Stress ball morphogenesis: How the lizard builds its lung

This study reveals how pressure drives the morphogenesis of cellular sheets into complex 3D architectures.

Abstract

The function of the lung is closely coupled to its structural anatomy, which varies greatly across vertebrates. Although architecturally simple, a complex pattern of airflow is thought to be achieved in the lizard lung due to its cavernous central lumen and honeycomb-shaped wall. We find that the wall of the lizard lung is generated from an initially smooth epithelial sheet, which is pushed through holes in a hexagonal smooth muscle meshwork by forces from fluid pressure, similar to a stress ball. Combining transcriptomics with time-lapse imaging reveals that the hexagonal meshwork self-assembles in response to circumferential and axial stresses downstream of pressure. A computational model predicts the pressure-driven changes in epithelial topology, which we probe using optogenetically driven contraction of 3D-printed engineered muscle. These results reveal the physical principles used to sculpt the unusual architecture of the lizard lung, which could be exploited as a novel strategy to engineer tissues.

INTRODUCTION

Function dictates form, and as a consequence, the physiology of many organ systems across the evolutionary tree shows conservation in underlying anatomy. The lungs, however, are radically different across classes of vertebrates. Both mammals and birds have lungs that are structured anatomically into distinct tissue compartments that physically segregate the conduction of air (through bronchi and air sacs, respectively) from gas exchange (through alveoli and parabronchi), despite the fact that air flows tidally in the mammal but unidirectionally in the bird. In contrast, the lungs of many reptiles are simple sacs in which both conduction and gas exchange take place in the same anatomic chamber. Unidirectional airflow was thought to require the complex anatomy of the parabronchial lung until the recent discovery of unidirectional flow patterns in the simple sac-like lungs of the green iguana lizard (1). This pattern of airflow is hypothesized to depend in part on the unique, honeycomb-shaped structure of the wall of the lizard lung (2), but the biological and physical basis of its morphogenesis has not been reported.

RESULTS AND DISCUSSION

To define the physical mechanisms that sculpt the wall of the lizard lung, we established the brown anole (Anolis sagrei) as a model system. We selected this species because of its small size, short incubation time (~30 days) and high breeding potential (3), and because a reference genome for the Anolis genus has been published (4). The lung of the adult anole is a single-chambered (unicameral) hollow lumen surrounded by a simple cuboidal epithelium. The lizard lung is faveolar, meaning that septae or trabeculae generate shallow primary and secondary corrugations in a hexagonal, honeycomb-shaped pattern that increases the surface area available for gas exchange (Fig. 1, A and B). In the anole embryo, the lung buds into a simple wishbone-shaped structure that separates from the ventral foregut, similar to mammalian and avian lungs (Fig. 1C). Between embryonic days (E) 5 and 6, the lumen of the wishbone inflates (Fig. 1C), resulting in a marked decrease in the aspect ratio of the lung (Fig. 1, C and D, and fig. S1A). Inflation is characterized by high levels of proliferation throughout the entire organ (fig. S1B) as well as apical-basal thinning that increases the cross-sectional area of the epithelial cells (Fig. 1, E and F). At E7, the initially smooth epithelium (fig. S1C) forms into the rounded corrugations (Fig. 1C) that eventually give rise to the faveoli, which are alveolus-like structures lined by a thin, squamous epithelium used for gas exchange (5). The formation of epithelial corrugations coincides with an increase in the aspect ratio of the lung from E6 to E7 (Fig. 1D and fig. S1A).

Fig. 1. The faveolar lung develops from epithelial corrugations that protrude through gaps within a smooth muscle meshwork.

(A) Immunofluorescence analysis for E-cadherin showing the surface (left) and central lumen (right) of the adult anole lung. Dotted outline shows area projected in (B). Scale bars, 5 mm. Ecad, E-cadherin. (B) 3D rendering of adult anole lung showing inner surface of faveolae. Depth is denoted using color-coding (blue = 1 mm). (C) Immunofluorescence analysis for CK showing the transition from simple wishbone shape (left) to inflated lung (middle) to corrugations (right). L, length; W, width. Scale bars, 100 μm. (D) Graph of the aspect ratio of the lung at each stage. (E) Immunofluorescence analysis for CK showing the epithelial thinning that takes place as the lung transitions to the inflated stage. Scale bars, 50 μm. (F) Graphs of the apical-basal thickness and cross-sectional area of the epithelial cells during the wishbone and inflated stages; schematic illustrates the corresponding change in epithelial cell shape. (G to I) Immunofluorescence analysis for CK and αSMA showing the formation of bundles of αSMA⁺ cells that organize into a meshwork around the lung epithelium and emergence of epithelial corrugations through gaps in this meshwork. Scale bars, 100 μm. (J) Schematic illustrating the processes of smooth muscle differentiation and epithelial morphogenesis. Shown are means ± SEM of n = 3, 7, and 6 (D) and n = 3 and 3 (F) independent replicates. **P < 0.01 and ***P < 0.001 per one-way analysis of variance (ANOVA) or two-sided t test.

Smooth muscle shapes the developing lung epithelium of the mouse (6, 7) and chicken (8) and also drives epithelial morphogenesis in other organs including the mouse gut (9, 10) and prostate (11). Mature trabeculae in adult lizard lungs contain a smooth muscle core (5), contraction of which maintains the lung structure and promotes airflow (12). We therefore mapped the spatial pattern of α-smooth muscle actin (αSMA)–expressing cells over developmental time in the embryonic anole lung. During the inflation stage at E6, αSMA⁺ cells are spread uniformly over the basal surface of the epithelium (Fig. 1G). As epithelial corrugations appear at E7, the αSMA⁺ cells form a hexagonal meshwork of thick bundles (Fig. 1, H and I) that creates a contractile cage around the entire epithelium (movie S1), somewhat reminiscent of the myofibroblast network around the alveoli in the mammalian lung (13) but at a much larger length scale. Epithelial corrugations only emerge from the gaps within the hexagonal mesh (Fig. 1, I and J), which is localized immediately adjacent to the regions of the highest epithelial curvature (fig. S1D), suggesting that the differentiation of this contractile tissue might be linked to morphogenesis of the epithelium.

High-magnification imaging revealed that the initially uniform αSMA⁺ cell population contains predominantly isotropic actin filaments (Fig. 2, A and F). As development proceeds, the actin filaments align as the αSMA⁺ cells coalesce into horizontal bundles along the medial-lateral axis of the lung (Fig. 2, B, C, and F, and fig. S2A). These horizontal bundles then thicken (Fig. 2D and fig. S2A) and are later joined by thin connective bundles along the anterior-posterior axis (Fig. 2E and fig. S2A), thus generating the smooth muscle meshwork.

Fig. 2. Smooth muscle meshwork is required for formation of epithelial corrugations.

(A to E) Immunofluorescence analysis for CK and αSMA showing formation of horizontal, followed by connective bundles of smooth muscle in the meshwork. Scale bars, 100 μm. (F) Rose plots of αSMA fiber orientation immediately after differentiation and after horizontal alignment has occurred. (G and H) UMAPs of cell clusters identified through scRNA-seq analysis of E5 and E6 anole lungs. (I and J) UMAPs of cell clusters at E5 and E6 labeled by the αSMA expression level. (K) Venn diagrams showing overlap of gene expression profiles for smooth muscle cells in the anole lung and smooth muscle cells or alveolar myofibroblasts in the embryonic mouse lung. (L) Diffusion analysis of mesenchymal cells differentiating into smooth muscle cells in the developing anole lung. Diffusion component 1 (DC1) represents the smooth muscle differentiation trajectory. (M) Expression level of Shh-associated genes along DC1. (N) Immunofluorescence analysis for CK and αSMA in lung explants treated with vehicle control (dimethyl sulfoxide), cyclopamine, or SAG. Scale bars, 100 μm. (O) Graph showing the percentage of the epithelial surface covered by smooth muscle in lung explants treated with vehicle control, cyclopamine, or SAG. (P) Graph showing the number of rows of corrugations in lung explants treated with vehicle control, cyclopamine, or SAG. (Q) Outlines of the epithelium from lung explants treated with vehicle control, cyclopamine, or SAG, color-coded by local curvature. (R) Heatmap of curvature at each position along the perimeter of lung explants treated with vehicle control, cyclopamine, or SAG, moving counterclockwise from black arrows in (Q). Shown are means ± SEM of n = 10, 5, and 6 (O and P) independent replicates. **P < 0.01 and ***P < 0.001 per one-way ANOVA.

To transcriptionally characterize these αSMA⁺ cells, we performed single-cell RNA-sequencing (scRNA-seq) analysis on lungs isolated before (E5) and during (E6) their appearance (fig. S2B). Clustering was performed using the Seurat pipeline (14), and epithelial, mesenchymal, endothelial, and blood cells were identified using known markers (Fig. 2, G and H). Among the mesenchymal clusters, we identified a population of cells that expresses high levels of αSMA and several other markers (15) of visceral smooth muscle (Fig. 2, I and J). The gene expression profile of this population in the anole shows a greater overlap with that of airway smooth muscle in the mouse than with that of the morphologically similar alveolar myofibroblast (Fig. 2K). We used diffusion analysis (16) to computationally reconstruct the differentiation trajectory of anole lung smooth muscle (Fig. 2L), which revealed that differentiation correlates with the expression of genes regulated by sonic hedgehog (Shh) (Fig. 2M and fig. S2C), which promotes airway smooth muscle differentiation in the developing mouse lung (6, 7, 17). Consistently, we found that inhibiting Shh signaling by treating anole lung explants with cyclopamine (fig. S2D) blocks smooth muscle differentiation and formation of the hexagonal smooth muscle meshwork (Fig. 2, N to O) and impedes the formation of epithelial corrugations (Fig. 2, N and P to R, and fig. S2E). Conversely, activating Shh signaling by treating lung explants with smoothened agonist (SAG) (fig. S2D) results in ectopic smooth muscle coverage over the basal surface of the epithelium (Fig. 2, N to O) and likewise hinders development of epithelial corrugations (Fig. 2, N and P to R, and fig. S2E). Smooth muscle differentiation and assembly into a meshwork are therefore required for epithelial morphogenesis into the corrugations that later become faveolae.

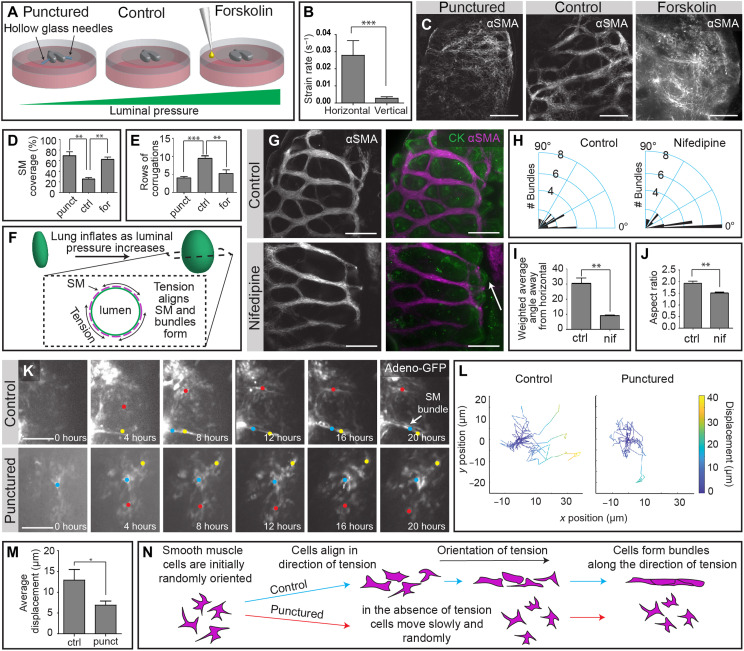
A uniform tissue layer could give rise to a hexagonal mesh by patterned cell death or cellular rearrangements. Immunofluorescence analysis of cleaved caspase-3 revealed minimal apoptosis in the smooth muscle cell layer, indicating that the holes in the mesh are not generated by cell death (fig. S3A). Randomly oriented mammalian smooth muscle cells are induced to align into bundles by the application of tension in culture (18, 19) and in vivo (9), and the changes in aspect ratio from E5 to E7 (Fig. 1D) suggested that the anole lung is under tension. To disrupt tension within the developing lung, we used a needle to puncture the epithelium (Fig. 3A), which resulted in rapid expulsion of luminal fluid (movie S2), decreased lung volume (fig. S3, B and C), and revealed a significantly higher strain rate along the horizontal (circumferential) axis of the organ than along the vertical axis (Fig. 3B), thus confirming that the direction of tension in the lung correlates with the orientation of smooth muscle bundles. Disrupting tension permitted smooth muscle differentiation but blocked the formation of the smooth muscle meshwork (Fig. 3, C and D) and impeded epithelial corrugations (Fig. 3E and fig. S3, D and E). To increase tension within the developing lung, we either inflated the lungs mechanically using microfluidic approaches (fig. S3F) (20) or treated explants with the adenylyl cyclase activator forskolin (Fig. 3A) (21), both of which increased the volume of fluid within the lung (fig. S3, B, C, and G) and likewise disrupted the formation of the smooth muscle meshwork (Fig. 3, C and D, and fig. S3, H and I) and epithelial corrugations (Fig. 3E and fig. S3, D and E). Optimal levels of inflation and the resulting circumferential tension are therefore required for smooth muscle cells to align and coalesce into horizontal bundles in the embryonic anole lung (Fig. 3F).

Fig. 3. Horizontal and connective smooth muscle bundles are formed sequentially in response to circumferential and vertical tension.

(A) Schematic illustrating experimental approaches used to manipulate luminal pressure within the embryonic anole lung. (B) Graph showing the average initial strain rate in the horizontal and vertical directions of punctured lung explants. (C) Immunofluorescence analysis for αSMA in control, punctured, and forskolin-treated lungs. Scale bars, 100 μm. (D) Graph showing the percentage of the epithelial surface covered by smooth muscle in control, punctured, and forskolin-treated lungs. (E) Graph showing the number of rows of epithelial corrugations in control, punctured, and forskolin-treated lungs. (F) Schematic illustrating circumferential tension in the epithelium resulting from inflation. (G) Immunofluorescence analysis for αSMA and CK in lungs treated with vehicle control and nifedipine. Scale bars, 100 μm. Arrow indicates epithelial corrugation. (H) Rose plots of smooth muscle bundle orientation relative to the horizontal axis in control and nifedipine-treated lungs. (I) Graph of the average angle of smooth muscle bundles away from the horizontal, normalized to thickness of the bundle, in control and nifedipine-treated lungs. (J) Graph of the average aspect ratio of lung explants after 48 hours of treatment with vehicle control or nifedipine. (K) Still images from time-lapse videos of GFP-expressing mesenchymal cells in control and punctured embryonic anole lungs. Scale bars, 100 μm. (L) Plots of trajectories of GFP-expressing mesenchymal cells from control and punctured lungs. (M) Graph of the average displacement of GFP-expressing mesenchymal cells in control and punctured lungs. (N) Schematic illustrating migration and bundling of smooth muscle cells in the direction of tension. Shown are means ± SEM of n = 3, 3, and 3 (A, D, and E), n = 4 and 4 (H to J), and n = 16 and 18 (M) independent replicates. *P < 0.05, **P < 0.01, and ***P < 0.001 per one-way ANOVA or two-sided t test.

After the horizontal bundles have formed, the aspect ratio of the lung increases (Fig. 1D) and connective bundles develop in the smooth muscle layer (Fig. 2E). Contraction of the horizontal bundles appears to play a role in both events. We found that inhibiting smooth muscle contractility after the appearance of horizontal bundles by blocking l-type calcium channels with nifedipine (22) leads to a significant decrease in connective bundles (Fig. 3, G to I) and a reduction in the aspect ratio of the lung (Fig. 3J). Similarly, puncturing the lungs after horizontal bundles have formed prevents the buildup of axial tension, permits the circumferential smooth muscle to collapse the unpressurized epithelium (fig. S3J), and significantly reduces the formation of connective bundles (fig. S3, K to M). These data suggest that circumferential tension (hoop stress) promotes the formation of horizontal bundles, the contraction of which generates a vertical tension (axial stress) that induces the formation of connective bundles to complete the smooth muscle meshwork.

To visualize the rearrangements of smooth muscle cells into a meshwork, we used an adenoviral approach to label individual mesenchymal cells with green fluorescent protein (GFP) and tracked these cells in real time. In control lung explants, mesenchymal cells were highly motile, and a subpopulation migrated and coalesced into horizontal bundles (Fig. 3, K and L, and movie S3). In punctured lung explants, which fail to generate horizontal bundles (Fig. 3C), we observed attenuated and random motility (Fig. 3, K and L; fig. S3N; and movie S4) and decreased average displacement of mesenchymal cells (Fig. 3M). Smooth muscle cells thus migrate and coalesce to form bundles along the direction of tension in the developing anole lung (Fig. 3N), suggesting that tension orients motility to enable morphogenesis of the unique meshwork geometry of this tissue.

There are two possible mechanisms by which epithelial corrugations could be sculpted by a smooth muscle mesh (Fig. 4A). The smooth muscle meshwork could actively contract to deform the underlying epithelium. Alternatively, luminal fluid pressure could push the epithelial sheet through the holes within a passive but stiff meshwork. To understand the changes in epithelial topology that can be induced by an actively contracting mesh, we used three-dimensional (3D) printing to construct a physical model of the embryonic anole lung (Fig. 4B). We generated thin films of silicone elastomer floating on water to mimic the epithelial sheet, on which we 3D-printed a synthetic hectorite clay in a hexagonal mesh to mimic the smooth muscle. The clay contracted as it dried (Fig. 4, C and D), resulting in corrugations within the silicone sheet that emerged through the gaps in the mesh (Fig. 4, C and E). Active contraction of a mesh can therefore generate corrugations of an underlying sheet, with a topology that matches that of the developing anole lung.

Fig. 4. Epithelial corrugations result from pressure-driven expansion through a stiff smooth muscle mesh.

(A) Possible mechanisms to form epithelial corrugations. (B) Procedure for generating a physical model of the embryonic anole lung. (C) Images of physical model at 0 and 24 hours after fabrication, showing the formation of corrugations as the clay dries and contracts. Scale bars, 2.5 mm. (D) Outlines of the clay at 0 and 24 hours, showing the strain induced by drying. (E) Topology plot of silicone film after the formation of corrugations. Color-coding indicates depth. (F) Immunofluorescence analysis for actin, α-actinin, and nuclei in 3D-printed hexagonal mesh of muscle cells. Scale bars, 1 mm for left image and 100 μm for three right images. (G) Optogenetic system used to induce calcium influx and contraction of muscle cells. CRAC, calcium release-activated calcium channel; CRY2, cryptochrome-2. (H) Images of bio/synthetic engineered tissue model with or without cells at 0 and 24 hours after stimulation with light, showing the formation of corrugations. Scale bars, 1 mm. (I) Outlines of cell-free and 3D-printed cell meshes at 0 and 24 hours, showing the cell-induced strain. (J) Topology plot of bio/synthetic engineered tissue model after 24 hours of cell-induced strain. (K) Tissue layers in the computational model. (L) Results of simulations, showing pressure-induced formation of epithelial corrugations through a passive smooth muscle mesh. (M) Results of simulations of lung puncture, showing elongation of epithelial corrugations. (N) Graph of the ratio between corrugation depth and width in simulations with and without puncture. (O) Schematic illustrating predicted change in epithelial morphology after puncturing an E7-stage lung. (P) Immunofluorescence analysis for CK and αSMA in an E7-stage lung explant that was punctured. Scale bars, 25 μm. (Q) Immunofluorescence analysis for CK and αSMA in an E7-stage lung explant that was punctured in the presence of nifedipine. Scale bars, 25 μm.

To determine whether a meshwork of smooth muscle cells can generate sufficient strain to deform an epithelial sheet into corrugations, we used 3D printing and optogenetics to create a bio/synthetic hybrid engineered tissue model (fig. S4A). We began by calculating the flexural rigidity, $D=\frac{E_e{h_e}^3}{12(1-{\mathrm{\upsilon }}^2)}$, of the lung epithelium, using known values of elastic modulus, E_e (23), Poisson’s ratio, υ (24), and our experimental measurements of epithelial tissue thickness, h_e (fig. S4B). We then generated thin films of silicone elastomer that approximated the flexural rigidity and thus the mechanical properties of the lung epithelium and used 3D printing approaches (25) to construct a hexagonal meshwork of differentiated muscle cells (Fig. 4F) in which contraction could be promoted by stimulating calcium influx optogenetically (Fig. 4G, fig. S4C, and movie S5), yielding temporal control over the magnitude of contraction. The hexagonal mesh of muscle cells contracted upon stimulation with light (Fig. 4H, fig. S4D, and movie S6), generating strain (Fig. 4I) that induced wrinkles in the silicone sheet (Fig. 4H and fig. S5, A and B) and 3D corrugations through the holes in the mesh (Fig. 4J; fig. S5, A and B; and movie S7). The corrugations generated in the bio/synthetic engineered tissue model are deeper than those induced by the clay in the physical model, but both are significantly shallower than the corrugations observed in the anole lung in vivo (fig. S5C). Consistently, the anole lung epithelium still forms corrugations when smooth muscle contraction is blocked pharmacologically (Fig. 3G, arrow), suggesting that active contraction is not the primary mechanism that drives formation of the honeycomb-shaped wall of the lizard lung.

To determine whether a passive smooth muscle mesh can promote corrugations of a pressurized epithelial sheet, we generated a computational model of the developing anole lung based on measured geometrical and biophysical parameters. We started by considering a smooth, spheroidal epithelial surface, with thickness and diameter that mimic the inflation-stage anole lung epithelium. We imposed a pressure on the fluid within the lumen and surrounded the basal surface of the epithelium with a stiff hexagonal lattice to mimic the geometry and mechanical properties of the smooth muscle meshwork (Fig. 4K). Our simulations revealed that increasing the pressure within the lumen causes the epithelial sheet to expand through the holes within the stiff hexagonal lattice, thus generating corrugations on the surface (Fig. 4L and movie S8). Our simulations also predicted that once the corrugations have formed, a sudden drop in luminal pressure would decrease the resistance to contraction of the elastic meshwork and result in elongation of the sheet through the holes in the mesh (Fig. 4, M and N, and movie S9). To test this prediction experimentally, we used needles to puncture corrugation-stage anole lungs (Fig. 4O). As predicted by our model, decreasing luminal pressure at this stage led to elongated epithelial corrugations, separated by a contracted smooth muscle meshwork (Fig. 4P and fig. S5D); simultaneous treatment with nifedipine prevented elongation of the corrugations in the punctured lungs (Fig. 4Q and fig. S5, E and F). Our simulations thus reveal that fluid pressure induces the formation of the corrugated epithelium of the lizard lung, in addition to driving morphogenesis of the hexagonal mesh of smooth muscle cells.

Fluid pressure opens the zebrafish gut tube (26), inflates the ventricles of the developing brain (27), elongates the vertebrate notochord (28), promotes coalescence or coarsening of microlumens into a single lumen in zebrafish Kupffer’s vesicle (29) and the early mouse blastocyst (30), and has been implicated in development of the mammalian lung (31–33). Despite its ubiquity, the mechanisms by which fluid pressure exerts its effects remain unclear for most developing systems. In the lizard lung, the transmission of mechanical forces from fluid pressure provides directional cues that permit smooth muscle cells to self-organize into a unique meshwork architecture, which generates a stiff, contractile template that guides pressure-induced expansion of the epithelium into a corrugated structure, akin to deformation of a stress ball (Fig. 5). This mechanism is distinct from that which generates the architecturally similar mammalian alveolus, which is thought to be sculpted by myofibroblast contraction (34, 35) rather than by luminal pressure. Collectively, these observations illustrate a novel morphogenetic mechanism by which mechanical forces from fluid pressure induce both the self-assembly of mesenchymal cells into a hexagonal geometry as well as extrusion of an epithelial sheet through the holes in the resulting rigid meshwork. The transcriptome of the differentiating reptilian smooth muscle cells has some overlap with that of mouse smooth muscle but is also quite distinct. Given the ubiquity of pressurized epithelial cavities, further work is needed to uncover whether mesenchymal cells within other developing organs are similarly guided by directional stress gradients downstream of luminal pressure.

Fig. 5. Schematic summarizing the physical mechanisms that give rise to the architecture of the anole lung.

Shown are several key developmental stages and the relative luminal pressure and oriented tension associated with each.

Regardless, formation of this stiff, contractile, hexagonal mesh guides the morphogenesis of a planar epithelium into the complex, 3D, honeycomb-shaped faveolar wall. Our physical and bio/synthetic models suggest that the principles of stress ball morphogenesis could be exploited to engineer predictable and reproducible epithelial tissues ex vivo, including organoids that mimic the alveolar gas exchange surface of the mammalian lung. Uncovering the physical principles that drive the morphogenesis of other noncanonical model organisms has the potential to reveal the developmental basis of anatomical diversity across the evolutionary tree and generate a toolbox of novel tissue engineering strategies.

MATERIALS AND METHODS

Anole husbandry and egg collection

Wild-caught brown anoles (A. sagrei) were obtained through a commercial vendor (Snakes at Sunset) and maintained in a temperature (75° to 85°F), humidity (>80%), and light-controlled environment (14 hours light/10 hours dark) at a ratio of one male to three females per tank, following Princeton Institutional Animal Care and Use Committee–approved protocols and the National Institutes of Health (NIH) Guide for the Care and Use of Laboratory Animals. Tanks were inspected daily, and eggs were removed and incubated in a benchtop incubator at 30°C and 80% humidity until the desired stage. Embryos were dissected under a stereoscope to isolate the lungs, which were either fixed and stained immediately after dissection or cultured as explants.

Explant culture

Lung explants were cultured at 37°C for 48 hours on a semipermeable membrane (25 mm in diameter, 8-μm pore; Whatman) floating on Dulbecco’s modified Eagle’s medium (DMEM)/F-12 medium (Hyclone) supplemented with 5% fetal bovine serum (FBS; Gemini Bioproducts). Pharmacological inhibitors were added directly to the culture medium at the indicated concentrations: SAG (5 μM; Calbiochem), cyclopamine (1 μM; Tocris), forskolin (5 μM; Sigma-Aldrich), nifedipine (20 μM; Sigma-Aldrich). The medium was replaced after 24 hours. For time-lapse analysis of mesenchymal cell rearrangements, recombinant adenovirus encoding GFP (AdGFP; Vector Biolabs) was injected into the mesenchyme using a hollow glass needle and a pressurized injection system (PV 820 Pneumatic PicoPump, World Precision Instruments). Time-lapse imaging was carried out in a stage-top incubator mounted on the microscope to maintain temperature (37°C) and humidity. Proliferation was visualized using an EdU kit (Thermo Fisher Scientific); EdU was added to the culture medium for 15 min before fixation.

Microfluidic control of luminal pressure

Microfluidic devices consisted of two chambers joined by a glass capillary and were constructed as described previously (20). Lungs were dissected from embryos at early E6; the trachea was intubated with the glass capillary and sutured in place within one of the chambers. The other chamber was fitted with a tower that was subsequently filled with culture medium to generate a given hydrostatic pressure through the needle.

Immunofluorescence analysis of lung explants

Embryonic lungs were fixed in 4% paraformaldehyde (PFA) in phosphate-buffered saline (PBS) for 15 min at room temperature. Adult lungs were inflated with and submerged in 4% PFA for 1 hour at room temperature. Samples were then washed in 0.1% Triton X-100 (Sigma-Aldrich) in PBS (PBST) at 15-min intervals for a total wash time of 1 hour and then blocked for 1 hour at room temperature in a solution of 5% goat serum (Sigma-Aldrich) and 0.1% bovine serum albumin (Sigma-Aldrich) in PBST. Samples were labeled using antibodies specific for epithelial cytokeratins (CKs) (1:400; Dako, Z0622), αSMA (1:400; Sigma-Aldrich, 1A4), and/or cleaved caspase-3 (1:200; Cell Signaling Technology, 9661) overnight at 4°C. Samples were washed in PBST at 15-min intervals for a total of 1 hour, blocked again for 1 hour, and then incubated in secondary antibodies (1:200; Invitrogen) overnight at 4°C. Nuclei were counterstained using Hoechst 33342 (1:1000; Invitrogen) for 20 min at room temperature. Stained samples were dehydrated with serial dilutions of ethanol and either cleared using Murray’s clear (1:2 ratio of benzyl alcohol to benzyl benzoate; Sigma-Aldrich) or cleared without dehydration by using serial dilutions of glycerol (25, 50, 75, and 100% every 30 min) in PBS and then imaged under confocal microscopy.

Imaging of anole lung explants

Fluorescent images of embryonic lungs were captured using a spinning disk confocal (X-Light V2tp, Crest Optics) fitted to an inverted microscope (Nikon Eclipse Ti) with either a 10× air, 20× air, or 40× oil objective. Fluorescent images of adult lungs were captured using a Nikon A1R-Si HD confocal microscope with a digital micromirror device and 10× air objective.

Image analysis and statistics

Z projections were assembled using ImageJ. Quantitative image analysis for calculating lengths and angles was also performed using ImageJ. Percent smooth muscle coverage was determined by thresholding images to the same intensity, outlining the lung, and calculating the percent of the outlined region that contained signal. The correlation between the curvature of the epithelium and the immediately adjacent staining intensity of αSMA was determined using a Pearson correlation. Data were confirmed to be normally distributed using the Shapiro-Wilk test, and significant difference between two means was calculated using a t test or one-way analysis of variance (ANOVA) with Tukey’s post hoc test and noted as (*) for P < 0.05, (**) for P < 0.01, and (***) for P < 0.001. Cell tracking was performed using Imaris (Oxford Instruments).

scRNA-seq experiments

Lungs were dissected from the embryo at the stages of interest and then dissociated with dispase (Corning) at room temperature for 10 min to generate a single-cell suspension. Cell suspensions were processed by the Princeton Genomics Core Facility. Cells were loaded and processed using the Chromium Single-Cell 3′ Library and Gel Bead Kit v3 (10x Genomics) on the Chromium Controller (10x Genomics) following the manufacturer’s protocols. Individual cells were encapsulated in droplets with individual gel beads carrying unique barcoded primers and lysed. Fragments of cDNA were synthesized, barcoded, and amplified by polymerase chain reaction (PCR). Illumina sequencing libraries were prepared from the amplified cDNA from each sample group using the Nextra DNA library prep kit (Illumina). Libraries were sequenced on NovaSeq 6000 S Prime flow cells (Illumina) as paired-end 28 + 94 nucleotide reads, following the manufacturer’s protocols. Base calling was performed, and raw sequencing reads were filtered using the Illumina sequencer control software to keep only pass-filtered reads for downstream analysis. The 10× Cell Ranger software version 3.0.2 was used to run the count pipeline with default settings on all FASTQ files from each sample to generate gene-barcode matrices using the Anolis carolinensis reference genome AnoCar2.0.

Quantitative reverse transcription PCR analysis

Embryonic anole lungs were extracted and preserved in TRIzol (Thermo Fisher Scientific) before being ground up using a BioMasher (VWR). RNA was extracted and then cDNA was generated using Verso cDNA synthesis (Thermo Fisher Scientific). Quantitative PCR analysis was carried out using custom primers and iTaq SYBR Green Supermix (Bio-Rad) following the manufacturer’s protocols.

scRNA-seq data analysis

scRNA-seq data were exported from Cell Ranger and then imported into R. The data were then processed using the Seurat package (14). Datasets were normalized and integrated using the Seurat function FindVariableFeatures based on 2000 genes. The integrated dataset was then scaled before being analyzed using the Seurat functions FindNeighbors and FindClusters to find neighbors and clusters. Last, we visualized clusters using the uniform manifold approximation and projection (UMAP) dimensional reduction. For initial analyses, all cells were used, which revealed large clusters of blood and immune cells, which we then removed as they were not the cell types of interest. We then adjusted the dataset to account for cell cycle stage using the Seurat package. All subsequent analyses were carried out using this resulting filtered and adjusted dataset. Cluster identities were then assigned based on known markers of cell types in the lung. To investigate mesenchymal cells specifically, we repeated the Seurat pipeline outlined above including only cells from clusters expressing mesenchymal markers.

Diffusion analysis of mesenchymal cells

To reconstruct smooth muscle differentiation trajectories, we applied the Destiny package to the cell-by-gene matrix generated using the Seurat algorithm in R (16). Only clusters expressing mesenchymal markers were used in this analysis.

Curvature analysis

To measure curvature, we created an image analysis pipeline in MATLAB (MathWorks). First, contours of the epithelium were manually traced and then smoothed. Local curvature for every point in the contour, P_i, was then calculated using P_i − 5, P_i, and P_i + 5 to eliminate noise and obtain a smoother readout of local curvature. To determine whether the local curvature was positive or negative with respect to the center of the lung, we took the dot product of the curvature vector and the unit vector pointing from the geometric center of the contour to P_i. To visualize curvature for single samples in 2D, we color-coded the contour based on the magnitude and direction of local curvature. To compare multiple samples, we generated heatmaps in which every column represents a sample and that are color-coded based on the magnitude and direction of local curvature.

Preparation of thin elastomeric films

To prepare thin elastomeric films for the physical model of the anole lung, polydimethylsiloxane (PDMS) (Sylgard 184) prepolymer was mixed with the PDMS curing agent at a 10:1 (w/w) ratio. Next, 75 μl of the PDMS mixture was drop-cast onto the surface of 2 ml of water in a 35-mm-diameter tissue culture dish. The PDMS was cured at room temperature (~20°C) overnight and then at 65°C for 30 min before use in experiments. Floating films of PDMS were used within 24 hours of fabrication. To prepare thin elastic films for the bio/synthetic hybrid model, films of Ecoflex 00-10 (Smooth-On, Macungie, PA) were generated on 25-mm-diameter circular glass coverslips using an approach adapted from a previous study (36). Briefly, glass coverslips were first treated in an ultraviolet/ozone (UVO) cleaner (Jelight Company, Irvine, CA) for 7 min. Next, 125 μl of sterile-filtered dextran solution [10% (w/v) dextran (Sigma-Aldrich) in 25% isopropyl alcohol] was spin-coated onto the glass coverslips at 6000 rpm for 1 min to generate a water-soluble sacrificial layer. A total of 400 μl of a 1:2 Ecoflex:hexanes (v/v) solution was then spin-coated onto the coverslip at 6000 rpm for 1 min, and the coated coverslips were cured at room temperature overnight. After curing, Ecoflex-coated coverslips were stored at room temperature. Immediately before printing collagen-Matrigel inks, Ecoflex-coated coverslips were sterilized with ethanol, air-dried, and treated in a UVO cleaner for 7 min.

Calculation of flexural rigidity

The flexural rigidity, D, of Ecoflex and an epithelial monolayer were calculated using the equation $D=\frac{E_e{h_e}^3}{12(1-{\mathrm{\upsilon }}^2)}$, where E_e is the Young’s modulus of the material, h_e is the elastic thickness of the material, and υ is the Poisson’s ratio. We measured the thickness of our thin films by laying them on a block of PDMS, sectioning the block, and then imaging using confocal microscopy. Assuming that the Poisson’s ratios for our thin film and for an epithelium are approximately equal, we can determine a ratio of the flexural rigidity of our materials of interest as related to only E_e [E_ecoflex ~ 50 kPa (37); E_epithelium ~ 1 kPa (23)] and h_e (h_e,Ecoflex ~ 8 μm; h_e,epithelium ~ 15 μm), yielding a flexural rigidity ratio D_Ecoflex/D_epithelium of ~8.

Preparation of 3D printing inks

Laponite XLG synthetic hectorite clay (BYK Additive and Instruments, Gonzales, TX) was dissolved in water at a concentration of 5% (w/v) and stored at room temperature for 24 hours before 3D printing. Collagen-Matrigel inks consisted of acid-solubilized bovine type I collagen (Advanced BioMatrix, Carlsbad, CA) and growth factor–reduced Matrigel (Corning, Corning, NY). The final concentrations of Matrigel and collagen were 2.34 and 2.14 mg/ml, respectively, and the pH was adjusted to ~8 using the collagen neutralizing solution from the manufacturer (Advanced BioMatrix). pH-adjusted collagen-Matrigel inks were stored on ice for 1 hour before 3D printing.

3D microextrusion printing

Synthetic hectorite clay and collagen-Matrigel inks were 3D-printed at room temperature using a bioprinter (Inkredible+, CELLINK, Sweden), as described previously (25). All printing was performed using 254-μm-diameter conical polyethylene nozzles (Nordson EFD, Robbinsville, NJ). Printing speed and pressure varied from 20 to 80 mm/s and 1 to 40 kPa, respectively, and the distance between the printing nozzle and the substratum was ~0.1 mm. Custom printing paths were generated manually in G-code. After printing, clay samples were stored at room temperature, and collagen-Matrigel samples were placed in an incubator at 37°C and 5% CO₂ for 30 min. To improve mechanical coupling between cells and Ecoflex films, collagen-Matrigel constructs were allowed to completely dry before seeding cells. After incubation, samples were immersed in 1% (w/v) Pluronic F108 for 15 min to block cell adhesion to exposed Ecoflex films.

Topology analysis

Topology maps of PDMS thin films that were deformed by 3D-printed hectorite clay were generated using a Leica DCM3D confocal microscope and a 5× 0.15–numerical aperture air objective. To enable topology mapping, glass beads (75 μm in diameter; Supelco) were added uniformly onto the surface of the deformed PDMS.

Cell culture

C2C12 mouse mesenchymal progenitor cells (American Type Culture Collection) were cultured in high-glucose DMEM without sodium pyruvate (Hyclone, Logan, UT), supplemented with 10% FBS and 1% penicillin-streptomycin (Thermo Fisher Scientific). Cells were seeded onto collagen-Matrigel constructs and cultured to confluence at 37°C and 5% CO₂. To promote differentiation, cells were cultured in high-glucose DMEM without sodium pyruvate supplemented with 2% heat-inactivated horse serum (Thermo Fisher Scientific) for 7 to 10 days.

Immunofluorescence analysis of cells on films

Cells on Ecoflex films were rinsed three times with PBS and then fixed in 4% PFA in PBS for 15 min at room temperature. Samples were then washed three times in 0.3% PBST for 15 min each and blocked for 1 hour at room temperature in 1:30 goat serum in PBST. Samples were labeled using an antibody specific for sarcomeric α-actinin (1:500; Invitrogen, EA-53) overnight at 4°C to detect differentiated muscle cells. Samples were washed in PBST three times for 5 min each, incubated in secondary antibody (1:500; Invitrogen) and Alexa Fluor 568 phalloidin (Invitrogen) in blocking buffer for 2 hours at room temperature, and then washed three times for 15 min in PBST. Hoechst 33342 (1:1000) was included in the second wash step to counterstain the nuclei. Stained samples were mounted using Fluoromount-G (SouthernBiotech).

Optogenetics

The optogenetic tool optoSTIM1 (GFP-Cry2-STIM1ct) (38) and the calcium sensor R-GECO1.2 (39) were cloned into pHR lentiviral expression vectors. Lentivirus was produced using Lenti-X 293 T cells as previously described (40). C2C12 cells were then transduced with optoSTIM1 lentivirus and bulk-sorted using fluorescence-activated cell sorting to generate a stable cell line. The optoSTIM1-expressing C2C12 cells were then transduced with R-GECO1.2 lentivirus to create a double-expressing cell line. To induce calcium influx and contraction, cells were stimulated every 10 s to 2 min for 0.5 to 1.5 s each using a light-emitting diode light source (490 nm) connected to an inverted epifluorescence microscope (Nikon). In parallel, R-GECO1.2 fluorescence was imaged as a readout of intracellular calcium levels. To quantify calcium waves induced by stimulation of optoSTIM1, individual cells were outlined in ImageJ, and the mean R-GECO1.2 intensity values were recorded for each frame and normalized to the first frame. To visualize cell contractions, kymograph analyses were performed by drawing a line (19.5-μm wide) along the center of each C2C12 cell in ImageJ as an input for the KymographBuilder plugin (41).

Imaging of the bio/synthetic engineered tissue model

Immunostained muscle cells cultured on 3D-printed hexagonal meshes on Ecoflex films were imaged using a spinning disk confocal (X-LIGHT V2tp, Crest Optics) fitted to an inverted microscope (Nikon Eclipse Ti) with a 20× air objective (Nikon Plan Apo VC). Tiles were acquired and stitched using MetaMorph. Transmission light and backlight images were acquired before and after peeling the films off the underlying glass slide using a stereo microscope (Leica M205FA) equipped with a camera and a motorized stage. A 1× objective was used for images of the entire structure and for z-stacks at 4× zoom to analyze the depth of corrugations generated in the Ecoflex film by cell contraction. To enhance cell contraction, optogenetic cells were stimulated by light on an inverted epifluorescence microscope (Nikon Eclipse Ti) for 1 hour using a 2× objective and tiling. 3D stereographs were acquired 24 hours after peeling by taking images through the left and right oculars of the stereomicroscope with a cell phone camera. The red/cyan anaglyph was created from the stereo images by removing the green and blue channels from the left image and the red channel from the right image before overlaying them and adjusting the offset to align the 3D image in Adobe Photoshop.

Computational modeling

In the model, the lizard lung is composed of two physical compartments, viz., the epithelium, modeled as a spherical shell, and the smooth muscle, modeled as a thick hexagonal lattice on the outer surface of the epithelium (fig. S6A). The epithelium and smooth muscle are assumed to be elastic solids characterized by different physical properties, and these tissues are denoted by subscripts “ep” and “sm,” respectively.

To model growing tissues, we adopted the method of deformation gradient decomposition (42), where the total deformation from the reference state is decomposed into one contribution due to growth/contraction and another due to elastic deformation. We assumed that growth and contraction of smooth muscle are much slower than mechanical relaxation, and hence, the system is always in quasi-mechanical equilibrium, which was achieved by minimizing the total elastic energy as described below.

Supposing that the initial reference volume is Ω, we introduced a fixed Cartesian coordinate system with an orthonormal basis {e₁, e₂, e₃} and spatial coordinates given as (X₁, X₂, X₃), denoted as X = X_ie_i where summation over repeated indices is implied. At some later time t, the system was deformed to a volume Ω_t , and the Cartesian coordinates were mapped to a different vector field, denoted as x = φ_t(X). Using this notation, we follow finite deformation theory (43) and define the deformation gradient tensor as $F_{\text{ij}}=\frac{ \mathrm{\partial }{x}_i}{{\mathrm{\partial }X}_j}$.

The total deformation gradient was decomposed as F = F_eF_g, where it was assumed that growth/contraction induce an intermediate stress-free state with a deformation gradient F_g (referred to as growth tensor from here on) and that there is an additional elastic deformation of this intermediate stress-free state to the final deformed state due to the elastic deformation gradient F_e (42).

To account for large material deformation, we assumed the tissues to be Neo-Hookean solids with the elastic energy storage density defined as (43)

$$\mathrm{\psi }({\mathbf{F}}_{\mathbf{e}},\mathit{X})=\frac{\mathrm{\mu }(\mathit{X})}{2}(I_c^e-3-2\text{ln}{J}^e)+\frac{\mathrm{\lambda }(\mathit{X})}{2}{(\text{ln}{J}^{\mathrm{e}})}^2.$$

λ and μ are the Lamé constants that are related to the Young’s modulus E and Poisson’s ratio 𝜐 as

$$\mathrm{\lambda }=\frac{E\mathrm{\nu }}{(1+\mathrm{\nu })(1-2\mathrm{\nu })} \text{and} \mathrm{\mu }=\frac{E}{2(1+\mathrm{\nu })}$$

where $I_{\mathrm{c}}^{\mathrm{e}}=\text{tr}(\mathbf{C})$is the trace of the right Cauchy-Green deformation tensor $\mathbf{C}\mathbf{=}{\mathbf{F}}_{\mathbf{e}}^{\mathbf{T}}{\mathbf{F}}_{\mathbf{e}}$ and J^e = det (F_e) > 0 is the Jacobian of the elastic deformation gradient. Note that the explicit dependence of ψ(F_e, X) on position X enters via elastic constants that are different for the epithelium and smooth muscle, but each tissue has homogeneous material properties.

Deformation due to growth and contraction is uniquely determined by the growth tensor F_g. For simplicity, we neglected epithelial proliferation to focus on the effect of mechanical forces, i.e., F_g,ep=I.We assumed that smooth muscle contraction was uniform and either isotropic or anisotropic (contraction only along the fiber length). For isotropic contraction, the growth deformation tensor was taken as F_g,sm = (1 + g_sm)I, where g_sm is the strain associated with contraction. For anisotropic contraction, we assume the stretch in the smooth muscle is (1 + g_sm) along the fiber direction f⁰ with no contraction in the orthogonal directions and the growth deformation tensor is given by (44)

$${\mathbf{F}}_{\mathbf{g},\mathbf{sm}}=\mathbf{I}+g_{\text{sm}}{\mathit{f}}^{\mathbf{0}}⨂{\mathit{f}}^{\mathbf{0}}.$$

We modeled smooth muscle contraction as negative growth (−1 < g_sm ≤ 0).

The outer surface of the lung was considered to be traction free. The presence of a lumen inside the lung was modeled by a positive normal pressure acting on the inner surface of the spherical epithelial shell. This pressure is in the opposite direction of the outer normal n on the current deformed boundary of the mesh, i.e., on the inner surface the traction force t can be written as t = −pn where p is the luminal pressure (fig. S6A).

The finite element method, a standard method in computational mechanics to numerically solve for the deformation field under given boundary conditions (45), was used to calculate the displacement field u = x − X that minimizes the total potential energy Π(u, λ_tr, λ_rot.) for a prescribed luminal pressure p and smooth muscle contraction profile with deformation gradient F_g, where the Lagrange multipliers λ_tr and λ_rot constrain rigid body translation and rotation, respectively. The total potential energy can be written as (46)

$$\begin{array}{c}\mathrm{\Pi }(\mathit{u},{\mathbf{\lambda }}_{\text{tr}},{\mathbf{\lambda }}_{\mathbf{rot}})=\\ {\int }_{\mathrm{\Omega }}{\mathbf{J}}_{\mathrm{g}}\mathbf{\psi }({\mathbf{F}}_{\mathbf{e}},\mathit{X})\mathrm{d}V-{\int }_{\mathrm{\partial }{\mathrm{\Omega }}_{\mathrm{t}}^{\text{in}}}\mathit{t}·\mathit{u} \mathrm{d}s-{\int }_{\mathrm{\Omega }}{\mathbf{\lambda }}_{\text{tr}}·\mathit{u}\mathit{dV}–{\int }_{\mathrm{\Omega }}{\mathbf{\lambda }}_{\text{rot}}·(\mathit{X} \times \mathit{u})\mathit{dV}\end{array}$$

The unknown displacement field u is then obtained via the variation of the potential energy function Π(u, λ_tr, λ_rot) with respect to u, λ_tr, and λ_rot and solving

$$\begin{array}{c}\mathrm{\delta }\mathrm{\Pi }={\int }_{\mathrm{\Omega }}\left[{\mathbf{J}}_{\mathrm{g}}\frac{\mathrm{\partial }\mathbf{\psi }({\mathit{F}}_{\mathit{e}},\mathit{X})}{\mathrm{\partial }\mathit{u}}\right]·\mathrm{\delta }\mathit{u} \mathrm{d}V-{\int }_{\mathrm{\partial }{\mathrm{\Omega }}_t^{\text{in}}}\mathit{t}·\mathrm{\delta }\mathit{u} \mathrm{d}s\\ -{\int }_{\mathrm{\Omega }}{\mathbf{\lambda }}_{\text{tr}}·\mathrm{\delta }\mathit{u}\mathit{dV}–{\int }_{\mathrm{\Omega }}{\mathbf{\lambda }}_{\text{rot}}·(\mathit{X}\times \mathrm{\delta }\mathit{u})\mathit{dV}\\ -{\int }_{\mathrm{\Omega }}{\mathrm{\delta }\mathbf{\lambda }}_{\text{tr}}·\mathit{u}\mathit{dV}–{\int }_{\mathrm{\Omega }}{\mathrm{\delta }\mathbf{\lambda }}_{\text{rot}}·(\mathit{X}\times \mathit{u})\mathit{dV}=0,\end{array}$$

$$\begin{array}{c}\mathrm{\delta }\mathrm{\Pi }={\int }_{\mathrm{\Omega }}\left[J_g\frac{\mathrm{\partial }\mathrm{\psi }({\mathit{F}}_{\mathit{e}},\mathit{X})}{\mathrm{\partial }\mathit{u}}\right]·\mathrm{\delta }\mathit{u} \mathrm{d}V-{\int }_{\mathrm{\partial }{\mathrm{\Omega }}^{\text{in}}}p({J\mathbf{F}}^{\mathbf{-}\mathbf{T}}\mathit{N})·\mathrm{\delta }\mathit{u} \mathrm{d}S\\ -{\int }_{\mathrm{\Omega }}{\mathbf{\lambda }}_{\text{tr}}·\mathrm{\delta }\mathit{u}\mathit{dV}–{\int }_{\mathrm{\Omega }}{\mathbf{\lambda }}_{\text{rot}}·(\mathit{X}\times \mathrm{\delta }\mathit{u})\mathit{dV}\\ -{\int }_{\mathrm{\Omega }}{\mathrm{\delta }\mathbf{\lambda }}_{\text{tr}}·\mathit{u}\mathit{dV}–{\int }_{\mathrm{\Omega }}{\mathrm{\delta }\mathbf{\lambda }}_{\text{rot}}·(\mathit{X}\times \mathit{u})\mathit{dV}=0.\end{array}$$

Here, J_g = det (F_g) > 0 is the Jacobian of the deformation gradient due to growth/contraction. dS, ∂Ωⁱⁿ, and ds, $\mathrm{\partial }{\mathrm{\Omega }}_t^{\text{in}}$ are the infinitesimal surface elements and the inner surface boundary in the reference and deformed configuration, respectively. J = det (F) > 0 is the Jacobian of the total deformation tensor. The virtual work due to pressure p in the second line of the equation above is translated to the undeformed reference configuration by using Nanson’s formula, where N is the outer normal in the reference configuration (43).

To numerically solve the above minimization problem, the domain Ω was discretized using first-order tetrahedral elements that were generated with the help of an open source software Gmsh (47). Then, the potential energy minimization problem was implemented in the open-source computing platform FEniCS (48). The Newton-Raphson algorithm (49) was used to find the displacement field that minimized the total potential energy. The entire lung structure contained ~230,000 tetrahedral elements, which were divided between the smooth muscle (~85,000) and epithelium (~145,000), and the final mesh contained ~57,000 vertices/nodes and ~170,000 degrees of freedom. Accuracy of the obtained results was tested against mesh refinements.

During the inflation stage, luminal pressure was linearly increased from 0 to p_fin as p = n Δp_i, where n is the number of time steps, and we assumed no smooth muscle contraction, i.e., g_sm = 0. During lung puncture, the luminal pressure was reduced to a fraction of its inflated value linearly as p = p_fin + n Δp_d where Δp_d < 0, while smooth muscle contraction was increased linearly from 0 as g_sm = n Δg_sm with Δg_sm < 0. At each time step, we computed the equilibrium configuration x by solving for displacements from the energy minimization. The results were visualized using Paraview software (50). The corrugation depths were calculated as the difference between the maximum and minimum values of radial displacement u · N of the epithelium.

The geometrical parameters were chosen based on experimentally measured values and are expressed relative to the outer radius R_ep of the hollow epithelial sphere. The thickness of the epithelial sheet and smooth muscle lattice were h_ep/R_ep = 0.05 and h_sm/R_ep = 0.075, respectively. The circumferential width of the smooth muscle lattice is expressed relative to the spacing between muscle fibers as $w_{\text{sm}}/\sqrt{3}{l}_{\text{sm}}=0.1$, where l_sm is the edge length of the hexagonal lattice and l_sm/R_ep = 0.304. The Young’s moduli were set to E_sm/E_ep = 75.0, and the luminal pressure was measured relative to E_ep (51). The Poisson’s ratios of both tissues were taken to be ν_sm = ν_ep = 0.30.

For simulating inflation, the final pressure was set to p_fin/E_ep = 0.11 and Δp_i = p_fin/100, and inflation was achieved in 100 time steps. For simulating lung puncture, pressure was reduced in steps of Δp_d = −0.1 p_fin/200 and anisotropic contraction of smooth muscle along the fibers was increased in steps of Δg_sm = −0.4/200, thus resulting in a drop of 10% in luminal pressure and smooth muscle contraction of 40% at the end of 200 time steps. The results were not dependent on the number of steps.

Smooth muscle contraction was implemented via both isotropic and anisotropic growth tensors, but there was no significant change in the deformation of the lizard lung during the simulated puncturing (Fig. 4M and fig. S6, B and C). The aspect ratio of the corrugations was measured as the ratio of protrusion height of the epithelium and the spacing between the muscle fibers in the inflated/punctured lung configuration. The corrugation aspect ratio measured from simulations and experiments increase after puncturing (Fig. 4N and fig. S5D).

We conducted sensitivity analysis by changing the parameters, viz., E_sm/E_ep to 50 and 100, p_fin ± 5%, and reducing smooth muscle contraction to 20% during puncturing. The resulting deformation was qualitatively similar and is quantified by the aspect ratio of corrugations (fig. S6, D to K).

Supplementary Materials

This PDF file includes:

Figs. S1 to S6

Legends for movies S1 to S9

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S9

View/request a protocol for this paper from Bio-protocol.