Binding free energy of protein/ligand complexes calculated using dissociation Parallel Cascade Selection Molecular Dynamics and Markov state model

Abstract

We recently proposed a computational procedure to simulate the dissociation of protein/ligand complexes using the dissociation Parallel Cascade Selection Molecular Dynamics simulation (dPaCS-MD) method and to analyze the generated trajectories using the Markov state model (MSM). This procedure, called dPaCS-MD/MSM, enables calculation of the dissociation free energy profile and the standard binding free energy. To examine whether this method can reproduce experimentally determined binding free energies for a variety of systems, we used it to investigate the dissociation of three protein/ligand complexes: trypsin/benzamine, FKBP/FK506, and adenosine A_2A receptor/T4E. First, dPaCS-MD generated multiple dissociation pathways within a reasonable computational time for all the complexes, although the complexes differed significantly in the size of the molecules and in intermolecular interactions. Subsequent MSM analyses produced free energy profiles for the dissociations, which provided insights into how each ligand dissociates from the protein. The standard binding free energies obtained by dPaCS-MD/MSM are in good agreement with experimental values for all the complexes. We conclude that dPaCS-MD/MSM can accurately calculate the binding free energies of these complexes.

Significance

We benchmarked the combination of dissociation Parallel Cascade Selection Molecular Dynamics simulations and the Markov State Model, called dPaCS-MD/MSM, using three protein/ligand complexes: trypsin/benzamine, FKBP/FK506, and adenosine A_2A receptor/T4E. The obtained standard binding free energies indicate that dPaCS-MD/MSM can efficiently calculate the binding affinities of the given complexes.

Introduction

Molecular binding/unbinding is involved in most molecular-level biological processes. Thus, understanding how biomolecules recognize each other and function upon binding is essential for furthering our understanding of biology and for drug development. Binding free energy is often used to determine the affinity of biomolecular interactions and the efficacy of drugs. Complete characterization of binding-competent protein conformations, ligand binding poses, and binding/unbinding kinetics is therefore needed for a thorough understanding of protein/ligand binding. Obtaining such information on drugs would significantly enhance the computational drug design process and maximize drug efficacy. Numerous methods for free energy calculation have been developed and applied to the binding of small compounds (ligands) with proteins, such as thermodynamic integration, free energy perturbation, and the adaptive biasing force technique [1,2].

Molecular dynamics (MD) is a computer simulation technique now routinely used in many fields related to biomolecules for examining dynamic properties and processes. Many features can be investigated by all-atom MD, such as the stability of biological macromolecules [3], conformational properties, the impact of dynamics on enzyme activity [4], molecular recognition and properties of complexes [5], protein association [6], protein folding [7], and other aspects. MD and related methods are widely used for binding free energy calculations [8]. Moreover, MD simulations can provide atomic details of interaction dynamics between proteins, ligands, and solvent molecules, and thus structural flexibility and entropic effects are explicitly considered in free energy calculations. However, MD simulations cannot sample across multiple energy minima within an affordable computational time if high energy barriers separate the minima. Accordingly, conventional MD simulations of protein/ligand binding and unbinding processes or other time-consuming events still require substantial computational resources, although the use of specialized MD engines for graphical processing units (GPUs) greatly reduce the computational cost [9,10]. Considerable recent research thus focuses on developing novel methods to improve the sampling of time-consuming events to overcome the limitations of conventional MD simulations [11].

The processes of binding/unbinding must be observed to calculate the free energy profile along the processes. To this end, various enhanced sampling methods have been developed, e.g., umbrella sampling [12], replica exchange MD [13], accelerated MD [14], steered MD [15], targeted MD [16], and metadynamics [17]. Some of the methods effectively enhance the movements of molecules by applying a bias force, which requires careful parameter tuning to avoid artifacts. Alternatively, parallel cascade selection molecular dynamics (PaCS-MD) is an enhanced simulation method that does not apply a bias force [18,19], similar to other simulation methods conducted as combinations of multiple unbiased MD methods, such as forward flux sampling [20,21], weighted ensemble [22,23], and milestoning [24,25]. These methods improve sampling efficiency and enable ligand binding/unbinding simulations of proteins. PaCS-MD comprises cycles of multiple parallel short (typically 0.1 ns) MD simulations combined with initial structure selection. The repetition of parallel MD simulations from selected promising structures with regenerated initial atom velocities drastically enhances the probability of observing the dissociation of protein/ligand complexes by selecting snapshots with longer protein‒ligand distances [26–28]. Cycles of PaCS-MD generate dissociation pathways as a series of multiple MD trajectories that mutually overlap in conformational space.

The use of an appropriate method to analyze these trajectories is a critical step in determining the binding free energy of a complex. The Markov state model (MSM) is a powerful analysis method in computational biology for identifying stationary states and kinetic details of protein dynamics from MD simulation data [29]. MSM provides information on the physical process defined as a set of transitions between discretized metastable states. A dynamic description of simulated unbinding processes can be obtained by constructing an MSM from many short PaCS-MD trajectories. By selecting snapshots with longer intermolecular distances, our group previously used dissociation PaCS-MD (dPaCS-MD) to generate dissociation pathways of tri-N-acetyl-D-glucosamine from hen egg white lysozyme [26], of the transactivation domain of p53 (p53-TAD) from murine double-minute clone 2 protein (MDM2) [30], and of an N-terminal fragment of the bacterial flagellar rotor protein FliM from the signaling protein CheY [28]. We built an MSM model using dPaCS-MD trajectories to investigate the dissociation mechanisms by describing states based on ligand/protein geometry [29,30]. Using this combination, we obtained binding free energies of the protein/ligand complexes in accordance with the experimentally determined values. These successes motivated us to extend dPaCS-MD/MSM to different types of protein/ligand complexes to demonstrate accuracy and computational efficiency in binding free energy calculations.

In this work, we investigated the dissociation of three protein/ligand complexes: trypsin/benzamine, FKBP/FK506, and adenosine A_2A receptor/T4E. The first complex comprises the inhibitor benzamidine bound to bovine trypsin, an enzyme that degrades dietary proteins [31]. We investigated the dissociation process of a relatively small ligand using this complex. The second complex investigated was FK506 (tacrolimus), which inhibits T-cell activation and is effective in organ transplantation because it binds to FK506 binding protein (FKBP). FKBP is an immunophilin protein involved in the regulation of T-cell activation and inhibition of the enzymatic activity, thus affecting different signal transduction pathways [32]. FK506 is larger and more flexible than benzamine. Both systems are commonly used as benchmarks for calculating binding energy and kinetic rates and have been measured both experimentally and computationally. The third complex involves adenosine A_2A receptor (A_2A), a member of the G protein-coupled receptor (GPCR) superfamily. A_2A drugs have been developed to address wound healing, vascular diseases such as atherosclerosis, restenosis, and platelet activation, and inflammation and cancer [33]. 4-(3-Amino-5-phenyl-1,2,4-triazin-6-yl)-2-chlorophenol (T4E) was developed as an antagonist of A_2A [34]. The A_2A receptor/T4E complex is a more challenging target compared to the other two because T4E binds deeply inside the binding cavity of A_2A. Here, we applied the dPaCS-MD/MSM scheme to each of the three complexes by conducting multiple dPaCS-MD and free energy calculations with MSM. The unbinding pathways obtained by dPaCS-MD showed differences between the unbinding mechanisms of the complexes. Subsequent MSM analyses provided free energy profiles along the dissociation pathway. Finally, we compared the standard finding free energies calculated by dPaCS-MD/MSM with the experimental values, thereby demonstrating that dPaCS-MD/MSM can accurately calculate the binding free energies of these complexes.

Materials and Methods

Simulation systems

The simulated protein/ligand complexes are listed in Table 1. For the trypsin/benzamine complex, the crystal structure [PDB ID: 3atl] was immersed in a cubic water box with an edge length of 111 Å and containing KCl at a concentration of 150 mM (approximately 140,000 atoms, Fig. 1a). Protonation states at pH 7 were chosen using PDB2PQR [35]. For the FKBP/FK506 complex, the crystal structure [PDB ID: 1fkf] was placed in a cubic water box with an edge length of 117 Å and containing NaCl at a concentration of 150 mM (~120,000 atoms, Fig. 2a). Protonation states were chosen using AmberTools [36]. For the A_2A/T4E complex, the crystal structure [PDB ID: 3uzc] was embedded in a membrane using CHARMM-GUI [37], which contains 210 DMPC lipid molecules. The initial box size was 82×82×138 ų. The Amber ff14SB force field [38] and the SPC/E_b water model [39] were used for all simulations. The ligand parameters were generated using the Antechamber module in the AmberTools package with GAFF and AM1-BCC [40, 41].

Table 1 .

Free energies calculated by dPaCS-MD/MSM and comparison with experimental values

Complex	−ΔG (kcal/mol)	ΔGv (kcal/mol)	ΔG° (kcal/mol)	ΔGexp (kcal/mol)
Trypsin/benzamidine	−6.6±0.2	0.5±0.2	−6.1±0.1	−6.4 [65] −7.3 [66]
FKBP/FK506	−14.2±1.5	0.6±0.1	−13.6±1.6	−12.9 [31]
Adenosine A2A/T4E	−15.5±1.2	1.2±0.2	−14.3±1.2	−13.2 [34]

The values after ‘±’ indicate standard errors.

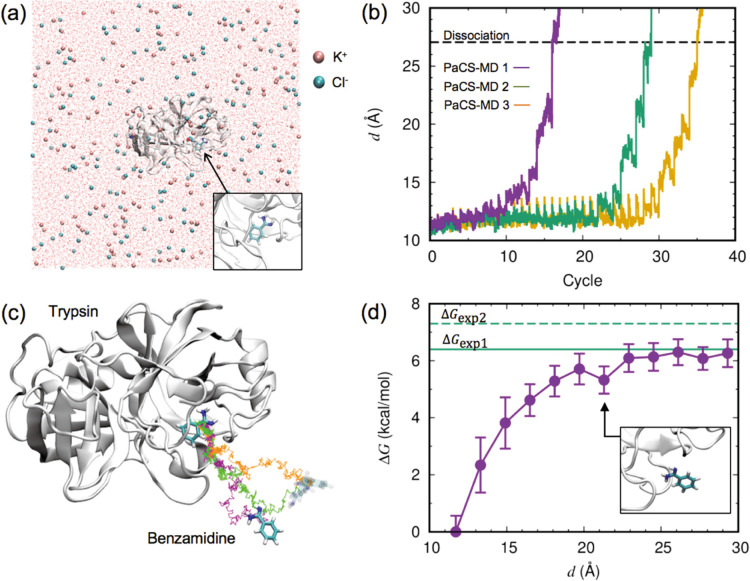
Figure 1 .

Binding free energy calculation for the trypsin/benzamidine complex. (a) Initial configuration of the complex, ions, and water oxygen in the simulation box. A close-up view of benzamidine with trypsin is shown in the inset. (b) The distance between the center-of-mass (COM) positions of trypsin and benzamidine, d, plotted as a function of the PaCS-MD cycles. Three independent simulations are shown in different colors. The dashed line indicates the average value of d where the complex totally dissociated. (c) Representative dissociation pathways of benzamidine from trypsin obtained by PaCS-MD simulations. Colored lines show the trace of the benzamidine COM position along representative concatenated trajectories. Colors are the same as in (b). The initial and final structures of benzamidine in the first PaCS-MD trial are shown in the stick model, and in transparent color for the other trials. (d) Free energy profile against d calculated by PaCS-MD/MSM. The error bars indicate the standard deviation of three PaCS-MD/MSM trials. Green lines indicate the experimentally determined values of the binding free energy. The inset shows a close-up view of a benzamidine structure with d=21.1 Å In this paper, the molecular structure was visualized using VMD [64].

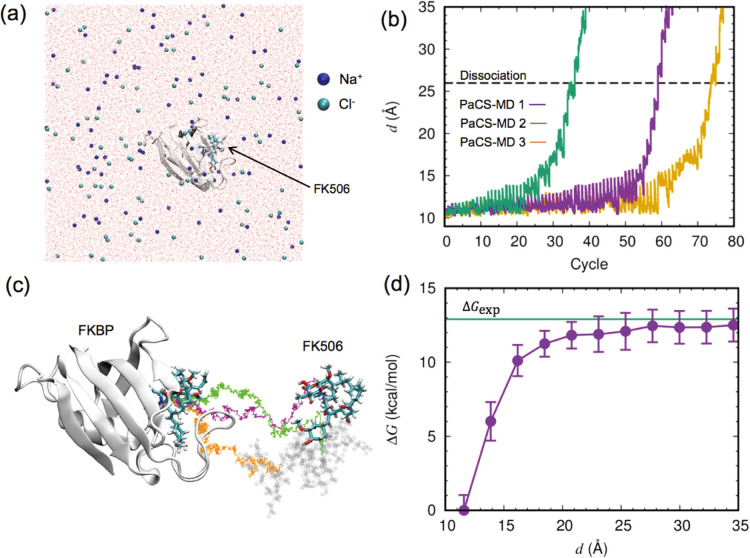
Figure 2 .

Binding free energy calculation for the FKBP/FK506 complex, shown in a similar manner to that for the trypsin/benzamidine complex in Fig. 1. (a) Overall view of the system simulated. (b) Evolution of d against the PaCS-MD cycles. (c) Dissociation pathways obtained by three PaCS-MD simulations. (d) The average free energy profile from three independent PaCS-MD/MSM calculations. The experimentally determined binding free energy is indicated by a green line.

Simulation procedure

The soluble trypsin/benzamine and FKBP/FK506 complexes were simulated using the GPU implementation [42] of the PMEMD module in the Amber package, and the A_2A/T4E complex embedded in a membrane was simulated by using GROMACS [43]. For the first two cases, the system was energy minimized and equilibrated in an NPT ensemble (300 K, 1 bar) for 10 ns by conventional MD simulation. For the A_2A/T4E complex, a 100 ns relaxation MD was conducted with positional restrains imposed on the protein and ligand, followed by free equilibration by 100 ns MD without restraints. A Langevin thermostat [44] with a friction parameter of 2 ps⁻¹ and a Berendsen barostat [45] were used for temperature and pressure control, respectively. Equations of motion were integrated with a time step of 2 fs. Covalent bonds involving hydrogens were constrained using the SHAKE algorithm [46], and the water molecules were kept rigid using the SETTLE algorithm [47]. The long-range Coulomb energy was evaluated using the particle mesh Ewald method [48], while real space non-bonded interactions were evaluated at a cutoff distance of 12 Å For the A_2A/T4E complex, the same settings were used except that the covalent bonds involving hydrogens were constrained using the LINCS algorithm [49] and the temperature and pressure were controlled by a Hoover-Nose thermostat [50,51] and a MTTK barostat [52], respectively. Three trials of PaCS-MD were conducted for the first two cases and five trials were performed for the A_2A/T4E complex.

The dissociation of protein/ligand complexes simulated using dPaCS-MD [26, 27] according to the procedure was described earlier [28]. Ten parallel MDs (replicas) were used for the trypsin/benzamine and FKBP/FK506 complexes and 30 replicas were employed for A_2A/T4E. As the initial structures for dPaCS-MD, ten structures were selected every 1 ns from the 10 ns conventional MD trajectories for the first two cases. For the A_2A/T4E complex, the equilibration MD was extended for 1 μs, the obtained trajectories were clustered into 30 clusters, and these representative 30 structures were used as the initial structures. For each cycle of dPaCS-MD, 0.1 ns MD simulations were conducted in parallel. Molecular structures were saved every 40 fs and used for MSM analysis. The structures obtained every 1 ps from each cycle were rank-ordered according to the distance d between the center-of-mass positions of the protein and ligand, and the top ten structures were selected as the initial structures for the next PaCS-MD cycle. dPaCS-MD was stopped when two molecules were sufficiently separated (d=35, 40 and 60 Å for trypsin/benzamine, FKBP/FK506, and A_2A/T4E, respectively). MD trajectories were analyzed using the cpptraj module [53] in the AmberTools14 package. The number of intermolecular contacts was calculated from heavy-atom contacts between the protein and ligand with a distance threshold of 4.5 Å.

Free energy calculation

The Gibbs free energy change ΔG with the dissociation of a protein-ligand complex was calculated by MSM analysis of the MD trajectories generated by each PaCS-MD trial according to the procedure described previously [27,28]. The calculation methods of the standard binding free energy based on the 1D free energy profile has been already well established [9,54], and we applied this concept to our MSM analysis. Binding free energy is defined as the free energy difference between the bound and completely unbound states. Although the bound state is a well-defined complex state, but the completely unbound state can be any states in which interactions between a protein and ligand of interest are negligible. Even in the cases that a ligand dissociated to very different positions, they are equivalent in free energy and all of them are considered as the completely unbound state because protein and ligand does not interact. In the previous work [27], we investigated a protein/peptide binding affinity by three different MSM methods: one-dimensional MSM based on the inter-center of mass (inter-COM) distance between the two molecules (1D-MSM); three-dimensional MSM based on the COM position of the peptide relative to the protein (3D-MSM); and by Cα coordinates of the peptide (Cα-MSM). The standard binding free energy obtained by the combination with 1D-, 3D- or Cα-MSM was in good agreement with those determined experimentally. Since 1D-MSM requires the least computational time for the calculation of the standard free energy, we adopt 1D-MSM in this work. To achieve sufficient statistics to construct a reasonable MSM, molecular structures were additionally sampled by multiple 0.1 ns MD simulations started from the PaCS-MD initial structures of each cycle with different random velocities until the implied time scale sufficiently converged to a plateau value [55]. For the trypsin/benzamidine complex, the total number of MD structures was tripled by additional MD simulations for two of the three observed pathways, whereas the third pathway did not require additional MD simulation. For the FKBP/FK506 complex, the total number of MD structures was tripled for all three pathways by additional MD simulations. For the A_2A/T4E complex, 30 replicas were used in dPaCS-MD, and no additional MD simulation was required.

MSM analysis was performed using MSMBuilder 3.5.0 [56]. Microstates were determined by k-means clustering (k=25) for d values. The initial guess of cluster centers is performed by k-means++ [57]. Supplementary Fig. S1 shows implied timescale versus lag time relation for the three slowest motions obtained for a representative 1D-MSM for each complex. Lag times of 48 ps (trypsin/benzamidine), 32 ps (FKBP/FK506) and 50 ps (A_2A/T4E) were selected based on the implied time scale test [55]. The ΔG value for the i-th microstate ΔG_i was calculated from the stationary probability of the microstate π_i:

$$\mathrm{\Delta }{G}_i=-k_{B}T\ln \frac{{\pi }_i}{{max}_j{\pi }_j}$$ (1)

where k_B is the Boltzmann constant and T is the absolute temperature [27]. The standard binding free energy ΔG° was obtained from the free energy profile and the correction term ΔG_v originating from the difference between the sampled bound volume V_b and the standard volume V° (=1661 ų) [58]:

$$\mathrm{\Delta }G°=-\mathrm{\Delta }G+\mathrm{\Delta }{G}_v$$ (2)

where ΔG is the average value of ΔG_i included in the unbound state when the corresponding value in the bound state is set to zero. ΔG_v was calculated by:

$$\mathrm{\Delta }{G}_v=-k_{B}T\ln \frac{V_b}{V°}$$ (3)

The bound state was defined as a region before the free energy curve becomes flat, i.e., a d of 22 Å for the trypsin/benzamine and FKBP/FK506 complexes, and a d of 27 Å for A_2A/T4E. The range in which the energy curve is flat was defined as the unbound state, which was 30 Å (trypsin/benzamidine), 35 Å (FKBP/FK506), and 45 Å (A_2A/T4E). The value of V_b was obtained as the volume of the convex hull defined by the center-of-mass coordinates of the ligand in the bound state relative to the center-of-mass of the protein at the origin. The convex hull calculation was performed for each dissociation simulation using Qhull [59].

Results and Discussion

Trypsin/benzamidine complex

Trypsin is a protease found in many vertebrate species and benzamidine is a competitive inhibitor of trypsin [60]. The binding between trypsin and benzamidine has been thoroughly investigated as an exemplar of biomolecular binding [61], and the binding free energy of the complex has been measured both experimentally [62] and computationally [58,63].

Dissociation of the trypsin/benzamidine complex was simulated three times by dPaCS-MD. The distance between the center-of-mass positions of trypsin and benzamidine, d, gradually increased with increasing number of PaCS-MD cycles, with back-and-forth motions of benzamidine around trypsin (Fig. 1b). At d=27.1±0.7 Å (average±SD of the three simulations), the complex dissociated completely, i.e., the number of inter-molecular contacts became zero (Fig. 1b, broken line). The number of PaCS-MD cycles required for the complete dissociation was 27±10. The corresponding computational time was 2.7 ns (0.1 ns×27 cycles) on average, and the total computational cost was 107 ns (0.1 ns×27 cycles×(10+an additional 30 replicas)). The experimental dissociation rate constant k_off was 600 s⁻¹, and the corresponding dissociation time was 1.67 ms [62], which means that PaCS-MD observed the dissociation within a computational time shorter by six orders of magnitude than the actual dissociation time.

Figure 1c depicts the dissociation pathways for benzamidine from trypsin shown by the representative PaCS-MD trajectories (from each cycle, the trajectory with maximum d was selected). Since PaCS-MD did not apply any artificial bias force to enhance dissociation, the observed possible dissociation pathways indicate how benzamidine unbinds from trypsin. All the pathways behaved similarly at the beginning of dissociation, but clearly differed after detachment from trypsin. Since benzamidine is mostly buried in trypsin in the bound state, the dissociation direction is strictly restrained in the initial process of dissociation. This is in agreement with the binding process reported previously using massive MD simulations combined with MSM, showing several binding pathways from the surface of trypsin to its binding pocket [58].

The Gibbs free energy change ΔG along the dissociation pathway was obtained by MSM analysis (Fig. 1d). Statistically reliable MSMs were constructed using MD trajectories obtained from PaCS-MD and additional MD simulations (see Methods for details). Similar to the result presented in Fig. 6 of the literature [26], each 1D-MSM was constructed around the regions around the pathways shown in Fig. 1c. To calculate the binding free energy, ΔG values are expected to converge into a certain value in long d ranges. In the range d<22 Å, the ΔG value increased, then flattened where the intermolecular interactions were insubstantial. Thus, MD structures included in the flat region were defined as the unbound state, and the other region was considered as the bound state. We found a local free energy minimum at d~21 Å in the position where benzamidine was located around the surface of trypsin (Fig. 1d, inset), in agreement with several metastable states in a simulation of the binding process [58].

The standard binding free energy ΔG° was calculated from the free energy difference between the bound and unbound states with a correction for ligand concentration (Table 1). The calculated ΔG° value was −6.1±0.1 kcal/mol, in good agreement with the experimental values of −6.4 [65] and −7.3 kcal/mol [66]. The difference between the calculated and measured values is within the limit of force field accuracy, believed to be 1 to 2 kcal/mol [67].

FKBP/FK506 complex

FK506 binding protein (FKBP) has been identified in many eukaryotes, from yeast to human, and possesses prolylisomerase activity. FK506 is a flexible ligand and is much larger than benzamidine. The dissociation of FK506 from FKBP was simulated three times by PaCS-MD (Fig. 2b). The dissociation completed at d=26.0±3.6 Å (Fig. 2b, dashed line) corresponds to a total computational time of 6±2 ns, which is twice that required for trypsin/benzamidine dissociation. The computational time spent observing dissociation should be related to the probability of escaping the free energy minima, i.e., the affinity of the protein/ligand complex. The experimental binding free energies are −12.9 kcal/mol [31] for the FKBP/FK506 complex (Table 1). However, previous studies reported that the number of dPaCS-MD cycles strongly depends on the number of trials when a small number of MD replicas run in each PaCS-MD cycle due to low probabilities of fluctuation occurrence toward dissociation [26,28]. If the number of replicas is not sufficient for MSM, additional MD simulations should be conducted as in the cases of trypsin/benzamine and FKBP/FK506. Estimating the relative affinities of protein/ligand complexes directly from the PaCS-MD trajectories may require a sufficient number of MD replicas (≥30 at least).

The obtained three FKBP/FK506 pathways were different from the beginning of dissociation, unlike those for the trypsin-benzamidine complex (compare Fig. 2c and Fig. 1c). Since FK506 is bulky, it is not buried in the binding pocket of FKBP (Fig. 2a), and thus from the beginning, FK506 can move in multiple directions towards outside the pocket.

The free energy landscape of FKBP/FK506 dissociation obtained by PaCS-MD/MSM is shown in Fig. 2d. The ΔG value continuously increased along the dissociation pathways until d~22 Å and then became flat, showing no metastable states during dissociation. The structures with d<22 Å were defined as the bound state and the outside structures were considered as the unbound state. The calculated ΔG° value of −13.6±1.6 kcal/mol agrees well with the experimental value of −12.9 kcal/mol (Table 1).

Adenosine A_2A receptor/T4E complex

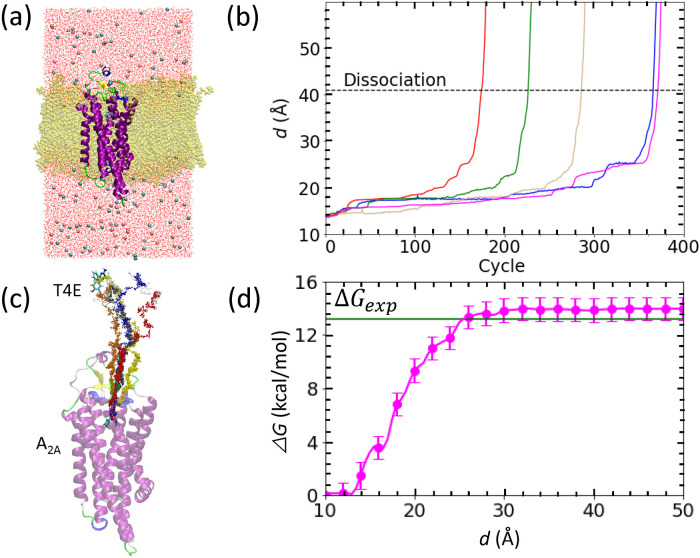
The third target in this study was the T4E ligand dissociating from its complex with the adenosine A_2A receptor (Fig. 3b). The dissociation processes were complete at d=41.0±2.2 Å (dashed line in Fig. 3b). The computational time required to reach the dissociated state was 28.0±7.9 ns. Since T4E is located deep inside the well-defined ligand binding pocket of the A_2A receptor in the bound state, the ligand requires significant time in the initial dissociation process to move from the native binding position to the entrance of the binding pocket (from a d value of 17 to 21 Å). Interestingly, all the trials required many cycles (132±18 cycles) for d between 16.9 to 18.2 Å, during which the ligand tried to find an escape path to reach bulk water by exchanging positions with water molecules and attempting to break hydrogen bonds, specifically with Ala266 in extracellular loop 3 (EL3) and Ile81 in transmembrane helix 3 (TM3). In addition, water-mediated contacts with Asn254 in transmembrane helix 6 (TM6) via two water molecules contributed to this trap. In all trials, T4E first escaped the binding pocket by breaking interactions of its NH₂ group with the A_2A receptor.

Figure 3 .

Binding free energy calculation for the adenosine A_2A/T4E complex shown in a similar manner to that for the trypsin/benzamidine complex in Fig. 1. (a) Configuration of the simulated system after careful relaxation. The protein is shown in a cartoon representation while the T4E ligand (atom-type coloring) and lipid membrane (yellow) are shown as licorice models. The pink and cyan spheres represent chloride and sodium ions, respectively, and water molecules are shown as line representations with atom-type coloring. (b) Evolution of d against the PaCS-MD cycles. (c) Unbinding pathways obtained by five PaCS-MD simulations. (d) The inter-COM free energy profile from five independent PaCS-MD/MSM calculations. The experimentally determined binding free energy is indicated by a green line. The inset of panel (d) displays the binding to the entrance of binding pocket of T4E.

The obtained free energy plot of the dissociation process of T4E out of the A_2A receptor is shown in Fig. 3d. The free energy increased from d ~ 12.5 Å and reached a constant value at 32 Å. The subtle local minimum at ~ 17 Å is consistent with the position of the trap observed during the PaCS-MD simulations. The calculated ΔG° value of −14.3±1.2 kcal/mol is in good agreement with the experimental value of −13.2 kcal/mol [34].

Conclusion

In this study, we applied dPaCS-MD/MSM to three distinct protein/ligand complexes and evaluated the binding free energies. dPaCS-MD generated multiple dissociation pathways within a reasonable computational time for all three complexes, despite the complexes comprising significantly different sized molecules and involving different intermolecular interactions. The MSM analyses produced free energy profiles for the dissociations, providing insights into how the ligand dissociates from the protein. The calculated standard binding free energies agreed well with previously published experimental values. We therefore conclude that dPaCS-MD/MSM can accurately calculate the binding free energies of these complexes.

Although dPaCS-MD/MSM can be applied to different protein/ligand complexes, some factors should be considered. First, dPaCS-MD is conducted in a cubic water box, which freely allows rotation and dissociation of the complex in any direction. Howenver, PaCS-MD has a higher computational cost for larger non-globular complexes. One way to avoid this is the use of positional restraints to stop the rotation of the protein, and the use of a rectangular box, with the long axis positioned along the direction of dissociation [26], although the dissociation directions are limited in this case. Second, a larger number of PaCS-MD cycles might be needed to observe the dissociation of a ligand bound deep inside the protein. In this case, dissociation might be enhanced by introducing other corrective variables for structure selection in PaCS-MD [68]. However, T4E situated deeply inside the binding cavity of adenosine A_2A receptor successfully dissociated only by the use of d as shown in this work. This was also confirmed for other A_2A ligands which are in progress in our laboratory.

Many MD calculations are distributed as replicas and conducted in parallel in PaCS-MD, and synchronization among the replicas within each cycle is not required. This advantage enables the production of unbiased dissociation pathways and accurate free energy profiles of protein/ligand dissociation within a reasonable computational time. Although the total computational cost might be large for larger systems or strongly bound complexes, parallelizability is suited for calculations using parallel computing supercomputers such as Summit, Sierra, and Fugaku, as well as distributed computing. In addition, PaCS-MD/MSM can be used to investigate not only the thermodynamics but also the kinetics of biomolecular interactions [27]. Calculations of kinetic rate constants (k_on, k_off, residence time, etc.) using PaCS-MD/MSM are currently under investigation in our laboratory.

Conflict of Interest

The authors declare no competing financial interest.

Author Contributions

H.H., D.P.T., and A.K. contributed to the design of the work. H.H., D.P.T., M.M.S., and A.K. conducted the overall analyses, and wrote the manuscript; H.H. and D.P.T. performed the computations.

A preliminary version of this work, doi: 10.33774/chemrxiv-2021-51bwf, was deposited in the ChemRxiv on August 19, 2021.