Covid-19 pandemic and spillover effects in stock markets: A financial network approach

Abstract

This paper examines the impact of the COVID-19 pandemic on 51 major stock markets, both emerging and developed. We isolated the countries susceptible to shock transmissions, and evaluated countries with immunity, during the lockdown. Specifically, using dependence dynamics and network analysis on a bivariate basis, we identify volatility and contagion risk among stock markets during the COVID-19 pandemic. The empirical findings add to the existing body of literature, given that previous work has not placed emphasis on network topologic metrics when it comes to financial networks, specifically during the COVID-19. The evidence shows instant financial contagion a result of the lockdown and the spread of the novel coronavirus. The methodological framework outlines important information for investors and policymakers on using financial networks to improve portfolio selection, by placing an emphasis on assets according to centrality.

1. Introduction

The World Health Organization (WHO) first announced COVID-191 a health emergency during January 2020. The novel coronavirus has since spread to over 200 countries and has mushroomed into a global public health and economic disaster, impacting the $90 trillion global economy. Its adverse impact is of such a magnitude that a comparable event has not been witnessed for at least a century. This pandemic is expected to trim economic growth around the world by over 3–6% during the year 2020. The subsequent year may experience some recovery, provided that a second wave does not present itself (Bank for International Settlements, 2020). This economic fallout runs the risk of a global recession event, one that can push unemployment levels up by a large margin – similar to what was observed during the great depression during the 1930s. The people that have died during the pandemic will build up a very real human cost, which will have a deep impact on the global economy itself. This is on top of the already increasing levels of unemployment, poverty, social unrest, and more. Some estimates suggest that worldwide trade will see an overall fall of between 13 and 32%. The overall situation will have a detrimental impact on trade-dependent economies, both emerging and developing countries included (International Monetary Fund, 2020). The extent of the damage is not yet known because of the evolving nature of the pandemic.

The Coronavirus seems to have produced numerous problems and affected sectors, including supply shortages, global financial markets, agriculture, manufacturing, arts, entertainment and sport, publishing, retail, business closures, restaurants, science and technology, tourism, transportation and unemployment. It is obvious that the global economy will struggle to handle a second lockdown. In addition, the solution to this issue should be a blended model with a list of recovery policies and regional lockdowns to enhance the economy and simultaneously control the spread of the Covid-19.

Globally, the economic conditions are extremely fluid. This is true for many regions and countries. There is great unsurety about the duration and extent of this pandemic, and its long-term economic impact. These issues have in turn created instability in the financial markets, which has had a serious impact on the corporate decision-making process (Im, Kang, & Shon, 2020). Furthermore, the uncertain future of the novel coronavirus and its spread puts into question the efficacy of public policies developed to curb its run and ensure a second wave does not come to be. This has further added to the volatility being observed in the market. The global economy takes on the shape of a financial network because of the workings of urbanization, globalization, and environmental change. Covid-19's spread has deeply impacted global financial markets.

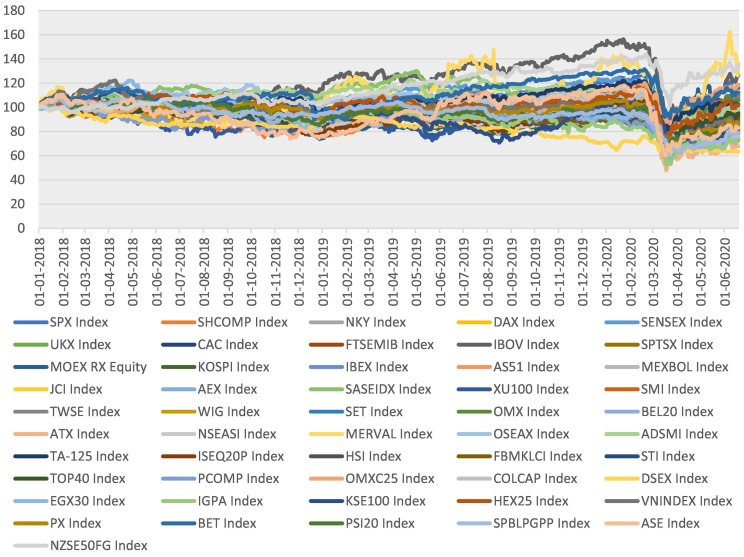
The S&P dropped by 7% in just four minutes on March 9. This was triggered soon after the exchange opened for business, leading to a circuit breaker for the first time since the crisis of 2007–2008. It caused trade to come to a stop for over 15 min (Fig. 1 ). Stock markets around the world observed serious drops in value, where STOXX Europe 600 fell by over 20% below the high that was seen during the start of the year. The yield on 10 and 30-year US Treasury Securities experienced record falls, with the 30-year options settling below 1% for the first time in their history. On March 12, the stock markets in Asia-Pacific shut down with Tokyo Stock Exchange's Nikkei 225 dropping below 20% of its original 52-week position. European stock markets fell 11%, the worst decline observed during a single day in all of history. The S&P 500 was down 9.5%, and these falls led to a cessation of trade at the NY Stock Exchange for the second time in that time period.

Fig. 1.

Covid-19 impact on stock markets.

Notes: Time series of 51 major indices from various economies selected by the countries' GDP. Sample includes daily data from 1/12018 till 18/6/2020. Data is rebased to 100 in order to illustrate the impact of the Covid-19 and the lockdowns.

Regarding that the daily number of COVID-19 cases increases there is a significant negative relationship with various stock indices. The source of financial contagion can be initiated from the imposed lockdowns; if one country imposes a lockdown, this decision/information is negatively transferred to other countries as well (due to the uncertainty and the panic). As a result, this increases the possibility of contagion within the network. This paper looks at the likely financial contagion risk, by identifying co-movements and spillover effects from the Covid-19 and lockdowns to other countries. Specifically, our main goal is to find contagion and spillover evidence from stocks' indices, within a financial network developed through correlations.

The Covid-19 crisis has demonstrated the part played by financial connectedness in terms of a possible source of macroeconomic instability and systemic risk (Goodell, 2020; Rizwan, Ahmad, & Ashraf, 2020). This pandemic has additionally showcased how important it is to understand whether a rise in this connectivity results in a larger likelihood of a financial crisis becoming a reality. The work of Forbes and Rigobon (2002) noted that a contagion can lead to a significant rise in disruptions in the market, which can be caused when one sector or channel of the economy experiences a shock. In particular, it has to do with the condition through which we can see financial disturbances spread from one region or country to other region(s) or country(ies), or from one channel or sector to another. Furthermore, where two indices produce a large amount of co-movement within peaceful periods, they will continue to sustain this link when a shock appears in the market, where this disruption may not be attributed to a financial contagion. Other research work has explained contagions as serious hikes in correlation between nations where the crisis occurs, and other countries (e.g., Agosto, Ahelegbey, & Giudici, 2020; Apergis, Christou, & Kynigakis, 2019; Baele, 2005; Bhanot, Burns, Hunter, & Williams, 2014; Corsetti, Pericoli, & Sbracia, 2005; Dungey, Flavin, & Lagoa-Varela, 2020; Geraci & Gnabo, 2018; Masson, 1998; Pericoli & Sbracia, 2003; Reboredo, Rivera-Castro, & Ugolini, 2016; Samitas, Kampouris, & Kenourgios, 2020). Dornbusch, Park, and Claessens (2000) and Collet and Ielpo (2018) explain contagion as the spread of disturbances in the market, basically in the context of negative side effects, where one market is affected because of another. Furthermore, the work of Bekaert, Harvey, and Ng (2005) and Audrino and Tetereva (2019) looks at contagion that exists in financial markets, where the conditions that cause movement in the indices essentially brings them closer together when crises emerge. On the other hand, Sachs, Tornell, and Velasco (1996) demonstrate this as a substantial hike in cross-country correlations of volatilities and stock market returns.

This pandemic has pushed for new research on how the modern financial system operates in terms of its interconnectedness. A fresh body of work also looks at how this impacts the fragility of the system. Network connections lead to market diversification, where a diversifying pattern is observed in risk exposures. On the other hand, they also help develop modes through which the contagion can spread shocks. This paper looks to add to the existing literature on links network connectivity in the given context, i.e. the global financial sector, and in specific the channels of stock indices. This is looked at in the context of likely contagion risk brought on by the pandemic. More specifically, the paper computes dynamic conditional correlations shared by all sets of stock indices and develops dynamic financial networks as per said sets. These networks are then deployed to find likely contagion risk during the period that the novel coronavirus lasts.

This paper adds to existing literature through its examination of whether contagion risk measures, devised on the concept of the global financial system as a network, detect spillover effects in stock markets during the Covid-19 pandemic crisis. Through this, we put together network analysis and dependence dynamics to develop a precise model to find shock events and volatile periods of contagion.

Our work differs from others in several facets:

• ➢This work is the first of its kind to look at and quantify the effects of lockdown in the global financial markets. We deployed an effective, efficient and advanced methodology to quantify and measure the spillover impact of Covid-19, in terms of the stock markets.
• ➢Most studies that use dynamic conditional correlations show contagion channels, and later the source of spillover. Our sample looked at data from 51 countries, selected by their GDP size and the best available data, and extracted correlations for all possible combinations. In particular, we calculated 1275 pairs of correlations for stocks indices to cover all possible combinations for these countries. To the best of our knowledge, this has not been covered in the literature. With this approach we have the ability to test and analyze the behavior of the correlations between countries and subsequently, quantify the extent of the interdependence in stock markets. Additionally, we categorize the dynamic conditional correlations based on the geographical position of the countries and provide significant evidence about how the markets react to financial crises.
• ➢This is the first time that a very large sample was used to depict and exact data, and in a network from the global financial system of markets with joints of correlations for stocks indices. In this way, we have the ability to see the structure of the global financial networks during the Covid-19 period. Specifically, we create financial networks of stock indices and analyze factors such as which countries have the strongest ties, which are more vulnerable to transferring uncertainty to markets and which others are less prone to the most significant shocks during the pandemic crisis.
• ➢This study showcases the unique evolution of the networks in question, alongside their centralities, and core nodes. The sample chosen is particularly large and allows us to examine not just how the networks are changing as time passes but also which countries becomes significant players in the global markets. Our study places a focus on the timeline of the lockdowns during the pandemic. This has enabled us to assert that market forces can be elaborated on through other aspects, and therefore providing more data to quantity and interpret the contagion's existence in the market.
• ➢Lastly, existing literature for financial contagions and Covid-19 is not particularly vast. We use hypotheses testing to develop a model from dynamic conditional correlations and dynamic centralities and analyze the possible existence of contagion risk inside the financial networks during the pandemic crisis. The model seems to be highly accurate in that it detects many of the critical dates of Covid-19 (1/27/2020: WHO addressed Covid-19 as global threat, 2/24/2020: significant rise in Covid-19 cases outside China and 3/9/2020: lockdown implementation started globally).

The rest of the paper is structured in the following manner: Section 2 looks at the reviewed literature. Section 3 discusses the testing framework, including the model for testing that allows for the identification of contagion within the setting in question, the data used for empirical framework, and the risk specifications for the contagion. The findings are outlined in Section 4, while the last section i.e. Section 5 looks at the conclusions.

2. Literature review

This paper looks at the likelihood of contagion risk within structured financial networks, in the context of stock markets, within the Covid-19 period. Since our methodological approach is multidimensional, we organize the literature review as follows. First, we review the current “traditional” literature on financial contagion and spillover effects in time series (because financial networks are dynamic), after which we present the part of the literature that covers the financial network and specifically financial contagion within networks. Also, there is no literature regarding spillover effects and contagion in stock markets during the Covid-19 or previous pandemic crises.2

2.1. Interdependence and contagion in stock markets

In terms of the methodology, a dependence structure when looking at market indices is the main problem for much of the research that exists. Most works deploy the multivariate GARCH models to look into transmission modes, correlation dynamics and volatility in financial market settings. Some studies also make use of copula functions to quantify the effects of the contagion. The first study of this kind was produced by Bollerslev, Engle, and Wooldridge (1988), who outlined that the VECH specification could prove useful. Engle and Kroner (1995) then pushed the BEKK asymmetric model, which is linked to the problem of dimensionality. Engle (2002) evolved Bollerslev (1990)’s CCC or Constant Conditional Correlation model. Here the correlation varies by time and can record changes over a given period. Cappiello, Engle, and Sheppard (2006) modified Engle's (2002) work and suggested the asymmetric (A-DCC) model to measure conditional variances and correlation dynamics in the context of asymmetry. On the other hand, copula functions were used in many pieces of research looking at the quantification of the financial contagion phenomenon (Bhatti & Nguyen, 2012; Durante & Jaworski, 2010; Rodriquez, 2007). Copulas are thought to be advanced methods to examine market dependence and are largely used for the same.

Recent studies on spillover effects and contagion (e.g., Apergis et al., 2019; Bayona & Peia, 2020; Bhanot et al., 2014; Bucci, Torre La, Liuzzi, & Marsiglio, 2019; Kalbaska & Gatkowski, 2012; Leventides, Loukaki, & Papavassiliou, 2019; Piccotti, 2017; Reboredo et al., 2016) tested various modifications of covolatility approaches to check for cross-country spillover effects. In the same framework, studies as Dungey et al. (2020), Guidolin, Hansen, and Pedio (2019), Collet and Ielpo (2018), Alter and Beyer (2014), Claeys and Vasicek (2014), and Jiang, Konstantinidi, and Skiadopoulos (2012) focused on VAR models to conclude for financial contagion. Among other studies, Audrino and Tetereva (2019) applied Granger causality to extract spillovers effects from US and EU stocks while Nguyen, Mateut, and Chevapatrakul (2020) and Green, Larsson, Lumina, and Nilsson (2018) used multivariate GARCH models to examine likely time-variant spillover effects from their sample data.

This paper makes use of an A-DCC model to quantify the correlations observed in all country pairs (sovereign bonds, CDS and stock indices), because this is a simple method through which the correlations in question can be measured. Existing literature has demonstrated that this is an adequate and appropriate approach.

2.2. Financial networks and volatility spillover in finance

Stock markets and modern banking are extremely interlinked. Regardless of many advantages, links between banks include a contagion risk (Babus, 2016). Hausenblas, Kubicova, and Lesanovska (2015) looked at the likely risk of contagion in the Czech banking system through their interbank exposures in terms of domestic banks. These banks are enriched through a liquidity channel and an asset price channel. A computational model of structure and size was used, alongside the banks' regulatory characteristics and balance sheet. The study found that credit losses on interbank exposures made for a limited likelihood of contagion. Meanwhile, Minoiu, Kang, Subrahmanian, and Berea (2015) studied the capacity of the connectivity in the global financial linkage networks to forecast crises for systemic banking. The findings showed that a rise in the connectedness relating to a country, and a fall in the connectedness of a neighboring country, are linked to a larger likelihood of there being a banking crises, after macroeconomic fundamentals had been controlled.

Within this framework, Tse, Liu, and Lau (2010) created networks to examine the links between US stocks' closing prices. Here, the stocks were taken as the nodes, and the connections were found through the variations in stock prices, trading volumes, and price returns within a specific period of time, which became the cross correlations. The study discovered that stock price variations are significantly impacted by a genuinely small amount of stocks. In the same vein, Qiao, Li, and Xia (2015) modeled currency networks by using the real effective exchange rate, i.e. REER. The MST was used alongside the rolling-window approach. Through these, correlation-based and time-varying networks were developed which helped examine the linking impact between various currencies. The work showed that apparent linking affects exist among currency networks and the euro (EUR), which is seen as a global currency around the world. Similarly, Eryigit and Eryigit (2009) examined networks developed through cross-correlation of stock market indices. The study demonstrated that European and North American markets had a stronger connectivity between themselves as opposed to other geographical regions, where they did not enjoy similar integration. Likewise, Brida and Risso (2010) and Kantar, Deviren, and Keskin (2011) found similar evidence, which links to the Turkish and German economies. Other works, including Samitas et al. (2020), Agosto et al. (2020), Duffy, Karadimitropoulou, and Parravano (2018), Li, Milne, and Qiu (2016), Yang, Li, and Zhang (2014), Chuluun, Prevost, and Upadhyay (2017), Chen, Luo, and Wang (2015), Gilmore, Lucey, and Boscia (2010), Eom, Oh, Jeong, and Kim (2009), Coelho, Hutzler, Lucey, and Richmond (2007), Coelho, Hutzler, Repetowicz, and Richmond (2007), Ulusoy, Keskin, Shirvani, Deviren, and Kantar (2012) and Tabak, Serra, and Cajueiro (2010) used vast variants of constructed networks to examine the correlations and likely spillovers impacts in the data.

Using a dynamic financial network framework, Sensoy and Tabak (2014) proposed dynamic spanning trees constructed by the ARMA-FIEGARCH-cDCC process to examine interconnections in the Asia-Pacific stock market. The study found that networks reduce in size as time passes. It noted that the market in Hong Kong was the main player. Moreover, the study found a heightened interdependence between the stock markets in the Asia-Pacific region during the last 20 years. This is the evidence for a contagion to have existing during the financial crises of 1997 and 2008. Qiao, Xia, and Li (2016) employed dynamic conditional correlations (DCC) approach to find a similar effect within the China stock market and found the impact of network linkage effects on the magnitude of security returns through varying sectors. They examined stock interdependence within the network of the China Securities Index (CSI) industry index basket and found that linkage effects were present within stock networks. The two aforementioned papers used time-varying highest centrality measures to analyze the dynamic evolution of the network structure. This purpose fulfills the investigation for network stability and the extent of shrinkage during a stock market crisis.

This paper uses A-DCC to develop networks using MST and therefore works to find centrality measures to examine the main nodes, and likely contagion impacts, within the networks. To the best of our knowledge, a similar study looking at the combination of a network analysis and financial contagion within the Covid-19 period is not present.

3. Modeling strategy

3.1. Data

For our analysis, we tried to find evidence for co-movements and contagion evidence from the data collected during the lockdown period. We tried to show that negative impacts were transferred between countries. Specifically, our main goal is to find spillover and contagion evidence from stocks indices within a financial network constructed by correlations. Through this method we examine the contagion risk that is linked to a network of stocks. We started this by measuring the interdependence ratio, which was acquired through the correlations of the applied econometric model. Given that we are examining the global stock exchange market environment, the main players in this field include the US, Europe, and Asian markets. Furthermore, there is no doubt that all other major emerging and developed economies have the capacity for significant co-movements and contagion in capital markets.

Daily data returns were used to calculate the interdependence ratio from the correlations. The period chosen was between January 1, 2018 and June 18, 2020 (the date this paper was written). Major stock indices were taken from the sample country picked from the different regions under study, i.e. Europe, EU, Eurozone, the Americas, Asia and Africa. Bloomberg was used to collect sample data on 51 economies (i.e. stocks – large cap main indices). The countries can be observed in Table 1 , along with related descriptive stats from this study. The countries were chosen as per the available data and the size of their GDP. We include more than 98% of the global GDP in our study.

Table 1.

Descriptive statistics.

	Mean	Median	Standard Deviation	Sample Variance	Kurtosis	Skewness	Range	Minimum	Maximum	Sum	Jarque - Bera Probability
Malaysia	1.843E-18	0.0003	0.0081	0.00007	13.481	−0.502	0.1203	−0.054	0.067	1.19E−15	0.00
Nigeria	-1.049E-17	0.0003	0.0098	0.00010	6.022	−0.998	0.0875	−0.056	0.031	−6.75E-15	0.00
Hong Kong	9.857E-18	0.0004	0.0125	0.00016	2.459	−0.467	0.1065	−0.057	0.050	6.35E-15	0.00
Japan	−3.052E-18	0.0000	0.0129	0.00017	5.899	−0.125	0.1400	−0.063	0.077	−1.97E-15	0.00
Vietnam	8.717E-18	0.0006	0.0123	0.00015	4.865	−1.011	0.1134	−0.065	0.049	5.61E-15	0.00
Taiwan	2.494E-18	0.0001	0.0103	0.00011	9.703	−1.058	0.1269	−0.065	0.062	1.61E-15	0.00
Mexico	5.980E-19	0.0004	0.0118	0.00014	4.834	−0.670	0.1138	−0.066	0.048	3.85E-16	0.00
Indonesia	1.100E-17	0.0004	0.0118	0.00014	11.327	0.068	0.1651	−0.068	0.097	7.08E-15	0.00
Pakistan	8.781E-18	0.0003	0.0130	0.00017	4.358	−0.612	0.1179	−0.071	0.047	5.66E-15	0.00
Singapore	4.690E-18	0.0004	0.0107	0.00011	10.345	−0.744	0.1353	−0.076	0.059	3.02E-15	0.00
New Zealand	7.723E-18	0.0001	0.0093	0.00009	16.475	−0.923	0.1483	−0.079	0.069	4.97E-15	0.00
China	3.121E-10	0.0002	0.0119	0.00014	5.705	−0.813	0.1349	−0.080	0.055	2.01E-07	0.00
Czech Republic	−2.518E-18	0.0003	0.0105	0.00011	18.098	−1.474	0.1553	−0.081	0.074	−1.62E-15	0.00
Denmark	7.553E-18	−0.0002	0.0106	0.00011	8.043	−1.215	0.1238	−0.084	0.040	4.86E−15	0.00
Turkey	-1.284E-17	0.0001	0.0144	0.00021	4.050	−0.785	0.1423	−0.084	0.058	−8.27E-15	0.00
South Korea	−3.300E-18	0.0003	0.0123	0.00015	11.239	−0.230	0.1702	−0.087	0.083	−2.13E-15	0.00
Russia	3.138E-18	−0.0003	0.0147	0.00022	5.471	0.022	0.1772	−0.089	0.088	2.02E-15	0.00
Bangladesh	3.315E-18	0.0007	0.0103	0.00011	33.512	−0.219	0.1885	−0.090	0.099	2.13E−15	0.00
Norway	-1.138E-18	0.0002	0.0127	0.00016	12.153	−1.616	0.1567	−0.098	0.058	−7.33E-16	0.00
Switzerland	7.852E-19	0.0001	0.0110	0.00012	15.805	−1.373	0.1691	−0.101	0.068	5.06E-16	0.00
Australia	−9.712E-18	0.0006	0.0125	0.00016	16.045	−1.609	0.1697	−0.102	0.068	−6.25E-15	0.00
Portugal	1.131E-19	0.0003	0.0116	0.00013	18.651	−1.613	0.1780	−0.102	0.076	7.29E-17	0.00
South Africa	4.501E-18	0.0001	0.0142	0.00020	9.947	−0.929	0.1836	−0.104	0.079	2.90E-15	0.00
Finland	1.013E-17	0.0000	0.0130	0.00017	11.022	−1.094	0.1734	−0.107	0.067	6.52E-15	0.00
Ireland	−8.844E-18	0.0003	0.0141	0.00020	11.163	−1.016	0.1829	−0.108	0.075	−5.70E-15	0.00
Peru	6.112E-18	0.0005	0.0104	0.00011	24.370	−2.493	0.1508	−0.110	0.041	3.94E−15	0.00
Sweden	-1.082E-17	0.0003	0.0129	0.00017	11.272	−1.193	0.1802	−0.112	0.068	−6.97E-15	0.00
Netherlands	−8.108E-19	0.0007	0.0124	0.00015	18.016	−1.451	0.1997	−0.114	0.086	−5.22E-16	0.00
Thailand	7.494E-18	0.0004	0.0120	0.00015	27.693	−2.417	0.1908	−0.114	0.077	4.83E-15	0.00
UK	1.206E-17	0.0005	0.0123	0.00015	19.031	−1.515	0.2018	−0.115	0.087	7.77E-15	0.00
Israel	7.151E-19	0.0000	0.0119	0.00014	21.876	−2.045	0.1876	−0.115	0.072	4.61E-16	0.00
Romania	−8.271E-18	0.0003	0.0129	0.00017	21.909	−2.201	0.1871	−0.119	0.068	−5.33E-15	0.00
USA	−2.795E-10	0.0004	0.0152	0.00023	16.664	−1.008	0.2173	−0.128	0.089	−1.80E-07	0.00
Germany	−1.090E-18	0.0004	0.0142	0.00020	18.243	−1.114	0.2347	−0.130	0.104	−7.02E-16	0.00
France	5.681E-18	0.0007	0.0137	0.00019	18.679	−1.822	0.2115	−0.131	0.081	3.66E-15	0.00
Canada	3.446E-18	0.0006	0.0136	0.00019	37.380	−1.977	0.2447	−0.132	0.113	2.22E−15	0.00
Poland	-1.388E-17	0.0004	0.0128	0.00016	22.495	−2.125	0.1916	−0.135	0.057	−8.94E-15	0.00
Chile	−4.253E-18	0.0005	0.0133	0.00018	32.102	−2.528	0.2149	−0.138	0.077	−2.74E-15	0.00
UAE	8.009E-19	0.0000	0.0133	0.00018	31.120	−2.151	0.2200	−0.139	0.081	5.16E−16	0.00
India	-1.541E-18	0.0000	0.0139	0.00019	25.083	−1.874	0.2270	−0.141	0.086	−9.92E−16	0.00
Philippines	-1.137E-17	0.0005	0.0148	0.00022	20.138	−2.085	0.2149	−0.143	0.072	−7.32E−15	0.00
Greece	-1.600E-17	0.0003	0.0181	0.00033	15.107	−1.672	0.2249	−0.143	0.081	−1.03E-14	0.00
Austria	5.121E-18	0.0006	0.0156	0.00024	22.008	−1.795	0.2488	−0.146	0.103	3.30E-15	0.00
Spain	8.297E-18	0.0006	0.0138	0.00019	27.936	−2.447	0.2268	−0.151	0.076	5.34E-15	0.00
Belgium	−7.470E-18	0.0007	0.0141	0.00020	25.876	−2.508	0.2269	−0.153	0.074	−4.81E-15	0.00
Brazil	−4.256E-19	−0.0002	0.0200	0.00040	18.845	−1.636	0.2902	−0.160	0.130	−2.74E-16	0.00
Colombia	5.382E-18	0.0004	0.0152	0.00023	41.631	−2.230	0.2876	−0.162	0.125	3.47E−15	0.00
Saudi Arabia	-1.617E-18	0.0000	0.0129	0.00017	48.874	−3.840	0.2359	−0.168	0.068	−1.04E-15	0.00
Egypt	4.931E-18	0.0005	0.0149	0.00022	35.390	−3.177	0.2591	−0.171	0.088	3.18E-15	0.00
Italy	−7.839E-19	0.0008	0.0158	0.00025	35.861	−3.115	0.2709	−0.185	0.086	−5.05E-16	0.00
Argentina	7.327E-19	−0.0005	0.0345	0.00119	58.223	−4.403	0.5747	−0.477	0.097	4.72E-16	0.00

Notes: The Indices for each economy are the following: USA -SPX Index, China -SHCOMP Index, Japan -NKY Index, Germany -DAX Index, India -SENSEX, Index, UK -UKX Index, France -CAC Index, Italy -FTSEMIB Index, Brazil -IBOV Index, Canada -SPTSX Index, Russia -MOEX RX Equity, South Korea -KOSPI Index, Spain -IBEX Index, Australia -AS51 Index, Mexico -MEXBOL Index, Indonesia -JCI Index, Netherlands -AEX Index, Saudi Arabia -SASEIDX Index, Turkey -XU100 Index, Switzerland -SMI Index, Taiwan -TWSE Index, Poland -WIG Index, Thailand -SET Index, Sweden -OMX Index, Belgium -BEL20 Index, Austria -ATX Index, Nigeria -NSEASI Index, Argentina -MERVAL Index, Norway -OSEAX Index, UAE -ADSMI Index, Israel -TA-125 Index, Ireland -ISEQ20P Index, Hong Kong -HSI Index, Malaysia -FBMKLCI Index, Singapore -STI Index, South Africa -TOP40 Index, Philippines -PCOMP Index, Denmark -OMXC25 Index, Colombia -COLCAP Index, Bangladesh -DSEX Index, Egypt -EGX30 Index, Chile -IGPA Index, Pakistan -KSE100 Index, Finland -HEX25 Index, Vietnam -VNINDEX Index, Czech Republic -PX Index, Romania -BET Index, Portugal -PSI20 Index, Peru -SPBLPGPP Index, Greece -ASE Index, New Zealand -NZSE50FG Index. Data obtained from Bloomberg.

The descriptive stats demonstrated that in most cases, the mean value is much lower than the median. In addition, the mean value is positive in 29 indices. Additionally, Argentina, Brazil, Greece and Italy experienced the most volatility, while New Zealand, Nigeria, and Malaysia experienced the least as per the standard deviations. Almost all countries were negative skewed. In addition, almost all countries had kurtosis higher than 3. All indices present high values of skewness and kurtosis, indicating that extreme changes tend to occur more frequently. Finally, the Jarque-Bera test showed that none of the indices are normally distributed. For this case, we used the residuals from the AR, MA and ARMA models, depending on which one fits better. However, in almost all cases, the AR (1) fit properly to locate asymmetry and excess kurtosis through the time series. Finally, in all cases, the minimum value is the day of the lockdown's announcement (3/9/2020), which points out that the resultant financial volatility (see Fig. 1) raised issues concerning the size of financial contagion within the network of stocks.

3.2. Empirical approach

For the purpose of measuring interdependence and the contagion risk specification, we chose the most current and advanced econometric methods, as per the reviewed literature. The methodological strategy that we used has a few steps. To start with, we use the (A-DCC) model put forward by Cappiello et al. (2006) to find correlations. In the next step, we convert correlations to distance metrics between each pair. For the third step, we employed the distance metrics to develop financial networks through use of Kruskal's (1956) MST algorithm. In the fourth step, centralities (degree, betweenness, eigenvector and closeness) were extracted from the networks created to quantify the key nodes i.e. the most important countries, within the financial networks. It is pertinent to mention that centralities were extracted for all dynamic conditional correlations for all indices of stocks. In specific, we looked at daily centralities as per the sample data. Through the tracing of daily centralities, we want to quantify the centralities' behavior in terms of the main countries, and sort them by rank into the top three positions for each centrality category outlined. Finally, we settle on a hypothesis to outline contagion risk within the financial network.

3.3. Asymmetric DCC model

To examine the contagion and co-movements, we focused on the mediums through which shocks are transferred from one place to another, in which case countries. It is important to quantify the ratio of interdependence that can be gauged from the correlations found through the econometric models deployed. Cappiello et al. (2006)’s model for correlation detection was used for this study. Furthermore, we look at the correlation behavior evidence from stock market returns. The A-DCC model measures the conditional asymmetries in the correlation dynamics directly by estimating the correlation coefficients using standardized residuals. This method is frequently used in combination with more sophisticated methods, since it accounts for the likely time-varying nature of correlations and structural shifts in data. As mentioned in the literature review is the most reliable and accurate econometric technique to deal with dynamic time series correlations.

From our sample, we can see that all indices show significant values of kurtosis and skewness, outlining that in all the cases considered, significant modifications are observed at a more frequent pace. A model such as the AR(1)-GJR-GARCH (Glosten-Jagannathan-Runkle GARCH model of Glosten, Jagannathan, & Runkle, 1993) fits properly to locate asymmetry and excess kurtosis channels through the time series. We use GJR –GARCH models into the A-DCC model to check for co-movements among assets.

The A-DCC model of Cappiello et al. (2006) can yield acceptable evidence since it records time-varying conditional correlations shared by the indices, and at the same time it has the capacity to check for leverage effect; asymmetry in variances (where negative shocks at time t − 1 tend to have stronger impact in the variance at time t than positive shocks). The A-DCC model was created in a way that makes it possible for two-stage estimation of the conditional covariance matrix. Where the first stage data cleaning takes place for all-time series.

In most cases, an AR (1) model was adequate for the residuals. Then, we estimate a univariate GARCH model for each return series. Despite the fact that we can find numerous univariate GARCH models in the literature, we applied the GJR-GARCH model of Glosten et al. (1993). The GJR-GARCH model is capable of capturing asymmetry and excess kurtosis in cases when data are not normally distributed.

The GJR-GARCH model makes use of the given form for conditional heteroskedasticity:

$${\sigma }_t^2=\omega +\left(a+\gamma {{\rm I}}_{t-1}\right){\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2$$

where

$$I_{t-1}=\left\{\begin{array}{c}0\mathit{if}{r}_{t-1}\ge \mu \\ 1\mathit{if}{r}_{t-1}<\mu \end{array}\right)$$

The GJR-GARCH model provides the empirically observed fact that negative shocks at time t − 1 have a stronger impact in the variance at time t than positive shocks. The observed asymmetry should be the leverage effect. The increase in risk is originated from the increased leverage induced by a negative shock. The generalized model to capture more lags has the following form [GJR-GARCH (p, q)]:

$${\sigma }_t^2=\omega +\sum _{i=1}^p\left(a+\gamma {{\rm I}}_{t-1}\right){\epsilon }_{t-1}^2+\sum _{j=1}^q\beta {\sigma }_{t-1}^2$$

The best lags can be chosen from the Akaike Information Criterion and the Bayesian Information Criterion. However, in nearly all cases, p = 1 and q = 1 best fit the data.

The second stage of the A-DCC estimation uses the residuals taken from the univariate GARCH models and transformed by their estimated standard deviations. Subsequently, the results are used to estimate the parameters of the conditional correlations for the A-DCC model. The A-DCC model estimates the conditional asymmetries in dynamic conditional correlations and explains the heteroskedasticity directly by estimating the correlation parameters using the standardized residuals from the first stage of estimation. In Engle's (2002) DCC model, the correlation matrix R_t in addition to the variance covariance matrix H_t are time varying and have the following decomposition:

$$H_t=D_t{R}_t{D}_t$$

where $D_t=\mathit{diag}\left\{\sqrt{h_{i,t}}\right\}$ is the diagonal matrix of the conditional standard deviations and R _t = {ρ _{ij, t}} the correlation matrix, which is time varying. The correlation matrix can also be denoted as:

$$R_t={\left(Q_t^{\ast }\right)}^{-1}{Q}_t{\left(Q_t^{\ast }\right)}^{-1}$$

$$\text{where}{Q}_t=\left[1-\alpha \left(1\right)-\beta \left(1\right)\right]\Gamma +\alpha \left(L\right){\eta }_{t-1}{\eta }_{t-1}^{\prime }+\beta \left(L\right)Q_{t-1}$$

Qt^⁎ is a diagonal matrix with a square root of the i ^th diagonal of Qt on its i ^th diagonal position. Namely, in the Q_t matrix, the model estimates the elements of correlations, which are calculated by the coefficients. Cappiello et al. (2006) presented a transformation of the original DCC model, which can capture asymmetries in the conditional variances, covariances and correlations of the time series. This asymmetric variation of the DCC model has the following form:

$$Q_t=\left(1-a-b\right)\overline{Q}-q\overline{N}+a{z}_{t-1}z{\prime }_{t-1}+b{Q}_{t-1}+g{n}_{t-1}n{\prime }_{t-1}$$

where α and β are the scalar parameters, g the asymmetry coefficient and $\overline{Q}$ and $\overline{N}$ are the unconditional correlation matrices of z _t and n _t. As presented in the literature review, the A-DCC model is suitable for quantifying the correlation and subsequently the dependence among stock market time series.

As the sample constitutes 51 countries, the correlation matrix for stock indices contains 1275 pairs to have each correlation for all possible combinations. All calculations were made in a bivariate case.

3.4. Financial networks

We transform the extracted correlations to distance metrics between each pair of indices as in Mantegna (1999):

$$d_{\mathit{ij}}^t=\sqrt{2\left(1-{\rho }_{\mathit{ij}}^t\right)}$$

Mantegna (1999) also mentioned that linkages between stock returns can be examined by applying a simple transformation of the elements of the correlation matrix of returns into distances. A connected graph is constructed in which the ‘nodes’ correspond to countries and the ‘distances’, or ‘edges’, between them are obtained from the appropriate transformation of the correlation coefficients. This formula fulfills the requirements of distance. Next, the N × N distance matrix is used to determine the Minimum Spanning Tree (MST), which is constructed using Kruskal's (1956) algorithm. Specifically, we utilize Kruskal's algorithm to construct a Minimum Spanning Tree (MST) to examine the extent and evolution of interdependence among indices. No matter the fact that the literature provides many others approaches to construct networks, the MST technique gives a reasonable explanation about how the correlations can be defined as distance measures (weights) within a network. A brief description of MST construction is proposed by Mantegna (1999):

• ➢Step 1. Regard each index as node and linkage effect as edge in a network. Consider each node as an isolated branch and sort the edges by their weights, which denote the degree of linkage effects among indices.
• ➢Step 2. Pass through the network once and search an edge with the minimum weight and ensure no closed loop is created. This edge is added to the minimum spanning tree set if all the requirements are met. Otherwise, continue to traverse the network to seek a next edge with the minimum weight.
• ➢Step 3. Recursively repeats the former steps, until n-1 edges have been identified (if the network has n nodes, the minimum spanning tree should have n − 1 edges since there are no closed loops in MST). Then, the searching process terminates, and the network's minimum spanning tree is obtained by selecting the most important correlations between the index returns.

After the construction of the financial networks, we extract the centralities to measure the most important countries inside the financial networks. We extract centralities on a daily basis to analyze their behavior. The constructed financial networks are 642 (daily data from 01 January 2018 until 18 June 2020). We tracked the centralities of networks and observed and analyzed their behavior thereafter. We repeat the procedure for second and third highest centrality scores of all categories. We used the most well-known centrality types of the literature as we assume, they are sufficient to extract accurate and reliable results about the most important nodes of the financial networks. The centralities used in this paper are betweenness, degree, eigenvector and closeness.

3.4.1. Betweenness centrality

Betweenness centrality measures the number of times a node behaves as a bridge between two other nodes whose path passes through it. The betweenness centrality index can be represented as

$$C_B\left(n_i\right)=\sum _{f<d}\frac{g_{\mathit{fd}}\left(n_i\right)}{g_{\mathit{fd}}}$$

where g _fd is the total number of shortest paths from f to node d and g _fd (n _i ) is the number of those paths that pass through n _i. The standardized version is calculated as

$$C_B^{\prime }\left(n_i\right)=\frac{C_B\left(n_i\right)}{\left[\left(g-1\right)\left(g-2\right)/2\right]}$$

Simply put, a central node is between two other (or more) nodes that have not collaborated/interacted with each other but have connected with the central node.

3.4.2. Degree centrality

Degree centrality measures the links to which the node is connected. In other words, degree centrality measures the number of times an author (or institution or country) interacted with other authors. The degree centrality of a network is as follows:

$$C_D=\frac{\sum _{i=1}^g\left[C_d\left(n^{\ast }\right)-C_d\left(n_i\right)\right]}{\left[\left(g-1\right)\left(g-2\right)\right]}$$

The C _d (n _i ) in the numerator are the g nodes degree indices, while C _d (n ^⁎ ) is the largest observed value. However, eigenvector centrality measures a node's influence over other nodes within the network.

3.4.3. Eigenvector centrality

For a given network, if vertex i is linked to vertex j and R _ij is the adjacency matrix, the eigenvector centrality is calculated by the eigenvector equation λe = Re and is expressed as

$$e_i=\frac{\sum _J{R}_{\mathit{ij}}{e}_j}{\lambda }$$

where e is the eigenvector of R _ij and λ the associated eigenvalue. The eigenvalue is a constant required so that the equations have nonzero solutions. Various eigenvalues exist for which an eigenvector solution also exists. Despite this, only the greatest eigenvalue outcomes in the preferred centrality measure. It's appropriate to assume that only the largest eigenvalue λ is the needed measure to quantify the eigenvector centrality (Bonacich, 1987). Nodes with high eigenvector centrality are nodes that are connected to several others, which are at their own end also connected to several more.

3.4.4. Closeness centrality

Finally, closeness centrality has to do with the shortest paths and is outlined as the range of collaboration in terms of connected nodes. The closeness centrality C _c of a node n is defined as

$$C_c={\left[\frac{\sum _{J=1}^{N}d\left(n_i{n}_j\right)}{N-1}\right]}^{-1}$$

where d(n _i n _j) is the length of the shortest path between two nodes n _i and n _j. The closeness centrality of each node is a number between 0 and 1. The higher a node's closeness centrality is, the lower its distance is to every connected node. More detail on social network analysis and centralities can be obtained from Wasserman and Faust (1994).

3.5. Contagion risk specification

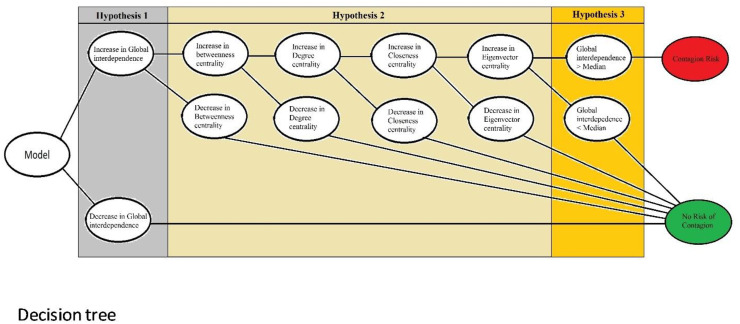
During the next stage, we create a hypothesis to find out whether the likelihood of contagion risk exists within the network as per the data available for daily correlations, alongside data on corresponding centralities. The outcome shows that we found a rise in centralities in the same spots where correlations of all cases were found in the first, second and third highest centralities. At the same time, the dates of the rise have to be linked to the pandemic and the lockdown. In specific, the dates where the global economy experiences spikes or extensively heightened instability – as shown in Fig. 3. The significant rise in correlations is indicative of the fact that there is a significantly large amount of interdependence, and there is also a higher likelihood of financial contagion being present in the given date range. We strongly advocate that there is a connection between countries' correlations and the extracted centralities of the financial networks. This connection triggers dynamics of contagion risk from the key node players. To put it more clearly, we assume that the structure of the networks favors the appearance of contagion when we have a simultaneous increase in already high correlations and the centralities. To answer this assumption, we use hypotheses that suggest that contagion risk exists inside the network when all the following Hypotheses are fulfilled:

• ➢

  Hypothesis 1

  Increase in correlations (global interdependence), otherwise no risk of contagion.

• ➢

  Hypothesis 2

  Rise in all the given segments for centrality, otherwise no risk of contagion.

• ➢

  Hypothesis 3

  The correlation has a higher value than the median (nodes with values smaller than the median are not as well connected than those with the opposite.

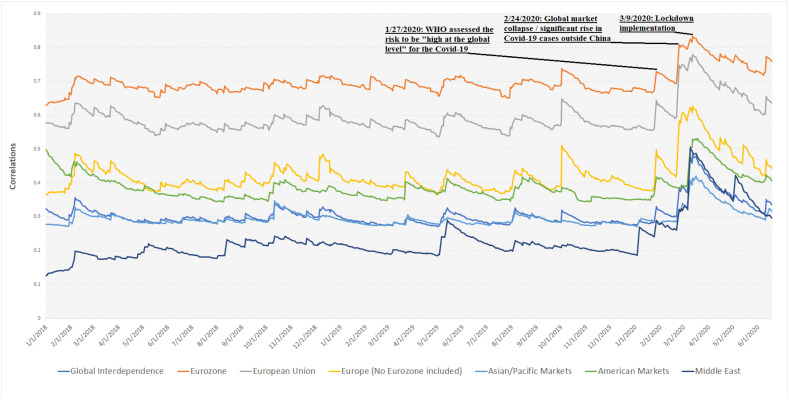
Fig. 3.

Global Interdependence (Asymmetric – Dynamic Conditional Correlations).

Notes: Time series asymmetric dynamic conditional correlations from 1/1/2018 till 18/6/2020. The dynamic conditional correlation matrix contains 1275 correlations (for 51 countries) and it is grouped by the geolocational position of its country.

For all other cases, we are of the view that the likelihood of contagion risk does not exist in the networks. A diagram explaining the model and our hypotheses can be observed through Fig. 2 .

Fig. 2.

Contagion risk specification.

4. Empirical results

Fig. 3 demonstrates how correlations grouped by their location – in this case geographic regions – have evolved. There was an instant increase observed in correlations related to Covid-19 and lockdowns throughout the period chosen. The most important outcome to be noted here is that correlations increased dramatically the critical dates of Covid-19 (1/27/2020: WHO addressed Covid-19 as global threat, 2/24/2020: significant rise in Covid-19 cases outside China and 3/9/2020: lockdown implementation started globally). Also, the regional correlations in question exhibit nearly identical behavior. This is a clear indication that, despite possible differences in the timings of preventive measures, the market dynamics share similar behaviors where conditional correlations can be observed. The entire duration studied in the data in this study has the same behaviors prevalent throughout.

Fig. 4 outlines the financial networks' structural data. In particular, the networks that were acquired from the median correlations of the complete sample every time (before / after lockdown and whole sample). Starting from the main network, it is clear that the topological composition of the financial networks is fairly near the actual country location. In specific, the connected countries or the correlations are more linked to neighboring units/countries as opposed to other units/countries in the entirety of the networks under study. An example of this is the Eurozone, where all countries are connected. Similarly, the same can be observed in American and Asian countries. This helps us see that the developed networks can be interpreted through a substantial portion of the real location where the markets exist. This evidence confirms the quality and veracity of our model and helps act as a robustness test for the financial networks that were extracted. The topological framework provides a logical elaboration of how the network connectivity manifests in the cases under discussion. This correlation behavior is based on issues within the neighborhood; substantial state and commercial transactions shared by countries, add to worldwide exports and imports. Nevertheless, in terms of the network's after lockdown became a reality globally, we observe that connections were differentiated compared to the network before the lockdown. This behavior can be explained due to the large volatility in the second period. Extensive uncertainty due to the Covid-19 pandemic crisis triggered strong volatility to stock markets resulting in allocations in the connectedness of the network after the lockdown.

Fig. 4.

Financial Networks before/after lockdown and main network.

Notes: Financial networks of stock markets. The networks were constructed by average correlations which transformed into network weights (distance measure). The connections of the network severely affected by the lockdown as can been observed from the figure (upper right). Extensive volatility impacted the correlations all over the world.

In terms of characteristics, Europe and the Eurozone are typically thought to connect with Asia and America across many countries within all the networks. In specific, as discussed earlier, the correlations' conversion, in terms of network distance, provide a geographical structure that's similar to the actual geolocation of the countries and their neighborhoods. In the same manner, evidence pertaining to properties of topology were observed in the works of Kanter et al. (201) and Eryigit and Eryigit (2009). It is pertinent to note that these findings revolved around a separate form of financial network set altogether. One significant element in the network analysis that we identified the fact that indices that come from the same region will naturally come together. This helps support and give evidence that stock market indices synchronize and exhibit clustering behavior that conforms to their locational properties. It also confirms that the network depicts the actual economic scenario empirically and theoretically. In simple words, a greater clustering impact is observed between indices that are from a related region as opposed to those with diverse regions. Furthermore, counties in the Eurozone share a currency, which means that their connection is considerably weighted, and a substantially high correlation can be observed therein. This aspect can be corroborated for all the networks under study, before the lockdown took place and after it did.

Table 2 depicts the centrality rankings that each country holds with respect to stock networks. The overall weighted financial network of stocks can be observed through Figs. 5, 6, and 7 in the supplementary online appendix. The same figures also depict their corresponding centrality. Germany and France seem to be the most central countries followed by Hong Kong. For France, we can see that this is the same as the work of Kantar et al. (2011), Gilmore, Lucey, and Boscia (2008) and Eryigit and Eryigit (2009). In Europe, and particularly the Eurozone itself, countries become central nodes and dominate the networks. Here, we observe a joint distribution that aligns with Asian and American markets. In the same vein, Qiao et al. (2015)’s work found similar evidence of such a network center.

Table 2.

Centrality rankings.

	Main Network				Before Lockdown				After Lockdown
	Degree	Closeness	Betweenness	Eigenvector	Degree	Closeness	Betweenness	Eigenvector	Degree	Closeness	Betweenness	Eigenvector
1	France	Germany	Germany	France	France	Germany	France	France	Germany	Germany	Germany	Germany
2	Germany	South Africa	France	Germany	Germany	France	Germany	Germany	France	France	France	France
3	Hong Kong	France	Hong Kong	Peru	Hong Kong	South Africa	Hong Kong	USA	Hong Kong	South Africa	Hong Kong	Sweden
4	Japan	Hong Kong	South Africa	Belgium	USA	Hong Kong	South Africa	Belgium	UK	Sweden	South Africa	South Africa
5	Sweden	Sweden	South Korea	USA	Sweden	Sweden	Taiwan	Netherlands	Canada	Netherlands	Netherlands	Netherlands
6	South Africa	Portugal	Malaysia	UK	Netherlands	Belgium	Belgium	Peru	Netherlands	Belgium	Sweden	Belgium
7	Philippines	Greece	Philippines	Italy	Saudi Arabia	USA	USA	Spain	Sweden	USA	Norway	Poland
8	Peru	Ireland	Taiwan	Mexico	Taiwan	Netherlands	Singapore	Switzerland	Belgium	Poland	Belgium	USA
9	USA	Romania	Indonesia	Netherlands	Belgium	Poland	Sweden	Sweden	Austria	Italy	UK	Italy
10	UK	Peru	Japan	Switzerland	Singapore	Ireland	Netherlands	South Africa	UAE	Ireland	USA	Ireland
11	Italy	Poland	UAE	Spain	Philippines	Portugal	Malaysia	Hong Kong	Singapore	Romania	Israel	Romania
12	South Korea	Belgium	Sweden	South Africa	Peru	Peru	Peru	Poland	Peru	Portugal	Canada	Portugal
13	Mexico	South Korea	Peru	Sweden	China	Spain	Saudi Arabia	Ireland	USA	Hong Kong	Singapore	Greece
14	Indonesia	USA	Belgium	Portugal	Japan	Switzerland	Philippines	Portugal	Japan	Greece	Saudi Arabia	Spain
15	Netherlands	UK	Egypt	Greece	UK	Taiwan	South Korea	Canada	South Korea	Spain	Austria	Mexico
16	Saudi Arabia	Italy	Portugal	Ireland	Canada	Singapore	Austria	Brazil	Indonesia	Mexico	Peru	Hong Kong
17	Switzerland	Mexico	Greece	Romania	South Korea	South Korea	Spain	Mexico	Saudi Arabia	Norway	UAE	UK
18	Taiwan	Netherlands	Poland	Hong Kong	Spain	China	Switzerland	Austria	Switzerland	UK	South Korea	Norway
19	Poland	Switzerland	USA	Austria	Switzerland	India	China	Greece	Taiwan	Finland	Poland	Austria
20	Belgium	Spain	UK	Argentina	Austria	Austria	Greece	UK	Poland	Switzerland	Greece	Switzerland
21	Austria	Taiwan	Italy	Chile	Malaysia	Greece	Canada	Turkey	Argentina	Canada	Switzerland	Canada
22	UAE	China	Mexico	Brazil	South Africa	Norway	UK	Colombia	Norway	Austria	Taiwan	Finland
23	Malaysia	India	Netherlands	Canada	Vietnam	Israel	Vietnam	Chile	Israel	Singapore	Argentina	Turkey
24	Egypt	Singapore	Switzerland	Turkey	Czech Republic	Finland	Japan	Italy	South Africa	Turkey	Indonesia	Thailand
25	Portugal	Malaysia	Austria	Norway	Greece	Canada	Czech Republic	Denmark	Greece	Thailand	Japan	Singapore
26	Greece	Israel	Saudi Arabia	Denmark	India	UK	Poland	Norway	China	South Korea	Italy	New Zealand
27	China	Finland	Ireland	Colombia	Italy	Brazil	Ireland	Israel	India	Taiwan	Ireland	South Korea
28	India	Russia	Romania	Poland	Brazil	Mexico	Portugal	Finland	Italy	China	Romania	Taiwan
29	Brazil	New Zealand	Spain	Israel	Russia	Turkey	India	Taiwan	Brazil	India	Portugal	China
30	Canada	Austria	China	Finland	Australia	Colombia	Norway	Singapore	Russia	New Zealand	Spain	India
31	Russia	Argentina	India	New Zealand	Mexico	Chile	Israel	South Korea	Spain	Israel	Mexico	Peru
32	Spain	Chile	Singapore	Russia	Indonesia	Italy	Finland	China	Australia	Peru	Finland	Israel
33	Australia	Pakistan	Israel	Taiwan	Turkey	Denmark	Brazil	India	Mexico	Russia	Turkey	Russia
34	Turkey	Brazil	Finland	South Korea	Poland	Malaysia	Mexico	Argentina	Turkey	Argentina	Thailand	Argentina
35	Thailand	Canada	Russia	China	Thailand	Vietnam	Turkey	Czech Republic	Thailand	Denmark	China	Pakistan
36	Nigeria	Turkey	New Zealand	India	Nigeria	Saudi Arabia	Colombia	New Zealand	Nigeria	Nigeria	India	Czech Republic
37	Argentina	Norway	Argentina	Singapore	Argentina	Thailand	Chile	Russia	Ireland	Pakistan	New Zealand	Denmark
38	Norway	Denmark	Chile	Czech Republic	Norway	Japan	Italy	Saudi Arabia	Malaysia	Czech Republic	Russia	Nigeria
39	Israel	Colombia	Pakistan	Pakistan	UAE	Pakistan	Denmark	Malaysia	Philippines	Indonesia	Denmark	Indonesia
40	Ireland	Japan	Brazil	Japan	Israel	Czech Republic	Thailand	Vietnam	Denmark	Japan	Nigeria	Malaysia
41	Singapore	Philippines	Canada	Malaysia	Ireland	New Zealand	Pakistan	Thailand	Colombia	Malaysia	Pakistan	Japan
42	Denmark	Czech Republic	Turkey	Thailand	Denmark	Argentina	New Zealand	Japan	Bangladesh	Vietnam	Czech Republic	Vietnam
43	Colombia	Australia	Norway	Australia	Colombia	Russia	Argentina	Pakistan	Egypt	Saudi Arabia	Malaysia	Colombia
44	Bangladesh	Thailand	Denmark	Vietnam	Bangladesh	Philippines	Russia	Romania	Chile	Colombia	Vietnam	Chile
45	Chile	Vietnam	Colombia	Philippines	Egypt	Bangladesh	Bangladesh	Philippines	Pakistan	Chile	Colombia	Saudi Arabia
46	Pakistan	Indonesia	Czech Republic	Indonesia	Chile	UAE	UAE	UAE	Finland	Brazil	Chile	Brazil
47	Finland	Nigeria	Australia	Nigeria	Pakistan	Egypt	Egypt	Egypt	Vietnam	Philippines	Brazil	Philippines
48	Vietnam	UAE	Thailand	UAE	Finland	Australia	Australia	Bangladesh	Czech Republic	Australia	Philippines	Australia
49	Czech Republic	Egypt	Vietnam	Egypt	Romania	Romania	Romania	Australia	Romania	UAE	Australia	UAE
50	Romania	Saudi Arabia	Nigeria	Saudi Arabia	Portugal	Indonesia	Indonesia	Indonesia	Portugal	Bangladesh	Bangladesh	Bangladesh
51	New Zealand	Bangladesh	Bangladesh	Bangladesh	New Zealand	Nigeria	Nigeria	Nigeria	New Zealand	Egypt	Egypt	Egypt

Notes: The four most common measures of centrality (Degree, Closeness, Betweenness and Eigenvector) were used to depict and reveal the most central economies during the Covid-19 pandemic crisis. Rankings categorized by before/after lockdown and the main network for the whole sample. The higher the ranking is, the more influence has the country in the network.

Interestingly, South Africa and Sweden appear higher in the centrality rankings than, for example, the USA and the UK. We consider this finding as stemming from the nature and methodology MST formulation. MST construction is based on considering each node as an isolated branch and then sorting the edges by their weights, which denote the degree of linkage effects among indices. As the algorithm does not allow closed loops, considering the included sample and the correlations between the nodes, this (intuitively unexpected) outcome can be considered as a limitation of the MST algorithm.

Figs. 9 to 32 in the supplementary online appendix show the dynamic evolution of the centralities across time for the first, second and third highest central country each time. In addition, we provide the corresponding frequency of the most central countries in first, second and third position across the sample for all networks. As far as the dynamic presence of the frequency of the countries, for all centralities, France, Germany and Hong Kong seem to dominate their appearance in the first, second and third and most central positions; they seem to be the most central and most important core nodes for the global financial markets network (not only in the main network but also before and after lockdown periods).

Moreover, the dynamic evolution of the network structure shows that the network experiences a relative stability over a given time period. Specifically, the Eurozone has the most central nodes and they are extremely connected or correlated to several other indices. This can be attributed to significant posts of European corresponding countries. By virtue of this, they have a significant, crucial part in stock networks and can consistently project substantial influences on the propagation of fundamental shocks in the global financial environment. As a result, regulators and investors need to remain aware that during the Covid-19 pandemic crisis period, the central nodes in the stock network merit increased attention as the major permanent source of risk contagion in the vast universe of equity markets, despite the perspective of financial risk supervision or earnings pursuit. That said, eye-catching changes have taken place in the network during three exceptional observations/days: the 1/27/2020 where WHO announced the high risk in a global level for the Covid-19, the 2/24/2020 where new cases appeared all over the world causing significant negative shock to markets and the 3/9/2020 where countries started imposing curfew and lockdowns. We believe that this can be attributed to the increased uncertainty following these events. We note that interdependence relationships in the network strengthened substantially, suggesting that variation of co-movements may originate, at least in part, from the contagion effect of influential pandemic crisis in reality. Increased correlations are a clear sign of significant presence of interdependence, resulting in higher likelihood of financial contagion in the given date range. There is thus a connection between countries' correlations and the extracted centralities of the financial networks. This connection triggers volatility and dynamics of contagion risk from the key node players, since we assume that the structure of the networks favors the appearance of contagion when we have a simultaneous increase in high correlations and centralities.

Figs. 9–32 depict the most important evidence, which essentially shows that there is a global interdependence present and correlations are volatile alongside centralities that have similar instability. In specific, the correlations have substantial shocks because of the pandemic, and this leads to substantial volatility for all centralities. The pattern is the same for the second and third most central nations within all categories of networks. Furthermore, the larger the shock of the correlation is, the higher the volatility in centralities becomes. This is true for all networks and centralities.

Based on this evidence and as demonstrated in the methodology, we develop hypotheses to see if a contagion risk exists within the network. The results of said risk specification within the complex networks of stocks can be observed in Fig. 8 . The results prove that our hypothesis is accurate, since they show that contagion risk is present during the dates we studied. There was a substantial rise seen in centralities and correlations. In specific, in many cases where we saw a serious hike in correlations, we also found a larger likelihood of contagion risk. In addition, it can be easily observed that there is significant risk of contagion on the dates related with the Covid-19 pandemic crisis (1/27/2020, 2/24/2020 and 3/9/2020).

Fig. 8.

Contagion risk specification.

Notes: Time series asymmetric dynamic conditional correlations from 1/1/2018 till 18/6/2020. The red vertical lines denote the presence of contagion risk specified by the decision tree and the hypotheses.

The evidence shows that we can now use additional methods instead of dynamic conditional correlations to quantify the risk of financial contagion inside the financial networks of markets. The overall methodological approach contributes to the existing literature, giving motivation for further research into this particular field in finance and the spillover effects in networks during the Covid-19 pandemic crisis. In addition, this paper clarifies the asset pricing mechanism of the stock market during the Covid-19 period. Although stock market networks have been extensively explored, we have extended this line of study to the effects of network topological properties on stock returns. Our model indicates that dynamic correlations and centralities tend to keep pace together, thereby representing evidence that future stock returns are significantly affected by the extent of the increased interdependence for a given stock in the concerned equity markets. In fact, the closeness for a stock represents the degree of its inherent correlation risk. More specifically, the stock index with the most connections to its network obtains the largest expected returns among the central nodes, while the stock that is most influenced by its ‘hub’ obtains larger risk premium among periphery nodes. From the perspective of trade factors, stock market investors tend to be risk averse, and this tendency magnifies during crisis periods. In addition, investors require high returns for those assets posited at the center of the network structure as a premium for the magnified contagion risk. In this way, network co-movement plays a critically important role in determining the asset pricing mechanism and deserves a positive risk price. This evidence is also in line with Qiao et al. (2016) and Samitas et al. (2020).

The findings of this paper are important because similar work focusing on financial networks in terms of network topology metrics, keeping Covid-19 in mind, has not been produced. The methodology we have chosen gives important insights for the construction of a diversified portfolio or risk management in terms of topological placement within stock networks. In specific, investors may bring down the number of investments when portfolio allocations are being made for highly related assets, and they can instead turn their attention to trends and patterns of regionally linked countries. Therefore, the proposed method gives useful insights into the implications that can help regulators and investors analyze stocks in a better fashion. It also shows that they need to place special focus on the ‘nucleus’ nodes as opposed to keeping an eye on every single one within the network. These findings are also in line with earlier work produced by Qiao et al. (2016) and Samitas et al. (2020).

The Covid-19 pandemic has increased at an alarming rate with massive impact on the global economy and consequently, academics, researchers, policy makers, and industry professionals are emphasizing on understanding its direct as well as indirect impacts on the overall global economy. In this research, the effects of Covid-19 have been studied and analyzed in multidimensional framework. The findings indicate that because of this global pandemic, the global economy has come under recession, affecting different countries worldwide irrespective of adopting strategies to minimize it effects. The findings of the research demonstrate that a global integrated approach is required to tackle the Covid-19 pandemic.

The global pandemic is considered to be first of its kind, which has been responsible for disrupting the entire global supply chain networks and supply and demand. In terms of supply, covid-19 is responsible for affecting the supply of products, goods and services, loss of labors, loss of organizational performance and productivity, while at the same time, it social distancing and lock downs are responsible for affecting the overall business activities and processes. In terms of demand, unemployment rates have increases significantly, while business and household incomes have decreased. Through this global pandemic, both businesses and consumers have been affected, which have resulted in financial losses, high unemployment rates, and significant loss of investments. In terms of empirical investigation pertaining to Covid-19's economic analysis, the focus is on its non-linear impacts, cross-country spillovers, and risks associated with it because of its varying nature.

The synthesis of current literature demonstrates that recessions have significant impact on GDP. This is because the demand and supply sides are disrupted by the cyclical shocks through various mediums. The impacts of these shocks have been identified as long-term trends. Because of the unpredictable nature of Covid-19, its impacts on the global economy cannot be predicted easily. Evaluation of the existing effects of the pandemic might help in understanding its impact to reach suitable conclusions, it is still difficult to predict them. The European Central Bank stated that pandemics like Covid-19 have short-lived effects, which disappear after a period of two years. This statement was made based on past pandemics. However, Covid-19 pandemic cannot be compared with past pandemics because of its unpredictable nature and its influence on the overall global economy, leading to significant negative outcomes at macroeconomics level.

The fluctuations in the global economy are further complicated by factors such as lack of investments due to risks and uncertainty conditions, increasing cost associated with raising capital, and high levels of precautionary savings. Global recession has increased because of Covid-19, which has significantly increased global volatility. We had conducted a country-by-country analysis, which indicates that global volatility is an important concept in terms of output growth.

Our findings indicated that spillovers effect has been observed in all the cases subjected to analysis, regardless the different policies being adopted to manage the pandemic. Evidence suggests that no economy is immune to the negative outcomes of Covid-19 and therefore, it has been classified as global shock.

The results of our analysis demonstrate that Covid-19's negative impacts are evident throughout the global economy. Both US and Europe have experienced the negative consequences of the pandemic, which highlight that the entire global economy is under its threat. As compared to Asian markets, Non-Asian markets are more vulnerable to the pandemic. The findings indicate the need and adoption of global monetary and economic policy to manage the negative outcomes of Covid-19 pandemic. Policies should also focus on efficient deployment of medical resources such as vaccines and medications, while at the same time, restoring the functionality of international financial markets. An international risk management system needs to be identified to reduce the negative outcomes of the pandemic. These endeavors can be beneficial in reducing the negative outcomes of Covid-19 on the global economy. In the meantime, the research in this paper tries to assist investors and policymakers to better prepare for the challenging issues of the pandemic.

5. Conclusions

The pandemic crisis of Covid-19 sparked a renewed interest in crisis forecasting models. It further reemphasized the financial interconnectedness of markets, and the likelihood of there being risk of financial contagion. This paper seeks to isolate contagion and spillover evidence by demonstrating that data from stock indices is conveyed from one country to another country (or multiple countries) in a negative manner within a financial network developed through correlations during the Covid-19 period and implied lockdowns. To study the correlations' interdependence ratio, we made use of daily data returns. Major stock indices were used from every country sampled from several regions, including European Union, Eurozone, Europe, the Americans, Asia, Middle East and Africa. The sample data looked at stock indices from 51 economies. These were chosen through the size of their GDP3 and as per the best possible data available. An Asymmetric Dynamic Conditional Correlation (A-DCC) model was applied on a bivariate basis for the purpose of this research. In the second step, we transformed the acquired correlations to distance metrics shared between each country pair with Mantegna (1999)’s work. The third step involved extraction of the distance metrics to develop financial networks through Kruskal (1956)’s Minimum Spanning Tree (MST) algorithm. In the fourth step, we extracted centralities from the daily financial networks that were developed, including the degree, betweenness, eigenvector and closeness observed every day. This was done to find the countries that were the most important key nodes. In specific, we examine daily centralities keeping Covid-19 in mind, specifically the lockdowns that took place globally. By keeping an eye on centralities on a daily basis we are aiming to quantify the behavior patterns of the key players i.e. the countries that are the first, second and third place in each category of centrality. After this we define a final hypothesis through which we will assess the contagion risk. The hypothesis that we settled on is as follows: a rise in global interdependence correlations, a rise in all centralities, and the correlation is much higher than the median value. That is, the nodes with values lower than the median are not as connected as those with higher values. In all other cases, the study shows that no likelihood of contagion exists within the networks.

Our results are significant because they help outline the likely financial contagion that plagues financial networks in the time that Covid-19 has become more and more relevant. In terms of the stock indices' correlations, an immediate rise is linked to financial turbulence throughout the time period. Furthermore, all correlations in the same region exhibit the same behavior; this is especially true for the Eurozone, Asian and American markets. The fact that they all operate at different hours does not cause any impact on regional interdependence. On the other hand, where financial networks were under consideration, the financial networks' topological structure appeared fairly similar to the actual location of the nodes (countries). For instance, Eurozone countries were observed to be connected, as were countries located in North or South America. The same phenomenon was observed in Asian countries. The financial networks were interpreted through a substantial portion of the real location of these markets. Long before and after the lockdowns took place, networks' connectivity did not change significantly. This evidence can verify the significance of our model and work as a robustness test for the extracted financial networks. This behavior of the correlations seems to be neighborhood driven in that transactions between countries contribute to global imports and exports. In addition, the Eurozone countries that have a common currency show a strong weighted connection to a significant extent, and they depict remarkably high correlations in the entire sample. France and Germany seem to be the most central countries followed by Hong Kong. A small sub-group of ‘old’ EU markets, sharing high levels of development and/or close geographical proximity, has consistently constituted the most tightly linked set of markets. The Eurozone dominates the networks and acts as a joint distribution with the American and the Asian markets. Additionally, as far as the dynamic presence of the frequency of the countries is concerned, for all centralities in the networks of stock indices, again France, Germany and Hong Kong seem to be the most central and most important core nodes for the global financial markets network during the pandemic crisis of Covid-19 (both before and after lockdowns). The most significant evidence from financial networks is that the volatility of the correlations (global interdependence) largely follows the volatility of the centralities where significant shocks in the correlations trigger huge volatility in all centralities (specifically during the exceptional observations/days of Covid-19). Based on this evidence we use hypothesis testing to determine the possibility of contagion risk inside the network. The results verify the presence of contagion risk on the dates where we observe a significant increase in the correlations (global interdependence) and centralities.4 This verifies that our approach is highly effective in identifying and predicting contagion inside financial networks. This evidence allows us to expand the literature and use additional methods instead of dynamic conditional correlations to quantify the risk of financial contagion inside the financial networks of markets.

The framework created here adds to existing literature and helps enrich our capacity to empirically comprehend and quantify contagion and spillover data during Covid-19, with regards to stock indices that are negatively transferred from one country to one or more countries that exist within the same financial network, which was earlier developed through correlations. Resultantly, our model gives considerable data that can prove useful not just for institutions or policymakers but also investors. They can use this information on understanding how contagion risk can manifest within a financial network in the context of a crisis that is at a pandemic level. This paper's most important contribution is using the financial market network as a device to help augment portfolio selection by focusing on an asset group based on its centrality. Furthermore, the outcome is significant because it allows for more robust policymaking which in turn helps develop stock markets. This is useful for not just practitioners but academics as well. This analysis can also be used by regulators that are working on surveilling the core nodes to make sure that the entire market remains stable. Investors can use it to improve their portfolio allocations and make better investment decisions. This paper's methodology can be used to further research in many areas. One direction that we plan to go into is to look at the expansion of our parameters and come up with more modern econometric approaches. The models can be deployed for the efficient measurement in time series, while using dummy variables on dependence aspects, keeping the daily financial network framework intact for the purpose of crosschecking findings and producing more irrefutable data that can assist economies against the Covid-19 and its consequences.

A possible way forward for future research could be to investigate changes in the pattern of centrality rankings following pandemic (or other crisis) news, where studies could focus on more crises than the Covid-19 pandemic. Indeed, it could be useful to examine the different market responses to other crises in the recent history, whether health or financial in nature. As the research of volatile and contagion using financial network is still a developing issue, we believe that significant contributions can be achieved by further studies on this topic, both in term of methodology and theoretical interpretation.

Appendix A. Supplementary data

Supplementary material