Skip to main content
NCBI home page
Journal of Peking University (Health Sciences) logoLink to Journal of Peking University (Health Sciences)
. 2021 Sep 8;53(6):1163–1170. [Article in Chinese] doi: 10.19723/j.issn.1671-167X.2021.06.026

基于机器学习的重症监护室超长入住时长预测

Predicting prolonged length of intensive care unit stay via machine learning

吴 静依 1,2, 林 瑜 1, 蔺 轲 1, 胡 永华 1,3, 孔 桂兰 2,4,*
PMCID: PMC8695140  PMID: 34916699

Abstract

目的

基于三种机器学习算法——支持向量机(support vector machine，SVM)、分类回归树(classification and regression tree，CART)和随机森林(random forest，RF), 构建重症监护室(intensive care unit，ICU)患者的ICU入住时长(length of ICU stay，LOS-ICU)分类预测模型，并与传统的定制版简化急性生理功能评分Ⅱ(simplified acute physiology score Ⅱ，SAPS-Ⅱ)模型进行比较。

方法

使用美国大型重症医疗数据库(medical information mart for intensive care Ⅲ，MIMIC-Ⅲ)，以ICU患者是否发生超长LOS-ICU(prolonged LOS-ICU，pLOS-ICU)作为结局指标，构建定制版SAPS-Ⅱ、SVM、CART和RF模型，使用递归特征消除法进行特征选择，基于五折交叉验证找出最佳预测模型。模型的预测性能评价指标包括Brier评分、受试者工作特征(receiver operation characteristic，ROC)曲线下面积(area under the ROC curve，AUROC)和估计校准度指数(estimated calibration index，ECI), 模型性能指标之间的比较使用双侧t检验。使用本研究中预测性能最好的模型识别出来的各预测变量重要性排序结果，给出重要性排序前五位的预测变量。

结果

最终共纳入40 200例ICU患者，发生pLOS-ICU的患者23.7%。其中，男性患者57.6%，患者平均年龄为(61.9±16.5)岁。五折交叉验证结果显示，相比于定制版SAPS-Ⅱ模型，三种机器学习模型的预测性能在各个指标上均有明显提升，且差异均具有统计学意义(P < 0.01)。其中，RF模型在综合预测性能、区分度与校准度三个方面均表现最优，其Brier评分、AUROC和ECI分别为0.145、0.770和7.259。校准曲线结果显示，在高pLOS-ICU发生风险的ICU人群中，RF模型倾向于略微高估其风险；在低pLOS-ICU发生风险的ICU人群中，RF模型倾向于略微低估其风险。基于性能最优的RF模型识别的对pLOS-ICU预测最重要的五个变量依次为年龄、心率、收缩压、体温和动脉血氧分压与吸入氧分数之比。

结论

基于机器学习构建ICU患者的pLOS-ICU预测模型相比于传统的定制版SAPS-Ⅱ模型，预测性能均有明显提升，其中，基于RF方法的pLOS-ICU预测模型性能最优，具有很大的临床应用潜力。

Keywords: 重症监护室, 住院时长, 机器学习, 随机森林, 简化急性生理功能评分

重症监护室(intensive care unit，ICU)是为医院内危重患者提供持续护理、密切监测以及最优化医疗支持的医疗场所。ICU患者病情严重程度较高，常见的病症包括呼吸窘迫综合征、创伤、多器官衰竭和败血症等[1]。由于ICU对医疗设施和医疗人员都有严格的质量要求，在经济水平较低的地区，ICU资源往往供不应求[2]。因此，如何根据患者病情严重程度合理做出医疗干预，以提高医疗效率并改善患者预后就显得尤为重要。

ICU入住时长(length of ICU stay，LOS-ICU)是判断患者病情严重程度、评价医院医疗卫生资源利用效率的有效指标[3]。研究表明，临床医师很难在患者入住ICU初始阶段准确地预测患者的LOS-ICU[4]。因此，利用历史累积的ICU临床数据，识别影响患者LOS-ICU的重要因素，构建有效的LOS-ICU预测模型，可以辅助临床医师对ICU患者进行危险度分层，做出合适的临床干预并合理安排医疗资源，这对提高医疗质量并改善患者预后至关重要。简化急性生理功能评分Ⅱ(simplified acute physiology score Ⅱ，SAPS-Ⅱ)[5]、急性生理学和慢性健康状况评分Ⅳ(acute physiology and chronic health evaluation Ⅳ，APACHE-Ⅳ)[6]等ICU常用的危重症病情评分系统是量化患者病情严重程度最常用的手段之一。目前已有一些研究基于上述危重症病情评分系统进行改良，构建定制版的危重症病情评分系统用于预测患者的LOS-ICU[7-8]。然而研究结果表明，这类定制版的LOS-ICU预测评分系统的预测准确性有限。近年来，数据挖掘技术与机器学习模型不断发展，并在多种不同的医疗决策支持领域表现出优良的预测性能[9-10]，这为开发新的LOS-ICU预测模型提供了方法支持。另外，随着医疗信息化程度不断提高，许多医疗信息得以实现电子化保存，这为构建LOS-ICU预测模型提供了可靠的数据支持。

本文以国外大型重症医疗数据库(medical information mart for intensive care Ⅲ，MIMIC-Ⅲ)[11]为数据源，基于三种机器学习模型：支持向量机(support vector machine，SVM)、分类回归树(classification and regression tree，CART)和随机森林(random forest，RF)，构建患者是否发生超长LOS-ICU(prolonged LOS-ICU，pLOS-ICU)的预测模型，并比较其与传统定制版SAPS-Ⅱ评分系统的预测性能。

1. 资料与方法

1.1. 数据来源

本研究基于美国大型公开重症医疗数据库MIMIC-Ⅲ[11]进行数据分析与模型构建。

1.2. 患者纳入与排除标准

纳入标准：年龄≥18岁且≤90岁的ICU患者。排除标准：院内死亡；LOS-ICU缺失；变量缺失率达30%及以上的ICU患者。对于单次住院期间多次入住ICU的患者随机抽取一条ICU入住记录。

1.3. 研究结局与预测变量

本研究的结局指标为二分类变量，即ICU患者是否发生pLOS-ICU。既往研究将ICU患者发生pLOS-ICU的界限值定义为LOS-ICU的第三四分位数(Q3)[12-13]，基于此，本研究中符合纳入标准患者的LOS-ICU的Q3值为4 d，即LOS-ICU超过4 d的患者定义为发生pLOS-ICU。

为了更加客观地比较三种机器学习模型(SVM、CART和RF)与传统定制版SAPS-Ⅱ评分系统的预测性能，本研究使用SAPS-Ⅱ中涉及到的所有变量作为构建SVM、CART与RF模型的基础特征集，再使用递归特征消除法(recursive feature elimination)[14]进行特征选择。本研究使用RF模型的预测性能作为特征子集的评价准则，向后逐步回归筛选特征，每一次迭代将变量重要性排在最后一位的特征去除，直至模型中仅剩余一个预测变量，最后在遍历的特征子集中选取使得RF模型的预测性能达到最优的特征子集作为最终预测变量集。基础预测变量包括：年龄，ICU入住类型(计划手术、非计划手术、无手术)，是否合并艾滋病、血液系统恶性肿瘤、转移癌，以及12项生理学指标[心率、收缩压、体温、动脉血氧分压与吸入氧分数之比(ratio of arterial oxygen tension to the fraction of inspired oxygen，PaO2/FiO2)、尿量、血清尿素氮水平、白细胞计数、血清钾水平、血清钠水平、血碳酸氢盐水平、血胆红素水平、Glasgow昏迷评分]。其中12项生理学指标取患者入住ICU后第一个24 h内的测量值，一些变量(如心率、体温等)为重复测量指标。在SAPS-Ⅱ模型中，对于只有唯一取值的变量(如年龄、性别等)，根据变量的取值赋予相应的分值；对于重复测量的变量，取患者入住ICU后第一个24 h内的最差值(最大值或最小值)，并赋予相应的分值[5]。在SVM、CART和RF模型中，对于唯一取值的变量，直接取该变量的原始值纳入模型；对于重复测量的变量，则提取患者入住ICU后第一个24 h内的最大值和最小值同时纳入模型。

1.4. SVM模型

SVM是20世纪90年代中期开发的一种有监督机器学习算法[15]。当数据集线性不可分时，SVM可通过映射函数ϕ(x)将线性不可分的数据从原始特征空间映射到一个更高维的特征空间，在高维空间中找到一个最佳的分隔平面(最大间隔超平面)，从而将不同类别的样本区分开来。给定包含N个样本点的训练数据集：D={(x1, y1), …, (x2, y2), …, (xN, yN)}，其中，(xi, yi)称为第i个样本点，xi∈Rn，yi∈{-1, 1}。SVM通过映射函数ϕ(x)将训练数据集D投射到更高维的特征空间。在高维特征空间，分隔超平面可表示为：wTϕ(x)+b=0，其中，w是和高维特征平面维数相同的法向量，b是误差项。距离分隔超平面最近的样本点称为支持向量，支持向量满足：Inline graphic。在高维特征空间，支持向量距离分隔超平面的距离R为：

1.4.

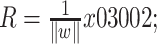SVM的学习目标是在投射后的高维空间内找到一个最大间隔超平面，使得支持向量到超平面的距离R最大。为了处理高维空间存在的爆炸性计算问题，SVM引入了核函数降低高维计算量。常用的核函数包括线性核函数、多项式核函数、径向基核函数和指数核函数。SVM模型在处理非线性可分、高维数据分类问题和泛化能力方面都表现出特有的优势[16]。

本研究中SVM模型的参数寻优结合五折交叉验证与网格搜索法。网格搜索法是指通过循环遍历给定的参数组合来实现参数寻优。最终采用的SVM模型的参数为：核函数为径向基核函数，惩罚因子C为100，核函数参数gamma为0.1，C和gamma共同控制SVM模型在训练集的拟合程度与泛化能力的平衡。

1.5. CART模型

CART是一种二分递归式的树状结构的决策树模型[17]。CART模型生成的决策树可解释性好，因此在临床决策中被广泛应用。CART模型的核心是通过计算信息增益选择决策树局部的最优划分特征建立决策节点，从而逐步构建决策树。一般来讲，一棵CART决策树包含一个根节点、若干个内部节点和若干个叶节点。其中，根节点包含样本全集，根节点与内部节点均为决策节点，每个决策节点对应于一个特征决策，每个叶节点对应于一种决策结果。CART算法采用二分递归分割算法，总是根据特征决策将当前样本集分割为两个子样本集，使得生成的决策树的每个非叶节点都只有两个分支，因此，CART算法生成的决策树是结构简洁的二叉树。

在每个决策节点，CART模型使用Gini指数减少量作为信息增益的度量指标来选择该节点的最优划分特征。若一个数据集D包含J个类别的样本，则该数据集D的Gini指数为：

1.5.

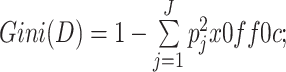其中，pj为第j个类别的样本在数据集D中所占的比例。若根据某个特征A将数据集D划分为两个子数据集D1和D2，则该特征A对应的Gini指数减少量S=Gini(D)-Gini(D1)-Gini(D2)。Gini指数减少量最大的特征将用于划分该节点。相比于传统的线性回归模型，CART模型不需要预测变量与结局变量满足复杂的关系假设，并且适用于处理预测变量与结局变量之间的非线性相关关系[18]。

本研究中CART模型的参数寻优结合五折交叉验证与网格搜索法。最终采用的CART模型的参数为：决策树最大深度为6，内部节点再划分所需最小样本数为200。

1.6. RF模型

RF是由Breiman[19]提出的基于树模型构建的一种常见的集成学习模型。集成学习通过综合多个弱分类器的分类结果，可进一步提升模型的性能。研究表明，集成学习模型的性能一般优于单个的基础分类器[9, 20-21]。RF使用决策树作为基础分类器，待分类样本的分类结果由所有相互独立的决策树的分类结果投票决定。RF的具体分类流程为：(1)训练样本随机采样：使用自助法(Bootstrap)在整个训练数据集D中重采样，随机产生K个训练子集D1, D2, …, DK，采样比例为1-[1-1/N]N，其中，N为整个训练数据集D的样本总数，当N趋向无穷时，采样比例约为2/3。(2)随机特征训练决策树：基于每个重采样训练子集训练一棵决策树，在决策树的每个节点，从所有M个特征中随机选取F个特征作为当前节点的特征子集，并以特征子集中信息增益最大的特征对该节点进行分裂，从而逐步构建决策树T1, T2, …, TK；决策树的生成依据信息增益最大化原则，常用的信息增益度量指标为Gini指数减少值。(3)决策树投票判别：采用投票法得到K个决策树中输出最多的类别作为待分类样本的分类结果。RF模型中的两次随机化过程——训练样本随机化和特征随机化，使得RF在处理高维数据问题时更有优势，也提供了更强大的泛化能力[22]。

本研究中RF模型的参数寻优结合五折交叉验证与网格搜索法。最终采用的RF模型参数为：决策树个数(K)为300，决策树每个节点选择的随机特征数量(F)为5，决策树最大深度为13。

1.7. 定制版SAPS-Ⅱ模型

SAPS-Ⅱ是Le Gall等[5]于1993年使用12 997例ICU患者的数据基于逻辑回归(Logistic regression，LR)算法开发的危重症评分系统。SAPS-Ⅱ模型由两部分组成：SAPS-Ⅱ评分和概率计算。SAPS-Ⅱ评分由17项变量构成，每项变量依据患者情况进行打分，最低0分，最高26分，总分0~163分。将所得SAPS-Ⅱ评分代入概率计算公式，即可得到ICU患者的死亡风险。具体公式为：

1.7.

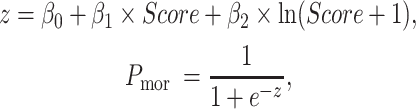其中，Score为SAPS-Ⅱ评分所得总分，β0、β1、β2为原始文献基于LR计算得到的各变量的系数，Pmor为ICU患者的死亡风险。

SAPS-Ⅱ模型最初是用于预测ICU患者的死亡风险，现有的一些研究基于SAPS-Ⅱ进行改良，定制用于预测ICU患者LOS-ICU的SAPS-Ⅱ模型[7-8]。本研究参照Vasilevskis等[7]的方法，使用MIMIC-Ⅲ数据库基于LR算法定制了预测ICU患者发生pLOS-ICU风险的SAPS-Ⅱ模型，作为其他三种机器学习模型的比较对象。具体的定制方法为：

1.7.

其中，β′0、β′1、β′2为基于MIMIC-Ⅲ数据库计算的各变量的系数，PpLOS-ICU为ICU患者发生pLOS-ICU的风险概率。

1.8. 统计分析与模型比较

本研究中数据的提取与清洗使用Postgre SQL软件，数据分析与模型构建使用Python 3.3.6软件。各变量的缺失值使用该变量的正常值填补。变量的正常值定义为SAPS-Ⅱ评分系统中该变量评分为0时所对应的变量取值，或者变量值区间的最大值和最小值的平均值。

模型预测性能的比较基于五折交叉验证所得的预测性能的平均值。模型的预测性能使用三种指标进行评价：(1)Brier评分：评价模型的综合预测性能；(2)受试者工作特征曲线下面积(area under the receiver operation characteristic curve，AUROC)：评价模型的区分度；(3)估计校准度指数(estimated calibration index，ECI)：评价模型的校准度[23-24]。Brier评分反映模型的预测结果与实际结果之间的误差，Brier评分越小，模型的综合预测性能越优。模型的区分度是指模型能够正确区分正样本(发生pLOS-ICU)与负样本(不发生pLOS-ICU)的能力，AUROC越接近于1，模型的区分度越优。模型的校准度是指模型预测的结局发生风险与实际发生风险之间的一致性程度，ECI越小，模型的校准度越优。使用校准曲线图进一步直观化评价模型的校准度。校准曲线图的横坐标为实际的结局发生风险，纵坐标为模型预测的结局发生风险，理想的模型校准曲线应为一条对角线，即模型预测的结局发生风险与实际的结局发生风险完全一致。校准曲线图可以反映在由低到高不同的结局发生风险人群中，模型预测的结局发生风险与实际结局发生风险的差异。模型性能指标之间的比较使用双侧t检验，以P < 0.05为差异具有统计学意义的判断标准。使用本研究中预测性能最好的模型识别出来的各预测变量重要性排序结果，给出重要性排序前五位的预测变量。

2. 结果

2.1. 基本特征

经过数据清洗，本研究共纳入40 200例符合条件的ICU患者，LOS-ICU的中位数为2.1 d(1.2~3.9 d)，发生pLOS-ICU的患者有9 514例，占比23.7%。患者平均年龄为(61.9±16.5)岁，男性患者23 145例，占比57.6%。ICU患者的详细信息见表 1。

表 1.

MIMIC-Ⅲ数据库中ICU患者的基本特征(n=40 200)

Characteristics of ICU patients in MIMIC-Ⅲ (n=40 200)

Items Data
SAPS-Ⅱ, simplified acute physiology score Ⅱ; ICU, intensive care unit; LOS-ICU, length of ICU stay; pLOS-ICU, prolonged LOS-ICU.
Age/years 61.9±16.5
Gender, n (%)
  Male 23 145 (57.6)
  Female 17 055 (42.4)
SAPS-Ⅱ score 32.5 ± 12.6
LOS-ICU / d, M (Q1-Q3) 2.1 (1.2-3.9)
pLOS-ICU, n (%) 9 514 (23.7)
Open in a new tab

图 1为患者的pLOS-ICU发生率依年龄、性别分层的金字塔图，可见随着年龄的上升，pLOS-ICU发生率在男性与女性患者中均呈上升趋势。30岁以上患者中，各年龄层的女性患者pLOS-ICU发生率略高于男性。

图 1.

ICU患者pLOS-ICU发生率依年龄、性别分层的金字塔图

The pLOS-ICU proportion pyramid stratified by age and gender

pLOS-ICU, prolonged length of ICU stay.

图 1

Open in a new tab

单因素假设检验结果显示，全部26个预测变量中，除体温最小值、血碳酸氢盐最小值、血胆红素最小值以及是否合并艾滋病等4个预测变量外，其余22个预测变量与结局pLOS-ICU均显著相关(P < 0.05)。

2.2. 特征选择

使用SAPS-Ⅱ中涉及到的所有变量作为基础特征集，在递归特征消除的过程中，建模特征的个数与RF模型性能的关系曲线如图 2所示。随着纳入特征数量的减少，RF模型的AUROC呈下降趋势；当纳入全部26个特征时，RF模型的AUROC最大。因此，最终用于建模的变量数目为26个。

图 2.

建模特征的个数与RF模型性能的关系曲线

The relationship curve that the prediction performanceof RF model varies with the number of selected features

AUROC, area under the receiver operation characteristic curve.

图 2

Open in a new tab

2.3. 模型的预测性能比较

SVM、CART、RF和定制版SAPS-Ⅱ模型的预测性能(Brier分值、AUROC、ECI)比较见表 2。五折交叉验证结果显示，四个模型中，RF模型在综合预测性能、区分度与校准度三个方面均表现最优，其达到了最优的Brier评分、AUROC和ECI，分别为0.145、0.770和7.259。相比于定制版SAPS-Ⅱ模型，三个机器学习模型在综合预测性能(Brier评分)、区分度(AUROC)和校准度(ECI)三个方面均有明显提升，且差异具有统计学意义(P < 0.01)。

表 2.

四种模型的预测性能比较

Prediction performance of the four models

Model Brier value AUROC ECI
AUROC, area under the receiver operation characteristic curve; ECI, estimated calibration index; SAPS-Ⅱ, simplified acute physiology score Ⅱ; SVM, support vector machine; CART, classification and regression tree; RF, random forest. *P < 0.01, vs. customized SAPS-Ⅱ model (t test).
Customized SAPS-Ⅱ 0.169 0.666 8.435
SVM 0.152* 0.738* 7.596*
CART 0.154* 0.730* 7.712*
RF 0.145* 0.770* 7.259*
Open in a new tab

2.4. RF模型的校准曲线分析结果

从RF模型的校准曲线(图 3)可以看出，在高pLOS-ICU发生风险的ICU人群中，RF模型略微高估了其风险；在低pLOS-ICU发生风险的ICU人群中，RF模型略微低估了其风险。

图 3.

RF模型的校准曲线

Calibration plot of RF model

RF, random forest.

图 3

Open in a new tab

2.5. RF模型识别的变量重要性排序

基于RF模型识别的变量重要性，对pLOS-ICU预测最重要的五个变量依次为年龄、心率、收缩压、体温和PaO2/FiO2。

3. 讨论

LOS作为评价医院效率与医疗资源利用率的有效指标，近年来在各个医疗领域被广泛研究。本研究使用美国大型重症医疗数据库MIMIC-Ⅲ，基于三种机器学习模型(SVM、CART和RF)构建ICU患者是否发生pLOS-ICU的预测模型，并比较其与传统的定制版SAPS-Ⅱ模型的预测性能。研究结果显示，RF模型在综合预测性能、区分度与校准度三个方面均表现最优，且相比于定制版SAPS-Ⅱ模型，其性能提升有统计学意义。

MIMIC-Ⅲ数据库由美国麻省理工学院(Massachusetts Institute of Technology，MIT)计算生理学实验室、美国哈佛医学院贝斯以色列迪康医学中心(Beth Israel Deaconess Medical Center, BIDMC)于2015年8月合作建立并维护。MIMIC-Ⅲ数据库为单中心数据库，储存了2001—2012年超过4万例ICU患者的临床信息记录，包括每例患者的人口学特征、诊断编码、生命体征测量数据、实验室检查数据、用药记录、生存结局等。其数据经过了严格的去隐私处理，患者的隐私信息如姓名、职业、联系方式等均不予记录。MIMIC-Ⅲ数据库不仅样本量大、数据类型丰富，而且数据质量高、可靠性好。

本研究基于三种机器学习模型(SVM、CART和RF)构建ICU患者是否发生pLOS-ICU的预测模型，研究中所使用的三种机器学习模型在实践中均有自己的优势所在，没有一个机器学习模型绝对优于另一种模型。具体建模实践时，则需根据数据集的特点及应用需求综合选择最为有效的机器学习模型。本研究结果提示，在预测ICU患者是否发生pLOS-ICU的应用中，RF模型在综合预测性能、区分度与校准度三个方面均表现最优，且相比于传统的定制版SAPS-Ⅱ模型，其性能提升有统计学意义。SAPS-Ⅱ本质上是基于LR算法开发的预测模型，传统的LR算法能够处理的样本数据量和特征维度有限，而且无法解决变量间的共线性问题，其预测性能也因此受到限制。相比于传统的LR模型，RF模型特有两种随机化思想——训练样本随机化和特征随机化，可在构建基础决策树时减少训练集的维度与样本量，使得RF模型在处理高维度、大样本数据时更有优势。

RF模型的预测性能在各个方面均优于SVM和CART模型。不同于SVM和CART模型，RF模型是以决策树为基础分类器的集成学习模型，RF基于随机采样的训练数据子集生成大量相互独立的决策树，其最终的模型预测结果综合了所有生成决策树的输出结果。在RF模型所有子决策树中，每棵决策树都可挖掘到预测变量与结局间相关性的一部分信息，RF则集成所有决策树预测结果，以减小发生在单个决策树中的预测误差。大量研究表明，相比于单个的基础分类器，集成学习模型的预测性能往往更为优异，其泛化能力也更为强大[9, 20-21]，与本研究的结果相一致。RF模型的校准曲线分析结果显示，RF模型会略微高估高风险ICU患者的pLOS-ICU发生风险，并略微低估低风险ICU患者的pLOS-ICU发生风险，说明RF模型倾向于拉开高风险人群与低风险人群的pLOS-ICU预测发生概率，这有助于更好地将高风险人群与低风险人群区分开来。

基于RF模型识别出的对pLOS-ICU预测最为重要的五个变量依次为年龄、心率、收缩压、体温和PaO2/FiO2。既往研究表明，年龄是影响ICU患者预后及医疗资源使用的一个重要因素[25-27]。高龄患者的身体机能下降，同时易合并多种慢性疾病，这增加了高龄ICU患者发生不良预后及消耗更多医疗资源的风险[28]。心率、收缩压和体温是衡量患者各器官代谢机能及状态的基本指标，本研究结果表明这三个基础指标对ICU患者的预后有重要的预测作用，与既往研究结果一致[29-31]。PaO2/FiO2是ICU患者使用机械通气的一个测量指标，其对ICU患者预后的独立预测作用也已在既往研究中被证实[32]。

本研究构建的pLOS-ICU预测模型对于我国ICU患者有一定的可适用性。第一，既往文献中报告的我国ICU患者的LOS-ICU的中位数为3 d[33]，与本研究所使用的MIMIC-Ⅲ数据库中ICU患者的LOS-ICU的中位数(2.1 d)相近，且两者的LOS-ICU分布有一定的相似性，均为右偏分布。第二，本研究建模所使用的预测变量大部分为我国ICU常规收集的医疗数据，数据获取方便[34]。第三，汪洋等[35]使用我国ICU患者的数据，基于RF算法构建的ICU患者的死亡预测模型达到了较高的准确率(AUROC=0.836)，这表明RF模型在预测ICU患者的预后方面对我国ICU患者的医疗数据有着一定的可适用性与应用前景。但另一方面，由于我国的人种特征、ICU的治疗模式与技术水平仍与美国有一定差异，本研究所构建的pLOS-ICU预测模型在应用于我国ICU的临床实践前，有待进一步的本地化修正与临床效应评估。

本研究有以下几点优势：(1)所使用的数据库样本量大，数据类型丰富；(2)建模所使用的预测变量均可在入住ICU后24 h内获得，因此，可在入住ICU早期使用pLOS-ICU预测模型，及时辅助医生进行临床决策；(3)使用五折交叉验证方法验证预测模型，所得结果较为稳健。但本研究也有一定的局限性：第一，MIMIC-Ⅲ数据库是一个美国的单中心数据库，且仅包含2001—2012年的数据，因而本研究所构建的pLOS-ICU预测模型的外推性可能会受到一定的限制，鉴于此，在应用于临床实践前，该pLOS-ICU预测模型有待进一步的本地数据修正与临床效应评估。第二，本研究样本可能存在一定的选择偏差，因为排除了在ICU内死亡的患者，其LOS-ICU的发展规律可能与生存患者的LOS-ICU的发展规律不一致，所以，所构建的pLOS-ICU预测模型可能不适用于在ICU内死亡的患者。第三，为了客观地比较机器学习模型与传统SAPS-Ⅱ模型的预测性能，本研究只使用了SAPS-Ⅱ中涉及到的变量构建机器学习模型，一些潜在的与LOS-ICU相关的特征可能未能纳入本研究的预测模型之中。

综上所述，本研究基于三种不同的机器学习算法构建ICU患者的pLOS-ICU预测模型，其中RF模型的预测性能最佳。基于RF的pLOS-ICU预测模型有很大的潜力辅助临床医护人员对ICU患者进行危险分层，从而进行合理的临床干预并改善患者预后。

Funding Statement

国家自然科学基金(81771938，91846101)、北京市自然科学基金(7212201)、科技创新2030项目(2018AAA0102100)和北京大学医学部-密歇根大学医学院转化医学与临床研究联合研究所项目(BMU2020JI011)

Supported by National Natural Science Foundation of China (81771938, 91846101), Beijing Municipal Science & Technology Commission (7212201), Chinese Scientific and Technical Innovation Project 2030 (2018AAA0102100), and the University of Michigan Health System-Peking University Health Science Center Joint Institute for Translational and Clinical Research (BMU2020JI011)

References

  • 1.Bin D, Youzhong A, Yan K, et al. Characteristics of critically ill patients in ICUs in mainland China. Crit Care Med. 2013;41(1):84–92. doi: 10.1097/CCM.0b013e31826a4082. [DOI] [PubMed] [Google Scholar]
  • 2.Milbrandt EB, Kersten A, Rahim MT, et al. Growth of intensive care unit resource use and its estimated cost in Medicare. Crit Care Med. 2008;36(9):2504–2510. doi: 10.1097/CCM.0b013e318183ef84. [DOI] [PubMed] [Google Scholar]
  • 3.Tsai PF, Chen PC, Chen YY, et al. Length of hospital stay prediction at the admission stage for cardiology patients using artificial neural network. J Healthc Eng. 2016;2016:7035463. doi: 10.1155/2016/7035463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Nassar AP, Caruso P. ICU physicians are unable to accurately predict length of stay at admission: A prospective study. Int J Qual Health Care. 2016;28(1):99–103. doi: 10.1093/intqhc/mzv112. [DOI] [PubMed] [Google Scholar]
  • 5.Le Gall JR, Lemeshow S, Saulnier F. A new simplified acute physiology ccore (SAPSⅡ) based on a European/North American multicenter study. JAMA. 1993;270(24):2957–2963. doi: 10.1001/jama.1993.03510240069035. [DOI] [PubMed] [Google Scholar]
  • 6.Zimmerman JE, Kramer AA, Mcnair DS, et al. Acute physiology and chronic health evaluation (APACHE) Ⅳ: Hospital mortality assessment for today's critically ill patients. Crit Care Med. 2006;34(5):1297–1310. doi: 10.1097/01.CCM.0000215112.84523.F0. [DOI] [PubMed] [Google Scholar]
  • 7.Vasilevskis EE, Kuzniewicz MW, Cason BA, et al. Mortality probability model Ⅲ and simplified acute physiology scoreⅡassessing their value in predicting length of stay and comparison to APACHE Ⅳ. Chest. 2009;136(1):89–101. doi: 10.1378/chest.08-2591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Zimmerman JE, Kramer AA, Mcnair DS, et al. Intensive care unit length of stay: Benchmarking based on acute physiology and chronic health evaluation (APACHE) Ⅳ. Crit Care Med. 2006;34(10):2517–2529. doi: 10.1097/01.CCM.0000240233.01711.D9. [DOI] [PubMed] [Google Scholar]
  • 9.Lin K, Hu Y, Kong G. Predicting in-hospital mortality of patients with acute kidney injury in the ICU using random forest model. Int J Med Inform. 2019;125:55–61. doi: 10.1016/j.ijmedinf.2019.02.002. [DOI] [PubMed] [Google Scholar]
  • 10.Saria S, Rajani AK, Gould J, et al. Integration of early physiolo-gical responses predicts later illness severity in preterm infants. Sci Transl Med. 2010;2(48):48–65. doi: 10.1126/scitranslmed.3001304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Johnson AEW, Pollard TJ, Shen L, et al. MIMIC-Ⅲ, a freely accessible critical care database. Sci Data. 2016;3:160035. doi: 10.1038/sdata.2016.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Agrawal S, Chen L, Tergas A I, et al. Characteristics associated with prolonged length of stay after hysterectomy for benign gynecologic conditions. Am J Obstet Gynecol. 2018;219(1):89.e1–89.e15. doi: 10.1016/j.ajog.2018.05.001. [DOI] [PubMed] [Google Scholar]
  • 13.Wolff J, Mccrone P, Patel A, et al. Predictors of length of stay in psychiatry: Analyses of electronic medical records. BMC Psychiatry. 2015;15:238. doi: 10.1186/s12888-015-0623-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Louw N, Steel SJ. Variable selection in kernel Fisher discriminant analysis by means of recursive feature elimination. Comput Stat Data Anal. 2006;51(3):2043–2055. doi: 10.1016/j.csda.2005.12.018. [DOI] [Google Scholar]
  • 15.Boser BE, Guyon IM, Vapnik VN. A training algorithm for optimal margin classifiers[C]//Proceedings of the fifth annual workshop on computational learning theory. New York: Association for Computing Machinery, 1992: 144-152.
  • 16.Furey TS, Cristianini N, Duffy N, et al. Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics. 2000;16(10):906–914. doi: 10.1093/bioinformatics/16.10.906. [DOI] [PubMed] [Google Scholar]
  • 17.Breiman L, Friedman JH, Olshen RA, et al. Classification and regression trees. Spain: Routledge; 2017. [Google Scholar]
  • 18.Austin PC. A comparison of regression trees, logistic regression, generalized additive models, and multivariate adaptive regression splines for predicting AMI mortality. Stat Med. 2007;26(15):2937–2957. doi: 10.1002/sim.2770. [DOI] [PubMed] [Google Scholar]
  • 19.Breiman L. Random forests. Machine Learning. 2001;45(1):5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
  • 20.Supatcha L, Chinae T, Chakarida N, et al. Heterogeneous ensemble approach with discriminative features and modified-SMOTE bagging for pre-miRNA classification. Nucleic Acids Res. 2013;41(1):e21. doi: 10.1093/nar/gks878. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Wang SQ, Yang J, Chou KC. Using stacked generalization to predict membrane protein types based on pseudo-amino acid composition. J Theor Biol. 2006;242(4):941–946. doi: 10.1016/j.jtbi.2006.05.006. [DOI] [PubMed] [Google Scholar]
  • 22.Touw WG, Bayjanov JR, Overmars L, et al. Data mining in the life sciences with random forest: A walk in the park or lost in the jungle? Brief Bioinformatics. 2013;14(3):315–326. doi: 10.1093/bib/bbs034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models a framework for traditional and novel measures. Epidemiology. 2010;21(1):128–138. doi: 10.1097/EDE.0b013e3181c30fb2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.van Hoorde K, van Huffel S, Timmerman D, et al. A spline-based tool to assess and visualize the calibration of multiclass risk predictions. J Biomed Inform. 2015;54:283–293. doi: 10.1016/j.jbi.2014.12.016. [DOI] [PubMed] [Google Scholar]
  • 25.Peigne V, Somme D, Guerot E, et al. Treatment intensity, age and outcome in medical ICU patients: Results of a French admi-nistrative database. Ann Intensive Care. 2016;6(1):7. doi: 10.1186/s13613-016-0107-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Fallenius M, Skrifvars MB, Reinikainen M, et al. Common intensive care scoring systems do not outperform age and glasgow coma scale score in predicting mid-term mortality in patients with spontaneous intracerebral hemorrhage treated in the intensive care unit. Scand J Trauma Resusc Emerg Med. 2017;25(1):102. doi: 10.1186/s13049-017-0448-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Szalados JE. Long-term mortality and quality of life after prolonged mechanical ventilation. Age and functional status as determinants of intensive care unit outcome: Sound basis for health policy or tip of the outcomes iceberg. Crit Care Med. 2004;32(1):291–293. doi: 10.1097/01.CCM.0000098851.97631.4C. [DOI] [PubMed] [Google Scholar]
  • 28.Brandberg C, Blomqvist H, Jirwe M. What is the importance of age on treatment of the elderly in the intensive care unit? Acta Anaesthesiol Scand. 2013;57(6):698–703. doi: 10.1111/aas.12073. [DOI] [PubMed] [Google Scholar]
  • 29.Diringer MN, Reaven NL, Funk SE, et al. Elevated body temperature independently contributes to increased length of stay in neurologic intensive care unit patients. Crit Care Med. 2004;32(7):1489–1495. doi: 10.1097/01.CCM.0000129484.61912.84. [DOI] [PubMed] [Google Scholar]
  • 30.Yien HW, Hseu SS, Lee LC, et al. Spectral analysis of systemic arterial pressure and heart rate signals as a prognostic tool for the prediction of patient outcome in the intensive care unit. Crit Care Med. 1997;25(2):258–266. doi: 10.1097/00003246-199702000-00011. [DOI] [PubMed] [Google Scholar]
  • 31.Grander W, Mullauer K, Koller B, et al. Heart rate before ICU discharge: a simple and readily available predictor of short- and long-term mortality from critical illness. Clin Res Cardiol. 2013;102(8):599–606. doi: 10.1007/s00392-013-0571-4. [DOI] [PubMed] [Google Scholar]
  • 32.Esteve F, Lopez-Delgado JC, Javierre C, et al. Evaluation of the PaO2/FiO2 ratio after cardiac surgery as a predictor of outcome during hospital stay. BMC Anesthesiol. 2014;14:83. doi: 10.1186/1471-2253-14-83. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Hu BJ, Tao LL, Rosenthal VD, et al. Device-associated infection rates, device use, length of stay, and mortality in intensive care units of 4 Chinese hospitals: International Nosocomial Control Consortium findings. Am J Infect Control. 2013;41(4):301–306. doi: 10.1016/j.ajic.2012.03.037. [DOI] [PubMed] [Google Scholar]
  • 34.徐 文秀, 方 理超, 刘 励军. APACHE Ⅱ评分和SAPSⅡ评分预测危重症患者病死率的应用价值分析. 中国血液流变学杂志. 2010;(2):245–247. [Google Scholar]
  • 35.汪 洋, 陈 上仲, 胡 才宝, et al. 基于随机森林法的严重脓毒症/脓毒性休克预后评估模型对患者28 d死亡的预测价值. 中华危重病急救医学. 2017;29(12):1071–1076. doi: 10.3760/cma.j.issn.2095-4352.2017.12.004. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Peking University (Health Sciences) are provided here courtesy of Editorial Office of Beijing Da Xue Xue Bao Yi Xue Ban, Peking University Health Science Center

RESOURCES