Skip to main content
NCBI home page
RSC Advances logoLink to RSC Advances
. 2021 Mar 4;11(16):9600–9607. doi: 10.1039/d1ra00837d

Predissociation resonances and accurate ab initio calculations of dication HF2+

Dong Liu 1, Rui Li 2, Juan Ren 1,3, Yongjun Cheng 1, Bing Yan 4, Yong Wu 5, Jian Guo Wang 5, Song Bin Zhang 1,✉
PMCID: PMC8695458  PMID: 35423438

Abstract

It is very interesting and challenging to investigate the electronic structures of diatomic dications, due to the nature of coulombic repulsive and bound attractive dissociation limits and their avoided diabatic interactions. Using the multi-reference configuration interaction approach, comprehensive ab initio calculations of the first 36 electronic states, corresponding to 15 dissociation limits, of dication HF2+ are reported. Good agreements for the vertical excitation energies and dissociation limits are achieved with the available references. Besides the common interesting quantities as adiabatic potential energy curves, dipole moments and spectral constants for the bound states, the nonadiabatic radial coupling matrix elements for the 1,3Π states are also presented. A showcase for the diabatic potentials of 3Π states are presented and discussed. Furthermore, predissociation states from the nonadiabatic couplings or avoided crossing of potential energy curves, known as shape resonances in collisions, are also investigated by using the WKB and scattering methods.

Highly accurate adiabatic potential curves of the 36 electronic states of the HF2+ dication by MRCI calculations. Panels (a), (b) and (c) correspond to the 16 singlet, 15 triplet and 4 quintet states, respectively. The nine bound states are highlighted and given in panel (d).graphic file with name d1ra00837d-ga.jpg

I. Introduction

The studies of multiply charged ions and highly charged ions have been a long-standing interest due to their important participations in various dynamic processes as in astrophysics,1–4 plasma physics,5 planetary ionospheres,6 interstellar chemistry,7 mass spectrometry8 and so on. In this work, we focus on the investigations of doubly charged diatomic dications, which have received much attention lying not only on their importance in diverse areas, but also on their interesting physical properties. Different from the highly charged and neutral systems, both Coulomb repulsive and chemical attractive interaction in diatomic dications play important roles, and avoided crossings between the potentials in short internuclear distances and metastable states could appear resulting from their diabatic interplay.8–10 The metastable states of dications are of particular interest for both experiments and theories11–15 as in absorption and emission spectroscopy,16,17 fragmentations,18,19 ion scatterings20,21 and so on. Furthermore, the recently developed X-ray free-electron laser facilities can generate ultra-short and ultra-intense X-ray pulses,22,23 and provide versatile Auger electron spectroscopy and kinetic energy release spectra to manipulate the nuclear dynamics of dications. These applications urgently ask for highly accurate electronic structures as potential energy curves (PEC) of dications,24–26 which is also highly required for the charged transfer investigations in heavy ion collisions.3

As a typical diatomic dication, it is interesting that not too many works of HF2+ have been recorded. HF2+ can be obtained by kicking out two electrons of HF molecule, while HF gas can easily dissolve in water as extremely strong and caustic acid, very few related experiments have been performed.27 This fact asks for much more investigations from the theoretical and computational aspects for HF2+ dication. The lowest PEC of HF2+ is a repulsive one, corresponding to the dissociation limit of ground-(F+ + H+). The ionization potentials (IP) of F+ ion and H atom are 35.970 eV and 13.598 eV, respectively. The first excited energy of H atom is 10.199 eV, so the HF2+ excited states with dissociation limits less than 31.571 eV (above the ground-(F+ + H+)) correspond to the repulsive ones-(F+* + H+) and attractive ones-(F2+* + H). For example, the dissociation limit of the lowest attractive curve is the ground-(F2+ + H), 21.372 eV above the ground-(F+ + H+). The Coulomb repulsion dominates the whole internuclear interactions of HF2+, interplayed by the excited attractive PECs. These facts lead to the difficulties to investigate the electronic structures and metastable states of dications by both theory and experiment.28

The first comprehensive work about HF2+ electronic structures could be the measurements of Auger electron spectra of HF molecule excited by X-ray photoionization in 1975 by Shaw et.al.,27 where most of the final states in HF2+ have been identified. Relevant theoretical investigations of the Auger electron spectra have been performed by Cederbaum's group24,29 in 1990s, where the complete active space self-consistent field (CASSCF) method has been employed to calculate the repulsive electronic structures of HF2+. However, the correlations from the attractive states are not sufficiently introduced in the calculations and the PECs are restricted in the short internuclear distances of 0.4–2 Å. Up to now, the most advanced studies of HF2+ electronic structures could be the calculations by the multi-reference single- and double-excitation configuration interaction (MRDCI) method by Bruna et.al. in 2006, where the vertical transition energies up to the first bound state (15Σ−) have been comprehensively calculated. Bearing in mind that the X-ray free-electron laser facilities have supplied more advanced degrees of freedom to investigate the dications. The present electronic structures of HF2+ are apparently far less and accurate enough. More comprehensive investigations for a broad internuclear distance and enough electronic states in high-level investigations are highly required.

In the present work, the highly accurate 36 potential energy curves of HF2+ are comprehensively investigated by the multi-reference configuration interaction approach (MRCI).30 These states correspond to 12 repulsive dissociation limits (F+* + H+) and 3 attractive dissociation limits (F2+* + H). The spectral constants of 9 bound states, transition dipole moments between the states, radial coupling matrix elements for 1,3Π states are given. The diabatic potentials of 3Π states are also presented and discussed, and the position and decay width of predissociation states are jointly investigated by using the WKB31 and scattering methods.32,33

II. Computation methods

A. Multi-reference configuration interaction calculations

All the calculations were performed using in the Molpro 2012 quantum chemistry ab initio package.34,35 Different basis sets have been tested and finally the correlation-consistent aug-cc-pV5Z basis set36–38 for F (15s9p5d4f3g2h → 7s6p5d4f3g2h) and H (9s5p4d3f2g → 6s5p4d3f2g) are employed. The irreducible representations of C2v is used to describe the linear molecule of C∞v as Σ+ = A1, Σ− = A2, Π = B1 + B2 and Δ = A1 + A2. Since both states Δ and Σ+ share the same A1, the unnatural avoid crossing or interplay in the PECs between A1 of Δ and A1 of Σ+ should be corrected; so do the PECs for states Σ− and Δ.

To obtain more accurate PECs of HF2+, MRCI is adopted in the calculations for each internuclear distance, with the reference wave functions generated by a state averaged-CASSCF (SA-CASSCF) procedure.39,40 In SA-CASSCF calculations, the initial molecular orbitals (MOs) are prepared by Hartree–Fock method, the active MOs for both singlet and triplet states are 5a1, 3b1 and 3b2 (termed as (5330)), and the quintuplet states use the active MOs of (6220), all 8 electrons are active. The relativistic correction for the valance energies of F+ and F2+ is in the order of 0.01 eV,41 that the spin–orbit interaction could be safely ignored in the calculations.

Note that the key point for the application of multi-reference methods is the rational selections of active space. However, for dications, the conventional scheme of building active space according to the dissociation limit is not adequate enough than for the neutral diatomics. Due to the avoided crossing and interplay between repulsive and attractive adiabatic PECs, a low-lying excited state in the dissociation limit could result from a highly excited state at the small internuclear distance after interplaying several times. The avoided crossing changes the active space with the variations of internuclear distance, a larger active space would be expected for dications to provide consistent results for the whole internuclear region. After lots of preliminary checking, the large active space (5330) for the singlet and triplet sates, and (6220) for the quintuplet states are implemented to generate 36 accurate PECs of HF2+, corresponding to 15 dissociation limits.

B. Adiabatic to diabatic transformation

Generally speaking, the PECs are calculated in the adiabatic representation, and the nonadiabatic couplings are quite weak between PECs away from each other. When two adiabatic PECs of the same symmetry approach each other and even interplay as the avoided crossing in a narrow region, the diabatic couplings should be taken into account seriously.3,42 For the PECs with strong diabatic couplings, it would be more convenient to transform the PECs into the diabatic representation.33 Since in the adiabatic representation, the nonadiabatic radial coupling matrix A(R) would change rapidly and appear as sharp peaks in the avoided crossing regions, while the off-diagonal potential/Hamiltonian in the diabatic representation indicating the diabatic radial coupling evolve slowly with respect to the internuclear distance, bringing in less instabilities for the numerical investigations in molecular dissociation, ion collision and so on.3 The adiabatic PECs Va can be transformed into the diabatic ones Vd by the unitary matrix C(R) as Vd = C†VaC. The transformation matrix C(R) satisfies Inline graphic with C(R → ∞) → I.3

Practically, the radial coupling matrix elements can be calculated numerically by finite difference method as Inline graphic32,33 which can be implemented in MOLPRO with the subroutine OVERLAP,35 and ΔR = 0.001 a.u. in the present calculations. The important radial coupling matrix elements for 1,3Π states have been calculated, and the diabatic potentials of 3Π states are transformed and discussed as a showcase.

C. Vibrational levels and spectroscopic constants

Once we get the potential energy curve of an electronic state, the vibrational energy levels can be obtained by numerically solving the radial Schrodinger equation Inline graphic where μ is the reduced mass of the system, J is the rotational quantum number, R is the internuclear distance, and the rotationless (electronic) potential V(R) plus a centrifugal term forms the effective one-dimensional potential VJ(R). The piecewise exact power series expansions method43 has been employed to efficiently solve the ro-vibrational levels in the present work. Generally speaking, the spectroscopic constants for a single bound state can be extracted from the numerical potential energy curves. For diatomic molecules, the potential energy curves of electronic states are simple and well-shaped, and the first few vibrational levels could be well represented by Morse potential.44 Therefore, the parameters including the equilibrium distance (Re), the well depth (De), the vertical transition energy (Te), the harmonic frequency (ωe), and the anharmonic constant (ωeχe) can be obtained by fitting the vibrational levels. The other spectroscopic constants, such as rotational constant (Be), can be generated by fitting the rovibrational levels as,45,46Ev,J = G(v) + Bv[J(J + 1)] − Dv[J(J + 1)]2 + Hv[J(J + 1)]3 + … = ∑m=0Km(v)[J(J + 1)]m, where G(v) is the vibrational energy level, Bv is rotational constant, Dv, Hv, … are anharmonicity.

D. Tunneling-predissociation states

When the PEC has a potential barrier above its dissociation limit, and the barrier is strong enough to temporally support localized states, these states will ultimately decay into the continuum through tunneling. These states are known as the tunneling-predissociation quasi-bound states, or shape resonances in particle collisions.3,33,42 The state/resonance position and decay width are quite important to understand the predissociation dynamics of dications. For the tunneling states with very long lifetimes, the state levels could be well approximated as the bound levels within the potential barrier,42 and the classical WKB method31 can be efficiently employed to calculate the tunneling lifetime as τ = tvib/ω, where tvib is the oscillation period in the potential well, and ω is the probability per collision of tunneling through the barrier. Precisely, Inline graphic and Inline graphic, where E is the bound energy level, U(R) = V(R) + [J(J + 1)/R2](ℏ2/2μ) is the effective potential, μ is the reduced mass of the system, v and J are the vibration and rotation quantum numbers, respectively. R1(E), R2(E) and R3(E) are the first three classical turning points.31 Note that the LEVEL program by Le Roy47 has implemented the WKB method.

It has shown that the long-lived tunneling states close to the bottom of the potential well could be well studied by the WKB method, while for the states close to the barrier top, WKB calculations would introduce uncertainties up to 10% or more.48–50 In such a case, an alternative quantum scattering method3 can be employed by treating the collisions of A+ + B+ in the potential of AB2+. The phase shift δ(E) of the free state fragments carries the information of scattering between A+ + B+, and the existence of resonance states would increase the phase shift by almost π,51 and the resonance position Er and width Γ can be well extracted by fitting δ(E) using the Breit–Wigner formula51,52 as Inline graphic. δ0(E) is the background phase shift near the resonance, and varies slowly, so the resonance parameters can be efficiently calculated as Inline graphic, where Inline graphic is the maximum derivative value of the δ(E) with respect to the energy, and the corresponding energy is Er as the resonance position.53 Note that the electron potential scattering code RADIAL can be properly modified to efficiently calculate the particle scattering phases.54,55

III. Results and discussion

With the help of Wigner–Witmer principle,56 the electronic states of HF2+ can be determined by the atomic states in its corresponding dissociation limit, e.g., 4Su + 2Sg = 5Σ− and 3Σ−. With the data of energy levels (F+, F2+ and H) from NIST,41 the tens of dissociation limits including Rydberg series up to F2+(2s22p3) + H(2s) are listed and shown in Table 1, the combinations between different excited F2+(2s22p3) and H(1s) result into the 3 attractive dissociation limits, and the repulsive ones are from the interactions between F+* and H. Note that Rydberg states with dissociation limit F+(2s22p3nl) + H+ below the limit F2+(2s22p3) + H(2s) can not be precisely calculated, states up to 12 repulsive dissociation limits and all 3 attractive dissociation limits are carefully investigated in the present work. In the calculations, the energies of dissociation limits could be obtained as the energy differences from the ground state at large R0 (50 a.u. in the present work) for the attractive states; while for the repulsive curves, such energy differences at large R0 minus 1/R0 produce the expected energies of dissociation limits, where 1/R0 represents the left positive repulsive coulomb potential.

The dissociation limits of HF2+ up to F2+(2s22p3) + H(2s) with the corresponding 36 electronic states (states up to 51Σ+, 21Σ−, 61Π, 31Δ, 23Σ+, 63Σ−, 63Π, 23Δ, 35Σ− and 15Π) calculated in the present MRCI. The relative excitation energies (eV, to states 13Σ−) for the dissociation limits are compared with that of NIST,41 the ratio of differences Inline graphic are within 0.8%.

Atomic state Term State ΔENIST ΔEpresent Ratio of difference
F+(2s22p4) + H+ 3Pg 13Σ−, 13Π 0 0 0
F+(2s22p4) + H+ 1Dg 11Σ+, 11Π, 11Δ 2.588 2.572 0.61%
F+(2s22p4) + H+ 1Sg 21Σ+ 5.569 5.531 0.68%
F+(2s2p5) + H+ 3Pu 13Σ+, 23Π 20.432 20.460 0.14%
F2+(2s22p3) + H(1s) 4Su + 2Sg 15Σ−, 23Σ− 21.371 21.198 0.81%
F+(2s22p33s) + H+ 5Su 25Σ− 21.882 21.791 0.42%
F+(2s22p33s) + H+ 3Su 33Σ− 22.672 22.594 0.34%
F+(2s22p33s) + H+ 5Pg 15Π, 35Σ− 25.101 24.984 0.46%
F2+(2s22p3) + H(1s) 2Du + 2Sg 21Δ, 21Π, 11Σ−; 13Δ, 33Π, 43Σ− 25.597 25.459 0.54%
F+(2s22p33p) + H+ 3Pg 43Π, 53Σ− 25.751 25.701 0.19%
F+(2s22p33s) + H+ 3Du 53Π, 63Σ−, 23Δ 26.268 26.190 0.30%
F+(2s22p33s) + H+ 1Du 31Π, 21Σ−, 31Δ 26.665 26.584 0.30%
F2+(2s22p3) + H(1s) 2Pu + 2Sg 41Π, 31Σ+; 63Π, 23Σ+ 27.762 27.605 0.57%
F+(2s22p33s) + H+ 1Pu 41Σ+, 51Π 28.173 28.187 0.04%
F+(2s22p33s) + H+ 3Pu 43Σ+, 73Π 28.461 — —
F+(2s22p33d) + H+ 3Du 83Π, 73Σ−, 33Δ 28.772 — —
F+(2s22p34s) + H+ 5Su 45Σ− 29.155 — —
F+(2s22p33p) + H+ 1Pg 31Σ−, 61Π 29.216 29.383 0.57%
F+(2s22p3nl) + H+ — — — — —
F2+(2s22p3) + H(2s) 4Su + 2Pu 3,5Σ−, 3,5Π 31.569 — —
Open in a new tab

In Table 1, the first and second column indicate different dissociation limits and its atomic terms. The corresponding molecular states is given in the third column. The fourth and fifth column are the NIST (ΔENIST) and present (ΔEpresent) calculated excitation energies by MRCI with respect to the lowest dissociation limit F+(2s22p4) + H+. The ratio of difference Inline graphic is given in the last column. Practically, 15–17th dissociation limits are not precisely calculated, the calculations show that very tiny improvement of the accuracy for states 7–93Π requires huge active space and are very expensive, while such a small improvement of these states tiny affect other lower triplet states. Thus it turns much cheaper to lose the accuracy of the three dissociation limits and related states, and the accuracy for other dissociation limits and states can be properly achieved. Besides, such a treatment do not affect the 18th dissociation limit of singlet states. So in Table 1, states up to 51Σ+, 21Σ−, 61Π, 31Δ, 23Σ+, 63Σ−, 63Π, 23Δ, 35Σ− and 15Π, 36 electronic states in total corresponding to 15 dissociation limits are reported. As it shows, the present relative energies by MRCI for the dissociation limits agree quite well with that of the NIST data.41 The absolute difference and difference ratio are within 0.18 eV and 0.8%, respectively.

The corresponding adiabatic potential energy curves of HF2+ dication by MRCI for the 36 electronic states listed in Table 1, are presented in Fig. 1 in a broad internuclear distances of R = 0.7–50 a.u. The PECs in large internuclear distance (>10 a.u.) for states sharing the same dissociation limits almost overlap with each other, and the attractive and repulsive branches could interchange at large internuclear distances, such as the crossing around 30 a.u. between states 31Π and 41Π. The nonadiabatic coupling results into the interplay or avoided crossing between PECs, and the positions of these avoided crossings are listed in Table 2. The nonadiabatic coupling and avoided crossing play a very important role in the electron-nuclear correlated dynamics, such as the photoabsorption spectra, molecular dissociation yield, charge transfer in ion collisions and so on.3,18,58 What is more, the related transition dipole moment (TDM) and permanent dipole moment (PDM) would surely be affected and even interchanged by the nonadiabatic couplings. The strength of nonadiabatic coupling is imprinted by the radial coupling matrix A(R), which must be firstly supplied to transform the PECs into diabatic representation. All these relevant quantities will be presented below.

Fig. 1. Highly accurate adiabatic potential curves of the 36 electronic states (states up to 51Σ+, 21Σ−, 61Π, 31Δ, 23Σ+, 63Σ−, 63Π, 23Δ, 35Σ− and 15Π) of HF2+ dication by MRCI calculations, see Table 1 for more information of the states. Panels (a), (b) and (c) correspond to the 16 singlet, 15 triplet and 4 quintet states, respectively. The nine bound states are highlighted and given in panel (d).

Fig. 1

Open in a new tab

The positions Rc (a.u.) of avoided crossings between the adiabatic potential energy curves.

States R c States R c
23Π–33Π 5.75 31Π–41Π 1.85, 27
33Π–43Π 2.85 41Π–51Π 1.55, 3.55
43Π–53Π 1.5, 14.5 51Π–61Π 1.3
53Π–63Π 1.6, 19 33Σ−–43Σ− 9.1
Open in a new tab

Besides carefully checking of the convergence, the accuracy of the present PECs could also be roughly estimated from several points. The PECs smoothly vary with respect to R. The repulsive brunches (F+ + H+) in large R decrease as the coulombic potential 1/R and the attractive ones reach constant limits. The relative energies for the dissociation limits show very good agreements with that of NIST data,41 where the absolute differences are less than 0.1 eV for repulsive states and about 0.15 eV for attractive states (Table 1). Further more, the vertical excitation energies at R = 2.2 a.u. agree quite well with that of the available MRD-CI results by Pablo et.al.57 shown in Table 3. The minor differences could be from different basis sets and different levels of calculations.

Vertical excitation energies ΔEv (eV) relative to 13Σ− at R = 2.2 a.u.

Present MRD-CI data57
11Δ 2.70 2.86
11Σ+ 4.23 4.39
13Π 2.22 2.29
11Π 4.72 4.92
21Σ+ 8.41 8.61
15Σ− 17.37 17.33
Open in a new tab

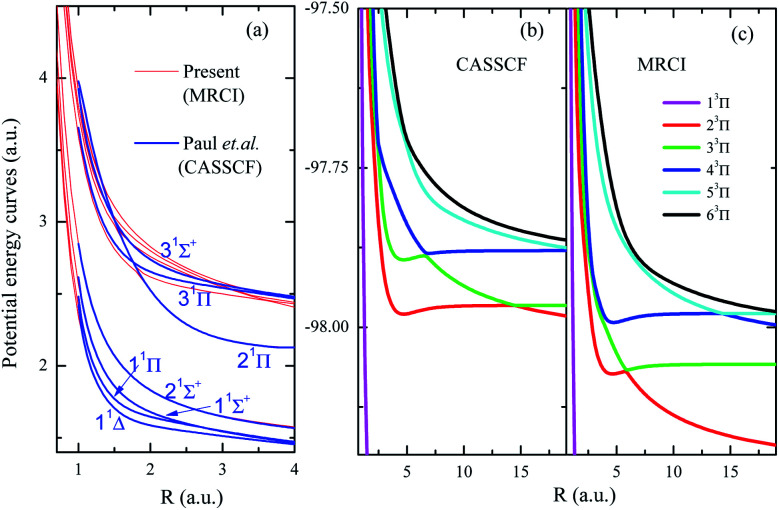
To show the importance of including the dynamic electron correlations in the calculations, PECs of low-lying excited states by previous CASSCF24 and present MRCI are shown in Fig. 2a. The CASSCF results of Pahl et.al.24 include seven singlet states and two triplet states given at R = 1–4 a.u., the present MRCI results are matched at R = 4 a.u. for 11Δ state. As Fig. 2a shows, PECs of low-lying states (11Δ, 11Π, 11Σ+, and 22Σ+) show excellent agreements between the previous CASSCF and present MRCI, however, significant discrepancies appear for higher excited states. The fact is that the dynamic electronic correlation is not fully considered in the CASSCF calculations, and such correlations should be more important for the description of highly excited states. Especially for the states involving nonadiabatic coupling and avoided crossing, more accurate descriptions of the dynamic electronic correlation are required. PECs of (1–6)3Π states by present CASSCF and MRCI are also presented in Fig. 2b and c, respectively, to further reveal the importance of including dynamic electron correlations. As it clearly shows, for these states with important nonadiabatic couplings, the inclusion of dynamic electron correlations shift back the avoided crossings into smaller internuclear region, therefore the electronic structures at small internuclear distances by CASSCF may be not reliable. CASSCF method could not be a proper choice to treat doubly charged HF2+ dications, especially for the states with nonadiabatic couplings. These features definitely indicate the importance of using high-level calculation methods instead of CASSCF method for dications.

Fig. 2. Panel (a) shows the PECs of some lowing excited states of HF2+ in the present MRCI level and the CASSCF level by Paul et al.;24 the PECs of 3Π of HF2+ by present CASSCF and MRCI calculations are given in panels (b) and (c), respectively.

Fig. 2

Open in a new tab

Fig. 1 also reveals nine shallow bound states, 15Σ−, 23Σ−, and 11Σ−, 21Δ, 21Π, 13Δ, and 31Σ+, 31Π, 43Π, locating at around 4.5 a.u., with binding energy of about 0.4 eV. The first two, the third to sixth, and the last three states are in the same dissociation limits F2+(2s22p3)4Su + H(1s)2Sg, F2+(2s22p3)2Du + H(1s)2Sg, and F2+(2s22p3)2Pu + H(1s)2Sg, respectively. Detailed spectral constants of these nine bound states are presented in Table 4. About five vibrational states could be supported. The leading configuration and its weight around the equilibrium of each state are also given. It shows the configuration interactions are quite important for all these bound states. There are two leading configurations for both states 15Σ− and 21Π, while besides two leading configurations for states 31Σ+, 31Π and 43Π, the listed additional 3% one also plays a very important role in MRCI calculations. Dynamic correlations are very important for the precise calculations.

Spectral constants and leading configurations of nine bound states.

States R e/a.u. ω e/cm−1 D e/eV ω e χ e/cm−1 B e/cm−1 Leading configuration and weight at R
15Σ− 4.51 675 0.47 30 3.1 0.64 3σ4σ05σ1π2 + 0.34 3σ4σ1π2 at R = 4.5 a.u.
15Σ− (ref. 57) 4.34 670
23Σ− 4.97 558 0.32 31 2.9 0.97 3σ4σ1π2 at R = 5.0 a.u.
11Σ− 4.62 639 0.41 30 3.0 0.97 3σ4σ1π2 at R = 4.6 a.u.
21Δ 5.00 551 0.31 31 2.5 0.97 3σ4σ1π2 at R = 5.0 a.u.
21Π 4.72 616 0.39 31 2.8 0.49 3σ04σ1π3 + 0.49 3σ24σ25σ1π0 at R = 4.7 a.u.
13Δ 4.54 666 0.45 30 3.1 0.97 3σ4σ1π2 at R = 4.5 a.u.
31Π 4.69 623 0.39 31 2.9 0.47 3σ04σ1π3 + 0.48 3σ24σ1π + 0.03 2σ03σ24σ1π3 at R = 4.7 a.u.
43Π 4.71 654 0.40 33 2.8 0.45 3σ04σ1π3 + 0.48 3σ24σ1π + 0.03 2σ03σ24σ1π3 at R = 4.7 a.u.
31Σ+ 4.97 562 0.32 31 2.5 0.47 3σ04σ1π3 + 0.47 3σ24σ1π + 0.03 2σ03σ4σ1π4 at R = 5.0 a.u.
Open in a new tab

The permanent dipole moment (PDM), transition dipole moment (TDM), radial coupling matrix element (RCME) for the typical low-lying states are also presented in Fig. 3–5, based on the MRCI calculations. These molecular parameters are indispensable to describe the dynamic processes such as spontaneous emission (Einstein coefficient), photo excitation and dissociation, charge transfer in ion collisions and so on. Fig. 3 has shown the PDM and TDM for the quintet states of HF2+. The value of PDM depends on the reference point of coordinates for charged specifies,59 the mass center of molecule is chosen as the reference point in this work, then the PDM at large R shows nearly linear behavior with respect to R, for the repulsive branches with one charge in each fragment. Similar features broadly appear in many systems with charged repulsive and even attractive branches.60–62 Note that 15Σ− is the lowest quintet state, and its dipole spontaneous emission is forbidden, 15Σ− could be a long-lived stable candidate for HF2+. The leading configuration for 35Σ− is 0.99 1σ22σ23σ4σ05σ06σ1π2, requiring the active orbitals up to at least 6a12b12b2 in state-averaged CASSCF calculations.

Fig. 3. Permanent dipole moments and transition dipole moments of quintet states.

Fig. 3

Open in a new tab

Fig. 4. Permanent dipole moments, transition dipole moments and important radial coupling matrix elements between 1Π states.

Fig. 4

Open in a new tab

Fig. 5. Same as in Fig. 4 but for 3Π.

Fig. 5

Open in a new tab

Both singlet and triplet Π states show avoided crossings, the PDM, TDM and RCME for states 1,3Π are presented in Fig. 4 and 5. The linear behavior of the PDM at large R is apparently, the abrupt changes for PDM with respect to R correspond to the regions of avoided crossings (see Table 2), featured as significant peaks for RCME. Both PDM and TDM show much more complex variations compared with that of quintet states without nonadiabatic interactions (see Fig. 3). We would expect the nuclear wavepacket dynamics on excited Π states should seriously include the nonadiabatic couplings. Note that the main configurations for states 23Π and 33Π are 1σ22σ3σ21π3 and 0.49 1σ22σ3σ04σ1π3 + 0.48 1σ22σ23σ24σ1π, respectively, indicating the importance of implementing the multi-configuration method.

As a showcase for the treatments of nonadiabatic system in the diabatic representation, the strongly coupled (2, 3, 4)3Π states have been transformed into diabatic representation and their diabatic PECs (including off-diagonal couplings) are shown in Fig. 6. As it shows, the repulsive diabatic PEC VD11 crosses through both attractive ones VD22 and VD33, and the diabatic off-diagonal couplings evolve normally with respect to R. Such a transformation has depleted the difficulties induced by the sharp radical coupling matrix A(R) in the studies related to the nuclear wavepacket dynamics. It turns out that the diabatic representation is more suitable for system with intense nonadiabatic couplings.

Fig. 6. The diabatic potential energy curves from the transformations of adiabatic potential energy curves using the radial coupling matrix elements for showcase of 3Π states. (a) and (b) are the diabatic potential energy curves and off-diagonal diabatic interactions, respectively.

Fig. 6

Open in a new tab

Finally, as a consequence of interchange between the PECs, tunneling-predissociation levels exist in this system. These states are also known as shape resonances or quasibound states in ion-atom collisions, they decay through the nonradiative tunneling process. As has mentioned in Sec. II, both WKB method and scattering method have been employed to calculate the predissociation level and width in a complementary way. Table 5 has shown the predissociation levels (relative to its dissociation limit) and widths for both states 33Σ− and 23Π. Note that there are six and only one predissociation states for states 33Σ− and 23Π, respectively. The WKB calculations show that the widths for ν = 5, 6 (33Σ−) and ν = 0 (23Π) are quite large, their positions and widths have been corrected by performing the scattering method. Typically, states ν = 6 (33Σ−) and ν = 0 (23Π) can tunneling decay as fast as in picosecond.

The resonance parameters of the tunneling-predissociation levels with the rotation quantum number J = 0. WKB method has been employed to calculate the resonance parameters for states ν = 1–4 of 33Σ−, and to be more accurately, the scattering method is used for 33Σ− states with ν = 5, 6 and the 23Π states.

ν Position (eV) Width (cm−1) Lifetime (s)
3 3 Σ −
0 2.45297 1.396 × 10−23 1.521 × 1012
1 2.52746 7.850 × 10−18 2.706 × 106
2 2.59519 5.964 × 10−13 3.560 × 101
3 2.6558 8.742 × 10−9 2.430 × 10−3
4 2.7089 2.820 × 10−5 7.530 × 10−7
5 2.75408 8.470 × 10−3 1.254 × 10−9
6 2.79094 1.164 × 100 9.117 × 10−12
 
2 3 Π
0 4.5129 4.566 × 100 2.325 × 10−12
Open in a new tab

IV. Conclusion

In this work, accurate ab initio calculations have been implemented on the electronic structure of HF2+ dication. 36 potential energy curves, corresponding to 12 repulsive dissociation limits F+* + H+ and 3 attractive dissociation limits F2+ + H(1s), are obtained by multi-reference configuration interaction approach. Good agreement have been achieved with existing theoretical results with respect to dissociation limits and vertical excitation energies. Spectroscopic constants for bound states, dipole moments and the radial coupling matrix elements for typical showcases are also presented. Furthermore, the tunneling-predissociation levels, due to the nonadiabatic coupling or avoided crossing of PECs, are investigated by WKB method complemented by the scattering method. To achieve reliable results for dications, the dynamic electron correlations should be seriously taken into account, high-level calculations beyond CASSCF as MRCI are expected.

Conflicts of interest

There are no conflicts of interest to declare.

Supplementary Material

Acknowledgments

Grants from NSFC (No. 11934004, 11974230), the Science Challenge Program of China (TZ2018005) are acknowledged.

References

  1. Butler S. Dalgarno A. Astrophys. J. 1980;241:838. doi: 10.1086/158395. [DOI] [Google Scholar]
  2. Janev R. K., Presnyakov L. P., and Shevelko V. P., Physics of highly charged ions, vol. 13, Springer Science & Business Media, 2012 [Google Scholar]
  3. Bransden B. H. and McDowell M. R. C., Charge exchange and the theory of ion-atom collisions, Clarendon Press, 1992 [Google Scholar]
  4. Rybicki G. B. and Lightman A. P., Radiative processes in astrophysics, John Wiley & Sons, 2008 [Google Scholar]
  5. Alves T. V. Hermoso W. Franzreb K. Ornellas F. R. Phys. Chem. Chem. Phys. 2011;13:18297. doi: 10.1039/C1CP20735K. [DOI] [PubMed] [Google Scholar]
  6. Thissen R. Witasse O. Dutuit O. Wedlund C. S. Gronoff G. Lilensten J. Phys. Chem. Chem. Phys. 2011;13:18264. doi: 10.1039/C1CP21957J. [DOI] [PubMed] [Google Scholar]
  7. Böhme D. K. Phys. Chem. Chem. Phys. 2011;13:18253. doi: 10.1039/C1CP21814J. [DOI] [PubMed] [Google Scholar]
  8. Price S. D. Roithová J. Phys. Chem. Chem. Phys. 2011;13:18251. doi: 10.1039/C1CP90163J. [DOI] [PubMed] [Google Scholar]
  9. Nenajdenko V. G. Shevchenko N. E. Balenkova E. S. Alabugin I. V. Chem. Rev. 2003;103:229. doi: 10.1021/cr0000628. [DOI] [PubMed] [Google Scholar]
  10. Sabzyan H. Keshavarz E. Noorisafa Z. J. Iran. Chem. Soc. 2014;11:871. doi: 10.1007/s13738-013-0359-5. [DOI] [Google Scholar]
  11. Mullin A. S. Szaflarski D. M. Yokoyama K. Gerber G. Lineberger W. J. Chem. Phys. 1992;96:3636. doi: 10.1063/1.461917. [DOI] [Google Scholar]
  12. Mathur D. Andersen L. Hvelplund P. Kella D. Safvan C. J. Phys. B: At., Mol. Opt. Phys. 1995;28:3415. doi: 10.1088/0953-4075/28/15/027. [DOI] [Google Scholar]
  13. Hogreve H. Chem. Phys. Lett. 2004;394:32. doi: 10.1016/j.cplett.2004.06.099. [DOI] [Google Scholar]
  14. Kolbuszewski M. Wright J. S. Buenker R. J. J. Chem. Phys. 1995;102:7519. doi: 10.1063/1.469083. [DOI] [Google Scholar]
  15. Sabzyan H. Keshavarz E. Noorisafa Z. J. Iran. Chem. Soc. 2014;11:871. doi: 10.1007/s13738-013-0359-5. [DOI] [Google Scholar]
  16. Fano U. Cooper J. W. Phys. Rev. 1965;137:A1364. doi: 10.1103/PhysRev.137.A1364. [DOI] [Google Scholar]
  17. Ott C. Kaldun A. Raith P. Meyer K. Laux M. Evers J. Keitel C. H. Greene C. H. Pfeifer T. Science. 2013;340:716. doi: 10.1126/science.1234407. [DOI] [PubMed] [Google Scholar]
  18. Van Dishoeck E. F. Van Hemert M. C. Allison A. C. Dalgarno A. J. Chem. Phys. 1984;81:5709. doi: 10.1063/1.447622. [DOI] [Google Scholar]
  19. Heays A. N. Bosman A. D. Van Dishoeck E. F. Astron. Astrophys. 2017;602:A105. doi: 10.1051/0004-6361/201628742. [DOI] [Google Scholar]
  20. Zygelman B. Dalgarno A. Kimura M. Lane N. F. Phys. Rev. A. 1989;40:2340. doi: 10.1103/PhysRevA.40.2340. [DOI] [PubMed] [Google Scholar]
  21. Wu Y. Lin X. H. Yan B. Wang J. G. Janev R. K. J. Phys. B: At., Mol. Opt. Phys. 2016;49:035203. doi: 10.1088/0953-4075/49/3/035203. [DOI] [Google Scholar]
  22. Bostedt C. Boutet S. Fritz D. M. Huang Z. Lee H. J. Lemke H. T. Robert A. Schlotter W. F. Turner J. J. Williams G. J. Rev. Mod. Phys. 2016;88:015007. doi: 10.1103/RevModPhys.88.015007. [DOI] [Google Scholar]
  23. Young L. Ueda K. Gühr M. Bucksbaum P. H. Simon M. Mukamel S. Rohringer N. Prince K. C. Masciovecchio C. Meyer M. J. Phys. B: At., Mol. Opt. Phys. 2018;51:032003. doi: 10.1088/1361-6455/aa9735. [DOI] [Google Scholar]
  24. Pahl E. Meyer H. Cederbaum L. S. Minelli D. Tarantelli F. J. Chem. Phys. 1996;105:9175. doi: 10.1063/1.472751. [DOI] [Google Scholar]
  25. Song S. Ding B. Xu W. Nicolas C. Patanen M. Nandi S. Bozek J. Miron C. Xiao Z. Liu X.-J. Phys. Rev. A. 2019;99:022511. doi: 10.1103/PhysRevA.99.022511. [DOI] [Google Scholar]
  26. Ullrich J. Rudenko A. Moshammer R. Annu. Rev. Phys. Chem. 2012;63:635. doi: 10.1146/annurev-physchem-032511-143720. [DOI] [PubMed] [Google Scholar]
  27. Shaw R. W. Thomas T. D. Phys. Rev. A. 1975;11:1491. doi: 10.1103/PhysRevA.11.1491. [DOI] [Google Scholar]
  28. Alagia M. Brunetti B. G. Candori P. Falcinelli S. Moix Teixidor M. Pirani F. Richter R. Stranges S. Vecchiocattivi F. J. Chem. Phys. 2006;124:204318. doi: 10.1063/1.2201742. [DOI] [PubMed] [Google Scholar]
  29. Zähringer K. Meyer H. D. Cederbaum L. S. Tarantelli F. Sgamellotti A. Chem. Phys. Lett. 1993;206:247. doi: 10.1016/0009-2614(93)85548-3. [DOI] [Google Scholar]
  30. Werner H. Knowles P. J. J. Chem. Phys. 1988;89:5803. doi: 10.1063/1.455556. [DOI] [Google Scholar]
  31. Ford K. W. Hill D. L. Wakano M. Wheeler J. A. Ann. Phys. 1959;7:239. [Google Scholar]
  32. Zygelman B. Cooper D. L. Ford M. J. Dalgarno A. Gerratt J. Raimondi M. Phys. Rev. A. 1992;46:3846. doi: 10.1103/PhysRevA.46.3846. [DOI] [PubMed] [Google Scholar]
  33. Zhang S. B. Wu Y. Wang J. G. J. Chem. Phys. 2016;145:224306. doi: 10.1063/1.4971296. [DOI] [PubMed] [Google Scholar]
  34. Werner H.-J. Knowles P. J. Knizia G. Manby F. R. Schütz M. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012;2:242. [Google Scholar]
  35. Werner H.-J., Knowles P. J., Knizia G., Manby F. R., Schütz M., Celani P., Korona T., Lindh R., Mitrushenkov A., Rauhut G., et al., see, http://www.molpro.net, 2012
  36. Peterson K. A. Dunning Jr T. H. J. Chem. Phys. 2002;117:10548. doi: 10.1063/1.1520138. [DOI] [Google Scholar]
  37. Dunning Jr T. H. J. Chem. Phys. 1989;90:1007. doi: 10.1063/1.456153. [DOI] [Google Scholar]
  38. Kendall R. A. Dunning Jr T. H. Harrison R. J. J. Chem. Phys. 1992;96:6796. doi: 10.1063/1.462569. [DOI] [Google Scholar]
  39. Knowles P. J. Werner H.-J. Chem. Phys. Lett. 1985;115:259. doi: 10.1016/0009-2614(85)80025-7. [DOI] [Google Scholar]
  40. Werner H. Knowles P. J. J. Chem. Phys. 1985;82:5053. doi: 10.1063/1.448627. [DOI] [Google Scholar]
  41. Kramida A., Ralchenko Yu. and J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.7.1). National Institute of Standards and Technology, Gaithersburg, MD. 2019, [online]. available: https://physics.nist.gov/asd, 2020, July 14 [Google Scholar]
  42. Yang Y. K. Cheng Y. Wu Y. Qu Y. Z. Wang J. G. Zhang S. B. New J. Phys. 2020;22:123022. doi: 10.1088/1367-2630/abcfed. [DOI] [Google Scholar]
  43. Salvat F. Fernández-Varea J. Williamson Jr W. Comput. Phys. Commun. 1995;90:151. doi: 10.1016/0010-4655(95)00039-I. [DOI] [Google Scholar]
  44. Morse P. M. Phys. Rev. 1929;34:57. doi: 10.1103/PhysRev.34.57. [DOI] [Google Scholar]
  45. Dunham J. L. Phys. Rev. 1932;41:721. doi: 10.1103/PhysRev.41.721. [DOI] [Google Scholar]
  46. Herzberg G., Molecular spectra and molecular structure. Vol.1: Spectra of diatomic molecules, 1950 [Google Scholar]
  47. Le Roy R. J. J. Quant. Spectrosc. Radiat. Transfer. 2017;186:167. doi: 10.1016/j.jqsrt.2016.05.028. [DOI] [Google Scholar]
  48. Le Roy R. J. Bernstein R. B. J. Chem. Phys. 1971;54:5114. doi: 10.1063/1.1674805. [DOI] [Google Scholar]
  49. Le Roy R. J. Liu W. J. Chem. Phys. 1978;69:3622. doi: 10.1063/1.437070. [DOI] [Google Scholar]
  50. Le Roy R. J. Comput. Phys. Commun. 1989;52:383. doi: 10.1016/0010-4655(89)90113-6. [DOI] [Google Scholar]
  51. Taylor J. R., Scattering theory: the quantum theory of nonrelativistic collisions, Courier Corporation, 2006 [Google Scholar]
  52. Friedrich H. and Friedrich H., Theoretical atomic physics, vol. 3, Springer, 2006 [Google Scholar]
  53. Zhang S. B. Wang J. G. Janev R. K. Phys. Rev. A. 2010;81:032707. doi: 10.1103/PhysRevA.81.032707. [DOI] [Google Scholar]
  54. Salvat F. Fernández-Varea J. Williamson Jr W. Comput. Phys. Commun. 1995;90:151. doi: 10.1016/0010-4655(95)00039-I. [DOI] [Google Scholar]
  55. Yang Y. K. Cheng Y. Peng Y. G. Wu Y. Wang J. G. Qu Y. Z. Zhang S. B. J. Quant. Spectrosc. Radiat. Transfer. 2020;254:107203. doi: 10.1016/j.jqsrt.2020.107203. [DOI] [Google Scholar]
  56. Wigner E. Witmer E. E. J. Appl. Phys. 1928;51:859. [Google Scholar]
  57. Bruna P. J. Grein F. J. Phys. Chem. A. 2006;110:4906. doi: 10.1021/jp0572838. [DOI] [PubMed] [Google Scholar]
  58. Van Dishoeck E. F. J. Chem. Phys. 1987;86:196. doi: 10.1063/1.452610. [DOI] [Google Scholar]
  59. Buckingham A. Q. Rev., Chem. Soc. 1959;13:183. doi: 10.1039/QR9591300183. [DOI] [Google Scholar]
  60. Khelifi N. Zrafi W. Oujia B. Gadea F. X. Phys. Rev. A. 2002;65:042513. doi: 10.1103/PhysRevA.65.042513. [DOI] [Google Scholar]
  61. Senekowitsch J. ONeil S. V. Werner H.-J. Knowles P. J. J. Chem. Phys. 1990;93:562. doi: 10.1063/1.459557. [DOI] [Google Scholar]
  62. Khelifi N. J. Phys. Chem. A. 2009;113:8425. doi: 10.1021/jp9040138. [DOI] [PubMed] [Google Scholar]

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES