Applications of density functional theory in COVID-19 drug modeling

Abstract

The rapidly evolving Coronavirus 2019 (COVID-19) pandemic has led to millions of deaths around the world, highlighting the pressing need to develop effective antiviral pharmaceuticals. Recent efforts with computer-aided rational drug discovery have allowed detailed examination of drug–macromolecule interactions primarily by molecular mechanics (MM) techniques. Less widely applied in COVID-19 drug modeling is density functional theory (DFT), a quantum mechanics (QM) method that enables electronic structure calculations and elucidations of reaction mechanisms. Here, we review recent advances in applying DFT in molecular modeling studies of COVID-19 pharmaceuticals. We start by providing an overview of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) drugs and targets, followed by a brief introduction to DFT. We then provide a discussion of different approaches by which DFT has been applied. Finally, we discuss essential factors to consider when incorporating DFT in future drug modeling research.

Introduction

The ongoing COVID-19 global pandemic has caused millions of deaths around the globe. Although effective COVID-19 vaccines have been developed within unprecedented timeframes, it is only recently that two small-molecule antiviral drug candidates were shown clinically to be capable of inhibiting the disease-causing coronavirus, SARS-CoV-2.1., 2., 3 The lack of effective antiviral pharmaceuticals highlights the pressing need to develop novel antiviral drugs to assist in combating the COVID-19 pandemic, to prevent more severe COVID-19 resulting in hospitalization and death.³

However, developing a lead molecule and an effective drug is challenging, even with known biological targets.⁴ During the early stage of drug development, rational drug design is an essential step for preclinical evaluations of drug properties.⁴ Fortunately, because of advances in both structural biology and computer-aided methodologies, drug discovery has evolved from the empirical-design era to the current rational-design era, making the process more efficient.⁵ Once the structures of biological targets are determined, modern computing technology enables the applications of chemo/bioinformatics and molecular modeling techniques to the study of drugs and medicines, which all significantly accelerated drug discovery efforts toward combating COVID-19.⁵

Molecular modeling of pharmaceuticals typically requires computations of large, complex, and often solvated biological systems, such that techniques with high computational costs (time and computing resources) are rendered impractical. Therefore, force field-based MM is an attractive approach given its low costs and relatively high calculation speed.⁶ MM is based on Newtonian-level calculations, such that its algorithm disregards changes at the electronic level and treats nuclei and electrons surrounding nuclei as perfect spheres. Atoms are treated as balls, and bonds as springs. Nonbonding atoms interact through van der Waals and electrostatic interactions.⁷ Therefore, biological systems comprising hundreds or even thousands of atoms are computationally suitable for MM treatments to describe receptor–ligand interactions. A major drawback of MM is its lack of chemical accuracy and, thus, it is not amenable for calculations of electronic properties. When chemical bonds break and new bonds form, MM can no longer afford energetic or geometric predictions because these changes occur at an electronic (quantum) level. Thus, QM-based calculations are favored for such detailed studies. In the context of the molecular modeling of drugs, QM studies allow close examination of the enzyme catalytic processes at the active site, and the mechanisms by which the inhibitor inhibits the catalytic activity of an enzyme. QM methods are also capable of providing energetic landscapes when such reactions happen.

DFT is the most popular and widely applied quantum theory to calculate the electronic structures of atoms and molecules. In drug modeling research, DFT is applied to study detailed electronic properties of isolated drug molecules and drug delivery systems, and is also applied in synergy with MM-based methodologies to study drug–receptor interactions. DFT provides the chemical accuracy otherwise unattainable by MM, making it particularly useful for describing reaction mechanisms when drug molecules act on enzyme active sites. Therefore, DFT serves well to both describe drug properties and their inhibitory actions on drug targets. To the best of our knowledge, no articles have been published that systematically review applications of DFT in COVID-19 drug modeling research. Therefore, here we introduce SARS-CoV-2 drug targets and drug compounds, fundamentals of DFT, followed by a review of literature grouped by applications of DFT in these studies. Finally, we discuss insights from COVID-19 drug modeling research so far and suggest essential factors to consider when setting up and incorporating DFT in future computational studies.

COVID-19 drug discovery: Biological targets and their inhibitors

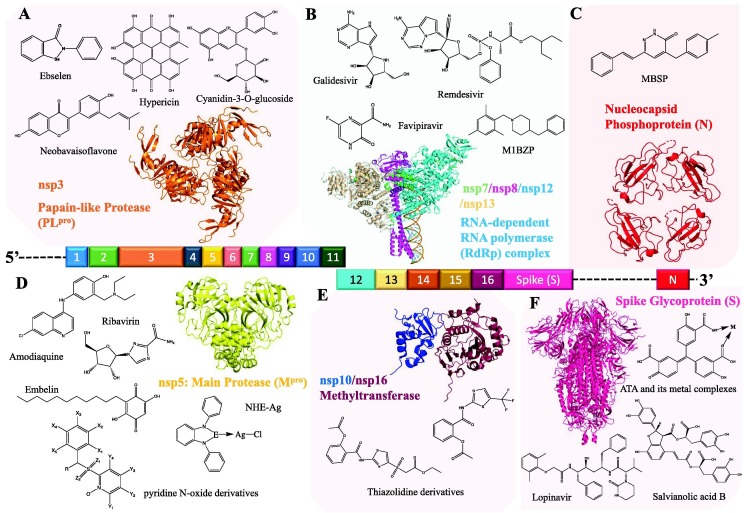
The key initial step in drug discovery is identifying target biomolecules that drug molecules bind to, and inhibit. Examination of the SARS-CoV-2 virology and its lifecycle reveals a range of proteins promising as drug targets, which are widely used for such purposes.¹ However, not every protein encoded by the SARS-CoV-2 genome is suitable for drug design; for instance, accessory proteins, which are involved in viral replication, assembly, and virus–host interactions, are poor drug targets because of their high mutation rates.⁸ Among all SARS-CoV-2 drug targets, six targets were found to be most popular among COVID-19 drug discovery research (Fig. 1 ).

Figure 1.

Map of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) protein targets, their positions on the viral RNA genome, and molecular structures of drug molecules targeting these proteins. The string represents the open reading frame (ORF) genome, with numbers corresponding to nonstructural protein (nsp) gene pieces. (a) The papain-like protease (PL^pro) [Protein Data Bank (PDB) ID: 6W9C] (J. Osipiuk et al., unpublished data, 2021) ebselen,¹⁷ hypericin and cyanidin-3-O-glucoside,²² neobavaisoflavone,²³(b) The RNA-dependent RNA polymerase complex, with its co-factor proteins (PDB ID: 6XEZ¹². Galidesevir,²⁴ remdesivir and its nucleotide analogs,¹⁸ 4-benzyl-1-(2,4,6-trimethyl-benzyl)-piperidine (M1BZP),¹⁹ favipiravir.²⁵(c) Nucleocapsid phosphoprotein (N) (PDB ID: 6WKP) (C. Chang et al., unpublished data, 2021). (E)-4-(4-methylbenzyl)-6-styrylpyridazin-3(2H)-one (MBSP).²⁶(d) Main protease (M^pro) (PDB ID: 6LU7²⁷. Amodiaquine and ribavirin,¹⁴ embelin,¹⁶ NHE–Ag (E = C, Si, and Ge) complex,²⁸ pyridine N-oxide derivatives.²⁹(e) Methyltransferase (PDB ID: 6W4H³⁰. Thiazolidine derivatives.¹⁵(f) Spike glycoprotein (S) (PDB ID: 6VXX³¹. Lopinavir and aurintricarboxylic acid (ATA) with its metal complexes,³² salvianolic acid B.³³

Among the six targets, the main protease (M^pro) of SARS-CoV-2, also known as the chymotrypsin-like cysteine protease (3CL^pro), is the most promising target, and is targeted the most in drug modeling studies. M^pro [Protein Data Bank (PDB) ID: 6LU7] is a crucial protease of coronaviruses and has the essential role of mediating viral replication and transcription, making it one of the most attractive drug targets for SARS-CoV-2.9., 10. Coronaviruses are subject to extensive mutagenesis; however, key proteins, such as M^pro, are highly conserved, because mutations in key proteins are often lethal to the virus. Thus, drugs that target the highly conserved M^pro are often effective in preventing viral proliferation processes and display broad-spectrum antiviral activity.¹¹ The M^pro active site contains a Cys − His catalytic dyad, and drugs that inhibit M^pro activity either form an irreversible covalent linkage with this dyad, or reversibly block substrate entry to the active site.

The RNA-dependent RNA polymerase (RdRp) is another promising macromolecular target: remdesivir, as the first US Food and Drug Administration (FDA)-approved antiviral drug, targets this enzyme. RdRp (PDB ID: 6XEZ) catalyzes the synthesis of viral RNA and, thus, also has a central role in the viral transcription cycle.¹² Drugs that target RdRp generally achieve inhibition via different mechanisms; remdesivir is a nucleotide analog and, when RdRp effectively incorporates its active remdesivir-triphosphate form, the RNA synthesis process is stalled.¹³ DFT has been applied the most in COVID-19 drug modeling studies that target these two enzymes: M^pro (e.g.,14., 15., 16., 17.) and RdRp(e.g.,18., 19.).

Small molecules have also shown promise as drug lead compounds for COVID-19 by acting on these targets (Fig. 1). The ligands (drugs) in these studies are diverse: natural products (e.g., embelin, hypericin, and naringin), repurposed antiviral pharmaceuticals (e.g., remdesivir, lopinavir, galidesivir, and amodiaquine), metal complexes of known ligands (e.g., ATA metal complexes and NHE–metal complexes), and newly synthesized compounds (e.g., M1BZP). Fig. 1 provides the molecular structures of these compounds and references to corresponding literature. In addition to small-molecule antiviral drugs, properties of drug delivery systems, such as C60 fullerene²⁰ or metallofullerenes,²¹ are also evaluated by DFT to assess their abilities as carriers of pharmaceutical compounds.

DFT overview

Here, we provide an overview of DFT to introduce fundamental concepts to nonexpert readers, especially those that are essential to understand in the context of computational drug modeling. We recommend that readers refer to tutorials or books, such as³⁸, for a more comprehensive guide to DFT.

Since Hohenberg and Kohn published their theorems of DFT during the 1960s, DFT has become a common computational method for electronic structure calculations. Instead of solving the many-electron Schrodinger Equation (wave function theory), which is a 3N-spatial-coordinate problem for N electrons, DFT shifts the focus to solving electron density $\rho$(r) with only three spatial coordinates.34., 35. Under the Born–Oppenheimer approximation, electronic energy and electronic properties of a system could be uniquely defined by the ground-state electron density $\rho$(r).35., 36., 37. Therefore, DFT has become one of the most popular methods over traditional wave function theory in computational chemistry for its low complexity and high accuracy. Here, we discuss Kohn–Sham (KS) DFT, the most common DFT formalism that approximates the kinetic energy in terms of fictitious single-particles orbitals within a non-interacting reference system.34., 36., 38. For a detailed description of KS-DFT, we refer readers to the book by Koch and Haolthausen.³⁸

Exchange-correlation functionals

Here, we provide a brief overview of DFT functionals; for further discussion, we refer readers to³⁶. For a given system, the electronic energy could be regarded as the sum of four parts: non-interacting electronic kinetic energy; nuclear–electron attraction; classical electron–electron repulsion; and the exchange–correlation (XC) energy, E_XC.34., 36. KS-DFT is formally exact, but the form of XC functional E_XC[$\rho$(r)] is not known exactly, and the search for accurate XC functionals remains one of the greatest challenges in DFT. Generally, the XC functional can be treated as a summation of the exchange term E_X[$\rho$(r)] and the correlation term E_C[$\rho$(r)].35., 36.

Types of functionals

The early generation of XC functionals uses the local density approximation (LDA), which assumes the XC energy for any given point in space depends only on the electron density at that point.34., 35. Generalized gradient approximation (GGA) reduces limitations of LDA functionals by considering that the real particle system is spatially inhomogeneous by adding the gradient of the density $\mathrm{\nabla }\rho$ into the XC functional,³⁵ such as the Perdew–Burke–Ernzerhof (PBE) exchange-correlational functional (Table 1 ). Meta-GGA functionals take two more additional variables from GGA into account: the kinetic energy density ${\tau }_{\sigma }$, and the Laplacian of the density ${\mathrm{\nabla }}^2{\rho }_{\sigma }$.35., 36., 37. Typically, Meta-GGA functionals perform better on predicting electronic properties, such as atomization energies.³⁵

Table 1.

Summary of the DFT XC functionals in recent (2020–2021) COVID-19 molecular modeling studies.^a, ^b

Functional	Type	$\mathit{\chi }$c	Exchange functional	Correlation functional	DC class	Description	Selected basis sets in study	Refs
PBE	LDA					Not used in studies reviewed
	GGA	0	PBE	PBE	None	Used to study inactivation mechanism Good at predicting solid-state properties Inaccurate in determining atomization energies and reaction barriers for molecular reactions.	Not mentioned	35., 36., 41.
	Meta-GGA					Not used in studies reviewed
B3LYP	Hybrid GGA	20	B88	Lee-Yang-Parr (LYP)	None	Widely used for many different types of ligand because of its relatively high accuracy and low cost; B3LYP is more suitable for main-group elements than for transition metals	6-31G, 6-31G* 6-311G(d,p) 6-311G* LANL2DZ def2-SVP	14., 15., 18., 20., 25., 32., 33., 37., 42.
B3PW91		20	B88	Perdew-Wang91	None	B3PW91 is similar to B3LYP; performs better for systems with uniform density	6-311++G**	36., 43.
PBE0		25	PBE	PBE	None	PBE0 is PBE functional with a 25% HF exchange functional; used to study inactivation mechanisms through covalent binding	6-31G* 6-311++G**	43., 44
PBE0-D3		25	PBE	PBE	III	PBE0-D3 is PBE0 with semiclassical correction on dispersion; describes thermochemistry better with low numerical complexity; dispersion correction does not affect density expression of system; used to study enzyme–substrate complex dynamical properties	6-31G**	39., 45.
M06-2X	Hybrid meta-GGA	54	M06-2X	M06-2X	II	Performs well in determining main-group thermochemical properties, noncovalent interactions, and barrier heights; however, not suitable for transition metal chemistry	6-311(d,p)	29, 37.
ωB97X-D	RSH GGA	22, 100d	Becke97	Becke97	III	Performs well for bonded interactions and barrier heights	def2-TZVP 6-31+G(d,p)	21., 36., 43.

^aThe types of XC functional are sorted by their levels of accuracy and computational complexity from low (top rows) to high (bottom rows). Some information is from35., 36., 37., 39., 46..

^bAbbreviations: DC Class, Dispersion-Correction Class (defined in³⁹GGA, generalized gradient approximation; GH, global hybrid; RSH, range-separation hybrid.

^c$\chi$: magnitude of the percentage of HF exchange functional in the total exchange functional part.

^d20 for short range exchange functional and 100 for long range exchange functional.

Functionals that consider Hartee–Fock (HF) exchange are hybrid functionals. Introducing HF exchange to GGA functionals significantly enhances their ability to describe self-interactions.³⁶ One of the most common functionals, B3LYP, is a hybrid GGA, and is used extensively in COVID-19 molecular modeling studies because of its proper balance between accuracy and cost. Global hybrid (GH) functionals treat the HF exchange as a global fraction, replacing a fraction of the exchange functional.³⁶ To accurately describe self-interaction further, more advanced functionals could be constructed through range separation.³⁶ Given its high accuracy, many COVID-19 modeling studies use ωB97X-D, an advanced range-separation hybrid (RSH) GGA functional created over the past decade (Table 1).

Dispersion correction

Dispersion interaction being described incorrectly is a major problem for many functionals. For example, B3LYP describes the long-range interaction as purely repulsive, which ignores the dispersion interaction.³⁹ To reduce such error, dispersion-correction terms are added in density functionals. Four classes of dispersion correction are described by Grimme.³⁹

When selecting appropriate functionals for DFT calculations, several factors need to be considered: desired chemical accuracy, computing resources available (computer clusters and time), and the given system (ligand and target). Table 1 details the accuracy and complexity of functionals.

Basis sets

In DFT, basis sets are sets of basis functions that are used to represent electronic wavefunctions. Basis functions are used to construct molecular orbitals (MOs), in which a large number of atomic orbitals (AOs) are expanded in linear combination to achieve a more flexible representation of MOs.⁴⁰ In practical density functionals, basis sets often make use of Gaussian-type functions, basis functions that resemble the true hydrogen AO functions and allow for easier computations. For a detailed description of different types of basis sets, refer to.⁴⁰ Table 1 lists basis sets that are selected in COVID-19 drug modeling studies for each corresponding functionals. The selection of basis sets must consider the balance between accuracy and costs. To more adequately describe wavefunctions, two types of addition could be incorporated in the basis sets: polarization functions that describe atomic charge polarizations in AOs, and diffuse functions that more accurately describe the portion of AOs distant from atomic nuclei.⁴⁰

DFT as a stand-alone technique for electronic property calculations

In the COVID-19 molecular modeling research reviewed here, DFT is extensively applied on isolated drug molecules. Molecular properties, such as reactivities, could be determined from DFT calculations, because they have the distinct advantage of providing electronic insight. Without studying protein–ligand interactions, electronic structures provided by DFT calculations could inform how drug compounds preferentially bind to their targets. The relationship between drug properties and resulting biological processes is dependent on the electronic properties of the target compounds.²⁵ Electronic properties of drug molecules determined by DFT in COVID-19 research are discussed in Table 2 ; studies that applied DFT for examining these properties of drug compounds are also cited.

Table 2.

Molecular electronic properties calculated by DFT.

DFT functions and calculated properties	Descriptions	Refs
Geometry optimization	Generates the lowest energy structures of molecules in a given system from an arbitrary starting state. Together with energy calculations, optimized geometry provides crucial structural insights into the relaxed structure of drug molecules and when they bind to their receptors	14., 20., 21., 28., 29, 32., 42., 48.
FMO	HOMO and LUMO together form FMOs. FMO governs reactivity of molecules and can be used to calculated multiple chemical reactivity descriptors, such as electronegativity, electrophilicity, and global hardness and softness	14., 15., 18., 20., 21., 25., 28., 32., 33., 42., 48., 49.
MEPs	EP correlates with dipole moment, electronegativity, and partial charges distributed in a molecule. Therefore, MEP provides a visual method to understand the relative polarity of a molecule	14., 20., 32., 42.
Mulliken atomic charges/natural population analysis	Both Mulliken atomic charge and natural population analysis are used to determine the partial charges of a molecule. Natural population analysis is an improved method with increased numerical stability and precision in calculation	14., 20., 26., 28., 48.
Spectral properties	DFT is applied to assist in interpreting experimental spectral data and provides competent calculations of excited state properties based on a time-dependent DFT (TD-DFT) method	21., 25., 32.

Geometry optimization is at the core of small-molecule DFT calculations. Optimized molecular geometry informs the lowest-energy conformation of the drug species, which is especially useful for complex ligand systems. Bui et al. examined tetrylene metal complexes as potential COVID-19 drug molecules. Their optimized molecular geometry allowed detailed structural characterizations of ligands binding to the metal centers and the resulting complexes.²⁸ Similarly, DFT allowed analyses of geometric properties of first-row transition metal-doped metallofullerenes, which are potential COVID-19 drug carriers, and their complexes when drug molecules bind.²¹

Another important property to study by DFT is frontier molecular orbital (FMO) calculations. FMO are the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), which govern the electron donating (HOMO) and accepting (LUMO) capabilities of a molecule. The HOMO–LUMO energy gap (E_HOMO-E_LUMO) is inversely correlated with the stabilization interactions of the compounds in protein–ligand interactions: a large HOMO–LUMO gap suggests high stability, large stabilizing interactions with the receptor, and poor reactivity of a molecule.²⁰ By this principle, FMOs are extensively calculated for drug stability and reactivity evaluations (see references in Table 2).

Molecular electrostatic potentials (MEPs) are another useful electronic property in COVID-19 drug modeling.⁴⁷ MEP allows for visualizations of molecular charge distributions and charge-related properties, such as reactive sites of the molecule prone to nucleophilic (most positive region) or electrophilic (most negative region) attacks.¹⁴ This informs molecular potentials for electrostatic interactions, such as van der Waals or hydrogen bonding interactions, also suggesting sites of potential covalent interactions upon binding to macromolecules.²⁰ In an evaluation of N-heterocycles as candidates of COVID-19 antiviral drugs,¹⁴ MEP maps identified electrophilic centers of the molecules that are electron-rich and prone to electron density donations. This informs binding modes and reaction potentials when these drugs bind to their targets.

DFT used in synergy with other modeling methodologies

MM techniques: molecular docking and molecular dynamics

Given high computational costs, direct application of DFT in complex biomolecular systems is limited. However, effective drug modeling relies on accurate depiction of drug–receptor interactions; this is when MM-based techniques have a role in COVID-19 drug modeling studies along with DFT.

Molecular docking treats the macromolecule (protein target) as rigid and allows the ligand (drug molecule) to be flexible within the defined grid, which is usually the active site of an enzyme. To compensate for the unrealistic nature of this rigid system, motions of this protein–ligand complex are then simulated by molecular dynamics (MD) calculations, described using classical Newtonian mechanics. Results of docking and MD studies provide pictures of binding modes between small–molecule drugs and the targets, together with potential noncovalent interactions. These resulting binding poses can be further analyzed in detail by DFT calculations: a common approach found in COVID-19 drug modeling research so far is to analyze using DFT the drug molecules shown to have the highest binding affinities with the target revealed by molecular docking or MD simulations. For instance, Rasool et al. studied the inhibitory potentials of 19 thiazolide derivatives on the M^pro and methyltransferase.¹⁵ DFT was executed for reactivity evaluations of compounds with the highest binding affinities. Evaluations were based on HOMO–LUMO gaps, which identified promising drugs with high reactivities as well as favored binding modes to the targets.¹⁵

More importantly, MM calculation results can be interpreted by electronic structures and properties of the drug compounds calculated by DFT. For example, MEP provides insights relating to charge distributions along the molecular surface, which informs regions that are prone to electrophilic or nucleophilic attacks during enzymatic reactions. Noncovalent bonding, such as van der Waals interactions and hydrogen bonds, could also be predicted by docking results combined with DFT-calculated electronic properties of drug molecules. Similarly, when comparing charge transfer potentials of drugs, FMO informs likely electron donors and acceptors. In fact, this DFT docking–MD approach is common in COVID-19 drug modeling studies.14., 15.

Such a combination of DFT and MM-based techniques allows for a detailed analysis of both molecular properties of the drug molecule and its interaction with target biomolecules. However, the separate application of DFT and MM-based techniques complicates the computational modeling procedure and reduces chemical accuracy. The more QM is applied, the more accurate depiction of chemical processes it provides at a molecular level, concerning changes of electronic structures. Here, we introduce the combined QM/MM method and its applications in COVID-19 drug modeling research.

QM/MM hybrid approach

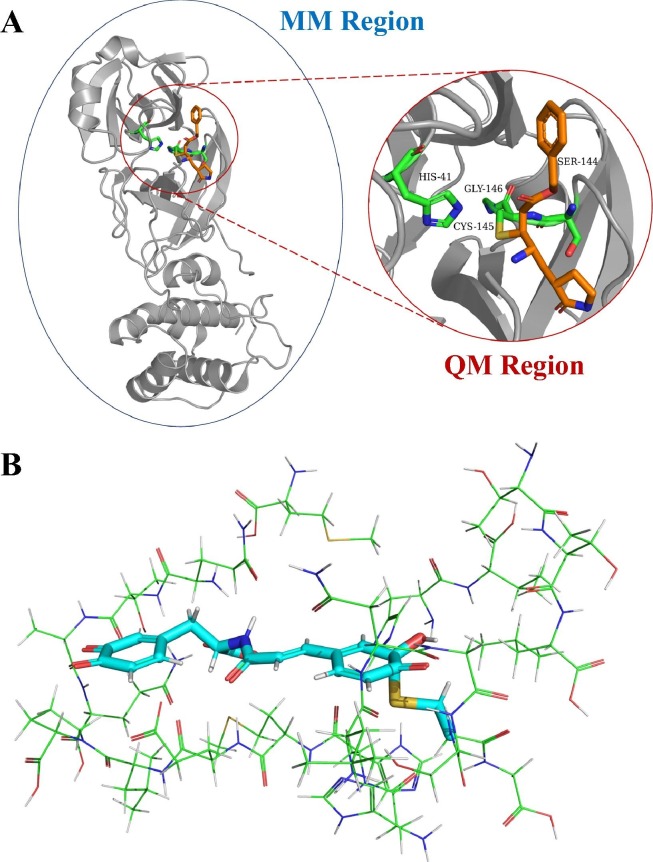
QM/MM is an integrated, hybrid mean of modeling chemical reactions in large biomolecular systems.⁵⁰ The QM/MM approach uses a QM method, usually DFT, for the chemically active enzymatic catalysis region (where bonds break and new bonds form), and combines it with an MM treatment for the rest of the macromolecule (Fig. 2 a).⁵¹ As a result, the complex macromolecular portion (comprising hundreds of atoms) can be effectively simulated by force field-based MM methods; the detailed description of chemical reactions or other electronic-level chemical processes, such as charge transfer at enzymatic active sites, would be calculated by QM methods.50., 51. This hybrid approach ensures the balance between affordable computational costs and necessary levels of chemical accuracy. A distinct advantage of QM/MM is that it directly provides information on both noncovalent (e.g., electrostatic interactions) and covalent interactions that occur between the ligand and the macromolecule.⁵⁰

Figure 2.

Hybrid quantum mechanics/molecular mechanics (QM/MM) and QM-cluster approaches. (a) The hybrid QM/MM approach. Blue oval circle indicates the QM region, which includes the whole protein. Shown is the monomer of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) M^pro in complex with inhibitor N3 [Protein Data Bank (PDB) ID: 6LU7]. Red circle indicates the QM region, which includes the inhibitor (ligand, shown in orange sticks) and selected amino acid residues (shown in green sticks) in the active site that often involve in the catalytic mechanism. (b) The QM-cluster approach. This figure provides a conformation of the active site of the protease–inhibitor complex after density functional theory (DFT) geometry optimization. Shown in green-line representations are the active site residues and in cyan-stick representation is the inhibitor, the clovamide molecule. It clearly suggests that a covalent bond is formed between one carbon on the quinone ring and the sulfur atom in the C145 catalytic residue. For details, refer to Ye et al.⁵⁹ Adapted with permission from⁵⁹.

In COVID-19 drug modeling research, QM/MM is less common than the DFT-MM approach, but is largely applied for the elucidation of reaction mechanisms of two types: catalysis mechanisms of SARS-CoV-2 enzymes52., 53. and inhibitory mechanisms of potential antiviral drugs on these enzymes.54., 55., 56., 57.

Arafet et al. used a hybrid M06-2X/6-31+G(d,p):AM1/MM method to investigate inhibition mechanisms of a known M^pro inhibitor, N3, and created energy profiles for covalent complex formation with the M^pro.⁵⁵ Two other designed covalent inhibitors were also studied by applying DFT/MM approach to evaluate their inhibitory potentials and mechanisms. QM/MM approach also enables researchers to gain novel insights into the catalytic mechanism of SARS-CoV-2 enzymes, which are crucial for mechanism-based rational drug design: QM/MM at a DLPNO-CCSD(T)/CBS//B3LYP/6-31G(d,p):AMBER level was applied to re-examine the mechanism of M^pro catalysis with detailed parameters: transition states, rate-limiting step, energy barriers, and free energy profiles of each step in the catalysis.⁵² In other studies, MD simulations are also combined with QM/MM methods to study the noncovalent enzyme–inhibitor/substrate complexes, before close examinations of reaction mechanisms by DFT/MM approaches.53., 57. Khrenova et al. performed a detailed dynamic study of the enzyme–substrate complex of M^pro.⁴⁵ They evaluated the electronic density features of the complex and showed that QM/MM-MD trajectories disclose substrate reactivity in M^pro, and were in good agreement with relevant experimental data.

Less applied in COVID-19 drug modeling studies is the QM-cluster approach, which treats the small-molecule drug and a truncated model of an enzyme receptor (usually dozens of surrounding amino acid residues in the active site) explicitly at an QM level.⁵⁸ Compared with QM/MM, this method applies only QM, providing high-level chemical accuracy particularly at enzyme catalytic regions to closely examine protein–ligand interactions and reaction mechanisms. However, one downside of this method is its high computational cost, because as it typically involves hundreds of atoms to be treated by DFT. Ye et al. applied the QM-cluster approach in their modeling of the inhibitory effects of a small molecule, clovamide, on M^pro.⁵⁹ Fig. 2b shows the 22 amino acids and the inhibitor ligand included in the study, in which the QM-cluster method provided crucial insights into covalent modifications by the inhibitor of the catalytic residues of M^pro.⁵⁹

Integrating DFT calculations in drug modeling research

Here, we propose a roadmap that highlights important factors to consider when developing a DFT-based drug modeling methodology. First, when developing an methodology that is based directly on modeling purposes, the general approach of how DFT is applied in a study is strongly dependent on the objectives. These studies can be categorized into three types: (i) studies intended to study solely molecular properties of isolated drug molecules at an electronic level. In this case, DFT is used as a stand-alone methodology20., 21., 49.; (ii) studies intended to study drug–receptor interactions would usually incorporate MM methodologies; and (iii) for those that examine mechanisms of inhibition reactions by a potential COVID-19 drug, QM/MM is often used and should be considered for future studies. A review⁵⁰ contains detailed information pertaining to the QM/MM method and its set-up, and is a great source for biochemists considering applying QM/MM in their studies.

Next, successful DFT calculations rely on appropriate set-ups. The two most important parameters to consider, functionals and basis sets, were introduced above. A list of computer codes and programs used to run DFT calculations can be found in Table S1 in the supplemental information online. Table S1 in the supplemental information online also supplies information regarding open-access options.

As discussed previously, the highly accurate nature of DFT has determined its limited applicability to macromolecular systems, which can be computationally expensive, time-consuming, and limiting regarding treatable size of given systems. A potential solution to circumvent these limitations is by parallel implementations of DFT programs, which makes DFT applicable to larger systems that encapsulate a larger portion of protein molecules.⁶⁰ This could be applied to QM/MM studies and effectively enlarges the QM region treatable by DFT. Linear-scaling DFT approaches (loaded in codes such as ONETEP⁶¹, allow such expansion of scopes and scales. Parallel implementation of DFT on graphical processing units (GPUs) are also shown to be capable of providing rapid and accurate electronic structure calculations.⁶² In the list provided in Table S1 in the supplemental information online, TeraChem is a GPU-based program that provides calculations with higher speed and, hence, improved efficiency.

Recently, semiempirical quantum mechanical methods GFNn-xTB (where n = 1, 2) were developed on the basis of density functional tight binding (DFTB) theory for equilibrium structure determination of both organic and metalloproteins.63., 64. These methods, particularly GFD2-xTB, provide an impressive level of accuracy in protein structure optimization with minimal deviation from experimental X-ray crystal structures compared with other force-field based MM methods.⁶⁴ The GFNn-xTB methods incorporate highly accurate, well-established D3 or D4 dispersion correction, two advanced successors that belong to the Class III dispersion correction mentioned in Table 1, allowing improved accuracy in macromolecular modeling.64., 65. In addition, these novel methods provide alternative approaches with affordable computational cost (even the largest proteins with up to 5000 atoms could be optimized in a few days on a small work-station), by which proteins and drug modeling research could be performed.⁶⁴ Given its low computational cost for a QM method, GFNn-xTB opens up new avenues for computational protein research and in silico rational, structure-based drug discovery.⁶⁴

Concluding remarks and future perspectives

The molecular modeling studies of COVID-19 pharmaceuticals reviewed in this article highlight the extensive application of DFT in the evaluation of molecular electronic properties of drug compounds. Most frequently, DFT is used to calculate electronic structures and properties of a given small molecule (Table 2). These electronic details correlate with properties of drug molecules and directly govern their binding modes with receptors. The most common purpose of application of DFT in studying small molecules is reactivity evaluations revealed by energy gaps of the FMO. The combined application of MM-based techniques along with DFT is common among COVID-19 drug modeling research. Moreover, when it comes to studying reaction mechanisms (inhibitory mechanisms by drug inhibitors or catalytic mechanisms by substrates), hybrid QM/MM is the prevalent approach because of its high efficiency in both tasks: examining drug–receptor bindings (MM) and predicting chemical reactions (QM). Integrating QM and MM calculations into one package, QM/MM offers researchers great convenience and efficiency. However, only those studies that investigate mechanisms are likely to apply this approach because of the complex nature involved in setting up QM/MM calculations in large biological systems. QM-cluster is a less applied, but relatively accurate approach to examine protein–ligand interactions at enzyme active sites and to predict reaction mechanisms.

Future drug modeling efforts should pay special attention to developing an appropriate methodology with proper set-ups (including codes, programs, levels of theory, etc.). MM techniques are fast, efficient, and easy approaches to describe how drug molecules bind macromolecular targets, but they lack chemical accuracy and are unable to provide electronic insights. QM techniques, represented by DFT, are capable of offering electronic details and predict reaction mechanisms (flow of electrons) between drug molecules and receptors, but are computationally expensive and time-consuming. QM/MM requires expertise in both QM and MM and sufficient computing resources. Developing a method that is suitable for research objectives while balancing computational costs and chemical accuracy is at the core of drug modeling studies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

The following are the Supplementary data to this article: