Webbing a network of reliable thermochemistry around lignin building blocks: tri-methoxy-benzenes

Abstract

Methoxy-substituted benzenes are the simplest fragments from the lignin separation feedstock. Extensive experimental thermochemical studies of these compounds were carried out, including vapor pressure measurements, combustion and differential scanning calorimetry. These data were evaluated using empirical, semi-empirical and quantum chemical methods. The consistent sets of evaluated thermodynamic data were used to design the method for predicting enthalpies of vaporisation and enthalpies of formation of di- and tri-substituted benzenes. It has been found that the agglomeration of substituents on the benzene ring has dramatic consequences for the energetics of the molecule (in terms of the enthalpy of formation), as well as for the energetics of intermolecular interactions (in terms of the enthalpy of vaporisation). These observations are essential to reliably assess the energetics of the molecules that appear in reaction products of lignin transformations in value-adding chemicals and materials.

Methoxy-substituted benzenes are the simplest fragments from the lignin separation feedstock.

1. Introduction

Lignin has received considerable attention as a renewable source of aromatics.¹ Catalytic processing or pyrolysis of lignin is important for a sustainable production of platform chemicals and biofuels. A better understanding of lignin processing at the molecular level is indispensable for developing process control strategies to optimize the product formation.² In order to understand the energetics and mechanisms that control the entire monomer formation and distribution, reliable thermodynamic data must be collected and evaluated for building blocks that result from the thermal conversion of lignin. The basic properties such as enthalpies of formation and enthalpies of phase transitions (vaporisation, sublimation and fusion) are required for energy balance calculations and dynamic equilibrium determinations in valorization reactions.^3–6

The correlation of thermodynamic properties of lignin constituting monomers with their molecular structures can open a window of opportunity for reliable predicting the energetics of large lignin building blocks. Such a prediction is crucial for optimizing the lignin conversion into value-adding and sustainable platform chemicals.

The aim of this work is to use experimental and computational methods to obtain reliable thermodynamic information for the development of quantitative structure–property relationships in molecules that are relevant for the valorization of lignin. In order to facilitate the understanding of the reactions of the lignin conversion and to control the chemical processes, “model compounds” (which imitate the structural units present in lignin) can be examined instead.^7–9 The tri-methoxy-substituted benzenes modelling lignin structural units examined in this work are shown in Fig. 1.

Fig. 1. Tri-methoxy-benzenes studied in this work: 1,2,3-tri-methoxy-benzene, 1,2,4-tri-methoxy-benzene, 1,3,5-tri-methoxy-benzene, 3,4,5-tri-methoxy-toluene.

The thermochemical information available on trimethoxy-benzenes is scarce.^8,9 Enthalpies of sublimation and enthalpies of formation of 1,2,3-trimethoxy and 1,3,5-trimethoxy-benzene were determined by using drop and combustion calorimetry by Matos et al.⁸ The enthalpy of vaporisation of 1,3,5-trimethoxybenzene is reported from the correlation gas-chromatography.⁹

This paper continues our previous systematic studies^{5–7,10–12} on the investigation of model compounds relevant to the valorization of biomass. Here we present results on enthalpies of formation, phase transitions, and vapor pressures of a series of tri-methoxy-benzenes of general formulas given in Fig. 1. The data available in the literature and new experimental results were evaluated and checked for internal consistency. The consistent thermochemical data sets for tri-methoxy-benzenes have been used for the design and the development of a “centerpiece” group-contribution approach being necessary for appraisal of enthalpies of formation and enthalpies of vaporisation of substituted benzenes important for downstream processing of lignin-derived feedstock into end products.

2. Experimental procedure

2.1. Materials

Commercially available samples of tri-methoxy-substituted benzenes (see Table S1†) with purities of 0.98 to 0.99 mass fraction were additionally purified. Solid samples were purified using fractional sublimation under reduced pressure. Liquid samples were purified using fractional vacuum distillation. Purities were determined using a gas chromatograph equipped with a capillary column HP-5 and a flame ionization detector. No impurities (greater than the mass fraction 0.0009) were detected. We used the Mettler Toledo DL38 Karl Fischer Titrator for analyzing the water content in samples. A negligible mass fraction of water close to the detection level was detected by using the HYDRANAL™ as the reagent.

2.2. Experimental and theoretical thermochemical methods

The gas-phase standard molar enthalpy of formation, Δ_fH^o_m(g), of a compound under study is the comprehensive experimental thermochemical property that includes all enthalpies of phase transitions (sublimation, evaporation, and fusion) in combination with combustion enthalpy. Vapor pressures of tri-methoxy-benzenes at different temperatures were measured by the transpiration.^13–15 The standard molar enthalpies of sublimation, Δ^g_crH^o_m, and the standard molar enthalpies of vaporisation, Δ^g_lH^o_m, were derived from vapor pressures temperature dependences. A high-precision self-made combustion calorimeter equipped with a static bomb was used to derive liquid and crystalline phase standard molar enthalpies of formation, Δ_fH^o_m(cr or liq), of tri-methoxy-benzenes. The experimental procedures have been described elsewhere.^16,17 The standard molar heat capacity C^o_p,m(cr) of 1,2,3-trimethoxybenzene and the standard molar enthalpies of fusion, Δ^l_crH^o_m, of tri-methoxy-benzenes were measured by using differential scanning calorimetry (DSC).¹⁸

We used quantum-chemical calculations to get theoretical standard molar gas-phase enthalpies of formation of tri-methoxy-benzenes. Conformational analysis was performed with the ADF program¹⁹ with the methods M06L/TZ2P and M06/QZ4P based on the Slater–Cartesian functions. The convergence of energy was better than 10⁻⁶ a.u. and for the gradients (forces) not more than 10⁻⁶ a.u. Å⁻¹. The fundamental harmonic frequencies of methoxy-substituted benzenes were obtained using M06L/TZ2P and corrected to anharmonic using a cubic polynomial. For this we found the harmonic frequencies of benzoquinone and methyl-benzoquinone²⁰ according to the M06L/TZ2P method, which contain a similar amount of atoms and well-established spectra, and the parameters of the third degree approximation polynomial were calculated based on the total set of frequencies available for the two molecules compared to the experimental values. The composite G4,²¹ and G3MP2 (ref. 22) methods from Gaussian 09 software²³ as well as the M06/QZ4P²⁴ method were used for calculations of enthalpies H₂₉₈-values, which were finally converted to the Δ_fH^o_m(g) and discussed. Calculations were performed for the most stable conformer of each compound.

3. Results and discussion

3.1. Standard molar heat capacity, C^o_p,m, measurements

Experimental heat capacity measurements are important in order to calculate heat balances in technological processes. In addition, heat capacities are required for adjustment sublimation/vaporisation enthalpies to any temperature of interest, and to reduce the results of combustion calorimetry to the standard conditions. From our experiences, the empirical group contribution method developed by Chickos et al.²⁵ (see Table S2†) can be reliably applied for capacity C^o_p,m(cr) and capacity C^o_p,m(liq) estimations. However, the validity of this approach towards tri-methoxy-benzenes have to be checked. In this work we measured heat capacity of 1,2,3-trimethoxy-benzene. Primary experimental results are given in Table S2 in the ESI.† The experimental value C^o_p,m(cr, 298.15 K) = 240.9 J K⁻¹ mol⁻¹ (see Table S3†) is in excellent agreement with the estimate C^o_p,m(cr, 298.15 K) = 243.3 J K⁻¹ mol⁻¹ (see Table S2†). Hence, the heat capacities at the reference temperature T = 298.15 K estimated according to Chickos et al.²⁵ (see Table S2†) have been used for the temperature adjustments of experimental vaporisation enthalpies as it shown in Section 3.2.

3.2. Thermodynamics of sublimation/vaporisation

The experimental vapor pressures p_i for the tri-methoxy-benzenes (see Table S4†) at different temperatures were measured with help of the transpiration method. They were fitted with the following equation:¹³

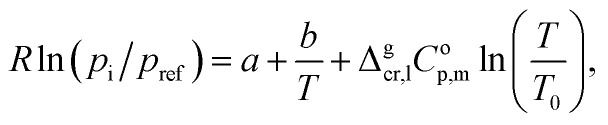1

where Δ^g_cr,lC^o_p,m is the difference of the molar heat capacities of the gas and the crystal (or liquid) phases respectively (see Table S2†), a and b are adjustable parameters, R = 8.31446 J K⁻¹ mol⁻¹ is the molar gas constant, and the reference pressure p_ref = 1 Pa. The temperature T₀ appearing in eqn (1) is generally an arbitrarily chosen reference temperature. In this work it was chosen to be T₀ = 298.15 K.

Vapor pressure measured at different temperatures, T, measured in this work have been used to derive the enthalpies of sublimation/vaporisation of tri-methoxy-benzenes using the following equation:

Δ^g_cr,lH^o_m(T) = −b + Δ^g_cr,lC^o_p,m × T 2

Sublimation/vaporisation entropies at temperatures T were also derived from the vapor pressures temperature dependences using eqn (3):

Δ^g_cr,lS^o_m(T) = Δ^g_cr,lH^o_m/T + R ln(p_i/p_ref) 3

Primary experimental vapor pressures measured at different temperatures by the transpiration method, coefficients a and b of eqn (1), as well as values of Δ^g_cr,lH^o_m(T) and Δ^g_cr,lS^o_m(T) are given in Table S4.† A short compilation of these data referenced to T = 298.15 K is given in Table 1. The method for calculating the combined uncertainties of the vaporisation/sublimation enthalpies includes uncertainties from the experimental conditions of transpiration, uncertainties in vapor pressure and uncertainties due to the temperature adjustment to T = 298.15 K as described elsewhere.^14,15

Results from the transpiration method: coefficient a and b of eqn (1), standard molar sublimation/vaporisation enthalpies Δ^g_cr,lH^o_m, standard molar sublimation/vaporisation entropies Δ^g_cr,lS^o_m, and standard molar vaporisation Gibbs energies Δ^g_cr,lG^o_m at the reference temperature T = 298.15 K^a.

	a	−b	−ΔglCop,mb, J K−1 mol−1	ΔglHomc, kJ mol−1	ΔglSomd, J K−1 mol−1	ΔglGom, kJ mol−1
1,2,3-Tri-methoxy-benzene (cr)	348.4	103 494.0	37.2	92.4 ± 0.7	215.5 ± 1.3	28.2 ± 0.1
1,2,3-Tri-methoxy-benzene (liq)	348.3	102 212.3	97.9	73.0 ± 0.5	154.6 ± 1.2	26.9 ± 0.1
1,2,4-Tri-methoxy-benzene (liq)	350.8	104 844.6	97.9	75.7 ± 0.5	157.2 ± 1.2	28.8 ± 0.1
1,3,5-Tri-methoxy-benzene (cr)	333.9	101 366.0	37.2	90.3 ± 0.5	201.0 ± 1.1	30.4 ± 0.1
1,3,5-Tri-methoxy-benzene (liq)	329.3	97 850.6	97.9	68.7 ± 0.4	135.7 ± 0.5	28.2 ± 0.1
3,4,5-Tri-methoxy-toluene (liq)	366.9	109 273.7	105.8	77.7 ± 0.5	165.3 ± 1.0	28.4 ± 0.1

^aUncertainties are expressed as the standard uncertainty (at 0.68 level of confidence, k = 1).

^bFrom Table S2.

^cCalculated by eqn (2) (see primary data in Table S4).

^dCalculated by eqn (3) (see primary data in Table S4).

Vapor pressures of tri-methoxy-benzenes have been measured for the first time. However, the sublimation enthalpies of 1,2,3-tri-methoxy- and 1,3,5-trimethoxy-benzenes were measured at 375 K (see Table 2) using the “vacuum sublimation” drop microcalorimetric method.⁸ The observed enthalpies of sublimation were adjusted to the reference temperature T = 298.15 K by using values of Δ^T_{298.15 K}H^o_m(g) estimated by a group-contribution method with values from Stull et al.²⁶ These results are listed in Table 2 for the sake of comparison with values derived in this work. However, in contrast to our transpiration results, the original uncertainties reported for the calorimetric values do not include the uncertainties due to the temperature adjustments. In order to get a fair comparison, we assumed that the uncertainties in the temperature adjustment of vaporisation/sublimation enthalpies from the experimental T to the reference temperature add 20% to the total adjustment.²⁷ The calorimetric results for 1,2,3-tri-methoxy- and 1,3,5-trimethoxy-benzenes with the re-assessed uncertainties are listed in Table 2 (column 5). As can be seen from this table, our “indirect” transpiration values are in disagreement with the “direct” calorimetric results even taking into account large experimental uncertainties of the latter values. There is no plausible explanation for this disagreement and we decided to validate our new experimental results as follows in Section 3.3.

Compilation of enthalpies of sublimation/vaporisation Δ^g_cr,lH^o_m of tri-methoxy-benzenes.

Compound/CAS	Methoda	T-Range, K	Δgcr,lHom(Tav), kJ mol−1	Δgcr,lHom(298.15 K)b, kJ mol−1	Ref.
1,2,3-Tri-methoxy-benzene (cr)	DC	375	113.4 ± 0.8	(98.0 ± 3.2)	8
	T	288.2–314.3	92.3 ± 0.4	92.4 ± 0.7	This work
	F			92.0 ± 0.7	Table 5
				92.2 ± 1.0 c	Average
1,2,3-Tri-methoxy-benzene (liq)	T	318.1–346.3	69.7 ± 0.3	73.0 ± 0.5	This work
	J x			72.9 ± 0.5	Table 3
				73.0 ± 0.7 c	Average
1,2,4-Tri-methoxy-benzene (liq)	T	309.7–350.1	72.5 ± 0.3	75.7 ± 0.5	This work
	J x			76.0 ± 0.5	Table 3
				75.9 ± 0.7 c	Average
1,3,5-Tri-methoxy-benzene (cr)	DC	375	116.0 ± 1.9	(100.6 ± 3.6)	8
	T	288.0–326.2	89.9 ± 0.3	90.3 ± 0.5	This work
	F			90.7 ± 0.7	Table 5
				90.4 ± 0.8 c	Average
1,3,5-Tri-methoxy-benzene (liq)	CGC	298		68.2 ± 2.0	9
	T	330.5–375.3	63.4 ± 0.2	68.7 ± 0.4	This work
	J x			69.0 ± 1.0	Table 4
				68.7 ± 0.8 c	Average
3,4,5-Tri-methoxy-toluene (liq)	T	327.2–366.2	72.7 ± 0.3	77.7 ± 0.5	This work
	J x			77.6 ± 0.5	Table 3
				77.7 ± 0.7 c	Average

^aTechniques: DC = drop calorimetry; T = transpiration method; J_x – derived from correlation of experimental vaporisation enthalpies with Kovats's indices (see text); CGC – correlation gas-chromatographic method (see text). F = derived from experimental data according to eqn (6) (see text).

^bUncertainties of the vaporisation and sublimation enthalpies is expressed as the standard uncertainty (0.683 level of confidence, k = 1). They were calculated according to a procedure described elsewhere.^21,22 Uncertainties include uncertainties from the experimental conditions and the fitting equation, vapor pressures, and uncertainties from adjustment of vaporisation/sublimation enthalpies to the reference temperature T = 298.15 K.

^cWeighted mean value (the uncertainty was taken as the weighing factor). Uncertainty of the vaporisation/sublimation enthalpy is expressed as the expanded uncertainty (0.95 level of confidence, k = 2). Values in brackets were not included in the averaging. Values highlighted in bold were recommended for thermochemical calculations.

3.3. Kovats's retention indices for validation of experimental vaporisation enthalpies

The disagreement of sublimation enthalpies observed for 1,2,3-tri-methoxy-benzene and 1,3,5-tri-methoxy-benzene have prompted the search for additional methods to validate our new transpiration results. In this context, we have applied our experiences with the Correlation Gas-Chromatographic (CGC) method.^6,7,9 This method is a valuable option to establish the consistency of the experimental results for investigated compounds by correlating the experimental Δ^g_lH^o_m(298.15 K)-values with their Kovats's indices²⁸ (see details in the ESI†). The literature data available on the Kovats's retention indices, J_x, for methoxy substituted benzenes were taken for correlation with the Δ^g_lH^o_m(298.15 K)-values measured in this work (see Table 1). Results from these correlations are given in Tables 3 and 4.

Correlation of vaporisation enthalpies, Δ^g_lH^o_m(298.15 K), of 1,2-di-methoxy-substituted benzenes with their Kovats's indices (J_x)^a.

Compound	J x b	ΔglHom(298.15 K)exp, kJ mol−1	ΔglHom(298.15 K)calcc, kJ mol−1	Δ d, kJ mol−1
1,2-Di-methoxy-benzene	1146	64.5 ± 0.3 (ref. 5)	64.5	0.0
1,2,3-Tri-methoxy-benzene	1315	73.0 ± 0.5e	72.9	0.1
1,2,4-Tri-methoxy-benzene	1378	75.7 ± 0.5e	76.0	−0.3
3,4,5-Tri-methoxy-toluene	1410	77.7 ± 0.5e	77.6	0.1
2,3,5-Tri-methoxy-toluene	1527	—	83.3	—

^aUncertainty is given as the standard uncertainty (0.683 level of confidence, k = 1).

^bKovats's indices, J_x, on standard non-polar columns from ref. 29.

^cCalculated using eqn (4).

^dDifference between experimental and calculated by eqn (4) values (columns 3 and 4).

^eExperimental data measured by using the transpiration method from (see Table 1).

Correlation of vaporisation enthalpies, Δ^g_lH^o_m(298.15 K), of 1,3- and 1,4-di-methoxy-substituted benzenes with their Kovats's indices (J_x)^a.

Compound	J x b	ΔglHom(298.15 K)exp, kJ mol−1	ΔglHom(298.15 K)calcc, kJ mol−1	Δ d, kJ mol−1
1,3-Dimethoxy-benzene	1143	59.7 ± 0.2 (ref. 5)	60.6	−0.9
1,4-Dimethoxy-benzene	1158	61.6 ± 0.2 (ref. 5)	61.1	0.5
3,5-Dimethoxy-toluene	1233	64.5 ± 1.2 (ref. 30)	63.5	1.0
1,3,5-Tri-methoxy-benzene	1405	68.7 ± 0.4e	69.0	−0.3
2,4,6-Tri-methoxy-toluene	1486	—	71.6	—

^aUncertainties are given as the standard uncertainty (0.683 level of confidence, k = 1).

^bKovats's indices, J_x, on standard non-polar columns from ref. 29.

^cCalculated using eqn (5).

^dDifference between experimental and calculated by eqn (5) values (columns 3 and 4).

^eExperimental data measured by using the transpiration method from (see Table 1).

It is known, that the Δ^g_lH^o_m(298.15 K)-values correlate linearly with Kovats's indices in various homologous series of alkylbenzenes, alkanes, aliphatic ethers, alcohols, or in a series of structurally similar compounds.³¹ As expected, the Δ^g_lH^o_m(298.15 K)-values correlated linearly with J_x values of methoxy-substituted benzenes, but it has turned out that the 1,2-dimethoxy-substituted species (see Table 3) and the 1,3- together with the 1,4-dimethoxy-substituted species (see Table 4) belong to the different lines. For the set of the methoxy-benzenes collected in Table 3, the following linear correlation was obtained:

Δ^g_lH^o_m(298.15 K)/(kJ mol⁻¹) = 7.9 + 0.0494 × J_x with (R² = 0.999) 4

For the set of the methoxy-benzenes collected in Table 4, the following linear correlation was obtained:

Δ^g_lH^o_m(298.15 K)/(kJ mol⁻¹) = 24.3 + 0.0318 × J_x with (R² = 0.953) 5

The results of the correlations with Kovats's indices are in a good agreement with those of the transpiration method (see Table 1). Such good agreement can be seen as additional validation of the experimental data measured in this work by using the transpiration method (see Tables 1 and 2). It can be seen from Table 3, that differences between experimental and calculated according to eqn (4) are mostly below 0.5 kJ mol⁻¹. Results given in Table 4, show that differences between experimental and calculated according to eqn (5) are mostly below 1.0 kJ mol⁻¹. Hence, the uncertainties of enthalpies of vaporisation which are estimated from the correlation the Δ^g_lH^o_m(298.15 K) − J_x are evaluated with these uncertainties of ±0.5 kJ mol⁻¹ (see Table 3) and of ±1.0 kJ mol⁻¹ (see Table 4).

3.4. Thermodynamics of liquid–gas, solid–gas, and solid–liquid phase transitions

Another valuable option for establishing the consistency of experimental data on phase transitions (liquid–gas, solid–gas, and solid–liquid) for the compound examined is the common thermochemical equation:

Δ^g_crH^o_m(298.15 K) = Δ^g_lH^o_m(298.15 K) + Δ^l_crH^o_m(298.15 K) 6

We have used this option for 1,2,3-tri-methoxy-benzene and 1,3,5-tri-methoxy-benzene. Indeed, for 1,2,3-tri-methoxy-benzene, the sublimation enthalpy Δ^g_crH^o_m(298.15 K) = 92.4 ± 0.7 kJ mol⁻¹ was measured using the transpiration method below the melting point (see Table 1) and the vaporisation enthalpy Δ^g_lH^o_m(298.15 K) = 73.0 ± 0.5 kJ mol⁻¹ was derived from vapor pressures measured above the melting point (see Table 1). The latter value is also in agreement with those from J_x-correlation Δ^g_lH^o_m(298.15 K) = 72.9 ± 0.5 kJ mol⁻¹ (see Table 3). The consistency of phase transitions available for 1,2,3-tri-methoxy-benzene can be easily established with help of eqn (6) and the experimental enthalpy of fusion for this compound Δ^l_crH^o_m(298.15 K) = 19.0 ± 0.5 kJ mol⁻¹ (see Table 5) as follows:

Δ^g_crH^o_m(298.15 K, 1,2,3-tri-methoxy-benzene) = 73.0 + 19.0 = 92.0 ± 0.7 kJ mol⁻¹ 7

Phase transitions thermodynamics of tri-methoxy-benzenes (in kJ mol⁻¹)^a.

Compounds	T fus, K	ΔlcrHom at Tfus	ΔlcrHomb	ΔglHomc	ΔgcrHomd
			298.15 K
1	2	3	5	6	7
1,2,3-Tri-methoxy-benzene	318.3 ± 0.5	20.2 ± 0.3	19.0 ± 0.5	73.0 ± 0.5	92.0 ± 0.7
1,3,5-Tri-methoxy-benzene	329.4 ± 0.5	23.9 ± 0.3	22.0 ± 0.6	68.7 ± 0.4	90.7 ± 0.7

^aUncertainty is expressed as the standard uncertainty (0.683 level of confidence, k = 1).

^bThe experimental enthalpies of fusion Δ^l_crH^o_m measured at T_fus were adjusted to 298.15 K with help of the equation:²⁷ Δ^l_crH^o_m(298.15 K)/(J mol⁻¹) = Δ^l_crH^o_m(T_fus/K) − (Δ^g_crC^o_p,m − Δ^g_lC^o_p,m) × [(T_fus/K) − 298.15 K], where Δ^g_crC^o_p,m and Δ^g_lC^o_p,m were taken from Table S2. Uncertainties in the temperature adjustment of fusion enthalpies from T_fus to the reference temperature are estimated to account with 30% to the total adjustment.²⁷

^cFrom Table 1.

^dCalculated as the sum of columns 5 and 6 in this table.

This estimate is in an excellent agreement with the transpiration experiment Δ^g_crH^o_m(298.15 K) = 92.4 ± 0.7 kJ mol⁻¹ (see Table 1). In the same way we checked the consistency of phase transitions for 1,2,3-tri-methoxy-benzene with the data compiled in Table 5. The estimated according to eqn (6) sublimation enthalpy Δ^g_crH^o_m(298.15 K) = 90.7 ± 0.7 kJ mol⁻¹ (see Table 5) is an excellent agreement with the transpiration experiment Δ^g_crH^o_m(298.15 K) = 90.3 ± 0.5 kJ mol⁻¹ (see Table 1).

The consistency of the solid–liquid, solid–gas, and liquid–gas phase transitions for 1,2,3-tri-methoxy-benzene and 1,2,3-tri-methoxy-benzene derived in this work could be regarded as an indirect support of the reliability of our new transpiration results.

3.5. Standard molar enthalpies of formation from combustion calorimetry

Specific energies of combustion, Δ_cu°, of highly pure samples of 1,2,3-tri-methoxy-benzene, 1,2,4-tri-methoxy-benzene, and 3,4,5-tri-methoxy-toluene were measured by using combustion calorimetry. Auxiliary data required for the reduction of the combustion results are presented in Table S5.† Typical examples of combustion experiments are given in Table S6.† The standard molar enthalpies of combustion Δ_cH^o_m(cr) and the standard molar enthalpies of formation Δ_fH^o_m(cr) were derived (see Table 6) from the specific energies of combustion. Combustion results for Δ_cu° and Δ_cH^o_m are referenced to the reaction for the tri-methoxy-benzenes:

C₉H₁₂O₃(cr,l) + 10.5 × O₂(g) = 9 × CO₂(g) + 6 × H₂O(liq) 8

and for the 3,4,5-trimethoxy-toluene:

C₁₀H₁₄O₃(liq) + 12 × O₂(g) = 10 × CO₂(g) + 7 × H₂O(liq) 9

All results for combustion experiments at T = 298.15 K (p° = 0.1 MPa) of the methoxy substituted benzenes^a.

	1,2,3-Tri-methoxy-benzene (cr)	1,2,4-Tri-methoxy-benzene (liq)	3,4,5-Tri-methoxy-toluene (liq)
	28 633.2	28 640.8	30 018.3
	28 617.4	28 649.1	30 020.6
	28 631.6	28 631.5	30 002.9
	28 620.0	28 640.3	30 014.5
	28 610.2	28 621.4	30 025.5
			30 034.9
Δcu°(cr or liq)/(J g−1)a	−28622.5 ± 4.4	−28636.6 ± 4.7	−30019.5 ± 4.4
ΔcHom(cr or liq)/(kJ mol−1)b	−4817.7 ± 1.8	−4820.1 ± 1.9	−5475.0 ± 2.0
ΔfHom(cr or liq)/(kJ mol−1)b	−438.9 ± 2.1	−436.5 ± 2.2	−460.9 ± 2.4

^aUncertainty of combustion energy is expressed as standard deviation of the mean.

^bUncertainties are expressed as the twice standard deviation of the mean.

The conventional procedure³² was used for reduction of the combustion energy to the standard state. Uncertainties related to combustion experiments are calculated according to the guidelines developed by Olofsson.³³ The Δ_fH^o_m(cr,l)-values of methoxy-substituted benzenes were obtained (see Table 6) applying the Hess's law to eqn (8) or (9) with the help of recommended by CODATA³⁴ standard molar enthalpies of formation of H₂O(liq) and CO₂(g).

Compilation of thermochemical data for methoxy-substituted benzenes is given in Table 7.

Thermochemical data for methoxy-substituted benzenes at T = 298.15 K (p° = 0.1 MPa, in kJ mol⁻¹)^a.

Compound	−ΔcHom(cr,l)	ΔfHom(cr,l)exp	Δgcr,lHomb	ΔfHom(g)exp	ΔfHom(g)theorc
1	2	3	4	5	6
1,2,3-Tri-methoxy-benzene (cr)	4819.5 ± 2.5 (ref. 8)	−437.0 ± 2.8
	4817.7 ± 1.8d	−438.9 ± 2.1
		−438.2 ± 1.7	92.2 ± 1.0	−346.0 ± 2.0	−350.6 ± 2.4
1,2,4-Tri-methoxy-benzene (liq)	−4820.1 ± 1.9d	−436.5 ± 2.2	75.9 ± 0.7	−360.6 ± 2.3	−360.6 ± 2.3
1,3,5-Tri-methoxy-benzene (cr)	4784.6 ± 2.9 (ref. 8)	−472.0 ± 3.1	90.4 ± 0.8	−381.6 ± 3.2	−382.1 ± 1.2
3,4,5-Tri-methoxy-toluene (liq)	−5475.0 ± 2.0d	−460.9 ± 2.4	77.7 ± 0.7	−383.2 ± 2.5	−382.1 ± 1.2

^aThe uncertainties are given as the twice standard deviation. Value given in bold is the weighted average and it was used for thermochemical calculations.

^bFrom Table 2.

^cTheoretical value calculated as the average from G4, G3MP2, and M06/QZ4P results (see Table 8).

^dMeasured in this work.

The Δ_fH^o_m(liq)-values of 1,2,4-tri-methoxy-benzene and 3,4,5-tri-methoxy-toluene were measured for the first time. The Δ_fH^o_m(cr,l)-values for 1,2,3-tri-methoxy-benzene and 1,3,5-tri-methoxy-benzene were previously reported by Matos et al.⁸ (see Table 7). Our new result for 1,2,3-tri-methoxy-benzene agrees well with their result. Nevertheless, it is reasonable to validate all available results for the methoxy-substituted benzenes with help of quantum-chemical calculations as it shown in Section 3.6.

3.6. Gas-phase enthalpies of formation: experiment and theory

The experimental gas-phase standard molar enthalpies of formation Δ_fH^o_m(g)_exp are derived from experimental results on sublimation/vaporisation enthalpies (see Table 2) and results from the combustion calorimetry (see Table 6) according to the common thermochemical equations:

Δ_fH^o_m(g, 298.15 K)_exp = Δ^g_crH^o_m(298.15 K) + Δ_fH^o_m(cr, 298.15 K)_exp 10

Δ_fH^o_m(g, 298.15 K)_exp = Δ^g_lH^o_m(298.15 K) + Δ_fH^o_m(liq, 298.15 K)_exp 11

Results derived with help eqn (10) and (11) are listed in Table 7, column 5.

In the last ten years, the quantum chemical (QC) composite methods have become a valuable tool for obtaining theoretical Δ_fH^o_m(g, 298.15)-values with “chemical accuracy”^35,36 at the level of 4–5 kJ mol⁻¹. However, the QC methods differ considerably in terms of time and computing power. In this work, we tested G4, G3MP2, and M06/QZ4P methods to get the theoretical Δ_fH^o_m(g, 298.15 K)-values of methoxy-substituted benzenes for validation of our new experimental results. A disagreement or agreement between the theoretical and experimental Δ_fH^o_m(g, 298.15 K)-values provides a valuable indicator of the data mutual consistency.

Conformational analysis and optimization of structures of methoxy-substituted benzenes were carried out within the framework of molecular mechanics in a force field UFF.¹⁹ In almost all molecules we have located several low-lying conformers, but their energies have been found to be close to each other within 1–2 kJ mol⁻¹. The subsequent geometry optimization with the M06L/TZ2P method¹⁹ led to some permutations between them. Therefore, the conformers of all structures were also optimized with G3MP2 method.²² The resulting energy distribution confirmed the M06L/Z2P results. The harmonic and anharmonic frequencies of the most stable conformers of methoxy-substituted benzenes were used to determine the zero point of energy and temperature contributions to enthalpy for M06/QZ4P in the “rigid rotator–anharmonic oscillator” (RRAO) approximation. Enthalpies H₂₉₈ of the most stable conformers for each isomer (see Fig. S1†) were calculated by using the G4, G3MP2, and M06/QZ4P methods.

The H₂₉₈-values have been converted to the standard molar enthalpies of formation Δ_fH^o_m(g, 298.15 K)_theor using the atomization (AT), as well as using the “well-balanced reactions” (WBR).^36,37 The atomization reaction is given by the following equation:

C_mH_nO_k = m × C + n × H + k × O 12

Based on our experience with the quantum chemical calculations, the enthalpies of formation from the atomization reaction sometimes systematically deviate from the experimental values.³⁸ However, a simple linear correlation could be found between calculated by the atomisation reaction and experimental enthalpies of formation of methoxy substituted benzenes (details are given in Tables S11–S13†):

Δ_fH^o_m(g)_theor/kJ mol⁻¹ = 1.0023 × Δ_fH^o_m(g, AT) + 4.1 with R² = 0.9992 for G4 13

Δ_fH^o_m(g)_theor/kJ mol⁻¹ = 1.0064 × Δ_fH^o_m(g, AT) + 8.7 with R² = 0.9993 for G3MP2 14

Δ_fH^o_m(g)_theor/kJ mol⁻¹ = 0.9739 × Δ_fH^o_m(g, AT) + 2.1 with R² = 0.9992 for M06/Q4P 15

Using these correlations, the “corrected” enthalpies of formation of substituted benzene have been calculated (see Table 8).

Comparison of the experimental, Δ_fH^o_m(g)_exp, and theoretical, Δ_fH^o_m(g)_theor, gas-phase standard molar enthalpies of formation of methoxy-substituted benzenes at T = 298.15 K and p° = 0.1 MPa (in kJ mol⁻¹).

Compound	ΔfHom(g)exp	G4	G4	G3MP2	G3MP2	M06/QZ4P	M06/QZ4P	ΔfHom(g)theor
	Exp.a	ATb	WBRc	ATb	WBRc	ATb	WBRc	Average
1,2,3-Trimethoxybenzene	−346.0 ± 2.0	−351.8	−352.2	−350.2	−351.5	−348.3	−349.3	−350.6 ± 2.4
1,2,4-Trimethoxybenzene	−360.6 ± 2.3	−360.7	−361.0	−359.8	−361.1	−358.5	−360.8	−360.3 ± 1.6
1,3,5-Trimethoxybenzene	−381.6 ± 3.2	−382.0	−382.3	−381.1	−382.2	−381.5	−383.4	−382.1 ± 1.2
3,4,5-Trimethoxytoluene	−383.2 ± 2.5	−383.4	−381.8	−382.3	−381.2	−381.6d	−382.1e	−382.1 ± 1.2

^aFrom Table 7. The uncertainties are given as the twice standard deviation.

^bCalculated by the G4, G3MP2, or M06/QZ4P method according to the standard atomization procedure and corrected with empirical equations specific for each method (see text).

^cCalculated by the G4, G3MP2 or M06/QZ4P methods with help of reactions (R1)–(R4) using experimental Δ_fH^o_m(g)-values for the reaction participants (see Table S7). Numerical data for reactions (R1)–(R4) are given in Tables S11 to S14 in ESI.

^dCalculated by the G4MP2 according to the standard atomization procedure.

^eCalculated by the G4MP2 method with help of reaction (R4) using experimental values for the reaction participants (see Table S6). Numerical data for reaction (R4) is given in Table S13 in ESI.

The following general reactions were used for the WBR method (detailed reactions are given in Fig. S2 and S3 in ESI†):

x,x,x-trimethoxy-benzene + 2 × benzene = 3 × methoxybenzene R1–R3

x,x,x-trimethoxy-toluene + 2 × benzene = 3 × methoxy-benzene + toluene R4

Using the reliable experimental gas-phase enthalpies of formation Δ_fH^o_m(g, 298.15 K) of benzene, methoxybenzene, and toluene from Table S7,† the theoretical enthalpies of formation of substituted benzenes were derived by using the G4, G3MP2, and M06/QZ4P methods. The results of quantum-chemical calculations are summarized in Table 8.

As can be seen from Table 8, a very good agreement with the experimental results is evident for all four quantum-chemical methods (G4, G3MP2, and M06/QZ4P) used, as well as for both atomization and WBR procedures. For this reason we have averaged the theoretical values for each compound and the final theoretical gas-phase enthalpies of formation, Δ_fH^o_m(g)_theor, are given in the last column of Table 7. The good agreement between the experimental and theoretical standard molar enthalpies of formation for benzene derivatives can be seen as proof of the internal consistency of the thermochemical results evaluated in this work (see Table 7), which can now be recommended as reliable benchmark properties for further thermochemical calculations with substituted benzene.

3.7. Development of a “centerpiece” group-contribution approach

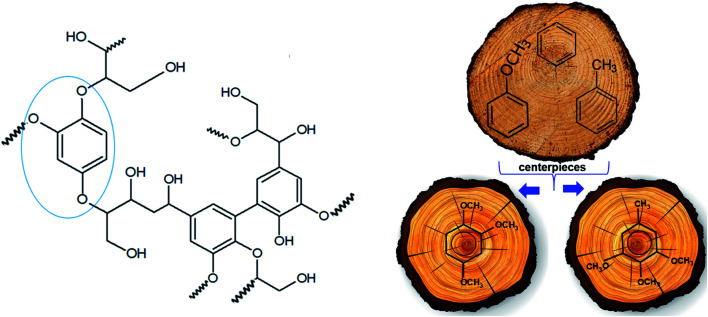
The polyphenolic lignin structure is well known as a complex 3D molecular structure that comprises a great variety of bonds with naturally around 50% ether linkages.³⁹ An idealized structural unit of lignin is given in Fig. 2. It is obvious that all components of this unit are arranged in close proximity and interact energetically with each other. The total energetics of the structural unit of lignin consists of enthalpic contributions from structural elements (e.g. OH, OCH₃, C_bH etc.), and the contribution from mutual non-bonded interactions among these structural elements. The first contribution could be approximated with any kind of group-additivity.^40,41 An exact accounting of the non-bonded interactions even for the simplified lignin unit is hardly possible due to the complex 3D molecular structure. The only way to assess the lignin energetics is therefore to develop an approach that requires a certain degree of simplification of the real structure.

Fig. 2. Idealized structural unit of lignin (left) and graphical presentation of the idea of a “centerpiece” group-contribution approach (right).

In our previous studies^{5–7,10–12} we have already launched the systematic study of the energetics of compounds that can be considered as the renewable feedstock and the lignin-broken bits (e.g. anethole, eugenol, hydroxy-, methoxy- etc.). These compounds are not only relevant for the processing of lignin, but also model the constituent elements of the lignin units. These preliminary studies have helped to envisage a “centerpiece” group-contribution approach which is necessary for a basic evaluation of the energetics (enthalpies of formation and enthalpies of vaporisation) of substituted benzenes, which make the main contributions to the lignin structure units.

The consistent sets of thermochemical data for tri-methoxy-benzenes evaluated in Table 7 have been used for the development of a “centerpiece” group-contribution approach as follows.

3.7.1. Construction of a strain-free theoretical framework

It is obvious from the idealized structural unit of lignin (see Fig. 2, left) that alkoxy-substituted benzenes (see Fig. 2, right) can also be seen as one of the constituent “building blocks”. For this work, however, it is more important to consider these molecules as “models” in order to develop an approach for a quick assessment of the energetics of the lignin building blocks.

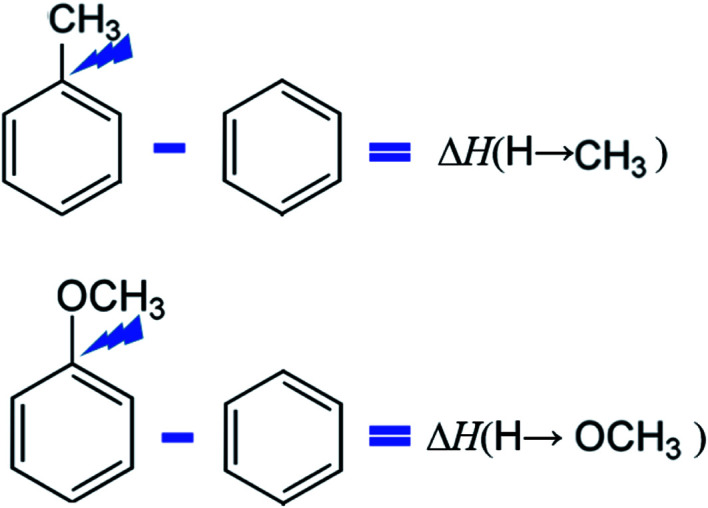
The idea of this approach is that to select a “centerpiece” molecule (e.g. benzene or methoxybenzene, or toluene or etc.) with the well-established thermodynamic properties. Various substituents (mostly relevant for the lignin are alkoxy, hydroxy and carbonyl substituents) can be attached to these “centerpieces” in different positions on the benzene ring. The enthalpic contributions for these substituents can be easily quantified (see Fig. 3) from the differences between the enthalpy of the substituted benzene and the enthalpy of the benzene itself. Using this scheme, the contributions ΔH(H→CH₃) and ΔH(H→CH₃O) were derived (see Table 9) using the reliable thermochemical data for toluene, methoxybenzene, and benzene compiled in Table S7.† Details on calculations conducted in this section are given in Tables S15 to S16 in ESI.†

Fig. 3. Example for the quantification of the enthalpic contributions for the methyl- and methoxy-substituents. The scheme is valid for the gas-phase standard molar enthalpies of formation, as well as for the standard molar enthalpies of vaporisation.

Parameters and pairwise nearest and non-nearest neighbour interactions of substituents on the “centerpieces” for calculation of thermodynamic properties of substituted benzenes at 298.15 K (in kJ mol⁻¹).

Contribution	ΔfHom(g)a	ΔglHomb
Benzene	82.9	33.9
ΔH(H→CH3O)	−153.6	12.5
ΔH(H→CH3)	−32.8	4.2
ortho CH3O–CH3O	14.3	5.6
meta CH3O–CH3O	−0.5	0.8
para CH3O–CH3O	7.4	2.7
ortho CH3O–CH3	−3.1	−0.4
meta CH3O–CH3	0.9	2.2
para CH3O–CH3	4.5	2.7

^aValues were calculated as given in Tables S15 and S16.

^bValues were calculated as given in Tables S17 and S18.

These enthalpic contributions ΔH(H→CH₃O) and ΔH(H→CH₃) can be now applied to construct a framework of any desired methoxy-substituted benzene or toluene (e.g. see 1,2,4-trimethoxy-benzene or 3,4,5-trimethoxy-toluene given in Fig. 2, right), arbitrary starting from the one of the “centerpieces” namely methoxybenzene or toluene, or even starting from the benzene itself. In terms of energy, however, this framework is not perfect due to the lack of energetics of the interactions between the substituents.

3.7.2. Pairwise interactions of substituents on the benzene ring

Nearest (e.g. ortho-interactions) and non-nearest neighbour interactions (e.g. meta- or para-interactions) of substituents on the “centerpieces” (benzene, methoxybenzene, and toluene) are generally stipulating the overall amount of the non-additive interactions specific for the particular structural unit of the lignin (see Fig. 2, left).

For practical reasons, however, it is first necessary to subdivide the entire non-additive interactions into easily definable pairwise interactions. The mutual enthalpic pairwise interactions of substituents in the benzene ring can be accounted for by the three types of contributions that are specific for the ortho, para, and meta positions of substituents placed in the benzene ring. How the pairwise interactions can be derived is shown in Fig. 4. Indeed, to quantify the enthalpic contribution “meta CH₃O–CH₃O” for the non-bonded interaction of the CH₃O-groups in the meta-position on the methoxybenzene (taken as the “centerpiece”) we must first construct the “theoretical framework” of the 1,3-dimethoxy-benzene (see Fig. 4, middle). To do that, we simply add the contribution ΔH(H→CH₃O) from Table 9 to the experimental enthalpy (enthalpy of formation or enthalpy of vaporisation) of the methoxybenzene from Table S7.† Alternatively, we could add two contributions ΔH(H→CH₃O) to the benzene as the “centerpiece”. This “theoretical framework” of 1,3-dimethoxy-benzene does not contain the “meta CH₃O–CH₃O” interaction. However, this interaction is present in the real 1,3-dimethoxy-benzene (it is symbolised in Fig. 4 with a blue arrow). The arithmetic difference between the experimental enthalpy (enthalpy of formation or enthalpy of vaporisation) of 1,3-dimethoxy-benzene and the enthalpy of the “theoretical framework” therefore provides the quantitative size of the pairwise interaction “meta CH₃O–CH₃O” directly (see Table 9). Using the same logic, the enthalpic contributions for the “ortho CH₃O–CH₃O” and “para CH₃O–CH₃” shown in Fig. 4 can be derived (see Table 9) by using the parameters ΔH(H→CH₃O) and ΔH(H→CH₃) respectively. In the same way, the required enthalpic contributions for the ortho-, meta-, and para-pairwise interactions of substituents were obtained and summarized in Table 9.

Fig. 4. Example for a quantification of the enthalpic contributions “CH₃O–R” for the non-nearest neighbour interactions of the CH₃O-group with the methoxy or methyl substituents attached in the different positions to the “centerpieces”. The scheme is valid for the gas-phase standard molar enthalpies of formation, as well as for the standard molar enthalpies of vaporisation.

Quantitatively, the strength of the interactions depends strongly on the type of ortho-, meta- or para-pairs. Let us consider the intensity of pairwise interaction in terms of Δ_fH^o_m(g). From Table 9 it can be seen that the ortho-dimethoxy-benzene shows a strong destabilization of 14.3 kJ mol⁻¹ due to the sterical repulsions of bulky methoxy groups.⁵ In contrast, the ortho-substituted methoxy-toluene is noticeably stabilized of −3.1 kJ mol⁻¹, however the reason for such stabilization is not quite apparent.³⁵ From our experiences, the meta- and para-interactions of substituents on the benzene ring are less profound compared to ortho-interactions.^5,7 Indeed, the meta-interactions of the substituents examined can be considered as negligible since they are below 1 kJ mol⁻¹ (see Table 9). In contrast, the significant destabilization at the level from 4.5 to 7.4 kJ mol⁻¹ is observed for the para-isomers of dimethoxy-benzene and methoxy-toluene. These noticeable destabilizing effects can be explained by the specific electron density distribution within the substituted benzene ring.

The discussion of the magnitudes of the pairwise interactions with respect to Δ^g_lH^o_m is rather limited, since these contributions reflect the tightness of the molecular packing in the liquid. However, these contributions are not of negligible size (see Table 9, last column) and they have to be considered as empirical constants for the correct prediction of the vaporisation energetics.

3.7.3. Effect of agglomeration of substituents on the benzene ring

It is apparent (see blue arrows in Fig. 5), that the introduction of the third and fourth substituents in the benzene ring is expected to increase the intensity of the mutual interactions of the substituents compared to two substituents. As can be seen in Fig. 5, all three possible types of ortho-, meta-, and para-interactions are present simultaneously in the 3,4,5-trimethoxy-toluene. Does the energetics of these interactions additive with the growing number of substituents? Can we just summarize the individual contributions given in Table 9? Or are there additional effects due to a perturbation in the electron density within the congested benzene ring?

Fig. 5. Agglomeration of the enthalpic contributions for the nearest and non-nearest neighbour interactions in the three and four substituted benzene derivatives.

In order to get the answer in terms of Δ_fH^o_m(g), we calculated the “theoretical framework” for each investigated molecule (see Table S15†). The difference between the Δ_fH^o_m(g) of the real molecule and the enthalpy of its model represented by the “theoretical framework” (see Tables S16 and S17†) provides the total amount of pairwise nearest and non-nearest neighbour interactions of substituents on the “centerpieces” in terms of Δ_fH^o_m(g). The numerical results of these differences are compiled in Table 10.

Analysis of the total amount of pairwise nearest and non-nearest neighbour interactions of substituents on the “centerpieces” in terms of Δ_fH^o_m(g) for tri-methoxy-substituted benzenes at 298.15 K (in kJ mol⁻¹).

Compound	ΔfHom(g)a	Actual amount of interactionsb	Theoretical amount of interactionsb	Δ c
1	2	3	4	5
1,2,3-Trimethoxybenzene	−350.6 ± 2.4	27.3	28.1	−0.8
1,2,4-Trimethoxybenzene	−360.3 ± 1.6	17.6	21.2	−3.6
1,3,5-Trimethoxybenzene	−382.1 ± 1.2	−4.2	−1.5	−2.7
3,4,5-Trimethoxytoluene	−382.1 ± 1.2	28.6	34.4	−5.8

^aResults from Table 7.

^bCalculated in Tables S16 an S17.

^cDifference between columns 3 and 4.

The actual amount of interactions in tri-methoxy-substituted benzenes is given in Table 10, column 3 and it is quite comparable (within uncertainties ascribed to Δ_fH^o_m(g)-values) to the theoretical sum of nearest and non-nearest neighbour interactions of substituents (Table 10, column 4). At first glance, no additional interactions between three substituents in the benzene ring appear to occur. It is noticeable, however, that the theoretical amount of interactions is systematically overestimated up to 3.6 kJ mol⁻¹ (see Table 10, column 5). This trend is more apparent for 3,4,5-trimethoxytoluene, in which the theoretical amount of interactions is already overestimated of −5.8 kJ mol⁻¹ (see Table 10, last column). This observation contradicts our expectations, but it could be explained that the “real” molecule of the tri-methoxy-benzenes becomes noticeably more relaxed compared to the di-methoxy-substituted benzene (see Fig. 6), despite the introduction of the third substituent.

Fig. 6. Extinguishing of mutual interactions of substituents in tri-methoxy-substituted benzenes compared to the strong pairwise interactions in the dimethoxy-substituted benzenes.

To summarize observations regarding the Δ_fH^o_m(g)-values we can conclude, that overall interactions of three methoxy-substituents placed in the benzene ring are systematically decreasing by 3 to 4 kJ mol⁻¹ compared to the theoretical value (collected from the sum of the pairwise interactions).

Analysis of the total amount of pairwise nearest and non-nearest neighbour interactions of substituents on the “centerpieces” in terms of Δ^g_lH^o_m for tri-methoxy-substituted benzenes is given in Table 11.

Analysis of the total amount of pairwise nearest and non-nearest neighbour interactions of substituents on the “centerpieces” in terms of Δ^g_lH^o_m for trimethoxy-substituted benzenes at 298.15 K (in kJ mol⁻¹).

Compound	ΔglHoma	Actual amount of interactionsb	Theoretical amount of interactionsb	Δ c
1	2	3	4	5
1,2,3-Trimethoxybenzene	73.0 ± 0.7	1.6	12.0	−10.4
1,2,4-Trimethoxybenzene	75.9 ± 0.7	4.5	9.1	−4.6
1,3,5-Trimethoxybenzene	68.7 ± 0.8	−2.7	2.4	−5.1
3,4,5-Trimethoxytoluene	77.7 ± 0.7	2.1	19.1	−17.0

^aResults from Tables 1 and 2.

^bCalculated in Table S17.

^cDifference between columns 3 and 4.

As can be seen from Table 11 (and more detailed from Tables S18 to S20†), the vaporisation enthalpies of the “real” tri-methoxy-benzenes are in most cases only somewhat higher in comparison to those for the “theoretical framework” (see Table 11, column 3). It means, that contrary to our expectations the large values of theoretical amount of interactions (collected from the pairwise interactions given in Table 9) is virtually disappears in the “real” tri-methoxy-benzenes! Most noticeable is the difference of −10.4 kJ mol⁻¹ (see Table 11, column 5) observed for the 1,2,3-trimethoxy-benzene, since the theoretical value for this compound is expected to be 12.0 kJ mol⁻¹ (see Table 11, column 4). This trend can be seen more profoundly for 3,4,5-trimethoxytoluene, in which the difference of −17.0 kJ mol⁻¹ (see Table 11, column 5) is observed. This means that the liquid phase for these both compounds is significantly more isotropic compared to the di-methoxy-substituted benzenes due to the less favourable intermolecular networking.

To summarize observations regarding the Δ^g_lH^o_m values, we assume that vaporisation enthalpies of substituted benzene derivatives approximately (with an uncertainty of 2 to 3 kJ mol⁻¹) equal to the value of “theoretical framework”. This assumption is very practical for the quick appraisal of vaporisation enthalpies of poly-substituted benzenes considered as the building blocks of the lignin. However, this assumption requires further investigation.

The parameters and pair-wise interactions of substituents in the benzene ring listed in Table 9 are aimed at predicting Δ_fH^o_m(g, 298.15 K) and Δ^g_lH^o_m(298.15 K) values for benzene derivatives resulting from the lignin valorization technologies. Taking into account the complex structure of the lignin fragments, the question of the energetic consequences of the agglomeration of substituents in the benzene ring deserves further systematic investigations. This is a comprehensive program and will be reported on in forthcoming publications.

4. Conclusions

The consistent sets of standard molar thermodynamic properties of formation and phase transitions for tri-methoxy-benzenes were measured in this work. These data were evaluated with help of complementary measurements of vapor pressures, fusion and combustion enthalpies, as well as with help of empirical and high-level quantum-chemical calculations. Thermodynamic properties of trimethoxy-substituted benzene derivatives, which modeling lignin structural units, were recommended as reliable benchmark properties for thermochemical calculations of the energetics of the lignin fragments. The evaluated vaporisation and formation enthalpies were used to design and develop the “centerpiece” approach for prediction of thermodynamic properties of the lignin broken bits. It has been found that the agglomeration of substituents on the benzene ring has dramatic consequences for the energetics of the molecule (in terms of the enthalpy of formation), as well as for the energetics of intermolecular interactions (in terms of the enthalpy of vaporisation). It has turned out that the mutual interactions of substituents in tri-methoxy-substituted benzenes are extinguishing compared to the strong pairwise interactions in the dimethoxy-substituted benzenes. Moreover, the pairwise contributions to the vaporisation enthalpy specific for the di-substituted benzenes also become insignificant with the growing agglomeration of substituents on the benzene ring. These observations are essential to reliably assess the energetics of the molecules that occur during the conversion of lignin into the value-adding platform chemicals and biofuels.

Conflicts of interest

There are no conflicts to declare.