Pepsin-like aspartic proteases (PAPs) as model systems for combining biomolecular simulation with biophysical experiments

Abstract

Pepsin-like aspartic proteases (PAPs) are a class of aspartic proteases which shares tremendous structural similarity with human pepsin. One of the key structural features of PAPs is the presence of a β-hairpin motif otherwise known as flap. The biological function of the PAPs is highly dependent on the conformational dynamics of the flap region. In apo PAPs, the conformational dynamics of the flap is dominated by the rotational degrees of freedom associated with χ1 and χ2 angles of conserved Tyr (or Phe in some cases). However it is plausible that dihedral order parameters associated with several other residues might play crucial roles in the conformational dynamics of apo PAPs. Due to their size, complexities associated with conformational dynamics and clinical significance (drug targets for malaria, Alzheimer's disease etc.), PAPs provide a challenging testing ground for computational and experimental methods focusing on understanding conformational dynamics and molecular recognition in biomolecules. The opening of the flap region is necessary to accommodate substrate/ligand in the active site of the PAPs. The BIG challenge is to gain atomistic details into how reversible ligand binding/unbinding (molecular recognition) affects the conformational dynamics. Recent reports of kinetics (K_i, K_d) and thermodynamic parameters (ΔH, TΔS, and ΔG) associated with macro-cyclic ligands bound to BACE1 (belongs to PAP family) provide a perfect challenge (how to deal with big ligands with multiple torsional angles and select optimum order parameters to study reversible ligand binding/unbinding) for computational methods to predict binding free energies and kinetics beyond typical test systems e.g. benzamide–trypsin. In this work, i reviewed several order parameters which were proposed to capture the conformational dynamics and molecular recognition in PAPs. I further highlighted how machine learning methods can be used as order parameters in the context of PAPs. I then proposed some open ideas and challenges in the context of molecular simulation and put forward my case on how biophysical experiments e.g. NMR, time-resolved FRET etc. can be used in conjunction with biomolecular simulation to gain complete atomistic insights into the conformational dynamics of PAPs.

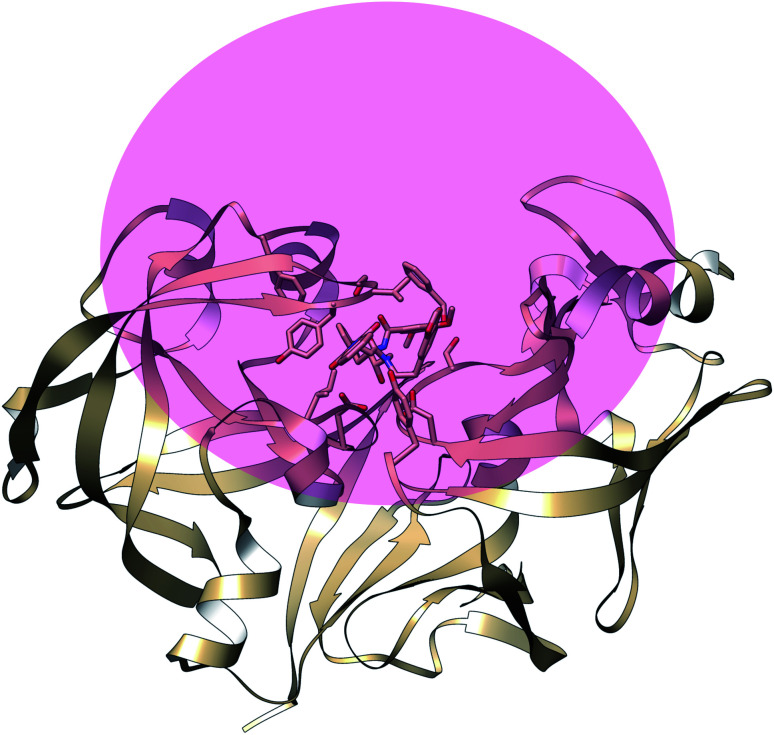
Pepsin-like aspartic proteases (PAPs) are a class of aspartic proteases which shares tremendous structural similarity with human pepsin.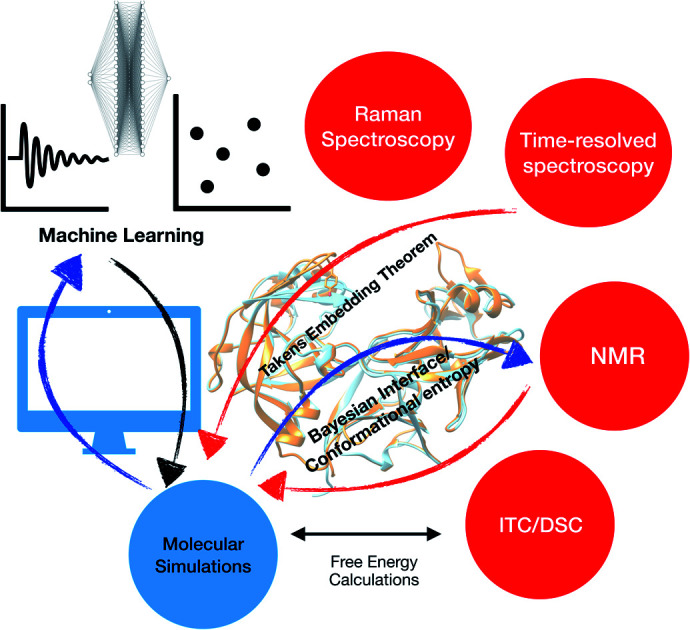

Introduction

Aspartic proteases are a class of enzymes which consist of two highly conserved aspartates in the active site. These enzymes use an active water molecule bound (by H-bond interaction) to aspartate for catalysis of their substrates. Based on their three-dimensional structural similarity, aspartic proteases can be categorised into two categories: (1) pepsin-like aspartic proteases (PAPs) and (2) retroviral aspartic proteases (RAPs).¹ PAPs belong to the A01 family whereas RAPs belong to the A02 family of proteases within the MEROPS database² (Table 1).

Structures (PDB IDs) and members of a few representative aspartic proteases. Abbreviations: BACE: β-secretase, HIV: human immunodeficiency viruses, SIV: simian immunodeficiency virus.

PAPs (MEROPS: A01)	PDBs	RAPs (MEROPS: A02)	PDBs
Human pepsin	1PSN, 1QRP, 1PSO	HIV-1	4L1A, 1TW7, 4NKK, 2PC0
Human renin	1RNE, 1HRN, 3D91	HIV-2	1IDA
BACE-1	1W50, 3TPL, 1SGZ	SIV	1TCW, 1AZ5, 1SIP
BACE-2	3ZKG, 3ZKI, 2EWY
Cathepsin D	1LYA, 1LYB
Plasmepsin I	4CKU, 3QRV
Plasmepsin II	1LF4, 1LF3, 4CKU, 4Z22, 1SME, 2BJU
Plasmepsin IV	1LS5
Plasmepsin V	4ZL4, 6C4G
Plasmepsin IX	N/A
Plasmepsin X	N/A
Penicillopepsin	1APW, 1PPM, 1PPK, 1APU

In recent years, HIV protease (belongs to RAPs) gained significant attention in context of structural and computational biology due to its role in HIV/AIDS.³ Similar argument can be put forward for β-secretase enzyme, BACE1 which belongs to PAPs and it is a promising drug target for Alzheimer's disease. One of the comprehensive reviews‡ on PAPs have been published by Ben Dunn in 2002.¹ Since then several blockbuster drug molecules have been proposed targeting BACE1.⁴ However, conformational dynamics and molecular recognition in PAPs have not been extensively studied by biophysical experiments e.g. NMR, single molecule FRET, Raman spectroscopy etc. Recent computational studies on BACE1 and plasmepsins (malarial PAP) have identified key order parameters (dynamical structural properties) that can be further explored by biophysical experiments combined with state-of-the art molecular simulation.^5–10 The purpose of this review is to highlight common order parameters that governs conformational dynamics and molecular recognition of PAPs and to highlight the need of integrated computational and experimental approaches to gain atomistic insights into molecular mechanism of PAPs. I will also highlight how machine learning methods can be used for this purpose and will put forward my case on using PAPs as a test system for methodological development in computational and experimental frontiers. In this review, i will use plasmepsins (Plms) and BACE1 as test systems to guide the discussion. PAPs share incredible structural similarity, hence i believe computational/experimental methodologies applied on the aforementioned proteins will be broadly applicable to other enzymes of this class. Biophysical experiments, machine learning and biomolecular simulation are the three pillars which governs drug discovery in 21st century.¹¹ I will further discuss how structural similarity of PAPs can be exploited in the context of drug re-purposing towards plasmepsins (drug target for malaria).

Structural features

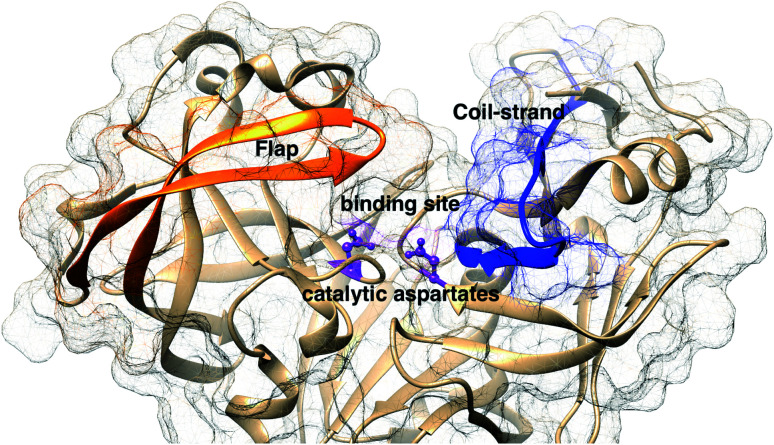
The main aim of this section is to clarify the language, organize the concepts and define structural features across a few representative PAPs. Common sequential features that are conserved in PAPs are as follows: (1) presence of two catalytic aspartates (often known as catalytic site) and (2) the presence of –Asp–Thr–Gly–Ser– sequence (Fig. 1). Structurally PAPs can be characterised by two main domains (1) the flap region and (2) the coil region.^3,5,6 The name coil region is not accurate. The so called coiled region consists of β-strand and coil structures. In this review, it will be denoted as CS region (coil-strand region) (Fig. 2 and Table 2).

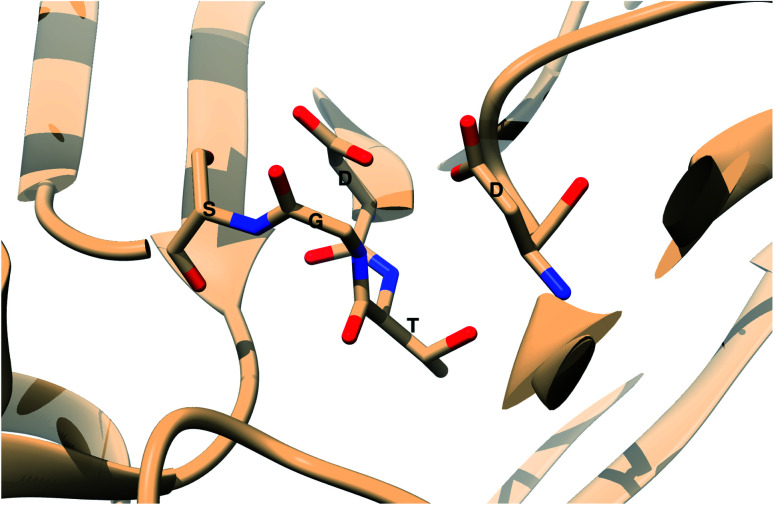
Fig. 1. Common structural features in PAPs: location of two conserved aspartates and the presence of –Asp–Thr–Gly–Ser– sequence. Figure was created using PDB:3TPL.¹² Amino acids are highlighted as one letter codes.

Fig. 2. Flap (resid 67–88) and coil-strand (resid 282–302) regions are two of the common structural features of PAPs. The flap acts as a lid over the catalytic aspartates. Opening of the flap exposes the binding site which enables ligand binding. Figure was created using PDB:1LF4.¹³.

Residue numbers of the flap and CS region in PlmII and BACE1.

Protein	Flap	CS region
PlmII	58–88	282–302
BACE1	52–82	314–334

The flap region acts as a lid over the catalytic site which governs the entry of the substrate or small molecule inhibitors. The extent of flap opening (described in detail in later sections) also dictates the volume of the binding site i.e. open flap conformation increases the volume of the binding site which can accommodate bigger ligands. The CS domain also plays a role in ligand/substrate binding but its role is not as pronounced as the flap region.

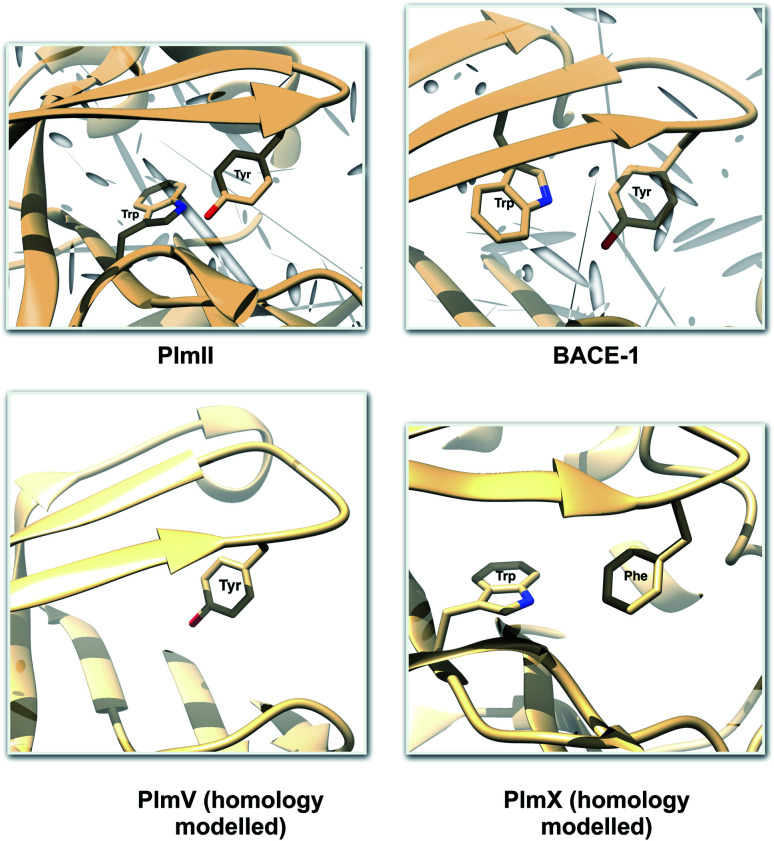
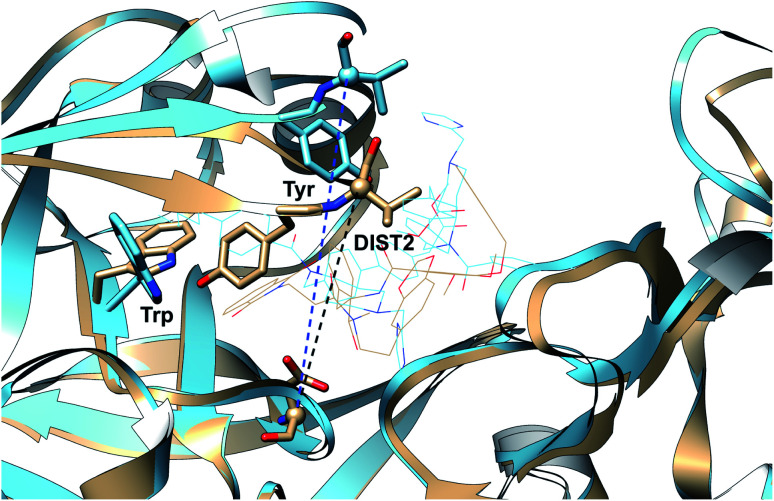
One of the startling structural features of PAPs is the presence of conserved tyrosine and tryptophan residue. The tyrosine (Tyr) residue is highly conserved in the flap region of most of the PAPs. Tryptophan (Trp) is another conserved residue that is present in the PAPs. In most cases, Trp is present at the S1 region (Fig. 3). However in case of BACE1 and BACE2, the conserved Trp is a part of the flap region (Fig. 3). Plasmepsin V (PlmV), an emerging drug target against malaria doesn't possess the conserved Trp residue.¹⁴ Whereas in PlmIX and X, the conserved Tyr residue is replaced by phenylalanine (Phe) (Fig. 3). Visual inspection of several 3D crystal structure of Plm and BACE-1 shows that the orientation of Tyr and Trp influences the extent of flap opening (Fig. 4). In the next section, i will propose/review several order parameters that can be used to study the extent of flap opening and its connection with orientation of Tyr and Trp.

Fig. 3. Location of conserved Tyr and Trp. For most of the PAPs, the Trp belongs to the S1 region (substrate binding region 1) as depicted in PlmII. Whereas in case of BACE1, the Trp is a part of the flap region. Exceptions: PlmV doesn't possess the conserved Trp and in case of PlmIX/X the Tyr is replaced by Phe. The homology modelled structures were generated using SwissModel¹⁵ and can be accessed in the corresponding Github profile.

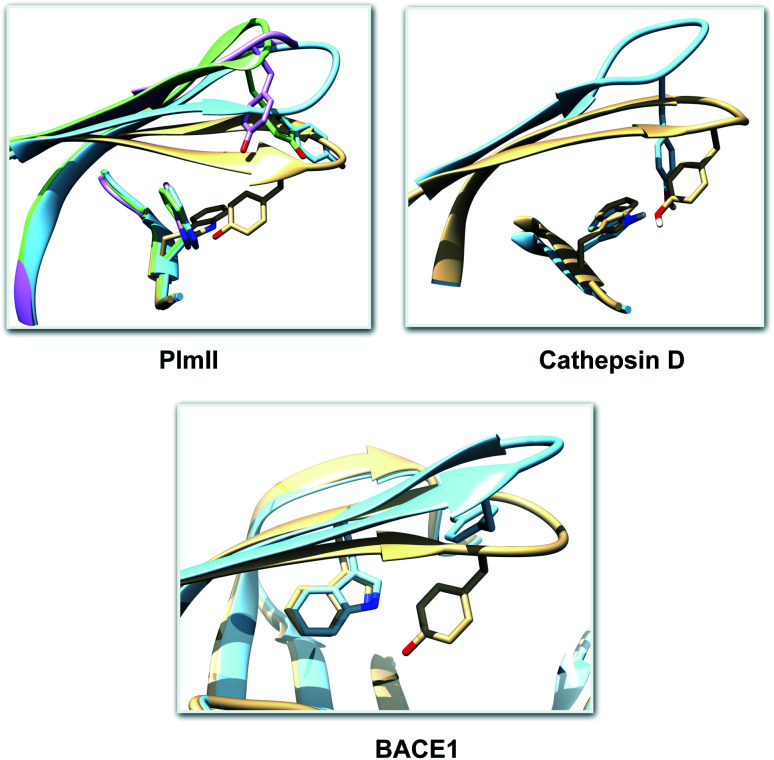
Fig. 4. Visual inspection of 3D structures of PAPs shows how orientation of Tyr and Trp alters flap elevation. In case of PlmII, altered Trp and Tyr orientation (PDB:2BJU,¹⁶2IGY¹⁷ and 4Z22 (ref. 18)) leads to expansion of the binding site (grey: 1LF4, blue: 2BJU, green: 2IGY, magenta: 4Z22). In case of cathepsin-D, high pH alters the conformation of Tyr which leads to flap elevation (blue: 1LYW,¹⁹ grey: 1LYA²⁰). Alternative conformation of Tyr was also observed in case of BACE-1 (blue: 1SGZ, grey: 3TPL).

Order parameters to study conformational dynamics

Order parameter is a commonly used term in physical chemistry. A poor man's working definition of order parameter (sometimes referred as reaction co-ordinate) in context of biomolecular conformational dynamics can be expressed as follows: ‘geometric or abstract co-ordinate systems which captures conformational changes along a pathway’. In biomolecular simulation, order parameters are often known as collective variables (CVs). Some of the commonly used geometric order parameters are distance between two atoms, bond lengths, torsional angles etc. Abstract order parameters include vectorised linear combinations e.g. principal components. Time independent components, latent variable from variational auto-encoder etc. In this section, i will discuss how geometric and abstract order parameters can be used to capture conformational dynamics and molecular recognition in PAPs.

Geometric order parameters

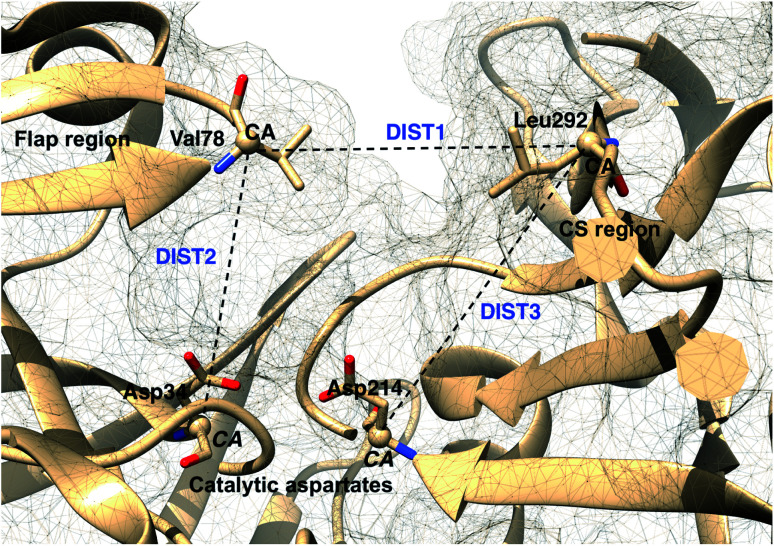
Karubiu et al. proposed the Cα–Cα distance (DIST2) between catalytic Asp and the flap tip residue (flap tip residue varies across different PAPs) in PlmII as order parameters to capture the extent of flap opening in unbiased all-atom molecular dynamics (MD) simulation.⁵

Rule of thumb to select flap tip residue

Residue number of the conserved Tyr/Phe + 1. For example, in PlmII it will be Val78 (77(Tyr) + 1).

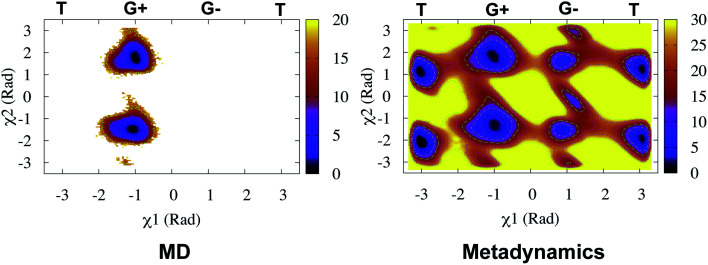
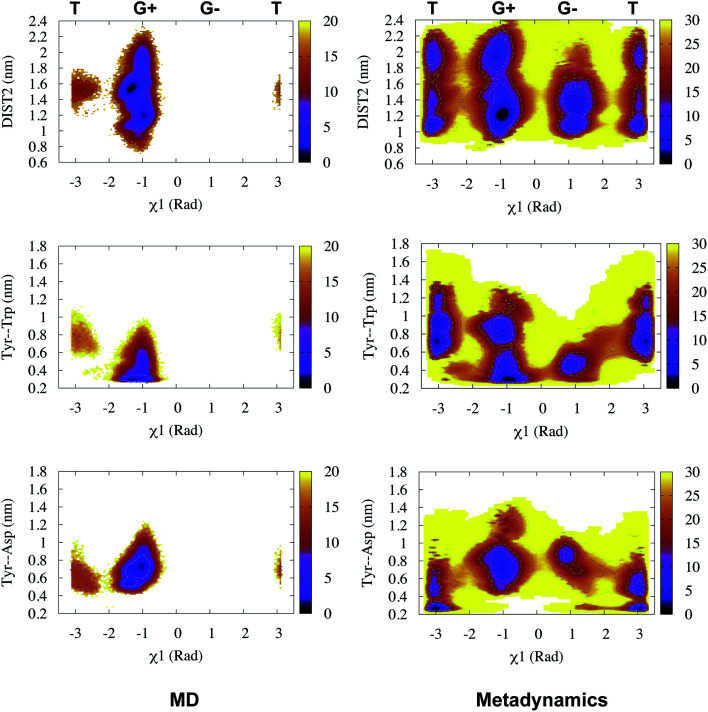
This distance criteria was inspired by the order parameter proposed to study spontaneous flap opening and closing in apo HIV protease.^21,22 Karubiu et al. further proposed a distance metric (DIST3) which can capture opening/closing motion associated with CS domain (Fig. 5). Recent study by Bhakat and Söderhjelm⁶ showed that the fluctuation of these two order parameters (DIST2 and DIST3) are uncorrelated which led to the hypothesis that in apo PAPs, the conformational dynamics of flap and CS domains are independent of each other (Fig. 12). Both DIST2 and DIST3 were further applied on BACE1 and other plasmepsins in order to gain insights into conformational dynamics from classical MD simulations. Bhakat and Söderhjelm performed test calculations (not published) where they have used DIST2 and DIST3 as CVs within metadynamics framework. The authors observed that the metadynamics biasing along these distances led to distorted flap conformations which suggests that these distance based order parameters are not the optimum choices to capture reversible conformational dynamics in PAPs but rather can be used as a quantitative measurement to capture the extent of flap/CS opening/closing. The authors further proposed two additional distance based order parameters COM_flap and COM_CS in case of PlmII with an aim that both these order parameters will simultaneously act as quantitative measurement of the conformational dynamics and CVs in enhanced sampling calculations e.g. metadynamics.

Fig. 5. Different distance based order parameters proposed by Karubiu et al. DIST2 measures the extent of flap opening whereas DIST3 accounts for opening of CS region. Fig. 12 shows that DIST2 and DIST3 are uncorrelated which gives an indication that in apo PAPs, the dynamics of flap and CS region are independent of each other. DIST1 acted as an auxiliary order parameter. These distance based order parameters can be generalised for other PAPs. The image was created using PDB:1LF4.

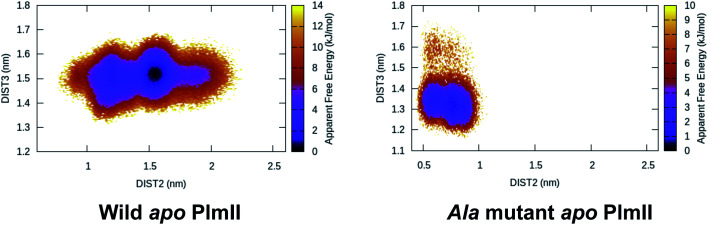
Fig. 12. Tyr to Ala mutation shows complete flap collapse in apo PlmII as captured by DIST2 in MD simulation. Similar results were obtained in case of BACE1 (ref. 6). This observation is in agreement with experiments where Tyr to Ala mutation resulted in loss of enzyme activity.

COM_flap: distance between centre of mass (COM) of the catalytic aspartates (only Cα atoms of catalytic aspartates) and COM of the flap region (Cα atoms of residues 58–88).

COM_CS: distance between COM of the catalytic aspartates (only Cα atoms of catalytic aspartates) and COM of the CS region (Cα atoms of residues 282–302).

Authors further used COM_flap and COM_CS as CVs in two – dimensional well-tempered metadynamics simulation. Metadynamics simulations with COM CVs showed significant hysteresis and lack of reversible sampling of the conformational landscape as these CVs doesn't represent slow order parameters (more on this later) necessary for optimum conformational sampling (Fig. 13).

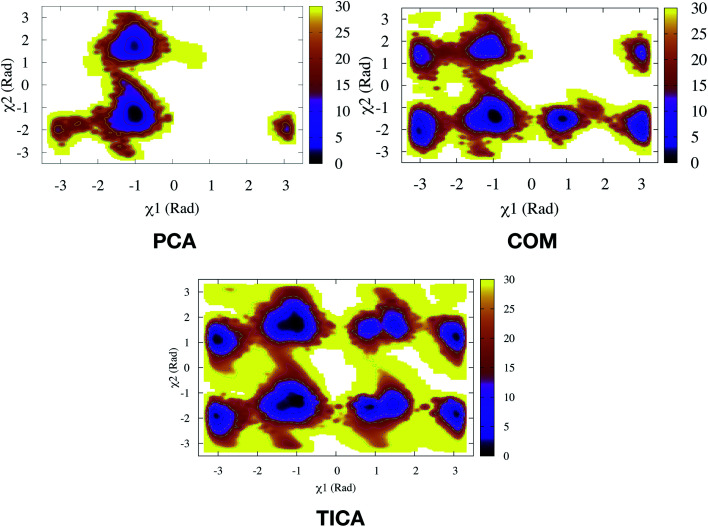
Fig. 13. Sampling of conformational space of apo PlmII using PC1 and PC2 as CVs in metadynamics (PCA). The authors also performed metadynamics simulations with COM CVs (COM). The sampling can be compared with metadynamics with χ1 and χ2 CVs (Fig. 9).Both PCA and COM based metadynamics didn't explicitly bias the torsional order parameters of conserved Tyr. Well-tempered metadynamics simulation with TIC1 and TIC3 as order parameters (TICA) did better sampling compared to PCA and COM CVs (ref. 6).

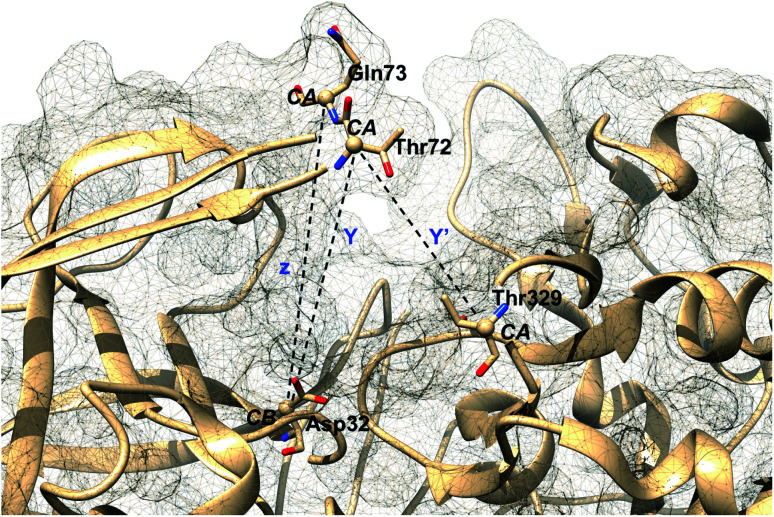
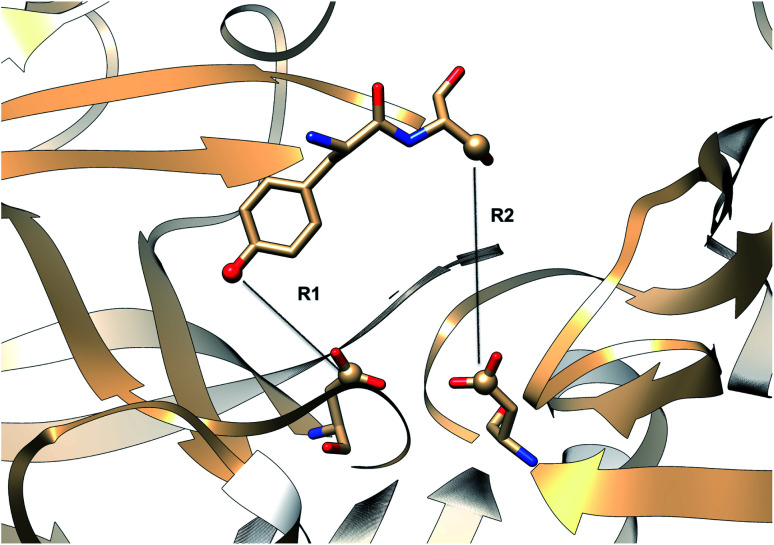
Karubiu et al. further proposed a distance based order parameter (Fig. 5) which measures the distance (DIST1) between flap and CS region as a function of time. Due to uncorrelated dynamics of these regions, DIST1 doesn't provide any additional information compared to DIST2/DIST3. A few other distance based order parameter has also been proposed by different research groups. Gorfe and Caflisch⁹ proposed (in context of BACE1) the distance between the Cα of the flap tip residue Thr72 and Cβ of the catalytic aspartate as a measure of flap opening (Y). This order parameter is almost identical to the DIST2 proposed by Karubiu et al. The authors further proposed an analogous distance criteria of DIST1: distance between Cα atoms of flap tip Thr72 and Thr329 of CS region (Y′). Spronk and Carlson¹⁰ introduced an analogous distance parameter (in BACE1) of DIST2 (denoted as z) which measures the distance between the Cα of the Gln73 and the Cβ of Asp32 (Fig. 6). Due to their similarity, either DIST2 or z can be applicable in PAPs to capture the extent of flap opening. Recently Shen and co-workers²³ proposed the following distance parameters to measure the extent of flap opening in human renin: (1) distance between Tyr-83-OH and Asp-38-CG and (2) distance between Ser-84-CB and Asp-226-CG (Fig. 27 in ESI†). The distance between Tyr-83-OH and Asp-38-CG can be a deceptive measurement of the flap opening as the orientation of Tyr-83-OH is highly dependent on the rotational degrees (χ1 and χ2) of freedom of Tyr. Flipping (discussed later) of Tyr side-chain can change the orientation of the Tyr-83-OH. In that case, the distance between Tyr-83-OH and Asp-38-CG will not measure the true extent of flap opening. Distance between Ser-84-CB and Asp-38-CG consist of two stable anchor points which can act as an alternative to Tyr-83-OH and Asp-38-CG.

Fig. 6. Distance based order parameters proposed by other research groups in context of BACE1. One can easily see that Y and z are analogous to DIST2 whereas Y′ is analogous to DIST1 (Fig. 5). The image was created using PDB:1W50.²⁴.

Fig. 27. Distance parameters proposed by Shen and co-workers. R1: distance between Tyr-83-OH and Asp-38-CG and R2: Ser-84-CB and Asp-38-CG. The figure was created using PDB:2REN.

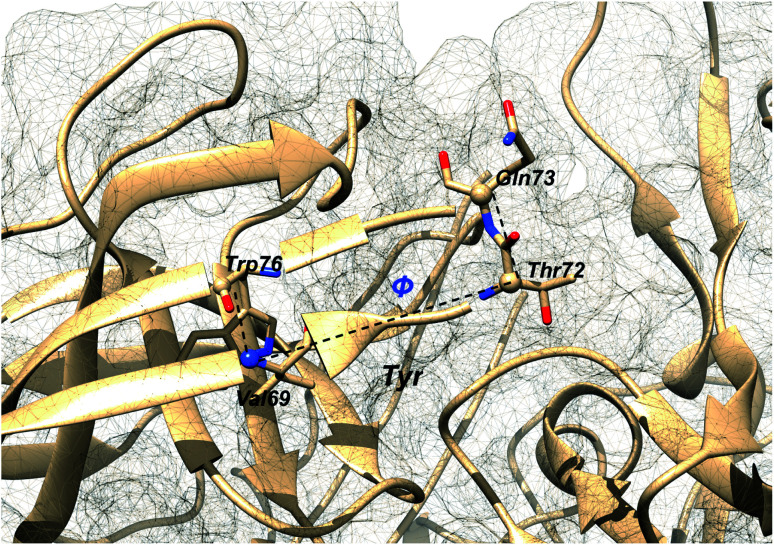
Additional order parameters have been proposed to capture flap twisting. Spronk and Carlson proposed flap twisting angle, ϕ as the dihedral angle involving Trp76C–Val69N–Thr72CA–Gln73CA (Fig. 7). However, this definition is specialised for BACE1. A general order parameter for capturing flap twisting in PAPs can be expressed as a dihedral angle involving following residues:

Fig. 7. Dihedral order parameter, ϕ proposed by Spronk and Carlson to account for flap twisting. The position of conserved Tyr is highlighted in order to give an idea on the relative position of other residues. The image was created using PDB:1W50.

i + 5 − C–i − 2 − N–i + 1 − CA–i + 2 − CA where i is the residue number of conserved Tyr.

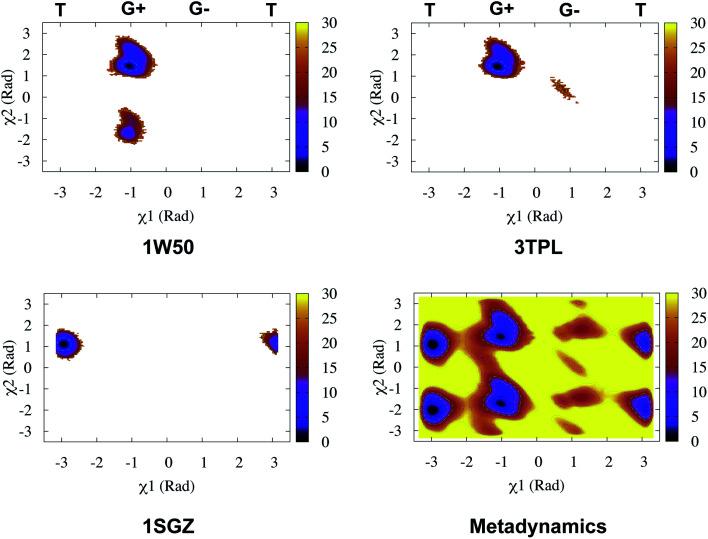
Recently, Bhakat and Söderhjelm proposed the torsion angles (χ1 and χ2) of conserved Tyr (in PlmII and BACE1) as order parameters to capture conformational dynamics in PAPs.⁶ A typical free energy profile of Tyr (along χ1) has three free energy minimas which corresponds to three different side-chain orientations: gauche⁺, gauche⁻ and trans. MD and metadynamics investigations using PlmII and BACE1 predicted that in apo PAPs both gauche⁺ and trans conformations are equally populated§ (Fig. 8 and 9). Gauche⁺ is stabilised by side-chain H-bond interaction between Tyr and Trp (denoted as normal state) whereas the trans conformation is stabilised by side-chain H-bond interaction between Tyr and one of catalytic Asp (denoted as flipped state, recently Shen and co-workers sampled this interaction using constant pH molecular dynamics on human renin) (Fig. 10). Gauche⁻ predicted to be the minor population which in case of BACE1 is stabilised by side-chain H-bond interaction between Tyr and Lys (PDB:1SGZ²⁵) (Fig. 4 and 8). A typical way to understand the rotation of Tyr and its connection with flap elevation is to plot a free energy profile involving DIST2/z against χ1 (Fig. 10).¶

Fig. 8. Sampling of χ1 and χ2 angles in classical MD simulations (∼ 500ns) starting with three different starting conformations of BACE1 (PDB ID: 1W50, 3TPL and 1SGZ differs in flap elevation and orientation of Tyr. For detail refer⁶). As one can see simulations starting with 1W50 and 3TPL only sampled gauche⁺ (G⁺) conformation. Whereas, simulation starting with 1SGZ only sampled trans (T) conformation. Metadynamics simulation with χ1 and χ2 order parameters did a enhanced sampling of the conformational space. Looking at apparent free energy values (z axis unit in kJ mol⁻¹) tells us that in apo BACE1 the flap remains in dynamic equilibrium between gauche⁺ and trans conformations. Gauche⁻ (G⁻) is the minor population which was stabilised by H-bond interaction between Tyr and Lys.

Fig. 9. Sampling of χ1 and χ2 order parameters in MD and metadynamics simulations starting with apo PlmII (PDB ID:1LF4). Sampling of MD and metadynamics was quite similar to Fig. 8.

Fig. 10. Sampling of χ1 and DIST2 order parameters in MD (∼600ns) and metadynamics simulations starting with apo PlmII (PDB ID:1LF4). The open flap conformation centres around DIST2 ∼ 2.0 nm. The gauche⁺ conformation was stabilised by H-bond interaction between Tyr and Trp whereas the trans conformation was stabilised by H-bond interaction between Tyr and catalytic Asp. The typical H-bond distance is 0.3–0.35 nm. z axis in the contour plot shows apparent free energy in kJ mol⁻¹.

Investigation of crystal structures of plasmepsin have shown that not only Tyr but the conserved Trp can also adapt flipped orientation (Fig. 11). Flipping of Trp (Table 3) combined with flap opening (measured using DIST2, see Table 4) leads to expansion of the binding pocket which can accommodate open flap inhibitors. The interplay between flap opening and dihedral order parameters of Tyr and Trp have further being exploited by Oefner and colleagues in human renin.²⁶ By increasing flap elevation by 1 Å, rotating Tyr by −120° (flipped conformation) and displacing Trp slightly led to expansion of the binding site|| which led to identification of novel piperidine based inhibitors with micro-molar k_i value. Further computational and experimental studies (X-ray crystallography and NMR) are necessary to understand if the combined flipping of Tyr and Trp is rare or a common phenomena in PAPs that correlates with flap opening and expansion of the binding site.

Fig. 11. Flipped orientation of Tyr and Trp in PlmII which led to flap opening (measured by DIST2) and expansion of the binding site. The expanded binding site can accommodate bigger ligands (represented as wire-frames). These inhibitors are often dubbed as open flap inhibitors.²⁷ In this case the rotation of Trp side-chain opens up space so that it can accommodate the alkane side-chain of non-peptidomimetic inhibitor. Blue represents PDB ID:2BJU and grey represents PDB ID:1LF3.¹³.

Dihedral order parameters χ1 and χ2 (values in radian) shows different conformational states of Trp in Plm-II.

PDBs	χ1	χ2
1LF4	1.22	−1.74
2BJU	−1.04	1.43

Crystal structures of Plasmepsin-II (PDB:1LF4, 2BJU, 2IGY, 4Z22), bovine chymosin protease (PDB:1CMS²⁸), human cathepsin-D (1LYA, 1LYW) and BACE-1 (3TPL, 1W50, 1SGZ) show different conformational states of Tyr. Crystallographic structures of these PAPs shows the variation in flap opening (DIST2). In case of human cathepsin-D, pH alters the extent of flap opening and the orientation of Tyr.

PDB	χ 1 (radian)	DIST2 (nm)	State
1LF4	−1.12	1.19	Gauche +
2BJU	−3.12	1.50	Trans
2IGY	−2.6	1.74	Trans
4Z22	−1.02	2.11	Gauche +
1CMS	3.08	1.28	Trans
1LYA	−1.29	1.20	Gauche +
1LYW	0.96	1.78	Gauche −
3TPL	−1.31	1.23	Gauche +
1W50	−1.06	1.76	Gauche+
1SGZ	0.87	1.61	Gauche−

Mutation of Tyr and its effect on conformational dynamics

Mutation of Tyr to Ala (amino acid with no bulky side-chain) in apo PlmII and BACE1 led to complete flap collapse in MD simulation which was captured by DIST2 (Fig. 12). This observation is consistent with previous experimental study by Suzuki and co-workers²⁹ which shows that Tyr to Ala mutation resulted in loss of enzyme activity in human renin. Further, mutation of Tyr to Thr, Ile, Val in chymosin also led to loss of enzyme activity. MD simulation based mutational study together with experiments led us to conclude that the conserved Tyr plays a critical role in enzyme activity. In future, similar experiments on PlmII and BACE1 are necessary to generalise the aforementioned claim.

Substitution of Tyr to Phe in pepsin retains the enzyme activity. Structural investigation of Toxoplasma gondii PAP, PlmIX, PlmX and PlmV reveals the presence of Phe in place of Tyr (Fig. 4). Since Phe possess rotational degrees of freedom along χ1 and χ2 order parameters hence it dictates the flap dynamics in the aforementioned PAPs. In future, this assumption can be validated by mutating Phe to Ala which results in loss of enzyme activity and flap collapse in MD simulation.

Mutation of Trp

Mutation of Trp and its effect on enzyme activity of PAPs has not been studied extensively. Park et al.³⁰ mutated conserved Trp (Trp39) of R. pusillus PAP with other residues and observed decreased enzyme activity. However, crystal structures of PlmV¹⁴ from P. vivax and P. falciparum (homology modelled) doesn't possess conserved Trp. In future detailed computational and experimental studies are required in order to decipher the exact role of Trp in conformational dynamics of PAPs.

Abstract order parameters

MD simulations of PAPs can produce high-dimensional dataset with million or more data points. These data points in together describes conformational motion associated with protein. Recently several dimensionality reduction techniques (e.g. PCA,^31–33 tICA,^34–38 tSNE,^39–42 diffusion map^43,44) have been proposed which can extract useful informations related to conformational dynamics from the plethora of the data generated during MD simulations.

Principal component analysis

Principal component analysis (PCA) does a linear transformation which (in context of MD simulation) aims at finding motions that maximize the variance. Before I dive into how it can be used as an order parameter to capture conformational dynamics associated with PAPs, I will briefly introduce the fundamental concept behind PCA.

The first principal component (often denoted as PC1, PCA1 or z₁) is the linear trans formation of the original variables x₁, x₂, …., x_p with α. Mathematically this transformation can be expressed as:

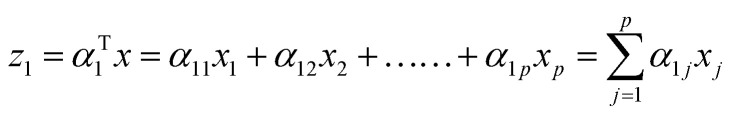1

The weight components (α₁₁, α₁₂, …, α_1p) maximizes the variance of the original data x subject to the following constraint (normalization):

α₁₁² + α₁₂² + …… + α_1p² = 1 2

Generally speaking k^th PC can be expressed as z_k = α^T_kx,* has the maximum variance and uncorrelated with z₁, z₂, …, z_k−1. x is the eigenvector matrix. Cartesian coordinates for each time-step in a MD simulation defines each of the rows in x whereas, p columns of x consist of 3N cartesian co-ordinates for each atom. For detailed description of PCA in context of MD simulation please refer ref. 32 and³³.

PCA algorithm as a post processing tool for MD simulation have been implemented in several state-of-the art software packages e.g. Gromacs,⁴⁵ MSMBuilder,⁴⁶ MDTraj⁴⁷etc. In practice, first few principal components capture the motions of maximal variance from MD trajectories. Bhakat and Söderhjelm performed two independent MD simulations (∼500 ns) of PlmII and performed PCA using the Cα atoms of the combined trajectory (ignoring the tail part) using g_covar tool integrated with Gromacs. The authors thought that first few PCs will capture degrees of freedom associated with the flap opening of PlmII. Metadynamics simulations using PC1 and PC2 as order parameters did a poor sampling of the conformational space of apo PlmII. PCA using the Cα atomic co-ordinates didn't take into account the dihedral angles associated with Tyr (as described in previous section) hence it is not a surprise that the metadynamics with PC1 and PC2 as order parameters failed to enhanced the sampling of the conformational space in apo PlmII (Fig. 13). An alternative approach will be to perform PCA on the dihedral (often known as dihedral PCA³¹) space (using χ1 and χ2 angles of the flap region in apo PlmII) which in principle should able to capture Tyr mediated flap dynamics in PAPs.

Independent component analysis

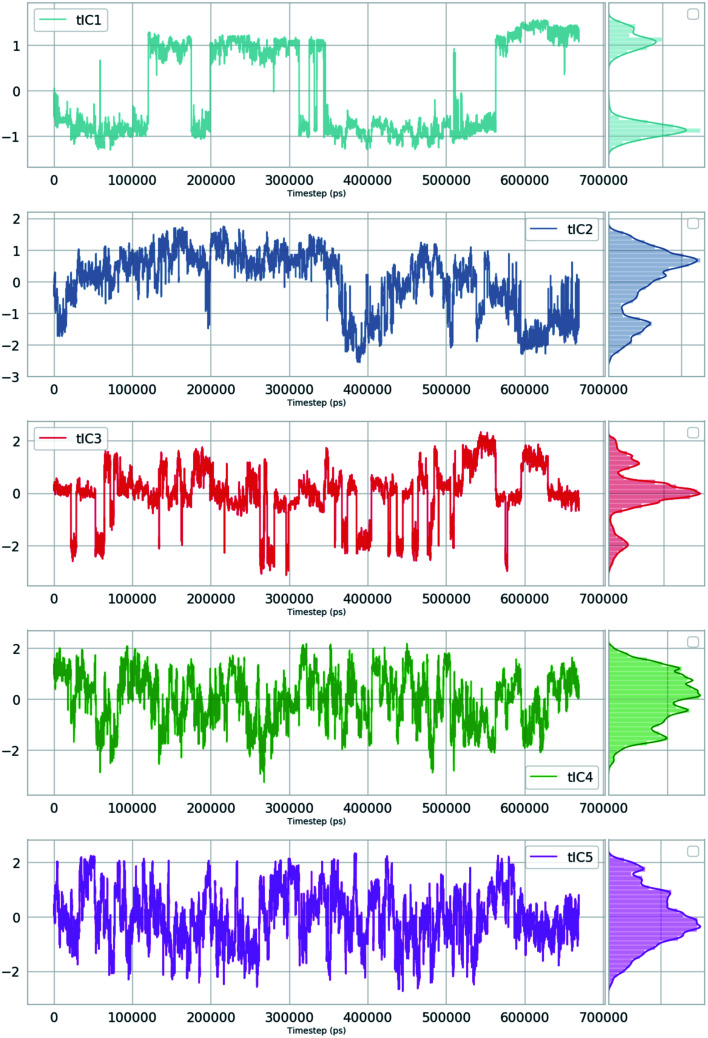
Second order independent component analysis (ICA) or otherwise known as time-lagged ICA (TICA) has also been applied in context of PAPs. While in PCA the aim was to find orthogonal linear transformations (PCs) that maximizes the variance, the goal in TICA is to identify linear transformations where the vectors (ICs) are statistically independent and maximizes auto-correlation (Fig. 14). ICA based approaches have been used widely to analyze time-series data from fMRI⁴⁸ and EEG⁴⁹ experiments. The first TIC component/vector (often denoted as TIC1) captures the slow (in context of timescale of biomolecular motions) dynamical mode from input high-dimensional time-series data (dihedral order parameters of the flap region in PAPs). TIC vectors can also be used as order parameters to perform well-tempered metadynamics simulations. Bhakat and Söderhjelm performed TICA analysis (for full mathematical description of TICA please refer³⁸ and³⁶) on the MD trajectory of apo PlmII to identify key dihedral order parameters (more precisely linear combination of dihedral angles with different weights for each angle) that captures slow dynamical modes from MD trajectory (Fig. 15 and 16). The authors further used TIC vectors as order parameters in metadynamics simulation which enhances the sampling of flap dynamics compared to classical MD simulations (Fig. 13).

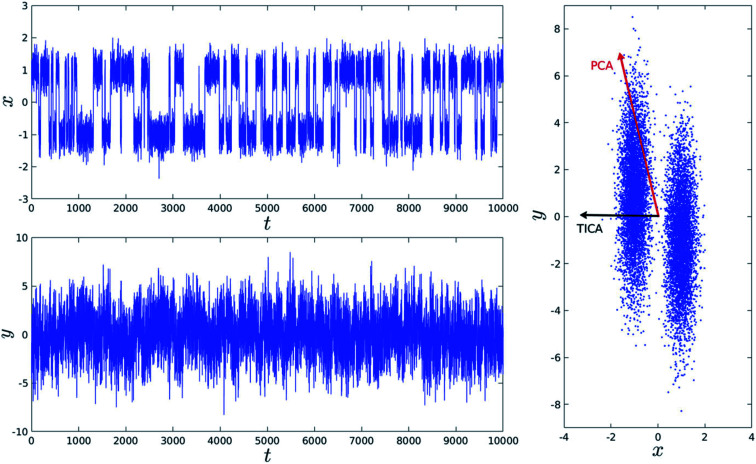
Fig. 14. Top and bottom plot shows time (t) series projection of two arbitrary order parameters, x and y. Right panel shows the dominant PCA and TICA vectors projected on x and y. Figure is adapted from ref. 50.

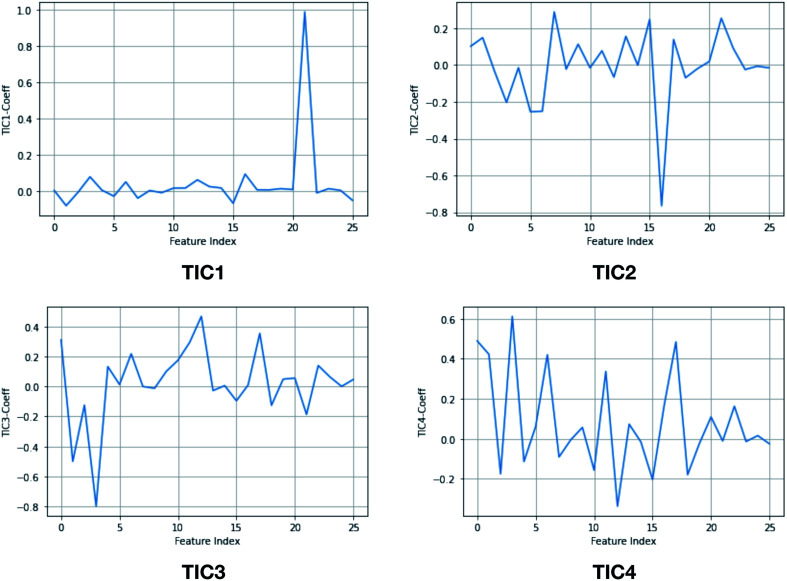
Fig. 15. TIC vectors and corresponding weights assign to each features. In case of TIC1, feature index 21 has significant weight which corresponds to sin  χ2. Whereas in case of TIC3, feature index 3 has most significant weight which corresponds to sin  χ1. 2D well-tempered metadynamics simulations with TIC1 and TIC3 as CVs did a better sampling of the conformational space of apo PlmII compared to classical MD simulation (Fig. 13). Note: technically it is possible to perform metadynamics simulations with all five TICs using parallel-bias metadynamics.

Fig. 16. TIC1–5 projected as a function of time for an unbiased ∼600 ns MD simulation with TIP4P water model of apo PlmII.

In principle analogous methods of TICA⁵¹i.e. VAC⁵² and SGOOP⁵³†† can also be applied on PAPs to identify and bias order parameters which capture slow dynamical modes (from the MD trajectory) corresponds to flap dynamics.

Integration of several ICA algorithms e.g. Infomax,⁵⁵ kernel ICA,³⁷ JADE,⁵⁷ Fast ICA⁵⁸ with programming interfaces such as Python opens up the door to test the effectiveness of these methods in identifying order parameters from the high-dimensional dihedral space of PAPs.

Binary classifiers

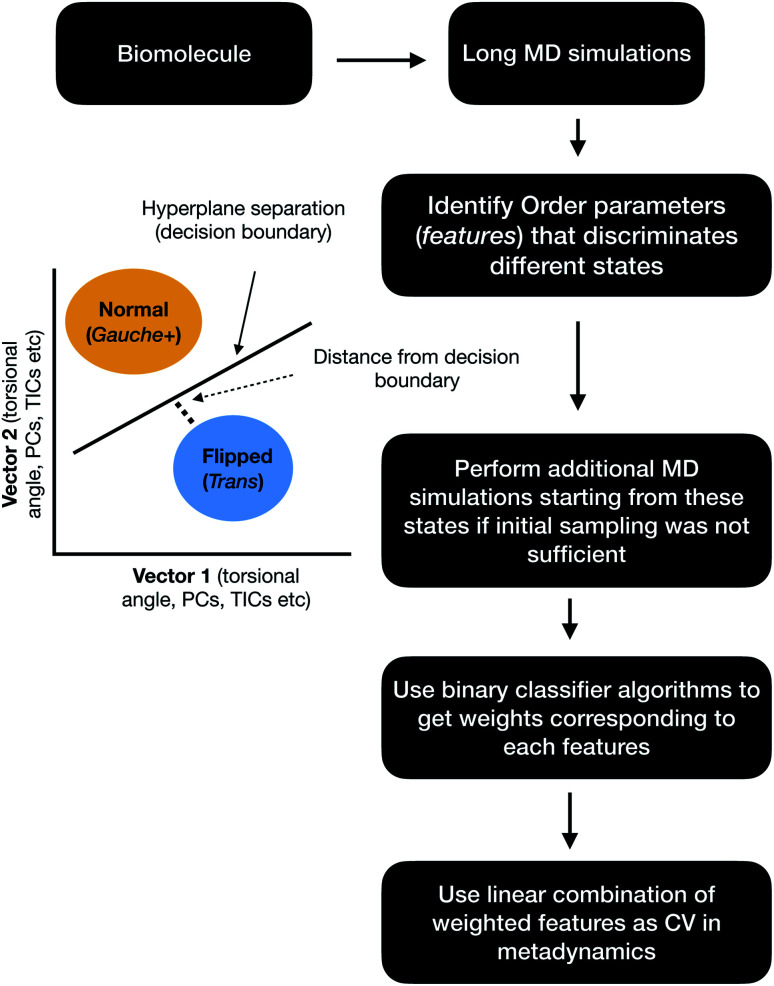
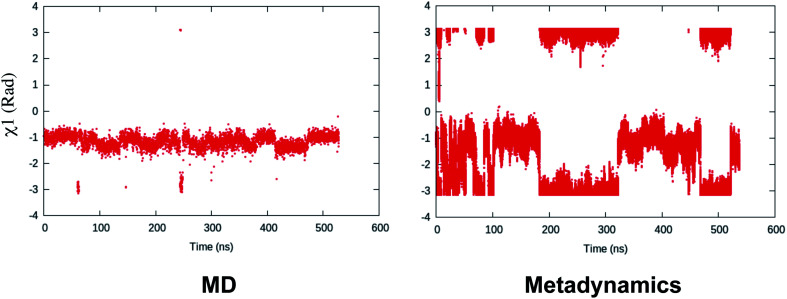
Binary classifiers are a set of supervised machine learning algorithms which aims at classifying an object into one of the two possible categories e.g. classifying the pictures of cats from dogs. The concept of using binary classifiers in automated selection of order parameters was first introduced by Sultan and Pande.⁵⁹ However, one prerequisite of using binary classifiers is that one has to sample the start and end states. In case of PAPs, these two states (otherwise known as state A and state B) can be normal and flipped states. If one extracts co-ordinates correspond to normal and flipped states from MD trajectory then the next step is to generate subset of order parameters (e.g. χ1 and χ2 angles of the flap region) which represents these two states. This is followed by training of the binary classifier e.g. support vector machine (SVM),⁶⁰ passive-aggressive (PasAg) classifier,⁶¹ logistic regression,⁶² perceptron⁶³ on the subset of order parameters. In case of PasAg classifier, the classifier decision boundary can be used as a order parameter to drive enhanced sampling calculation (Fig. 17). One advantage of using binary classifier based order parameters in metadynamics is that one can simultaneously bias multiple degrees of freedom (using parallel-bias metadynamics) which can lead to faster convergence (less chance for metadynamics to remain stuck along arbitrary orthogonal slow degrees of freedom) of metadynamics simulations. For example, if transition between normal to flipped state requires change in both χ1 and χ2 angles of Tyr and additional χ1 and χ2 angles of other amino acids (of the flap region), then binary classifier based order parameter would allow addition of metadynamics bias along these additional features using a single order parameter (classifier decision boundary). Initial calculations (unpublished) by the author have shown the effectiveness order parameters in sampling normal to flipped transition in apo PlmII (Fig. 18 and 19).

Fig. 17. Schematic diagram showing the steps involved in the application of binary classifier algorithms in context of biomolecular simulation. In case of PAPs vector1 and vector2 can be the χ1 and χ2 angles of the flap region. The χ1 and χ2 angles of Tyr plays dominating role in discriminating normal and flipped states. One can also use states separated along abstract order parameters (PCs, TICs) as classification problem.

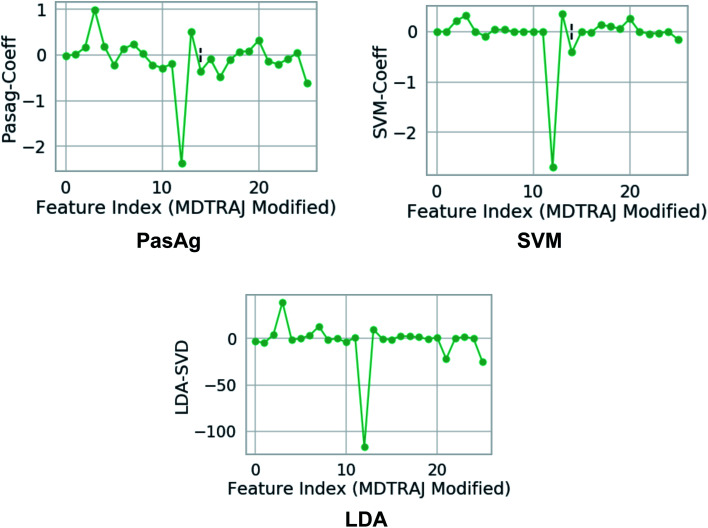
Fig. 18. Weights assign to each features which were used as inputs. Feature 3 and 12 corresponds to χ1 angle (3 and 12 represents sin χ1 and cos χ1 respectively) of Tyr (see Github for more details). One can clearly see that the weights corresponds to χ1 angle is higher compared to other side-chains angle of the flap region. This gives a clear signal that the χ1 angle of the conserved Tyr dictates transition between normal and flipped conformations. In case of LDA, the single value decomposition (LDA-SVD) was used as a solver (see scikit-learn for more options).

Fig. 19. Fluctuation of χ1 order parameter during MD simulation of apo PlmII. Metadynamics simulation with PasAg classifier based order parameter shows enhanced fluctuation along χ1. The plumed input files and tpr files for reproducing this result can be available at Github.

Another method that can be applied in capturing normal to flipped transition in PAPs is Fisher's linear discriminant analysis (LDA)⁶⁴ (Fig. 18). LDA has been routinely used in machine learning as a robust supervised classification method. Recently, Parrinello and co-workers have proposed a modified version of LDA, harmonic linear discriminant analysis (HLDA)⁶⁵ based order parameter which can be applied in context of normal to flipped transition in PAPs. However from a sampling point of view, i believe HLDA will not provide any additional benefits compared to binary classifier e.g. SVM, PasAg, logistic regression etc.

PAPs: testing ground for computational method development

‘If you know the answer beforehand it is easier to test new methods’

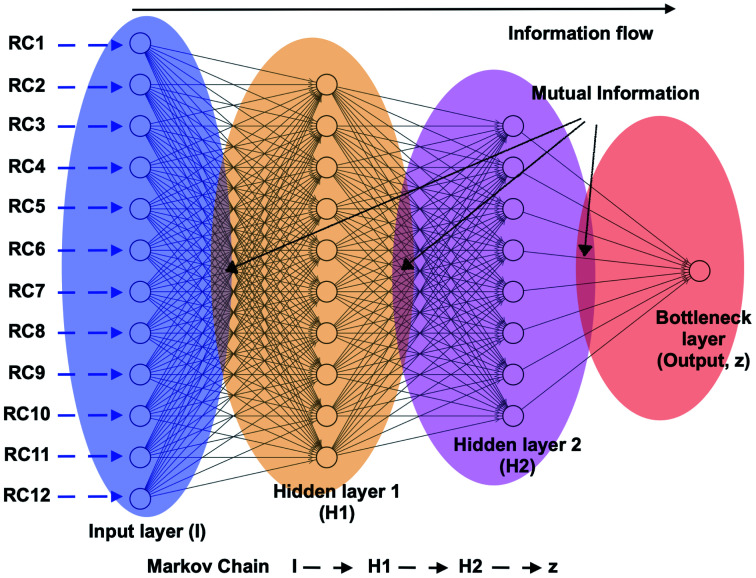
This was the philosophy behind using alanine dipeptide, chignolin, BPTI (together these systems known as the mice model for simulation methods) as typical test systems for novel computational methods directed towards order parameter selection. As discussed before the χ1 and χ2 order parameters⁶ of Tyr plays a critical role in conformational dynamics of apo PAPs. The rotation degrees of freedom associated with Tyr is believed to be one of the slow degrees of freedom which governs conformational dynamics of the flap. However, rotation degrees of freedom associated with conserved Trp and other residues present in the flap region also plays crucial role in overall conformational dynamics of PAPs. High dimensionality associated with dihedral angles of PAPs makes it an ideal play ground to test neural network based latent variable order parameters. In mathematical terms, latent variables are transformations that are not directly observed (probability distributions of dihedral angles) but are rather emerged (using mathematical transformations) from observed variables. Latent variable from bottleneck layer of neural network can effectively capture slow degrees of freedom from unbiased MD trajectories (Fig. 21 and 20). This type of neural network based order parameter can be further used to drive enhanced sampling calculations. Sidky et al.⁶⁶ and Wang et al.⁶⁷ laid out several machine learning algorithms that have been tested in context of biomolecular simulation. I believe most of these algorithms can be applied on PAPs with an aim to automatise identification of order parameters that governs its conformational dynamics. Bigger size of PAPs and prior knowledge on the role of conserved Tyr in flap dynamics (makes it easier to interpreted abstract order parameters) makes PAPs an ideal testing ground for novel machine learning algorithms (e.g. slow feature analyses,⁶⁸ LSTM⁶⁹ or transformer⁷⁰ like recurrent neural network).

Fig. 21. Schematic representation of a feed forward artificial neural network (ANN) architecture. A typical input to ANN can be multiple RCs which in context of PAPs can be probability distributions of χ1 and χ2 angles of the residues in the flap region, tIC/PC/SGOOP vectors sampled during trial MD simulation. The output layer (z) (also known as bottleneck layer) provides a non-linear transformation (sigmoid transformation) of the input features which can be used as a CV in metadynamics simulations. If we think I to z as Markov chains, then it is possible to calculate information flow within ANN by calculating mutual information between each layer (ref. 73 and 74). The hypothesis is that the information output from z will follow principle of maximum entropy (the output will be dominated by input RCs with maximal information entropy).

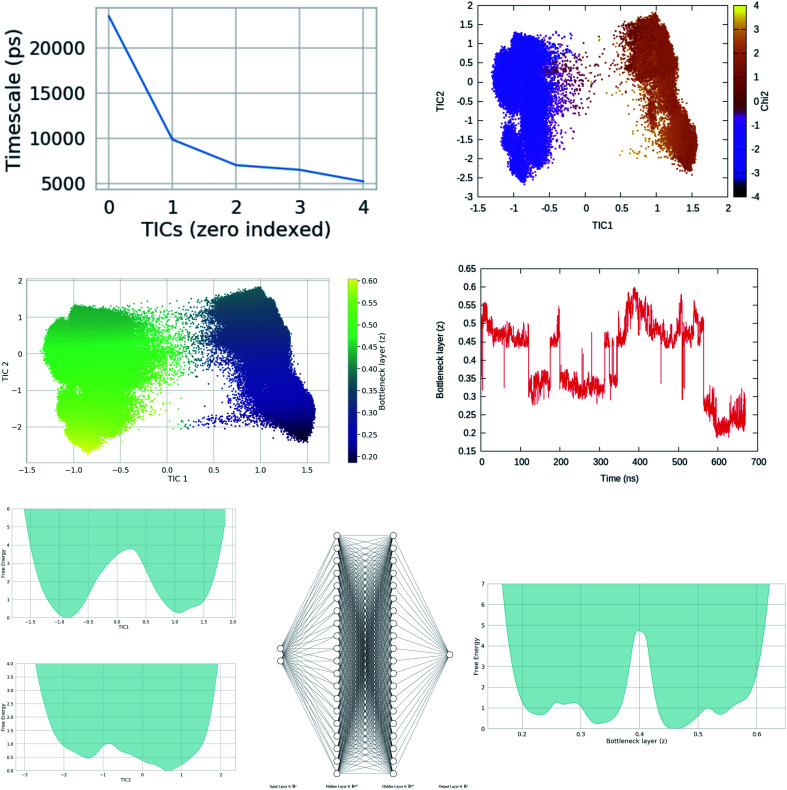
Fig. 20. Upper panel: timescale separation (otherwise known as spectral gap) along different TIC vectors (unbiased MD simulation of apo PlmII with length of ∼600 ns). TIC1 and TIC2 projected along χ2 angle of Tyr-79 shows that χ2 is one of the slow degrees of freedom in plasmepsin-II (corresponds with the higher weight on sin  χ2 in Fig. 15. Middle panel: bottleneck layer of a variational autoencoder (VAE)⁷¹ projected along TIC1 and TIC2. TIC1–2 were used as inputs in VAE. Different values of bottleneck layer represents different points along TIC vectors. One can see that the bottleneck layer did a better job in separating different metastable states compared to χ2. Further, time-series projection of the bottleneck layer shows its fluctuation during MD simulation. The coefficients (weights) of the bottleneck layer can be used as order parameters in metadynamics simulations. This method in principal similar to combining RAVE⁷² with SGOOP.⁵³ See the Github profile corresponding this article to see step-by-step guide on how to use variational autoencoder. Bottom panel: shows apparent free energy surface projected along TIC1, TIC2 and bottleneck layer. In this case, i have used a variational autoencoder with the following hyper-parameters: number of hidden layers = 2, number of neurons in each hidden layer = 20, number of epochs = 100, batch size = 500, learning rate = 1e − 2.

Open idea

Can one design a deep learning algorithm which will take multiple X-ray structures as inputs and predict trial CVs that captures slow degrees of freedom which governs conformational dynamics of a biomolecule? One can use PAPs as a test case in this project. The variations in PDB structures of BACE1 and PlmII are mainly dominated by torsional order parameters associated with conserved Tyr. An output trial CV from a deep learning architecture should give higher weights to torsional order parameters associated with Tyr. Besides, it must capture some non-linear combinations of other torsional order parameters that vary among these X-ray structures. The trial CVs can be iteratively optimized using a metadynamics framework similar to VAC.⁵²

Order parameters to capture ligand binding/unbinding

Ligand or substrate binding with PAPs require conformational change i.e. opening of the flap so that ligand/substrate can bind to the active site. Flap opening in PAPs is similar to the flap opening in HIV/SIV protease.⁷⁵ A generalised order parameter that can describe ligand binding/unbinding can be defined as follows:

‘COM_unbind: the distance between COM of the ligand heavy atoms and the COM of the catalytic aspartates (Cα atoms)’

Plotting the aforementioned order parameter COM_unbind in combination of DIST2 gives an indication of the extent of flap opening during ligand binding/unbinding. Further, plotting COM_unbind with χ1 and χ2 angles of Tyr can give an idea on how flipping of conserved Tyr residue affects ligand binding/unbinding.

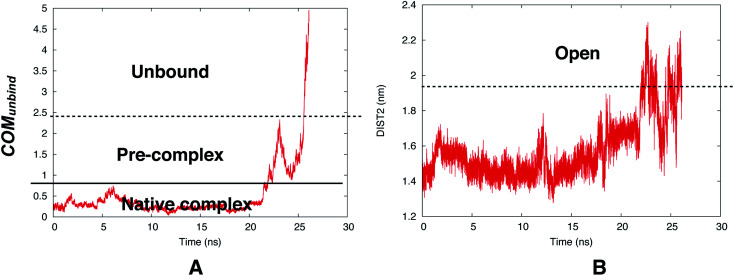
However, reversible sampling of ligand binding/unbinding using physical order parameters such as COM_unbind is not a trivial task. In one such initial effort Bhakat and Söderhjelm used COM_unbind order parameter within well-tempered metadynamics simulation. The results showed that flap opening is necessary for ligand unbinding (Fig. 22). However, the challenge is to multiple reversible sampling of ligand binding/unbinding in order to validate the role of flap opening with statistical certainty. Another open question which goes hand in hand with ligand binding: ‘does flipping of conserved Tyr/Phe in PAPs necessary during ligand binding to accommodate the ligand in the active site?’ Recently, Limongelli⁷⁷ reviewed several pathway based simulation methods that can capture conformational change induced ligand binding/unbinding. One of these simulation methods include funnel metadynamics⁷⁸ (facilitates frequent ligand binding/unbinding by using a funnel like restraint potential which reduces the sampling of the unbound state) and its variant volume-biased (sphere shaped restraint potential instead of funnel) metadynamics.⁷⁹ In theory it is possible to use COM_unbind order parameter within funnel/volume biased‡‡ metadynamics framework to understand how conformational changes in PAPs induce ligand binding/unbinding (Fig. 23 and 24). Other enhanced sampling methods such as accelerated MD (aMD),^80–82 weighted ensemble (WE) method,^83–85 adiabatic-biased MD (ABMD)^86,87etc can also be tested on PAPs to explore conformational dynamics, kinetics and free energy associated with ligand binding/unbinding.

Fig. 22. Time evolution of COM_unbind during metadynamics simulations (A). Plotting DIST2 as a function of time shows how flap opening is necessary in order to transit from pre-complex to unbound state. The conserved Tyr remained in gauche⁺ conformation during the unbinding process. The simulation was carried out using PlmII-ligand complex (PDB ID:4Y6M⁷⁶).

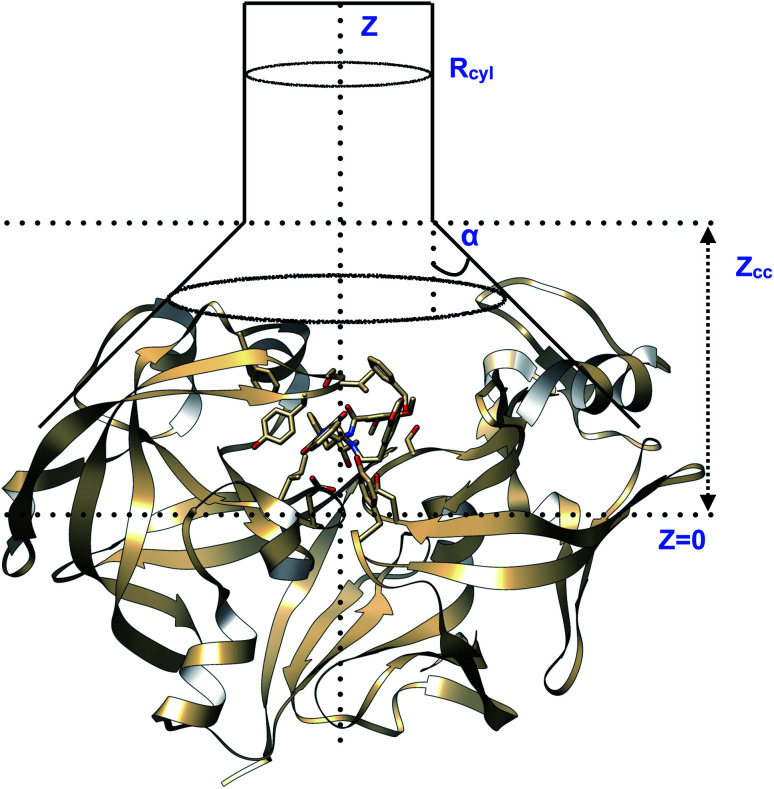
Fig. 23. Pictorial representation of a model funnel shaped potential that can be used to calculate binding free energy and binding/unbinding induced conformational changes in PAPs.R_cyl describes the radius of the cylindrical section and Z defines the axis to study binding/unbinding. Z can be COM_unbind or some other distance based order parameter. Z_cc is the distance where the potential switches from cone to cylindrical shape. The effect of restraint potential can be rigorously calculated as described in ref. 92. R_cyl should be adjusted such that it doesn't affect the natural conformational dynamics of the ligand binding/unbinding. PAP-inhibitor complex provides a true challenge (compared to T4-lysozyme and other systems where the ligand has few torsional degrees of freedom and protein is relatively rigid) for funnel metadynamics as the ligands have large number of torsion angles and the protein undergoes large conformational changes during binding/unbinding. Abstract order parameters e.g. TICA/SGOOP/VAC, path CVs can address this challenge. Funnel metadynamics using open flap inhibitors can in principle give insights into how flipping of Tyr and Trp accommodate bigger ligands which has direct application in ligand design.

Fig. 24. Pictorial representation of sphere shaped restraint potential applied in case of volume-biased metadynamics. Unlike funnel metadynamics, the sphere shape restraint potential is more general and doesn't assume any prior knowledge of the binding site. This method has been used to identify novel ligand binding pathways in T4-lysozyme. Using this method on PAP-ligand complex can find alternative ligand binding pathways as well as path CVs for binding/unbinding transition. The challenge is to set the radius of the sphere so that it doesn't hamper the large scale conformational dynamics of PAPs upon ligand binding/unbinding.

Challenge to the simulation community

Recently, macro-cyclic ligand bound structures of BACE1 were reported by Yen et al.⁸⁸ (PDB IDs: 6NV7, 6NV9, 6NW3). The authors further reported experimental K_i and K_d values as well as several thermodynamic parameters (ΔH, TΔS, and ΔG) of ligand binding (thermodynamic parameters were calculated using isothermal titration calorimetry (ITC) experiments). Keeping in mind the availability of experimental datas, size and number of torsion angles of the macro-cyclic ligands and large scale conformational dynamics of BACE1, it will be the perfect challenge for methods e.g. funnel metadynamics, volume biased metadynamics, variational autoencoder driven infrequent metadynamics,^89,90 WE,⁹¹ aMD etc. To predict binding free energies and kinetics on clinically important protein-ligand systems beyond typical test cases e.g. benzamide–trypsin and on systems where the ligand is relatively small with fewer torsional angles and there is no large scale conformational dynamics upon ligand binding.

Combining experiment with molecular simulation

Rotation of Tyr side-chain and opening of the flap region makes PAPs an ideal case to apply methods that combines molecular simulations with biophysical experiments. Combining MD simulation with NMR spin relaxation derived dynamical information^93–97 to capture residue-wise backbone/side-chain configurational entropy is a powerful method to understand stability of proteins and its changes upon perturbation. An analytical approach to capture configurational entropy is to measure residue-wise O² (often written as S²) from MD simulations. It has been shown that configurational entropy of protein can be described from dihedral distribution sampled during MD simulations.⁹⁵ For each side-chain dihedral angle ω_j, the probability distribution p(ω_j) is determined by von-Mises kernel estimation which contributes toward the configurational entropy S:

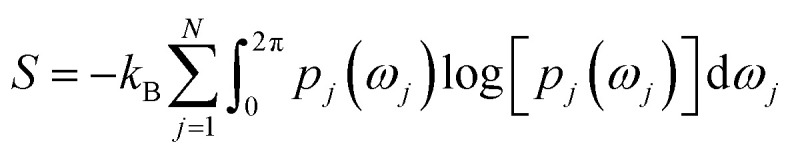3

O² is mathematically connected with S using the following equation:

S = k_BM[A + Bf(1 − O_NMR²)] 4

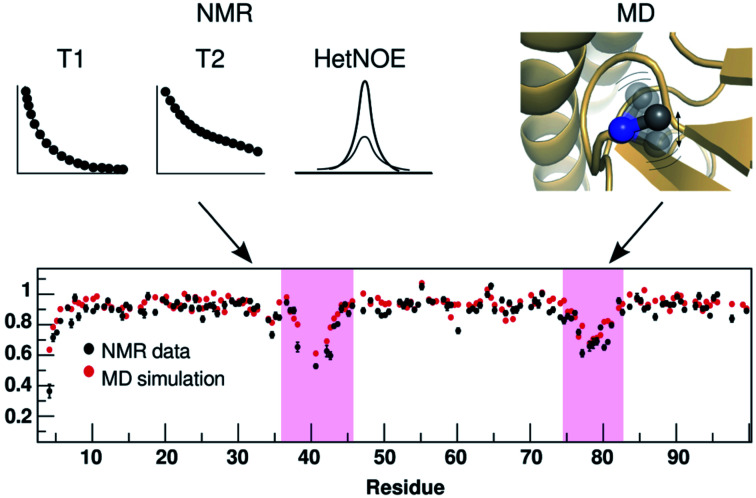
where M denotes number of side-chain dihedral angles, A and B are fitted parameters. One way to capture O² from MD simulation is to use principal component based method otherwise known as isotropic reorientation eigenmode dynamics (iRED).⁹⁸ In principal, O² derived from MD simulation can be compared with NMR spin relaxation experiments which can give us an idea of residue-wise dynamics associated with the flap region of PAPs (Fig. 25). NMR experiments can further give insights (both dynamics and kinetics) into ring flip associated with conserved Tyr/Phe and Trp in PAPs (ref. 99–101).

Fig. 25. Comparison of residue-wise dynamical properties measured by NMR and MD derived order parameter O² (y axis in the bottom panel). The backbone order parameter provides information on the amplitude of fluctuation of NH and CH bond vectors. The magenta shadowed area shows the residues with higher backbone flexibility (lower O² corresponds to higher flexibility). Experimental parameters can be calculated by T1, T2 and heteronuclear NOE relaxation experiments. Often short MD simulations are sufficient to produce O² which can capture motions in ps to ns timescale but for slower relaxation motions one needs longer simulations (μs to ms). Comparison of NMR and MD derived O² in PAPs can give insights into how flap flexibility varies between apo and ligand-bound conformations. See ref. 95 and 96 for comparison of conformational dynamics using MD and NMR. The figure was adapted from ref. 102.

Besides combining NMR with MD simulation, time resolved fluorescence spectroscopy, FRET and Raman spectroscopy§§ can be applied to capture conformational dynamics of PAPs. This is an open area of research which didn't gain much attention from the biophysical or structural biology community. In theory, time-dependent order parameters from experiments (e.g. FRET) can be integrated with MD simulations using embedding theorem e.g. Taken's embedding theorem (ref. 104). Ligand binding to PAPs can be calculated using isothermal titration calorimetry (ITC)¹⁰⁵ or differential scanning calorimetry (DSC)¹⁰⁶ which measures different thermodynamic parameters involved in the binding process. The major challenge in front of the simulation community is to calculate thermodynamic parameters from pathway based simulation methods (or from enhanced sampling calculations) that agrees with experiment. This is a growing area of research within biophysical community and PAPs can be an ideal test system for integrating biophysical experiments with biomolecular simulation.

Ideal playing field for drug repurposing

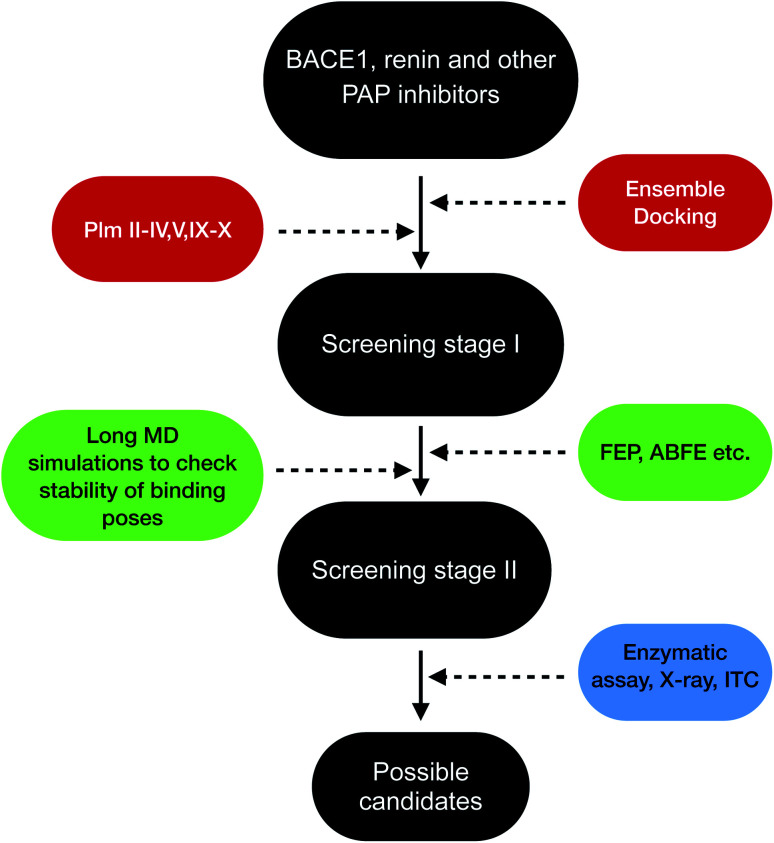
Plasmepsins (especially PlmII, PlmIV, PlmV, PlmIX and X) are drug targets for malaria.^107,108 Artemisinin and chloroquine are the two major blockbuster drugs against malaria. Emergence of artemisinin¹⁰⁹ and chloroquine¹¹⁰ resistant P. falciparum possess a huge risk towards eradication efforts towards malaria in Africa and South-East Asia. This calls for identification of novel drug targets against malaria and plasmepsins has potential to become the next big target against malaria. BACE-1 is a promising drug target for Alzheimer's disease with several inhibitors in different stages clinical trials and several ligand bound crystal structures deposited in PDB. Due to structural similarity and similar mechanism of action which governs conformational dynamics of apo PlmII and BACE-1 (in general all PAPs), the ligands targeting BACE-1 can be re-purposed on plasmepsins. Machine learning based methods (e.g. convolutional neural network) combined with molecular docking,^111–113 free energy calculations¹¹⁴ (e.g. FEP, ABFE, MM/PBSA or MM/GBSA) and biochemical assay can then be used to identify BACE-1 inhibitors (in broad sense this concept is applicable for other PAP inhibitors e.g. human renin inhibitor) as potential plasmepsin inhibitors. This repurposing strategy can help to identify scaffolds¶¶ that can be further modified by synthetic chemists to develop potent molecules targeting plasmepsins (Fig. 26). I believe in future machine learning driven molecular docking combined with experiment will play an important role in repurposing other PAP inhibitors against plasmepsins.

Fig. 26. Schematic diagram showing a workflow on how computational predictions and experiments can work coherently in order to re-purpose BACE1 and other PAP inhibitors on plasmepsins. Growing interest of artificial intelligence (AI) based drug discovery companies (e.g. Atomwise) within drug repurposing in the wake of COVID19 shows that AI can also be used within drug repurposing workflow in context of plasmepsins.

Conclusions and future directions

The main aim of this review was to highlight the possibilities of using PAPs as model systems to test novel simulation methods and to combine biomolecular simulation with biophysical experiments. In order to kick-start this effort I have curated a Github profile which contains inputs for performing biomolecular simulation and order parameters that can be monitored during molecular simulation. Although in practice there has been a few advances in application of state-of-the art biomolecular simulations on PAPs, a combination of biophysical experiments with biomolecular simulation (otherwise known as integrative structural biology¹¹⁵) is far from a standard practice. Dynamic nature of PAPs makes it an ideal case to integrate experiment with molecular simulation using methods such as Bayesian-maximum entropy¹¹⁶etc. which can provide both atomic-level description and mechanistic understanding (e.g. population of normal/flipped states, role of force field and water models in population of different states, role of Tyr/Phe in conformational dynamics and ligand binding, extent of flap opening etc.) of the PAPs.

Finally, COVID-19 pandemic shows a resurgence of drug repurposing by combining molecular simulation with biochemical experiments. Projects like COVID Moonshot shows how an old simulation technique (free energy perturbation) can be effectively used in order to hunt novel drug candidates against COVID. Similar simulation strategies (AI driven molecular docking, free energy perturbation etc.) can be applied to re-purpose BACE1, human renin, pepsin inhibitors against plasmepsins followed up by experimental validation (biochemical assay, X-ray crystallography, NMR etc.). Further keeping in mind the neglected¹¹⁷ status of malaria it is of utmost importance to share computational and experimental protocols openly using public data/code-sharing platforms e.g. Jupyter Notebook, Github, Google Collab etc. Finally, bigger and dynamical nature PAPs and their role in human disease makes it an ideal model system for experimentalists and computational chemists to work together towards developing new methods and applying old methods which will have direct application towards developing novel therapeutics against malaria, Alzheimer's disease etc.

Note

To date, no pathway based simulation methods able to predict thermodynamics and kinetic parameters of HIV protease inhibitors (for the sake of sample size we can focus on nine clinically approved drugs) and compare it with experiments. Even in the year 2020, the most widely used method for small molecule drug discovery (clinically relevant) is molecular docking (often followed by visual inspection and FEP) which is computationally less expensive compared to physical pathway based methods. Two major problems of molecular docking are approximated energy functions and lack of sampling (especially of the protein). The remedy to this is a skin-in-the game problem.

‘when the solution is about solving this very problem-Nassim Nicholas Taleb’.

Observation

In D3R Grand Challenge 4 (ref. 118) which aims at predicting binding pose and free energy using BACE1, the top performing submissions didn't use pathway based sampling methods.

Conflicts of interest

Author declares no potential conflicts of interest.