Mechanical behaviors and probabilistic multiphase network model of polyvinyl alcohol hydrogel after being immersed in sodium hydroxide solution

Abstract

Because of the advantages of a uniform distribution of reinforcing particles and in situ preparation, in situ precipitation has become an important way to prepare magnetic and other smart hydrogels. An important step in this process is to immerse hydrogels in alkaline solution to implant magnetic particles. Previous studies generally have ignored the effect of this process on the network structure and mechanical properties of hydrogels. In this study, we immersed polyvinyl alcohol (PVA) hydrogel samples in sodium hydroxide solutions of different concentrations to study changes in mechanical properties, such as stress–strain relationship, self-recovery, and fracture failure. The results showed that after the immersion process, the hydrogel's tensile and compressive properties changed significantly, and the failure behavior changed from brittle fracture to ductile fracture. Through a microscopic mechanism, the alkaline solution caused a high degree of phase separation and crystallization within the polymer network, thereby changing the PVA hydrogel network from a single phase to a multiphase. Hence, we used a continuous multiphase network model with a certain probability distribution to describe this tensile behavior. This model well described the stress–strain relationship of the hydrogel from stretching to fracture and revealed that the macroscopic failure corresponded to the peak of fracture distribution. Studies have shown that attention should be paid to the influence of the in situ precipitation on the mechanical properties, and the probabilistic multiphase network model can be used to predict the mechanical behavior of hydrogels with multiple phase separation.

Phase separation occurs in polyvinyl alcohol hydrogel after being immersed in sodium hydroxide solution. The change of the network structure leads to significant changes in the mechanical behaviors.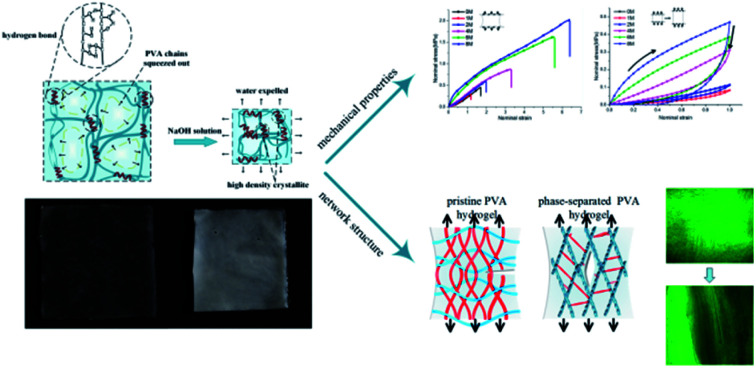

Introduction

Hydrogels consist of a three-dimensional network of hydrophilic polymer chains. The water content and hardness of some hydrogels are similar to that of soft tissues in the human body;¹ hence, hydrogels have wide application prospects in the biomechanical field. As a synthetic material with better mechanical properties,² physical crosslinked hydrogels often have better biocompatibility than chemical crosslinked hydrogels,³ thus becoming the focus of biomechanical research.

Physically crosslinked polyvinyl alcohol (PVA) hydrogels have attracted wide attention because of their good physical properties and biocompatibility.^4,5 Peppas and Merrill first reported the physical crosslinked PVA hydrogel preparation in 1976.⁶ The PVA solution was frozen and thawed to prepare hydrogels with a stable structure, high water content, and good biocompatibility. Some researchers have reported that physical PVA hydrogel was used as a base material to obtain intelligent PVA hydrogels with both biocompatibility and environmental sensitivity. Among these hydrogels, magnetic PVA hydrogel has great values. It has the ability to respond to the external magnetic field remotely, like other magnetically controlled nanocarriers, and has been shown to be an effective drug delivery system. Use of the thermal and magnetic response of the hydrogel under alternating magnetic field to control drug release can greatly overcome the lack of spatial and temporal control existing in conventional methods.^7,8 Researchers have demonstrated that magnetic PVA hydrogels have good responses to an external magnetic field and have investigated applying the material in biomechanics, including the use of magnetic hydrogels to move drugs to the target area or regulate the release rate of the drugs by adjusting the external magnetic field.^8,9

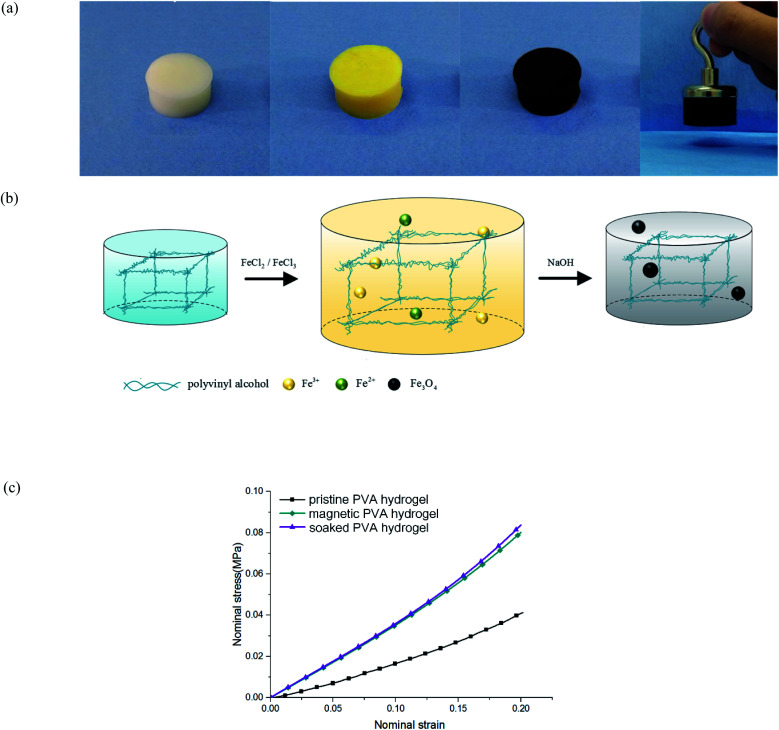
The preparation of traditional magnetic PVA hydrogel is to mix PVA solution and magnetic particles directly (i.e., γ-Fe₂O₃/Fe₃O₄). This process is simple and effective, but it has the shortcoming of uneven particle distribution: because the polymer network in the early freezing stage was not completely formed, magnetic particles could not be fixed in the fiber network; thus, they would sink to the bottom under gravity. Therefore, its magnetism is obviously uneven along the vertical direction. In addition, the mechanical properties and stability of magnetic PVA hydrogel are restricted by the base material, which limits its applications in some aspects. For example, when magnetic PVA hydrogel was used in thermal anticancer therapy,^10,11 the hydrogen bonds of physical crosslinked PVA hydrogels would break at a high temperature, which led to the collapse of the polymer network.¹² As a result, the hydrogels not only could not work properly, but also may have caused problems such as magnetic particle exudation and biological toxicity.¹³ If a PVA hydrogel was used for bearing or driving, it would face problems of insufficient hardness (0.1–0.2 MPa) or toughness (10² to 10³ J m⁻²).¹⁴ Researchers have proposed some methods, such as dry-anneal,¹⁵ cast-dry¹⁶ or cyclic pre-stretching.¹⁷ Although the mechanical properties of the material were improved, it took a longer preparation cycle and introduced more complex procedures. The preparation of magnetic hydrogels by an in situ precipitation method could address these problems. To obtain the magnetic PVA hydrogel through in situ precipitation, the PVA hydrogel was immersed in an Fe²⁺/Fe³⁺ solution and sodium hydroxide (NaOH) aqueous solution successively to produce nano Fe₃O₄ particles (Fig. 1(a) and (b)). This method has several advantages: first, relying on the intact three-dimensional network structure, the magnetic particles produced are evenly distributed. Second, the mechanical properties of PVA hydrogels were obviously improved. By comparing the compression curves of hydrogel immersed in NaOH aqueous solution, magnetic hydrogel, and pristine hydrogel, we found that its immersing process affected the properties of hydrogel (Fig. 1(c)). This effect was often neglected in the studies of magnetic hydrogel. We found that the improvement of mechanical properties was mainly due to the process of PVA hydrogel immersing in an alkaline solution, and the degree of enhancement was directly related to the concentration.

Fig. 1. Magnetic PVA hydrogel: (a) magnetic PVA hydrogel prepared by in situ precipitation method, hydrogels exhibited good magnetic properties; (b) schematic of the in situ precipitation preparation of magnetic hydrogels; and (c) stress curves of different hydrogels under uniaxial compression.

The modification of hydrogels after being immersed in solution has attracted much attention in the past few years. Studies have shown that hydrogels may produce salting-out under immersion and may affect the macroscopic properties of materials.¹⁸ When polyacrylamide hydrogel was immersed in a high concentration of dimethylamide solution, it lost water and shrank, the hardness was increased, and the transparency was reduced.¹⁹ Poly-dimethylpropionamide (PDMA) hydrogel had similar behavior in NaOH aqueous solution, which could be used to prepare a high-toughness magnetic PDMA hydrogel.²⁰ Polyvinyl alcohol/sodium alginate (PVA/SA) composite hydrogel had better mechanical properties and higher conductivity after being immersed in saturated sodium chloride (NaCl) solution.²¹ Darabi et al. discussed the reaction between PVA and NaOH solution, and revealed that the acid–base reaction was the primary reason that led to the hydrogen bonding and crystallite formation inside the polymer. Therefore, the physical and chemical properties of the material would be changed obviously.²² Sato et al. thought that when the hydrogel was immersed in good solution, it would absorb water and swell, and that in poor solution, it would lose water. They found, however, that the mechanical properties were enhanced, and this enhancement was attributed to the phase separation of the polymer network.¹⁹ Few researchers, however, have established a mechanical model to analyze this mechanism.

In this study, we first demonstrated the existence of an interaction between physical PVA hydrogel and NaOH solution. We then proved that NaOH solution caused this phase separation, which increased the microcrystalline in the polymer network. As a result, the hardness, toughness, and self-recovery of the hydrogel were improved. The relationship between mechanical properties and solution concentration was studied quantitatively. We also demonstrated that the essence of the effect of solution immersion on the mechanical properties was the energy dissipation mechanism. The phase separation significantly affected the mechanical behavior of the material during tensile failure, which resulted in the transformation from fast fracture to ductile fracture. Finally, we proposed a multiphase network model with continuous distribution to describe the tension behavior.

Experimental methods

Hydrogel synthesis

We prepared the PVA hydrogel according to the freeze–thaw method: PVA dry powder and deionized water were mixed with a mass ratio of 1 : 4, and then placed in a high-temperature environment above 120 °C to obtain a transparent PVA aqueous solution. Then the solution was placed into the vacuum environment. After the air bubbles were removed, the solution was poured into molds. We performed five cycles of freezing and thawing for 12 h per stage (freezing at −20 °C and thawing at 25 °C). Finally, we obtained PVA hydrogels with 20% fiber content.

To obtain the magnetic PVA hydrogel, the hydrogel was immersed in the mixture solution of FeCl₂ and FeCl₃ at a concentration ratio of 1 : 2. After swelling to equilibrium, the opaque hydrogel turned orange. Finally, the Fe²⁺/Fe³⁺ loaded hydrogel was transferred to the NaOH aqueous solution to generate magnetic particles into the polymer network. Then, the following reaction occurred: 2Fe³⁺ + Fe²⁺ + 8OH⁻ → Fe₃O₄(↓) + 4H₂O.

To obtain the phase-separated PVA hydrogel with high mechanical property, we immersed the pristine PVA hydrogels directly in the NaOH aqueous solution until it reached the equilibrium. Afterward, we immersed the sample in deionized water to remove the excess ions. The volume and transparency of the hydrogel were tuned by changing the concentration of the NaOH solution.

Wide-angle X-ray diffraction measurement

We collected wide-angle X-ray powder diffraction (XRD) profiles at room temperature 25 °C in the degree 2θ range of 10°–50°.

Tension test

The intact and pre-notched hydrogel samples of rectangular cross sections were fixed at both ends. We conducted quasi-static tensile tests using an INSTRON5567 testing machine. The strain rate was fixed as 0.01 s⁻¹. For the uniaxial tensile test, we carried out the tensile loading until the material tore. For the cyclic loading experiment, when the tension reached the predetermined length, the machine would unload. The second loading would start when stress was reduced to 0, and the unloading rate was controlled to be the same.

Compressive tests

We subjected cylindrical hydrogels to uniaxial compression. The strain rate was controlled at a constant 0.005 s⁻¹ and the maximum compressive strain was 0.25. We recorded the experimental data by the testing machine.

Confocal imaging of PVA hydrogels

To visualize the microstructures of the PVA hydrogels, we used a fluorescent dye (i.e., 5-[(4,6-dichlorotriazin-2yl)amino]) fluorescein hydrochloride [5-DTAF]) to label the PVA sides groups. PVA hydrogels were first immersed in a large volume of weak alkaline solution (pH = 9.0) for 12 h to equilibrate the pH within the samples. The 5 mg of 5-DTAF dissolved in 1.0 mL of anhydrous dimethyl sulfoxide was immersed in 100 mL of alkaline solution (pH = 9.0) to form a reactive dye solution. The previous PVA samples were immersed in the dye solution for 12 h at 5 °C in a dark environment to form conjugated fluorochromes. Then the PVA samples were rinsed several times with deionized water to wash away the nonconjugated dyes. After the noted pretreatment, we could use the PVA samples for observation under a confocal microscope.

Digital image processing method

To obtain the real stress state of the material at each moment during the loading process, we used a camera to take a full picture of the sample through the entire process. Because the hydrogel is opaque and white, we placed a blackboard behind the sample to increase contrast so that we could use edge detection technology to distinguish the boundary of the sample clearly. By calculating the distance of the edges of each photo, we obtained the width and thickness of the sample at each moment, and furthermore, we obtained the true stress–strain relationship of the material.

Results and discussion

Characterization of PVA hydrogel

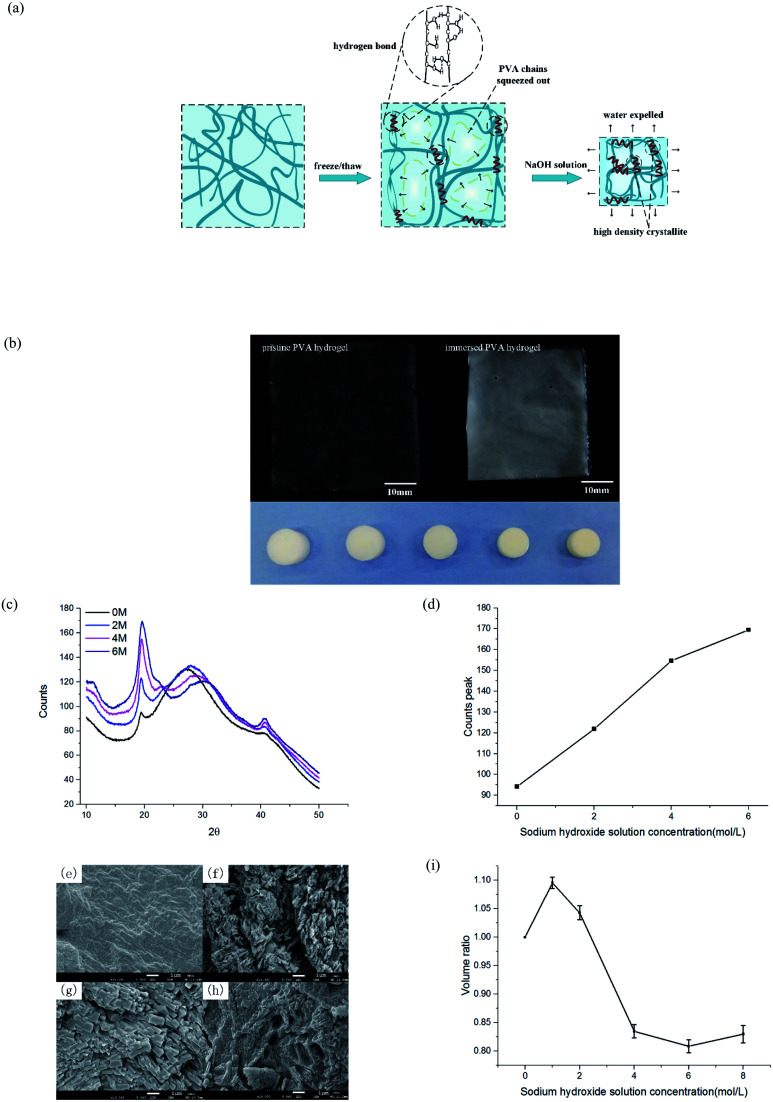
After freezing and thawing, the physical PVA hydrogel obtained had low transparency. During the freezing process, the water in the solution froze and PVA chains were discharged, forming dense regions with high PVA density and sparse regions with low PVA density (Fig. 2(a)). The hydrogen bonding interaction between the polymer chains in the dense regions drove the formation of the microcrystals. As a result, the hydrogels turned opaque.²³ After the PVA hydrogel was immersed in the NaOH solution, the hardness increased, but the swelling ratio and transparency decreased further (Fig. 2(b)).

Fig. 2. Characterization of PVA hydrogel after immersion. (a) Schematic of phase separation mechanism of freeze–thaw and solution immersion; (b) transparency and volume changes induced by NaOH solution immersion, the photos were taken by a camera; (c) XRD patterns under different concentrations of immersion; (d) statistics of crystallization peaks of XRD patterns at four concentrations; (e)–(h) surface morphology of hydrogels immersed in 0, 2, 4, and 6 M NaOH solution, respectively; and (i) volume ratio of hydrogels immersed in different NaOH concentrations.

To prove that phase separation existed and led to an increase of microcrystalline, we tested the samples by wide-angle XRD and observed their surface morphology under an electron microscope. PVA hydrogels containing 80% water were immersed in 0, 2, 4, and 6 mol L⁻¹ NaOH solution, respectively. The spectrum of the hydrogel contained diffraction peaks at the 2θ angles of 19.5° (Fig. 2(c)). This result was consistent with a previous study²⁴ that also indicated the formation of PVA crystallites. With the increasing of NaOH solution concentration, the diffraction peaks also increased obviously. Fig. 2(d) displays the statistical result of peak intensity. The calculation of crystallinity was

φ = I_c/(I_c + I_a) 1

where I_c represents the intensity of the crystallization peak, which can be calculated by the area surrounded by the crystallization peak curve; and I_a is the intensity of the amorphous peak. It is clear that crystallinity enhanced obviously. Fig. 2(e)–(h) show the microsurface morphology of different samples observed under scanning electron microscope. After being immersed in a high-concentration solution, an obvious microcrystallite formation could be seen. The transparency of PVA hydrogel depended on the volume and density of internal crystallites;²⁵ hence, the immersed PVA hydrogels had a lower transparency. The volume ratio V_i/V_p of different experimental groups is shown in Fig. 2(i), where V_i is the volume of immersed hydrogels and V_p is the volume of pristine hydrogels. When the solution concentration was higher than 4 M, the water content and transparency of the material no longer changed, but its mechanical properties were still enhanced with the concentration, which suggested that the network structure of the hydrogel changed.

Tension and compression behavior of phase-separated PVA hydrogels

To study the mechanical properties of PVA hydrogel immersed in NaOH solution, we conducted uniaxial tensile and compressive tests. NaOH solution concentrations were 0, 1, 2, 4, 6, and 8 M. The experimental results showed that the mechanical properties of PVA hydrogels increased significantly after being immersed in high-concentration solution.

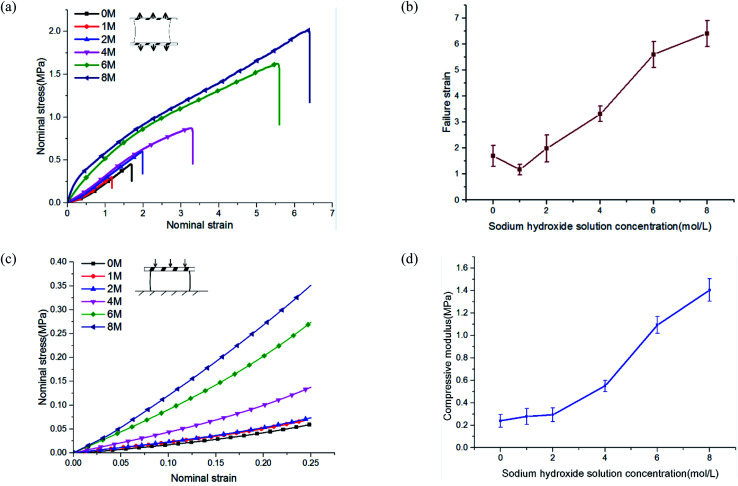
The stress–strain curves under uniaxial tensile are shown in Fig. 3(a). The failure strain of hydrogels immersed in 8 M concentration reached more than four times that of pristine PVA hydrogel (Fig. 3(b)). The tensile stress of pristine PVA hydrogel showed nonlinearity: with increases in stretching, the stress increased faster, which was consistent with previous results.²⁶ For hydrogels immersed in NaOH solution, the results showed an opposite trend: in the early stage of stretching, the stress increased rapidly, but in the late stage of stretching, the slope of the stress curve decreased. The shape of the stress curve changed from “lower convex” of the pristine PVA hydrogel to “upward convex” of the PVA hydrogel immersed in NaOH solution. This may have resulted from a gradual destruction inside the polymer network: the decrease in the number of stressed fibers resulted in a decrease in the tangent slope of the stress curve. In terms of compressive behavior (see the stress–strain curves in Fig. 3(c)), the modulus of PVA hydrogels immersed in 8 M NaOH concentration reached seven times that of the pristine PVA hydrogel (Fig. 3(d)).

Fig. 3. Tension and compression behavior of phase-separated PVA hydrogels: (a) the stress–strain curve under uniaxial tension; (b) failure strain statistics; (c) the stress–strain curve under uniaxial compression; and (d) the compression modulus of PVA hydrogels.

The enhancement of mechanical properties in tension and compression may have been due to two mechanisms. First, the fiber content increased because of a decrease in the swelling ratio. The mechanical properties of the hydrogels were directly related to their fiber content. The mechanical properties of the material could be affected in this way only when the concentration of NaOH solution was lower than 4 M. Previous experiments showed that when the concentration was higher than 4 M, the swelling ratio no longer changed. Second, phase separation changed the polymer structure and further led to the enhancement of mechanical properties. This indicated that multiphase networks with different mechanical properties may have been formed in the polymer network. Moreover, the chemical mechanism of phase separation induced by the interaction of NaOH and PVA has been discussed in detail by Darabi et al.²²

Energy dissipation and self-recovery of phase-separated PVA hydrogels

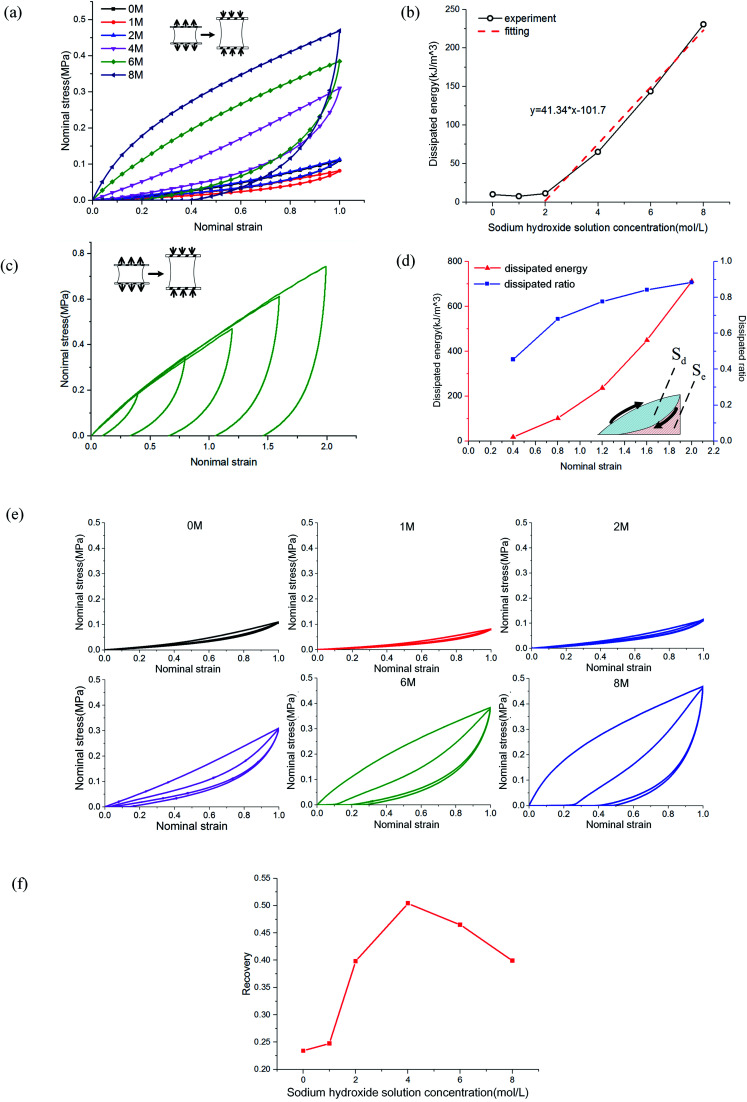
The mechanism of improving the mechanical properties for phase-separated hydrogels was similar to double-network hydrogels. The interactions between polymer chains in dense regions were enhanced and more microcrystals could serve as sacrificial bonds to dissipate energy during stretching to protect the entire polymer network from being destroyed, which has been explained in detail by Gong.²⁷ This mechanism can be proved by the hysteresis phenomenon in loading and unloading tests. The stress curves of six groups immersed in different NaOH concentrations within one cycle are shown in Fig. 4(a). The dissipated energy U_hys is the area S_d enclosed by the loading curve and unloading curve:¹⁹

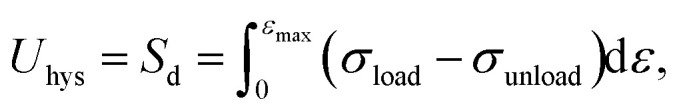2

where σ_load and σ_unload are the stress of the loading and unloading process.

Fig. 4. Cyclic load tests: (a) the single loading and unloading curves of PVA samples immersed in different NaOH concentration; (b) energy dissipation statistics of (a); (c) the loading and unloading curves of PVA immersed in 8 M NaOH solution with different tensile strains; (d) statistics of energy dissipation and dissipation ratio of (c); (e) double cycle curves of immersed PVA hydrogel samples; and (f) self-recovery ratio of PVA hydrogels immersed in NaOH solution.

The area enclosed by the tensile curve and x-axis (S_d + S_e) was the work done by external force during the stretching process, and the difference S_e was the potential energy stored in the polymer network (Fig. 4(d)). When the NaOH solution concentration was higher than 2 M, the energy dissipated through the network increased obviously, and a linear correlation was evident, as shown in Fig. 4(b). We defined S_d/(S_d + S_e) as the external work dissipated ratio. This value reflected the working effect of the mechanism. When nominal strain reached 1.0, the dissipation ratio of pristine PVA hydrogel was 0.23, and that of the samples immersed in 8 M NaOH concentration was 0.7. For pristine PVA hydrogel, most of the external force work was stored as potential energy, which retained the ability to restore the material to its original state. In phase-separated PVA hydrogel, this work left little as stored energy, and most of the energy was consumed through microcrystal expansion. As a result, the sample had obvious residual strain. Fig. 4(c) shows the loading and unloading curves of PVA hydrogel immersed in 8 M NaOH concentration solution under different maximum strains, and the dissipated energy and ratio increased obviously with strain (Fig. 4(d)), which indicated that the dissipation mechanism took more effect as the materials deformed.

Furthermore, we studied the effect of NaOH solution on the self-recovery characteristics of PVA hydrogel. As a feature of hydrogen-bonded hydrogels, self-recovery often has been used to design double-network hydrogels with self-recovery ability.²⁴ This feature is due to the low requirements of PVA chains to interact. Fig. 4(e) shows the stress curves of double cycles of loading and unloading for phase-separated PVA hydrogels. There was no interval between cycles. We explored the recovery degree of polymer networks during the unloading time. The degree of self-recovery was defined as the ratio of the two enclosed areas of stress curve U_hys1 and U_hys2:²⁴

ϕ = U_hys2/U_hys1, 3

where ϕ represented the recovery of network to dissipate energy; the results are shown in Fig. 4(f). The self-recovery degree of pristine PVA hydrogel was fairly low, but after it was immersed, it could reach ϕ = 0.45 ± 0.05. For phase-separated PVA hydrogels, the self-recovery ability was related to several factors, including standing time and stretching degree. If samples were left standing in solution after unloading for some time, the recovery coefficient ϕ would increase.²⁷ Under large deformation, too much energy dissipation led to the loss of the ability to pull back the PVA chains. Therefore, it became difficult for the chains to interact with each other, and the recovery degree also decreased.

Tearing behavior of phase-separated PVA hydrogels

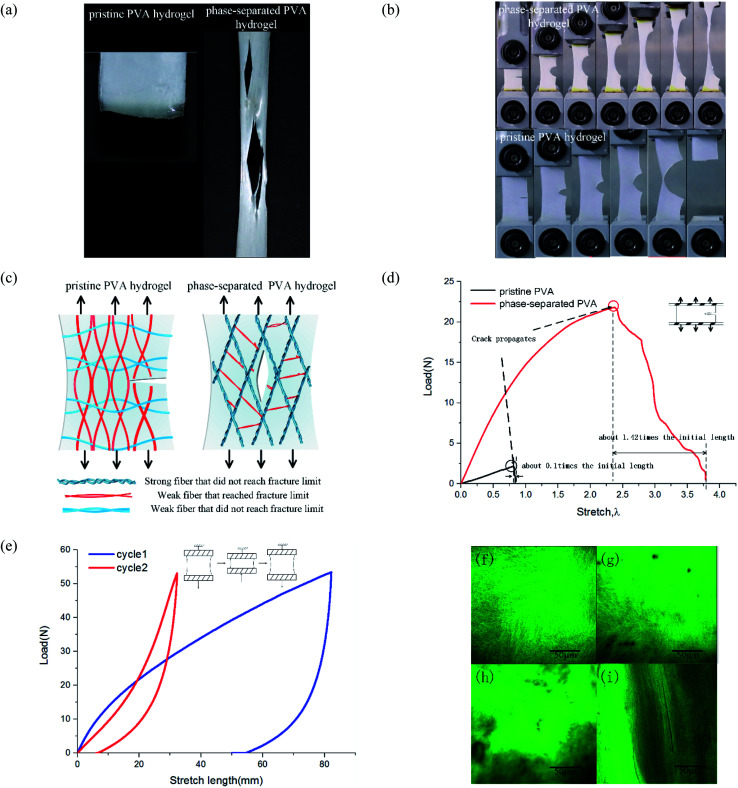
To study tearing behavior, we conducted uniaxial tensile tests from loading until complete tear for hydrogels. The results showed that their tear modes were quite different. For pristine PVA hydrogel, the crack generated when stress reached a threshold, and then it extended along the transverse direction and directly led to the sample's failure. The subsequent time from crack initiation until the sample completely tore was short, and so the fracture mode was fast fracture.²⁸ For phase-separated PVA hydrogels, as stress increased, multiple cracks appeared and expanded along the loading direction, which was quite different from the pristine PVA hydrogel (Fig. 5(a)). Most of the cracks propagated slowly and suspended at a certain stress, which was not as fast or continuous as in the pristine PVA hydrogel. Thus, the failure mode was ductile fracture.

Fig. 5. Characterization of tear behavior of phase-separated PVA hydrogels: (a) tensile-fractured pristine PVA hydrogel and phase-separated PVA hydrogels; (b) schematic of different failure modes; (c) uniaxial tensile failure of pre-notched samples; (d) the load–stretch curve of pre-notched samples; (e) the load–displacement curve of phase-separated PVA hydrogels of double cyclic loading test; and (f)–(i) microstructure of materials observed by confocal microscope.

To calculate the toughness of materials, we conducted pure-shear tests for pre-notched samples (Fig. 5(b)). Loading curves are shown in Fig. 5(d). Toughness is equal to²⁹

Γ = hW(λ) 4

where Γ is the energy release rate at the tip of crack propagation, h is the initial length of sample, and W(λ) is the strain energy density that can be obtained by calculating the area enclosed by the stress–strain curve of an intact sample under uniaxial tension. The toughness of pristine PVA hydrogel was ∼1.02 × 10³ J m⁻², whereas toughness of the 8 M phase-separated PVA hydrogel reached ∼4.2 × 10⁴ J m⁻². Thus, we found that the toughness of hydrogels was greatly improved.

These results showed that the phase separation induced by NaOH solution immersion affected both the toughness and failure mode for PVA hydrogel. To explain this change, we proposed a multiphase network theory. When phase separation occurred, the homogeneous polymer network was separated into dense regions and sparse regions.¹⁹ Suppose that in fiber dense regions, the interaction reinforced the screw fibers as strong fibers, and those strong fibers with the same mechanical properties then formed a strong phase network. Thus, the polymer network of phase-separated PVA hydrogels could be characterized by multiphase networks. The modulus and fracture stress varied from different phases. The pristine PVA hydrogel could be regarded as a single-phase network, which meant that the modulus and strengths of all the fibers were close. In the polymer network, those fibers along the loading direction were stressed. When part of these fibers surpassed their fracture limit and were about to break, the surrounding fibers also reached a critical value, and thus, the sample tore apart quickly and the expanding direction was perpendicular to the loading direction (Fig. 5(c)). Strictly speaking, the pristine PVA hydrogel was not a single-phase network because the freeze–thaw process resulted in phase separation, but because of its brittleness and fast fracture behavior, we could simplify it as a single-phase network. For phase-separated PVA hydrogels, fibers could withstand a very high stress, and the strong fibers changed their orientation into loading direction under a high stress, whereas the weak fibers broke early. After those weak fibers that connected the strong fibers broke, the strong fibers separated from each other and the shape of the cracks became the contour formed by the strong fibers (Fig. 5(c)). The crack growth process could be interpreted as the continuous fracture of weak fibers between the strong fibers. Because stress needed for the weak fiber fracture to the strong fiber fracture was discontinuous, the crack propagation was also discontinuous.

We provide the longitudinal arrangement of fibers by a double cyclic loading test and observation under a confocal microscope. When the loading direction was consistent with the direction of the fiber orientation, the material showed better mechanical properties. As shown in Fig. 5(e), the material in the second loading stage showed better mechanical property. Fig. 5(f)–(i) show the network microstructure results. We used the fluorescence dye to label the PVA side groups. Fig. 5(f) and (g) show the observation of pristine PVA hydrogels before and after tensile fracture. Stretching to the fracture did not change the uniformity and isotropy of the network. In Fig. 5(h), the high bright green area represented the dense fiber area, and the dark area represented the sparse area. Fig. 5(i) shows that after stretching, the orientation of fibers changed toward the tensile direction, and thus the hydrogels were no longer isotropic.

Probabilistic multiphase network model

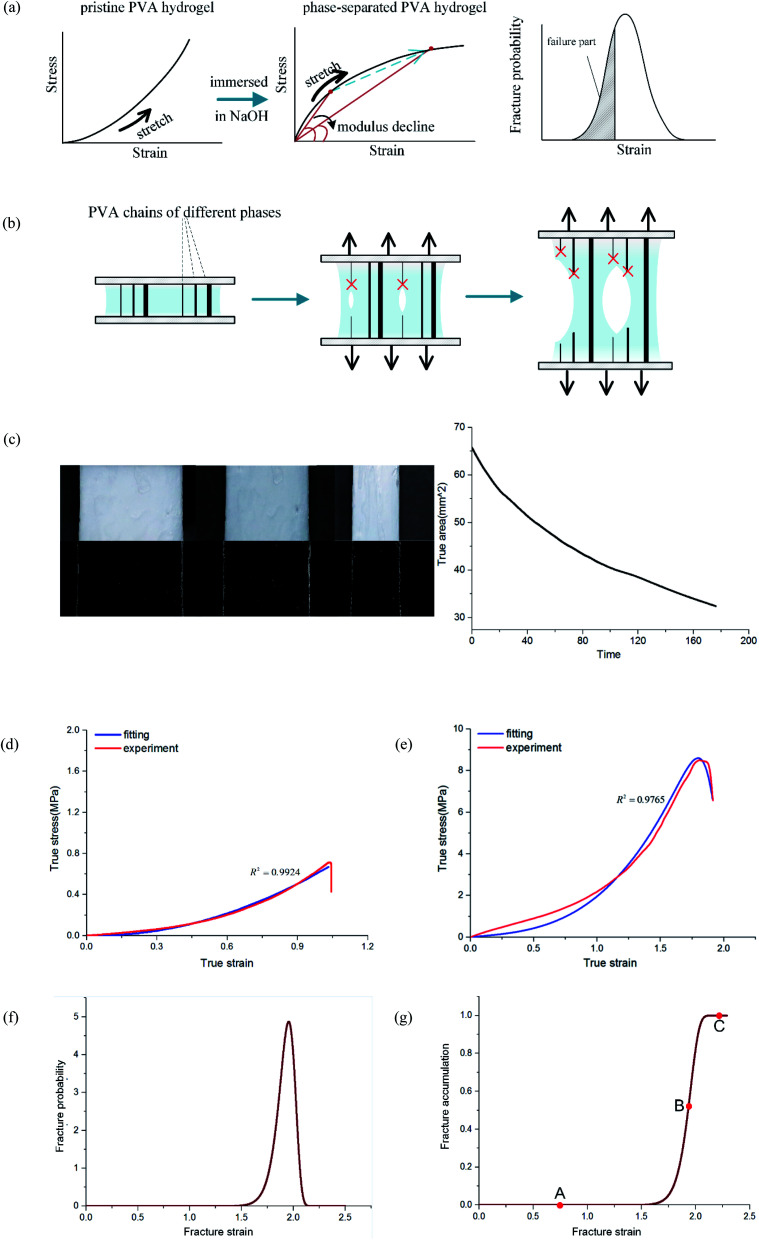
In the previous discussion, we explained that NaOH solution immersion caused phase separation in the polymer network, and the interactions in the dense region were enhanced. Thus, we regarded the dense regions as a strong phase network. We next used a multiphase parallel model to explain the tension behavior. Two mechanical parameters representing the mechanical properties of the network were tensile modulus and fracture strain. In the previous experiments, the tangent modulus of the tensile curve for phase-separated PVA hydrogels decreased gradually as stretching, which was quite different from pristine PVA hydrogels (Fig. 6(a)). To explain this difference, we adopted a continuous distribution model. The modulus and fracture strain of the different phases conformed to this continuous probability distribution. During stretching, fibers of different phases broke continuously, and the accumulation of damage led to the appearance of macro cracks, which caused the material to fail completely (Fig. 6(b)).

Fig. 6. Continuous multiphase network theory: (a) the stress curve change of PVA hydrogel before and after being immersed in NaOH solution; (b) schematic of ductile fracture; (c) edge detection technology method used to measure the true area in real-time; (d) the fitting and experiment data of the pristine PVA hydrogel; (e) the fitting and experiment data of the phase-separated PVA hydrogel; (f) the probability distribution of fracture; and (g) the cumulative distribution of fracture.

The constitutive equation of pristine PVA hydrogel during uniaxial tension follows:³⁰

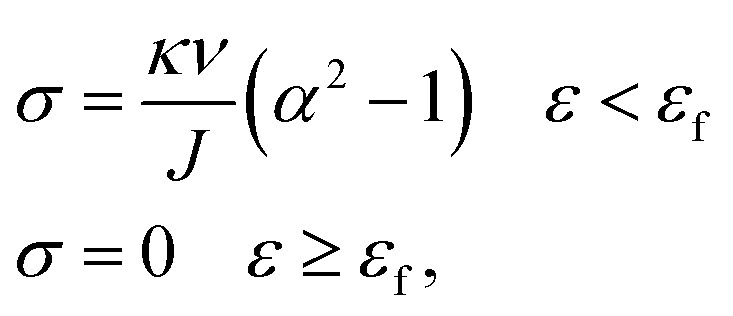5

where κ is the Boltzmann constant, ν is the number of chains in the polymer network, and σ is the stress under uniaxial tension. For single-phase hydrogel, κν determines its tension behavior, which is related to the type and water content of hydrogel; J is volume fraction, and this parameter strictly varies with tensile strength. It is difficult to measure J in real time, and if the material is regarded as the volume being unchangeable, it is also far from the real situation. For convenience, we separated J into two constant parameters, J₁ and J₂, and thus avoided the measurement of J. We also obtained an equation that described the tension behavior well in a large range, where α is the main elongation, and the relationship between strain ε and α is α = 1 + ε. Thus, we can obtain

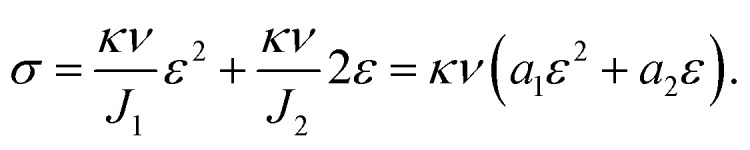6

We used this formula to obtain an equation that described the tensile behavior of the pristine PVA hydrogel, where σ and ε are true stress and true strain, respectively. Usually, we can directly measure only the nominal stress–strain in the experiment, and thus we need to transfer the nominal stress–strain into true stress–strain. The relationship between nominal stress–strain and true stress–strain is as follows:

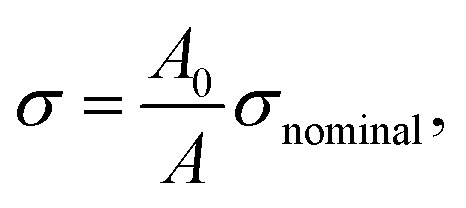7

ε = ln(1 + ε_nominal), 8

where A₀ is nominal area and A is true area. The thickness and width of the sample were dynamic because of the Poisson ratio effect, and thus the true area was also dynamic. To accurately obtain the true area at each moment, we used a camera to take real-time photos of samples and used a digital image technology method to calculate the real-time transverse size of the sample (Fig. 6(c)). Thus, we obtained the true stress of the sample.

Because Weibull distribution often has been used to describe the strength and life-related parameters of materials,³¹ we assumed that modulus and fracture strain of different phase networks also satisfy this distribution:

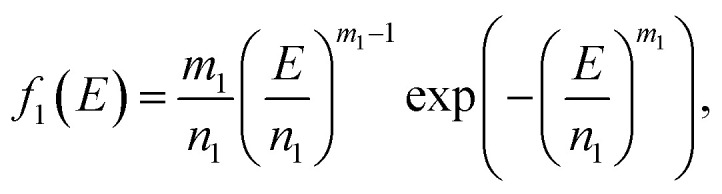9

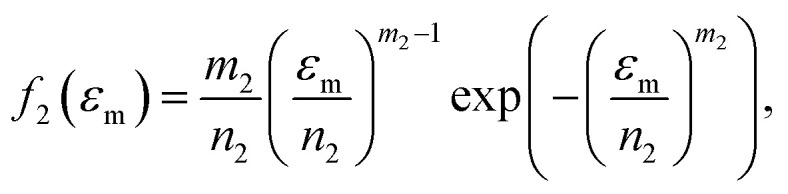10

where E is tensile modulus and ε_m is fracture strain; m₁, n₁, m₂, n₂ are four independent parameters that determine the distribution of the two parameters.

We assumed that different phase networks were in parallel, and every phase had the same strain ε when stretching. Considering the continuous distribution of modulus, the number of networks with modulus E was f(E)dE. Thus, the constitutive equation of the whole network is as follows:

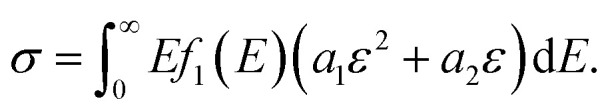11

Furthermore, when fracture is considered, the amount that breaks 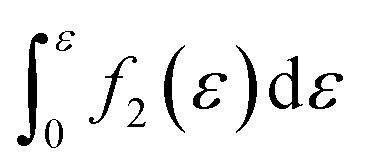is a cumulative area function. This part of the network loses its loading capacity, and thus the constitutive equation becomes

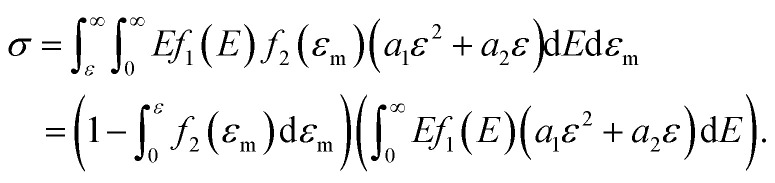12

Substitute eqn (5) and (6) into eqn (12).

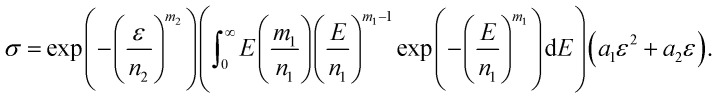13

After integration, we obtain

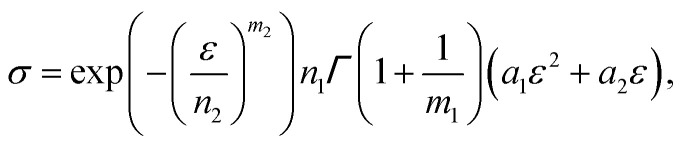14

where 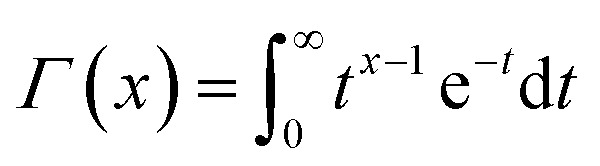is a gamma function, where t = (E/n₁)^m₁.

We used the uniaxial tensile test data of the phase-separated PVA hydrogel with 20% fiber content immersed in 6 M NaOH solution for fitting. First, we fitted the constitutive equation of the pristine PVA hydrogel (2) and obtained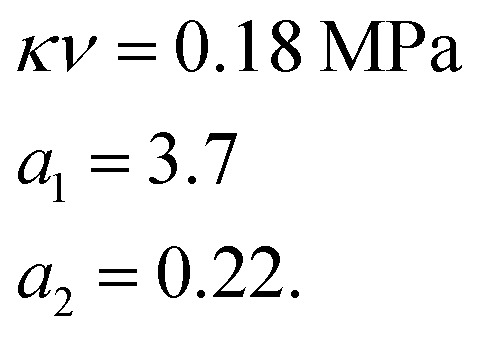

The comparison between fitting and experimental was shown in Fig. 6(d). Then we fitted the experimental data of the phase-separated PVA hydrogels to calculate the four parameters m₁, n₁, m₂, n₂ in the probability distribution.

The results were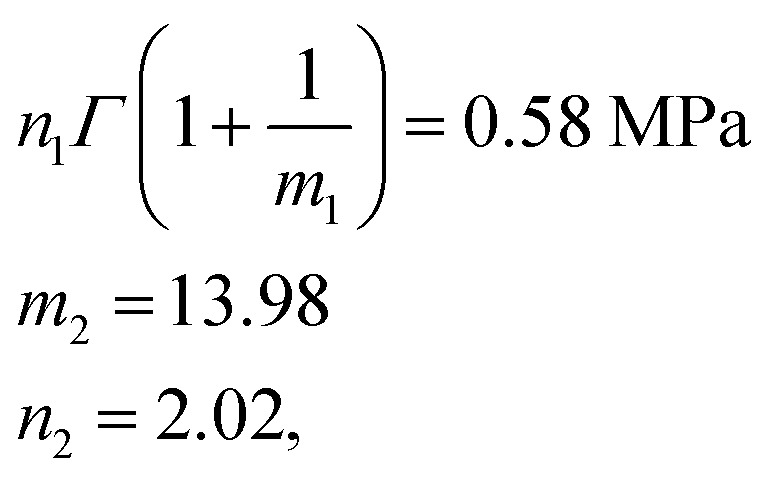where n₁Γ(1 + 1/m₁) represents the mean of modulus distribution, which is equal to the average modulus of phase-separated PVA hydrogel, which compared with κν shows the hardness increase affected by the NaOH solution. The experimental and fitting results of the phase-separated hydrogels are shown (Fig. 6(e)). In the fitting curve, the strain and stress corresponding to the peak were 1.80 and 8.6 MPa, respectively, whereas the experimental results were 1.80 and 8.5 MPa, respectively.

After obtaining the noted parameters, we obtained the probability distribution and cumulative distribution of the fracture function, as shown in Fig. 6(f) and (g):

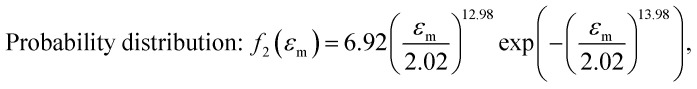15

16

For pristine PVA hydrogel, when the strain reached the fracture limit, the material tore rapidly. It is not meaningful to discuss the mechanical behavior in the failure stage for fast fracture behavior. Therefore, the existing constitutive theories are valuable before fracture happens. For phase-separated PVA hydrogel, however, the failure mode of the material was ductile fracture. Thus, it was necessary to study the fracture behavior during the failure stage. By introducing the continuous probability distribution of failure and combining the constitutive theory of the single-phase network, we well described the mechanical behavior of the material for a considerable period of time after fracture happens. Considering that the relationship between real strain and nominal strain was ε = ln(1 + ε_nominal), the real stress range seemed to be a short time in the middle and late stages of loading, which actually had quite dense experimental data points, and the loading time was quite long.

Fig. 6(g) shows the fracture of phase-separated hydrogel had three stages. When the strain was relatively low, corresponding to stage A in the graph, fibers were hardly broken, and the stress curve of the phase-separated hydrogels was similar to that of the pristine hydrogel (ε < 1.5). After strain exceeded a critical value, the fracture started to accumulate (stage B), and the stress changed from growth to a gradual decline (1.5 < ε < 2.0). When most fibers fractured, the material was completely destroyed, which corresponded to stage C (ε > 2.0). In comparison, the fracture cumulative distribution function of the pristine PVA hydrogel could be regarded as the following step function:

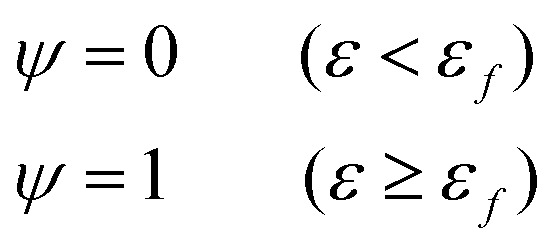17

where ψ is fracture accumulation.

In the middle-late stage, the fibers followed a longitudinal direction. This was similar to the parallel mode that we used in the model; therefore, the fitting result was in better agreement with the experiment. In the fracture probability distribution diagram (Fig. 6(f)), the strain corresponding to the peak was 1.9, which meant that the probability of failure of networks at this point reached the maximum. The strain corresponding to failure was 1.8 in the experiment, which indicated that most of the breaks in the networks led to the failure of the macrostructure. The continuous phase network distribution model not only was in good agreement with the tensile curve but also described the failure behavior of the material. We admit that the theory was not always satisfactory in some aspects. As a simple network model, our hypothesis is still quite different from the real network structure in PVA hydrogels.

Conclusion

Alkaline solution immersion is an important step to prepare magnetic hydrogel in in situ precipitation. Our study indicated that immersion in high-concentration NaOH solution enhanced the mechanical properties of physical PVA hydrogel, including its elastic modulus, failure strength, toughness, and self-recovery ability. The mechanical properties changed obviously with the solution concentration.

The enhancement of mechanical properties of the material was mainly due to the change of the structure of hydrogel. Phase separation led the polymer structure to change from a homogeneous network to an inhomogeneous network consisting of multiple phases with different strength and modulus. The sacrifice of weak phases gave the network a high toughness and the existence of strong phases allowed the hydrogel to endure a high stress. The enhancement also changed the failure mode from fast fracture to ductile fracture.

On the basis of the aforementioned experiments, we proposed a model of a continuous multiphase network. The model is in good agreement with the experimental results under uniaxial tension. Additionally, the probability peak corresponding to the macroscopic failure of the materials further explained the failure behavior of the hydrogel. These basic experiments may enhance our understanding of PVA hydrogels and thus improve practical applications.

Author contributions

L. Z. and L. T., conceived the project. Z. Z. and Y. Z. synthesized the samples; performed the mechanical tests, XRD tests, and SEM tests; and processed the data. Z. Z., Y. Z., Z. L., Z. J., and Y. L. discussed and analyzed the results. Z. Z., L. T., and Y. Z. wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.