Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2021 Jun 25;38(1):289–290. doi: 10.1093/bioinformatics/btab469

MomentClosure.jl: automated moment closure approximations in Julia

Augustinas Sukys 1,2,✉, Ramon Grima 3,✉
Editor: Lenore Cowen
PMCID: PMC8696096  PMID: 34170295

Abstract

Summary

MomentClosure.jl is a Julia package providing automated derivation of the time-evolution equations of the moments of molecule numbers for virtually any chemical reaction network using a wide range of moment closure approximations. It extends the capabilities of modelling stochastic biochemical systems in Julia and can be particularly useful when exact analytic solutions of the chemical master equation are unavailable and when Monte Carlo simulations are computationally expensive.

Availability and implementation

MomentClosure.jl is freely accessible under the MIT licence. Source code and documentation are available at https://github.com/augustinas1/MomentClosure.jl.

1 Introduction

The stochastic dynamics of biochemical systems under well-mixed conditions are governed by the chemical master equation (CME). The CME cannot be solved analytically except for simple systems and its exact stochastic simulation (Gillespie, 1977) can be computationally expensive, in turn motivating the development of more efficient approximation methods (Schnoerr et al., 2017).

One approach is to approximate the whole probability distribution solution of the CME in terms of its first few moments: starting from the CME, we can derive a set of ordinary differential equations (ODEs) describing the time-evolution of moments for the molecule numbers of each species in a system, e.g. means and (co)variances. However, if a chemical reaction network is non-linear, we end up with an infinite hierarchy of coupled moment equations that cannot be solved directly as each moment will depend on higher order moments. Nevertheless, this problem can be tackled using one of many moment closure approximations (MAs) that express all moments above a certain order in terms of lower order moments using various (usually distributional) assumptions, effectively closing the hierarchy and enabling a numerical solution (Lakatos et al., 2015; Schnoerr et al., 2015; Soltani et al., 2015).

Deriving the moment equations and applying MAs manually can be a cumbersome and error prone process, especially when large systems and high-order MAs are considered. For this reason, a number of software tools have been developed over the years, allowing automatic derivation of the closed moment equations for a specified chemical reaction network (Azunre et al., 2011; Fan et al., 2016; Gillespie, 2009; Hespanha, 2008; Kazeroonian et al., 2016; Schnoerr et al., 2015). However, these packages are either outdated or unmaintained, offer limited functionality (implementing only few types of MAs and restricted to mass action reactions) or require proprietary expensive software, limiting the potential user base.

We present MomentClosure.jl, the first Julia package to automatically derive the closed time-evolution equations of moments up to an arbitrary order for any chemical reaction network supporting both non-polynomial and time-dependent propensity functions, and implementing a variety of MAs commonly used in stochastic biochemical kinetics. A comprehensive review of MAs and tutorials on using the software can be found at https://github.com/augustinas1/MomentClosure.jl.

2 Materials and methods

In what follows, we discuss the main implementation details of MomentClosure.jl and its integration within the broader Julia package ecosystem enabling a streamlined moment-based modelling workflow in which we can easily define a biochemical system, generate the corresponding moment equations using MAs and solve the resulting system of ODEs numerically. In Figure 1, we summarize the workflow and compare the accuracy of different MAs applied to a simple stochastic model of an auto-regulatory genetic feedback loop.

Fig. 1.

Fig. 1.

Open in a new tab

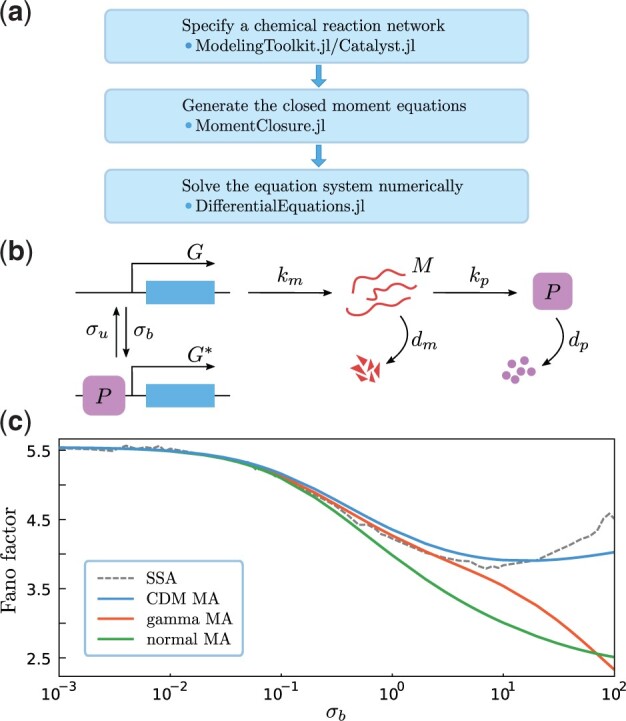
(a) The general workflow of moment-based modelling in Julia using MomentClosure.jl and related packages. (b) Model of a negative auto-regulative genetic feedback loop. If a gene is active (G), an mRNA molecule (M) is produced with rate km which can be subsequently translated into proteins (P) with rate kp (both degrade with rates dm and dp, respectively). The negative feedback is introduced via protein binding to the gene with rate σb, switching the promoter OFF (G*) and preventing the transcription (in contrast, switching ON occurs with rate σu). (c) Fano factor of the steady-state protein number as a function of σb where we have truncated the moment hierarchy at the second order using normal, gamma and CDM MAs, and compared the results to the true values predicted by the stochastic simulation algorithm (Gillespie, 1977) (averaged over 105 realizations). The initial condition is zero protein and mRNA molecules (set to 0.001 for MAs to ensure numerical stability) in state G, and the parameters are fixed as σu=10,km=3,kp=50,dm=10 and dp = 1

2.1 Model definition

Modelling of chemical reaction networks in Julia is made easy by Catalyst.jl (https://github.com/SciML/Catalyst.jl) that leverages a powerful symbolic-numeric modelling framework provided by ModelingToolkit.jl (Ma et al., 2021): a model can be constructed by simply specifying the reaction stoichiometry and the propensities using symbolic variables. MomentClosure.jl is fully compatible with models defined through the two packages, allowing systems containing any number of molecular species and reactions with any type of smooth propensity functions. The only assumption made is that reactions occur in a single compartment of fixed volume. We note that networks involving multiple dynamically interacting compartments can be considered using Compartor (Pietzsch et al., 2021), albeit the software is restricted to reactions with polynomial rate laws and supports only mean-field and gamma MAs.

2.2 Moment equations

Using MomentClosure.jl, we can automatically obtain a system of ODEs describing the time evolution of moments up to any order. Internally, the raw moment equations are derived in a straightforward manner from the CME when the kinetics of a system are governed by the law of mass action. The derivation becomes more involved if the propensity functions take a non-polynomial form: here, we adopt a general moment expansion framework based on Taylor-expanding the propensities around the mean, allowing us to obtain equations for the means and higher order central moments, as first formulated by (Lee, 2013) and (Ale et al., 2013).

The moment equations generated up to the specified order m can then be decoupled from all the higher order moments they depend on using one of the implemented MAs, i.e. expressing the moments above order m in terms of mth and lower order moments using MA-specific assumptions. MomentClosure.jl currently supports zero, normal, Poisson, log-normal, gamma, derivative matching, conditional Gaussian and conditional derivative matching (CDM) closures (Lakatos et al., 2015; Schnoerr et al., 2015; Soltani et al., 2015). We note that conditional MAs are available in only one other package (Cerena, see Kazeroonian et al. (2016)) and have been found to be particularly effective in modelling gene networks with promoter switching dynamics (Cao and Grima, 2019; Soltani et al., 2015).

Finally, the closed moment equations can be solved numerically using any high-performance ODE solver implemented in DifferentialEquations.jl (Rackauckas and Nie, 2017), which also provides a number of numerical analysis and parameter estimation tools enabling even further study of the resulting ODE system.

3 Conclusion

MomentClosure.jl provides automated moment equation generation and closure approximations up to any desired expansion order. It is easily applicable to chemical reaction networks of any size containing reactions with smooth linear and non-linear propensity functions. Moreover, utilizing the popular ModellingToolkit.jl and DifferentialEquations.jl packages, MomentClosure.jl makes the stochastic modelling of biochemical reaction kinetics using MAs efficient and accessible for Julia newcomers and experts alike.

Funding

This work was supported by the Alan Turing Institute Doctoral Studentship [EPSRC grant EP/N510129/1 to A.S.] and a Leverhulme Trust grant [grant no. RPG-2018-423 to R.G.].

Conflict of Interest: none declared.

Contributor Information

Augustinas Sukys, SynthSys, School of Biological Sciences, University of Edinburgh, Edinburgh EH9 3JD, UK; The Alan Turing Institute, London NW1 2DB, UK.

Ramon Grima, SynthSys, School of Biological Sciences, University of Edinburgh, Edinburgh EH9 3JD, UK.

References

  1. Ale A.  et al. (2013) A general moment expansion method for stochastic kinetic models. J. Chem. Phys., 138, 174101. [DOI] [PubMed] [Google Scholar]
  2. Azunre P.  et al. (2011) Mass fluctuation kinetics: analysis and computation of equilibria and local dynamics. IET Syst. Biol., 5, 325–335. [DOI] [PubMed] [Google Scholar]
  3. Cao Z., Grima R. (2019) Accuracy of parameter estimation for auto-regulatory transcriptional feedback loops from noisy data. J. R. Soc. Interf., 16, 20180967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Fan S.  et al. (2016) MEANS: python package for moment expansion approximation, iNference and simulation. Bioinformatics, 32, 2863–2865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gillespie C. (2009) Moment-closure approximations for mass-action models. IET Syst. Biol., 3, 52–58. [DOI] [PubMed] [Google Scholar]
  6. Gillespie D.T. (1977) Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem., 81, 2340–2361. [Google Scholar]
  7. Hespanha J. (2008) Moment closure for biochemical networks. In: IEEE Proc. of the 3rd International Symposium on Communications, Control and Signal Processing, Malta. pp. 142–147.
  8. Kazeroonian A.  et al. (2016) CERENA: ChEmical REaction Network Analyzer—a toolbox for the simulation and analysis of stochastic chemical kinetics. PLoS One, 11, e0146732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Lakatos E.  et al. (2015) Multivariate moment closure techniques for stochastic kinetic models. J. Chem. Phys., 143, 094107. [DOI] [PubMed] [Google Scholar]
  10. Lee C.H. (2013) A moment closure method for stochastic chemical reaction networks with general kinetics. MATCH Commun. Math. Comput. Chem., 70, 785–800. [Google Scholar]
  11. Ma Y.  et al. (2021) ModelingToolkit: a composable graph transformation system for equation-based modeling.
  12. Pietzsch T.  et al. (2021) Compartor: a toolbox for the automatic generation of moment equations for dynamic compartment populations. Bioinformatics, btab058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Rackauckas C., Nie Q. (2017) DifferentialEquations.jl–a performant and feature-rich ecosystem for solving differential equations in Julia. J. Open Res. Software, 5, 15. [Google Scholar]
  14. Schnoerr D.  et al. (2015) Comparison of different moment-closure approximations for stochastic chemical kinetics. J. Chem. Phys., 143, 185101. [DOI] [PubMed] [Google Scholar]
  15. Schnoerr D.  et al. (2017) Approximation and inference methods for stochastic biochemical kinetics—a tutorial review. J. Phys. A: Math. Theor., 50, 093001. [Google Scholar]
  16. Soltani M.  et al. (2015) Conditional moment closure schemes for studying stochastic dynamics of genetic circuits. IEEE Trans. Biomed. Circuits Syst., 9, 518–526. [DOI] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES