Abstract
Motivation
Single-cell multi-omics sequencing data can provide a comprehensive molecular view of cells. However, effective approaches for the integrative analysis of such data are challenging. Existing manifold alignment methods demonstrated the state-of-the-art performance on single-cell multi-omics data integration, but they are often limited by requiring that single-cell datasets be derived from the same underlying cellular structure.
Results
In this study, we present Pamona, a partial Gromov-Wasserstein distance-based manifold alignment framework that integrates heterogeneous single-cell multi-omics datasets with the aim of delineating and representing the shared and dataset-specific cellular structures across modalities. We formulate this task as a partial manifold alignment problem and develop a partial Gromov-Wasserstein optimal transport framework to solve it. Pamona identifies both shared and dataset-specific cells based on the computed probabilistic couplings of cells across datasets, and it aligns cellular modalities in a common low-dimensional space, while simultaneously preserving both shared and dataset-specific structures. Our framework can easily incorporate prior information, such as cell type annotations or cell-cell correspondence, to further improve alignment quality. We evaluated Pamona on a comprehensive set of publicly available benchmark datasets. We demonstrated that Pamona can accurately identify shared and dataset-specific cells, as well as faithfully recover and align cellular structures of heterogeneous single-cell modalities in a common space, outperforming the comparable existing methods.
Availabilityand implementation
Pamona software is available at https://github.com/caokai1073/Pamona.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The latest developments in high-throughput single-cell multi-omics sequencing technologies, e.g. single-cell RNA-sequencing (scRNA-seq) and ATAC-sequencing (scATAC-seq), enable cell-resolved investigation of heterogeneous cellular populations that make up tissues, the dynamics of developmental processes and the underlying regulatory mechanisms that control cellular functions (Stuart and Satija, 2019). The integration of emerging single-cell multi-omics datasets, however, poses fresh data integration challenges such as unmatched/distinct features and/or unpaired cells across datasets (Efremova and Teichmann, 2020; Scherer et al., 2021). Integrative methods have been developed to enable joint learning across multiple types of data. For example, the celebrated single-cell data analysis platform Seurat (Stuart et al., 2019) projected (distinct) feature spaces across datasets into a common subspace using canonical correlation analysis (CCA), which maximizes inter-dataset correlation, and selected mutual nearest-neighbors (MNNs) (Haghverdi et al., 2018) as anchors to align datasets. Although it achieved success in batch effect correction, Seurat relies on the linear mapping of CCA and the linear alignments of MNNs, thus weakening its ability to handle non-linear geometrical deformations and rotations of intrinsic manifolds embedded across cellular modalities. A growing number of supervised methods, which require cross-correspondence of cells given as a priori, have been developed for single-cell multi-omics integration. For example, Multi-Omics Factor Analysis (MOFA) (Argelaguet et al., 2018) employed a Bayesian Group Factor Analysis approach; IntNMF (Chalise and Fridley, 2017) and scAI (Jin et al., 2020) adopted the non-negative matrix factorization (NMF) approach; scMVAE (Zuo and Chen, 2021) proposed a single-cell multimodal variational autoencoder model and achieved state-of-the-art performance in jointly clustering of cells across modalities.
Recently, manifold alignment approaches, which aimed to align embedded low-dimensional manifolds, have been developed for holistic representation of the intrinsic cellular structures across cellular modalities, without requiring any correspondence information, either among cells or among features, e.g. MATCHER (Welch et al., 2017), MMD-MA (Liu et al., 2019; Singh et al., 2020), UnionCom (Cao et al., 2020) and SCOT (Demetci et al., 2021). These methods were derived under various advanced machine learning techniques, such as linear trajectory alignment using the latent Gaussian process, as in MATCHER (Welch et al., 2017); kernel space matching based on maximum mean discrepancy, as in MMD-MA (Liu et al., 2019); metric space matching based on the graph-matching/quadratic assignment formulation, as in UnionCom (Cao et al., 2020), or the optimal transport formulation, as in SCOT (Demetci et al., 2021). Although these state-of-the-art methods have achieved integrative performance with encouraging results (Demetci et al., 2021), current manifold alignment methods often automatically assume that all datasets share the same underlying structure across cellular modalities. Such assumption can be easily nullified by presenting dataset-specific cell types/structures across the heterogeneous single-cell datasets. The dataset-specific cell types/structures may be introduced by differences due to experimental batch, sample collection or experimental technology (Hie et al., 2019a). Therefore, it remains computationally challenging for state-of-the-art manifold alignment algorithms to preserve both shared and dataset-specific cellular structures across datasets during integration.
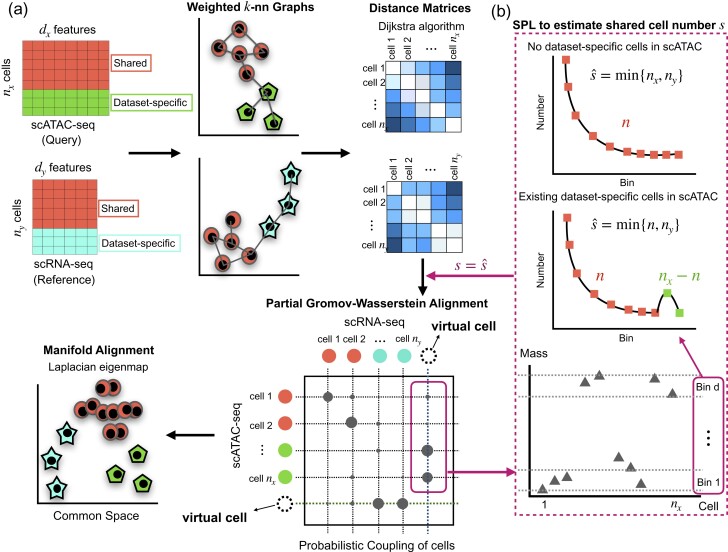
Here, we present Pamona, a partial Gromov-Wasserstein-based manifold alignment algorithm, that integrates heterogeneous single-cell multi-omics datasets to delineate and represent both shared and dataset-specific cellular structures (Fig. 1a and Section 2). Optimal transport (OT) is a powerful tool in the analysis of complex data, as it learns an optimal cost-effective mapping between data distributions (Peyré and Cuturi, 2019). Although OT has a wide range of successful applications including computer vision (Solomon et al., 2015) or domain adaptation (Courty et al., 2017), it relies on the assumption of the same feature space. Gromov-Wasserstein (GW) distance, a generalized OT which overcomes the lack of intrinsic correspondence between feature spaces, has been proven to be increasingly valuable for diverse fields (Mémoli, 2011; Peyré and Cuturi, 2019). In the single-cell data analysis community, GW has been applied to the spatial reconstruction of gene expression cartography by novoSpaRc (Nitzan et al., 2019) and single-cell multi-omics data integration by SCOT (Demetci et al., 2021). While GW seeks a transportation map that preserves the total mass between the two probability distributions (Mémoli, 2011; Peyré and Cuturi, 2019), partial-GW extends the GW framework by allowing only a fraction of the total mass to be transported (Chapel et al., 2020). The spirit of partial-GW is built upon adding virtual or dummy points onto the marginals and enforcing points with large discrepancies absorbed by the virtual points (Caffarelli and McCann, 2010; Chapel et al., 2020). As such, partial-GW enables Pamona to reconstruct the probabilistic couplings of cells across datasets to identify both shared and dataset-specific cells. Based on the probabilistic couplings, Pamona further aligns single-cell multi-omics datasets in a common low-dimensional space, while preserving both shared and dataset-specific cellular structures across modalities.
Fig. 1.
Overview of Pamona. Pamona is a partial manifold alignment algorithm for heterogeneous single-cell multi-omics data integration. Given inputs of multiple cellular modalities (e.g. scATAC-seq and scRNA-seq), it identifies both shared and dataset-specific cells based on the computed probabilistic couplings of cells across datasets, and it aligns cellular modalities in a common low-dimensional space, while simultaneously preserving both shared and dataset-specific structures. (a) Pamona constructs a weighted k-nn graph of cells for each dataset (step 1), computes the geodesic distance matrix of cells within each dataset (step 2), computes the probabilistic coupling matrices of cells based on the partial Gromov-Wasserstein optimal transport (step 3), and aligns cellular modalities with distinct unmatched features in a common low-dimensional space to holistically represent the cellular structures (step 4). (b) A Scree-Plot-Like (SPL) method is proposed to estimate the shared cell number s when it is not available
Before Pamona, only a few methods were developed specifically for integrating single-cell datasets with dataset-specific cell types/structures. For example, Scanorama (Hie et al., 2019a) efficiently integrated multiple scRNA-seq datasets based on a generalized MNN matching technique for ‘panorama stitching’ of heterogeneous scRNA-seq datasets. Liger (Welch et al., 2019), which employed an integrative NMF approach to find the shared and dataset-specific components across datasets, required pre-matched common feature space across modalities and could not integrate datasets into a common space. The manifold alignment method UnionCom (Cao et al., 2020) showed its ability to accommodate dataset-specific cells, but remains to be further explored.
Notably, Pamona can perform both global and partial manifold alignments for single-cell multi-omics data integration. In this study, we propose a Scree-Plot-Like (SPL) method paralleled with Pamona to estimate the shared cell number which needs to be specified by the partial-GW framework (Fig. 1b and Supplementary Note S4). With no inherent reliance on any prior information, our framework offers the flexibility to match prior information, e.g. cell type annotations or cell-cell correspondence, when available. To assess its performance, we applied Pamona to 2 simulated and 4 real single-cell multi-omics datasets on various tasks. We demonstrate that Pamona can accurately identify shared and dataset-specific cells, as well as faithfully recover and align intrinsic manifolds across heterogeneous cellular modalities in the common space.
2 Materials and methods
2.1 Overview of Pamona
Pamona is a partial manifold alignment algorithm for heterogeneous single-cell multi-omics data integration based on the foundation of partial-GW framework (Chapel et al., 2020). The main inputs of Pamona are the data matrices of single-cell multimodal profiles, e.g. gene expression, chromatin accessibility and DNA methylation. The main outputs of Pamona are (i) the probabilistic couplings of cells across datasets in order to identify both shared and dataset-specific cells and (ii) the common low-dimensional space that recovers and aligns intrinsic structures of heterogeneous cellular modalities.
2.2 Mathematical formulation of Pamona
The procedure used by Pamona includes four major steps (see Fig. 1a and Supplementary Note S1 for the pseudocode).
First, suppose that and are the inputs of two single-cell multi-omics datasets where and are the number of features and cells for X(Y). We compute the weighted k-nn graphs for each of the two datasets where the nodes of each graph correspond to cells within the dataset, and edges have weights based on pairwise Euclidean distances between cells. In case the k-nn graph for a given k is not connected, we adopt the same procedure as that in Klimovskaia et al. (2020) to enforce connectivity.
Second, we compute the geodesic distances of cells within the same dataset by calculating the shortest distance between each pair of nodes (cells) on the k-nn graph using the Dijkstra algorithm, which was proposed by UnionCom (Cao et al., 2020) and then followed by SCOT (Demetci et al., 2021). The path with the shortest distance will approximate to geodesic distance on the embedded manifold (Tenenbaum et al., 2000). We denote the geodesic distance matrices for X and Y as and , respectively.
Third, we compute the probabilistic cell-cell correspondence between X and Y to identify the shared and dataset-specific cells. Here, we formulate the problem as the partial-GW optimal transport framework (Chapel et al., 2020). Partial-GW extends the GW optimal transport to allow only a fraction of the total mass to be matched/transported (Peyré and Cuturi, 2019).
Specifically, we assign each cell from each of the two datasets with a point mass , where . Partial-GW aims to match (transport) a fraction of s/N mass from X to Y. Here, needs to be specified, and it can be regarded as the number of shared cells between X and Y. Partial-GW finds a probabilistic coupling matrix from nx cells in X to ny cells in Y able to minimize discrepancy between the geodesic distances in and , that is
| (1) |
where is the relative probability that matches cell i in X to cell j in Y, satisfying the constraints on the set of all admissible coupling as
| (2) |
where and are the uniform mass marginal distributions for X and Y, which was proposed by SCOT (Demetci et al., 2021). Here, denotes an n-dimensional vector of ones, and the superscript denotes the transpose of a vector or matrix. The equality in enforces the relaxed requirement that only a fraction of s/N cells needs to be matched/transported between the two datasets.
We write in matrix form and add an entropic regularization penalty to the original problem, resulting in the entropic regularized partial-GW metric as follows:
| (3) |
where denotes Frobenius dot product of matrices, denotes an cost matrix with its (i, j)th element defined as , the discrepancy between geodesic distances , the entropic regularization term and ϵ is a tradeoff parameter between and .
To solve the optimization problem of , Pamona adds virtual points onto the marginals as in Chapel et al. (2020). The virtual points are used as buffers when comparing distributions with different probability masses. In this way, the partial-GW problem is equivalent to a point (cell) augmented, but still standard GW problem, which can be efficiently solved by Sinkhorn iterations (Cuturi, 2013; Peyré et al., 2016). Here, different from the optimization framework of partial-GW which resorted to a Frank-Wolfe method (Chapel et al., 2020), Pamona adds the entropic regularization term in Equation (3) and applies the efficient mirror descent algorithm to solve this problem (Peyré et al., 2016; Solomon et al., 2016). Pamona solves it iteratively as follows: for each iteration k:
A1.Update the cost matrix as follows:
| (4) |
where represents the cost of aligning cell i in X to cell j in Y at iteration k.
A2.Add two virtual points (cells), one to X and the other to Y, resulting in augmented cost matrix and marginal distributions () defined as follows:
| (5) |
| (6) |
where the variable is set as a relatively large value greater than the elements of the cost matrix , with the aim of preventing the alignment within virtual cells between two datasets. In practice, α can be chosen as any value such that , and the performance of Pamona is robust to the choice of α (see Supplementary Fig. S2e and f). The mass of virtual cell in X is set as in , and the mass of virtual cell in Y is set as in . The ξ is a bounded scalar and should be (Chapel et al., 2020).
A3.Compute GW optimal transport plan with and (). We first normalize and to construct probability distributions. Afterwards, we formulate the problem as
| (7) |
where
| (8) |
which is a standard entropic regularized optimal transport problem. The is efficiently solved by Sinkhorn iterations (Cuturi, 2013). Once is obtained, we remove the last row and column of to obtain as in Chapel et al. (2020).
The mechanism of adding virtual points with the designed augmented cost matrix and marginal distributions (), as defined above, is based on the theory that the virtual cell in X attracts mass of cells in Y, with large values in corresponding columns of the cost matrix , and that the virtual cell in Y attracts mass of cells in X, with large values in corresponding rows of the cost matrix . Equation (8) enforces that a fraction of s/N cells needs to be transported between the two datasets, regardless of the transport cost between datasets and virtual cells.
Four, we align cellular modalities with distinct unmatched features in a common low-dimensional space for feature comparability. The common space should preserve both shared and dataset-specific structures across cellular modalities. Suppose we have datasets. As in Seurat (Stuart et al., 2019), we fix a dataset as the reference dataset, and the other datasets as the query datasets. We apply partial-GW to and Y in the three steps above and obtain the probabilistic coupling matrices s of cells between s and Y, respectively, as the probabilistic cell-cell correspondence information.
We then align s and Y in a de-dimensional common space, resulting in the new embeddings of , and . To preserve the local neighborhood relationship, we construct the graph Laplacian matrices of , and of Y, as other manifold learning algorithms have done (Belkin and Niyogi, 2003; Cui et al., 2014; Roweis and Saul, 2000). Besides, we also introduce the rotation-invariant constraints and find the embeddings of cells by solving the optimization problem as
| (9) |
where
| (10) |
| (11) |
| (12) |
and is the trace of matrix (see Supplementary Note S2 for details). We solve this optimization problem using the eigenvalue decomposition method as in Hardoon et al. (2004) and Cui et al. (2014). This step is computationally efficient since its computational cost mainly depends on feature dimension and does not increase substantially with the increasing number of samples/cells.
In addition, Pamona has the flexibility to incorporate existing prior information during the alignment, such as cell types or cell-cell correspondence, similar to the labeled graph matching problem (Zaslavskiy et al., 2009). See Supplementary Note S3 for details. By incorporate existing prior information, Pamona can greatly increase the accuracy of data integration tasks and reduce the ambiguity of manifold alignment (See Section 3.5).
3 Results
3.1 Pamona improved heterogeneous single-cell multi-omics data integration
In the following, we compared Pamona to current state-of-the-art single-cell multi-omics integration methods, including Seurat v3 (Stuart et al., 2019), MMD-MA (Liu et al., 2019), UnionCom (Cao et al., 2020) and SCOT (Demetci et al., 2021). To the best of our knowledge, SCOT is the first application of Gromov-Wasserstein optimal transport to align single-cell multi-omics data.
For this purpose, we employed two simulated and four real-world single-cell multi-omics datasets as follows: a simulated dataset from MMD-MA (Liu et al., 2019), hereinafter denoted as Simulation 1; a simulated dataset from UnionCom (Cao et al., 2020), hereinafter denoted as Simulation 2; the single-cell analysis of genotype, expression and methylation dataset from Cheow et al. (2016), hereinafter denoted as sc-GEM; the single-cell nucleosome, methylome and transcriptome dataset from Argelaguet et al. (2019), hereinafter denoted as scNMT-seq; the single-nucleus chromatin accessibility and mRNA expression dataset from Chen et al. (2019), hereinafter denoted as SNARE-seq; and the 10X Genomics scRNA-seq and scATAC-seq dataset of human peripheral blood mononuclear cells from Wang et al. (2020), hereinafter denoted as PBMC. Detailed information of these datasets is provided in Supplementary Notes S6 and S7.
We mainly employed two scores to assess the performance of single-cell multi-omics data integration: (i) Label Transfer Accuracy to measure the ability to transfer labels of the shared cells from one dataset to another and (ii) Alignment Score to measure the ability to preserve both shared and dataset-specific structures. What is noteworthy is that Label Transfer Accuracy characterizes the local structure preservation across modalities, while Alignment Score characterizes global structure preservation. In addition, we adopted the FOSCTTM score to measure the preservation of cell-cell correspondence across datasets for the SNARE-seq dataset. All three scores work on the basis of the common space by integrative methods (See Supplementary Note S5).
In general, Pamona improved various partial manifold alignment tasks with the highest scores of Label Transfer Accuracy and Alignment Score on Simulation 1, Simulation 2, sc-GEM and scNMT-seq (Supplementary Fig. S1). Especially, Pamona increased the Alignment Score markedly on the partial manifold alignment tasks. On the global manifold alignment task of the scNMT-seq dataset, Pamona achieved the second highest performance, slightly below the highest one achieved by SCOT (Supplementary Fig. S1d). Detailed results and comparison will be provided in the following sections. Meanwhile, Pamona is robust to the hyperparameter choices (Supplementary Fig. S2 and Supplementary Note S8).
We demonstrated with detailed results that Pamona (i) resolved the partial manifold alignment on simulated datasets of Simulation 1 and 2 (Section 3.2); (ii) identified informative genes in delineating the shared and dataset-specific cellular structures of the sc-GEM dataset (Section 3.3); (iii) resolved the integration of the scNMT-seq dataset in both global and partial manifold alignment tasks (Section 3.4); (iv) improved the integration of the SNARE-seq dataset by incorporating partial cell-cell correspondence information (Supplementary Result S1); (v) resolved the integration of the heterogeneous PBMC dataset by incorporating cell type annotation information (Section 3.5); (vi) achieved high accuracy on jointly clustering of cells across modalities of SNARE-seq dataset in the common space (Section 3.6).
3.2 Pamona resolved the partial manifold alignment on simulated datasets
We assessed the performance of Pamona on partial manifold alignment using Simulation 1 and Simulation 2, and global manifold alignment using 3 simulated datasets (denoted as Sim.1, Sim. 2 and Sim. 3) in MMD-MA (Liu et al., 2019).
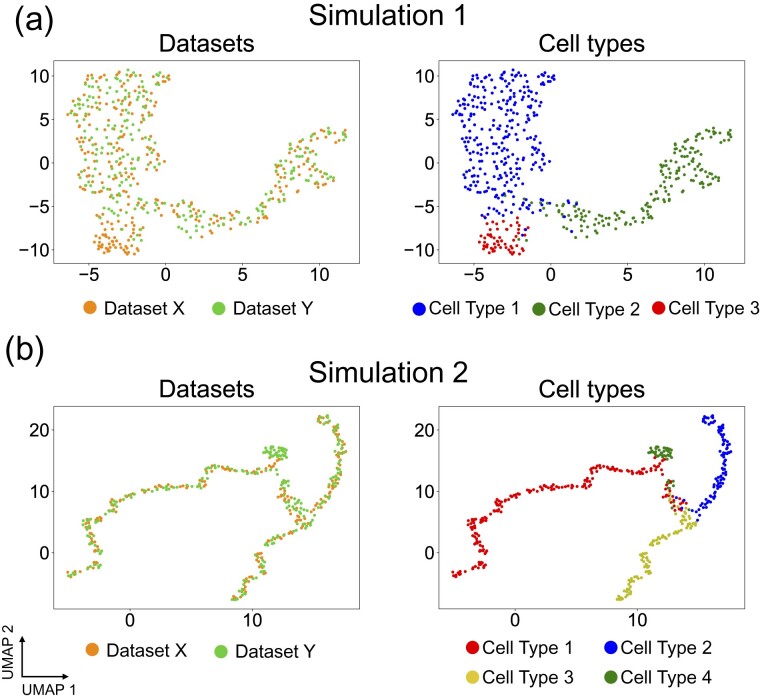
In Simulation 1, dataset X contains an embedded bifurcated tree with three branches denoted as Type 1 (blue points), Type 2 (green points) and Type 3 (red points), respectively (Supplementary Fig. S3a). The original dataset Y also contains an embedded bifurcated tree with cell types corresponding to those in Dataset X. To construct a partial manifold alignment task, we removed the cells of Type 3 from dataset Y, resulting in a lineage structure constituted only by cells of Type 1 (blue points) and Type 2 (green points) (Supplementary Fig. S3a). Therefore, Type 3 becomes an X-specific branch. When we applied Pamona to integrate X and Y, it aligned the shared cells of Type 1 (blue points) and Type 2 (green points), accordingly, and preserved the cells of Type 3 as the X-specific branch in the common space (Fig. 2a), achieving the highest Alignment Score of 0.834 and Label Transfer Accuracy of 97.92%. In contrast, Seurat v3, MMD-MA, UnionCom and SCOT did not preserve either shared or dataset-specific structures very well (Supplementary Fig. S4), resulting in sharp drops of Alignment Score (Seurat v3, 0.215; MMD-MA, 0.507; UnionCom, 0.596; SCOT, 0.601) (Supplementary Fig. S1a). MMD-MA has a lower Alignment Score since it mixed cells of Type 1 and Type 2 (Supplementary Fig. S4c). Meanwhile, MMD-MA, SCOT and UnionCom achieved Label Transfer Accuracy similar to that of Pamona (MMD-MA, 95.85%; SCOT, 95.02%; UnionCom, 97.91%), while Seurat v3 had the lowest Label Transfer Accuracy of 70.12% (Supplementary Fig. S1a).
Fig. 2.
Pamona integrated two simulated datasets in partial manifold alignment tasks. (a) Visualizations of the common space of the partial alignment of the two aligned datasets in Simulation 1 by Pamona using UMAP: left panel: cells are colored according to their corresponding datasets; right panel: cells are colored according to their corresponding types. (b) Visualizations of the common space of the partial alignment of the two aligned datasets in Simulation 2 by Pamona using UMAP
In Simulation 2, dataset X contains an embedded bifurcated tree with three branches denoted as Type 1 (red points), Type 2 (blue points) and Type 3 (yellow points), respectively; dataset Y contains an embedded trifurcated tree with three branches corresponding to those in dataset X and a Y-specific branch of cells from Type 4 (green points) (Supplementary Fig. S3b). When we applied Pamona to integrate X and Y, it aligned the shared cells of Type 1 (red points), Type 2 (blue points) and Type 3 (yellow points), accordingly, and preserved the cells of Type 4 as the Y-specific branch in the common space (Fig. 2b). It had the highest Alignment Score of 0.885 and Label Transfer Accuracy of 93.5% (Supplementary Fig. S1b). In comparison, UnionCom also integrated X and Y quite well (Supplementary Fig. S5b) and had the second highest Alignment Score of 0.698d Label Transfer Accuracy of 86.5% (Supplementary Fig. S1b). In contrast, Seurat v3, MMD-MA and SCOT did not perform well on the partial manifold task (Supplementary Fig. S5), showing sharp drops of Alignment Score (Supplementary Fig. S1b).
In three global alignment tasks, Pamona achieved the highest Label Transfer Accuracy of 95.00% and 98.00%, and highest FOSTCTTM scores of 0.073 and 0.011 in Sim. 1 and Sim. 2, respectively (Supplementary Table S1). SCOT achieved the highest Label Transfer Accuracy of 95.77%, and highest FOSTCTTM scores of 0.009 in Sim. 3 (Supplementary Table S1).
3.3 Pamona identified informative genes in delineating the shared and dataset-specific cellular structures of the sc-GEM dataset
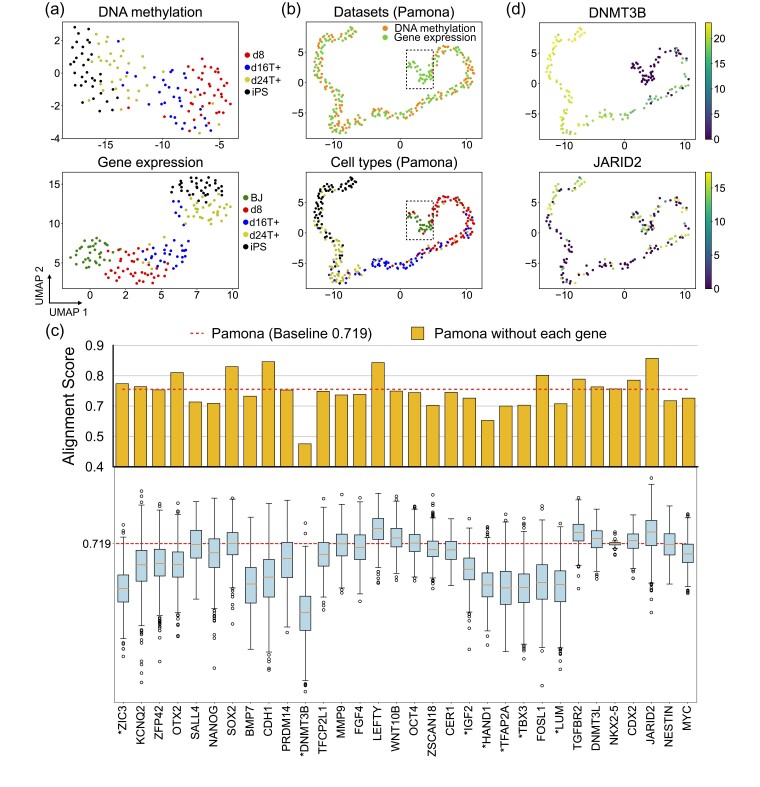
We applied Pamona to the sc-GEM dataset of gene expression and DNA methylation on samples of human cells undergoing reprogramming to induced pluripotent stem (iPS) cells. In a previous study, we applied UnionCom to this same dataset for a global manifold alignment task (Cao et al., 2020). However, in this study, we removed the human foreskin fibroblast (BJ) cells from the DNA methylation dataset to construct a partial manifold alignment task. Both gene expression and DNA methylation datasets demonstrated similar linear structures with the same cell type orders when visualized using Uniform Manifold Approximation and Projection (UMAP) (Becht et al., 2019; McInnes et al., 2018) separately (Fig. 3a). The gene expression dataset showed the dataset-specific cell type BJ (green points) located at one end of the linear trajectory (Fig. 3a, lower panel).
Fig. 3.
Pamona integrated the sc-GEM dataset and identified informative genes in delineating the shared and dataset-specific cellular structures. (a) Visualizations of the DNA methylation (upper panel) and gene expression (lower panel) datasets separately using UMAP before alignment. BJ cells (green points) comprise the gene expression dataset-specific cells. (b) Visualizations of the common space of the two aligned datasets by Pamona using UMAP: upper panel: cells are colored according to their corresponding datasets; lower panel: cells are colored according to their corresponding types. (c) Alignment score of Pamona using expression profile with all 32 genes (red dashed line, baseline 0.719) and without each of the 32 genes separately (upper panel, orange bars), or the permuted Alignment Scores by randomly shuffling the expression values of each of the 32 genes across cells 1000 times (lower panel, blue boxes). The genes with significant P-values less than 0.05 are denoted with ‘*’. (d) Gene expression of cells in the common space: upper panel: DNMT3B (informative gene); lower panel: JARID2 (non-informative gene)
Pamona aligned the shared cells of d8 (red points), d16T+ (blue points), d24T+ (yellow points) and iPS (black points), accordingly, and preserved BJ cells as the gene expression dataset-specific cells in the common space (Fig. 3b). It achieved the highest Alignment Score of 0.719 and Label Transfer Accuracy of 66.2% (Supplementary Fig. S1c). In comparison, UnionCom achieved the second highest Alignment Score of 0.592 and Label Transfer Accuracy of 45.77% (Supplementary Fig. S1c). SCOT and UnionCom did not separate BJ cells from d8 cells (Supplementary Fig. S6a and b); MMD-MA and Seurat v3 failed to align the shared cells across the two datasets (Supplementary Fig. S6c and d) and showed relatively low accuracy (Supplementary Fig. S1c).
We further assessed the importance of all 32 genes from the gene expression profile in delineating the shared and dataset-specific cellular structures. We set the Alignment Score achieved by Pamona at 0.719 as baseline (Fig. 3c, upper panel, blue line). We removed each gene from the gene expression profile, applied Pamona and computed the Alignment Score separately (Fig. 3c, upper panel, orange bars). We found that (i) removing each of DNMT3B, HAND1, TFAP2A and TBX3 genes resulted in a dramatic lose of Alignment Score, suggesting that these genes are informative features for the partial alignment task, but that (ii) removing each of the LEFTY and JARID2 genes resulted in a significant gain of Alignment Score, suggesting that these genes are non-informative features for the partial alignment task. To evaluate the significancy of the results, we performed the permutation test on each gene as follows: (i) we randomly shuffled the given gene’s expression values across cells and calculated the corresponding permuted Alignment Score; (ii) we repeated the step (1) for 1000 times to obtain the permutation distribution which served as a reference to access the significance of the given gene in the alignment; (iii) we computed the P-value of the given gene by calculating the fraction of the permuted Alignment Scores that are above the baseline 0.719 (Fig. 3c, lower panel). All the informative genes DNMT3B, HAND1, TFAP2A and TBX3 have significant P-values less than 0.05, but not for the non-informative genes LEFTY and JARID2 (see the listed P-values of all 32 genes in Supplementary Table S2). It also can be evidenced that the informative gene DNMT3B was highly expressed in the shared cells, but not expressed in BJ cells, which are dataset-specific cells (Fig. 3d, upper panel). The non-informative gene JARID2 was uniformly expressed in both shared and dataset-specific cells (Fig. 3d, lower panel).
3.4 Pamona resolved the integration of the scNMT-seq dataset in both global and partial manifold alignment tasks
We applied Pamona to the scNMT-seq dataset of chromatin accessibility, DNA methylation and gene expression on mouse gastrulation samples collected at four time stages, i.e. embryonic day 4.5 (E4.5), E5.5, E6.5 and E7.5 (Argelaguet et al., 2019).
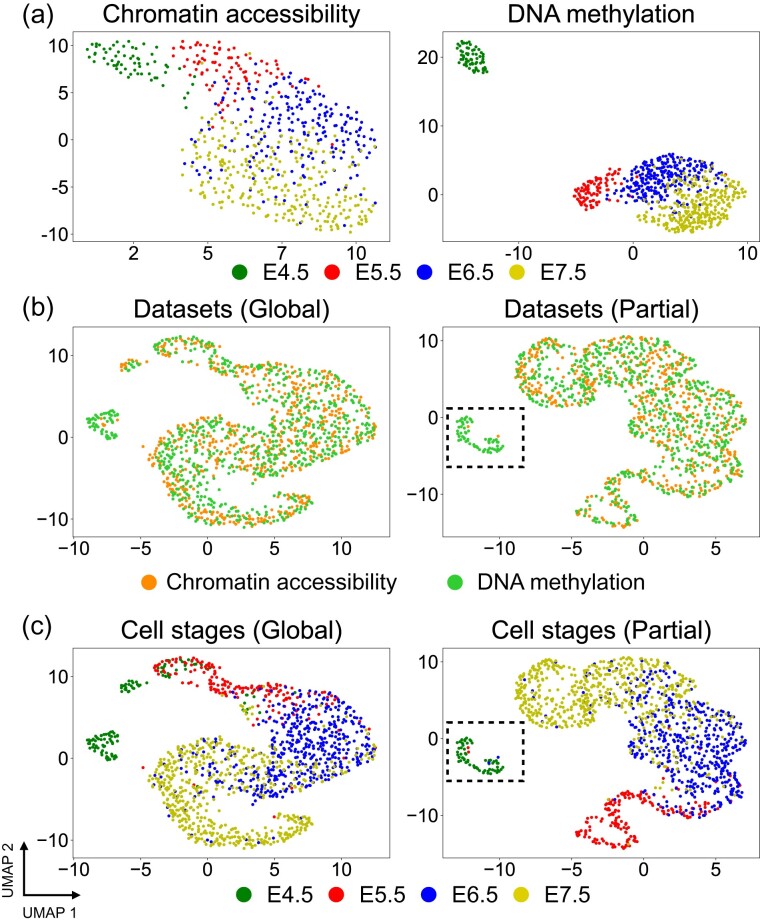
We conducted a global manifold alignment task to integrate the two cellular modalities of chromatin accessibility and DNA methylation. Both datasets demonstrated similar linear structures which preserve the time stage orders when visualized using UMAP separately (Fig. 4a). Pamona aligned the two datasets in a common space and also preserved the time stage orders (Fig. 4b). Pamona achieved the second highest Alignment Score of 0.866 and Label Transfer Accuracy of 70.79%, slightly below the highest scores achieved by SCOT (Alignment Score 0.88; Label Transfer Accuracy 74.03%). See Supplementary Figures S7a–d and S1d for more results of the 4 compared methods.
Fig. 4.
Pamona integrated the scNMT-seq dataset in both global and partial manifold alignment tasks. (a) Visualizations of chromatin accessibility (upper panel) and DNA methylation (lower panel) datasets separately using UMAP before alignment. (b) Visualizations of the common space of the global alignment of the two datasets by Pamona using UMAP: upper panel: cells are colored according to their corresponding datasets; lower panel: cells are colored according to their corresponding types. (c) Visualizations of the common space of the partial alignment of the two datasets (cells of E4.5 were removed from the chromatin accessibility dataset) by Pamona using UMAP
Next, we constructed a partial manifold alignment task by removing the cells of time stage E4.5 from the chromatin accessibility dataset. Pamona aligned the shared cells from E5.5 to E7.5, accordingly, and preserved the cells of E4.5 as the DNA methylation dataset-specific cells in the common space (Fig. 4c). It achieved the highest Alignment Score of 0.907 and Label Transfer Accuracy of 75.34% (Supplementary Fig. S1e). In comparison, UnionCom achieved the second highest Alignment Score of 0.669 and Label Transfer Accuracy of 64.72%. SCOT, which was designed with the underlying assumption of global manifold alignment, dropped its accuracy markedly (Alignment Score 0.297; Label Transfer Accuracy 62.67%). See Supplementary Figures S7e–h and S1e for more results of the 4 compared methods.
Finally, we conducted a partial manifold alignment task to integrate the three cellular modalities of chromatin accessibility, gene expression and DNA methylation by removing the cells of time stage E4.5 from the chromatin accessibility dataset (Supplementary Fig. S8a). Pamona successfully integrated the three modalities by aligning the shared cells according to their time stages and preserving the cells of E4.5 as the DNA methylation- and gene expression-specific cells in the common space (Supplementary Fig. S8b). In contrast, UnionCom, which can also handle multiple datasets, did not clearly separate the cells of E4.5 of the DNA methylation and gene expression datasets from the cells of the chromatin accessibility dataset (Supplementary Fig. S8c).
3.5 Pamona resolved the integration of the heterogeneous PBMC dataset by incorporating cell type annotation information
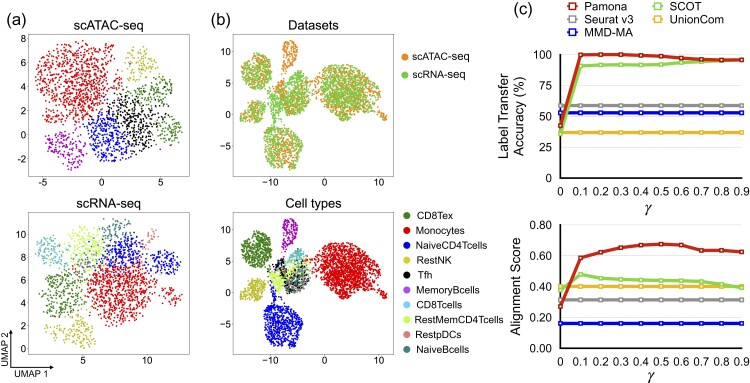
We applied Pamona to integrate the heterogeneous PBMC dataset by incorporating cell type annotation information. The PBMC dataset consisting of gene expression (scRNA-seq) and chromatin accessibility (scATAC-seq) was derived from samples of human peripheral blood mononuclear cells released by 10X Genomics, and it was previously analyzed by MAESTRO (Wang et al., 2020). We adopted the annotations provided by MAESTRO (Wang et al., 2020) as the benchmark to assess the performance of the methods (see Fig. 5a for the annotated cell types of scRNA-seq and scATAC-seq datasets on UMAP visualizations separately). Since both scRNA-seq and scATAC-seq have dataset-specific cell types annotated by MAESTRO (Fig. 5a), such data integrative analysis is a partial manifold alignment task.
Fig. 5.
Pamona integrated the heterogeneous PBMC dataset by incorporating cell type annotation information. (a) Visualizations of the scATAC-seq (upper panel) and scRNA-seq (lower panel) datasets separately using UMAP before alignment. (b) Visualizations of the common space of the two aligned datasets by Pamona by incorporating cell type annotation information (): upper panel: cells are colored according to their corresponding datasets; lower panel: cells are colored according to their corresponding types. (c) The Label Transfer Accuracy and Alignment Score of Pamona and SCOT when γ in the disagreement matrix M was set from 0 to 0.9, which is equivalent to the growing influence of cell annotations compared to data structure. We similarly incorporated prior information for SCOT. Results by Seurat v3, MMD-MA and UnionCom did not incorporate cell type annotation information
Here, the regulation parameter , which is defined in Supplementary Note S3, represents a tradeoff between cost of individual matchings and faithfulness to the data structure. When γ = 0, no prior information is incorporated. When no prior information was used, all five methods tested had low scores of Label Transfer Accuracy and Alignment Score (Fig. 5c). None of the 5 methods tested could integrate the two modalities since they failed to preserve both shared and dataset-specific cellular structures (Supplementary Fig. S10). For example, Pamona could not align shared NaiveCD4T cells across the two datasets in the common space (Supplementary Fig. S10).
When incorporating cell type annotation information, however, Pamona aligned the shared cells, accordingly, and preserved the dataset-specific cells in the common space (Fig. 5b) with demonstrably improved integrative accuracy in that the scores of Label Transfer Accuracy and Alignment Score increased as the γ increased (Fig. 5c). We also incorporated cell type annotation information for SCOT, as we did for Pamona, but SCOT only slightly improved its Alignment Score (Fig. 5c) since it lacks a partial manifold alignment strategy to separate out dataset-specific cells from the shared cells in the common space. Pamona dropped its accuracy when γ was set greater than 0.5, which indicates that is an appropriate trade-off parameter between cost of individual matchings and faithfulness to the data structure.
3.6 Pamona achieved high accuracy on jointly clustering of cells across modalities of SNARE-seq dataset in the common space constructed
We benchmarked the performance of Pamona with the state-of-the-art supervised integration methods, MOFA and scMVAE, on jointly clustering of single-cell multi-omics dataset of SNARE-seq (See Supplementary Note S7 and Supplementary Result S1 for the information about the SNARE-seq dataset). Both MOFA and scMVAE, which were developed for parallel sequencing with multi-modality in the same cell, took the information of cross-correspondence of cells as a prior. We also included the unsupervised integration methods Seurat and CCA as comparisons. We adopted the Kappa coefficient utilized by scMVAE (Zuo and Chen, 2021) to measure consistency between cell clusters predicted by each omic data. A higher Kappa coefficient is indicative of higher accuracy. The calculated Kappa coefficients of Seurat, CCA, MOFA and scMVAE on the SNARE-seq dataset was directly adopted from Zuo and Chen (2021). We also calculated the Adjusted Rand Index (ARI) and Normalized Mutual Information (NMI) indexes of Pamona for evaluation of clustering performance.
We performed manifold alignment by Pamona without incorporating information of cross-correspondence of cells, and mapped the cells into the common space. We then jointly clustered cells across modalities in the common space into 4 clusters, the same number of clusters as in scMVAE (Zuo and Chen, 2021), with the K-Means clustering algorithm. It is worth note that Pamona achieved second highest Kappa coefficient of 0.955, slightly below the highest coefficient of 0.985 by scMVAE (Supplementary Fig. S15). Besides, Pamona also achieved high scores of ARI (0.92) and NMI (0.87).
4 Discussion
In this study, we propose Pamona, a partial manifold alignment algorithm, for heterogeneous single-cell multi-omics data integration. Pamona delineates and represents the shared and dataset-specific cell structures in the common space across modalities. It easily incorporates prior information, such as cell type annotations or cell-cell correspondence, to further improve alignment quality. When applied to two simulated and four real single-cell multi-omics datasets, Pamona accurately identified shared and dataset-specific cells, and it faithfully recovered and aligned cellular structures of heterogeneous cellular modalities in the common space.
Pamona was developed based on the recently proposed partial-GW optimal transport framework (Chapel et al., 2020). The key technique of partial-GW is adding virtual/dummy points onto the marginals to enforce points with large discrepancies absorbed by the virtual points (Caffarelli and McCann, 2010; Chapel et al., 2020). Virtual points have also been discussed in the partial graph matching problem (Zaslavskiy et al., 2009). As we can see from the computed probabilistic coupling matrices by Pamona, the virtual points achieved the goal of absorbing the dataset-specific cells (Supplementary Figs S11–S13). We also proposed an SPL method to estimate the shared cell number across datasets. We demonstrate that SPL is very accurate and robust in our tested datasets (Supplementary Note S4, Supplementary Fig. S14).
Pamona is a computationally efficient algorithm (Table 1, Supplementary Note S9). However, it requires memory consumption in the storage of distance matrices. Therefore, it may not perform well when sample size is in large-scale (e.g. > 1 million cells). As large-scale single-cell multi-omics datasets are emerging, it is challenging to resolve the scalability problem for Pamona. One approach to tackle this problem is to develop a distributed storage and distributed computational framework for Pamona. Meanwhile, since large-scale single-cell datasets can be highly redundant, we can take the alternative approach by 1) adopting the state-of-the-art neural network with mini-batch framework (Cho et al., 2018), or 2) selecting a subset of informative samples using the advanced geometric sketching tool (Hie et al., 2019b) prior to applying Pamona. We plan to pursue these topics in our future work.
Table 1.
Running time of Pamona and other methods
| Method | Simulation1 | Simulation2 | scGEM | scNMT-seq | PBMC |
|---|---|---|---|---|---|
| Seurat | 3.81 | 2.50 | 2.20 | 5.52 | 9.54 |
| MMD-MA | 19.76 | 19.35 | 17.05 | 41.70 | 88.47 |
| UnionCom | 53.00 | 38.23 | 32.58 | 74.06 | 462.65 |
| SCOT | 18.07 | 8.89 | 71.04 | 54.19 | 124.51 |
| Pamona | 17.00 | 7.17 | 17.64 | 30.92 | 102.18 |
Note: Time unit: Second.
Funding
This work was supported by the National Key R&D Program of China under Grant 2019YFA0709501, the National Natural Science Foundation of China [61733018, 12071466], Shanghai Municipal Science and Technology Major Project [2021SHZDZX010], the Fundamental Research Funds for the Central Universities and LSC of CAS.
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Kai Cao, LSC, NCMIS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China; School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China.
Yiguang Hong, LSC, NCMIS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China; Department of Control Science and Engineering, Tongji University, Shanghai 200092, China.
Lin Wan, LSC, NCMIS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China; School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China.
References
- Argelaguet R. et al. (2018) Multi-omics factor analysis—a framework for unsupervised integration of multi-omics data sets. Mol. Syst. Biol., 14, e8124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Argelaguet R. et al. (2019) Multi-omics profiling of mouse gastrulation at single-cell resolution. Nature, 576, 487–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becht E. et al. (2019) Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol., 37, 38–44. [DOI] [PubMed] [Google Scholar]
- Belkin M., Niyogi P. (2003) Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput., 15, 1373–1396. [Google Scholar]
- Caffarelli L.A., McCann R.J. (2010) Free boundaries in optimal transport and Monge-Ampere obstacle problems. Ann. Math., 171, 673–730. [Google Scholar]
- Cao K. et al. (2020) Unsupervised topological alignment for single-cell multi-omics integration. Bioinformatics, 36, i48–i56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalise P., Fridley B.L. (2017) Integrative clustering of multi-level ’omic data based on non-negative matrix factorization algorithm. PLoS One, 12, e0176278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapel L. et al. (2020) Partial optimal tranport with applications on positive-unlabeled learning. In: Advances in Neural Information Processing Systems, Vancouver, British Columbia, Canada, Vol. 33, pp. 2900–2910.
- Chen S. et al. (2019) High-throughput sequencing of the transcriptome and chromatin accessibility in the same cell. Nat. Biotechnol., 37, 1452–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheow L.F. et al. (2016) Single-cell multimodal profiling reveals cellular epigenetic heterogeneity. Nat. Methods, 13, 833–836. [DOI] [PubMed] [Google Scholar]
- Cho H. et al. (2018) Generalizable and scalable visualization of single-cell data using neural networks. Cell Syst., 7, 185–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courty N. et al. (2017) Optimal transport for domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell., 39, 1853–1865. [DOI] [PubMed] [Google Scholar]
- Cui Z. et al. (2014) Generalized unsupervised manifold alignment. In: Advances in Neural Information Processing Systems, Montreal, Canada, Vol. 27, pp. 2429–2437.
- Cuturi M. (2013) Sinkhorn distances: lightspeed computation of optimal transport. In: Advances in Neural Information Processing Systems, Harrahs and Harveys, Lake Tahoe, Vol. 26, pp. 2292–2300.
- Demetci P. et al. (2021) Gromov–Wasserstein optimal transport to align single-cell multi-omics data. In: Proceedings of the 25th International Conference on Research in Computational Molecular Biology.
- Efremova M., Teichmann S.A. (2020) Computational methods for single-cell omics across modalities. Nat. Methods, 17, 14–17. [DOI] [PubMed] [Google Scholar]
- Haghverdi L. et al. (2018) Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nat. Biotechnol., 36, 421–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardoon D.R. et al. (2004) Canonical correlation analysis: an overview with application to learning methods. Neural Comput., 16, 2639–2664. [DOI] [PubMed] [Google Scholar]
- Hie B. et al. (2019a) Efficient integration of heterogeneous single-cell transcriptomes using scanorama. Nat. Biotechnol., 37, 685–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hie B. et al. (2019b) Geometric sketching compactly summarizes the single-cell transcriptomic landscape. Cell Syst., 8, 483–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin S. et al. (2020) scAI: an unsupervised approach for the integrative analysis of parallel single-cell transcriptomic and epigenomic profiles. Genome Biol., 21, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klimovskaia A. et al. (2020) Poincaré maps for analyzing complex hierarchies in single-cell data. Nat. Commun., 11, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. et al. (2019) Jointly embedding multiple single-cell omics measurements. In: 19th International Workshop on Algorithms in Bioinformatics (WABI 2019), LIPICS, Vol. 143, pages 10:1–10:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McInnes L. et al. (2018) Umap: Uniform manifold approximation and projection for dimension reduction. arXiv preprint arXiv:1802.03426.
- Mémoli F. (2011) Gromov–Wasserstein distances and the metric approach to object matching. Found. Comput. Math., 11, 417–487. [Google Scholar]
- Nitzan M. et al. (2019) Gene expression cartography. Nature, 576, 132–137. [DOI] [PubMed] [Google Scholar]
- Peyré G. et al. (2016) Gromov-Wasserstein averaging of kernel and distance matrices. In: International Conference on Machine Learning, New York City, NY, USA, Vol. 48, pp. 2664–2672.
- Peyré G., Cuturi M. (2019) Computational optimal transport. Found. Trends Mach. Learn., 11, 355–607. [Google Scholar]
- Roweis S.T., Saul L.K. (2000) Nonlinear dimensionality reduction by locally linear embedding. Science, 290, 2323–2326. [DOI] [PubMed] [Google Scholar]
- Scherer M. et al. (2021) Machine learning for deciphering cell heterogeneity and gene regulation. Nat. Comput. Sci., 1, 183–189. [DOI] [PubMed] [Google Scholar]
- Singh R. et al. (2020) Unsupervised manifold alignment for single-cell multi-omics data. In: Proceedings of the 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, BCB ’20. Association for Computing Machinery. [DOI] [PMC free article] [PubMed]
- Solomon J. et al. (2015) Convolutional Wasserstein distances: efficient optimal transportation on geometric domains. ACM Trans. Graph., 34, 1. [Google Scholar]
- Solomon J. et al. (2016) Entropic metric alignment for correspondence problems. ACM Trans. Graph., 35, 1. [Google Scholar]
- Stuart T., Satija R. (2019) Integrative single-cell analysis. Nat. Rev. Genet., 20, 257–272. [DOI] [PubMed] [Google Scholar]
- Stuart T. et al. (2019) Comprehensive integration of single-cell data. Cell, 177, 1888–1902.e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenenbaum J.B. et al. (2000) A global geometric framework for nonlinear dimensionality reduction. Science, 290, 2319–2323. [DOI] [PubMed] [Google Scholar]
- Wang C. et al. (2020) Integrative analyses of single-cell transcriptome and regulome using MAESTRO. Genome Biol., 21, 198–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch J.D. et al. (2017) MATCHER: manifold alignment reveals correspondence between single cell transcriptome and epigenome dynamics. Genome Biol., 18, 138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch J.D. et al. (2019) Single-cell multi-omic integration compares and contrasts features of brain cell identity. Cell, 177, 1873–1887.e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaslavskiy M. et al. (2009) A path following algorithm for the graph matching problem. IEEE Trans. Pattern Anal. Mach. Intell., 31, 2227–2242. [DOI] [PubMed] [Google Scholar]
- Zuo C., Chen L. (2021) Deep-joint-learning analysis model of single cell transcriptome and open chromatin accessibility data. Brief. Bioinf. 22, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.