Protein pK_a Prediction with Machine Learning

Abstract

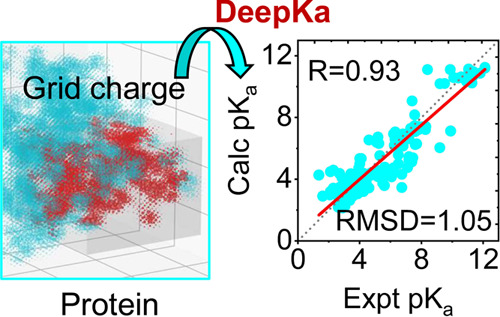
Protein pK_a prediction is essential for the investigation of the pH-associated relationship between protein structure and function. In this work, we introduce a deep learning-based protein pK_a predictor DeepKa, which is trained and validated with the pK_a values derived from continuous constant-pH molecular dynamics (CpHMD) simulations of 279 soluble proteins. Here, the CpHMD implemented in the Amber molecular dynamics package has been employed (Huang Y.et al. J. Chem. Inf. Model. 2018, 58, 1372−1383). Notably, to avoid discontinuities at the boundary, grid charges are proposed to represent protein electrostatics. We show that the prediction accuracy by DeepKa is close to that by CpHMD benchmarking simulations, validating DeepKa as an efficient protein pK_a predictor. In addition, the training and validation sets created in this study can be applied to the development of machine learning-based protein pK_a predictors in the future. Finally, the grid charge representation is general and applicable to other topics, such as the protein–ligand binding affinity prediction.

1. Introduction

Solution pH plays a key role in many biological events, such as proton-coupled transport of ions¹ or small molecules² across the cellular membrane, enzyme catalyses that require proton donors in the active sites to carry out the catalytic functions,³ and pH-gradient-driven ATP synthesis in the cellular energy metabolism.⁴ pK_a on the other hand measures how tight a proton is held by an ionizable site and the resulting microscopic protonation and deprotonation equilibria at a certain pH condition. Thus, the predictions of pK_a’s are essential to understand the molecular mechanisms of pH-mediated processes in biology and chemistry. pK_a’s can be determined by experiments, typically nuclear magnetic resonance (NMR) for biomolecules.^5,6 However, NMR experiments are often expensive and time-consuming, making theoretical methods more favored.

A fast way to compute pK_a’s is coming up with a simple empirical function, such as PropKa that calculates pK_a shifts contributed by desolvation, hydrogen-bonding, and charge–charge interactions.⁷⁻¹⁰ However, the construction of such an empirical function requires the knowledge of pK_a’s determinants. In addition, measured pK_a’s are needed to determine model coefficients. On the other hand, in the framework of a classic force field, like CHARMM¹¹ and Amber,¹² the pK_a shift can be achieved by estimating the free energy perturbation (FEP) of transferring an ionizable group from an aqueous solution to a biomolecule.¹³ For instance, FEP can be approximated numerically with the Poisson–Boltzmann (PB)-based methods, such as MCCE,¹⁴ H++,¹⁵ and DelphipKa.¹⁶⁻¹⁸ PB-based approaches assume that the structure and charge distribution of a biomolecule are fixed. As a consequence, the calculated pK_a value of an ionizable group might be biased to a specific conformation, which is known as microscopic pK_a.

Alternatively, constant-pH molecular dynamics (CpHMD) simulations have been developed to calculate FEP and the resulting pK_a’s. CpHMD methods can be divided into two classes. One is the discrete CpHMD that periodically updates the protonation states stochastically in the Monte-Carlo step followed by a short molecular dynamics simulation.¹⁹ The other is the continuous CpHMD that propagates simultaneously the spatial and titration coordinates in the framework of λ dynamics.^20,21 During CpHMD simulations, molecular conformations are coupled with protonation states. Besides, the interplay of titration events is elucidated. Thus, macroscopic pK_a’s can be obtained with CpHMD simulations, in accordance with the apparent pK_a’s measured by experiments. Recently, CpHMD simulations have been proved applicable to those challenging systems that are very dynamic, such as enzymes²²⁻²⁴ and membrane proteins,²⁵⁻²⁷ demonstrating high robustness. Apart from the CpHMD methods, a hybrid Rosetta-MCCE protocol provides the pK_a’s where the conformational changes coupled to ionization states are considered too.²⁸ However, the price comes that either CpHMD simulations or the hybrid Rosetta-MCCE protocol are time-consuming when compared with other state-of-the-art methods. Thus, a cheap method is demanded that offers comparable precision with that by a CpHMD method.

Unlike the knowledge-based approaches above, machine learning (ML) methods build algorithms on sample data to accomplish complex tasks.²⁹ For instance, ML methods have been successful in predicting pK_a’s for aliphatic amines,³⁰ protein–ligand binding affinity,^31,32 and protein secondary/tertiary structure.³³⁻³⁵ Similar to the protein–ligand binding affinity, the pK_a value of an ionizable group is governed by the protein environment.²² Thus, exploiting the complex protein environment patterns is the primary task to model a protein pK_a predictor. A valid training data set is fundamental to an ML model. However, the protein pK_a data set is quite a lack. At present, experimental pK_a values of 1350 ionizable residues in 157 proteins are available in the pK_a database PKAD,³⁶ which is far not enough for rational modeling with ML.

In this work, a deep learning-based protein pK_a predictor DeepKa has been developed and evaluated. The training and validation sets that include 11368 and 1441 pK_a’s, respectively, have been created based on continuous CpHMD simulations of 279 soluble proteins.^37,38 The deep learning architecture proposed by Stepniewska-Dziubinska and co-workers has been applied with minor modifications.³¹ To reduce the computational cost, typically a cubic box³¹ or, in another study, a sphere³⁹ is defined as model input, instead of the entire protein. Such a truncation scheme excludes the protein electrostatics beyond the cutoff. In physics, energy fluctuations could be observed at the cutoff,⁴⁰ which may result in an artificial pK_a shift. Noting that electrostatics is the major contributor to pK_a shifts,¹³ it is of importance to eliminate the cutoff-induced discontinuities. In this study, a general solution has been proposed to smooth the charge distribution and the resulting electrostatic energy. Finally, based on the PKAD database mentioned above, the test set that contains 167 pK_a’s was created to evaluate DeepKa. To find out the theoretical limit, CpHMD simulations of benchmark proteins in the test set were carried out. The prediction accuracy by DeepKa will be compared with that by CpHMD simulations as well as the PropKa method to examine the predictive power of the present deep learning model. Finally, the effectiveness of the cropped cubic box as well as the proposed grid charge representation will be discussed.

2. Methods and Materials

2.1. Feature Representation

The protein environment of an ionizable group should be transformed and encoded to make it readable by a neural network. Instead of the entire protein, a 20 Å cubic box or grid was defined to present the protein environment.³¹ The center of the box is the titratable site of interest. As a result, the minimal distance from the center to the edge of the box is 10 Å. Then, heavy atoms were mapped to the 3D grid with 1 Å resolution.³¹ Discretized Cartesian coordinates of grid points that provide the spatial information are set as the model input. As a consequence, a 4D tensor was created where the first three dimensions correspond to the Cartesian coordinates and the last dimension contains 20 features that describe a grid point. As listed below, the first 17 features resemble the ones applied by Stepniewska-Dziubinska and co-workers in their Pafnucy model³¹

• 9 bits (one-hot or all null) that encode atom types, including B, C, N, O, P, S, Se, halogens, and metals

• 1 integer (1, 2, or 3) that indicates atom hybridization

• 1 integer that counts the number of bonded heavy atoms

• 1 integer that counts the number of bonded hetero atoms

• 5 bits (1 if present) that encode the five properties defined with SMARTS patterns, namely, hydrophobic, aromatic, acceptor, donor, and ring⁴¹

• 1 float with a grid charge

• 1 bit (1 if belonging to the titratable residue at the center of the box)

• 1 integer that indicates the ionizable residue type at the center of the box (0, 1, 2, and 3 corresponding to Asp, Glu, Lys, and His, respectively)

In this work, grid charges are proposed to prevent discontinuities at the cutoff. In specific, atomic charges assigned by a force field were spread over the grid with a B-spline interpolation algorithm, which will be elucidated in detail below. If more than one atom is assigned to a grid point, which is rare for a 1 Å grid unit, features from all colliding atoms were added.³¹ As to the grid points that have no atom assigned to, all features were set zero,³¹ except for the ionizable residue-type feature. These grid points will be recognized as water molecules by the model. The last two features indicate the titratable residue at the center of the cubic box and the corresponding residue type, respectively. The 20 features were scaled with z-score normalization.

2.2. Charge Spreading

In this work, each atomic charge in a protein was distributed to n × n × n grid points with the B-spline interpolation algorithm, where n denotes the interpolation order that equals 4, the default value used by smoothed particle-mesh Ewald summation in the CHARMM package.^40,42 Here, we take a two-dimensional mesh with two identical atomic charges as an example (Figure 1a). As illustrated in Figure 1b, each charge is spread to 4 × 4 grid points with B-spline interpolation. The weights of the two atomic charges at a grid point are determined individually by the B-spline coefficients, which can be formulated as below for one dimension.⁴²

1

2

where u is a real number that denotes the scaled fractional coordinate and the B-spline coefficients obey the normalization condition.

Figure 1.

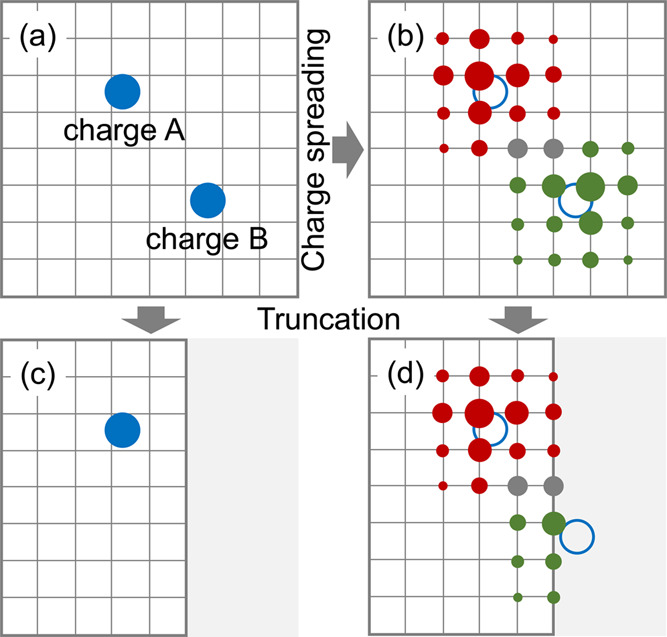
Schematic diagram of spreading two identical atomic charges to a 2D grid. (a) Atomic charges A and B are represented by two blue solid circles. (b) B-spline interpolation algorithm is utilized to distribute charges A and B over the grid with an interpolation order of 4. Open circles indicate that charges A and B have been spread to the grid. Red and green solid circles represent the distributions of charges A and B, respectively, over the grid. The grid points with accumulated contributions by two charges are in gray. The radii of circles indicate the accumulated weights of atomic charges at grid points. The 2D grid is truncated in (c) and (d). Charge B is removed in (c), and the grid charges that belong to the truncated area (gray) are removed in (d).

From Figure 1b, one can see that the distribution of an atomic charge over the grid is diffusive. The contributions from two atomic charges at a grid point are accumulated (gray solid circles in Figure 1b). To explain the potential artifact with atomic charges, the grid is truncated. As a result, charge B is fully excluded even though it’s close in position to the boundary (Figure 1c). On the contrary, charge B can be partly captured when represented with grid charges (Figure 1d).

2.3. Data Set Preparation

Following the Pafnucy model proposed by Stepniewska-Dziubinska and co-workers, atomic features were calculated with Open Babel.⁴³ In particular, the atomic charges were assigned based on Amber ff14SB force field¹² by UCSF Chimera.⁴⁴ In this work, the atomic charges were spread over the grid. SWISS-MODEL was utilized to build the positions of missing residues in the protein crystal structures.⁴⁵ At present, four titratable residue types, namely, Asp, Glu, His, and Lys, are considered.

2.3.1. Training and Validation Sets PHMD252 and PHMD27

The pK_a values for training and validation were calculated with continuous CpHMD simulations. Hereinafter, CpHMD denotes continuous CpHMD. The training set PHMD252 contains 11368 pK_a values that correspond to 3237 Asp, 3672 Glu, 1268 His, and 3191 Lys in 252 proteins (Table S1). The validation set PHMD27 contains 1441 pK_a values for 363 Asp, 499 Glu, 151 His, and 428 Lys in 27 proteins (Table S1). The proteins in PHMD252 and PHMD27 were selected randomly from data set TR6614, which was used previously as the training set for protein secondary structure prediction.⁴⁶ The predictive power of a CpHMD method is governed mainly by the solvation energy that can be estimated by implicit or explicit solvent models. Accordingly, implicit,^20,21,37 hybrid,^47,48 or explicit^49,50 solvent-based CpHMD methods have been developed and implemented in two popular molecular dynamics engines, CHARMM⁴⁰ and Amber.⁵¹ In theory, the particle-mesh Ewald (PME)-based explicit solvent CpHMD scheme is applicable to any protein that a classical force field can describe, including membrane proteins.⁵⁰ However, explicit solvent CpHMD methods are time-consuming and slow to reach pK_a convergence.⁵⁰ Thus, pK_a values in both PHMD252 and PHMD27 were computed with the GBNeck2-based implicit solvent CpHMD method,³⁷ which had been implemented in the GPU-accelerated pmemd program of the Amber package.^38,51 GBNeck2-based implicit solvent is limited to soluble proteins; thus, there is no membrane protein in the current training and validation sets. CpHMD simulation details can be found below.

2.3.2. Test Set EXP67S

Test set EXP67S is the subset of data set EXP67. The pK_a values in EXP67 were extracted from the PKAD database that collects from the literature the experimentally measured pK_a values of ionizable groups in proteins.³⁶ Original PKAD contains pK_a data of 1350 residues in 157 wild-type proteins. The residues with pK_a values outside the experimental pH ranges were excluded. Besides, if a residue is measured more than once and the pK_a’s are similar, only one measurement is used to avoid data duplication. It is noticed that the absolute pK_a shifts of Lys are all smaller than 2.0 in PKAD. To examine the predictive power of DeepKa for Lys residues with high pK_a shifts, the measured pK_a’s of three Lys residues in three SNase mutants (PDB ID: 3RUZ, 4HMI, and 3C1E) were added to the test set.⁵² Notably, the absolute pK_a shifts of the three Lys residues are larger than 2.0. To avoid the potential overfitting due to sequence homology, sequence identity calculations have been done with the FASTA package (version 36.3.8h) to exclude the proteins in the test set that have the sequence identities larger than 30% with those in the training or validation set. Finally, data set EXP67 contains 470 pK_a values for 151 Asp, 176 Glu, 75 His, and 68 Lys in 67 proteins. It is found that the distributions of pK_a values around model pK_a’s are dense, which would lead to overestimated accuracy and underestimated correlation between calculated and measured pK_a values. Thus, the subset of EXP67, namely, EXP67S that satisfies the normal distribution of pK_a values, was utilized as the test set to evaluate the model. In specific, the absolute pK_a shift was divided into five windows, namely, [0,0.5), [0.5,1.0), [1.0,1.5), [1.5,2.0), and [2.0,+∞). To balance the populations among the windows and reach the normal distribution, some data points in the regions of [0,0.5) and [0.5,1.0) have been selected randomly and removed. The number distribution of absolute pK_a shifts in the resulting EXP67S can be found in Table S1. Finally, EXP67S contains 167 pK_a’s for 46 Asp, 60 Glu, 31 His, and 30 Lys in 52 proteins. Notably, the pK_a values around model pK_a’s are less populated (Table S1).

In contrast to previous CpHMD research studies,^37,38,50 much more benchmark pK_a’s have been collected, especially for His and Lys, enabling definitive conclusions regarding the GBNeck2-based implicit solvent CpHMD method.

2.4. CpHMD Simulation Protocols

2.4.1. Structure Preparation

The initial structures of proteins in PHMD252, PHMD27, and EXP67 were obtained from the protein data bank (PDB) by providing the PDB codes. For the proteins in PHMD252 and PHMD27, the first chain in the crystal structure or the first conformation in the NMR models was selected. All proteins were acetylated at N-terminus (ACE) and amidated at C-terminus (CT2). Disulfide bonds if any were built and missing hydrogens were added.⁵³ Residue name HIS in the PDB files was substituted with HSP, which denotes the protonated state of His. Restraining the heavy atoms with a harmonic force constant of 50 kcal/mol.Ų, hydrogen atoms were relaxed by 50 steps of steepest descent and then 10 steps of Newton–Raphson minimization in the GBSW implicit solvent with an ionic strength of 0.15 M.⁵⁴ Here, the CHARMM22/CMAP additive force field was utilized to represent proteins.^11,55 To mimic proton buffers, dummy hydrogens bonded to the carboxyl oxygens of Asp/Glu were added and placed in the syn position. The structures were minimized following the scheme mentioned above. The aforementioned steps were accomplished with the CHARMM program (version c45a1).⁴⁰ The resulting PDB files were then converted into Amber-style PDB files with the MMTSB toolset.⁵⁶ The residue names ASP, GLU, and HSP were replaced manually by AS2, GL2, and HIP, respectively, such that Asp/Glu/His can be identified as ionizable by Amber. If two Cys residues form a disulfide bond, their residue names were renamed too, which is from CYS to CYX. The interaction between two dummy hydrogens was excluded to remove the artificial effect of nearby dummy hydrogens. In addition, the intrinsic Born radii of the His hydrogens was reduced from 1.3 Å, the default value for GBNeck2, to 1.17 Å.³⁸ Providing the PDB files as inputs, the parameter and coordinate files were generated with the LEaP utility in Amber where proteins were represented by ff14SB Amber force field,¹² in consistence with the force field utilized by the grid charge representation mentioned above. Finally, with the same harmonic force constant of 50 kcal/mol·Å² applied to heavy atoms, hydrogen atoms were relaxed by 100 steps of steepest descent followed by 200 steps of Newton–Raphson minimization in the GBNeck2 implicit solvent (igb=8) with an ionic strength of 0.15 M and the mbondi3 intrinsic Born radii.

2.4.2. Equilibration

After minimization, each structure undergoes four equilibration simulations where the restraints on heavy atoms reduced gradually from 5 to 0 kcal/mol·Å². The GPU-accelerated GBNeck2 implicit-solvent-based CpHMD model was selected (iphmd=1), and Asp, Glu, His, and Lys were set titratable.^37,38 The pH value of 7 that represents neutral aqueous solution was applied during the equilibration stage. The Langevin algorithm with a collision frequency of 1.0 p^–1 was utilized for constant-temperature (300 K) simulations (ntt=3). The SHAKE algorithm was used to constrain the bonds involving hydrogen atoms.⁵⁷ As a result, a time step of 2 fs can be used. The running length for each stage is 4 ps.

2.4.3. Production

A pH-based asynchronous replica-exchange protocol was utilized to improve the sampling of conformations as well as protonation states.^47,58 From the block analysis as illustrated in Figure S1, it is evident that most pK_a’s are converged within 2 ns per replica, consistent with that by Harris and Shen.³⁸ Thus, unless otherwise noted, each replica was run for 2 ns and the first 0.2 ns was discarded for later pK_a calculations. Exchanges were attempted every 1000 MD steps or 2 ps. Replica pH ranges from 0.0 to 12.5 with an interval of 0.5. As a result, there are 26 replicas in total and the accumulative running length is 52 ns for each protein. The pH-based asynchronous replica-exchange CpHMD simulations were carried out on two NVIDIA RTX 2080TI graphics processing units (GPUs) each with 11 gigabyte (GB) memory.

2.4.4. pK_a Calculation

The unprotonated fraction S at a pH condition can be calculated as below.

3

where N^unpro and N^pro denote the counts of unprotonated (λ > 0.8) and protonated (λ < 0.2) states, respectively. The variable λ that ranges from 0 to 1 is the titration coordinate of an ionizable group. Then, residue-specific pK_a’s can be computed by fitting S at different pH conditions to the generalized Henderson–Hasselbalch equation

4

where the Hill coefficient h is the slope of the titration curve that represents the coupling between ionizable groups.

2.5. Deep Learning Architecture

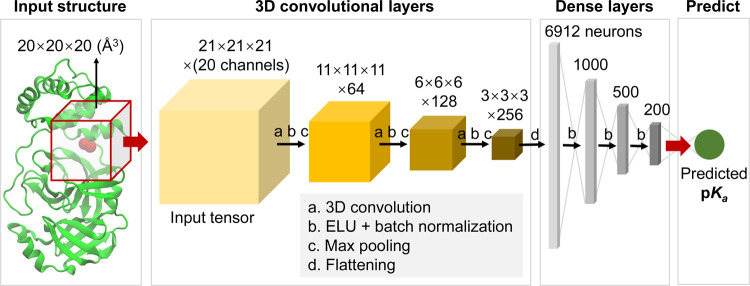
Convolutional neural network (CNN) has been succeeded in different areas. In particular, CNN was validated recently by Stepniewska-Dziubinska and co-workers in predicting the protein–ligand binding affinity that plays a key role in drug design.³¹ In fact, the pK_a value of an ionizable site reflects the binding affinity of a proton to this site at a certain pH condition. Thus, the deep learning architecture proposed by Stepniewska-Dziubinska and co-workers has been applied in this work,³¹ aiming at discovering protein environment patterns of proton binding sites and the resulting pK_a’s. As illustrated in Figure 2, a cubic box centralized at the titratable site of interest was cropped from a protein. The cubic box was then transformed to a 4D tensor as the input of the CNN (Figure 2, input tensor). Followed were three convolutional layers with 64, 128, and 256 cubic filters (5 × 5 × 5), respectively. For each convolutional layer, a 3D convolution was coupled with max pooling, in the middle of which an action function named exponential linear unit (ELU) and a batch normalization (BN) were utilized to speed up network convergence. Here, the max pooling uses a 2 × 2 × 2 cubic patch. Notably, the BN layers were not considered by Stepniewska-Dziubinska and co-workers in their model.³¹ The output 4D tensor of the convolution block is a 3 × 3 × 3 grid, the fourth vector of which contains 256 channels. The tensor was then flattened into a 1D array with 6912 neurons. This array was fed to four consecutive dense or fully connected layers. To overcome overfitting and vanishing, ELU functions and BN operations were applied to the dense layers too. Finally, the messages in the 200-neuron array were integrated by a single node where the pK_a value was predicted.

Figure 2.

3D convolutional neural network architecture of DeepKa. The crystal structure of the protein as an example is visualized with the NewCartoon model by VMD.⁵⁹ The titratable carboxyal oxygens of an Asp residue are highlighted with red balls. The input structure is the 20 Å open red cubic box centralized at the center of mass of the two carboxyl oxygens. The four solid boxes represent 4D tensors with the grid sizes of 21 × 21 × 21, 11 × 11 × 11, 6 × 6 × 6, and 3 × 3 × 3, respectively, and the channel counts per grid point are 20, 64, 128, and 256, respectively. In the dense block, the input layer includes 6912 neurons and the following three hidden layers have 1000, 500, and 200 neurons, respectively. The output layer with one single node (green) is the predicted pK_a.

2.6. Implementation Details

First, the Kaiming algorithm embedded in the PyTorch environment was used to initialize the training.⁶⁰ More precisely, the weights and biases were initialized with uniform distribution. The network was then trained with the Adam optimizer. The learning rate was set to 10^–3. To reduce overfitting, dropout was applied to the dense layers. A large mini-batch size of 128 was used, which is favored in the presence of BN layers. To reduce unexpected sensitivity to the orientation of a protein structure, the cubic box was rotated before entering the network.³¹ There are 24 combinations of 90° rotations around three axes for a cubic box. It should be noted that the selection of 90° is a balance between computational cost and speed. A smaller degree of rotation may reduce the effect of orientation, but the computational cost will increase. Finally, 720 epochs in total were carried out to make sure each orientation was visited randomly 30 times on average. After three rounds of training and validation, the model with the lowest root-mean-square deviation from the validation set PHMD27 was selected as the final model. The experiments were implemented under the PyTorch (version 1.8.1) environment, and the model was trained on a single NVIDIA RTX 2080TI GPU with 11 GB memory.

2.7. Performance Evaluation

Root-mean-square deviation (RMSD) or mean absolute error (MAE) is often used to measure the overall accuracy, whereas Pearson’s correlation coefficient (R) is indispensable for investigating the robustness of a model. pK_a shifts from the reference values tell to what extent ionizable sites are affected by proteins. The reference pK_a values for Asp, Glu, His, and Lys are 3.67, 4.25, 6.54,⁶¹ and 10.40,⁶² respectively. In the following section, pK_a shifts will be employed to examine the ability of DeepKa in capturing the protein environment of an ionizable site.

2.8. PropKa

PropKa (version 3.0)⁸ is utilized to see how well an existing method works on the same test data set EXP67S. The input of PropKa is the PDB code of a protein. To calculate pK_a shifts, a different set of reference pK_a values should be used for PropKa, which are 3.8, 4.5, 6.5, and 10.5 for Asp, Glu, His, and Lys, respectively.⁶³⁻⁶⁵

3. Results and Discussion

3.1. Protein pK_a Prediction Accuracy

Unless otherwise noted, the following analyses are based on the test set EXP67S. Nevertheless, pK_a values in EXP67 are displayed too in Figure 3 as background. As illustrated in Figure 3, both RMSD and R values by the proposed DeepKa model (Figure 3a,b) agree with those by the benchmark CpHMD simulations (Figure 3c,d). However, from the linear regression slopes, one can see that the pK_a shifts are underestimated systematically by both DeepKa (Figure 3b) and CpHMD (Figure 3d). In fact, it is the intrinsic error of the GBNeck2-based implicit solvent applied by CpHMD that desolvation penalties are underestimated.³⁷ Now that the present training and validation sets are created by GBNeck2-based CpHMD simulations, it is acceptable that the systematic error of the CpHMD scheme is inherited by deep learning. To get rid of such errors, a more accurate CpHMD approach, like PME-based CpHMD, is demanded.⁵⁰

Figure 3.

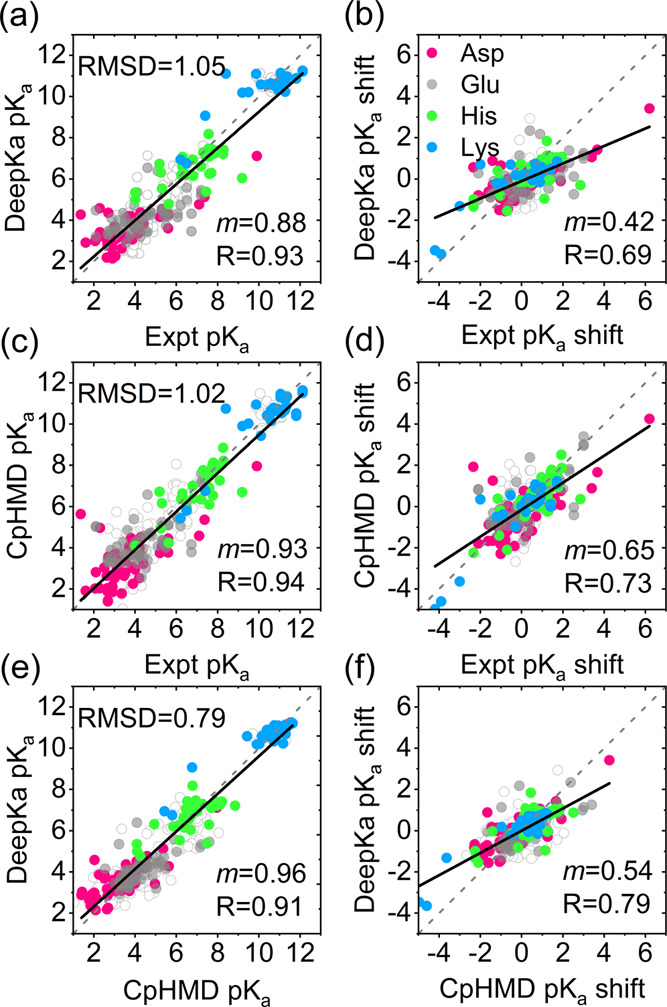
Pairwise comparison of the pK_a’s (a, c, e) and pK_a shifts (b, d, f) from DeepKa, experimental (Expt), and CpHMD simulations (CpHMD). Data for Asp, Glu, His, and Lys residues in the test set EXP67S, the subset of EXP67, are colored pink, gray, green, and blue, respectively. The diagonal (y = x) and linear regression lines are colored gray (dashed) and black (solid), respectively. The open circles are data for the residues in EXP67. RMSD, regression slope (m), and R are displayed.

Notably, the regression slope m by DeepKa (Figure 3b) is 0.23 lower than that by CpHMD (Figure 3d), implying other errors arising from deep learning. Thus, to examine the prediction accuracy of DeepKa with respect to CpHMD, the correlation of pK_a’s or pK_a shifts produced by DeepKa and CpHMD simulations was computed, where the intrinsic error of CpHMD can be canceled out. From the RMSD, m, and R values, one can see that the pK_a’s or pK_a shifts by DeepKa are close to those by CpHMD simulations (Figure 3e,f) than the measured values (Figure 3a,b), which is normal as DeepKa model parameters are established by the pK_a’s calculated with CpHMD simulations. At the same time, these quantities, especially the regression slope m in Figure 3f, still have measurable deviations from the ideal values of 0.0, 1.0, and 1.0 for RMSD, m, and R, respectively, that correspond to two identical data sets.

From the regression slope m in Figure 3f, one can see that the pK_a shifts are generally underestimated by DeepKa when compared with those by CpHMD simulations. As shown in Table 1, four ionizable residue types were examined individually. In addition to the RMSD, R, and regression slope m, mean absolute error (MAE) and maximum absolute deviation (max) are considered too. Now that R and m were calculated for individual residue types, the analyses on pK_a’s are equivalent to those on pK_a shifts. Indeed, as summarized in Table 1, m or R values for Glu are most underestimated by both DeepKa and CpHMD when compared with those for another three residue types. It is found from PHMD252 that 67.1, 81.6, 64.8, and 85.8% of pK_a shifts for Asp, Glu, His, and Lys, respectively, are smaller than 1.0 (Table S1), which might lead to the prediction biased to the reference pK_a’s and therefore reduced correlation with the experiment. According to the solvent-accessible surface area (SASA) calculations of the four residue types in PHMD252,⁶⁶⁻⁶⁸ most are solvent-accessible (Figure S2), which is responsible for the abundance of pK_a’s nearby the reference values. Encouragingly, though the distribution of pK_a’s for Lys is concentrated around the reference pK_a’s, like that for Glu, the measured pK_a downshifts of the three Lys residues that belong to the 3 SNase mutants are captured by DeepKa, resulting in a higher R value of 0.84 for Lys. Noting that the three Lys residues are all highly buried, we suggest that the pK_a downshifts for Lys be dominated by desolvation, which facilitates the learning of large downshifts based on a small sample. Once the three data points are removed, the correlation coefficient for Lys reduces significantly from 0.84 to 0.38. On the other hand, the prediction of pK_a upshifts for Glu is much worse by DeepKa. In contrast to Lys, a buried Glu would involve in a complex hydrogen-bonding network, which leads to pK_a downshift and therefore compensates to some extent desolvation-induced pK_a upshift.²² Concentrated distribution of training pK_a’s around the reference values would result in low sensitivity of DeepKa to the varying protein environment. Thus, more sufficient pK_a’s for the buried residues in the training data set are desired to improve the predicting accuracy. The training and validation sets proposed in this work obey the population of protein pK_a’s in nature. Thus, simply adding protein samples to the training set is not likely to change the distribution of pK_a’s and the resulting accuracy. It is possible to improve the accuracy via manipulating the distribution of pK_a’s in PHMD252 and PHMD27. However, this is beyond the scope of the present work and will be investigated in the future.

Table 1. Comparisons of pK_a Values by DeepKa, CpHMD Simulations, PropKa, and Experiments.

res	MAE	RMSD	max	R	m
DeepKa vs experiment
All	0.81	1.05	3.27	0.69	0.42
Asp	0.79	1.08	2.91	0.74	0.42
Glu	0.94	1.15	3.27	0.54	0.31
His	0.78	1.01	3.15	0.63	0.42
Lys	0.63	0.84	2.71	0.84	0.59
CpHMD vs experiment
All	0.74	1.02	4.27	0.73	0.65
Asp	0.93	1.24	4.27	0.67	0.54
Glu	0.78	1.06	2.94	0.62	0.50
His	0.57	0.80	2.49	0.80	0.77
Lys	0.53	0.72	2.35	0.89	0.91
DeepKa vs CpHMD
All	0.58	0.79	2.55	0.79	0.54
Asp	0.61	0.82	2.55	0.79	0.56
Glu	0.57	0.82	2.30	0.66	0.46
His	0.66	0.83	2.11	0.72	0.49
Lys	0.45	0.66	2.31	0.94	0.65
PropKa vs experiment
All	0.87	1.12	3.66	0.63	0.45
Asp	0.80	1.05	2.96	0.75	0.47
Glu	0.76	1.06	3.66	0.69	0.65
His	1.20	1.44	3.47	0.19	0.08
Lys	0.81	0.95	2.00	0.80	0.50

In addition to CpHMD, the proposed DeepKa is compared with another pK_a predictor PropKa that has become popular due to its high efficiency.⁸ Like DeepKa, pK_a calculations for one protein can be done in seconds by PropKa. From Table 1, one can see that the overall accuracy by DeepKa is higher than that by PropKa. In particular, DeepKa outperforms PropKa on His and Lys. As to Asp, the two methods show similar performances. Nevertheless, PropKa performs better than DeepKa with respect to Glu. As illustrated in Figure S3, PropKa provides an accurate prediction of large pK_a upshift for Glu, while the pK_a shifts for His are underestimated significantly. The results above can be explained by the focus of PropKa development on Asp and Glu.⁸

To further investigate the accuracy and robustness of DeepKa, the histograms of pK_a differences between DeepKa/CpHMD and the experiment have been computed. Data set EXP67 that contains more pK_a values was utilized. As illustrated in Figure 4, the distributions by DeepKa are similar to those by CpHMD. The distributions for Glu, His, and Lys by CpHMD simulations are concentrated around zero, demonstrating the high robustness of the CpHMD model. On the other hand, the distributions for the three residue types are centralized around −0.5 by DeepKa, revealing a systematic error in DeepKa. As illustrated in Figure 4a, such a systematic error is made by CpHMD for Asp, whereas DeepKa gives a more symmetric distribution around zero. Notably, the trend above is consistent with that in Table 1.

Figure 4.

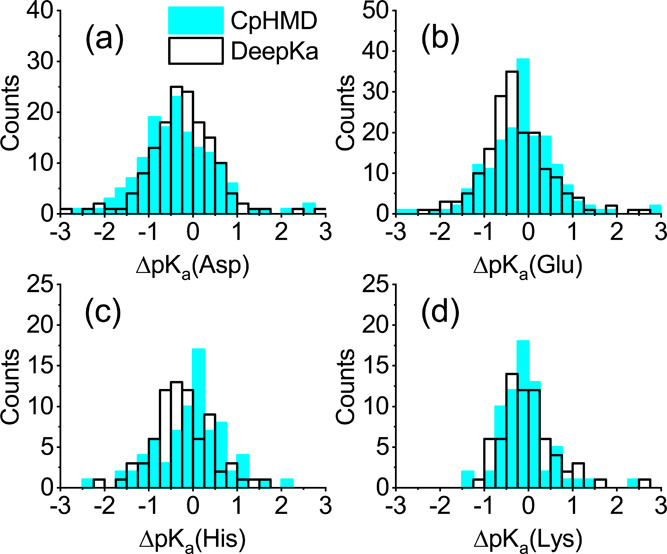
Comparison of the pK_a error histograms for (a) Asp, (b) Glu, (c) His, and (d) Lys by CpHMD simulations (cyan) and DeepKa (black). ΔpK_a is the deviation of calculated pK_a’s by CpHMD/DeepKa from measured values.

From the statistics for PHMD252 (Table S1), one can see that the counts of pK_a values with the absolute shifts larger than 1.0 for Asp, Glu, His, and Lys are 1065, 676, 446, and 454, respectively, where Asp has the most. The training data with large pK_a shifts are indispensable for capturing the diversity of protein environments, which might to some extent explain the robustness of DeepKa for Asp. Now that DeepKa and CpHMD are examined by the same independent set of measured pK_a values, it is possible that DeepKa outperforms CpHMD in some circumstances.

3.2. Validity of Grid Charge Representation

In this work, the atomic charges assigned by force field were substituted by grid charges to represent protein electrostatics, the principal contributor of pK_a shifts.²² As illustrated in Figure 5a, the atoms in the SNase mutant V74K (PDB ID: 3RUZ) are colored based on the atomic charges that are discrete in space. When the atomic charges are distributed over the grid by the B-spline interpolation algorithm, one can see from Figure 5b that the charge density is smoothed.

Figure 5.

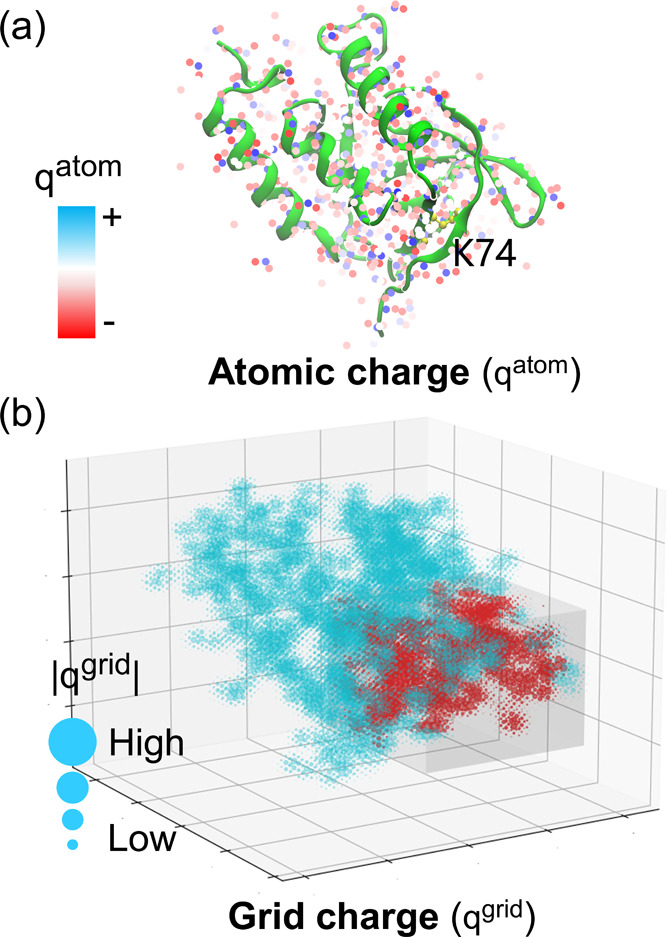
(a) Atomic and (b) grid charge representations of SNase mutant V74K (PDB ID: 3RUZ). (a) Each atom is represented with a point model and colored according to the atomic charge (q^atom) assigned by the Amber ff14SB force field.¹² The side chain of K74 is highlighted with a stick and ball model and colored yellow. The crystal structure is displayed with the NewCartoon model by VMD.⁵⁹ (b) Atomic charges are distributed over the grid with the B-spline interpolation algorithm, where the interpolation order equals 4. A 20 Å cubic box centralized at the side chain nitrogen of K74 is cropped. The grid charges inside the box are colored red. To make the plot clean, the sign is not displayed. The absolute values of grid charges (|q^grid|) are coupled with the radii of circles.

To investigate the validity of grid charge representation, atomic charge representation has been tested. In specific, each atomic charge assigned by the force field was mapped to the nearest grid point. Likewise, the atomic charge-based model was trained, validated, and tested by PHMD252, PHMD27, and EXP67S, respectively. From Figure 6a,b, one can see that the overall accuracy by the atomic charge-based model is similar to that by the grid charge-based model, as illustrated in Figure 3a,b. From Figure 6c,d, one can see that the grid charge-based model reproduces the pK_a’s by the atomic charge-based model, validating the grid charge representation.

Figure 6.

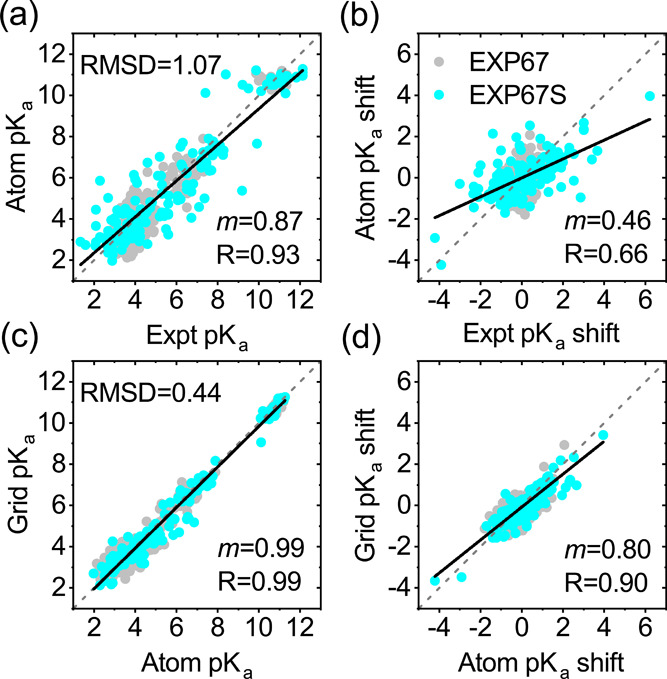
Comparison of the pK_a’s and pK_a shifts (a, b) from atomic charge-based DeepKa to the experiment and (c, d) from grid charge-based DeepKa to atomic charge-based DeepKa. The subset of EXP67, namely, test set EXP67S, is colored cyan. The diagonal (y = x) and linear regression lines are colored gray (dashed) and black (solid), respectively. The gray circles are data for the residues in EXP67. RMSD, regression slope (m), and R are displayed.

3.3. Effects of Cropped Cubic Box Size and Rotation

A cubic box is cropped to express the protein environment of an ionizable residue.³¹ The scope of the protein environment is determined by the box size, whereas the box rotating in the training process is essential for robust prediction upon distinct orientations of a protein. Therefore, it is of importance to test the effects of the box size and rotation on prediction accuracy. In the meantime, the feasibility of the box size of 20 Å as well as the 90° rotation suggested by Stepniewska-Dziubinska and co-workers in their Pafnucy model and employed in the present work can be evaluated. As a result, another two box sizes, namely, 18 and 22 Å, have been tested. As shown in Table 2, the overall accuracy with 18 Å is slightly lower than that with 20 or 22 Å, indicating that nontrivial information has been missed with 18 Å. On the other hand, the performance with 22 Å is no better than that with 20 Å, which means that 20 Å is valid. Next, to examine the effectiveness of 90° rotation, different orientation counts in the training process have been tested. For example, the model was trained with 0° and 180° rotations, which result in 1 and 4 orientations, respectively. Besides, 20 orientations were tested by discarding 4 from the 24 combinations of 90° rotations. From Table 2, it is evident that the overall accuracy increases as the orientation count and converges at 20 orientations, demonstrating that 24 orientations from 90° rotations are sufficient.

Table 2. Performances of DeepKa With Different Orientation Counts (OCs) and Sizes of Cropped Cubic Boxes.

OC	size (Å)	MAE	RMSD	R	m
24	18	0.85	1.11	0.65	0.41
24	20	0.81	1.05	0.69	0.42
24	22	0.82	1.08	0.66	0.41
20	20	0.81	1.09	0.69	0.36
4	20	0.92	1.20	0.58	0.29
1	20	0.92	1.26	0.51	0.20

4. Concluding Remarks

In this work, the training (PHMD252) and validation (PHMD27) sets that include 12809 protein pK_a values in total have been created based on continuous constant-pH molecular dynamics (CpHMD) simulations of 279 soluble proteins. To the best of our knowledge, PHMD252 is the first training data set available for machine learning of protein pK_a’s. Based on PHMD252 and PHMD27, a deep learning-based protein pK_a predictor DeepKa has been established. DeepKa is examined by test set EXP67S that contains 167 measured pK_a’s, most of which are from the PKAD database. Encouragingly, the prediction accuracy yielded by DeepKa is close to that by CpHMD simulations and comparable with that by a fast protein pK_a calculator PropKa, validating DeepKa as an efficient protein pK_a predictor.

The success of DeepKa tells that the protein pK_a data sets created in this study enable future developments of machine learning-based protein pK_a predictors. In the meantime, the training and validation sets PHMD252 and PHMD27 will keep updating to improve the population of high pK_a shifts. Due to the lack of measured large pK_a shifts, currently, the validation set is based on implicit solvent CpHMD simulations, which would hinder the effective adjustment of the hyperparameters. Alternatively, the hyperparameters could be optimized further with the pKa’s calculated by more accurate but less efficient CpHMD models, such as the PME-based explicit solvent CpHMD, which has been implemented in CHARMM.⁵⁰

Instead of previously used atomic charges, grid charges have been proposed to represent electrostatics. The grid charge representation is general and has been applied to the prediction of protein–ligand binding affinity that also requires an accurate description of electrostatics, especially when a ligand is charged (data not published).

Extensive CpHMD simulations performed in this work have verified that, in addition to Asp and Glu, the GBNeck2-based implicit solvent CpHMD offers an accurate prediction of pK_a’s for His or Lys, which is not for sure because of the lack of benchmark proteins in previous research studies.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c05440.

• Supplemental figures and tables including the convergence analysis of pK_a’s by CpHMD simulations, distributions of pK_a’s in data sets, distribution of solvent accessibility, and cross plots by PropKa (PDF)

Author Contributions

^† Z.C. and F.L. contributed equally to this work and are joint first authors. Y.H. conceived, designed, and supervised the study. Z.C. performed CpHMD simulations and wrote the code of DeepKa. F.L. and Y.W. implemented charge spreading in DeepKa. Y.W. performed sequence identity calculations with FASTA. Z.C. carried out data collection and the training, validation, and testing of DeepKa. E.L. performed pK_a calculations with PropKa. Y.H., Z.C., and F.L. analyzed the data. Y.H. wrote and revised the manuscript. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Notes

The code of DeepKa and the relevant data can be downloaded from https://gitlab.com/yandonghuang/deepka.