Phase Change Dispersion Made by Condensation–Emulsification

Abstract

Cooling processes require heat transfer fluids with high specific heat capacity. For cooling processes below 0 °C, water has to be diluted with organic liquids to prevent freezing, with the undesired effect of reduced specific heat capacity. Phase change dispersions, PCDs, consist of a phase change material, PCM, being dispersed in a continuous phase. This allows for using the PCD as heat transfer fluid with a very high apparent specific heat capacity within a specified, limited temperature range. So far, the PCMs being reported in the literature are paraffins, fatty acids, or esters and are used for isothermal cooling applications between +4 and +50 °C. They are manufactured by high shear equipment like rotor-stator systems. A recently published method to produce emulsions by the direct condensation of the dispersed phase into the emulsifier-containing continuous phase is applied on this PCD. n-Decane is used as PCM, and the melting temperature is −30 °C. The achieved apparent specific heat capacity lies above 15 kJ/kg·K, more than 3 times the value of water. This paper presents experimental methods and data, formulation details, and thermophysical and rheological properties of such new PCD. Food conservation or isothermal cooling of lithium-ion batteries is a potential application for the presented method. The properties of the developed PCD were determined, and the successful application of such a PCD at −30 °C has been demonstrated.

1. Introduction

Cooling and tempering are important processes in many industries. Cold can only be supplied while consuming pure exergy within cycling processes. Any temperature in the thermodynamic cycle below the target of the application reduces the efficiency (lower COP). Further, in many applications, cold has to be supplied at the “best temperature”. One reason can be to keep the device being cooled isothermal for reasons like the precision of machine spindles or high-voltage thyristor cooling.^1,2 Another reason is the prevention of damage to the product if the temperatures are too low or too high.

In the food industry, quick freezing of goods is essential for quality. Depending on the application, different temperature levels exist. Temperatures of −30 °C are commonly used to freeze meat and vegetable for storage. The distribution of the cold in warehouses requires thermal fluids with very low freezing temperatures like the water–glycol systems. Compared to pure water, such carrier fluids have lower specific heat capacity (typically only about 60%) requiring higher flow rates and energy consumption. The following work will describe a new thermal fluid that provides at −30° an apparent specific heat capacity exceeding that of water by a factor of 3.

A major part of future mobility will be electric. In comparison to conventional combustion-based propulsion systems, electric vehicles require meticulous thermal management. Batteries and electric components need time-shifted cooling and heating. Further, heating or cooling of the passenger area requires valuable electric energy (exergy), reducing the overall vehicle mileage. Vehicles are exposed to a range of ambient temperatures. Depending on the region they are operated in, this may range from −40 to +50 °C. The low temperature requires water–glycol (or glycerin) systems to prevent freezing, a standard in the present-day automotive industry. Additionally, batteries or electric components are sensitive to conductive coolants.¹ Manufacturers of battery systems are therefore investigating alternatives like low viscosity oils and/or other dielectric liquids. However, any such solution will have specific heat capacities (usually around 2 kJ/kg·K) far below that of water (around 4.2 kJ/kg·K), resulting in higher flow rates, lesser efficiencies, and greater energy losses. Hence, solutions are required where the liquid has a freezing point below ambient temperature (in cold season) and a high specific heat capacity at the desired application, for batteries, e.g., at 25 °C.

Analytical instruments or control devices often dissipate heat and are exposed to fluctuating ambient conditions. Change in temperature of the instrument itself may result in reduced accuracy or even breakdown. In the case of active cooling, the heat transfer fluid in operation should have a high specific heat capacity at the operating range of temperatures.

For all of the above-mentioned applications (and others), phase change dispersions (PCDs) are a potential solution.¹⁻⁴ Phase change dispersions, PCDs, have attracted recent attention on account of their ability to transfer heat within a narrow temperature range with a higher specific heat capacity and heat transfer coefficients compared to water.⁴ A PCD consists of a dispersed phase being an appropriate phase change material, PCM, a continuous phase being immiscible with the PCM and emulsifier to stabilize the dispersed phase. In certain cases, additional ingredients to suppress supercooling are required as well.

Within phase change dispersions (PCDs), the PCM changes its state from liquid (while melted) to solid (while frozen) and therefore the fluid changes from emulsion to suspension; a picture of a typical PCD is shown in Figure 1. A phase change dispersion requires, like all emulsions, a well-balanced emulsifier system. A nice overview may be found in refs (5, 6). As the phase change material shows the effect of supercooling, nucleation agents need to be added to mitigate the effect.^7,8

Figure 1.

System level, flow level, and emulsion level schematics of phase change dispersions.

To prepare a phase change dispersion, the emulsifier is dissolved in one of the two (dispersed or continuous) phases. Both phases are heated up to a temperature above the melting point of all of the ingredients and shear forces are applied until the drop size is small enough and drop size distribution is narrow. Background information may be found in ref (3).

Paraffins are well known for their use as PCM and particularly in PCD. However, at a higher temperature, their vapor pressure and other physical properties are disadvantageous. The applications investigated so far in the literature focus on temperatures above the melting point of water. Many of them are for cooling or air-conditioning purposes.^2,3,5,9,10

However, there is a significant dearth in the literature of PCDs operating at temperatures below 0 °C. To make use of such PCDs, the continuous phase (usually water) must be modified. Chemicals like salts or low-freezing organic materials like glycerin or glycols have to be added. It should be noted that such organic materials do have an influence on the mutual solubility of the PCM. No literature is found on this area until now.

Guha et al.¹¹ reported a new approach to produce small particle size emulsions by a new method that may be referred to as “condensation–emulsification”. The dispersed phase (aqueous) was evaporated and transferred to the continuous phase, already including the emulsifier. The resulting emulsion is a water-in-oil (W/O) type, and the drop sizes are well below 1 μm. This method does not require shear force and corresponding equipment. However, it is required that the boiling temperature of the continuous phase should be significantly higher than that of the dispersed phase (here water), which is the case for many organic oils or PCM. Furthermore, very specific requirements on the emulsifier system and its concentration are needed to ensure cloaking for small drop sizes and narrow particle size distribution.¹¹ Additionally, their system was static and a depletion of the emulsifier at the surface with increasing concentration was observed. Further, most technical emulsions are, however, not of the water-in-oil (W/O) type but of the oil-in-water (O/W) type. And this is in particular for phase change dispersions, where the continuous phase is water and the dispersed phase is the PCM.

In this work, the authors combine the former knowledge to prepare for the first time a phase change dispersion at temperatures below the freezing point of water, namely, at −30 °C. Further, the preparation of such PCD is done by the condensation–emulsification method for the first time of the O/W type. We have opted to use the O/W-type emulsion so that the technique can serve as a modification to the existing propylene glycol-based system currently used for subzero applications instead of introducing an entirely new continuous phase. To overcome the dilemma of the boiling temperature and emulsifier depletion, the process is done under vacuum and condensation is done on a thin liquid film in a packed bed. For property comparison, the PCD is also manufactured by a conventional rotor-stator homogenizer.

2. Materials

Following the goal of using the condensation–emulsification method at temperatures where the continuous phase must be liquid and the dispersed phase (PCM) must have significant vapor pressure, 60% propylene glycol–water mixture (PG60) and n-decane were chosen as the continuous and dispersed phases, respectively. PEG-monooleate was used as an emulsifier.

2.1. Properties of the Dispersed Phase

Technical-grade n-decane (95% purity), which has a melting point of −30 °C, was used as the dispersed phase. The boiling temperatures of this material were measured and compared to theoretical values,¹² as shown in Figure 2. To evaporate the n-decane at reasonable temperatures (∼100 °C), it was maintained at 150 hPa. To allow for the condensation of n-decane on the water–propylene glycol mixture, a pressure of 60 hPa was chosen so that the 60% water–propylene glycol mixture does not evaporate.

Figure 2.

Calculated (lines) vapor pressures of n-decane and water. Comparison with own measurements for technical-grade n-decane.

2.2. Properties of the Continuous Phase

The main component of the continuous phase is deionized water, with an electric conductivity of 0.6 μS/cm. Hence, the function as PCD is only possible with a melting point of the continuous phase to be below −30 °C. Propylene glycol, 1,2-propane-diol, C₃H₆(OH)₂, was used for this purpose. In,¹³ the melting temperature for a mix of 60% propylene glycol in water (PG60) was reported to be below −50 °C.

2.3. Emulsifier System

A low melting effective material was necessary as an emulsifier. A polyethylene glycol (400) oleic acid ester (CAS-9004-96-0), PEG-monooleate, was used. It has a melting temperature of 3 °C and is miscible with water and paraffin. The reported hydrophilic–lipophilic balance (HLB) value is 11.4. Its molecular weight is 460 g/mol (Table 1).

Table 1. Composition of PG60 and the PCD in Mass %.

material	PG60	PCD	refraction index14
water	40	36.4	1.3315
emulsifier, PEG-monooleate		1.8	nm
propylene glycol, PPG	60	54.5	1.4324
PCM, n-decane		7.3	1.4090
total	100	100

The similarity of the refraction index of PPG and n-decane explains why emulsions made on the basis of only water in the continuous phase appear whiter compared to the emulsions made on the basis of water–PPG.

3. Methods and Analysis

3.1. Determination of the Interfacial Tension and Spreading Behavior

Surface tension measurements were done using a Rame’ Hart Goniometer model: the interfacial tension of five systems was measured using the pendant drop method, namely, (i) water (w)–n-decane (o), (ii) 60% propylene glycol and water mixture (pg60)–n-decane (o), (iii) water (w)–air (a), (iv) 60% propylene glycol and water mixture (pg60)–air (a), and (v) n-decane (o)–air (a). Henceforth, the subscripts mentioned above will be used to represent the respective phases.

Interfacial tension measurements were done by varying the concentration of the emulsifier PEG-monooleate (MW = 460 g/mol). In all of the systems, the emulsifier was added to the aqueous phase (w or pg60), which was then suspended as a droplet in decane or air. The variation of the interfacial tension for the various systems is plotted in Figure 3. Here, a 10^–1 M concentration of emulsifier corresponds to a mass concentration of 74% w/w for water and 40.2% w/w for pg60 (Table 1).

Figure 3.

Variation of interfacial tension with the concentration of emulsifier for (a) pg60 and water in n-decane and (b) pg60, water, and n-decane in air. Note that the values for no emulsifier are given in Table 2. (The standard deviation in values is less than 1%.).

Table 2. Nonemulsifier (Pure Substance) Interfacial Tension Value for the Various Systems.

system	interfacial tension (mN/m)
pg60/a	40 ± 0.4
w/a	72 ± 0.7
w/o	43 ± 0.4
pg60/o	19 ± 0.2

There is almost no variation in the interfacial tension of the n-decane and air (o/a) system with the concentration of the emulsifier (being constant around 24 mN/m). This can be explained because both phases (o and a) here are hydrophobic and hence are not stabilized by the emulsifier.⁵ There is a considerable drop in the surface tension for the water–air (w/a) and the pg60–air (pg60/a) systems already with very low emulsifier concentrations. This indicates a stabilization of these interfaces by the emulsifier. For the water–air (w/a) system and pg60–air (pg60/a) system, the CMC is attained at an emulsifier concentration of about 10^–4 M. For the oil–water (o/w) system and pg60–oil (pg60/o) system, the decrease in surface tension at CMC occurs as well around 10^–4 M emulsifier concentration. The drop is much steeper for the water–oil system and the pg60–oil system. Compared to the literature,¹⁵ the value of 43 mN/m is comparably low. This can be explained using a technical-grade decane with a purity of only 95%. For the envisaged application of making a stable and finely dispersed emulsion, the interfacial tension of the pg60/o and w/o systems above their CMC is of particular interest. The interfacial tension drops to very low values, around 1 mN/m, which made the measurements discerning and demonstrate the eligibility of the emulsifier.

For the application being considered in this work, we need to distinguish two possible types of emulsions. The oil-in-water emulsions (o/w), where the continuous phase is water and the dispersed phase is oil, or water-in-oil emulsions (w/o), where the continuous phase is oil and the dispersed phase is water. These emulsions are stabilized with the help of an emulsifier. The two different systems would need two different emulsifiers. Whereas a w/o emulsion will require HLB values below 7, the o/w systems favor HLB values above 10.^5,6

The emulsifier serves two purposes—first, to stabilize the oil/water interface and second, to allow cloaking of one phase by the other, particularly in the case of condensation–emulsification. The emulsifier serves the first purpose by forming a bilayer that reduces the interfacial tension. The second purpose is the wetting behavior, particularly important in the case where the emulsions are formed by condensing one phase on the other. The mechanism of spreading can be understood by looking at the spreading coefficient given by¹¹

1

2

for a water-in-oil emulsion and an oil-in-water emulsion, respectively. Here, S_ij is the spreading coefficient for the spreading of phase “i” over phase “j”, and γ_ij is the interfacial tension between phases i and j. Full spreading occurs when the surface energy of the continuous phase is higher than the combined surface energy of the dispersed phase and the interface of the continuous and dispersed phases (i.e., S_wo, S_ow > 0). Figure 4 shows a schematic of the same for the case of a w/o-type emulsion, as used in Guha et al.¹¹ As soon as the water droplet condenses on the surface of the oil, it is cloaked by the oil. This effect is further enhanced by the emulsifier, and the criterion to look at is the spreading of the oil on water that determines the cloaking of the water droplet. Note that in the case of the water-in-oil emulsion, the emulsifier is added to the oil and hence the interfacial tension of the water/air interface is independent of the emulsifier concentration. In the system dealt with in this paper, we are looking at the formation of an oil-in-water emulsion. Hence, we would be looking at effective cloaking of the oil drop by water (S_ow > 0) to form an emulsion. Here, the variation of the water–air interfacial tension with emulsifier concentration is taken into account while calculating the spreading coefficient.

Figure 4.

Spreading of the oil phase over the water droplet in the case of a water-in-oil emulsion made by condensation–emulsification.

In the case where the conditions are unfavorable for complete cloaking (i.e., S_ow < 0), we can look at the three-phase contact angles to gauge the extent of cloaking. Figure 5a shows a schematic of the three-phase contact angles. These are given by

3

4

where θ₁ and θ₂ are defined in Figure 5a. The different behaviors for the different angles are also shown in Figure 5. When both θ₁ and θ₂ go to 0, it results in complete spreading. On plugging these into eqs 3 and 4, we can obtain the criteria S_wo > 0 and S_ow < 0 for complete spreading. When θ₁ goes to 0 while θ₂ goes to 180°, it results in complete cloaking. On plugging into eqs 3 and 4, this simplifies to the conditions S_ow > 0 and S_wo < 0. These are shown in Figure 5b. However, in the case where both S_ow and S_wo are negative, several possibilities arise that are shown in Figure 5c.

Figure 5.

(a) Schematic of the three-phase contact angles for the oil–pg60–air interface. (b) Criteria for fully spreading and cloaking cases. (c) Intermediate cases of a three-phase contact angle when S_ow, S_wo < 0.

3.2. Mixing and Dispersing

To assess the quality of the condensation–emulsification, a standard shear-based system was applied as well. A Polytron 10-35 GT lab rotor-stator homogenizer from Kinematica, Switzerland, was used for dispersing the PCM phase into the continuous phase. The outer diameter of the rotor rim is 26 mm, and the inner diameter of the outer stator rim is 26.5 mm. The shear rate was varied, and a setting of γ̇ = 50 000 1/s (9200 rpm) and a dispersing time of 5 or 20 min were applied.

3.3. Thermal Analysis with Differential Scanning Calorimetry (DSC)

Differential scanning calorimetry (DSC) was used to measure the phase change enthalpy and melting temperature range. An 823e DSC from Mettler Toledo based on heat exchange calorimetry was used. The typical sample size was 10–15 mg, and a heating rate of 2 K/min was applied. The experimental uncertainty in the determination of latent heat and specific heat capacity is less than 1%.

3.4. Particle Size Distribution

A Beckman Coulter LS 13320 with polarization intensity differential scattering (PIDS) and laser diffraction was used. The measuring range lies between 0.04 and 2000 μm, and typical particle sizes were expected to lie between 500 nm and 5 μm.

3.5. Rheology

An MCR 302 Anton Paar Rheometer with a cone-and-plate (20 mm) geometry was used to measure dynamic viscosity. Two measured series were executed for the sample: at 20 °C, the shear rate was varied between 1 and 200 1/s, and at a shear rate of 100 1/s, the temperature was varied between 0 and 28 °C. The value at 20 and 100 1/s was used for checking the consistency of the two series. The uncertainty in measurements is ±3%.

3.6. Apparatus for Condensation–Emulsification

As outlined in the Introduction section, a “continuous” process is required to prevent depletion and a thin film system to create drop formation. To realize the experiment at reasonably low temperatures accounting for the vapor pressure of n-decane, vacuum needs to be applied. The schematic of the setup is shown in Figure 6, with details listed in Table 3.

Figure 6.

Left: schematic of the setup. Right: photo of the apparatus. Top right: details of the inlet connector before thermal insulation. The emulsion is collected at the outlet of the packed column.

Table 3. Parameter in Test Setup for Condensation–Emulsification.

item	description
1	reservoir, filled initially with 42 g of n-decane, boiling at about T = 110 and 90 °C, at p = 150 mbar, resp. 60 mbar
2	stirrer and heater, T = 130 °C, resp. 110 °C
3	packed column, glass beads, diameter = 3 mm, column inner diameter = 20 mm, filled height = 175 mm, volume = 55 mL
4	reservoir filled initially with 160 g of aqueous phase, kept at 5 or 20 °C temperature
5	centrifugal pump, flow rate = 1 L/min
6	vacuum membrane pump, p = 150 mbar, 60 mbar

3.7. Application Test

To verify the function of a PCD at −30 °C for the purpose of cooling, a comparison test between PG60 and PCD was performed. A certain amount of fluid was placed on a Petri dish with an initial low temperature of −40 °C. The bottom and side of the Petri dish were insulated, while the top side is exposed to the ambient air at 23 °C. The temperature of the fluid was logged vs time, and an IR camera monitored the temperature optically (Figure 7). The results are discussed in the next section (Table 4).

Figure 7.

Schematic for the application test.

Table 4. Test Setup for Application Test: (3) Insulation, (2) PCD or pg60, (1) Ambient Air, and (4) IR Camera.

item	description
1	air at ambient temperature is flowing by free convection into a chamber at 23° for heating
2	a Petri dish with PG60 or PCD with a thickness of 10 mL initially –40 °C is placed on the insulation. At this temperature, the PCD is “loaded”, which means the PCM is in solid state
3	insulation for an adiabatic boundary condition
4	infrared camera

4. Heat Transfer within a PCD

4.1. Specific Heat Capacity

For a PCD, the “apparent” specific heat capacity combines the sensible heat of all involved liquids and the latent heat. To account for both sensible heat and enthalpy of fusion (melting) during the melting process, an apparent heat capacity can be calculated.

Melting will never occur at exactly one certain temperature. The melting temperature range (mtr) depends on different parameters, as discussed in ref (15). Therefore, it must be taken into account that the considered temperature range, ΔT_c, of the application could be larger or smaller than the melting temperature range, ΔT_mtr, of the PCM. It shall be noted that the sensible heat of the PCM is included within the latent heat for the phase change, Δh_m,mtr. As derived in ref (15), this result is a reduced (considered) melting enthalpy Δh_m,c, which can be expressed as follows

5

where Δh_m,c (ΔT) is the true exploitable latent heat and

6

is an approach ref (15) for the part c_r of the totally available latent heat Δh_m,mtr. In case the considered temperature range is larger than the melting temperature range ΔT_c< ΔT_mtr, the factor c_r becomes 1. For many technical applications and considering fluctuations in temperature controls, the applied temperature range is about the order of the melting range ΔT_c = ΔT_mtr and lies around 3–5 Kelvin. If the mass content of the dispersed phase ψ in the PCD is defined as

7

and c_r = 1, the apparent specific heat capacity for a PCD, c̅_P,PCD, can be calculated according to eq 8

8

Quantitative results of the expression above for different temperature ranges with values from Table 7 are shown in Figure 8a. As Figure 8a implies, high content of dispersed phase is desired to use the latent heat of fusion, thereby increasing the heat capacity of the PCD. Also, it is of advantage to distribute this latent heat across a smaller temperature range.

Table 7. Comparing the Thermophysical Properties of PCM, PCD, Water, and Water–Propylene Glycol.

property		unit	n-decane14	water14	PG6014	PCDw	PCDpg60
specific heat capacity at 25 °C	cp	kJ/kg·K	1.70	4.19	2.32	3.69	2.20
density at 25 °C	ρ	kg/m3	902	997	1051	988	1012
latent heat	Δhpc	kJ/kg	197	333	93	32	13
heat conductivity at 25 °C	k	W/(m·K)	0.23	0.61	0.22	0.529	0.39
viscosity at 100 1/s at 20 °C	η	mPa·s	solid	0.9	29.5	3.1	17.0

Figure 8.

(a) Apparent heat capacity c̅_P,PCD in dependence on the mass content of the dispersed phase according to eq 8, applying values from Table 7. (b) Viscosity of the PCD_w as a function of the content of the dispersed phase, measured at 20 °C and at a shear rate of 100 1/s. (c) Capacity increase factor (according to eqs 13 and 15) for laminar and turbulent flows, with data from Table 7 combining the information from panels (a,b).

4.2. Viscosity

With the increasing content of the dispersed phase, the viscosity of the PCD increases. PCDs are non-Newtonian fluids. Its apparent viscosity is a complex function of shear rate, the content of the dispersed phase, and temperature (liquid or solid PCM). In ref (1), detailed information on this behavior is described. For the purpose of assessment of the increase in the content of the dispersed phase, a single curve at a constant shear rate shall be the basis, as depicted in Figure 8b. Heat transfer fluids with viscosities above 100 mPa·s are not appropriate in practical applications.^16,17 Already, from Figure 8b, it can be seen that the mass content of the dispersed phase will always be below 40%.

4.3. Capacity Increase Factor

The 60% water–propylene glycol (PG60) mix is the benchmark for the PCD in the application at −30 °C. Low viscosity and high specific heat capacity guarantee a good trade-off between pressure drop to heat capacity flow rate. However, the case of low melting PCD has remarkable high viscosities already for the continuous phase. The difference of viscosities of pure water to a PCD without propylene glycol is therefore the more illustrative one and shall be elaborated in the following.

To assess the situation of a heat transfer fluid with or without PCM, the assumption of an identical pressure drop shall be made. To illustrate the situation, the simple and descriptive laminar pipe flow case is described first. The laminar flow is a worst-case scenario (for the PCD) as the pressure drop is linearly dependent on the viscosity.

Pressure drop, Δp, in a laminar pipe flow

9

where η is the viscosity, v is the velocity, L is the length of the pipe, and d is the diameter of the pipe. Equating the pressure drop of PCD and water–propylene glycol (pg60) yields

10

Using the fact that

11

where ṁ is the mass flow rate, V̇ is the volume flow rate, ρ is the density of the fluid, and A is the area of cross section. The heat capacity flow rate is defined as the product of mass flow and specific heat capacity. The ratio C of the two cases of PCD or only water–propylene glycol as a possible figure of merit is defined as the heat capacity rate of PCD over water–propylene glycol

12

and finally using the fact that ρ_PCD ≈ ρ_wg for small ψ and for the case of laminar flow

13

This equation illustrates for the simple case of laminar pipe flow that any gain in capacity due to the content of PCM has to be evaluated against the unfortunate increase in viscosity in a linear manner.

In heat exchangers, laminar flow is usually not applied as heat transfer rates are poor. In this case, a simple equation for the pressure drop in the turbulent pipe, valid for microencapsulated PCM as derived from ref (1), shall be applied in a simplified form (based on the original form from Blasius)

14

where Re is the Reynolds number. Following the same procedure as for laminar flow, the capacity increase factor for turbulent flow is now

15

The increase in viscosity of a PCD is less critical for turbulent flow than it is for laminar flow though.

Combining the data and evolution of heat capacity and viscosity with increasing content of dispersed phase, the capacity increase factor as a function of the applied temperature range ΔT_c for the situation of laminar flow and turbulent flow is depicted in Figure 8c.

There is an optimum of the content of dispersed phase that lies between 10 and 20%. The lower the applied temperature range for the heat transfer is (3 instead of 5), the higher is the gain. A capacity increase of 100% and more at turbulent flow conditions is feasible and proves the high potential of this class of heat transfer fluids. Loading the PCD with higher values of the dispersed phase content, e.g., 40 or 60%, may be useful in case the storage function is of importance; however, for heat transfer, the viscosity increase will result in a drop in performance.

4.4. Melting of an Ideal Sphere

To address the heat exchange during a cooling application with a PCD, it will be necessary to consider

• (a)Melting of a PCM sphere at the particle level.
• (b)Heat transfer from the continuous phase to the particle (dispersed phase).
• (c)Heat transfer from the PCD to/from the wall of the heat exchanger.

The mathematical description of the melting process occurring in a material during heating is well known as the Stefan problem.¹⁸ Solutions are generally obtained by solving the heat conduction equation in both phases and specifying the Stefan condition at the interface between the liquid and solid. The Stefan condition results from a simple energy balance on the infinitesimal volume that undergoes the phase change and merely represents the physical fact that the phase change enthalpy released or absorbed is equal to the heat flux in or out of this infinitesimal volume.¹⁸

There are various approximate analytical solutions for simplified geometries, one of which is called the quasi-stationary approach.^19,20 If the sensible heat within the melting part is negligible compared to the latent heat, the transient part of the heat conduction equation cancels out. If additionally all properties are assumed to be approximately constant and if there is no heat generation within the melting part, the analogy of thermal resistance can be used to obtain the heat flux. For engineering practices, this approximation is known to give good results for Stefan numbers St = c_pΔT/Δh < 1/7.¹⁹ It is therefore acceptable for the PCM in question to consider temperature differences between the two phases of up to 6 K.

In the following section, the quasi-stationary approach discussed above is applied to the general case of a spherical PCM particle being encapsulated. Should the particle be nonencapsulated, as it is the case for the presented PCD, the thickness of the shell can be simply set to zero. However, it may be useful to have the complete derivation as the microencapsulated PCM is discussed widely. It also delivers the information needed to assess the increase in thermal resistance due to an eventual polymeric shell.

In addition to the assumptions mentioned above, the following is required as outlined in ref (19). The equations become less convoluted by assuming that the temperature ϑ_E of the PCM particle core is assumed to be constant while melting. The same assumption applies to the outside temperature ϑ₀ of the continuous phase. Furthermore, only one mean density for the dispersed phase is considered

16

In Figure 9a, the principle setup is illustrated, where an encapsulated PCM particle is melting. The outer layer is liquid, whereas some part of the core is still solid. The melting front is moving from the shell to the center of the sphere. The overall thermal resistance for this specific case includes convection around the particle surface (wall or shell), conduction through the encapsulation material (with thermal conductivity k_W) of thickness δ_W, and conduction within the melted PCM. Natural convection inside the melted PCM is neglected. During melting or freezing, the interphase between the liquid and solid is moving inwards. The growth of the melted or solidified region is represented by the layer thickness (position) s in the interval 0 ≤ s ≤ R.

Figure 9.

(a) Spherical PCM particle with an outer layer δ_W (encapsulated PCM), an inner solid core, and an outer liquid (melted) layer. The case of melting is depicted. (b) Melting PCM particle. The PCM is heated up, and the melting front moves in the opposite direction of r. The layer thickness s indicates the melted region. (c) Melting times for varying particle sizes and Nusselt = 2 based on the thermophysical properties of a PCD according to Table 7. The assumed temperature difference between the core and surrounding is ΔT = 1 K. The dot illustrates the time when the melting front s arrived at the center of the particle and the particle is entirely melted.

In Figure 9b, a more detailed picture of the situation at the melting region (s and ds) is shown. The energy absorbed in an infinitesimal element ds that undergoes the phase change is given by the expression

17

Furthermore, the heat transfer rate due to the temperature difference ΔT between the surrounding (ϑ = ϑ_O) and the interface where the phase change occurs (ϑ = ϑ_E) is given by the equation

18

By combining these two equations and integrating the resulting expression, the time as a function of the melted thickness s, t(s) can be calculated (in some cases analytically) by integration

19

R_th denotes the overall thermal resistance between the core temperature and the dispersed phase and is defined for a spherical geometry by

20

h: heat transfer coefficient for the convective heat transfer outside the shell.

k_W: the heat conductivity of the wall/shell.

k_PCM: the heat conductivity of the PCM alongside the inner side of the shell. It will be the k_PCM,l in case of melting.

The term A(s) represents the time-dependent surface of the boundary layer where the PCM-phase change occurs

21

Finally, differential eq 18 ends up as eq 22 with its general solution given by eq 23. All of the equations are valid for both the melting and solidification process when k_PCM is substituted by k_l,PCM and k_s,PCM, respectively

22

23

Depending on the properties and assumptions, different cases can be distinguished. Assuming

24

For the general case, we have

25

With 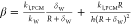. Similarly, for the nonencapsulated particle (δ_W = 0), we have

26

With . An important unknown in expression eqs 25 and 26 for the melting time is the value of the outside heat transfer coefficient h

27

Using the PCD as a heat transfer fluid implies the assumption that the continuous phase and dispersed phase move at an identical velocity (low Stokes numbers).²¹ Hence, even though the liquid is flowing at a high overall velocity and most probably under turbulent conditions, the assumption for a “worst case” in terms of lowest heat transfer can be made that the relative velocity of the dispersed phase to the continuous phase is close to zero.

In this case, the analytical solution for quasi-stationary heat conduction of a sphere with Nusselt number = 2 may be applied, resulting in

28

For small particles on the order of magnitude below 1 μm, the calculated heat transfer coefficient can reach several hundred thousand W/(m²·K)! A well-known effect as, e.g., exploited in spray drying. It therefore can be assumed that the thermal resistance in a “worst-case” scenario lies just within the particle itself or at the boundary layer of the heat transfer fluid with the heat exchanger wall (Table 5).

Table 5. Maximum Biot Numbers for Fully Liquid Particles and Properties According to Table 7.

Nu	Bi
0.001	0.0004
0.01	0.0036
0.1	0.0356
2	0.7107

To further assess the determining resistance, the Biot number may be written (here for the case of melting)

29

At Bi numbers above 1, the resistance can be considered as mainly within the sphere. The outside heat transfer coefficient does not have to be considered therefore and assuming the minimum Nu = 2 leads to a simplification of β in eq 26

30

At high Nusselt numbers (2 would already be high!), the heat transfer into the particle is only limited by the conduction within the dispersed phase, which is determined by the amount of melted material. From the engineering point, it can therefore be assumed that Nu > 2 and all resistance for the heat transfer lies within the PCD particle. The calculated melting time for the particles has to be compared to the typical exposure time of the PCD to the heat/cold source. Ideally, the melting time is shorter than the exposure time to melt all PCM particles completely and thus achieve a significant cooling effect.

As shown in Figure 9c, the melting times for typical particle sizes within the μm region lie below 0.25 ms. Therefore, even for very fast cooling applications such as impinging jets, the feasibility of a PCD should be promising.

5. Experimental Results and Discussion

5.1. Interfacial Tension Cloaking and Spreading Behavior

From the interfacial tensions measured for our systems (Figure 3), the spreading coefficients (eqs 1 and 2) were calculated for a water-in-oil (w/o), water-in-pg60 (w/pg60), oil-in-water (o/w), and an oil-in-pg60 (o/pg60) emulsion as a function of the emulsifier concentrations and are shown in Figure 10. Note that a value of S > 0 is required for cloaking, which is the essential mechanism to form a dispersion by condensation–emulsification. Note that while calculating the spreading coefficients for o/w (or) o/pg60 emulsions (using eq 1), we need to take into account the variation of the interfacial tension of the w/a (or) pg60/a interface. This is because the interfacial tension of w/a (or) pg60/a is dependent on the concentration of the emulsifier (as seen in Figure 3). For the w/o and pg60/o emulsion formation through condensation–emulsification, the emulsifier is added to the oil and hence does not affect the w/a (or) pg60/a interface.

Figure 10.

Variation of the spreading coefficient with the emulsifier concentration. Immediate spreading occurs for S > 0, resulting in contact angles of 0°. For S < 0, only partial spreading occurs (SD < 1%).

It can be seen here that beyond the critical micelle concentration (CMC), the spreading coefficients are favorable for the formation of water-in-oil (w/o) and pg60-in-oil (pg60/o) emulsions by cloaking with the condensation–emulsification method. On the other hand, the water-in-oil (w/o) and pg60-in-oil (pg60/o) spreading coefficients are negative or very close to zero for concentrations beyond the CMC, indicating that we have to look at the contact angles to understand the spreading behavior more thoroughly. At lower emulsifier concentrations, the formation of all emulsions (o/w, o/pg60, w/o, and w/pg60) is unfavorable.

Contact angles are plotted in Figure 11 for the case of the oil-in-water (o/w) and oil-in-pg60 (o/pg60) emulsions from the interfacial tension values shown in Figure 3 using eqs 3 and 4. The schematic in Figure 11 (inset) shows the two angles calculated using eqs 3 and 4. It represents the angles made by a drop of oil with the water–air or pg60–air interface on either side. Ideally, for complete cloaking, θ₁ must go to zero and θ₂ must tend to 180°. It can be seen in the case of oil-in-water (o/w) emulsions that the contact angle, θ₁, tends to zero and θ₂ tends to higher angles, indicating a possible cloaking-like behavior at very high emulsifier concentrations. The contact angles (both θ₁ and θ₂) in the case of oil-in-pg60 emulsions tend to zero, indicating a fully spreading behavior. The condensed oil will form a film and spread and will not form a drop that is cloaked.

Figure 11.

Variation of the contact angle of an n-decane drop on water/pg60 with variation of the emulsifier concentration in the water/pg60 (SD < 1%).

This indicates that in the case of condensation–emulsification the mechanism of droplet formation is different for the two cases: o/pg60 (our work) and w/o (as presented in ref (11)). For the case of w/o emulsions, the condensation of water droplets combined with cloaking of the water phase by (emulsifier-containing) oil phase in air causes the formation of the emulsion. This would not be possible in the case of o/pg60, as the oil prefers the air interface more than the pg60 does, and this would have led to film formation instead of cloaking.

To further understand the cloaking and spreading behavior, the emulsifier concentration in both the decane and the water was varied. A 1 μL drop of decane was added to a bath of water, and the resulting behavior was observed.

The decane droplet is seen to be most spreading at an emulsifier concentration of 1 × 10^–5 to 1 × 10^–4 M. Above this concentration, the interfacial tension of the water–oil interface reduces drastically, and the system prefers a cloaking state. This can be observed by noticing the distance of the spread of the decane drop on water at different concentrations of the emulsifier, as shown in Figure 12. This closely corresponds to the contact angle measurements in Figure 11.

Figure 12.

Spreading of a decane droplet on water is shown for different concentrations of the emulsifier.

Based on similar reasoning, it would be expected that the o/pg60 system would show a spreading behavior at a higher emulsifier concentration. This would result in the formation of a film of decane on the pg60. However, similar measurements could not be done for the decane–pg60 system (putting a decane drop onto pg60) as the drop boundary was not clearly visible due to similar refractive indices and vapor-mediated phenomena. Figure 13a shows the time lapse of such a vapor-mediated phenomenon when 1 μL of decane is dropped in a pg60 + emulsifier (5 × 10^–2 M) bath. Figure 13b shows similar vapor-mediated phenomena but on a borosilicate glass slide (such bursting is not observed when there is no emulsifier).

Figure 13.

(a) Left, the time lapse shows the bursting seen when a decane drop lands on a bath of PG60 + emulsifier. (b) Top right shows vapor-mediated interactions between a decane drop and PG60 + emulsifier drop on a glass slide.

An additional factor to consider is the solubility of the emulsifier in pg60. This could lead to an Ouzoo effect type of breakage enhanced by the vapor-mediated interactions. Figure 14 shows the solubility of the emulsifier in decane, water, and pg60. It is clear that the emulsifier phase separates at concentrations above 1 × 10^–3 M in pg60 and 1 × 10^–2 M in water. The emulsifier is soluble in decane in all proportions, as seen in Figure 14c. It seems like a combination of these phenomena could contribute to the break-up of the film.

Figure 14.

Solubility of the emulsifier in PG60, water, and decane at different concentrations.

5.2. Flow-Induced Breakage of Decane Film and Final Particle Size Distribution of the Emulsion

To force the breakage of the film, we set up a flow of the pg60 through a packed bed of glass beads (refer to Figure 15a for a schematic; the actual setup is shown in Figure 6). A film of about 1 mm thick pg60 + emulsifier was rinsed through the trickled bed system. It was ensured that the entire glass column was wet by the pg60 + emulsifier and that the film was thick enough so that the decane does not displace the pg60 from the glass. Figure 15b shows the variation of the contact angle of pg60 on a borosilicate glass slide in the presence of n-decane with varying concentration of the emulsifier. It can be seen that at higher emulsifier concentrations, the n-decane wets the glass more than the pg60. Therefore, a thick enough film of pg60 must be present prior to the evaporation and condensation of n-decane to avoid this scenario. Once this was done, the n-decane was vaporized and allowed to form a thin film on the pg60 film. Due to the flow of the film through the porous constrictions, the n-decane film is broken up into droplets and the decane is forced into the bulk forming an emulsion. All of the flow conditions used in the experiment are listed in Table 6. Figure 15c shows the particle distributions obtained for different evaporation conditions (shown in Table 6).

Figure 15.

(a) Schematic of the formation of the emulsion through flow. (b) Contact angle of the PG60 + emulsifier on a borosilicate glass slide in n-decane at different emulsifier concentrations. (c) Particle size distribution for the emulsion obtained from different methods.

Table 6. Experiments and Specific Parameters According to Figure 15c.

identifier	description	technical conditions
cond.-emuls.	condensation–emulsification of n-decane into an aqueous phase, containing an emulsifier.	p = 150 mbar, Tevap = 110 °C, Tcond = 5 °C, evaporation time of 10 min
		p = 60 mbar, Tevap = 90 °C, Tcond = 20 °C, evaporation time of 30 min
rotor stator	emulsification by rotor stator, n-decane was added to the aqueous phase containing the emulsifier	rotor stator, t = 5 min, shear rate = 20 000 1/s
high shear	the dispersion was made with a specific high energy input in both terms of time and shear rate to evaluate the possible minimum particle size	rotor stator, t = 20 min, shear rate = 50 000 1/s
PCDwg	the continuous phase of the PCD contained water and propylene glycol (PG60) plus emulsifier	water/propylene glycol = 40:60
PCDw	the continuous phase of the PCD contained only water plus emulsifier

Particle size distribution was measured for the experiments on condensation–emulsification with the setup, as shown in Figure 15c, as well as for the experiments with a rotor-stator unit, as described in Section 3.2. The experimental conditions are summarized in Table 6. It can be seen that the mean particle size distribution is shifted to larger drops at higher pressures. This could be explained by the fact that the evaporation rates are faster at higher temperature and pressure, causing the formation of a thicker film and thereby larger emulsion particle size. The primary goal of this work was to understand the mechanism and to invent a method of dispersing without any mechanical shear forces. Further studies need to be done to understand the dependence of the particle size on different parameters pertaining to the flow. Such investigations may be useful for many applications of w/o emulsions.

5.3. DSC of n-Decane and PCD

In the following, the measured DSC of technical-grade n-decane (Figure 16) and the PCD was obtained during the manufacturing with a rotor stator. Please refer to Table 7.

Figure 16.

(a) DSC measurement of PCD. The theoretical value of the capacity is 0.0727 ×197 kJ/kg = 13.4 kJ/kg. (b) DSC measurement of pure n-decane. Measured values fit to literature data.

5.4. Thermophysical Properties

The properties of the materials used are listed in Table 7. The properties were either derived from the literature or measured with the devices as described in Section 3.

5.5. Cooling Effect

On exposing the PCD (with the same composition as in Table 1) to ambient air at 23 °C and observing the cooling through temperature measurements and IR imaging, it can be seen clearly that in the range of operation (−35 to −25 °C), the apparent specific heat capacity of the PCD is higher than that of the water–propylene glycol (pg60) system. This is shown in Figure 17. This proves the effectiveness of the system for our applications. The IR thermograph clearly shows a longer residence at a temperature of around −30 °C in the case of the PCD.

Figure 17.

Left: the variation of the temperature with time for the PCD and plain water–propylene glycol when exposed to the ambient. Right: the IR image of the Petri dish at time 200 s containing the specimen exposed to the ambient.

6. Conclusions and Outlook

In this research, we have successfully manufactured and demonstrated a phase change dispersion (PCD) for subzero applications (−30 °C). For this phase change dispersion, we chose n-decane as the phase change material (PCM) and a mixture of water and propylene glycol as the carrier fluid (dispersed phase). The PCD therefore qualifies as an oil-in-water emulsion. Further, we manufactured the phase change dispersion using both condensation–emulsification and rotor-stator homogenizer. It was observed that the particles obtained from condensation–emulsification were of a similar size as those obtained from rotor-stator homogenization (∼1 μm). To better understand the mechanism of PCD formation through condensation–emulsification, we measured the interfacial tension and calculated the spreading coefficients for oil-in-water emulsions. We concluded that the mechanism of formation was not due to cloaking but was due to film formation and subsequent breaking. Further studies will focus on identifying the exact mechanism of the formation of the PCD.

We modeled the apparent specific heat capacity and viscosity of the PCD for different mass fractions of the PCM and found that although the apparent specific heat capacity increased with the percentage of n-decane, the viscosity also increased with higher loading of the n-decane. These counteracting effects caused the capacity increase to max out at around 20% mass fraction of the PCM for turbulent flows. We also modeled the melting time for the PCM using the quasi-stationary approximation to the Stephan problem. It was concluded that particles in the μm size range melted in a few milliseconds, therefore making the PCD applicable for fast cooling jets. DSC measurements for the PCD showed a peak heat capacity at −29.7 °C. Further, the apparent specific heat capacity of the PCD was above 15 kJ/kg·K, which is more than 3 times that of water. Finally, on leaving the PCD and PG60 to ambient cooling, it was seen that the PCD was able to hold the temperature of −30 °C for almost 5 min! This was visualized using an IR camera.

It is, therefore, possible to create PCD for applications below 0 °C with organic PCM and an aqueous continuous phase by adding organic matter like glycols. As pure glycol may dissolve most of the organic PCM, there may be limitations to this method for lower temperatures or other PCMs. Further, in the next iteration, we would look at water-free PCD where the continuous phase is nonaqueous. These could find use in thermal management for batteries due to their nonconductive and dielectric nature. Future work will also look at the long-term stability of the emulsions and effective ways to re-emulsify these PCDs.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The project was executed without external funding.

The authors declare no competing financial interest.