Abstract
The pure component properties are estimated for active pharmaceutical ingredients that are related or proposed for the treatment of severe acute respiratory syndrome-CoronaVirus-2. These include Baricitinib, Camostat, Chloroquine, Dexamethasone, Hydroxychloroquine, Fingolimod, Favipiravir, Thalidomide, and Umifenovir. The estimations are based on group contribution+ (GC) models that contain combined group contribution and atom connectivity index with uncertainties in the estimated property values. The thermodynamic properties that are reported include boiling point, critical temperature, critical pressure, critical volume, melting point, standard Gibb's energy of formation, standard enthalpy of formation, enthalpy of fusion, enthalpy of vaporization at 298 K, enthalpy of vaporization at boiling point, entropy of vaporization at boiling point, flash point, Hildebrand solubility parameter, octanol/water partition coefficient, acentric factor, and liquid molar volume at 298 K. The reported properties are not available in the literature and thereby is an incremental development for reliable process engineering.
Keywords: Thermodynamic Estimations, Active Pharmaceutical Ingredient, COVID-19, Pure Component Properties, Group Contribution Method
Abbreviation: , normal boiling point; , critical temperature; , critical pressure; , critical volume; , normal melting point; , standard Gibbs energy of formation; , standard enthalpy of formation; , normal enthalpy of fusion; , enthalpy of vaporization at 298 K; , enthalpy of vaporization at the normal boiling point; , the entropy of vaporization at the normal boiling point; , flash point; , auto-ignition temperature; δDδPδH, Hansen solubility parameters; , Hildebrand solubility parameter; , octanol/water partition coefficient; ω, acentric factor; , liquid molar volume at 298 K
1. Introduction
The Global Pandemic COVID-19 also known as Severe Acute Respiratory Syndrome-CoronaVirus-2 (SARS-CoV-2) has affected the entire world. The pandemic has involved clinicians around the globe to put in an unprecedented effort to develop a better healthcare system. To date, the World health organization (WHO) has issued an emergency use listing for the Pfizer COVID-19 vaccine (BNT162b2), AstraZeneca/Oxford COVID-19 vaccine, and Ad26.COV2. S (Johnson & Johnson). The other includes Sputnik V (Russia), Covaxin (India) Corovac (China), Sinopharm (China), Kexing (China), and Moderna (USA). Ramdesivir has been approved by FDA and has shown clinical evidence for specific treatment against SARS-CoV-2 [1]. Furthermore, the different vaccines are being underdeveloped around and are at various stages of trials. This pandemic as of November 2021, has resulted in 261,926,070 confirmed cases with 5220, 328 deaths, and 236,538,716 recovery cases, while among the active cases, 20,038,269 cases are in mild condition and 83,757 cases in a serious or critical condition [2]. Apart from the vaccine, the treatment of the patient by physicians are mainly dependents on the symptom they possess and for the critically ill patients, mainly oxygen therapy or ventilator support is provided. The drugs/ active pharmaceutical ingredient (API) that are presently used or in combination for the treatment of mild symptoms are hydroxychloroquine [3], chloroquine [4] combination of are hydroxychloroquine and azithromycin [5], remdesivir [6], [7], lopinavir [8], [9] and ritonavir [10]. The candidate drugs in combination are still in clinical trials to combat COVID-19 by various pharmaceutical companies. Likewise, antimalarial drugs such as chloroquine by Sanofi (Aralen) and hydroxychloroquine by CaoSanofi (Plaquenil); Mylan, Teva, Novartis, Bayer, Rising Pharmaceuticals. While the antivirals to combat COVID-19 are Remdesivir by Gilead Sciences; Favipiravir by Fujifilm Toyama Chemical and Umifenovir by Pharm standard. The other drugs such as Baricitinib by Concert Pharmaceuticals, Inc., USA; Dexamethasone by the University of Oxford; Phase-II/III) and fingolimod by Fujian Medical University/Novartis; the clinical stage is presently developed to combat COVID-19.
Once the aforementioned drugs are clinically approved, there will be a requirement of their bulk scale production which in turn requires their physical and chemical thermodynamic properties data set. This data is useful for chemical/process engineers to perform tasks or understand the process design, simulation, and optimization for product development. For the estimation of properties of compounds, the Quantity Structure-Property Relationship method can be used that contains an empirical relationship [11]. This method uses the chemical structure of the compound in which atoms, bonds, groups of atoms in the molecule, topological indices, and molecular descriptors are used for the estimation of properties. Over the year's different empirical relationships based on group contribution (GC) methods such as Joback and Reid, Lydersen, Klincewicz and Reid, Constantino and Gani, and Marrero and Gani has been reported for the estimation of properties of pure organic, inorganic, organometallic, polysaccharides, polymers, and lipid compounds and their mixtures [12], [13], [14], [15], [16], [17], [18], [19], [20]. This property includes critical properties [21], [22], [23], parameters of state equations [24], [25] acentric factor [26], [27], activity coefficients [28], vapor pressure [29], [30], liquid viscosity [31], gas viscosity [32], heat capacity [33], enthalpy of vaporization [34], entropy of vaporization [34], normal boiling temperature [20], [21], liquid thermal conductivity [35], gas thermal conductivity [36], gas permeability and diffusion coefficients [37], liquid density [38], [39], surface tension [40] and flash temperatures [41]. The application range and reliability of this method are largely dependent on several factors such as the group definitions used to represent the molecular structure of the pure components; the property model and the quantity and quality of the experimental dataset used in the regression to estimate the model parameters. These GC methods generally do not have all the needed parameters, such as groups and/or their contributions for drugs or larger and complex molecular weight compounds for a specific property. For such special cases, where the molecular structure of a given component is not completely described by any of the available groups, the atom connectivity index (CI) method can be employed together with the GC method to create the missing groups and to predict their contributions. This combined approach leads to the development of a group-contribution+ (GC+) method of a wider application range than before since the missing groups and their contributions can now be easily predicted through the regressed contributions of connectivity indices. The statistical indicators that are used are assessing the parameters for the group contribution method includes standard deviation, average absolute or relative error, and regression coefficient. The inclusion of uncertainty into model parameters are added advantages that are not generally reported. This uncertainty in properties plays an important role in the design and simulations of unit operations such as distillation, liquid-liquid extraction, and others [42]. P.M. Mathias [43] and Hajipour and Satyro [44] have shown the necessity and effect of uncertainties on the optimization calculations using computer-aided software (ASPEN, CAMD, MD). So, in consideration of its importance for reliable and accurate property prediction calculations in engineering design, the present work estimates the properties of important compounds based on GC+ property models. This model is developed by A. S. Hukkerikar et al. [45] that considers a systematic property modeling procedure with an extended CAPEC database that includes new experimental data on various polyfunctional, polycyclic, and complex components with their experimental uncertainty. A total of 3510 compounds that include hydrocarbon, oxygenated, nitrogenated, chlorinated, fluorinated, brominated, iodinated, sulfonated, multifunction compounds are used as data set for the regression and parameter estimation. The model helps to estimate the properties of the compound based on their molecular structure and has shown good accuracy for predicting the properties of the chemical, biochemical, and pharmaceutical compounds.
The present study estimates the pure component properties for 9 APIs that include Baricitinib, Camostat, Chloroquine, Dexamethasone, Hydroxychloroquine, Fingolimod, Favipiravir, Thalidomide, and Umifenovir based on the GC method (Table 1 ). A total of 16 pure component properties are estimated that includes the normal boiling point , critical temperature , critical pressure , critical volume , normal melting point , standard Gibbs energy of formation , standard enthalpy of formation , normal enthalpy of fusion , enthalpy of vaporization at 298 K , enthalpy of vaporization at the normal boiling point , the entropy of vaporization at the normal boiling point , flash point , auto-ignition temperature , Hansen solubility parameters , Hildebrand solubility parameter , octanol/water partition coefficient , acentric factor (ω), and liquid molar volume at 298 K . Thereby, the present work is an important source for knowledge about possible drug candidates or active pharma ingredients that are of prime interest shortly
Table 1.
Details on the compounds.
| Molecule Name | Structure | Formula | Molar Mass (g/mol) | CAS No. |
|---|---|---|---|---|
| Baricitinib | 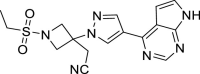 |
C16H17N7O2S | 371.42 | 1,187,594–09–7 |
| Camostat | 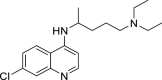 |
C20H22N4O5 | 398.412 | 59,721–29–8 |
| Chloroquine | 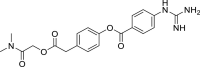 |
C18H26ClN3 | 319.872 | 54–05–7 |
| Dexamethasone | 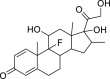 |
C22H29FO5 | 392.464 | 50–02–2 |
| Favipiravir |  |
C5H4FN3O2 | 157.104 | 259,793–96–9 |
| Fingolimod |  |
C19H33NO2 | 307.471 | 162,359–55–9 |
| Hydroxychloroquine |  |
C18H26ClN3O | 335.872 | 118–42–3 |
| Thalidomide |  |
C13H10N2O4 | 258.23 | 50–35–1 |
| Umifenovir |  |
C22H25BrN2O3S | 477.414 | 131,707–23–8 |
2. Model and methodology
The details about the model development and methodology are reported by A.S. Hukkerikar et al. [45] and Marrero and Gani (MG) [46]. In brief, the estimation of properties is based on a collection of 3 different types of groups viz. 1st order, 2nd order, and 3rd order are present in the compound. In the 1st order, simple molecules are considered that allow estimating the contributions to the property of different classes of organic compounds. The larger group or polycyclic, polyfunctional, and heterocyclic are not be considered here and each group is be kept as small as possible. The entire molecule needs to be covered and no fragments of the given should be left out in 1st order estimations. The overlapping is not allowed and the contributions are independent of the molecule in which the group has occurred. While in the case of 2nd and 3rd order groups, the information/contribution of the molecular fragments or the structural information is considered that otherwise is not provided by the 1st order group. The contributions of the polyfunctional and isomeric compounds are better described by the 2nd order group and the entire molecule need not be covered/described as that in the case of 1st order. Partial overlapping is allowed but one group should not completely overlap the others and in such case the molecule with the complete overlapping need to be considered. 2nd order group fails to provide the information of multi-ring compounds. The information about a multi-ring compound or fused aromatic rings, non-aromatic rings, and non-fused rings joined by chains with the different functional groups are covered in the 3rd order groups. The property prediction model with multilevel successive contribution can be described by the following general Eq. (1) given by MG:
| (1) |
In this equation, the function is dependent on the property . The is the contribution of the 1st order group of type that has an occurrence of times, is the contribution of the 2nd order group of type that has an occurrence of times and is the contribution of the 3rd order group of type that has an occurrence of times in the molecule. In the first step, the value of and are set zero for the 1st level of estimation of a given property with contribution. In the second step case of the 2nd level of estimation, the constants and are assigned unity and zero values, respectively because only 1st and 2nd order groups are involved while in the 3rd level, both and are set to unity values. The property function is used to define the different properties and is detailed in Table 2 . The universal constant/adjustable parameters required for the estimation of 16 thermodynamic properties are reported in Table 3 . The MG method reported herein is analyzed through step-wise regression method (STRM) and simultaneous regression method (SIRM) and the results are detailed in the next section.
Table 2.
Property, function and group contributions for the estimation of properties of the compound.
| Property | Function | Group Contribution terms |
|---|---|---|
| Normal boiling point | ||
| Critical temperature | ||
| Critical pressure | ||
| Critical volume | ||
| Normal melting point | ||
| Standard Gibbs energy of formation | ||
| Standard enthalpy of formation | ||
| Standard enthalpy of vaporization at 298 K | ||
| Normal enthalpy of fusion | ||
| Octanol/Water partition coefficient | ||
| Flash point | ||
| Enthalpy of vaporization at normal boiling point | ||
| Entropy of vaporization at normal boiling point | ||
| Hildebrand solubility parameter | ||
| Acentric factor ( | ||
| Liquid molar volume |
Table 3.
Value of universal constants for different methods.
| Universal Constants | Units | Values | |
|---|---|---|---|
| Step-wise Method | Simultaneous Method | ||
| 244.5165 | 244.7889 | ||
| 181.6716 | 181.6738 | ||
| 0.0519 | 0.0519 | ||
| 0.1347 | 0.1155 | ||
| 28.0018 | 14.6182 | ||
| 143.5706 | 144.0977 | ||
| −1.3385 | 8.5016 | ||
| 35.1778 | 83.9657 | ||
| −1.7795 | −1.2993 | ||
| 0.4876 | 0.752 | ||
| 170.7058 | 150.0218 | ||
| 9.6127 | 10.4327 | ||
| 15.4199 | 15.0884 | ||
| 21.6654 | 20.7339 | ||
| 0.908 | 0.9132 | ||
| 0.1055 | 0.0447 | ||
| 1.0012 | 1.0039 | ||
| 0.016 | 0.0123 | ||
| 0 | 71.2584 | ||
| 0 | 525.93 | ||
The deviation in the estimated thermodynamic properties was used using absolute relative deviation (ARD) that is defined as
| (2) |
Here, is the experimental thermodynamic property and is predicated on the thermodynamic property based on STRM and SIRM.
3. Result and discussion
The thermodynamic properties of the API were estimated based on the group contribution+ (GC) model that contains combined group contribution and the atom connectivity index. The model parameters considered have standard uncertainties in the prediction of the thermodynamic property. Each drug/molecule is split into different subgroups at each level for the estimation of the property. Table 4 reports the subgroups, group number, and their occurrence that are considered for predicting the thermodynamic properties of Baricitinib, Camostat, Chloroquine, Dexamethasone, Hydroxychloroquine, Fingolimod, Favipiravir, Thalidomide, and Umifenovir. Based on their contribution at each level i.e., contributions to 1st order group, 2nd order group, and 3rd order groups, the overall contribution to thermodynamic functions is calculated using Eq. (1). Table S1 reports the detailed contribution that is considered for the estimation of thermodynamic properties (, , , , , , , , , , , ,, , ω, and ) based stepwise (STRM) and simultaneous (SIRM) regression methods. While the estimated thermodynamic properties are reported in Table 5 . Among the 16 thermodynamic properties estimated for the 9 APIs, only the experimental normal melting point and for a few octanol/water partition coefficients is reported in the open literature and is mentioned also mentioned in Table 5. The other thermodynamic properties are not found in the literature to the best of our knowledge. The estimated normal melting point and octanol/water partition coefficient was therefore compared with that of literature for the performance evaluation of the mentioned GC method. The statistical performance indicator used in the present study is an absolute relative deviation (ARD).
Table 4.
Group orders, group number and their occurrence in each compound for the estimation of thermodynamic properties.
| Baricitinib | Camostat | Chloroquine | Dexamethasone | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Groups | Gr. No. | FN | Groups | Gr. No. | FN | Groups | Gr. No. | FN | Groups | Gr. No | FN | ||||||
| First-order | First-order | First-order | First-order | ||||||||||||||
| CH3 | 1 | 1 | CH3 | 1 | 1 | CH3 | 1 | 1 | CH3 | 1 | 3 | ||||||
| CH2 | 2 | 1 | CH2 | 2 | 9 | CH2 | 2 | 9 | OH | 29 | 3 | ||||||
| aCH | 15 | 5 | aCH | 15 | 4 | CH | 3 | 1 | CH2CO | 34 | 1 | ||||||
| aC fused with aromatic ring | 16 | 2 | aC except as above | 18 | 1 | aCH | 15 | 4 | CF | 116 | 1 | ||||||
| aC except as above | 18 | 2 | CH2CO | 34 | 1 | aC fused with aromatic ring | 16 | 1 | CH2 (cyclic) | 168 | 4 | ||||||
| aN in-aromatic ring | 19 | 5 | aC—CO | 37 | 1 | aN in-aromatic ring | 19 | 2 | CH(cyclic) | 169 | 4 | ||||||
| CH2CN | 68 | 1 | CH2—COO | 41 | 1 | CH2N | 61 | 2 | C (cyclic) | 170 | 3 | ||||||
| SO2 | 149 | 1 | aC—O | 53 | 1 | aC—NH | 63 | 1 | CH CH (cyclic) | 171 | 1 | ||||||
| CH2 (cyclic) | 168 | 2 | CH3N | 60 | 1 | aC—Cl | 123 | 1 | CH C (cyclic) | 172 | 1 | ||||||
| C (cyclic) | 170 | 1 | aC—NH | 63 | 1 | CO (cyclic) | 180 | 1 | |||||||||
| N (cyclic) | 176 | 1 | NH2 expect as above | 65 | 1 | ||||||||||||
| C = N | 67 | 1 | |||||||||||||||
| Second-order | Second-order | Second-order | Second-order | ||||||||||||||
| Ccyc-CH2 | 100 | 1 | aC—CH2—COO | 64 | 1 | No Occurrences | CHcyc-OH | 84 | 1 | ||||||||
| AROMRING s1s4 | 106 | 1 | AROMRING s1s4 | 106 | 2 | Ccyc-CH3 | 99 | 2 | |||||||||
| Ccyc-OH | 101 | 1 | |||||||||||||||
| CHcyc-CH3 | 76 | 1 | |||||||||||||||
| Third orders | Third-order | Third-order | Third-order | ||||||||||||||
| aC- aC (different ring) | 15 | 1 | aC—O-C-aC (different rings) | 47 | 1 | ARMOFUSED [2]S1S4 | 55 | 1 | CH multiring | 22 | 2 | ||||||
| AROMFUSED S1 | 52 | 1 | |||||||||||||||
| Favipiravir | Fingolimod | Hydroxychloroquine | Thalidomide | Umifenovir | |||||||||||||
| Groups | Gr. No. | FN | Groups | Gr. No. | FN | Groups | Gr. No. | FN | Groups | Gr. No | FN | Groups | Gr. No. | FN | |||
| First-order | First-order | First-order | First-order | First-order | |||||||||||||
| aCH | 15 | 1 | CH3 | 1 | 1 | CH3 | 1 | 2 | aCH | 15 | 4 | CH3 | 1 | 1 | |||
| aN in- AR | 19 | 2 | CH2 | 2 | 9 | CH2 | 2 | 5 | aC fused with non-AR | 17 | 2 | CH2 | 2 | 9 | |||
| aC—OH | 30 | 1 | aCH | 15 | 4 | CH | 3 | 1 | CH(cyclic) | 169 | 1 | aCH | 15 | 4 | |||
| aC—CONH2 | 94 | 1 | C | 4 | 1 | aCH | 15 | 1 | CH2 (cyclic) | 168 | 2 | aC fused with AR | 16 | 1 | |||
| NH2 expect as above | 65 | 1 | NH2 expect as above | 65 | 1 | aC fused with AR | 16 | 2 | NHCO except as above | 107 | 1 | aN in- AR | 19 | 2 | |||
| aC—CO | 37 | 1 | OH | 29 | 2 | aN in- AR | 19 | 2 | N(cyclic) | 176 | 1 | aCH2 | 21 | 2 | |||
| aC-F | 124 | 1 | aC—CH2 | 21 | 2 | OH | 29 | 1 | CO(cyclic) | 180 | 3 | aC—OH | 30 | 1 | |||
| CH2N | 61 | 1 | aC—COO | 45 | 1 | ||||||||||||
| aC—Cl | 123 | 1 | CH3N | 60 | 1 | ||||||||||||
| aC-Br | 126 | 1 | |||||||||||||||
| aC-S- | 147 | 1 | |||||||||||||||
| Second-order | Second-order | Second-order | Second Order | Second Order | |||||||||||||
| AROMRING s1 s2s4 | 108 | 1 | No Occurrences | No Occurrences | AROMFUSED [2] | 51 | 1 | ||||||||||
| aC—CH2-S- | 59 | 1 | |||||||||||||||
| Third-order | Third-order | Third-order | Third-order | ||||||||||||||
| No Occurrences | ARMOFUSED [2]S1S4 | 55 | 1 | aC- CO cyc (Fused rings) | 32 | 2 | PYRIDINE FUSED [2] | 64 | 1 | ||||||||
| AROMFUSED [2] | 51 | 1 | |||||||||||||||
FN: Occurrences.
Gr.No: Group Number.
AR: Aromatic Ring.
Table 5.
Estimated properties of compounds based on stepwise regression method (STRM) and simultaneous regression method (SIRM).
| Property | Units | Baricitinib | Camostat | Chloroquine | Dexamethasone | Favipiravir | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| STRM | SIRM | [47] | STRM | SIRM | [49] | STRM | SIRM | [50] | STRM | SIRM | [51] | STRM | SIRM | [52] | |||
| [K] | 794.469 | 760.077 | 757.482 | 771.300 | 688.550 | 682.652 | 722.347 | 717.264 | 618.948 | 688.871 | |||||||
| [K] | 997.035 | 973.995 | 934.420 | 949.155 | 907.967 | 907.964 | 905.005 | 905.004 | 815.160 | 815.158 | |||||||
| [bar] | 0.076 | 0.091 | 0.140 | 0.145 | 0.152 | 0.147 | 0.100 | 0.109 | 0.063 | 0.064 | |||||||
| [cc/mol] | 58.885 | 903.061 | 1381.063 | 1410.628 | 1196.016 | 1175.118 | −1061.953 | 1080.050 | 299.645 | 326.270 | |||||||
| [K] | 492.478 | 458.127 | 487.15 | 453.792 | 468.250 | 467.15 | 393.375 | 385.545 | 363.15 | 467.128 | 462.022 | 524.15 | 465.514 | 497.056 | 450.15 | ||
| [kJ/mol] | 632.951 | 395.881 | −122.228 | −121.518 | 737.893 | 757.660 | −536.591 | −574.299 | −187.165 | −173.038 | |||||||
| [kJ/mol] | 223.416 | 107.378 | −706.079 | −634.774 | 145.400 | 259.584 | −1054.777 | −994.887 | −385.972 | −417.504 | |||||||
| [kJ/mol] | 100.855 | 49.657 | 66.271 | 66.260 | 70.036 | 51.288 | 32.559 | 33.055 | 53.974 | 46.568 | |||||||
| 0.5811 | 2.32 | 5.4578 | 3.6913 | 5.463 | 6.0219 | 1.743 | 1.844 | −0.867 | −2.097 | ||||||||
| [K] | – | 607.007 | – | 150.022 | 570.936 | 552.786 | 723.751 | 736.511 | – | – | |||||||
| [kJ/mol] | – | 118.800 | – | 10.433 | 149.382 | 154.790 | 184.173 | 182.672 | 118.959 | 124.073 | |||||||
| [kJ/mol] | – | – | – | – | – | – | 143.507 | 144.740 | – | – | |||||||
| [kJ/mol] | – | – | – | – | – | – | 204.871 | 207.947 | – | – | |||||||
| [MPa1/2] | 27.197 | 27.445 | 23.924 | 26.165 | 14.350 | 16.843 | 27.291 | 26.661 | 27.886 | 27.635 | |||||||
| 0.013 | −0.002 | 0.023 | – | 0.013 | −0.001 | 0.024 | 0.018 | 0.015 | −0.001 | ||||||||
| [cc/kmol] | 0.251 | 0.301 | 0.507 | – | 0.333 | 0.333 | 0.278 | 0.462 | 0.134 | 0.129 | |||||||
| Property | Units | Fingolimod | Hydroxychloroquine | Thalidomide | Umifenovir | ||||||||||||
| STRM | SIRM | [53] | STRM | SIRM | [55] | STRM | SIRM | [57] | STRM | SIRM | [58] | ||||||
| [K] | 687.396 | 689.003 | 681.390 | 714.345 | 648.734 | 650.895 | 776.060 | 772.496 | |||||||||
| [K] | 848.840 | 848.839 | 909.231 | 920.028 | 936.906 | 931.518 | 973.718 | 973.718 | |||||||||
| [bar] | 0.106 | 0.115 | 1.335 | 0.142 | 2.419 | 0.069 | 0.142 | 0.146 | |||||||||
| [cc/mol] | 1058.116 | 1069.218 | 865.489 | 1199.529 | 566.423 | 575.560 | 1292.282 | – | |||||||||
| [K] | 398.693 | 396.310 | 400.15 | 417.170 | 414.588 | 367.1 | 441.490 | 440.390 | 543.15 | 447.213 | 448.603 | 415 | |||||
| [kJ/mol] | −21.235 | −2.948 | 346.872 | 595.810 | −229.399 | −255.484 | 171.261 | – | |||||||||
| [kJ/mol] | −478.253 | −448.244 | −63.171 | 45.765 | −456.385 | −446.716 | −397.082 | – | |||||||||
| [kJ/mol] | 48.469 | 46.357 | 58.150 | 55.237 | 23.906 | 32.053 | 70.472 | – | |||||||||
| 4.532 | 4.064 | 3.2266 | 4.6854 | 0.0915 | 0.3946 | 6.251 | 6.1162 | ||||||||||
| [K] | 615.936 | 616.728 | 594.016 | 640.443 | 567.197 | 570.199 | – | – | |||||||||
| [kJ/mol] | 162.707 | 162.094 | 144.748 | 178.760 | 147.419 | 152.094 | – | – | |||||||||
| [kJ/mol] | 98.831 | – | – | – | 99.785 | 159.024 | – | – | |||||||||
| [kJ/mol] | 134.617 | – | – | – | 168.272 | 181.299 | – | – | |||||||||
| [MPa1/2] | 28.506 | 29.829 | 18.645 | 19.895 | 23.247 | 27.758 | 21.665 | – | |||||||||
| 0.022 | – | 0.013 | – | 0.011 | −0.002 | 0.019 | −0.013 | ||||||||||
| [cc/kmol] | 0.360 | 0.294 | 14.941 | 0.337 | 0.168 | 0.160 | 0.419 | −1.453 | |||||||||
The estimated for the Baricitinib was found to be 492.478 K that showed an ARD of 1.093 (STRM) with that of reported A. S. Alshetaili et al. [47]. While the enthalpy of fusion showed a high ARD of 18.7 with that reported in the literature [47]. The Hansen solubility for the Baricitinib was found to be 27.197 MPa1/2 and was closer with reported literature [47] with a value of 28.90 MPa1/2. While the octanol/water partition coefficient is estimated to be 0.252 and consistent with Pengfei Xu et al. (0.24) [48]. The Camostat estimated was found to be 497.05 K (SIRM) with an ARD of 2.85 with that of experimental data reported by J. Yin et al. [49]. While the Chloroquine estimated was found to be 385.54 K against the reported value of 363.15 K by M. Staderini et al. [50]. The estimated for Dexamethasone showed an ARD of 10.87 with that of reported of 524.60 K [51] and was mainly with complex structure and fluorinated compounds present in it. Also, the normal enthalpy of fusion was found to be 32.55 kJ/mol and that showed very high ARD (29.27) with reported by X. Cai et al. [50]. The estimated for Favipiravir was found to be 465.51 K with a relatively low deviation of 3.41 K with that reported by Q. Guo et al. [52]. Fingolimod showed the lowest ARD with an estimated of 398.69 K and 396.30 K based on STRM and SIRM method. An ARD of 0.36 and 0.95 was found with that reported by S. R. Shaikh et al. [53]. H. Gunaydin reported the octanol/water partition coefficient of 2.8 that has a percentage ARD of 0.29 with STRM (4.5) [54] The estimated for Hydroxychloroquine is 417.16 K (STRM) with an ARD 12.05 [55]. Also, the estimated octanol/water partition coefficient based on STRM (3.22) was found coherent with that reported by M. Nimgampalle et al. with a value of 3.58 [56]. Similar to dexamethasone, Thalidomide estimated should a high ARD of 18.71 with that of reported of 543.15 K by et al. B.D. Vu et al. [57]. The presence of carboxyl carbonyl groups and fused aromatic rings are the possible reason for larger deviations. The Umifenovir estimated was found to be 447.21 K (STRM) with an ARD of 7.72 58. A. Kons et al. [58].
Based on the above statistical analysis of the overall average relative deviation for all the APIs was found to be 7.27 and 8.39 for STRM and SIRM methods, respectively. This relative deviation in the predicted properties is related to the experimental data set that was used for regression and the estimation of universal constants for empirical correlations. The group-contribution+ (GC+) method used in the present work is developed from the DIPPR 801® databank that has used experimental data with reported uncertainties. The experimental data itself has standard uncertainties in the measurements. For example, the normal boiling point [K] with data points of 1306 has an experimental average measurement error of 6.32% while that of predication based on the GC + method has 6.17%. Similarly, the deviations are seen for Normal melting point [K] with data points of 1385 has an experimental average measurement error of 5.10 while that of predication has 15.99. It has been found that for the 16 estimated properties the prediction error is lower than (or at least comparable to) the average measurement error, except for the case of normal melting point and standard enthalpy of fusion . For these two properties, group contribution methods, in general, have difficulties in providing a reliable estimation. This is mainly due to the strong dependency of the melting point on intermolecular interaction and molecular symmetry. With low deviation in STRM and SIRM method, the present GC+ method showed its capability to accurately predict the thermodynamic properties. The predicted thermodynamic properties not perfect/exact (lack of experimental value) still provide the basis for engineering design.
4. Conclusion
The group contribution (GC) method was used to estimate thermodynamic properties for the drugs/compounds/API that are related or proposed for the treatment of severe acute respiratory syndrome-CoronaVirus-2. The GC method based on stepwise regression parameters showed a low average deviation for the melting point. A total of 16 thermodynamic properties are reported for 9 API which is helpful in the product-process design, simulation, and optimization calculations. The properties contribute to reliable and robust engineering solutions for pharmaceutical product development.
Disclosure statement
No potential conflict of interest was reported by the authors.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We thank Director, CSIR-IICT (Ms. No. IICT/Pubs./2021/113) for providing all the required facilities to carry out the work. The authors also acknowledge financial support sponsored by CSIR under IICT-FBR Project (MLP0073).
References
- 1.https://www.who.int/news–room/q–a–detail/coronavirus–disease–(covid–19)–vaccines.
- 2.https://www.worldometers.info/coronavirus/?fbclid=IwAR35ZFiRZJ8tyBCwazX2N–k7yJjZOLDQiZSA_MsJAfdK74s8f2a_Dgx4iVk.
- 3.Yao X., Ye F., Zhang M., Cui C., Huang B., Niu P., Liu X., Zhao L., Dong E., Song C., Zhan S., Lu R., Li H., Tan W., Liu D. In vitro antiviral activity and projection of optimized dosing design of hydroxychloroquine for the treatment of severe acute respiratory syndrome coronavirus 2 (SARS–CoV–2) Clin. Infect. Dis. 2020;71:732–739. doi: 10.1093/cid/ciaa237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fantini J., Scala C.D., Chahinian H., Yahi N. Structural and molecular modelling studies reveal a new mechanism of action of chloroquine and hydroxychloroquine against SARSCoV–2 infection. Int. J. Antimicrob. Agents. 2020;55 doi: 10.1016/j.ijantimicag.2020.105960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gautret P., Lagier J.C., Parolaa P., Hoang V.T., Meddeba L., Mailhea M., Doudier B., Courjone J., Giordanengo V., Vieira V.E., Dupont H.T., Honoréi S., Colsona P., Chabrièrea E., Scolaa B.L., Rolaina J.M., Brouqui P., Raoult D. Hydroxychloroquine and azithromycin as a treatment of COVID–19: results of an open–label non–randomized clinical trial. Int. J. Antimicrob. Agents. 2020;56 doi: 10.1016/j.ijantimicag.2020.105949. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 6.Wang M., Cao R., Zhanget L. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019–nCoV) in vitro. Cell Res. 2020;30:269–271. doi: 10.1038/s41422-020-0282-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cao B., Wang Y., Wen D., Liu W., Wang J., Fan G., Ruan L., Song B., Cai Y., Wei M., Li X., Xia J. A Trial of Lopinavir–Ritonavir in Adults Hospitalized with Severe Covid–19. N Engl J Med. 2020;382:1787–1799. doi: 10.1056/NEJMoa2001282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Clinical Trials. Gov website: https://clinicaltrials.gov/ct2/show/NCT04470427, 2020, A Study to Evaluate Efficacy, Safety, and Immunogenicity of mRNA–1273 Vaccine in Adults Aged 18 Years and Older to Prevent COVID–19.
- 9.Williams J.D. New Mexico State Univ.; Las Cruces, NM, USA: 1997. Prediction of melting and heat capacity of inorganic liquids by the method of group contributions. Thesis. [Google Scholar]
- 10.Briard A.J., Bouroukba M., Petitjean D., Dirand M. Models for Estimation of Pure n–Alkanes' Thermodynamic Properties as a Function of Carbon Chain Length. J. Chem. Eng. 2003;48:1508–1516. [Google Scholar]
- 11.Majer V., Svoboda V., Pick J. Elsevier; 1989. 1989 Heats of Vaporization of Fluids. [Google Scholar]
- 12.Costa A.J.L., Esperança J.M.S.S., Marrucho I.M., Rebelo L.P.N. Densities and Viscosities of 1–Ethyl–3–methylimidazolium n–Alkyl Sulfates. J. Chem. Eng. Data. 2011;56:3433–3441. [Google Scholar]
- 13.Nikitin E.D., Popov A.P., Yatluk Y.G., Simakina V.A. Critical Temperatures and Pressures of Some Tetraalkoxytitaniums. J. Chem. Eng. Data. 2010;55:178–183. [Google Scholar]
- 14.Papaioannou A., Morin S., Cheung A.M., Atkinson S., Brown J.P., Feldman S., Hanley D.A., Hodsman A., Jamal S.A., Kaiser S.M., Kvern B., Siminoski K., Leslie W.D. Clinical practice guidelines for the diagnosis and management of osteoporosis in Canada: summary. Can. Med. Assoc. J. 2010;182:1864–1873. doi: 10.1503/cmaj.100771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lobanova O., Mueller K., Mokrushina L., Arlt W. Estimation of Thermodynamic Properties of Polysaccharides. Chem. Eng. Technol. 2011;34:867–876. [Google Scholar]
- 16.Satyanarayana K.C., Gani R., Abildskov J. Polymer property modeling using grid technology for design of structured products. Fluid Ph. Equilibria. 2007;261:58–63. [Google Scholar]
- 17.Oh S.Y., Bae Y.C. Group contribution method for group contribution method for estimation of vapor liquid equilibria in polymer solutions. Macromol. Res. 2009;17:829–841. [Google Scholar]
- 18.Tovar C.A.D., Gani R., Sarup B. Lipid technology: property prediction and process design/analysis in the edible oil and biodiesel industries. Fluid Ph. Equilibria. 2011;302:284–293. [Google Scholar]
- 19.Browna J.S., Ziliob C., Cavallini A. Thermodynamic properties of eight fluorinated olefins. Int J Refrig. 2010;33:235–241. [Google Scholar]
- 20.Gani R., Constantinou L. Molecular structure–based estimation of properties for process design, Fluid Ph. Equilibria. 1996;116:75–86. [Google Scholar]
- 21.Joback K.G., Reid R.C. Estimation of pure–component properties from group–contributions. Chem. Eng. Commun. 1987;57:233–243. [Google Scholar]
- 22.Ambrose D. Correlation and Estimation of Vapour–Liquid Critical Properties. II. Critical Pressures and Volumes of Organic Compounds. National Physical Laboratory, Teddington: NPL Rep. Chem. 1979;98 [Google Scholar]
- 23.Ambrose D. Correlation and Estimation of Vapour–Liquid Critical Properties. I. Critical Temperatures of Organic Compounds. National Physical Laboratory, Teddington: NPL Rep. Chem. 1978;92 [Google Scholar]
- 24.S. Pereda, E. Brignole, S. Bottini, Equations of state in chemical reacting systems. In: applied Thermodynamics of Fluids, Royal Society of Chemistry; 1st Ed. (2011) 433–459.
- 25.B. Schmid, J. Gmehling, Revised parameters and typical results of the VTPR group contribution equation of state, Fluid Ph. Equilibria. 317 (1012) 110–126.
- 26.Constantinou L., Gani R. New group contribution method for estimating properties of pure compounds. AIChE J. 1994;40:1697–1710. [Google Scholar]
- 27.Manago K., Otobrise C. Estimation of pure–component properties of fatty acids and esters from group contributions. J. Chem. Soc. Nigeria. 2010 [Google Scholar]
- 28.Tochigi K., Kurita S., Okitsu Y., Kurihara K. Measurement and Prediction of Activity Coefficients of Solvents in Polymer Solutions Using Gas Chromatography and a Cubic–Perturbed Equation of State with Group Contribution. Fluid Ph. Equilibria. 2005;228:527–533. [Google Scholar]
- 29.B.E. Poling, J.M. Prausnitz, J.P. O’ Connell, The properties of gases and liquids, Fifth Edition, ISBN: 9780070116825, McGraw-Hill Education.
- 30.Miller D.G. Estimating Vapor Pressures–Comparison of Equations. Ind. Eng. Chem. 1964;56:46–57. [Google Scholar]
- 31.Conte E., Martinho A., Matos H.A., Gani R. Combined Group–Contribution and Atom Connectivity Index–Based Methods for Estimation of Surface Tension and Viscosity, nd. Eng. Chem. Res. 2008;47:7940–7954. [Google Scholar]
- 32.Reichenberg D. New methods for the estimation of the viscosity coefficients of pure gases at moderate pressures (with particular reference to organic vapors) AIChE Journal. 1975;21:181–183. [Google Scholar]
- 33.Jr V.R., Domalski E.S. Estimation of the Heat–Capacities of Organic Liquids as a Function of Temperature Using Group Additivity. 1. Hydrocarbon Compounds. J Phys Chem Ref Data. 1993;22:597. [Google Scholar]
- 34.Kolská Z., Růžička V., Gani R. Estimation of the Enthalpy of Vaporization and the Entropy of Vaporization for Pure Organic Compounds at 298.15 K and at Normal Boiling Temperature by a Group Contribution Method. Ind. Eng. Chem. Res. 2005;44:8436–8454. [Google Scholar]
- 35.Nagvekar M., Daubert T.E. A Group Contribution Method for Liquid Thermal Conductivity. Ind. Eng. Chem. Res. 1987;26:1362–1365. [Google Scholar]
- 36.Chung T.H., Lee L.L., Starling K.E. Applications of Kinetic Gas Theories and Multiparameter Correlation for Prediction of Dilute Gas Viscosity and Thermal Conductivity. Ind. Eng. Chem. Fundam. 1984;23:8–13. [Google Scholar]
- 37.Yampolskii Y., Shishatskii S., Alentiev A., Loza K. Group Contribution Method for Transport Property Predictions of Glassy Polymers: focus on Polyimides and Polynorbornenes. J. Membr. Sci. 1998;149:203–220. [Google Scholar]
- 38.Cruz M.S., Aca G.A., Daza O.S., Arenas T.L. Predicting critical properties, density and viscosity of fatty acids, triacylglycerols and methyl esters by group contribution methods. Computer–Aided Chemical Engineering. 2010 [Google Scholar]
- 39.Shahbaz K., Baroutian S., Mjalli F.S., Hashim M.A. Densities of ammonium and phosphonium based deep eutectic solvents: prediction using artificial intelligence and group contribution techniques. Thermochim Acta. 2012;527:59–66. [Google Scholar]
- 40.Awasthi A., Tripathi B.S., Awasthi A. Applicability of corresponding–states group–contribution methods for the estimation of surface tension of multicomponent liquid mixtures at 298.15 K, Fluid Ph. Equilibria. 2010;287(2):151–154. [Google Scholar]
- 41.Liaw H., Gerbaud V., Li Y. Prediction of miscible mixtures flash–point from UNIFAC group contribution methods, Fluid Ph. Equilibria. 2011;300:70–82. [Google Scholar]
- 42.Aniya V., Singh A., De D., Satyavathi B. An energy efficient route for the dehydration of 2–Methylpropan–2–ol: experimental investigation, modeling and process optimization, Sep. Purif. Technol. 2015;156:738–753. [Google Scholar]
- 43.Mathias P.M., Soto A., Fele–Zilnik L., de Hemptinne J.C., Bazyleva A., Abildskov J. Data Quality and Assessment, Validation Methods and Error Propagation through the Simulation Software: report from the Round–Table Discussion at the 10th World Congress of Chemical Engineering in Barcelona (October 1–5, 2017) Chem Eng Res Des. 2018;137:A1–A8. doi: 10.1016/j.cherd.2018.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mathias P.M., Soto A., Fele–Zilnik L., de Hemptinne J.C., Bazyleva A., Abildskov J., Hajipour S., Satyro M.A., Foley M.W. Uncertainty Analysis Applied to Thermodynamic Models and Fuel Properties – Natural Gas Dew Points and Gasoline Reid Vapor Pressures. Energy Fuels. 2014;28:1569–1578. [Google Scholar]
- 45.Shivajirao A., Bent H., Antoon S., Katec T., Abildskova J., Sina G., Gania R. Group–contribution+ (GC+) based estimation of properties of pure components: improved property estimation and uncertainty analysis. Fluid Ph. Equilibria. 2012;321:25–43. [Google Scholar]
- 46.Marrero J., Gani R. Group-contribution based estimation of pure component properties. Fluid Ph. Equilibria. 2001;183–184:183–208. [Google Scholar]
- 47.Alshetaili A.S. Solubility and Solution Thermodynamics of Baricitinib in Six Different Pharmaceutically Used Solvents at Different Temperatures. Z. Phys. Chem. 2019;233:1129–1144. [Google Scholar]
- 48.P.Xu P.Shen, Wang H., Qin L., Ren J., Sun Q., R.Ge J.Bian, Zhong Y., Li Z., Wang J., Qiu Z. Discovery of imidazopyrrolopyridines derivatives as novel and selective inhibitors of JAK2. Eur. J. Med. Chem. 2021;218 doi: 10.1016/j.ejmech.2021.113394. [DOI] [PubMed] [Google Scholar]
- 49.Yin J., Noda Y., Hazemoto N., Yotsuyanagi Toshihisa. Distribution of Protease Inhibitors in Lipid Emulsions: gabexate Mesilate and Camostat Mesilate. Chem. Pharm. Bull. 2005;53(8):893–898. doi: 10.1248/cpb.53.893. [DOI] [PubMed] [Google Scholar]
- 50.Staderini M., Bolognesi M.L., Menndez J.C. Lewis Acid-Catalyzed Generation of C–C and C–N Bonds on π-Deficient Heterocyclic Substrates. Adv. Synth. Catal. 2015;357(1):185–195. [Google Scholar]
- 51.Cai X., Grant D.J.W., Wiedmann T.S. Analysis of the Solubilization of Steroids by Bile Salt Micelles. J. Pharm. Sci. 1997;86:372–377. doi: 10.1021/js9602148. [DOI] [PubMed] [Google Scholar]
- 52.Guo Q., Xu M., Guo S., Zhu F., Xie Y., Shen J. The complete synthesis of favipiravir from 2–aminopyrazine. Chem. pap. 2019;73:1043–1051. [Google Scholar]
- 53.Shaikh R.S., Schilson S.S., Wagner S., Hermann S., Keul P., Levkau B., Schäfers M., Haufe G. Synthesis and Evaluation of Fluorinated Fingolimod (FTY720) Analogues for Sphingosine–1–Phosphate Receptor Molecular Imaging by Positron Emission Tomography. J. Med. Chem. 2015;58:3471–3484. doi: 10.1021/jm502021d. [DOI] [PubMed] [Google Scholar]
- 54.Gunaydin H. Probabilistic Approach to Generating MPOs and Its Application as a Scoring Function for CNS Drugs. ACS Med. Chem. Lett. 2016;7:89–93. doi: 10.1021/acsmedchemlett.5b00390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Joshi P., Dhaneshwar S. Novel drug delivery of dual acting prodrugs of hydroxychloroquine with aryl acetic acid NSAIDs: design, kinetics and pharmacological study. Drug Deliv. and Transl. Res. 2017;7:709–730. doi: 10.1007/s13346-017-0420-5. [DOI] [PubMed] [Google Scholar]
- 56.Nimgampalle M., Devanathan V., Saxena A. Screening of Chloroquine, Hydroxychloroquine and its derivatives for their binding affinity to multiple SARS-CoV-2 protein drug targets. J. Biomol. Struct. Dyn. 2020 doi: 10.1080/07391102.2020.1782265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Vu B.D., Ba N.M.H., Phan D.C. Facile Synthesis of Thalidomide,Org. Process Res. Dev. 2019;23:1374–1377. [Google Scholar]
- 58.Kons A., Berzins A., Krukle-Berzina K., Actins A. Characterization and physicochemical evaluation of molecular complexes formed between umifenovir and dicarboxylic acids. Latv. J. Chem. 2014;52:28–40. [Google Scholar]


