Abstract

During coal seam mining, a large amount of low-concentration mine gas will be produced, and it is the main utilization way to pass it into a thermal storage oxidation device to obtain heat energy. The thermal storage oxidation process is carried out in an ultra-high temperature environment. The excessive gas concentration not only reduces the production efficiency but also presents an explosion hazard. To solve the abovementioned problems, the lower explosion limit of a low-concentration gas at ultra-high temperatures (900–1200 °C) was studied through a self-developed high-temperature explosion experimental device. Fluent software was used to simulate the reaction of a low-concentration gas in a high-temperature environment, and the experimental results were verified according to the maximum explosion pressure. Through analysis and discussion, the following are found: (1) the relationship between the instantaneous explosion pressure of the low-concentration gas and the gas concentration as well as the relationship between the maximum explosion pressure near the lower explosion limit and the gas concentration are in accordance with the Boltzmann function. (2) When the temperature rises from 900 to 1200 °C, the lower limit of gas explosion obtained from experiments is reduced from 2.33 to 1.36%. (3) The lower limit of gas explosion decreases with increasing temperature at ultra-high temperatures and the downward trend slows down, this is similar to the change rule of the lower limit of gas explosion at temperatures below 200 °C. These findings have certain practical significance for improving the utilization efficiency of the low-concentration gas in heat storage oxidation.
1. Introduction
Since 2018, China’s utilization of mine gas has reached 5.31 billion cubic meters and has continued to rise. The scale of underground gas utilization is increasing year by year, but the utilization rate of gas is at a relatively low level. In 2018, the utilization rate of underground gas was only 40.91%.1 At present, more than 70% of gas drainage comes from the underground windblown mine gas with a concentration of less than 1% and thus an important utilization method is to make ultra-low concentration gas flow through a thermal storage oxidation device to obtain heat energy.2 In the standard state, methane gas has an explosion limit range of 5–16%. In the ultra-high temperature environment, where the heat storage oxidation process is carried out, the lower limit of gas explosion decreases significantly because as the temperature rises, the mine gas molecules become more active.3 Therefore, it is necessary to study the lower explosion limit of a low-concentration gas at ultra-high temperatures. This study can provide a corresponding theoretical reference for the utilization of thermal storage oxidation and other aspects and improve the efficiency of gas utilization on the premise of ensuring safety.
At present, many researchers have achieved remarkable results in the research of gas explosion characteristics.4−9 Zhu10 explored the influence of different ambient temperature and environmental humidity conditions on the concentration limit of methane explosion through a 20 L spherical explosive device. His results showed that when the initial environmental temperature increased from 25 to 200 °C, the lower limit of methane explosion was reduced from 5.03 to 4.23%, and the rate of decrease was 15.9%. Huang11 studied the maximum explosion pressure change of methane gas with a concentration of 10.1% at an ambient temperature of 20 to 200 °C and found that the maximum explosion pressure decreased from 0.894 MPa at 20 °C to 0.502 MPa at 200 °C and that the maximum pressure rise rate was relatively stable. Gao et al.12 investigated the explosion pressure of methane under different initial temperature conditions with a 20 L spherical experimental device. Their experimental results showed that as the initial temperature continued to increase, the maximum explosion pressure decreased, the reaction rate increased, and the explosion risk increased accordingly. Wan, Zhang, and Shen13 proposed a model for predicting the explosion limit based on relevant data. Through their prediction model, they found that the lower limit of the flammable concentration of the methane–air mixture at a normal pressure and a high temperature of 1200 K was 1.0–1.5%. Yang, Liu, and Yang14 examined the explosion characteristics of the methane–air mixture under different working conditions by means of a spherical explosion test device. They found that as the methane concentration continued to decrease, the maximum explosion pressure and the maximum pressure rise rate of the mixed gas would gradually decrease near the lower explosion limit, but the downward trend became weaker. Faghih et al.15 discussed the effect of different initial temperatures and initial pressures on the explosion pressure of the methane-contained gas and pointed out that the initial temperature had no obvious effect on the maximum explosion pressure rise rate of methane gas, while the initial pressure had a significant effect. Cammarota et al.16 investigated the influence of initial pressure on the explosion characteristics of a hydrogen/methane/air mixture and believed that the maximum explosion pressure and the maximum explosion pressure rise rate were positively correlated with the initial pressure. In addition, the scholar17 also used a 5 L closed cylindrical container to study the explosive behavior of n-dodecane under an environment of −130 °C, 160 °C, −1 bar, 2 bar, and 3 bar and found that the initial temperature or pressure increases. The scholar found that the flammable range of n-dodecane on the fuel-rich side was expanded, and the explosion behavior was not sensitive to changes in the initial temperature, but it responded more to changes in the initial pressure. Ren et al.18 analyzed the influence of the oxygen concentration, initial temperature, initial humidity, and other factors on the explosion limit of a combustible gas mixture and reported that the explosion limit range of most hydrocarbon combustible gases expanded with increasing temperature and initial pressure and presented an approximately linear relationship. Salzano et al.19 studied the effects of factors such as the oxygen enrichment factor and equivalent ratio on the explosion characteristics and laminar combustion speed of H2/CO/O2/N2/CO2 mixtures through experiments and numerical simulations. The results show that when the laminar combustion rate of the mixed gas is high, the main influencing factor of CO2 on the laminar combustion rate is heat; when the laminar combustion rate is low, the main influence of CO2 on the laminar combustion rate is thermal and kinetic effects. Cui et al.20 found that in an ambient temperature range of 123–273 K, with the increase of the temperature and initial pressure, the upper explosion limit of methane gas was increased, and the lower explosion limit was decreased, both of which had a linear relationship with the temperature. They also pointed out that the explosion container had a significant impact on the explosion limit of flammable gases. Xu et al.21 tested the explosion limit of mine gas by using a self-developed 1 L explosion test device and showed that in the range of 25–400 °C, the gas explosion limit was roughly linear with the initial temperature, the upper explosion limit was increased by 7.7%, the lower explosion limit was decreased by 1.53%, and that the gas explosion range became larger. Li et al.22 conducted explosion experiments on a methane–air mixture in the range of 150–300 K with stainless-steel cylinders and found that with the increase of the temperature, the upper and lower explosion limits of the mixed gas showed linear changes.
In the above studies, most researchers discussed the influence of the ambient temperature, initial pressure, ambient humidity, and other factors on the gas explosion characteristics at temperatures below 200 °C. However, relatively few studies have been done on the gas explosion reaction at ultra-high temperatures. With the wide application of the thermal storage oxidation technology in China’s mining areas, the process of thermal storage oxidation is usually carried out at a temperature above 900 °C. This places strict requirements on the gas concentration. Therefore, 1–2% low-concentration gas explosion experiments at a temperature of 900–1200 °C are conducted through a self-developed, high-temperature, and low-concentration gas explosion apparatus in this paper. This serves as the basic research for the analysis of the explosion characteristics of mine gas at ultra-high temperatures and provides theoretical guidance for the related fields such as the utilization of thermal storage oxidation.
2. Experimental Apparatus and Method
2.1. Experimental Apparatus
The high-temperature and low-concentration gas explosion experimental apparatus used in this experiment is mainly composed of four parts: a high-temperature oxidation furnace chamber, a rapid inflation system, a scale monitoring system, and a data collection and control system, as shown in Figure 1.
Figure 1.
Diagram of the experimental system.
The high-temperature oxidation furnace chamber has a volume of 8.5 L and can withstand a high temperature of 1500 °C. A resistance wire (nickel–chromium alloy) is attached to the outer wall of the oxidation chamber for heating. An insulation layer of about 25 cm thickness is arranged on the periphery, and a ventilation pipe is set at the bottom of the chamber. A rupture disk is located at the entrance of the pipe. When the gas pressure reaches the rupture disk pressure, the gas in the constant volume gas storage tank quickly enters the oxidation chamber. Then, the displacement of the top cover after the gas reaction and the displacement time are monitored by a high-speed camera. There are three control valves in the system, of which k1 controls the entry of gas, k2 controls the drainage of replacement gas, and k3 must be closed when pressure is applied to the gas. The specific parameters of each part of the experimental apparatus are shown in Table 1.
Table 1. Parameters of Various Parts of the Experimental Apparatus.
| volume of the oxidation chamber | temperature resistance of the reaction chamber | thickness of the insulation wall | volume of the constant volume gas storage tank | pressure resistance of the bursting disc | high-speed camera |
|---|---|---|---|---|---|
| 8.5 L | 1500 °C | 25 cm | 1 L | 0.5 MPa | 1000 fps/s |
2.2. Experimental Content and Method
The experimental procedure is described as follows. First, the temperature of the oxidation chamber is raised to a predetermined value through the computer control system. Next, the air in the pipeline is replaced with mine gas, which is discharged through k2. Then, with k1, k2, and k3 closed, a gas pump with a set pressure of 0.5 MPa is started, and 1 L of mine gas (including the volume of the pipeline) is forced into a high-temperature oxidation chamber. Finally, the experimental data are recorded by a high-speed camera. In addition, the experimental gas is prepared at a ratio of CH4/O2/N2 = 1:21:78. According to the above procedure, the explosion experiment with a gas concentration of 1.0 to 2.0% (with a step size of 0.2%) is carried out at 900, 1000, 1100, and 1200 °C, and five experiments are conducted in each experimental group, as shown in Figure 2.
Figure 2.
Experimental flowchart.
Due to the use of ultra-high temperatures in the experiment, further analysis is carried out by studying the instantaneous state when the top cover has an initial displacement of 1 mm. In order to ensure the relative accuracy of the calculation results, the time for the top cover to produce an initial displacement of 2 mm is used to calculate the instantaneous velocity at the time of 1 mm initial displacement of the top cover and then the instantaneous explosion pressure of the low-concentration gas. This can avoid the appearance of a large pressure relief space that may lead to large errors in the calculation results. The calculation process is as follows
| 1 |
| 2 |
where Δs = 2 mm; Δt is the time for the pointer to produce an initial displacement of 2 mm, ms; Vt is the instantaneous velocity when the pointer is initially displaced by 1 mm; V0 is the initial velocity of the pointer, which is 0; and a is the acceleration of the pointer.
Combining eqs 1 and 2 as well as Newton’s second law F = ma, the following equation is obtained
| 3 |
With eq 3 substituted into the pressure formula P = F/S, eq 4 is obtained
| 4 |
where S is the bottom surface area of the top cover, which equals 0.0025π m2; m = (top cover gravity – spring tension)/g. Because the mass of the top cover is known to be 11 kg, and the top cover is pulled by three identical stainless-steel springs with an elasticity coefficient k = 1000 N/m and the amount of deformation is 0.02 m, the gravity of the top cover is 11 × 9.8–3 × 1000 × 0.02 = 47.8 N. The downward force generated by the deformed part of the springs on the top cover is 3 × 1000 × 0.002 = 6 N. Hence, m = (47.8 + 6)/9.8 = 5.49 kg, and the instantaneous pressure at a time of 1 mm initial displacement of the top cover is
| 5 |
3. Experimental Results and Analysis
3.1. Instantaneous Explosion Pressure
The instantaneous explosion pressure generated after the reaction of different concentrations of gas is obtained by calculation. In order to obtain an accurate result, the average value of each group of data (Table 2) is taken, and the fitting curve is shown in Figure 3.
Table 2. Experimental Results.
| temperature (°C) | concentration (%) | explosion pressure (kPa) |
|---|---|---|
| 900 | 1 | 10.9 |
| 1.2 | 12.1 | |
| 1.4 | 14.2 | |
| 1.6 | 15.8 | |
| 1.8 | 17.8 | |
| 2 | 21.1 | |
| 2.2 | 22.5 | |
| 2.4 | 49.7 | |
| 2.6 | 57.1 | |
| 2.8 | 58.3 | |
| 1000 | 1 | 13.5 |
| 1.2 | 15.1 | |
| 1.4 | 16.5 | |
| 1.6 | 19.4 | |
| 1.8 | 43.7 | |
| 2 | 48.4 | |
| 1100 | 1 | 15.1 |
| 1.2 | 17.9 | |
| 1.4 | 23.9 | |
| 1.6 | 57.1 | |
| 1.8 | 72.7 | |
| 2 | 77.7 | |
| 1200 | 1 | 15.8 |
| 1.2 | 21.2 | |
| 1.4 | 77.7 | |
| 1.6 | 103.4 | |
| 1.8 | 111.8 | |
| 2 | 115 |
Figure 3.

Instantaneous explosion pressures after the reaction of different concentrations of mine gas at the time of 1 mm initial displacement of the top cover.
As shown in Figure 3, at 900 °C, the instantaneous pressure generated by mine gas with a concentration of 1 to 2% does not show a sharp increase trend. In order to obtain the relationship between the instantaneous explosion pressure and the gas concentration at 900 °C, further explosion experiments are carried out on gas with concentrations of 2.2, 2.4, 2.6, and 2.8%. To ensure safety, only simple predictions are made based on the result trend under other conditions.
Figure 3 shows that when the gas concentration is constant, the instantaneous explosion pressure increases with the rise of the temperature, and when the gas concentration is lower than 1.2%, the instantaneous explosion pressures at 900, 1000, 1100, and 1200 °C are relatively close. Because the concentration of the introduced mine gas is too low, the heat emitted by the oxidation reaction of the mine gas in the furnace chamber is not enough to cause a violent explosive reaction, and thus, the displacement of the top cover is small and the instantaneous explosion pressure is basically below 20 kPa. At 900 °C, the trend of the instantaneous explosion pressure generated by the reaction of the gas with a concentration of 1.0–2.0% is relatively gentle, and the relationship between the pressure and concentration is approximately linear, indicating that the concentration of the introduced gas has not reached the lower explosion limit. At 1000, 1100, or 1200 °C, the fitting curve of the instantaneous explosion pressure has a slow-fast-slow change trend, and the relationship between the pressure and concentration conforms to the Boltzmann function.
When the gas concentration is lower than 1.6, 1.4, and 1.2% at 1000–1200 °C, the three fitting curves change smoothly. The reason is that although the excessively low concentration of the mine gas is oxidized and burns quickly in a high-temperature environment, the reaction rate is relatively slow because air and other gases account for a relatively large amount and have a certain inhibitory effect on the chemical reaction. Consequently, the heat generated by the reaction is difficult to cause a violent movement of the surrounding gas molecules. This results in a lower instantaneous explosion pressure and a smoother fitting curve. At 1000–1200 °C, when the gas concentration is about 1.6–1.8, 1.4–1.7, and 1.2–1.5%, the fitting curve has a significant upward trend, and the instantaneous explosion pressure is increased from 19.4, 23.9, and 21.2 to 43.7, 69.1, and 99.8 kPa, respectively, and the net increase in the instantaneous explosion pressure is also increased with the increase of the temperature. This is because when the mine gas reaches a certain concentration, more methane molecules in the mine gas participate in the reaction, the reaction rate is greater, and the impact on the surroundings is also greater. As a result, the phenomenon of gas deflagration occurs, which makes the instantaneous explosion pressure rise significantly. In addition, at the same concentration, the frequency of collisions between the gas molecules increases with the increase of the temperature, which is also the main reason for the more violent explosion reaction. Therefore, the instantaneous explosion pressure and the net increase in the instantaneous explosion pressure also increase with the increase of the temperature. When the gas concentration is greater than 1.8, 1.7, and 1.5%, the pressure fitting curve becomes flat again. When the gas concentration is greater than the lower limit of the gas explosion, the gas undergoes an incomplete explosion reaction. Because a small amount of methane undergoes an exothermic oxidation reaction and does not participate in the explosion reaction process, it does not contribute much to the increase of the instantaneous pressure, and thus the fitting curve tends to be flat again.
3.2. Lower Explosion Limit
In order to obtain an accurate explosion limit value, the secondary derivative processing is performed on the instantaneous explosion pressure fitting curve at 900, 1000, 1100, and 1200 °C, respectively, and thus, the gas concentration values for the most violent gas explosion reaction are 2.33, 1.66, 1.57, and 1.36%, respectively. Finally, the trend of the lower explosion limit is obtained, as shown in Figure 4.
Figure 4.

Trend of lower limit of gas explosion.
Figure 4 shows that the lower limit of the gas explosion decreases as the temperature rises, but the downward trend gradually slows down. Due to the increase in temperature, the internal energy and collision frequency of the gas molecules increase, which makes more gas participate in the explosive reaction. Moreover, the chemical reaction rate increases, which causes a stable system to become an explosive system. Therefore, the lower limit of gas explosion is reduced. In addition, when the ambient temperature is constant, the gas concentration near the lower explosion limit is low, and the reaction process is in an oxygen-rich environment. Furthermore, the nitrogen in the air acts as an inert gas and reduces the chance of collision between methane and oxygen molecules,23 making it difficult to maintain the chain reaction. Therefore, the lower limit of gas explosion does not decrease linearly.
4. Numerical Simulation and Result Analysis
4.1. Mathematical Model
4.1.1. Model Assumptions
The process of gas explosion is rapid and complicated. In order to make the calculation simple and to simulate the changes of the flow field more accurately, some reasonable assumptions need to be made before the simulation:
1The gas in the space is real gas, which satisfies the real gas state equation.
2The specific reaction process of CH4 and O2 was ignored, the reaction between the two is irreversible in a single step.
3The walls of the model are all adiabatic walls, and there is no heat transfer between the mixed gas and the wall.
4The model wall is rigid, and the fluid–solid coupling between the wall and the gas is not considered.
4.1.2. Basic Equation
The combustion and explosion of methane can be regarded as the thermal expansion of an ideal gas. This can be expressed by the mass conservation equation, momentum conservation equation, and energy conservation equation.24,25 The continuity equation is
Mass equation
| 6 |
The momentum equation is
| 7 |
The momentum conservation equation is
| 8 |
The chemical composition balance equation is
| 9 |
where p is the gas density; x is the space coordinate; t is the time
coordinate; h is the enthalpy per unit volume; p is the pressure; u is the velocity component; i, j, and k are the different
directions of the space; μeff is the effective viscosity;
μeff = μ1 + μ2,
μ1 is the molecular viscosity, μi = Cμρk2/ε, Cμ is the empirical constant; 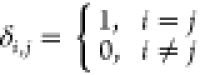 , σ is
the Prandtl number; Sh,rad is the radiation
source term caused by
coupled radiation; Yfu is the mass fraction
of the methane gas; and Rfu is the average
combustion rate of the mixed gas.
, σ is
the Prandtl number; Sh,rad is the radiation
source term caused by
coupled radiation; Yfu is the mass fraction
of the methane gas; and Rfu is the average
combustion rate of the mixed gas.
4.1.3. Turbulence Model
According to the characteristics of gas explosion, the k−ε turbulence model is selected to describe the turbulence characteristics of the gas explosion process. The equation is
| 10 |
The ε equation is
| 11 |
In eqs 10 and 11, G = Gk + Gb, where Gk is the turbulent energy production term caused by the laminar flow velocity, Gb is the turbulent energy produced by the buoyancy effect, ε is the turbulent energy dissipation rate, C1 and C2 are the empirical coefficients, and δij is the viscous heat. Gk and Gb are described by the following equations.
| 12 |
| 13 |
4.1.4. Combustion Model
The chemical reaction mechanism of methane combustion and explosion is relatively complicated, so for the convenience of calculation, the article adopts a single-step irreversible reaction model, which can be expressed as
| 14 |
For the explosion reaction of the gas mixture, the article uses the laminar finite-rate/Eddy-dissipation model to describe. In the turbulent combustion zone, the combustion and explosion of the gas needs to consider the control of the Arrhenius reaction mechanism, and the specific equations as follows
| 15 |
where Rfu,A is the Arrhenius chemical reaction rate, J s–1 and Rfu,T is the turbulent burning rate, J s–1, and their expressions are
| 16 |
| 17 |
where B is the pre-exponential factor, Ea is the activation energy, J mol–1, R is the Platts gas constant, CEBU is the empirical constant (0.34–0.4), Y1 is the mass fraction of fuel, Y2 is the mass fraction of oxide, and Y3 is the mass fraction of combustion products.
4.1.5. Initial Conditions and Boundary Conditions
1The wall temperature and the temperature of the reaction field are constant as the experimental setting values (1173, 1273, 1373, and 1473 K).
2For a cylindrical reaction chamber, it can be simplified as an axisymmetric model, and the symmetry axis satisfies: v = 0, ∂vx/∂x = 0, ∂Yi/∂x = 0, ∂T/∂x = 0.
3The gas temperature is set to 293 K, the inlet form is a mass rate inlet, and the inlet rate is set according to the gas composition in the experimental plan.
4The outlet boundary condition is set to the pressure outlet, and the pressure of the pressure outlet is set to 0.
4.1.6. Meshing
In order to ensure the calculation efficiency and the accuracy of the simulation results, mesh refinement processing is carried out in the gas inlet area and the central area of the model, and the other areas are evenly divided into rectangular grids. The total number of grids is about 64,200 (Figure 5).
Figure 5.

Schematic diagram of grid encryption.
4.1.7. Physical Model
Because the change of the explosive reaction flow field in the cavity presents a two-dimensional feature to a large extent, a two-dimensional model consistent with the cross-sectional dimension of the oxidation chamber is established based on software ICEM CFD. The model has a height of 400 mm, a width of 165 mm, and a gas inlet diameter is 32 mm, as shown in Figure 6.
Figure 6.

Numerical model.
4.2. Numerical Simulation Results and Analysis
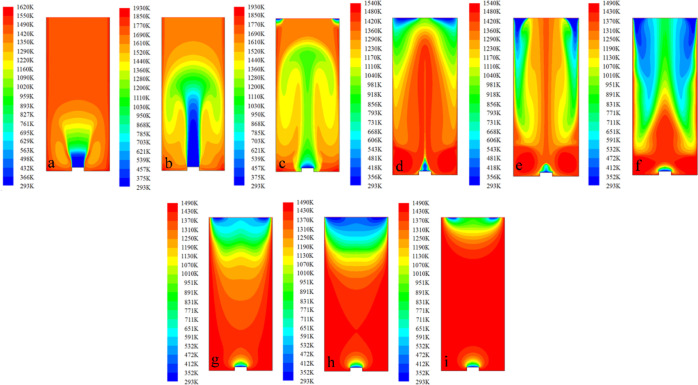
The explosion reaction of the low-concentration gas in the oxidation chamber at 900–1200 °C is simulated, and the gas explosion reaction process is described by the change in the temperature field of the chamber. Figures 7–10 show the simulated gas explosion reaction process at 900, 1000, 1100, and 1200 °C, respectively.
Figure 7.
Temperature change process of the gas explosion reaction in the oxidation chamber at 900 °C: (a) 10; (b) 20; (c) 30; (d) 37; (e) 48; (f) 58; (g) 70; (h) 83; and (i) 200 ms.
Figure 10.
Temperature change process of the gas explosion reaction in the oxidation chamber at 1200 °C. (a) 12; (b) 22; (c) 28; (d) 43; (e) 49; (f) 55; (g) 65; (h) 73; and (i) 83 ms.
Figures 7–10 indicate that the results of the temperature field distribution in the oxidation chamber after gas explosion at different temperatures are generally similar. The general process of low-concentration gas explosion in the oxidation chamber is as follows:
First, after the low-concentration gas is compressed, part of the gas enters the oxidation chamber and undergoes a preliminary reaction. Owing to the high initial temperature and small inlet diameter, part of the gas entering the chamber reacts at the front end, resulting in changes in the local temperature field. The local temperature rises along the radial direction and the wall direction and shows a fan-shaped development trend in the two-dimensional plane, as shown in Figures 7a, 8a, 9a and 10a.
Figure 8.
Temperature change process of the gas explosion reaction in the oxidation chamber at 1000 °C: (a) 12; (b) 22; (c) 29; (d) 38; (e) 49; (f) 55; (g) 66; (h) 89; and (i) 180 ms.
Figure 9.
Temperature change process of the gas explosion reaction in the oxidation chamber at 1100 °C. (a) 12; (b) 22; (c) 31; (d) 38; (e) 49; (f) 55; (g) 61; (h) 70; (i) 82; and (g) 180 ms.
After about 10 ms, most of the gas enters the oxidation chamber. At this time, the temperature in the chamber changes significantly. As the gas continues to enter, a considerable part of the gas undergoes an exothermic combustion reaction. Limited by the wall of the chamber, the fan-shaped temperature field continues to develop to the top and bottom, as shown in Figures 7b, 8b, 9b and 10b.
Next, 1 L of gas enters the chamber. Except for the remaining part of the gas in the central area of the chamber that has not yet fully reacted, most of the gas participates in the chain reaction. At this time, the temperature in the chamber rises as a whole, and the impact generated by the gas explosion reaction causes the top cover of the oxidation chamber to move, and the external room-temperature air starts to enter the chamber from the top edge, as shown in Figures 7c,d, 8c,d, 9c,d, and 10c.
After the gas reaction, there is a pressure relief space at the top of the oxidation chamber, and outside air flows into the chamber from the edge. During this process, due to the cooling effect of the room-temperature air and the gas reaction in the later stage, the temperature in the chamber gradually drops. Specifically, the temperature is high in the center of the chamber, and lower than the initial temperature near the wall. In the later stages of the gas reaction, the energy generated after the explosion reaction is exhausted, and the air entering the upper part of the cavity will be gradually heated, the temperature field in the chamber presents a relatively regular wave-shaped zonal distribution from the bottom to the top, as shown in Figures 7g, 8g, 9h, and 10g. This means that the closer to the pressure relief port, the lower the temperature.
In the process of closing the pressure relief outlet through the top cover, the final reaction products of the gas, namely, CO2, CO, H2, and H2O, no longer exist.26 Because the gas is regulated by the outside room-temperature air and a constant heating field exists around the oxidation chamber, the temperature in the chamber gradually returns to the set temperature, and this process takes a relatively long time. In order to verify the accuracy of the experimental results, the chamber wall is taken as the monitored object. At 900–1200 °C, the pressure-time curve at gas concentrations of 2.0–2.5, 1.3–1.8, 1.3–1.8, and 1.0–1.5% near the lower explosion limit is obtained, as shown in Figure 11.
Figure 11.
Pressure–time curves of the chamber wall near lower explosion limits at different temperatures: (a) 900; (b) 1000; (c) 1100; and (d) 1200 °C.
In Figure 11, the maximum explosion pressure curve generally shows the following two situations at different temperatures. When the gas concentration is higher than the lower explosion limit, the gas explosion reaction causes the pressure to rise rapidly. After the pressure relief space appears at the top cover, the pressure in the chamber drops rapidly. When the gas concentration is lower than the lower explosion limit, the reaction rate is relatively slow because the gas reaction is not violent. As a result, the rise and fall of the pressure on the chamber wall are relatively slow. In addition, at the same temperature, mine gas with a higher concentration contains more methane molecules, which promotes its chain reaction, and thus the time to reach the pressure peak after the gas reaction is shorter.
As shown in Figure 11a, at 900 °C, when the gas concentrations are 2.0 and 2.1%, the maximum gas reaction pressures reach 57 and 63 kPa, respectively. When the gas concentrations are 2.3, 2.4, and 2.5%, the maximum explosion pressures on the chamber wall are 151, 157, and 166 kPa, respectively, which are much higher than the pressure produced at other gas concentrations. This figure indicates that the pressure generated by the gas with a concentration of 2.1% reaches its peak value at 35 ms, and then the reaction pressure drops very slowly. When the gas concentration increases to 2.2%, the pressure peak rises significantly. After the pressure peak, the pressure drops relatively quickly. The pressure change in this concentration interval is obvious, and similar changes also appear in Figure 11b–d.
In order to visually display the change trend of the maximum explosion pressure produced by the gas with a concentration near the lower explosive limit at each temperature, the maximum pressure fitting trend is obtained, as shown in Figure 12. Through the same processing method, the curvature of the fitting curve is obtained. Finally, the experimental and simulated lower explosion limits are compared in Figure 13.
Figure 12.

Fitting curves of the maximum explosion pressure of gas near a lower limit concentration of explosion.
Figure 13.

Experimental and simulated lower explosion limit values and trends.
Figure 12 indicates that the trend of the maximum explosion pressure of the gas near the lower explosion limit at each temperature is similar to the previous fitting trend of the instantaneous explosion pressure, and the relationship between the maximum explosion pressure and the gas concentration also conforms to the Boltzmann function. However, the causes are different. When the gas concentration is lower than the lower explosion limit, also owing to the low methane content, the gas only undergoes a violent oxidation and combustion process, which results in a relatively small maximum explosion pressure. When the gas concentration exceeds the lower explosion limit, methane reacts with oxygen to produce more water vapor. Because water vapor has a large specific heat capacity, it can absorb more heat during the explosion reaction, which has an inhibitory effect on the increase of explosion pressure. Therefore, the maximum explosion pressure no longer continues to increase obviously.27,28 As shown in Figure 13, the lower explosion limit obtained through a numerical simulation is slightly lower than the experimental value. Moreover, the simulated and experimental lower explosion limits decrease with the increase of the temperature, and the simulated and experimental downward trends slow down. After the two sets of data are analyzed, the error between the simulated and experimental values of the lower limit of gas explosion at the four temperatures is 5.2, 7.8, 3.8, and 9.5%, respectively. The error range generally shows a tendency to gradually become larger, reflecting to a certain extent that when the experimental temperature rises to 1200 °C, this puts greater pressure on the experimental system, so the experimental data obtained have relatively large fluctuations. In addition, considering that in the actual operation process, there are some unavoidable practical factors such as long gas pipelines and too many connections, which may cause the overall experimental result to be higher than the simulation result, but the error range does not exceed 10%, which still can verify that the lower limit of gas explosion at 900–1200 °C obtained through the self-developed ultra-high temperature gas explosion experimental apparatus is relatively correct.
5. Discussion
At present, many researchers have conducted comprehensive and in-depth research on the explosion characteristics of mine gas at low initial ambient temperature through different methods. Zhu10 and Kondo et al.29 obtained experimental results at temperatures below 200 °C (Figure 14). In this paper, the lower explosion limit of the gas in an ultra-high temperature environment is obtained through the newly developed high-temperature gas explosion experiment apparatus (Figure 4), and it is found that the change rule is similar to that at temperatures below 200 °C, that is, the lower explosion limit of the gas decreases with the increase of the temperature, and the downward trend gradually slows down.
Figure 14.

Trend of the lower explosion limit of methane at temperatures below 200 °C.
According to the experimental data, the fitting relationship between the lower limit of gas explosion and the ambient temperature at an ultra-high temperature is obtained, as shown in eq 18
| 18 |
where T is the initial ambient temperature and LEL is the lower limit of gas explosion at initial temperature T. The above equation is applicable to the calculation of the lower limit of gas explosion at 900–1200 °C.
In this paper, basic research on the explosion characteristics of gas at ultra-high temperatures is conducted. At present, many mining areas generally mix ultra-low concentration underground gas (<0.75%) with air, then perform thermal storage oxidation treatment, and control the gas concentration below 1.2% (≈1000 °C). In this paper, through experiments and simulation methods, it is found that the gas with a concentration of 1.53 to 1.66% at 1000 °C may have an explosion hazard. The experimental results have a certain reference value for the restriction standards. If the gas concentration can be increased in the future, it will greatly promote the macroscopic aspects such as saving energy and improving regional efficiency. In view of the above shortcomings, based on the current actual situation, mixing methane with other conventional gases to obtain the explosive parameters of the mixed gas is a work that can be carried out in the near future.
6. Conclusions
In this paper, the lower explosion limits of different concentrations of the gas in the oxidation chamber at 900, 1000, 1100, and 1200 °C are analyzed through the high-temperature and low-concentration gas explosion experimental apparatus and the simulation software Fluent. After discussion, the following conclusions are drawn:
-
(1)
For the gas with a concentration range of 1–2.8%, the relationship between the instantaneous explosion pressure and the gas concentration at a time of 1 mm initial displacement of the top cover at 900–1200 °C conforms the Boltzmann function. Through numerical simulation, the relationship between the maximum explosion pressure of the gas and the gas concentration near the lower explosion limit is also in accordance with the Boltzmann function.
-
(2)
As the temperature rises, the lower explosion limit of the gas gradually decreases. The lower explosion limit obtained through the experiment is reduced from 2.33% at 900 °C to 1.36% at 1200 °C by 0.97%. The lower explosion limit obtained through the numerical simulation is reduced from 2.21% at 900 °C to 1.23% at 1200 °C by 0.98%. At 900, 1000, 1100, and 1200 °C, the error between the simulated and experimental values of the lower limit of gas explosion is 5.2, 7.8, 3.8, and 9.5%, respectively.
-
(3)
At a temperature of 900–1200 °C, the change rule of the lower explosion limit of gas is similar to that at temperatures below 200 °C, that is, the lower explosion limit decreases as the temperature rises, and the downward trend slows down.
Acknowledgments
This work was supported by the Key Project of the National 13th-five year research program of China (project no. 2017YFC0805207) and the State Key Laboratory Cultivation Base for Gas Geology and Gas Control (Henan Polytechnic University) (project no. WS2020B06).
The authors declare no competing financial interest.
References
- Si R.; Li R. Dynamic characteristics of low-concentration oxygen-containing gas explosion and key technologies for prevention and control. Coal Sci. Technol. 2020, 48, 7–36. 10.13199/j.cnki.cst.2020.10.002. [DOI] [Google Scholar]
- Wang G.; Yang S.; Zhang S.; Liu X. Current Status and Prospects of Gas Drainage and Utilization Technology in Xinjiang Coal Mining Area. Coal Sci. Technol. 2020, 48, 154–161. 10.13199/j.cnki.cst.2020.03.018. [DOI] [Google Scholar]
- Pilkington G.; Paik S. High speed measurement of the lower flammable limits in a rapidly changing vapor stream. Process Saf. Environ. Prot. 2005, 83, 430–436. 10.1205/psep.04216. [DOI] [Google Scholar]
- Li Q.; Lin B.; Dai H.; Zhao S. Explosion characteristics of H2/CH4/air and CH4/coal dust/air mixtures. Powder Technol. 2012, 229, 222–228. 10.1016/j.powtec.2012.06.036. [DOI] [Google Scholar]
- Wang G.; Xie J.; Xue S.; Wang H. Laboratory study on low-temperature coal spontaneous combustion in the air of reduced oxygen and low methane concentration. Tech. Gaz. - Univ. Osijek 2015, 22, 1319–1325. 10.1016/j.jhazmat.2020.123680. [DOI] [Google Scholar]
- Luo Z.; Zhang Q.; Wang H.; Cheng F.; Wang T.; Deng J. Numerical simulation of gas explosion in confined space based on FLACS. J. China Coal Soc. 2013, 38, 1381–1387. [Google Scholar]; CNKI:SUN:MTXB.0.2013-08-014
- Gieras M.; Klemens R.; Rarata G.; Wolański P. Determination of explosion parameters of methane-air mixtures in the chamber of 40 dm3 at normal and elevated temperature. J. Loss Prev. Process Ind. 2006, 19, 263–270. 10.1016/j.jlp.2005.05.004. [DOI] [Google Scholar]
- Li R.-z.; Huang Z.-c.; Si R.-j. The Influence of Ambient Temperature on Gas Explosion Pressure and Pressure Rising Rate. Explos. Shock Waves 2013, 33, 415–418. [Google Scholar]; CNKI:SUN:BZCJ.0.2013-04-013
- Liu J.; Meng X.; Yan K.; Wang Z.; Dai W.; Wang Z.; Li F.; Yang P.; Liu Y. Study on the Effect and Mechanism of Ca(H2PO4)2 and CaCO3 powders on inhibiting the explosion of titanium powder. Powder Technol. 2021, 395, 158–167. 10.1016/j.powtec.2021.09.067. [DOI] [Google Scholar]
- Zhu P. Study on the Influence of Environmental Factors on the Limit Concentration of Methane Explosion. Coal Technol. 2019, 38, 108–111. 10.13301/j.cnki.ct.2019.06.038. [DOI] [Google Scholar]
- Huang Z. The Influence of Ambient Temperature on the Explosion Characteristics of Premixed Gas. Saf. Coal Mines 2021, 52, 1–6. 10.13347/j.cnki.mkaq.2021.02.002. [DOI] [Google Scholar]
- Gao N.; Zhang Y.; Hu Y. Experimental Study on the Coupling Effect of Temperature and Pressure on the Explosion Limit of Methane-Air Mixture. Explos. Shock Waves 2017, 37, 453–458. [Google Scholar]; CNKI:SUN:BZCJ.0.2017-03-010
- Wan X.; Zhang Q.; Shen S. L. Theoretical estimation of the lower flammability limit of fuel-air mixtures at elevated temperatures and pressures. J. Loss Prev. Process Ind. 2015, 36, 13–19. 10.1016/j.jlp.2015.05.001. [DOI] [Google Scholar]
- Yang L.; Liu Y.; Yang C. Explosion characteristics of methane-air mixture under different humidity and near lower explosion limit. Explos. Shock Waves 2021, 41, 166–175. 10.11883/bzycj-2020-0093. [DOI] [Google Scholar]
- Faghih M.; Gou X.; Chen Z. The explosion characteristics of methane, hydrogen and their mixtures: A computational study. J. Loss Prev. Process Ind. 2016, 40, 131–138. 10.1016/j.jlp.2015.12.015. [DOI] [Google Scholar]
- Cammarota F.; Di Benedetto A.; Di Sarli V.; Salzano E.; Russo G. Combined effects of initial pressure and turbulence on explosions of hydrogen-enriched methane/air mixtures. J. Loss Prev. Process Ind. 2009, 22, 607–613. 10.1016/j.jlp.2009.05.001. [DOI] [Google Scholar]
- Cammarota F.; Di Benedetto A.; Di Sarli V.; Salzano E. Influence of initial temperature and pressure on the explosion behavior of n-dodecane/air mixtures. J. Loss Prev. Process Ind. 2019, 62, 103920. 10.1016/j.jlp.2019.103920. [DOI] [Google Scholar]
- Ren C.; Zhang X.; Zhang Y.; Sun X.; Li J. Research on the Influence Characteristics of the Explosion Limit of Combustible Gas and Its Mixture. Fire Sci. Technol. 2017, 36, 1500–1503. [Google Scholar]; CNKI:SUN:XFKJ.0.2017-11-008
- Salzano E.; Basco A.; Cammarota F.; Di Sarli V.; Di Benedetto A. Explosions of Syngas/CO2 Mixtures in Oxygen-Enriched Air. Ind. Eng. Chem. Res. 2012, 51, 7671–7678. 10.1021/ie201734u. [DOI] [Google Scholar]
- Cui G.; Li Z.; Yang C. Experimental study of flammability limits of methane/air mixtures at low temperatures and elevated pressures. Fuel 2016, 181, 1074–1080. 10.1016/j.fuel.2016.04.116. [DOI] [Google Scholar]
- Xu C.; Si R.; Li R. Study on the law of gas explosion limit change under extremely high temperature. Saf. Coal Mines 2015, 46, 1–4. 10.13347/j.cnki.mkaq.2015.04.001. [DOI] [Google Scholar]
- Li Z.; Gong M.; Sun E.; Wu J.; Zhou Y. Effect of low temperature on the flammability limits of methane/nitrogen mixtures. Energy 2011, 36, 5521–5524. 10.1016/j.energy.2011.07.023. [DOI] [Google Scholar]
- Si R.; Li R.. Research on gas explosion characteristics under special environmental conditions, 1st ed.; Li J., Ed.; Academic Press: China; 2020; pp 77–94. [Google Scholar]
- Middha P.; Hansen O. R. Predicting deflagration to detonation transition in hydrogen explosions. Process Saf. Prog. 2008, 27, 192–204. 10.1002/prs.10242. [DOI] [Google Scholar]
- Shi B.; Mu C.; Ma H.; Jiao Z.; Qi J. Characteristics of Cavity Affecting Shock Wave Propagation of Methane Explosion in Whole Tunnel. J. China Coal Soc. 2020, 45, 841–849. 10.13225/j.cnki.jccs.2020.0791. [DOI] [Google Scholar]
- Deng J.; Li H.; Yang Y.; Hou S.; Wen Z. Micro-kinetics and thermodynamic analysis of gas explosion. J. China Coal Soc. 2006, 31, 487–791. [Google Scholar]; DOI: CNKI:SUN:MTXB.0.2006-04-017
- Qi S.; Du Y.; Zhang P.; Li G.; Zhou Y.; Wang B. Effects of concentration, temperature, humidity, and nitrogen inert dilution on the gasoline vapor explosion. J. Hazard. Mater. 2017, 323, 593–601. 10.1016/j.jhazmat.2016.06.040. [DOI] [PubMed] [Google Scholar]
- Zhang P.; Du Y.; Wu S.; Zhou Y.; Zhou J.; Xu J. Experiments of the secondary ignition of gasoline-air mixture in a confined tunnel. J. Therm. Anal. Calorim. 2014, 118, 1773–1780. 10.1007/s10973-014-4082-y. [DOI] [Google Scholar]
- Kondo S.; Takizawa K.; Takahashi A.; Tokuhashi K. On the temperature dependence of flammability limits of gases. J. Hazard. Mater. 2011, 187, 585–590. 10.1016/j.jhazmat.2011.01.037. [DOI] [PubMed] [Google Scholar]