High-pressure phase transition of AB₃-type compounds: case of tellurium trioxide

Abstract

Tellurium trioxide, TeO₃, is the only example of a trioxide adopting at ambient conditions the VF₃-type structure (a distorted variant of the cubic ReO₃ structure). Here we present a combined experimental (Raman scattering) and theoretical (DFT modelling) study on the influence of high pressure (exceeding 100 GPa) on the phase stability of this compound. In experiments the ambient-pressure VF₃-type structure (R3̄c symmetry) is preserved up to 110 GPa. In contrast, calculations indicate that above 66 GPa the R3̄c structure should transform to a YF₃-type polymorph (Pnma symmetry) with the coordination number of Te⁶⁺ increasing from 6 to 8 upon the transition. The lack of this transition in the room-temperature experiment is most probably connected with energetic barriers, in analogy to what is found for compressed WO₃. The YF₃-type phase is predicted to be stable up to 220 GPa when it should transform to a novel structure of R3̄ symmetry and Z = 18. We analyse the influence of pressure on the band gap of TeO₃, and discuss the present findings in the context of structural transformations of trioxides and trifluorides adopting an extended structure in the solid state.

Tellurium trioxide, TeO₃, is the only example of a trioxide adopting at ambient conditions the VF₃-type structure (a distorted variant of the cubic ReO₃ structure).

Introduction

Tellurium, one of the heaviest metalloids, has recently attracted significant attention due to its role in manufacturing highly efficient photovoltaic panels,^1,2 and investigations of superconductivity in iron-based compounds.³ In these systems tellurium is found as an anion (Te²⁻), but materials containing this element as a cation are also of great interest, as exemplified by the acousto-optic and nonlinear optoelectronic properties of tellurium dioxide (TeO₂).^4,5

Apart from TeO₂, four other oxides of tellurium are known in the solid state: tellurium trioxide (TeO₃) and two mixed-valent compounds containing both Te⁴⁺ and Te⁶⁺ ions (Te₄O₉ and Te₂O₅).^6,7 The phase transitions of TeO₂ induced by pressures exceeding 1 GPa (=10 kbar) were studied intensively both experimentally,^8–13 and by Density Functional Theory (DFT) modelling.^13–16 Compression induces a substantial volume reduction in TeO₂ (by about 36% up to 70 GPa), and an increase in the coordination number (CN) of Te⁴⁺ from 4 to 9.¹²

In contrast, the high-pressure phase transitions of TeO₃, which contains the much smaller Te⁶⁺ cation, were not studied up to date. One of the probable reasons for such lack of research is connected with the poor availability of the starting material. Tellurium trioxide cannot be prepared by direct oxidation of Te or TeO₂, but requires performing the thermal decomposition of orthotelluric acid, Te(OH)₆. Moreover, there is some variation in the published recipes for the synthesis.^17–21

TeO₃ is reported to exhibit four different phases: three of them are crystalline (marked I, II, III following the notation introduced in ref. 21) and one is amorphous (IV). Full structural information is available only for phase I (often referred to as β-TeO₃), which adopts a VF₃-type structure (Fig. 1) exhibiting a coordination number (CN) of Te⁶⁺ equal to 6.^18,20,21 Phase II is reported to adopt a hexagonal unit cell, while for phase III only information on unindexed powder X-ray diffraction lines is available.²¹

Fig. 1. The ambient-pressure VF₃-type structure of TeO₃ (R3̄c) symmetry.

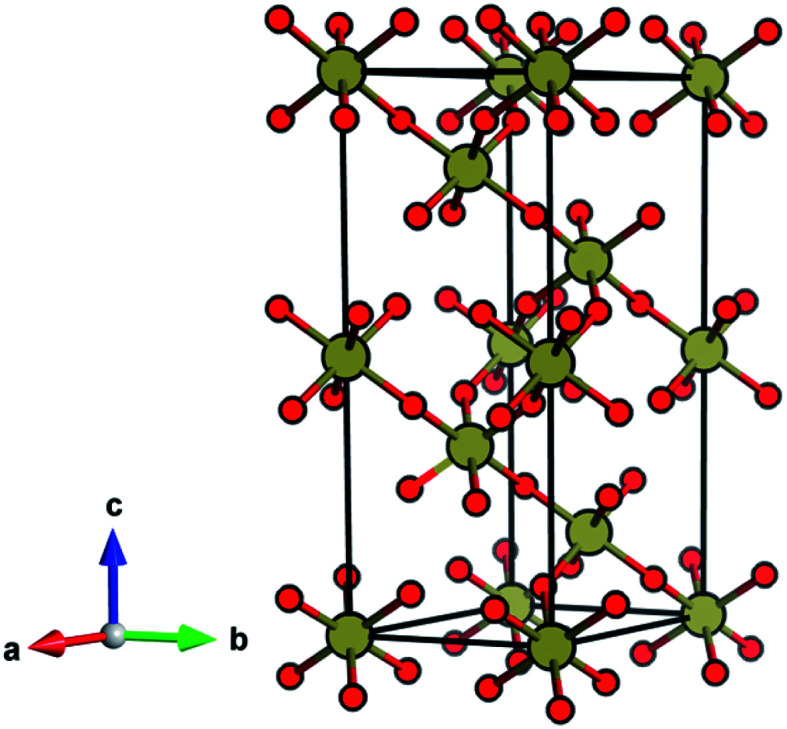
The ambient-pressure VF₃-type structure (R3̄c symmetry, Z = 6)^20,21 is composed of corner-sharing TeO₆ octahedra with all six Te–O contacts equal in length. This geometry can be viewed as a perovskite-type ABX₃ structure with vacant A-sites and tilting of the BX₆ octahedra. The VF₃ polytype can be derived from the non-tilted ReO₃ structure (Pm3̄m, Z = 1)²² by enforcing tilting of the octahedra (a⁻a⁻a⁻ type tilting in Glazer's notation).²³

It's noteworthy to point out that phase I of TeO₃ is the only example of a trioxide adopting the VF₃-type structure. This polytype is more commonly encountered in trifluorides. In this context, it is of interest to explore the high-pressure phase transformations of TeO₃, and compare them with those of trifluorides,^24–26 and trioxides, in particular, WO₃,^27–31 and ReO₃ itself.^32–35

Here we present a combined experimental (Raman scattering) and theoretical (DFT modelling) study on the influence of high pressure on the structure stability of TeO₃. Our experimental results indicate that the ambient-pressure VF₃-type structure (R3̄c symmetry) is preserved up to 110 GPa. In contrast, calculations indicate that above 66 GPa the R3̄c structure should transform to a YF₃-type polymorph (Pnma symmetry) with a subsequent increase in the CN of Te⁶⁺ from 6 to 8. This transition is not observed in an experiment most probably due to large energetic barriers, in analogy to what is found for compressed WO₃. Another transition from the Pnma structure to a rhombohedral phase (R3̄, Z = 18) with a 10-fold coordination of Te⁶⁺ is predicted at 220 GPa. We analyse the influence of pressure on the band gap of TeO₃ and discuss the present findings in the context of structural transformations of trioxides and trifluorides adopting an extended structure in the solid state (in contrast to SbF₃,³⁶ or AsF₃,³⁷ which form molecular crystals).

Experimental and computational details

Sample preparation

TeO₃ was prepared by heating Te(OH)₆, purchased from Aldrich, in a thick glass ampoule at a 350–450 °C temperature range. The best material was obtained by reaction conducted at 450 °C for 20 hours. The purity of the sample was verified by powder X-ray diffraction and Raman spectroscopy (see Fig. S1 in the ESI†).

High-pressure experiments

Three high-pressure runs were conducted with the use of a diamond anvil cell (DAC) equipped with diamonds with a bevelled 300 μm tip (bevel angle of 8°). The sample was enclosed by a stainless-steel gasket pre-indented to a thickness of ca. 30 μm. The gasket hole with a radius of 120 μm was laser-drilled. No pressure-transmitting medium was used. The pressure was determined with the use of the ruby fluorescence scale as proposed by Dewaele et al.,³⁸ as well as the shift of the first-order Raman spectra of the diamond anvil as given by Akahama and Kawamura.³⁹

Raman spectroscopy

The spectra in the first two runs were collected in backscattered geometry using custom designed setup for micro-Raman measurements based on Jobin Yvon THR1000 monochromator equipped with a single grating (with 1200 grooves mm⁻¹) giving a resolution of ∼1 cm⁻¹, notch filters (Keiser Optical Systems) and thermoelectrically cooled (−65 °C) CCD (Horiba Synapse) detection. A He–Ne laser (Melles-Griot) red line (632.8 nm) was used for sample excitation.

The spectra in the third run were acquired with the Alpha300M+ confocal microscope (Witec Gmbh) equipped with a motorized stage. We used a 532 nm laser line delivered to the microscope through a single-mode optical fiber. The laser power at the sample did not exceed 20 mW. The backscattered Raman signal was collected through a 20× long working distance objective, and passed through a multi-mode optical fiber (50 μm core diameter) to a lens based spectrometer (Witec UHTS 300, f/4 aperture, focal length 300 mm) coupled with a back-illuminated Andor iDUS 401 detector thermoelectrically cooled to −60 °C. The spectra were collected in the range of Raman shifts from 70 to 1720 cm⁻¹ with the use of an 1800 mm grating resulting in a 1.2 cm⁻¹ spectral resolution. The acquisition time was 1 s with 30 accumulations. The spectra were post-processed (background subtraction and cosmic-ray removal) with the Project FIVE software (Witec Gmbh). The position of Raman bands was established with the Fityk 1.3.1 software by fitting the observed bands with Pseudo-Voigt profiles.⁴⁰ During the experiment we did not observe any Raman bands that could be assigned to the O₂ vibron,⁴¹ which excludes decomposition of TeO₃ into O₂ and lower-valence tellurium oxides.

DFT calculations

Periodic DFT calculations of the geometry and enthalpy of various polymorphs of TeO₃ utilized the SCAN meta-GGA functional.⁴² This functional was found to offer an accurate description of the high-pressure properties for a wide range of compounds.^43–47 We found that it reproduces very well the geometry and the vibration frequencies of the ambient pressure structure of TeO₃ (see Table S1†), and yields a similar pressure of the VF₃-type TeO₃ → YF₃-type TeO₃ phase transition to the more computational demanding hybrid HSE06 functional (Table S2†).⁴⁸ Thermodynamic stability of various TeO₃ polymorphs was judged by comparing their enthalpy (H), and thus the calculations formally correspond to T = 0 K at which the Gibbs free energy (G = H − ST, where S is the entropy) is equal to H.

The projector-augmented-wave (PAW) method was used in the calculations,⁴⁹ as implemented in the VASP 5.4 code.^50,51 The cut-off energy of the plane waves was set to 800 eV with a self-consistent-field convergence criterion of 10⁻⁸ eV. Valence electrons (Te: 5s², 5p⁴; O: 2s², 2p⁴) were treated explicitly, while standard VASP pseudopotentials were used for the description of core electrons. We verified that using an extended basis set for Te, with the 3d, 4s, and 4p electrons included explicitly, did not alter the obtained results. The k-point mesh spacing was set to 2π × 0.03 Å⁻¹. All structures were optimized until the forces acting on the atoms were smaller than 1 meV Å⁻¹. Calculations of vibration frequencies (also using SCAN) were conducted with the finite-displacement method with 0.007 Å displacement. We did not apply any scaling of the theoretical vibration frequencies when comparing them with experimental values.

At selected pressures, we additionally calculated the intensity of Γ-point Raman-active vibrational modes using density-functional perturbation theory (DFPT),⁵² as implemented in the CASTEP code (academic release version 19.11).⁵³ Due to the large computational cost of these calculations we employed the Local Density Approximation (LDA). This approach was previously successfully used to model the Raman spectrum of Te(ii) and Te(iii) oxides,^54,55 as well as the pressure-induced changes in the Raman spectrum of inorganic fluorides.^46,47 In our calculations we employed norm-conserving pseudopotentials and a cut-off energy of 1020 eV. The Raman activity of each vibrational mode (S_i) was converted into the intensity (I_i) assuming the following relation:where ν₀ is the laser frequency, ν_i is the mode frequency, T is the temperature (taken as equal to 293 K).

We performed evolutionary algorithm searches for lowest-enthalpy structures of TeO₃. For this, we used the XtalOpt software (version r12)⁵⁶ coupled with periodic DFT calculations utilizing the Perdew–Burke–Ernzerhof (PBE) functional.⁵⁷ These searches were conducted at 50, 60, 100, 150, and 200 GPa for Z up to 6 (an additional search at 60 GPa with Z = 12 was also conducted) yielding nearly 5000 crystal structures.

Visualization of all structures was performed with the VESTA software package.⁵⁸ For symmetry recognition we used the FINDSYM program.⁵⁹ Group theory analysis of the vibrational modes was performed with the use of the Bilbao Crystallographic Server.⁶⁰

Results and discussion

High-pressure Raman scattering

Previous studies showed that at ambient pressure all of the four Raman-active vibrational modes of the R3̄c structure (A_1g + 3 × E_g) can be detected, with the A_1g mode having a considerable higher intensity than the E_g modes.^19,54,55 In our diamond anvil cell (DAC) high-pressure experiments we could follow the frequency change of all of these modes up 35 GPa (Fig. 2). Above that pressure, the highest-frequency E_g mode (3E_g) could not be detected due to an increase in the background fluorescence. The lowest-frequency E_g mode (1E_g) could be followed up to 90 GPa, while the medium-frequency E_g mode (2E_g) is shadowed by the A_1g band at approximately the same pressure.

Fig. 2. Raman spectrum (black curves) of the R3̄c polymorph of TeO₃ at low (a) and high (b) pressures. The spectra are offset for clarity. Red bars indicate the intensities of Raman bands obtained with LDA simulations performed for the R3̄c structure at 1 and 40 GPa. Arrows mark the position of a new band developing above 60 GPa.

Up to the highest pressure reached in this study (110 GPa) the observed shifts in the frequency of the Raman bands are in good accordance with those predicted for the VF₃ structure (Fig. 3). However, above 60 GPa we observe a new band developing on the high-frequency side of the A_1g mode (Fig. 2b). The emergence of this band is most probably a result of non-hydrostatic conditions inside the DAC which, present even at lower pressures but amplified by compression, lead for a part of the sample to shifting of the frequency of the A_1g mode to higher values (see Fig. S2†). The changes in the Raman spectrum were observed in all three experimental runs and at different positions in the DAC. The spectrum after decompression to 1 atm was identical to the initial spectrum.

Fig. 3. Pressure dependence of the frequencies of Raman bands of solid TeO₃ measured at room-temperature compression (black points). Stars mark the position of the new Raman band which develops above 60 GPa due to non-hydrostatic conditions (see text). Solid red curves mark frequencies of Raman-active bands calculated for the R3̄c structure with the SCAN functional.

DFT calculations

To gain more insight in the pressure-induced phase transitions of TeO₃, we have conducted evolutionary algorithm searches for the most stable high-pressure polymorphs of this compound (for details see the Methods section). These searches identified two low-enthalpy structures (Fig. 4a and b): one with Pnma symmetry (Z = 4), the other with R3̄ symmetry (Z = 18). The first of these polymorphs is isostructural to YF₃ and exhibits 8-fold coordination of Te⁶⁺ by O²⁻ in the form of a distorted square antiprism. Searches in the Inorganic Crystal Structure Database (FIZ Karlsruhe)⁶¹ indicate that the R3̄ structure, exhibiting 10-fold coordination of Te⁶⁺, has not been previously reported for any AB₃-type compound.

Fig. 4. The high pressure structures of TeO₃:YF₃-type (Pnma symmetry, Z = 6) (a), structure of R3̄ symmetry (Z = 18) (b), HP-WO₃-type (P2₁/c, Z = 4) (c). Coordination numbers of Te⁶⁺ are given for each structure. The R3̄ polymorph is shown in the rhombohedral representation.

Analysis of the pressure dependence of the relative enthalpy of various TeO₃ polymorphs is given in Fig. 5a. Calculations indicate that the VF₃-type structure is the most stable one at ambient conditions (≈0 GPa) – in accordance with experiment. Upon compression, a first order transition from this structure into the YF₃-type polymorph (Pnma symmetry) is predicted at 66 GPa. However, the spectral changes observed in the experiment cannot be assigned to this transition, as the predicted Raman spectrum of the Pnma structure is very different from the experimental one (Fig. S3†). Calculation indicate one more phase transition at 220 GPa from the YF₃-type structure to a polymorph of R3̄ symmetry. This process leads to an increase in CN from 8 to 10 and a volume reduction of nearly 3% (Fig. 5b).

Fig. 5. Pressure dependence of the (a) relative enthalpy (referenced to that of Pnma) of the high-pressure polymorphs of TeO₃ (SCAN calculations), and (b) their volume. Numbers in (a) indicate the pressures corresponding to the R3̄c → Pnma and Pnma → R3̄ phase transitions. Predicted volume changes at these transitions are given in (b).

The lack of the transition between VF₃- and YF₃-type structures in our room-temperature experiment is most probably due to significant kinetic barriers accompanying this process. These are a result of large changes in the Te coordination environment and molar volume (Fig. 5b). This notion is supported by the fact that the VF₃ polymorph is dynamically stable at 66 GPa (vide infra). The lack of the VF₃ → YF₃ phase transition in TeO₃ resembles the situation found for MgF₂ and SnO₂ where large energy barriers hinder the thermodynamically favoured phase transition from the TiO₂-type structure to an α-PbO₂ polymorph.^62,63 To overcome these barriers laser heating of the sample would be required, in analogy to high-pressure experiments conducted for TeO₂.¹² However our current experimental setup does not allow us to perform laser heating of samples enclosed in a diamond anvil cell. Moreover leaser heating could lead to thermal decomposition of TeO₃ (at ambient conditions this compound decomposes above 400 °C).²¹

The fact that the VF₃ structure of TeO₃ is metastable up to 110 GPa is further supported by phonon dispersion calculations. In the 0 to 141 GPa pressure range the R3̄c polymorph does not exhibit any vibrations with imaginary frequencies. However, upon compression, a softening of one phonon branch is observed at the F-point of the Brillouin zone, (1/2, 1/2, 0) vector, which leads to the appearance of imaginary modes at this point above 141 GPa. This behaviour was also observed at high pressure for the VF₃ structure of FeF₃.²⁵

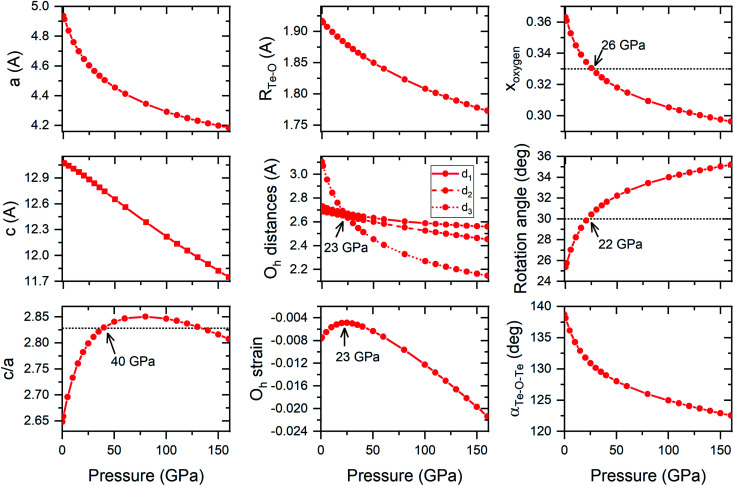
Both FeF₃ and TeO₃ exhibit a similar pressure dependence of structural parameters (although in different pressure ranges). For both compounds pressure initially induces a change in the structural parameters towards an ideal hexagonally close-packing (hcp) packing of O²⁻ anions.^24,25 For example, the c/a ratio increases upon compression up to a point where it exceeds that predicted for a perfect hcp packing (Fig. 6). After reaching a maximum (found at 20 GPa for FeF₃, and 80 GPa for TeO₃ – see Fig. 6) this ratio decreases upon compression. Interestingly in both FeF₃ and TeO₃ the F-point phonon instability appears at the point when this ratio becomes again smaller than the value predicted for a perfect hcp packing.

Fig. 6. Calculated evolution of the structural parameters of the R3̄c structure upon compression. The d₁ and d₂ distances are O–O distances within the TeO₆ octahedra (d₁ within the ab plane, d₂ out of plane), while d₃ is the O–O distance between the octahedra located in the same ab plane. The octahedral (O_h) strain is calculated as equal to (d₂ − d₁)/(d₂ + d₁), negative values indicate compression of the TeO₆ octahedron along the c cell vector. The rotation angle is calculated with respect to the 〈111〉 direction of the ideal cubic ReO₃ cell; α_Te–O–Te is the angle of the Te–O–Te bridge. Dotted horizontal lines indicate c/a, x_o, and rotation angle values expected for a perfect hexagonal close-packing packing of O²⁻ anions.

Distorting the R3̄c structure along the eigenvector of the imaginary mode, and subsequent geometry optimization, leads to a structure with four TeO₃ units per unit cell and P2₁/c symmetry (this space group is the highest-symmetry sub-group of R3̄c along the (1/2, 1/2, 0) modulation vector). This structure, shown in Fig. 4c, is a distorted variant of the high-pressure phase of WO₃ (HP-WO₃),²⁸ and exhibits 7-fold coordination of Te⁶⁺ (increasing to 8-fold upon compression). The R3̄c → P2₁/c transition is of first order (ΔV/V = −5.8% at 141 GPa). However, given the fact that it is connected with a phonon instability, it might be characterized by a small energetic barrier. It, therefore, could be observed during room-temperature compression.

SCAN calculation of the pressure dependence of the electronic band gap (E_g) for the high-pressure structures of TeO₃ is shown in Fig. 7. The E_g value obtained at ambient conditions for the VF₃ structure (1.55 eV) is underestimated compared with the experimental value (3.25 eV), but larger than that obtained in calculations utilizing the PBE functional (1.21 eV).^64,65 Compression induces an increase of the band gap in all TeO₃ polymorphs, especially for the VF₃-type structure exhibiting octahedral coordination of Te⁶⁺. This trend is similar to what is found for ionic difluorides (MF₂, M = Be, Mg, Ca),⁶⁶ and in contrast to TeO₂ where much smaller variations of E_g are seen.¹⁵ The band gap is predicted to decrease abruptly upon the R3̄c → Pnma (p = 60 GPa) and the Pnma → R3̄ (p = 220 GPa) phase transition.

Fig. 7. Dependence of the electronic band gap upon compression for the high-pressure structures of TeO₃. Predicted changes in E_g at the R3̄c → Pnma (p = 60 GPa) and Pnma → R3̄ (p = 220 GPa) transitions are given.

Conclusions

High-pressure Raman measurements indicate that the ambient-pressure VF₃-type structure (R3̄c symmetry) persists up to 110 GPa. Calculations confirm the dynamic stability of this polymorph up to a pressure of 141 GPa. At larger compression a phonon instability should lead to a transition into a distorted variant of the high-pressure phase of WO₃ (P2₁/c symmetry) with a subsequent increase of the Te⁶⁺ coordination number from 6 to 7. We argue that a similar transition could be observed for FeF₃, which exhibits the same type of instability.²⁵ The HP-WO₃ phase can also be a candidate for a post-VF₃ phase of ReO₃.³²

Calculations indicate that the persistence of the VF₃-type structure above 66 GPa is a kinetic effect as this polymorph, as well as the HP-WO₃ structure, are thermodynamically less stable than a YF₃-type polymorph (Pnma space group), which exhibits 8-fold coordination of Te⁶⁺. The lack of the VF₃ → YF₃ phase transition in room-temperature compression experiments is most probably a result of the large energetic barriers associated with it. It's noteworthy to mention that a similar situation is found for WO₃. For this compound calculations indicate that a YF₃ structure is the ground state structure above 20 GPa.³¹ However, it has not been observed in experiments conducted up to 40 GPa.²⁹

We predict that above 220 GPa TeO₃ should enter a post-YF₃ phase with R3̄ symmetry (Z = 18) and 10-fold coordination of Te⁶⁺. We do not find evidence for a possible transition into the 12-fold coordinated LaF₃-type structure (P3̄c1) adopted by rare earth trifluorides, nor to the 9-fold coordinated Cmcm phase proposed for WO₃.³¹ Finally, we show that high pressure and compression-induced phase transitions lead to large variations of the electronic band gap of TeO₃. The possibility of pressure-tuning of the band structure of TeO₃ polymorphs is also of interest in the context of non-linear properties of this material.⁶⁴

Conflicts of interest

The authors declare no competing financial interest.