The effect of enzyme loading, alcohol/acid ratio and temperature on the enzymatic esterification of levulinic acid with methanol for methyl levulinate production: a kinetic study

Abstract

As an important bio-based chemical, methyl levulinate (ML) can be produced via enzymatic esterification of levulinic acid with methanol. A kinetic model is developed in this work based on the law of mass action and reaction reversibility, to investigate the effect of enzyme loading, alcohol/acid ratio and temperature on ML yield. Data analysis shows that newly developed binary regression is apparently more persuasive than the commonly used unitary regression. Kinetic study reveals: (1) rate constants of esterification/hydrolysis increase with increasing enzyme loading, while their ratio (equilibrium constant) remains invariant. (2) Methanol has no toxicity towards lipase, and hence, neither the rate constants of esterification/hydrolysis nor the equilibrium constant are affected by alcohol/acid ratio. (3) Both rate constants of esterification/hydrolysis and the equilibrium constant increase with temperature elevation, and their relationships agree with Arrhenius equation and Van't Hoff equation, respectively. (4) The esterification is endothermic and spontaneous. In total, the application of binary regression analysis for the developed model to study the enzymatic esterification kinetics is quite successful.

Based on reaction reversibility and the law of mass action, a mathematical model was developed. By the developed model, the effect of enzyme loading, molar alcohol/acid ratio, and temperature on methyl levulinate yield was kinetically analyzed.

1. Introduction

As an important bio-based chemical, methyl levulinate (ML) can be used as a gasoline/diesel additive, a green solvent, and a plasticizing and antifreeze agent.^1–3 ML is mostly produced from enzymatic or chemical esterification of levulinic acid (LA).^1,4 Compared to chemical catalysis, enzymatic catalysis has many benefits such as mild operation conditions, high product specificity and low pollution.^5–7 Esterification is reversible, and H₂O is also a product, which can promote reverse esterification (hydrolysis).⁸ Hence, in order to obtain high ML yield, the esterification should be carried out in non-aqueous systems (organic phase).^7,9 However, organic solvents and alcohols are always toxic toward lipase, hence, direct use of free lipase cannot obtain efficient esterification. Lipase must be immobilized to improve its tolerance.^10–12 Moreover, immobilization can provide the recyclability of the biocatalyst for possible-reuse, which can sharply reduce the lipase cost. Therefore, lipase immobilization gains more and more attention, and the enzymatic esterification becomes a heterogeneous reaction owing to the insolubility of the immobilized lipase.

To quantitively describe the effect of lipase loading, alcohol/acid ratio and temperature on ML yield, it is desirable to study the enzymatic esterification kinetics.^13–15 Besides, the development of kinetic models always helps to predict the reaction results and gain insight into the mechanism.^14,16 However, complex heterogeneous systems make it difficult to develop a kinetic model for reversible esterification. The typical Michaelis–Menten theory based on homogeneous systems cannot been applied to the heterogeneous process.

Based on reaction reversibility and law of mass action, a second-order model has been developed and it has gained much popularity.^8,17–21 However, during the application of the model, either the rate constants vary with substrate concentration or the equilibrium constant varies with substrate concentration and enzyme loading.^17–19,21 Further, irregular variation in the rate and equilibrium constants always occurs when the temperature increases.^18,20,21 Obviously, it is unreasonable. Toward this, some constraint conditions are added in this study to revise the data analysis, in which the relationship between rate/equilibrium constants and various factors exhibits rationale rules.

2. Experimental

2.1. Materials

LA, ML and methanol were purchased from Aladdin (Shanghai, China). An organic solvent namely 1-butyl-3-methylimidazolium hexafluorophosphate ([bmim][PF₆]) was purchased from Zhejiang Xinming Chemical Co., Ltd. (Ningbo, China). Immobilized lipase CAL-B (Candida Antarctica Lipase B) was purchased from Novozymes Co., Ltd. (Tianjin, China). 3Å molecular sieves were purchased from Tianjin Kemiou Chemical Reagent Co., Ltd. (Tianjin, China).

2.2. Dehydration of organic solvent

3Å molecular sieves were activated in a muffle furnace at 550 °C for 5 h, and cooled to room temperature in a desiccator. In order to dehydrate the organic solvent, the solvent and the activated molecular sieves were mixed at 150 rpm and room temperature. After 24 h, the molecular sieves were separated, and the obtained organic solvent was used as the dehydrated solvent for esterification reaction.

2.3. Esterification reaction

LA and methanol were mixed in a molar ratio of 1 : 3 in a brown Erlenmeyer flask, and then [bmim][PF₆] was added with methanol volume of 3 times. To start the reaction, 10 g L⁻¹ CAL-B was added. The reaction temperature and rotation speed were 30 °C and 150 rpm, respectively. At 3 h, 5 h, 7 h, 9 h, 18 h and 24 h, 0.4 g samples were taken out and diluted with methanol in a 5 mL volumetric flask. The diluted samples were then filtered with 0.22 μm filters and used for ML analysis by gas chromatography as per our previous report.⁶

2.4. Model development

Based on the law of mass action and reaction reversibility, eqn (1) was firstly proposed by Han et al.:⁸

1

Solving eqn (1) with the boundary condition (Y = 0, at t = 0), Y can be expressed as shown in eqn (2) and (3):

2

3

3. Results and discussion

3.1. Kinetic study on the effect of enzyme loading

The amount of enzyme loading C_E directly decides the reaction rate and the time for the reaction to reach equilibrium. CAL-B predominantly exhibits esterification activity over hydrolytic activity.⁶ Therefore, the more C_E is, the higher Y is at the same reaction time (Fig. 1 (symbol points)). With increase in C_E, the binding of enzyme and substrate becomes more and more saturated, and hence the trend of increase in Y become progressively lower. Over 50% ML was produced within the first 5 h except for C_E = 2 g L⁻¹. The slowdown of reaction rate could be caused by enzyme deactivation,^22,23 product inhibition²⁴ and attainment of chemical equilibrium¹³ as others have demonstrated. Increase in C_E can cause high cost even if Y is improved. Therefore, C_E = 8 g L⁻¹ may be the optimum choice.

Fig. 1. Experimental data versus fitted lines of ML yield for lipase-catalysed esterification of LA and methanol at different enzyme loadings. Temperature: 303.15 K; molar alcohol/acid ratio: 3.

Firstly, unitary regression was used to analyse the experimental Y, as shown in Fig. 1 (symbol points), where only t was taken as the independent variable and experimental Y at each C_E were separately fitted by eqn (2). As shown in Fig. 1 (dotted lines), the fitting accuracy is very high, as verified by R² (Table 1 (unitary regression)). As shown in Table 1, k₂ decreases with the increase in C_E although k₁ increases with its increase, which has also been reported by others.¹⁹ Normally, both k₁ and k₂ should present a positive correlation with C_E. Since the present results show the opposite, therefore, a significant problem exists for unitary regression. Besides, equilibrium constant K_e, defined by eqn (4), varies with C_E (Table 1 (unitary regression)). Clearly, it is also unreasonable because K_e is related only to temperature. Similar issues exists in other reports, but further elaboration and analysis is still lacking.^17–19,21 Both k₁ and k₂ increase with the increase in C_E as per Tomke and Rathod's report, however, K_e at each C_E is still different.²¹

4

Fitted values of k₁ and k₂ from unitary and binary regression analyses of experimental data at each C_E.

Fitting method	Parameter	Unit	C E (g L−1)
			2	4	6	8	10
Unitary regression	k 1	L h−1 mol−1	0.007354	0.03006	0.06844	0.09960	0.1142
	k 2	L h−1 mol−1	0.1925	0.08964	0.05690	0.03965	0.02193
	K e		0.034	0.34	1.204	2.514	5.21
	R 2		0.9937	0.9909	0.9935	0.9974	0.9997
Binary regression	k 1	L h−1 mol−1	0.006006	0.02109	0.04399	0.07409	0.1110
	k 2	L h−1 mol−1	0.001337	0.004695	0.009790	0.01649	0.02471
	K e		4.49
	R 2		0.9411	0.9112	0.9289	0.9770	0.9996

To solve the above problems, the fitting has been revised in the present work by adding some constraint conditions as shown in eqn (5):

k_i = k_i,E × C_E^m, i = 1 or 2 5

The enzymatic promotion factor m must be identical for esterification and hydrolysis reactions. Otherwise, K_e will become different at different C_E, as reported in our previous study.¹³ Binary regression is proposed by combining eqn (2) and (5), where both C_E and t are taken as independent variables.

The proposed binary regression can ensure the increase in the rate constant and invariance of K_e with C_E increase. Table 2 lists the parametric values fitted through binary regression, where k_1,E is larger than k_2,E. Hence, k₁ is always larger than k₂ at any C_E according to eqn (5), and their ratio is the constant K_e. The value of m quantitatively describes the effect of C_E on k₁ and k₂. The larger m is, the faster k₁ and k₂ increase with the increase in C_E. As shown in Fig. 1 (solid lines), the experimental Y is also very close to the fitted lines, as verified by R² (Table 1 (binary regression)), although the fitting accuracy is no better than that obtained through unitary regression. What's more, the proposed binary regression ensures the regular variance of k₁ and k₂, and invariance of K_e, compared to unitary regression.

Fitted parametric values of intrinsic rate constant and enzymatic promotion factor from binary regression analysis of experimental data at various enzyme loadings.

Parameter	k 1,E	k 2,E	m	R 2
Unit	g L−1 mol−1	g L−1 mol−1
	0.001710	0.0003806	1.8124	0.9679

3.2. Effect of alcohol/acid ratio

Alcohol, as a substrate of esterification, can favourably shift the reaction toward ML production (esterification). Hence, increasing R_m accelerates the esterification process and enhances Y as shown in Fig. 2 (symbol points). However, the increase in the trend becomes progressively smaller with increasing R_m. The increase in Y is very significant when R_m increases from 0.5 to 1.0 and from 1.0 to 1.5, while only a slight increase is observed when R_m increases from 1.5 to 2, from 2 to 2.5, and from 2.5 to 3.

Fig. 2. Experimental data versus fitted lines of Y for lipase-catalyzed esterification of LA and methanol at different R_m. Enzyme loading: 10 g L⁻¹; temperature: 303.15 K.

Besides, R_m increase results in the decrease in the conversion rate of alcohol, although the conversion rate of LA increases. Therefore, R_m = 1.5 may be the best choice. Similarly, unitary regression was initially used to fit the experimental Y in Fig. 2 (symbol points), where only t was taken as the independent variable and experimental Y at each R_m were separately substituted to eqn (2).

Fig. 2 (dotted lines) shows a very high fitting accuracy, as verified by R² > 0.98 in Table 3 (unitary regression). The table also shows that both k₁ and k₂ do not present a corresponding relationship with R_m. The variance in both k₁ and k₂ with the increase in R_m seems to be irregular, and even k₂ = 0 when R_m = 1.5. Similar problems have been presented in other reports, but no major discussion or resolution has been proposed.^18,20,21 Although both k₁ and k₂ decease as R_m increases as reported by Alves et al. (heptane as the solvent), the value of K_e is not identical at each R_m.¹⁸ Therefore, the fitting should be revised to overcome the problem.

Fitted values of k₁ and k₂ from unitary and binary regression analyses of experimental data for each R_m.

Fitting method	Parameter	Unit	R m
			0.5	1.0	1.5	2.0	2.5	3.0
Unitary regression	k 1	L h−1 mol−1	0.1343	0.1035	0.08362	0.07394	0.1321	0.1142
	k 2	L h−1 mol−1	0.02127	0.01203	0	0.006472	0.02711	0.02193
	K e		6.31	8.60	+∞	11.42	4.87	5.21
	R 2		0.9966	0.9777	0.9837	0.9901	0.9915	0.9997
Binary regression	k 1	L h−1 mol−1	0.1110
	k 2	L h−1 mol−1	0.02471
	K e		4.49
	R 2		0.9939	0.9778	0.9636	0.9615	0.9864	0.9996

Generally, neither k₁ nor k₂ is related to substrate concentration. However, alcohol is a unique substrate which always has some toxicity toward the enzyme. It has been reported that alcohols, especially short-chain alcohols can seriously inhibit the activity of some lipases.^25,26 In this study, the inhibition of alcohol on lipase activity is described by rate constant as shown in eqn (6):

k_i = k_i,Rm × C_M0⁻ⁿ = k_i,Rm × (R_m × C_S0)⁻ⁿ, i = 1 or 2 6

From eqn (6), it can be concluded that both k₁ and k₂ decrease with the increase in R_m. Using eqn (6) as constraint condition, the binary regression is used to fit the experimental data in Fig. 2 (symbol points) by eqn (2), where both t and R_m are considered as independent variables.

Surprisingly, the fitted value of n is 0, which validates that alcohol doesn't have any toxicity towards CAL-B. Hence, k₁ and k₂ are identical at each R_m. This outcome may be due to CAL-B being an immobilized lipase, and the high tolerance against alcohol is attained via immobilization.^10,12 Substituting the same values of k₁ and k₂ in eqn (2), the correlation coefficient (R² > 0.96) shows a very high fitting accuracy. Of course, the fitting performance is not superior to that of unitary regression, but confirms the invariance of K_e at each R_m.

3.3. Effect of temperature

T is another important parameter for enzymatic reaction.^27,28 Both esterification and hydrolysis rate constants can be improved by evaluating T. However, the improvement is limited within a certain range due to inevitable denaturation and deactivation of lipase at high temperatures.²⁹ As shown in Fig. 3 (symbol points), Y increased with the increase in T.

Fig. 3. Experimental data versus fitted lines of Y for lipase-catalyzed esterification of LA and methanol at different T. Enzyme loading: 10 g L⁻¹; molar alcohol/acid ratio: 3.

Similarly, unitary regression was initially used to fit the experimental Y in Fig. 3 (symbol points), where only t was taken as the independent variable. For the proposed unitary regression, experimental Y at each T was substituted into eqn (2). The fitted parametric values are listed in Table 4. Although k₁ increases with T elevation, k₂ decreases. Obviously, the fitting based on unitary regression is unreasonable. Similar issues were also reported by others, but further analysis and resolution is still lacking.^17,19 Besides, completely irregular variance of k₁ and k₂ at different T, has also been reported.^18,20,21 To this end, some constraint conditions must be added to revise the fitting.

Fitted values of k₁ and k₂ from unitary and binary regression analyses of experimental data at each molar alcohol/acid ratio.

Fitting method	Parameter	Unit	T (K)
			293.15	298.15	303.15
Unitary regression	k 1	L h−1 mol−1	0.02935	0.03761	0.1142
	k 2	L h−1 mol−1	0.09462	0.02751	0.02192
	K e		0.31	1.37	5.21
	R 2		0.9953	0.9916	0.9997
Binary regression	k 1	L h−1 mol−1	0.01720	0.04439	0.1110
	k 2	L h−1 mol−1	0.004205	0.01035	0.02471
	K e		4.09	4.29	4.49
	R 2		0.8980	0.9902	0.9996

It is widely accepted that the relationship between the rate constant and temperature always agrees with Arrhenius equation, as shown in eqn (7):

7

Using eqn (7) as the constraint condition, binary regression is proposed for eqn (2) to analyse the experimental Y at all T, where both t and Y are taken as independent variables. The fitted lines and parametric values are shown Fig. 3 (dotted lines) and Table 5, respectively.

Fitted parametric values of intrinsic rate constant and enzymatic promotion factor from binary regression analysis of experimental data at various temperatures.

Parameter	E a,1	E a,2	A 1	A 2	R 2
Unit	kJ mol−1	kJ mol−1	L h−1 mol−1	L h−1 mol−1
	138	131	6.15 × 1022	8.79 × 1020	0.9611

E _a,1 > E_a,2, indicates that the occurrence of esterification reaction requires a higher activation energy compared to the hydrolysis reaction. As a result of A₁ being much larger than A₂, the value of k₁ is still higher than that of k₂, although E_a,1 > E_a,2.

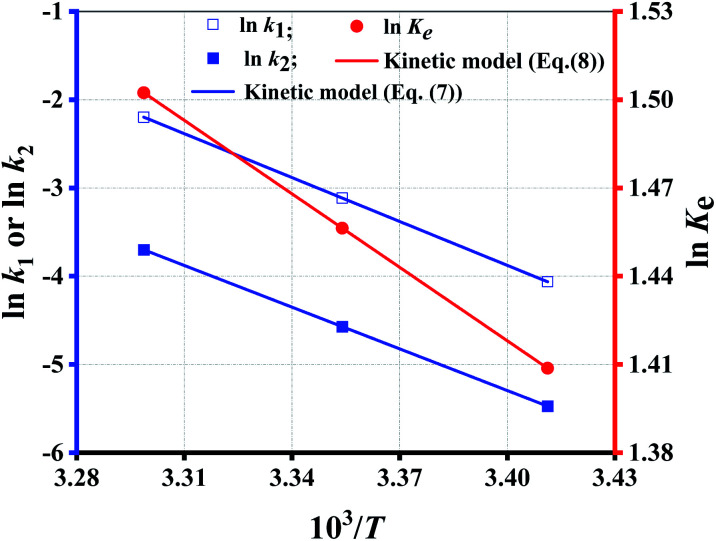
Since eqn (7) is a constraint condition, the relationship between ln k₁ (or ln k₂) and 1/T is fully linear (Fig. 4). Taking the data from Table 5, the values of k₁ or k₂ are calculated using eqn (7) (Table 4 (binary regression)). Thereafter, the kinetics lines are drawn using eqn (7) (Fig. 3 (dotted lines)). The figure shows that experimental data is very close to the kinetics lines, indicative of a very good fitting, as verified by the R² values listed in Table 4. Overall, the fitting accuracy at high temperatures is apparently higher than at low temperatures.

Fig. 4. The fitting of rate/equilibrium constant with temperature.

Reaction equilibrium can be changed by T other than by C_E and R_m. The effect of T on the reaction equilibrium is evaluated by K_e at each T, as defined by eqn (8):

8

Taking the values of k₁ and k₂ listed in Table 4 (binary regression) into eqn (8), value of K_e is calculated at each T. According to Van't Hoff equation, the relationship between K_e and T can be described by eqn (9):

9

Fig. 4 shows that the fitting is rather perfect, and the values of ΔH and ΔS are 6919 J mol⁻¹, and 35.31 J mol⁻¹ K⁻¹, respectively. K_e increases with T elevation, and so ΔH > 0, which indicates that esterification is an endothermic reaction. Hence, the elevation of T can shift the equilibrium to esterification, which is beneficial to obtain higher Y. As result of K_e > 1, ΔG > 0 at any T, which demonstrates that the esterification occurs spontaneously.

4. Conclusions

Compared to unitary regression, binary regression has been demonstrated to be more suitable for the developed model to analyze the effect of C_E, R_m and T on enzymatic esterification of LA with methanol. Both k₁ and k₂ increase with the increase in C_E and T, while kept invariant at all R_m. K_e is not related to C_E and R_m, but increases with T elevation. Besides, kinetic study also shows that the esterification is endothermic and spontaneous.

Nomenclature

Y

ML yield (%)

t

Reaction time (h)

k ₁

Rate constant of esterification (L h⁻¹ mol⁻¹)

k ₂

Rate constant of hydrolysis (L h⁻¹ mol⁻¹)

C _S0

Initial substrate LA concentration (mol L⁻¹)

C _M0

Initial substrate methanol concentration (mol L⁻¹)

R _m

Initial molar alcohol/acid ratio (C_M0/C_S0)

K

Apparent rate constant (L h⁻¹ mol⁻¹)

C _E

Lipase loading (g L⁻¹)

K _e

Equilibrium constant

k _1,E

Intrinsic esterification rate constant of related to enzyme (L h⁻¹ mol⁻¹)

k _2,E

Intrinsic hydrolysis rate constant of related to the enzyme (L h⁻¹ mol⁻¹)

m

Enzymatic promotion factor

k _1,Rm

Intrinsic esterification rate constant of related to alcohol(L h⁻¹ mol⁻¹)

k _2,Rm

Intrinsic hydrolysis rate constant of related to alcohol (L h⁻¹ mol⁻¹)

n

Alcohol inhibition factor

A ₁

Pre-exponential factor of esterification ((L h⁻¹ mol⁻¹))

A ₂

Pre-exponential factor of hydrolysis (L h⁻¹ mol⁻¹)

E _a,1

Activation energy of esterification (kJ mol⁻¹)

E _a,2

Activation energy of hydrolysis (kJ mol⁻¹)

R

Molar gas constant (J mol⁻¹ K⁻¹)

T

Temperature (K)

ΔG

Gibbs free energy (J mol⁻¹)

ΔH

Enthalpy change (J mol⁻¹)

ΔS

Entropy change (J mol⁻¹ K⁻¹)

Author contributions

All authors contributed to the writing of the manuscript. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.