Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Dec 23.
Published in final edited form as: Proc SPIE Int Soc Opt Eng. 2021 Feb 15;11603:116030Q. doi: 10.1117/12.2582330

Automatic detection of head and neck squamous cell carcinoma on pathologic slides using polarized hyperspectral imaging and machine learning

Ximing Zhou a, Ling Ma a, William Brown a, James V Little b, Amy Y Chen c, Larry L Myers d, Baran D Sumer d, Baowei Fei a,e,f,*
PMCID: PMC8699168  NIHMSID: NIHMS1762461  PMID: 34955584

Abstract

The aim of this study is to incorporate polarized hyperspectral imaging (PHSI) with machine learning for automatic detection of head and neck squamous cell carcinoma (SCC) on hematoxylin and eosin (H&E) stained tissue slides. A polarized hyperspectral imaging microscope had been developed in our group. In this paper, we imaged 20 H&E stained tissue slides from 10 patients with SCC of the larynx by the PHSI microscope. Several machine learning algorithms, including support vector machine (SVM), random forest, Gaussian naive Bayes, and logistic regression, were applied to the collected image data for the automatic detection of SCC on the H&E stained tissue slides. The performance of these methods was compared among the collected PHSI data, the pseudo-RGB images generated from the PHSI data, and the PHSI data after applying the principal component analysis (PCA) transformation. The results suggest that SVM is a superior classifier for the classification task based on the PHSI data cubes compared to the other three classifiers. The incorporate of four Stokes vector parameters improved the classification accuracy. Finally, the PCA transformed image data did not improve the accuracy as it might lose some important information from the original PHSI data. The preliminary results show that polarized hyperspectral imaging can have many potential applications in digital pathology.

Keywords: Polarized hyperspectral imaging, Stokes vector, head and neck cancer, machine learning, histologic slides, digital pathology

1. INTRODUCTION

Head and neck squamous cell carcinoma (SCC) is originated from the mucosal epithelium in the oral cavity, pharynx and larynx and is the major head and neck malignancies [1]. Computational pathology, also known as digital pathology, is an emerging technology that promises quantitative diagnosis of pathological samples, and traditional computational pathology relies on RGB digitized histology images [2]. Multidimensional optical imaging has grown rapidly in the recent years. Rather than measuring only the two-dimensional spatial distribution of light as in the conventional photography, multidimensional optical imaging captures unprecedented information about photons’ spatial coordinates, emittance angles, wavelength, time, and polarization [3].

Hyperspectral imaging (HSI) is an optical imaging method that was originally used in remote sensing, and it has been extended to the applications in several other promising fields including biomedical applications [4]. Hyperspectral imaging acquires the spectra of the pixels in a two-dimensional (2D) images and constructs a three-dimensional (3D) data cube, where rich spatial and spectral information can be obtained simultaneously. Hyperspectral imaging has been implemented on the detection of head and neck cancer. A hyperspectral endoscope was developed with a star-shaped filter to image larynx cancer in vivo, assisted by a classification algorithm for the identification of healthy and cancerous tissues, which took image registration, noise removal and specular reflectance detection into consideration [5, 6]. Yushkov et al [7] developed an acoustic-optic hyperspectral imaging system with an amplitude mask, which improved the contrast for phase visualization in the stained and unstained histological sections of human thyroid cancer. A pilot study was implemented to test the feasibility of a hyperspectral imaging system for in vivo delineating the preoperatively lateral margins of ill-defined BCCs on the head and neck region [8]. Our group has investigated several machine learning and deep learning algorithms for head and neck cancer detection based on hyperspectral imaging, including principal component analysis (PCA) [9], tensor-based computation and modeling [10], the incorporation of support vector machine (SVM) into a minimum spanning forest [11, 12], non-negative matrix factorization (NMF) [13], the combination of super pixels, PCA, and SVM [14], as well as convolutional neural networks (CNN) [15, 16, 17, 18, 19].

Polarized light imaging is an effective optical imaging technique to explore the structure and morphology of biological tissues through obtaining their polarization characteristics. It can acquire the 2D spatial polarization information of the tissue, which reflects various physical properties of the tissue, including surface texture, surface roughness, and surface morphology information [20, 21, 22, 23, 24]. The categories of polarized light imaging techniques, namely linear polarization imaging [25, 26, 27], Muller matrix imaging [28, 29], and Stokes vector imaging [30], have been applied on head and neck cancer detection. Orthogonal polarization spectral (OPS) imaging method, which is a type of linear polarization imaging method, was implemented for evaluation of anti-vascular tumor treatment and oral squamous cell carcinoma on tissue [25, 26]. A multispectral digital microscope (MDM) with an orthogonal polarized reflectance (OPR) imaging mode was developed for in vivo detection of oral neoplasia [27]. A 4×4 Muller matrix imaging and polar decomposition method were applied for diagnosis of oral precancer [29], and the researchers adopted a 3×3 Muller Matrix imaging method for oral cancer detection [28]. In our previous study, we developed a novel polarized hyperspectral imaging microscope, which is able to distinguish squamous cell carcinoma from normal tissue on hematoxylin and eosin (H&E) stained slides from larynx based on the spectra of Stokes vector [30].

Polarized hyperspectral imaging (PHSI) is a combination of polarization measurement, hyperspectral analysis, and space imaging technology. It can obtain the polarization, spectral and morphological information of the object simultaneously [31, 32, 33]. In this paper, we are developing a novel dual-modality optical imaging microscope by combining hyperspectral imaging and polarized light imaging. The microscope is capable of acquiring polarization, spectral and spatial information of an object simultaneously, and provides more image information for digital pathology compared to RGB digitized histology images. We incorporated the polarized hyperspectral imaging microscope with machine learning algorithms for automatic detection of SCC on H&E stained tissue slides. We also investigated the ability of using machine learning algorithms to classify the data collected with the polarized hyperspectral imaging microscope. To the best of our knowledge, this is the first study to use polarized hyperspectral imaging for the detection of head and neck cancer based on full Stokes polarized hyperspectral imaging datasets.

2. METHODS

2.1. Polarized hyperspectral imaging system setup

The setup of our home-made polarized hyperspectral microscope has been described in [30]. The system is capable of full Stokes polarized light hyperspectral imaging, which acquires the images of four Stokes vector parameters (S0, S1, S2, S3) in the wavelength range from 486 nm to 700 nm. The images were collected under 10× magnification with an image size of 1088 × 1088 pixels, and the field of view of the imaging system was 595 um × 595 um. The core components of the imaging system include an optical microscope, two polarizers, two liquid crystal variable retarders (LCVR), and a novel SnapScan hyperspectral camera, as shown in Figure 1. The LCVRs and polarizers in the system are for polarized light imaging. The SnapScan hyperspectral camera is able to acquire data through the translation of the imaging sensor inside of the camera. The polarized light imaging components and hyperspectral imaging components work together in the image acquisition progress to obtain the Stokes vector parameters in the visible wavelength range. In the polarized hyperspectral imaging dataset obtained by the system, each Stokes vector parameter corresponds to a 3D data cube with two spatial dimensions and one spectral dimension, as shown in Figure 2.

Figure 1.

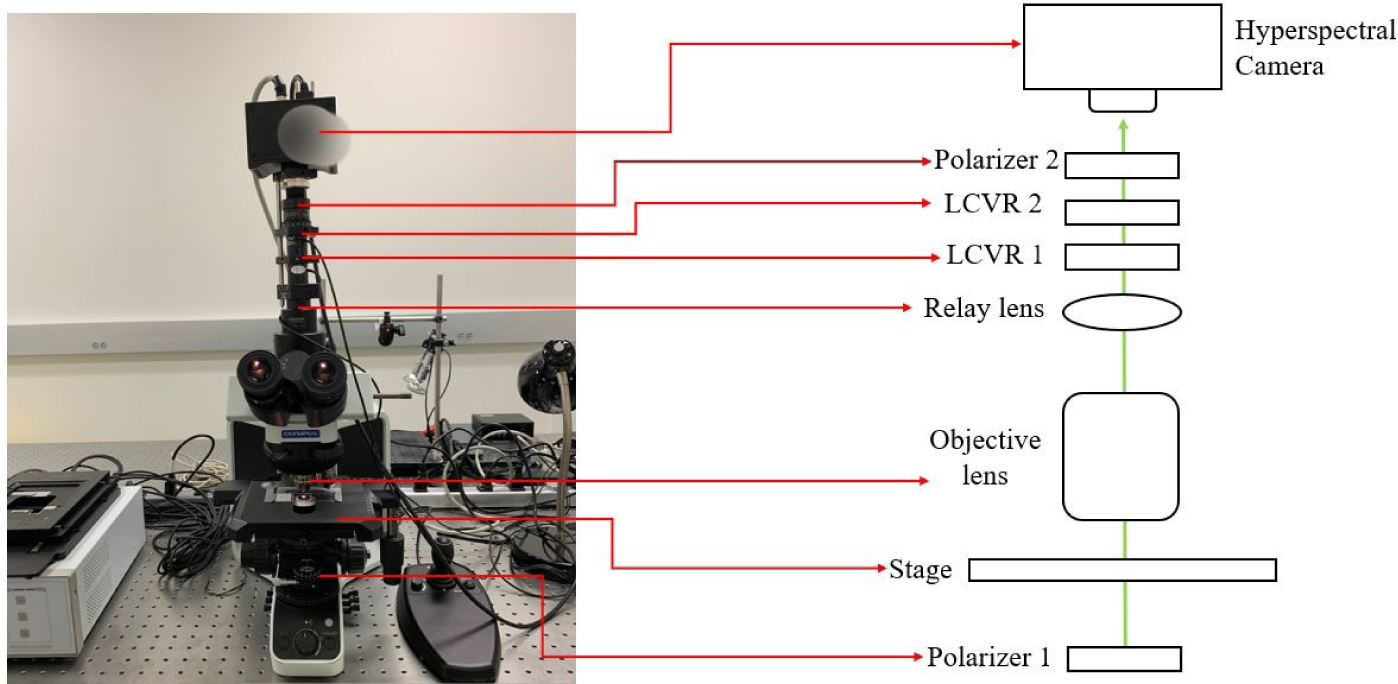
Figure 1.

Open in a new tab

The setup of the polarized hyperspectral imaging microscope. The polarized imaging components include two polarizers (one polarizer was placed at the bottom near the light source, the other polarizer was placed right before the hyperspectral camera), and two LCVRs placed between the objective lens and polarizer 2. The SnapScan hyperspectral camera was placed at the top of the system.

Figure 2.

Figure 2.

Open in a new tab

Diagram of full-polarization hyperspectral imaging data cubes. The data cube of each Stokes parameter (S0, S1, S2, S3) has three dimensions including two spatial dimensions (x, y) and one spectral dimension (λ).

2.2. Stokes vector acquisition

Polarized light imaging is realized by the two polarizers and two LCVRs. Figure 3 demonstrates the schematic of the imaging system with fast axis orientations of polarizers and LCVRs. Polarizer 1 was set at 45 degrees, and polarizer 2 was set at 0 degrees. LCVR 1 was set at 0 degrees, and LCVR 2 was set at 45 degrees. The system is capable of full Stokes polarimetric imaging, which produces all four components of the Stokes vector. Thus, the system can completely define the polarization properties of transmitted light. The way to calculate the four elements of Stokes vector (S0, S1, S2, and S3) is expressed in the following Equation (1):

S0=Ih+IvS1=Ih+IvS2=Ih+Iv−I+45S3=Ilc+Irc (1)

where Ih represent the light intensity measured with a horizontal linear analyzer, in which the retardations of LCVR 1 and LCVR 2 are both set at 0 rad; Iv represents the light intensity measured with a vertical linear analyzer, in which LCVR 1 is set at 0 rad retardation and LCVR 2 is set at π rad retardation; I+45 represents the light intensity measured with a +45 degrees oriented linear analyzer, in which LCVR 1 and LCVR 2 are both set at π/2 rad retardation; Ilc represents the light intensity measured with left circular analyzer, in which LCVR 1 is set at 0 rad retardation and LCVR 2 is set at π/2 rad retardation; Irc represents the light intensity measured with right circular analyzer, in which LCVR 1 is set at π rad retardation and LCVR 2 is set at π/2 rad retardation. The phase retardation of LCVR is determined by different values of voltage applied on it. In addition, the value of S0 is equal to the value of total light intensity.

Figure 3.

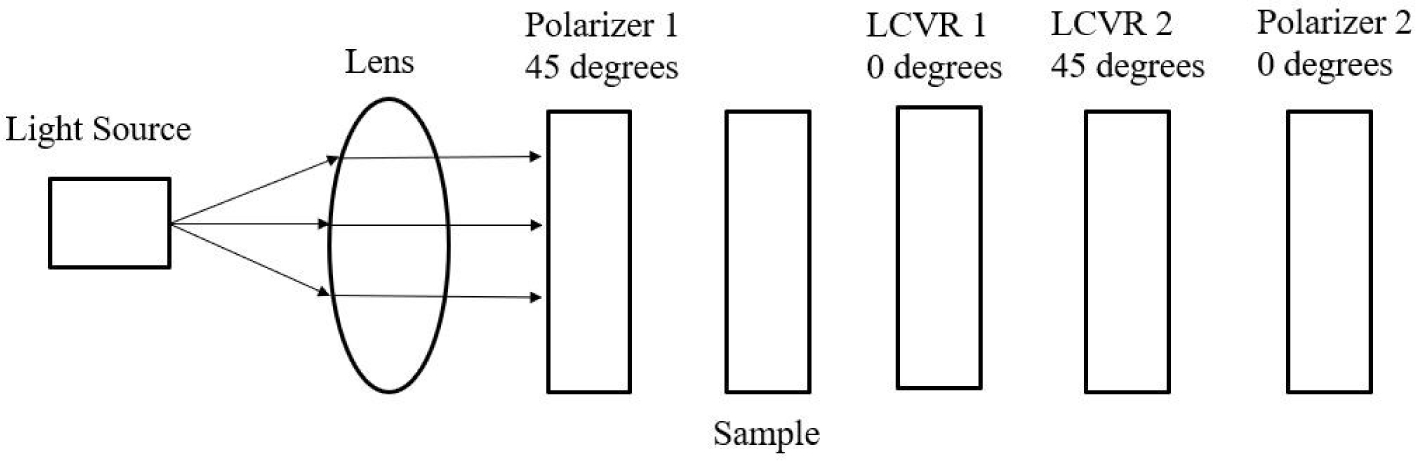
Figure 3.

Open in a new tab

Schematic of the polarized light imaging system. The fast axis orientation of polarizer 1 was set at 45 degrees, and polarizer 2 was set at 0 degrees. The fast axis orientation LCVR 1 was set at 0 degrees, and LCVR 2 was set at 45 degrees.

2.3. Sample preparation and data acquisition

Fresh surgical tissue samples were obtained from patients who underwent surgical resection of head and neck cancer [34]. Of each patient, a sample of the primary tumor, a normal tissue sample, and a sample at the tumor-normal margin were collected. Fresh ex-vivo tissues were formalin fixed, paraffin embedded, sectioned, stained with hematoxylin and eosin, and digitized using whole-slide scanning. Then, a board-certified pathologist with expertise in head and neck pathology outlined the cancer margin on the digital slides using Aperio ImageScope (Leica Biosystems Inc, Buffalo Grove, IL, USA). The annotations were used as histology ground truth in this study.

In the image acquisition progress, we acquired images of Ih, Iv, I+45, Irc, and then calculated the Stokes vector parameters (S0, S1, S2, and S3). We collected the image data from 20 H&E stained tissue slides of 10 patients with squamous cell carcinoma from the larynx. The slides of the normal tissue sample and tumor tissue sample of each patient were used. The selected areas to be imaged on normal tissue slides were from healthy stratified squamous epithelium, and the selected areas to be imaged on cancerous tissue slides were at or close to cancer nests. We cropped the original images with the image size of 1088 × 1088 pixels into image patches with a patch size of 40 × 40 pixels. The patches generated from the images of normal tissue slides were normal patches and labelled as 0, and the image patches of cancerous tissue slides were cancerous patches and labelled as 1.

2.4. Machine Learning

The implementation of machine learning algorithms is the main focus of this paper. In this project, we applied machine learning algorithms to our novel polarized hyperspectral imaging dataset. Four different machine learning methods, namely the support vector machine (SVM), random forest, Gaussian naive Bayes, and logistic regression, were trained and tested using the collected image data of 10 patients. We conducted the image classification based on the full Stokes vector polarized hyperspectral data cube, the synthetic RGB images generated from the full data cube, and the synthetic images based on the first three principal components of the polarized hyperspectral data cube. The machine learning algorithms were implemented using scikit-learn.

SVM is a kernel-based machine learning classifier that is widely used in image classification, and it is effective in high-dimensional spaces. SVM classifiers can be trained on either the linear kernel or the nonlinear kernel. We trained the SVM classifier based on the linear kernel, applied L2 regularization, and set the inverse of regularization strength at 1. Random forest is a type of ensemble machine learning method, which is operated based on an ensemble of decision trees. In the training process of random forest algorithm, we set the number of trees at 100, the maximum depth of the tree at 10, and used Gini function to measure the quality of a split. Naive Bayes classifiers are based on applying Bayes’ theorem with naïve independence assumptions among the features. In the Gaussian naive bayes classifier, a typical assumption is that the continuous values related to each class are distributed obeying a Gaussian distribution. In the training process of Gaussian naive bayes classifier, we set the value for the portion of the largest variance that is added to variances at 10−9 for calculation stability. Logistic regression is a machine learning classifier using a logistic function to model a binary dependent variable. In the training process of logistic regression classifier, we applied L2 regularization, and set the inverse of regularization strength at 1. These four machine learning algorithms applied were all supervised learning algorithms, which were trained on the labelled normal and cancerous image patches.

2.5. Data processing

We used 4500 image patches (40 × 40 pixels) generated from 20 images of 20 pathologic tissue slides of 10 patients. 2250 of them are normal image patches, while the other 2250 patches are cancerous image patches. We took accuracy as the evaluation metric, which is defined as the ratio of the number of correctly classified image patches to the total number of image patches in the ground truth, as is expressed in equation (2):

Accuracy=TP+TN/(TP+TN+FP+FN) (2)

where true positive (TP) refers to the number of correctly classified cancerous image patches, true negative (TN) refers to the number of correctly classified normal image patches, false positive (FP) refers to the number of normal image patches classified into cancerous image patches, and false negative (FN) refers to the number of cancerous image patches classified into normal image patches.

Before training the machine learning classifiers, we divided the image patches into training and testing groups. We utilized three types of image datasets for training and testing, respectively: the polarized hyperspectral data cubes, the synthesized RGB images, and PCA transformed images. To begin with, we trained the machine learning classifiers based on the original polarized hyperspectral data cubes. For each image patch, we calculated the average value of all pixel on (S0, S1, S2, S3) across all the 66 wavelength bands within the range of 486 nm and 700 nm, then represented each image patch with a feature matrix with the shape of 4 × 66 (average value of 4 Stokes vector parameters across 66 wavelength bands). Next, we formed an overall feature matrix of all 4500 image patches, which was a 4500 × 4 × 66 matrix. Then, leave-one-patient-out validation was carried out. Feature data in the overall feature matrix of one single patient were left out for validation in each fold, and the rest of the feature data in the matrix were used as the training data. So, we carried out 10 times of training in total. We calculated the validation accuracy for each fold as well as the average accuracy of all 10 folds.

Similar training processes were applied to the synthetic RGB images and the PCA transformed images. For synthetic RGB images, we adopted a transformation function similar to the spectral response of human eye and modified it for our data to generate the synthetic RGB images [35]. The transformation is shown in Figure 4. The formed feature matrix for a single RGB image patch had a shape of 4 × 3 (average value of 4 Stokes vector parameters under red, green, and blue bands), and the formed overall feature matrix had a shape of 4500 × 4 × 3. For the PCA transformed image data, we took the first, second, and third principal components to form a 4 × 3 feature matrix for each image patch, and the overall feature matrix was at the size of 4500 × 4 × 3.

Figure 4.

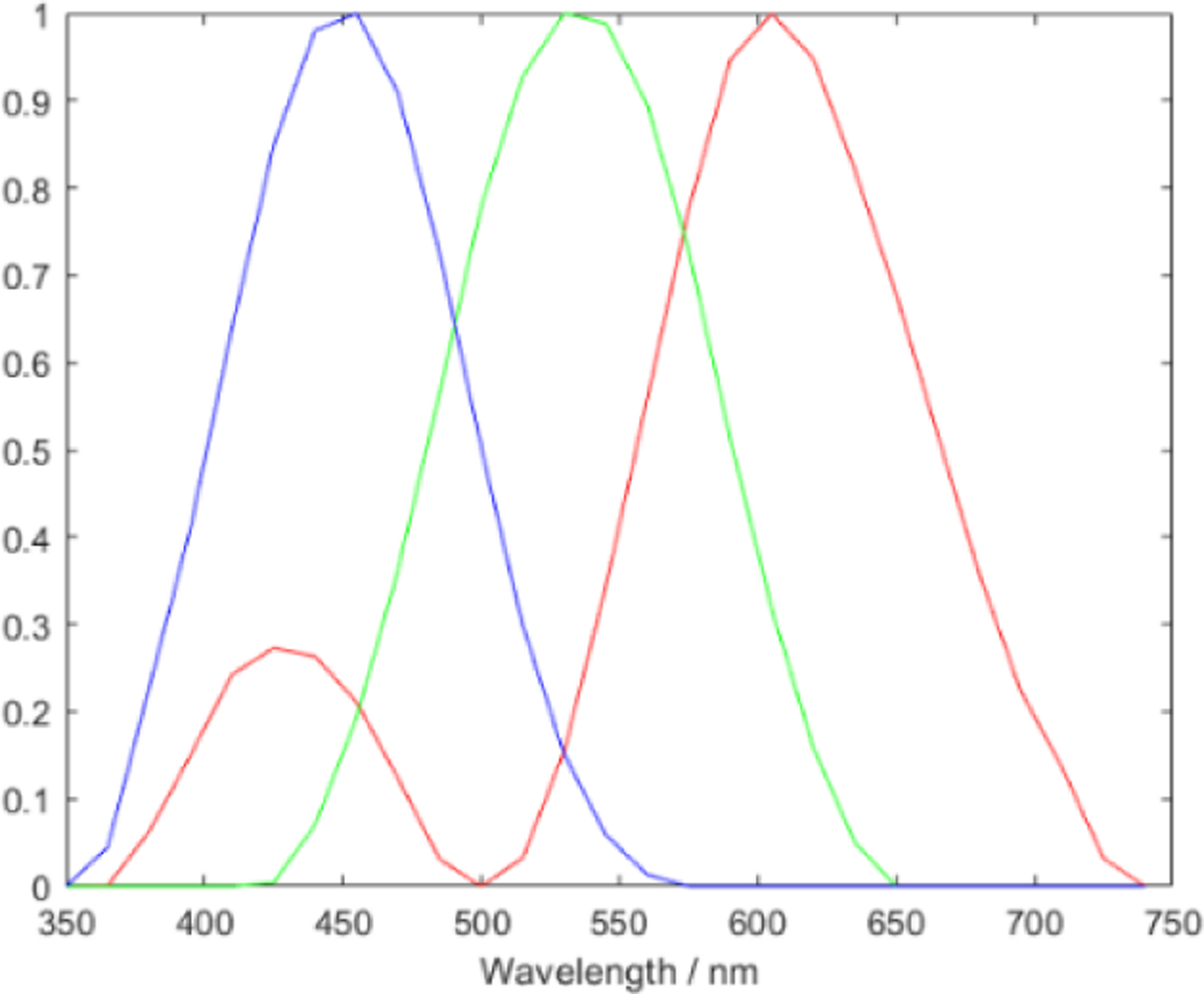
Figure 4.

Open in a new tab

Transformation function to synthesize pseudo-RGB images from the polarized hyperspectral data.

3. RESULTS

3.1. Comparison of the different components (S0, S1, S2, S3)

In Figure 5, we demonstrates the synthetic RGB images of Stokes vector parameters (S0, S1, S2, and S3) from a normal image patch of the normal slide and a cancerous image patch of the tumor slide from the same patient.

Figure 5.

Figure 5.

Open in a new tab

The color image representation of S0, S1, S2, and S3 (left to right) from a normal area on the normal slide (top) and a cancerous area on the tumor slide (bottom) of the same patient.

We also tested these four types of machine learning methods on the PCA transformed image data of the original polarized hyperspectral image data cube. Figure 6 demonstrates the synthetic three-channel pseudo-color images based on the first, second, and third principal components of the Stokes vectors (S0, S1, S2, and S3) from a normal area on the normal slide and a cancerous area on the tumor slide of the same patient.

Figure 6.

Figure 6.

Open in a new tab

The representation of the synthetic three-channel images based on the first, second, and third principal components of the Stokes vectors (S0, S1, S2, S3 are from left to right) from a normal area on the normal slide (top) and a cancerous area on the tumor slide (bottom) of the same patient.

3.2. Performances of machine learning algorithms

Leave-one-patient-out cross validation was conducted on image patches from 10 patients using four different machine learning algorithms (SVM, Random Forest, Gaussian NB, Logistic Regression), and the average validation accuracy of the 10 folds using different classifiers are reported. Table 1 shows the accuracies of four classifiers utilizing the full wavelength range (486 nm to 700 nm) of four Stokes vector parameters. The highest accuracy of 93.5% is achieved by SVM on S3. Table 2 shows the accuracies of four types of classifiers utilizing synthetic RGB images of four Stokes vector parameters. The highest accuracy of 92.6% is achieved by SVM on S3. Table 3 shows the accuracies of four types of classifiers utilizing the first three principal components of four Stokes vector parameters. The highest accuracy of 93.3% is achieved by logistic regression on S3.

Table 1.

Average validation accuracies of four types of classifiers utilizing the full wavelength range (486 nm to 700 nm) of four Stokes vector parameters (S0, S1, S2, S3).

Accuracy S0 S1 S2 S3
SVM 92.0% 92.9% 80.3% 93.5%
Random Forest 77.1% 90.4% 76.3% 88.4%
Gaussian NB 89.2% 75.8% 77.2% 76.2%
Logistic Regression 77.5% 89.8% 83.7% 87.5%
Open in a new tab

Table 2.

Average validation accuracies of four classifiers utilizing the pseudo-RGB patches of four Stokes vector parameters.

Accuracy S0 S1 S2 S3
SVM 90.2% 91.5% 78.8% 92.6%
Random Forest 80.8% 88.2% 77.1% 90.4%
Gaussian NB 83.7% 92.2% 74.0% 82.6%
Logistic Regression 86.3% 82.9% 81.2% 87.3%
Open in a new tab

Table 3.

Average validation accuracies of four classifiers utilizing the three principal components of four Stokes vector parameters.

Accuracy S0 S1 S2 S3
SVM 86.9% 88.2% 76.7% 89.2%
Random Forest 77.4% 91.4% 80.2% 91.8%
Gaussian NB 81.6% 92.1% 78.9% 87.4%
Logistic Regression 83.2% 83.7% 86.1% 93.3%
Open in a new tab

4. CONCLUSIONS AND DISCUSSIONS

In this work, we developed a novel polarized hyperspectral imaging microscope, which is able to acquire the full Stokes vector polarized hyperspectral imaging data cube, and has the potential to distinguish normal and cancerous area on H&E stained tissue slides of head and neck cancer. We developed an image classification framework based on machine learning methods to classify the normal and cancerous image patches generated from our collected polarized hyperspectral data cube. To the best of our knowledge, this is the first study of head and neck cancer detection in pathologic slides based on polarized hyperspectral imaging and machine learning methods. According to the results, SVM classifier achieved the highest accuracies (93.5% on S3) for the original polarized hyperspectral imaging data cube and the synthetic RGB image data (92.6% on S3), and for the classification using PCA transformed image data, logistic regression achieved the highest accuracy (93.3% on S3). The results suggest that SVM is a superior classifier for classification tasks based on polarized hyperspectral image data compared to the other three types of classifiers (random forest, Gaussian NB, and logistic regression).

Furthermore, the incorporate of the four Stokes vector parameters can improve the overall classification accuracy of the light-intensity image data (S0). The accuracies were improved by using S1 and S3 as the classification parameters for all types of image data (polarized hyperspectral data cube, synthesized RGB image data, and PCA transformed image data). In addition, S3 achieved the best accuracy for all types of image data (93.5% for polarized hyperspectral data cube, 92.6% for RGB image data, and 93.3% for PCA transformed image data). The results suggest that S3 is a superior parameter for classification tasks based on polarized hyperspectral image data.

Finally, the PCA transformed image data did not improve the best accuracy from the polarized hyperspectral imaging data cube, as it might lose some important information from the original polarized hyperspectral imaging data cube, but it did improve the best accuracy when compared to the performance of synthetic RGB image data.

Two recent researches of applying Stokes vector in cancer detection has shown the potential of using circular polarized light related parameter S3 in cancer detection on tissue samples [36, 37], which is consistent with what we found in our results. More work need to be performed on the statistical analysis of Stokes vector parameters on a larger dataset with more patients. Furthermore, we plan to carry out image analysis on whole-slide images, and apply deep learning algorithms in the analysis for future work.

ACKNOWLEDGMENTS

This research was supported in part by the U.S. National Institutes of Health (NIH) grants (R01CA156775, R01CA204254, R01HL140325, and R21CA231911) and by the Cancer Prevention and Research Institute of Texas (CPRIT) grant RP190588.

REFERENCES

  • 1.Johnson, Daniel E et al. , “Head and neck squamous cell carcinoma,” Nature Reviews Disease Primers 6(1), 1–22 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Ortega Samuel, et al. , “Hyperspectral and multispectral imaging in digital and computational pathology: a systematic review,” Biomedical Optics Express 11(6), 3195–3233 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Gao Liang, and Wang Lihong V., “A review of snapshot multidimensional optical imaging: measuring photon tags in parallel,” Physics reports 616, 1–37 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Lu G, and Fei B, “Medical hyperspectral imaging: a review,” Journal of biomedical optics 19(1), 010901 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Regeling B et al. , “Development of an image pre-processor for operational hyperspectral laryngeal cancer detection,” Journal of biophotonics 9(3), 235–245 (2016). [DOI] [PubMed] [Google Scholar]
  • 6.Regeling B et al. , “Hyperspectral Imaging Using Flexible Endoscopy for Laryngeal Cancer Detection,” Sensors 16(8), 1288 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Yushkov KB, and Molchanov VY, “Hyperspectral imaging acousto-optic system with spatial filtering for optical phase visualization,” Journal of biomedical optics 22(6), 066017 (2017). [DOI] [PubMed] [Google Scholar]
  • 8.Salmivuori M et al. , “Hyperspectral Imaging System in the Delineation of Ill-defined Basal Cell Carcinomas: A Pilot Study,” Journal of the European Academy of Dermatology and Venereology (2018). [DOI] [PubMed] [Google Scholar]
  • 9.Lu Guolan, et al. , “Hyperspectral imaging for cancer surgical margin delineation: registration of hyperspectral and histological images,” Medical Imaging 2014: Image-Guided Procedures, Robotic Interventions, and Modeling. Vol. 9036. International Society for Optics and Photonics, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Lu G et al. , “Spectral-spatial classification using tensor modeling for cancer detection with hyperspectral imaging,” Medical Imaging 2014: Image Processing 903413 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Pike R et al. , “A minimum spanning forest based hyperspectral image classification method for cancerous tissue detection,” Medical Imaging 2014: Image Processing 90341W (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Pike R et al. , “A Minimum Spanning Forest-Based Method for Noninvasive Cancer Detection With Hyperspectral Imaging,” IEEE Trans. Biomed. Engineering 63(3), 653–663 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Lu G et al. , “Estimation of tissue optical parameters with hyperspectral imaging and spectral unmixing,” Medical Imaging 2015: Biomedical Applications in Molecular, Structural, and Functional Imaging 94170Q (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Chung H et al. , “Superpixel-based spectral classification for the detection of head and neck cancer with hyperspectral imaging,” Medical Imaging 2016: Biomedical Applications in Molecular, Structural, and Functional Imaging, 978813 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Halicek M et al. , “Tumor margin classification of head and neck cancer using hyperspectral imaging and convolutional neural networks,” Proceedings of SPIE--the International Society for Optical Engineering (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Halicek M et al. , “Deep convolutional neural networks for classifying head and neck cancer using hyperspectral imaging,” Journal of biomedical optics 22(6), 060503 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Halicek M et al. , “ Optical biopsy of head and neck cancer using hyperspectral imaging and convolutional neural networks,” Journal of biomedical optics 24(3), 060503 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Halicek M et al. , “ Hyperspectral imaging of head and neck squamous cell carcinoma for cancer margin detection in surgical specimens from 102 patients using deep learning,” Cancers 11(9), (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Halicek M et al. , “ Tumor detection of the thyroid and salivary glands using hyperspectral imaging and deep learning,” Biomedical Optics Express 11(3), (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Anderson RR, “Polarized light examination and photography of the skin,” Arch. Dermatol 127(7), 1000–1005 (1991). [PubMed] [Google Scholar]
  • 21.Pierangelo A et al. , “Polarimetric imaging of uterine cervix: a case study,” Optics express 21(12), 14120–14130 (2013). [DOI] [PubMed] [Google Scholar]
  • 22.Raković MJ et al. , “Light backscattering polarization patterns from turbid media: theory and experiment,” Applied optics 38(15), 3399–3408 (1999). [DOI] [PubMed] [Google Scholar]
  • 23.Liu B et al. , “Mueller polarimetric imaging for characterizing the collagen microstructures of breast cancer tissues in different genotypes,” Optics Communications 433(60–67 (2019). [Google Scholar]
  • 24.Chang J et al. , “Division of focal plane polarimeter-based 3× 4 Mueller matrix microscope: a potential tool for quick diagnosis of human carcinoma tissues,” Journal of biomedical optics 21(5), 056002 (2016). [DOI] [PubMed] [Google Scholar]
  • 25.Lindeboom JA, Mathura KR, and Ince C, “Orthogonal polarization spectral (OPS) imaging and topographical characteristics of oral squamous cell carcinoma,” Oral oncology 42(6), 581–585 (2006). [DOI] [PubMed] [Google Scholar]
  • 26.Pahernik S et al. , “Orthogonal polarisation spectral imaging as a new tool for the assessment of antivascular tumour treatment in vivo: a validation study,” British journal of cancer 86(10), 1622 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Roblyer DM et al. , “Multispectral optical imaging device for in vivo detection of oral neoplasia,” Journal of biomedical optics 13(2), 024019 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Manhas S et al. , “Polarized diffuse reflectance measurements on cancerous and noncancerous tissues,” Journal of biophotonics 2(10), 581–587 (2009). [DOI] [PubMed] [Google Scholar]
  • 29.Chung J et al. , “Use of polar decomposition for the diagnosis of oral precancer,” Applied optics 46(15), 3038–3045 (2007). [DOI] [PubMed] [Google Scholar]
  • 30.Zhou Ximing, et al. , “Development of a new polarized hyperspectral imaging microscope,” Imaging, Therapeutics, and Advanced Technology in Head and Neck Surgery and Otolaryngology 2020. Vol. 11213. International Society for Optics and Photonics; (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Dong Y et al. , “Quantitatively characterizing the microstructural features of breast ductal carcinoma tissues in different progression stages by Mueller matrix microscope,” Biomedical optics express 8(8), 3643–3655 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Vasefi F et al. , “Polarization-sensitive hyperspectral imaging in vivo: a multimode dermoscope for skin analysis,” Scientific reports 4(4924 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Wang Z et al. , “Polarization-resolved hyperspectral stimulated Raman scattering microscopy for label-free biomolecular imaging of the tooth,” Applied Physics Letters 108(3), 033701 (2016). [Google Scholar]
  • 34.Lu G et al. , “Detection of head and neck cancer in surgical specimens using quantitative hyperspectral imaging,” Clinical Cancer Research, 5426–5436, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Ling Ma, et al. , “Hyperspectral microscopic imaging for automatic detection of head and neck squamous cell carcinoma using histologic image and machine learning,” Medical Imaging 2020: Digital Pathology. Vol. 11320, International Society for Optics and Photonics, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Britt Kunnen, et al. , “Application of circularly polarized light for non-invasive diagnosis of cancerous tissues and turbid tissue-like scattering media,” Journal of biophotonics 8(4), 317–323, (2015). [DOI] [PubMed] [Google Scholar]
  • 37.Deyan Ivanov, et al. , “Colon cancer detection by using Poincaré sphere and 2D polarimetric mapping of ex vivo colon samples,” Journal of Biophotonics, e202000082, (2020) [DOI] [PubMed] [Google Scholar]

RESOURCES