Abstract
Moth-flame optimization (MFO) algorithm inspired by the transverse orientation of moths toward the light source is an effective approach to solve global optimization problems. However, the MFO algorithm suffers from issues such as premature convergence, low population diversity, local optima entrapment, and imbalance between exploration and exploitation. In this study, therefore, an improved moth-flame optimization (I-MFO) algorithm is proposed to cope with canonical MFO’s issues by locating trapped moths in local optimum via defining memory for each moth. The trapped moths tend to escape from the local optima by taking advantage of the adapted wandering around search (AWAS) strategy. The efficiency of the proposed I-MFO is evaluated by CEC 2018 benchmark functions and compared against other well-known metaheuristic algorithms. Moreover, the obtained results are statistically analyzed by the Friedman test on 30, 50, and 100 dimensions. Finally, the ability of the I-MFO algorithm to find the best optimal solutions for mechanical engineering problems is evaluated with three problems from the latest test-suite CEC 2020. The experimental and statistical results demonstrate that the proposed I-MFO is significantly superior to the contender algorithms and it successfully upgrades the shortcomings of the canonical MFO.
Keywords: optimization, metaheuristic algorithms, swarm intelligence algorithm, moth-flame optimization, mechanical engineering problems
1. Introduction
In the majority of real-world optimization problems, a large number of decision variables are interacted with together, which is a very time-consuming process for finding an exact solution [1,2,3,4,5,6,7]. Metaheuristic algorithms have been widely used in recent years to approximate near-optimal solutions for real-world problems in various applications such as discrete optimization [8,9,10,11,12,13,14,15,16,17], continuous optimization [18,19,20,21,22], and constrained engineering problems [23,24,25,26,27,28,29,30,31,32,33]. Moreover, a novel research field has emerged in this area which successfully combines machine learning and swarm intelligence approaches to obtain outstanding results in different areas [34,35,36]. Metaheuristic algorithms can be classified into two main categories of non-nature-inspired and nature-inspired [2]. Simulated annealing (SA) [37], tabu search (TS) [38], adaptive dimensional search (ADS) [39], and iterated local search (ILS) [40] are some well-known non-nature-inspired metaheuristic algorithms. Although these algorithms have demonstrated remarkable local search capabilities, they may easily be trapped in local optimum in complex problems [2,3].
Nature-inspired algorithms consist of three main categories: evolutionary, physics-based, and swarm intelligence (SI). Evolutionary algorithms are mostly inspired by Darwin’s theory of evolution. Some examples are: genetic algorithm (GA) [41,42], genetic programming (GP) [43], differential evolution (DE) [44], evolution strategy (ES) [45], and quantum-based avian navigation optimizer (QANA) [46]. Ensemble of mutation strategies and parameters in differential evolution (EPSDE) algorithm [47], multi-population ensemble DE (MPEDE) [48], ensemble of differential evolution variants (EDEV) [49], and multi-trial vector-based differential evolution (MTDE) [50] are some successful improvements on evolutionary algorithms. Physics-based algorithms propose meaningful search strategies inspired by physics and mathematics laws to solve optimization problems. The big bang–big crunch (BB-BC) [51], charged system search (CSS) [52], ray optimization (RO) [53], atom search optimization (ASO) [54], arithmetic optimization algorithm (AOA) [55], and atomic orbital search (AOS) [56] are some of the successful physics-based algorithms in the literature.
Swarm intelligence (SI) algorithms are mainly derived from the social interaction behavior of terrestrial animals, aquatic animals, birds, and insects in nature [57]. Grey wolf optimizer (GWO) [58], chimp optimization algorithm (ChOA) [59], and gorilla troops optimizer (GTO) [60] are inspired by the behavior of terrestrial animals to solve optimization problems. Despite their simplicity and broad use, they may suffer from common drawbacks such as low population diversity, sinking into local optimum, and premature convergence problems. Therefore, there have been many improvements with different approaches applied to overcome their weaknesses [61,62,63,64]. Some SI algorithms are inspired by the behavior of aquatic animals such as prey besieging and foraging, which have been modeled in krill herd (KH) [65], dolphin echolocation (DE) [66], and whale optimization algorithm (WOA) [67]. The social intelligence behaviors of birds and insects encourage researchers to propose a new generation of SI algorithms that are modeled by foraging, hunting, and navigation behavior. Ant colony optimization (ACO) [68], ant lion optimizer (ALO) [69], social spider algorithm (SSA) [70], crow search algorithm (CSA) [71], African vultures optimization algorithm (AVOA) [72], Aquila optimizer (AO) [73], and moth-flame optimization (MFO) [74] are popular SI algorithms inspired by the behaviors of birds and insects.
The moth-flame optimizer (MFO) is a prominent SI algorithm inspired by the moths’ locomotion toward the light source. The MFO is appealing because of its ease of implementation, acceptable time complexity, and small number of parameters, which make it applicable in real-world optimization problems such as image segmentation [75,76,77], feature selection [78,79,80,81,82], food processing [83,84,85], and engineering optimization [86,87,88,89,90,91]. Consequently, many MFO variants have been developed such as Lévy-flight moth-flame optimization (LMFO) [92], non-dominated sorting moth flame optimization (NS-MFO) [93], enhanced moth-flame optimization (EMFO) [94], water cycle–moth-flame optimization (WCMFO) [95], and sine-cosine moth-flame optimization (SMFO) [96]. However, MFO and its variants cannot satisfy the needs of the optimization process for challenging problems, and they still suffer from some weaknesses such as low population diversity [97,98], premature convergence, local optima trapping [99,100], and imbalance between exploration and exploitation [101]. The main reason for these MFO’s weaknesses is that the majority of moths are trapped in the local optima in the early iterations which results in low population diversity. The question of this study is how moths can escape the local optima trapping and be moved to promising zones?
This paper proposes an improved MFO algorithm named I-MFO which uses moths’ memory mechanism and an adapted version of the wandering around search (WAS) strategy introduced in our prior study [57] to find and possibly free trapped moths. In the I-MFO algorithm, trapped moths are detected by comparing their best experienced flame fitness (Fbest) with their current positions’ fitness (OM). If the current position of each moth is not better than its memory, the moth is considered to be a trapped moth, and the adapted wandering around search (AWAS) strategy is employed to possibly free it from local optima by performing some random short flights, which also leads to amelioration of the premature convergence. Moreover, the fl parameter is used to strike a balance between exploration and exploitation by limiting the moths’ flight range. In the end, the new position and its fitness value replace the previous ones if the new fitness value is better than its Fbest.
The proposed I-MFO is comprehensively investigated by the benchmark functions CEC 2018 [102] in different dimensions of 30, 50, and 100, and compared with the state-of-the-art metaheuristic algorithms and three MFO variants including SA, continuous genetic algorithm (CGA) [42], GWO, MFO, WOA, LMFO, WCMFO, ChOA, AOA, and SMFO. The results demonstrate that the I-MFO can avoid local optima trapping, maintain population diversity, mitigate premature convergence, and strike a balance between exploration and exploitation. The I-MFO algorithm is statistically evaluated by the Friedman test and post hoc analysis to prove the superiority of the algorithm. Moreover, the applicability of I-MFO to solve real-world optimization problems was evaluated by three mechanical engineering problems from the latest test-suite CEC 2020 [103]. All experimental evaluations and statistical tests indicate that the I-MFO algorithm outperforms contender algorithms with an overall effectiveness of 92%.
In the rest of this study, the MFO and its variants are discussed in Section 2. Section 3 illustrates the structure of the proposed I-MFO. The results of I-MFO in solving CEC 2018 benchmark test functions are given and analyzed in Section 4, and the results are proven by statistical analysis in Section 5. The applicability of the proposed I-MFO for solving real-world mechanical engineering problems is tested by three problems from the latest test-suite CEC 2020 in Section 6. Finally, conclusions and future directions are given in Section 7.
2. Related Works
In this section, the MFO algorithm is first described in detail, and then its variants are reviewed from the perspective of overcoming the MFO weaknesses.
The MFO algorithm proposed in [74] is a population-based SI algorithm that mimics moths’ navigation behavior toward light sources. The moths navigate toward the real-light source (moon) with a straight path and a fixed angle which is called transverse orientation. Moreover, moths are highly attracted to artificial lights such as flames, and because of the close distance, they change their flight angles continuously, which forms a spiral path. This behavior is modeled by the MFO algorithm to solve optimization problems and is reviewed in [104,105,106]. In this algorithm, both moths and flames are considered as solutions. First, moths scatter in the search space randomly and their positions are saved in a matrix M, where rows indicate the number of moths (N), and columns represent dimensions (D). Then, the fitness value of M is evaluated and stored in an array OM as represented below.
The positions and fitness values of flames are considered in a matrix F and an array OF, respectively. In the first iteration, the OF is initiated based on ascending order of OM, and the corresponding sorted positions are assigned to the matrix F. In the next iterations, the F will be updated by the best N search agents from F and current M populations. In the optimization process, each moth Mi(t) in the current iteration t moves around its corresponding flame Fj using a logarithmic spiral defined in Equation (1), where Disi is computed by Equation (2), b determines the shape of the logarithmic spiral, and k is a random number value between interval (−1, 1).
| (1) |
| (2) |
In this algorithm, the number of flames is computed by Equation (3), where t indicates the current iteration, and N and MaxIt are the number of search agents and the maximum number of iterations, respectively.
| (3) |
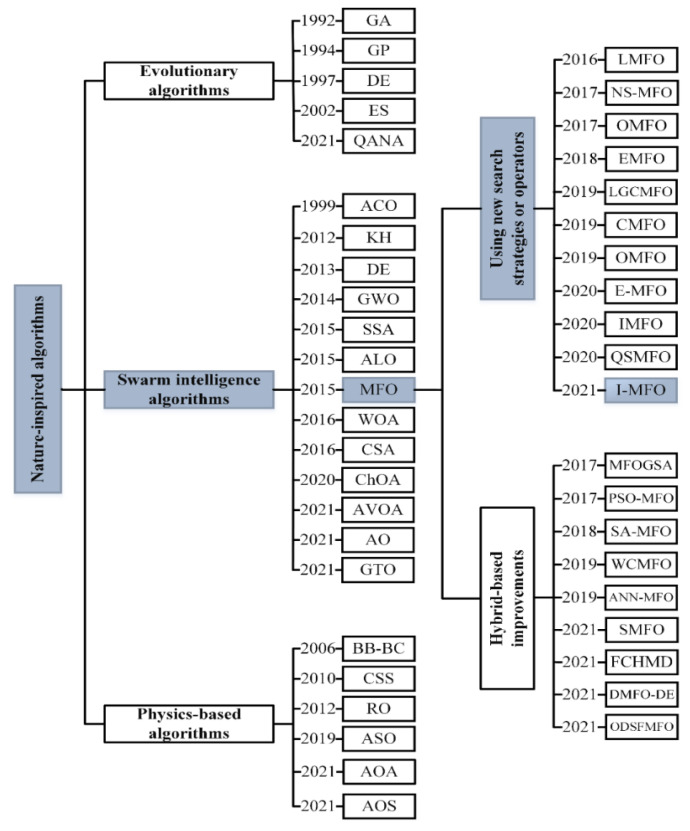
The MFO algorithm is an effective problem solver that is widely applied for real-world optimization problems. However, MFO is prone to being trapped in local optimum and suffers premature convergence due to its loss of population diversity and imbalance between the two tendencies of exploration and exploitation. Therefore, many variants have been proposed to boost the MFO algorithm, which can be categorized in improved algorithms based on using new search strategies or operators and hybrid-based improvements with other algorithms. Figure 1 shows the classification of SI algorithms and MFO variants.
Figure 1.
The classification of nature-inspired algorithms and MFO variants.
Many algorithms have been proposed by using new search strategies or operators in the canonical MFO. Li et al. [92] proposed the LMFO algorithm by employing the Lévy-flight strategy to increase the population diversity. Savsani et al. [93] proposed the effective non-dominated moth-flame optimization algorithm (NS-MFO) to solve multi-objective problems using the elitist non-dominated sorting method. The opposition-based moth-flame optimization (OMFO) [107] presents an opposition-based scheme in the canonical MFO to avoid local optimum and increase global exploration. In the EMFO [94], the Gaussian mutation (GM) was added to MFO to increase the diversity. In LGCMFO [100], Xu et al. used new operators such as Gaussian mutation (GM), Lévy mutation (LM), and Cauchy mutation (CM) to boost exploration and exploitation capabilities and encounter the local optima trapping of the MFO. In addition, Hongwei et al. [99] presented the chaos-enhanced moth-flame optimization (CMFO) with ten chaotic maps to cope with the MFO deficiency. Sapre et al. [108] brought up OMFO to cope with premature convergence and local optima trapping by proposing a combination of opposition-based, Cauchy mutation and evolutionary boundary constraint handling. In 2020, Kaur et al. [97] proposed E-MFO by adding a Cauchy mutation (CM) to improve the distribution of the algorithm in the search space. An improved moth-flame optimization (IMFO) [98] algorithm proposes a new flame generation strategy and divides optimization iterations into three phases to encounter low population diversity and enhance MFO’s search balance, respectively. An improved MFO algorithm called QSMFO was proposed by [109] to boost MFO’s exploitation capabilities while enhancing the exploration rate by introducing the simulated annealing strategy and quantum rotation gate, respectively.
Some variants proposed hybrid-based improvements to the MFO algorithm to boost its performance. MFOGSA [83] is a combination of MFO with gravitational search algorithm (GSA) to utilize MFO’s exploration and GSA’s exploitation capabilities. Bhesdadiya et al. [110] proposed a hybrid PSO-MFO algorithm to solve optimization problems. SA-MFO [111] combines MFO with simulated annealing (SA) to overcome local optima trapping and low convergence rate. Khalilpourazari et al. [95] proposed WCMFO to encounter MFO’s entrapping at local optima and low convergence rate, while taking advantage of the water cycle algorithm (WCA). A combination of MFO and artificial neural network (ANN-MFO) was proposed by Singh et al. [112] to solve multi-objective problems in magnetic abrasive finishing of aluminum. Chen et al. [96] introduced SMFO to improve the exploration capability of MFO by integrating it with the sine cosine strategy. An enhanced MFO algorithm was proposed by MP Dang et al. [113] which is a hybridization of MFO and three different methods to solve the design problem of a flexure hinge. Mittal [114] brought up an enhanced moth-flame optimization by integrating MFO and variable neighborhood search to boost search capabilities and convergence accuracy of the canonical MFO. In a recent study, Abd Elaziz et al. [115] proposed the FCHMD algorithm which is a hybridization of Harris hawks optimizer and MFO. In this algorithm, fractional-order Gauss and 2xmod1 chaotic maps are used to generate the initial population. Moreover, the FCHMD algorithm ameliorates premature convergence and stagnation in local optima by applying evolutionary population dynamics. Ahmed et al. [116] brought up DMFO-DE which is a discrete hybrid algorithm developed by integrating differential evolution and MFO to encounter the local optima problem and ameliorate the convergence speed and prevent the local optima problem. Li et al. [117] proposed the ODSFMFO algorithm which consists of an improved flame generation mechanism based on opposition-based learning (OBL) and differential evolution (DE) algorithm, and an enhanced local search mechanism based on shuffled frog leaping algorithm (SFLA) and death mechanism.
Based on the above review on MFO and its proposed variants, the most serious drawbacks of MFO are premature convergence, getting stuck in local optimum, low population diversity, and deficient balance between exploration and exploitation. Therefore, in this study, the improved moth-flame optimization (I-MFO) algorithm is proposed to encounter MFO’s shortcomings by introducing a memory mechanism and an adapted version of the wandering around search (WAS) strategy [57], called AWAS strategy, to the canonical MFO.
3. Proposed Algorithm
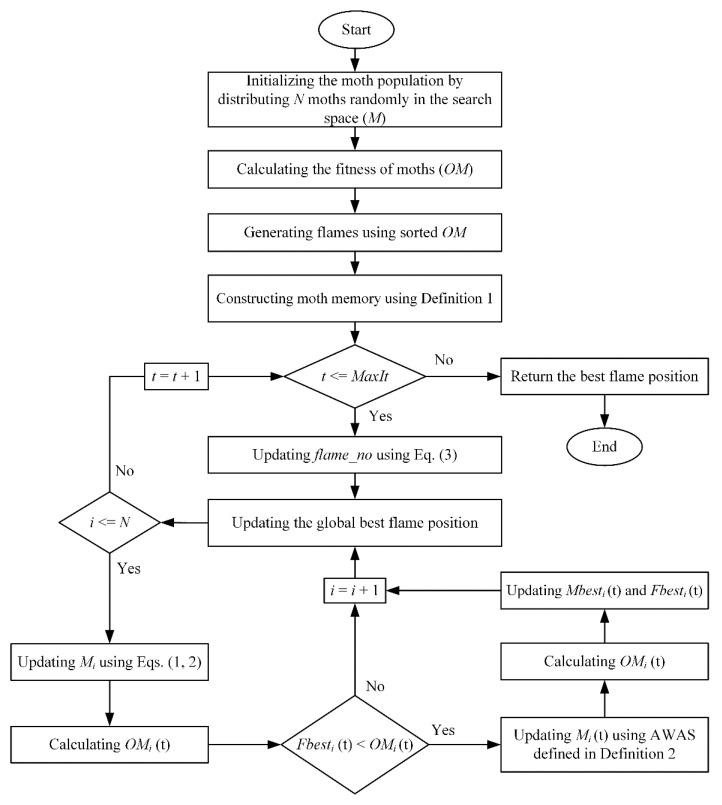
The proposed improved moth-flame optimization (I-MFO) algorithm is boosted using a moth memory mechanism and the adapted wandering around search (AWAS) strategy to overcome the mentioned shortcomings of the canonical MFO algorithm. The moth memory mechanism is inspired by moths’ behavior in nature in remembering their experiences [118], which is defined by Definition 1. Moreover, the AWAS strategy is introduced in Definition 2, to possibly escape the trapped moths from the local optima and alleviate the premature convergence. The pseudo-code and the flowchart of the proposed I-MFO are shown in Algorithm 1 and Figure 2, respectively.
Figure 2.
The flowchart of improved moth-flame optimization (I-MFO) algorithm.
Definition 1 (Moth memory construction).
Suppose Mem = {Mem1, Mem2, …, Memi, …, MemN} is finite set of N moths’ memories. The moth memory Mi is denoted by Memi = (Mbesti, Fbesti), where Mbesti is the best position of Mi obtained so far, and Fbesti is the fitness value of Mbesti. In the first iteration t, the best position Mbesti (t = 1) ← Mi (t = 1) and Fbesti (t = 1) ← OMi (t = 1). For the rest of the iterations, Mbesti (t > 1) ← Mi (P) and Fbesti (t > 1) ← OMi (P) such that {OMi (P) < Fbesti, P = 2, …, t}. The moth memory construction is formulated in Equation (4).
| (4) |
| Algorithm 1. The pseudo-code of I-MFO | |
| Algorithm of improved moth-flame optimization (I-MFO) | |
| Input: Maximum iterations (MaxIt), Number of moths (N), and Dimension size (D). | |
| Output: The best flame position and its fitness value. | |
| 1 | Begin |
| 2 | Randomly distributing M moths in the D-dimensional search space. |
| 3 | Calculating moths’ fitness (OM). |
| 4 | Set t = 1. |
| 5 | OF ← sort (OM). |
| 6 | F ← sort (M). |
| 7 | Defining the moth memory Mbest and Fbest using Definition 1. |
| 8 | While t ≤ MaxIt |
| 9 | Updating F and OF by the best N moths from F and current M. |
| 10 | Updating flame_no using Equation (3) |
| 11 | For i = 1: N |
| 12 | Computing the distance between moth Mi (t) and flame Fj (t) using Equation (2). |
| 13 | Updating the position of Mi (t) using Equation (1). |
| 14 | Computing the fitness value of Mi (t) and update OMi (t). |
| 15 | If Fbesti (t) < OMi (t) |
| 16 | Selecting a random moth Mr (t). |
| 17 | Updating the position of Mi (t) using AWAS defined in Definition 2. |
| 18 | Updating the fitness value OMi (t). |
| 19 | End if |
| 20 | Updating the moth memory Mi using Definition 1. |
| 21 | End for |
| 22 | Updating the position and fitness value of the global best flame. |
| 23 | t = t + 1. |
| 24 | End while |
Definition 2
(AWAS strategy). Consider TM (t) = {M1, …, Mi, …} as a finite set of moths trapped in the current iteration t such that Mi could not dominate its Memi (OMi (t) > Fbesti). Then, to possibly free the trapped moth Mi (t + 1) from the local optimum, its new position is computed by Equation (5), where Fgbest j (t) is the jth dimension of the global best flame, ri is a random number between interval (0, 1), Mrj (t) is the value of a random moth position. The flight length fli (t) for moth Mi is computed by Equation (6), where δ1 and δ2 are defined by the user, NF is the number of flights determined randomly in [1, D], and q is the current flight number. In fact, using AWAS strategy with the random NF provides advantage through which the trapped moth Mi can be moved to a better position.
| (5) |
| (6) |
4. Numerical Experiment and Analysis
In this section, the performance of the proposed I-MFO has been evaluated using the CEC 2018 [102] benchmark. Moreover, the proposed algorithm was compared with the state-of-the-art metaheuristic algorithms including SA [37], CGA [42], GWO [58], WOA [67], ChOA [59], AOA [55], canonical MFO [74], and its variants such as LMFO [92], WCMFO [95], and SMFO [96]. The parameter settings of comparative algorithms are adjusted as in their original papers and are reported in Table 1. The obtained results are reported in Table 2, Table 3 and Table 4, where the bold values show the winner algorithm. Furthermore, at the end of each table, the symbols W, T, and L demonstrate the number of wins, ties, and losses of each algorithm, respectively.
Table 1.
Parameter settings of the I-MFO and other contender algorithms.
| Algorithms | Parameter Settings |
|---|---|
| SA | T0 = 10. |
| CGA | IPMut = 0.9, PXcross = 0.5. |
| GWO | The parameter a is linearly decreased from 2 to 0. |
| MFO | b = 1, a is decreased linearly from −1 to −2. |
| WOA | α variable decreases linearly from 2 to 0, b = 1. |
| LMFO | β = 1.5, µ and v are normal distributions, Γ is the gamma function. |
| WCMFO | The number of rivers and sea = 4. |
| ChOA | f decreases linearly from 2 to 0. |
| AOA | µ = 0.5, α = 5. |
| SMFO | r4 = random number between interval (0, 1). |
| I-MFO | δ1 = 2.02, δ2 = 1.08, NF = random number between 1 and D. |
Table 2.
Comparison of optimization results obtained from unimodal and multimodal test functions.
| F | D | Metrics | SA (1983) |
CGA (2000) |
GWO (2014) |
MFO (2015) |
WOA (2016) |
LMFO (2016) |
WCMFO (2019) |
ChOA (2020) |
AOA (2021) |
SMFO (2021) |
I-MFO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 30 | Avg | 2.251 × 1010 | 3.794 × 1010 | 8.223 × 108 | 6.952 × 109 | 1.906 × 106 | 2.402 × 107 | 1.328 × 104 | 2.238 × 1010 | 3.943 × 1010 | 3.091 × 1010 | 5.859 × 103 |
| Min | 1.897 × 1010 | 2.437 × 1010 | 4.404 × 107 | 1.027 × 109 | 5.654 × 105 | 1.731 × 107 | 1.214 × 102 | 1.123 × 1010 | 2.791 × 1010 | 2.010 × 1010 | 1.488 × 102 | ||
| 50 | Avg | 7.170 × 1010 | 1.126 × 1011 | 4.522 × 109 | 3.099 × 1010 | 7.172 × 106 | 1.091 × 108 | 2.826 × 104 | 4.407 × 1010 | 9.968 × 1010 | 6.933 × 1010 | 1.430 × 104 | |
| Min | 6.279 × 1010 | 9.612 × 1010 | 1.231 × 109 | 7.095 × 109 | 1.980 × 106 | 7.284 × 107 | 6.883 × 102 | 3.201 × 1010 | 8.424 × 1010 | 4.945 × 1010 | 1.948 × 102 | ||
| 100 | Avg | 2.830 × 1011 | 3.547 × 1011 | 3.207 × 1010 | 1.173 × 1011 | 3.677 × 107 | 7.525 × 108 | 2.017 × 105 | 1.457 × 1011 | 2.617 × 1011 | 1.908 × 1011 | 2.881 × 104 | |
| Min | 2.638 × 1011 | 3.147 × 1011 | 1.634 × 1010 | 6.748 × 1010 | 1.409 × 107 | 6.332 × 108 | 1.093 × 104 | 1.282 × 1011 | 2.343 × 1011 | 1.527 × 1011 | 1.033 × 102 | ||
| F3 | 30 | Avg | 1.439 × 105 | 1.095 × 105 | 2.993 × 104 | 1.009 × 105 | 1.715 × 105 | 2.786 × 103 | 1.887 × 103 | 5.221 × 104 | 7.488 × 104 | 8.189 × 104 | 6.106 × 102 |
| Min | 1.029 × 105 | 9.312 × 104 | 1.576 × 104 | 1.920 × 103 | 8.481 × 104 | 1.424 × 103 | 3.092 × 102 | 3.954 × 104 | 5.445 × 104 | 7.186 × 104 | 3.388 × 102 | ||
| 50 | Avg | 2.994 × 105 | 2.241 × 105 | 7.147 × 104 | 1.650 × 105 | 6.180 × 104 | 3.151 × 104 | 1.150 × 104 | 1.306 × 105 | 1.648 × 105 | 1.775 × 105 | 1.460 × 104 | |
| Min | 2.647 × 105 | 1.648 × 105 | 3.628 × 104 | 1.176 × 104 | 3.098 × 104 | 2.291 × 104 | 7.428 × 102 | 1.006 × 105 | 1.249 × 105 | 1.273 × 105 | 7.827 × 103 | ||
| 100 | Avg | 8.110 × 105 | 5.742 × 105 | 2.023 × 105 | 4.556 × 105 | 5.928 × 105 | 2.495 × 105 | 7.361 × 104 | 3.071 × 105 | 3.330 × 105 | 3.366 × 105 | 7.625 × 104 | |
| Min | 7.298 × 105 | 4.725 × 105 | 1.595 × 105 | 1.191 × 105 | 3.355 × 105 | 1.819 × 105 | 3.430 × 104 | 2.701 × 105 | 3.027 × 105 | 3.182 × 105 | 6.767 × 104 | ||
| F4 | 30 | Avg | 1.587 × 103 | 7.327 × 103 | 5.441 × 102 | 9.082 × 102 | 5.476 × 102 | 4.928 × 102 | 4.886 × 102 | 2.971 × 103 | 8.808 × 103 | 5.977 × 103 | 4.868 × 102 |
| Min | 1.354 × 103 | 6.137 × 103 | 4.963 × 102 | 5.424 × 102 | 4.995 × 102 | 4.755 × 102 | 4.239 × 102 | 1.134 × 103 | 3.824 × 103 | 3.030 × 103 | 4.704 × 102 | ||
| 50 | Avg | 7.832 × 103 | 2.608 × 104 | 8.767 × 102 | 4.097 × 103 | 6.676 × 102 | 5.907 × 102 | 5.493 × 102 | 9.176 × 103 | 2.582 × 104 | 1.879 × 104 | 5.550 × 102 | |
| Min | 6.386 × 103 | 1.598 × 104 | 6.745 × 102 | 1.216 × 103 | 5.138 × 102 | 5.084 × 102 | 4.849 × 102 | 5.017 × 103 | 1.686 × 104 | 1.005 × 104 | 4.210 × 102 | ||
| 100 | Avg | 4.778 × 104 | 1.033 × 105 | 2.812 × 103 | 2.348 × 104 | 9.992 × 102 | 7.215 × 102 | 6.423 × 102 | 2.760 × 104 | 7.703 × 104 | 5.544 × 104 | 6.318 × 102 | |
| Min | 3.845 × 104 | 8.305 × 104 | 1.870 × 103 | 6.742 × 103 | 8.615 × 102 | 6.726 × 102 | 5.980 × 102 | 2.116 × 104 | 6.019 × 104 | 3.485 × 104 | 5.772 × 102 | ||
| F5 | 30 | Avg | 8.120 × 102 | 8.777 × 102 | 5.855 × 102 | 6.894 × 102 | 8.044 × 102 | 6.278 × 102 | 6.744 × 102 | 7.877 × 102 | 7.905 × 102 | 8.721 × 102 | 5.499 × 102 |
| Min | 7.865 × 102 | 8.259 × 102 | 5.508 × 102 | 6.280 × 102 | 7.242 × 102 | 5.707 × 102 | 6.104 × 102 | 7.471 × 102 | 7.217 × 102 | 8.041 × 102 | 5.308 × 102 | ||
| 50 | Avg | 1.167 × 103 | 1.273 × 103 | 6.892 × 102 | 8.934 × 102 | 9.209 × 102 | 8.152 × 102 | 8.940 × 102 | 1.037 × 103 | 1.078 × 103 | 1.118 × 103 | 6.348 × 102 | |
| Min | 1.142 × 103 | 1.184 × 103 | 6.379 × 102 | 7.731 × 102 | 8.081 × 102 | 7.287 × 102 | 7.743 × 102 | 9.853 × 102 | 9.951 × 102 | 1.053 × 103 | 5.836 × 102 | ||
| 100 | Avg | 2.180 × 103 | 2.374 × 103 | 1.058 × 103 | 1.666 × 103 | 1.413 × 103 | 1.456 × 103 | 1.726 × 103 | 1.789 × 103 | 1.955 × 103 | 1.985 × 103 | 8.613 × 102 | |
| Min | 2.098 × 103 | 2.255 × 103 | 9.864 × 102 | 1.455 × 103 | 1.329 × 103 | 1.226 × 103 | 1.328 × 103 | 1.724 × 103 | 1.842 × 103 | 1.875 × 103 | 7.885 × 102 | ||
| F6 | 30 | Avg | 6.582 × 102 | 6.734 × 102 | 6.043 × 102 | 6.267 × 102 | 6.671 × 102 | 6.038 × 102 | 6.225 × 102 | 6.604 × 102 | 6.655 × 102 | 6.830 × 102 | 6.000 × 102 |
| Min | 6.468 × 102 | 6.612 × 102 | 6.011 × 102 | 6.144 × 102 | 6.410 × 102 | 6.017 × 102 | 6.095 × 102 | 6.386 × 102 | 6.476 × 102 | 6.615 × 102 | 6.000 × 102 | ||
| 50 | Avg | 6.835 × 102 | 6.936 × 102 | 6.105 × 102 | 6.437 × 102 | 6.760 × 102 | 6.094 × 102 | 6.400 × 102 | 6.720 × 102 | 6.837 × 102 | 6.890 × 102 | 6.000 × 102 | |
| Min | 6.691 × 102 | 6.784 × 102 | 6.052 × 102 | 6.270 × 102 | 6.638 × 102 | 6.034 × 102 | 6.165 × 102 | 6.608 × 102 | 6.747 × 102 | 6.780 × 102 | 6.000 × 102 | ||
| 100 | Avg | 7.210 × 102 | 7.176 × 102 | 6.275 × 102 | 6.648 × 102 | 6.768 × 102 | 6.398 × 102 | 6.664 × 102 | 6.860 × 102 | 7.028 × 102 | 7.030 × 102 | 6.000 × 102 | |
| Min | 7.164 × 102 | 7.143 × 102 | 6.229 × 102 | 6.466 × 102 | 6.676 × 102 | 6.222 × 102 | 6.526 × 102 | 6.761 × 102 | 6.970 × 102 | 6.865 × 102 | 6.000 × 102 | ||
| F7 | 30 | Avg | 1.728 × 103 | 1.965 × 103 | 8.418 × 102 | 1.011 × 103 | 1.238 × 103 | 8.735 × 102 | 8.985 × 102 | 1.190 × 103 | 1.295 × 103 | 1.349 × 103 | 7.964 × 102 |
| Min | 1.593 × 103 | 1.798 × 103 | 7.801 × 102 | 8.671 × 102 | 1.089 × 103 | 8.438 × 102 | 8.402 × 102 | 1.063 × 103 | 1.154 × 103 | 1.175 × 103 | 7.595 × 102 | ||
| 50 | Avg | 3.572 × 103 | 3.656 × 103 | 1.015 × 103 | 1.701 × 103 | 1.684 × 103 | 1.092 × 103 | 1.141 × 103 | 1.663 × 103 | 1.860 × 103 | 1.919 × 103 | 9.208 × 102 | |
| Min | 3.305 × 103 | 3.300 × 103 | 9.654 × 102 | 1.113 × 103 | 1.500 × 103 | 1.065 × 103 | 1.020 × 103 | 1.464 × 103 | 1.744 × 103 | 1.769 × 103 | 8.168 × 102 | ||
| 100 | Avg | 1.014 × 104 | 9.052 × 103 | 1.710 × 103 | 4.169 × 103 | 3.250 × 103 | 1.736 × 103 | 1.988 × 103 | 3.320 × 103 | 3.712 × 103 | 3.891 × 103 | 1.356 × 103 | |
| Min | 9.035 × 103 | 8.338 × 103 | 1.542 × 103 | 2.576 × 103 | 2.814 × 103 | 1.649 × 103 | 1.531 × 103 | 3.127 × 103 | 3.579 × 103 | 3.536 × 103 | 1.140 × 103 | ||
| F8 | 30 | Avg | 1.116 × 103 | 1.166 × 103 | 8.713 × 102 | 9.790 × 102 | 1.000 × 103 | 9.379 × 102 | 9.841 × 102 | 1.032 × 103 | 1.041 × 103 | 1.096 × 103 | 8.574 × 102 |
| Min | 1.074 × 103 | 1.144 × 103 | 8.435 × 102 | 8.938 × 102 | 9.488 × 102 | 8.797 × 102 | 9.344 × 102 | 9.726 × 102 | 1.002 × 103 | 1.058 × 103 | 8.418 × 102 | ||
| 50 | Avg | 1.467 × 103 | 1.573 × 103 | 9.792 × 102 | 1.229 × 103 | 1.249 × 103 | 1.119 × 103 | 1.213 × 103 | 1.305 × 103 | 1.426 × 103 | 1.404 × 103 | 9.201 × 102 | |
| Min | 1.427 × 103 | 1.519 × 103 | 9.384 × 102 | 1.118 × 103 | 1.132 × 103 | 1.062 × 103 | 1.087 × 103 | 1.251 × 103 | 1.339 × 103 | 1.320 × 103 | 8.796 × 102 | ||
| 100 | Avg | 2.499 × 103 | 2.751 × 103 | 1.397 × 103 | 1.968 × 103 | 1.897 × 103 | 1.740 × 103 | 2.026 × 103 | 2.157 × 103 | 2.404 × 103 | 2.422 × 103 | 1.160 × 103 | |
| Min | 2.448 × 103 | 2.620 × 103 | 1.225 × 103 | 1.717 × 103 | 1.716 × 103 | 1.531 × 103 | 1.756 × 103 | 2.052 × 103 | 2.248 × 103 | 2.276 × 103 | 1.087 × 103 | ||
| F9 | 30 | Avg | 1.079 × 104 | 1.239 × 104 | 1.384 × 103 | 6.278 × 103 | 7.233 × 103 | 1.015 × 103 | 8.747 × 103 | 6.612 × 103 | 5.570 × 103 | 9.591 × 103 | 9.882 × 102 |
| Min | 9.017 × 103 | 8.805 × 103 | 1.025 × 103 | 4.471 × 103 | 4.425 × 103 | 9.056 × 102 | 5.118 × 103 | 4.627 × 103 | 4.101 × 103 | 7.754 × 103 | 9.065 × 102 | ||
| 50 | Avg | 3.302 × 104 | 4.335 × 104 | 4.571 × 103 | 1.644 × 104 | 1.783 × 104 | 1.306 × 103 | 2.195 × 104 | 2.591 × 104 | 2.277 × 104 | 3.066 × 104 | 1.305 × 103 | |
| Min | 2.622 × 104 | 3.603 × 104 | 2.135 × 103 | 8.748 × 103 | 1.187 × 104 | 9.481 × 102 | 1.190 × 104 | 1.969 × 104 | 1.804 × 104 | 1.925 × 104 | 9.853 × 102 | ||
| 100 | Avg | 1.197 × 105 | 1.243 × 105 | 2.638 × 104 | 4.507 × 104 | 3.820 × 104 | 1.421 × 104 | 5.208 × 104 | 6.813 × 104 | 5.374 × 104 | 6.959 × 104 | 7.081 × 103 | |
| Min | 1.034 × 105 | 1.079 × 105 | 1.102 × 104 | 3.679 × 104 | 2.557 × 104 | 3.037 × 103 | 3.986 × 104 | 5.806 × 104 | 4.673 × 104 | 5.852 × 104 | 4.038 × 103 | ||
| F10 | 30 | Avg | 7.764 × 103 | 8.149 × 103 | 3.909 × 103 | 5.130 × 103 | 6.156 × 103 | 4.422 × 103 | 4.808 × 103 | 8.037 × 103 | 6.487 × 103 | 8.363 × 103 | 2.745 × 103 |
| Min | 6.721 × 103 | 7.474 × 103 | 2.718 × 103 | 3.575 × 103 | 4.506 × 103 | 3.149 × 103 | 3.332 × 103 | 7.199 × 103 | 5.410 × 103 | 7.473 × 103 | 1.941 × 103 | ||
| 50 | Avg | 1.426 × 104 | 1.446 × 104 | 6.428 × 103 | 8.566 × 103 | 9.478 × 103 | 7.081 × 103 | 7.956 × 103 | 1.419 × 104 | 1.223 × 104 | 1.368 × 104 | 4.799 × 103 | |
| Min | 1.337 × 104 | 1.342 × 104 | 4.582 × 103 | 6.288 × 103 | 6.969 × 103 | 6.045 × 103 | 6.204 × 103 | 1.301 × 104 | 1.058 × 104 | 1.234 × 104 | 3.734 × 103 | ||
| 100 | Avg | 3.136 × 104 | 3.121 × 104 | 1.497 × 104 | 1.728 × 104 | 2.012 × 104 | 1.758 × 104 | 1.618 × 104 | 3.141 × 104 | 2.783 × 104 | 3.071 × 104 | 1.168 × 104 | |
| Min | 3.040 × 104 | 2.990 × 104 | 1.141 × 104 | 1.417 × 104 | 1.687 × 104 | 1.631 × 104 | 1.147 × 104 | 3.035 × 104 | 2.582 × 104 | 2.843 × 104 | 9.083 × 103 | ||
| Ranking | 30 | W|T|L | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 9/0/0 |
| 50 | W|T|L | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 2/0/7 | 0/0/9 | 0/0/9 | 0/0/9 | 7/0/2 | |
| 100 | W|T|L | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 1/0/8 | 0/0/9 | 0/0/9 | 0/0/9 | 8/0/1 |
Table 3.
Comparison of optimization results obtained from hybrid test functions.
| F | D | Metrics | SA (1983) |
CGA (2000) |
GWO (2014) |
MFO (2015) |
WOA (2016) |
LMFO (2016) |
WCMFO (2019) |
ChOA (2020) |
AOA (2021) |
SMFO (2021) |
I-MFO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F11 | 30 | Avg | 3.124 × 103 | 5.262 × 103 | 1.406 × 103 | 3.749 × 103 | 1.462 × 103 | 1.292 × 103 | 1.336 × 103 | 3.361 × 103 | 3.325 × 103 | 5.265 × 103 | 1.188 × 103 |
| Min | 2.512 × 103 | 3.284 × 103 | 1.271 × 103 | 1.363 × 103 | 1.282 × 103 | 1.177 × 103 | 1.254 × 103 | 1.731 × 103 | 1.739 × 103 | 2.547 × 103 | 1.119 × 103 | ||
| 50 | Avg | 1.128 × 104 | 1.978 × 104 | 3.078 × 103 | 7.297 × 103 | 1.591 × 103 | 1.532 × 103 | 1.491 × 103 | 8.609 × 103 | 1.605 × 104 | 1.426 × 104 | 1.326 × 103 | |
| Min | 9.143 × 103 | 1.250 × 104 | 1.480 × 103 | 1.574 × 103 | 1.421 × 103 | 1.380 × 103 | 1.344 × 103 | 6.220 × 103 | 9.287 × 103 | 8.985 × 103 | 1.212 × 103 | ||
| 100 | Avg | 1.883 × 105 | 2.174 × 105 | 3.531 × 104 | 1.257 × 105 | 7.762 × 103 | 3.319 × 103 | 2.191 × 103 | 7.211 × 104 | 1.625 × 105 | 2.086 × 105 | 1.776 × 103 | |
| Min | 1.465 × 105 | 1.629 × 105 | 1.647 × 104 | 2.137 × 104 | 4.463 × 103 | 2.955 × 103 | 1.840 × 103 | 6.100 × 104 | 1.167 × 105 | 1.399 × 105 | 1.464 × 103 | ||
| F12 | 30 | Avg | 7.895 × 108 | 3.540 × 109 | 3.900 × 107 | 6.158 × 107 | 3.770 × 107 | 5.460 × 106 | 1.254 × 106 | 3.360 × 109 | 7.828 × 109 | 4.462 × 109 | 2.499 × 105 |
| Min | 3.859 × 108 | 1.934 × 109 | 2.109 × 106 | 7.305 × 104 | 2.509 × 106 | 1.046 × 106 | 3.718 × 104 | 6.620 × 108 | 3.034 × 109 | 1.749 × 109 | 5.318 × 104 | ||
| 50 | Avg | 9.643 × 109 | 2.939 × 1010 | 4.764 × 108 | 2.475 × 109 | 1.861 × 108 | 4.882 × 107 | 7.229 × 106 | 1.887 × 1010 | 5.350 × 1010 | 3.075 × 1010 | 1.599 × 106 | |
| Min | 5.659 × 109 | 2.161 × 1010 | 7.558 × 107 | 1.646 × 107 | 5.114 × 107 | 2.169 × 107 | 1.549 × 106 | 1.045 × 1010 | 2.948 × 1010 | 1.600 × 1010 | 3.874 × 105 | ||
| 100 | Avg | 6.862 × 1010 | 1.398 × 1011 | 4.919 × 109 | 3.523 × 1010 | 6.875 × 108 | 3.370 × 108 | 3.428 × 107 | 6.764 × 1010 | 1.766 × 1011 | 9.544 × 1010 | 3.131 × 106 | |
| Min | 5.696 × 1010 | 1.132 × 1011 | 1.450 × 109 | 1.435 × 1010 | 2.918 × 108 | 2.296 × 108 | 3.806 × 106 | 4.928 × 1010 | 1.296 × 1011 | 5.096 × 1010 | 1.250 × 106 | ||
| F13 | 30 | Avg | 9.518 × 107 | 8.620 × 108 | 8.368 × 105 | 7.958 × 106 | 1.463 × 105 | 4.494 × 105 | 1.047 × 105 | 8.863 × 108 | 4.348 × 104 | 8.738 × 108 | 1.994 × 104 |
| Min | 4.048 × 107 | 3.361 × 108 | 1.991 × 104 | 1.122 × 104 | 2.283 × 104 | 2.705 × 105 | 1.436 × 104 | 3.327 × 107 | 2.158 × 104 | 2.189 × 108 | 1.396 × 103 | ||
| 50 | Avg | 1.722 × 109 | 8.709 × 109 | 1.532 × 108 | 2.427 × 108 | 1.657 × 105 | 2.510 × 106 | 8.895 × 104 | 5.260 × 109 | 3.917 × 109 | 1.288 × 1010 | 1.434 × 104 | |
| Min | 1.103 × 109 | 5.824 × 109 | 1.312 × 105 | 1.136 × 105 | 4.764 × 104 | 1.415 × 106 | 2.174 × 104 | 5.002 × 108 | 1.041 × 107 | 1.435 × 109 | 1.582 × 103 | ||
| 100 | Avg | 8.436 × 109 | 2.634 × 1010 | 4.163 × 108 | 4.053 × 109 | 8.423 × 104 | 1.168 × 107 | 1.378 × 105 | 1.915 × 1010 | 3.479 × 1010 | 1.965 × 1010 | 1.105 × 104 | |
| Min | 6.140 × 109 | 1.992 × 1010 | 1.579 × 106 | 2.629 × 108 | 3.701 × 104 | 9.896 × 106 | 3.658 × 104 | 1.137 × 1010 | 2.155 × 1010 | 1.073 × 1010 | 1.651 × 103 | ||
| F14 | 30 | Avg | 1.022 × 105 | 3.619 × 105 | 1.438 × 105 | 8.969 × 104 | 9.075 × 105 | 2.614 × 104 | 2.073 × 104 | 3.244 × 105 | 4.223 × 104 | 1.548 × 106 | 1.671 × 104 |
| Min | 3.932 × 104 | 7.165 × 104 | 3.679 × 103 | 2.197 × 103 | 1.364 × 105 | 2.724 × 103 | 6.252 × 103 | 4.503 × 104 | 2.213 × 103 | 7.879 × 104 | 5.615 × 103 | ||
| 50 | Avg | 1.285 × 106 | 5.160 × 106 | 4.016 × 105 | 3.086 × 105 | 6.358 × 105 | 1.086 × 105 | 8.151 × 104 | 1.206 × 106 | 3.933 × 105 | 2.634 × 107 | 8.426 × 104 | |
| Min | 8.972 × 105 | 2.700 × 106 | 4.749 × 104 | 1.071 × 104 | 9.639 × 104 | 2.360 × 104 | 1.194 × 104 | 5.706 × 105 | 4.727 × 104 | 8.185 × 105 | 8.798 × 103 | ||
| 100 | Avg | 2.710 × 107 | 6.024 × 107 | 3.480 × 106 | 7.558 × 106 | 1.876 × 106 | 1.207 × 106 | 3.627 × 105 | 7.928 × 106 | 2.267 × 107 | 3.200 × 107 | 3.439 × 105 | |
| Min | 2.008 × 107 | 3.524 × 107 | 1.056 × 106 | 3.097 × 105 | 6.461 × 105 | 1.938 × 105 | 1.387 × 105 | 4.302 × 106 | 4.241 × 106 | 7.455 × 106 | 1.557 × 105 | ||
| F15 | 30 | Avg | 2.966 × 106 | 4.746 × 107 | 3.637 × 105 | 3.412 × 104 | 8.683 × 104 | 9.006 × 104 | 3.448 × 104 | 5.434 × 106 | 2.498 × 104 | 4.469 × 107 | 1.983 × 104 |
| Min | 1.113 × 106 | 6.971 × 106 | 1.847 × 104 | 3.640 × 103 | 1.368 × 104 | 5.002 × 104 | 2.547 × 103 | 1.019 × 106 | 1.454 × 104 | 2.375 × 106 | 2.006 × 103 | ||
| 50 | Avg | 1.739 × 108 | 1.276 × 109 | 9.314 × 106 | 2.145 × 107 | 7.839 × 104 | 5.206 × 105 | 7.164 × 104 | 1.070 × 108 | 3.131 × 104 | 8.129 × 108 | 9.247 × 103 | |
| Min | 6.074 × 107 | 5.105 × 108 | 1.565 × 104 | 4.235 × 104 | 2.225 × 104 | 3.594 × 105 | 1.422 × 104 | 5.379 × 107 | 1.979 × 104 | 1.237 × 108 | 1.622 × 103 | ||
| 100 | Avg | 2.250 × 109 | 8.426 × 109 | 9.478 × 107 | 1.045 × 109 | 2.527 × 105 | 2.824 × 106 | 9.337 × 104 | 4.851 × 109 | 4.659 × 109 | 8.332 × 109 | 7.383 × 103 | |
| Min | 1.743 × 109 | 6.068 × 109 | 5.864 × 105 | 1.058 × 105 | 2.549 × 104 | 1.949 × 106 | 1.223 × 104 | 1.096 × 109 | 1.070 × 109 | 1.272 × 109 | 1.752 × 103 | ||
| F16 | 30 | Avg | 3.496 × 103 | 4.179 × 103 | 2.287 × 103 | 2.995 × 103 | 3.519 × 103 | 2.640 × 103 | 2.807 × 103 | 3.475 × 103 | 3.676 × 103 | 4.402 × 103 | 1.928 × 103 |
| Min | 3.252 × 103 | 3.709 × 103 | 1.744 × 103 | 2.487 × 103 | 2.728 × 103 | 2.110 × 103 | 2.095 × 103 | 2.940 × 103 | 2.867 × 103 | 3.607 × 103 | 1.617 × 103 | ||
| 50 | Avg | 5.575 × 103 | 6.744 × 103 | 2.791 × 103 | 4.150 × 103 | 4.689 × 103 | 3.621 × 103 | 3.778 × 103 | 5.240 × 103 | 6.261 × 103 | 6.930 × 103 | 2.546 × 103 | |
| Min | 5.216 × 103 | 6.027 × 103 | 2.209 × 103 | 3.133 × 103 | 3.895 × 103 | 2.949 × 103 | 3.014 × 103 | 4.488 × 103 | 3.693 × 103 | 5.302 × 103 | 2.186 × 103 | ||
| 100 | Avg | 1.236 × 104 | 1.660 × 104 | 5.610 × 103 | 8.085 × 103 | 9.811 × 103 | 6.439 × 103 | 6.869 × 103 | 1.231 × 104 | 1.814 × 104 | 1.679 × 104 | 4.533 × 103 | |
| Min | 1.111 × 104 | 1.563 × 104 | 4.748 × 103 | 6.389 × 103 | 7.512 × 103 | 5.301 × 103 | 4.978 × 103 | 1.047 × 104 | 1.301 × 104 | 1.394 × 104 | 3.471 × 103 | ||
| F17 | 30 | Avg | 2.410 × 103 | 2.789 × 103 | 1.956 × 103 | 2.411 × 103 | 2.520 × 103 | 2.203 × 103 | 2.315 × 103 | 2.598 × 103 | 2.620 × 103 | 2.752 × 103 | 1.875 × 103 |
| Min | 2.242 × 103 | 2.467 × 103 | 1.777 × 103 | 1.975 × 103 | 1.931 × 103 | 1.801 × 103 | 1.942 × 103 | 2.275 × 103 | 2.085 × 103 | 2.359 × 103 | 1.736 × 103 | ||
| 50 | Avg | 4.770 × 103 | 5.784 × 103 | 2.676 × 103 | 3.708 × 103 | 3.892 × 103 | 3.155 × 103 | 3.758 × 103 | 4.205 × 103 | 4.226 × 103 | 5.316 × 103 | 2.573 × 103 | |
| Min | 4.087 × 103 | 4.805 × 103 | 2.257 × 103 | 2.866 × 103 | 3.106 × 103 | 2.538 × 103 | 2.931 × 103 | 3.304 × 103 | 3.228 × 103 | 3.873 × 103 | 2.176 × 103 | ||
| 100 | Avg | 1.132 × 104 | 9.223 × 104 | 4.439 × 103 | 7.668 × 103 | 7.212 × 103 | 5.693 × 103 | 6.345 × 103 | 1.240 × 104 | 2.886 × 105 | 4.082 × 105 | 4.247 × 103 | |
| Min | 1.036 × 104 | 1.996 × 104 | 3.338 × 103 | 5.623 × 103 | 5.421 × 103 | 4.630 × 103 | 4.935 × 103 | 9.483 × 103 | 1.665 × 104 | 1.263 × 104 | 2.980 × 103 | ||
| F18 | 30 | Avg | 2.207 × 106 | 7.273 × 106 | 6.631 × 105 | 3.177 × 106 | 2.408 × 106 | 3.682 × 105 | 1.734 × 105 | 1.487 × 106 | 7.850 × 105 | 2.844 × 107 | 8.793 × 104 |
| Min | 1.112 × 106 | 1.967 × 106 | 8.000 × 104 | 3.737 × 104 | 1.933 × 105 | 8.629 × 104 | 3.793 × 104 | 4.340 × 105 | 1.205 × 105 | 2.007 × 106 | 3.279 × 103 | ||
| 50 | Avg | 1.242 × 107 | 4.494 × 107 | 3.300 × 106 | 3.443 × 106 | 4.272 × 106 | 7.009 × 105 | 4.064 × 105 | 8.349 × 106 | 2.081 × 107 | 7.061 × 107 | 3.192 × 105 | |
| Min | 5.637 × 106 | 1.275 × 107 | 2.968 × 105 | 1.807 × 105 | 1.009 × 106 | 3.224 × 105 | 1.508 × 105 | 3.517 × 106 | 8.364 × 105 | 1.412 × 107 | 3.532 × 104 | ||
| 100 | Avg | 5.093 × 107 | 1.121 × 108 | 4.158 × 106 | 1.162 × 107 | 2.020 × 106 | 2.306 × 106 | 8.326 × 105 | 1.088 × 107 | 3.135 × 107 | 5.663 × 107 | 1.164 × 106 | |
| Min | 3.392 × 107 | 6.823 × 107 | 7.431 × 105 | 4.881 × 105 | 8.476 × 105 | 1.032 × 106 | 3.782 × 105 | 5.042 × 106 | 9.728 × 106 | 9.819 × 106 | 2.003 × 105 | ||
| F19 | 30 | Avg | 1.278 × 107 | 9.064 × 107 | 2.913 × 105 | 4.071 × 106 | 2.647 × 106 | 6.193 × 104 | 3.223 × 104 | 4.950 × 107 | 1.071 × 106 | 1.072 × 108 | 2.012 × 104 |
| Min | 6.005 × 106 | 3.289 × 107 | 9.466 × 103 | 2.093 × 103 | 1.744 × 105 | 1.764 × 104 | 2.168 × 103 | 2.507 × 106 | 8.696 × 105 | 5.192 × 106 | 1.940 × 103 | ||
| 50 | Avg | 9.348 × 107 | 6.178 × 108 | 2.362 × 106 | 6.151 × 106 | 2.457 × 106 | 2.445 × 105 | 2.361 × 104 | 3.031 × 108 | 4.614 × 105 | 9.214 × 108 | 1.409 × 104 | |
| Min | 4.313 × 107 | 2.829 × 108 | 6.908 × 104 | 5.030 × 103 | 1.534 × 105 | 1.272 × 105 | 2.700 × 103 | 3.918 × 107 | 4.438 × 105 | 1.580 × 108 | 2.081 × 103 | ||
| 100 | Avg | 2.062 × 109 | 8.505 × 109 | 1.003 × 108 | 3.561 × 108 | 1.528 × 107 | 4.435 × 106 | 7.032 × 104 | 3.211 × 109 | 4.723 × 109 | 5.975 × 109 | 1.009 × 104 | |
| Min | 1.411 × 109 | 6.413 × 109 | 2.250 × 106 | 2.761 × 106 | 5.273 × 106 | 2.123 × 106 | 1.223 × 104 | 7.255 × 108 | 1.529 × 109 | 2.984 × 109 | 2.081 × 103 | ||
| F20 | 30 | Avg | 2.533 × 103 | 2.656 × 103 | 2.288 × 103 | 2.600 × 103 | 2.702 × 103 | 2.498 × 103 | 2.468 × 103 | 2.921 × 103 | 2.638 × 103 | 2.847 × 103 | 2.116 × 103 |
| Min | 2.461 × 103 | 2.473 × 103 | 2.154 × 103 | 2.215 × 103 | 2.327 × 103 | 2.180 × 103 | 2.072 × 103 | 2.560 × 103 | 2.327 × 103 | 2.454 × 103 | 2.018 × 103 | ||
| 50 | Avg | 3.891 × 103 | 3.930 × 103 | 2.736 × 103 | 3.557 × 103 | 3.628 × 103 | 3.060 × 103 | 3.431 × 103 | 3.932 × 103 | 3.346 × 103 | 3.929 × 103 | 2.297 × 103 | |
| Min | 3.535 × 103 | 3.587 × 103 | 2.422 × 103 | 2.897 × 103 | 2.664 × 103 | 2.586 × 103 | 2.655 × 103 | 3.576 × 103 | 2.634 × 103 | 3.493 × 103 | 2.097 × 103 | ||
| 100 | Avg | 7.466 × 103 | 7.382 × 103 | 4.469 × 103 | 5.692 × 103 | 5.875 × 103 | 5.054 × 103 | 5.740 × 103 | 6.931 × 103 | 5.751 × 103 | 6.923 × 103 | 3.566 × 103 | |
| Min | 6.910 × 103 | 6.809 × 103 | 3.301 × 103 | 4.194 × 103 | 4.326 × 103 | 4.139 × 103 | 4.438 × 103 | 6.030 × 103 | 4.700 × 103 | 6.187 × 103 | 3.093 × 103 | ||
| Ranking | 30 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 10/0/0 |
| 50 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 1/0/9 | 0/0/10 | 0/0/10 | 0/0/10 | 9/0/1 | |
| 100 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 1/0/9 | 0/0/10 | 0/0/10 | 0/0/10 | 9/0/1 |
Table 4.
Comparison of optimization results obtained from composition test functions.
| F | D | Metrics | SA (1983) |
CGA (2000) |
GWO (2014) |
MFO (2015) |
WOA (2016) |
LMFO (2016) |
WCMFO (2019) |
ChOA (2020) |
AOA (2021) |
SMFO (2021) |
I-MFO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F21 | 30 | Avg | 2.593 × 103 | 2.655 × 103 | 2.383 × 103 | 2.476 × 103 | 2.558 × 103 | 2.439 × 103 | 2.493 × 103 | 2.565 × 103 | 2.604 × 103 | 2.653 × 103 | 2.363 × 103 |
| Min | 2.565 × 103 | 2.626 × 103 | 2.352 × 103 | 2.421 × 103 | 2.463 × 103 | 2.378 × 103 | 2.398 × 103 | 2.503 × 103 | 2.515 × 103 | 2.551 × 103 | 2.334 × 103 | ||
| 50 | Avg | 2.945 × 103 | 3.065 × 103 | 2.485 × 103 | 2.694 × 103 | 2.888 × 103 | 2.609 × 103 | 2.694 × 103 | 2.886 × 103 | 3.002 × 103 | 3.064 × 103 | 2.430 × 103 | |
| Min | 2.893 × 103 | 3.026 × 103 | 2.440 × 103 | 2.575 × 103 | 2.744 × 103 | 2.542 × 103 | 2.580 × 103 | 2.819 × 103 | 2.885 × 103 | 2.935 × 103 | 2.399 × 103 | ||
| 100 | Avg | 4.058 × 103 | 4.393 × 103 | 2.845 × 103 | 3.594 × 103 | 3.884 × 103 | 3.280 × 103 | 3.539 × 103 | 4.044 × 103 | 4.581 × 103 | 4.394 × 103 | 2.738 × 103 | |
| Min | 3.956 × 103 | 4.275 × 103 | 2.751 × 103 | 3.262 × 103 | 3.502 × 103 | 3.106 × 103 | 3.233 × 103 | 3.804 × 103 | 4.161 × 103 | 4.128 × 103 | 2.652 × 103 | ||
| F22 | 30 | Avg | 6.618 × 103 | 6.787 × 103 | 4.413 × 103 | 5.842 × 103 | 5.949 × 103 | 5.006 × 103 | 6.637 × 103 | 9.124 × 103 | 7.785 × 103 | 8.654 × 103 | 2.889 × 103 |
| Min | 4.837 × 103 | 5.363 × 103 | 2.420 × 103 | 3.150 × 103 | 2.315 × 103 | 2.325 × 103 | 5.330 × 103 | 8.503 × 103 | 5.492 × 103 | 5.677 × 103 | 2.300 × 103 | ||
| 50 | Avg | 1.569 × 104 | 1.600 × 104 | 8.634 × 103 | 1.029 × 104 | 1.208 × 104 | 8.858 × 103 | 1.001 × 104 | 1.655 × 104 | 1.468 × 104 | 1.616 × 104 | 6.525 × 103 | |
| Min | 1.464 × 104 | 1.489 × 104 | 7.065 × 103 | 7.958 × 103 | 8.721 × 103 | 7.176 × 103 | 8.609 × 103 | 1.554 × 104 | 1.304 × 104 | 1.529 × 104 | 5.551 × 103 | ||
| 100 | Avg | 3.336 × 104 | 3.346 × 104 | 1.777 × 104 | 2.032 × 104 | 2.397 × 104 | 1.948 × 104 | 1.943 × 104 | 3.374 × 104 | 3.092 × 104 | 3.277 × 104 | 1.393 × 104 | |
| Min | 3.264 × 104 | 3.169 × 104 | 1.413 × 104 | 1.778 × 104 | 2.087 × 104 | 1.791 × 104 | 1.671 × 104 | 3.233 × 104 | 2.790 × 104 | 3.043 × 104 | 1.189 × 104 | ||
| F23 | 30 | Avg | 2.916 × 103 | 3.149 × 103 | 2.731 × 103 | 2.801 × 103 | 3.032 × 103 | 2.759 × 103 | 2.785 × 103 | 3.011 × 103 | 3.312 × 103 | 3.283 × 103 | 2.700 × 103 |
| Min | 2.819 × 103 | 3.102 × 103 | 2.695 × 103 | 2.762 × 103 | 2.886 × 103 | 2.710 × 103 | 2.721 × 103 | 2.930 × 103 | 3.093 × 103 | 3.027 × 103 | 2.680 × 103 | ||
| 50 | Avg | 3.380 × 103 | 3.816 × 103 | 2.907 × 103 | 3.135 × 103 | 3.592 × 103 | 3.027 × 103 | 3.104 × 103 | 3.515 × 103 | 4.310 × 103 | 3.929 × 103 | 2.858 × 103 | |
| Min | 3.345 × 103 | 3.644 × 103 | 2.835 × 103 | 3.046 × 103 | 3.377 × 103 | 2.990 × 103 | 2.980 × 103 | 3.373 × 103 | 3.850 × 103 | 3.594 × 103 | 2.820 × 103 | ||
| 100 | Avg | 4.322 × 103 | 5.475 × 103 | 3.405 × 103 | 3.716 × 103 | 4.823 × 103 | 3.475 × 103 | 3.545 × 103 | 4.661 × 103 | 6.745 × 103 | 6.024 × 103 | 3.035 × 103 | |
| Min | 4.238 × 103 | 5.225 × 103 | 3.289 × 103 | 3.547 × 103 | 4.263 × 103 | 3.366 × 103 | 3.306 × 103 | 4.424 × 103 | 6.011 × 103 | 5.104 × 103 | 2.971 × 103 | ||
| F24 | 30 | Avg | 3.084 × 103 | 3.342 × 103 | 2.904 × 103 | 2.974 × 103 | 3.167 × 103 | 2.927 × 103 | 2.978 × 103 | 3.201 × 103 | 3.682 × 103 | 3.433 × 103 | 2.871 × 103 |
| Min | 3.063 × 103 | 3.270 × 103 | 2.855 × 103 | 2.910 × 103 | 3.021 × 103 | 2.897 × 103 | 2.928 × 103 | 3.128 × 103 | 3.473 × 103 | 3.217 × 103 | 2.852 × 103 | ||
| 50 | Avg | 3.459 × 103 | 4.039 × 103 | 3.087 × 103 | 3.227 × 103 | 3.733 × 103 | 3.136 × 103 | 3.231 × 103 | 3.713 × 103 | 4.749 × 103 | 4.359 × 103 | 3.008 × 103 | |
| Min | 3.416 × 103 | 3.856 × 103 | 3.000 × 103 | 3.152 × 103 | 3.545 × 103 | 3.071 × 103 | 3.135 × 103 | 3.588 × 103 | 4.340 × 103 | 3.875 × 103 | 2.964 × 103 | ||
| 100 | Avg | 5.059 × 103 | 8.073 × 103 | 3.962 × 103 | 4.272 × 103 | 5.854 × 103 | 4.086 × 103 | 4.293 × 103 | 5.913 × 103 | 1.065 × 104 | 8.875 × 103 | 3.651 × 103 | |
| Min | 4.961 × 103 | 7.435 × 103 | 3.819 × 103 | 4.124 × 103 | 5.238 × 103 | 3.976 × 103 | 4.048 × 103 | 5.524 × 103 | 8.928 × 103 | 6.869 × 103 | 3.556 × 103 | ||
| F25 | 30 | Avg | 4.148 × 103 | 5.436 × 103 | 2.957 × 103 | 3.107 × 103 | 2.945 × 103 | 2.889 × 103 | 2.887 × 103 | 4.099 × 103 | 4.426 × 103 | 3.940 × 103 | 2.888 × 103 |
| Min | 3.828 × 103 | 4.615 × 103 | 2.913 × 103 | 2.889 × 103 | 2.898 × 103 | 2.888 × 103 | 2.884 × 103 | 3.456 × 103 | 3.635 × 103 | 3.463 × 103 | 2.887 × 103 | ||
| 50 | Avg | 1.054 × 104 | 1.824 × 104 | 3.371 × 103 | 4.930 × 103 | 3.155 × 103 | 3.043 × 103 | 3.041 × 103 | 8.621 × 103 | 1.388 × 104 | 1.083 × 104 | 3.000 × 103 | |
| Min | 7.933 × 103 | 1.397 × 104 | 3.055 × 103 | 3.159 × 103 | 3.039 × 103 | 2.994 × 103 | 2.962 × 103 | 6.928 × 103 | 1.101 × 104 | 7.534 × 103 | 2.978 × 103 | ||
| 100 | Avg | 5.160 × 104 | 5.583 × 104 | 5.277 × 103 | 1.123 × 104 | 3.590 × 103 | 3.456 × 103 | 3.321 × 103 | 1.363 × 104 | 2.328 × 104 | 2.002 × 104 | 3.262 × 103 | |
| Min | 4.633 × 104 | 4.701 × 104 | 4.686 × 103 | 4.792 × 103 | 3.464 × 103 | 3.365 × 103 | 3.206 × 103 | 1.142 × 104 | 1.986 × 104 | 1.680 × 104 | 3.116 × 103 | ||
| F26 | 30 | Avg | 6.408 × 103 | 8.876 × 103 | 4.424 × 103 | 5.689 × 103 | 7.599 × 103 | 5.012 × 103 | 5.447 × 103 | 6.328 × 103 | 9.412 × 103 | 8.871 × 103 | 4.300 × 103 |
| Min | 5.542 × 103 | 7.735 × 103 | 3.954 × 103 | 4.921 × 103 | 5.975 × 103 | 4.607 × 103 | 4.955 × 103 | 5.882 × 103 | 7.702 × 103 | 5.057 × 103 | 2.900 × 103 | ||
| 50 | Avg | 1.063 × 104 | 1.594 × 104 | 5.735 × 103 | 8.121 × 103 | 1.306 × 104 | 7.041 × 103 | 8.059 × 103 | 1.028 × 104 | 1.546 × 104 | 1.587 × 104 | 5.179 × 103 | |
| Min | 1.002 × 104 | 1.454 × 104 | 5.192 × 103 | 6.910 × 103 | 9.977 × 103 | 6.161 × 103 | 7.062 × 103 | 9.047 × 103 | 1.326 × 104 | 1.396 × 104 | 4.512 × 103 | ||
| 100 | Avg | 2.452 × 104 | 4.461 × 104 | 1.263 × 104 | 1.741 × 104 | 3.111 × 104 | 1.493 × 104 | 1.752 × 104 | 2.492 × 104 | 4.995 × 104 | 4.315 × 104 | 9.748 × 103 | |
| Min | 2.363 × 104 | 4.099 × 104 | 1.124 × 104 | 1.526 × 104 | 2.326 × 104 | 1.333 × 104 | 1.518 × 104 | 2.276 × 104 | 4.219 × 104 | 3.583 × 104 | 9.123 × 103 | ||
| F27 | 30 | Avg | 3.279 × 103 | 3.667 × 103 | 3.229 × 103 | 3.236 × 103 | 3.346 × 103 | 3.221 × 103 | 3.228 × 103 | 3.493 × 103 | 4.286 × 103 | 3.688 × 103 | 3.213 × 103 |
| Min | 3.250 × 103 | 3.497 × 103 | 3.212 × 103 | 3.208 × 103 | 3.282 × 103 | 3.200 × 103 | 3.201 × 103 | 3.355 × 103 | 3.633 × 103 | 3.397 × 103 | 3.184 × 103 | ||
| 50 | Avg | 3.730 × 103 | 5.183 × 103 | 3.471 × 103 | 3.550 × 103 | 4.305 × 103 | 3.356 × 103 | 3.504 × 103 | 4.272 × 103 | 6.565 × 103 | 5.306 × 103 | 3.337 × 103 | |
| Min | 3.669 × 103 | 4.697 × 103 | 3.342 × 103 | 3.407 × 103 | 3.678 × 103 | 3.249 × 103 | 3.377 × 103 | 3.997 × 103 | 5.687 × 103 | 4.453 × 103 | 3.231 × 103 | ||
| 100 | Avg | 4.858 × 103 | 8.855 × 103 | 3.854 × 103 | 3.867 × 103 | 4.945 × 103 | 3.500 × 103 | 3.607 × 103 | 5.656 × 103 | 1.177 × 104 | 9.335 × 103 | 3.467 × 103 | |
| Min | 4.700 × 103 | 7.573 × 103 | 3.594 × 103 | 3.655 × 103 | 3.909 × 103 | 3.389 × 103 | 3.482 × 103 | 5.033 × 103 | 9.541 × 103 | 5.884 × 103 | 3.381 × 103 | ||
| F28 | 30 | Avg | 4.040 × 103 | 5.557 × 103 | 3.339 × 103 | 3.721 × 103 | 3.303 × 103 | 3.255 × 103 | 3.194 × 103 | 4.295 × 103 | 5.958 × 103 | 5.524 × 103 | 3.226 × 103 |
| Min | 3.927 × 103 | 4.829 × 103 | 3.269 × 103 | 3.318 × 103 | 3.269 × 103 | 3.209 × 103 | 3.100 × 103 | 3.565 × 103 | 4.603 × 103 | 4.419 × 103 | 3.155 × 103 | ||
| 50 | Avg | 8.098 × 103 | 1.147 × 104 | 3.873 × 103 | 8.080 × 103 | 3.424 × 103 | 3.316 × 103 | 3.298 × 103 | 6.101 × 103 | 1.102 × 104 | 9.557 × 103 | 3.278 × 103 | |
| Min | 6.921 × 103 | 8.816 × 103 | 3.653 × 103 | 5.324 × 103 | 3.344 × 103 | 3.274 × 103 | 3.259 × 103 | 5.216 × 103 | 9.574 × 103 | 8.008 × 103 | 3.259 × 103 | ||
| 100 | Avg | 2.499 × 104 | 3.958 × 104 | 6.692 × 103 | 1.749 × 104 | 3.721 × 103 | 1.149 × 104 | 7.644 × 103 | 1.204 × 104 | 2.938 × 104 | 2.320 × 104 | 3.357 × 103 | |
| Min | 2.393 × 104 | 3.584 × 104 | 4.771 × 103 | 1.485 × 104 | 3.598 × 103 | 3.439 × 103 | 3.333 × 103 | 9.983 × 103 | 2.587 × 104 | 1.831 × 104 | 3.321 × 103 | ||
| F29 | 30 | Avg | 4.387 × 103 | 5.321 × 103 | 3.645 × 103 | 4.003 × 103 | 4.751 × 103 | 3.785 × 103 | 3.965 × 103 | 4.348 × 103 | 5.689 × 103 | 5.698 × 103 | 3.465 × 103 |
| Min | 4.114 × 103 | 4.426 × 103 | 3.459 × 103 | 3.603 × 103 | 4.062 × 103 | 3.596 × 103 | 3.650 × 103 | 4.057 × 103 | 4.626 × 103 | 4.728 × 103 | 3.343 × 103 | ||
| 50 | Avg | 6.503 × 103 | 9.644 × 103 | 4.214 × 103 | 5.076 × 103 | 7.281 × 103 | 4.337 × 103 | 4.671 × 103 | 6.906 × 103 | 1.548 × 104 | 1.622 × 104 | 3.589 × 103 | |
| Min | 5.954 × 103 | 7.327 × 103 | 3.750 × 103 | 4.271 × 103 | 6.025 × 103 | 3.820 × 103 | 3.992 × 103 | 5.462 × 103 | 8.398 × 103 | 8.290 × 103 | 3.288 × 103 | ||
| 100 | Avg | 1.758 × 104 | 5.024 × 104 | 7.229 × 103 | 1.370 × 104 | 1.413 × 104 | 6.953 × 103 | 7.986 × 103 | 1.940 × 104 | 8.567 × 104 | 5.425 × 104 | 5.805 × 103 | |
| Min | 1.557 × 104 | 2.701 × 104 | 6.385 × 103 | 7.555 × 103 | 1.053 × 104 | 5.760 × 103 | 7.019 × 103 | 1.268 × 104 | 3.350 × 104 | 1.727 × 104 | 5.194 × 103 | ||
| F30 | 30 | Avg | 1.398 × 107 | 1.149 × 108 | 7.020 × 106 | 3.271 × 105 | 6.709 × 106 | 1.579 × 105 | 2.811 × 104 | 3.527 × 107 | 4.703 × 107 | 3.278 × 108 | 1.064 × 104 |
| Min | 4.880 × 106 | 2.608 × 107 | 8.829 × 105 | 1.393 × 104 | 4.463 × 105 | 4.934 × 104 | 1.582 × 104 | 1.030 × 107 | 1.875 × 106 | 3.212 × 107 | 5.336 × 103 | ||
| 50 | Avg | 3.257 × 108 | 1.521 × 109 | 6.713 × 107 | 8.852 × 107 | 8.101 × 107 | 5.293 × 106 | 2.475 × 106 | 5.299 × 108 | 5.682 × 108 | 2.207 × 109 | 1.323 × 106 | |
| Min | 1.906 × 108 | 7.735 × 108 | 3.536 × 107 | 2.389 × 106 | 4.041 × 107 | 3.797 × 106 | 1.155 × 106 | 1.890 × 108 | 1.863 × 108 | 2.782 × 108 | 7.972 × 105 | ||
| 100 | Avg | 3.841 × 109 | 1.351 × 1010 | 3.958 × 108 | 1.283 × 109 | 1.922 × 108 | 1.283 × 107 | 1.932 × 106 | 1.185 × 1010 | 3.055 × 1010 | 1.581 × 1010 | 7.578 × 103 | |
| Min | 3.148 × 109 | 8.053 × 109 | 5.455 × 107 | 3.821 × 107 | 7.264 × 107 | 7.913 × 106 | 3.637 × 105 | 8.263 × 109 | 1.450 × 1010 | 4.669 × 109 | 5.286 × 103 | ||
| 30 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 2/0/8 | 0/0/10 | 0/0/10 | 0/0/10 | 8/0/2 | |
| Ranking | 50 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 10/0/0 |
| 100 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 10/0/0 |
4.1. Benchmark Test Functions and Experimental Environment
The performance of the proposed algorithm is evaluated using the CEC 2018 benchmark functions with various dimensions of 30, 50, and 100. This benchmark contains 29 test functions with a diverse set of characteristics: unimodal, simple multimodal, hybrid, and composition. Test functions F1 and F3 are unimodal functions and they are adequate for evaluating the exploitation of algorithms. Test functions F4–F10 are multimodal with many local optima which are suitable to assess the exploration abilities of algorithms. Test functions F11–F20 are hybrid and F21–F30 are composition functions that can evaluate the local optima avoidance ability and balance between exploration and exploitation.
Due to the randomization of SI algorithms and to guarantee that the comparisons are fair, all experiments for each function are repeated 30 times separately on a laptop with characteristics: Intel Core i7-10750H CPU (2.60 GHz) and 24 GB of memory. The MATLAB programming language version R2020a and Windows 10 operating system were used to conduct all experiments. All algorithms were run under the same conditions, with the population size (N) 100 and the maximum number of iterations (MaxIt) (D × 104)/N.
4.2. Exploitation and Exploration Analysis
In this experimental evaluation, the unimodal functions F1 and F3 are considered to assess the exploitation abilities, while the multimodal test functions F4–F10 are dedicated to evaluating the exploration capabilities.
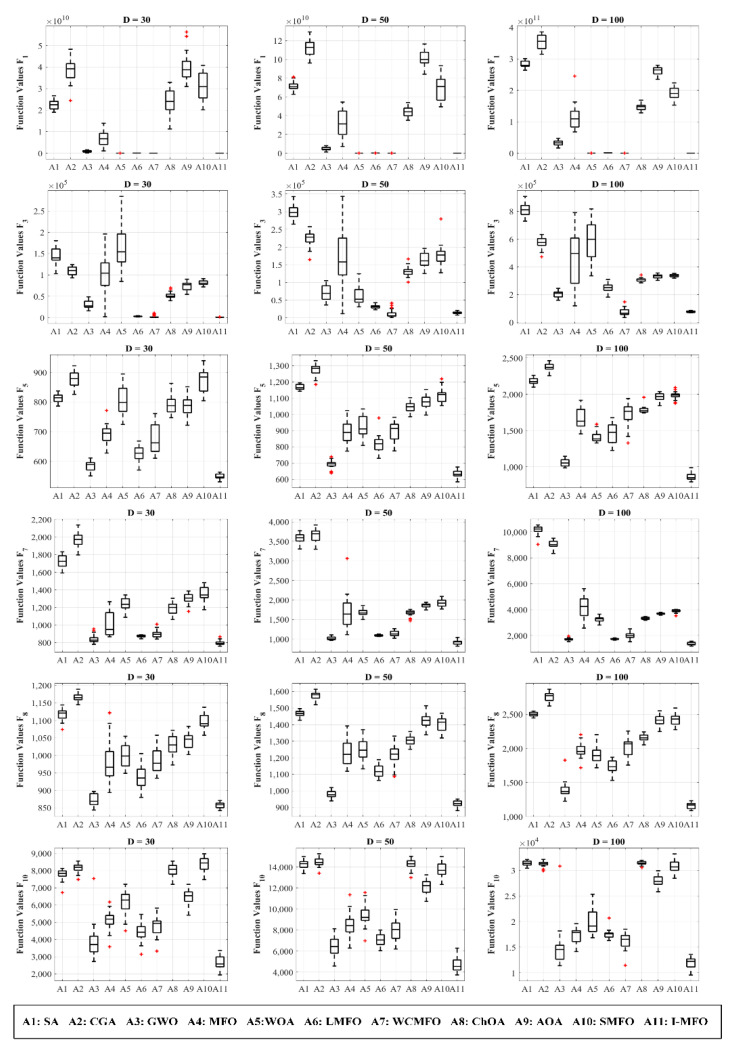
According to Table 2, the results prove that the I-MFO provides superior exploitation abilities around the optimum solution for all dimensions, particularly on test function F1. The results of multimodal test functions are evidence that the exploration capability of the I-MFO significantly outperforms all other algorithms in different dimensions. The comparison and reported results lead to the conclusion that the proposed I-MFO has an effective exploration ability due to the randomness movements of trapped moths by the AWAS strategy. Meanwhile, considering the best flame position and limited value of flight length (fl) causes the exploitation ability to remain functional in the course of iterations. Moreover, the comparison of fitness distribution is shown by box and whiskers diagrams in Figure 3. The diagrams predominately demonstrate that the proposed I-MFO can find the best solutions during the optimization process, which verifies that its exploration and exploitation abilities are more sufficient than other competitors.
Figure 3.
The comparison of fitness distribution on unimodal and multimodal functions.
4.3. Local Optima Avoidance Evaluation
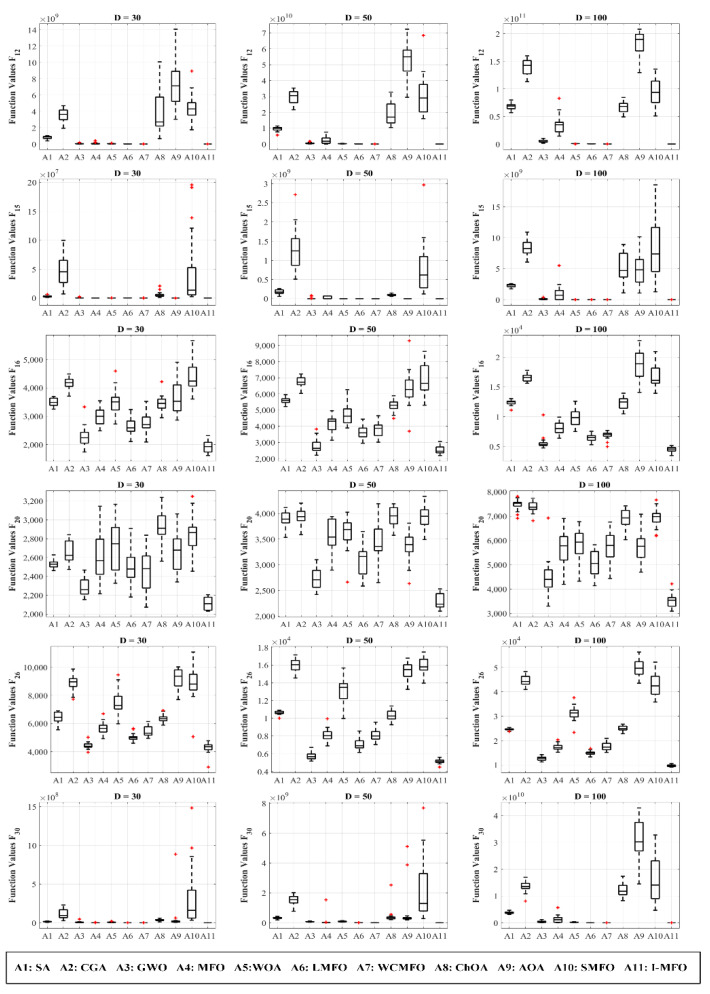
This experimental evaluation is benchmarking the ability of the proposed algorithm against the contender algorithms in terms of local optima avoidance and striking a balance between exploration and exploitation by considering hybrid and composition function results. The obtained results tabulated in Table 3 and Table 4 indicate that the proposed I-MFO algorithm is superior to the contender algorithms in dimensions 30, 50, and 100. The main reason is that the AWAS strategy helps trapped moths to escape the local optima and obtain a better position by changing random dimensions of trapped moths with dimensions of the best flame and a random moth’s position. The random moth causes the trapped moth to explore the search space and increases the population diversity while considering the best flame enhances the exploitation capabilities of the algorithm simultaneously. Furthermore, Figure 4 visualizes the comparison of fitness distribution using box and whiskers diagrams in which almost all diagrams demonstrate that the proposed I-MFO can find the best solutions during the optimization process. It verifies that I-MFO can provide satisfactory equilibration between exploration and exploitation.
Figure 4.
The comparison of fitness distribution on hybrid and composition functions.
4.4. I-MFO Overall Effectiveness
The overall effectiveness (OE) [50] of the I-MFO and other contender algorithms is computed by using results reported in Table 2, Table 3 and Table 4. The OE results tabulated in Table 5 are calculated using Equation (7), where N indicates the number of test functions and L is the number of losses of each algorithm. The results reveal that I-MFO with overall effectiveness of 92% is the most effective algorithm for all dimensions: 30, 50, and 100.
| (7) |
Table 5.
The overall effectiveness of the I-MFO and contender algorithms.
| Algorithms | SA (W/T/L) |
CGA (W/T/L) |
GWO (W/T/L) |
MFO (W/T/L) |
WOA (W/T/L) |
LMFO (W/T/L) |
WCMFO (W/T/L) |
ChOA (W/T/L) |
AOA (W/T/L) |
SMFO (W/T/L) |
I-MFO (W/T/L) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| D = 30 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 2/0/27 | 0/0/29 | 0/0/29 | 0/0/29 | 27/0/2 |
| D = 50 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 3/0/26 | 0/0/29 | 0/0/29 | 0/0/29 | 26/0/3 |
| D = 100 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 2/0/27 | 0/0/29 | 0/0/29 | 0/0/29 | 27/0/2 |
| Total | 0/0/87 | 0/0/87 | 0/0/87 | 0/0/87 | 0/0/87 | 0/0/87 | 7/0/80 | 0/0/87 | 0/0/87 | 0/0/87 | 80/0/7 |
| OE | 0% | 0% | 0% | 0% | 0% | 0% | 8% | 0% | 0% | 0% | 92% |
4.5. Convergence Behavior Analysis
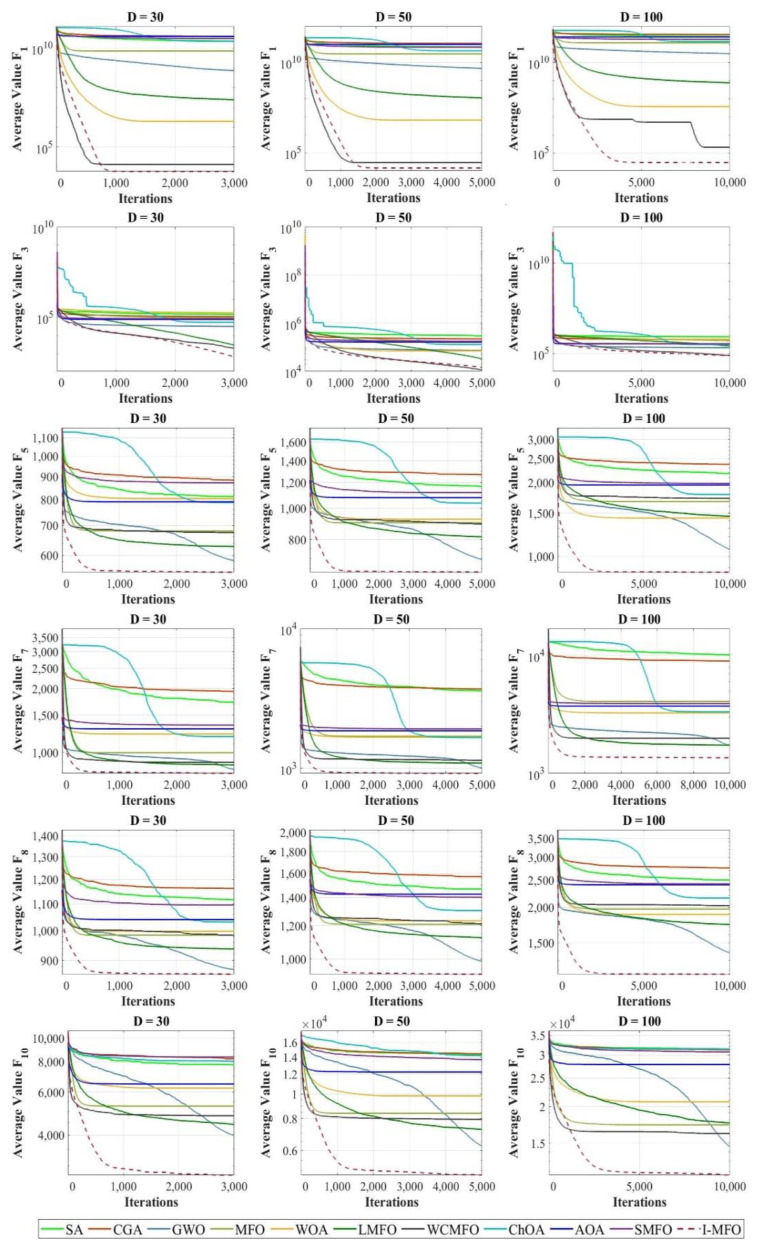
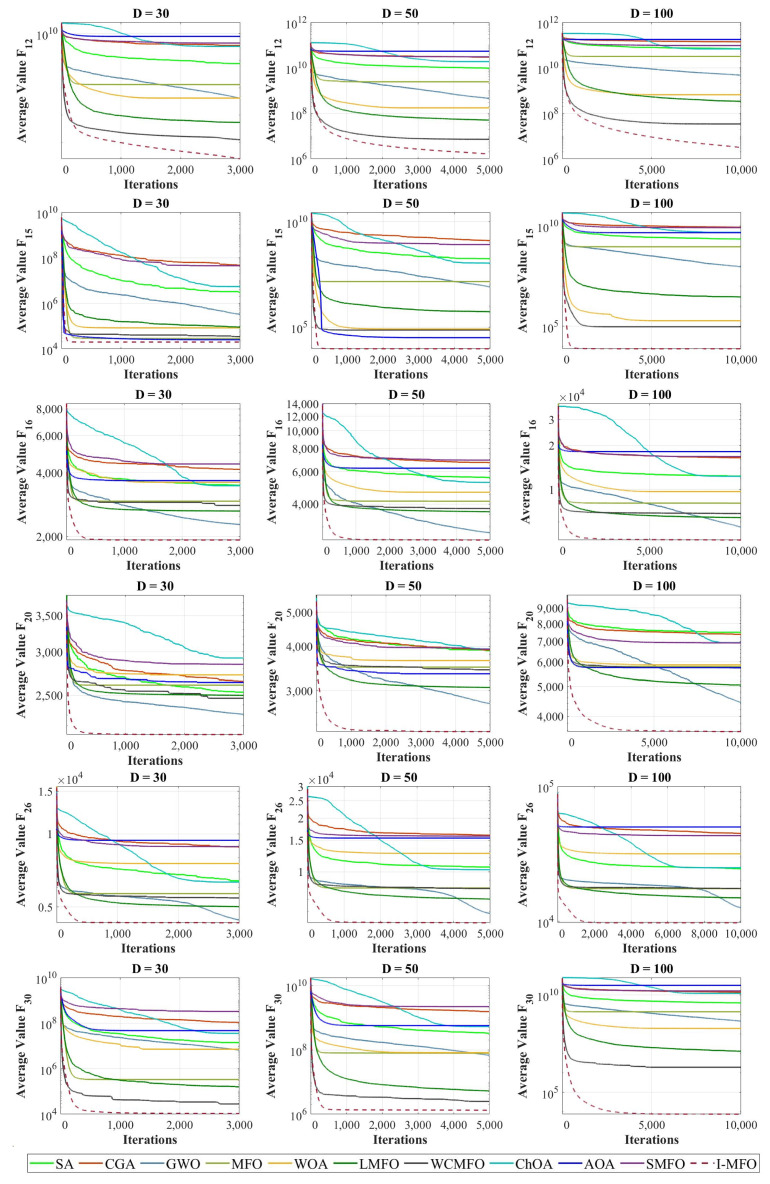
In this section, the convergence behavior of I-MFO is assessed and compared with contender algorithms on some selected functions with dimensions 30, 50, and 100. The convergence curves of the best fitness values obtained by each algorithm on unimodal and multimodal test functions are plotted in Figure 5. Moreover, the convergence curves of hybrid and composition test functions are plotted in Figure 6.
Figure 5.
The convergence curves of algorithms in unimodal and multimodal test functions.
Figure 6.
The convergence curves of algorithms in hybrid and composition test functions.
Investigating convergence behaviors of the I-MFO reveals that it shows various convergence behaviors. The most common behavior is an accelerated descent with the fastest accurate solutions toward the promising area in the early iterations, which can be seen in 30D (F5, F15, F16, F26), 50D (F6, F15, F16, F26, F30), and 100D (F5, F7, F8, F15, F16, F26). For some functions such as 30D (F1, F7, F8, F18, F30), 50D (F1, F8, F18), and 100D (F1, F10, F18, F30), the I-MFO shows abrupt movements in the first half of iterations and very low variations for the second half, which proves the efficient balance between exploration and exploitation. Finally, for 30D (F3, F7, F10, F12 F20), 50D (F3, F5, F8, F10, F12, F18, F20), and 100D (F3, F12, F18, F20), the I-MFO starts its convergence with a steep descent slope and then changes to a gradual trend toward the optimum solutions until final iterations. This behavior demonstrates the ability of the I-MFO in escaping from the local optimum and taking advantage of the last iterations.
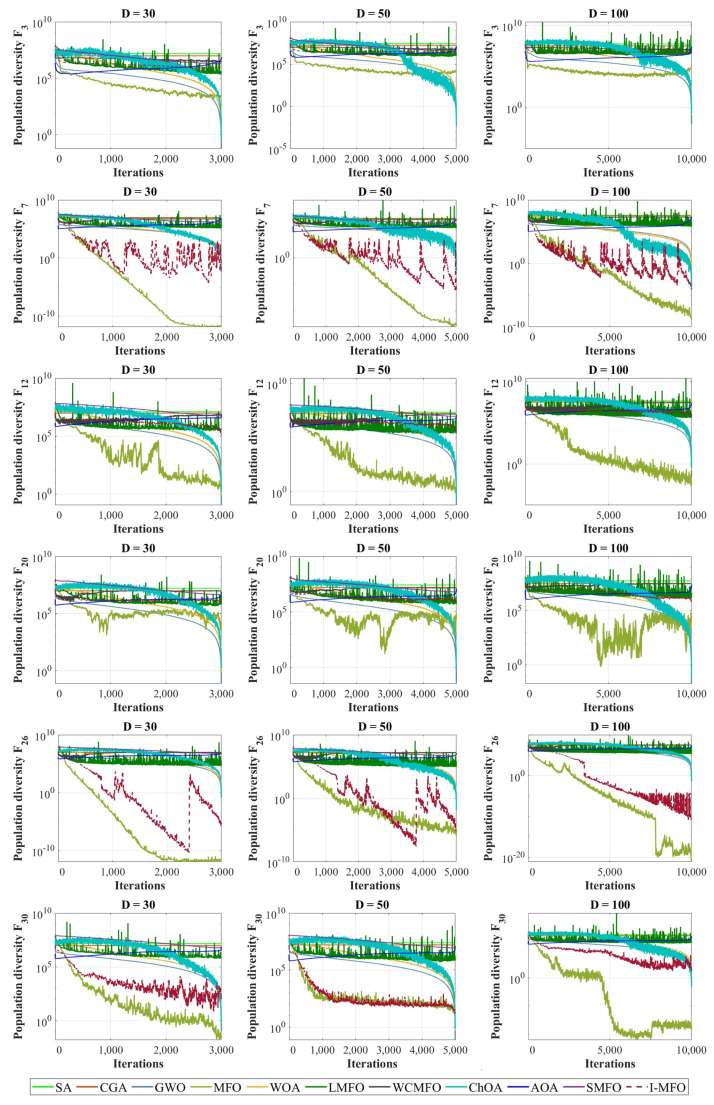
4.6. Population Diversity Analysis
In metaheuristic algorithms, the population diversity maintenance is important throughout the optimization process. The low diversity among search agents may cause the algorithm to plunge into the local optimum. In this experiment, the population diversity of the proposed I-MFO and contender algorithms is measured by a moment of inertia (Ic) [119], where the Ic is the spreading of each individual from their mass center given by Equation (8) and the mass center cj for j = 1, 2 … D is calculated by Equation (9).
| (8) |
| (9) |
The presented population diversity measures the distribution of search agents, and the diversity’s changing slope for the proposed algorithm and contender algorithms is plotted in Figure 7. This experiment is conducted on some CEC 2018 benchmark functions with dimensions 30, 50, and 100. Comparing the convergence curves in Figure 5 and Figure 6 and the plotted diversity in Figure 8 reveals that I-MFO can effectively maintain diversification among solutions until the near-optimal solution is met.
Figure 7.
The population diversity of algorithms in different test functions.
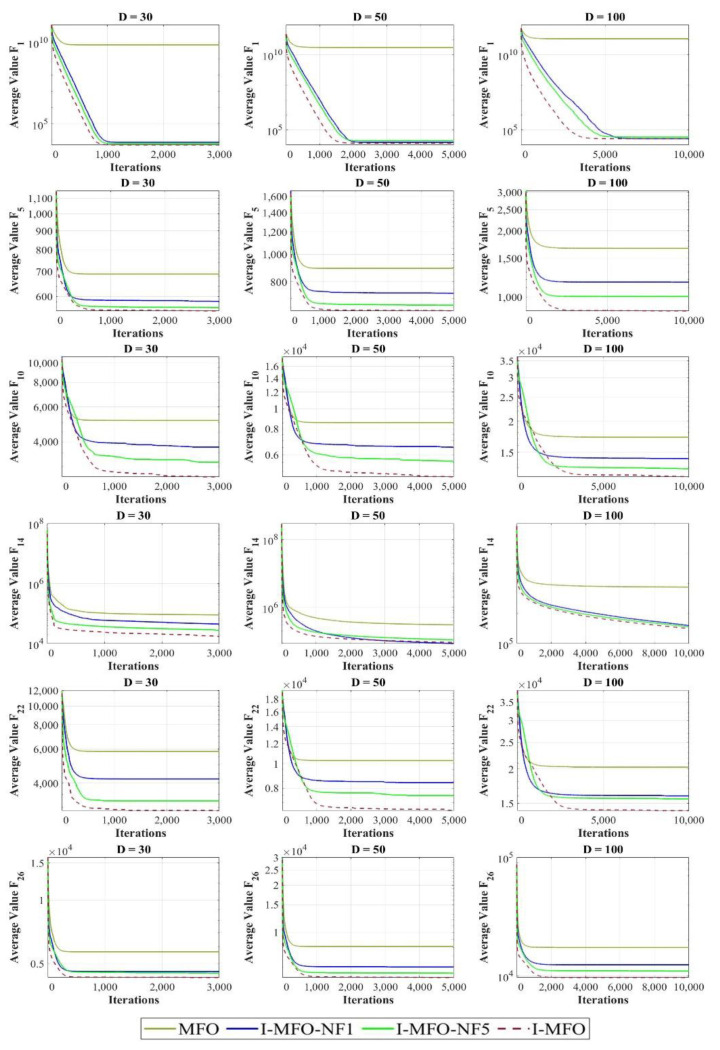
Figure 8.
The sensitivity analysis on the NF parameter.
4.7. Sensitivity Analysis on the Number of Flight (NF) Parameter
As discussed in Definition 2, the NF parameter is the number of opportunities for each trapped moth to fly in the search space and possibly obtain a better position. Hence, in this experiment, the impact of considering different values for the NF parameter is evaluated and discussed. The plotted curves in Figure 8 illustrate the convergence behavior of the MFO compared with different variants of I-MFO algorithm. In I-MFO-NF1 and I-MFO-NF5, the value of NF is considered by 1 and 5 while in I-MFO, the value of NF is set by a random number in [1, D]. The results gained for different dimensions 30, 50, and 100 reveal that setting NF by a random number limited by the dimension has an advantage for trapped moths to possibly escape from the local optima for different test functions.
4.8. Impact Analysis of Applying AWAS Strategy
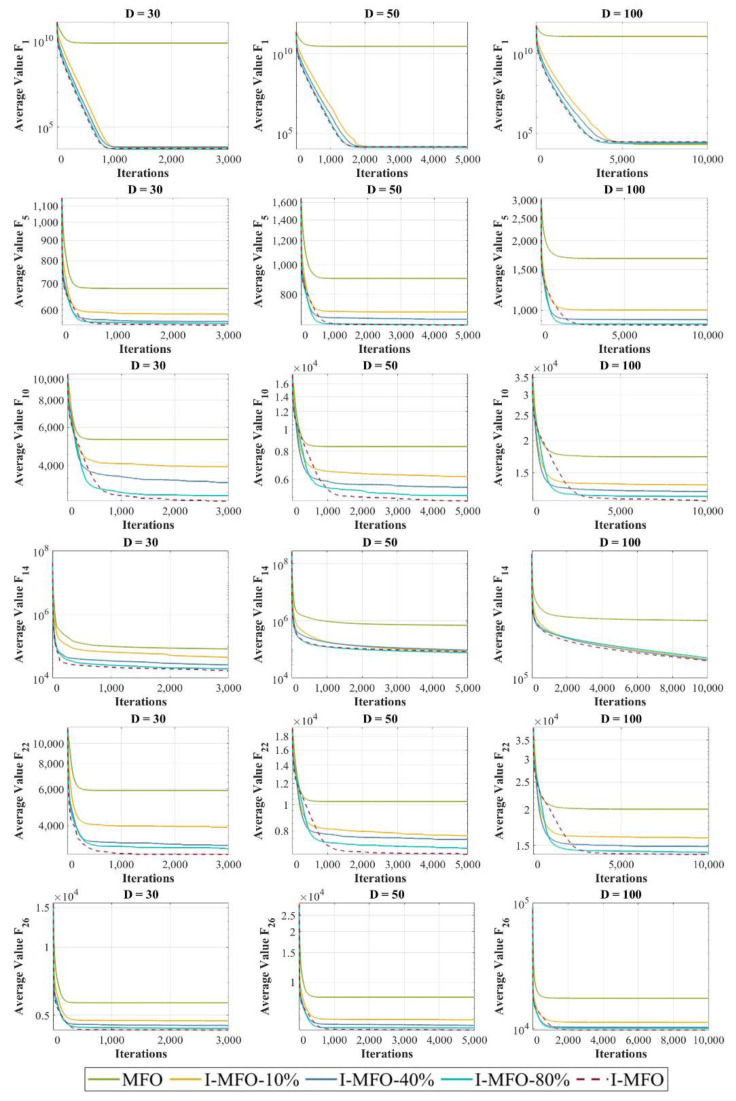
In this experiment, the impact of applying the AWAS strategy is analyzed on some selected functions of the CEC 2018 benchmark for different dimensions 30, 50, and 100. The proposed AWAS strategy can ameliorate the MFO’s weaknesses described in Section 2. To adequately assess the impact of applying the AWAS strategy, in this experiment we consider MFO, I-MFO, and its three variations including I-MFO-10%, I-MFO-40%, and I-MFO-80% which indicate the percentage of trapped moths that are randomly selected to possibly escape from the local optima using the proposed AWAS strategy.
The first row of Figure 9 indicates convergence curves for unimodal F1, where the I-MFO and its variations outperform the MFO for all dimensions. Specifically, for dimension 100, the I-MFO-10% offers superior outcomes while it has less computational cost compared to the I-MFO. The curves provided for multimodal F5 and F10 indicate that the I-MFO offers better solutions, while in the next ranks, I-MFO-80%, I-MFO-40%, and I-MFO-10% outperform the MFO. The hybrid test function is shown in the fourth row of Figure 9, where the I-MFO and its variations keep converging toward the global optimum with a steep slope until the final iterations. The I-MFO and its variations can also find better solutions for the composition functions F22 and F26, wherein for these functions, as the number of dimensions grows, the significance of the AWAS strategy in guiding the population toward the global optimum region and avoiding local optima entrapment becomes clearer. Although the provided results demonstrate that the I-MFO with 100% of trapped moths applied to AWAS strategy mostly provides better solutions for different dimensions and search spaces, other variations of the I-MFO can also provide competitive performance while they have the advantage of lower computational cost compared to the I-MFO.
Figure 9.
Impact analysis of applying AWAS strategy on different percentages of trapped moths.
5. Statistical Analysis
In this section, the results obtained in the preceding section are first statistically analyzed using the non-parametric Friedman test. The Bonferroni and Tukey post hoc producers are then conducted to establish proper comparisons between the proposed algorithm and comparative algorithms.
5.1. Non-Parametric Friedman Test
The Friedman test is performed to rank the significance of the superiority algorithms statistically [120,121]. The obtained results for unimodal and multimodal test functions are tabulated in Table 6 and the results for hybrid and composition functions are reported in Table 7. This statistical analysis shows that the I-MFO is first rank on all test functions for dimensions of 30, 50, and 100.
Table 6.
Friedman test for unimodal and multimodal functions of the CEC 2018.
| Functions | Unimodal Functions | Multimodal Functions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 50 | 100 | 30 | 50 | 100 | ||||||
| Algorithms | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank |
| SA | 9.22 | 10 | 9.77 | 10 | 10.50 | 11 | 8.67 | 9 | 9.45 | 10 | 10.15 | 10 |
| CGA | 9.75 | 11 | 10.42 | 11 | 10.25 | 10 | 10.49 | 11 | 10.74 | 11 | 10.29 | 11 |
| GWO | 4.57 | 4 | 5.12 | 5 | 4.12 | 3 | 2.52 | 2 | 2.66 | 2 | 2.578 | 2 |
| MFO | 6.30 | 6 | 6.07 | 6 | 6.30 | 7 | 4.65 | 5 | 4.67 | 5 | 5.26 | 6 |
| WOA | 6.70 | 7 | 3.60 | 4 | 6.10 | 5 | 6.21 | 6 | 5.45 | 6 | 4.53 | 4 |
| LMFO | 3.45 | 3 | 3.57 | 3 | 4.15 | 4 | 2.99 | 3 | 2.85 | 3 | 3.29 | 3 |
| WCMFO | 1.77 | 2 | 1.62 | 2 | 1.70 | 2 | 4.61 | 4 | 4.52 | 4 | 4.67 | 5 |
| ChOA | 6.17 | 5 | 6.70 | 7 | 6.17 | 6 | 7.19 | 7 | 7.27 | 7 | 7.34 | 7 |
| AOA | 8.12 | 8 | 9.02 | 9 | 7.80 | 9 | 7.67 | 8 | 8.04 | 8 | 7.98 | 8 |
| SMFO | 8.57 | 9 | 8.57 | 8 | 7.57 | 8 | 9.75 | 10 | 9.14 | 9 | 8.82 | 9 |
| I-MFO | 1.35 | 1 | 1.50 | 1 | 1.32 | 1 | 1.20 | 1 | 1.17 | 1 | 1.06 | 1 |
Table 7.
Friedman test for hybrid and composition functions of the CEC 2018.
| Functions | Hybrid Functions | Composition Functions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 50 | 100 | 30 | 50 | 100 | ||||||
| Algorithms | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank |
| SA | 7.96 | 8 | 8.74 | 9 | 8.52 | 8 | 7.20 | 7 | 8.74 | 9 | 7.68 | 8 |
| CGA | 9.94 | 10 | 10.19 | 11 | 10.20 | 11 | 9.50 | 9 | 10.19 | 11 | 9.65 | 10 |
| GWO | 3.79 | 2 | 3.79 | 3 | 4.17 | 5 | 3.12 | 2 | 3.795 | 3 | 3.14 | 2 |
| MFO | 3.87 | 4 | 4.56 | 5 | 5.4 | 6 | 4.36 | 5 | 4.56 | 5 | 4.95 | 5 |
| WOA | 6.49 | 7 | 5.14 | 6 | 4.04 | 4 | 6.05 | 6 | 5.14 | 6 | 5.83 | 6 |
| LMFO | 4.63 | 5 | 4.06 | 4 | 3.65 | 3 | 3.39 | 3 | 4.06 | 4 | 3.23 | 3 |
| WCMFO | 3.86 | 3 | 3.57 | 2 | 2.95 | 2 | 3.99 | 4 | 3.57 | 2 | 3.55 | 4 |
| ChOA | 8.18 | 9 | 7.74 | 8 | 7.48 | 7 | 7.70 | 8 | 7.74 | 8 | 7.4 | 7 |
| AOA | 5.81 | 6 | 6.96 | 7 | 8.8 | 9 | 9.64 | 10 | 6.96 | 7 | 10.15 | 11 |
| SMFO | 10.21 | 11 | 10.12 | 10 | 9.62 | 10 | 9.90 | 11 | 10.12 | 10 | 9.36 | 9 |
| I-MFO | 1.23 | 1 | 1.10 | 1 | 1.09 | 1 | 1.12 | 1 | 1.10 | 1 | 1.03 | 1 |
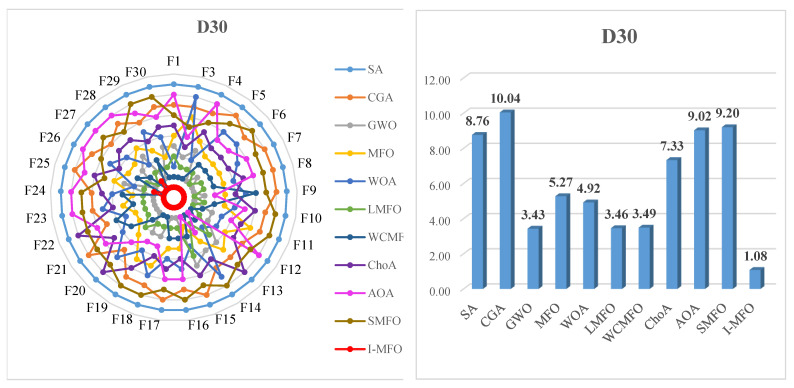
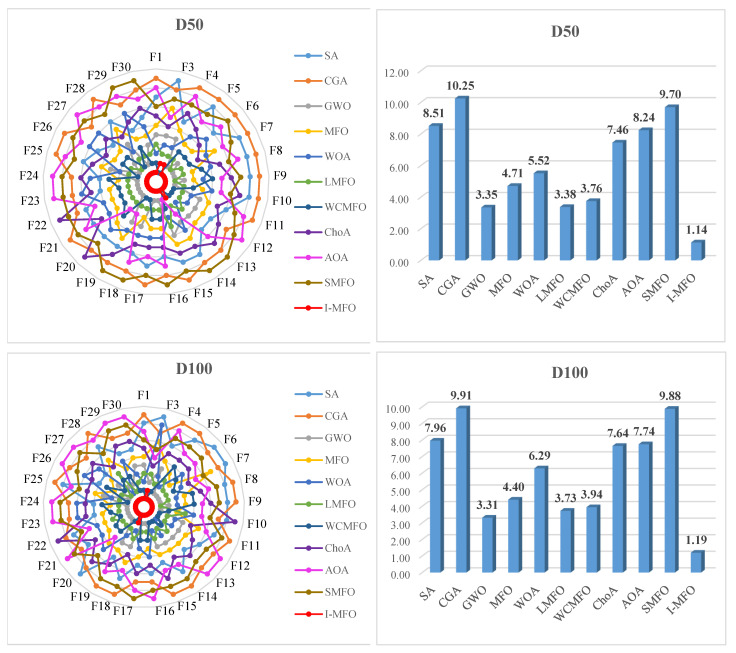
Figure 10 contains six charts to visually show the ranking of the I-MFO and contender algorithms in different dimensions. The left side illustrates the ranking of algorithms in various functions of the CEC 2018 benchmark, while the right side shows the bar chart of Friedman test average results. The radar graph shows that the I-MFO outperforms other algorithms in different dimensions as the smaller size of the I-MFO indicates its first and second rank for all functions. The bar chart provided on the right side reveals that the I-MFO is superior to other comparative algorithms as it has the shortest bar in various dimensions of 30, 50, and 100.
Figure 10.
The radar graphs and bar charts of algorithms in different dimensions.
5.2. Post Hoc Analysis
In the post hoc analysis [120], we evaluated the proposed hypothesis between the control method and the rest of the compared methods in Table 8 by employing Bonferroni and Tukey’s multiple comparison producers. In this experiment, the level of significance is α = 0.05, which determines whether or not a hypothesis is acceptable by comparing the significant difference (p-value) between each pair of algorithms. Since gained p-values for all dimensions 30, 50, and 100 are less than α = 0.05, it reveals that there are significant differences between the performances of the I-MFO and other compared algorithms.
Table 8.
Adjusted p-values for the Friedman test on different dimensions (I-MFO is the control method).
| Dimensions | 30 | 50 | 100 | |||
|---|---|---|---|---|---|---|
| Algorithms | Bonferroni p-Value |
Tukey p-Value |
Bonferroni p-Value |
Tukey p-Value |
Bonferroni p-Value |
Tukey p-Value |
| SA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10-08 |
| CGA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| GWO | 5.337 × 10−7 | 5.338 × 10−7 | 5.337 × 10−7 | 5.338 × 10−7 | 7.238 × 10−8 | 7.247 × 10−8 |
| MFO | 5.337 × 10−7 | 5.338 × 10−7 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| WOA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| LMFO | 3.444 × 10−6 | 3.444 × 10−6 | 5.337 × 10−7 | 5.338 × 10−7 | 5.337 × 10−7 | 5.338 × 10−7 |
| WCMFO | 1.595 × 10−3 | 1.595 × 10−3 | 3.444 × 10−6 | 3.444 × 10−6 | 3.444 × 10−6 | 3.444 × 10−6 |
| ChOA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| AOA | 5.337 × 10−7 | 5.338 × 10−7 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| SMFO | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
6. Applicability of I-MFO Algorithm to Solve Mechanical Engineering Problems
In this section, three constrained mechanical engineering problems from the latest test-suite CEC 2020 [103] are considered to evaluate the applicability of the I-MFO algorithm in real-world applications. To achieve a fair comparison, the algorithms were run 20 times with the population size (N) 20 and maximum iterations (MaxIt) (D × 104)/N. In this experimental evaluation, the proposed algorithm and contender algorithms compete to solve three different problems that consist of a gas transmission compressor design problem, three-bar truss, and tension/compression spring design.
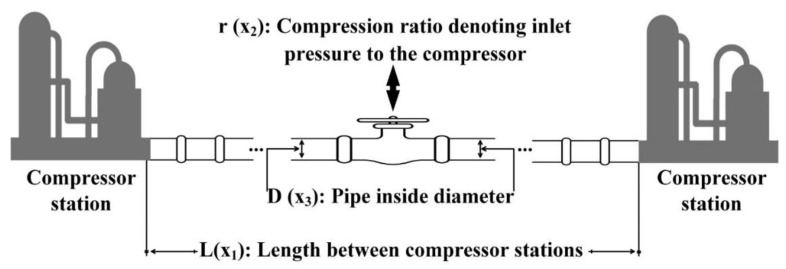
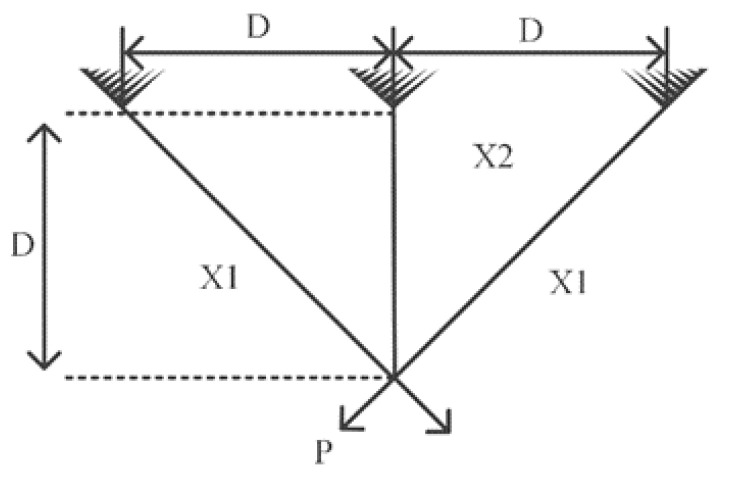
P1: Gas transmission compressor design problem
Minimization of the objective function using four design variables is the main goal of the gas transmission compressor design problem. This problem is illustrated and formulated in Figure 11 and Equation (10). The performance of the proposed algorithm is evaluated against the contender algorithms to solve this problem and the obtained results are tabulated in Table 9. As shown in this table, the I-MFO is superior in addressing this issue.
| (10) |
Figure 11.
Gas transmission compressor design problem.
Table 9.
Results of the gas transmission compressor design problem.
| Algorithms | Optimal Values for Variables | Optimal Cost | |||
|---|---|---|---|---|---|
| x 1 | x 2 | x 3 | x 4 | ||
| SA | 46.76 | 1.62 | 25.79 | 0.55 | 4.390311 × 106 |
| CGA | 49.97 | 20.01 | 31.47 | 49.83 | 1.735023 × 107 |
| GWO | 20.00 | 7.81 | 20.00 | 60.00 | 2.964974 × 106 |
| MFO | 50.00 | 1.18 | 24.57 | 0.39 | 2.964902 × 106 |
| WOA | 50.00 | 1.18 | 24.86 | 0.39 | 2.965002 × 106 |
| LMFO | 49.46 | 1.18 | 24.64 | 0.39 | 2.965456 × 106 |
| WCMFO | 50.00 | 1.18 | 24.61 | 0.39 | 2.964897 × 106 |
| ChOA | 50.00 | 1.19 | 24.24 | 0.41 | 2.966828 × 106 |
| AOA | 50.00 | 1.23 | 20.00 | 0.51 | 3.014615 × 106 |
| SMFO | 23.66 | 1.09 | 23.66 | 0.19 | 3.052254 × 106 |
| I-MFO | 50.00 | 1.18 | 24.60 | 0.39 | 2.964896 × 106 |
P2: Three-bar truss problem
In this problem, three constraints and two variables are utilized to formulate the objective function, which is the weight of the bar structures. The schematic and formulation of this problem are represented in Figure 12 and Equation (11), respectively. The proposed I-MFO algorithm and comparative algorithms are compared for solving this problem. The attained results from this experiment are tabulated in Table 10, in which the I-MFO algorithm outperforms other algorithms in approximating the optimal values for variables with minimum weight.
| (11) |
Figure 12.
Three-bar truss problem.
Table 10.
Results of the three-bar truss problem.
| Algorithms | Optimal Values for Variables | Optimal Weight | |
|---|---|---|---|
| x 1 | x 2 | ||
| SA | 0.768630 | 0.474232 | 2.6482456 × 102 |
| CGA | 0.792428 | 0.397752 | 2.6390770 × 102 |
| GWO | 0.787771 | 0.410872 | 2.6389619 × 102 |
| MFO | 0.789186 | 0.406806 | 2.6389603 × 102 |
| WOA | 0.787713 | 0.410977 | 2.6389653 × 102 |
| LMFO | 0.791713 | 0.399909 | 2.6392114 × 102 |
| WCMFO | 0.788472 | 0.408822 | 2.6389589 × 102 |
| ChOA | 0.787802 | 0.410724 | 2.6389653 × 102 |
| AOA | 0.792789 | 0.396906 | 2.6392526 × 102 |
| SMFO | 0.792044 | 0.398859 | 2.6390973 × 102 |
| I-MFO | 0.788792 | 0.407919 | 2.6389585 × 102 |
P3: Tension/compression spring design problem
In the tension/compression spring design problem, the objective is to minimize the weight of the tension/compression spring by considering three variables and four constraints. As shown in Figure 13, the variables are wire diameter (d), the number of active coils (N), and mean coil diameter (D). The problem and its constraints are described in Equation (12) and results are reported in Table 11.
| (12) |
Figure 13.
Tension/compression spring design problem.
Table 11.
Results for tension/compression spring design problem.
| Algorithms | Optimal Values for Variables | Optimum Weight | ||
|---|---|---|---|---|
| d | D | N | ||
| SA | 0.075935 | 0.993094 | 3.879891 | 0.033670 |
| CGA | 0.071031 | 1.019975 | 1.726076 | 0.019749 |
| GWO | 0.051231 | 0.345699 | 11.970135 | 0.012676 |
| MFO | 0.053064 | 0.390718 | 9.542437 | 0.012699 |
| WOA | 0.050451 | 0.327675 | 13.219341 | 0.012694 |
| LMFO | 0.050000 | 0.317154 | 14.107156 | 0.012771 |
| WCMFO | 0.051509 | 0.352411 | 11.545969 | 0.012666 |
| ChOA | 0.051069 | 0.341746 | 12.251078 | 0.012702 |
| AOA | 0.050000 | 0.310475 | 15.000000 | 0.013195 |
| SMFO | 0.050000 | 0.314692 | 14.696505 | 0.013136 |
| I-MFO | 0.051710 | 0.357217 | 11.259785 | 0.012665 |
The results of the mechanical engineering problems tabulated in Table 9, Table 10 and Table 11 demonstrate the fact that the I-MFO is superior to other algorithms for solving real-world mechanical engineering problems.
7. Conclusions and Future Works
The transverse orientation behavior of moths while encountering artificial lights is the main inspiration behind the MFO algorithm to successfully solve optimization problems. However, as with most of the SI algorithms, the MFO suffers from premature convergence, local optima entrapping, low population diversity, and imbalance between exploration and exploitation. These drawbacks make the MFO uncompetitive in solving complex and real-world optimization problems. Therefore, an improved version of the MFO named I-MFO is proposed to improve the MFO algorithm from the perspective of alleviating premature convergence, maintaining population diversity, avoiding local optima trapping, and striking a balance between exploration and exploitation.
To detect local optima-trapped moths, a memory mechanism is defined for each moth. Then, the adapted wandering around search (AWAS) strategy is introduced to possibly free detected trapped moths from local optima by changing their positions while considering the best flame and a random moth position. The CEC 2018 benchmark tasks were conducted to evaluate the performance of the I-MFO, where the reported results in Table 2, Table 3 and Table 4 and OE in Table 5 prove I-MFO’s superior performance over 92% of test functions. The multimodal test function results reported in Table 2 are clear evidence of the fact that the I-MFO boosts exploration rate, especially in more complex problems. The hybrid and composition test function results tabulated in Table 3 and Table 4 support the claim that the proposed I-MFO enhances the balance between exploration and exploitation, by which the I-MFO can get out of local optima effectively. The convergence curves also show the local optima avoidance ability and enhanced balance between exploration and exploitation. Moreover, it can be deduced from the population diversity plots that the I-MFO successfully maintains population diversity until a near-optimal solution emerges.
The sensitivity of the AWAS strategy and NF parameter is evaluated on some CEC 2018 benchmark functions for different dimensions, where the results reveal that although the I-MFO offers better solutions in most test functions, other variations of the I-MFO can also provide competitive outcomes for some functions and dimensions. The statistical efficiency of the I-MFO is investigated by the Friedman test and post-hoc analysis, which revealed that the proposed I-MFO outperforms other contender algorithms for various test functions. In the end, the outcomes of the mechanical engineering problems from the latest test-suite CEC 2020 demonstrate that the proposed I-MFO is applicable for solving real-world mechanical engineering problems. Although I-MFO provides competitive results for solving global optimization and engineering tasks, like most improvements, it consumes more time compared to the canonical MFO because it uses the AWAS strategy. Hence, in practice, the I-MFO may not be suitable for solving large-scale real-time problems. For future works, a multi-objective version of I-MFO can be developed for solving continuous multi-objective problems. Moreover, extending I-MFO to the discrete version for solving discrete optimization tasks such as the community detection problem is a worthwhile direction.
Author Contributions
Conceptualization, M.H.N.-S.; methodology, M.H.N.-S. and H.Z.; software, M.H.N.-S., A.F. and H.Z.; validation, M.H.N.-S. and H.Z.; formal analysis, M.H.N.-S., A.F. and H.Z.; investigation, M.H.N.-S., A.F. and H.Z.; resources, M.H.N.-S., S.M. and L.A.; data curation, M.H.N.-S., A.F. and H.Z.; writing, M.H.N.-S., A.F. and H.Z.; original draft preparation, M.H.N.-S., A.F. and H.Z.; writing—review and editing, M.H.N.-S., A.F., H.Z., S.M. and L.A.; visualization, M.H.N.-S., A.F. and H.Z.; supervision, M.H.N.-S. and S.M.; project administration, M.H.N.-S. and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and code used in the research may be obtained from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Del Ser J., Osaba E., Molina D., Yang X., Salcedo-Sanz S., Camacho D., Das S., Suganthan P., Coello C.C., Herrera F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput. 2019;48:220–250. doi: 10.1016/j.swevo.2019.04.008. [DOI] [Google Scholar]
- 2.Talbi E.-G. Metaheuristics: From Design to Implementation. Volume 74 John Wiley & Sons; New York, NY, USA: 2009. [Google Scholar]
- 3.Kar A.K. Bio inspired computing—A review of algorithms and scope of applications. Expert Syst. Appl. 2016;59:20–32. doi: 10.1016/j.eswa.2016.04.018. [DOI] [Google Scholar]
- 4.Dezfouli M.B., Nadimi-Shahraki M.H., Zamani H. A novel tour planning model using big data; Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP); Malatya, Turkey. 28–30 September 2018; pp. 1–6. [Google Scholar]
- 5.Zahrani H.K., Nadimi-Shahraki M.H., Sayarshad H.R. An intelligent social-based method for rail-car fleet sizing problem. J. Rail Transp. Plan. Manag. 2021;17:100231. doi: 10.1016/j.jrtpm.2020.100231. [DOI] [Google Scholar]
- 6.Javadian N., Sayarshad H.R., Najafi S. Using simulated annealing for determination of the capacity of yard stations in a railway industry. Appl. Soft Comput. 2011;11:1899–1907. doi: 10.1016/j.asoc.2010.06.006. [DOI] [Google Scholar]
- 7.Sayarshad H.R., Javadian N., Tavakkoli-Moghaddam R., Forghani N. Solving multi-objective optimization formulation for fleet planning in a railway industry. Ann. Oper. Res. 2010;181:185–197. doi: 10.1007/s10479-010-0714-1. [DOI] [Google Scholar]
- 8.Abdollahzadeh B., Gharehchopogh F.S. A multi-objective optimization algorithm for feature selection problems. Eng. Comput. 2021:1–19. doi: 10.1007/s00366-021-01369-9. [DOI] [Google Scholar]
- 9.Ewees A.A., Al-qaness M.A.A., Abualigah L., Oliva D., Algamal Z.Y., Anter A.M., Ali Ibrahim R., Ghoniem R.M., Abd Elaziz M. Boosting Arithmetic Optimization Algorithm with Genetic Algorithm Operators for Feature Selection: Case Study on Cox Proportional Hazards Model. Mathematics. 2021;9:2321. doi: 10.3390/math9182321. [DOI] [Google Scholar]
- 10.Mienye I.D., Sun Y. Improved Heart Disease Prediction Using Particle Swarm Optimization Based Stacked Sparse Autoencoder. Electronics. 2021;10:2347. doi: 10.3390/electronics10192347. [DOI] [Google Scholar]
- 11.Taghian S., Nadimi-Shahraki M.H., Zamani H. Comparative analysis of transfer function-based binary Metaheuristic algorithms for feature selection; Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP); Malatya, Turkey. 28–30 September 2018; pp. 1–6. [Google Scholar]
- 12.Zamani H., Nadimi-Shahraki M.H. Swarm intelligence approach for breast cancer diagnosis. Int. J. Comput. Appl. 2016;151:40–44. doi: 10.5120/ijca2016911667. [DOI] [Google Scholar]
- 13.Zamani H., Nadimi-Shahraki M.H. Feature selection based on whale optimization algorithm for diseases diagnosis. Int. J. Comput. Sci. Inf. Secur. 2016;14:1243. [Google Scholar]
- 14.Ibrahim R.A., Abualigah L., Ewees A.A., Al-Qaness M.A., Yousri D., Alshathri S., Abd Elaziz M. An Electric Fish-Based Arithmetic Optimization Algorithm for Feature Selection. Entropy. 2021;23:1189. doi: 10.3390/e23091189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang L., Shi R., Dong J. A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems. Entropy. 2021;23:598. doi: 10.3390/e23050598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee J., Park J., Kim H.-C., Kim D.-W. Competitive Particle Swarm Optimization for Multi-Category Text Feature Selection. Entropy. 2019;21:602. doi: 10.3390/e21060602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nadimi-Shahraki M.H., Moeini E., Taghian S., Mirjalili S. DMFO-CD: A Discrete Moth-Flame Optimization Algorithm for Community Detection. Algorithms. 2021;14:314. doi: 10.3390/a14110314. [DOI] [Google Scholar]
- 18.Alsalibi B., Abualigah L., Khader A.T. A novel bat algorithm with dynamic membrane structure for optimization problems. Appl. Intell. 2021;51:1992–2017. doi: 10.1007/s10489-020-01898-8. [DOI] [Google Scholar]
- 19.Asghari K., Masdari M., Gharehchopogh F.S., Saneifard R. A chaotic and hybrid gray wolf-whale algorithm for solving continuous optimization problems. Prog. Artif. Intell. 2021;10:349–374. doi: 10.1007/s13748-021-00244-4. [DOI] [Google Scholar]
- 20.Goldanloo M.J., Gharehchopogh F.S. A hybrid OBL-based firefly algorithm with symbiotic organisms search algorithm for solving continuous optimization problems. J. Supercomput. 2021:1–34. doi: 10.1007/s11227-021-04015-9. [DOI] [Google Scholar]
- 21.Zaman H.R.R., Gharehchopogh F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2021:1–35. doi: 10.1007/s00366-021-01431-6. [DOI] [Google Scholar]
- 22.Doumari S.A., Givi H., Dehghani M., Montazeri Z., Leiva V., Guerrero J.M. A New Two-Stage Algorithm for Solving Optimization Problems. Entropy. 2021;23:491. doi: 10.3390/e23040491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Abd Elaziz M., Elsheikh A.H., Oliva D., Abualigah L., Lu S., Ewees A.A. Advanced Metaheuristic Techniques for Mechanical Design Problems. Arch. Comput. Methods Eng. 2021:1–22. doi: 10.1007/s11831-021-09589-4. [DOI] [Google Scholar]
- 24.Akay B., Karaboga D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012;23:1001–1014. doi: 10.1007/s10845-010-0393-4. [DOI] [Google Scholar]
- 25.Aloui M., Hamidi F., Jerbi H., Omri M., Popescu D., Abbassi R. A Chaotic Krill Herd Optimization Algorithm for Global Numerical Estimation of the Attraction Domain for Nonlinear Systems. Mathematics. 2021;9:1743. doi: 10.3390/math9151743. [DOI] [Google Scholar]
- 26.Gharehchopogh F.S., Farnad B., Alizadeh A. A farmland fertility algorithm for solving constrained engineering problems. Concurr. Comput. Pract. Exp. 2021;33:e6310. doi: 10.1002/cpe.6310. [DOI] [Google Scholar]
- 27.Ivanov O., Neagu B.-C., Grigoraș G., Scarlatache F., Gavrilaș M. A Metaheuristic Algorithm for Flexible Energy Storage Management in Residential Electricity Distribution Grids. Mathematics. 2021;9:2375. doi: 10.3390/math9192375. [DOI] [Google Scholar]
- 28.Wang S., Jia H., Abualigah L., Liu Q., Zheng R. An Improved Hybrid Aquila Optimizer and Harris Hawks Algorithm for Solving Industrial Engineering Optimization Problems. Processes. 2021;9:1551. doi: 10.3390/pr9091551. [DOI] [Google Scholar]
- 29.Ziadeh A., Abualigah L., Abd Elaziz M., Şahin C.B., Almazroi A.A., Omari M. Augmented grasshopper optimization algorithm by differential evolution: A power scheduling application in smart homes. Multimed. Tools Appl. 2021;80:31569–31597. doi: 10.1007/s11042-021-11099-1. [DOI] [Google Scholar]
- 30.Varaee H., Ghasemi M.R. Engineering optimization based on ideal gas molecular movement algorithm. Eng. Comput. 2017;33:71–93. doi: 10.1007/s00366-016-0457-y. [DOI] [Google Scholar]
- 31.Ghasemi M.R., Varaee H. A fast multi-objective optimization using an efficient ideal gas molecular movement algorithm. Eng. Comput. 2017;33:477–496. doi: 10.1007/s00366-016-0485-7. [DOI] [Google Scholar]
- 32.Hua Z., Xiao Y., Cao J. Misalignment Fault Prediction of Wind Turbines Based on Improved Artificial Fish Swarm Algorithm. Entropy. 2021;23:692. doi: 10.3390/e23060692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang S., Liu Q., Liu Y., Jia H., Abualigah L., Zheng R., Wu D. A Hybrid SSA and SMA with Mutation Opposition-Based Learning for Constrained Engineering Problems. Comput. Intell. Neurosci. 2021;2021:6379469. doi: 10.1155/2021/6379469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Selvaraj S., Choi E. Swarm Intelligence Algorithms in Text Document Clustering with Various Benchmarks. Sensors. 2021;21:3196. doi: 10.3390/s21093196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bacanin N., Bezdan T., Venkatachalam K., Al-Turjman F. Optimized convolutional neural network by firefly algorithm for magnetic resonance image classification of glioma brain tumor grade. J. Real-Time Image Process. 2021;18:1085–1098. doi: 10.1007/s11554-021-01106-x. [DOI] [Google Scholar]
- 36.Bacanin N., Bezdan T., Tuba E., Strumberger I., Tuba M. Optimizing convolutional neural network hyperparameters by enhanced swarm intelligence metaheuristics. Algorithms. 2020;13:67. doi: 10.3390/a13030067. [DOI] [Google Scholar]
- 37.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 38.Glover F., Laguna M. Handbook of Combinatorial Optimization. Springer; Boston, MA, USA: 1998. Tabu search; pp. 2093–2229. [Google Scholar]
- 39.Hasançebi O., Azad S.K. Adaptive dimensional search: A new metaheuristic algorithm for discrete truss sizing optimization. Comput. Struct. 2015;154:1–16. doi: 10.1016/j.compstruc.2015.03.014. [DOI] [Google Scholar]
- 40.Lourenço H.R., Martin O.C., Stützle T. Handbook of Metaheuristics. Springer; Cham, Switzerland: 2019. Iterated local search: Framework and applications; pp. 129–168. [Google Scholar]
- 41.Holland J.H. Genetic algorithms. Sci. Am. 1992;267:66–73. doi: 10.1038/scientificamerican0792-66. [DOI] [Google Scholar]
- 42.Chelouah R., Siarry P. A continuous genetic algorithm designed for the global optimization of multimodal functions. J. Heuristics. 2000;6:191–213. doi: 10.1023/A:1009626110229. [DOI] [Google Scholar]
- 43.Koza J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994;4:87–112. doi: 10.1007/BF00175355. [DOI] [Google Scholar]
- 44.Storn R., Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 45.Beyer H.-G., Schwefel H.-P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002;1:3–52. doi: 10.1023/A:1015059928466. [DOI] [Google Scholar]
- 46.Zamani H., Nadimi-Shahraki M.H., Gandomi A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021;104:104314. doi: 10.1016/j.engappai.2021.104314. [DOI] [Google Scholar]
- 47.Mallipeddi R., Suganthan P.N., Pan Q.-K., Tasgetiren M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011;11:1679–1696. doi: 10.1016/j.asoc.2010.04.024. [DOI] [Google Scholar]
- 48.Wu G., Mallipeddi R., Suganthan P.N., Wang R., Chen H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016;329:329–345. doi: 10.1016/j.ins.2015.09.009. [DOI] [Google Scholar]
- 49.Wu G., Shen X., Li H., Chen H., Lin A., Suganthan P.N. Ensemble of differential evolution variants. Inf. Sci. 2018;423:172–186. doi: 10.1016/j.ins.2017.09.053. [DOI] [Google Scholar]
- 50.Nadimi-Shahraki M.H., Taghian S., Mirjalili S., Faris H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020;97:106761. doi: 10.1016/j.asoc.2020.106761. [DOI] [Google Scholar]
- 51.Erol O.K., Eksin I. A new optimization method: Big bang—Big crunch. Adv. Eng. Softw. 2006;37:106–111. doi: 10.1016/j.advengsoft.2005.04.005. [DOI] [Google Scholar]
- 52.Kaveh A., Talatahari S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010;213:267–289. doi: 10.1007/s00707-009-0270-4. [DOI] [Google Scholar]
- 53.Kaveh A., Khayatazad M. A new meta-heuristic method: Ray optimization. Comput. Struct. 2012;112:283–294. doi: 10.1016/j.compstruc.2012.09.003. [DOI] [Google Scholar]
- 54.Zhao W., Wang L., Zhang Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019;163:283–304. doi: 10.1016/j.knosys.2018.08.030. [DOI] [Google Scholar]
- 55.Abualigah L., Diabat A., Mirjalili S., Abd Elaziz M., Gandomi A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021;376:113609. doi: 10.1016/j.cma.2020.113609. [DOI] [Google Scholar]
- 56.Azizi M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021;93:657–683. doi: 10.1016/j.apm.2020.12.021. [DOI] [Google Scholar]
- 57.Zamani H., Nadimi-Shahraki M.H., Gandomi A.H. CCSA: Conscious neighborhood-based crow search algorithm for solving global optimization problems. Appl. Soft Comput. 2019;85:105583. doi: 10.1016/j.asoc.2019.105583. [DOI] [Google Scholar]
- 58.Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 59.Khishe M., Mosavi M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020;149:113338. doi: 10.1016/j.eswa.2020.113338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Abdollahzadeh B., Soleimanian Gharehchopogh F., Mirjalili S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021;36:5887–5958. doi: 10.1002/int.22535. [DOI] [Google Scholar]
- 61.Nadimi-Shahraki M.H., Taghian S., Mirjalili S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021;166:113917. doi: 10.1016/j.eswa.2020.113917. [DOI] [Google Scholar]
- 62.Jia H., Sun K., Zhang W., Leng X. An enhanced chimp optimization algorithm for continuous optimization domains. Complex Intell. Syst. 2021:1–18. doi: 10.1007/s40747-021-00346-5. [DOI] [Google Scholar]
- 63.Liu Y., Sun J., Yu H., Wang Y., Zhou X. An Improved Grey Wolf Optimizer Based on Differential Evolution and OTSU Algorithm. Appl. Sci. 2020;10:6343. doi: 10.3390/app10186343. [DOI] [Google Scholar]
- 64.Chen C., Wang X., Chen H., Wu C., Mafarja M., Turabieh H. Towards Precision Fertilization: Multi-Strategy Grey Wolf Optimizer Based Model Evaluation and Yield Estimation. Electronics. 2021;10:2183. doi: 10.3390/electronics10182183. [DOI] [Google Scholar]
- 65.Gandomi A.H., Alavi A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012;17:4831–4845. doi: 10.1016/j.cnsns.2012.05.010. [DOI] [Google Scholar]
- 66.Kaveh A., Farhoudi N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013;59:53–70. doi: 10.1016/j.advengsoft.2013.03.004. [DOI] [Google Scholar]
- 67.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 68.Dorigo M., Di Caro G. Ant colony optimization: A new meta-heuristic; Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406); Washington, DC, USA. 6–9 July 1999; pp. 1470–1477. [Google Scholar]
- 69.Mirjalili S. The ant lion optimizer. Adv. Eng. Softw. 2015;83:80–98. doi: 10.1016/j.advengsoft.2015.01.010. [DOI] [Google Scholar]
- 70.James J., Li V.O. A social spider algorithm for global optimization. Appl. Soft Comput. 2015;30:614–627. [Google Scholar]
- 71.Askarzadeh A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016;169:1–12. doi: 10.1016/j.compstruc.2016.03.001. [DOI] [Google Scholar]
- 72.Abdollahzadeh B., Gharehchopogh F.S., Mirjalili S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021;158:107408. doi: 10.1016/j.cie.2021.107408. [DOI] [Google Scholar]
- 73.Abualigah L., Yousri D., Abd Elaziz M., Ewees A.A., Al-qaness M.A., Gandomi A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021;157:107250. doi: 10.1016/j.cie.2021.107250. [DOI] [Google Scholar]
- 74.Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015;89:228–249. doi: 10.1016/j.knosys.2015.07.006. [DOI] [Google Scholar]
- 75.Abd El Aziz M., Ewees A.A., Hassanien A.E. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017;83:242–256. doi: 10.1016/j.eswa.2017.04.023. [DOI] [Google Scholar]
- 76.Jia H., Ma J., Song W. Multilevel thresholding segmentation for color image using modified moth-flame optimization. IEEE Access. 2019;7:44097–44134. doi: 10.1109/ACCESS.2019.2908718. [DOI] [Google Scholar]
- 77.Khan M.A., Sharif M., Akram T., Damaševičius R., Maskeliūnas R. Skin Lesion Segmentation and Multiclass Classification Using Deep Learning Features and Improved Moth Flame Optimization. Diagnostics. 2021;11:811. doi: 10.3390/diagnostics11050811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Abd Elaziz M., Ewees A.A., Ibrahim R.A., Lu S. Opposition-based moth-flame optimization improved by differential evolution for feature selection. Math. Comput. Simul. 2020;168:48–75. doi: 10.1016/j.matcom.2019.06.017. [DOI] [Google Scholar]
- 79.Gupta D., Ahlawat A.K., Sharma A., Rodrigues J.J. Feature selection and evaluation for software usability model using modified moth-flame optimization. Computing. 2020;102:1503–1520. doi: 10.1007/s00607-020-00809-6. [DOI] [Google Scholar]
- 80.Tumar I., Hassouneh Y., Turabieh H., Thaher T. Enhanced binary moth flame optimization as a feature selection algorithm to predict software fault prediction. IEEE Access. 2020;8:8041–8055. doi: 10.1109/ACCESS.2020.2964321. [DOI] [Google Scholar]
- 81.Abu Khurmaa R., Aljarah I., Sharieh A. An intelligent feature selection approach based on moth flame optimization for medical diagnosis. Neural Comput. Appl. 2021;33:7165–7204. doi: 10.1007/s00521-020-05483-5. [DOI] [Google Scholar]
- 82.Nadimi-Shahraki M.H., Banaie-Dezfouli M., Zamani H., Taghian S., Mirjalili S. B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets. Computers. 2021;10:136. doi: 10.3390/computers10110136. [DOI] [Google Scholar]
- 83.Sarma A., Bhutani A., Goel L. Hybridization of moth flame optimization and gravitational search algorithm and its application to detection of food quality; Proceedings of the 2017 Intelligent Systems Conference (IntelliSys); London, UK. 7–8 September 2017; pp. 52–60. [Google Scholar]
- 84.Hassanien A.E., Gaber T., Mokhtar U., Hefny H. An improved moth flame optimization algorithm based on rough sets for tomato diseases detection. Comput. Electron. Agric. 2017;136:86–96. doi: 10.1016/j.compag.2017.02.026. [DOI] [Google Scholar]
- 85.Lei X., Fang M., Fujita H. Moth–flame optimization-based algorithm with synthetic dynamic PPI networks for discovering protein complexes. Knowl.-Based Syst. 2019;172:76–85. doi: 10.1016/j.knosys.2019.02.011. [DOI] [Google Scholar]
- 86.Li C., Li S., Liu Y. A least squares support vector machine model optimized by moth-flame optimization algorithm for annual power load forecasting. Appl. Intell. 2016;45:1166–1178. doi: 10.1007/s10489-016-0810-2. [DOI] [Google Scholar]
- 87.Mei R.N.S., Sulaiman M.H., Mustaffa Z., Daniyal H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017;59:210–222. [Google Scholar]
- 88.Allam D., Yousri D., Eteiba M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016;123:535–548. doi: 10.1016/j.enconman.2016.06.052. [DOI] [Google Scholar]
- 89.Ebrahim M.A., Becherif M., Abdelaziz A.Y. Dynamic performance enhancement for wind energy conversion system using Moth-Flame Optimization based blade pitch controller. Sustain. Energy Technol. Assess. 2018;27:206–212. doi: 10.1016/j.seta.2018.04.012. [DOI] [Google Scholar]
- 90.Raju K., Madurai Elavarasan R., Mihet-Popa L. An assessment of onshore and offshore wind energy potential in India using moth flame optimization. Energies. 2020;13:3063. doi: 10.3390/en13123063. [DOI] [Google Scholar]
- 91.Rezk H., Ali Z.M., Abdalla O., Younis O., Gomaa M.R., Hashim M. Hybrid moth-flame optimization algorithm and incremental conductance for tracking maximum power of solar PV/thermoelectric system under different conditions. Mathematics. 2019;7:875. doi: 10.3390/math7100875. [DOI] [Google Scholar]
- 92.Li Z., Zhou Y., Zhang S., Song J. Lévy-flight moth-flame algorithm for function optimization and engineering design problems. Math. Probl. Eng. 2016;2016:1423930. doi: 10.1155/2016/1423930. [DOI] [Google Scholar]
- 93.Savsani V., Tawhid M.A. Non-dominated sorting moth flame optimization (NS-MFO) for multi-objective problems. Eng. Appl. Artif. Intell. 2017;63:20–32. doi: 10.1016/j.engappai.2017.04.018. [DOI] [Google Scholar]
- 94.Xu L., Li Y., Li K., Beng G.H., Jiang Z., Wang C., Liu N. Enhanced moth-flame optimization based on cultural learning and Gaussian mutation. J. Bionic Eng. 2018;15:751–763. doi: 10.1007/s42235-018-0063-3. [DOI] [Google Scholar]
- 95.Khalilpourazari S., Khalilpourazary S. An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput. 2019;23:1699–1722. doi: 10.1007/s00500-017-2894-y. [DOI] [Google Scholar]
- 96.Chen C., Wang X., Yu H., Wang M., Chen H. Dealing with multi-modality using synthesis of Moth-flame optimizer with sine cosine mechanisms. Math. Comput. Simul. 2021;188:291–318. doi: 10.1016/j.matcom.2021.04.006. [DOI] [Google Scholar]
- 97.Kaur K., Singh U., Salgotra R. An enhanced moth flame optimization. Neural Comput. Appl. 2020;32:2315–2349. doi: 10.1007/s00521-018-3821-6. [DOI] [Google Scholar]
- 98.Pelusi D., Mascella R., Tallini L., Nayak J., Naik B., Deng Y. An Improved Moth-Flame Optimization algorithm with hybrid search phase. Knowl.-Based Syst. 2020;191:105277. doi: 10.1016/j.knosys.2019.105277. [DOI] [Google Scholar]
- 99.Hongwei L., Jianyong L., Liang C., Jingbo B., Yangyang S., Kai L. Chaos-enhanced moth-flame optimization algorithm for global optimization. J. Syst. Eng. Electron. 2019;30:1144–1159. [Google Scholar]
- 100.Xu Y., Chen H., Luo J., Zhang Q., Jiao S., Zhang X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019;492:181–203. doi: 10.1016/j.ins.2019.04.022. [DOI] [Google Scholar]
- 101.Li Y., Zhu X., Liu J. An improved moth-flame optimization algorithm for engineering problems. Symmetry. 2020;12:1234. doi: 10.3390/sym12081234. [DOI] [Google Scholar]
- 102.Awad N., Ali M., Liang J., Qu B., Suganthan P. Technical Report. Nanyang Technological University; Singapore: 2016. Problem definitions and evaluation criteria for the cec 2017 special sessionand competition on single objective bound constrained real-parameter numerical optimization. [Google Scholar]
- 103.Kumar A., Wu G., Ali M.Z., Mallipeddi R., Suganthan P.N., Das S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput. 2020;56:100693. doi: 10.1016/j.swevo.2020.100693. [DOI] [Google Scholar]
- 104.Hussien A.G., Amin M., Abd El Aziz M. A comprehensive review of moth-flame optimisation: Variants, hybrids, and applications. J. Exp. Theor. Artif. Intell. 2020;32:705–725. doi: 10.1080/0952813X.2020.1737246. [DOI] [Google Scholar]
- 105.Mehne S.H.H., Mirjalili S. Nature-Inspired Optimizers. Springer; Cham, Switzerland: 2020. Moth-flame optimization algorithm: Theory, literature review, and application in optimal nonlinear feedback control design; pp. 143–166. [Google Scholar]
- 106.Shehab M., Abualigah L., Al Hamad H., Alabool H., Alshinwan M., Khasawneh A.M. Moth–flame optimization algorithm: Variants and applications. Neural Comput. Appl. 2020;32:9859–9884. doi: 10.1007/s00521-019-04570-6. [DOI] [Google Scholar]
- 107.Apinantanakon W., Sunat K. Omfo: A new opposition-based moth-flame optimization algorithm for solving unconstrained optimization problems; Proceedings of the International Conference on Computing and Information Technology; Singapore. 27–29 December 2017; pp. 22–31. [Google Scholar]
- 108.Sapre S., Mini S. Opposition-based moth flame optimization with Cauchy mutation and evolutionary boundary constraint handling for global optimization. Soft Comput. 2019;23:6023–6041. doi: 10.1007/s00500-018-3586-y. [DOI] [Google Scholar]
- 109.Yu C., Heidari A.A., Chen H. A quantum-behaved simulated annealing algorithm-based moth-flame optimization method. Appl. Math. Model. 2020;87:1–19. doi: 10.1016/j.apm.2020.04.019. [DOI] [Google Scholar]
- 110.Bhesdadiya R., Trivedi I.N., Jangir P., Kumar A., Jangir N., Totlani R. Advances in Computer and Computational Sciences. Springer; Singapore: 2017. A novel hybrid approach particle swarm optimizer with moth-flame optimizer algorithm; pp. 569–577. [Google Scholar]
- 111.Sayed G.I., Hassanien A.E. A hybrid SA-MFO algorithm for function optimization and engineering design problems. Complex Intell. Syst. 2018;4:195–212. doi: 10.1007/s40747-018-0066-z. [DOI] [Google Scholar]
- 112.Singh R.K., Gangwar S., Singh D., Pathak V.K. A novel hybridization of artificial neural network and moth-flame optimization (ANN–MFO) for multi-objective optimization in magnetic abrasive finishing of aluminium 6060. J. Braz. Soc. Mech. Sci. Eng. 2019;41:270. doi: 10.1007/s40430-019-1778-8. [DOI] [Google Scholar]
- 113.Dang M.P., Le H.G., Chau N.L., Dao T.-P. Optimization for a flexure hinge using an effective hybrid approach of fuzzy logic and moth-flame optimization algorithm. Math. Probl. Eng. 2021;2021:6622655. doi: 10.1155/2021/6622655. [DOI] [Google Scholar]
- 114.Mittal T. A hybrid moth flame optimization and variable neighbourhood search technique for optimal design of IIR filters. Neural Comput. Appl. 2021:1–16. doi: 10.1007/s00521-021-06379-8. [DOI] [Google Scholar]
- 115.Abd Elaziz M., Yousri D., Mirjalili S. A hybrid Harris hawks-moth-flame optimization algorithm including fractional-order chaos maps and evolutionary population dynamics. Adv. Eng. Softw. 2021;154:102973. doi: 10.1016/j.advengsoft.2021.102973. [DOI] [Google Scholar]
- 116.Ahmed O.H., Lu J., Xu Q., Ahmed A.M., Rahmani A.M., Hosseinzadeh M. Using differential evolution and Moth–Flame optimization for scientific workflow scheduling in fog computing. Appl. Soft Comput. 2021;112:107744. doi: 10.1016/j.asoc.2021.107744. [DOI] [Google Scholar]
- 117.Li Z., Zeng J., Chen Y., Ma G., Liu G. Death mechanism-based moth–flame optimization with improved flame generation mechanism for global optimization tasks. Expert Syst. Appl. 2021;183:115436. doi: 10.1016/j.eswa.2021.115436. [DOI] [Google Scholar]
- 118.Blackiston D.J., Silva Casey E., Weiss M.R. Retention of memory through metamorphosis: Can a moth remember what it learned as a caterpillar? PLoS ONE. 2008;3:e1736. doi: 10.1371/journal.pone.0001736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Morrison R.W. Designing Evolutionary Algorithms for Dynamic Environments. Springer Science & Business Media; Berlin/Heidelberg, Germany: 2004. [Google Scholar]
- 120.Derrac J., García S., Molina D., Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011;1:3–18. doi: 10.1016/j.swevo.2011.02.002. [DOI] [Google Scholar]
- 121.Friedman M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940;11:86–92. doi: 10.1214/aoms/1177731944. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data and code used in the research may be obtained from the corresponding author upon request.