Predictably Engineering the Viscoelastic Behavior of Dynamic Hydrogels via Correlation with Molecular Parameters

Abstract

Rational design of dynamic hydrogels with desirable viscoelastic behaviors relies on an in-depth understanding of the principles correlating molecular parameters and macroscopic properties. To quantitatively elucidate such principles, we designed a series of dynamic covalent hydrogels crosslinked via hydrazone bonds. We tuned the exchange rate of hydrazone bond by varying the concentration of an organic catalyst, while maintaining the crosslinking density unchanged. This strategy of independently tuning exchange dynamics of crosslinks and crosslinking density allowed unambiguous analysis of the viscoelastic response of the dynamic hydrogels as a function of their network parameters. We found that the terminal relaxation time of the dynamic hydrogels is primarily determined by two factors: the exchange rate of crosslinks and the number of effective crosslinks per polymer chain, and is independent of the network architecture. Furthermore, a universal correlation is identified between the terminal relaxation time determined from stress relaxation and the exchange rate determined via reaction kinetics, which can be generalized to any viscoelastic hydrogel networks in principle. This quantitative correlation facilitates the development of dynamic hydrogels with variable desired viscoelastic response based on molecular design.

Graphical Abstract

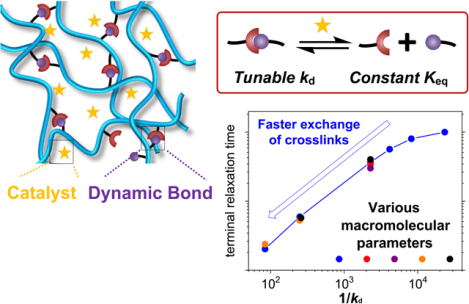
Molecular parameters of dynamic covalent hydrogels are independently varied to investigate their effects on the viscoelastic behavior of hydrogels. Universal correlations are identified to quantitatively predict the viscoelastic properties of dynamic hydrogels with different network topologies based on the exchange rate of crosslinks and the number of effective crosslinks per polymer chain.

Hydrogels crosslinked via dynamic bonds are a class of increasingly important materials with viscoelastic behaviors.^[1] Dynamic hydrogels exhibit many desired properties, including adaptability to external mechanical stimuli and molding,^[2] injectability,^[3] self-healing,^[4] energy dissipation,^[5] and tough bonding to surfaces.^[6] Designing and controlling the desired dynamic parameters, such as the rate of creeping, stress relaxation, or self-healing, is key to precisely engineer viscoelastic materials for different applications.^[7] This requires quantitative and comprehensive understanding of the molecular contributions to the dynamic properties of materials, which is, however, often a difficult task.

Although physical models for viscoelastic bulk polymer networks have been developed in the past,^[8] a quantitative description of the viscoelastic behavior of hydrogels still lacks due to the challenge of decoupling kinetic and thermodynamic parameters of a hydrogel system and the complexity of such systems. Several dynamic gel systems have been developed using reversible crosslinking with variable lifetime of the crosslinks.^[9] But it is often difficult to vary the thermodynamics that control the equilibrium and the kinetics that control the rate of crosslink exchange independently. Holten-Andersen and coworkers used multiple mixed metal-ligand complexes with distinct exchange kinetics as crosslinks and reported coexistence of multiple relaxation processes in the formed hydrogels that correspond to the lifetimes of different crosslinks.^[9b] However, the metal-ligand complexes used in dynamic hydrogels are under equilibrium of multiple coordination numbers at different stoichiometric ratios, thus leading to uncertainty in the structure and topology of the networks.^[10] Using gels crosslinked by different metal-ligand complexes or dynamic boronic esters, the Craig group and the Tibbitt group reported a quantitative correlation between the dissociation rate constant of the crosslinks and time-dependent mechanical properties.^[9a,9i] They observed excellent superposition for different crosslinks when plotting the storage modulus as a function of frequency and scaling by the dissociation rate constant. However, changing crosslinking kinetics by varying the chemical structures of crosslinks or the pH values of media inevitably resulted in large variation in equilibrium constants of the crosslinking in these systems, and thus the kinetic and thermodynamic parameters of dynamic networks cannot be independently varied. Other dynamic chemistry used as transient crosslinking is often limited in tunability.^[9c,9f,9h] As a result, it remains difficult to cleanly separate the contributions to viscoelastic response from the exchange of crosslinks and the crosslinking density, which are controlled by the kinetics and thermodynamics of dynamic crosslinks, respectively. Therefore, it remains unclear how the viscoelastic properties are quantitatively correlated with molecular parameters of the crosslinks and network structures. Moreover, most of the reported systems require high polymer concentrations to form stable hydrogels and cytotoxic crosslinking chemistry, limiting their potential applications as biomaterials.

To overcome these issues, we designed an approach to independently tune the crosslinking density and exchange kinetics of crosslinks in hydrogel systems using catalyst-modulated hydrazone bonds.^[3c,11] Incorporation of an organic catalyst allowed tuning of the exchange kinetics of hydrazone crosslinking by two orders of magnitude without affecting the network thermodynamic structures. This design has enabled us to unambiguously correlate molecular parameters with macroscopic stress relaxation of dynamic hydrogels. We quantitatively captured the time-dependent characteristics of hydrogels by two parameters, the exchange rate of dynamic crosslinks and the number of effective crosslinks per chain, and independent of polymer concentration. We also confirmed that these correlations are applicable to two different and common network topologies. These results provide quantitative guidelines to predictably engineer dynamic hydrogels with controlled and tunable viscoelastic properties.

We and others have reported using dynamic covalent hydrazone chemistry as transient crosslinking to synthesize viscoelastic hydrogels for biological applications.^[3c,11,12] We have used aminomethyl benzimidazole as an organic catalyst to accelerate the dynamic exchange of hydrazone bond and temporally enhance the injectability of the formed hydrogels (Figure 1).^[3c,13] Addition of a catalyst lowers the activation energy of an exchange reaction without affecting its equilibrium constant. Therefore, we rationalized that varying the amount of catalyst should allow continuous tuning of the exchange kinetics of crosslinking without altering the crosslinking density at equilibrium, thus decoupling crosslinking dynamics and crosslinking density for viscoelastic hydrogels. We applied this strategy to investigate viscoelastic properties of hydrogels in two most commonly used network topologies: crosslinking linear polymers through multiple sites along each chain (Figure 1a) and crosslinking multi-arm star polymers through end-linking (Figure 1b).

Figure 1.

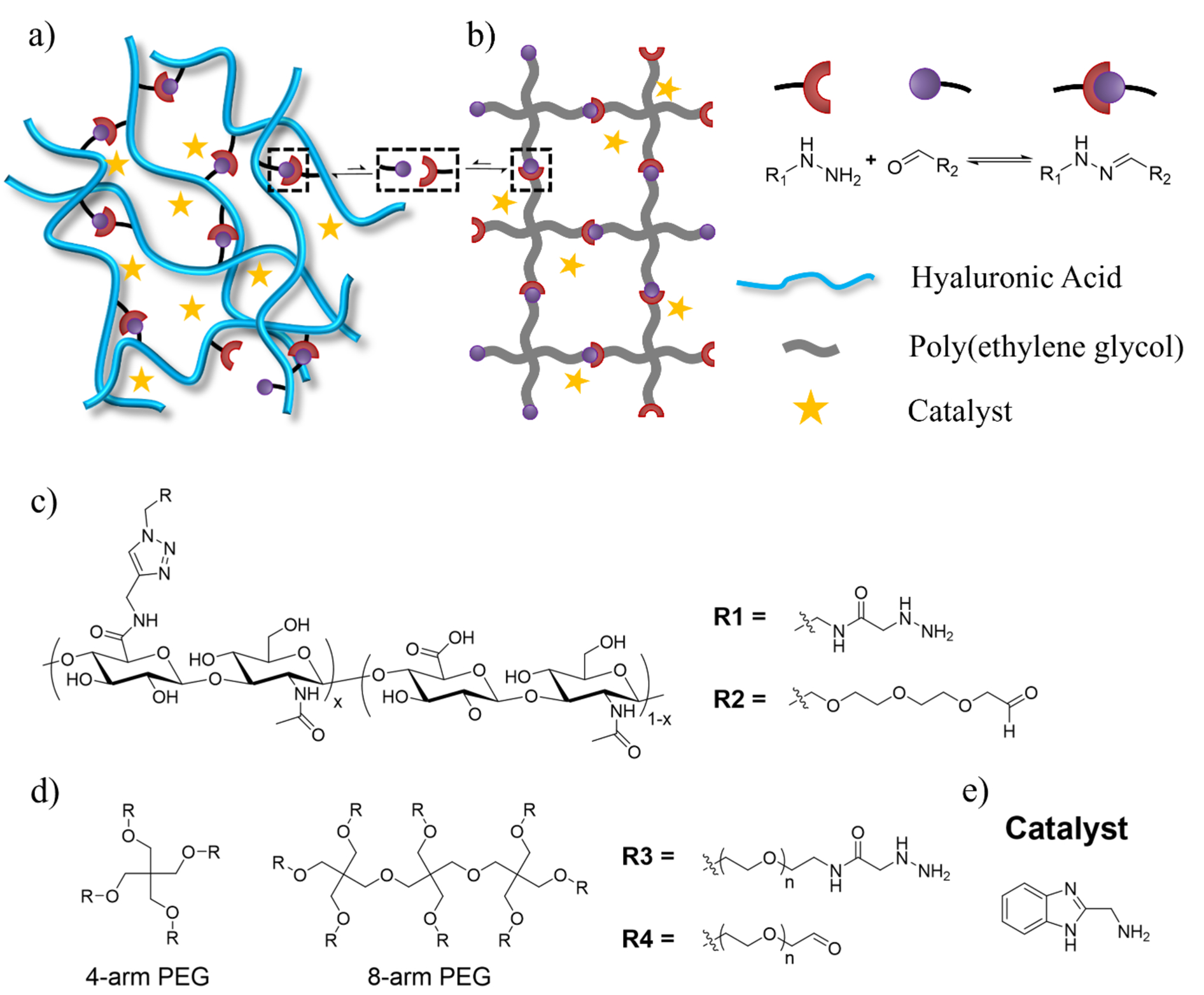
Schematic representation of two polymer network architectures, a) crosslinking of linear polymers and b) end-linking of star-shaped polymers. Chemical structures of c) hydrazine and aldehyde functionalized HA, d) hydrazine and aldehyde functionalized PEG, and e) catalyst used to accelerate hydrazone exchange.

We first investigated hydrogels crosslinked through multiple sites along linear polymers (Figure 1a). We modified hyaluronic acid (HA), an abundant polysaccharide in tissues, with hydrazine and aldehyde using our previously reported two-step protocol (Figure 1c).^[11] To investigate the effects of crosslinking density and polymer length on hydrogel viscoelasticity, we modified 12%, 15% and 20% of the carboxylate groups on a HA of 39 kDa with either hydrazine or aldehyde (Figure S1–S3); we also modified HAs of 45 and 75 kDa both at 12% to vary the chain length.

Using these modified HAs with different MWs and degrees of functionalization, we prepared dynamic HA hydrogels by mixing dilute solutions of hydrazine and aldehyde functionalized HAs at 1:1 stoichiometry and a total HA concentration of 2 wt% in phosphate buffered saline (PBS, pH 7.4) at 37 °C. To study the viscoelastic properties of these hydrogels, we performed stress-relaxation test, which measures the stress decay over time upon application of a small step strain. These time-dependent mechanical properties depend on two processes: a fast process related to the relaxation of polymer chain segments and a slow process related to the relaxation of dynamic crosslinks. The exchange of hydrazone bonds is relatively slow under physiological conditions, occurring at a time scale that is significantly longer compared to the relaxation of polymer chain segments. Therefore, the dynamics of crosslinks almost entirely dictates the stress relaxation with a minimum effect from the fast process. However, this relatively slow relaxation is practically difficult to measure using small amplitude oscillatory frequency sweep, which is the most common method to study viscoelastic behavior. Time temperature superposition (TTS) is used to capture viscoelastic behavior in a wide range of time scales for polymer melts with a single horizontal shift factor.^[14] However, a single shift factor cannot account for the changes in equilibrium constant and exchange kinetics at different temperatures,^[8d] and therefore TTS is not appropriate for studying dynamic hydrogels. Instead, stress relaxation tests capture the viscoelastic characteristics across a wide range of time scales, and can be converted directly to the storage and loss moduli obtained from oscillatory frequency sweeps (Figure 2). Therefore, it is the preferred method for quantitative analysis of our system.

Figure 2.

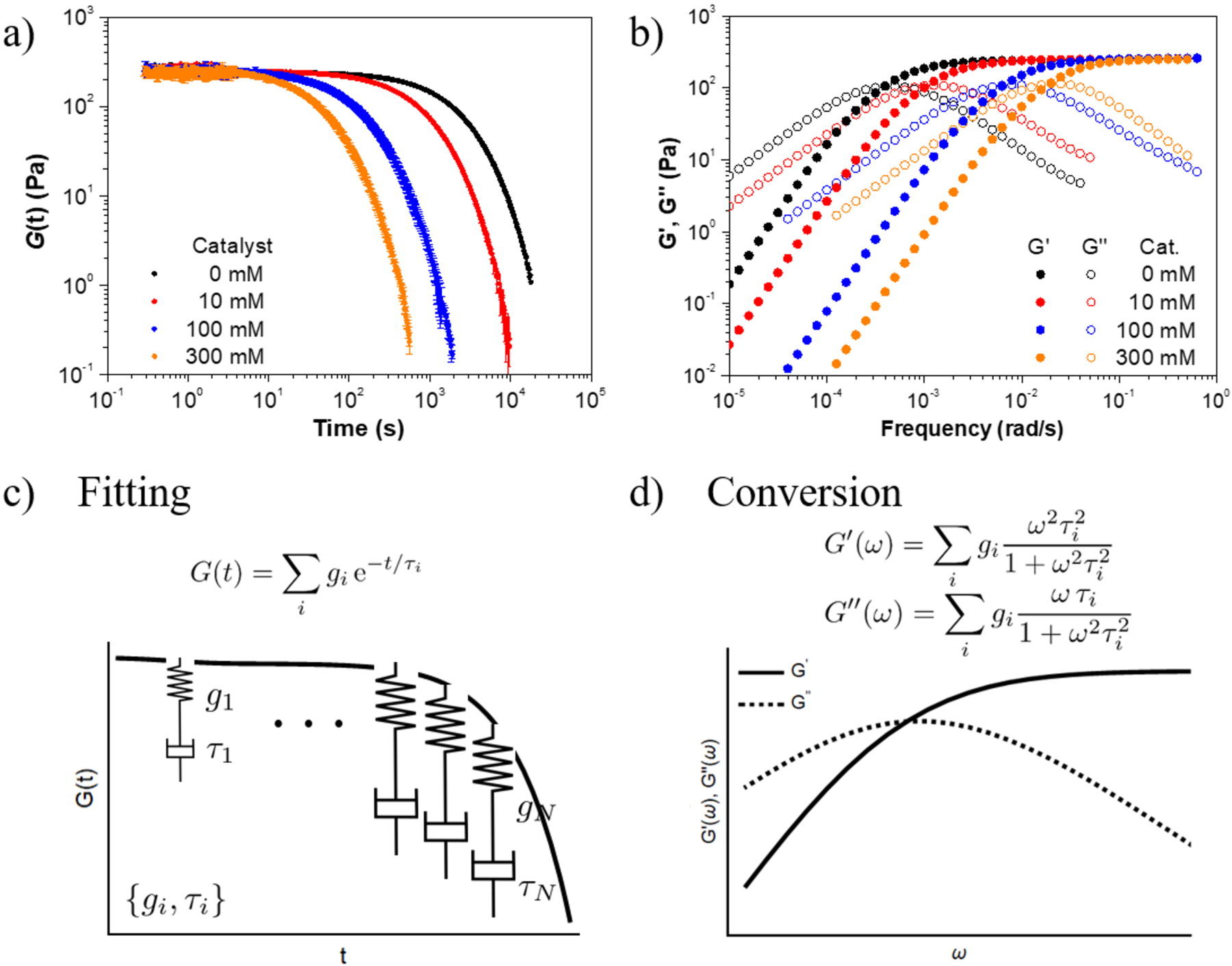
a) Stress relaxation profiles of a hydrogel from 39 kDa HA with 12% functionalization at different catalyst loadings. Each trace is an average of three independent experiments. b) Oscillatory frequency sweep data converted from stress relaxation profiles by fitting and interpolation. c) Fitting of stress relaxation profiles by a series of Maxwell elements with a set of stiffness and relaxation time {g_i, τ_i}. d) Conversion between the stress-relaxation modulus and the complex modulus using analytical formulas for the Fourier transform of the G(t) model to calculate the storage modulus (G′) and loss modulus (G″) according to g_i and τ_i obtained from fitting experimental data.

Stress relaxation experiments were first performed on hydrogels formed from HA of 39 kDa and 12% functionalization in the presence of different concentrations of aminomethyl benzimidazole as the catalyst (Figure 2a). The modulus of hydrogel was identical regardless of the catalyst loading from 0 to 300 mM (corresponding to molar ratio of [catalyst]/[hydrazine] from 0 to 100), confirming that addition of catalyst had a negligible effect on the equilibrium crosslinking density. Importantly, addition of catalyst markedly enhanced the rate of stress relaxation and shifted the stress relaxation curve to shorter time scales without changing its shape or slope. This effect of varying catalyst loading on shifting the rheological spectrum was also observed for hydrogels using HAs with different molecular weights (MWs) or degrees of functionalization. However, variation of MW or degree of functionalization at a constant catalyst concentration has marked effects on the relaxation curves and changes their shape and the slopes (Figure S4–S5). These observations indicate that the network structural factors and crosslinking dynamics contribute to stress relaxation differently. The initial modulus also increased with increasing MW or degree of functionalization of HA as expected, due to an increase in crosslinking density. By varying these macromolecular parameters, the modulus of these hydrogels can be tuned from tens Pa to thousands of Pa, which covers the stiffness of most natural tissues (Figure S6, Table S1). The impact of adding a catalyst on the viscoelastic behavior of hydrogel was also examined by tensile and compression tests. Addition of a catalyst did not affect the elastic modulus but significantly enhanced hysteresis as expected (Figure S7–S9).

Next, we converted the stress relaxation data to the frequency domain (Figure 2b) by first fitting the stress relaxation function G(t) to a sum of exponential decays (Figure 2c), then converting the fitted exponentials to storage and loss moduli analytically (Figure 2d, S10–S14). The results showed that increasing the catalyst loading does not affect the shape of curves but significantly shifts the curves to higher frequencies (Figure 2b). The crossover frequency, where G′ = G″ in frequency sweep curve, is the inverse of terminal relaxation time, τ_t, which is the timescale for the transition from liquid-like to solid-like response. At frequencies below 1/τ_t, the moduli followed the scaling of G′(ω) ~ ω² and G″(ω) ~ ω. At frequencies above 1/τ_t, the storage modulus G′(ω) reached a plateau that corresponds to the stiffness of the material. The obtained values for the plateau moduli and the terminal relaxation times as a function of polymer MW, degree of hydrazine/aldehyde functionalization of the polymer, and catalyst loading, are summarized in Table 1. Although the dynamics of HA hydrogels is generally too slow to capture by frequency sweep experiment, we performed frequency sweep test on HA hydrogel with the highest loading (35 kDa, 12% functionalization, 300 mM catalyst) to compare with the fitting result. The crossover frequency obtained from frequency sweep experiment agreed with that from the model fitting (Figure S15).

Table 1.

Mechanical properties of investigated HA hydrogels.

Polymer MW (kDa)	Degree of functionalization	[Cat]a (mM)	Modulus (Pa)	τtb (s)
39	12%	0	257	15946
39	12%	2	244	12779
39	12%	5	249	9018
39	12%	10	263	5838
39	12%	100	259	948
39	12%	300	250	324
39	15%	0	647	21216
39	15%	10	651	7320
39	15%	100	681	1144
39	20%	0	1762	69460
39	20%	10	1902	18796
45	12%	0	324	18660
45	12%	10	322	7503
45	12%	100	326	987
45	12%	300	317	446
75	12%	0	851	50144
75	12%	10	904	20153
75	12%	100	934	2882

^aconcentration of the catalyst, aminomethyl benzimidazole.

^bterminal relaxation time.

We next correlated τ_t with the exchange kinetics of the crosslinks. To measure the acceleration of exchange kinetics of the hydrazone bond in the presence of the catalyst, we investigated a small molecule model reaction between an aliphatic aldehyde and a hydrazine that closely resemble the structures used to form hydrogel crosslinking.^[3c] The conversions for each reactant in the presence of 0, 1, or 2 mM aminomethyl benzimidazole were monitored using HPLC. The association (k_a) and dissociation (k_d) rate constants were obtained by modeling the reaction kinetics for a reversible second order reaction (Figure S16). Both k_a and k_d increased with the addition of catalyst and exhibited first-order dependence on the catalyst concentration (Figure S17).^[13] Since the reaction at high catalyst concentrations cannot be easily monitored due to very fast conversion of hydrazine and aldehyde, k_a and k_d were calculated assuming first order kinetics of the catalyst (Table S2). The equilibrium constant (K_eq) was calculated from k_a/k_d, which remained the same regardless of catalyst concentration (Table S2). With the addition of 100 mM catalyst, k_a and k_d can both be enhanced by two orders of magnitude while the equilibrium constant remains unchanged under physiological conditions (pH 7.4, 37 °C).

We plotted τ_t against 1/k_d for 2 wt% hydrogels at different catalyst concentrations and τ_t decreased monotonically with decreasing 1/k_d as expected (Figure 3a), and similar trends were obtained for different HA MWs or degrees of functionalization. To decouple the exchange kinetics of crosslinks from the network structural parameters (e.g. polymer MW, number of crosslinking sites per chain), we normalized τ_t of the hydrogels with the same structural parameters at different catalyst loadings to the longest terminal relaxation time without added catalyst. After normalization, τ_t’s of hydrogels from HAs with different MWs or degrees of functionalization all collapse onto a master curve (Figure 3b). The excellent superposition of normalized τ_t over 1/k_d unambiguously demonstrates that the dynamics of crosslinks and crosslinking density at equilibrium are fully decoupled. Using this normalized master curve, the viscoelastic behavior of a hydrogel, especially τ_t, can be simply predicted from k_d of dynamic crosslinks in the range of k_d examined.

Figure 3.

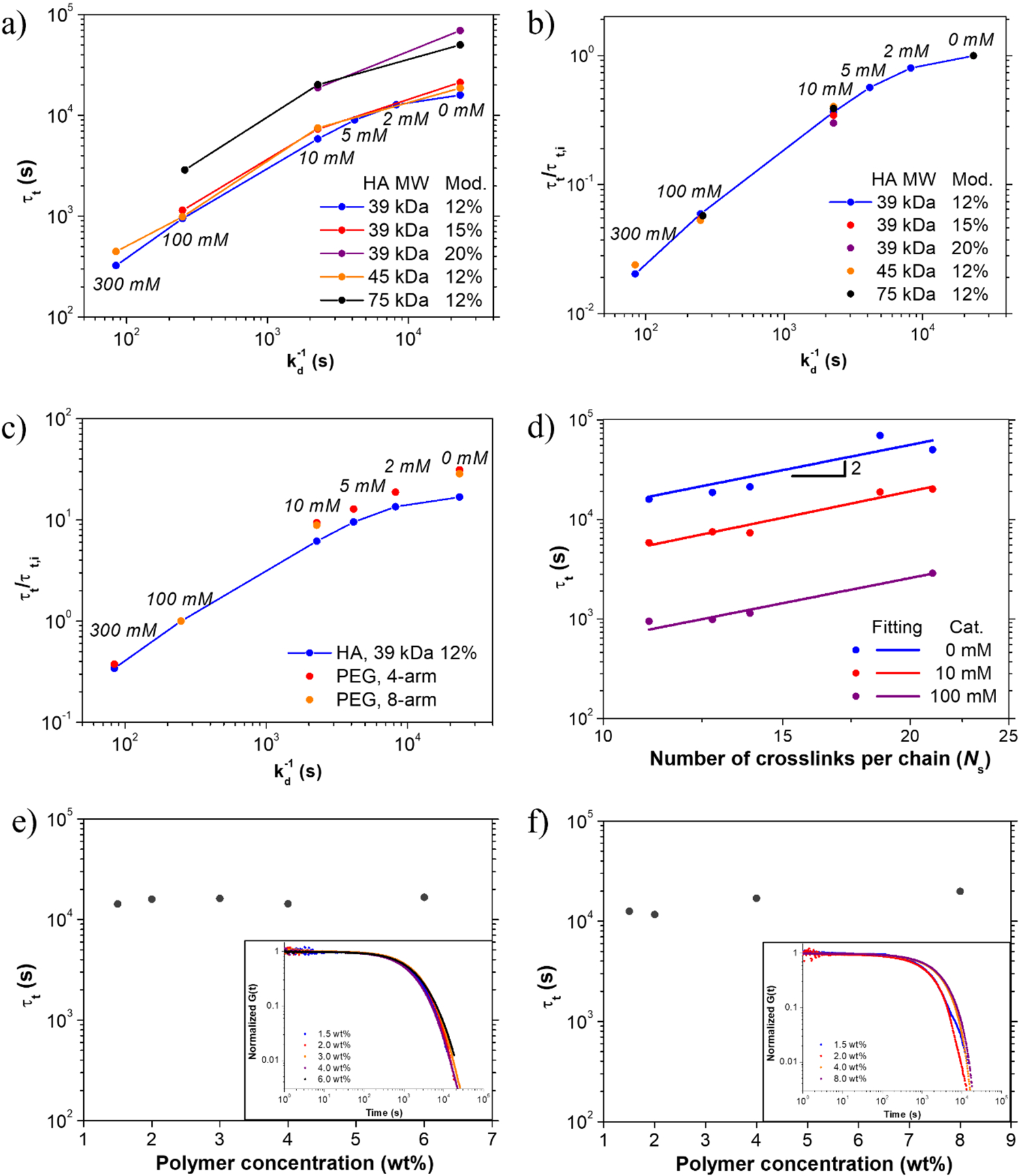
a) Terminal relaxation time τ_t as a function of 1/k_d at different catalyst loadings for HA-based hydrogels with different polymer MWs or degrees of functionalization. b) Normalized τ_t as a function of 1/k_d in log-log scale, showing superposition regardless of polymer MW. τ_t’s with the same structural parameters at different catalyst loadings are normalized to the longest terminal relaxation time without added catalyst. c) Normalized τ_t as a function of 1/k_d, showing superposition regardless of the network architecture. τ_t’s with the same structural parameters at different catalyst loadings are normalized to the terminal relaxation time with 100 mM catalyst. d) τ_t as a function of number of effective crosslinks per chain N_s at different catalyst loading for HA-based hydrogels. e) τ_t’s of hydrogels using 39 kDa HA with 12% functionalization at HA concentrations of 1.5, 2, 3, 4, and 6 wt%. (insert: normalized stress relaxation traces of hydrogels at different HA concentrations) f) τ_t’s of hydrogels using 4-arm PEG at concentrations of 1.5, 2, 4, and 8 wt% (insert: normalized stress relaxation traces of hydrogels at different PEG concentrations).

To test the generality of this correlation, we then examined the network architecture formed from multi-arm star polymers by end-linking 4-arm and 8-arm PEGs via hydrazone bonds (Figure 1b). The 4-arm and 8-arm PEGs with hydrazine or aldehyde end groups were obtained by modifying the amino or hydroxyl end groups of PEGs, respectively (Figure 1d, S18–S20). In order to compare the difference between different hydrogel systems, we normalized τ_t to its terminal relaxation time at 100 mM catalyst. Interestingly, the number of PEG arms does not affect the normalized τ_t, and more importantly, despite the different network architectures and polymer structures, the end-linked star PEG hydrogels and the side chain linked linear HA hydrogels exhibited almost the same quantitative correlation for normalized τ_t vs 1/k_d (Figure 3c, Table 2).

Table 2.

Mechanical properties of investigated star-shaped PEG hydrogels

Polymer MW (kDa)	Degree of functionalization	[Cat]a (mM)	Modulus (Pa)	τtb (s)
10	4-arm	0	220	11672
10	4-arm	2	236	7078
10	4-arm	5	233	5062
10	4-arm	10	223	3282
10	4-arm	100	228	396
10	4-arm	300	244	132
20	8-arm	0	259	47813
20	8-arm	10	251	14904
20	8-arm	100	257	1469

^aconcentration of the catalyst, aminomethyl benzimidazole.

^bterminal relaxation time

For both network topologies, slight deviation from linearity was observed in the log-log plot of normalized τ_t vs 1/k_d at low catalyst concentrations. This deviation could be attributed to the limit of experimentally measurable G(t) values in stress relaxation measurements at long time scales for the slowly relaxing hydrogels. For the samples with the lowest catalyst concentrations, it is possible that the duration (~5 h) of experimental measurement was not enough to capture some of the slower relaxation modes. This would result in missing contributions in the fitted spectra, leading to smaller terminal relaxation times and the observed nonlinearity in the collapsed curves of Figure 3c.

After demonstrating the correlation between τ_t and exchange kinetics of crosslinks, we investigated the effect of other molecular parameters, including MW, degree of functionalization for linear HA hydrogels, and the number of arms for star PEG hydrogels. In the HA system, at the same catalyst loading, increasing the MW or degree of functionalization both led to an increase in the plateau modulus and τ_t. To simplify the analysis of polymer parameters, we used a single parameter, average effective crosslinks (N_s), which represents the number of crosslinks per chain under equilibrium in a hydrogel. In our system, N_s can be directly calculated from the macromolecular parameters and equilibrium constant (Table S3). When τ_t’s of hydrogels in the presence of 0, 10 or 100 mM catalyst were plotted against N_s in log-log scale, a power law close to 2 was observed for all the three catalyst concentrations (Figure 3d). This power law agrees with the prediction by the Sticky-Rouse model,^[8] which shows that τ_t is proportional to N_s².^[15] Similar correlation was also observed in star-shape PEG system. At the same catalyst loading, τ_t of hydrogels composed of 8-arm PEG (N_s = 8) were about 4 times larger than τ_t of hydrogels composed of 4-arm PEG (N_s = 4) (Table 2). This observed trend also highlights the importance of equilibrium constant of dynamic crosslinks, which changes N_s and thus affects the dynamic properties of hydrogels.

Finally, we investigated the effect of polymer concentration on stress relaxation in both network topologies. We measured the stress relaxation curves of HA hydrogels at 1.5, 2, 3, 4 and 6 wt% using 39 kDa HA with 12% functionalization without added catalyst. τ_t’s of these hydrogels at different polymer concentrations were almost identical and the stress relaxation curves superimposed with each other after normalization to their initial modulus (Figure 3e), showing concentration-independent stress relaxation as predicted by the Sticky-Rouse model in the examined concentration range from 1.5 to 6 wt%.^[15] The same insignificant effect of polymer concentration on the stress relaxation behavior of hydrogels was also observed for hydrogels consisting of star-shaped PEG’s (Figure 3f), similar to the results reported by Zhao and coworkers using multi-arm PEG hydrogels crosslinked via dynamic boronic acid-diol complexation.^[16] Therefore, we can independently manipulate the stiffness of hydrogels via polymer concentrations without affecting their stress relaxation properties in the two common polymer network topologies.

In summary, we have developed a new strategy to decouple crosslinking density and exchange kinetics of crosslinks in viscoelastic hydrogels by using an organic catalyst. Varying catalyst concentrations allowed tuning of the exchange kinetics of dynamic covalent hydrazone crosslinks over two orders of magnitude without affecting the equilibrium constant, thus providing a convenient means to control the stress relaxation behavior of viscoelastic hydrogels. This strategy has enabled us to investigate the impact of various molecular and macromolecular parameters independently on stress relaxation using two most common network topologies in hydrogel biomaterials. A quantitative correlation between time-dependent mechanical behavior of hydrogels and the dissociation rate constant of dynamic crosslinks was observed regardless of the crosslinking density, polymer structures, and network topologies. We also found the number of effective crosslinks per chain to be another important factor regulating the viscoelastic characteristics in both network topologies. These results elucidate the fundamental mechanisms that determine the viscoelastic properties of hydrogels and provide guidelines to precisely and predictably engineer the viscoelastic properties of hydrogels for various biological applications, including studying mechano-biology, therapeutic cell delivery, and tissue engineering.