Abstract
Purpose
Patients with repaired Tetralogy of Fallot (rTOF) will develop dilation of the right ventricle (RV) from chronic pulmonary insufficiency and require pulmonary valve replacement (PVR). Cardiac MRI (cMRI) is used to guide therapy but has limitations in studying novel intracardiac flow parameters. This pilot study aimed to demonstrate feasibility of reconstructing RV motion and simulating intracardiac flow in rTOF patients, exclusively using conventional cMRI and an immersed-boundary method computational fluid dynamic (CFD) solver.
Methods
Four rTOF patients and three normal controls underwent cMRI including 4D flow. 3D RV models were segmented from cMRI images. Feature-tracking software captured RV endocardial contours from cMRI long-axis and short-axis cine stacks. RV motion was reconstructed via diffeomorphic mapping (Deformetrica, deformetrica.org), serving as the domain boundary for CFD. Fully-resolved direct numerical simulations were performed over several cardiac cycles. Intracardiac vorticity, kinetic energy (KE) and turbulent kinetic energy (TKE) was measured. For validation, RV motion was compared to manual tracings, results of KE were compared between CFD and 4D flow.
Results
Diastolic vorticity and TKE in rTOF patients were 4.12±2.42mJ/L and 115±27/s, compared to 2.96±2.16mJ/L and 78±45/s in controls. There was good agreement between RV motion and manual tracings. The difference in diastolic KE between CFD and 4D flow by Bland-Altman analysis was −0.89910-2 mJ/mL (95% limits of agreement: - 1.351*10−2mJ/mL to 1.171*10−2mJ/mL).
Conclusion
This CFD framework can produce intracardiac flow in rTOF patients. CFD has the potential for predicting the effects of PVR in rTOF patients and improve the clinical indications guided by cMRI.
Keywords: Cardiac Magnetic Resonance Imaging, Tetralogy of Fallot, Computational Fluid Dynamics
Background
Tetralogy of Fallot (TOF) is the most common cyanotic congenital heart defect [1], consisting of a large ventricular septal defect and right ventricular outflow tract (RVOT) obstruction. The repair of TOF typically occurs in infancy, involving patch closure of the ventricular septal defect and transannular patch across the RVOT. As a result, patients with repaired Tetralogy of Fallot (rTOF) will often have the surgical sequelae of chronic pulmonary valvar insufficiency (PI). Chronic PI leads to right ventricular (RV) enlargement and energy loss [2], increasing the risk of RV deterioration, ventricular arrhythmias and mortality [3]. Older rTOF patients will require pulmonary valve replacement (PVR) to treat these sequelae [4, 5].
Timing of PVR is the focus of most recent studies related to rTOF [4, 6, 7]. There are risks associated with early or late PVR: on one hand, RV dysfunction may be irreversible if PVR is postponed until rTOF patients develop clinical symptoms [8, 9]. On the other hand, implanted pulmonary valves have limited durability (surgical PVR estimated to be approximately 15 years, percutaneous PVR potentially shorter) [10], and aggressive early intervention leads to increased number of future interventions with incremental risk. Thus, methods to guide PVR therapy and predict the hemodynamic benefit of PVR are desired.
Measurements of RV size by cardiac magnetic resonance imaging (cMRI) have provided critical thresholds for PVR intervention [5, 6]. These measurements include indexed RV end-diastolic volume (RVEDVi), indexed RV end-systolic volume (RVESVi) and RV ejection fraction (RVEF). However, current guidelines acknowledge the inconsistent use of conventional cMRI measurements alone to dictate therapy [5, 6]. Conventional cMRI measurements do not incorporate the diverse RV morphological changes and RV motion in rTOF [11, 12]. The link between abnormal RV morphology and PI in rTOF patients has not been clarified. The post-operative RV motion and intracardiac flow abnormalities have not been comprehensively studied.
Recent advances in cMRI now allow for time resolved three-dimensional imaging (4D flow) of intracardiac flow. With 4D flow, it is observed that intracardiac flow parameters such as vorticity (the local spinning motion of blood), kinetic energy (KE) and turbulent kinetic energy (TKE) are altered in rTOF patients [13-15]. Intracardiac flow parameters are thus promising hemodynamic biomarkers to potentially guide timing of PVR. However, 4D flow imaging have limitations in spatial and temporal resolution [16], prohibiting detailed visualization and study of intracardiac flow abnormalities. Additionally, the use of 4D flow alone cannot predict the changes in RV intracardiac flow to guide PVR therapy.
Computational modeling such as computational fluid dynamics (CFD) is key to comprehensive flow analysis and prediction of hemodynamic changes after procedural interventions [17]. Computational models have been previously developed to estimate functional changes based on RV material parameter values (such as elasticity) in rTOF patients after PVR, relying on cMRI geometric data and cardiac catheterization pressure recordings [18, 19]. In similar fashion, a CFD-based method could change input boundary conditions, removing the intracardiac and morphological effect of PI and determine changes to intracardiac flow. CFD may further predict the effect of varying PVR techniques, including surgical placement with or without RVOT plication, percutaneous placement, or “hybrid” approaches [20, 21]. Thus, CFD potentially offers risk-benefit analysis of PVR based on specific clinical data, allowing for a customized and optimized approach for each individual patient.
In this pilot study, we aim to develop a comprehensive method to reconstruct RV motion and simulate intracardiac flow in rTOF patients. This method exclusively uses conventional two-dimensional cMRI cine images, diffeomorphic mapping software, and a robust immersed-boundary method CFD solver [22]. We hypothesize that such a CFD approach to RV intracardiac flow is feasible using boundary conditions generated from cMRI data, and that this approach can identify important intracardiac flow abnormalities in rTOF patients.
Methods
CMR imaging
This study was approved by the Institutional Review Boards of all participating institutions, with all patients prospectively enrolled after informed consent. Four rTOF patients and three normal controls underwent clinically-indicated cMRI studies using a Siemens 1.5T scanner. The rTOF patients all had undergone transannular patch with no significant residual ventricular septal defect, tricuspid regurgitation or pulmonary stenosis. cMRI data included cine imaging (long-axis and short-axis cine), contrast-enhanced magnetic resonance angiography (MRA), three-dimensional steady state free precession imaging (3D SSFP), two-dimensional phase contrast (2D-PC) across the pulmonary valve (Venc set between 2 m/s – 2.5 m/s) and 4D flow sequences. The cine sequence parameters included FOV = 350 x 220 mm, matrix = 256 x 155, TE = 1.19 ms, TR = 31.13 ms, slice thickness = 6-8 mm. All cines were reconstructed into 30 images per cardiac cycle. The MRA and 3D SSFP covered the entire heart with voxel size ~ 1.4 x 1.4 x 1.4 mm. The 4D flow sequence parameters included FOV = 400–480 x 190–230 mm, matrix = 160 x 77, TE = 2.19 ms, TR = 37.9 ms, slice thickness = 2.5–3 mm and venc between 2 m/s - 2.5 m/s. The 4D flow data was only used for validation purposes.
3D Model
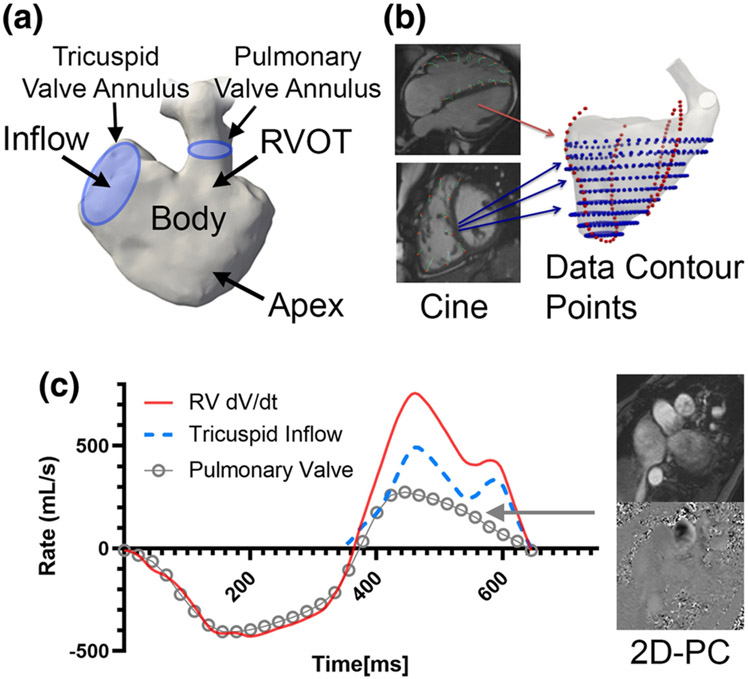
3D end-diastolic models of the RV were created from MRA and 3D SSFP datasets, according to lab standard segmentation [23, 24] using commercially available software (Mimics; Materialise, Leuven, Netherlands). The three-dimensional (3D) models incorporated the three components of the RV including RV inflow, RV body/apex, and RVOT, with extra delineation of tricuspid valve annulus and pulmonary valve annulus (Figure 1a).
Figure 1. Clinical imaging data used for reconstruction of right ventricular (RV) motion and simulation.
a) Standard segmentation techniques were applied to recreate the right ventricle. The tricuspid valve annlus and pulmonary valve annulus are also demarcated to establish inflow/outflow. b) Feature tracking was applied to cine imaging in both short-axis and long-axis views (blue points and red points respectively). c) Inflow boundary condition across the tricupisd valve are derived from mass conservation, by subtracting RV volumetric change (dV/dt) against the flow rate of pulmonary insufficiency from 2D phase contrast (2D-PC).
RV motion reconstruction with Feature Tracking and Diffeomorphic Mapping Software
Cines acquired in continuous short axis slices were obtained to evaluate wall motion. Each short-axis cine was used for feature tracking analysis with QStrain V2.0 (Medis Medical Imaging Systems, Leiden, Netherlands), a semi-automated process that requires manual contour of the end-diastolic RV endocardial border to initiate tracking. In cases of insufficient tracking with apparent deviations, the RV endocardial contours were manually adjusted. The same process was also applied to long-axis views (Figure 1b). The moving endocardial borders of the entire RV were then extracted and formatted as data contour points.
To create a continuous representation of RV motion, the data contour points from QStrain were combined with the 3D end-diastolic model of the RV using smooth mappings known as diffeomorphism. A similar method has been previously demonstrated by Biffi et al on the left ventricle in aortic stenosis patients [25]. The approach relied on an image registration technique based on a control-point instance of the Large Deformation Diffeomorphic Geometric Mapping (LDDMM) implemented into the open-source software Deformetrica [26]. Using Deformetrica, the motion of the surface mesh from the 3D model throughout the cardiac cycle was guided by endocardial data contour points in both short-axis and long-axis trajectories. The data contour points were used to compute mappings (diffeomorphisms) that transformed a given reference phase (e.g. diastole) into each of the 30 phases of the cardiac cycle. The final transformation was obtained by linear superposition of the two mappings in the short-axis and long-axis planes. The computed diffeomorphisms were then applied to the end-diastolic, 3D triangulated surface mesh, to yield 30 meshes with the same connectivity properties that served as boundary conditions for the simulations. Trigonometric interpolation with N/2 Fourier modes, where N=30 is the number of reconstructed cardiac phases, was eventually used to increase the temporal resolution as required for accurate time integration of the Navier-Stokes equations. This procedure also provided the time history of the RV volume over the cardiac cycle.
Immersed Boundary Method
Direct numerical simulations were performed using an in-house CFD solver based on the immersed boundary method (IBM) to solve the Navier-Stokes equations for incompressible flow, assuming a Newtonian model for the blood with μ = 4 x 10−3 Pa · s and ρ = 1 kg/m3 [27]. Spatial discretization relied on a staggered second-order scheme, while time advancement employed a fractional-step formulation, where both advective and diffusive terms were advanced with an explicit third-order Runge-Kutta scheme. The moving RV geometry was immersed in a cubic domain, with periodic boundaries along two directions, and inlet/outlet boundary conditions along the third one to ensure proper washout of the fluid domain outside the RV. The position and velocity of each point discretizing the RV wall, which is not aligned with the computational grid, was obtained from the trigonometric interpolation procedure described above and enforced using a moving least-squares IBM approach. The details on the overall formulation can be found in [22, 28]. The overall mesh size was on average of ~10 million grid points, leading to a typical spatial resolution of ~0.60 mm. The time step size in all computations was primarily dictated by accuracy considerations. In direct-forcing IBM, such as the one utilized in the present work, it is well known that due to the operator splitting between the IBM and the fractional-step scheme, the boundary conditions on the immersed body are only accurate to order O(Dt^2) [29] potentially leading to spurious transpiration through the boundary. We found that a time step size equal to 2x10−5s was able to guarantee negligible errors for the global mass conservation within the immersed body. The computations took on average 20 hours per cardiac cycle when run in parallel on 16 processors at a high-end workstation.
Boundary Conditions
The tricuspid valve annulus and pulmonary valve annulus were represented by simple planes whose permeability was modulated depending on the phase of the cardiac cycle. The positions of these planes were guided by clinical imaging (see subsection “3D model”, Figure 1a) and followed the corresponding changes in RV wall motion. The boundary conditions were derived as follows:
The tricuspid inflow boundary condition was derived from mass conservation. For normal controls, the tricuspid inflow was directly related to RV volumetric change (dV/dt). For rTOF patients, the tricuspid valve flow rate was computed by subtracting RV dV/dt against the diastolic PI flow rate from 2D-PC (Figure 1c), then uniformly distributed across the tricuspid valve plane. The velocity at the tricuspid valve annulus plane was explicitly imposed using the IBM.
For outflow boundary condition in controls, the pulmonary valve was assumed to be either fully open/closed in systole and diastole respectively. For rTOF patients, the pulmonary valve was assumed to be fully open during systole; during diastole, the pulmonary valve was also assumed to be open, absent of residual pulmonary valve tissue. As the tricuspid inflow and RV dV/dt is already prescribed in the simulation, the regurgitant volume and regurgitant fraction by 2D-PC measurement is maintained by mass conservation (Figure 1c).
Quantification of Intracardiac Flow
The CFD velocity fields were extracted using in-house MATLAB codes. The ventricular reconstruction used to define the boundary conditions for the simulations was also exploited for post-processing purposes. The segmented and moving RV geometry, including the RVOT, was used to isolate the domain of interest for extraction of the results. KE, TKE and vorticity were computed for each phase of the cardiac cycle and spatially integrated over the RV volume to yield their mean values. KE, TKE and vorticity were defined as:
Where ρ is density, v is velocity over the three orthogonal directions (x, y and z); u’, v’ and w’ are standard deviation of velocities (i.e. fluctuation), and ∇ is the gradient operator of the velocity field); u’, v’ and w’ were computed with respect to phase-averaged velocity fields, with statistics accumulated over 5 cardiac cycles. Values of these parameters in diastole were singled out for further analysis. In addition, the Q-criterion [30] was used to visualize the topology of coherent vortical structures, creating isosurfaces with Q Criterion > 5000. Phase-averaged velocity fields were visualized using velocity vectors to allow for direct comparison with 4D flow.
Reynolds calculation
The peak Reynolds number [27] across the tricuspid valve and pulmonary valve was also calculated in early diastole, using the following equation:
Where Re = Reynolds number, ρ = 1 kg/m3, μ = 4 x 10−3 Pa · s, D is the local diameter and v is velocity. D was locally obtained by measuring the area across the TV and PV. v across the TV and PV was obtained by spatially averaging the total flow over the measured area.
Validation of RV motion reconstruction with cine imaging
For each patient, a specific slice of cMRI cine imaging not used for feature tracing (axial cine or separate RVOT cine) was selected for validation of RV motion reconstruction process. In each specific slice, the contour of the RV and main pulmonary artery was manual traced through the cardiac cycle. An overlay of reconstructed RV motion was compared against manual tracing. The similarity and degree of overlap with manual tracings were represented as the Dice coefficient [31], with 0 = no overlap; 1 = complete overlap.
Comparison between CFD and 4D flow
CFD results were compared against 4D flow using both qualitatively and quantitatively. For quantitative comparison, the diastolic KE was computed from 4D flow, using the same procedure described above (see subsection “Quantification of Intracardiac Flows”). The diastolic KE computed from CFD was then normalized over time and directly compared to 4D flow results. Paraview V4.3 [32] and MATLAB were used for qualitative comparison by visualizing the phase-averaged velocity fields during late diastolic filling across a longitudinal slice of the RV, such that the tricuspid valve plane and portion of the RVOT were included. The flow pattern in this longitudinal slice was qualitatively compared between CFD and 4D flow.
Statistical Evaluation
Statistical analysis was performed with Prism 8.4.0 (GraphPad Software, California, USA). For RV motion, the mean Dice coefficient is reported. Good agreement was defined as Dice coefficient >0.700 [33]. Bland-Altman analysis was also performed to plot the agreement between CFD and 4D flow.
Results
Demographics
Four rTOF patients (aged 15 ± 9 years, body surface area 1.5 ± 0.3 m2) and three normal controls (aged 15 ± 5 years, body surface area 1.5 ± 0.4 m2) and were included (Table 1). All rTOF patients had increased RV size – the mean RVEDVi was 150±29 mL/m2, RVESVi was 78±23 mL/m2, and RVEF was 48±5%. Using current guidelines [5], rTOF 2 would have been considered a potential PVR candidate based on cMRI criteria alone.
Table 1.
Patient Demographics included in pilot study.
| Subject | Age | BSA (m2) | RVEDVi (mL/m2) |
RVESVi (mL/m2) |
RVEF (%) | PVRF (%) |
|---|---|---|---|---|---|---|
| rTOF 1 | 6 | 1.02 | 148 | 75 | 50 | 40 |
| rTOF 2 | 12 | 1.29 | 191 | 114 | 41 | 50 |
| rTOF 3 | 17 | 1.38 | 158 | 85 | 46 | 30 |
| rTOF 4 | 30 | 1.83 | 148 | 68 | 54 | 30 |
| Control 1 | 10 | 1.09 | 108 | 50 | 53 | n/a |
| Control 2 | 17 | 1.53 | 87 | 42 | 53 | n/a |
| Control 3 | 19 | 1.91 | 85 | 38 | 55 | n/a |
Three normal controls and four repaired Tetralogy of Fallot (rTOF) patients were included in the study. Age, body surface area (BSA), indexed RV end-diastolic volume (RVEDVi), indexed RV end-systolic volume (RVESVi), RV ejection fraction (RVEF) and pulmonary valve regurgitant fraction (PVRF) were reported.
Intracardiac Flow Quantification
Vorticity and TKE results for rTOF patients and controls for both early and late peak diastole are shown in Table 2. The mean TKE of rTOF patients was 2.48 ± 1.86 mJ/L and 4.12 ± 2.42 mJ/L respectively, compared to 1.40 ± 1.06 mJ/L and 2.96 ± 2.16 mJ/L for controls. The mean vorticity of rTOF patients was 115 ± 27 /s and 93 ± 43 L/s respectively, compared to 78 ± 45 /s and 77 ± 38 /s for control. For all rTOF cases, the peak Reynolds number at early diastole at both tricuspid inflow (3800 ± 700) and PI jet (2700 ± 1100) was in the upper transitional range for turbulence [27]. The control cases had an early-diastolic Reynolds number of 2600 ± 890 at tricuspid inflow (Table 3).
Table 2.
Intracardiac Flow Quantification Results by Computational Fluid Dynamic simulation (CFD).
| Subject | TKE in early diastole (mJ/L) |
TKE in late diastole (mJ/L) |
Vorticity in early diastole (1/s) |
Vorticity in late diastole (1/s) |
|---|---|---|---|---|
| rTOF 1 | 1.2 | 2.4 | 103 | 62 |
| rTOF 2 | 5.1 | 6.5 | 107 | 123 |
| rTOF 3 | 2.5 | 5.9 | 156 | 136 |
| rTOF 4 | 1.1 | 1.7 | 96 | 51 |
| Control 1 | 0.2 | 0.5 | 43 | 38 |
| Control 2 | 2.2 | 4.5 | 130 | 115 |
| Control 3 | 1.8 | 3.9 | 63 | 78 |
The CFD results of three normal controls and four repaired Tetralogy of Fallot (rTOF) patients are shown for both early diastole and late diastole. The mean TKE of rTOF patients was 2.48 ± 1.86 mJ/L and 4.12 ± 2.42 mJ/L respectively, compared to 1.40 ± 1.06 mJ/L and 2.96 ± 2.16 mJ/L for controls. The mean vorticity of rTOF patients was 115 ± 27 /s and 93 ± 43 L/s respectively, compared to 78 ± 45 /s and 77 ± 38 /s for control.
Table 3.
Local Reynolds (Re) number across the tricuspid valve (TV), and from pulmonary insufficiency (PI) in early diastole.
| Subject | Re across TV in early diastole | Re from PI in early diastole |
|---|---|---|
| rTOF 1 | 4380 | 2580 |
| rTOF 2 | 2800 | 4000 |
| rTOF 3 | 4160 | 2900 |
| rTOF 4 | 3900 | 1300 |
| Control 1 | 1800 | N/A (no PI) |
| Control 2 | 3570 | N/A (no PI) |
| Control 3 | 2450 | N/A (no PI) |
Qualitative Observations of RV Motion Reconstruction
The reconstructed RV motion of one normal control and rTOF patients are depicted in Supplementary Video 1. The RV of the normal control had an expected pyramidal shape that contracted in longitudinal fashion. Meanwhile, the four rTOF cases had different, heterogenous RV morphology and motion, despite some having similar indexed size and ejection fraction (rTOF 1 and rTOF 4). The rTOF cases demonstrated larger circumferential motion in comparison to the normal control.
Qualitative Observations of Intracardiac Flow
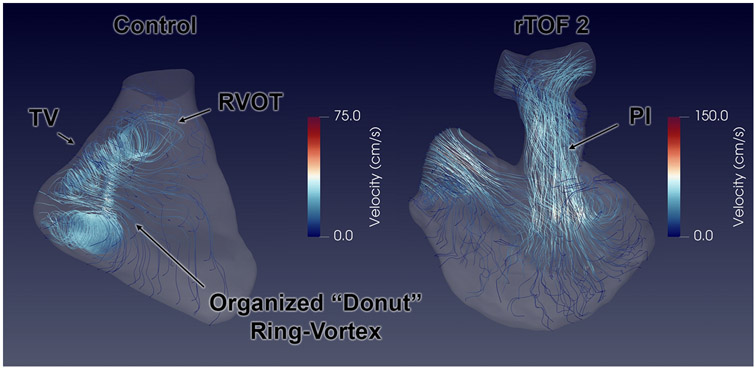
The relative differences in flow are demonstrated as vector flow streamlines (Figure 2) and the topology of vorticity isosurfaces (Figure 3, Supplementary Video 2). In control cases, an organized, “donut”-shaped ring-vortex was visualized surrounding the tricuspid inflow during diastole. The superior edge of the diastolic vortex propagated in a counterclockwise pattern directly towards the RVOT. Most of these flow features dissipated before reaching the RV apex. During systole, the flow translated into a helical twist along the RVOT. In comparison, the rTOF simulations in diastole demonstrated turbulent-like, chaotic flow formation starting in the RVOT, propagating through the RV body into the apex. The diastolic vortex from the tricuspid valve, whilst also present in rTOF patients, was disrupted by the jet of PI.
Figure 2. Vector flow streamlines representing right ventricular (RV) intracardiac flow simulation between normal control and repaired Tetralogy of Fallot (rTOF) patient.
In the control case, an organized “donut” ring-vortex is formed from the tricuspid valve (TV) inflow, with the superior edge propagating towards the right ventricular outflow tract (RVOT). The rTOF cases are characterized by collision of pulmonary insufficiency (PI) and TV inflow in the RV body.
Figure 3. Vorticity isosurfaces representing right ventricular (RV) intracardiac flow simulation between normal control and repaired Tetralogy of Fallot (rTOF) patients.
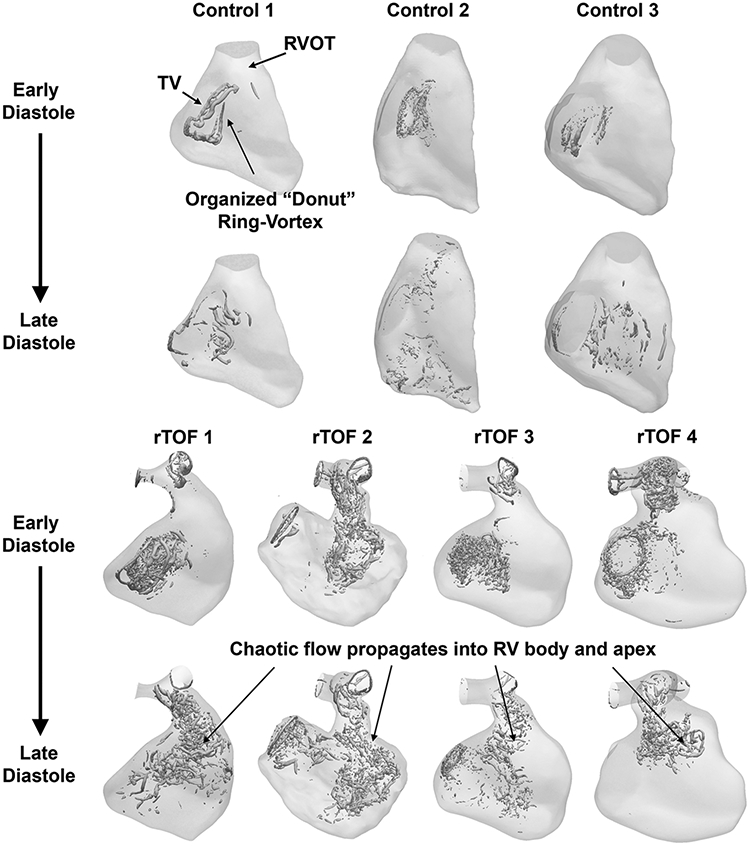
Vortical isosurfaces were created with Q Criterion > 5000. In rTOF patients, there is chaotic flow that propagates into RV body and apex.
Cine validation of RV motion reconstruction
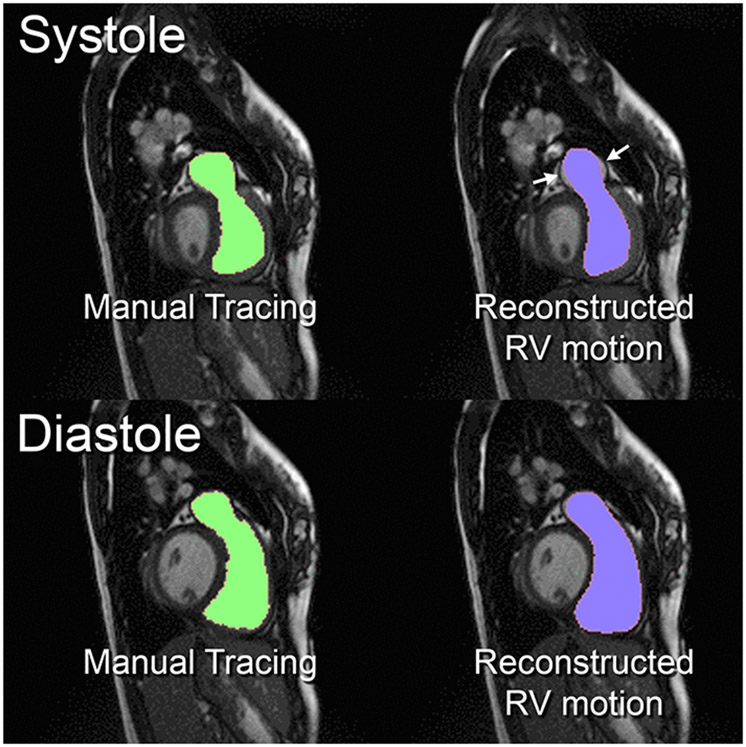
The mean Dice coefficient was calculated to be 0.887±0.0197, demonstrating good agreement between manual tracings and reconstructed RV motion. The main source of discrepancy was noted in the distal pulmonary arteries, a result of pulmonary artery pulsations that were not fully captured by cine imaging (Figure 4, Supplementary Video 3).
Figure 4. Comparison of endocardial border between manual tracings and reconstructed right ventricular (RV) motion.
The end-systolic and end-diastolic frames for case rTOF 3 were shown as an example. Good agreement noted through systole (top pictures) and diastole (bottom pictures). The main discrepancies were noted in the distal pulmonary artery during systole (white arrows).
Comparison between Intracardiac Flow Simulation and 4D Flow
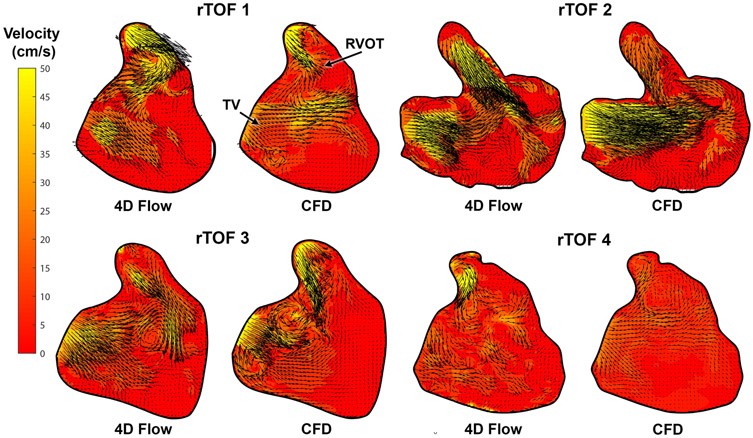
The comparison of diastolic KE profiles between 4D flow and CFD are shown in Figure 5 and Figure 6. The difference between CFD and 4D flow by Bland-Altman analysis (Figure 6) was −0.899 *10−2 mJ/mL (95% limits of agreement: −1.351 *10−2 mJ/mL to 1.171*10−2 mJ/mL). Comparisons between CFD and 4D flow phase-averaged velocity fields at late diastolic filling are shown in Figure 7. In the CFD simulations at this phase of the cardiac cycle, the RV was characterized by a complex flow pattern resulting from the interaction between the tricuspid diastolic vortex and the jet of PI. Overall, the chaotic flow formation from this interaction is also displayed by 4D flow. The main source of discrepancy appeared to be magnitude and direction of flow acceleration across tricuspid valve annulus and pulmonary valve annulus, where interaction with tissue (particularly residual pulmonary valve tissue) were not incorporated into the CFD model.
Figure 5. Comparison of diastolic kinetic energy (KE) between 4D flow and Computational Fluid Dynamic simulation (CFD) of repaired Tetralogy of Fallot (rTOF) patients.
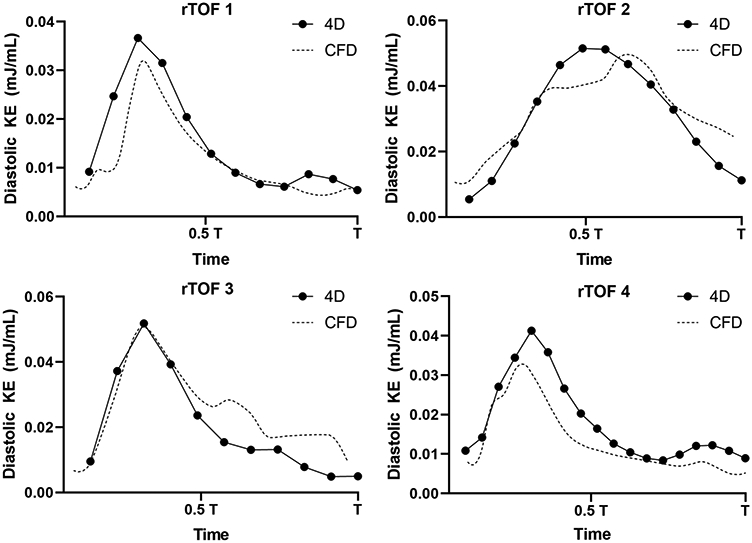
Four rTOF patients had 4D flow measurements for comparison against CFD results. Flow curves were adjusted to the same time scale T. The diastolic KE as measured by CFD (dotted line) overall strongly correlated with 4D flow measurements (r = 0.854, p < 0.0001).
Figure 6. Bland-Altman analysis of diastolic kinetic energy (KE) measurement profile between 4D flow and Computational Fluid Dynamic simulation (CFD) of repaired Tetralogy of Fallot (rTOF) patients.
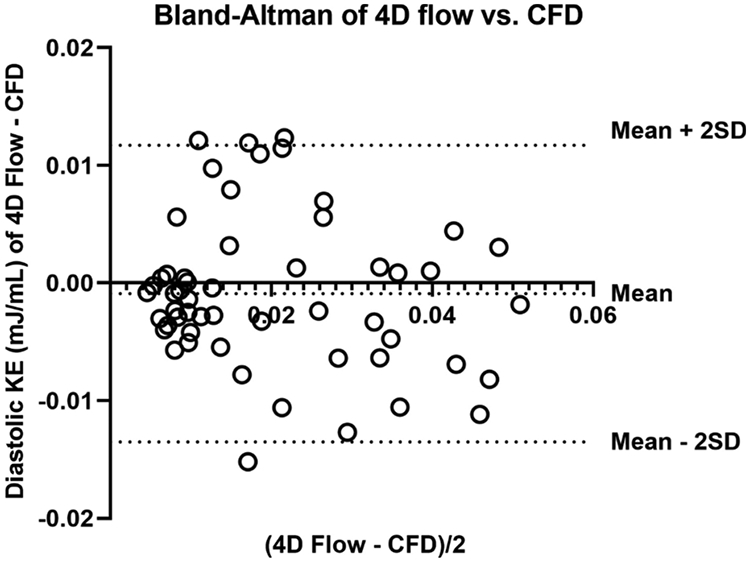
The mean difference between 4D flow and CFD was −0.0008987 mJ/mL (95% limits of agreement: −0.01351 mJ/mL to 0.01171 mJ/mL).
Figure 7. Comparison of diastolic intracardiac flow profile between 4D flow and Computational Fluid Dynamic simulation (CFD) of repaired Tetralogy of Fallot (rTOF) patients.
Overall, the chaotic flow pattern predicted by CFD is also noted by 4D flow, with notable discrepancies in flow magnitude and direction at the native pulmonary valve annulus.
Discussion
This is the first study to exclusively use clinical cMRI data and create direct numerical simulations of RV intracardiac flow in rTOF patients. The main findings of this pilot study include: (1) feasibility of methodology in normal control and rTOF patients, (2) validation of RV motion reconstruction from cMRI images for boundary conditions and (3) alterations to diastolic intracardiac flow of the rTOF patients when compared to normal controls.
Conventional cMRI volumetric measurements provide critical information to inform the timing of PVR. However, we conjecture that there are patient-specific, clinically relevant RV abnormalities not captured by volumetric measurements. Comprehensive visualization of patient-specific intracardiac flow must be taken into consideration to demonstrate this complex interplay between RV shape, RV motion and PI. Statistical shape modeling studies have demonstrated morphological changes beyond “simple” measurements of RVEDVi and RVESVi [11, 12]. Leonardi et al and Mansi et al developed a shape analysis framework that correlated end-diastolic RV shape with PI and RV dilation [11, 34]. Akinesis of the RVOT free wall, a result of the transannular patch, also varies with surgical technique and peri-operative conditions [35]. The efficiency of the RV is decreased in rTOF patients [2, 36]; Shibata et al demonstrated that diastolic flow energy losses correlated with cardiac enlargement and RV deterioration [36]. Potential mechanical sources of energy loss include volume overload from PI, viscous dissipation from turbulent flows, and impaired diastolic filling.
The comparison of diastolic intracardiac flow topology between control and rTOF patients in our small exploratory series is striking, as demonstrated in Figure 3. In control cases, the “donut” of diastolic vortex from tricuspid inflow is consistent with earlier computational studies of RV intracardiac flow (derived from 3D echocardiography) [37-39] and in-vivo observations of 4D flow [40]. Early work by Dr. Pasipoularides demonstrated the role of the diastolic vortex in reducing the “convective deceleration load” from tricuspid inflow and improve ventricular filling [38]. The direct propagation of the RV vortex into the RVOT also facilitates the helical twist observed in systole [41], that in turn may prevent flow separation at the branch pulmonary arteries [42]. In rTOF simulations, the native diastolic vortex has reduced significance in the dilated RV, another observation seen in Pasipoularides’ work [37].
More importantly, the diastolic vortex is significantly disrupted by collision with PI and results in less coherent vortical structures in the RV. This phenomenon of “kinematic obstruction” is also observed with in-vitro planar time-resolved particle image velocimetry of aortic regurgitation in the left ventricle [43], and more recently in an RV double activation simulator mimicking PR in rTOF patients [44]. PI blocks the formation of a coherent “donut” ring-vortex from tricuspid inflow into the RV and leads to viscous energy dissipation. When PI is severe, it generates the dominant vortical flow in the RV [44] and in turn propagates disturbed flow into RV apex, altering the mechanotransductive environment and likely contributing to RV shape adaptations [45, 46]. The source of TKE and vorticity in rTOF is likely from this flow propagation, in combination with the higher Reynolds number across both the tricuspid inflow and PI jet observed in this study. The degree of flow disturbance is affected by multiple factors, including timing of the PI jet, its relative direction, position and magnitude to the diastolic vortex, as well as boundary layer changes from RV motion. Of note, the tricuspid vortex also demonstrates physiologic variation in both structure and magnitude, as demonstrated by Figure 3 and the quantitative results of TKE and vorticity (particularly Control 2, likely a result of the higher Reynolds number from tricuspid inflow). Thus, it will be important to consider the regional contributions of the tricuspid inflow vs. RVOT towards TKE and vorticity, beyond measuring these intracardiac flow globally.
cMRI remains the best imaging modality to provide boundary conditions for RV simulation in rTOF. cMRI allows for visualization and quantification of regional wall motion via feature tracking [47-49]. With improved techniques in feature tracking and segmentation, there are now semi-automated/fully automated methods to model RV kinematics directly from image data [50-52]. In rTOF patients, there are alterations to longitudinal and circumferential wall motion in rTOF patients [48, 49]. The normal RV wall motion is usually derived from longitudinal contraction, recognized by tricuspid annular plane systolic excursion or longitudinal strain [53]. However for rTOF patients, the post-operative RVOT patch modification and chronic physiology of PI leads to RVOT akinesia, adaptive changes to increased volume load, and electro-mechanical dyssychrony from right bundle branch block [49], all of which affect the circumferential motion of the RV. Thus, both long-axis and short-axis views are needed to represent RV motion in rTOF patients. 3D modeling by cMRI can also demonstrate adaptive remodeling in different regions of the RV. In rTOF patients, the RV has regional enlargement of the apex and RVOT, and a reduction in curvature along the ventricular septum [12]. The RVOT also has heterogenous shape features [54] which influence flow characteristics of PI. Thus, patient-specific CFD simulations need cMRI data in order to incorporate complex RV shapes and RV motion, particularly the longitudinal contraction of the RV.
Our study coupled cMRI data with an IBM-solver, a logical next step in studying RV intracardiac flow patterns. The use of computational solvers to study intracardiac flow is well documented [55], initially focusing on two-dimensional flow patterns across heart valves [56]. Solvers have now advanced to incorporate full 3D models with increasingly realistic interactions between blood and wall motion over time [57-59]. The IBM method has been widely employed for the simulation of left ventricular flow dynamics in conjunction with cMRI or computed tomography [60]. For the RV, IBM solvers have been previously coupled with 3D echocardiography [39]. In this work we employ a robust IBM technique that ensures smoothness of the flow fields while maintaining good overall accuracy. This method is compatible with cMRI, ensuring boundary conditions from data with diagnostic-quality spatial/temporal resolution and high reproducibility [61]. The resulting computational framework is remarkably flexible and suitable for potential incorporation into clinical workflow. The unique combination with diffeomorphic mapping software also informed the longitudinal movement of the tricuspid inflow, which likely has a role in diastolic vortex formation. By relying only on cine and 2D-PC, the methodology allows for larger retrospective studies of rTOF cohorts (including studies where 4D flow is not available) to identify clinically relevant ranges of intracardiac vorticity and TKE, similar to Haggerty et al when they performed computational modeling of 100 patient-specific Fontan patients derived from conventional cMRI imaging [62]. To predict the effect of PVR, we envision a process that will: (1) incorporate a pulmonary valve with fully resolved opening/closing motion, (2) anticipate the resulting change in RV wall motion [63, 64] and (3) repeat numerical simulation to estimate the alterations in flow.
Tang et al has previously developed a computational method relying on cMRI and cardiac catheterization data to estimate functional changes after surgical PVR and plication of the RVOT, based on RV elasticity [18, 19]. Our approach differs significantly from this methodology in several aspects: (1) the exclusive use of non-invasive clinical data, whereas Tang et al’s method also relies on pressure recordings from invasive cardiac catheterization; (2) incorporating patient-specific longitudinal and circumferential motion in one continuous model, whereas Tang et al’s method uses a “shrink” estimation process to define RV shape in systole and diastole as separate phases; and (3) specific focus on intracardiac flow, whereas Tang et al’s method aims to simulate stress, strain and Young’s modulus of the RV myocardium.
The alterations in vorticity and TKE in rTOF patients are consistent with in-vivo 4D flow studies. Hirtler et al and Frediksson et al have prospectively demonstrated flow abnormalities in rTOF patients with 4D flow [13, 15]. Hirtler et al demonstrated significant differences in vorticity between rTOF patients and normal controls. Significant correlations were also found between vorticity, PI and RVEDVi [13]. Frediksson demonstrated that rTOF patients with worse PI had higher TKE values when compared to normal controls. Furthermore, peak total RV TKE was significantly correlated with RVEDVi [15]. These studies demonstrate the relationship between flow abnormalities, energy loss and functional impairment in rTOF patients, as well as the potential for using intracardiac flow biomarkers that are more sensitive than volumetry. Our CFD framework now provides a path to develop a fundamental understanding of the interactions between PI and RV motion. This research will guide the development of metrics derived from 4D flow measurements, and potentially develop a prediction model to study the effect of PVR on abnormal vorticity and TKE.
Study Limitations and Future Work
This pilot study is limited by the small number of rTOF and control cases used for simulation, thus no statistical analysis was performed to compare the two groups; further studies are needed before the qualitative observations of intracardiac flow are generalizable for rTOF patients. Another major limitation includes the significant differences in spatial and temporal resolution between acquired cMRI data (used to create the boundary conditions) and CFD, which impacts the comparison between the two methodologies. Some notable discrepancies were observed between CFD and 4D flow. Potential sources for discrepancy include the lack of residual pulmonary valve tissue during diastole, which likely created the localized regions of flow acceleration in the 4D flow datasets. The addition of residual pulmonary valve tissue will be essential in determining the magnitude and direction of PI flow back into the RV. Additionally, the 3D end-diastolic model of the RV, which was smoothed to facilitate diffeomorphic mapping. The segmentation/smoothing process removes RV trabeculations and papillary muscles, and the loss of endocardial detail may influence vortex mechanics in the CFD simulation [65]. The current methodology also assumed fully open/closed states across the tricuspid valve thus would not account for tricuspid regurgitation. The right atrium was also not incorporated as conventional cMRI imaging of rTOF do not focus on its features. Furthermore, direct clinical measurement of tricuspid inflow (a critical boundary condition) by 2D-PC was not feasible and instead derived from mass conservation. The sensitivity of these features to intracardiac flow results require further study, however these limitations will likely improve with advances in cMRI techniques that allow for dynamic whole-heart 3D imaging [66] and accurate valve-tracking flow measurements by 4D flow [67].
Future work includes incorporation of tricuspid valve/residual pulmonary valve tissue into CFD simulation to add potential effects of pulmonary stenosis or tricuspid regurgitation. We plan to investigate the regional contributions of PI in the RVOT towards TKE and vorticity, by varying the boundary conditions in the same model similarly to other in-vitro studies [43, 44], or by comparing TKE and vorticity to other forms of volume-overloaded RVs from atrial-level shunts. We plan to simulate of a broad cohort of rTOF patients to correlate intracardiac flow parameters with RV morphology and clinical outcomes, identifying key physiologic flow features that relate to clinical RV dysfunction and exercise intolerance [9]. Our long-term goal is to develop a CFD-based method that can remove the intracardiac and morphological effect of PI to determine the benefit of PVR. This would likely include predicting the alterations to RV shape using statistical shape modeling [11, 34] and RV kinematics by coupling strain with fluid-structure-electrophysiology interactions [59, 63, 64].
Conclusion
Our study is the first to use exclusively use conventional cMRI images to simulate RV intracardiac flow in rTOF patients. With this CFD method, highly resolved intracardiac flow can be recreated and directly quantified. This computational framework has the potential to predict intracardiac changes after PVR, improving its clinical indications guided by cMRI.
Supplementary Material
Sources of Funding
This publication was supported by Award Number UL1TR001876 from the NIH National Center for Advancing Translational Sciences. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Center for Advancing Translational Sciences or the National Institutes of Health. This work was also supported by institutional funding through Children’s National Hospital (Board of Visitors grant) to pay for licensing of segmentation software (Mimics, Materialise). Dr. Francesco Capuano was supported by Università degli Studi di Napoli “Federico II”.
Disclosures
Dr. Yue-Hin Loke receives partial salary support from NIH R01 HL143468-01 and R21 HL156045. Dr. Francesco Capuano also received support from NIH UL1TR001876.
Footnotes
Human subjects/informed consent statement
All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1975, as revised in 2000. Informed consent was obtained from all patients for being included in the study
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
References
- 1.Nies M, & Brenner JI (2013). Tetralogy of Fallot: epidemiology meets real-world management: lessons from the Baltimore-Washington Infant Study. Cardiology in the Young, 23(6), 867–870. 10.1017/S1047951113001698 [DOI] [PubMed] [Google Scholar]
- 2.Fogel MA, Sundareswaran KS, de Zelicourt D, Dasi LP, Pawlowski T, Rome J, & Yoganathan AP (2012). Power loss and right ventricular efficiency in patients after tetralogy of Fallot repair with pulmonary insufficiency: Clinical implications. The Journal of Thoracic and Cardiovascular Surgery, 143(6), 1279–1285. 10.1016/j.jtcvs.2011.10.066 [DOI] [PubMed] [Google Scholar]
- 3.Bhatt AB, Foster E, Kuehl K, Alpert J, Brabeck S, Crumb S, … American Heart Association Council on Clinical Cardiology. (2015). Congenital heart disease in the older adult: a scientific statement from the American Heart Association. Circulation, 131(21), 1884–1931. 10.1161/CIR.0000000000000204 [DOI] [PubMed] [Google Scholar]
- 4.Egbe AC, Vallabhajosyula S, & Connolly HM (2019). Trends and outcomes of pulmonary valve replacement in tetralogy of Fallot. International Journal of Cardiology. 10.1016/j.ijcard.2019.07.063 [DOI] [PubMed] [Google Scholar]
- 5.Stout KK, Daniels CJ, Aboulhosn JA, Bozkurt B, Broberg CS, Colman JM, … Van Hare GF (2019). 2018 AHA/ACC Guideline for the Management of Adults With Congenital Heart Disease: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation, 139(14). 10.1161/CIR.0000000000000603 [DOI] [PubMed] [Google Scholar]
- 6.Geva T (2013). Indications for Pulmonary Valve Replacement in Repaired Tetralogy of Fallot: The Quest Continues. Circulation, 128(17), 1855–1857. 10.1161/CIRCULATIONAHA.113.005878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.O’Byrne ML, Glatz AC, Mercer-Rosa L, Gillespie MJ, Dori Y, Goldmuntz E, … Rome JJ (2015). Trends in pulmonary valve replacement in children and adults with tetralogy of fallot. The American Journal of Cardiology, 115(1), 118–124. 10.1016/j.amjcard.2014.09.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Therrien J, Siu SC, McLaughlin PR, Liu PP, Williams WG, & Webb GD (2000). Pulmonary valve replacement in adults late after repair of tetralogy of fallot: are we operating too late? Journal of the American College of Cardiology, 36(5), 1670–1675. [DOI] [PubMed] [Google Scholar]
- 9.Van den Eynde J, Sà MPBO, Vervoort D, Roever L, Meyns B, Budts W, … Weymann A (2020). Pulmonary Valve Replacement in Tetralogy of Fallot: An Updated Meta-Analysis. The Annals of Thoracic Surgery, S0003497520321731. 10.1016/j.athoracsur.2020.11.040 [DOI] [PubMed] [Google Scholar]
- 10.Bhagra CJ, Hickey EJ, Van De Bruaene A, Roche SL, Horlick EM, & Wald RM (2017). Pulmonary Valve Procedures Late After Repair of Tetralogy of Fallot: Current Perspectives and Contemporary Approaches to Management. Canadian Journal of Cardiology, 33(9), 1138–1149. 10.1016/j.cjca.2017.06.011 [DOI] [PubMed] [Google Scholar]
- 11.Leonardi B, Taylor AM, Mansi T, Voigt I, Sermesant M, Pennec X, … Pongiglione G (2013). Computational modelling of the right ventricle in repaired tetralogy of Fallot: can it provide insight into patient treatment? European Heart Journal - Cardiovascular Imaging, 14(4), 381–386. 10.1093/ehjci/jes239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zaidi SJ, Cossor W, Singh A, Maffesanti F, Kawaji K, Woo J, … Patel AR (2018). Three-dimensional analysis of regional right ventricular shape and function in repaired tetralogy of Fallot using cardiovascular magnetic resonance. Clinical Imaging, 52, 106–112. 10.1016/j.clinimag.2018.07.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hirtler D, Garcia J, Barker AJ, & Geiger J (2016). Assessment of intracardiac flow and vorticity in the right heart of patients after repair of tetralogy of Fallot by flow-sensitive 4D MRI. European Radiology, 26(10), 3598–3607. 10.1007/s00330-015-4186-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Francois CJ, Srinivasan S, Schiebler ML, Reeder SB, Niespodzany E, Landgraf BR, … Frydrychowicz A (2012). 4D cardiovascular magnetic resonance velocity mapping of alterations of right heart flow patterns and main pulmonary artery hemodynamics in tetralogy of Fallot. Journal of Cardiovascular Magnetic Resonance, 14(1), 16. 10.1186/1532-429X-14-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fredriksson A, Trzebiatowska-Krzynska A, Dyverfeldt P, Engvall J, Ebbers T, & Carlhäll C-J (2018). Turbulent kinetic energy in the right ventricle: Potential MR marker for risk stratification of adults with repaired Tetralogy of Fallot. Journal of magnetic resonance imaging: JMRI, 47(4), 1043–1053. 10.1002/jmri.25830 [DOI] [PubMed] [Google Scholar]
- 16.Itatani K, Miyazaki S, Furusawa T, Numata S, Yamazaki S, Morimoto K, … Yaku H (2017). New imaging tools in cardiovascular medicine: computational fluid dynamics and 4D flow MRI. General Thoracic and Cardiovascular Surgery, 65(11), 611–621. 10.1007/s11748-017-0834-5 [DOI] [PubMed] [Google Scholar]
- 17.Biglino G, Capelli C, Bruse J, Bosi GM, Taylor AM, & Schievano S (2017). Computational modelling for congenital heart disease: how far are we from clinical translation? Heart, 103(2), 98–103. 10.1136/heartjnl-2016-310423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tang D, del Nido PJ, Yang C, Zuo H, Huang X, Rathod RH, … Geva T (2016). Patient-Specific MRI-Based Right Ventricle Models Using Different Zero-Load Diastole and Systole Geometries for Better Cardiac Stress and Strain Calculations and Pulmonary Valve Replacement Surgical Outcome Predictions. PLOS ONE, 11(9), e0162986. 10.1371/journal.pone.0162986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yu H, del Nido PJ, Geva T, Yang C, Tang A, Wu Z, … Tang D (2019). Patient-specific in vivo right ventricle material parameter estimation for patients with tetralogy of Fallot using MRI-based models with different zero-load diastole and systole morphologies. International Journal of Cardiology, 276, 93–99. 10.1016/j.ijcard.2018.09.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ou-Yang W-B, Qureshi S, Ge J-B, Hu S-S, Li S-J, Yang K-M, … Pan X-B (2020). Multicenter Comparison of Percutaneous and Surgical Pulmonary Valve Replacement in Large RVOT. The Annals of Thoracic Surgery, 110(3), 980–987. 10.1016/j.athoracsur.2020.01.009 [DOI] [PubMed] [Google Scholar]
- 21.Phillips ABM, Nevin P, Shah A, Olshove V, Garg R, & Zahn EM (2016). Development of a novel hybrid strategy for transcatheter pulmonary valve placement in patients following transannular patch repair of tetralogy of fallot: Hybrid Pulmonary Valve Implantation. Catheterization and Cardiovascular Interventions, 87(3), 403–410. 10.1002/ccd.26315 [DOI] [PubMed] [Google Scholar]
- 22.Posa A, Vanella M, & Balaras E (2017). An adaptive reconstruction for Lagrangian, direct-forcing, immersed-boundary methods. Journal of Computational Physics, 351, 422–436. 10.1016/j.jcp.2017.09.047 [DOI] [Google Scholar]
- 23.Loke Y-H, Krieger A, Sable C, & Olivieri L (2016). Novel Uses for Three-Dimensional Printing in Congenital Heart Disease. Current Pediatrics Reports, 4(2), 28–34. 10.1007/s40124-016-0099-y [DOI] [Google Scholar]
- 24.Loke Y-H, Harahsheh AS, Krieger A, & Olivieri LJ (2017). Usage of 3D models of tetralogy of Fallot for medical education: impact on learning congenital heart disease. BMC Medical Education, 17(1). 10.1186/s12909-017-0889-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Biffi B, Bruse JL, Zuluaga MA, Ntsinjana HN, Taylor AM, & Schievano S (2017). Investigating Cardiac Motion Patterns Using Synthetic High-Resolution 3D Cardiovascular Magnetic Resonance Images and Statistical Shape Analysis. Frontiers in Pediatrics, 5. 10.3389/fped.2017.00034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Durrleman S, Prastawa M, Charon N, Korenberg JR, Joshi S, Gerig G, & Trouvé A (2014). Morphometry of anatomical shape complexes with dense deformations and sparse parameters. NeuroImage, 101, 35–49. 10.1016/j.neuroimage.2014.06.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Berger SA, & Jou L-D (2000). Flows in Stenotic Vessels. Annual Review of Fluid Mechanics, 32(1), 347–382. 10.1146/annurev.fluid.32.1.347 [DOI] [Google Scholar]
- 28.Vanella M, & Balaras E (2009). A moving-least-squares reconstruction for embedded-boundary formulations. Journal of Computational Physics, 228(18), 6617–6628. 10.1016/j.jcp.2009.06.003 [DOI] [Google Scholar]
- 29.Kim J, Kim D, & Choi H (2001). An Immersed-Boundary Finite-Volume Method for Simulations of Flow in Complex Geometries. Journal of Computational Physics, 171(1), 132–150. 10.1006/jcph.2001.6778 [DOI] [Google Scholar]
- 30.Hunt JC, Wray AA, & Moin P (1988). Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research. [Google Scholar]
- 31.Zou KH, Warfield SK, Bharatha A, Tempany CMC, Kaus MR, Haker SJ, … Kikinis R (2004). Statistical validation of image segmentation quality based on a spatial overlap index. Academic Radiology, 11(2), 178–189. 10.1016/s1076-6332(03)00671-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ayachit U (2015). The ParaView guide: updated for ParaView version 4.3. (Avila L, Ed.) (Full color version.). Los Alamos: Kitware. [Google Scholar]
- 33.Zijdenbos AP, Dawant BM, Margolin RA, & Palmer AC (1994). Morphometric analysis of white matter lesions in MR images: method and validation. IEEE transactions on medical imaging, 13(4), 716–724. 10.1109/42.363096 [DOI] [PubMed] [Google Scholar]
- 34.Mansi T, Voigt I, Leonardi B, Pennec X, Durrleman S, Sermesant M, … Ayache N (2011). A statistical model for quantification and prediction of cardiac remodelling: application to tetralogy of Fallot. IEEE transactions on medical imaging, 30(9), 1605–1616. 10.1109/TMI.2011.2135375 [DOI] [PubMed] [Google Scholar]
- 35.Heng EL, Gatzoulis MA, Uebing A, Sethia B, Uemura H, Smith GC, … Babu-Narayan SV (2017). Immediate and Midterm Cardiac Remodeling After Surgical Pulmonary Valve Replacement in Adults With Repaired Tetralogy of Fallot: A Prospective Cardiovascular Magnetic Resonance and Clinical Study. Circulation, 136(18), 1703–1713. 10.1161/CIRCULATIONAHA.117.027402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shibata M, Itatani K, Hayashi T, Honda T, Kitagawa A, Miyaji K, & Ono M (2018). Flow Energy Loss as a Predictive Parameter for Right Ventricular Deterioration Caused by Pulmonary Regurgitation After Tetralogy of Fallot Repair. Pediatric Cardiology. 10.1007/s00246-018-1813-z [DOI] [PubMed] [Google Scholar]
- 37.Pasipoularides A, Shu M, Shah A, Womack MS, & Glower DD (2003). Diastolic right ventricular filling vortex in normal and volume overload states. American Journal of Physiology-Heart and Circulatory Physiology, 284(4), H1064–H1072. 10.1152/ajpheart.00804.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pasipoularides A (2013). Evaluation of Right and Left Ventricular Diastolic Filling. Journal of Cardiovascular Translational Research, 6(4), 623–639. 10.1007/s12265-013-9461-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mangual JO, Domenichini F, & Pedrizzetti G (2012). Describing the Highly Three Dimensional Right Ventricle Flow. Annals of Biomedical Engineering, 40(8), 1790–1801. 10.1007/s10439-012-0540-5 [DOI] [PubMed] [Google Scholar]
- 40.Fredriksson AG, Zajac J, Eriksson J, Dyverfeldt P, Bolger AF, Ebbers T, & Carlhäll C-J (2011). 4-D blood flow in the human right ventricle. American Journal of Physiology-Heart and Circulatory Physiology, 301(6), H2344–H2350. 10.1152/ajpheart.00622.2011 [DOI] [PubMed] [Google Scholar]
- 41.Mangual JO, Domenichini F, & Pedrizzetti G (2012). Three dimensional numerical assessment of the right ventricular flow using 4D echocardiography boundary data. European Journal of Mechanics - B/Fluids, 35, 25–30. 10.1016/j.euromechflu.2012.01.022 [DOI] [Google Scholar]
- 42.Capuano F, Loke Y-H, & Balaras E (2019). Blood Flow Dynamics at the Pulmonary Artery Bifurcation. Fluids, 4(4), 190. 10.3390/fluids4040190 [DOI] [Google Scholar]
- 43.Okafor I, Raghav V, Condado JF, Midha PA, Kumar G, & Yoganathan AP (2017). Aortic Regurgitation Generates a Kinematic Obstruction Which Hinders Left Ventricular Filling. Annals of Biomedical Engineering, 45(5), 1305–1314. 10.1007/s10439-017-1790-z [DOI] [PubMed] [Google Scholar]
- 44.Mikhail A, Labbio GD, Darwish A, & Kadem L (2020). How pulmonary valve regurgitation after tetralogy of fallot repair changes the flow dynamics in the right ventricle: An in vitro study. Medical Engineering & Physics, 83, 48–55. 10.1016/j.medengphy.2020.07.014 [DOI] [PubMed] [Google Scholar]
- 45.Pasipoularides A (2015). Mechanotransduction Mechanisms for Intraventricular Diastolic Vortex Forces and Myocardial Deformations: Part 1. Journal of Cardiovascular Translational Research, 8(1), 76–87. 10.1007/s12265-015-9611-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pasipoularides A (2015). Mechanotransduction Mechanisms for Intraventricular Diastolic Vortex Forces and Myocardial Deformations: Part 2. Journal of Cardiovascular Translational Research, 8(5), 293–318. 10.1007/s12265-015-9630-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu B, Dardeer AM, Moody WE, Edwards NC, Hudsmith LE, & Steeds RP (2018). Normal values for myocardial deformation within the right heart measured by feature-tracking cardiovascular magnetic resonance imaging. International Journal of Cardiology, 252, 220–223. 10.1016/j.ijcard.2017.10.106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Berganza FM, de Alba CG, Özcelik N, & Adebo D (2017). Cardiac Magnetic Resonance Feature Tracking Biventricular Two-Dimensional and Three-Dimensional Strains to Evaluate Ventricular Function in Children After Repaired Tetralogy of Fallot as Compared with Healthy Children. Pediatric Cardiology, 38(3), 566–574. 10.1007/s00246-016-1549-6 [DOI] [PubMed] [Google Scholar]
- 49.Kalaitzidis P, Orwat S, Kempny A, Robert R, Peters B, Sarikouch S, … Diller G-P (2018). Biventricular dyssynchrony on cardiac magnetic resonance imaging and its correlation with myocardial deformation, ventricular function and objective exercise capacity in patients with repaired tetralogy of Fallot. International Journal of Cardiology, 264, 53–57. 10.1016/j.ijcard.2018.04.005 [DOI] [PubMed] [Google Scholar]
- 50.Ringenberg J, Deo M, Devabhaktuni V, Berenfeld O, Boyers P, & Gold J (2014). Fast, accurate, and fully automatic segmentation of the right ventricle in short-axis cardiac MRI. Computerized Medical Imaging and Graphics, 38(3), 190–201. 10.1016/j.compmedimag.2013.12.011 [DOI] [PubMed] [Google Scholar]
- 51.Yilmaz P, Wallecan K, Kristanto W, Aben J-P, & Moelker A (2018). Evaluation of a Semi-automatic Right Ventricle Segmentation Method on Short-Axis MR Images. Journal of Digital Imaging, 31(5), 670–679. 10.1007/s10278-018-0061-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Yang F, Zhang Y, Lei P, Wang L, Miao Y, Xie H, & Zeng Z (2019). A Deep Learning Segmentation Approach in Free-Breathing Real-Time Cardiac Magnetic Resonance Imaging. BioMed Research International, 2019, 5636423. 10.1155/2019/5636423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Dutta T, & Aronow WS (2017). Echocardiographic evaluation of the right ventricle: Clinical implications. Clinical Cardiology, 40(8), 542–548. 10.1002/clc.22694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Schievano S, Coats L, Migliavacca F, Norman W, Frigiola A, Deanfield J, … Taylor AM (2007). Variations in right ventricular outflow tract morphology following repair of congenital heart disease: implications for percutaneous pulmonary valve implantation. Journal of Cardiovascular Magnetic Resonance: Official Journal of the Society for Cardiovascular Magnetic Resonance, 9(4), 687–695. 10.1080/10976640601187596 [DOI] [PubMed] [Google Scholar]
- 55.Peskin CS (1977). Numerical analysis of blood flow in the heart. Journal of Computational Physics, 25(3), 220–252. 10.1016/0021-9991(77)90100-0 [DOI] [Google Scholar]
- 56.Dumont K, Stijnen JMA, Vierendeels J, van de Vosse FN, & Verdonck PR (2004). Validation of a fluid-structure interaction model of a heart valve using the dynamic mesh method in fluent. Computer Methods in Biomechanics and Biomedical Engineering, 7(3), 139–146. 10.1080/10255840410001715222 [DOI] [PubMed] [Google Scholar]
- 57.Vedula V, George R, Younes L, & Mittal R (2015). Hemodynamics in the Left Atrium and Its Effect on Ventricular Flow Patterns. Journal of Biomechanical Engineering, 137(11), 111003. 10.1115/1.4031487 [DOI] [PubMed] [Google Scholar]
- 58.Hasan A, Kolahdouz EM, Enquobahrie A, Caranasos TG, Vavalle JP, & Griffith BE (2017). Image-based immersed boundary model of the aortic root. Medical Engineering & Physics, 47, 72–84. 10.1016/j.medengphy.2017.05.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Viola F, Meschini V, & Verzicco R (2020). Fluid–Structure-Electrophysiology interaction (FSEI) in the left-heart: A multi-way coupled computational model. European Journal of Mechanics - B/Fluids, 79, 212–232. 10.1016/j.euromechflu.2019.09.006 [DOI] [Google Scholar]
- 60.Mittal R, Seo JH, Vedula V, Choi YJ, Liu H, Huang HH, … George RT (2016). Computational modeling of cardiac hemodynamics: Current status and future outlook. Journal of Computational Physics, 305, 1065–1082. 10.1016/j.jcp.2015.11.022 [DOI] [Google Scholar]
- 61.Mooij CF, de Wit CJ, Graham DA, Powell AJ, & Geva T (2008). Reproducibility of MRI measurements of right ventricular size and function in patients with normal and dilated ventricles. Journal of Magnetic Resonance Imaging, 28(1), 67–73. 10.1002/jmri.21407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Haggerty CM, Restrepo M, Tang E, de Zélicourt DA, Sundareswaran KS, Mirabella L, … Yoganathan AP (2014). Fontan hemodynamics from 100 patient-specific cardiac magnetic resonance studies: A computational fluid dynamics analysis. The Journal of Thoracic and Cardiovascular Surgery, 148(4), 1481–1489. 10.1016/j.jtcvs.2013.11.060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Harrild DM, Marcus E, Hasan B, Alexander ME, Powell AJ, Geva T, & McElhinney DB (2013). Impact of Transcatheter Pulmonary Valve Replacement on Biventricular Strain and Synchrony Assessed by Cardiac Magnetic Resonance Feature Tracking. Circulation: Cardiovascular Interventions, 6(6), 680–687. 10.1161/CIRCINTERVENTIONS.113.000690 [DOI] [PubMed] [Google Scholar]
- 64.Balasubramanian S, Harrild DM, Kerur B, Marcus E, del Nido P, Geva T, & Powell AJ (2018). Impact of surgical pulmonary valve replacement on ventricular strain and synchrony in patients with repaired tetralogy of Fallot: a cardiovascular magnetic resonance feature tracking study. Journal of Cardiovascular Magnetic Resonance, 20(1), 37. 10.1186/s12968-018-0460-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sacco F, Paun B, Lehmkuhl O, Iles TL, Iaizzo PA, Houzeaux G, … Aguado-Sierra J (2018). Evaluating the roles of detailed endocardial structures on right ventricular haemodynamics by means of CFD simulations. International Journal for Numerical Methods in Biomedical Engineering, 34(9), e3115. 10.1002/cnm.3115 [DOI] [PubMed] [Google Scholar]
- 66.Nguyen K-L, Han F, Zhou Z, Brunengraber DZ, Ayad I, Levi DS, … Finn JP (2017). 4D MUSIC CMR: value-based imaging of neonates and infants with congenital heart disease. Journal of Cardiovascular Magnetic Resonance, 19(1), 40. 10.1186/s12968-017-0352-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jacobs K, Rigdon J, Chan F, Cheng JY, Alley MT, Vasanawala S, & Maskatia SA (2020). Direct measurement of atrioventricular valve regurgitant jets using 4D flow cardiovascular magnetic resonance is accurate and reliable for children with congenital heart disease: a retrospective cohort study. Journal of Cardiovascular Magnetic Resonance, 22(1), 33. 10.1186/s12968-020-00612-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.