Computational Methods for Analyzing Dynamic Regulatory Networks

Abstract

Regulatory and other networks in the cell change in a highly dynamic way over time and in response to internal and external stimuli. While several different types of high-throughput experimental procedures are available to study systems in the cell, most only measure static properties of such networks. Information derived from sequence data is inherently static, and most interaction data sets are measured in a static way as well. In this chapter we discuss one of the few abundant sources for temporal information, time series expression data. We provide an overview of the methods suggested for clustering this type of data to identify functionally related genes. We also discuss methods for inferring causality and interactions using lagged correlations and regression analysis. Finally, we present methods for combining time series expression data with static data to reconstruct dynamic regulatory networks. We point to software tools implementing the methods discussed in this chapter. As more temporal measurements become available, the importance of analyzing such data and of combining it with other types of data will greatly increase.

1. Introduction

Biological systems are inherently dynamic in nature as they change in response to external and internal stimuli and over time (1–3). While several different types of high-throughput genomic data sets are being collected, most are static or measured in a static way. For example, DNA sequences are inherently static and do not change over years. Information derived from such data including DNA and miRNA binding motifs (4) is also static. Other types of data, including interaction data are often measured in a static way. For example, large-scale protein–DNA binding (5), protein–protein interactions (6, 7), and miRNA–mRNA (8) interactions are all performed as a snapshot experiment and do not provide information about changes over time.

To understand the dynamics of regulatory networks, researchers must be able to obtain and analyze temporal data sets regarding the activity of such systems. So far the most abundant data source for this task has been time series gene expression data (seeFig. 24.1). This chapter will focus on how we can extract information about the regulation of biological systems from this type of data and how it can be integrated with other (mostly static) data sets to reconstruct models for the activity of these networks in the cell. Other types of dynamic data, most notably imaging data, are also becoming available for some of these systems. However, since they are so far limited to a small number of biological systems and relatively little computational work has been performed to use these data sets, we would not discuss them in this chapter.

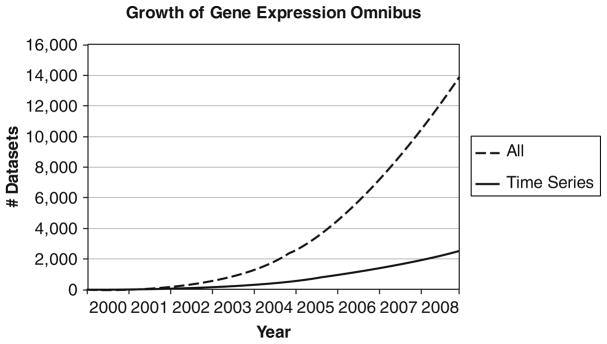
Fig. 24.1.

Growth in the number of expression data sets deposited in GEO over the last decade. The solid curve represents the data sets from time series experiments. Over 2,000 time series data sets were deposited in GEO by the end of 2008, representing almost 20% of all gene expression experiments. Methods that can adequately analyze these data sets and that can combine them with other high-throughput data sets are required so that we can fully utilize the information obtained in these experiments.

Figure 24.2 presents four analysis levels that are often performed when using high-throughput data sets to study biological systems. While these should be considered for all high-throughput experiments, different types of data raise different sets of questions that should be addressed at each level. For example, while gene expression experiments can be used to study either static (snapshot) or dynamic processes, there are a number of unique issues when using time series expression data. When designing time series experiments, one needs to decide how many time points to use and what the sampling rates should be. When analyzing such data one should decide how to represent it (a collection of points, some interpolated curve or a specific function). Similarly, while many clustering algorithms can be used for both static and time series data, these often do not make adequate use of the temporal information. Algorithms that are specifically designed for time series data may lead to better results for such data. In a previous review, we focused primarily on the lower two analysis levels: experimental design and data analysis (9). Here we focus on the upper two levels, clustering and systems biology. We discuss several new approaches for these tasks that have been developed since 2004. We also highlight the importance of data integration, specifically of time series and static data, which can lead to dynamic models while still relying on abundant static data.

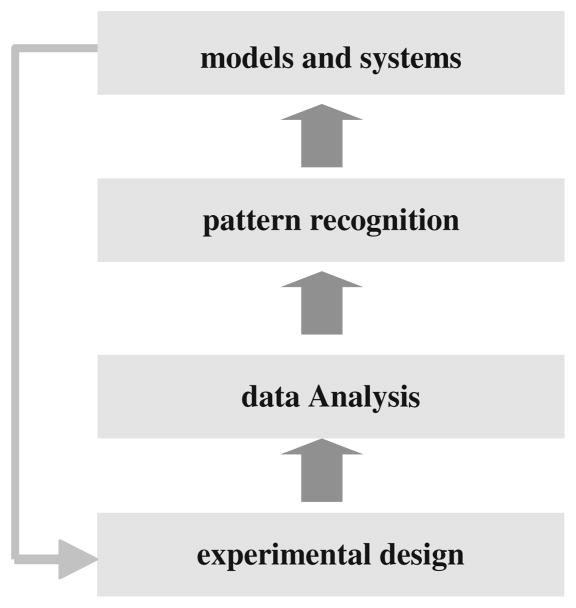
Fig. 24.2.

Analysis levels for high-throughput experiments. Studies using high-throughput data sets often address issues related to these four analysis levels. Here we discuss issues that relate to the analysis of time series data sets and dynamic regulatory networks focusing on the upper two levels (pattern recognition and modeling).

The Methods section of this chapter is organized into three parts. Section 3.1 discusses clustering methods for time series expression data. These methods are often used to obtain a first, global, view of the expression data. They are also used to infer groupings and large-scale organization and can provide functional information about unknown genes that are grouped with known genes. Section 3.2 discusses methods that try to infer interactions and causality from temporal data sets. These methods rely on the observation that in many cases genes that are active at early time points will activate genes at later time points. Such an analysis can provide information about regulatory interactions between genes. While the first two sections focus on inference that can be drawn from expression data alone, Section 3.3 describes methods that try to integrate additional data sets for this task. This helps to overcome the dimensionality problem that often exists in high-throughput experiments (relatively few samples and a large number of genes) by using additional data sources to constrain the set of parameters and their values. For each of these sections, we provide a list of software tools that implement some of the methods we discuss so that researchers may try these ideas on their own data. We conclude this chapter by discussing open problems and directions for future work.

2. Software

In this chapter we discuss several methods for analyzing dynamic regulatory networks. Some of these methods have been implemented and can be downloaded and used by researchers. Below we provide the links for these software packages. The links are arranged according to the sections that discuss the methods they implement.

2.1. Clustering

The Eisen lab provides implementation for several general purpose clustering algorithms, including hierarchical clustering, self-organizing maps, and K-means. The software (Cluster) can be downloaded from http://rana.lbl.gov/EisenSoftware.htm. The STEM software for clustering short time series expression data is available from http://www.cs.cmu.edu/~jernst/stem/.

2.2. Regression and Dynamic Bayesian Networks (DBNs)

Kevin Murphy wrote a popular Bayesian Networks toolbox for MATLAB, which also contains DBN procedures. It can be down-loaded from http://people.cs.ubc.ca/~murphyk/Software/BNT/bnt.html. A MATLAB implementation for aligning time series data sets studying the same system under different experimental conditions is available from http://www.sb.cs.cmu.edu/pages/software.html. An implementation of the method for combining experiments from different conditions can be found here: http://www.cs.cmu.edu/~yanxins/regulation_inference/Matlab.html.

2.3. Data-Integrated Methods

An R implementation of Inferelator, which combines time series and motif data, is available at http://err.bio.nyu.edu/inferelator. Perl scripts for the various components of the Statistical Analysis of Network Dynamics (SANDY) algorithm can be found under the “data download” section here: http://sandy.topnet.gersteinlab.org. The Network Component Analysis tool-box for MATLAB can be downloaded from http://www.seas.ucla.edu/~liaoj/download.htm. A MATLAB implementation of the post-transcriptional modification model, which combines sequence and expression data, can be downloaded at http://www.sb.cs.cmu.edu/PTMM/PTMM.html. The Dynamic Regulatory Events Miner (DREM) executable and Java source code can be obtained here: http://www.sb.cs.cmu.edu/drem.

3. Methods

3.1. Clustering Time Series Expression Data

In a gene expression time series experiment, one can observe the activity of thousands of genes over periods of time. To obtain a global view and facilitate further analysis, it is often useful to divide genes into smaller groups based on their temporal expression patterns. This can be done by cluster analysis, which assigns genes to subsets (clusters) such that genes in the same cluster exhibit similar expression patterns, while genes in distinct clusters do not. Cluster analysis has been used to discover co-regulated genes and genes sharing related functions (10).

There are a number of challenges when applying cluster analysis to gene expression time series. First, many general clustering methods do not take into account the order of time points. In contrast, methods specifically designed for time series may be better suited to the task. Second, most of the expression time series have relatively few (3–8) time points (11). As a result, methods that work well with long time series may tend to overfit when applied to such data sets. Third, because the number of genes observed is large, patterns may arise just by chance. One needs a way to distinguish between real patterns versus patterns arising by chance.

Several methods have been used to cluster time series data. However, general clustering algorithms do not take time into account. While we mention some of these here because of their popularity, our goal in this section is to focus on methods developed for clustering time series.

3.1.1. General Clustering Methods

The most popular methods for clustering expression data, which have also been used to cluster time series data, include hierarchical clustering, K-means, and projection-based methods. Hierarchical clustering groups genes either using a bottom-up (10) or a top-down (12) approach. In both cases, the resulting clusters are represented as a tree with leafs corresponding to genes and subtrees corresponding to clusters. K-means clustering (12) is an iterative algorithm that starts from k randomly selected clusters. In each iteration, genes are assigned to the cluster with the nearest mean, and the k means are updated by calculating the average expression profile within each cluster. Projection-based methods, including principal component analysis (13, 14) and independent component analysis (15, 16), work by first mapping the gene expression to a new space and then clustering genes there.

Unlike the general clustering methods described above, several recent algorithms were developed specifically for clustering time series expression data. These methods utilize the dynamic information to improve the clustering results and often are shown to outperform the general clustering methods.

3.1.2. Clustering Using Continuous Representation

Time series experiments only generate snapshots at certain time points of the gene expression levels, which may be more naturally modeled by a continuous curve. One way is to represent the gene expression level by splines, piecewise polynomials with bounded constraints. Bar-Joseph et al. (17) proposed to use B-splines for this purpose, and the resulting model has fewer basis coefficients than the number of time points, which helps to avoid overfitting. The clustering method assumes a mixture model where each mixture component corresponds to a cluster, and the expression of each gene is generated through a noisy process from the model expression curve. Bar-Joseph et al. (17) describe a method that simultaneously estimates the parameters for the continuous representation and the assignment of genes to clusters.

Closely related methods have been proposed to represent expression time series by piece-wise linear (18), quadratic (19), or higher-order interpolation (20). In Magni et al. (18) and Liu et al. (19), the learned models are transformed into symbolic representations, which are in turn used to cluster genes, while Wang et al. (20) cluster genes directly based on the learned polynomials.

3.1.3. Clustering Using Dynamic Features

In these methods, features reflecting temporal patterns are extracted from expression time series and used for clustering. Kim and Kim (21) use first- and second-order differences between adjacent time points as temporal features. Genes are clustered based on the pattern determined by the sequence of features. One limitation of the method is that it requires several replicate experiments and most time series expression data sets are measured with very few or no replicates. Déjean et al. (22) represent genes by smoothing splines, and use the derivatives at some discretization points as features. Genes are clustered by applying hierarchical clustering to the extracted derivatives. Li et al. (23) convert expression time series to a sequence of slopes, and use an unsupervised conditional random field model to cluster the genes.

3.1.4. Clustering Using Hidden Markov Models

Schliep et al. (24) developed a hidden Markov model (HMM) method to model the dependency between observations of adjacent time points. An HMM is specified by a set of hidden states, the probability of starting at a given state, the probability of transition from one state to the other, and the probability of generating the gene expression level at each state. The clustering is modeled by a mixture of HMMs, where each HMM corresponds to a cluster. Gene assignment and model parameters are estimated by maximizing the likelihood of the observed expression time series using an Expectation Maximization (EM) style algorithm (see Chapters 6 and 7). The number of clusters is determined by a heuristic procedure that removes clusters with too few genes and splits clusters with too many genes.

In (24), a gene is assigned to the cluster corresponding to the most probable HMM. Schliep et al. (25) suggest a method to improve the assignment by grouping genes with ambiguous membership into a separate cluster, and show that the resulting groups are more robust to noise in the data. Schliep et al. (25) also propose an approach to incorporate prior biological knowledge to improve the clustering.

We note that while HMM-based methods works well for long time series, they require the number of time points to be much larger than the number of states, which may be problematic for short time series.

3.1.5. Clustering Methods Based on Stochastic Processes

In this section we discuss regression models for determining the effects genes have on other genes. These ideas can also be used for clustering by relying on an autoregressive model (26). An autoregressive model of order p assumes the expression level at a given time point is a linear function of the expression levels of the same gene in the previous p time points. The clustering algorithm uses an agglomerative procedure to search for the most probable set of clusters. It starts by assuming every expression time series is generated by a different process. In the next step, it computes the model likelihood for all possible pair-wise merges. The method then identifies the merge that results in the highest model likelihood, and, if it is higher than the current model likelihood, merges the two clusters. The procedure stops when the model likelihood cannot be improved by merging anymore. A closely related method by Zhou and Wakefield (27) models gene dynamics by a random walk, and uses birth-death MCMC to determine the number of clusters.

3.1.6. Clustering Using Model Profiles

Short Time-series Expression Miner (STEM) is designed specifically for short time series (28) (Fig. 24.3). The method starts by selecting a set of potential model profiles that can represent any expression profile. The number of potential profiles is controlled by a user parameter that determines the amount of change a gene can exhibit between two adjacent time points. A subset of the m profiles is selected by a procedure that maximizes the minimum distance between any two profiles. The rationale is to select a distinctive set of profiles that covers the entire space of possible expression profiles. Given a set of model profiles, each gene is assigned to the closest model profile. The significance of the model profiles is computed by hypothesis testing where the null hypothesis is that any profile observed is resulted from random fluctuation of the model profile.

Fig. 24.3.

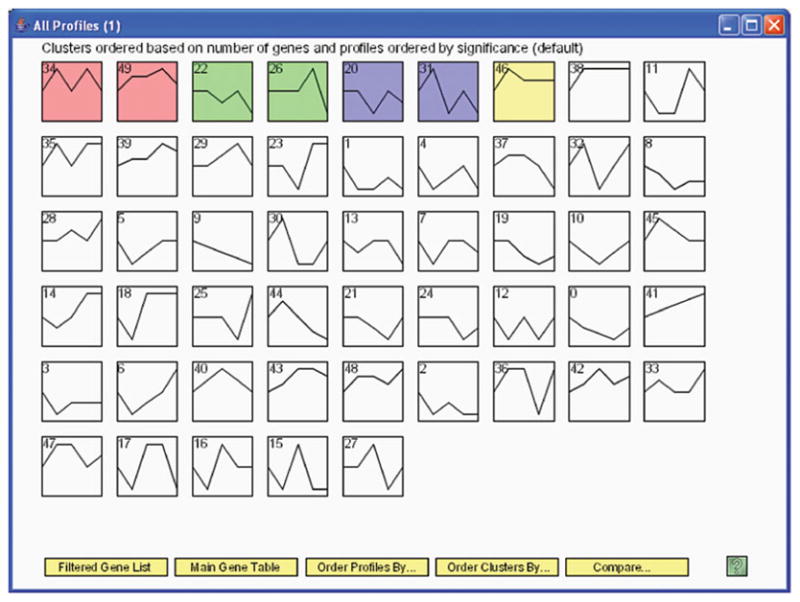
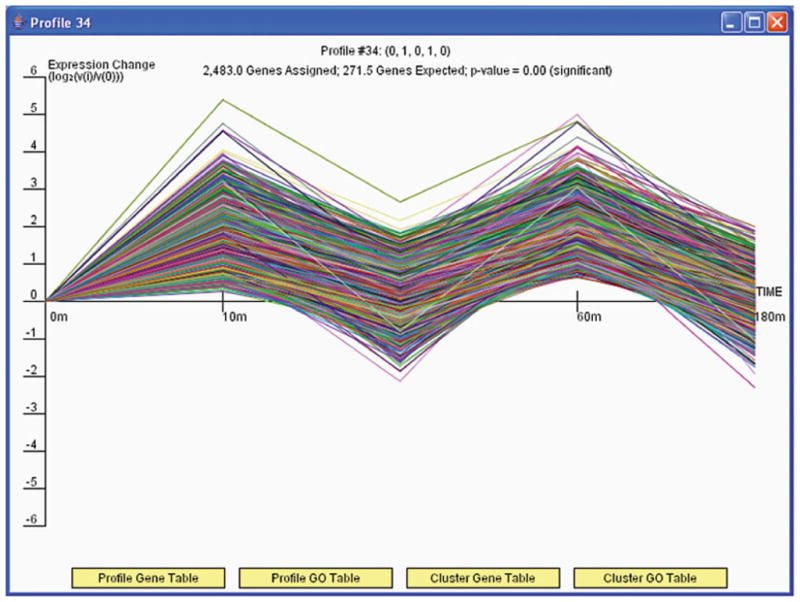
Short time-series expression miner (STEM) example. The data are from experiments studying a serum response factor, SRF-VP16, of wild-type embryonic stem cells. Samples were taken at five time points: 0, 10, 30, 60, and 180 min (76). (A) Overview of clustering results. The number in the top left-hand corner of a profile box is the profile ID number. The colored profiles had a statistically significant number of genes assigned, and those non-white profiles of the same color are similar and assigned to the same cluster of profiles. (B) Zoom in on profile 34. The figure displays all genes assigned to that profile. It also lists the expected and actual number of genes assigned to this profile and the p-value for having so many genes assigned to this profile.

Anand et al. (29) suggest a number of ways to improve this method by assigning genes to model profiles based on a fuzzy membership function, and selecting model profiles using an evolutionary algorithm that finds trade-off between minimizing quantization errors and minimizing the number of profiles. They show that in certain situations the proposed method improves the clustering quality.

3.2. Regression Analysis for Causal Inference in Time Series Data

There are two primary sources for inferring regulatory relationships from gene expression data. The first are perturbation experiments (either knockout or knockdown) that inactivate a gene or a pair of genes and study the downstream affects (30, 31). The second are time series experiments in which researchers use lagged correlations to search for regulatory relationships (32).

Unlike perturbation experiments, which usually start with a single perturbed gene, time series data allow researchers to study several different regulators at once. On the other hand, the application of methods for inferring lagged correlations to a data set containing measurements of thousands of genes over a relatively small number of time points may lead to a large number of false positives. In such a data set, many of the inferred regulatory relationships may result from noise or from unrelated sources (co-occurrence as opposed to activation). To address this problem, most algorithms developed for this task are focused on trying to limit overfitting by tightly controlling the algorithms used to learn the interaction parameters. Another possible solution to this problem is to combine different data sets (measuring the same set of genes under different experimental conditions) and search for regulatory relationships that are present in a subset of these data sets.

We divide the set of methods developed for lagged regulatory analysis into those that can only be applied to a single data set and those that can be applied to multiple data sets at once. Most of the work applied to a single data set relied on regression analysis to identify causal genes. Most of the work applied to multiple data sets used correlation coefficients (implicitly assuming a fixed delay of 0 in all experiments) though more recently researchers have used regression analysis for multiple data sets as well.

3.2.1. Time-Lagged Inference from a Single Data Set

Qian et al. (32) were among the first to use time series data for inferring interactions among genes. Their method relied on aligning the measured values for a pair of genes. To identify causal relationships they have used local alignment algorithms to find cases where a later expression of one gene matches an earlier expression of another gene and link these two genes. They have also looked at inverted relationships that could identify repression effects. Schmitt et al. (33) applied a similar analysis to a much larger data set from the photosynthetic cyanobacterium Synechocystis sp. The analysis identified networks of interactions and allowed inference of putative effects of light on this organism. The final network comprised 50 different groups containing 259 genes. Most of these gene groups possess known light-stimulated gene clusters while others represent novel findings in that work. Balasubramaniyan et al. (34) developed a tool called CLARITY (Clustering with Local shApe-based similaRITY). This tool uses the Spearman rank correlation as a shape-based similarity measure to compute the correlation between genes in a single time series expression data set. The method can also identify time-shifted (lagged) correlations, which can be used to infer causal relationships.

3.2.2. Dynamic Bayesian Networks (DBNs)

Another direction for determining causal relationships from time series data is the use of various graph theory-based methods also known as graphical models. These models include Bayesian networks (35) that have been successfully applied to study static expression data. An extension of Bayesian networks, Dynamic Bayesian Networks (DBNs) can be used to determine regulatory relationships from time series data, often improving on the static version for this type of data (36). For example, Ong et al. (37) applied DBNs to study Escherichia coli time series data. While Ong et al. used discretized expression values (up or down regulation) in their DBNs, most follow-up studies worked with continuous values and regression analysis. To illustrate the general concept of using DBNs for time series expression data, consider the graph in Fig. 24.4. This figure presents five genes in two consecutive time points. Genes A and C on the left are connected to gene B indicating that their expression levels in a previous time point affect the expression of B in the next time point. This could represent transcription factors (TFs) regulating some of their targets (note that A also regulates C so the figure represents a temporal feed-forward loop). We denote the node representing A on the left as a parent of B and C. The exact nature of this effect is indicated by the Conditional Probability for B, which is specified in the figure. This function assumes that B is expressed as a linear function of A and C plus some noise. More generally, we usually use functions of the form:

$$x_i^t=\sum _{j\in p(i)}{w}_{i,j}f(x_i^{t-1})+\epsilon$$

where at time t the $x_i^t$ expression of gene i is dependent on the expression of its parents (p(i)) at the previous time point (t−1). w_i,j represents the strength of the influence of parent j on gene i. ε accounts for experimental and other types of noise and is assumed to be independent of the measurements and distributed as a Gaussian with 0 mean (ε ~ N (0, σ²)). The dependency between parents and genes can either be linear (in which case f is the identity function, as in Fig. 24.4) or nonlinear (in which case f can take an arbitrary form). More generally, given a vector of expression levels at time t − 1(X ^t−1), we can model the levels at time t using the following equation:

$$X^t=Wf(X^{t-1})+\mathbf{e}$$

where W is a sparse matrix and e is a vector of normally distributed random noise variables.

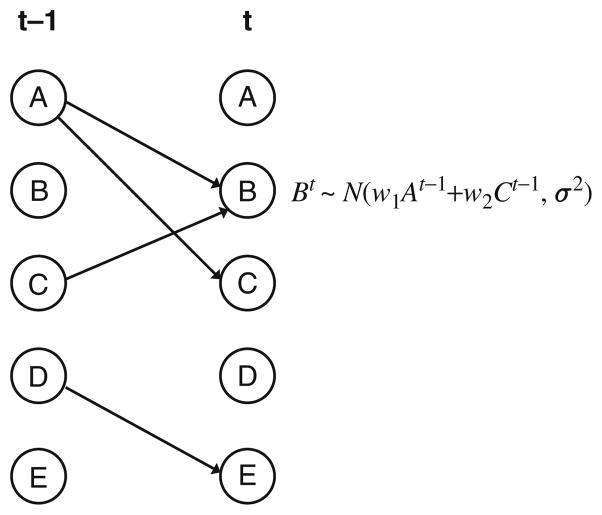
Fig. 24.4.

Dynamic Bayesian network (DBN) example. Five genes are represented using a DBN. Edges represent conditional dependence between levels of genes in two consecutive time points. The probability distribution for gene B is specified. Since both A and C connect to B, this probability is a function of the level of these two genes at the previous time point plus some noise term. Note that in the DBN in the picture we only allow connections between time points. In general, DBNs connections are also allowed within a time point, but most applications using DBNs for time series expression data only use the between time points connections.

The major challenge associated with learning such networks from data is the condition that we need to estimate a large number of parameters from a relatively small number of data points. Time series experiments are very short (often no longer than 8 time points, (11)), which means that we face the curse of dimensionality problem when trying to infer DBNs from a single time series data set. To address this problem, researchers have used a number of regularization methods. These include L1 penalty terms on the values of the weight parameters (effectively minimizing the number of parents for each node) (38), information theoretic penalty terms on the number of parameters (39, 40), limiting possible parents to a coherent subset of the genes (41), and constraints on the time distance between the activation of the regulator and the activation of its target (42).

Recently, Ahmed and Xing (43) developed a method termed TESLA for learning time-varying networks. This method combines ideas from both static and dynamic network analyses. A regression network is constructed for each time point. However, the networks for consecutive time points are linked so that the presence of edges in one time point depends on their presence in the previous time point allowing TESLA to uncover the evolvability of the networks over time.

3.2.3. Interaction Inference from Multiple Temporal Data Sets

Combining multiple time series data sets when learning DBNs or other time lag models may help in overcoming the skewed dimensionality problem. However, combining multiple data sets for this task is a non-trivial problem. First, sampling rates differ between different data sets, making it hard to determine a common temporal unit for DBNs. Second, for a specific interaction pair (a TF and its target gene) the actual time lag may differ between different experiments since the time scale of the series data may change. For example, using different arrest methods leads to very different cell cycle durations (44). These different cell cycle durations translate to differences on the molecular level, which affect the time it takes a TF to activate the genes it regulates. Finally, even for a pair of genes displaying time lagged regulation, this relationship might exist in only a subset of the data sets since different pathways may be activated under different conditions.

A possible way to combine multiple data sets is to ignore the time lag and rely instead on correlation between the profiles of genes in the data set. This effectively assumes a time lag of 0 for all pairs. For example, Lee et al. (45) used the correlation method to combine a large number of human expression data sets to search for correlated pairs. Another way to address this issue, which is appropriate for combining experiments that study the same system under different conditions (for example, different cell cycle arrest methods) is to align the data sets assuming that genes behave in the same way in all experiments though with different time units. The alignment process determines the appropriate transformation from one time series to another. Once the alignment is determined, we can transform the different data sets into a common temporal representation and they can then be used to infer DBNs and other lagged models as discussed above. Various alignment techniques have been suggested including methods based on dynamic programming (46), methods based on continuous representations and alignment of curves (47), a combination of dynamic programming and continuous representation (48), and HMM-based methods (49). There have been a few attempts at using aligned data sets for reconstructing DBNs, most notably for cell cycle studies in yeast and human (50). Note however, that all of these alignment methods assume that the data sets measure the same system. However, when combining more diverse experiments (for example, cell cycle and stress experiments), such an assumption cannot be expected to hold anymore. Thus, unlike static BNs that have been used to combine a large number of data sets from a wide range of experimental conditions, DBNs have so far been limited to modeling individual data sets or similar data sets for the same biological system.

Shi et al. (51) presented method that may overcome this problem and allow researchers to combine experiments from different conditions in a single DBN. These authors presented an algorithm that uses a set of known interacting pairs to compute a temporal transformation between every two data sets, regardless of the condition they study. The underlying idea is that some interactions would be present in both data sets and these can be used to learn the temporal transformation between the two data sets. Using an EM algorithm, they align all time series data sets to a common reference data set (usually the longest) and use the aligned experiments to search for additional regulatory interactions, not used in the learning phase, that are present in multiple data sets. From 16 yeast time series data sets from cell cycle, various stress conditions, and DNA damage response experiments, the method was able to greatly improve upon the accuracy of models constructed from a single data set.

3.3. Integrating Additional Data for Improved Network Inference

As discussed in the previous section, network inference techniques that rely solely on time series gene expression data often suffer because there are many more parameters to fit than time points. To remedy this problem, inference algorithms can incorporate other data sources to impose additional constraints and reduce the number of feasible models.

Adding new types of data to existing models gives rise to its own set of challenges. Such information can be used in a pre- and/or post-processing step to eliminate inconsistent networks or can be tightly coupled with the network inference algorithm, which may require a fundamentally different computational framework. Furthermore, not all types of data are prevalent in certain species. For instance, whereas sequence data are readily available for many species of interest, genome-wide protein–DNA binding studies have only been performed for a few species (see Chapters ??, (52)). In addition, as noted earlier, sequence data are inherently static and protein–DNA binding, protein–protein interactions (PPI), and miRNA–mRNA interactions are generally measured at a single time point in a single condition. Thus, it is not always straightforward to use this information to provide additional insight into dynamic regulatory processes.

The data-integrative methods we present here are broadly grouped by the types of additional information they utilize: sequence and motif data, protein–DNA binding interactions, and/or other types of interactions.

3.3.1. Combining Time Series Expression and Sequence Data

In the context of inferring dynamic regulatory networks, sequence data are most often used to predict protein–DNA binding by identifying TF binding site motifs in genes’ promoter regions. Kundaje et al. (53) combined time series gene expression profiles and occurrence counts of known motifs to learn transcriptional modules. Splines were used to model the dynamic expression data, and the modules were learned by using Expectation Maximization to optimize a generative probabilistic graph model. Ramsey et al. (54) extended the time-lagged correlation method discussed in the previous section to include a motif scanning step. Differentially expressed genes were clustered, a time lagged correlation procedure calculated significance for TF-gene pairs, and the significance scores were combined to yield TF-cluster scores. Position-weight matrices were used to scan the promoter regions of the differentially expressed genes and motif enrichments were computed for each cluster. Inferelator (55) first formed biclusters based on gene expression data, regulatory motifs in promoter regions, and a network of functional associations. Kinetic equations were then fit to determine the regulatory impacts between predictor variables, TFs and external stimuli, and the biclusters. This method also models pairwise combinatorial interactions between predictors. An extension to Inferelator (56) adopts a Bayesian approach to improve predictions under long time scales.

3.3.2. Utilizing Protein–DNA Binding Interactions

While incorporating sequence data is appealing due to its prevalence in many species, motif-based binding predictions are not as informative as experimental protein–DNA binding interaction data. The availability of genome-wide ChIP–chip data in model organisms such as Saccharomyces cerevisiae (5) has given rise to techniques that make use of such information, sometimes in conjunction with sequence data.

Luscombe et al. (57) presented Statistical Analysis of Network Dynamics (SANDY), a tool for calculating network statistics for dynamic systems. Differentially expressed genes were assigned to a stage in the cell cycle, and an iterative trace-back algorithm was applied to isolate the active TFs and sub-network at that stage. Sub-networks were subsequently compared based on graph statistics such as topology, presence of network motifs, and TF usage. A rule-based method by Chawade et al. (58) clustered genes such that their promoter regions were enriched for a common set of motifs that are known to be bound by a TF. In addition, each gene in a cluster must be first significantly expressed at the same time point or immediately after the TF regulating that cluster is first expressed, and the expression profiles of the clustered genes must be correlated. We previously discussed integrating time lagged correlation models with motifs (54), and Wu and Li (59) extended this class of models by incorporating TF binding and deletion gene expression data as well. Lin et al. (60) employed a first-order nonlinear differential equation to combine cell cycle TF binding data and dynamic gene expression data and extract dynamic interactions among the TFs. Network Component Analysis (61) decomposes a data matrix containing dynamic gene expression levels into a connectivity matrix and a signal matrix and provides criteria for doing so uniquely. The signal matrix corresponds to the activity levels of TFs over time, and the connectivity matrix quantifies how strongly TFs regulate their target genes. Protein–DNA binding data are used to constrain the connectivity matrix so that TFs cannot regulate genes they do not bind, and extensions to Network Component Analysis (62, 63) use gene knockout data to further constrain the signal matrix.

Several regression-based methods also include protein–DNA binding data to guide the estimation of model parameters. Cokus et al. (64) applied linear regression to time series gene expression data and binding interaction data to estimate dynamic TF activity levels at each time point. The authors then used least squares to estimate a transition matrix that specifies how TFs affect each other’s activity levels over time. Multivariate Random Forests, developed by Xiao and Segal (65), consist of a random forest of multivariate regression trees that use protein–DNA binding and motif data as input and temporal gene expression levels as outcomes. The resulting proximity matrix specifies pairwise gene similarity based on both time series expression and binding information. The authors used the proximity matrix as input to a guided clustering method to identify regulatory cliques.

Probabilistic graphical models have also benefitted from the integration of TF binding information. Dynamic Bayesian Networks, discussed in the previous section, were adapted to include TF binding data as a prior by Bernard and Hartemink (66). The strength of the prior for the presence of an edge is greater for binding interactions with lower p-values, and the prior is factorable in order to enable efficient computation. Sanguinetti et al. (67) incorporated ChIP–chip data in their Kalman filter model to represent network connectivity. They applied a variational Expectation Maximization inference algorithm to learn TFs’ dynamic protein concentration levels and regulatory influences on their target genes. The post-transcriptional modification model presented by Shi et al. (68) learns temporal TF activity levels via a switching model that determines whether a TF is regulated transcriptionally or post-transcriptionally. TFs’ activity levels can then be respectively inferred from either their own gene expression levels or the expression levels of their regulatory targets. Protein–DNA binding data are incorporated as prior in the log-likelihood score function to penalize TF-gene regulatory interactions in the model that disagree with the ChIP–chip data. Below we present one type of graphical model applied to this problem, an extension of HMMs, in greater detail.

3.3.3. Dynamic Regulatory Events Miner

Dynamic Regulatory Events Miner (DREM) (69) takes a unique approach by focusing its modeling of temporal regulatory interactions on bifurcation points. Bifurcation events occur when a set of genes share a similar expression trajectory up to a certain time point and then diverge (Fig. 24.5). To identify these splits, groups of genes are assigned to the hidden states of an input–output hidden Markov model (IOHMM). IOHMM is an extension of hidden Markov models that allows static input, in this case TF-gene interaction data, to influence the state transition probabilities. At each state that has more than one child state, an L1-penalized logistic regression classifier maps the subsets of TFs that are potentially active at that state to transition probabilities for the genes assigned to that state. After DREM assigns each gene’s expression profile to one of the paths along hidden states in the model, it uses protein–DNA binding or motif data to determine which TFs are responsible for the bifurcations by calculating enrichment scores based on the hypergeometric distribution.

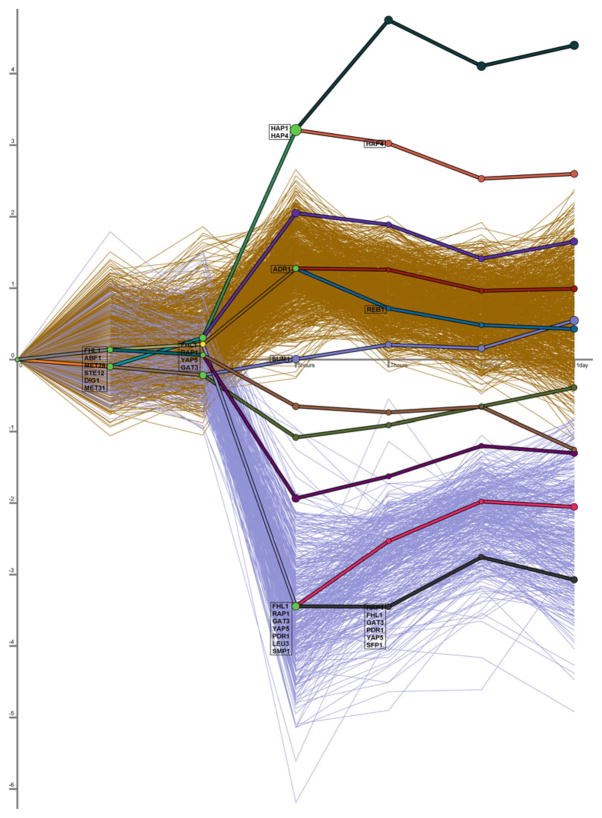
Fig. 24.5.

Dynamic regulatory events miner (DREM) example. Here DREM has been applied to stationary phase expression data from a Saccharomyces cerevisiae strain in which the gene encoding for the TF Ypl230w had been deleted (77). Because protein–DNA binding data specific to this condition are not available, general binding interactions (5) were used. Thick lines show the paths between states in the input–output hidden Markov model and thin lines indicate the expression levels of individual genes. A bifurcation event at the second time point has been selected so that only genes that pass through the corresponding hidden state (represented by a yellow node) are shown. These genes share a common response through the first two time steps, exhibiting relatively little response to the stimulus. However, after the second time point this set of genes diverges into two distinct groups, one of which is significantly repressed. DREM identifies Fhl1, Rap1, Gat3, Yap5, and Smp1 as the TFs responsible for this bifurcation. Several predictions made by DREM were experimentally validated as discussed in the main text.

Because DREM infers the times at which TFs regulate their targets, it can differentiate master regulators that control the immediate response to a stimulus from secondary regulators that are active later. Determining the time at which a TF is most active also enables DREM to identify the best time to conduct binding experiments for particular TFs to experimentally verify their role in the stimulus response. DREM was so far applied to yeast and E. coli (70) and in both cases led to specific temporal predictions, which were experimentally verified.

3.3.4. Integrating Additional Interactions Beyond Protein–DNA Binding

As techniques for integrating static sequence and protein–DNA binding data with time series gene expression data continue to become more commonplace, it becomes increasingly interesting to explore how other types of interactions that influence regulatory networks can be incorporated into dynamic models. Protein–protein interaction data are widely available for the most commonly studied species, but it is not obvious how such protein interactions dynamically control gene regulation. One preliminary approach by Vu and Vohradsky (71) applied a neural network-based ordinary differential equation model that combined PPI data with time series gene expression, sequence, and ChIP–chip binding data. PPI were used to model the regulation of a gene by a protein complex in the case where not all members of the complex directly bind the promoter region. However, this method only allowed for complexes of two proteins, and general integration of PPI data remains an open problem.

Post-translational modifications (PTMs) of histones and TFs are another promising source of interaction data. TSAP (72) focused on integrating dynamic histone PTMs to infer regulatory states and model the trajectories of genes between those regulatory states over time, where a regulatory state was defined by a joint gene expression and histone PTM pattern. It extended the Affinity Propagation (73) algorithm to cluster genes at each interval in a time series gene expression experiment such that each cluster is dependent on clusters at other time points. Histone PTMs near genes’ start sites were incorporated as additional features in the clustering similarity measure between genes. Using TSAP on mouse data provided new insights into the regulation of Hox genes, which play an important role in motor neuron development.

4. Discussion

High-throughput data about the activity in the cell are rapidly accumulating. However, most of these data are static. To infer the dynamic activation of regulatory programs within the cell, researchers need temporal data. The most abundant source for such data is time series expression experiments, which now account for more than 20% of all expression studies.

When analyzing time series data, researchers need to use tools specifically designed for such data sets. These tools take advantage of the temporal ordering in the data sets and use these to infer groupings and causal relationships. A number of clustering methods have been specifically designed for these data sets and many provide an easy to use interface. Other methods use regression-based analysis to infer causality and interaction from time series data. Both types of methods have been applied to time series data sets from a large number of species.

While methods that analyze expression data provide useful information, they are limited by the large dimensionality of the data and the relatively few time points that are sampled in each study. To overcome this, researchers have been developing methods for integrating time series data with other data sources. This helps limit the parameter space and allows for temporal predictions regarding data that were measured in static way. These methods often lead to detailed hypotheses regarding the time of specific interactions, some of which have been experimentally tested and shown to be accurate.

4.1. Evaluation

Of the methods discussed in this chapter, clustering approaches are so far the most widely used. Almost every high-throughput study uses clustering to visualize and organize the results. While general clustering algorithms are still the most popular methods for analyzing time series data, the temporal clustering methods have been gaining ground recently and have been increasingly used when analyzing data from species ranging from bacteria to yeast to mammals.

The use of methods for causality inference in time series data, discussed in Section 3.2, has so far been primarily limited to computational reanalysis of expression and other types of biological data and has not been widely used by experimentalists. This may be because of the more complex nature of these methods or because, as discussed above, of the skewed dimensionality problem that leads to many false positives. However, even though it has not been very popular on its own, this types of analysis may prove to be very useful as part of the larger analysis framework, specifically when combined with other types of biological data.

Data integration methods for inferring dynamic networks are increasingly used by experimentalists. Many recent high profile papers (74, 75) use various forms of data integration to improve the inference of dynamic regulatory networks. Unlike clustering, this area is still in its infancy and so it remains to be seen which computational methods would prove the most beneficial. However, this direction has already led to important findings and is likely to remain an important research direction as we discuss below.

4.2. Future Work

While we believe that more temporal data will become available (including temporal data regarding binding of TFs to genes and protein interaction), some data sets are inherently static (most notably DNA). Thus, a major challenge remains to develop methods for combining these temporal data sets with static data sets for reconstructing dynamic modules for regulatory networks. Many methods can already successfully integrate time series expression data with protein–DNA interactions, but the important goal of connecting regulatory, signaling, and metabolic networks would require the use of other types of interactions including protein interactions and protein modification information. Methods for integrating all of these data sources would provide a much needed view for the dynamic activation of signaling and regulatory networks, which lie at the heart of any response system.