Investigating the impact of development and internal validation design when training prognostic models using a retrospective cohort in big US observational healthcare data

Abstract

Objective

The internal validation of prediction models aims to quantify the generalisability of a model. We aim to determine the impact, if any, that the choice of development and internal validation design has on the internal performance bias and model generalisability in big data (n~500 000).

Design

Retrospective cohort.

Setting

Primary and secondary care; three US claims databases.

Participants

1 200 769 patients pharmaceutically treated for their first occurrence of depression.

Methods

We investigated the impact of the development/validation design across 21 real-world prediction questions. Model discrimination and calibration were assessed. We trained LASSO logistic regression models using US claims data and internally validated the models using eight different designs: ‘no test/validation set’, ‘test/validation set’ and cross validation with 3-fold, 5-fold or 10-fold with and without a test set. We then externally validated each model in two new US claims databases. We estimated the internal validation bias per design by empirically comparing the differences between the estimated internal performance and external performance.

Results

The differences between the models’ internal estimated performances and external performances were largest for the ‘no test/validation set’ design. This indicates even with large data the ‘no test/validation set’ design causes models to overfit. The seven alternative designs included some validation process to select the hyperparameters and a fair testing process to estimate internal performance. These designs had similar internal performance estimates and performed similarly when externally validated in the two external databases.

Conclusions

Even with big data, it is important to use some validation process to select the optimal hyperparameters and fairly assess internal validation using a test set or cross-validation.

Strengths and limitations of this study.

• We developed and externally validated 840 prediction models using 8 different development/internal validation designs across 21 prediction problems.

• We focused on a target population of approximately 500 000 patients and predicted 21 different outcomes of various rareness.

• We empirically investigated the impact of development/internal validation design on internal discrimination estimate bias and model generalisability in big data.

Background

Prognostic models aim to use a patient’s current medical state, such as his medical history and demographics, to calculate a personalised estimate for the risk of some future medical event. If a model can make accurate predictions, then it can be used to help personalise medical decision making.¹ Big observational healthcare databases may provide a way to observe and follow large at-risk patient samples that could be used to develop prognostic models.² The initial step when using these datasets to learn a prognostic model is creating labelled data that can be used by binary classifiers. The labelled data consist of pairs of features and the outcome class for each patient in the at-risk patient sample.

Binary classification is a type of machine learning where labelled data are used to learn a model that can discriminate between two classes (eg, healthy vs unhealthy or will develop cancer vs will be cancer free) using patient features such as age, body mass index or a medical illness (also known as attributes, predictors or covariates). In terms of prognostic models in healthcare, a model uses current features of an at-risk patient to predict some future health state for the patient. It is hoped that a model learnt using labelled data from a sample of at-risk people will generalise to any new at-risk person. Unfortunately, sometimes a model incorrectly mistakes noise in the sample of labelled data as patterns. This is known as ‘overfitting’ and causes a model to appear to perform extremely well in the sample of labelled data but performs much worse when applied to new data.³ This means that the model makes incorrect predictions that could be dangerous. One way to address the issue of overfitting when developing a model is to ‘hold out’ some of the labelled data when learning the model and then evaluate the model on the held-out data. This process mimics evaluating the model in new data but reduces the size of the labelled data used to learn the model. Alternatively, the amount of overfitting can be quantified based on how stable the model performance is across different labelled data samples used to develop the model. This process is known as bootstrapping.⁴ Using the correct internal validation design is important as it results in more reliable model performance estimates and makes it possible to fairly assess a prognostic model. Research has shown that a bootstrapped approach is most suitable in smaller datasets (<10 000 at-risk patients and <100 features)^{5 6} but there is currently no research into the impact of validation design in data with a large at-risk sample (big n) and many features (big p). As healthcare datasets are growing, the a-risk samples used for model development are increasing, and the research insights found on smaller data may not extrapolate to big n and big p data. Research into the impact of development/validation design in big data is needed to ensure the most optimal models are being developed or limitations of certain designs are known.

Bootstrapping is the best approach to fairly evaluate a logistic regression model with small data due to the ‘held-out’ data being small and estimates being uncertain. In big n and big p data, training a model is often a slow process. Advanced machine learning methods such as deep learning can take days or weeks to train. This makes the bootstrap approach unsuitable as it requires training a model 100 s of times. In addition, in big n data, the development and ‘held-out’ data are both large, which may overcome the small data issue of estimates being uncertain. However, as the number of features (p) increases and more complex classifiers are trained, the chance of overfitting increases, so issues may still occur in big data. Classifiers often have hyperparameter that control the complexity. For example, regularised logistic regression models have a hyperparameter that adds a cost to the number of features (or size of the coefficients). This makes them suitable for learning in big p data, but the optimal hyperparameter needs to be identified. Identifying the optimal hyperparameters requires comparing hyperparameter performance in some labelled data that were not used to develop the model, otherwise overfitting may bias the hyperparameter evaluation. This means developing models in big p and big n data requires three data splits: the development data used to train the model, the validation data used to select the optimal hyperparameter and the test data that is held out and used to fairly evaluate the model.

The bigger the data used to develop a model, the less likely the model will overfit and the bigger the ‘held-out’ data used to evaluate a model the more stable the performance estimates. This prompts the idea of cross-validation (CV). CV requires splitting the labelled data into N independent subsets (N-folds) and then iterates over the subset by holding the subset out and developing the model using the combination of the N-1 other data subsets. The held-out dataset is then used to evaluate the model. This results in N performance estimates that are aggregated to provide a single estimate of performance. This provides a fair way to evaluate the model while also increasing the size of data used to develop the model. CV is often used to pick the optimal hyperparameters. In big n and big p data there is the choice of whether to use a held-out data set (test set), whether to use a validation set or CV and how many CV folds to use. The common designs used for big data are displayed in figure 1.

Figure 1.

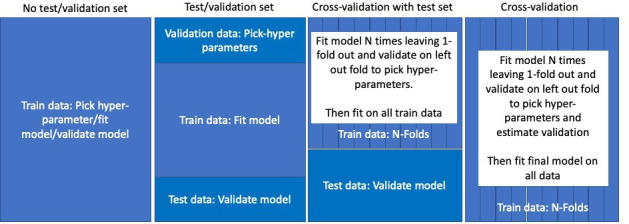
Possible development and internal validation design strategies for big data. The options include whether to use a test set (hold out some data from development that is used to fairly assess performance) and whether to use cross-validation (where the data are partitioned, and each partition is iteratively held out while the rest of the data are used to develop the model).

In this paper, we compare the impact of model development design on regularised logistic regression performance in big data. We focus on data with approximately 500 000 patients, >86 000 features and investigate performance estimates across 21 prediction problems with varying outcome event count rareness. We implemented eight different development designs per prediction problem. We repeated each design multiple times with different splits (folds or test sets) to estimate how stable and unbiased the performance estimates are. We then investigate whether the choice of design impacts model performance when externally validating the models in two new databases.

Methods

We use the OHDSI PatientLevelPrediction framework⁷ and R package to develop and evaluate the prediction models in this study.

Data

We developed models using a US claims database, IBM MarketScan Commercial Claims, that contains insurance claims data for individuals enrolled in US employer-sponsored insurance health plans. The data includes adjudicated health insurance claims (eg, inpatient, outpatient and outpatient pharmacy) as well as enrollment data from large employers and health plans who provide private healthcare coverage to employees, their spouses and dependents. The patients in this database are aged under 65. The database contains records for approximately 153 million patients between January 2000 and December 2019.

Models were externally validated using:

1. IBM MarketScan Medicare Supplemental Database (MDCR), a US claims database that represents health services of retirees (aged 65 or older) in the USA with primary or Medicare supplemental coverage) through privately insured fee-for-service, point-of-service, or capitated health plans. These data include adjudicated health insurance claims (eg, inpatient, outpatient, and outpatient pharmacy). The database contains approximately 10 million patients from January 2000 to January 2020.

2. IBM MarketScan Multi-state Medicaid Database (MDCD), a US database containing adjudicated US health insurance claims for Medicaid enrollees from multiple states. The database includes hospital discharge diagnoses, outpatient diagnoses and procedures, and outpatient pharmacy claims as well as ethnicity and Medicare eligibility. The database contains approximately 31 million patients from January 2006 to January 2020.

Patient and public involvement

No patient involved.

Study population

We extracted data for patients who are pharmaceutically treated for their first occurrence of depression to predict 21 outcomes occurring for the first time from 1 day after their depression diagnosis until 365 days after. In the development data we randomly sampled 500 000 patients from 1 964 494 treated for depression and this resulted in a range of outcome event count sizes during the 1-year follow-up. In the external validation data, we used all the data available, this corresponded to 160 956 patients in MDCR and 539 813 in MDCD.

Outcomes

We used the same 21 outcomes used by the PatientLevelPredicion framework study.⁷ Table 1 lists the 21 outcomes we predicted occurring 1 day after index until 365 days after index. The number of outcome events in the development data and validation data are also reported. As we are predicting first occurrence of each outcome, we excluded patients with the outcome prior to their depression, so the study populations slightly differed per outcome (eg, when predicting acute liver injury we exclude patients with a history of acute liver injury but when predicting ischaemic stroke we exclude patients with a history of ischaemic stroke).

Table 1.

Outcomes predicted in this study and the logic used to define the outcome in the data

Outcome	Phenotype	Event count in development data (N~500 000)	Event count in MDCR data (N~160 956)	Event count in MDCD data (N~539 813)
Open angle glaucoma	A first-time condition record of open-angle glaucoma with at least one condition record of open-angle glaucoma from a provider with ophthalmology, optometry or optician specialty within 1–365 days.	174	510	102
Acute liver injury	A first-time condition record of Acute liver injury during an emergency room visit or inpatient visit. No Acute liver injury exclusions 1 year prior to 60 days after.	184	67	352
Ventricular arrhythmia and sudden cardiac death	A first-time condition record of ventricular arrhythmia and sudden cardiac death during an emergency room visit or inpatient visit being the primary cause of the visit.	297	642	1188
Ischaemic stroke	A first-time condition record of ischaemic stroke during an inpatient visit	380	1153	674
Acute myocardial infarction	A first-time condition record of acute myocardial infarction during an emergency room visit or inpatient visit being the primary cause of the visit.	491	1080	1042
Gastrointestinal haemhorrage	A first-time condition record of gastrointestinal haemorrhage during an emergency room visit or inpatient visit being the primary cause of the visit.	509	963	1037
Delirium	A first-time condition record of delirium during an emergency room visit or inpatient visit	985	1298	1842
Seizure	A first-time condition record of seizure during an emergency room visit or inpatient visit	1494	935	4314
Decreased libido	A first-time condition record of decreased libido	1661	130	926
Alopecia	A first-time condition record of alopecia	2577	748	2674
Hyponatraemia	A first-time condition record of hyponatraemia or a first-time measurement of serum sodium between 1 and 136 millimole/L	2628	4276	6035
Fracture	A first-time condition record of fracture	2722	4071	4692
Vertigo	A first-time condition record of vertigo	3046	2086	2791
Tinnitus	A first-time condition record of tinnitus	3120	1824	3186
Hypotension	A first-time condition record of hypotension	4170	6399	10 738
Hypothyroidism	A condition record of hypothyroidism with another condition record of hypothyroidism within 90 days	6117	3853	6064
Suicide and suicidal ideation	A first-time condition record of suicide and suicidal ideation or a first-time observation of suicide and suicidal ideation	10 221	993	24 972
Constipation	A first-time condition record of constipation	10 672	7569	23 463
Diarrhoea	A first-time condition record of diarrhoea	14 875	7226	24 941
Nausea	A first-time condition record of nausea	19 754	7824	38 344
Insomnia	A first-time condition record of insomnia	20 806	6846	32 118

MDCD, Multi-state Medicaid Database.

Candidate predictors

We used one-hot encoding for any medical event, drug, procedure, observation or measurement recorded within 1 year prior to, or on, index (date of depression). This means we have a binary predictor per medical event/drug/procedure/observation/measurement recorded for any patient in our development study population within 1 year prior to index. For example, if a patient had a record of ‘type 2 diabetes’ 80 days prior to index, the value for the predictor ‘type 2 diabetes 1 year prior’ would be 1. If a patient never had type 2 diabetes recorded, their value for the predictor ‘type 2 diabetes 1 year prior’ would be 0. We also created one-hot encoded variables for any medical event, drug, procedure, observation, or measurement recorded within 30 days prior to, or on, index. In addition, we added one-hot encoded variables for age in 5-year groups (0–4, 5–9,…, 95–99), index month (for seasonality), ethnicity, race and gender. Finally, the number of visits in the prior 30 days was also used as a candidate predictor. This resulted in approximately 86 000 candidate predictors. In this paper we focus on the impact of study design on internal validation estimation and therefore do not present the final developed models.

Model development designs

We investigate developing and internally validating Least Absolute Shrinkage and Selection Operator (LASSO) logistic regression models⁸ using the designs in table 2. LASSO logistic regression is a generalised linear model that adds a penalty term to penalise the inclusion of predictors that are only weakly associated to the class label. This effectively performs feature selection during model training and is necessary due to using >86 000 candidate predictors. Due to the penalty term, only a small selection of predictors ends up being included in the final model. This makes the model less likely to overfit. The penalty amount is a hyperparameter that needs to be determined while training the model.

Table 2.

The different designs compared in this study.

Design	CV	Test set?	Hyperparameter selection	Model development	Internal validation
No test/validation set	0	No	Using all data	Using all data	Using all data
Test/validation set	0	Yes	Using 10% validation data	Using 80% training data	Using 10% test data
Threefold CV	3	No	Using threefold CV on all data	Using all data	Using threefold CV on all data
Threefold CV with test set	3	Yes	Using threefold CV on 80% training data	Using 80% training data	Using 20% test data
Fivefold CV	5	No	Using fivefold CV on all data	Using all data	Using fivefold CV on all data
Fivefold CV with test set	5	Yes	Using fivefold CV on 80% training data	Using 80% training data	Using 20% test data
Ten-fold CV	10	No	Using 10-fold CV on all data	Using all data	Using 10-fold CV on all data
Ten-fold CV with test set	10	Yes	Using 10-fold CV on 80% training data	Using 80% training data	Using 20% test data

CV, cross-validation.

We compare the estimated internal validation when developing models using:

• No test/validation set: the hyperparameters, final model and performance are determined using all the data. This has a high risk of overestimating the performance and is included as a worst-case scenario.

• Test/validation set: the hyperparameters are selected using the validation data, the model is fit using the training data and the performance is estimated using the test set. This is the quickest design apart from the no test/validation set.

• N-fold CV: CV on all the data is used to select the hyperparameters and estimate the performance. Final model is fit using all the data.

• N-fold CV with test set: CV on the training data is used to select the hyperparameters and the model is fit using all the training data. Performance is estimated using the test set.

The designs are summarised in table 2. We investigate the impact of the number of folds (N is 3, 5 or 10) when performing CV. All designs that use CV to select the optimal hyperparameters used the same hyperparameter grid search. The test/train splits were done stratified by outcome, so the % of people in the test/train data with the outcome were the same.

Evaluation of models

Discrimination: The area under the receiver operating curve (AUROC) and area under the precision recall curve (AUPRC) were used to evaluate the discriminative performance (how well it ranks based on predicted risk). The AUROC is a measure that ranges between 0 and 1, with values less than 0.5 corresponding to discrimination worse than randomly guessing risk (eg, patients who will experience the outcome are assigned a lower risk than patients who will not experience the outcome), a value of 0.5 corresponding to randomly guessing the risk and values great than 0.5 corresponding to better than random guessing. The closer the AUROC is to 1, the better the discrimination. For the AUROC estimated using N-fold CV we have N estimates of the AUROC (per fold). We calculate the 95% CI using the formula mean – 1.96*SD of the N estimates. For the test set AUROC we calculated the 95% CI using the SD based on the Mann-Whitney statistic. The AUPRC is a measure of discrimination that is impacted by how rare the outcome is. It is the area under the curve representing the precision (probability a patient predicted as having the outcome in the future will have the outcome) as a function of recall (aka sensitivity—proportion of patient who will experience the outcome that are correctly predicted to). AUPRC also ranges between 0 and 1, with 1 representing perfect discrimination and 0 poor discrimination. However, a ‘good’ AUPRC value depends on the outcome proportion, and this is prediction task specific.

Calibration: To measure the calibration of the model we calculated the average E-statistic.⁹ This value corresponds to the mean absolute calibration error (difference between the observed risk using a LOESS function and predicted risk). A smaller value indicates better calibration, a value of 0 means perfect calibration. The E-statistic is impacted by the outcome rareness, as a model predicting a rarer outcome will often predict lower risks and this will result in the mean error being smaller.

Model generalisability

To investigate whether some development/validation designs are more likely to cause a model to overfit (leading to optimistic internal performance estimates and making it less generalisable) we externally validated the models in two databases. The two external databases differ from the development database, so we expect some differences in model discrimination and calibration when externally validating the models. The MDCR database contains an older population and the MDCD database contains patients with a lower social economic status.

Although we expect some differences in the internal vs external performance due to data differences, very large decreases in performance when a model is applied externally may indicate that the model has overfit. To investigate this, we calculate the difference between the internal performance compared with the external performance. A higher value for the AUROC/AUPRC discrimination metric means better discrimination, so an overfit model will have a higher internal AUROC/AUPRC then external AUROC/AUPRC. The difference, internal AUROC/AUPRC—external AUROC/AUPRC, gives an indication of whether a model has overfit to the development dataset, where a value close to zero or less than zero indicates excellent model generalisability. A lower value for the E-statistic calibration metric means better calibration, so positive internal E-statistic—external E-statistic values indicate better calibration when externally validated.

Results

The characteristics of the development and validation study populations are displayed in table 3. The MDCR data patients were older with more comorbidities than the development data. The MDCD data patients were slightly younger and had slightly more comorbidities than the development data. The gender ratio was similar across datasets with ~70% female. The mean prior observation (number of days a patient has been active in the database prior to index) was >1200 days (>3 years) in all databases.

Table 3.

The characteristics of the study populations

	Development Data (N~5 00 000)	MDCR Data (N~1 60 956)	MDCD Data (N~5 39 813)
Mean Age in years (SD)	40 (15)	75 (7.8)	34 (16.6)
Male gender %	31	32	27.1
Mean days prior observation (SD)	1474 (1205)	1585 (1192)	1244 (885)
Condition recorded in prior year (% of patients)
Neoplastic disease	21.1	45.7	13.4
Pain	60.1	74.4	72.8
Anxiety	41.3	28.6	50.8
Respiratory tract infection	15.9	12.0	22.2
Dementia	0.0	0.9	0.1
Obesity	10.5	10.6	17.9
Diabetes mellitus	8.9	27.0	13.5
Hypertensive disorder	24.7	69.0	29.4
Heart disease	9.2	46.5	14.0
Hyperlipidaemia	23.3	56.3	19.8

MDCD, Multi-state Medicaid Database; MDCR, Medicare Supplemental Database.

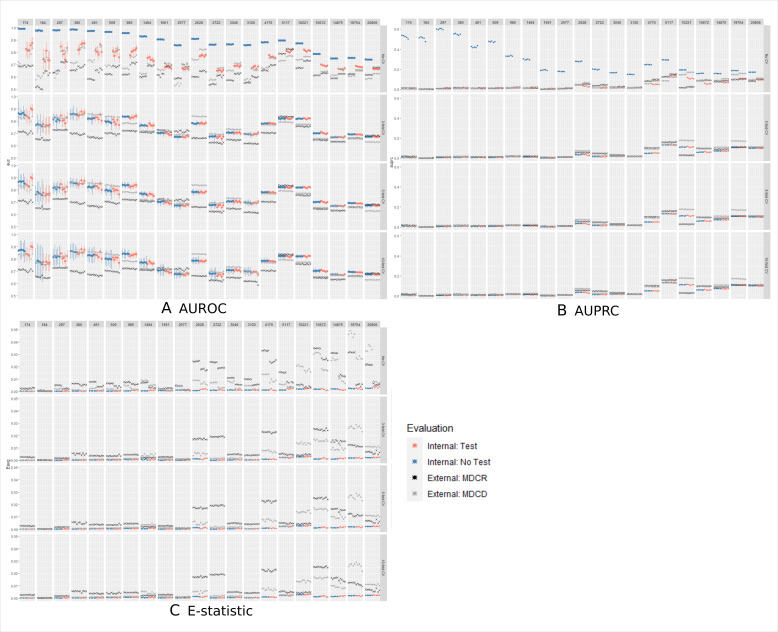
Figure 2A displays the results of the AUROC values and 95% CI across designs for five reputations of using a test set internal validation design(red dots) and using a CV internal validation or all data (blue dots). The rows correspond to the number of folds used by CV and the columns correspond to the 21 different outcomes. The rarest outcomes are on the left and the most common are on the right. The performance when CV was not used to select hyperparameters is the top row (no CV). In this row the ‘no test/validation set’ design (blue dots) had no validation or test set but the ‘test/validation set’ design (red dots) had a single validation set to select the hyperparameter and a test set. Blue dots represents the AUROC performances for designs where all the data (with or without CV) are used to estimate the internal performance, red dots represents the AUROC performances of designs where a test set is used to estimate the internal performance and black crosses/light grey pointers represents the external validation for each model across designs. The top row (no CV) differs from the rows 2 to 4, where we see that the ‘no test/validation design’ that picks the hyperparameter and fits the model using all the same data lead to highly overfit models. The AUROC performance varied across the outcomes. In general, the external validation on MDCR (black cross) was lower than all internal validation estimates, except for three outcomes (decreased libido, alopecia and hypothyroidism). The external validation on MDCD (light grey pointer) showed the external AUROC fluctuated around the internal AUROC. The internal validation estimates using a test set versus CV appear to be similar across outcomes and the external validation performances were often equivalent across designs. The number of folds used in CV (3, 5 or 10) does not appear to impact the internal or external validation estimates, except for rare outcomes where the CIs are wider. Similar trends were observed when considering the AUPRC and E-statistic, see figure 2B, C.

Figure 2.

The AUROC/AUPRC/E-statistic performance estimates for five repetitions per design per prediction task. The columns represent the prediction task, with the number representing the number of patients with the outcome during the time at-risk. For example, the first column corresponds to a prediction task where 174 patients had the outcome, whereas the last column corresponds to a prediction task where 20 806 patients had the outcome. The rows correspond to whether CV was used by the design (top row does not use CV) or the number of folds (3, 5 or 10). The internal validation performances of the designs that used a test set are coloured in red, and those not using a test set are blue (dots with vertical lines indicating the 95% confidence interval). The external validation performances for a model are the light grey pointers (MDCD) and black crosses (MDCR) that have the same x-coordinate and fall within the same row/column. AUPRC, area under the precision recall curve; AUROC, area under the receiver operating curve; CV, cross-validation; MDCD, Multi-state Medicaid Database; MDCR, Medicare Supplemental Database.

To investigate whether some development/validation designs are more likely to lead to optimistic internal discriminative estimates we calculated the difference between the internal validation performance and the external validation performance in MDCD and MDCR for each model. Figure 3 shows box plots for the difference between the internal performance and the external performance on the x-axis with the y-axis representing the design used to develop/validate each model. The red box plots are the differences when externally validated in MDCD and the blue box plots are differences when externally validated in MDCR. The AUROC, AUPRC and E-statistic performance metrics differences are displayed. The results show that the ‘no test/validation design’ resulted in optimistic AUROC and AUPRC, as the differences were large in both databases. The design also resulted in worse external calibration. The other designs had similar difference distributions in figure 3 and similar performances in figure 2.

Figure 3.

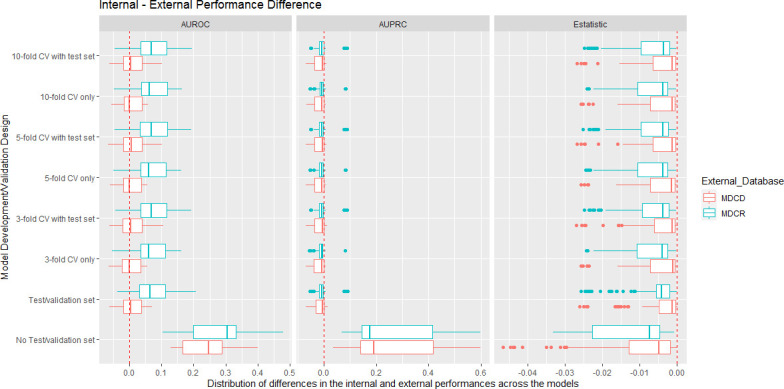
Box plots showing the internal performance estimate minus the external performance estimate per design and external database. The left side shows the AUROC differences, the centre shows the AUPRC differences, and the right side shows the E-statistic differences. For the AUROC, values near 0 indicate that the internal validation AUROC estimates were accurate as the external validation AUROCs were similar. For AUPRC and AUPRC values less than 0 indicate that the performance was better externally, values greater than 0 indicate the performance is worse externally. For the E-statistic, values less than 0 indicate worse calibration when the models were externally validated. AUPRC, area under the precision recall curve; AUROC, area under the receiver operating curve; CV, cross-validation; MDCD, Multi-state Medicaid Database; MDCR, Medicare Supplemental Database.

To see whether these results are consistent across different outcome counts, we also include the difference distributions broken up by prediction tasks with an outcome count less than 1000, outcome count between 1000 and 5000 and outcome count of 5000 or more, see online supplemental figures 1–3). The difference distributions were similar across all three metrics. figure 2A shows that when the outcome count is <1500, the AUROC performance fluctuated per replication for all designs except the overfit ‘no test/validation set’ design.

Discussion

In small data, it has been shown that the design used to development and internal validated a model impacts the internal performance estimate bias. In this study using big n (500 000) and big p (>86 000) data to develop LASSO logistic regression models we show that the impact of design has negligible impact if some fair validation process is implemented to select the optimal hyperparameter and some fair process is implemented to estimate the internal performances. The only design in this study that resulted in highly biased internal performance estimates was the ‘no test/validation’ design that leads to overfit models even with big data. The estimated performance of any prognostic model that is developed using the ‘no test/validation’ design cannot be trusted, and this design should be avoided.

Interestingly, in this study, the number of folds used by CV appeared to have negligible impact on the model’s internal and external performance in big data. This is a useful result, as increasing the number of folds makes the model development more complex and could slow down model development.

We sampled 500 000 target patients from the development database to reduce the lower value of outcome count range across the 21 outcomes. This enabled us to gain insight into the impact of low outcome count on the internal performance estimate per design. The number of outcomes has been shown to impact model performance.¹⁰ We can see from figure 2 that the split used to create the data used for selecting the hyperparameter and evaluating the model impacted the internal AUROC estimates when the outcome count was <1500 as the values varied across replication. This suggests that even in big data (n=5 00 000) and using an appropriate design, if the outcome is rare (<0.3%) the internal validation will have some error. The designs that used CV rather than a test set to estimate internal performance were more stable when the outcome was less common. This makes sense as holding out data for a test set reduces the amount of data used to develop the model and this will have an impact on performance if the outcome count is low.

The AUROC is not impacted by outcome rareness, so the difference in internal and external AUROC represents the difference in discriminative ability of the model in the development data and the external databases. The AUPRC and E-statistic are impacted by the outcome rareness, so differences between the internal and external performances for these metrics were impacted by differences in the outcome rate in the development data and external data. This explains why the AUPRC was often greater when models were applied to the external data.

The main strength of this study is that we were able to investigate the impact of development/validation design across a large number of outcomes. In total, we investigated 8 designs no test/validation set, test/validation set and 3-fold/5-fold/10-fold CV with/without a test set, 21 outcomes and 5 repetitions, resulting in the development of 840 models (8×21×5). In addition, we externally validated each of these models in two different databases. The percentage of the study population experiencing each outcome ranged between ~0.04% to ~4%, enabling us to investigate the impact of development/validation design in big data when the outcome count was small and large.

Limitations of this study include only investigating models developed in one US claims data and in future work it would be useful to repeat this study using more datasets to see whether the results hold. Similarly, we only used one target population, patients initially treated for depression, and future work should investigate whether the results hold across different study populations and outcomes. Finally, we have only investigated the impact of the model development design when developing a LASSO logistic regression. Our results may not generalise to all binary classifiers.

Conclusion

Our study is the first to investigate the impact of model development/validation design on the accuracy of the internal discrimination/calibration estimate and external validation performance when using big data (n=500 000). We compared designs that use (1) all the data to develop and validate a model (no test/validation set), (2) a train/test/validation set (test/validation set), (3) CV with a test set and (4) CV only to estimate the internal discriminative performance across 21 prediction problems. The results showed that the ‘no test/validation set’ design leads to overfitted models that have unrealistically high internal discrimination estimates but the other designs were able to limit overfitting equivalently. These results show that even in big data using a poor design to develop LASSO logistic regression models can impact the accuracy of the internal validation and compromise model generalisability. A useful design requires: (1) a fair process to pick any hyperparameters (eg, a validation set or CV) and (2) a fair process to evaluate the model internally (eg, a test set or CV).

Data availability statement

Data may be obtained from a third party and are not publicly available. The IBM MarketScan Commercial Claims, IBM MDCD and IBM MDCR data that support the findings of this study are available from IBM MarketScan Research Databases (contact at: https://www.ibm.com/products/marketscan-research-databases/databases) but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available.

Ethics statements

Patient consent for publication

Not applicable.

Ethics approval

The use of IBM MarketScan Commercial Claims, IBM MDCR and IBM MDCD was reviewed by the New England Institutional Review Board (IRB) and were determined to be exempt from broad IRB approval. Only deidentified data were used, and informed consent was not applicable.