Modeling the Waves of Covid-19

Abstract

The challenges with modeling the spread of Covid-19 are its power-type growth during the middle stages of the waves with the exponents depending on time, and that the saturation of the waves is mainly due to the protective measures and other restriction mechanisms working in the same direction. The two-phase solution we propose for modeling the total number of detected cases of Covid-19 describes the actual curves for many its waves and in many countries almost with the accuracy of physics laws. Bessel functions play the key role in our approach. The differential equations we obtain are of universal type and can be used in behavioral psychology, invasion ecology (transient processes), etc. The initial transmission rate and the intensity of the restriction mechanisms are the key parameters. This theory provides a convincing explanation of the surprising uniformity of the Covid-19 waves in many places, and can be used for forecasting the epidemic spread. For instance, the early projections for the 3rd wave in the USA appeared sufficiently exact. The Delta-waves (2021) in India, South Africa, UK, and the Netherlands are discussed at the end.

Introduction

The evidence is strong that the exponential growth of the total number of detected infections of Covid-19, denoted by u(t) in this work, can be observed only during short periods. This is in any countries and especially when the middle stages are considered. The corresponding curves are in fact of power type: $u(t)\sim t^r$ (approximately proportional to) in terms of the time t from the beginning of the current wave for some exponent r, which heavily depends on time:  r approaches 1 near the turning point of the spread and then continues to diminish closer to the end of the wave. In many countries (not all), this period (phase 1) is followed by a period of essentially linear-type growth of the total number of infections (phase 2 in our theory).

Methodologically, we consider epidemics as “invasions”, and focus on “transiencies”; momentum managing epidemics is clearly of transitory nature. The resulting theory appeared very exact for modeling Covid-19. This is actually similar to Hastings (2004): “The question of interest was the time course of the epidemic, rather than the final state, which is always one where the disease dies out”. The “predator-prey” system for us is when the protective measures (including self-imposed ones) play the role of “predator”, and the “prey” is the number of infections.

This is significantly different from the SIR-type models, applicable mostly to the initial periods of exponential spread and to final stages of epidemics. SIR-type models were suggested in early 20th century. Since then, it was developed, but the exponential growth until the herd immunity fully develops remains its essential feature. As we will show, the asymptotic periodicity of Bessel functions is absolutely relevant here. Generally, Bessel function and Bessel processes are important in mathematics and physics: they were not employed for epidemics and in invasion ecology as far as we know.

Our approach seems promising in ecology. More specifically, Bessel functions can presumably describe various continuous 2-species models. Following (Hastings 2004), the discretization, different time-scales, 3-species models are natural further steps. See also (Hethcote and Levin 1989; Lewis and Petrovskii 2016). Generally, basic hypergeometric functions and their variants are expected to occur.

The discretization will be discussed only a little. We also do not touch upon in this paper the concept of Momentum Risk Taking from Cherednik (2019), somewhat similar to Kahneman’s “thinking-fast”, which can be considered as a behavioral counterpart of the “transiencies” in ecology.

The most ambitious here are the expectations that the same ODE model the processes of momentum decision making in our brain, but this can be difficult to confirm. The number of neurons involved in the “momentum” analysis of an event is restricted here by the “predator”: restrictions on the allocation of resources of our brain for a particular task. The asymptotic periodicity of Bessel functions provides some “saturation” of its analysis in our brain before switching to something else. Generally, it is surprising that Bessel functions, invented by Daniel Bernoulli long ago, are not one of the main tools in mathematical theory of epidemics, ecology, behavioral science, and beyond.

The usage of the basic and current reproduction numbers $R_0,R$ is common for epidemics. The basic one, $R_0$, is defined as the initial average number of people infected by one person who contracted the virus; see (Carrasco-Hernandez et al. 2017; Cobey 2020; Cushing 2016; Diekmann and Heesterbeek 2014; Hethcote 2000; Hethcote and Levin 1989). However, R can be used only qualitatively for Covid-19 and other epidemics of power growth: the formula $u(t)\sim const{R}^t$ for the total number of infections will stop working very quickly and cannot be of real help for forecasting the spread of epidemics. Mathematically, this is an attempt to approximate power-type functions by exponential ones.

It is not unusual when R is reported as 2, 0.7 or so almost back-to-back in the middle stages of the waves of Covid-19; such fluctuations show that R is highly unstable. They are provided constantly by Robert Koch Institute (for Germany) and quite a few other centers. We replace R by c, the initial transmission rate; in our approach,   c  is a parameter of the whole wave of the epidemic (in a given area).

One of the possibilities to adjust SIR to the power growth of Covid-19 and epidemics of non-exponential type is to assume that $R\approx 1$, i.e. to invoke the theory of resonances. This results in some linear growth of the total number of infections, but resonances are very unstable, which contradicts to what we see with the waves of Covid-19. Our modeling is based on a combination of the local herd immunity, which provides $u(t)\sim t^r$, with the impact of prevention mechanisms, which eventually make $r\to 0$ and result in the saturation of the wave.

One of the most efficient prevention mechanisms is (and always was) the self-restriction of our contacts, for instance avoiding infected areas. The information from disease control centers on the spread of the epidemic is important here, which is obviously “active epidemic management”.

It was already intensively discussed in the literature that the herd immunity can influence the spread of Covid-19 well before it reaches the levels of $70\%$ or so. See e.g. Britton and Ball (2020). The protective measures play a significant role in this reduction. Vice versa, their relaxation can result in the recurrence of the waves of the infection.

We actually make the next step: claim that local herd immunity begins almost from day one and deduce from this the power-type growth of the total number of infections, $u(t)$. The dependence of r on time is captured in our theory via Bessel functions. This approach works very well for many waves (all we considered).

Our theory was posted in the middle of April 2020, when the saturation of the spread was observed only in several countries; they were mostly in phase one, under mode (A) in our terminology. We also provided a variant for phase two, under mode (B), when the hard measures are significantly reduced. The (B)-mode system of ODE appeared really necessary for modeling the spread correctly. Qualitatively, phase two is the switch to some less aggressive management: the phase with relatively low numbers of daily infections.

Generally, the parameter c is such that $u(t)\sim t^c$ in the beginning of the wave. It determines the corresponding Bessel function for the 1st phase. The second phase is described by $u(t)\sim t^{c/2}cos(dlog(t))$ for some d, and the same c. The Bessel-type formula (alone) for u(t) works well “almost” until the saturation for quite a few waves, and can be generally used to forecast their durations and magnitudes.

The spread of Covid-19 in the USA was mathematically quite a challenge for us; the results of our prior efforts are systematically reported in Cherednik (2020a). The first wave in the USA went through several stages, more than with any other countries we considered. Our understanding is that it was so mostly because the protective measures were constantly relaxed in the USA on the first signs of improvements, well before the saturation. This was in contrast to quite a few countries in Europe/Asia during the 1st waves.

The costs and consequences of hard measures, especially lockdowns, are huge. Moreover, the saturation due to the active management is generally not the end of the spread; recurrences of the epidemic are likely if the protective measures are reduced or abandoned. Our theory provides an approach to evaluating the efficiency of the measures and controlling them real-time. Such applications and forecasting the waves are always a challenge. See e.g. Fraser et al. (2004). Though we will provide quite a few examples when forecasting was doable.

Prior Approaches

There is an increasing number of works where the power growth of the total number of infections is considered for modeling Covid-19, though not many and mostly of experimental nature. Let us mention at least (Cherednik 2020a; Manchein et al. 2020; Meyer 2014; Thurner and Klimek 2020).

Well before Covid-19, an ambiguity with the definition and practical calculation of $R_0,R$ was discussed in Cushing (2016): “It is reassuring to know, however, that the sign of $R_0-1$ is independent of the decomposition used and that the prediction of exponential growth or decay is therefore correctly made by any of the counting schemes.” This is our impression too: the sign of $R-1$ is what is mainly used practically, not the exact value of R (calculated by some simple formulas). However the spread was mostly assumed of exponential type in Cushing (2016). Considering $R\approx 1$ was mentioned there: “As far as we know, little can be said in general about the exceptional case that $R_0$ is not strictly dominant”.

In Manchein et al. (2020), the authors comment on the power growth of the spread of Covid-19: “the nature is full of surprises”. In Thurner and Klimek (2020): “this new contamination regime is hard to explain by traditional models”. In our one: “power law of epidemics must be the starting point of any analysis if we want our mathematical models to be up to date”. See also Ray (2020) and works mentioned there concerning a potential usage of small-world interaction network, where individuals are assumed to contact (mostly) local neighbors and have occasional long-range connections.

In a different direction, paper (Britton and Ball 2020) and some other works suggest that the levels of herd immunity sufficient to impact the spread of Covid-19 can be lower than the “classical” 70%, or so: as low as 40% in some areas due to the population heterogeneity. We just make the next step in this direction. Our starting assumption is that local herd immunity shapes the spread from the very beginning of an epidemic and quickly reduces its exponential growth (if any) to the power one. This is related to the concept of small-world.

Spatial modeling. This approach is actually similar to the one via “small-world”. The graph of contacts, especially geographically related ones, is the key for spatial modeling. For instance, Fig. 8 in Bertrand (2021) shows the initial spread of Covid-19 in Germany, which is naturally related to the geographic locations. The authors change there the SEIRD model (susceptible- exposed- infected- recovered- deceased) to SEIQRD by adding the quarantined compartment. Obviously quarantines and travel restrictions are important to model epidemics. See also Fig. 2 from Kergaßner et al. (2020) (Germany too). The population heterogeneity is an important consideration here.

Producing meso-scale forecasts with specific information and for some concrete location is quite a challenge. See e.g. Jha et al. (2020) (for Texas). Partial differential reaction-diffusion equations are used there; see also Viguerie et al. (2021). The total number of detected cases for the whole country (in our approach) is obviously insufficient for those in charge of practical managing the epidemic.

Classical methods “least-squares”, “Bayes”, “k nearest neighbors”, and various statistical tools can be used for “meso-forecasts”. Machine learning is a possibility here, which we will not touch upon. Though this does not help much with theoretical understanding the spread: there are too many parameters and the uniqueness of the optimal ones is not granted.

Surprisingly, the dimension of the graph of contacts is “almost sufficient” for macro-forecasting the number of infections. This is our parameter  c; the total number of infections is then $\sim t^c$ in the beginning of the corresponding wave. Our ODE can be applicable for meso-forecasting, even to viral load in infected individuals, but generally this is a macro-phenomenon (at least in this paper). The uniformity of the curves of total numbers of detected infections in so many so different countries and for different waves is still mysterious to us, though we think that we found proper mathematical tools to address this.

Power growth. The main problem with modeling Covid-19 appeared actually not the power growth itself, “power law of epidemics”, a starting point for us. This alone is insufficient for forecasting. Understanding the saturation is (and always was) the key challenge for modeling epidemics. However, we must note here that even the power growth of the number of infections is not commonly accepted; this is in spite of ample evidence of the power growth during the Covid-19 pandemic.

Practically, the exponents  r in $u(t)\sim t^r$ heavily depend on the time passed from the beginning of the wave of the infection; we use Bessel functions to address this. Though there are quite a few examples of pure power growth of the total number of infections for sufficiently long periods (mostly due to a lack of hard measures): see e.g. Figs. 9, 18.

Fig. 9.

India: 3/20-10/7, $c=5.75,a=0.035,C=0.55$

Fig. 18.

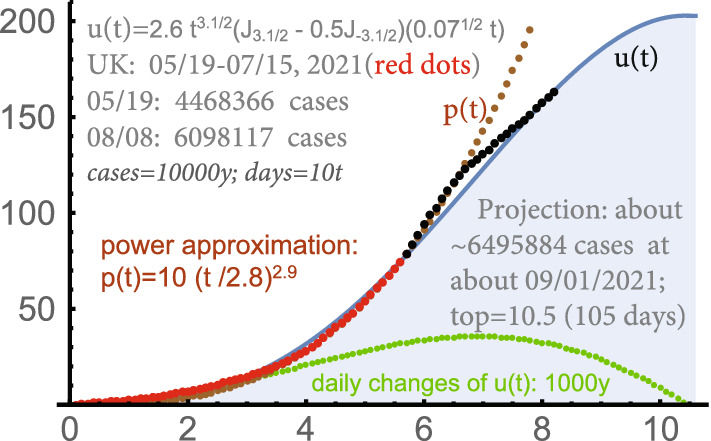
UK: 05/19-08/08, optimization for 05/19-07/15

By now, the power growth (after small initial periods) is obvious in all waves of Covid-19, including the Delta-waves; see e.g. Fig. 18. The theory of this phenomenon was suggested in Cherednik (2020a). There were other papers discussing the power growth. For instance, the data in Fig. 1 in Manchein et al. (2020) demonstrate that the spread is of power type piece-wise, where the exponents depend on the corresponding portions of the wave. This generally cannot be used for forecasting because the exponents change very much during the wave.

Our parameter c serves the whole wave (both phases); we suggest it as a replacement of the classical initial reproduction number $R_0$. Our exponents are quite different practically from the exponents obtained in Manchein et al. (2020) and other papers addressing the power growth. We note that the SEIR model (susceptible- exposed- infectious- removed) was used in Manchein et al. (2020) as a theoretical tool, which does not result in the power growth. However, “small world” is mentioned there as a possibility.

Paper (Thurner and Klimek 2020) is based on the Poissonian small-world network. This approach results in the linear growth ($\sim t$) of the total number of infections. The linear growth is indeed present near the turning points of the curves of total numbers of infections, but it is far from linear anywhere apart from these middle portions and the end of the waves. The explanation of the linear growth and the saturation in Thurner and Klimek (2020) is very different from what we proposed in Cherednik (2020a) and present in this paper.

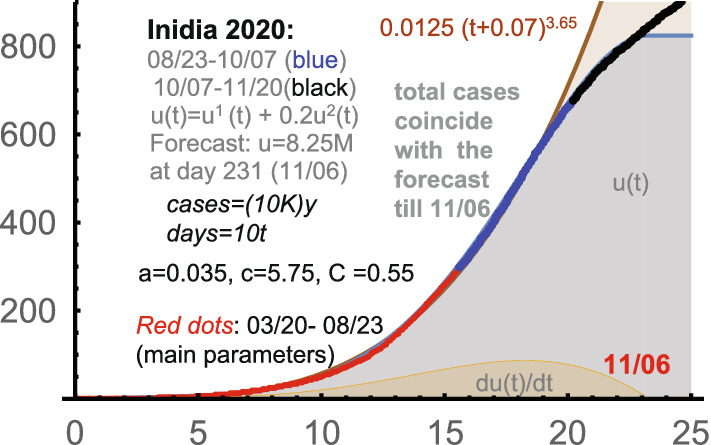
Among many confirmations of the power growth of the total number of infections of Covid-19, the period 3/20-10/7 (2020) in India is very convincing; see Fig. 9. Here $u(t)=const{t}^r$ for $r=3.65$ was practically exact (almost without modifications) for the total number of detected cases in India for a very long period: for at least 5 months (!).

In this figure, the main parameters were determined on 08/03. This forecast was posted on 10/07 (2020): the saturation was predicted on 11/06, which appeared quite exact. Here and in many countries, some linear-type growth was observed after the top of the Bessel-type curve u(t), which can be seen in the graph for India after 11/06.

In our theory, such late periods are described by the formula for mode (B); this is phase 2 in our terminology (for any waves). Generally, the same c serves both phases, and the starting point of both curves is the same: the beginning of the wave.

Saturation of Covid-19 Waves

For us, the saturation, followed by some linear-type growth of the total number of infections, is due to protective measures, mostly the hard ones, and other mechanisms restricting the spread. The key hard measure is detection-isolation-tracing, which includes closing the places where the spread of infection is the most likely. Its societal cost is huge, but it proved to reduced the spread efficiently. The vaccination is obviously a very hard measure, by any standards. Self-imposed restrictions, including reducing our contacts during epidemics, are (and always were) very important too.

Biological mechanisms that limit life of any virus strain or result in strains with mostly mild or asymptomatic cases work in the same direction. Consecutive transmissions mostly destroy or weaken the virus. At later stages, “weakened” genomes of the virus generally dominate, and the corresponding cases are more likely to become asymptomatic or mild. The biological factors can be necessary to explain why the waves can affect only small fractions of population and then “stop”, even with a lack of hard measures in a country.

The mutations that make the virus stronger are rare statistically, but they are always present and can lead to new strains and new waves of the infection. With Covid-19, its “proofreading ability” reduces the total number of mutations but significantly increases the fraction of “constructive ones”. The latter can occur in a single infected individual. It is rare when individuals are infected by 2 different strains at the same time, though such cases can lead to especially dangerous transformations of the virus.

Anyway, if the strain weakened by mutations dominates then the current wave of infection in this area is on its way to the (technical) saturation. Also, generally (not always) the strains with very high transmissibility can become less lethal.

The herd immunity, vaccinations and weakening the virus due to mutations are important factors. However it is not disputed that the saturation of the first 1–2 waves of Covid-19 were not due to these factors. The herd immunity and vaccinations require at least 40–60% (“classically” 70% or greater) of all susceptible population to be affected to start working (Britton and Ball 2020). It was very far from these levels during the first waves. Thus, the saturation mechanism of SIR-type models is not applicable here, at least for the initial waves of Covid-19.

The analysis of the 2nd waves confirms the validity of our approach, based on the prime role of protective measures, mostly the hard ones. Recurrence of epidemics is quite frequent; see e.g. Hethcote and Levin (1989). For Covid-19, the 2nd waves began too quickly, sometimes even on the top of the unfinished first waves, as it happened in the USA. The relaxation of hard measures closer to the end of the 1st (and other) waves definitely contributed to such a kind of recurrence (unusual for epidemics).

In 2020, the summer vacations and closed schools in Western Europe reduced the spread there, which factors worked in the same direction as hard measures. However, at the end of August (2020), the second waves began practically everywhere in Europe. The epidemic resumed in the USA too: approximately from the middle of September.

The parameter  c , which we call the initial transmission rate, appeared increasing from the first to the second wave in many countries. This parameter is one of the main in our theory; it reflects the virus transmissibility strength and the basic number of contacts in the area. We note that we determine   c  for the whole wave; the decrease of transmissiblity due to prevention mechanisms is incorporated via our ODE. Generally, the objective is to reach the best match for the whole wave, then c is taken somewhat different than that determined during the initial stages. The 2nd–3rd waves of Covid-19 appeared to be with greater c, partially due to the reduction of protective measures (including our own behavior). The virus intensified and reached broader areas.

The 2nd key parameter of our theory is a, the intensity of protective measures. It dropped very significantly for the 2nd waves, which was expected. The intensity of the hard measures during the 1st wave was difficult to sustain. The parameter a has a different meaning if the reduction of the spread is due to biological factors. Generally, diminishing   a  means that restrictions of any kind confining the spread are reduced or abandoned: protective measures, our own behavior or various biological factors.

Qualitatively, the duration of the wave is $\frac{1}{\sqrt{a}}$; quantitatively, Bessel functions must be used here. Mathematically, we essentially repeated the first waves, but now with lower levels of  a. Longer periods of intensive spread of infections and, generally, greater magnitudes of the curves of total number of detected infections can be expected if a decreases and c increases. Though, the magnitude depends very much on the ability of the virus to reach new areas, which is not directly connected with a, c. For instance, the 2nd wave in India was with much  greater magnitude for smaller c and greater a vs. the 1st wave there. Obviously the virus evolved and was able to reach new strata of the population during the 2nd wave in India.

Further waves. The mechanisms restricted the duration of the waves became somewhat different for Delta-waves, when the vaccination, herd immunity, and the transformations of the virus due to mutations began to take effect. Significantly longer “linear-type” 2nd phases occurred.

We note a striking similarity of the waves in South Africa and UK under the dominance of the Delta-strain of Covid-19 (March–August, 2021) and (later) in other countries. It indicates that there can be some biological limits for the durations of the waves of Covid-19. The countries can have very different situations (including their health care systems and vaccinations), but the corresponding curves of total number of detected infections appeared quite similar for the Delta-waves.

Analyzing the waves until Summer-Fall 2021, we think that, generally, protection-restriction mechanisms are:

(a): protective measures especially the hard ones, where “detection-isolation-tracing” of infected individuals is the key; (b): self-imposed restrictions by the population directly or indirectly based on the data provided by the authorities in charge; (c): herd immunity, the vaccination programs, and improvements of the treatment of infected individuals; (d): possible weakening the virus due to the mutations of destructive type upon sequences of consecutive transmissions, though the proofreading feature of Covid-19 is an important factor here.

Our ODE seem applicable to all 4. Our main assumption is that N “isolations” or “reductions” of those infected at the moment $t_0$ due to (a, b, c, d) diminish the total number of infections at the moment t by $(t-t_0)N$ with some coefficient of proportionality. Also, the number of “isolations” at $t_0$ is assumed proportional to $u(t_0)$, the total number of detected cases at $t_0$. In system (1) below: p(t), the protection function, is the number of “preventions” at t from all “isolations” that occurred before.

Power Law of Epidemics

With such complex processes as epidemics, there can be of course multiple factors contributing to the power growth, biological ones included (Castro et al. 2018). The “justification” from (Cherednik 2020a) goes as follows. First, we assume that infected people transmit the disease to their (susceptible) neighbors, colleagues, etc., and that the population is distributed uniformly. The second assumption is that the wave of the infections expands linearly in a proper graph of contacts. The third assumption, the principle of local herd immunity, is that people “inside the infection zone” do not transmit the disease because they are surrounded by those already infected or recovered, i.e. the border of this zone mostly contributes to the spread of this disease. This readily gives that $u(t)\sim t^c$ for the exponent 2 or greater (in the absence of protective measures). Indeed, the lowest c we observed was $c=2.2$ (the 1st wave in the USA).

People from infected zones work, do shopping, travel, visit friends. So the higher dimensions N are needed to imbed the graph of contacts into some $R^N$ providing that the geometric distances between points representing people are essentially the numbers of links between them, i.e. that the distance reflects the intensity of the contacts.

Upon this embedding, we assume the uniform distribution of the points in $R^N$ representing people, and the linear spread of the disease in $R^N$. This is basic physics. Then, indeed, $u(t)\sim C{t}^c$, where c is the “dimension” of the image of this graph, a number from 2 to N.

Next, we represent such u(t) as a solution of the differential equation $du(t)/dt=cu(t)/t$. This is standard when we need to add “external forces”, which will be protective measures, more generally, mechanisms restricting the spread of the virus. We argued above that the exponential growth is generally unsustainable. However the power growth is unsustainable in the long term too. This will be “corrected” as follows.

Adding Protection

Combining the initial power growth of the total number of detected infections u(t) with the impact of protective measures, or other factors working in the same directions, we obtain the following two systems of differential equations:

$$\left\{\frac{du(t)}{\mathit{dt}}=c\frac{u(t)}{t}-p(t),\frac{dp(t)}{\mathit{dt}}=au(t)\right\};$$ 1

$$\left\{\frac{du(t)}{\mathit{dt}}=c\frac{u(t)}{t}-\frac{p(t)}{t},\frac{dp(t)}{\mathit{dt}}=\frac{b}{t}u(t)\right\}.$$ 2

Here t is the time from the beginning of the intensive growth of infections, not always the very beginning of the corresponding wave of Covid-19 but sufficiently close to it. System (1) describes the impact of hard measures under the most aggressive response to the spread, or the effect of restriction mechanisms acting in the same direction. The second system describes the impact of the soft measures: some travel restrictions, wearing the protective masks and social distancing are typical. We called these two modes (A) and (B) in (Cherednik 2020a, b).

When $a=0$ in the 1st system and $b=c^2/4$ in the 2nd system, we obtain the power growth $u(t)\sim C{t}^c$. The parameter c can be measured experimentally during the early stages of Covid-19 and is supposed to be the same for (1) and (2). Mostly it was in the range $2.2-2.8$ for the first waves, but reached $c=4.5,5.5$ in Brazil and India during the first waves there.

There is a variant of these systems, when the second equation in (1) is replaced by that from (2), called the transitional (AB)-mode in Cherednik (2020a). It modeled reasonably the 1st waves in the USA, UK, and Brazil, but the usage of (1) and (2) in our two-phase solution appeared sufficient for many countries, without mode (AB).

The protection function p(t) for (1) is basically the number of transmission preventions at t. More exactly, $p(t)={\sum }_i(t-t_i)\approx a{\int }_0^{t}u(\tau )d\tau$, where the sum is over all infected individuals isolated at the moments $0<t_i<t$ for a measuring the intensity of “isolations”. We assume that if not isolated, these people would contribute p(t) to du(t)/dt (so the transmission rate is conditionally taken 1 for them). For (2), $p(t)\sim$ the number of people under various (self-)restrictions.

Logistic modification. Let us touch upon the modification of system (2) under the assumption that u(t) is bounded. We will rescale u(t): divide it by the total number of susceptible individuals. Thus $u(t)<1$ now, and we need to multiply the right-hand side of the 1st equation by $(1-u(t)),$ which models the interaction of infected individual with the remaining (susceptible) ones. We obtain:

$$\begin{array}{cc}& \frac{du(t)}{\mathit{dt}}=(1-u(t))\left(\frac{c}{t},,u,(t),-,\frac{1}{t},,p,(t)\right).\hfill \end{array}$$

In the absence of p(t), it is a well-known logistic equation with the following modification: the interaction is proportional now to 1/t.

The 2nd equation in (2) remains unchanged. It is not clear whether the corresponding solutions are more relevant than those for the original system (2). For the following modification of the 2nd equation, this system can be readily integrated: $\frac{dp(t)}{\mathit{dt}}=b\frac{du(t)}{\mathit{dt}},$ i.e. u(t)/t (the average rate of change) is replaced by the actual derivative (the momentum rate of change). One has:

$$\begin{array}{cc}& u(t)=(\beta +B{t}^{r-\beta })/(r+B{t}^{r-\beta }),r=c-b>0,\hfill \\ \hfill & p(t)=bu(t)+\beta ,\mathit{where}0\le \beta <r,B\ge 0.\hfill \end{array}$$

If $B>0,$ then $u(0)=\beta /r,p(0)=c\beta /r,u(\infty )=1,p(\infty )=b+\beta .$

Related Random Processes

Both systems above are actually from (Cherednik 2019), where they were used to describe the dynamic of the (relative) stock prices p(t) under news-driven momentum trading. The function u(t) there was the news propagation triggered by some event. It is of power growth in terms of time t passed since the event; the corresponding exponents c are generally significantly smaller than 1.

The arguments there were from behavioral finance. This is actually related; the behavioral aspects of epidemics are of obvious importance (Strong 1990). However financial news fades, and this happens quickly (so $c<1$); this is very different for the spread of epidemics ($c>2$). System (1) described in Cherednik (2019) profit taking in stock markets; the second one modeled the “usual” news-driven investing.

We think that these two systems are of very general nature. For instance, they are supposed to occur in any momentum risk taking. This concept, MRT  for short, is from (Cherednik 2019); it is somewhat similar to Kahneman’s “thinking-fast” (Kahneman 2011). Managing epidemics on the basis of the current data is very much momentum. As in stock markets, people and authorities in charge must react promptly to any change of the situation. Another example there is tree growth, though there were no p(t) and the deduction of the equation were somewhat different.

It was expected in Cherednik (2019, 2020a), though without biological evidence, that both systems of equations may describe real neural processes in our brain. Here u(t) is the number of neurons involved in the analysis of a particular event at the moment t, counted from the event, and p(t) is the expected importance of this event and the corresponding expected  brain resources needed for its analysis. I.e. p(t) is basically the expected allocation of resources, which are very limited in our brain. We do not know much about decision-making in our brain, but confirmations of the power laws and related saturations are solid in the stock markets and, as we demonstrate, in epidemics.

We note that a significant part of Cherednik (2019) is devoted to the discretization. Decision-making always requires some action potentials, i.e. it is discrete by its nature. With epidemics, the usage of ODE worked very well so far, though the discretization is expected to be of importance.

Tree growth. We mention that the equation $u_n=u_{n-1}+\frac{u_{n-2}}{n-2}$ describes reasonably middle stages of tree growth. This is a discrete version of $du(t)/dt=cu(t)/t$ for $c=1$ with the maturity set to 1 (1 time-unit, for instance, 1 year). Its obvious solution is $u_n=n$.

Under the initial conditions $u_1=0,u_2=1$, the corresponding solution tends to n/e. This solution is directly related to the derangements $D_n$ in combinatorics: $u_n=D_n/(n-1)!$.

The rationale for this model is that the volume of a tree is approximately proportional to $r^3$, when the area of the root system is essentially proportional to $r^2$, where r is the tree radius, which can be assumed to grow linearly. Thus the “nutrition” provided by the root system to one cubic unit of a tree is proportional to 1/r and to 1/(time). We omit the experimental support for this model; which is applicable to many trees during their middle stages.

The following recurrence is convenient to model the saturation stage of tree growth: $u_n=u_{n-1}+\frac{(n-1)}{(n-2)n(n+1)}{u}_{n-2}$. Its solution with the initial conditions $u_1=0,u_2=\frac{1}{3}$ tends to $2J_0(2)\approx 0.447782$ as $n\to \infty$, for $J_0(2)=1-1+\frac{1}{{(2!)}^2}-\frac{1}{{(3!)}^2}+\dots$; $u_n=\frac{n}{n+1}$ is another solution. We will publish the algebraic details somewhere. The term in front of $u_{n-1}$ is obviously adjusted to make this recurrence “solvable”.

Toward Discretization

We begin with some basics. Let $u_n$ be the total number of infections at the n th moment from the beginning of some epidemic. Infected individuals transmit the disease mostly during some initial period, which we will make the unit of time. Let it be 1 (about 1–2 weeks for Covid-19). The recurrence relation and the corresponding quadratic equation are:

$$\begin{array}{c}\hfill u_n=u_{n-1}+R_0(u_{n-1}-u_{n-2}),{\lambda }^2=(1+R_0)\lambda -R_0.\end{array}$$

Here $R_0$ is the initial reproduction number.

We obtain: ${\lambda }_{1,2}=\frac{(1+R_0)}{2}\pm \sqrt{{(1+R_0)}^2/4-R_0}=\{1,R_0\}$. Thus, $u_n=C_1+C_2{(R_0)}^n$ for some $C_1,C_2$. If $C_2\ne 0$ and $R_0>1$, the growth of the total number of infections will be exponential.

This is unless the herd immunity is expected to be reached, when a difference version of SIR is needed. We will not address this here.

Power growth. Basically, there are 3 main mathematical possibilities to ensure a power growth:

• (i)the presence of “predators”, forces restricting the epidemic spread, for example, various protective measures,
• (ii)when R approaches 1, which results in “resonances” and can potentially provide some linear growth,
• (iii)when the “birth rate”, the transmission rate in this context, becomes inversely proportional to time.

Obviously (i) is applicable: we do fight epidemics. The resonances and linear growth occur when $R\approx 1$, but this is unstable and does not seem of actual importance for modeling epidemics. We think, a combination of (i) and (iii) is the key in epidemics.

The spread of any disease is the growth of the “circles” of those infected; these are combinatorial circles, not geometric ones (in a map of the affected area). The contacts of infected people are not only with their immediate neighbors; people work, study, do shopping, travel. This is the concept of “small world” and the basis of spatial modeling. Our main assumption is that the rate of change of the radii of these circles can be expected constant. However they are not planar ones. The combinatorial distance is in the graph of connections (links) between people: “one’s co-worker” (the distance is 1), “a family member of one’s co-worker” (the distance is 2), and so on. The geographic connections are of course important here, but there are other links too.

The individuals at the frontier of such a circle transmit the disease the most because:

1. they are the “latest” and therefore in their most infectious stages,

2. people inside the circle are “surrounded” by those with immunity.

We assume that the infected people “inside the circle” contribute to the transmission of the disease significantly less than those at its boundary. Then the circle of infected people can be presented as a ball of dimension c; accordingly, the growth of $u_n$ will be $\sim n^c$. Here c can be any positive number, not only an integer. For instance, $c\approx 2$ if our contacts are mostly with those who live near us, but $c\approx 3.65$ in Fig. 9. We never saw countries with $c<2$ during the 1st and the 2nd waves. Recall that c, the initial transmission rate, reflects the virus transmissibility strength and the basic number of contacts in the area. It is constant for the whole wave in our model.

Disregarding the latent period when people are already infected but not infectious, the number of “newly infected people” is basically the area of the boundary of this “ball”, i.e. the area of the corresponding sphere. Presenting this number as $c{u}_{n-1}/(n-1)$, we arrive at the following recurrence: $u_n-u_{n-1}=c\frac{u_{n-1}}{(n-1)}.$ Asymptotically, $n^c$ is a solution of this recurrence. Let us comment on this.

We have $u_n=(1+\frac{c}{n-1})(1+\frac{c}{n-2})\cdots (1+c)u_1$. Therefore, $log(u_n)\approx log(u_1)+c{\sum }_{m=1}^n\frac{1}{m}\approx log(u_1)+clog(n)$ and $u_n\approx n^c{u}_1$. More exactly, $u_n\approx \frac{n^c}{\mathrm{\Gamma }(c+1)}{u}_1$ for the Gamma function $\mathrm{\Gamma }$. When $c=r$ for a positive integer r:  $u_n=u_1\frac{1+r}{1}\frac{2+r}{2}\cdots \frac{1+2r}{1+r}\cdots \frac{n-1}{n-r+1}\cdots \frac{n+r-1}{n-1}=\left(\begin{array}{c}n+r-1\\ r\end{array}\right)u_1$.

Adding protective measures. In the most aggressive variant of protective measures (or similar restriction mechanisms) we have:

$$\begin{array}{c}\hfill u_n-u_{n-1}=c\frac{u_{n-1}}{n-1}-p_{n-1},p_n-p_{n-1}=a{u}_{n-1},\end{array}$$ 3

where a is the intensity of hard measures (or other restriction mechanisms); $p_n$ is basically the number of “preventions” at n, which we subtract from the total number of infections in the 1st equation.

This is parallel to the differential case; see (1). The main point here is that the “isolation” of one infected individual prevents the number of future virus transmissions roughly proportional to the time passed from this isolation. Then $p_n-p_{n-1}$ is proportional to the current total number of infections.

Let us eliminate $p_n$ from these relations. We obtain that $p_{n-1}=\left(1,+,\frac{c}{n-1}\right)u_{n-1}-u_n$, $p_n=(1+\frac{c}{n})u_n-u_{n+1}$, and

$$p_n-p_{n-1}=\left(1+\frac{c}{n}\right)u_n-u_{n+1}-\left(1+\frac{c}{n-1}\right)u_{n-1}+u_n=\left(2+\frac{c}{n}\right)u_n-\left(1+\frac{c}{n-1}\right)u_{n-1}-u_{n+1}=a{u}_{n-1}.$$

Finally, we obtain the recurrence relation:

$$\begin{array}{c}\hfill u_{n+1}=(2+\frac{c}{n})u_n-(1+a+\frac{c}{n-1})u_{n-1}.\end{array}$$ 4

When $a=0$, we have the solution $u_n=n$ for any c. This is for $u_1=1,u_2=2$. For $a=0$ and arbitrary  initial conditions $u_1,u_2$, the “function” $u_n$ is essentially proportional to $n^c$, which follows from (3). When $c=0$, this equation is not applicable: $p_n=u_n-u_{n+1}$, the amount of protective measures, cannot be negative. Recall that $u_n$, the total  number of cases, cannot decrease.

Figure 1 is an example of the calculation with (4), where $a=0.1,c=2.2$, and we begin with $u_1=1,u_2=3$. We must stop at $n=8$ (week 8 if the unit is one week), which is the saturation; the total number of cases cannot decrease. We note that the whole u(t) (including its negative part) can be considered here and below, if u(t) is understood as the difference of the total numbers of infections in two different areas, say in 2 hemispheres.

Fig. 1.

Discrete modeling the number of infections

Two-Phase Solution

The solutions of (1) and (2) we need are

$$\begin{array}{cc}& u^{1,2}(t)=t^{(c+1)/2}{J}_{\pm \frac{c-1}{2}}(\sqrt{a}t),\hfill \\ \hfill & u_B(t)=t^{c/2}cos(dlog(Max(1,t))).\hfill \end{array}$$

Here $J_{\alpha }(x)={\sum }_{m=0}^{\infty }\frac{{(-1)}^m{(x/2)}^{2m+\alpha }}{m!\mathrm{\Gamma }(m+\alpha +1)}$ are Bessel functions  of the first kind; Watson (1944) (Ch.3, S 3.1). The solution $u^1(t)$ (the sign is $+$) is the main; the second (non-dominant) solution $u^2(t)$ is for −. The function $u_B$ is for $d=\sqrt{b-c^2/4}>0$, to be used to model later stages of the waves.

Our two-phase solution is the usage of a proper linear combination u(t) of $u^{1,2}$ for phase 1, which is until u(t) reaches its top or (mostly) somewhat before this moment, and then the usage of $u_B$ for phase 2. Importantly: $(a)$ the same c is used in both stages, and $(b)$ $u_B(t)$ is calculated from the beginning of the wave, though it will be “seen” only later.

The 2-phase solution proved to be quite exact for modeling the curves of total numbers of detected infections of Covid-19. For $t\approx 0$: $u^1(t)\approx t^c$ and $u^2(t)$ is approximately $\sim t$. I.e. $u^1$ dominates for such t. This holds for any time, though $u^2$ capture some features. For forecasting, $u^1(t)$ is mostly sufficient.

The second fundamental solution of system (2) is with $sin$ instead of $cos$, not used below. We note that when the protective measures are really modest, $D=c^2/4-b>0$. The leading fundamental solution is $t^r$ in this case, with $r=c/2+\sqrt{D}$, i.e. $t^c$ in the beginning of the spread diminishes to $t^{c/2}$ and then remains unchanged. This is of importance, but we will not touch the range $D>0$ in this work.

The 1st waves (2020). We mainly follow (Cherednik 2020a). In all figures, the horizontal t-axis is always the time measured in days from the beginning of the wave divided by 10. The y-axis gives the total number of detected cases from the beginning of the wave, and is divided by a proper power of 10. For all waves: it is 10K unless for Japan (1K,1M), USA (always 100K), and India (10K, 100K).

Italy: 2/22-5/22, 2020. Figure 2. The total number of infections was 17 on 2/22. We always subtract the initial value when calculating our dots and the total numbers of detected infections. One has:

$$\begin{array}{cc}& u^{1,2}(t)=0.8t^{(c+1)/2}{J}_{\pm \frac{c-1}{2}}(\sqrt{a}t),u(t)=u^1(t)-u^2(t),,\hfill \\ \hfill & u_B(t)=2.85t^{c/2}cos(dlog(Max(1,t))),c=2.6,a=0.2,d=0.5.\hfill \end{array}$$

We use here both fundamental solutions $u^{1,2}(t)$ of system (1).

Fig. 2.

Italy 2020: $c=2.6,a=0.2,d=0.5$

Germany: 3/07-5/22, 2020. See Fig. 3. We began with the initial number of total infections 684 (subtracted). This was approximately the moment when a systematic management began. One has:

$$\begin{array}{cc}& u(t)=1.3(t^{(c+1)/2}(J_{+\frac{c-1}{2}}-0.7J_{-\frac{c-1}{2}})(\sqrt{a}t)\mathit{for}c=2.6,\hfill \\ \hfill & u_B(t)=2.95t^{c/2}cos(dlog(Max(1,t))),a=0.35,d=0.56.\hfill \end{array}$$

Fig. 3.

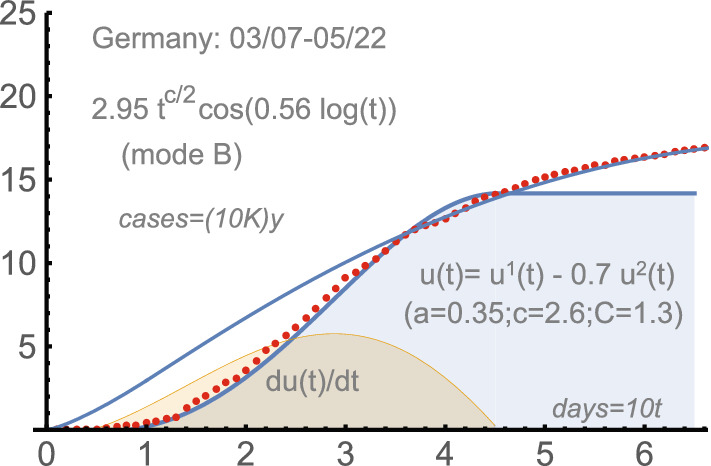
Germany 2020: $c=2.6,a=0.35,d=0.56$

Japan: 3/20- 5/22, 2020. See Fig. 4. There was some prior stage; we subtract 950, the total number of infections on March 20. The curve for Japan is not too smooth, which is not unusual. However it is managed well by our 2-phase solution :

$$\begin{array}{cc}& u(t)=1.5t^{(c+1)/2}(J_{+\frac{c-1}{2}}-0.4J_{-\frac{c-1}{2}}(\sqrt{a}t),c=2.6,\hfill \\ \hfill & u_B(t)=3.15t^{c/2}cos(dlog(Max(1,t))),a=0.3,d=0.6.\hfill \end{array}$$

Fig. 4.

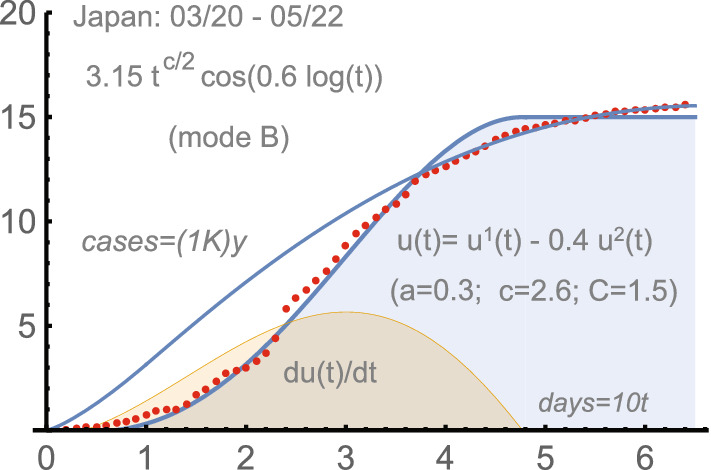
Japan 2020: $u=1.5t^{1.8}(J_{0.8}-0.4J_{-0.8})(t\sqrt{0.3})$

UK: 03/16-06/13, 2020. This country was a challenge for us, though it “eventually” managed to reach phase 2. Actually the red dots  for UK are modeled better with the transitional (AB)-mode. However, we prefer to stick to the “original” u(t) determined for the period till April 15. The two-phase solution is a combination of two phases separated by a linear period, about 10 days. See Fig. 5. The formulas are:

$$\begin{array}{cc}& u(t)=2.2t^{(c+1)/2}{J}_{\frac{c-1}{2}}(\sqrt{a}t),c=2.4,a=0.2,\hfill \\ \hfill & u_B(t)=4t^{c/2}cos(dlog(Max(1,t))),d=0.465.\hfill \end{array}$$

The Netherlands: 03/13-5/22, 2020. The u-function here is with the same a, c as for UK. The parameter $d=0.54$ is different from that for UK ($d=0.465$). This could be expected; the process toward the saturation of phase 2 was slower for UK.

Fig. 5.

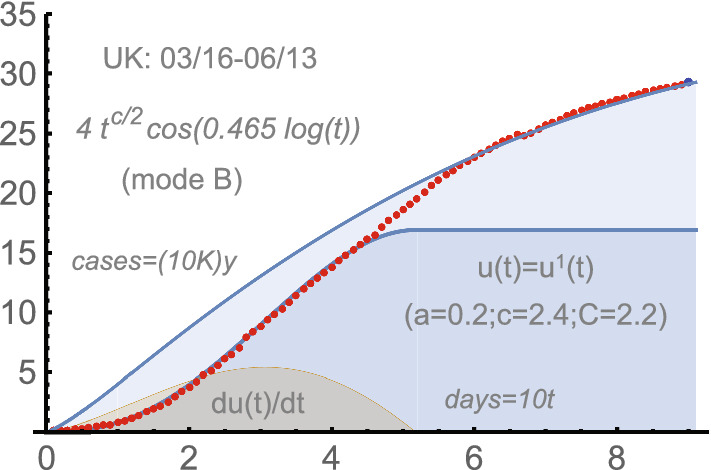
UK 2020: $u=2.2t^{1.7}{J}_{0.7}(t\sqrt{0.2})$

See Fig. 6. The number of the total case was 383 on 3/13, the beginning of the intensive spread from our perspective. The usage of the dominant $u^1$ appeared sufficient:

$$\begin{array}{cc}& u(t)=0.5t^{(c+1)/2}{J}_{\frac{c-1}{2}}(\sqrt{a}t),c=2.4,a=0.2,\hfill \\ \hfill & u_B(t)=0.86t^{c/2}cos(dlog(Max(1,t))),d=0.54.\hfill \end{array}$$

Fig. 6.

The Netherlands: $u=0.5t^{1.7}{J}_{0.7}(t\sqrt{0.2})$

Further Waves

The mathematical similarity of the 2nd–3rd waves to the 1st waves is very remarkable, a strong confirmation of our approach. The parameters a, c, b though changed, which is mostly in an understandable way. The 2nd waves were quite uniform in Western Europe. The Netherlands is convenient to demonstrate the evolution of our parameters because the corresponding u-function does no involve the second, non-dominating, Bessel-type solution.

The Netherlands: the 2nd wave, 08/24-11/23, 2020. The similarity of Figs. 6 and 7 is obvious. Compare with the similarity of the 1st, 2nd, and 3rd waves in the USA to be discussed below.

Fig. 7.

The 2nd wave in the Netherlands

For the second wave in the Netherlands, one has:

$$\begin{array}{cc}& u(t)=0.7t^{(c+1)/2}(J_{+\frac{c-1}{2}}(\sqrt{a}t),c=3.4,\hfill \\ \hfill & u_B(t)=1.65t^{c/2}cos(dlog(Max(1,t))),a=0.085,d=0.43.\hfill \end{array}$$

The parameter c significantly increased in the Netherlands: from 2.4 (the 1st wave) to 3.4 (the 2nd). The intensity of the hard measures understandably dropped: from 0.2 to 0.085. Such changes are actually common for the second waves in Europe. The parameter $d=0.43$ in $u_B$ diminished from the prior one: 0.54. Our projection worked well until the beginning of December, a pause before the 3rd wave.

In December of 2020, almost all Western Europe reached a modest linear-type growth of the total number of detected infections. Somewhat later, the 3rd waves began in Europe on top of the unfinished 2nd waves later. The usage of protective measures diminished, which can be partially due to the holiday season. The self-imposed restrictions are of obvious importance here; their reduction contributed too. The new strain, Alpha, was quite a factor of course. Anyway, the intensity parameter a diminished further for the 3rd waves in Europe.

Japan: the 4th wave. See Fig. 8. It began in March, 2021. We take the period 03/15-5/25, 2021. The formula for u(t) is:

$$\begin{array}{cc}& u(t)=0.23t^{c/2+0.5}(J_{c/2-0.5}(\sqrt{a}t)+0.53J_{0.5-c/2}(\sqrt{a}t)),\hfill \\ \hfill & wherec=2.8,a=0.08.\hfill \end{array}$$

The tendency for c to somewhat increase and for a to drop is similar for that in other countries we considered. Here we did not create the control period; all dots are red.

Fig. 8.

The 4th wave in Japan, 2021

The 1st wave in India: 3/20-10/07-11/20, 2020. This country provides important mathematical patterns of the dynamic of the spread of Covid-19. The (clear) first wave was later than in quite a few countries, but it was with the greatest c we observed. The starting number of detected cases was 191, which was subtracted.

The power function $0.0125{(t+0.07)}^{3.65}$ gave a surprisingly good approximation for more than 5 months; see Fig. 9: the whole red period and almost all blue period. Such a clear power growth is a very convincing argument in favor of the power law of epidemics. This kind of growth is the starting point of our approach.

The exponent r in $u(t)\sim t^r$ began to decrease to $r\approx 1$ (the turning point) much faster in other countries. Obviously, the size of population and its huge density in some parts of India are important factors. Also, the unusual stability of the exponent here, $r=3.65$, can be linked to a relatively low level of the active management of Covid-19 during the first wave in India (in the affected areas). In our theory, the waves under active management cannot be of pure power type too long.

In Fig. 9, the parameters a, c, C were determined around 08/03, 2020, i.e. actually before the turning point. They were considered conditional (to be improved later), but they worked until the saturation. After the turning point, they became significantly more reliable. Notice that $c=5.75$ is different from $r=3.65$ from the general approximation $u(t)\sim t^r$. The Bessel functions provide the time-evolution of the exponent from c to $1$, and then all the way to $0$.

The conditional projection was that a (technical) saturation could be around 11/6 with 8.25M of (total) cases. It matched the actual numbers. As almost always, a linear-type growth period (mode (B)) was expected somewhat before the top of the Bessel-type curve u(t). This period can be seen in the graph; it is described by $u_B(t)$. The parameter c is the same for phase 2 as it was for phase 1 (used in the Bessel-type u(t)). Recall that $u_B$ always begins from the starting point of the wave: “as if it were no phase 1”. We omit $u_B$ for India.

Let us mention here that our computer forecasting programs are for the 2nd phase only. They find the best $u_B(t)$ (from point 0) approximating the last 20 points. See below. It is not supposed to begin at 0, but it is frequently close enough to this point (unless there are recent significant changes of the trend). See e.g. Fig. 21.

Fig. 21.

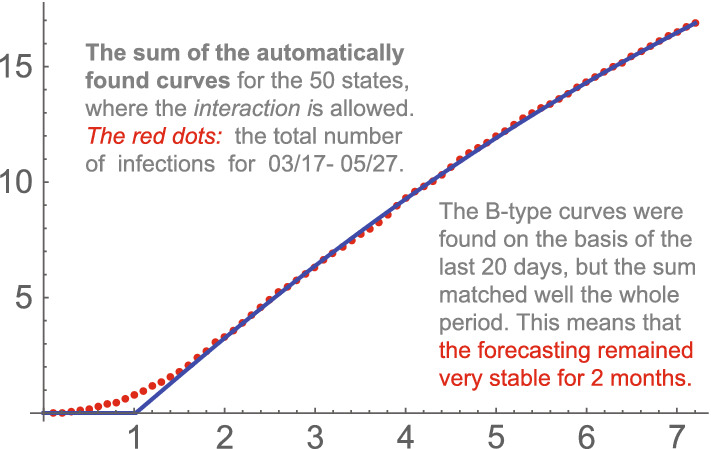
USA, the sum of the curves for individual states

In this figure, $y=$cases/10K; similarly, y is the total number of cases divided by proper powers of 10 in the other charts we will consider. It depends, for instance, we divided “cases” by 100K for the USA. The x-axis is always time in days divided by 10 from the beginning of the curve. The red-blue-black dots give the corresponding actual total numbers of the detected cases. The u-function for India (the 1st wave) is:

$$\begin{array}{c}\hfill u(t)=0.55t^{c/2+0.5}(J_{c/2-0.5}(\sqrt{a}t)+0.2J_{0.5-c/2}(\sqrt{a}t)),\end{array}$$

where $c=5.75,a=0.035$. It matched well the actual numbers of cases until the middle of December (until the 2nd phase of the 1st wave).

The 2nd wave in India: 03/25-05/25, 2021. The corresponding u-function is

$$\begin{array}{cc}& u(t)=15t^{c/2+0.5}(J_{c/2-0.5}(\sqrt{a}t)+0.4J_{0.5-c/2}(\sqrt{a}t)),\hfill \\ \hfill & \text{where}c=2.85,a=0.14.\hfill \end{array}$$

We note that the parameter c, which is the key, became smaller  than during the 1st wave in India, though there is a somewhat greater contribution of the second solution $u^2$, the term $0.4J_{0.5-c/2}(·)$.

Generally, the latter can influence c, a (but not too much). Its “role” in our calculations is mostly to adjust better the early stage of the wave. At later stages, $J_{0.5-c/2}(t)$ becomes negative. So its presence with a positive coefficient can require greater values of C. Recall, that this term was $0.2J_{0.5-c/2}(·)$ for the 1st wave in India. See Figs. 10, 11.

Fig. 10.

India: 2nd wave (1), $c=2.85,a=0.14,C=15.$

Fig. 11.

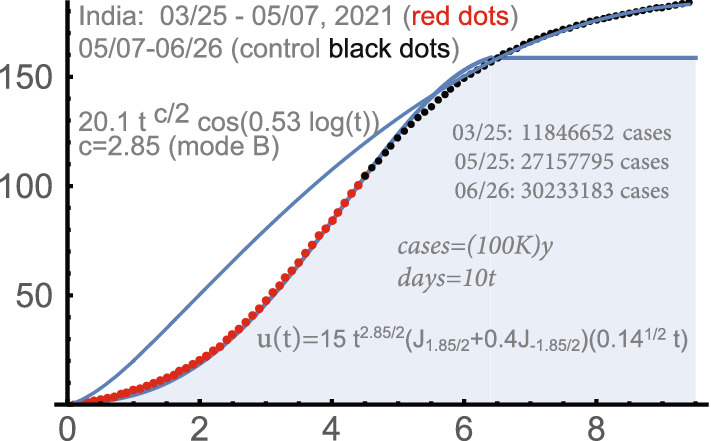
India: 2nd wave (2), 2-phase solution

The coefficient a for the 2nd wave is quite similar to those for the 1st waves in Europe, and greater than those for further waves in Europe and the USA. Recall that the duration of the wave is qualitatively proportional to $1/\sqrt{a}$. Indeed, the duration of the 2nd wave in India was smaller than that of the 2nd–3rd waves in the USA and Europe.

The coefficient c coincides  with that for the 3rd wave in the USA; it is much smaller than the one for the 1st wave in India, which was 5.75. Generally, this means that the population of India and the authorities in charge reacted faster when the 2nd wave arrived, and the number of contacts with those infected was reduced faster than with the 1st wave. The self-imposed restrictions are very efficient protective measures. This includes the restriction of contacts, prompt contacting the medical authorities, preemptive medicine, masks, physical distancing etc. The parameter a increased from 0.035 (the 1st wave) to 0.14.

India faced the Delta-strain during the 2nd wave, significantly more virulent. For instance, the likelihood increased dramatically for the whole family to become infected if one of its members is infectious vs. the 1st wave according to Indian medical officials. The virus acquired greater ability to penetrate practically all strata and age groups of this very large and diverse country. This resulted in a much  greater number of detected cases and in the jump of the magnitude C. The latter is just mathematical scaling. However, when comparing different waves in the same  country, it contains valuable information.

The control period was until 06/26/2021. The accuracy of the Bessel u(t), for the 1st phase of our 2-phase solution, was very high. As it was with many waves, the first phase “smoothly” switched for this one to the 2nd phase (mode (B)). The formula for the 2nd phase of this wave in India was : $u_B(t)=20.1t^{c/2}cos(0.53log(t))$.

We note that in the USA and Europe, the changes between the first 2–3 waves were mostly due to the relaxation of the hard measure (including self-restrictions), i.e. due to a very significant drop of the coefficient a. Some increase of c was of the same origin. However in India, c diminished, a increased, and the magnitude dramatically increased: so the virus itself evolved: became a “broader one”.

Generally, the changes of c, a, C can be used to analyze the trends in the virus’s evolution, though they are very much linked to our response to the threat, not really “biological”.

USA: Waves 2 and 3

We use these waves to adjust the forecasting component of our theory. The 3rd wave was especially useful to understand the possibility of “early forecasts” for sufficiently long periods. This appeared possible, assuming that the virus did not change too much. The Delta-strain can be managed too (wave 4 in the USA), but the early forecasts (before the turning point) appeared not too exact: the curves of total number of detected cases for this strain are somewhat different from the prior ones, though not significantly.

The 2nd wave in the USA: 06/16-9/12, 2020. The two-phase solution worked well for the 2nd wave in the USA. The accuracy is comparable with what we had above for the 1st waves in Japan, Italy, Germany, the Netherlands and UK. Upon subtracting 2.1M, the 2nd wave matched well the following functions:

$$\begin{array}{cc}& u(t)=3.4t^{(c+1)/2}(J_{+\frac{c-1}{2}}+0.6J_{-\frac{c-1}{2}}(\sqrt{a}t),c=2.65,\hfill \\ \hfill & u_B(t)=4.1t^{c/2}cos(dlog(Max(1,t))),a=0.06,d=0.435.\hfill \end{array}$$

We note that the initial transmission rate was $c=2.2$ for the USA during the first wave, so it increased. The parameters c, C and 0.6 in the first formula were determined for the period marked by the red dots; the black dots formed the control period. See Fig. 12. The projected saturation moment for $u_B$ (the 2nd phase) is given by the formula $t_{\mathit{end}}=exp(\frac{1}{d}ta{n}^{-1}(\frac{c}{2d}))$. Numerically, $t_{\mathit{end}}=17.8463$, which is 178 days from 06/16: December 11, 2020. This did not materialize since the USA entered the 3rd wave in the middle of September.

Fig. 12.

2-phase solution for the 2nd wave in the USA

USA: the 3rd wave, 2020-21. This wave was used for long-term forecasting, which we will describe in 3 figures.

The 3rd wave was on top of the unfinished 2nd wave; we subtract the starting total number of infections, which was about 6.9M on 9/24, when our u(t) begins. The red dots used to determine the parameters of u(t) were taken from 9/24 to 11/17/2020, before the 3rd wave in the USA reached the turning point. The early projections based on our approach can be valuable.

The 1st control period (black dots) was until 12/13. The match was good: see Fig. 13. The accuracy became even better later, in March.

Fig. 13.

The 3rd wave in the USA (1)

The formula obtained on 11/17 for u(t) was as follows:

$$\begin{array}{cc}& u(t)=5.5t^{(c+1)/2}(J_{+\frac{c-1}{2}}+0.65J_{-\frac{c-1}{2}}(\sqrt{a}t),\text{for}c=2.85,a=0.02.\hfill \end{array}$$

So the new c for this wave increased to 2.85 from $c=2.65$ for the 2nd wave, similarly to the passage from the 1st wave to the 2nd. The parameter a significantly dropped again: from $a=0.06$ for the 2nd wave to 0.02, i.e. threefold. We note that a was 0.2 for 1st wave, so the same tendency persisted. Recall that the duration of phase (A) is qualitatively $\sim \frac{1}{\sqrt{a}}$.

The projection for the saturation of the 3rd wave in the USA was 03/05/2021. It was supposed to be followed by some period of modest (essentially linear) growth under the (B)-mode (the 2nd phase). This projection was posted on 11/17/2020; see Fig. 14. The 1st control period (black dots) was until 12/13. The match was good: see Fig. 13.

Fig. 14.

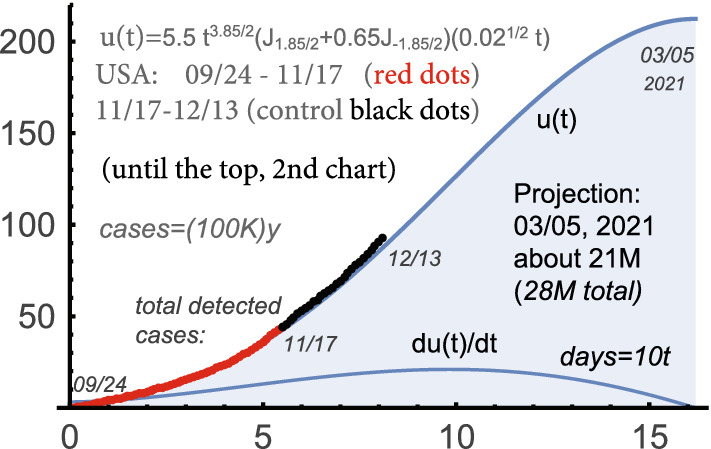
The 3rd wave in the USA (2)

The next control period was until the expected expiration; it is presented in Fig. 15. The accuracy of this forecast appeared even better in March than in December. The early forecasts can be sometimes no worse than later ones, but this is not really “scientific”.

Fig. 15.

The 3rd wave in the USA (3)

We mention that the 1st wave in the USA was with some “unusually long” linear-type periods in the middle. Because of this, forecasting the 1st wave was more difficult with the USA than in almost any other country we considered. This was not the case with the 3rd wave. Note that the massive vaccination began in the USA somewhat later; it did not influence the 3rd wave too much.

The 3rd wave in the USA was followed by some break until the 4th wave began. The 4th one was exceptionally small and short in the USA: until July 4 or so. The country already reached the first stages of the herd immunity (for the current strains) in the middle of March, the vaccination program began to contribute, and the summer time helped. However the new Delta-wave began in the USA in Summer 2021 after the 4th wave. It appeared quite possible to use our tools for its analysis, but we will focus on South Africa, UK, and the Netherlands.

Delta-Waves

Let us discuss the Delta-waves in UK and South Africa ($ZAF$), though it was not only under Delta in the latter. The curves of the total number of detected cases in these countries are similar, and this is applicable to other Delta-waves.

The Delta-waves were with 3 clear segments; a relatively slow growth presumably when the Delta-strain was establishing its dominance, then a period of fast power-type growth followed by a relatively fast decline of the number of daily cases until it became constant (though not a small one). In UK, the function $10{(t/2.8)}^{2.9}$ approximated well the number of total cases for the 2nd segment. This was similar to the Delta-waves in other countries. Such a 3-segment structure was not observed before, and made early forecasting more difficult (but doable).

The program of intensive vaccination of population in UK and summer vacations in July–August certainly contributed to the decline of the number of daily cases (in spite of the relaxation of the protective measures). It is quite possible that the biology of the virus was an important factor here. Generally, viruses can be expected to lose their strength after sufficiently long sequences of transmissions and to evolve in the direction of higher transmissibility but greater numbers of mild and asymptomatic cases. Recall that only detected cases matter for us.

The chart for South Africa is quite similar to that in UK. Obviously UK and South Africa are in very different situations concerning the health care systems, the vaccinations and other factors. These charts are similar to the graph of total number of detected infections for the Delta-wave in the Netherlands in Fig. 20, though the latter is somewhat sharper and the duration of phase (A) is relatively short. This is probably due to the impact of the summer vacations and the intensive vaccination. Importantly, the later stages of the curves for the Delta-waves were with high numbers of new daily cases.

Fig. 20.

The Netherlands-2021: the Delta-wave

For the Netherlands, we provide the corresponding 2-phase solution in Fig. 20. Phase (B) can be clearly seen for UK too. There are some changes here versus our usual approach: we change the c coefficient from that for phase (A). Generally, the parameters of phase (B) are supposed to be found by automated programs and  the beginning of $u_B(t)$ can be not the origin of the wave, imposed in our 2-phase solution. In October 2021, new waves began in both countries.

In these 3 countries, Israel and some others, phase (B) of the Delta-waves was with relatively high number of new daily detected infections, longer than we observed before, and with some oscillations (which we do not observed before). This can be related to the impact of the vaccinations. Namely, the infection continues to spread but the number of asymptomatic and mild cases significantly increases and the effect of vaccinations  fades in time, as well as the impact of natural immunity for those who had Covid-19 before. Such “essentially linear” periods after the end of phase (A) look more standard (for us) in India, South Africa, Japan etc.

In South Africa, one  u-curve was essentially sufficient to approximate all 3 segments; see Fig. 16. In UK, the spike during the 2nd segment was somewhat beyond the u-curve providing the optimal approximation which is presented in Fig. 18. The projections focused on the 2nd, the most intensive, segment (until 7/15) were naturally higher; compare Fig. 18 with 19, and Figs. 16 with 17.

Fig. 16.

South Africa: 05/04-08/08, with the focus mostly on the initial relatively slow period till 06/26

Fig. 19.

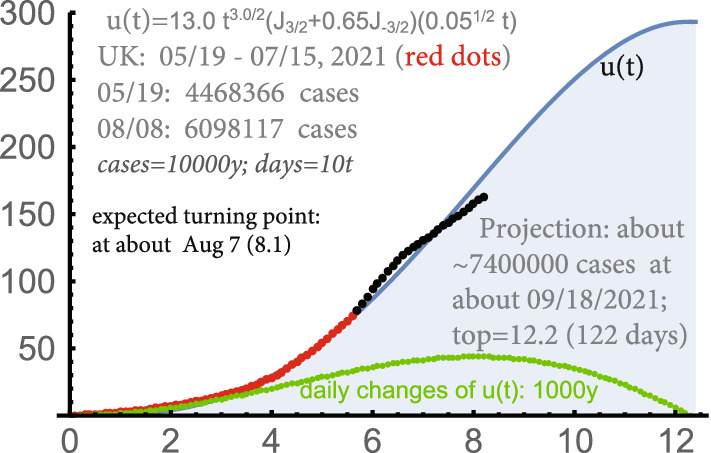
UK: 05/19-08/08, with the focus on 06/15-07/15

Fig. 17.

South Africa: 05/04-08/08, focus mostly on the period of relatively fast growth from 06/15

Figures 16 and 17 provide the projections for $ZAF$ with the red dots until 06/26/2021 and until 07/15/2021 respectively. For UK, this period was until 07/15/2021, but it was used somewhat differently in the figures. Recall that the dots, red and black (the control periods), are for the total number of detected cases minus the initial values. The projections are in terms of the absolute total numbers of detected cases (from the very beginning of the epidemic).

Auto-forecasting

We mostly did this for the USA and Western Europe, but any waves can be “processed” during their 2nd phases, which is under mode (B). Currently, there is no software for the 1st phases, i.e. for the periods “under” the Bessel-type modeling.

The USA: from 03 to 05, 2020. We will provide the automated forecast for 50 states based on the period 03/17-05/27; the data were from https://github.com/nytimes/covid-19-data. Every state was processed individually; see (Cherednik 2020a) for details. Here we allow the curves for individual states to become decreasing as far as the total sum increases, which is some kind of interaction motivated by physics.

Our program focuses on the last 20 days; however, the match with the total number of detected infections appeared almost from 03/17/2020. See Fig. 21 and compare it with Fig. 23.

Fig. 23.

A sample forecast in the USA: 06/09/2021

Such a high level of stability is rare in any forecasting, which made the chances good for reaching the saturation around 9/19/2020. This was our projection based on Fig. 21 and on the assumption that the level of protective measures would remain essentially unchanged. Recall that the saturation for phase 1 is of technical nature: it does not mean the end of the wave. Normally, it is followed by a period of modest linear growth of the total number of infections, which we model using $u_B(t)$; this is the 2nd phase. Also, there are always remaining and new clusters of infection and no country is really isolated. In some countries, mode (A) alone was almost sufficient until the end of the wave; however, the second phases were mostly present.

Concerning the projection 9/19/2020 in the USA, the hard measures were significantly reduced there at the end of May practically in all 50 states. As a result, the number of states that reached phase 2 dropped from about 22 at 5/27 to 8 at 7/12 (2020). Then, in the second half of June, the USA entered the second wave.

Similarly, the program was quite stable for phase 2 for the 2nd wave in the USA before it entered the 3rd wave in the middle of September of 2020. We recall that the program is written for the 2nd phase only, when constant adjustments of projections are needed. A posteriori, using the data for the whole  wave, we never had difficulties with finding the parameters b, d for the 2nd phase.

Europe: Summer 2020. The situation with Covid-19 was reasonably stable in Europe during Summer 2020. We provide in Fig. 22 a sample forecast our automated system produced for Western Europe till the end of July, 2020. It was for 45 countries.

Fig. 22.

An auto-forecast for Europe as of 7/14 (2020)

Here and below the curve average  is as follows. We consider the average of the 9 last curves $u_B(t)$ (for 9 consecutive days) and then find its maximum: the top value. The 9-day average  is the simple average of the corresponding maxima for these 9 curves, a usual moving average. The main source of Covid-19 data we used was: https://ourworldindata.org/coronavirus.

As of July 8, 2020, the forecasts were sufficiently stable, though Sweden, Poland, Portugal and some other countries did not reach phase 2 at that time. Such stability changed in Fall 2020 due to the end of the vacation periods and the beginning of the school year.

Summer 2021. Fig. 23 provides an auto-generated projection for the USA as of 06/09/2021. This was without the state-by-state analysis: the total number of detected infections for the whole country was used. Such projections are supposed to be constantly renewed during phase 2. The fact that the curve of (actual) detected cases was very well approximated by our $u_B(t)$ for the whole period of 90 days is very remarkable; only the last 20 days are used for finding the (current) parameters. This is a strong confirmation of our theory of the (B)-mode. The USA was in the middle of the intensive vaccination program during this period. Also, it approached the initial levels of herd immunity (for the current strains) in March–May.

For Europe in Summer 2021, a similar projection is provided in Fig. 24. Similarly to the USA, an almost perfect match with the actual data was for the whole period of 90 days (only the last 20 days were used by the program), so this is another indication of stability of such forecasts. The growth of the number of the cases was expected in Fall 2021 in Europe, the USA and other countries due to the continued impact of the Delta-strain and the end of summer vacations.

Fig. 24.

A sample forecast in Europe: 06/08/2021

We emphasize that generally we need to switch to auto-forecasting during phase (B), where c is not assumed to be the same as for (A), and the initial point can be different from the origin of the wave (which we imposed in out 2-phase solution).

The vaccines created for the initial strains appeared efficient for the Delta-strain and Alpha-strain, which was of great importance. Generally, significant modifications and recombinations of the existing strains can be expected to emerge, including new strains evading the existing vaccines. The vaccination programs and the natural herd immunity alone can be insufficient to stop the new waves: it is expected that the protective measures remain important to fight the epidemic. Much will depend of course on the further evolution of the virus. We note that the “classical” seasonal periodicity of the waves appeared not really applicable to Covid-19.

According to the latest data, the periodic vaccination of the population, improvements with the treatment of Covid-19, the sequence “detection-isolation-tracing”, and all kinds of imposed and self-imposed restrictions will continue to be the key.

Hopefully we will be better prepared to new cycles of Covid-19, including improved mathematical tool for forecasting the spread of epidemics, better understanding the uniformity of the waves of the infections, and automated methods for finding the parameters of the spread. The purpose is of course to make solid mathematical predictions for the durations and magnitudes of the waves of infections.

Concluding Remarks

Modeling Covid-19 appeared quite a challenge for existing mathematical methods, which are mostly based on the SIR-type approach, suggested in the early 20th century and remained without major revisions since then. The following features of Covid-19 obviously require such a revision.

1. The curves of total numbers of detected infections are mostly of power-type for Covid-19, where the exponent diminishes over time.

2. The saturation of the initial waves of Covid-19 was mostly because of the protective measures, not due to the herd immunity.

3. The range and intensity of the protective measures used to fight Covid-19 were exceptional in the history of epidemics.

These factors are not really new in epidemics, but they do require a new mathematical theory. The prior approaches appeared insufficient for modeling the spread of Covid-19. The power-type growth of the total number of infections and the role of hard measures cannot be addressed within the SIR-type models.

Our theory seems the first one designed to explain and model epidemics of power growth (quite a few) under active management. The resulting differential equations are in terms of the initial transmission rate and the intensity of the protective measures (and other restriction mechanisms). The  main parameter, c in this work, can be determined during early stages of the waves of Covid-19: it replaces $R_0$, the initial reproduction number.

The graphs of the total number of detected cases in many countries (all we considered) are described uniformly and with surprisingly high accuracy by our curves. The 2-phase solution is a combination of the Bessel-type curve for phase 1, which is the key in our approach, and its certain version for phase 2 (in terms of elementary functions). The second phase, called phase (B) in this paper, generally requires auto-forecasting tools; the transmission rate c and the origin of the approximation curve are determined by these tools automatically, which can be different from the initial values.

The saturation due to the protective measure is of unstable nature. It was of this kind for the first-second waves of Covid-19: mostly due to the active management of the pandemic. At least, it was such before Summer 2021 (the Delta waves). Reducing the protective measures may result (and resulted) in the recurrence of the pandemic. Modeling saturations of this kind requires sharp mathematical tools, which we try to provide.

With the Delta-strains, we see the first instances of the interaction of different strains. The original Delta-strain quickly suppressed the Alpha strain everywhere, and also appeared quite competitive vs. Gamma (at least in Brazil). Then we had the following sequence of the Delta-plus variants: Delta $\to$ AY.4.0 $\to$ AY.4.2 (and AY.33.1 too). Generally, hypergeometric functions can be necessary to describe the interaction of two competing strains under the protective measures. See equations (12),(13) in Cherednik (2019). The current data are insufficient for a quantitative theory: the genome sequencing is not too systematic for Covid-19. Qualitatively, there are 2 possible mechanisms:

1. A new strain can infect some strata of population not susceptible to the current strain due to immunity, vaccinations or other reasons.

2. A new strain has significantly greater transmission strength; a somewhat greater transmissibility can be insufficient here without (a).

When the new strain essentially exhausts its “new niche” under (a) and its transmissibility is not too different from that for the old one, then the ratio “old strain/new strain” for the daily infections can be expected (mathematically) to remain stable for some time. Presumably, the competition between the original Delta and AY.4.0 was of this kind. The way to dominance can be slow for sub-lineages of the initial strain unless they have really superior characteristics. As for AY.4.2, other Delta-plus strains and other strains, including recent Omicron, it remains to be seen.

Methods. The starting point of our approach to modeling the total number of infections during epidemics is the power growth hypothesis, which has solid confirmations with Covid-19 practically in all countries (beyond small initial periods). We deduce it from the principle of local herd immunity. This is without the impact of the epidemic management.

The saturation of the initial waves of the spread of Covid-19 was mainly due to the protective measures: active management of the epidemic and our own actions. Protective measures are not unique for Covid-19, but their range and intensity reached unprecedented levels. Our model interprets this kind of saturation via the asymptotic periodicity of Bessel functions, one of the deepest results in their theory.

This is very different from the classical approaches based on SID, SIR, SIER models and their variants, and the models used in the neighboring directions of invasion ecology. We note that if there are 2 strains at the same time, then hypergeometric functions are expected to be used instead of Bessel functions (3 species in invasion ecology).

The saturation for us is a dynamic equilibrium between the virus invasion and our protective measures, including very important self-imposed ones. This is mostly not because of the classical herd immunity; our approach is actually parallel to those in invasion ecology.

Due to a very limited number of parameters, 3 main and 5 totally, in our two-phase solution, the corresponding modeling is much more rigid than in any other approaches. The curves we obtain match very well the actual graphs of the total numbers of detected infections practically in all countries we examined (many). These parameters are quite meaningful mathematically and epidemiologically. The key are c, the initial transmission rate, and a, the intensity of hard protective measures, which can be determined reliably at relatively early stages of particular waves of the epidemic. Here a can reflect restriction mechanisms of any nature: vaccination programs, self-imposed restrictions, biological ones.

Accordingly, forecasting the waves can be potentially reduced to finding c, a, C and the coefficient of the non-dominant solution $u^2$ in (1). The challenge is to do this at early stages of the waves; presumably it is doable near or somewhat before the turning point of the wave. Currently we find these parameters “manually”, which is almost a formal procedure (but not a computer program by now). Deep machine learning is expected to be added here for better forecasting.

Our parameters are generally different for different waves, but we see some patterns here. The second waves were almost always with somewhat higher c and significantly lower a. Though the 2nd wave in India (the Delta-one) was exceptional: c dropped and a increased. Also, this wave was much broader than the 1st one: C, the magnification coefficient, was much greater. We attribute this to a high transmissibility of the Delta-strain and much stronger response by the population of India and the authorities in charge to the threat. As with the 1st wave, the match of the real curve with our u(t) was very good.

We obtain a very good match practically for the whole periods of the waves of Covid-19 in many countries. It is actually surprising for such stochastic processes as epidemics, and of course this is a strong confirmation of our assumptions. In spite of various simplifications we made, it appeared that the systems of differential equations (1) and (2) capture very well the dynamic of the waves of Covid-19. We obtain our ODE from some “first principles”, however the true rationale can be beyond our arguments: the universality of these differential equations.

The main part of our theory was created and posted in the middle of April 2020, which was mostly in the middle of the 1st waves of Covid-19. We had a unique and valuable opportunity to test our theory real-time: in the course of the epidemic. Namely, we systematically determined the parameters of our curves during relatively early stages, and then tested the corresponding projections for sufficiently long control periods.

Our usage of control periods is similar to routine testing the quality of the models used for forecasting share-prices in stock markets, where no approach can be accepted without real-time runs and carefully crafted historic experiments that exclude any “usage of future” as far as possible. This kind of “discipline” is not present in forecasting epidemics, at least by now. The results of such “real-time testing” our theory and the outputs of the corresponding automated forecasting programs we provide are an important part of Cherednik (2020a, b).

One of the main examples of early forecasts in this paper is that for the 3rd wave in the USA. It shows that our tools can be potentially used to obtain reasonable projections at relatively early stages of the waves. Also, we discuss in detail our forecasting the Delta-wave in UK.

Summary

We demonstrated that Bessel-type functions describe very well the growth of the total number of detected cases in many countries. Mathematically, we successfully model the passage from $\sim t^c$, describing the initial growth of the total number of detected cases, to $\sim t$ near the turning point, when the number of new (daily) cases stabilizes, and then almost all the way to the (technical) saturation of the wave. This is the 1st phase, which is mode (A) in this paper.

At the late stages of the waves of Covid-19, we switch to mode (B). The corresponding ODE describe a more relaxed management; their solutions are in terms of elementary functions. Though in some countries, mode (A) appeared “almost sufficient” until the end of the wave.

Here c is the initial transmission rate, which can be captured at relatively early stages of the waves of Covid-19. Theoretically it is the same for both modes, (A) and (B). Practically, it may change for the latter mode during the late stages of the waves. Capturing the 2nd key parameter a, the intensity of hard measures, generally requires longer periods than for c; it is the key for forecasting the durations of the waves.

Our differential equations describe epidemics under active management, the system of protective measures, where hard measures play the key role. The self-imposed restrictions of the contacts during epidemics are and always were important protective measures. Receiving reliable information on the course of the epidemic by the population is of obvious significance here. The travel restrictions, closing the places where the spread is the most likely and vaccination are classical state controlled measures.

The saturation due to active protection measures is of unstable nature unless the herd immunity and high levels of vaccination (for the current strains) become significant. Its forecasting requires an exact mathematical theory, which we try to provide. There will be an endless discussion of the efficiency of different measures and different management approaches until verifiable trustworthy mathematical models and the corresponding software are developed and implemented practically.

The verification of any models, including our one, does require algorithms that can be used by anyone, not only by their creators, which is considered the ultimate test of their validity. This is one of the reasons why we wrote our programs. They are posted in Cherednik (2020a, b) and can be used by anyone for any countries and regions, though only for the late stages of Covid-19 so far (mode (B)).

Our 2-phase solution seems a solid basis for reaching the next level, which is forecasting. It describes the curves of total numbers of detected infections with high accuracy and with surprisingly high quality of projections; we pay great attention to the stability of our auto-forecsating . Though forecasting (any) is always quite a challenge.

Basic parameters. The small number of the parameter we employ explains well the uniformity of the curves of total numbers of detected infections of Covid-19 in many so different countries, as well as the mathematical similarity of different waves. They are:

1. the initial transmission rate c, which can be determined at relatively early stages of the current wave (and it serves the whole phase 1),

2. the intensity a of hard measures be or any restriction mechanisms, which becomes sufficiently stable near the turning point of the wave,

3. the intensity b of the measures during the 2nd phase, which begins near the end of phase 1: the switch from mode (A) to mode (B).

We note that the same c is mostly applicable to both phases (modes (A), (B)), though we see some deviations for the 2nd phases in Delta-waves. Generally, our auto-forecasting programs determine c, b and the starting point of the corresponding (B)-type curve automatically strictly on the basis of the latest “points” (not many).

In contract to c, the parameters   a and b  (the intensity of the measures) are more time-dependent, but  a  appeared sufficiently stable for long periods. Concerning b, it must be adjusted constantly at the later stages: no country is really isolated and the management of the epidemic, including the self-imposed protection measures, becomes more flexible at later stages and less predictable mathematically.

Generally, the phase transition, from (A) to (B), is one of important conclusions of our paper. There must be interesting biology involved here: this passage can be not only due to diminishing the measures.

The scaling coefficient C in the Bessel-type formula for u(t) is adjusted to match the real numbers of cases. The coefficient of $u^2(t)$, the non-dominant solution of our system of ODE, is an additional parameter. It is mainly responsible for the “effects of the second order” and possibly can be disregarded for forecasting; the dominant Bessel-type solution $u^1(t)$ is expected to be sufficient for this. We confirmed in Cherednik (2020a) that both, $u^1(t)$ and $u^2(t)$, do occur; both are used in this paper too. We note that $u^2(t)$ can become negative when u(t) still remains increasing. Actually, the whole u(t), positive or negative, can become meaningful if it is interpreted as the difference of the numbers of infections in 2 areas.

The coefficient C is generally a technicality, to make the output convenient to present as a graph. However it provides valuable information when different waves of the epidemic are compared in the same country. An example is our analysis of the 1st and 2nd waves in India. The whole country was affected during the 2nd wave, when only some strata of this huge and diverse country were infected during the 1st wave. Accordingly, the coefficient C dramatically increased during the 2nd wave there, when c diminished and a increased, a mathematical indication that a new strain arrived, Delta. The match of our u(t) and the total number of detected cases was generally quite good for the Delta-waves, though the oscillations after phase (B) were new to us.

The fact that we were able to describe such complex stochastic processes as epidemics with only 3 basic parameters seems a real discovery. This worked very well almost everywhere (in all countries we considered), but it will take time to understand the scope of this new theory and to begin using it practically.

Obviously such a remarkable universality is supposed to have deep roots in general biology. Mathematically, the same system of ODE is expected to serve various different processes, including those in invasion ecology. An example is MRT, momentum risk-taking, which has applications for momentum trading in stock markets. The protection function p(t) in (1) is replaced by the price function in momentum trading. MRT was expected in Cherednik (2019) as an important part of processes in our brain, especially those related to decision-making.

Some biological aspects. Needless to say that the herd immunity and vaccinations make us well protected against the current strains of Covid-19, which were mostly Delta-strains in quite a few countries during Summer-Fall of 2021. There are many challenges here (Anderson et al. 2020). For instance, measuring the efficiency of the vaccination programs requires sharp mathematical tools. In our approach, this means measuring the impact of the vaccination on the parameters, especially our c and a. The Delta-waves were clearly affected by the vaccination programs in Europe, Israel, the USA and some other countries.

Technically, we are still in the 1st cycle of the epidemic (in 2021). Basically, the cycles of epidemics end when the current strains become less infectious due to the growing immunity, vaccinations, the change of a season and various other factors. A clear “break” must be present, which is still not the case with Covid-19.

The virus can be expected to weaken at the end of a cycle and the number of mild and asymptomatic cases can be expected to increase, though the transmissibility can remain very high. This change can be due to mutations, which are mostly of destructive type, and general trends of virus evolution. Understanding these processes requires greater biological research on Covid-19, especially due to its high stability under the mutations (its “proofreading feature”). The following is essential.

1. To determine experimentally the number of “passages” (consecutive experiments) that may increase or decrease the transmissibility of SARS-Covid-19.

2. To find the predominant mutations upon such sequences and their effect on the general abilities of the virus, including the transmissibility and immune evasion.

3. To observe and analyze how and when the general strength of the virus begins to fade after sufficiently many transmissions for real waves of Covid-19 infections.

Paper (Shiliaev 2021) give some preliminary answers to (a,b); the experiments described there (in consecutive Petri dishes) were aimed at boosting of transmissibility. Understanding (c) and the process of the real evolution of Covid-19 is quite a challenge. An important argument in favor of weakening the virus is that the waves of Covid-19 generally affected only some fractions of the susceptible population. The protective measures obviously restrict the waves of Covid-19, but this equally happens in quite a few countries with relatively low levels of active management of the epidemic.

For the Delta-waves, high vaccination rates, rising herd immunity and the evolution of the virus can be the reasons of relatively fast passage from phase 1 to phase 2 (from mode (A) to mode (B)). Though mode (B) for the Delta-strain lasted unusually long (vs. prior waves) with relatively high numbers of new daily cases and with some oscillations. Such oscillations and even some smaller waves can be clearly seen in UK and some other countries. Such prolonged 2nd phase can be due to the reduction of general protective measures, fading the strength of the vaccines and natural immunity over time, opening schools, the beginning of the fall-winter season and (of course) new strains.

After the end of the cycle in one area, the epidemic can continue somewhere else and in zoonotic reservoirs. Generally, a significant renewal of the strains is typical for new cycles. Covid-19 demonstrated its unique ability to produce many waves and many new strains one after another within one cycle, sometimes in the very same areas.

With new strains of Covid-19, about 6 months seem necessary for them to reach a significant presence counting from their “first appearance”, however it depends. The immunity after the recovery of infected individuals or upon the vaccination is (currently) expected to last about 6 months too. This may give us some time to become prepared for the next waves/cycles. Sharp mathematical tools will be needed to produce early forecasts when new waves begin.

The ability of Covid-19 to evolve resisting the vaccines and the treatment remains to be seen, but it can be expected ample. Generally, it can take only several infected individuals where the virus can “stay” for 1–3 months to generated a lot of potentially dangerous mutations, but fortunately only very few of them have a chance to reach any dominance. The mathematical theory of the spread of epidemics from (Cherednik 2020a, b) and in this paper can help to trace these developments. The effect of weakening the virus can be expected to be governed by the same ODE, but with a different meaning of the coefficients a, b.

Expected applications. Some practical objectives are as follows:

1. Forecasting the duration and the intensity of the waves of Covid-19 and for other epidemics with the spread of “power-type”.

2. Creating software for monitoring the dynamic of the waves of Covid-19, which is especially needed at their later stages.

3. Comparing different waves in the same region aimed at understanding the virus evolution and the impact of the measures.

4. Extending this theory to Invasion Ecology, more specifically, to transient processes of the interaction between 2 and 3 species.