Enabling realistic health data re-identification risk assessment through adversarial modeling

Abstract

Objective

Re-identification risk methods for biomedical data often assume a worst case, in which attackers know all identifiable features (eg, age and race) about a subject. Yet, worst-case adversarial modeling can overestimate risk and induce heavy editing of shared data. The objective of this study is to introduce a framework for assessing the risk considering the attacker’s resources and capabilities.

Materials and Methods

We integrate 3 established risk measures (ie, prosecutor, journalist, and marketer risks) and compute re-identification probabilities for data subjects. This probability is dependent on an attacker’s capabilities (eg, ability to obtain external identified resources) and the subject’s decision on whether to reveal their participation in a dataset. We illustrate the framework through case studies using data from over 1 000 000 patients from Vanderbilt University Medical Center and show how re-identification risk changes when attackers are pragmatic and use 2 known resources for attack: (1) voter registration lists and (2) social media posts.

Results

Our framework illustrates that the risk is substantially smaller in the pragmatic scenarios than in the worst case. Our experiments yield a median worst-case risk of 0.987 (where 0 is least risky and 1 is most risky); however, the median reduction in risk was 90.1% in the voter registration scenario and 100% in the social media posts scenario. Notably, these observations hold true for a wide range of adversarial capabilities.

Conclusions

This research illustrates that re-identification risk is situationally dependent and that appropriate adversarial modeling may permit biomedical data sharing on a wider scale than is currently the case.

INTRODUCTION

Large quantities of personal health data are generated in the clinical,^1–4 consumer,^5,6 and research domains. As examples of the latter, UK Biobank,⁷ China’s Kadoorie Biobank,⁸ and the All of Us Research Program of the U.S. National Institutes of Health⁹ collect diverse data about millions of individuals from various resources, including electronic health records (EHRs), lifestyle surveys, biospecimens, and radiological images. In addition, numerous consortia have rapidly formed to collect and share data on COVID-19 (coronavirus disease 2019) patients.^10–14 Broadening access to such data can accelerate numerous endeavors, ranging from policy analysis to novel scientific investigations in medicine and public health.^15–17

At the same time, there are concerns that sharing person-specific data may infringe on privacy interests or expectations, with a particular unease about anonymity.^18–20 Numerous approaches^21–28 have been developed to assess re-identification risk by estimating the extent to which the data subjects are unique with respect to the set of attributes that can distinguish them from other subjects, or what is often called a quasi-identifier (eg, date of birth, gender, and zip code of residence; a survey of these approaches is provided in Supplementary Appendix A). Yet these approaches were designed under the expectation that the number of quasi-identifying attributes is relatively small. When this is true, risk assessment typically focuses on the theoretical worst-case scenario, in which it is assumed that the data recipient knows the values for all of the quasi-identifying attributes for all of the individuals whose data will be shared. It thus follows that, as the number of quasi-identifying attributes grows, so too does worst-case risk. And, as an artifact, various re-identification studies have called into the question the extent to which anonymity can be assured as data collection and sharing efforts ramp up.^21,29–33 In fact, in a recent investigation, it was suggested that only 15 demographic attributes are required to make 99.98% of Americans unique.²⁸ Guided by the results of such re-identification risk assessments, organizations managing biomedical data typically adopt 1 of 2 stances: (1) substantially alter data to reduce the worst-case risk to an acceptable level or (2) rely more heavily on sociolegal controls (eg, data use agreements and credentialing of data recipients).

However, worst-case assessments make an assumption about an attacker’s capabilities that, in practice, may be far too strong.³⁴ For instance, it is nontrivial for would-be attackers to obtain accurate information about all quasi-identifiers for many of the subjects in a dataset.^35,36 Consequently, the amount of alteration applied to a biomedical dataset may be excessive. Just as adversarial modeling has enabled pragmatism in computer security³⁷ and war gaming,³⁸ there is a need for a principled risk analysis framework that makes defensible, and more realistic assumptions, about adversarial capacity and behavior with respect to biomedical data sharing.

To support this goal, we introduce a novel re-identification risk analysis framework that accounts for the information that is expected to be reasonably available to an attacker for re-identification purposes. This framework expands on the traditional notion of re-identification risk by allowing an organization to simulate threats under various degrees of completeness in an attacker’s knowledge about individuals in the dataset. It should be recognized from the outset, however, that this framework is designed to estimate the re-identification risk in records and is not a de-identification method in of itself. However, this framework can be combined with measures of data utility measures that are relevant to the context in which the data are to be shared, such that policies that balance privacy and utility can be uncovered.^39,40

To illustrate the potential of the framework, we performed a re-identification risk analysis for data derived from patient records at the Vanderbilt University Medical Center (VUMC) with respect to 2 types of datasets that have been invoked in re-identification attacks. The first dataset corresponds to voter registration records, which contain structured demographic data on a large proportion of the adult American population and have been successfully applied in various re-identification attacks against hospital discharge databases.^30,32 The second corresponds to social media data, a resource that was recently exploited for clinical trials re-identification purposes to assess the capabilities of a motivated intruder.³² Our findings indicate that the re-identification risk for attackers relying on such resources is, in many instances, significantly lower than that suggested by the worst-case scenario.

Materials and METHODS

This section begins with an introduction to the probabilistic representation of the data an attacker relies upon to re-identify subjects, which we refer to as the external identified dataset, and the definition and computation of re-identification risk measures under specific adversarial assumptions. Next, we provide a formal Bayesian network (BN) representation of overall re-identification probability given any attacker. We then describe the design of the case studies.

Reidentification threat model

For presentation purposes, we assume that the dataset to be shared $D$ is stored in a relational table, where each row represents the record of a subject (eg, a participant in a research study) and each column is a data attribute (eg, age or zip code of residence). Formally, the set of records is represented as $D=\{d_1,.,d_n\}$, where $n$ is the number of records in the dataset, and the set of attributes is represented as $F=\{f_1,\dots ,f_m\}$, where $m$ is the number of attributes in the dataset. We represent the subject associated with a record $d_i$ as $s_{d_i}$ and the set of subjects as $S=\{s_{d_1},\dots ,s_{d_n}\}$.

In our framework, we define a probabilistic model to represent if each attribute can be obtained from the external identified dataset for each subject. Owing to the fact that the attributes available in an external resource can vary by individual (eg, the voter registration lists of each U.S. state vary in what information they make known about its constituents),⁴⁵ our model represents the probability that the attacker knows the values of the attributes for each subject $s_{d_i}.$ This design supports a flexible model in which the probability that a certain attribute about a subject is known to the attacker can vary across subjects.

For each subject $s_{d_i}$, we partition the attributes into nonoverlapping subsets, in which each subset contains a set of attributes that is obtained simultaneously from an external resource. For instance, imagine that the data to be shared includes the following set of quasi-identifying attributes $\{$Race, Gender, Age, Marital Status, Education$\mathrm{ }\mathit{Level}\}$. An attacker has the ability to learn Gender and Age simultaneously from a voter registration database, Marital Status from vital records, and Education Level from social media (eg, LinkedIn). This implies that there are 3 attribute subsets: $\{$Race, Gender, Age$\}$, $\{\mathit{Marital} \mathit{Status}\}$, and $\{\mathit{Education} \mathit{Level}\}$. Given a subject, there is a probability that the attacker can obtain each subset of attributes. Formally, the probability model of the external identified dataset includes the specification of a set of attribute groups: $\{F{\mathrm{\text{'}}}_{i,1}$, …, $F{\mathrm{\text{'}}}_{i,h_i}\}$ for data subject $s_{d_i}$, each of which is a subset of the attribute set $F$, where $F{\mathrm{\text{'}}}_{i,a}\cap F{\mathrm{\text{'}}}_{i,b}=\mathrm{\varnothing }$ for any $a\ne b$. The attack model further defines variables $\{P{\mathrm{\text{'}}}_{i,1}$, …, $P{\mathrm{\text{'}}}_{i,h_i}\}$ as the probability that the attacker can obtain each attribute group from $\{F{\mathrm{\text{'}}}_{i,1}$, …, $F{\mathrm{\text{'}}}_{i,h_i}\}$ for an arbitrary subject $s_{d_i}$.

Re-identification risk measures

We refer to the set of records that match a subject on the attributes known to the attacker as the equivalence group. The framework integrates 3 re-identification risk measures based on existing attack models, which are informally referred to as prosecutor, journalist, and marketer risks.^41,42

The prosecutor model assumes that the attacker strives to discover the record of someone that they know is in the dataset. Based on this assumption, we define the first risk measure ${\mathit{Risk}}_{\mathit{prosecutor}}$ as the probability that a subject is unique in the dataset for the attributes in the external identified dataset. This attacker is successful when the subject’s record is found to be unique in the dataset because the attacker is guaranteed to correctly re-identify the subject.

By contrast, the journalist model assumes that the attacker does not know if someone is in the dataset. As a result, the attacker strives to discover the record of someone in the population from which the dataset has been sampled. The population itself is relative to the attacker’s knowledge. For instance, imagine that a dataset contains a subset of individuals who received outpatient care from a certain clinic in a large healthcare system. If the attacker knows that a subject of interest received care, but does not know at which clinic, then the population is composed of all the patients who visited the healthcare system. Thus, we define a second risk measure ${\mathit{Risk}}_{\mathit{journalist}}$ as the probability that a subject is unique in the population from which the subjects in the dataset have been drawn. When the subject is unique in the population, this attacker can confirm that a unique match between the subject and the corresponding record is correct without prior knowledge that the subject was in the dataset.

The third measure is defined as the marketer risk, which assumes the attacker will link a subject to a record from the corresponding equivalence groups at random with equal probability. In this adversarial situation, the probability that the selected record is correct is the inverse of the number of records in the equivalence group, which we define as the marketer risk ${\mathit{Risk}}_{\mathit{marketer}}.$

The framework implements a Monte Carlo simulation over a set of trials to compute ${\mathit{Risk}}_{\mathit{journalist}}$, ${\mathit{Risk}}_{\mathit{prosecutor}}$ and ${\mathit{Risk}}_{\mathit{marketer}}$ for each subject $s_{r_i}$. In each trial, we select a set of attributes according to the set of probabilities $\{P{\mathrm{\text{'}}}_{i,1}$, …, $P{\mathrm{\text{'}}}_{i,h_i}\}$. We then compute the size of the equivalence group by comparing the subject’s values to each record in the dataset. A record is considered to be a member of the equivalence group if the quasi-identifying attributes known to the attacker exhibit values that include the subject’s values. In other words, the values could be exactly the same or they could be some generalized version of the value. For instance, when the subject’s race is reported as Pacific Islander, but the record in the external dataset under consideration lists a race of Native American or Pacific Islander, then they should be considered a possible match. At this point, if the subject is unique in the dataset, we then compute the probability that the subject is also unique in the population using the Pitman method⁴³ as discussed subsequently.

We represent the equivalence group sizes obtained from the trials as $A=\{a_1,\mathrm{ }\dots ,a_{\theta }\}$ and the probability of that the subject is unique in the population as $B=\{b_1,\dots ,b_{\theta }\}$, where $\theta$ corresponds to the number of trials. The risk measures are then computed as follows:

$${\mathit{Risk}}_{\mathit{prosecutor}}=\frac{\sum _{i=1}^{i=\theta }g\left(a_i\right)}{\theta }, \text{where} g\left(x\right)=\left\{\begin{array}{c}1 \text{if} x=1\\ 0 \text{if} x>1\end{array}\right.,$$

 

$${\mathit{Risk}}_{\mathit{journalist}}=\frac{\sum _{i=1}^{i=\theta }{b}_i}{\theta }$$

and  

$${\mathit{Risk}}_{\mathit{marketer}}=\frac{\sum _{i=1}^{i=\theta }\frac{1}{a_i}}{\theta }.$$

Informally, $g\left(x\right)$ is an indicator function for when the equivalence group size is equal to 1, and ${\mathit{Risk}}_{\mathit{prosecutor}}$ corresponds to the proportion of the trials in which the subject is unique in the dataset. Similarly, ${\mathit{Risk}}_{\mathit{journalist}}\mathrm{ }$corresponds to the average probability that the subject is unique in a trial. ${\mathit{Risk}}_{\mathit{marketer}}$ corresponds to the average probability that the attacker will randomly select the correct record from the equivalence group.

Overall re-identification probability

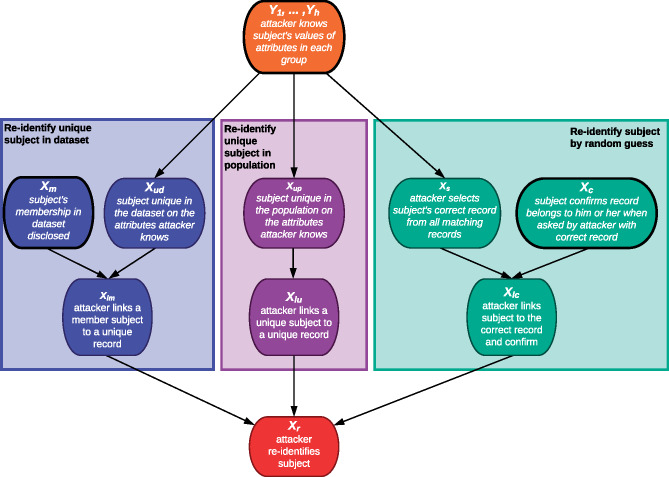
Each of the risk measures defined previously represent the re-identification risk for a particular type of attacker. However, the overall probability of re-identification needs to consider all of these risks together. To do so, we formalize the probability of re-identification using a BN as shown in Figure 1. The probability of re-identification depends on the external identified datasets and the variables of the BN, which are summarized in Table 1.

Figure 1.

A Bayesian network representation of the re-identification risk for a subject in a dataset.

Table 1.

A summary of the variables used in the framework

Variable	Description
$D=\{d_1,..,d_n\}$	The set of records in the dataset
$F=\{f_1,\dots ,f_m\}$	The set of attributes in the dataset
$S=\{s_{d_1},...,s_{d_n}\}$	The set of data subjects, $s_{d_i}$is the subject associated with a record $d_i$
$\{F{\mathrm{\text{'}}}_{i,1}$ , …, $F{\mathrm{\text{'}}}_{i,h_i}\}$	The set of attributes groups for dataset $s_{d_i}$, $F{\mathrm{\text{'}}}_{i,a}\mathrm{ }\subseteq F$, $F{\mathrm{\text{'}}}_{i,a}\cap F{\mathrm{\text{'}}}_{i,b}=\mathrm{\varnothing }$ for any $a\ne b$
$\{P{\mathrm{\text{'}}}_{i,1}$ , …, $P{\mathrm{\text{'}}}_{i,h_i}\}$	The probability that the attacker can obtain each attribute group from $\{F{\mathrm{\text{'}}}_{i,1}$, …, $F{\mathrm{\text{'}}}_{i,h_i}\}$ for an arbitrary subject $s_{d_i}$
$p_m$	$p_m=P(X_m=\mathit{True})$ , the probability that the subject’s presence in the de-identified dataset is disclosed to the attacker.
$p_c$	$p_c=P(X_c=\mathit{True})$ , the probability that the attacker confirms that a record corresponds to the subject of interest.
$p_{fm}$	$p_{fm}=(X_{lm}=\mathit{True}|{\mathrm{ }X}_m=\mathit{True}\mathrm{ }\mathit{and}$   $\mathrm{ }{X}_{ud}=\mathit{True})$, the probability that the attacker discovers that the subject is in the dataset given that the subject’s presence in the dataset is known.
$p_{cu}$	$p_{cu}=P\left(X_{lu}=\mathit{True}\right|\mathrm{ }{X}_{up}=\mathit{True})$ , the probability that the attacker confirms that a subject is unique in the population for a set of attributes given that the data subject is unique.

In Figure 1,$\{Y_1,\dots ,Y_h\}$ corresponds to a set of random variables that represent if the attacker knows each subset of attributes $\{F{\mathrm{\text{'}}}_{i,1}$, …, $F{\mathrm{\text{'}}}_{i,h_i}\}$ of subject $s_{r_i}$. The probabilities for these variables are defined in the model of the external identified dataset as $\{P{\mathrm{\text{'}}}_{i,1}$, …, $P{\mathrm{\text{'}}}_{i,h_i}\}$. The variable $X_r$ at the bottom of the BN represents if the attacker successfully re-identifies the subject, while the variables within each outlined box in Figure 1 are associated with each of the 3 routes of re-identification, which correspond to the 3 types of attackers). $X_r$ is true if any of these routes leads to a successful re-identification of the subject, as indicated by the 3 variables at the bottom of each box: $X_{lm}$, $X_{lu}$ and $X_{lc}$. We walk through the computation of the probability for each in the following sections.

Re-identification by a prosecutor

The variable $X_{lm}$ at the bottom of the left rectangle in Figure 1 indicates that a prosecutor type of attacker re-identifies a subject who is unique in the dataset. $X_{lm}$ is true when the attacker knows that the subject is in the dataset and is unique, which is represented by variable $X_{ud}$. Note that $X_{ud}$ is dependent on variables $Y_1$, …, $Y_h$.

$P(X_m=\mathit{True})$ is the probability that the subject’s presence in the dataset is disclosed, which is assigned to the input variable $p_m$ in Table 1. If $X_m$ is true, then there is a probability (assigned to input variable $p_{fm}$) that the attacker can figure out that the subject is in the dataset. Therefore, when both $X_{ud}$ and $X_m$ are true, then the probability that the attacker achieves a successful re-identification via the first route, or $P(X_{lm}=\mathit{True})$, is equal to $p_{fm}$, and is 0 otherwise.

Re-identification by a Journalist

Variable $X_{lu}$ at the bottom of the rectangle in the middle of Figure 1 represents the case in which a journalist type of attacker matches a subject to a unique record in the dataset and in which this record is also unique in the population based on the subset of attributes known to the attacker. In this scenario, it is assumed that the attacker does not know if the subject is in the dataset a priori. Therefore, to ascertain if the relationship between the subject and the record is correct, the attacker needs to confirm the uniqueness of the subject in the population.

Variable $X_{up}$ represents that the subject is unique in the population. This variable depends on variables $Y_1$, …, $Y_h$ and the population under consideration. There are various mechanisms to confirm if someone is unique in a population, such as one might use a population registry³⁵ or rely on a generative statistical model.²⁸ Given the set of attributes known to the attacker and the size of the population, we use the Pitman method,⁴³ which estimates the frequency of the equivalence group sizes on a set of attributes, to set $P(X_{up}=\mathit{true})$. Based on this frequency and the size of the population, we estimate the ratio of the number of records that are unique in the population to the total number of records that are unique in the dataset. If $X_{up}=\mathit{True}$, then there is a chance that the attacker can confirm the uniqueness of the subject in the population. Therefore, when $X_{up}$ is true, the probability that the attacker achieves successful re-identification via the second route, or $P(X_{lu}=\mathit{True})$, is $p_{cu}$ and is 0 otherwise.

Re-identification by a marketer

The marketer model assumes that the attacker will link a subject to a record in its equivalence group at random with equal probability. As such, we define the third route of re-identification as shown in the rectangle to the right in Figure 1. Specifically, variable $X_s$ represents if the selected record is the subject’s record. Therefore, $P(X_s=\mathit{true})$ is the inverse of the equivalence group size. At this point, the attacker needs to confirm that that link is correct, probability of which corresponds to $p_c$. Thus, when X_c and X_s are True, the probability that the attacker achieves a successful re-identification via the third route, P(X_lc = true) is 1, and is 0 otherwise.

We also run a Monte Carlo simulation to compute $P\left(X_r\right)$ for each subject $s_{r_i}$. In each trial, we compute (1) the equivalence group size and (2) the probability that the subject is unique in the population. We then simulate the values for the other random variables based on the probabilities. We represent the set of $X_r$ values of from the Monte Carlo trials as $E=\{e_1,\dots ,e_{\theta }\}$.

Finally, the re-identification probability, denoted as ${\mathit{Risk}}_{\mathit{overall}}$, is computed as

$${\mathit{Risk}}_{\mathit{overall}}=\frac{\sum _{i=1}^{i=\theta }{e}_i}{\theta }.$$

Case studies

To evaluate the re-identification risk framework, we created a dataset based on EHRs at VUMC and data from the U.S. Census Bureau. A summary of the attributes is provided in Table 2.

Table 2.

A summary of the attributes used in the case studies

Source	Attribute	Values
SD	Race	White, Black or African American, Asian, American Indian or Alaska Native, Native Hawaiian or Other Pacific Islander; other race; and a set of multiracial groups
	State	50 U.S. states and Washington, DC
	Ethnicity	Hispanic; non-Hispanic
	Sex	Male; female
	Year of birth	Before 1978
Simulated from Adult dataset	Education	Preschool, grades 1-4, grades 5-6, grades 7-8, grade 9, grade 10, grade 11, grade 12, high school graduate, some college, associate’s degree—vocational, associate’s degree—academic, bachelor’s degree, master’s degree, doctorate
	Marital status	Never married; married; divorced
	Work class	Government-federal; government-state; government-local; privately employed; self-employed-not incorporated; self-employed-incorporated; without pay
	Income level	≤$50 000; >$50 000
Simulated from population statistics	Country of birth	United States; outside of United States
	Homeowner	Own; rent
	Sexual orientation	Straight; other

SD: Vanderbilt University Medical Center Synthetic Derivative.

First, we selected records from the VUMC Synthetic Derivative (SD),⁴⁴ a de-identified version of the EHRs of more than 2 million VUMC patients. We specifically selected the following attributes: (1) year of birth, (2) sex, (3) state of residence, (4) race, and (5) ethnicity. To investigate re-identification risk in the context of a larger number of quasi-identifying attributes, we augmented the SD records with data from the U.S. Census. Specifically, we simulated the following attributes according to their age group–specific distribution in the Adult dataset⁴⁵: (6) education, (7) marital status, (8) work class, and (9) income level. Given that the Adult dataset is based on individuals born before 1978, we limited the simulation to this subpopulation of the SD. In addition, we simulated 3 attributes by randomly sampling according to the age group–specific distribution of the values in the U.S. population^46,47: (10) county of birth, (11) home owner or renter, and (12) sexual orientation. Further details about the age groups and how they guided the simulation are in Supplementary Appendix B. The resulting dataset contains 1 583 020 records. Given that we investigate the risks for individuals born before 1978, we assume that the population size is 100 000 000.

We compared the re-identification risk under the worst case and 2 scenarios based on external identified datasets that attackers have exploited to re-identify subjects:

Worst-case scenario. The attacker knows all of the values of the attributes available for the subject.

Voter registration scenario. The attacker has access to publicly available voter registration data in each U.S. state. We documented the attributes that are publicly available from the voter registration list for each state. Based on this information, we derived the probabilities that the attacker knows different groups of attributes, the details of which are provided in Supplementary Appendix C.

Social media scenario. In this study we focus on Twitter because this platform has been used for re-identification, and recent studies show how to infer Twitter user’s demographics from their posts. We estimate the probability that the attacker knows each attribute of a subject based on existing studies in predicting demographic variables for Twitter users.^48–53 Further details about this model are provided in Supplementary Appendix D.

We draw random samples of records from the simulated dataset to use as de-identified datasets with a size ranging from 1000 to 40000. We compute the 3 risk measures (ie, ${\mathit{Risk}}_{\mathit{prosecutor}}$, ${\mathit{Risk}}_{\mathit{journalist}}$, ${\mathit{Risk}}_{\mathit{marketer}}$) for each subject in each sample under the 3 different scenarios. We then compute the difference between the risk value based on each of the 2 external datasets and the worst case for each subject. We compare the probability distribution of the reduction of the values of the risk measures of the all the subjects in each sample in terms of the 25th percentile (Q1), median, and 75th percentile (Q3) percentiles. These percentiles indicate the proportion of subjects in each sample with a risk reduction above a certain level. For example, if the ${\mathit{Risk}}_{\mathit{marketer}}$ reduction under the Twitter scenario comparing to the worst case has a Q1 of 55%, indicating that over 75% of the subjects has a reduction in the${\mathit{Risk}}_{\mathit{marketer}}$ above 55%.

Finally, we assess how variation in the knowledge and capabilities of the attacker influence the re-identification probability of the subjects. We conduct this experiment using a sample set of 1000 subjects and parameters $p_m$, $p_c$, $p_{fm}$, and $p_{cu}$, each of which was assigned a value drawn from the set {0.2, 0.5, 0.8}. We compute ${\mathit{Risk}}_{\mathit{overall}}$ ($P_r$) for each subject for each of the 12 possible combinations of parameterizations. For example, when $p_m=0.5$, $p_c=0.$5, $p_{fm}=0.2$, and $p_{cu}=0.2$, there is a 50% chance that the subject will reveal their membership, a 50% chance that the attacker can confirm the record corresponds to a subject of interest, a 20% chance that the attacker can determine if someone is a member of the sample, and a 20% chance that the attacker can confirm that a subject is unique in the population. Similarly, we compute the Q1, median, and Q3 of the ${\mathit{Risk}}_{\mathit{overall}}$ reduction for each subject in each sample when shifting from the worst case to the 2 real world–identified external dataset–based scenarios.

RESULTS

Re-identification risk measures

This section reports on the re-identification risk for each type of attacker and then the overall re-identification probability given any attacker. We show how risk changes when shifting from the worst-case scenario to the scenarios associated with the specific external identified datasets. We close this section with an analysis of the distribution of the reduction of risk over the subjects in samples of varying sizes.

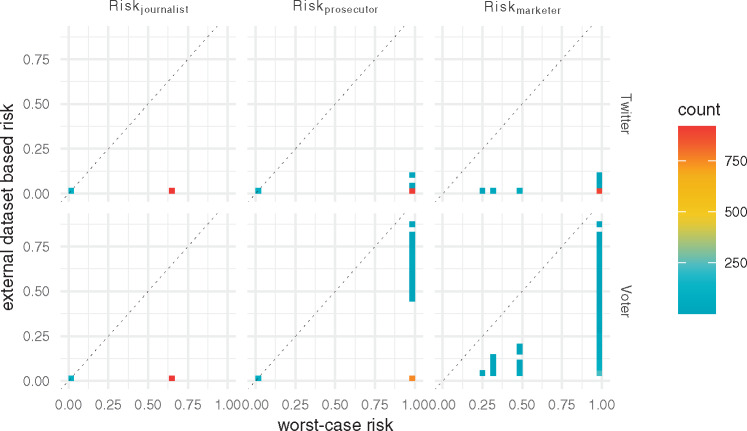
Figure 2 illustrates a heatmap of how the re-identification risk changes when shifting off the worst-case perspective using a random sample of 1000 subjects. There are 3 heatmaps each for the Twitter (the upper row) and the voter registration (the lower row) scenarios, 1 for each of the re-identification attacks.

Figure 2.

Heatmaps for risk measures Risk_journalist, Risk_prosecutor, and Risk_marketer in samples of 1000 records for the worst-case and pragmatic scenarios. The upper row is the worst-case risk (x-axis) vs the Twitter risk (y-axis). The bottom row is the worst-case risk vs voter registration risk. The points on the dashed line indicate that the worst-case risk is the same as the risk under the pragmatic attack scenario. The points on the x-axis indicate that the risk is reduced to 0 when shifting from the worst-case to the Twitter or voter registration list attack scenario.

First, we report on the results with respect to the journalist risk, shown as ${\mathit{Risk}}_{\mathit{journalist}}$. To orient the reader, we take a moment walk through the heatmap corresponding to ${\mathit{Risk}}_{\mathit{journalist}}$ for the Twitter scenario (shown in the top left). Similar interpretations can be applied to the other re-identification risk measures. In this figure, the x-axis corresponds to the worst-case risk, while the y-axis corresponds to the Twitter risk. If a point is on the diagonal line, then the worst-case risk is equal to the Twitter risk; in other words, the risk does not change. It can be seen that in this specific case, there are 2 points in the heatmap. The first point is the red square, which shows that the overwhelming majority of subjects (over 90%) have a worst-case risk of 0.66 but a value close 0 in the Twitter scenario. The second corresponds to the blue square near (0,0). This is expected because when the risk is close to 0 in the worst case, it must remain close to 0 in any other scenario. With respect to ${\mathit{Risk}}_{\mathit{journalist}}$ more generally, it can be seen that the heatmap of for the worst case vs the voter registration scenario is similar to the worst case vs the Twitter scenario.

Next, we considered the prosecutor risk ${\mathit{Risk}}_{\mathit{prosecutor}}$, which is shown in the middle column of Figure 2. It can be seen that the worst-case scenario exhibits 2 values only, 0 and 1, for all subjects. This is because, in the worst-case scenario, the attacker knows a fixed set of attributes of all subjects, such that if a subject is unique with respect to these attributes, then ${\mathit{Risk}}_{\mathit{prosecutor}}$ is 1, otherwise it is 0. By contrast, the majority of subjects with ${\mathit{Risk}}_{\mathit{prosecutor}}=1$ in the worst case reduce to near 0 for the voter registration and Twitter scenarios.

We then considered the marketer risk ${\mathit{Risk}}_{\mathit{marketer}}$, which is shown in the rightmost column of Figure 2. In the worst-case scenario, the subjects have different levels of ${\mathit{Risk}}_{\mathit{marketer}}$ corresponding to their equivalence group size in the dataset. In the Twitter scenario, for the majority of subjects, the value reduces to close to 0. By contrast, in the Voter registration list scenario, the rate of risk reduction varies by subject.

Table 3 shows that, for all samples, the Q1 of the reduction in ${\mathit{Risk}}_{\mathit{journalist}}$ and ${\mathit{Risk}}_{\mathit{prosecutor}}$ are 100%; in other words, at least 75% of the subjects, who are unique on presumed quasi-identifying attributes in the worst case, are not unique on the attributes available in the external datasets. For the risk measure ${\mathit{Risk}}_{\mathit{marketer}}$, the percent change grows with sample size. For example, given the voter registration lists scenario, the Q1, median, and Q3 of the percent change in ${\mathit{Risk}}_{\mathit{marketer}}$ are 67%, 87%, and 94%, respectively, for the sample dataset of 1000 subjects, while these values are 97%, 99%, and 99%, respectively, for the sample dataset of 40 000 subjects. This indicates that the size of a subject’s equivalence group (based on the attributes obtained by the attacker from the external dataset) grows faster in the Twitter and voter registration scenarios than in the worst-case scenario.

Table 3.

A summary of the percent reduction in re-identification risk for each subject when shifting from the worst case to the Twitter and voter registration scenarios

External Identified Dataset	Number of Subjects (×1000)	Risk Reduction
		Journalist	Prosecutor	Marketer
		Q1	Q1	Q1	Median	Q3
Twitter	1	100%	100%	99.48%	99.70%	99.81%
	4	100%	100%	99.82%	99.92%	99.95%
	7	100%	100%	99.88%	99.95%	99.97%
	20	100%	100%	99.94%	99.98%	99.99%
	40	100%	100%	99.95%	99.98%	99.99%
Voter Registration	1	100%	100%	67.47%	86.78%	93.86%
	4	100%	100%	88.16%	94.91%	97.87%
	7	100%	100%	92.22%	96.86%	98.67%
	20	100%	100%	95.83%	98.38%	99.32%
	40	100%	100%	96.63%	98.95%	99.57%

Q: quartile.

Overall probability of re-identification

Next, we considered how the scenario influenced the probability of re-identification ${\mathit{Risk}}_{\mathit{overall}}$. To do so, we created 10 sets of subjects, each of which contained 1000 subjects selected at random, and measured the change in the risk probability for each paramterization of the BN (ie, combination of $p_m$, $p_c$, $p_{fm}$, and $p_{cu}$ values) when shifting from the worst case to the Twitter and voter registration scenarios. In the worst-case scenario, the value of the Q1, median, and Q3 of ${\mathit{Risk}}_{\mathit{overall}}$ averaged across all the different parameterizations and all the samples is 0.448, 0.987, and 1 (where 0 is the least risk and 1 is the most risky). Table 4 reports the average (and SD) for several representative parameterizations, as well as the overall average (and SD). The results for all 81 parameterizations are provided in Supplementary Appendix E.

Table 4.

Robustness of the reduction in re-identification risk ${\mathit{Risk}}_{\mathit{overall}}$ when shifting from the worst case to the Twitter and the voter registration scenarios.

BN Parameter				Twitter			Voter
$p_m$	$p_c$	$p_{fm}$	$p_{cu}$	Q1	Median	Q3	Q1	Median	Q3
0.2	0.2	0.2	0.2	96.85 (0.17)	100.0 (0.0)	100.0 (0.0)	42.42 (2.03)	91.18 (0.61)	96.84 (0.16)
0.5	0.5	0.5	0.5	97.49 (0.37)	100.0 (0.0)	100.0 (0.0)	37.85 (1.54)	90.38 (0.71)	95.69 (0.35)
0.8	0.8	0.8	0.8	97.51 (0.31)	100.0 (0.0)	100.0 (0.0)	30.2 (0.72)	88.36 (0.92)	94.59 (0.37)
0.5	0.2	0.8	0.5	98.47 (0.03)	100.0 (0.0)	100.0 (0.0)	41.2 (1.81)	95.56 (0.23)	98.51 (0.03)
0.2	0.2	0.5	0.8	98.46 (0.08)	100.0 (0.0)	100.0 (0.0)	65.21 (1.48)	95.47 (0.45)	98.46 (0.08)
…	…	…	…	…	…	…	…	…	…
Average				97.73 (0.22)	100 (0)	100 (0)	38.69 (1.33)	90.89 (0.65)	95.98 (0.26)
SD				0.44 (0.15)	0 (0)	0 (0)	10.22 (0.48)	3.09 (0.25)	1.75 (0.15)

The first several rows report the average (and SD) of the Q1, median, and Q3 across 10 runs of 1000 subjects each for several representative BN parameterizations. The final 2 rows report the average and standard deviation across all BN parameterizations.

BN: Bayesian network; Q: quartile.

In the Twitter scenario, the results yielded an average Q1 risk reduction of 97.73% (ie, a risk reduction of 97.73% for over 75% of the subjects) and a median (and thus a Q3 as well) of 100% (ie, a risk reduction of 100% for half of the subjects). Note that in the Twitter scenario, the standard deviation of the Q1 and the median are very small, suggesting that the re-identification risk reduction is robust to variance in BN parameters. By contrast, the voter registration scenario leads to smaller reductions in re-identification risk. Specifically, we observe an average Q1 of 38.69%, average median was 91.135, and average Q3 of 95.98%. At the same time, the SD associated with these measures is higher than in the Twitter scenario, suggesting that the result is less stable. Though these reductions are smaller and more variable than the Twitter scenario, they remain quite high overall, which supports the claim that modeling adversaries in pragmatic scenarios leads to substantially lower estimates of re-identification risk.

DISCUSSION

It should be recognized that, from a computational perspective, the re-identification risk assessment framework is relatively lightweight. This is because it requires only probabilities that can be derived from identified external datasets, as opposed to the identified datasets themselves. This is notable because obtaining access to, as well as processing all resources in the public domain, can be prohibitively expensive for many organizations.

Still, the framework has several limitations which we believe serve as opportunities for future research. First, the proposed method only provides an estimated probability of re-identification of the individuals in the dataset. It does not predict with certainty whether or not an individual will actually be re-identified. However, predicting the exact re-identification potential for a record would require maintaining an up-to-date representation of all data available to an attacker. While we believe that this would be an ideal situation, the collection and maintenance of such a resource is unlikely to be cost-effective—and such resources will likely evolve over time—such that we believe it is prudent to rely on risk estimates in practice. Second, we assume that the re-identification of each study participant takes place independently. However, if a data recipient links an external resource with the released data, the re-identification of one individual’s record may make the re-identification of another person easier.⁵⁴ Third, the framework does not provide a systematic way to configure the probability parameters in the model, but should certainly be considered in future investigation. Currently, data sharers can still use the method by computing the risk given the combinations of a range of values for each of the probabilistic parameters as demonstrated in our experiments. Fourth, the framework does not consider the amount of effort the attacker will need to invest to conduct the re-identification attack or their decisions on whether or not to conduct an attack in the first place. This indicates that, in the future, game theoretic models³⁹ can be integrated with the framework to allow for analysis of costs and payoff functions for the attacker affect the re-identification risk. In addition to accounting for the attacker’s cost and payoff analysis, our method can be further extended to include a set of variables for profiling different types of attackers, such as a health insurance company or the neighbors of the subjects. Moreover, our risk assessment focuses on structured data only, and it is possible that unstructured data may yield inferences about the traits of an individual that could be leveraged for re-identification purposes as well. This is outside the scope of this investigation, but it is an important area for future research if unstructured data are to be taken into account in a re-identification risk analysis.

Furthermore, we acknowledge that there are several limitations to the case studies. First, the dataset relied on to compute risk is only partially based on a real dataset because a subset of its attributes are simulated from population statistics (eg, country of birth and sexual orientation). We simulated these attributes by assuming that they are dependent on the age of the individual only. Second, we computed the probability that a random adult is in the voter registration list by dividing the number of voters by the adult population size in each U.S. state, while the probability that someone is registered to vote varies based on their race, age, and other demographic and socioeconomic factors. Third, we limited the analysis of the effects of the parameters of the BN on the re-identification probability ${\mathit{Risk}}_{\mathit{overall}}$ of each subject to a sample of 1000 subjects. Still, despite these limitations, this investigation provides a clear illustration about adversarial modeling that takes into account the capabilities of the would-be attackers is critical for assessing the re-identification risk of the shared biomedical data.

CONCLUSION

Overall, the results show that the re-identification risk given attack scenarios based on the real-world, external identified datasets is often significantly lower than under the worst-case assumption. This holds true for all case studies regardless of the sizes of the dataset considered in turn, and implies that substantially more data could be shared for biomedical research.

FUNDING

This research was supported by National Institutes of Health grant numbers R01HG006844, RM1HG009034, and U2COD023196; National Library of Medicine grant number T15LM007450; and National Science Foundation grant numbers CNS2029651 and CNS2029661.

AUTHOR CONTRIBUTIONS

WX designed the framework and the empirical analysis, analyzed the experiment results, and drafted the manuscript. YL, SN, and ZW and assisted in framework design and empirical analysis, and revised the manuscript. EWC, MK, and YV provided guidance on framework and interpretation of the empirical findings, and revised the manuscript. BM designed and supervised the study, analyzed results, and revised the manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

DATA AVAILABILITY STATEMENT

Data available on request.

CONFLICT OF INTEREST STATEMENT

The authors have no competing interests to declare.