Skip to main content
PMC home page
CBE Life Sciences Education logoLink to CBE Life Sciences Education
. 2020 Fall;19(3):es5. doi: 10.1187/cbe.20-01-0016

“How Well Does Your Structural Equation Model Fit Your Data?”: Is Marcoulides and Yuan’s Equivalence Test the Answer?

James Peugh †,*, David F Feldon ‡
Editor: Erin L Dolan
PMCID: PMC8711809  PMID: 32510273

Abstract

Structural equation modeling is an ideal data analytical tool for testing complex relationships among many analytical variables. It can simultaneously test multiple mediating and moderating relationships, estimate latent variables on the basis of related measures, and address practical issues such as nonnormality and missing data. To test the extent to which a hypothesized model provides an appropriate characterization of the collective relationships among its variables, researchers must assess the “fit” between the model and the sample’s data. However, interpreting estimates of model fit is a problematic process. The traditional inferential test of model fit, the chi-square test, is biased due to sample size. Fit indices provide descriptive (i.e., noninferential) values of model fit (e.g., comparative fit index, root-mean-square error of approximation), but are unable to provide a definitive “acceptable” or “unacceptable” fit determination. Marcoulides and Yuan have introduced an equivalence-testing technique for assessing model fit that combines traditional descriptive fit indices with an inferential testing strategy in the form of confidence intervals to facilitate more definitive fit conclusions. In this paper, we explain this technique and demonstrate its application, highlighting the substantial advantages it offers the life sciences education community for drawing robust conclusions from structural equation models. A structural equation model and data set (N = 1902) drawn from previously published research are used to illustrate how to perform and interpret an equivalence test of model fit using Marcoulides and Yuan’s approach.

“HOW WELL DOES YOUR STRUCTURAL EQUATION MODEL FIT YOUR DATA?”: IS MARCOULIDES AND YUAN’S (2017) EQUIVALENCE TEST THE ANSWER?

The efforts of educational research to understand and characterize the interactions of persons, social and policy contexts, and interventions have led it to be called the “hardest science” (Berliner, 2002, p. 18). Interpreting these complex relationships quantitatively requires the application of multivariate statistical tools capable of predicting one or more outcomes through multiple possible pathways (e.g., mediation, moderation). For this reason, structural equation model analyses have become common in life sciences education research (e.g., Aragón et al., 2018; Corwin et al., 2018; Estrada et al., 2018) to explain complex sequential relationships among several analytical variables. Structural equation modeling (SEM) is ideally suited for analytical models involving the testing, for example, of multiple mediated pathways (Taylor et al., 2008; Williams and MacKinnon, 2008). Such an analytical model, by definition, involves testing multiple mediation variables that are both predicted by other variables, but also subsequently predict additional variables.

For example, in evaluating the direct and indirect effects of biology instructors’ beliefs about student intelligence on their implementation of active-learning practices, Aragón and colleagues (2018) estimated instructor mindset as a latent variable using participant responses to multiple questions and examined the latent variable’s ability to predict implementation of active-learning strategies both directly and as it impacted each preceding stage of a hypothesized process of adoption that led to implementation. Similarly, Corwin and colleagues (2018) examined the ability of course features to impact students’ cognitive and emotional ownership, which in turn were hypothesized to predict students’ postcourse career intentions. The authors used SEM analyses to determine that these relationships accounted for 11% of the variance in the sample, independent of the influence of students’ precourse career intentions.

Such complex analytical structural equation models immediately beg the question of model fit, which is broadly defined as the extent to which the quantified relationships among variables in the analytical model reproduce the relationships among the variables in the sample data. However, differently specified structural equation models might account for the same proportion of response variable variance. To assess which might be a better fit to the data, it is necessary to assess both the variance explained and model parsimony. Conceptually, parsimony reflects the efficiency with which an explanation can account for observed data. According to the maxim of Occam’s razor, if two competing explanations of a phenomenon equivalently account for the data available, the simpler of the two is preferable. In the context of SEM, parsimony can be quantified as the available degrees of freedom (df).

For example, a researcher might estimate a simple correlation matrix for variables of interest as an analytical model, but such a model is not ideal for two reasons. First, by definition, a correlation matrix makes no independent variable or dependent variable distinctions, so no directional relationships are tested. Second, a correlation matrix is a model that quantifies the extent to which every variable is related to all other variables. In SEM, such a model exhausts all df, such that df = 0 for a correlation matrix. In contrast, a structural equation model proposes specific and directional relationships among independent and dependent analytical variables, does not exhaust all df (df > 0 for most structural equation models), and is more parsimonious (i.e., specifies fewer relationship paths).

This again begs an immediate question of model fit: How well does a more parsimonious structural equation model (df > 0) reproduce relationships among variables as shown in a sample data correlation matrix (df = 0)? This is a crucial question, because a structural equation model is only as reliable and valid as its ability to accurately reproduce relationships known to exist.

Testing and interpreting how well structural equation models fit sample data has been a methodological challenge for decades. Inferential tests of model fit (e.g., chi-square) are biased due to sample size, and descriptive fit indices (e.g., comparative fit index [CFI; Bentler, 1990]; root-mean-square error of approximation [RMSEA; Steiger and Lind, 1980]) have no absolute cut-points to reliably differentiate “acceptable” from “unacceptable” fit (Hu and Bentler, 1999). The four purposes of this research methods Essay are to: 1) briefly summarize previous attempts to define, quantify, test, and evaluate model fit; 2) describe in detail a new technique for testing and evaluating model fit from Marcoulides and Yuan (2017); 3) demonstrate this technique with a sample data set and structural equation model typical of the types of studies published in LSE; and 4) offer both suggestions and cautions to researchers seeking to assess structural equation model fit.

Structural Equation Model Fit Defined

Structural equation model fit (see Glossary of Terms) is determined by the degree of similarity between the collective relationships specified in a given model (i.e., parameter estimates) and the covariance matrix (i.e., the unstandardized correlation matrix, which represents all pairwise relationships in the data set). 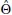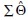If we denote a covariance matrix for a set of analytical variables obtained from a sample as S, and all parameter estimates from a structural equation model analyzed using the same sample data collectively as Inline graphic, the model fit question then becomes how to compare Inline graphic estimates with sample data covariance matrix S to determine fit. As shown elsewhere (Bollen, 1989), parameter estimates can be mathematically combined to create an alternative, or model-reproduced, covariance matrix, denoted Inline graphic that represents how well the structural equation model predicts all pairwise relationships among the variables analyzed. Model fit is determined by the extent to which the structural equation model–reproduced covariance matrix (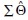Inline graphic) matches the sample data covariance matrix (S).

In hypothesis testing terms, this is:

graphic file with name cbe-19-es5-e005.jpg
graphic file with name cbe-19-es5-e006.jpg

where the null hypothesis states that the structural equation model (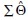Inline graphic) accurately captures the relationships among analytical variables in the population as estimated by the sample covariance matrix (S). This test of model fit implies that 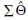Inline graphic can be statistically compared with S, and the null hypothesis of model fit either rejected or retained.

The test statistic (TS) needed for the above hypothesis test is defined as:

graphic file with name cbe-19-es5-e009.jpg

where f is a single value that quantifies the discrepancy between the sample data and model-reproduced covariance matrices (S − 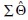Inline graphic). The fit function (f) is estimated along with the parameters for a given structural equation model using maximum likelihood (cf. Jöreskog, 1969; Browne, 1974, as cited in West et al., 2012). The resulting TS is assumed to be chi-square (χ2) distributed and is evaluated at df equal to [p(p + 1)/2] − q, where p is the number of analytical variables and q is the number of SEM parameters estimated. The intent of this chi-square test of model fit is to quantify the extent to which the model covariance matrix deviates from the sample covariance matrix and to test that deviation against a null hypothesis of zero (i.e., it is not significantly different).

However, this test of model fit has both conceptual and practical limitations. Conceptually, data can be collected in ways that minimize sample bias, but even in best-case scenarios, it is highly unlikely that the samples will be exact reflections of true population relationships. As such, many researchers view a null-hypothesis test of exact model fit as both unrealistic and unattainable (Steiger and Lind, 1980; Jöreskog and Sörbom, 1981; Cudeck and Henly, 1991; MacCallum et al., 2001).

Practically, the chi-square test of model fit is strongly influenced by sample size (i.e., statistical power increases as sample sizes increases). Smaller differences are easier to detect with larger samples, and larger differences can be missed in smaller samples. With smaller samples, the test statistic is less likely to be chi-square distributed, and a null hypothesis is more likely to be retained, even with a large discrepancy between the sample covariance matrix (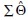Inline graphic) and the model covariance matrix (S). Conversely, with larger samples, the null hypothesis can be rejected for a negligibly small discrepancy (Tucker and Lewis, 1973; Box, 1979; Bentler and Bonett, 1980; James et al., 1982).

Despite its bias due to sample size, the chi-square test of model fit holds some intuitive appeal: the model fit question can be posed in terms of null and alternative hypotheses, a test statistic and p value can be obtained from the SEM parameter estimation process, and model fit can be judged definitively by retaining or rejecting the null hypothesis. In contrast, fit indices (e.g., CFI, RMSEA) view model fit as points along a continuum, reflecting “better fit” at one end of the continuum and “poorer fit” at the other. Accordingly, they are not inferential tests of model fit, because they do not enable researchers to retain or reject a null hypothesis. Instead, researchers look to suggested cut-point values along the fit continuum with the expectation that such cut-points may reliably distinguish well-fitting structural equation models from poorly fitting ones. Thus, common practice in current applications of SEM is to forego inferential tests of fit in favor of decreasing potential bias due to sample size through the application of model fit indices, such as RMSEA and CFI, which we summarize next.

Fit Indices: Definitions and Problems

Many fit indices have been developed as alternatives to the chi-square test of model fit (e.g., West et al., 2012, pp. 212–213). We focus in this Essay on the two of the most commonly used, RMSEA and CFI, which Marcoulides and Yuan (2017) used to develop their test of model fit. Both fit indexes are calculated using the SEM chi-square model fit statistic (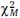Inline graphic) and df (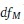Inline graphic). However, the RMSEA and CFI also differ in two important ways. First, the RMSEA uses sample size (N) in its computation, but the CFI does not. Second, the CFI uses the chi-square fit statistic (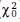Inline graphic) and df from a (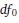Inline graphic) “null” model1 (Bentler and Bonett, 1980; Widaman and Thompson, 2003), but the RMSEA does not.

The RMSEA and CFI are computed as:

graphic file with name cbe-19-es5-e016.jpg
graphic file with name cbe-19-es5-e017.jpg

The RMSEA produces values ranging from 0 to 1 and reflects poorer fit as its value increases (i.e., values closer to zero reflect a lack of “poor fit”). The computation of RMSEA’s denominator includes both sample size and model df. Accordingly, RMSEA tends to reward complex models with high df estimated with large samples. It also tends to penalize simpler structural equation models estimated with fewer variables analyzed at smaller sample sizes (e.g., Mulaik, 2009, as cited in Kline, 2016; West et al., 2012).

In contrast, the CFI is an index of “good fit,” ranging from 0 to 1, which quantifies the proportional improvement in structural equation model fit over a “null” model (e.g., Bollen, 1989; Bentler, 1990; Kline, 2016). One advantage of the CFI is that it is less influenced by sample size. Another advantage is that it penalizes nonparsimonious models. However, the validity of the “null” comparison model for the CFI has also been questioned, because even if none of the relationships specified in a structural equation model were supported by the data, an externally valid and parsimonious “null” model would be highly unlikely. Thus, it has been argued that a null model provides an unrealistically extreme point of contrast that could yield overly generous assessments of model fit.

Hu and Bentler (1998, 1999) conducted fit index Monte Carlo simulations to determine the cut-point values that reliably distinguished “good-fitting” from “bad-fitting” structural equation models. Results suggested CFI values ≥0.95 and RMSEA values ≤0.08 distinguished well-fitting from poorly fitting structural equation models. However, subsequent research has shown that model fit index values can also be influenced by sample size (Marsh et al., 2004), df (Chen et al., 2008), the number of variables analyzed (i.e., model complexity; Kenny and McCoach, 2003), and missing data (Davey, 2005; Savalei, 2011). Despite these results and Hu and Bentler’s (1999) own warnings against doing so, their cut-point values have been accepted de facto as the SEM fit standard.

The widespread adoption of Hu and Bentler’s (1999) cut-point criteria has also led to a practical research problem (Barrett, 2007; Jellison et al., 2019). Researchers using structural equation models often provide multiple fit index values such as the chi-square test statistic and p value, CFI, RMSEA, and others. However, these fit indices may not provide uniform evidence for a well-fitting model, leaving readers to assess the strength of such a claim rather subjectively on the basis of a preponderance of often less than definitive evidence. For example, with Hu and Bentler’s (1999) recommended cut-points, models may yield borderline values (e.g., CFI = 0.943 and RMSEA = 0.087) or differ from one another based on which side of the cut score they land (e.g., CFI = 0.97 and RMSEA = 0.09; Marsh et al., 2004).

Papers often report fit indices that vary in terms of their ability to meet recommended cut-point criteria. As a result, authors characterize their findings based on personal opinion, using context-free descriptive adjectives such as “good,” “acceptable,” “close,” “adequate,” “marginal,” and so on to justify the validity of their SEM findings while simultaneously exploiting the uncertainty in the fit index empirical literature. Absent any additional definitive criteria, editorial decisions such as whether to publish a study with structural equation model fit index values that deviate to varying degrees from Hu and Bentler’s (1999) cut-points tend to become matters more of semantic subjectivity than empirical validity. As summarized by Barrett (2007):

Indeed, one gets the feeling that social scientists cannot actually contemplate that

most of their models do not fit their data, and so invent new ways of making sure

that by referencing some kind of ad hoc index, that tired old phrase, “acceptable approximate fit” may be rolled out as the required rubber stamp of validity (pp. 819–820).

Ultimately, researchers who use SEM are at an impasse. They can either assess model fit using an inferential test with well-known biases and limitations, or they can provide fit indices that reduce bias but often cannot provide clear, reliable, and valid boundaries for what values indicate good fit. However, the gap between these approaches could be bridged if confidence intervals (CIs) could be placed around CFI and RMSEA indices. This strategy would provide a measure of how certain the CFI and RMSEA indices are for a given sample and model, which would inform and quantify for researchers how certain they could be that their structural equation model is a good or poor fit to their data. This measure of certainty would need to be reliable and valid across various sample sizes, df values, model complexities, and missing data rates, while acknowledging a minimally acceptable amount of model misfit (Kline, 2016). Marcoulides and Yuan (2017) and Yuan et al. (2016) have developed an approach that accomplishes just this: an inferential equivalence test of model fit that can be used with conventional descriptive fit indices. In the following section, we describe their approach, followed by an example of how it is used to test model fit.

Equivalence Testing, Confidence Intervals, and Model Fit

Equivalence testing is based on two premises. First, traditional null-hypothesis statistical tests do not provide researchers with evidence in favor of an effect size being precisely zero in the population (i.e., it cannot prove a negative). Rather, these tests allow researchers to propose null hypotheses regarding the size of an effect, based on agreed-upon definitions of what constitutes a meaningful effect size. If the null is rejected, the test then provides inferential evidence for a lack of a meaningful difference (Wellek, 2010).

For example, if a researcher wished to compare two interventions, intervention A and intervention B, both thought to improve mean educational achievement 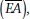Inline graphic, traditional two-sided null and alternative hypotheses could be posed as

graphic file with name cbe-19-es5-e019.jpg
graphic file with name cbe-19-es5-e020.jpg

In this scenario, retaining the null hypothesis does not provide evidence that the difference in effectiveness between the two interventions is exactly zero, but instead suggests that the mean difference in test scores observed between the two interventions was of insufficient magnitude to reject the null hypothesis. The possibility exists that the mean difference could still have resulted in a meaningful effect size and that retaining the null hypothesis was due to low statistical power. However, in the field of educational achievement, if a Cohen’s d effect size of 0.20 is considered a small but meaningful difference, equivalence testing allows for “two one-sided” null-hypothesis tests (Schuirman, 1987) to be posed

graphic file with name cbe-19-es5-e021.jpg
graphic file with name cbe-19-es5-e022.jpg

If both null hypotheses are rejected, the researcher can conclude that the observed mean difference between the two interventions falls within the bounds of a meaningful effect and that the two interventions equivalently improve educational achievement (Seaman and Serlin, 1998; Lakens, 2017).

It is through this equivalence-testing lens that Marcoulides and Yuan (2017) have proposed a new technique for quantifying and judging model fit. Their technique begins by forming CIs around the observed CFI and RMSEA fit indices. In general, the equation for a CI for any parameter estimate is:

graphic file with name cbe-19-es5-e023.jpg

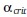where Inline graphic is a distributional critical value that determines the width of the CI (e.g., assuming a unit normal distribution, 1.96 is the distributional critical value for a two-tailed 95% CI) and standard error (SE) is calculated as a function of variance and sample size. The CI equation shown above can be rewritten consistent with Marcoulides and Yuan’s (2017) equivalence-testing technique as:

graphic file with name cbe-19-es5-e025.jpg

In this equation, 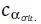Inline graphic is a cumulative probability distribution critical value that specifies a 95% CI. For SEM fit equivalence testing, the meaningful effect of interest is 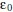Inline graphic, which quantifies a minimal acceptable value for SEM misfit (Wellek, 2010). Both the critical value (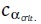Inline graphic) and the equivalence-testing value (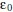Inline graphic) are calculated as a function of 1) sample size, 2) chi-square fit statistics for both the analytical and null models, 3) df, and 4) the number of analytical variables via syntax provided by Marcoulides and Yuan (2017). Because the CFI is a “good fit” index, we only need to consider the lower bound of the 95% CI. Conversely, because the RMSEA is a “poor fit” index, we only need to consider the upper bound of the 95% CI. Together, these two rescaled fit indices are referred to as “T-size” statistics (CFIT and RMSEAT), because the chi-square model fit statistic is often referred to in the SEM literature as a T-statistic. The T-statistic is needed to compute both the rescaled fit indices and their respective 95% CI bounds for use in equivalence testing.

It is important to note that interpreting CFIT and RMSEAT values in relation to conventional benchmark values for the CFI (0.99, 0.95, 0.92, 0.90) and RMSEA (0.01, 0.05, 0.08, 0.10; MacCallum et al., 1996) would be inappropriate, because the conventional values were not generated with any specific model in mind. Accordingly, the conventional values do not take into account sample size, model complexity, and df. However, Marcoulides and Yuan (2017) provide syntax2 that rescales the CFI and RMSEA, as well as their respective benchmarks,3,4 based on sample size and df, so model fit conclusions can be drawn with inferential certainty based on both rescaled fit statistics and rescaled benchmarks.

A STRUCTURAL EQUATION MODEL FIT EQUIVALENCE-TESTING EXAMPLE

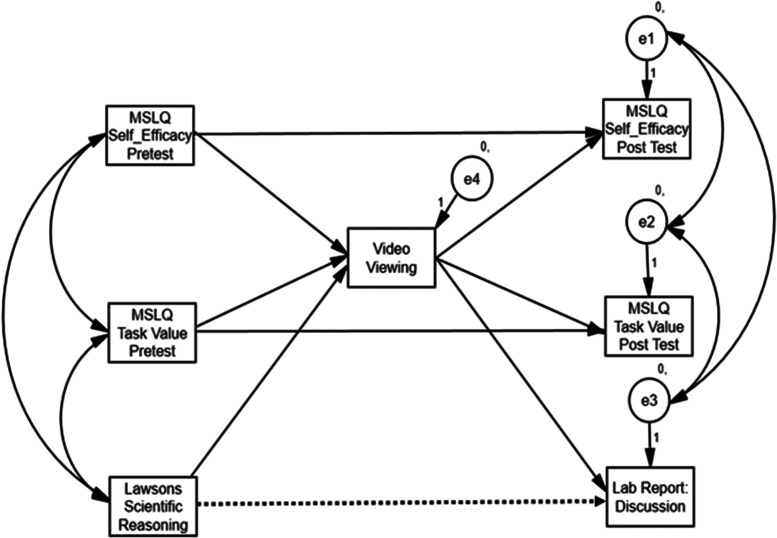
Here we describe an example of a test of SEM fit from a published study aimed at testing the effect of viewing an instructional video on students’ postintervention self-efficacy, task value, and lab report quality, controlling for preintervention self-efficacy, task value, and scientific reasoning scores (see Feldon et al., 2018). The example analytical structural equation model used is shown in Figure 1. SEM analysis was needed for three reasons: 1) the research question involves four correlated response variables; 2) the analytical model contains complex relationships: “video viewing” is both predicted by MSLQ pretest and Lawson’s scientific reasoning and predicts MSLQ posttest and lab report discussion section scores; and 3) the sample (N = 1902) has missing data (ranges from 0.9 to 31.4%) that can be handled correctly using maximum-likelihood estimation available in most SEM statistical analysis software packages. To show how to judge model fit using Marcoulides and Yuan’s (2017) procedure, we analyzed data from the study with both a “properly specified” model, defined as one consistent with Feldon et al.’s (2018) research question, and a “misspecified” model, defined as a model that is inconsistent with Feldon et al.’s (2018) research question, because it excluded a key prediction path. Specifically, as shown in Figure 1, the properly specified model included the dashed path, the misspecified model excluded the dashed path. We performed all analyses in Mplus (v. 8.4). The syntax we used to compute rescaled CFI and RMSEA fit statistic values and their respective rescaled benchmarks can be found online at www3.nd.edu/∼kyuan/EquivalenceTesting.

FIGURE 1.

FIGURE 1.

Open in a new tab

Example structural equation model based on Feldon et al. (2018).

Analyzing the misspecified version of the structural equation model (Figure 1) showed the following structural equation model fit results: 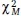Inline graphic = 60.404, df = 7, p < 0.001; CFI = 0.964; RMSEA = 0.063; 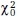Inline graphic = 1515.459, df = 18, P = 7 variables analyzed. According to conventional interpretations of the CFI and RMSEA using Hu and Bentler’s (1999) criteria, this model would have acceptable fit. However, entering this information into Marcoulides and Yuan’s (2017) equivalence-testing syntax files produced the following rescaled fit statistics values: CFIT = 0.9347 and RMSEAT = 0.0785. The generated5 interpretation guidelines for the rescaled CFI value (i.e., CFIT) based on rescaled benchmarks are: “poor” ≤ 0.881, “mediocre” = 0.881–0.903, “fair” = 0.903–0.935, “close” = 0.935–0.983, “excellent” ≥ 0.983. Likewise, the rescaled benchmarks for RMSEAT are: “poor” ≥ 0.113, “mediocre” = 0.094–0.113, “fair” = 0.066–0.094, “close” = 0.032–0.066, “excellent” ≤ 0.032. More importantly, when expressed as two one-sided null hypotheses consistent with conventional equivalence testing

graphic file with name cbe-19-es5-e032.jpg
graphic file with name cbe-19-es5-e033.jpg

the two one-sided null hypotheses are retained, which by equivalence-testing standards indicates that the model is not equivalent to a “close” model that acceptably fits the sample data. Stated differently, the rescaled fit statistic values for both the CFI and RMSEA fall within their respective “fair” rescaled benchmark intervals, which Marcoulides and Yuan deem an unacceptable fit of the structural equation model to the data.

Analyzing the properly specified version of the structural equation model in Figure 1 showed the following conventional fit statistics results: 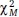Inline graphic = 28.547, df = 6, p < 0.001; CFI = 0.985; RMSEA = 0.044; 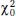Inline graphic = 1515.459, df = 18, P = 7 variables analyzed. Entering this information into Marcoulides and Yuan’s (2017) equivalence-testing syntax files produced the following rescaled fit statistics values and their respective rescaled benchmarks: CFIT = 0.9648 (“poor” ≤ 0.882, “mediocre” = 0.882–0.904, “fair” = 0.904–0.935, “close” = 0.935–0.983, “excellent” ≥ 0.983) and RMSEAT = 0.0615 (“poor” ≥ 0.114, “mediocre” = 0.095–0.114, “fair” = 0.067–0.095, “close” = 0.033–0.067, “excellent” ≤ 0.033). When again expressed as two one-sided null hypotheses consistent with conventional equivalence testing

graphic file with name cbe-19-es5-e036.jpg
graphic file with name cbe-19-es5-e037.jpg

both one-sided null hypotheses are rejected, which by equivalence-testing standards indicates that the model is equivalent to a “close” model that acceptably fits the sample data. Stated differently, the rescaled fit statistic values for both the CFI and RMSEA fall within their respective “close” benchmark intervals, indicating an acceptable model fit to the data.

Two key points warrant emphasis. First, Marcoulides and Yuan’s (2017) equivalence-testing technique allows researchers to state with 95% confidence that the population CFI is greater than 0.9648, and the population RMSEA is lower than 0.0615. Second, the rescaled “fair” benchmark interval upper bound for the CFIT and lower bound for the RMSEAT, respectively, essentially function as the new test statistics for judging structural equation model fit, determined on the basis of the tested model’s specific characteristics. Specifically, both the misspecified and properly specified models yielded results that would have been readily accepted under Hu and Bentler’s (1999) cut-point guidelines, despite the former excluding a parameter (Lawson’s → Lab report: Discussion) critical to answering the research question. Using Marcoulides and Yuan’s strategy, clear differences were found in model fit that identified the misspecified model as unacceptable and the properly specified model as acceptable. Further, this difference was not open to criticism that research beliefs biased the semantic characterization of model fit. The tests were inferential and accounted for both model specification and df differences between the two models when calculating the criterial T-size values.

CAUTIONS

The example illustrates the benefits of applying Marcoulides and Yuan’s (2017) approach. However, before wholesale adoption of equivalence testing to assess model fit, words of caution are warranted. First, there is currently no agreement in the empirical literature as to what constitutes correct specification for a null structural equation model—in other words, what an appropriate null model is (e.g., Widaman and Thompson, 2003). Currently, the null model is used as a baseline contrast against the specified model tested in a structural equation model to yield a CFI value. For instance, CFI = 0.95 would reflect a 95% improvement in model fit for the specified model over the null. As such, because the CFI is highly reliant on the null model test statistic and df for computation, equivalence-testing results can be greatly impacted based on how each SEM statistical analysis software package defines and specifies a null model. Researchers should note that different equivalence-testing results and conclusions could occur for the same model estimated in different statistical analysis software packages. For example, analyzing the misspecified version of the structural equation model shown in Figure 1 using AMOS (v. 24) showed that the CFIT value fell into the “close” benchmark interval, indicating acceptable model fit for the misspecified model. This result can be explained by the fact that the null model chi-square fit statistics differed by 1300 points and 10 df when estimated in AMOS versus Mplus.6 Accordingly, it is both prudent and necessary to report the statistical analysis software and version employed for a given SEM analysis.

Second, researchers using SEM have long been tempted to delete statistically nonsignificant model parameters, add model parameters suspected to be statistically significant based on modification index values, or both. Engaging in such parameter deletion or addition practices in the service of improving model fit is referred to in the SEM literature as specification search activities. Such specification searches have long been known to produce results that subsequent research typically fails to replicate (see MacCallum, 1986; MacCallum et al., 1992). A recent increase in dedicated software programs that automate specification searches (e.g., Brandmaier et al., 2016; Marcoulides and Falk, 2018; Gates et al., 2019) for the purpose of recommending additional model specification changes that would enhance fit exacerbates the concern that researchers are engaging in “HARKing” (hypothesizing after results are known), theoretically ungrounded data exploration, and p value hacking (Pan et al., 2017), which are antithetical to scientific inquiry. A lack of acceptable structural equation model fit should spur a re-examination of theory, not an analytical model specification search—the sample data “tail” should never wag the empirical “dog.” Shifting theoretical expectations to optimally suit the idiosyncrasies of a specific data sample are likely to result in significant findings that reflect coincidental features of the sample itself (i.e., sampling error) rather than those reflective of the true population.

Finally, this equivalence-testing example was based on a relatively large sample (N = 1902). Marcoulides and Yuan’s (2017) illustrative example was based on a generated data set of N = 600 hypothetical participants. These sample sizes are somewhat larger than the sample sizes typically seen across a variety of research disciplines, including studies published in LSE. Further, the rescaled values for the CFI and RMSEA, as well as their respective cut-points, are all calculated based on both the chi-square statistics for the analytical and “null” models (which are affected by sample size) and the sample size itself. How well Marcoulides and Yuan’s (2017) equivalence-testing technique performs at sample sizes more commonly seen in the published research literature has not yet been systematically investigated.

Further, we would argue that assessing SEM fit using equivalence testing is the best current practice, because it quantifies a minimal tolerable amount of model misspecification and specifies an inferential test of model fit using a strategy well supported by the mathematics underlying the approach. However, Marcoulides and Yuan’s (2017) equivalence-testing technique has yet to be tested extensively using wide ranges of sample sizes, model types, and data characteristics. In short, its status as state of the art does not mean it is infallible under all circumstances. As further statistical studies examine potential effects of sample size and other features on the precision of Marcoulides and Yuan’s generated T-size statistics, their application may change. For this reason, it is advisable for researchers using SEM to keep at least marginally abreast of developments in this area of statistics, as they should for any method they use. Findings relevant to the current issue are typically published in journals such as Psychological Methods, Structural Equation Modeling, and Multivariate Behavioral Research. Notwithstanding these potential limitations, the approach does reflect the most notable advance in structural equation model fit evaluation in over two decades and offers a new standard in best practice.

CONCLUSIONS

Many of us use SEM in our analyses without much thought to the underlying statistical mechanisms of statistical tools. Yet recent advances in assessments of model fit are worthy of our attention, because they provide a more robust basis for drawing conclusions regarding the validity of trends within our data. The equivalence-testing approach and accompanying code provided by Marcoulides and Yuan (2017) offer a ready resource for scholars to test and compare goodness of fit for structural equation models on an inferential basis. Using a CI approach for evaluating fit indices that incorporate characteristics of the specific model tested provides a greater level of precision for assessing the fit of proposed models. In turn, findings supported by Marcoulides and Yuan’s rigorous approach can offer greater benefit in both understanding the mechanisms of learning and informing evidence-based practices in life sciences education.

GLOSSARY OF TERMS

Covariance Matrix

Denoted by “S” in a sample of data, it is sometimes referred to as an “unstandardized correlation matrix,” because it quantifies all possible pairwise relationships among variables of interest in their original measurement scales, whereas a correlation matrix quantifies all possible pairwise relationships among variables of interest after all variables have been standardized (i.e., placed on a unit normal or z-score scale).

Parameter Estimates

Denoted collectively by 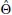Inline graphic, they are the result of mathematically and statistically imposing a structural equation model of interest upon a given sample of data. The goal of parameter estimates is to answer research questions regarding population realities based on information obtained from samples drawn randomly from the population. Such population realities, or parameters, are termed “estimates” to acknowledge that they were obtained under the assumption that information gathered from the sample will closely approximate the reality of interest in the population.

Model-Reproduced Covariance Matrix

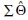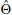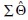Denoted Inline graphic, it is the result of using parameter estimates from a structural equation model of interest (Inline graphic) to solve SEM-specific covariance algebra equations shown elsewhere (e.g., Bollen, 1989) to quantify all possible pairwise relationships (Inline graphic) among variables as determined by the structural equation model of interest (i.e., Inline graphic).

Model Fit

The methodological process by which the internal validity, external validity, adequacy, and efficacy of a structural equation model is determined; model fit is defined and quantified as the extent to which the model-reproduced covariance matrix (Inline graphic) differs from the sample data covariance matrix (S).

Footnotes

1Varying approaches can be taken to specifying the null model (c.f. Widaman and Thompson, 2003), resulting in occasional disagreements between statistical analysis software packages. As a practical issue, this topic is briefly discussed in the Cautions section later in this paper.

5Interpretation guidelines are generated dynamically by the code published in Marcoulides and Yuan (2017) according to model parameters and sample characteristics. Thus, threshold values change as appropriate for each model tested.

6Specifically, for the misspecified model shown in Figure 1, both Mplus and AMOS define a null model’s df as the differences in df between the alternative (HA:) and null (H0:) baseline models as follows. In Mplus, the HA: baseline model has df values that are the sum of: 1) four variances, four means, and six covariances (14 total) among the response variables (i.e., Video Viewing, MLQ Self-Efficacy Posttest, MLQ Task Value Posttest, and Lab Report: Discussion), plus 2) all possible covariances between MLQ Self-Efficacy Posttest, MLQ Task Value Posttest, and Lab Report: Discussion with Video Viewing (six) plus all possible covariances between MLQ Self-Efficacy pretest, MLQ Task Value pretest, and Lawson’s test of Scientific Reasoning with Video Viewing (six; 12 total) for an HA: baseline model total of df = (14 + 12) = 26. The H0: baseline model in Mplus has df defined as the sum of four means and four variances (8 total) for the response variables (i.e., Video Viewing, MLQ Self-Efficacy Posttest, MLQ Task Value Posttest, and Lab report: Discussion). As such, in Mplus, the df for the null model is (df = HA: minus H0: = 26 – 8 = 18). In contrast, AMOS defines an HA: baseline model as having df equal to the sum of all possible variances and covariances among all seven analytical variables [(7*8) / 2 = 28] plus 7 means (28 + 7 = 35 total). AMOS defines an H0: baseline model as having df equal to seven variances for all analysis variables. As such, in AMOS, the df for the null model is (df = HA: minus H0: = 35 – 7 = 28). This explains the ten (28 – 18 = 10) df difference, and subsequent 1300 chi-square point difference, in null-model definition and estimation between Mplus and AMOS.

REFERENCES

  1. Aragón, O. R., Eddy, S. L., Graham, M. J. (2018). Faculty beliefs about intelligence are related to the adoption of active-learning practices. CBE—Life Sciences Education, 17, ar47. doi: 10.1187/cbe.17-05-0084 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barrett, P. (2007). Structural equation modelling: Adjudging model fit. Personality and Individual Differences, 42, 815–824. doi: 10.1016/j.paid.2006.09.018 [DOI] [Google Scholar]
  3. Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107, 238. doi: 10.1037/0033-2909.107.2.238 [DOI] [PubMed] [Google Scholar]
  4. Bentler, P. M., Bonett, D. G. (1980). Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin, 88(3), 588–606. [Google Scholar]
  5. Berliner, D. (2002). Educational research: The hardest science of all. Educational Researcher, 31(8), 18–20. [Google Scholar]
  6. Bollen, K. A. (1989). Structural equations with latent variables. New York: Wiley. [Google Scholar]
  7. Box, G. E. P. (1979). Robustness in the strategy of scientific model building. In Launer, R. L., Wilkinson, G. N. (Eds.), Robustness in statistics (pp. 201–236). Academic Press. [Google Scholar]
  8. Brandmaier, A. M., Prindle, J. J., McArdle, J. J., Lindenberger, U. (2016). Theory-guided exploration with structural equation model forests. Psychological Methods, 21, 566–582. doi: 10.1037/met0000090 [DOI] [PubMed] [Google Scholar]
  9. Browne, M. W. (1974). Generalized least squares estimators in the analysis of covariance structures. South African Statistical Journal, 8, 1–24. [Google Scholar]
  10. Chen, F., Curran, P. J., Bollen, K. A., Kirby, J., Paxton, P. (2008). An empirical evaluation of the use of fixed cutoff points in RMSEA test statistic in structural equation models. Sociological Methods & Research, 36, 462–494. doi: 10.1177/0049124108314720 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Corwin, L. A., Runyon, C. R., Ghanem, E., Sandy, M., Clark, G., Palmer, G. C., Dolan, E. L. (2018). Effects of discovery, iteration, and collaboration in laboratory courses on undergraduates’ research career intentions fully mediated by student ownership. CBE—Life Sciences Education, 17, ar20. doi: 10.1187/cbe.17-07-0141 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cudeck, R., Henly, S. J. (1991). Model selection in covariance structures analysis and the" problem" of sample size: A clarification. Psychological Bulletin, 109, 512–519. [DOI] [PubMed] [Google Scholar]
  13. Davey, A. (2005). Issues in evaluating model fit with missing data. Structural Equation Modeling: A Multidisciplinary Journal, 12, 578–597. doi: 10.1207/s15328007sem1204_4 [DOI] [Google Scholar]
  14. Estrada, M., Hernandez, P. R., Schultz, P. W. (2018). A longitudinal study of how quality mentorship and research experience integrate underrepresented minorities into STEM careers. CBE—Life Sciences Education, 17, ar9. doi: 10.1187/cbe.17-04-0066 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Feldon, D. F., Franco, J., Chao, J., Peugh, J., Maahs-Fladung, C. (2018). Self-efficacy change associated with a cognitive load-based intervention in an undergraduate biology course. Learning and Instruction, 56, 64–72. doi: 10.1016/j.learninstruc.2018.04.007 [DOI] [Google Scholar]
  16. Gates, K. M., Fisher, Z. F., Bollen, K. A. (2019). Latent variable GIMME using model implied instrumental variables (MIIVs). Psychological Methods, 25(2), 227–242. doi: 10.1037/met0000229 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hu, L. T., Bentler, P. M. (1998). Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods, 3, 424–453. [Google Scholar]
  18. Hu, L. T., Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6, 1–55. doi: 10.1080/10705519909540118 [DOI] [Google Scholar]
  19. James, L. R., Mulaik, S. A., Brett, J. M. (1982). Causal analysis. Beverly Hills, CA: Sage. [Google Scholar]
  20. Jellison, S., Roberts, W., Bowers, A., Combs, T., Beaman, J., Wayant, C., Vassar, M. (2019). Evaluation of spin in abstracts of papers in psychiatry and psychology journals. BMJ Evidence-Based Medicine. doi: 10.1136/bmjebm-2019-111176 [DOI] [PubMed] [Google Scholar]
  21. Jöreskog, K. G. (1969). A general approach to confirmatory maximum likelihood factor analysis. Psychometrika, 34, 183–202. [Google Scholar]
  22. Jöreskog, K. G., Sörbom, D. (1981). LISREL 5: Analysis of linear structural relationships by maximum likelihood and least squares methods[User’s guide]. Uppsala, Sweden: University of Uppsala. [Google Scholar]
  23. Kenny, D. A., McCoach, D. B. (2003). Effect of the number of variables on measures of fit in structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 10, 333–351. doi: 10.1207/S15328007SEM1003_1 [DOI] [Google Scholar]
  24. Kline, R. B. (2016). Principles and practice of structural equation modeling (4th ed.). New York: Guilford. [Google Scholar]
  25. Lakens, D. (2017). Equivalence tests: A practical primer for t tests, correlations, and meta-analyses. Social Psychological and Personality Science, 8, 355–362. doi: 10.1177/1948550617697177 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. MacCallum, R. (1986). Specification searches in covariance structure modeling. Psychological Bulletin, 100, 107–120. [Google Scholar]
  27. MacCallum, R. C., Browne, M. W., Sugawara, H. M. (1996). Power analysis and determination of sample size for covariance structure modeling. Psychological Methods, 1, 130–149. doi: 10.1037/1082-989X.1.2.130 [DOI] [Google Scholar]
  28. MacCallum, R. C., Roznowski, M., Necowitz, L. B. (1992). Model modifications in covariance structure analysis: The problem of capitalization on chance. Psychological Bulletin, 111, 490–504. [DOI] [PubMed] [Google Scholar]
  29. MacCallum, R. C., Widaman, K. F., Preacher, K. J., Hong, S. (2001). Sample size in factor analysis: The role of model error. Multivariate Behavioral Research, 36, 611–637. doi: 10.1207/S15327906MBR3604_06 [DOI] [PubMed] [Google Scholar]
  30. Marcoulides, K. M., Falk, C. F. (2018). Model specification searches in structural equation modeling with R. Structural Equation Modeling: A Multidisciplinary Journal, 25(3), 484–491. doi: 10.1080/10705511.2017.1409074 [DOI] [Google Scholar]
  31. Marcoulides, K. M., Yuan, K. H. (2017). New ways to evaluate goodness of fit: A note on using equivalence testing to assess structural equation models. Structural Equation Modeling: A Multidisciplinary Journal, 24, 148–153. doi: 10.1080/10705511.2015.1065414 [DOI] [Google Scholar]
  32. Marsh, H. W., Hau, K. T., Wen, Z. (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling: A Multidisciplinary Journal, 11, 320–341. [Google Scholar]
  33. Mulaik, S. A. (2009). Linear causal modeling with structural equations. New York: Chapman and Hall/CRC. [Google Scholar]
  34. Pan, J., Ip, E. H., Dubé, L. (2017). An alternative to post hoc model modification in confirmatory factor analysis: The Bayesian lasso. Psychological Methods, 22, 687–704. doi: 10.1037/met0000112 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Savalei, V. (2011). On asymptotic robustness of NT methods with missing data (UCLA Department of Statistics papers). Retrieved May 29, 2020, from https://escholarship.org/uc/item/7zt626nh [Google Scholar]
  36. Schuirman, D. J. (1987). A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability. Journal of Pharmacokinetics and Biopharmaceutics, 15, 657–680. [DOI] [PubMed] [Google Scholar]
  37. Seaman, M. A., Serlin, R. C. (1998). Equivalence confidence intervals for two-group comparison means. Psychological Methods, 3, 403–411. doi: 10.1037/1082-989X.3.4.403 [DOI] [Google Scholar]
  38. Steiger, J. H., Lind, J. C. (1980). Statistically based tests for the number of common factors. Paper presented at: annual meeting of the Psychometric Society (Iowa City, IA). [Google Scholar]
  39. Taylor, A. B., MacKinnon, D. P., Tein, J. Y. (2008). Tests of the three-path mediated effect. Organizational Research Methods, 11, 241–269. [Google Scholar]
  40. Tucker, L. R., Lewis, C. (1973). A reliability coefficient for maximum likelihood factor analysis. Psychometrika, 38, 1–10. [Google Scholar]
  41. Wellek, S. (2010). Testing statistical hypotheses of equivalence and non-inferiority (2nd ed.). Boca Raton, FL: Chapman & Hall/CRC. [Google Scholar]
  42. West, S. G., Taylor, A. B., Wu, W. (2012). Model fit and model selection in structural equation modeling. In Hoyle, R. (Ed.), Handbook of structural equation modeling (pp. 209–231). New York: Guilford. [Google Scholar]
  43. Widaman, K. F., Thompson, J. S. (2003). On specifying the null model for incremental fit indices in structural equation modeling. Psychological Methods, 8, 16–37. doi: 10.1037/1082-989X.8.1.16 [DOI] [PubMed] [Google Scholar]
  44. Williams, J., MacKinnon, D. P. (2008). Resampling and distribution of the product methods for testing indirect effects in complex models. Structural Equation Modeling: A Multidisciplinary Journal, 15, 23–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Yuan, K. H., Chan, W., Marcoulides, G. A., Bentler, P. M. (2016). Assessing structural equation models by equivalence testing with adjusted fit indexes. Structural Equation Modeling: A Multidisciplinary Journal, 23, 319–330. doi: 10.1080/10705511.2015.1065414 [DOI] [Google Scholar]

Articles from CBE Life Sciences Education are provided here courtesy of American Society for Cell Biology

RESOURCES