Skip to main content
PMC home page
The Journal of Advanced Prosthodontics logoLink to The Journal of Advanced Prosthodontics
. 2021 Dec 22;13(6):396–407. doi: 10.4047/jap.2021.13.6.396

Comparative finite element analysis of mandibular posterior single zirconia and titanium implants: a 3-dimensional finite element analysis

Sung-Min Choi 1, Hyunsuk Choi 2, Du-Hyeong Lee 3, Min-Ho Hong 4,✉
PMCID: PMC8712109  PMID: 35003555

Abstract

PURPOSE

Zirconia has exceptional biocompatibility and good mechanical properties in clinical situations. However, finite element analysis (FEA) studies on the biomechanical stability of two-piece zirconia implant systems are limited. Therefore, the aim of this study was to compare the biomechanical properties of the two-piece zirconia and titanium implants using FEA.

MATERIALS AND METHODS

Two groups of finite element (FE) models, the zirconia (Zircon) and titanium (Titan) models, were generated for the exam. Oblique (175 N) and vertical (175 N) loads were applied to the FE model generated for FEA simulation, and the stress levels and distributions were investigated.

RESULTS

In oblique loading, von Mises stress values were the highest in the abutment of the Zircon model. The von Mises stress values of the Titan model for the abutment screw and implant fixture were slightly higher than those of the Zircon model. Minimum principal stress in the cortical bone was higher in the Titan model than Zircon model under oblique and vertical loading. Under both vertical and oblique loads, stress concentrations in the implant components and bone occurred in the same area. Because the material itself has high stiffness and elastic modulus, the Zircon model exhibited a higher von Mises stress value in the abutments than the Titan model, but at a level lower than the fracture strength of the material.

CONCLUSION

Owing to the good esthetics and stress controllability of the Zircon model, it can be considered for clinical use.

Keywords: 3D model, Dental implant, Finite element analysis, Zirconia

INTRODUCTION

Dental implants are not only applicable to edentulous or partially edentulous patients, but are also an effective treatment option for patients who need to replace a single missing tooth.1 In the dental field, titanium is currently considered the gold standard for implant manufacturing because of its excellent biocompatibility, long-term scientific validation, and relative ease of manufacture.2 Titanium implants have demonstrated excellent long-term survival rates and clinical performance.3 However, esthetic issues may arise because of the metallic color of titanium. In some cases, the gray color of titanium can be visible through the mucosal tissues after soft tissue recession.4,5 In addition, despite the excellent properties of titanium, disadvantages such as allergic reactions, cellular sensitization, and galvanic current formation have been reported. Owing to these problems, there is an increasing demand for implant materials that are esthetically satisfactory and highly biocompatible.6,7

Various materials for the manufacture of implants and implant-related treatments have recently been introduced. Zirconia is a promising material for oral rehabilitation since it can replace titanium-based implant systems with excellent esthetics, biocompatibility, and mechanical and optical properties, properties that allow its use even in premolar and molar areas.8 Specifically, zirconia is made of yttria-stabilized tetragonal polycrystals (Y-TZP), which have high flexural strength, favorable hardness, high fracture toughness, and a Weibull parameter of 10 to 12.9 Y-TZP undergoes a phase transformation from a tetragonal phase to a monoclinic phase, especially when stress is induced. This property limits crack propagation by causing a volume expansion.10 In addition, its biocompatibility as a material for dental implants has been demonstrated in several animal studies.1,10,11,12

In most clinically commercialized zirconia implant systems, one-piece implants are preferred over two-piece ones.13,14 In some studies, one-piece zirconia implants showed good tissue response and a satisfactory degree of biocompatibility.15,16,17 In 3-year follow-up studies on the success and survival of one-piece zirconia implants, survival rates ranged from 97.5% to 98.5%, which are almost identical to those of titanium implants.18,19 However, from the perspective of reconstructing lost teeth, one-piece zirconia implants have somewhat less prosthetic flexibility than two-piece zirconia implants. Owing to these properties, prosthetic correction of one-piece zirconia implants that are not placed in the ideal position is difficult. Moreover, their use is limited when implants need to be submerged.13 In such cases, two-piece zirconia implants are more advantageous than one-piece ones because the abutment shape and angle can be flexibly modified.

Recently, two-piece zirconia implants have become widely accepted in implant dentistry.20,21 However, the available evidence for their long-term success is insufficient. In most of the previous studies that performed finite element analysis (FEA) on zirconia implants, only the stress transmitted to the support bone around the fixture was analyzed.8,20,22,23,24 The lack of widespread clinical adoption of two-piece zirconia implants is likely due to the properties of brittle ceramics such as microcracks.13,20

FEA simulation is one of the most frequently used tools to investigate stress distribution in implant-surrounding bone. It is well known that optimal stress occurring in the jawbone affects the success of dental implants. However, the biomechanical properties used to assess the suitability and safety of two-piece zirconia implants are not widely known. Thus, the aim of this FEA simulation project was to compare the biomechanical properties of the new two-piece zirconia and the existing titanium implants using FEA.

MATERIALS AND METHODS

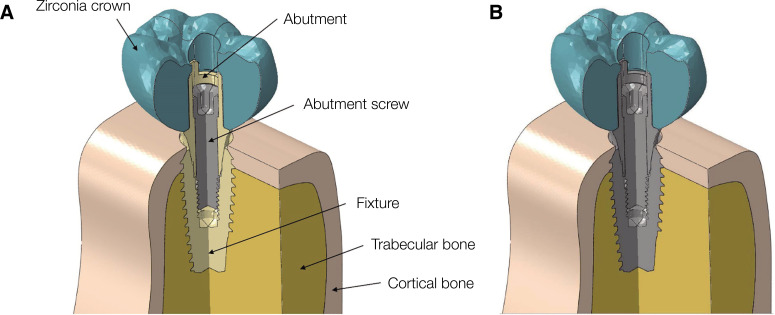
The 3D model used for the study was designed using a computer-aided design program (CATIA, Dassault Systemes, Velizy-Villacoublay, France), and a mandibular right first molar-shaped 3D model was fabricated. The models in the study were classified as zirconia (Zircon) and titanium (Titan) models. The implant, abutment screw, and bone (cortical and trabecular) geometries in both models were identical (Fig. 1). The zirconia crown used in this study was designed by editing artificial tooth (Dentiform, Nissin Dental Products, Kyoto, Japan) scan data in an NX program (NX10.0.0.24, SIEMENS, Munich, Germany). In addition, a reverse design of the natural tooth was carried out using the method of producing the surface based on STL (stereolithography) geometry. The zirconia crown used in this study was designed by editing natural tooth scan data in a CAD program. The cement thickness between the zirconia crown and the abutment was ignored to simplify the experimental models and to focus on the stress concentrations at implant and surrounding bone.25 The abutment used in this study (Milling abutment, Megagen, Daegu, Korea) was 4.5 mm in diameter and length. The abutment screw was 1.8 mm in diameter and 8.5 mm in length. The distance from the abutment screw head to the screw thread was 5.1 mm. The implant fixture (Anyone® Internal; Megagen, Daegu, Korea) was tapered implant with an internal hex connection and 5.0 mm in diameter and 11.5 mm in length. The mandible model, which was built based on the cross-sectional image of a human mandible, was 29.5 mm high and 14.0 mm wide. It was composed of trabecular bone surrounded by a cortical bone with the thickness of 1.4 to 3.7 mm. Implant fixture was applied on the mandible model at the cortical bone level.

Fig. 1. Cross-sectional view of the three-dimensional finite element models of dental implants with the internal assembly structure. (A) Zircon model and (B) Titan model.

Fig. 1

Open in a new tab

A meshing program (Altair Hypermesh v17.0; Altair Engineering, Troy, MI, USA) was used to discretize all 3D models. For the models applied in this study, 10 nodes of quadratic tetrahedral elements (mean size: 0.25 mm)26 were used. Table 1 shows the nodes, elements, and mesh sizes used in this study. The results for both models were derived through simulation using specific software (Abaqus FEA v6.12; Dassault Systems Simulia Corp., Providence, RI, USA). To simplify the models and the numerical calculations related to stress analysis using finite elements, it was assumed that the models had the following physical properties: homogeneity (the mechanical properties of the material are uniform), isotropy (material properties and mechanical behavior are the same in the three directions of the X, Y, and Z axes), and linear elasticity (the deformation or displacement of the structure is proportional to the applied force and independent of the amount of displacement). The implant and bone were assumed to be completely osseointegrated. The Young’s modulus and Poisson’s ratio of each component were chosen considering the physical properties used in previous studies (Table 2).1,27,28

Table 1. Nodes, elements, and mesh size of the FE models.

Components Nodes Elements Mesh size (μm)
Zirconia crown 12,809 58,892 250
Zirconia and titanium abutment 55,931 23,534
Zirconia and titanium fixture 96,051 23,534
Abutment screw 12,064 58,163
Cortical bone 60,134 280,089
Trabecular bone 50,931 247,142
Open in a new tab

Table 2. Mechanical properties of all simulated materials.

Material Young’s modulus (GPa) Poisson’s ratio Reference
Titanium abutment/fixture 110 0.35 [1, 24]
Zirconia abutment/fixture 210 0.30 [1, 24]
Abutment screw 110 0.35 [24]
Zirconia crown 210 0.26 [1]
Cortical bone 13.7 0.30 [24]
Trabecular bone 1.37 0.30 [24]
Open in a new tab

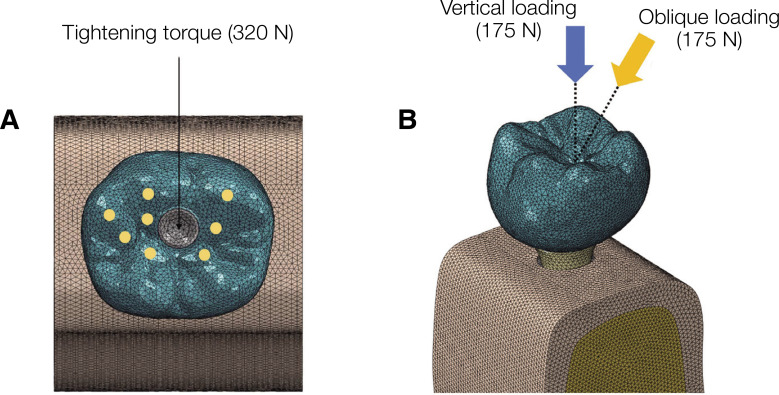
To prevent all mandible movements, the boundary condition constrained the mandible model in all three directions, X, Y, and Z. Deformation was allowed in the crown, fixture, and surrounding bone. Also, the model was assumed to be in the “tie contact,” in which the fixture is fixed to the support bone, and the screw is connected to the internal thread of the fixture. By tightening the screw torque, the abutment was connected to the fixture. However, the coefficient of friction between the inner surface of the abutment and the screw head was set to 0.5.29 A screw tightening torque of 320 N was applied, based on the formula provided in a previous study, to reproduce the preload generated in the stage before applying the occlusal force (Fig. 2).30,31

Fig. 2. Boundary and loading condition of the FEA models (Zircon and Titan models). Both groups of models are fixed in all directions. (A) A force of 320 N was applied in a direction parallel to the axis of the placed fixture, and the fixture and abutment were considered to be fully engaged. (B) Oblique and vertical loadings were obtained with the application of 175 N in two directions onto the eight occlusal areas.

Fig. 2

Open in a new tab

Two load conditions were applied to describe the occlusal load that may occur during mastication in the oral cavity. An inclined force (175 N) was applied at an inclination of 30° relative to the axis of the fixture (Fig. 2). In addition, a vertical force was applied relative to the axis of the fixture (175 N) (Fig. 2). The stress transmission of the abutment, abutment screw, and fixture were evaluated using von Mises stress analysis. In addition, the stress transmission of the cortical and trabecular bone structures was comparatively evaluated using principal stress values.

RESULTS

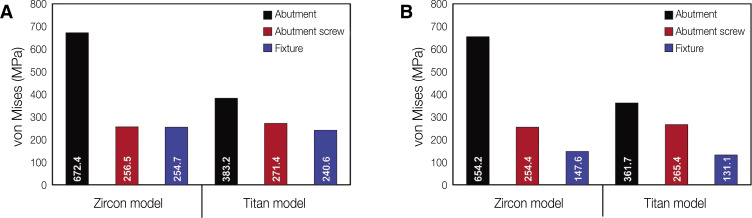
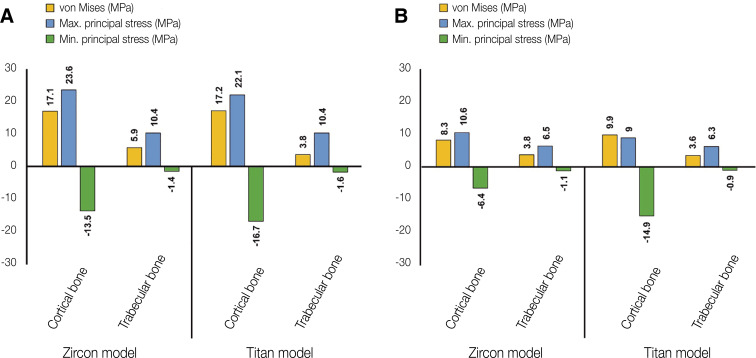
Figure 3 shows the von Mises stress values in abutment, abutment screw and fixture under oblique and vertical loading. The von Mises and principal stresses transmitted under oblique and vertical loading to the cortical and trabecular bone are shown in Fig. 4.

Fig. 3. von Mises stress values of abutment, screw, and fixture. (A) Oblique loading, (B) Vertical loading.

Fig. 3

Open in a new tab

Fig. 4. von Mises and principal stress values in cortical and trabecular bone. (A) Oblique loading, (B) Vertical loading.

Fig. 4

Open in a new tab

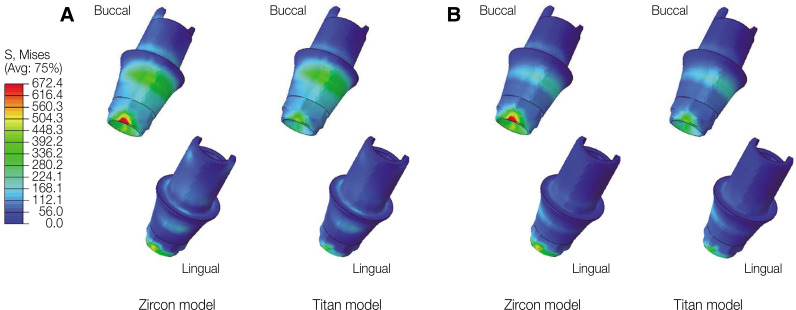
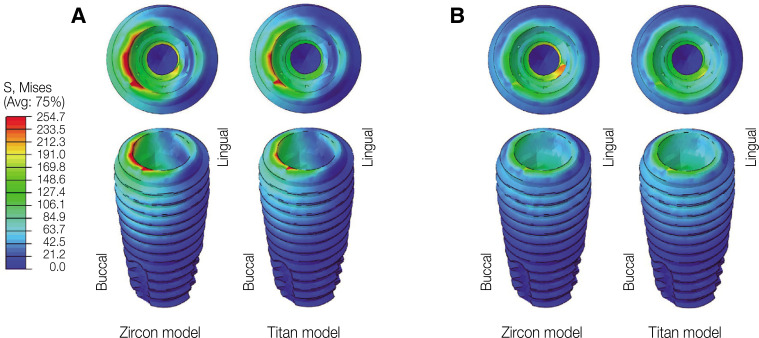
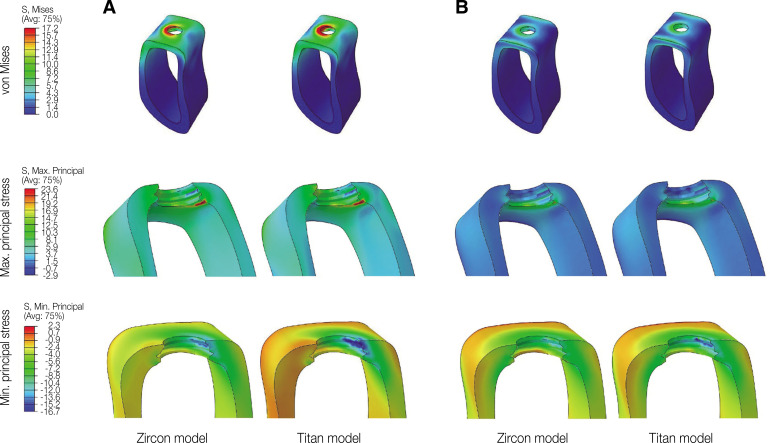
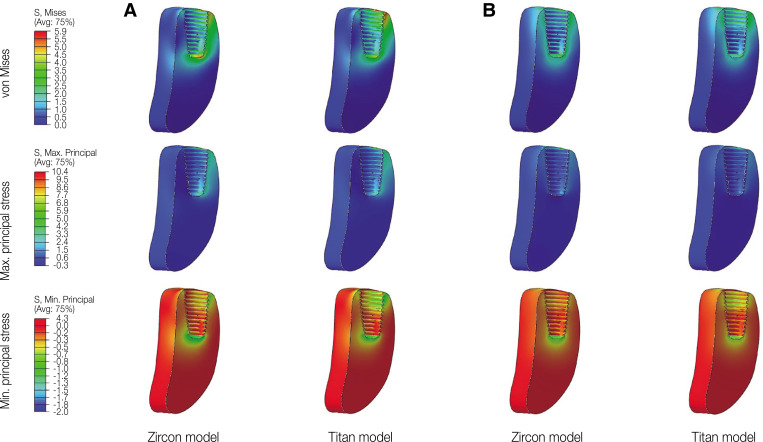
In oblique loading, the abutment exhibited the highest von Mises stress in the Zircon model (Fig. 3). The abutment screw revealed slightly higher von Mises stress in the Titan than in the Zircon model. In addition, the von Mises stress in the Titan model was also slightly higher than that in the Zircon model. Overall, the cortical bone showed higher maximum and minimum principal stress levels than the trabecular bone in all FE models. In addition, the stress concentration point was found to be similar in all FE models. In the abutment, the stress was concentrated on the inner surface of the fixture and the hex part of the abutment (Fig. 5A). Regarding the abutment screw, the stress was the highest at the third thread pitch and bottom of the screw head (Fig. 6A). The fixture showed stress concentration in the buccal neck region (Fig. 7A). In the case of maximum and minimum principal stresses, stress was concentrated in the buccal region of the cortical bone (Fig. 8A) and in the distal region of the trabecular bone (Fig. 9A).

Fig. 5. von Mises stress distribution in the abutment. (A) Oblique loading, (B) Vertical loading.

Fig. 5

Open in a new tab

Fig. 6. von Mises stress distribution in the abutment screw. (A) Oblique loading, (B) Vertical loading.

Fig. 6

Open in a new tab

Fig. 7. von Mises stress distribution in the fixture. (A) Oblique loading, (B) Vertical loading.

Fig. 7

Open in a new tab

Fig. 8. von Mises and principal stress distribution on cortical bone. (A) Oblique loading, (B) Vertical loading.

Fig. 8

Open in a new tab

Fig. 9. von Mises and principal stress distribution on trabecular bone. (A) Oblique loading, (B) Vertical loading.

Fig. 9

Open in a new tab

Under vertical loading, stress concentrations in the implant components and bones occurred in the same areas as under oblique loads (Fig. 5B, 6B, 7B, 8B and Fig. 9B). Overall, the stress value was slightly lower under the vertical than under the oblique load (Fig. 3B and 4B). In addition, when the same type of stress was applied, the stress distribution was also similar, and in all models the stress was mostly concentrated in the connection part where the implant and abutment were connected. In all models, the maximum and minimum principal stresses in the cortical and trabecular bones were similar.

In addition, von Mises and maximum principal stress in the cortical and trabecular bone were similar in the Zircon and Titan model under oblique and vertical loading. However, minimum principal stress in the cortical bone was higher in the Zircon model than in the Titan model under oblique and vertical loading.

DISCUSSION

In this study, the details and physical/mechanical properties of the simulation model were determined based on the validated numerical values to increase the accuracy of the FEA.32 Nevertheless, structural design and biomechanical analysis using FEA do not include all biomechanical conditions and biochemical contents found in the oral cavity of patients. However, FEA is very helpful in improving implant system design because its results allow to predict the stability and suitability of the structure in advance.32,33 In addition, even when laboratory experiments are not possible, FEA can help predict the dependence of outcomes on various parameters related to geometry, material, boundary, and load conditions.32

There have been previous studies to evaluate biomechanical behavior of zirconia and titanium implants through FEA. Brandão et al.23 evaluated zirconia and titanium implants placed in the anterior region, and de Matos et al.24 analyzed the results of 3-unit fixed partial dentures on zirconia and titanium implants placed in the posterior region. However, in the above studies, only the stress transmitted to the support bone around the fixture was analyzed. Therefore, in the present study, FEA was performed on the biomechanical behavior of abutment, abutment screw, fixture, cortical and trabecular bone when oblique and vertical loads were applied to single two-piece zirconia and titanium implants, respectively.

In the stress analysis using FEA performed in this study, it was assumed that the material was homogeneous and isotropic, to simplify the model and the numerical calculation of stress. In addition, the material properties were defined only by their elastic modulus and Poisson’s ratio. An ideal FE model is essential for achieving successful results.34 In previous studies, the results derived when the element size was larger than 300 µm were inappropriate.35 However, an element size of 150 µm or less extends the time required for analysis.35 Therefore, in this study, the average element size was set to 250 µm.

Various materials can be used in prosthetic implants. The selection of the optimal dental restorative material is a debatable topic, but there is a general agreement that implant survival is not affected by the dental restorative material. Therefore, in this study, a monolithic zirconia crown was selected. The distribution of occlusal loads on osseointegrated implants has a significant impact on their long-term prognosis. The von Mises stress is used as a major indicator to determine the fracture level of ductile metal materials such as abutments, abutment screws, and fixtures. On the other hand, because brittle materials such as the support bone are useful for judging failure by principal stress, the analytical results are presented using principal stress.

Under oblique and vertical loads, the Zircon model abutment showed the highest von Mises stress value of 672.4 MPa. This value did not exceed the maximum fracture strength of zirconia, which is 900 - 1200 MPa.9 In addition, under all loading conditions, the von Mises stress in the abutment screw was less than 550 MPa, which corresponds to the yield strength of titanium.36 Moreover, the abutment and fixture of the Titan model also exhibited von Mises stress values smaller than 550 MPa. The result of above are similar to the results of previous study that analyzed the same geometry of the implants. Brandão et al.23 reported that titanium fixture-zirconia abutment group obtained the higher values of tensions in implants and abutments compared to titanium fixture-titanium abutment group. This result is in agreement with other studies37,38 that observed a greater number of fractures in the region of connection with the implant for zirconia abutments compared to titanium. However, these higher stress values do not compromise the use of zirconia abutments in the posterior region of the oral cavity, since these abutments presented similar clinical performance to titanium abutments. In addition, this result shows that the abutment/implant interface also influences the stress distribution.

In previous studies, when stress was applied to the cortical bone, the maximum tensile stress was 100 - 130 MPa, and the compressive stress was 170 - 190 MPa.36,39 In the present study, neither the Zircon nor the Titan model exceeded the strength threshold of the cortical bone. However, in this study, vertical and oblique static loads of 175 N were applied to each model, and the stress distribution in each implant component and support bone was evaluated. Therefore, in clinical situations, repeated masticatory loads may lead to implant failure and unfavorable long-term prognosis.

In the present study, von Mises stress values in the implant and maximum and minimum principal stress concentrations in the cortical and trabecular bones were similar in all models, except for the abutment in Zircon models. In the vertical and oblique loading conditions, the stress distribution of the abutments of the Titan and Zircon models was observed to be similar. However, the zirconia implant abutment showed a significantly higher maximum equivalent stress value than the titanium implant abutment. This is due to the properties of zirconia, which has a modulus of elasticity nearly twice that of titanium.1,14,23

Due to such high modulus of elasticity, zirconia dissipates more stress and reduces the displacement of the surrounding soft tissue. Owing to these physical properties, zirconia implants exhibit high von Mises stress on their internal structure, and the equivalent strain value is low.14 In a recent FEA study of an implant model, zirconia was reported to be subjected to higher stress than titanium.40 The authors also stated that the Young’s modulus of the material can directly affect the stress applied to the implant, and that a harder material can withstand more stress.40 The results of their study may be the reason why the stress value of the Zircon model abutment was higher than that of the Titan model abutment in this study. Therefore, because the fracture strength of the zirconia abutment is more than twice that of the titanium abutment, it cannot be concluded that the zirconia abutment causes greater mechanical failure than the titanium abutment, considering the magnitude of the stress and the mechanical strength. In a clinical study using zirconia abutments, abutment fracture did not occur for an average of 49.2 months in single missing tooth restorations,41 and it has been reported that no abutment fracture has occurred for more than 5 years in clinical cases restored with all-ceramic crown restorations.42

The FEA in this study revealed that zirconia implants have competitiveness and potential over titanium implants. In addition, the stress values in MPa of the Zircon and Titan model were similar, but it can be seen that the Zircon model reduces the stress of the bone around the implant when compared with the Titan model. However, dental clinicians should also consider other clinical parameters such as esthetics, insertion torque, occlusion, parafunctional habits, restoration location, type of edentulous areas, etc.43,44,45 A prospective clinical study with a large number of patients will be needed to establish whether zirconia implants are an excellent alternative to titanium ones.

This study has several limitations as follows. First, the experimental design was limited to the posterior single crown, and in order to analyze the effect in the clinical situations, further studies on anterior implants or posterior fixed partial dentures will be necessary. Next, in this study, it was assumed that zirconia and titanium implants were completely osseointegrated. In the previous study, there was no significant difference in the degree of osseointegration between zirconia and titanium implants.46 However, as the difference in osseointegration appears depending on the microstructure and implant surface modification method, additional research is needed. In addition, as our study was conducted under the static load, follow-up studies on the effect of dynamic loading will also be needed.

CONCLUSION

Based on the FEA results for a mandibular first molar single implant, which mimics a general clinical scenario, the following conclusions were drawn: the Zircon model exhibited higher von Mises stress values in the abutment than the Titan model. In addition, the Zircon model showed more favorable results in terms of stress transmission to the support bone around the implant compared to the Titan model. These results are due to the high stiffness and elastic modulus of the zirconia, but the stress value was lower than the fracture strength of the material. Therefore, the Zircon model can be considered to have sufficient esthetic and stress-modulating properties for clinical use.

Footnotes

This research was supported by the Ministry of Trade, Industry & Energy (MOTIE), Korea Institute for Advancement of Technology (KIAT) [P0018960] and RESEARCH FUND (2021) offered from Catholic University of Pusan.

References

  • 1.Çaglar A, Bal BT, Karakoca S, Aydın C, Yılmaz H, Sarısoy S. Three-dimensional finite element analysis of titanium and yttrium-stabilized zirconium dioxide abutments and implants. Int J Oral Maxillofac Implants. 2011;26:961–969. [PubMed] [Google Scholar]
  • 2.Cionca N, Hashim D, Mombelli A. Zirconia dental implants: where are we now, and where are we heading? Periodontol 2000. 2017;73:241–258. doi: 10.1111/prd.12180. [DOI] [PubMed] [Google Scholar]
  • 3.Buser D, Janner SF, Wittneben JG, Brägger U, Ramseier CA, Salvi GE. 10-year survival and success rates of 511 titanium implants with a sandblasted and acid-etched surface: a retrospective study in 303 partially edentulous patients. Clin Implant Dent Relat Res. 2012;14:839–851. doi: 10.1111/j.1708-8208.2012.00456.x. [DOI] [PubMed] [Google Scholar]
  • 4.Bidra AS, Rungruanganunt P. Clinical outcomes of implant abutments in the anterior region: a systematic review. J Esthet Restor Dent. 2013;25:159–176. doi: 10.1111/jerd.12031. [DOI] [PubMed] [Google Scholar]
  • 5.Thoma DS, Naenni N, Figuero E, Hämmerle CHF, Schwarz F, Jung RE, Sanz-Sánchez I. Effects of soft tissue augmentation procedures on peri-implant health or disease: A systematic review and meta-analysis. Clin Oral Implants Res. 2018;29:32–49. doi: 10.1111/clr.13114. [DOI] [PubMed] [Google Scholar]
  • 6.Siddiqi A, Payne AGT, De Silva RK, Duncan WJ. Titanium allergy: could it affect dental implant integration? Clin Oral Implants Res. 2011;22:673–680. doi: 10.1111/j.1600-0501.2010.02081.x. [DOI] [PubMed] [Google Scholar]
  • 7.Sivaraman K, Chopra A, Narayan AI, Balakrishnan D. Is zirconia a viable alternative to titanium for oral implant? A critical review. J Prosthodont Res. 2018;62:121–133. doi: 10.1016/j.jpor.2017.07.003. [DOI] [PubMed] [Google Scholar]
  • 8.Becker J, John G, Becker K, Mainusch S, Diedrichs G, Schwarz F. Clinical performance of two-piece zirconia implants in the posterior mandible and maxilla: a prospective cohort study over 2 years. Clin Oral Implants Res. 2017;28:29–35. doi: 10.1111/clr.12610. [DOI] [PubMed] [Google Scholar]
  • 9.Depprich R, Naujoks C, Ommerborn M, Schwarz F, Kübler NR, Handschel J. Current findings regarding zirconia implants. Clin Implant Dent Relat Res. 2014;16:124–137. doi: 10.1111/j.1708-8208.2012.00454.x. [DOI] [PubMed] [Google Scholar]
  • 10.Denry I, Kelly JR. State of the art of zirconia for dental applications. Dent Mater. 2008;24:299–307. doi: 10.1016/j.dental.2007.05.007. [DOI] [PubMed] [Google Scholar]
  • 11.Al-Amleh B, Lyons K, Swain M. Clinical trials in zirconia: a systematic review. J Oral Rehabil. 2010;37:641–652. doi: 10.1111/j.1365-2842.2010.02094.x. [DOI] [PubMed] [Google Scholar]
  • 12.Gautam C, Joyner J, Gautam A, Rao J, Vajtai R. Zir-conia based dental ceramics: structure, mechanical properties, biocompatibility and applications. Dalton Trans. 2016;45:19194–19215. doi: 10.1039/c6dt03484e. [DOI] [PubMed] [Google Scholar]
  • 13.Joos M, Sailer I, Filippi A, Mukaddam K, Rosentritt M, Kühl S. Stability of screw-retention in two-piece zirconia implants: An in vitro study. Clin Oral Implants Res. 2020;31:607–614. doi: 10.1111/clr.13597. [DOI] [PubMed] [Google Scholar]
  • 14.Talmazov G, Veilleux N, Abdulmajeed A, Bencharit S. Finite element analysis of a one-piece zirconia implant in anterior single tooth implant applications. PLoS One. 2020;15:e0229360. doi: 10.1371/journal.pone.0229360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Liñares A, Grize L, Muñoz F, Pippenger BE, Dard M, Domken O, Blanco-Carrión J. Histological assessment of hard and soft tissues surrounding a novel ceramic implant: a pilot study in the minipig. J Clin Periodontol. 2016;43:538–546. doi: 10.1111/jcpe.12543. [DOI] [PubMed] [Google Scholar]
  • 16.Roehling S, Astasov-Frauenhoffer M, Hauser-Gerspach I, Braissant O, Woelfler H, Waltimo T, Kniha H, Gahlert M. In vitro biofilm formation on titanium and zirconia implant surfaces. J Periodontol. 2017;88:298–307. doi: 10.1902/jop.2016.160245. [DOI] [PubMed] [Google Scholar]
  • 17.Janner SFM, Gahlert M, Bosshardt DD, Roehling S, Milz S, Higginbottom F, Buser D, Cochran DL. Bone response to functionally loaded, two-piece zirconia implants: A preclinical histometric study. Clin Oral Implants Res. 2018;29:277–289. doi: 10.1111/clr.13112. [DOI] [PubMed] [Google Scholar]
  • 18.Balmer M, Spies BC, Vach K, Kohal RJ, Hämmerle CHF, Jung RE. Three-year analysis of zirconia implants used for single-tooth replacement and three-unit fixed dental prostheses: A prospective multicenter study. Clin Oral Implants Res. 2018;29:290–299. doi: 10.1111/clr.13115. [DOI] [PubMed] [Google Scholar]
  • 19.Bormann KH, Gellrich NC, Kniha H, Schild S, Weingart D, Gahlert M. A prospective clinical study to evaluate the performance of zirconium dioxide dental implants in single-tooth edentulous area: 3-year follow-up. BMC Oral Health. 2018;18:181. doi: 10.1186/s12903-018-0636-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Cionca N, Müller N, Mombelli A. Two-piece zirconia implants supporting all-ceramic crowns: a prospective clinical study. Clin Oral Implants Res. 2015;26:413–418. doi: 10.1111/clr.12370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Lopez CAV, Vasco MAA, Ruales E, Bedoya KA, Benfatti CM, Bezzon OL, Deliberador TM. Three-dimensional finite element analysis of stress distribution in zirconia and titanium dental implants. J Oral Implantol. 2018;44:409–415. doi: 10.1563/aaid-joi-D-16-00109. [DOI] [PubMed] [Google Scholar]
  • 22.Lin YT, Shen YF, Wei PC, Hsu KW. Clinical evaluation of two-piece zirconia abutments with bonded titanium inserts for implant-supported restorations. J Prosthet Dent. 2020;123:449–454. doi: 10.1016/j.prosdent.2019.01.006. [DOI] [PubMed] [Google Scholar]
  • 23.Brandão de Holanda KA, Armini Caldas R, Amaral M, da Silva Concilio LR, Pino Vitti R. Biomechanical evaluation of anterior implants associated with titanium and zirconia abutments and monotype zirconia implants. J Prosthodont Res. 2021;65:73–77. doi: 10.2186/jpr.JPOR_2019_527. [DOI] [PubMed] [Google Scholar]
  • 24.de Matos JDM, Lopes GDRS, Nakano LJN, Ramos NC, Vasconcelos JEL, Bottino MA, Tribst JPM. Biomechanical evaluation of 3-unit fixed partial dentures on monotype and two-piece zirconia dental implants. Comput Methods Biomech Biomed Engin. 2021:1–8. doi: 10.1080/10255842.2021.1946798. [DOI] [PubMed] [Google Scholar]
  • 25.Bulaqi HA, Mousavi Mashhadi M, Safari H, Samandari MM, Geramipanah F. Effect of increased crown height on stress distribution in short dental implant components and their surrounding bone: A finite element analysis. J Prosthet Dent. 2015;113:548–557. doi: 10.1016/j.prosdent.2014.11.007. [DOI] [PubMed] [Google Scholar]
  • 26.Bankoğlu Güngör M, Yılmaz H. Evaluation of stress distributions occurring on zirconia and titanium implant-supported prostheses: A three-dimensional finite element analysis. J Prosthet Dent. 2016;116:346–355. doi: 10.1016/j.prosdent.2016.01.022. [DOI] [PubMed] [Google Scholar]
  • 27.Kaleli N, Sarac D, Külünk S, Öztürk Ö. Effect of different restorative crown and customized abutment materials on stress distribution in single implants and peripheral bone: A three-dimensional finite element analysis study. J Prosthet Dent. 2018;119:437–445. doi: 10.1016/j.prosdent.2017.03.008. [DOI] [PubMed] [Google Scholar]
  • 28.Sannino G, Gloria F, Ottria L, Barlattani A. Influence of finish line in the distribution of stress trough an all ceramic implant-supported crown: A 3D finite element analysis. Oral Implantol (Rome) 2009;2:14–27. [PMC free article] [PubMed] [Google Scholar]
  • 29.Zhang G, Yuan H, Chen X, Wang W, Chen J, Liang J, Zhang P. A three-dimensional finite element study on the biomechanical simulation of various structured dental implants and their surrounding bone tissues. Int J Dent. 2016;2016:4867402. doi: 10.1155/2016/4867402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Kim WH, Lee JC, Lim D, Heo YK, Song ES, Lim YJ, Kim B. Optimized dental implant fixture design for the desirable stress distribution in the surrounding bone region: a biomechanical analysis. Materials (Basel) 2019;12:2749. doi: 10.3390/ma12172749. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Lee H, Park S, Kwon KR, Noh G. Effects of cementless fixation of implant prosthesis: A finite element study. J Adv Prosthodont. 2019;11:341–349. doi: 10.4047/jap.2019.11.6.341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Lin D, Li Q, Li W, Swain M. Dental implant induced bone remodeling and associated algorithms. J Mech Behav Biomed Mater. 2009;2:410–432. doi: 10.1016/j.jmbbm.2008.11.007. [DOI] [PubMed] [Google Scholar]
  • 33.Geng JP, Tan KB, Liu GR. Application of finite element analysis in implant dentistry: a review of the literature. J Prosthet Dent. 2001;85:585–598. doi: 10.1067/mpr.2001.115251. [DOI] [PubMed] [Google Scholar]
  • 34.Bal BT, Cağlar A, Aydin C, Yilmaz H, Bankoğlu M, Eser A. Finite element analysis of stress distribution with splinted and nonsplinted maxillary anterior fixed prostheses supported by zirconia or titanium implants. Int J Oral Maxillofac Implants. 2013;28:e27–e38. doi: 10.11607/jomi.2442. [DOI] [PubMed] [Google Scholar]
  • 35.Caglar A, Bal BT, Aydin C, Yilmaz H, Ozkan S. Evaluation of stresses occurring on three different zirconia dental implants: three-dimensional finite element analysis. Int J Oral Maxillofac Implants. 2010;25:95–103. [PubMed] [Google Scholar]
  • 36.Akça K, Iplikçioğlu H. Finite element stress analysis of the effect of short implant usage in place of cantilever extensions in mandibular posterior edentulism. J Oral Rehabil. 2002;29:350–356. doi: 10.1046/j.1365-2842.2002.00872.x. [DOI] [PubMed] [Google Scholar]
  • 37.Nakamura K, Kanno T, Milleding P, Ortengren U. Zirconia as a dental implant abutment material: a systematic review. Int J Prosthodont. 2010;23:299–309. [PubMed] [Google Scholar]
  • 38.Kim JS, Raigrodski AJ, Flinn BD, Rubenstein JE, Chung KH, Mancl LA. In vitro assessment of three types of zirconia implant abutments under static load. J Prosthet Dent. 2013;109:255–263. doi: 10.1016/S0022-3913(13)60054-2. [DOI] [PubMed] [Google Scholar]
  • 39.Reilly DT, Burstein AH. The elastic and ultimate properties of compact bone tissue. J Biomech. 1975;8:393–405. doi: 10.1016/0021-9290(75)90075-5. [DOI] [PubMed] [Google Scholar]
  • 40.Pérez-Pevida E, Brizuela-Velasco A, Chávarri-Prado D, Jiménez-Garrudo A, Sánchez-Lasheras F, Solaberrieta-Méndez E, Diéguez-Pereira M, Fernández-González FJ, Dehesa-Ibarra B, Monticelli F. Biomechanical consequences of the elastic properties of dental implant alloys on the supporting bone: finite element analysis. Biomed Res Int. 2016;2016:1850401. doi: 10.1155/2016/1850401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Glauser R, Sailer I, Wohlwend A, Studer S, Schibli M, Schärer P. Experimental zirconia abutments for implant-supported single-tooth restorations in esthetically demanding regions: 4-year results of a prospective clinical study. Int J Prosthodont. 2004;17:285–290. [PubMed] [Google Scholar]
  • 42.Yildirim M, Fischer H, Marx R, Edelhoff D. In vivo fracture resistance of implant-supported all-ceramic restorations. J Prosthet Dent. 2003;90:325–331. doi: 10.1016/s0022-3913(03)00514-6. [DOI] [PubMed] [Google Scholar]
  • 43.El-Anwar MI, El-Zawahry MM, Ibraheem EM, Nassani MZ, ElGabry H. New dental implant selection criterion based on implant design. Eur J Dent. 2017;11:186–191. doi: 10.4103/1305-7456.208432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Bryington M, De Kok IJ, Thalji G, Cooper LF. Patient selection and treatment planning for implant restorations. Dent Clin North Am. 2014;58:193–206. doi: 10.1016/j.cden.2013.09.009. [DOI] [PubMed] [Google Scholar]
  • 45.Brodt MD, Swan CC, Brown TD. Mechanical behavior of human morselized cancellous bone in triaxial compression testing. J Orthop Res. 1998;16:43–49. doi: 10.1002/jor.1100160108. [DOI] [PubMed] [Google Scholar]
  • 46.Webber LP, Chan HL, Wang HL. Will zirconia implants replace titanium implants? Appl Sci. 2021;11:6776 [Google Scholar]

Articles from The Journal of Advanced Prosthodontics are provided here courtesy of Korean Academy of Prosthodontics

RESOURCES