Low‐dose cone‐beam CT via raw counts domain low‐signal correction schemes: Performance assessment and task‐based parameter optimization (Part II. Task‐based parameter optimization)

Abstract

Purpose

Different low‐signal correction (LSC) methods have been shown to efficiently reduce noise streaks and noise level in CT to provide acceptable images at low‐radiation dose levels. These methods usually result in CT images with highly shift‐variant and anisotropic spatial resolution and noise, which makes the parameter optimization process highly nontrivial. The purpose of this work was to develop a local task‐based parameter optimization framework for LSC methods.

Methods

Two well‐known LSC methods, the adaptive trimmed mean (ATM) filter and the anisotropic diffusion (AD) filter, were used as examples to demonstrate how to use the task‐based framework to optimize filter parameter selection. Two parameters, denoted by the set $\mathcal{P}$, for each LSC method were included in the optimization problem. For the ATM filter, these parameters are the low‐ and high‐signal threshold levels p _l and p _h ; for the AD filter, the parameters are the exponents δ and γ in the brightness gradient function. The detectability index d′ under the non‐prewhitening (NPW) mathematical observer model was selected as the metric for parameter optimization. The optimization problem was formulated as an unconstrained optimization problem that consisted of maximizing an objective function $d^{\prime }(\mathcal{P})$, where i and j correspond to the i‐th imaging task and j‐th spatial location, respectively. Since there is no explicit mathematical function to describe the dependence of d′ on the set of parameters $\mathcal{P}$ for each LSC method, the optimization problem was solved via an experimentally measured d′ map over a densely sampled parameter space. In this work, three high‐contrast–high‐frequency discrimination imaging tasks were defined to explore the parameter space of each of the LSC methods: a vertical bar pattern (task I), a horizontal bar pattern (task II), and a multidirectional feature (task III). Two spatial locations were considered for the analysis, a posterior region‐of‐interest (ROI) located within the noise streaks region and an anterior ROI, located further from the noise streaks region. Optimal results derived from the task‐based detectability index metric were compared to other operating points in the parameter space with different noise and spatial resolution trade‐offs.

Results

The optimal operating points determined through the d′ metric depended on the interplay between the major spatial frequency components of each imaging task and the highly shift‐variant and anisotropic noise and spatial resolution properties associated with each operating point in the LSC parameter space. This interplay influenced imaging performance the most when the major spatial frequency component of a given imaging task coincided with the direction of spatial resolution loss or with the dominant noise spatial frequency component; this was the case of imaging task II. The performance of imaging tasks I and III was influenced by this interplay in a smaller scale than imaging task II, since the major frequency component of task I was perpendicular to imaging task II, and because imaging task III did not have strong directional dependence. For both LSC methods, there was a strong dependence of the overall d′ magnitude and shape of the contours on the spatial location within the phantom, particularly for imaging tasks II and III. The d′ value obtained at the optimal operating point for each spatial location and imaging task was similar when comparing the LSC methods studied in this work.

Conclusions

A local task‐based detectability framework to optimize the selection of parameters for LSC methods was developed. The framework takes into account the potential shift‐variant and anisotropic spatial resolution and noise properties to maximize the imaging performance of the CT system. Optimal parameters for a given LSC method depend strongly on the spatial location within the image object.

1. Introduction

Given the increasing concern about the potential risks associated with the use of ionizing radiation in x‐ray CT, multiple strategies to perform low‐dose CT while still providing acceptable image quality have been proposed. These range from the improvement of current CT imaging systems’ hardware to the development of novel methods to appropriately process the measured raw counts. Some of the most relevant improvements to the system's hardware are related to: detector efficiency,^{1, 2, 3, 4} x‐ray beam spectrum optimization,^{5, 6, 7, 8, 9, 10} and tube current modulation.^{11, 12, 13, 14} In terms of software methods, both analytical filtered backprojection (FBP) reconstruction in conjunction with denoising in either the image domain, sinogram domain, or raw counts domain as well as iterative reconstruction methods have been successfully implemented. A large portion of the analytical methods consists of performing a certain type of raw counts domain denoising, followed by the conventional FBP reconstruction.^{15, 16, 17} Independent of the underlying principle, the main goal of these methods is to preferentially correct for noisy data to provide the most accurate representation of the image object. These advances in software and hardware work in synergy to improve the imaging performance of low‐dose CT.

However, it is often challenging to optimize parameters used in a given low‐dose technique to obtain optimal imaging performance. This challenge becomes more complex when dealing with potentially nonlinear problems. One example are low‐signal correction (LSC) methods that use filters such as the adaptive trimmed mean filter (ATM)^{15, 18, 19, 20} and the anisotropic diffusion (AD)^{21, 22, 23, 24, 25, 26} filter. The criteria to optimize parameter selection for similar denoising methods either in the sinogram or raw counts domain^{15, 16, 17, 27, 28, 29, 30} have been limited to performing a denoising process such that there is a defined trade‐off between spatial resolution and noise. The different reported methodologies used to assess this criteria provide a partial understanding of how these noise and spatial resolution properties may vary under specific scenarios. Part I³¹ of this work presents a thorough characterization of the spatial resolution and noise properties of the ATM and the AD filters. It includes a systematic study of the parameter space of each LSC method and the characterization of their spatial resolution and noise properties through the measurement of the local modulation transfer function (MTF) and the local noise power spectrum (NPS) via an ensemble averaging approach.^{32, 33, 34} In that work, it was found that not only does the overall spatial resolution and noise magnitude depend on the spatial location and the LSC parameters used but also that the MTF directionality and the NPS directionality and coarseness depend strongly on these factors. Having shift‐variant and highly anisotropic MTF and NPS makes the LSC parameter selection process highly nontrivial, especially since it has been shown previously that in order to comprehensively assess the imaging performance of a CT system, the assessment of the potential trade‐off between spatial resolution and noise magnitude should be associated with a given imaging task.^{35, 36, 37}

A straightforward option that incorporates an imaging task into the parameter optimization process is a human observer study. However, not only are human observer studies expensive and time consuming but also these studies may be highly inefficient because of the multiple system parameters that need to be optimized for different imaging tasks. Fortunately, the MTF and NPS can be incorporated into the so‐called mathematical observer models.^{38, 39} The main advantage of these mathematical observer models is that besides being time‐efficient and inexpensive, these models can be targeted to a given imaging task, and most importantly, can model to some extent the characteristics of the human visual system and the behavior of human observers. These metrics have shown promising results for the assessment of the imaging performance of both linear and nonlinear imaging systems for a given imaging task through the detectability index (d′).^{32, 40, 41, 42, 43, 44, 45}

The purpose of this work is to develop a local task‐based parameter optimization framework for a given LSC method in the raw counts domain for low‐dose CT. More specifically, the framework will be experimentally implemented with the ATM and AD LSC methods using scans of an anthropomorphic phantom under severe photon starvation conditions. This work aims to emphasize the importance of performing task‐based parameter optimization for LSC methods instead of using traditional metrics of image quality, which may result in the selection of inappropriate parameters for a given imaging task. In addition, the goal of this work is not to explicitly compare one LSC method against the other, but to demonstrate the applicability of the optimization framework across different LSC methods.

2. Materials and methods

2.A. General strategy

Parameter optimization in LSC is not a trivial task since the noise statistics, which are associated with the attenuation properties and geometry of a given image object, will have a direct impact on the behavior of the LSC method and subsequently on the spatial resolution across the field of view (FOV) of the resulting CT image. The relationship between each of the critical parameters of a given LSC method and their influence on spatial resolution and noise is hard to predict analytically. Alternatively, spatial resolution and noise properties for a given LSC method can be experimentally measured under certain controlled conditions to allow for parameter optimization. However, even if the spatial resolution and noise characteristics are well understood, these image quality metrics do not fully characterize the imaging performance of a CT system, since the overall image quality must be inferred from the interplay among spatial resolution, noise spatial frequency distribution, and properties of the imaging task. In this regard, different mathematical observer models have shown good agreement with human observer performance by incorporating the MTF and the NPS into a single metric, d′, that can also factor in the spatial frequency information of a given imaging task as well as the response of the human visual system to certain stimuli.

To account for the different factors described above and to incorporate the detectability index measurement for parameter optimization, the following task‐based framework, depicted in Fig. 1 and summarized through the steps below, was proposed:

1. Identify the phantom with desirable attenuation properties and geometry to be included in the optimization process and perform repeated CT scans.

2. Define the parameter space of the specific LSC method and perform the respective CT image reconstructions for all repeated scans.

3. Perform measurements of the local MTF and NPS using ensemble averaging of the reconstructed LSC CT images from the repeated scans.

4. Measure the detectability index for a given imaging task and spatial location.

5. Determine the optimal parameter combination, ${\mathcal{P}}^{\ast }$, that maximizes d′.

Figure 1.

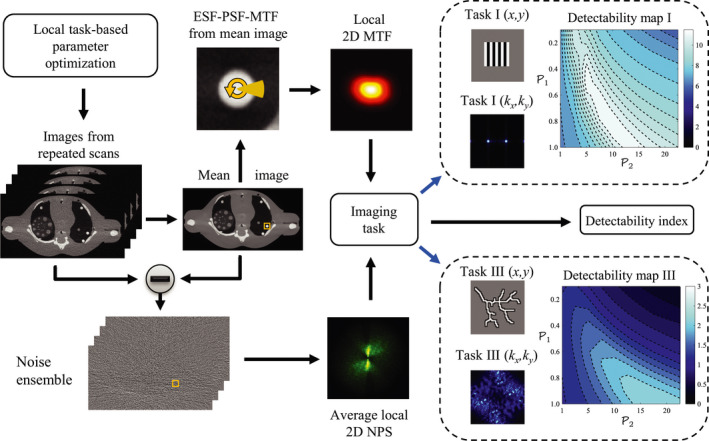
Workflow for the local task‐based detectability framework for parameter optimization. [Color figure can be viewed at wileyonlinelibrary.com]

The optimal LSC parameters are found by searching for the solution to the following unconstrained optimization problem:

$${\mathcal{P}}^{\ast }=\underset{\mathcal{P}}{\text{arg max}}{d}_{i,j}^{\prime }(\mathcal{P}),$$ (1)

where $\mathcal{P}$ corresponds to the set of parameters to be optimized for each LSC method and $d_{i,j}^{\prime }$ is the detectability index defined under a given mathematical observer model for a specific imaging task i and spatial location j.

The proposed framework can be applied to theoretical models (if available), numerical simulations, or experimental scans, and can be done either in 2D or 3D. In this work, it was applied to experimental phantom scans, and because of the long‐processing time for over 10,000 reconstructions, image quality measurements were limited to 2D but could be readily extended to 3D if desired.

2.B. Physical phantom data acquisition

In this section, the selection of the phantom and the experimental setup will be presented and justified. Experimentally, accurate and practical 2D spatial resolution measurements can only be performed on a few spatial locations, which limits the extent of the local detectability analysis across the FOV and consequently the assessment of the respective shift‐variance. However, by taking an experimental approach, physical factors that could influence imaging performance and cannot be fully modeled or simulated, can be incorporated into the parameter optimization process.

One anatomical region that generally poses big challenges for LSC methods is the chest, due to its highly anisotropic anatomy and very heterogeneous attenuation from the interactions of the lungs and shoulders. Therefore, the chest area of an anthropomorphic phantom (ATOM 10‐year‐old phantom, Model 706, CIRS Inc., Norfolk, VA) was studied in this work. A CBCT benchtop imaging system composed of a CsI flat panel energy‐integrating detector (PaxScan 4030CB, Varian, Salt Lake City, UT) and a rotating anode x‐ray tube (Varian G‐1592, Salt Lake City, UT) were used. The anthropomorphic phantom was scanned 50 times at a reduced dose of 0.5 mGy, to undergo each of the LSC processes, and at a dose of 1.9 mGy, for reference purposes. These doses corresponded to the CTDI_vol measured with a 16 cm cylindrical phantom. For more details about the anthropomorphic phantom, CBCT imaging system, and scan setup, please refer to Part I³¹ of this work.

2.C. Low‐signal correction parameter space

The implementation of the two LSC methods used in this work is described in detail in Part I;³¹ however, in order to justify the selection of the parameters to be optimized, the LSC methods and the roles of the selected parameters are briefly reviewed below.

2.C.1. Adaptive trimmed mean filter

Let $p_i^{\theta }$ represent the raw‐measured signal at view angle θ and detector index i corresponding to coordinates (u, v) in the detector plane. The ATM filter can be summarized in four steps: (a) determine the window width W as a function of the current signal value p at detector index i and view angle θ, (b) rank order the signal values falling within this adaptive window, (c) trim very high and very low values from the rank‐ordered set of values based on a trimming factor α, and finally (d) take the mean of the rank‐ordered and trimmed set and replace $p_i^{\theta }$ with this new value. The window width function was mathematically defined as

$$W(p)=\left\{\begin{array}{cc}{W}_0& p<p_l\\ {\displaystyle \frac{W_0(p_h-p_l)}{\left(W_0-1\right)(p-p_l)+(p_h-p_l)}}& p_l\le p\le p_h\\ 1& p>p_h,\end{array}\right.$$ (2)

where p _l and p _h (p _h  ≥ p _l ) correspond to low‐ and high‐signal threshold levels, and W ₀ represents the maximum window width used to define the neighborhood size that will be used for the filtration process. The trimming process was governed by a trimming factor α which was signal dependent and given by

$$\alpha (p)=\left\{\begin{array}{cc}0& p<p_l\\ 0.5\frac{p-p_l}{p_h-p_l}& p_l\le p\le p_h\\ 0.5& p>p_h.\end{array}\right.$$ (3)

In this work, α was allowed to increase linearly from 0 at p _l to 0.5 at p _h , so that regions with low and high SNR would tend toward a mean or a median filtration, respectively. For the sake of brevity, a fixed maximum window width was selected; its value was set empirically to W ₀ = 5. Therefore, the two free parameters to be optimized are the low‐ and high‐signal threshold levels,

$$\mathcal{P}=(p_l,p_h).$$ (4)

2.C.2. Anisotropic diffusion filter

Anisotropic diffusion in the imaging context is an iterative denoising process guided by diffusion coefficients whose values are computed from a brightness gradient function. The filter can be mathematically described in the discrete domain as

$$p_i^{\theta ,t+1}=p_i^{\theta ,t}+\mathrm{\Delta }\tau \sum _{b=1}^B{\mathrm{\nabla }}_b{D}_i^{\theta ,t}{\mathrm{\nabla }}_b{p}_i^{\theta ,t},$$ (5)

where ∆τ is the step size and the term ${\mathrm{\nabla }}_b{D}_i^{\theta ,t}$ is the diffusion coefficient specific to view angle θ, detector index i, iteration number t, and the directional derivative along the b‐th direction out of a total of B‐nearest neighbors.

The brightness gradient function, denoted by g, maps edge structural information from the raw detector data to determine the diffusion coefficients. The goal is to assign small coefficients (close to 0) to pixels where real edges should be preserved, and to assign high values (close to 1) to pixels where the signal fluctuations are considered to be noise. The brightness gradient function can be mathematically defined as⁴⁶

$$g\left(|{\mathrm{\nabla }}_b{p}_i^{\theta ,t}|\right)={\mathrm{\nabla }}_b{D}_i^{\theta ,t}=\frac{1}{{\left[1+{\left(\frac{|{\mathrm{\nabla }}_b{p}_i^{\theta ,t}|}{\beta }\right)}^{\delta }\right]}^{\gamma }},$$ (6)

where the parameters β, δ, and γ are scalars that determine the amount of diffusion (denoising) allowed for a local gradient value during a given iteration. The parameter β was updated at each time point t and view angle θ, and its value was determined automatically based on the expected gradient of structures present in a given raw data measurement. The parameters δ and γ determine the shape of the brightness gradient curve by adjusting the extent of the plateau at low‐gradient values and the slope, respectively.³¹ The number of iterations was fixed across view angles based on the global noise level associated with the given exposure and phantom; therefore, the optimization process in this implementation of anisotropic diffusion was reduced to the parameters:

$$\mathcal{P}=(\delta ,\gamma ).$$ (7)

Once the raw data underwent LSC through the ATM and AD methods and across each of the parameter spaces, FDK reconstruction with a ramp kernel was performed for each of the repeated scans.

2.D. Spatial resolution and noise measurement

To enable an accurate local measurement of spatial resolution and noise in such a challenging photon‐starved scenario, the ensemble averaging approach was taken.^{32, 33, 34} The image ensemble obtained from the repeated scans provides enough noise realizations at a given spatial location to allow one to separate the noise component of the CT image from the spatial resolution component. Subsequently, each of these locally shift‐variant image components can be treated and measured independently. For details of the specific measurement methodology for spatial resolution and noise, refer to Part I³¹ of this work. To assess the impact of the spatial resolution and noise shift‐variance on the imaging performance, local 2D MTF and 2D NPS measurements were performed at two spatial locations defined by two regions‐of‐interest (ROI) within the anthropomorphic phantom. These ROIs are the same as those used in Part I;³¹ (a) posterior: corresponding to a highly photon‐starved region along the path of largest attenuation and (b) anterior: corresponding to a region located distal from the photon‐starved measurements.

2.E. Noise and spatial resolution trade‐off

Optimizing parameter selection for LSC methods is a complex task since, as demonstrated in Part I of this work,³¹ there is a large variability, not only of noise magnitude and overall spatial resolution across the parameter space and across the FOV but also of the noise texture and the directional dependence of spatial resolution. Previous works have reported the use of noise and spatial resolution curves to assess the imaging performance of a specific denoising method.^{16, 29} These noise and spatial resolution curves are built by recording the noise magnitude and a surrogate of spatial resolution for a given operating point in the parameter space. This approach enables the analysis and comparison of the noise magnitude and spatial resolution trade‐off among specific denoising methods of interest and across the parameter space of a single method. The criteria to select an optimal operating point then reduces to: first identifying a spatial resolution level of interest based on a given imaging feature, and then choosing the operating point with the lowest noise magnitude that still meets the spatial resolution requirement.

Figure 2 displays how this approach is implemented for a given LSC method for the 2D parameter space defined in this study; in this case, an example is shown for AD at the anterior spatial location. Figure 2(a) displays all of the combinations of points in the parameter space with their specific noise (σ)‐spatial resolution (MTF_10/y ) pair. In this figure, the spatial resolution axis is divided into three zones with high (a), low (b), and moderate (c) spatial resolution. The multiple operating points in these zones offer different trade‐offs between spatial resolution and noise. Figure 2(b) displays these points in a 4D scatter plot to better understand the behavior of these trade‐offs across the parameter space. Finally Fig. 2(c) shows the labeled points belonging to each zone overlaid on the 2D parameter space. For a given zone, that is, spatial resolution interval, the operating point that provides the lowest noise magnitude can be selected. However, even though this process seems simple, the selection of the required spatial resolution interval is empirical. Furthermore, the analysis of the contribution of spatial resolution is limited to one dimension (along the k _y axis in this example), and it only takes into account the overall noise magnitude. Therefore, this method does not fully encompass the definition of a task‐based approach, since it is lacking the inclusion of essential information such as noise texture, the directional dependence of spatial resolution, and the shape and contrast of the imaging feature. Alternatively, these multidimensional image quality metrics as well as certain characteristics of the human visual system and behavior of human observers can be incorporated into mathematical observer models through the use of the so‐called detectability index.

Figure 2.

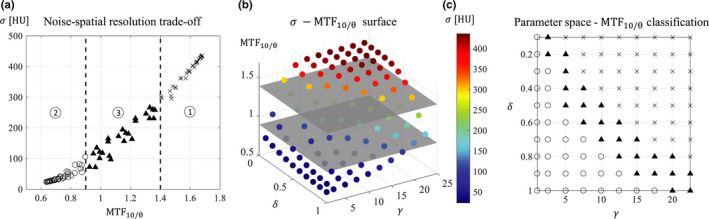
Noise and spatial resolution trade‐off analysis for AD at the anterior spatial location and along the y‐axis direction. (a) σ − MTF _10/θ values across the (δ, γ) 2D parameter space defined for AD; zones 1, 2, and 3 correspond to operating points that offer high, low, and moderate spatial resolution, respectively, and have different trade‐offs with noise. (b) Four‐dimensional scatter plot displaying the σ − MTF _10/θ trade‐off across the 2D parameter space. (c) Classification of the operating points across the parameter space based on the three zones defined in terms of spatial resolution performance. [Color figure can be viewed at wileyonlinelibrary.com]

2.F. Detectability index

2.F.1. Observer model

In this work, the task‐based detectability index was chosen as the image quality metric to optimize parameter selection for LSC methods. More specifically, the non‐prewhitening observer model⁴⁷ (NPW) was selected to demonstrate the application of the proposed parameter optimization framework. This observer model has shown good agreement with human observer performance for similar applications.^{40, 48, 49} The model is formulated using the expected signal as an internal cross‐correlation template and by taking into account the fact that humans are unable to decorrelate or prewhiten noise. This latter aspect is very important, since for a highly photon‐starved scenario, LSC methods may offer a wide variety of noise textures across the parameter space that may influence the observers’ performance and therefore need to be accounted for. The detectability index metric, d′, for the NPW model was then calculated using the following equation

$$d_{i,j}^{{\prime }^2}=\frac{{\left[\int \int |{\text{MTF}}_j(\mathbf{k},\mathcal{P})·{\tilde{T}}_i{(\mathbf{k})|}^2{\mathrm{d}}^2\mathbf{k}\right]}^2}{\int \int |{\text{MTF}}_j(\mathbf{k},\mathcal{P})·{\tilde{T}}_i{(\mathbf{k})|}^2{\text{NPS}}_j(\mathbf{k},\mathcal{P}){\mathrm{d}}^2\mathbf{k}},$$ (8)

where k = (k _x , k _y ) is a vector in the spatial frequency space, and ${\tilde{T}}_i(\mathbf{k})$ corresponds to the Fourier transform of the i‐th imaging task T _i (x).

2.F.2. Imaging tasks

The selection of the imaging tasks included in this study was motivated by the shift‐variant and highly anisotropic spatial resolution and noise properties of LSC methods found in Part I³¹ of this work. Consequently, three high‐resolution–high‐contrast discrimination imaging tasks with different directional dependence were defined to optimize the LSC methods presented in this work: a vertical bar pattern, a horizontal bar pattern, and a multidirectional feature that resemble the structure of lung bronchioles. Each of the discrimination tasks was mathematically defined as shown in Eq. (9)

$${\tilde{T}}_i(\mathbf{k})=\text{FT}\left\{T_i(\mathbf{x})\right\}=\text{FT}\left\{h_{A_i}(\mathbf{x})-h_{0_i}(\mathbf{x})\right\},$$ (9)

where h _Ai (x) and h _0i (x) are the alternative and null hypothesis, respectively, of the i‐th imaging task. Each hypothesis was defined as

$$\begin{array}{c}\hfill h_{A_i}(\mathbf{x})=C_{A_i}{f}_{A_i}(\mathbf{x})+s_i\\ \hfill h_{0_i}(\mathbf{x})=C_{0_i}{f}_{0_i}(\mathbf{x})+s_i,\end{array}$$ (10)

where s _i corresponds to the signal background level of the i‐th imaging task and C _Ai , C _0i , and f _Ai (x), f _0i (x) are contrast coefficients and binary images, respectively, specific to the alternative and null hypothesis of each imaging task. For high‐frequency–high‐contrast discrimination tasks, it has been shown that adjustments should be made to traditional observer models in order to better correlate with human observers’ performance.³⁷ In this work, an alternative approach was taken. In this approach, the imaging tasks are designed to place emphasis on the detection of the oscillations associated with each structure, rather than the detection of each structure as a whole. To achieve this, the average contrast of each imaging task, T _i (x), needs to be zero so that the low‐frequency component is suppressed,⁴² as can be seen in Figs. 3(d), 3(h), and 3(l). In other words, the condition stated in Eq. (11) needs to be satisfied.

Figure 3.

The top, middle, and bottom row correspond to imaging tasks I, II, and III, respectively. From left to right, the first and second column display the alternative and null hypotheses, respectively, while the third and fourth column show the spatial and spatial frequency domain representation of each imaging task, respectively. [Color figure can be viewed at wileyonlinelibrary.com]

$$\int \int \left[h_{A_i}(\mathbf{x})-h_{0_i}(\mathbf{x})\right]{\mathrm{d}}^2\mathbf{x}=0.$$ (11)

A relationship between C _Ai and C _0i can then easily be derived resulting in Eq. (12).

$$C_{0_i}=\frac{\int \int f_{A_i}(\mathbf{x}){\mathrm{d}}^2\mathbf{x}}{\int \int f_{0_i}(\mathbf{x}){\mathrm{d}}^2\mathbf{x}}{C}_{A_i}.$$ (12)

Figure 3 displays the alternative and null hypotheses and the corresponding imaging task in the spatial and spatial frequency domain for each of the imaging features used in this study.

• Imaging task I, shown in Figs. 3(c) and 3(d), consisted of the discrimination between a vertical bar pattern and a uniform rectangle of equal dimensions. The bar pattern was composed of five lines of 0.6 mm × 5 mm (8 line pairs/cm) with a contrast C _A  = 500 HU with respect to the background. The uniform rectangle had a contrast C ₀ = 278 HU with respect to the background. The dominant spatial frequency for this imaging task was along the k _x axis and between 0.8 and 0.9 mm ⁻¹. The specific magnitude and direction of imaging tasks I and II in the frequency domain were chosen to emphasize the different trade‐offs between spatial resolution and noise across the parameter space and spatial locations.

• Imaging task II, shown in Figs. 3(g) and 3(h), was exactly the same as the imaging task I, but oriented horizontally, therefore providing dominant frequencies along the k _y axis between 0.8–0.9 mm ⁻¹.

• Imaging task III, shown in Figs. 3(k) and 3(l), was designed as a multidirectional high‐contrast–high‐frequency discrimination imaging task. The alternative hypothesis consisted of a structure that resembles lung bronchioles with airway outer diameters between 0.2 and 0.4 mm and a contrast C _A  = 500 HU with respect to the background. The null hypothesis was defined as a thicker version (0.6–1.2 mm) of the alternative hypothesis with a contrast C ₀ = 166 HU with respect to the background.

The background level s was set to −1000 HU for all three imaging features.

2.F.3. Sample images

Hybrid images were generated for visual assessment of the imaging performance at a given operating point in the parameter space. These hybrid images were generated by convolving the alternative hypothesis of each imaging task with the experimentally measured point spread function (PSF), followed by the addition of experimentally acquired local noise‐only background. This methodology has been validated in previous work.³⁷ The hybrid image specific to a given imaging feature, spatial location, noise realization, and operating point of a given LSC method was obtained using

$${\mathrm{I}}_{i,j,r}^{\mathcal{P}}(\mathbf{x})=\left[h_i(\mathbf{x})\otimes {\text{PSF}}_j^{\mathcal{P}}(\mathbf{x})\right]+n_{j,r}^{\mathcal{P}}(\mathbf{x}),$$ (13)

where h _i (x) represents the alternative or null hypothesis of the i‐th imaging task, ⊗ denotes the 2D convolution operator, and ${\text{PSF}}_j^{\mathcal{P}}(\mathbf{\text{x}})$and $n_{j,r}^{\mathcal{P}}(\mathbf{\text{x}})$ are the point spread function and noise‐only background, respectively, corresponding to the j‐th spatial location and r‐th repeated scan processed at the operating point, $\mathcal{P}$, of a particular LSC method. In this work, hybrid images of the alternative hypothesis are provided for visual reference.

3. Results

Figures 4 and 5 display the detectability contour maps for ATM and AD, respectively. Each figure contains results from each of the imaging tasks at each spatial location. In order to highlight the different noise and spatial resolution trade‐offs across the parameter space and at both spatial locations, three points of interest belonging to each of the zones defined in Section 2.E and Fig. 2 — and indicated by the circular markers — were identified for each case. Operating points 1 and 2 are the same as those indicated in Part I of this work;³¹ point 1 corresponds to regions in the parameter space that favor high spatial resolution, while point 2 corresponds to regions that favor low noise magnitude. These two points are fixed for each LSC method: for ATM, point 1 is located at (0, 100) and point 2 at (180, 900), while for AD, point 1 and 2 are located at (0.1, 20) and (0.9, 2.5), respectively. The operating points labeled by the marker # 3 correspond to the optimal operating points obtained through the d′ metric and are different for each scenario. The optimal operating point should in principle provide the appropriate noise and spatial resolution trade‐off that maximizes detectability for a given imaging task. All of the optimal operating points indicated by these circular markers have a corresponding hybrid image in Figs. 6, 7, and 8. For the sake of brevity, hybrid images obtained with noise realization r = 1 are displayed. However, the reader should be aware that the correspondence between the d′ values from the mathematical observer model and the visual assessment of the hybrid images depends to some extent on the contribution of each noise realization to the estimation of the average NPS. Therefore, in order to provide a more accurate conclusion, a rigorous human observer study that includes multiple noise realizations and operating points in the parameter space would be required; this is a subject of current investigation.

Figure 4.

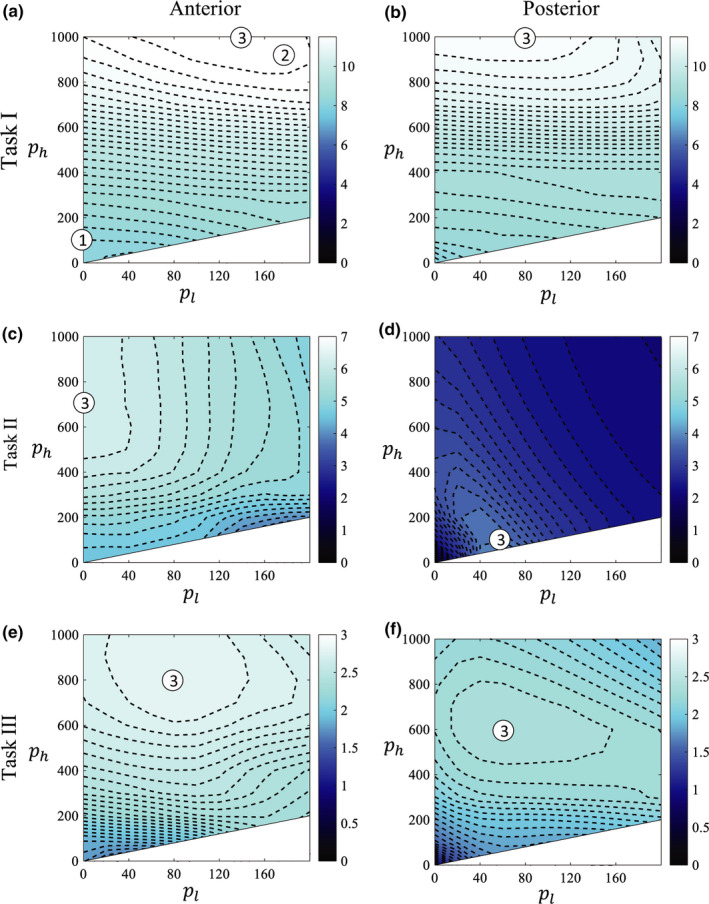
Detectability maps for each of the three imaging tasks and two spatial locations for the ATM filter. The circular markers # 1 and 2 (the same as those indicated in Part I of this work) correspond to points with high and low spatial resolution, respectively, and are fixed for all cases (a–f). Circular marker # 3 corresponds to the optimal operating point in each case based on maximizing d′. Markers for each case are associated with the hybrid images displayed in Figs. 6, 7, and 8. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 5.

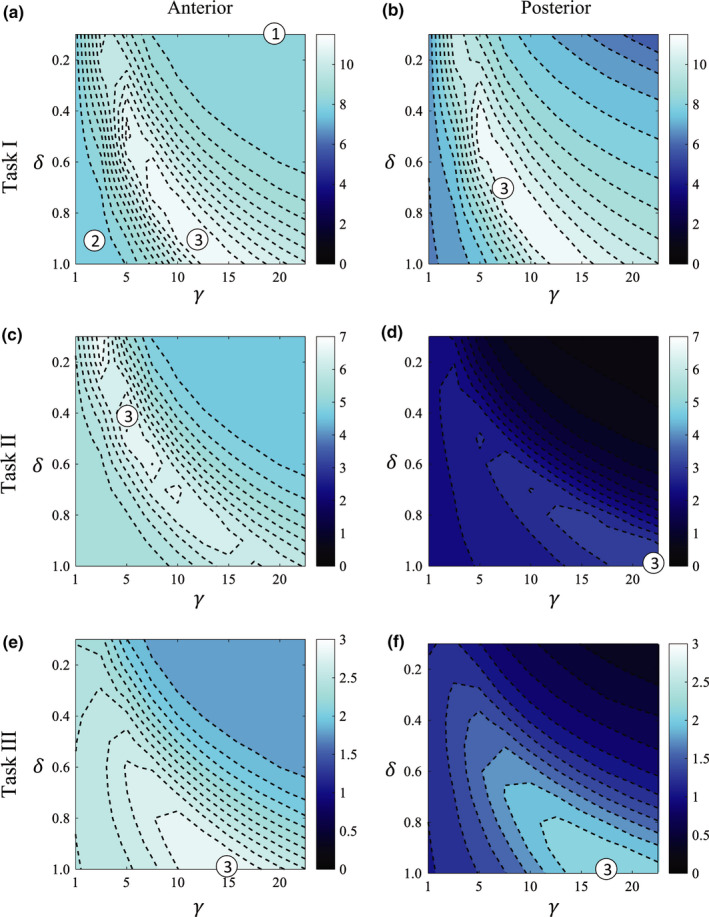
Detectability maps for each of the three imaging tasks and two spatial locations for the AD filter. The circular markers # 1 and 2 (the same as those indicated in Part I of this work) correspond to points with high and low spatial resolution, respectively, and are fixed for all cases (a–f). Circular marker # 3 corresponds to the optimal operating point in each case based on maximizing d′. Markers for each case are associated with the hybrid images displayed in Figs. 6, 7, and 8. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 6.

Sample hybrid images of the alternative hypothesis of imaging task I using a given LSC method at a given spatial location and noise realization with r = 1. (1–3) Correspond to the images from the operating points indicated in Figs. 4(a), 4(b) and 5(a), 5(b). In addition to the 0.5 mGy LSC images, hybrid images from scans at 1.9 and 0.5 mGy without undergoing LSC are displayed. Images displayed at [WW,WL] = [1600,−600].

Figure 7.

Sample hybrid images of the alternative hypothesis of imaging task II using a given LSC method at a given spatial location and noise realization with r = 1. (1–3) Correspond to the images from the operating points indicated in Figs. 4(c), 4(d) and 5(c), 5(d). In addition to the 0.5 mGy LSC images, hybrid images from scans at 1.9 and 0.5 mGy without undergoing LSC are displayed. Images displayed at [WW,WL] = [1600,−600].

Figure 8.

Sample hybrid images of the alternative hypothesis of imaging task III using a given LSC method at a given spatial location and noise realization with r = 1. (1–3) Correspond to the images from the operating points indicated in Figs. 4(e), 4(f) and 5(e), 5(f). In addition to the 0.5 mGy LSC images, hybrid images from scans at 1.9 and 0.5 mGy without undergoing LSC are displayed. Images displayed at [WW,WL] = [1600,−600].

For both LSC methods, the optimal operating points determined through the d′ metric were different for each imaging task and spatial location. This is due to the different properties of each imaging task in this study, more specifically in terms of image feature orientation and its interplay with the highly shift‐variant and anisotropic spatial resolution and noise properties. Additionally, for both LSC methods and all imaging tasks, the overall d′ value was higher or equal for the anterior spatial location compared to the posterior location, which is mainly caused by the larger noise magnitude in the posterior ROI. Furthermore, since the parameter space defined for the AD filter was “larger” in the sense that it could lead to more blurring (zone 2) or even streak enhancement (zone 1), the AD filter was capable of yielding lower d′ values than the ATM filter. However, the shape of the d′ contours for the AD method was more stable across different imaging tasks and spatial locations compared to the shape of the d′ contours for the ATM method. Finally, the d′ value for the optimal operating point for each spatial location and imaging task was similar across LSC methods.

3.A. Imaging task I

For imaging task I, the optimal operating points for the ATM filter for the anterior and posterior ROIs were (140, 1000) and (80, 1000), respectively; for the AD filter, the optimal operating points for each spatial location were (0.9, 12.5) and (0.7, 7.5), respectively. For both LSC methods, the overall d′ magnitude was very similar for both spatial locations because (a) the degradation of the spatial resolution along the k _x axis is minimal, even when performing strong LSC in the posterior spatial location and (b) the magnitude of the noise spatial frequency component along the k _x direction does not change much across spatial locations. Therefore, for both LSC methods, the visibility of the vertical bar pattern after LSC is almost independent of the spatial location, as can be confirmed in the optimal d′ hybrid images marked with the # 3 in Fig. 6. Finally, the visibility of the vertical bar pattern after LSC for both spatial locations at 0.5 mGy is higher than the uncorrected 0.5 mGy images and relatively close to the visibility obtained with the images at 1.9 mGy.

3.B. Imaging task II

The optimal operating points for this imaging task for ATM for the anterior and posterior spatial locations were (0, 700) and (60, 100), respectively; for AD, the optimal operating points for each spatial location were (0.4, 5.0) and (1.0, 22.5), respectively. The overall detectability for this imaging task for both LSC methods drops considerably when moving from the anterior to the posterior ROI. This is because of (a) the dominant degradation of the spatial resolution along the k _y axis and (b) the large magnitude of the noise spatial frequency component along the k _y direction for the posterior ROI. Additionally, the shape of the d′ contour maps for both ATM and AD methods had a high similarity with the shape of the corresponding NPS isotropy contours shown in Part I³¹ [Figs. 8(c), 8(d), and 9(c), 9(d) in that work]. This makes sense since an imaging task that potentially masquerades with a similarly oriented strong noise texture would be benefited with a more isotropic noise texture instead. Furthermore, the images shown in Fig. 7 corresponding to the # 1, 2, and 3 markers show larger visibility differences among them compared to imaging task I. The optimal operating point obtained through the d′ metric provided considerably better visibility of the horizontal bar pattern than when operating in the points indicated by markers # 1 and 2.

3.C. Imaging task III

For imaging task III, the optimal operating points for the ATM filter for the anterior and posterior ROIs were (80, 800) and (60, 600), respectively; for AD, the optimal points were (1.0, 15.0) and (1.0, 17.5) for each spatial location. This imaging task does not have a single‐dominant spatial frequency component, as can be seen in Fig. 3(l). Therefore, the shape of the d′ contours is a mixture of the previous contours from imaging task I and II. One difference, however, is that since the spatial resolution requirement of this imaging task is higher than that of previous imaging tasks, the overall detectability value is lower than that of imaging tasks I and II.

Hybrid images of task III at 0.5 and 1.9 mGy without LSC are displayed in Fig. 8. Due to the low noise magnitude at 1.9 mGy, the fine details of the structure are clearly discriminated from the background resulting in a large detectability. However, the visibility is degraded by the presence of noise streaks in the 0.5 mGy image without LSC, resulting in a lower d′ value. The LSC images suggested by the operating points in zone (2), particularly for the AD method, have a considerable loss in spatial resolution, which compromises the visual differentiation of the structure from the background. The optimal operating points in zone (1) provided images with good spatial resolution but with compromised structure visibility by the still strong noise texture. On the other hand, the optimal operating points indicated by marker # (3) determined using the d′ metric, provided images with good conspicuity, independently of the spatial location for both LSC methods.

Table 1 summarizes the optimal operating points obtained through the d′ metric. This table lists the optimal points for each LSC method, imaging task, and spatial location.

Table 1.

Optimal operating points for a given LSC method, spatial location, and imaging task, determined using the d’ metric

Task	ATM (p l , p h )		AD (δ, γ)
	Anterior	Posterior	Anterior	Posterior
I	(140, 1000)	(80, 1000)	(0.9, 12.5)	(0.7, 7.5)
II	(0, 700)	(60, 100)	(0.4, 5.0)	(1.0, 22.5)
III	(80, 800)	(60, 600)	(1.0, 15.0)	(1.0, 17.5)

4. Discussion

This work presented a task‐based framework to optimize parameters for a given LSC method. Parameter optimization is not a trivial task, particularly if the LSC method has a nonlinear behavior with shift‐variant spatial resolution and noise properties in the reconstructed CT image. Multiple signal filtration methods have been proposed in previous works, and their imaging performance has been assessed via numerous approaches, from the subjective assessment of noise streaks reduction to specific figures of merit that attempt to integrate spatial resolution and noise measurements.^{15, 16, 17, 27, 28, 29, 30} The proposed framework uses mathematical observer models to not only integrate frequency‐dependent metrics of spatial resolution (MTF) and noise (NPS), but to allow for the incorporation of a specific imaging task of interest and an observer model that can be adjusted to better correlate with human observer performance. The framework incorporates an ensemble averaging approach that enables the measurement of the highly shift‐variant spatial resolution and noise properties of LSC images.

The interplay between the major spatial frequency components of each imaging task and the highly shift‐variant and anisotropic noise and spatial resolution properties is essential for determining the shape and magnitude of the detectability contours and consequently the selection of the optimal operating point. This interplay influenced the imaging performance of task II the most, since its major frequency component coincided with both: the direction of spatial resolution loss and the dominant noise spatial frequency component corresponding to noise streaks. On the other hand, the performance of imaging task I was affected the least by this interplay, since the spatial resolution loss and dominant noise spatial frequency component were perpendicular to its major frequency component. Since imaging task III had no strong directional dependence, the impact of this interplay was moderate; however, since it required better spatial resolution performance than imaging tasks I and II, the overall detectability level was lower. The detectability index can assess this interplay and enable the selection of the optimal operating point in the LSC parameter space that provides the appropriate trade‐off between the different dimensions of spatial resolution and noise for a given imaging task.

It was found that the optimal operating point for each of the LSC methods depended strongly on the imaging task and spatial location. Even though in a clinical scenario is very rare to know the exact lesion properties and its location, it is still possible to optimize parameters using this task‐based framework. For instance, one could foresee optimizing parameters for two different scenarios in a head CT scan: one where it is important to have favorable low‐contrast detection performance for a central region in the brain, while another where it is more relevant to have better high‐frequency performance for peripheral regions near the skull.

Even though the main goal of this study was not to compare two LSC methods, it could be relevant to highlight some filter characteristics and comment briefly about their imaging performance. In terms of computational efficiency, even though the AD filter is an iterative denoising method, it can be as efficient as the ATM filter, and both filters if optimized appropriately could be adapted to a clinical scenario without significantly slowing down the usual workflow. In terms of imaging performance, the results show that even though the shape of the contour maps for the AD filter is more consistent across different scenarios compared to the ATM filter, the AD filter has some regions of the parameter space that preserve streaks and therefore these regions must be avoided. In regards to the task‐based performance, the optimal d′ values are very similar for both AD and ATM across the studied imaging tasks and spatial locations. However, it must be noted that these results from the NPW observer have not yet been validated with human observer studies.

This work has certain limitations. The optimal operating points found for each LSC method are specific to an imaging system, image object, scanning conditions, and of course imaging task; therefore, it is not expected that these optimal operating points are generalizable to other scenarios. On the other hand, it is the task‐based parameter optimization framework itself which is designed to be generalizable. In this work, the generalizability of the framework was demonstrated with two LSC methods and three imaging tasks. Further studies with different anthropomorphic phantoms and CT imaging systems would provide more insight into the parameter optimization framework. It would also be desirable to include a wider variety of imaging tasks to optimize the performance of a given LSC method according to the particular needs, for example, high spatial resolution or low‐contrast detectability. The translation of the optimal parameters determined for a given anthropomorphic phantom and imaging task also needs to be validated for in vivo data.

In principle, the PSF measured for a feature of given contrast should be associated with an imaging task of similar contrast. In this work, the PSF was measured using rods with 1,400 HU contrast and applied to imaging features with a contrast of 500 HU. However, since both of these are sufficiently high‐contrast levels, it is assumed that there is negligible spatial resolution dependence on contrast level for this study. Future work should include rigorous systematic studies to accurately characterize the potential spatial resolution dependence on contrast level for LSC methods.

The dependence of d′ values throughout the image object needs to be systematically studied. An experimental study to determine this dependence would require a special phantom that enables accurate spatial resolution measurements at numerous spatial locations. As an alternative, numerical simulations could be performed to facilitate such analyses.

In this work, the NPW observer model was used; the correlation of this model with human observers could be further improved by adding an eye filter and internal noise⁵⁰ (NPWEi). The eye filter accounts for the observer's visual response to different spatial frequencies, and the internal noise component accounts for inconsistencies in the human observer's performance. However, in order to find out which of the many available observer models better correlates with human observer's performance, detailed human observer studies are needed. This is a subject of current investigation.

5. Conclusion

In this work, a task‐based parameter optimization framework for LSC methods in low‐dose CT was presented. The framework takes into account the potential nonlinear behavior of a given LSC method and the associated shift‐variant and highly anisotropic spatial resolution and noise properties of the reconstructed CT image. The optimal parameters that maximized detectability were found to depend strongly on the spatial location within the image object.

Conflict of Interest

The authors have no conflicts to disclose.