Effect of vaccination, border testing, and quarantine requirements on the risk of COVID-19 in New Zealand: A modelling study

Abstract

We couple a simple model of quarantine and testing strategies for international travellers with a model for transmission of SARS-CoV-2 in a partly vaccinated population. We use this model to estimate the risk of an infectious traveller causing a community outbreak under various border control strategies and different levels of vaccine coverage in the population. Results are calculated from N = 100,000 independent realisations of the stochastic model. We find that strategies that rely on home isolation are significantly higher risk than the current mandatory 14-day stay in government-managed isolation. Nevertheless, combinations of testing and home isolation can still reduce the risk of a community outbreak to around one outbreak per 100 infected travellers. We also find that, under some circumstances, using daily lateral flow tests or a combination of lateral flow tests and polymerase chain reaction (PCR) tests can reduce risk to a comparable or lower level than using PCR tests alone. Combined with controls on the number of travellers from countries with high prevalence of COVID-19, our results allow different options for managing the risk of COVID-19 at the border to be compared. This can be used to inform strategies for relaxing border controls in a phased way, while limiting the risk of community outbreaks as vaccine coverage increases.

1. Introduction

From April 2020 until September 2021, New Zealand pursued a COVID-19 elimination strategy (Baker et al., 2020) and, through a combination of strict border controls and snap lockdowns when needed, has limited community transmission of SARS-CoV-2 to very low levels. As a result, New Zealand has negligible infection-acquired immunity to COVID-19 (Carlton et al., 2021). Australia has also relied on international border controls and a strong public health response to keep incidence of COVID-19 very low. New Zealand's vaccination programme began in February 2021 and is exclusively using the Pfizer/BioNTech mRNA vaccine. As of early December 2021, over 90% of New Zealand's eligible population (aged over 12 years) are fully vaccinated (Ministry of Health, 2021). As vaccine rollout programmes in New Zealand and Australia have progressed, both countries have begun to transition away from strict elimination strategies to managing COVID-19 in the community, accompanied by a phased relaxation of travel restrictions.

During 2021, the Delta variant of SARS-CoV-2 has displaced other variants and become dominant in many countries, including India, the UK and USA – countries with which New Zealand has close travel links. Because of the increased transmissibility of the Delta variant, it is unlikely that countries will be able to reach complete population immunity (i.e. a reproduction number that less than 1 in the absence of any other interventions) via vaccination alone (Moore et al., 2021; Steyn et al., 2021). Other public health measures will be needed to control the virus, although reliance on these will reduce as vaccine coverage increases. These measures may consist of a mixture of border controls designed to reduce the risk of cases being seeded into the population, and community measures designed to enhance surveillance and reduce the potential for transmission.

Recent modelling has shown that the increased transmissibility of the Delta variant has largely nullified the reduction in risk of quarantine breaches gained from vaccination of international travellers and quarantine workers (Zachreson et al., 2021). This means that strong border controls, including limits on travel volume and mandatory government-managed isolation for international arrivals, remain essential to prevent re-introduction of SARS-CoV-2 into populations until they are protected by high levels of vaccine coverage. Once vaccination rates are sufficiently high, it is likely that border controls can be gradually relaxed in conjunction with ongoing community public health measures (New Zealand Government, 2021). To do this safely, it will be important to quantify the relative risk of community outbreaks under different sets of mitigation measures for international travellers arriving to at the border. These may include different combinations of government-managed isolation and quarantine (MIQ), self-isolation at home, and pre-departure and post-arrival testing requirements. Between 1 February and September 15, 2021, 83% of New Zealand's border-related cases were detected in the first 7 days after arrival and 75% were detected in the first 5 days. This suggests that a reduced quarantine period of less than 14 days would catch the majority of cases, but other measures such as home isolation and follow-up testing after completion of quarantine testing may still be needed. Different sets of requirements could be applied to travellers depending on their risk profile, for example more stringent restrictions for people travelling from countries with high infection rates.

New Zealand has primarily used polymerase chain reaction (PCR) tests for SARS-CoV-2 testing throughout the pandemic, sometimes referred to as the gold standard test because of its high sensitivity. Around the world, countries are increasingly complementing PCR testing with lateral flow tests, also known as rapid antigen tests. These have lower sensitivity than PCR tests, particularly in the early and late stages of the infectious period (Bruemmer et al., 2021; Dinnes et al., 2021). However, they have the advantage that they return results very quickly (typically within 30 minutes), they are cheap, and they do not require laboratory processing. This means they can be used to test large numbers of people at high frequency (e.g. daily) without stretching laboratory capacity and with fast turnaround of results.

Travel volume is a key determinant of the risk posed by international travel. As a consequence of limited MIQ capacity and citizenship or residence requirements for entry, the volume of international arrivals to New Zealand has been approximately 2% of pre-pandemic levels (with the exception of arrivals from Australia during limited periods of quarantine-free travel). It is important to factor this into risk evaluations because if, for example, a given mitigation provides a 10-fold reduction in the risk per traveller, this will be offset if there is a simultaneous 10-fold increase in travel volume.

In this paper, we use a stochastic model of SARS-CoV-2 transmission and testing to compare the relative reduction in transmission potential from infected travellers under various mitigations and at different levels of vaccine coverage in the resident population. This paper is a policy-oriented application of the model developed by Steyn et al. (2021) to investigate the potential impact of COVID-19 at different stages in New Zealand's vaccination programme.

The model allows for different effectiveness of isolation under different circumstances, for example MIQ versus self-isolation at home during asymptomatic, pre-symptomatic, symptomatic or confirmed stage of infection (Steens et al., 2020). We compare different testing requirements, such as daily lateral flow tests (LFT) or less frequent PCR tests, allowing for the different sensitivity of these tests. The model also includes individual heterogeneity in transmission rates and the probability of returning a positive result if tested. We use the model to simulate community outbreaks seeded by international arrivals and calculate the probability that such an outbreak meets various pre-defined criteria. The aim is not to identify vaccination targets at which borders can be completely reopened, but rather to support evidence-based strategies for relaxation of travel restrictions by comparing the risk reduction from various policy options.

The modelling approach is similar to that of Quilty et al. (2021), which estimated the reduction in transmission potential from a range of traveller interventions. The model of Quilty et al. (2021) modelled individual heterogeneity in viral load trajectories and assumed that the transmission rate and the probability of testing positive are both functions of the viral load. This requires that there is a unique one-to-one mapping between the transmission rate at time $t$ and the probability of testing positive at time $t$. We found it difficult to reconcile this with the fact that there is significant pre-symptomatic transmission of SARS-CoV-2 and that the likelihood of individuals testing positive whilst pre-symptomatic stage appears to be significantly lower than after symptom onset. We therefore take a simpler approach based on an empirically estimated generation time interval and test positivity curve and we investigate the qualitative effects of different forms of heterogeneity in these.

2. Methods

In this section, we first define the stochastic age-structured model for transmission of SARS-CoV-2. This model includes the effects of vaccination and case-targeted controls (case isolation and contact tracing) once a border-related community outbreak is detected. We describe the model for different interventions that can be applied to international travellers and how these affect potential transmission from international arrivals into the community. We then describe the testing model, defined in terms of the sensitivity of PCR tests and of LFTs as a function of time since infection. Finally, we describe how international travellers, under a given set of border interventions, are used to seed the community transmission model and define the simulation outputs that are calculated.

2.1. Age-structured transmission model

We model transmission of SARS-CoV-2 in the community using a stochastic age-structured branching process model in partially vaccinated population (Steyn et al., 2021). Vaccine allocation is assumed to be static (i.e. we do not consider simultaneous dynamics of community transmission and an ongoing vaccination programme). We assume that 90% of those over 65 years old are vaccinated and consider different levels of vaccine coverage in the 12–64 year age band (70%, 80%, 90%). For simplicity, we assume all individuals are either fully vaccinated or non-vaccinated (i.e. we do not consider the effect of people who have had a single dose). We assume the vaccine prevents infection in $e_I=70\%$ of people, and reduces transmission by $e_T=50\%$ in breakthrough infections (Public Health England, 2021). This provides an overall reduction in transmission of 85%. We assume that breakthrough infections and primary infections are equally likely to cause symptomatic disease. This does not preclude breakthrough infections having a lower probability of severe illness or death, although we do not investigate these outcomes in this study.

Infected individuals are categorised as either clinical or subclinical, with the clinical fraction increasing with age (Hinch et al., 2021) (see Table 1). Subclinical individuals are assumed to be $\tau =50\%$ as infectious as clinical individuals (Davies et al., 2020). The incubation period is assumed to be Gamma distributed from infection time with mean 5.5 days and s.d. 3.3 days (Lauer et al., 2020). In the absence of interventions, we assume generation times follow a Weibull distribution with mean 5.0 days and s.d. 1.9 days (Ferretti et al., 2020). There is at present conflicting evidence in the literature as to whether the Delta variant of SARS-CoV-2 has a shorter mean generation time or mean incubation period than other variants (Kang et al., 2021; Li et al., 2021; Pung et al., 2021; Ryu et al., 2021; Zhang et al., 2021). Generation times are difficult to empirically measure because this requires the infection times of both cases in a transmission pair. If infection times are unavailable but symptom onset dates are known, the serial interval can be used as a proxy for generation time. However, serial interval measurements contain more noise as they depend on both individuals’ incubation periods. In addition, observed generation times and serial intervals are affected by interventions such as test, trace and isolate measures. To investigate the effect of some of these uncertainties, we perform a sensitivity analysis with a shorter generation time (mean 2.9 days, s.d. 1.9 days) and incubation period (mean 4.4 days, s.d. 1.9 days) (Zhang et al., 2021).

Table 1.

Model parameter values.

Parameter	Value
Basic reproduction number in the absence of control	$R_0=6$
Relative transmission rate for isolated individuals: -asymptomatic/pre-symptomatic -symptomatic unconfirmed -confirmed cases -in MIQ	$c_{asym}=0.4$ [0.6 in sensitivity] $c_{symp}=0.2$ [0.4 in sensitivity] $c_{conf}=0$ $c_{MIQ}=0$
Incubation period (gamma distributed) -default values -sensitivity analysis	Mean 5.5 days, s.d. 3.3 days Mean 4.4 days, s.d. 1.9 days
Generation interval (Weibull distributed) -default values -sensitivity analysis	Mean 5.0 days, s.d. 1.9 days Mean 2.9 days, s.d. 1.9 days
Relative infectiousness of subclinical individuals	$\tau =0.5$
Heterogeneity in individual reproduction numbers	$k=0.5$
Vaccine effectiveness: -against infection -against transmission in breakthrough infection	$e_I=0.7$ $e_T=0.5$
Probability of a clinical community case being tested: -before an outbreak is first detected -after an outbreak is detected	$p_{test,pre}=0.12$ $p_{test,outbreak}=0.4$
Mean time from symptom onset to test result: -before an outbreak is first detected -after an outbreak is detected	4 days 4 days
Probability of a community case being detected via contact tracing	$p_{trace}=0.7$
Mean time from infection to quarantine for traced contacts	6 days
Probability of testing positive by PCR on days $[1,\dots ,21]$ after infection	[0, 0.01, 0.04, 0.33, 0.62, 0.75, 0.79, 0.80, 0.79, 0.77, 0.73, 0.70, 0.66, 0.62, 0.57, 0.52, 0.48, 0.44, 0.40, 0.37, 0.34]
Probability of testing positive by LFT on being PCR positive on days $[4,\dots ,15]$ after infection: default values	[0.25, 0.35, 0.66, 0.73, 0.73, 0.70, 0.58, 0.49, 0.42, 0.19, 0.14, 0.03]
-sensitivity analysis	[0.19, 0.27, 0.51, 0.57, 0.57, 0.54, 0.45, 0.38, 0.33, 0.15, 0.11, 0.02]

Age-specific parameters
Age (yrs)	0–4	5–9	10–14	15–19	20–24	25–29	30–34	35–39	40–44	45–49	50–54	55–59	60–64	65–69	70–74	75+
% of popn	5.98	6.39	6.56	6.17	6.59	7.40	7.44	6.62	6.08	6.41	6.43	6.38	5.77	4.90	4.24	6.64
Pr (clinical) (%)	54.4	55.5	57.7	59.9	62.0	64.0	65.9	67.7	69.5	71.2	72.7	74.2	75.5	76.8	78.0	80.1
Susceptibilitya	0.46	0.46	0.45	0.56	0.80	0.93	0.97	0.98	0.94	0.93	0.94	0.97	1.00	0.98	0.90	0.86

^aSusceptibility $u_i$ for age group $i$ is stated relative to susceptibility for age 60–64 years.

Transmission between age groups is described by a next generation matrix. The $\left(i,j\right)$ entry of this matrix is defined to be the expected number of secondary infections in age group $i$ caused by an infected individual in age group $j$ in the absence of interventions and given a fully susceptible population:

$$NG{M}_{i,j}=U{u}_i{C}_{j,i}$$

where $u_i$ is the relative susceptibility to infection of age group $i$ (Davies et al., 2020), $C$ is a contact matrix describing mixing rates between and within age groups (Prem et al., 2017; Steyn et al., 2021), and $U$ is a constant representing the intrinsic transmissibility of the virus. The value of $U$ is chosen so that the average number of secondary infections caused by an infected individual is equal to the assumed value of $R_0$. We assume $R_0=6.0$ for all simulations, approximately representing the Delta variant of SARS-CoV-2 (Kang et al., 2021; Zhang et al., 2021; SPI-M-O, 2021).

Each individual $l$ is assigned a relative transmission parameter $Y_l$ that is gamma distributed with mean 1 and variance $1/k$. This allows for individual heterogeneity in transmission (Lloyd-Smith et al., 2005). We set $k=0.5$, consistent with estimates of the overdispersion of SARS-CoV-2 in New Zealand and internationally (James et al., 2020a; Riou & Althaus, 2020). Under the assumptions about transmission between age groups and vaccine effectiveness described above, the expected number of secondary cases infected by individual $l$ given a fully susceptible population in the absence of interventions (the individual reproduction number) is

$$R_l=(1-V_l{e}_T)Y_l\sum _{j=1}^{M}NG{M}_{j,a_l}$$

where $V_l=1$ if individual $l$ is vaccinated and zero otherwise, $e_T$ is the vaccine effectiveness against transmission conditional on infection, and $a_l$ is the age group of individual $l$. The expression above is multiplied by $\tau$ if individual $l$ is subclinical.

At each timestep of size $\text{Δ}t$, infected individuals generate a Poisson distributed number of putative secondary infections with mean:

$$\lambda \left(t\right)=R_l\underset{t}{\overset{t+\text{Δ}t}{\int }}{F}_l^c\left(x\right)\omega \left(x\right)dx$$

where $F_l^c\left(x\right)$ describes the reduction in transmission due to isolation or prevention of travel (see Border interventions section below) and $\omega \left(x\right)$ is the probability density function for the generation time distribution. Each putative secondary infection is assigned an age group $i$ with probability $NG{M}_{i,a_l}/\sum _{j=1}^{M}NG{M}_{j,a_l}$ and to the vaccinated class with probability $v_i$. To account for the effect of vaccination in preventing infection, the putative secondary infections in the vaccinated class are thinned with probability $e_I$. Immunity from prior infection is ignored in the model. This is reasonable because we only consider small community outbreaks and our model is applicable to populations, such as New Zealand and Australia, that have not yet experienced large-scale epidemics.

We use a simplified model for case-targeted controls in the community. We assume there are initially no controls in place in the period of time before the outbreak is detected (i.e. before the first positive test result is returned). Outbreaks can be detected either via a positive test result in the infected traveller or by community testing. During the period before the outbreak is detected, we assume that symptomatic individuals in the community are tested with probability $p_{test,pre}=0.12$. This value is based on previous findings that, during a period with no known community transmission of SARS-CoV-2 in New Zealand, an estimated 10–20% of people with Covid-like symptoms sought a test (Harvey, Mackenzie, O'Neale, & Turnbull, 2021a). These findings were derived from an estimate of the number of people with Covid-like symptoms made using FluTracking data (Harvey et al., 2021b). Once an outbreak has been detected, symptomatic testing rates typically increase significantly (Harvey et al., 2021a). We therefore assume that all existing and subsequent clinical cases in the outbreak are detected with probability $p_{test,outbreak}=0.4$. In all cases, there is a delay from symptom onset to the test result being returned, which we assume to be exponentially distributed with mean 4 days (James et al., 2020b). To model the effect of contact tracing, we also assume that, after an outbreak is detected, all infected individuals are traced with probability $p_{trace}=0.7$ and isolated with a mean delay of 6 days after infection (see Table 1).

2.2. Border interventions

We model the effects of alternative sets of interventions on the expected transmission from an infected traveller. We use $F_l^c\left(t\right)$ to denote the transmission rate of individual $l$ at time $t$ under a given intervention $c$, relative to their unmitigated transmission rate at time $t$. When $F_l^c\left(t\right)=1$, this means individual $l$ is not quarantined or isolated at time $t$; when $F_l^c\left(t\right)=0$, this means individual $l$ is fully isolated at time $t$ and cannot transmit the virus. Note that $F_l^c\left(t\right)$ is also defined to be zero if individual $l$ has not yet arrived at their destination, or has been prevented from travelling from pre-departure symptom checks or testing. The expected number of secondary cases caused by individual $l$ under interventions $c$ relative to no interventions is given by:

$$\frac{R_l^c}{R_l}=\underset{0}{\overset{\infty }{\int }}{F}_l^c\left(t\right)\omega \left(t\right)dt$$

where $\omega \left(t\right)$ is the probability density function for the generation time distribution.

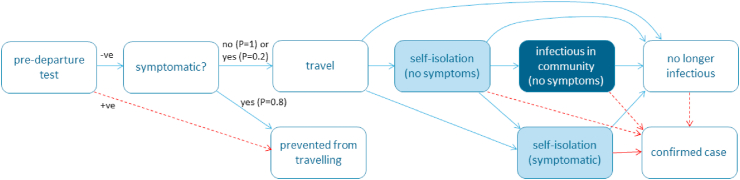
Interventions can be split into three categories: vaccination requirements, pre-departure tests, and post-arrival restrictions. We consider a few key policies for each category in Table 2. All scenarios assume a baseline level of screening of air passengers so that 80% of travellers who develop symptoms prior to departure are prevented from travelling, independent of any testing requirements. Fig. 1 shows a schematic diagram of the model with the different pathways travellers can take through the border control system.

Table 2.

Overview of key border interventions considered for international travellers. Interventions can be categorised as vaccination requirements, pre-departure testing requirements and post-arrival interventions.

Vaccination	Pre-departure	Post-arrival
Fully vaccinated	No test	No requirements
Not vaccinated	PCR on day −3	PCR test on days 0 and 4
	LFT on day −1	Daily LFT for 5 days
		5 day self-isolation with PCR test on days 0 and 4
		5 day self-isolation with daily LFT
		7 days MIQ with PCR test on day 5
		14 days MIQ with PCR test on days 3 and 12

Fig. 1.

Schematic diagram of the border model showing different potential pathways infected travellers can take through the system. States are shaded to indicate whether the infectious traveller poses: unmitigated risk of transmission to the community (dark blue); risk of transmission to the community mitigated by partially effective self-isolation (light blue); no risk of transmission to the community (white). Red arrows indicate transitions that are the result of a positive test result, either from a routine test on an asymptomatic or pre-symptomatic traveller (dashed red) or a symptom-triggered test (solid red).

Self-isolation after arrival can occur for any one of four reasons:

• 1.Due to a requirement to self-isolate while asymptomatic, assumed to reduce transmission to $F_l^c\left(t\right)=c_{asymp}$.
• 2.Due to onset of symptoms, assumed to reduce transmission to $F_l^c\left(t\right)=c_{symp}$, regardless of the border policy. Isolation is assumed to begin on the day following symptom onset. This represents a situation where recent arrivals are contacted by public health teams to encourage monitoring of symptoms.
• 3.Due to return of a positive test, assumed to reduce transmission to $F_l^c\left(t\right)=c_{conf}$, regardless of the border policy. Isolation is assumed to begin on the day following the return of a positive result.
• 4.Due to a requirement to enter MIQ. For simplicity, we assume there is no risk of transmission between travellers in MIQ facilities ($F_l^c\left(t\right)=c_{MIQ}=0$). Transmission between travellers in MIQ facilities is known to have occurred (Eichler et al., 2021; Grout et al., 2021), but this risk is likely to be much smaller than the risk of transmission from individuals in self-isolation at home.

Individuals isolate with the effectiveness of the strongest measure that applies at time $t$. In all scenarios, we assume that self-isolation prevents 100% of transmission from confirmed cases ($F_l^c\left(t\right)=c_{conf}$). Self-reported adherence to requested quarantine measures in a Norwegian study was 71% of those with COVID-19-compaible symptoms and 28% of those without (Steens et al., 2020). In the base scenario, we assume that self-isolation prevents 60% of transmission for travellers who are asymptomatic or pre-symptomatic ($c_{asymp}=0.4$), and prevents 80% of transmission for travellers who are symptomatic but have not yet received a positive test result ($c_{symp}=0.2$). We also perform a sensitivity analysis where self-isolation is less effective than in the base scenario ($c_{asymp}=0.6$ and $c_{symp}=0.4$).

This formulation assumes that all isolated individuals transmit at a reduced rate $c.$ However, we expect average model outputs to be very similar if we instead assumed that a fraction $c$ of isolated individuals transmit at the same rate as a non-isolated individual and a fraction $1-c$ do not transmit at all (Quilty et al., 2021). Individuals that develop symptoms after arrival seek a test with probability 80%. This test is assumed to be a PCR test taken with an exponentially distributed delay with mean 2 days after symptom onset and the result is returned the following day. If the individual is scheduled for any kind of test on the same day, they do not take the additional test.

2.3. Testing

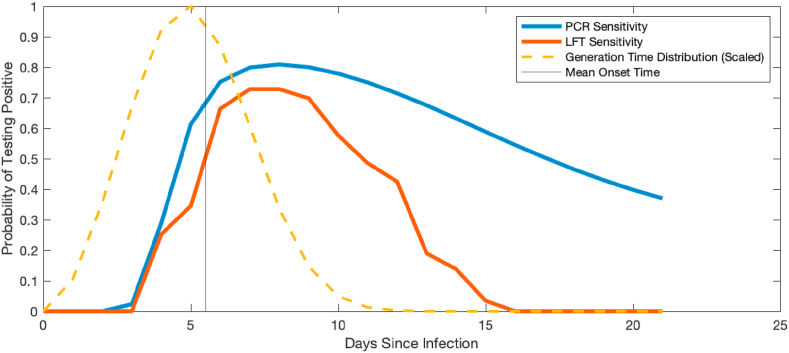
The probability of testing positive is modelled as a function of time since infection. For RT-PCR tests we use data from Kucirka et al. (2020), with a peak probability of testing positive of 81% eight days after infection (Fig. 2). We construct a similar function for the probability of testing positive by LFT based on data from Smith et al. (2021). These results showed that 24 out of 25 individuals tested returned a positive LFT on the day after first positive culture of the virus from a nasal swab. However, real-world test performance is likely to be lower than in a controlled laboratory study. We therefore scaled the data from Smith et al. (2021) so that the peak probability of testing positive was 73% (which is 90% of the PCR peak). We assumed that the peak occurs at the same time as the peak for the PCR test, i.e. eight days after infection (see Fig. 2). In addition, we assume that it is not possible to test negative by PCR and positive by LFT on the same day. To generate an LFT result, we therefore simulate the result of a putative PCR test where probability of a positive result is as shown by the blue curve in Fig. 2. If the putative PCR result is negative, we assume the LFT result is also negative. If the putative PCR result is positive, we assume the LFT result is positive with probability $P\left(LF{T}^{+}|PC{R}^{+}\right)=P_{LFT}^{+}\left(t\right)/P_{PCR}^{+}\left(t\right)$, which is the ratio of the red curve to the blue curve in Fig. 2.

Fig. 2.

Variation in assumed test sensitivity over time. Curves show the assumed probability of testing positive as a function of time since infection for PCR (blue) and LFT (red). Dashed curve shows the scaled generation time distribution, showing that a significant amount of transmission can occur prior to test positivity.

Note that, although the peak sensitivity of the LFT is assumed to be 90% of the peak sensitivity of a PCR test, the overall sensitivity of the LFT is lower than this because of the faster decay away from the peak (Fig. 2). Under the model assumptions, a PCR test taken on a random day in the one week or two weeks following symptom onset will detect 77% or 66% of infected individuals respectively, relative to 60% or 33% of infected individuals respectively for a LFT. Although precise characterisation of time-dependent test performance is difficult, this is broadly consistent with results showing that LFTs detected between 40% and 80% of PCR-positive cases (García-Fiñana et al., 2021; Schuit et al., 2021; Peto et al., 2021; Bruemmer et al., 2021; Pray, 2021). However, we also investigate a sensitivity analysis in which the peak sensitivity of the LFT is only 57%, which is 70% of the peak sensitivity of a PCR test (see Table 1 for time-dependent probabilities).

The probability of testing positive is assumed to be the same for subclinical and clinical individuals. Conditional on being infected, the probability of testing positive is assumed to be the same for vaccinated as for non-vaccinated individuals.

It is clear from Fig. 2 that, under these assumptions, a significant amount of transmission occurs before the infected person has a high probability of testing positive. This may seem pessimistic but it is consistent with the fact that pre-symptomatic transmission of SARS-CoV-2 is known to be common and with empirical data showing that the probability of testing positive prior to symptom onset is much smaller than after symptom onset (Kucirka et al., 2020). We also perform a sensitivity analysis to investigate the consequences of shifting the probability curves in Fig. 2 to the left by 2 days.

2.4. Model outputs

For each set of interventions $c$, we run $N=\mathrm{100,000}$ simulations, each initialised with one infected traveller. The traveller is assigned an age-group with a frequency proportional to the New Zealand age-structure, an infection time uniformly randomly distributed in the 14 days prior to arrival, and a clinical status that depends on age. The simulation returns the transmission potential of the infected traveller ($R_l^c$) and a list of any infections in the community. From these simulations, we report three model outputs defined as follows.

Output (1) is the transmission potential of infected travellers under interventions $c$ relative to the transmission potential in the absence of interventions. This is defined as $\overline{R_l^c}/\overline{R_l^0}$ where the bar denotes the mean of $N$ simulations.

Output (2) is the proportion of simulations meeting each of the following four criteria: (i) the infected traveller causes any onward transmission in the community; (ii) the infected traveller causes onward transmission in the community and is never detected; (iii) the infected traveller causes an outbreak that reaches 5 infections; (iv) the infected traveller causes an outbreak that reaches 50 infections. Note that because the reproduction number is significantly greater than 1 even at the highest vaccine coverage level considered (90% of over-12s), outbreaks that reach 50 infections are almost certain to continue to grow until control measures are introduced (or there is a build-up of population immunity). The size of an outbreak that would be concerning varies depending on context. The criteria of 50 infections is arbitrary, but is a convenient point at which to terminate simulations and indicates that community transmission has become established and stochastic extinction is unlikely.

Finally, output (3) is the number of infected travellers who would be expected to result in one large outbreak (that reaches 50 cases from one traveller). If, for example, an average of one outbreak per month is tolerable, then this is the number of infected travellers who would be tolerated per month. This is equal to the reciprocal of the probability that an infected traveller starts a large outbreak.

2.5. Model extension: individual heterogeneity in probability of testing positive

In the base model described above, we ignore heterogeneity between individuals in the probability of testing positive at a given time. In reality, there may be variability in the timing, magnitude and duration of the probability of testing positive, and these may be correlated with individual infectiousness. This could affect the performance of different risk mitigation strategies. Explicitly modelling these heterogeneities and correlations would require individual-level data on the probability of testing positive and infectiousness over time. In the absence of detailed data on this, we consider a simplified model for individual heterogeneity.

The base model includes heterogeneity in transmission, via the individual parameter $Y$ with mean 1 and variance $1/k$. This parameter encompasses two key contributors to heterogeneity: variability in contact rates (which is not correlated with probability of testing positive); and variability in viral shedding (which is likely to be correlated with probability of testing positive). We model these two contributions by writing $Y=Y_1{Y}_2$ where $Y_1$ and $Y_2$ are independent random variables, each with mean 1. Conceptually, $Y_1$ quantifies behavioural factors that affect transmission (i.e. contact rates during the infectious period), whereas $Y_2$ is related to biological characteristics of the infection (e.g. viral load) in a particular individual. We assume that the probability of returning a positive test result is an increasing function of $Y_2$ (see below). In the base model with no heterogeneity in probability of testing positive, $Var\left(Y_2\right)=0$ and heterogeneity in transmission is entirely due to individual differences in contact rates. Fixing $Var\left(Y\right)$ and increasing $Var\left(Y_2\right)$ does not change the intrinsic transmission dynamics, but increases the correlation between and individual's transmission rate and probability of testing positive.

To implement this model, we assume $Y_1$ is gamma distributed with mean 1 and variance $1/k^{\ast }$, and $Y_2$ is normally distributed with mean 1 and variance ${\sigma }^2$ truncated to non-negative values. If we set $k^{\ast }=k(1+{\sigma }^2)/(1-k{\sigma }^2)$ then, provided ${\sigma }^2$ is sufficiently small, the product $Y_1{Y}_2$ is approximately gamma distributed with mean 1 and variance $1/k$, as for the base model. We assume that the odds of testing positive are proportional to $Y_2$ and so we set the probability that a test on individual $l$ at time $t$ returns a positive result to be $\frac{Y_{2,l}{P}^{+}\left(t\right)}{1-(1-Y_{2,l})P^{+}\left(t\right)}$, where $P^{+}\left(t\right)$ is the relevant test positivity curve for either PCR or LFT shown in Fig. 2.

3. Results

3.1. Relative transmission potential

The relative transmission potential (model output 1) measures the reduction in the expected number of secondary cases per infected traveller as a result of a given border intervention $c$. By construction, this is independent of the assumed value of $R_0$ and of the level of vaccine coverage in the domestic population. For example, a relative transmission potential of 0.6 means that the expected number of community infections per infected traveller is 60% of what it would be with no interventions.

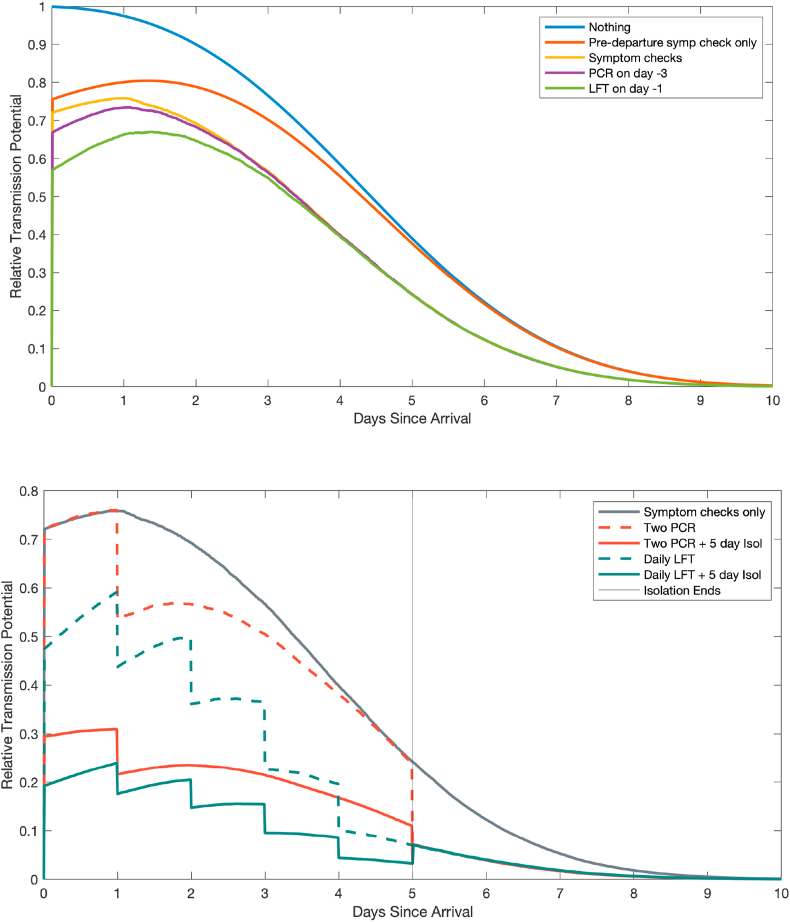
Fig. 3 shows the effect of alternative interventions on the average transmission potential of an infected traveller over time, relative to the unmitigated potential on day 0. The effect of scheduled tests can be seen as a drop in transmission potential (at the time results are returned) as detected cases are put into strict isolation. The overall transmission potential under a given intervention is proportional to the area under the corresponding curve shown in Fig. 3.

Fig. 3.

Effect of border interventions on transmission potential of infected travellers. Each curve shows the average transmission potential of an infected traveller as a function of time since arrival under a given set of interventions, relative to the transmission potential of an infected traveller on day 0 with no mitigation.

Table 3 shows the relative transmission potential of an average infected traveller under a given border policy. All results are relative to the same baseline, representing the transmission potential of a non-vaccinated traveller that faces no interventions other than a pre-departure symptom check. Conditional on being infected, a vaccinated individual is assumed to be 50% as infectious as a non-vaccinated individual (Table 1). Vaccinated individuals are less likely to be infected than non-vaccinated individuals. However, we do not attempt to model the epidemic dynamics in the traveller's country of origin so the results do not capture this effect.

Table 3.

Transmission potential of infected travellers under different border interventions (model output 1). Average remaining transmission potential (relative to that of a non-vaccinated traveller with no interventions other than a pre-departure symptom check) of infected travellers under various border controls. All scenarios assume pre-departures symptom checks, regular post-arrival symptom checks, and symptom-triggered testing are implemented, with the exception of the first row. Results are from 100,000 independent simulations representing 100,000 infected travellers.

Post-arrival	Pre-depart	Non-vacc traveller	Vacc traveller
None	Symp check only	100%	50%
Regular symptom checks	No test	78%	39%
	PCR on day −3	76%	38%
	LFT on day −1	73%	36%
PCR on days 0 & 4	No test	66%	33%
	PCR on day −3	66%	33%
	LFT on day −1	63%	32%
Daily LFT for 5 days	No test	45%	22%
	PCR on day −3	44%	22%
	LFT on day −1	43%	22%
5 day isolation + PCR on days 0 & 4	No test	29%	15%
	PCR on day −3	29%	15%
	LFT on day −1	28%	14%
5 day isolation + daily LFT	No test	20%	10%
	PCR on day −3	20%	10%
	LFT on day −1	19%	10%
7 day MIQ + PCR on days 0 & 4	No test	0.36%	0.18%
	PCR on day −3	0.35%	0.18%
	LFT on day −1	0.36%	0.18%
14 day MIQ + PCR on days 3 & 12	No test	0.0%	0.0%
	PCR on day −3	0.0%	0.0%
	LFT on day −1	0.0%	0.0%

Regular post-arrival symptom checks and isolation for symptomatic travellers (assumed to be 80% effective from the day following symptom onset) reduces the transmission potential to 78% of the baseline (unmitigated) transmission potential for non-vaccinated travellers and 39% for vaccinated travellers.

Requiring pre-departure testing reduces transmission potential only slightly (for vaccinated travellers from 39% with no pre-departure testing to 38% for PCR on day −3 or 36% for LFT on day −1). Although pre-departure testing and symptom checks screen out a significant fraction of infected travellers (approximately 34% for symptom-checks only, 54% with the addition of either test), many of these travellers would have been towards the end of their infectious period by the time they arrived at their destination. This explains why the reduction in transmission potential is relatively modest. The small difference between the effect of a PCR test on day −3 and a LFT on day −1 suggests the reduced sensitivity of the LFT is roughly offset by the fact it can be performed closer to the time of departure.

Of the post-arrival testing strategies, a daily LFT for 5 days is more effective (reducing transmission potential from 39% to 22% for vaccinated travellers) than PCR tests on day 0 and day 4 (39% to 33%). This shows that, under the assumed test characteristics, the lower sensitivity of LFT tests is outweighed by the increased frequency of testing and faster return of results.

Adding a requirement for five days self-isolation after arrival further reduces transmission potential (from 33% to 15% with the PCR testing strategy and from 22% to 10% with the LFT strategy, for vaccinated travellers). Finally, a seven-day stay in MIQ with two PCR tests reduces transmission potential to approximately 0.2% for vaccinated travellers, and a fourteen-day stay in MIQ with two PCR tests reduces the transmission potential to a negligible level. Note that the model does not attempt to include the risk of transmission within MIQ facilities.

3.2. Risk of onward transmission

Table 4 shows the probability that an infected traveller leads to any onward transmission in the community (model output 2.i). These risks all decrease as the vaccine coverage in the domestic population increases. The results are presented for both vaccinated and non-vaccinated travellers in the tables, although we focus on vaccinated travellers in the results described below.

Table 4.

Probability that an infected traveller causes onward transmission in the community (model output 2.i). Columns headings 0%, 70%, 80%, and 90% refer to the percentage of 12-to-64-year-olds that are vaccinated in the community; all scenarios (except 0% coverage) assume 90% of over 65-year-olds are fully vaccinated. Results are from 100,000 independent simulations representing 100,000 infected travellers.

Post-arrival		Non-vaccinated traveller				Vaccinated traveller
	Pre-depart	0%	70%	80%	90%	0%	70%	80%	90%
None	Symp check only	36%	33%	32%	31%	32%	28%	28%	27%
Regular symptom checks	No test	35%	31%	30%	29%	31%	26%	26%	25%
	PCR on day −3	32%	29%	28%	28%	28%	25%	24%	24%
	LFT on day −1	29%	26%	26%	25%	26%	23%	22%	21%
PCR on days 0 & 4	No test	33%	29%	29%	28%	29%	25%	24%	23%
	PCR on day −3	30%	27%	27%	26%	27%	23%	23%	22%
	LFT on day −1	28%	25%	24%	24%	25%	21%	21%	20%
Daily LFT for 5 days	No test	24%	22%	21%	20%	21%	18%	18%	17%
	PCR on day −3	23%	21%	20%	20%	21%	18%	17%	17%
	LFT on day −1	22%	20%	19%	19%	20%	17%	16%	16%
5 day isolation + PCR on days 0 & 4	No test	28%	24%	23%	22%	23%	19%	18%	17%
	PCR on day −3	26%	23%	22%	21%	22%	18%	17%	17%
	LFT on day −1	24%	21%	20%	19%	20%	17%	16%	15%
5 day isolation + daily LFT	No test	20%	17%	17%	16%	17%	14%	13%	13%
	PCR on day −3	20%	17%	17%	16%	17%	14%	13%	12%
	LFT on day −1	19%	16%	16%	15%	16%	13%	12%	12%
7 day MIQ + PCR on days 0 & 4	No test	1.32%	0.97%	0.91%	0.84%	0.92%	0.63%	0.58%	0.53%
	PCR on day −3	1.32%	0.97%	0.90%	0.83%	0.92%	0.63%	0.58%	0.53%
	LFT on day −1	1.33%	0.97%	0.91%	0.84%	0.93%	0.64%	0.59%	0.54%
14 day MIQ + PCR on days 3 & 12	No test	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
	PCR on day −3	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
	LFT on day −1	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%

When only pre-departure symptom checks are included, there is a 32% chance that an infected vaccinated traveller leads to onward transmission in a fully susceptible population. This decreases to 27% when 90% of the domestic population aged 12 years or over is vaccinated. Adding post-arrival symptom checks results in a modest reduction in the probability of onward transmission (31% without domestic vaccination, decreasing to 25% at 90% coverage of over-12s). This decreases to 28%/24% with the addition of a pre-departure PCR test, or to 26%/21% with the addition of a pre-departure LFT test.

Consistent with the results in Table 3, daily LFTs for 5 days after arrival make the risk of onward transmission smaller (21% with no vaccine coverage, dropping to 17% at 90% coverage of over-12s) than PCR tests on day 0 and day 4 (29% with no vaccine coverage, dropping to 23% at 90% coverage of over-12s). When five days of self-isolation are required, daily LFTs again perform better at preventing onward transmission (14% for LFT compared to 19% for PCR with no vaccine coverage). The probability of onward transmission following a 7-day MIQ stay is between 0.5% and 1% depending on vaccine coverage in the population.

The LFT-based strategies also perform better than the corresponding PCR strategies at reducing the probability that an infected traveller transmits the virus without ever being detected by testing (Table 5, model output 2.ii). This is important because detecting a travel-related case, even after they have passed the virus on in the community, allows contact tracing to begin. This may enable the outbreak to be eliminated in its early stages. However, the differences between the LFT and PCR strategies are relatively small because. Although daily LFTs detect a reasonably high proportion of cases before they can transmit, PCR tests are more sensitive in the later stages of the infection. Motivated by this, we also calculated the probability of undetected onward transmission under alternative strategies where travellers take daily LFTs on days 0–3 followed by a PCR test on day 4. We found that these strategies performed comparably to the LFT-only strategies at preventing onward transmission, but outperformed both the LFT-only and PCR-only strategies at preventing undetected onward transmission (Supplementary Table 1). For example, the probability of undetected onward transmission from an infected vaccinated traveller into a non-vaccinated population is 1.8% in the mixed testing strategy compared to 2.8% for LFT-only and 4.0% for PCR-only.

Table 5.

Probability that an infected traveller leads to onward transmission in the community and is never detected (model output 2.ii). Columns headings 0%, 70%, 80%, and 90% refer to the percentage of 12-to-64-year-olds that are vaccinated in the community; all scenarios (except 0% coverage) assume 90% of over 65-year-olds are fully vaccinated. Results are from 100,000 independent simulations representing 100,000 infected travellers.

Post-arrival		Non-vaccinated traveller				Vaccinated traveller
	Pre-depart	0%	70%	80%	90%	0%	70%	80%	90%
None	Symp check only	36%	33%	32%	31%	32%	28%	28%	27%
Regular symptom checks	No test	24%	21%	21%	20%	21%	18%	18%	17%
	PCR on day −3	21%	19%	19%	19%	19%	17%	16%	16%
	LFT on day −1	19%	18%	17%	17%	17%	15%	15%	14%
PCR on days 0 & 4	No test	4.4%	4.0%	4.0%	3.9%	4.0%	3.5%	3.4%	3.3%
	PCR on day −3	4.2%	3.9%	3.8%	3.7%	3.8%	3.4%	3.4%	3.3%
	LFT on day −1	4.0%	3.7%	3.6%	3.6%	3.7%	3.3%	3.2%	3.1%
Daily LFT for 5 days	No test	3.1%	2.9%	2.8%	2.8%	2.8%	2.5%	2.5%	2.4%
	PCR on day −3	3.1%	2.8%	2.8%	2.7%	2.8%	2.5%	2.4%	2.4%
	LFT on day −1	3.0%	2.8%	2.7%	2.7%	2.8%	2.5%	2.4%	2.4%
5 day isolation + PCR on days 0 & 4	No test	3.9%	3.5%	3.4%	3.3%	3.4%	2.9%	2.8%	2.7%
	PCR on day −3	3.9%	3.5%	3.4%	3.3%	3.4%	2.9%	2.8%	2.7%
	LFT on day −1	3.7%	3.3%	3.3%	3.2%	3.2%	2.8%	2.7%	2.6%
5 day isolation + daily LFT	No test	2.8%	2.5%	2.5%	2.4%	2.5%	2.2%	2.1%	2.1%
	PCR on day −3	2.8%	2.5%	2.5%	2.4%	2.5%	2.2%	2.1%	2.0%
	LFT on day −1	2.8%	2.5%	2.5%	2.4%	2.4%	2.1%	2.1%	2.0%
7 day MIQ + PCR on days 0 & 4	No test	1.14%	0.83%	0.78%	0.72%	0.78%	0.53%	0.49%	0.45%
	PCR on day −3	1.13%	0.82%	0.77%	0.71%	0.77%	0.53%	0.49%	0.44%
	LFT on day −1	1.13%	0.82%	0.77%	0.71%	0.79%	0.54%	0.50%	0.45%
14 day MIQ + PCR on days 3 & 12	No test	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
	PCR on day −3	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%
	LFT on day −1	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%	0.0%

3.3. Risk of community outbreaks

Table 6, Table 7 show the probability that an infected traveller starts an outbreak that causes at least 5 infections and at least 50 infections respectively (model output 2.iii and 2.iv). Comparing Table 6, Table 7 reveals that, in a non-vaccinated population, most outbreaks that reach 5 infections also go on to reach 50 infections, as the respective probabilities are very similar. As vaccine coverage increases, the probability of an outbreak reaching 50 infections drops below the probability of reaching 5 infections. This shows that, in a highly vaccinated population, outbreaks may cause a few cases but increasingly fail to establish. These scenarios assume effective contact tracing is implemented once an outbreak is detected (either via a positive test result in the traveller who triggered the outbreak or via symptomatic community testing), so while vaccination levels are low, additional controls would almost always be necessary to control an outbreak.

Table 6.

Probability of an infected vaccinated traveller starting an outbreak leading to at least 5 infections (model output 2.iii). Columns headings 0%, 70%, 80%, and 90% refer to the percentage of 12-to-64-year-olds that are vaccinated in the community; all scenarios (except 0% coverage) assume 90% of over 65-year-olds are fully vaccinated. Results are from 100,000 independent simulations representing 100,000 infected travellers.

Post-arrival	Pre-depart	0%	70%	80%	90%
None	Symp check only	16.7%	10.1%	8.8%	7.4%
Regular symptom checks	No test	14.5%	8.4%	7.3%	6.0%
	PCR on day −3	14.3%	8.2%	7.2%	5.9%
	LFT on day −1	13.1%	7.8%	6.9%	5.6%
PCR on days 0 & 4	No test	12.7%	7.0%	6.0%	4.9%
	PCR on day −3	12.3%	6.9%	6.0%	4.9%
	LFT on day −1	11.7%	6.6%	5.7%	4.6%
Daily LFT for 5 days	No test	9.2%	4.8%	4.2%	3.3%
	PCR on day −3	8.9%	4.9%	4.1%	3.3%
	LFT on day −1	8.7%	4.8%	4.0%	3.2%
5 day isolation + PCR on days 0 & 4	No test	7.8%	3.7%	3.1%	2.4%
	PCR on day −3	7.6%	3.8%	3.0%	2.4%
	LFT on day −1	7.4%	3.5%	2.8%	2.4%
5 day isolation + daily LFT	No test	5.5%	2.6%	2.1%	1.7%
	PCR on day −3	5.5%	2.5%	2.1%	1.6%
	LFT on day −1	5.2%	2.5%	2.0%	1.6%
7 day MIQ + PCR on days 0 & 4	No test	0.16%	0.06%	0.05%	0.03%
	PCR on day −3	0.16%	0.07%	0.05%	0.04%
	LFT on day −1	0.16%	0.05%	0.04%	0.04%
14 day MIQ + PCR on days 3 & 12	No test	0.0%	0.0%	0.0%	0.0%
	PCR on day −3	0.0%	0.0%	0.0%	0.0%
	LFT on day −1	0.0%	0.0%	0.0%	0.0%

Table 7.

Probability of an infected vaccinated traveller starting a large outbreak leading to at least 50 infections (model output 2.iv). Columns headings 0%, 70%, 80%, and 90% refer to the percentage of 12-to-64-year-olds that are vaccinated in the community; all scenarios (except 0% coverage) assume 90% of over 65-year-olds are fully vaccinated. Results are from 100,000 independent simulations representing 100,000 infected travellers.

Post-arrival	Pre-depart	0%	70%	80%	90%
None	Symp check only	16.4%	8.7%	6.7%	4.5%
Regular symptom checks	No test	14.2%	6.7%	5.0%	3.1%
	PCR on day −3	13.9%	6.5%	4.9%	3.1%
	LFT on day −1	12.8%	6.2%	4.7%	2.8%
PCR on days 0 & 4	No test	12.1%	4.9%	3.4%	1.9%
	PCR on day −3	11.7%	4.8%	3.3%	1.9%
	LFT on day −1	11.2%	4.6%	3.2%	1.8%
Daily LFT for 5 days	No test	8.7%	3.3%	2.3%	1.3%
	PCR on day −3	8.5%	3.4%	2.3%	1.2%
	LFT on day −1	8.2%	3.3%	2.2%	1.2%
5 day isolation + PCR on days 0 & 4	No test	7.4%	2.5%	1.7%	0.9%
	PCR on day −3	7.3%	2.6%	1.6%	0.9%
	LFT on day −1	7.0%	2.4%	1.5%	0.9%
5 day isolation + daily LFT	No test	5.2%	1.7%	1.1%	0.6%
	PCR on day −3	5.2%	1.7%	1.1%	0.6%
	LFT on day −1	4.9%	1.7%	1.0%	0.6%
7 day MIQ + PCR on days 0 & 4	No test	0.16%	0.06%	0.04%	0.02%
	PCR on day −3	0.16%	0.06%	0.04%	0.02%
	LFT on day −1	0.16%	0.04%	0.03%	0.02%
14 day MIQ + PCR on days 3 & 12	No test	0.0%	0.0%	0.0%	0.0%
	PCR on day −3	0.0%	0.0%	0.0%	0.0%
	LFT on day −1	0.0%	0.0%	0.0%	0.0%

High levels of community vaccine coverage decrease the risk that a vaccinated traveller with only pre-departure symptom checks starts a large outbreak from 16% with no vaccination, to 4.5% once 90% of over 12-year-olds are vaccinated. Introducing a pre-departure LFT and post-arrival symptom checks decreases this to 2.8%. Further introducing a PCR test on day 0 and 4 after arrival takes this to 1.8% while daily LFT for 5 days after arrival takes this to 1.2%. Requiring 5 days of self-isolation reduces the risk to 0.9% with the PCR testing strategy or 0.6% with the LFT testing strategy. A 7-day stay in MIQ reduces the risk to a much lower level (<0.05%).

These results can also be interpreted in terms of the number of infected travellers that are expected to lead to one large outbreak (Table 8, model output 3). Aside from those involving MIQ, the only scenario that consistently tolerates more than 80 infected travellers per large outbreak is 5-day self-isolation with daily LFTs and at least 80% domestic vaccine coverage, or 5-day self-isolation with two PCR tests and 90% vaccine coverage. Aside from MIQ, there is no scenario where domestic vaccine coverage is below 80% of over 12-year-olds and more than 80 infected travellers can be allowed to enter without a large outbreak being expected.

Table 8.

Expected number of infected vaccinated travellers per large outbreak (model output 3). Columns headings 0%, 70%, 80%, and 90% refer to the percentage of 12-to-64-year-olds that are vaccinated in the community; all scenarios (except 0% coverage) assume 90% of over 65-year-olds are fully vaccinated. Results are from 100,000 independent simulations representing 100,000 infected travellers. For scenarios in which less than 100 of the 100,000 simulations resulted in a large outbreak, the number of infected travellers per large outbreak is shown as >1000.

Post-arrival	Pre-depart	0%	70%	80%	90%
None	Symp check only	6	12	15	22
Regular symptom checks	No test	7	15	20	33
	PCR on day −3	7	15	20	32
	LFT on day −1	8	16	21	35
PCR on days 0 & 4	No test	8	21	30	52
	PCR on day −3	9	21	30	52
	LFT on day −1	9	22	31	56
Daily LFT for 5 days	No test	11	30	43	79
	PCR on day −3	12	30	44	82
	LFT on day −1	12	30	46	83
5 day isolation + PCR on days 0 & 4	No test	13	40	58	111
	PCR on day −3	14	39	61	109
	LFT on day −1	14	42	65	111
5 day isolation + daily LFT	No test	19	59	89	157
	PCR on day −3	19	58	90	154
	LFT on day −1	21	59	98	164
7 day MIQ + PCR on days 0 & 4	No test	649	>1000	>1000	>1000
	PCR on day −3	617	>1000	>1000	>1000
	LFT on day −1	641	>1000	>1000	>1000
14 day MIQ + PCR on days 3 & 12	No test	>1000	>1000	>1000	>1000
	PCR on day −3	>1000	>1000	>1000	>1000
	LFT on day −1	>1000	>1000	>1000	>1000

3.4. Sensitivity analyses

Results for the model with individual heterogeneity in the probability of testing positive (Supplementary Tables 2–4) show that this appears to be a relatively small part of the overall stochasticity of the simulation results. Including heterogeneity has very little effect on the average relative transmission potential, but slightly increases the risk of undetected onward transmission relative to the base model. This is because more infected individuals will be missed, even when tested on multiple occasions. Further modelling work and better data on test characteristics are needed to more completely understand the sensitivity of the results to heterogeneity, but it appears to have a relatively small effect on the outcomes considered here.

If individuals tend to test positive earlier in the course of their infection (shifting the curves in Fig. 2 to the left by 2 days), this decreases all measures of risk (Supplementary Tables 5–7), particularly for interventions involving daily LFT testing. Conversely, if the generation time and incubation period are shorter (mean 2.9 days and 4.4 days respectively), the relative transmission potential is higher (Supplementary Table 8). However, this is not a good basis for comparison with the default parameter values (see Table 1) because the baseline (unmitigated) transmission potential depends on generation time assumptions. The risk of onward transmission (Supplementary Tables 9–10) is a better basis for comparison and this is lower for the short generation time scenario. This is because most transmission occurs in the first few days following infection, so testing and a period of self-isolation after arrival are more effective at preventing contact with the community during the infectious period.

When the sensitivity of LFTs is assumed to be lower (see Table 1), strategies using LFTs still outperform the corresponding strategy using PCR tests at reducing the probability of onward transmission (Supplementary Tables S11–S12). LFT-based strategies become slightly worse than the corresponding PCR strategy at preventing onward transmission that is never detected (Supplementary Table S13). However, the difference is small and could be offset by a PCR test at the end of the self-isolation period (as described above). Finally, we performed a sensitivity analysis where self-isolation only prevents 40% of transmission from pre-symptomatic or asymptomatic arrivals in the community during and 60% of transmission from symptomatic arrivals (Supplementary Tables S13–S15), as opposed to 60% and 80% in the base scenarios). As expected, the risk metrics are higher under most interventions, particularly those involving a 5-day self-isolation period. However, the relative risk reductions of the different policies follow the same qualitative features described above.

4. Discussion

We have modelled the effect of different border controls on the risk of international travellers infected with SARS-CoV-2 transmitting the virus and triggering community outbreaks. Potential border measures include a requirement for travellers to be vaccinated, different combinations of pre-departure testing and post-arrival testing and quarantine. We investigated outcomes at different levels of vaccine coverage in the domestic population.

The aim of this study is not to identify an optimal set of border interventions at a given vaccination rate. Relaxing border restrictions will increase the risk of border-related community outbreaks, including the risk per infected traveller and potentially also the volume of travellers. However, the tolerance a government has for border-related outbreaks will vary depending on factors such as the domestic vaccination rate, prevalence of SARS-CoV-2, capacity of public health systems, and overall strategy for community outbreak management. Tolerance is likely to increase over time in countries, such as New Zealand, transitioning away from a strict elimination strategy towards managing ongoing community transmission of SARS-CoV-2. Conversely, the emergence of new variants of concern could prompt a reduction in risk tolerance and tightening of border restrictions. Our study provides a rigorous framework to support decision-makers to assess and manage risk at the border within a shifting epidemiological context.

Our results should be interpreted as estimates of the relative effectiveness of alternative mitigation strategies, rather than absolute predictions of risk. For example, the model estimates that pre-departure tests alone have a relatively small impact on the risk of a community outbreak. Adding post-arrival testing requirements provides a larger benefit and can cut the risk by around 50% relative to no testing. A further requirement for 5 days of self-isolation at home can cut the risk to around one third of the risk without mitigations. Our model assumes that travellers that test positive after arrival are strictly isolated and pose no further risk of transmission. This is a reasonable assumption when the volume of infectious arrivals is relatively low as confirmed cases can be accommodated in a dedicated facility. However, if the number of infectious arrivals is very high this assumption may no longer be justified and the risk profile will increase. The model results also clearly show the progressive reduction in risk as vaccine coverage in the domestic population increases: achieving 90% vaccine coverage amongst over-12-year-olds cuts the risk of a community outbreak by roughly a factor of 3.

Our results describe the risks per infected would-be traveller. The other key determinant of overall risk is the number of infected travellers, which is a product of the prevalence of infection amongst travellers and the travel volume. The latter variable is crucial because, although the restriction of travel to New Zealand residents and the limited availability of rooms in MIQ have seen travel volume reduce to approximately 2500 arrivals to New Zealand per week, this could increase substantially following a relaxation of border controls. For example, a hypothetical scenario with 50,000 arrivals per week (i.e. around 50% of pre-pandemic travel volume) and a very low prevalence of 0.2 infections per 1000 travellers (for example by restricting quarantine-free travel to low-risk countries) would mean around 10 infected arrivals per week. Under the more effective border control scenarios with high vaccine coverage and 5-day self-isolation and testing requirements, the model estimates the risk of a community outbreak to be around 1–2% per infected traveller. This would translate to around one new community outbreak every 5–10 weeks. If prevalence among travellers was 80 infections per 1000 (which is approximately the positivity rate seen in arrivals to MIQ up to June 2021 (ESR, 2020)), the same travel volume and border controls would translate to around 400 infectious arrivals per week and 4–8 new community outbreaks per week. The level of tolerance for new border-related outbreaks will vary over time depending on the domestic epidemiological situation. Our results provide a framework for assessing and managing risks at the border for countries transitioning away from a strict elimination strategy towards managing the impacts of COVID-19 in the population.

If vaccine coverage is sufficiently high, the majority of border-related outbreaks may be stamped out with targeted measures like intensive community testing and contact tracing (Steyn et al., 2021). However, this would likely require significantly higher capacity than has been used in previous outbreaks in New Zealand. In addition, some outbreaks may require broader interventions or even localised lockdowns, particularly if they affected population groups with relative low vaccine coverage or high contact rates. This suggests a staged approach to relaxing travel restrictions with a gradual as opposed to a sudden increase in travel volume, allowing case management and outbreak control systems to be tested.

The over-dispersed nature of SARS-CoV-2 transmission implies many infected people do not transmit the virus, or only infect one or two others, whereas a small minority of cases can infect a large number of other people. This means that, although the probability of an individual transmitting the virus may be low, the ones who do transmit can lead to outbreaks that grow faster than an average would suggest.

The assumed reduction in transmission from individuals in self-isolation at home does not capture any specific effects, such as the increased relative likelihood of transmission to household contacts. Policies such as requiring all household contacts of self-isolating travellers to be vaccinated or mandating the collection of contact tracing information would further mitigate risk. However, the effectiveness of home isolation is largely untested in the New Zealand context. Analysis of contact tracing data from March 2021 suggested that the introduction of a self-isolation requirement for international arrivals reduced transmission by 35% (James et al., 2020a), although this estimate was based on a small dataset that may not be representative of future cohorts of travellers.

Lateral flow tests have not been widely used in New Zealand previously. Our results suggest that there could be a place for LFTs as part of a comprehensive border management strategy. Although they are less sensitive than PCR tests, particularly in the early or late stages of infection (Dinnes et al., 2021), this can be compensated for by the fact that they can be used more frequently and provide results rapidly without the need for laboratory processing. For example, the model estimates that daily testing of arrivals with LFTs for 5 days provides a bigger risk reduction than a PCR test on days 0 and 4. Sensitivity analysis indicates that the magnitude of this advantage depends on factors such as individual heterogeneity in viral loads and the temporal correlation between infectiousness and likelihood of testing positive. Daily LFT testing combined with a PCR test on the last day could combine the benefits of regular testing in preventing transmission with the sensitivity of a PCR test for detecting cases that may have been missed by LFT. Trialling LFTs these alongside PCR tests in MIQ facilities and frontline border workers would allow for the collection of valuable real-world data to evaluate their sensitivity at different times relative to symptom onset.

We have assumed that vaccinated and non-vaccinated individuals, if infected, have the same probability of developing symptoms of COVID-19. If in reality vaccinated infected people may be less likely to develop symptoms, the effectiveness of post-arrival symptom checks and symptom-triggered testing in vaccinated travellers will be less than in the results shown here. However, this reduced effectiveness may be offset if likelihood of developing symptoms is correlated with infectiousness. Further work is needed to investigate this.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: This research was funded by a grant from the New Zealand Department of Prime Minister and Cabinet.

Handling editor: Dr HE DAIHAI HE

Appendix A. Supplementary data

The following are the Supplementary data to this article: