Abstract
We conducted a comparative study of the COVID-19 epidemic in three different settings: mainland China, the Guangdong province of China and South Korea, by formulating two disease transmission dynamics models which incorporate epidemic characteristics and setting-specific interventions, and fitting the models to multi-source data to identify initial and effective reproduction numbers and evaluate effectiveness of interventions. We estimated the initial basic reproduction number for South Korea, the Guangdong province and mainland China as 2.6 (95% confidence interval (CI): (2.5, 2.7)), 3.0 (95%CI: (2.6, 3.3)) and 3.8 (95%CI: (3.5,4.2)), respectively, given a serial interval with mean of 5 days with standard deviation of 3 days. We found that the effective reproduction number for the Guangdong province and mainland China has fallen below the threshold 1 since February 8th and 18th respectively, while the effective reproduction number for South Korea remains high until March 2nd Moreover our model-based analysis shows that the COVID-19 epidemics in South Korean is almost under control with the cumulative confirmed cases tending to be stable as of April 14th. Through sensitivity analysis, we show that a coherent and integrated approach with stringent public health interventions is the key to the success of containing the epidemic in China and especially its provinces outside its epicenter. In comparison, we find that the extremely high detection rate is the key factor determining the success in controlling the COVID-19 epidemics in South Korea. The experience of outbreak control in mainland China and South Korea should be a guiding reference for the rest of the world.
Keywords: COVID-19 epidemic, Multi-source data, Mathematical model, Mainland china and south korea, Comparative study
1. Introduction
Coronaviruses, enveloped viruses characterized by a single-stranded, positive-sense RNA, cause generally mild infections but occasionally lethal communicable disorders leading to the “Severe Acute Respiratory Syndrome” (SARS), the “Middle East Respiratory Syndrome” (MERS), and the current “Coronavirus 2019 Disease” (COVID-19) outbreak [1], [2], [3], [4], [5] that has gradually spread out from the initial epicenter of Wuhan (China) and affected more than 220 countries/territories and international conveyances including the cruise ship Diamond Princess harbored in Yokohama/Japan.
In the absence of effective treatments and vaccines, early adoption of stringent public health measures is crucial in mitigating the scale and burden of an outbreak. Unprecedented restrictive measures, including travel restrictions, contact tracing, quarantine, and lock-down of entire towns/cities adopted by the Chinese authorities have resulted in a significant reduction of the effective reproductive number of COVID-19 [6], [7]. However, these public health interventions have not been considered and/or implemented as effectively in other settings and contexts. Decision-making and implementations require, indeed, adaptations and modifications to take into account setting-specific characteristics in terms of community features, local epidemiology and risk assessment, social habits, juridical provisions, organizational coordination, and availability of economic-financial resources. For instance, particularly restrictive measures have been shown not to be effective in certain countries [8].
Several public health interventions can be implemented to counteract the threat posed by an emerging outbreak [9] with pandemic potential. These interventions can be basically classified into two major categories: the measures in the first category are aimed at protecting the borders and include interventions such as travel restrictions and border entry screening, whereas the measures in the second category have the objective of locally controlling the spreading of the virus and include enhanced epidemiological surveys and surveillance, contact tracing, school closure and other interventions that favor a reduction in the number of social contacts. The effectiveness of intervention measures is variable and, for some, is still under debate. Regarding, for example, extensive travel restrictions, a recent systematic review has shown that this intervention may contribute to delaying but not preventing the transmission and diffusion of a viral outbreak. As such, it is not recommended for implementation, if not within a broader package of public health measures aimed at rapidly containing the outbreak [10]. A similar conclusion can be reached for border entry screening, considered as ineffective or poorly effective per se, and therefore needs to be combined and provided together with other strategies [11]. School closure appears to be potentially effective in containing/reducing viral outbreaks, although further research is warranted to identify the best strategy in terms of timing and length of closure [12]. The measure of quarantine is also particularly controversial, since it raises ethical dilemmas, and political and social concerns [13], [14], and quantification of its real impact [13] is difficult due to high uncertainty in its efficacy. However, in the absence of effective medical interventions, for example, during the earlier stage of a pandemic, these measures must be implemented and the success of these measures, despite their disruptive impact on social-economic activities, depends heavily on how these measures are adapted to the specific scenario, in terms not only of clinical and epidemiological variables but also of social aspects, including social habits, juridical provisions, and economic-financial resources.
How differentiation and combination of these interventions within a coherent and systematic package of public health measures contribute to different outbreak outcomes is an urgent global health issue that must be addressed in order to ensure that lessons from countries that have early experienced COVID-19 outbreak can be learned by other countries in their preparedness and management of a likely pandemic.
Several mathematical models have been devised to predict the epidemiologic trend of the COVID-19 outbreak, including stochastic/mathematical (integer derivative [15], [16] or fractional-order [17], [18], [19]) models, mass-action, (spatial) structured metapopulation, agent-based networked, and other compartmentalized models [20], among others. According to a systematic survey of the literature, synthesizing 242 studies, 46.1% of studies used compartmental models, 31.8% statistical models (growth models and time series), 6.7%, 4.7%, 3.3%, 2.3% and 1.3% Artificial Intelligence-, Bayesian approach-, hybrid, network- and individual agent-based models, respectively [21].
In the present paper, we conducted a comparative study of the COVID-19 epidemic in three different settings: mainland China, the Guangdong province of China and South Korea.
In South Korea, the first COVID-19 case (a 36 year-old Chinese woman, with a recent travel history to Wuhan) was reported on January 8th 2020. A severe cluster of cases emerged in the city of Daegu, where on February 23rd 2020 a 61 years old woman spread the virus to hundreds of worshipers at Shincheonji Church of Jesus. On March 5th 2020, a further cluster of cases occurred at a nursing home in Gyeongsan, which has been declared a “special care zone” in an effort to contain the viral outbreak. As of March 8th 2020, South Korea has reported 7313 cases, with 130 total recovered cases and 50 deaths, with no sign that the epidemic was slowing down. As of June 8th 2021, a number of 164,028 total cases have been reported, with 2034 deaths and 151,923 total recovered cases. There were 1275 newly daily confirmed cases.
In comparison, intensive social contacts and massive mobility associated with the Chinese Traditional Spring Festival, combined with an initial delay in responding to the outbreak, resulted in exponential growth of infections in the (then) epicenter (Wuhan) and large case importations to other Chinese cities. On January 23rd 2020, the Chinese government decisively implemented a systematic package of measures in the epicenter, including the lock-down/quarantine of Wuhan city and other cities/towns of the Hubei province, intense contact tracing and isolation. This led to the rapid and effective mitigation of the COVID-19 epidemic. Case importation before the January 23rd lock-down also resulted in outbreaks in all Chinese provinces, but the systematic package of interventions implemented across the country led to an effective containment. On March 8th 2020, the newly confirmed cases in the entire country reduced to 40. As of June 8th 2021, a number of 91,966 total cases have been reported, with 4636 deaths and 86,883 total recovered cases. Newly daily confirmed cases were 17.
Particularly, Guangdong, the province with the largest population in China at present, with gross domestic product (GDP) ranked first since 1989 and with the level of middle- and upper-income countries and middle-developed countries, reported the first confirmed COVID-19 case on January 19th. On January 23rd, the government of Guangdong province announced the first-level response to major public health emergencies for controlling the spread of COVID-19. As of March 8th, there are a total of 1325 confirmed cases and 8 deaths in Guangdong province, and no new case is reported. In contrast to South Korea, there was a relatively large ratio of imported cases in Guangdong province, particularly, in Shenzhen (a megacity in Guangdong province) more than 70 percent of the confirmed cases are imported [22].
What differences in the intervention design and implementation between China and South Korea, and between South Korea and Guangdong have contributed to the different epidemic curves, and what projection can we make about the epidemic trend in South Korea under different scenarios if a portion or the entirety of the Chinese package of public health interventions is applied to South Korea? These are the questions we aim to answer by developing mathematical models tailored to different settings, including the entire country of China and its Guangdong province and South Korea.
The present paper is the fully peer-reviewed and final edited version of a draft initially submitted to the pre-print server of the World Health Organization, as mandated by the institution itself for rapid dissemination of COVID-19 related research during the pandemic to facilitate and assist quick implementation of public health policies in a data-driven and evidence-based way [1], [2].
2. Methods
2.1. Data
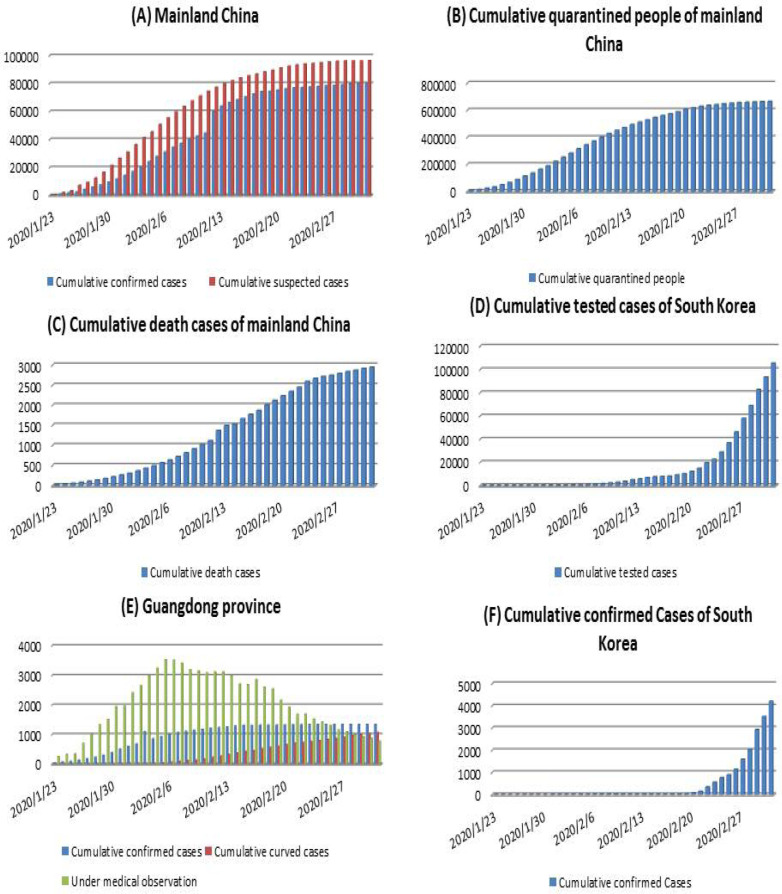
We obtained data of the confirmed COVID-19 cases, the cumulative number of quarantined individuals, cumulative death cases in mainland China from the “National Health Commission” of the People’s Republic of China [23]. Data information includes the newly reported cases, the cumulative number of reported confirmed cases, the cumulative number of cured/recovered cases and the number of death cases, as shown in Fig. 1(A–C). In addition, we obtained the data of the cumulative confirmed cases, cumulative cured cases and daily cases under medical observation for the Guangdong province (Fig. 1(E)) of China. We also obtained the data of cumulative confirmed cases and cumulative tested cases for South Korea from the Korea Centers for Disease Control and Prevention (KCDC) [24], [25], as shown in Fig. 1(D), and (F). The data were released and analyzed anonymously. Note that the first confirmed case was reported on January 23rd 2020 for South Korea, and also on January 23rd 2020 mainland China started the lock-down of Wuhan city, the epicenter, and implemented other interventions. Note that the data for reported cases, either confirmed or quarantined, or under medical observation or tested, was used in China or South Korea since January 23rd 2020.
Fig. 1.
The datasets related to the COVID-19 epidemics, including newly reported cases, cumulative number of reported cases, cumulative number of cured cases, cumulative number of death cases, cumulative quarantined cases and cumulative suspected cases for mainland China (A–C), the Guangdong province of China (E), and South Korea (F).
2.2. The model
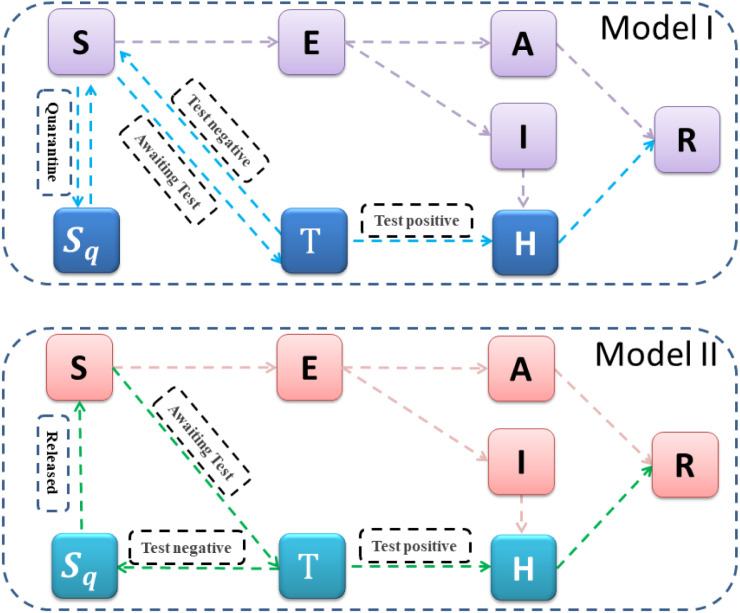
Our baseline model is the classical deterministic susceptible–exposed–infectious–removed(SEIR) epidemic model refined by incorporating contact tracing-quarantine-test-isolation strategies (Fig. 2). We stratify the population into susceptible , exposed (), symptomatic/asymptomatic infected (), hospitalized () and recovered () compartments, and we further stratify the population to include quarantined susceptible (), and quarantined suspected individuals (). These stratifications were used in our previous studies [6], [7], [26] and agreement of model predictions with real data provides a validation of the model structure reflecting the interventions implemented in Wuhan and in mainland China. Here, we add an additional quarantined suspected compartment, which consists of exposed infectious individuals resulting from contact tracing and individuals with common fever. These individuals with common fever but quarantined as COVID-19 suspected contributed to the difficulty of implementing an effective quarantine process due to the size of this compartment. In what follows, exposure, transmission and infection compartments are always used for modeling the COVID-19.
Fig. 2.
The illustration of the compartmental models incorporating important interventions and features of reporting systems, for mainland China (model I) including its Province of Guangdong, and for South Korea (model II).
In our model formulation, the transmission probability is denoted by and the contact rate is denoted by . By enforcing contact tracing, a proportion, , of individuals exposed is quarantined, and can either move to the compartment or with rate of (or ), depending on whether they are effectively infected or not [27], [28], while the other proportion, , consists of individuals exposed to the virus who are missed from contact tracing and move to the exposed compartment at rate of once effectively infected or stay in compartment otherwise. Note that contact tracing is not triggered by asymptomatic infected individuals, who can infect susceptible individuals. We use constant m to denote the transition rate from the susceptible compartment to the (COVID-19) suspected compartment due to fever and/or illness-like symptoms. The suspected individuals leave this compartment at a rate , with a proportion, f, if confirmed to be infected with COVID-19, going to the hospitalized compartment, whilst the other proportion, , is ruled out for COVID-19 infection and goes back to the susceptible compartment. Then, for mainland China, the model equations are as follows.
| (C1) |
where is the total population which is the sum of the populations of all the compartments. Keeping the time-dependent parameters in model (C1) as constants and using the next generation matrix method introduced in the studies [29], [30], we can calculate the basic reproduction number of model (C1) as follows:
here, , and . Then, substituting all the time-dependent parameters/variables into the formula of the basic reproduction number, we can obtain the effective reproduction number of model (C1), which is given by:
As the total population is very large, we can assume that , thus the effective reproduction number is reduced to
| (C2) |
In epidemiology, the basic reproduction number (R0), used to measure the transmission potential of a disease, is the average number of secondary infections produced by a typical case of an infection in a population where everyone is susceptible. Once the intervention implemented results effective, the effective transmission potential is measured by the effective reproductive number that can be time-dependent as intervention measures vary over time. If falls below 1 and remains below 1, there will be a decline in the number of cases.
The prevention and control interventions were gradually improved in mainland China, and there are several key time points when mitigation measures were gradually strengthened: (1) On January 23rd Wuhan was locked down, and most parts of China shortly adopted a similar strategy; (2) On January 26th, the government announced to extend the Chinese Traditional New Year Festival holiday so self-isolation/protection was maximized; (3) On February 7th the Chinese government created the partnership between each one of the 16 provinces to its sister-city in the epicenter, the Hubei province, to reinforce the health care workers and equipment in the sister-city in Hubei; (4) On February 12th the Hubei province started to include the clinically diagnosed cases into the confirmed cases to enhance its quarantine/isolation measure; (5) On February 14th, Wuhan refined its management protocol of residential quarters; (6) On February 16th, the National Health Commission of the People’s Republic of China revised its New Coronavirus Pneumonia Prevention and Control Plan to further clarify and enhance the public health interventions in four key areas: Quarantine high-risk individuals as much as possible, Test suspected individuals as much as possible;Treat patients as best as possible;and Receive and cure all the patients.
Corresponding to the package of gradually improved prevention and control interventions carried out by the governments, the parameters related to the interventions should be time-varying, i.e., functions of time . More in detail, as effect of the implementation of lockdown and limiting the population movement since January 23rd, the contact rate should be a decreasing function of time ; because of the enhanced close contact tracing and quarantine, the quarantine rate should be an increasing function of time ; since the improve testing capacity, the diagnosis rate should be an increasing function of time , correspondingly, the diagnosis period decreases over time. Here, we assume that all of the three rates are changing exponentially at the initial stage, then gradually slow down their speed and approach to a maximum/limit rate. Based on the above assumptions, the time-dependent contact rate , quarantined rate , and detection rate can be defined as follows:
| (C3) |
where denotes the initial contact rate (on January 23rd 2020) with , denotes the minimal contact rate with the intervention being implemented. Constant is the initial quarantined rate of exposed individuals with , is the maximum quarantined rate with . Similarly, constant is the initial diagnosis rate, is the fastest diagnose rate with .
For the Guangdong province, the recovery rate has been improved over the time, and this is reflected by the time- dependence of the recovery rate of the quarantined infected (isolated) population, given by
| (C4) |
with being the initial recovery rate and the fastest recovery rate, and the corresponding increasing rate of the recovery rate.
For South Korea, a similar contact tracing strategy has been implemented: all traced individuals are quarantined and are tested. Once tested, the suspected individuals leave the compartment at a rate , with a proportion, f, if confirmed to be COVID-19 infected, going to the hospitalized compartment, whilst the remaining proportion, , is recommended to remain quarantined and hence goes to the compartment [29], [30]. The transmission dynamics subject to this intervention practice is given by
| (K1) |
where has the same formula in Eq. (C3) while the other parameters are positive constants. Using a similar method for calculating the effective reproduction number as used for model (C1), we can obtain the effective reproduction number of model (K1), which is given by
| (K2) |
3. Model fitting process
When carrying out the parameter estimations, we first informed several parameters in model (C1) and model (K1) with fixed values retrieved from the scholarly literature. These include the transition rate of exposed individuals to the infected class , the rate at which the quarantined uninfected contacts were released into the wider community , and the recovery rate of the asymptomatic infections , as shown in Table 1. In addition, the initial values of suspected population, quarantined infected population, quarantined susceptible population, and recovered population are obtained from official statistical reports, epidemiological surveys and databases mentioned in the data section (Table 1). We used the least square (LS) method with a priori interval for each parameter to fit the proposed models to the data, where the objective function is the residual sum of squares between the real data and the predicted number by solving model (C1)/model (K1). The built-in function “ODE45” in Matlab is used to solve the ODE systems while the “fmincon” function is used to search for the optimal solutions of the objective functions. We generated 1000 time series of the cumulative cases, death cases and tested cases following a Poisson distribution with mean given by the real data, and fitted the models to each set. Consequently, we obtained the estimated mean values of the parameters, as listed in Table 1.
Table 1.
Parameter estimates for the COVID-19 epidemic in China, Guangdong Province of China and Korea.
| Parameter | Definitions | Estimated values |
Source | |||
|---|---|---|---|---|---|---|
| Guangdong | China | Korea | ||||
| Contact rate at the initial time | (Est) | 14.78 | 21.9 (Est) | [4] | ||
| Minimum contact rate under the current control strategies | 4.00 | 7.78 | 2.01 | Estimated | ||
| Exponential decreasing rate of contact rate | 0.01 | 2 | 0.1312 | Estimated | ||
| Probability of transmission per contact | 0.13 | 0.143 | 0.143 (F) | Estimated | ||
| Modification factor of the transmission probability of asymptotical infected individual | 0.02 | 0.0437 | 0.1758 | Estimated | ||
| Quarantined rate of exposed individuals at the initial time | 0.28 | – | Estimated | |||
| Maximum quarantined rate of exposed individuals under the current control strategies | 0.99 | 0.8 | – | Estimated | ||
| Exponential increasing rate of quarantined rate of exposed individuals | 0.0361 | 0.15 | – | Estimated | ||
| Constant quarantined rate | – | – | 02215 | Estimated | ||
| Transition rate of susceptible individuals to the suspected class | Estimated | |||||
| Detection rate of the suspected class | 0.0891 | 0.20 | 0.4004 | Estimated | ||
| Confirmation ratio: Transition rate of exposed individuals in the suspected class to the quarantined infected class | 0.01 | 0.50 | 0.001 | Estimated | ||
| Ratio of symptomatic infection | 0.5 | 0.4022 | 0.9409 | Estimated | ||
| Transition rate of exposed individuals to the infected class | [24] | |||||
| Rate at which the quarantined uninfected contacts were released into the wider community | [4] | |||||
| Initial transition rate of symptomatic infected individuals to the quarantined infected class | 0.12 (Est) | 0.1326 | – | [4] | ||
| Fastest diagnosis rate | 0.50 | 0.50 | – | Estimated | ||
| Exponential decreasing rate of diagnosis rate | 0.2410 | 0.10 | – | Estimated | ||
| Constant transition rate of symptomatic infected individuals to the quarantined infected class | – | – | 0.651 | Estimated | ||
| Recovery rate of asymptotic infected individuals | 0.1397 | 0.1397 | 0.1397 | [4] | ||
| Recovery rate of quarantined infected individuals at initial time | 0.001 | – | – | Estimated | ||
| Fastest recovery rate of quarantined infected individual | 0.2283 | – | – | Estimated | ||
| Exponential increasing rate of recovery rate of quarantined infected individuals | 0.01 | – | – | Estimated | ||
| Constant recovery rate of quarantined infected individuals | – | 0.2 | 0.2 (F) | Estimated | ||
| Disease-induced death rate | 0 (Assumed) | 0.0076 | 0.0076 (F) | Estimated | ||
| Initial values | Definitions | Estimated values |
Source | |||
| Guangdong | China | Korea | ||||
| Initial susceptible population | Estimated | |||||
| Initial exposed population | 250 | 204 | Estimated | |||
| Initial infected population | 378 | 108 | Estimated | |||
| Initial asymptotical population | 100 | 395 | Estimated | |||
| Initial suspected population | 258 | 1072 | 11 (Est) | Data | ||
| Initial quarantined susceptible population | 21 (Est) | 7347 | 7123 | Data | ||
| Initial quarantined infected population | 53 | 771 | 21 | Data | ||
| Initial recovered population | 2 | 34 | 9 | Data | ||
Note that, ‘Est’ means that the parameter values are estimated by fitting the models to the data when the source column indicates that they are not. ‘F’ means that the parameter values are fixed as the same as those estimated by fitting the proposed model to the multiple source data of China.
3.1. Model-free estimation for and
We employed the method developed by White and Pagano [31] to estimate the basic reproduction number . Let be the number of newly reported cases on day . Assume follows the Poisson distribution with a mean of , where is the probability, giving the serial interval distribution. Assume also that and are independent as long as . Given the distribution of the serial interval and the observed data on , the basic reproduction number can be estimated by the maximum likelihood estimates approach.
With the same notations and assumptions described above, we can also estimate the effective reproduction number following Cori et al. [32]. Namely, using within the Bayesian framework, we can obtain an analytical expression of the posterior distribution of by assuming a gamma prior distribution for . Then we can get the posterior means and confidence intervals of .
4. Main results
4.1. Model-free estimation for and
By using the number of daily newly reported cases from January 10th to January 23rd 2020, we estimate for mainland China, and using the newly reported cases from January 19th to January 31st 2020 we estimate for the Guangdong province. Also, we estimate for South Korea based on the number of daily newly reported cases from January 23rd to March 2nd 2020.
All the estimates are given in Table 2. In particular, given the serial interval with mean of 5 and standard deviation of 3, for mainland China, the Guangdong Province and South Korea is estimated to be 3.8 (95%CI: (3.5, 4.2)), 3.0 (95%CI: (2.6, 3.3)) and 2.6 (95%CI: (2.5, 2.7)), respectively. In particular, the initial COVID-19 reproduction rate in South Korea was smaller than that in the Guangdong Province.
Table 2.
Estimated basic reproduction number for mainland China, Guangdong province of China, Korea for various serial intervals.
| Std = 3 | E = 4 | E = 5 | E = 6 | E = 7 | E = 8 |
| Mainland China | 2.9 (2.6, 3.2) | 3.8 (3.5, 4.2) | 5.4 (4.9, 6.0) | 7.8 (7.1, 8.6) | 11.1 (10.0, 12.2) |
| Guangdong | 2.4 (2.1, 2.7) | 3.0 (2.6, 3.3) | 3.8 (3.4, 4.3) | 5.1 (4.5, 5.8) | 6.9 (6.1, 7.8) |
| South Korea | 2.1 (2.0, 2.2) | 2.6 (2.5, 2.7) | 3.4 (3.2, 3.5) | 4.5 (4.3, 4.7) | 6.0 (5.7, 6.3) |
| Std = 4 | E = 4 | E = 5 | E = 6 | E = 7 | E = 8 |
| Mainland China | 2.8 (2.5, 3.1) | 3.4 (3.1, 3.7) | 4.4 (4.0, 4.9) | 6.0 (5.4, 6.6) | 8.4 (7.6, 9.2) |
| Guangdong | 2.4 (2.1, 2.7) | 2.8 (2.5, 3.1) | 3.4 (3.0, 3.9) | 4.4 (3.9, 4.9) | 5.8 (5.1, 6.5) |
| South Korea | 2.1 (2.0, 2.1) | 2.4 (2.3, 2.5) | 3.0 (2.8, 3.1) | 3.8 (3.7, 4.0) | 5.0 (4.8, 5.3) |
| Std = 5 | E = 4 | E = 5 | E = 6 | E = 7 | E = 8 |
| Mainland China | 2.8 (2.5, 3.1) | 3.2 (2.9, 3.5) | 3.9 (3.5, 4.3) | 4.9 (4.5, 5.6) | 6.6 (5.9, 7.2) |
| Guangdong | 2.4 (2.1, 2.7) | 2.7 (2.4, 3.0) | 3.2 (2.8, 3.6) | 3.9 (3.4, 4.3) | 4.9 (4.3, 5.5) |
| South Korea | 2.1 (2.0, 2.2) | 2.3 (2.2, 2.4) | 2.7 (2.6, 2.9) | 3.4 (3.2, 3.5) | 4.3 (4.1, 4.4) |
E: mean of serial interval, Std: standard deviation of serial interval.
In order to investigate the variation of with respect to the serial interval, we carry out a sensitivity analysis by changing the mean of the serial interval from 4 to 8 days, the standard deviation (Std) from 3 to 5. The sensitivity analysis is reported in Table 2, and we notice that increases when the mean of the serial interval increases, and we remark that serial interval examined by recent studies is shorter than that earlier estimation [33], [34], [35]. It also follows from Table 2 that increasing Std of the serial interval only slightly decreases the estimated for a given mean of the serial interval.
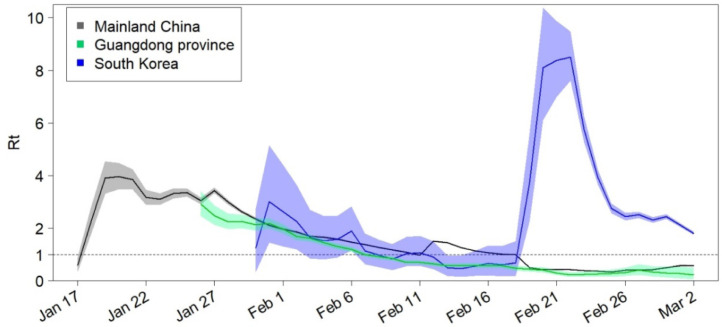
We also estimate the effective reproduction numbers for the considered regions, using the number of daily newly reported cases from the date the first case was reported until March 2nd 2020 (Fig. 3). It shows that the effective reproduction number in mainland China and in its Guandong province has fallen below the threshold 1 since February 18th and February 7th, while the effective reproduction number of South Korea remains very high, indicating that there is still room for improving the interventions in South Korea.
Fig. 3.
Estimated effective reproduction number over sliding weekly windows for the entire country of China, the Guangdong province of China, and Korea. The solid lines show the posterior means and the colored zones show the 95% confidence intervals; the horizontal dashed line indicates .(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
5. Model-based prediction and interventions efficacy evaluation
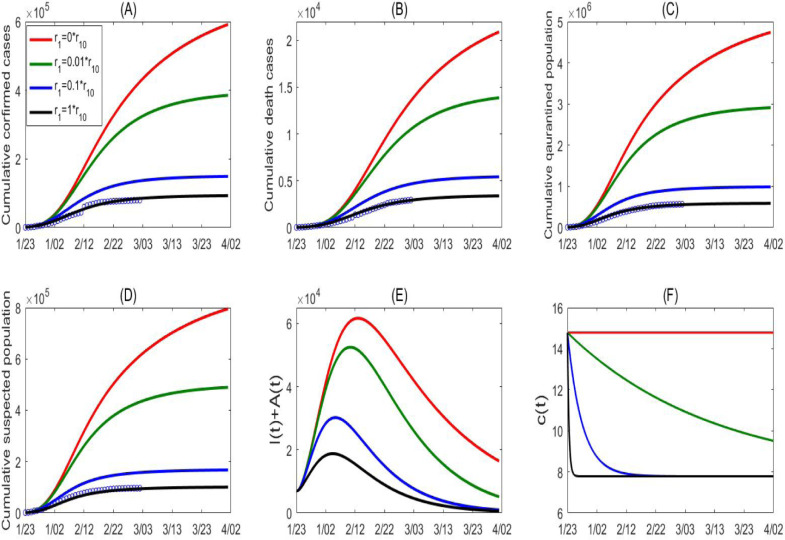
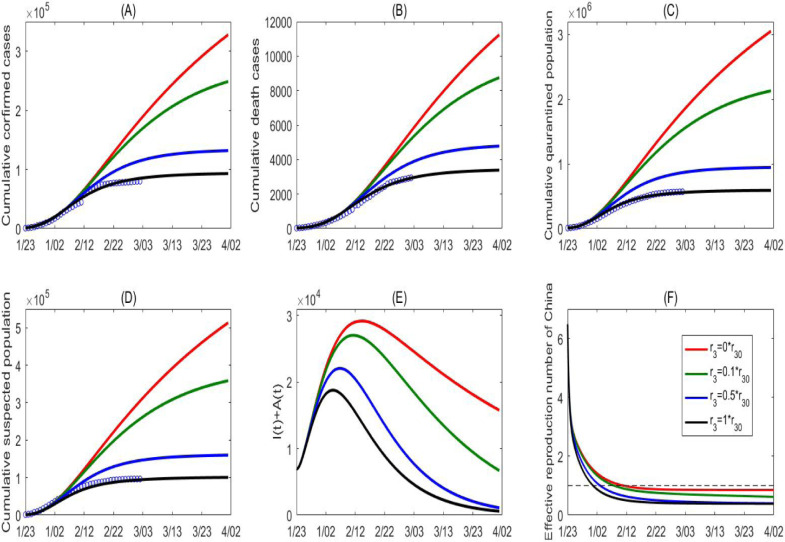
By simultaneously fitting the model (C1) to the multiple source data on the cumulative number of reported cases, deaths, quarantined and suspected cases in mainland China, we obtain estimations for unknown parameters and initial conditions, listed in Table 1. The best fitting result is shown as black curves in Fig. 4 with the estimated baseline exponential decreasing rate () in the contact rate function. We then conduct a sensitivity analysis of the cumulative reported, death, quarantined, suspected cases, and the infected (asymptomatic/symptomatic) individuals by shrinking the exponential index , representing the weakening of the control interventions relevant to the contact rate. As shown in Fig. 6, the numbers of cumulative reported, death, quarantined, suspected cases, and the peak value of the infected all increase significantly. In particular, with corresponding to no reduction of the contact rate from the initial period, the number of cumulative confirmed cases increases by more than six times as of April 1st (600,000 cases) and the peak value of the infected will increase by more than 3 times, in comparison with the actual situation under the strong control measures implemented by the Chinese government.
Fig. 4.
Model fitting results (curves marked as black) and variations in cumulative number of reported cases (A), death cases (B), quarantined cases (C) and suspected cases (D) for mainland China. (E) Variation in number of infected (asymptomatic/symptomatic) individuals with contact rate function . (F) Here the contact rate function is changed by varying the exponential decreasing rate , representing the variation in intensity of control measures. denotes the estimated baseline value of .
Fig. 6.
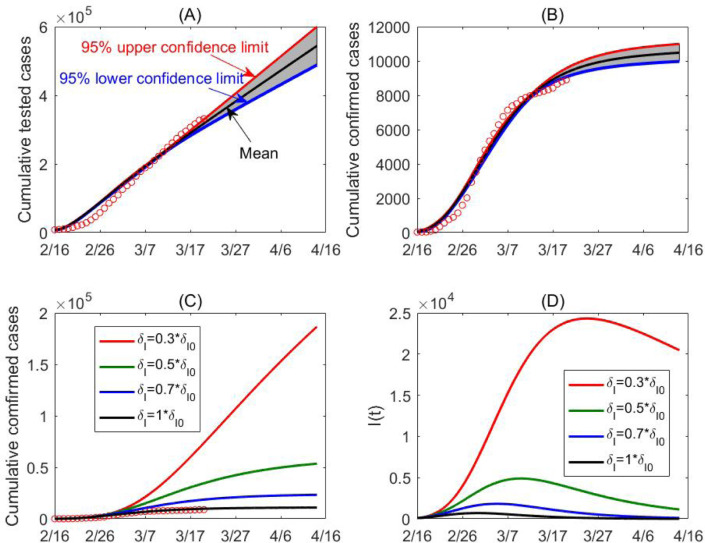
(A–B) Model fitting results and the impact of the randomness of the data set including the cumulative number of tested cases and the cumulative number of reported cases on the COVID-19 epidemic in Korea. The 95% confidence intervals have been given and the mean curve is marked as black. The red cycles denote the real data. (C–D) Sensitivity analysis. The impact of the diagnose rate on the cumulative confirmed cases and the infected populations in South Korea. Here, denotes the estimated baseline value of the diagnose rate.. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
We also conduct a sensitivity analysis regarding the detection rate , by decreasing the value of . We obtain a similar conclusion that the cumulative confirmed cases would reach the number of 350,000 cases as of April 1st with a constant detection rate (no improvement of detection), shown in Fig. 6. As illustrated in Fig. 6(F), we can observe that while decreasing the detection rate would not affect the decreasing trend of the effective reproduction number, it however postpones the time when the threshold value of 1 is reached. Therefore, the outcome in the mainland China, both in terms of the infections avoided and the timing when the outbreak begins to be under control, is the consequence of a systematic package of social distancing (self-isolation and self-protection), contacting tracing, and detection/diagnosis.
Similarly, by simultaneously fitting the proposed model (K1) to the cumulative number of reported and tested cases for South Korea, we obtain the estimations for the unknown parameters and initial conditions, listed in Table 1. The best fitting result is shown as black curves in Fig. 7. Comparing the estimated values of the detection rate in China and South Korea, we find an important difference that the diagnosis rate in South Korea (a constant value of 0.651) is much higher than that in China, being even higher than the maximal diagnosis rate in China. This is in line with the real control interventions adopted by the Korean government, that is to say, the government has actively coordinated the production of testing kits of COVID-19, consequently, the testing kits have been always available, even during the peak period of the epidemic. Apparently, as shown in Fig. 7(A–B), the COVID-19 epidemics in Korea will be almost under control as of April 14th with the confirmed cases tending to be stable. In order to test whether the extremely high detection rate is the key factor determining the success in controlling the COVID-19 in South Korea, we plotted the cumulative confirmed cases and the infectious population by decreasing the detection rate by 70%, 50% and 30%, respectively, as shown in Fig. 7(C–D). It follows from Fig. 7(C) that the number of the cumulative reported cases can reach 186,000 as of April 14th if the detection rate decreases by 70 percent (the red curve), which is around 17 times the predicted number of the best fitting result (the black curve). Furthermore, from Fig. 7(D), we find that the peak value of the infectious population can increase significantly as well (around 30 times) if the detection rate is decreased by 70%, while the peak time is postponed a lot with a lower detection rate of the infectious individuals.
Fig. 7.
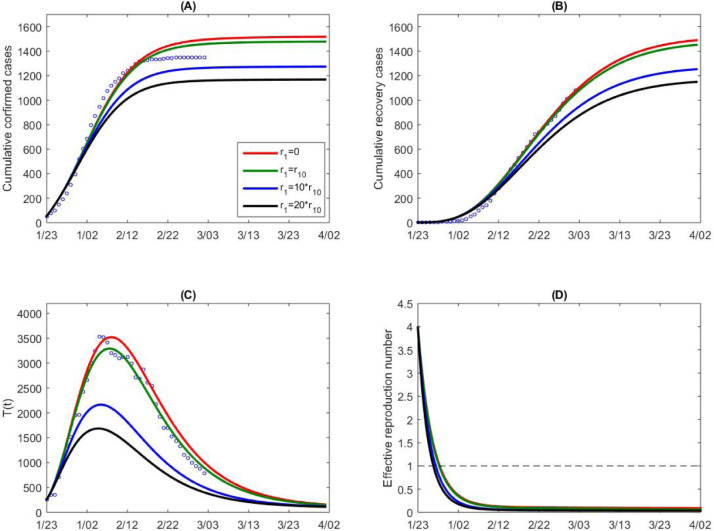
Model fitting results (curves marked as green) and variations in cumulative number of reported cases (A), recovery cases (B), and suspected cases (C) for Guangdong province. (D) Variation in the effective reproduction number with parameter in contact rate function . Here the contact rate function is changed by varying the exponential decreasing rate , representing the variation in intensity of control measures. denotes the estimated baseline value for parameter .. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
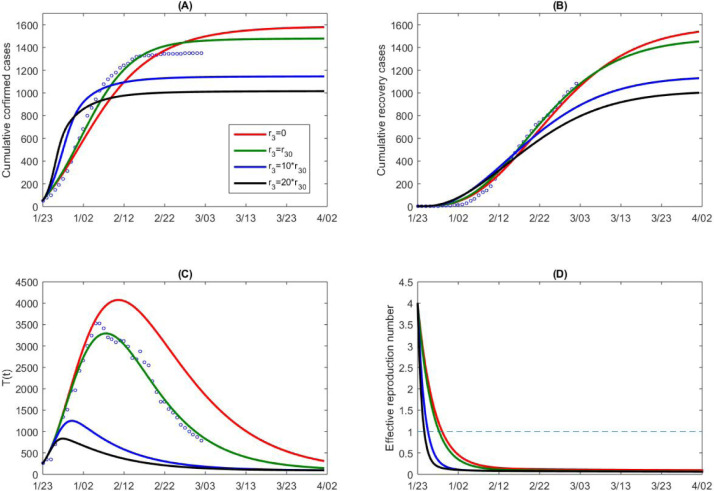
Further, by simultaneously fitting the model (C1) to the multiple source data on the cumulative number of reported cases, recovery and suspected cases of Guangdong province, we parameterize the model and obtain the estimations for the unknown parameters and initial conditions, listed in Table 1. The best fitting result is shown as green curves in Fig. 8. Similarly, we consider the variation in the epidemic by means of the parameter , representing the variation in the intensity of the control measures implemented. It follows from Fig. 8(A–C) that increasing the parameter reduces the disease infections and the number of suspected individuals, while decreasing the parameter (to zero) slightly affects the disease infections, shown in green curves () and red curves () in Fig. 8(A–C). This conversely implies that the prevention and control strategies in Guangdong province were relatively strong from the early stage of the outbreak. This can also be confirmed by the continuously declining trend of the effective reproduction number, as shown in Fig. 3, Fig. 8(D). Again, we performed the sensitivity analysis by decreasing the value of in the detection rate and obtained similar results, as shown in Fig. 8.
Fig. 8.
Goodness of fit (green curves) and variations in cumulative number of reported cases (A), recovery cases (B), and suspected cases (C) for Guangdong province. (D) Variation in the effective reproduction number with parameter in detection rate function . Here the detection rate function is changed by varying the exponential decreasing rate , representing the variation in intensity of control measures. denotes the estimated baseline value of .. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
6. Discussion
After some initial delay in the response to the COVID-19 outbreak, the Chinese government started implementing drastic public health measures on January 23rd 2020, including the lock-down of Wuhan city, contact tracing, quarantine, and isolation. This decisive and systematically implemented package of interventions has contributed to rapid mitigation, providing a window of opportunity for the preparedness, prevention and control of COVID-19 in other Chinese cities and around the world. As we showed in this modeling study, a systematic approach incorporating coherent and complementary public health measures rapidly implemented is the key for containing the viral outbreak.
In this study, we formulated a dynamic model and parameterized it by using multi-source data for the different settings within South Korea, China and Guangdong province. We predicted that the trend of cumulative reported cases would be very serious, reaching around 600 thousand as of April 1st 2020 given no control measures being implemented (Fig. 5(A)). Hence a comparison with the current COVID-19 epidemic: the cumulative reported cases are around 80,651 as of March 6th, 2020, supporting the efficacy of the ongoing strengthening of prevention and control measures implemented in mainland China.
Fig. 5.
Model fitting results (curves marked as black) and variations in cumulative number of reported cases (A), cumulative number of death cases (B), quarantined cases (C) and suspected cases (D) for mainland China. (E) Variation in number of infected (asymptomatic/symptomatic) individuals with detection rate function . (F) Variation in the effective reproduction number of China. Here the detection rate function is changed by varying the exponential decreasing rate , representing the variation in intensity of control measures. denotes the estimated baseline value of .
In Guangdong, the province with the largest population in China, most cases at the initial phase of the COVID-19 outbreak are imported, and immediately after the lockdown of Wuhan on January 23rd 2020, the province implemented a systematic approach towards prevention and control, with gradual enhancement, leading to the effective control of otherwise potentially catastrophic outcomes.
In comparison with South Korea, Guangdong has more inhabitants and a less developed economy. Also, from our model-free estimation, the basic reproduction number in South Korea is less than that computed for the Guangdong province. Therefore, the COVID-19 epidemic potential in South Korea was initially weaker than that in Guangdong. Our model-based analysis shows that the COVID-19 epidemics in South Korea is almost under control because of the high detection rate of the infectious individuals. Our simulation results indicate that the COVID-19 epidemic in South Korea will change from a slow to a quick increase in terms of the cumulative number of the confirmed cases and the infected population if the detection rate is decreased, as shown in Fig. 7(C–D). This indicates that the high detection rate is actually the key of the success in controlling the epidemics in South Korea. It is worth to mention that we assumed in our model that all the confirmed cases are isolated in the hospital, hence cannot infect other populations, which should be also a very important factor determining the success in controlling the COVID-19 epidemics. In other words, with the high detection rate, receiving and curing the patients as much as possible, instead of just asking the patients staying at home, is also important.
More in detail, a comparison of the parameter estimations of the Guangdong province and the entire country of China shows that
(1) the initial and maximum quarantine rates in Guangdong were much higher than those in the entire country China, while the initial and minimum contact rates were lower than those in the country, contributing to the observed better control effect in the province than the national average.
(2) the confirmation ratios of the Guangdong province and South Korea were much lower than the ratio of the entire country China, indicating the increased efficiency of contact tracing and testing in the Guangdong province and South Korea than that in the entire country of China.
Carrying out the sensitivity analysis of confirmed cases of China and Guangdong province with respect to the contact rate function, and further with respect to the detection rate of South Korea is in support of the effectiveness of the control measures implemented in other countries. Other countries or territories experiencing large-scale outbreaks of COVID-19 should capitalize on this lesson: convincing all the citizens to stay at home by self-isolation and becoming aware of the implications of self-protection is of crucial importance, but not enough. Improving the diagnosis rate of the infectious individuals and hospitalizing all the patients instead of staying at home have been fundamental for controlling the spreading of COVID-19 epidemic.
We note that future works may aim to address items of major public health concern such as: based on how a given regional epidemic situation is evolving, inform the decision-making for switching of intervention tactics and control measures. For instance, at which point does a country/territory make the decision to switch from tactics based on strict contact tracing to those based on travel restriction and mass quarantine? While contact tracing may be effective in controlling an outbreak with few initial cases, strong response efforts, and low pathogen transmissibility, this effectiveness may fade as cases accumulate [36]. In other words, the effectiveness of control measures may be dependent on the time and epidemic state at which they are implemented; therefore, switching tactics based on the local epidemic evolution may be optimal for regional and hence global control.
Through the parametrization and simulation of disease transmission models with intervention mechanisms and informed with multiple data sources, regional demographics, and regional intervention features, our work provides a foundational framework for the intervention evaluation and intervention scenario analysis. This study highlights the opportunity for evaluation of control measures and the learning from select regions to inform the future decision-making for the preparedness, real-time management as well as risk assessment of COVID-19.
It should be mentioned that several studies have provided evidence of pre-symptomatic transmission of COVID-19 [36], [37]. As reported in the study conducted by Subramanian et al. [38], ignoring pre-symptomatic transmission may lead to the underestimation of the basic reproduction number. Not accounting for the infectivity of the exposed class is a limitation of our model, which warrants future studies.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Tang B, Xia F, Bragazzi NL, McCarthy Z, Wang X, He S et al. Lessons drawn from China and South Korea for managing COVID-19 epidemic: Insights from a comparative modeling study [Preprint]. Bull World Health Organ, 2020. [DOI] [PMC free article] [PubMed]
- 2.Tang B., Xia F., Bragazzi NL., Wang X., He S., Sun X., et al. 2020. Lessons drawn from China and South Korea for managing COVID-19 epidemic: Insights from a comparative modeling study. medRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fehr AR., Perlman S. Coronaviruses: An overview of their replication and pathogenesis. Methods Mol Biol. 2015;1282:1–23. doi: 10.1007/978-1-4939-2438-7_1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lu H., Stratton CW., Tang YW. The Wuhan SARS-CoV-2 - What’s next for China. J Med Virol. 2020;92(6):546–547. doi: 10.1002/jmv.25738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rothan HA., Byrareddy SN. The epidemiology and pathogenesis of Coronavirus disease (COVID-19) outbreak. J Autoimmun. 2020 doi: 10.1016/j.jaut.2020.102433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tang B., Wang X., Li Q., Bragazzi NL., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019-ncov and its implication for public health interventions. J Clin Med. 2020;9(2):E462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tang B., Bragazzi NL., Li Q., Tang S., Xiao Y., Wu J. An updated estimation of the risk of transmission of the novel Coronavirus (2019-nCov) Infect Dis Model. 2020;5:248–255. doi: 10.1016/j.idm.2020.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cuijpers P., de Graaf I., Bohlmeijer E. Adapting and disseminating effective public health interventions in another country: Towards a systematic approach. Eur J Pub Health. 2005;15(2):166–169. doi: 10.1093/eurpub/cki124. [DOI] [PubMed] [Google Scholar]
- 9.Zhang L., Liu Y. Potential interventions for novel coronavirus in China: A systematic review. J Med Virol. 2020;92(5):479–490. doi: 10.1002/jmv.25707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mateus AL., Otete HE., Beck CR., Dolan GP., Nguyen-Van-Tam JS. Effectiveness of travel restrictions in the rapid containment of human influenza: A systematic review. Bull World Health Organ. 2014;92(12):868–880. doi: 10.2471/BLT.14.135590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mouchtouri VA., Christoforidou EP., An der Heiden M., Menel Lemos C., Fanos M., Rexroth U., Grote U., Belfroid E., Swaan C., Hadjichristodoulou C. Exit and entry screening practices for infectious diseases among travelers at points of entry: Looking for evidence on public health impact. Int J Environ Res Public Health. 2019;16(23):4638. doi: 10.3390/ijerph16234638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jackson C., Vynnycky E., Hawker J., Olowokure B., Mangtani P. School closures and influenza: Systematic review of epidemiological studies. BMJ Open. 2013;3(2) doi: 10.1136/bmjopen-2012-002149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bensimon CM., Upshur RE. Evidence and effectiveness in decision making for quarantine. Am J Public Health. 2007;97(Suppl 1):S44–S48. doi: 10.2105/AJPH.2005.077305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tognotti E. Lessons from the history of quarantine, from plague to influenza A. Emerg Infect Diseases. 2013;19(2):254–259. doi: 10.3201/eid1902.120312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nabi KN., Abboubakar H., Kumar P. Forecasting of COVID-19 pandemic: From integer derivatives to fractional derivatives. Chaos Solitons Fractals. 2020;141 doi: 10.1016/j.chaos.2020.110283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kumar P., Erturk VS., Abboubakar H., Nisar KS. Prediction studies of the epidemic peak of Coronavirus disease in Brazil via new generalised Caputo type fractional derivatives. Alex Eng J. 2021;60(3):3189–3204. [Google Scholar]
- 17.Rajagopal K., Hasanzadeh N., Parastesh F., Hamarash II., Jafari S., Hussain I. A fractional-order model for the novel Coronavirus (COVID-19) outbreak. Nonlinear Dyn. 2020:1–8. doi: 10.1007/s11071-020-05757-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mohammad M., Trounev A. On the dynamical modeling of COVID-19 involving Atangana-Baleanu fractional derivative and based on Daubechies framelet simulations. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Naik PA., Yavuz M., Qureshi S., Zu J., Townley S. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur Phys J Plus. 2020;135(10):795. doi: 10.1140/epjp/s13360-020-00819-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Adiga A., Dubhashi D., Lewis B., Marathe M., Venkatramanan S., Vullikanti A. Mathematical models for COVID-19 pandemic: A comparative analysis. J Indian Inst Sci. 2020:1–15. doi: 10.1007/s41745-020-00200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gnanvi JE., Salako KV., Kotanmi GB., Glèlè Kakaï R. On the reliability of predictions on covid-19 dynamics: A systematic and critical review of modelling techniques. Infect Dis Model. 2021;6:258–272. doi: 10.1016/j.idm.2020.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.2020. Health commission of Guangdong province. Available online: http://wsjkw.gd.gov.cn/. [Accessed 8 March 2020] [Google Scholar]
- 23.2020. National health commission of the people’s republic of China. http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml [Accessed 8 2020] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.2020. Korea centers for diseases control and prevention (KCDC) https://www.cdc.go.kr/board/board.es?mid=a30402000000&bid=0030 [Accessed 6 March 2020] [Google Scholar]
- 25.2020. Korea centers for disease control and prevention (KCDC) http://www.cdc.go.kr/board.es?mid=a20507020000&bid=0019&act=view&list_no=366481 [Accessed on 8 March 2020] [Google Scholar]
- 26.Tang S., Tang B., Bragazzi NL., Xia F., Li T., He S., et al. Analysis of COVID-19 epidemic traced data and stochastic discrete transmission dynamic model. Sci Sin Math. 2020;50:1–16. [Google Scholar]
- 27.van den Driessche P. Reproduction numbers of infectious disease models. Infect Dis Model. 2017;2(3):288–303. doi: 10.1016/j.idm.2017.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 29.Castillo-Chavez C., Castillo-Garsow CW., Yakubu A. Mathematical models of isolation and quarantine. JAMA. 2003;290:2876–2877. doi: 10.1001/jama.290.21.2876. [DOI] [PubMed] [Google Scholar]
- 30.Keeling MJ., Rohnai P. Princeton University Press; 2008. Modeling infectious diseases in humans and animals; pp. 313–320. [Google Scholar]
- 31.White LF., Pagano M. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Stat Med. 2008;27(16):2999–3016. doi: 10.1002/sim.3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cori A., Ferguson NM., Fraser C., Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. 2013;178(9):1505–1512. doi: 10.1093/aje/kwt133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Special Expert Group for Control of the Epidemic of Novel Coronavirus Pneumonia of the Chinese Preventive Medicine Association, The Chinese Preventive Medicine Association An update on the epidemiological characteristics of novel Coronavirus pneumonia (COVID-19) Chin J Epidemiol. 2020;41:139–144. doi: 10.3760/cma.j.issn.0254-6450.2020.02.002. [DOI] [PubMed] [Google Scholar]
- 34.Du Z., Xu X., Wu Y., Wang L., Cowling BJ., Meyers LA. The serial interval of COVID-19 from publicly reported confirmed cases. Emerg Infect Diseases. 2020;26(6):1341–1343. doi: 10.3201/eid2606.200357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nishiura H., Linton NM., Akhmetzhanov AR. Serial interval of novel Coronavirus (COVID-19) infections. Int J Infect Dis. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gatto M., Bertuzzo E., Mari L., Miccoli S., Carraro L., Casagrandi R., et al. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc Natl Acad Sci USA. 2020;117(19):10484–10491. doi: 10.1073/pnas.2004978117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tindale LC., Stockdale JE., Coombe M., Garlock ES., Lau WYV., Saraswat M., et al. Evidence for transmission of COVID-19 prior to symptom onset. eLife. 2020;9:e57149. doi: 10.7554/eLife.57149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Subramanian R., He Q., Pascual M. Quantifying asymptomatic infection and transmission of COVID-19 in New York city using observed cases, serology, and testing capacity. Proc Natl Acad Sci USA. 2021;118(9) doi: 10.1073/pnas.2019716118. [DOI] [PMC free article] [PubMed] [Google Scholar]