The effect of simulation strategies on prediction of power deposition in the tissue around electronic implants during magnetic resonance imaging

Abstract

Numerical simulations are increasingly employed in safety assessment of high-field magnetic resonance imaging (MRI) in patients with conductive medical implants such as those with deep brain stimulation (DBS) devices. Performing numerical simulations with realistic patient models and implant geometry is the preferred method as it provides the most accurate results; however, in many cases such an approach is infeasible due to limitation of computational resources. The difficulties in reconstructing realistic patient and device models and obtaining accurate electrical properties of tissue have compelled researchers to adopt compromises, either to exceedingly simplify implant structure and geometry, or the complexity of the body model. This study examines the effect of variations in anatomical details of the human body model and implant geometry on predicted values of specific absorption rate (SAR) values during MRI in a patient with a DBS implant. We used a patient-derived model of a fully implanted DBS implant and performed numerical simulations to calculate the maximum SAR during MRI at 1.5T (64 MHz) and 3T (127 MHz). We then assessed the effect of uncertainties in dielectric properties of tissue, complexity of body model, truncation of body/DBS model, and DBS lead geometry on SAR. Our results showed that 40% variation in the conductivity of individual tissues in a heterogeneous body model caused a peak of 7% variation in maximum SAR value at 64 MHz, and 10.6% variation in SAR at 127 MHz. SAR predictions from a homogeneous body model with a conductivity range of 0.01 S m⁻¹ → 1 S m⁻¹ could cover the full range of SAR variations predicted by the heterogeneous body model. Truncation of body model below the implanted pulse generator changed the predicted SAR by 16% at 1.5T and 32% at 3T while saving 250% and 148% in computational time and memory allocation, respectively. In contrast, variation in DBS lead geometry significantly changed the SAR by up to 51% at 64 MHz and 67% at 127 MHz. These results suggest that the error introduced by simplifying the implant’s geometry could negate the benefit of using a realistic body model, should such model be used at the expense of oversimplifying implant geometry.

1. Introduction

With an aging population and increased indications for implanted neuromodulation and electronic cardiovascular devices, there are an increasing number of cases where patients with conductive implants are referred for magnetic resonance imaging (MRI) exams. Until recently, MRI was contraindicated in most patients with electronically active medical implants due to concerns for hazardous interactions between MRI fields and the implanted device. Since the first report of such harmful effects in 1989 (Pavlicek et al 1983) significant improvement has been made in implant design and manufacturing leading to the first generation of MR-conditional devices that obtained FDA approval in 2011. Such improvements include, for example, reduction of ferromagnetic material to reduce the risk of device dislodgement due to static magnetic fields (Shellock et al 2007), enhanced device programming to reduce the risk of device malfunction (Sommer et al 2006), and improved lead structure to reduce radiofrequency (RF) heating (Dublin et al 2006, Wahlstrand et al 2007). Despite these advances, RF heating of the tissue surrounding the implanted leads remains a major issue, especially in cases where leads are implanted in sensitive organs such as the brain (Rezai et al 2004, Bhusal et al 2018, Golestanirad et al 2019c, Bhusal et al 2020). Consequently, manufacturers have strict guidelines regarding MRI in patients with devices such as deep brain stimulation (DBS) implants (Medtronic 2015), preventing application of the majority of clinically useful imaging sequences.

Predicting RF heating of medical implants in MRI environment is notoriously complex (Mattei et al 2008) yet it has become increasingly in demand. The major safety concern is known as the ‘antenna effect’, wherein the electric field of the MRI transmit coil couples with conductive implanted leads and amplifies the energy deposition in the tissue. In turn, this can lead to excessive heating that can damage the examined tissue. While novel approaches have been suggested to reduce these safety risks through the modification of MRI hardware and implant trajectory, the clinical implementation of these practices has been hindered due to the lack of a quantitative measurements of tissue heating in realistic scenarios.

Historically, MRI safety studies have relied on RF heating measurements using box-shaped phantoms filled with a tissue-mimicking gel and implanted with the device under test (ISO/TS 2018). There were also several in vivo experimental studies where porcine brains were used instead of tissue mimicking gels to measure RF heating in real tissues near DBS electrodes (Shrivastava et al 2010, Shrivastava et al 2012). Recently, numerical simulations have been increasingly used as an alternative approach to phantom experiments, especially as the importance of using realistic representation of human body has been emphasized (Wolf et al 2013, Murbach et al 2015, Fujimoto et al 2018, Guerin et al 2018). Nevertheless, performing simulations with the dynamic spatial resolution that spans details of implant geometry (~ 500 μm), multi-compartment body models (~ 1 mm), and MRI equipment (~ 1 m) is still impractical even with the latest advancement in computing technology. A common limitation of commercially available electromagnetics solvers is the problem of modeling electrically small and large objects simultaneously, as it leads to difficulties in mesh generation. For example, popular numerical methods such as the finite difference time domain (FDTD) technique typically discretize the spatial space with equal-sized cubical mesh elements. This means that to accurately simulate a complex system, the mesh size should be small enough to capture details of the smallest structure. This will lead to an enormously large number of mesh elements in systems with a large spatial range of dimensions. In addition, to ensure the numerical stability of the FDTD method, the time increment cannot exceed the Courant limit that is defined by the mesh size (Taflove and Brodwin 1975). Small mesh size leads to small time step size, and therefore, extremely long computation time is required to perform the simulation of complex system. Finite element (FEM) techniques on the other hand, offer greater flexibility as they allow unstructured and adaptive tetrahedral mesh scheme, however they require high memory usage if direct matrix inversion is used to obtain the solution. As a result, numerical solutions for MRI on human body models in the presence of implanted devices with sub-millimeter details are computationally expensive to the extent of being infeasible in many cases even with support of modern computers. Therefore, there is a need for evidence-based studies that systematically evaluate the effect of different simplification approaches while maintaining reliable specific absorption rate (SAR) prediction.

To date, it is still controversial what level of simplifications of numerical model are acceptable. Despite the extensive literature on effects of various model parameters on simulated SAR values in healthy subjects (Chen et al 1998, Wang et al 2007, Murbach et al 2011, Yeo et al 2011, Wolf et al 2013), to our knowledge this issue has not been well explored in the context of implant safety. In this work, we systematically studied the impacts of different parameters / assumptions (i.e. dielectric properties of tissue, complexity of body model, truncation of body/implant model, and internal geometry of the implant) on prediction of SAR values in a patient with a DBS implant undergoing MRI at 1.5T and 3T. The major goal was to determine factors that affected the SAR prediction the most. This could in turn help find a compromise allowing simplifications of the model while maintaining confidence in prediction of worst-case SAR scenarios.

2. Materials and methods

2.1. Body model

We simulated a patient with a fully implanted DBS device to assess the effects of body model complexity, model truncation, and implant internal geometry on calculated SAR. A heterogeneous body model was used consisting of 184 individual body parts categorized into 30 tissue classes. The body model was constructed by stitching a lab-made head model to the torso of ANSYS human body model (ANSYS Human Body Model V3, accessed 2020). The head model was a fine-grain 1 mm × 1 mm × 1 mm phantom consisting of 15 tissue types created based on MRI of a healthy volunteer. Details of image segmentation and model creation are given elsewhere (Makris et al 2008). Table 1 gives different tissue types along with the implant components and the nominal values of their permittivity and conductivity as reported in the literature. The average value of permittivity and conductivity of the whole set of tissues in the body model are calculated and given in table 2.

Table 1.

Dielectric parameters of tissues in heterogeneous body and implant components.

Tissue name	Volume (mm3)	Conductivity (S m−1) at 64 MHz	Relative permittivity at 64 MHz
Air	110,840	0.00	1.00
Blood	165,717	1.20	86.44
BoneCancellous	552,421	0.16	30.87
BoneCortical	1,187,984	0.06	16.68
BoneMarrow	27,157	0.02	7.21
BrainGreyMatter	934,384	0.51	97.43
BrainWhiteMatter	311,491	0.29	67.84
Cartilage	206,814	0.45	62.92
Cerebellum	140,440	0.72	116.35
CerebroSpinalFluid	209,039	2.07	97.31
Fat	209,864	0.04	6.51
Gallbladder	1,844	0.97	87.40
Gland	21,364	0.78	73.95
Heart	217,552	0.68	106.51
Kidney	36,980	0.74	118.56
Liver	409,020	0.45	80.56
LungInflated	3,434,294	0.29	37.10
Muscle	3,567,303	0.69	72.24
Nerve	11,999	0.31	55.06
Oesophagus	69,198	0.88	85.82
Pancreas	8,141	0.78	73.95
Retina	13,303	0.88	75.30
SmallIntestine	60,365	1.59	118.36
SpinalCord	33,681	0.31	55.06
Spleen	6,731	0.74	110.56
Stomach	145,851	0.88	85.82
SubCut	244,363	0.43	35.35
Trachea	33,593	0.53	58.89
VitreousHumor	6,748	1.50	69.13
Lumen	202	0.00	1.00
Insulation	974	0.00	3.50
IPG	9,055	4,000,000	1.00
Lead	20	4,000,000	1.00

Table 2.

Average dielectric parameters.

Average conductivity at 64 MHz	~ 0.5 S m−1
Average relative permittivity at 64 MHz	~ 60

2.2. Model of DBS device

A typical DBS device includes a lead the tip of which is implanted in deep brain nucleolus of interest, an implanted pulse generator (IPG) usually implanted in the pectoral region, and an extension that subcutaneously connects the lead to the IPG. We used computed tomography (CT) images of a patient with a DBS device to reconstruct the implant’s trajectory. The image segmentation and DBS device modeling was similar to what was described our previous works (Golestanirad et al 2017a, Golestanirad et al 2017b, Golestanirad et al 2019c). In brief, Amira 5.3 (Thermo Fisher Scientific, Waltham MA) was used to construct preliminary masks and 3D surfaces of the lead, extension and the IPG. To do so, a thresholding mask was applied to select the hyper dense metallic components from CT images using Amira’s segmentation module, with threshold values selected manually such that the resulting mask covered the center of the artifact but not the surrounding tissue such as bone. Labels were smoothed and the resulting mask was used to generate preliminary 3D surfaces of the lead and extension trajectories. 3D lead surfaces were exported to a CAD tool (Rhino3D®, Robert McNeal and Associates, Seattle, WA) in which lead trajectory lines were manually reconstructed. Adjustments were made as necessary to ensure there was more than 1.27 mm gap between overlapping segments, so that reconstructed lead/extension did not intersect itself after addition of the insulation layer. The reconstructed trajectory lines were exported to ANSYS HFSS where models of electrode contacts, core, and insulation layers were reconstructed around them. Models were composed of four cylindrical contacts (outer diameter = 1.27 mm, wall thickness = 150 μm), connected through a solid straight or helical central core (section 2.5) and embedded in polyurethane insulation (diameter = 1.27 mm, σ = 10⁻¹⁰ S m⁻¹, ε_r = 3.5 (Elwassif et al 2006)). Electrode contacts were made of 90%:10% platinum-iridium (Pt:Ir, σ = 4 × 10⁶ S m⁻¹) positioned 0.5–1.5 mm apart (Medtronic 2003). The reconstructed device was incorporated into the heterogeneous human body model with minor adjustments to ensure all parts of the DBS model were embedded inside the body model.

2.3. MRI RF coils and SAR calculation

Electromagnetic simulations were implemented in ANSYS Electronics Desktop (HFSS 18.1, Designer, ANSYS Inc. Canonsburg, PA) on a server with 1.5 TB memory and 2× Xenon(R) Gold 6140 CPUs each having 32 processing cores. Numerical model of a 16-rung high-pass birdcage body coil (62 cm length) was implemented and tuned to its respective Larmor frequency at 64 MHz (1.5T) or 127 MHz (3T) using lumped capacitors C_t distributed at the end-ring gaps and matched to 50 Ω using a single capacitor C_m at each port in series with an ideal voltage source with a 50 Ω internal resistance. A quadrature excitation was implemented by feeding the coils at two ports on the bottom end-ring that were 90° apart in position and phase (figure 1). The multi-compartment body model with DBS implant was positioned in the coil such that the head was at the iso-center. For all simulations, the input power of the coil was adjusted to generate head SAR of radio-frequency energy of 3.2 W kg⁻¹. The head SAR was calculated within a cylindrical region at the center of the coil having height and radius of 33 cm and 25 cm, respectively. More specifically, we calculated the net power flow through the closed surface of the cylinder shown in figure 1, by integrating the Poynting vector normal to that surface to determine power deposited within the cylinder’s volume as below

$$W=\underset{S}{{\displaystyle \int }}\mathrm{Re}(\overrightarrow{P})\cdot \overrightarrow{n}dS$$ (1)

where S is the cylinder’s surface that is used to calculate the power and $\overrightarrow{n}$ is the normal vector to the surface S. Because of conservation of energy, the loss power W is the deposited power to the body part that intersects with the cylinder. The MaxSAR1g was then normalized as

$$MaxSAR1g_{normalized}=\frac{3.2\times m}{W}\times MaxSAR1g,$$ (2)

where m is weight of the cylinder-intersected body part, i.e. body model’s head. 1g-averaged SAR was calculated according to IEEE STD P1 528.4 recommendation, using the built-in SAR calculation module in ANSYS HFSS. The maximum of normalized 1g-averaged SAR in a 2 cm × 2 cm × 2 cm cubic area surrounding all DBS electrode contacts was calculated and reported as MaxSAR1g.

Figure 1.

Multicompartment human model in a body coil.

2.4. Tissue properties

The dielectric properties of tissue, i.e. the conductivity and the permittivity are important input parameters that are difficult to accurately obtain; establishing dielectric properties in realistic conditions requires careful experiments and complex interpretation with often widely varying results (Gabriel et al 1996a). Often these parameters are set to the population averages and thus do not reflect the range of values that might be encountered in a population. We assessed the effect of conductivity variations of five major tissues surrounding the implant, namely grey matter (0.3 S m⁻¹ → 0.7 S m⁻¹), white matter (0.18 S m⁻¹ → 0.42 S m⁻¹), CSF (1.2 S m⁻¹ → 2.8 S m⁻¹), fat (0.018 S m⁻¹ → 0.042 S m⁻¹) and muscle (0.4 S m⁻¹ → 1 S m⁻¹), on SAR by changing the conductivity of each tissue in the body model while keeping the conductivity of all other tissues constant (figure 2). In the next step, we assessed the variability of the SAR predicted by a homogeneous body model. To do this, we assigned the averages permittivity of the whole tissue set to a homogeneous body model while varying its conductivity from 0.01 S m⁻¹ → 1 S m⁻¹ covering a wide range of low to high tissue conductivities. Our goal was to determine whether or not by changing the conductivity value of a homogeneous body model, one can predict the worst-case SAR scenario that is predicted by a heterogeneous model. We also studied the impact of truncating the body/implant model by simulating two additional scenarios where one homogeneous body model was truncated right below the IPG and the other model was truncated below neck (figure 3).

Figure 2.

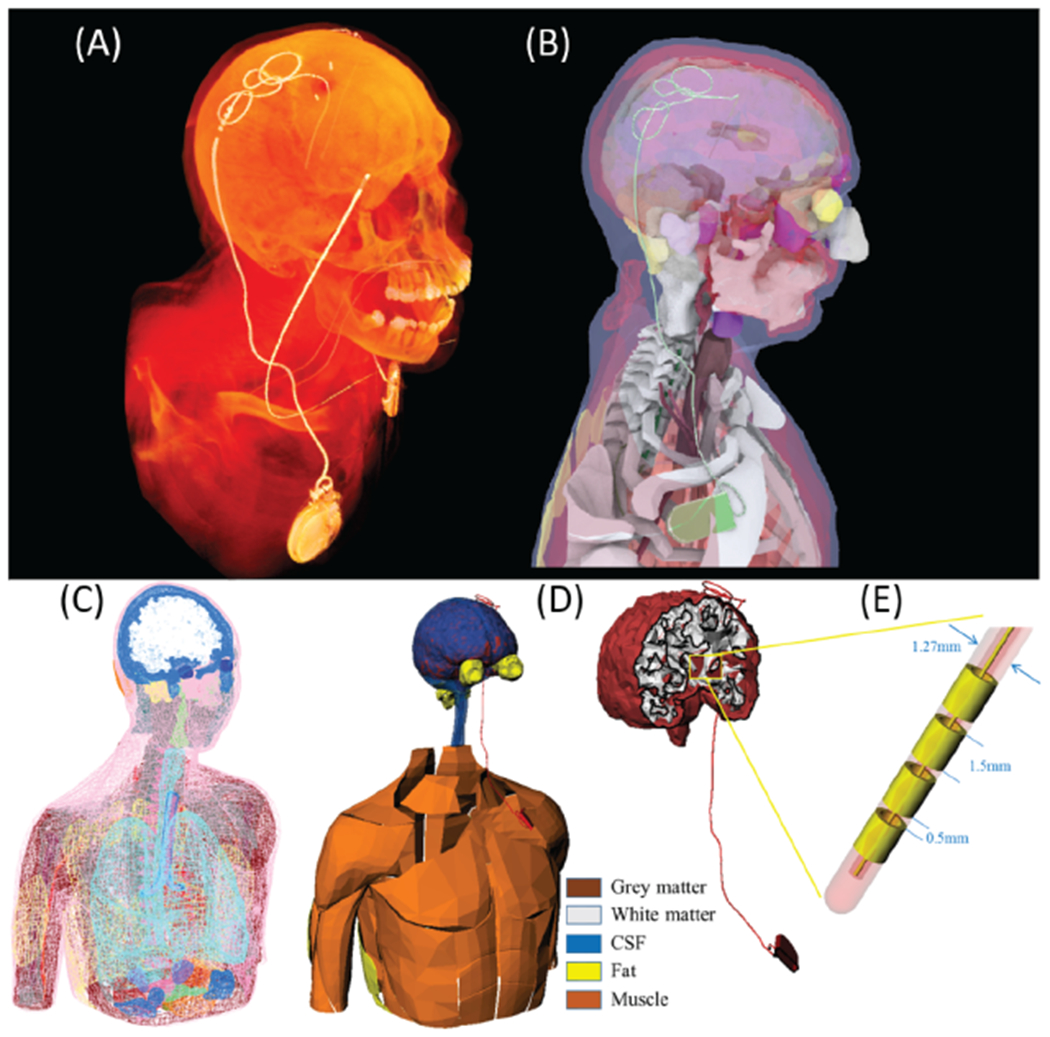
(A) and (B) CT image of a patient with an implanted DBS implant. Device trajectory was manually segmented and a 3D model of the implant was constructed and registered to a heterogeneous human body model consisting of 184 individual body parts categorized into 30 tissue classes. (C) and (D) Conductivity of five major tissues surrounding DBS device was varied by ± 40% around their nominal values while other tissue conductivities were kept constant. (E) DBS lead model consisting of 4 electrode contacts, a hollow insulation, and a straight core.

Figure 3.

Truncated body/implant models to assess the effect of truncation zone on predicted SAR.

2.5. Effect of implant geometry

The majority of simulation studies that involve electronically active implants in the human body have simplified the implant’s geometry in some form or another. Many have used simple solid wires to represent leads such as those in cardiac or neuromodulation devices (Park et al 2007, Angelone et al 2010). Others have included more detail of the lead geometry such as individual electrode contacts and insulation layers (Golestanirad et al 2017a, Golestanirad et al 2017c), however, even in these cases the internal wires that connect electrode contacts are usually simplified and modelled as straight wires. In practice, cardiac or DBS leads have multiple interleaved tightly-coiled helical wires that connect electrodes to the IPG. To investigate the effect of internal geometry of the leads, we simulated and compared SAR of a simplified DBS lead with a straight wire with the SAR generated by DBS leads with tightly-coiled helical wires of different pitch (pitch of 1.2, 0.9 and 0.6 mm) as shown in figure 4.

Figure 4.

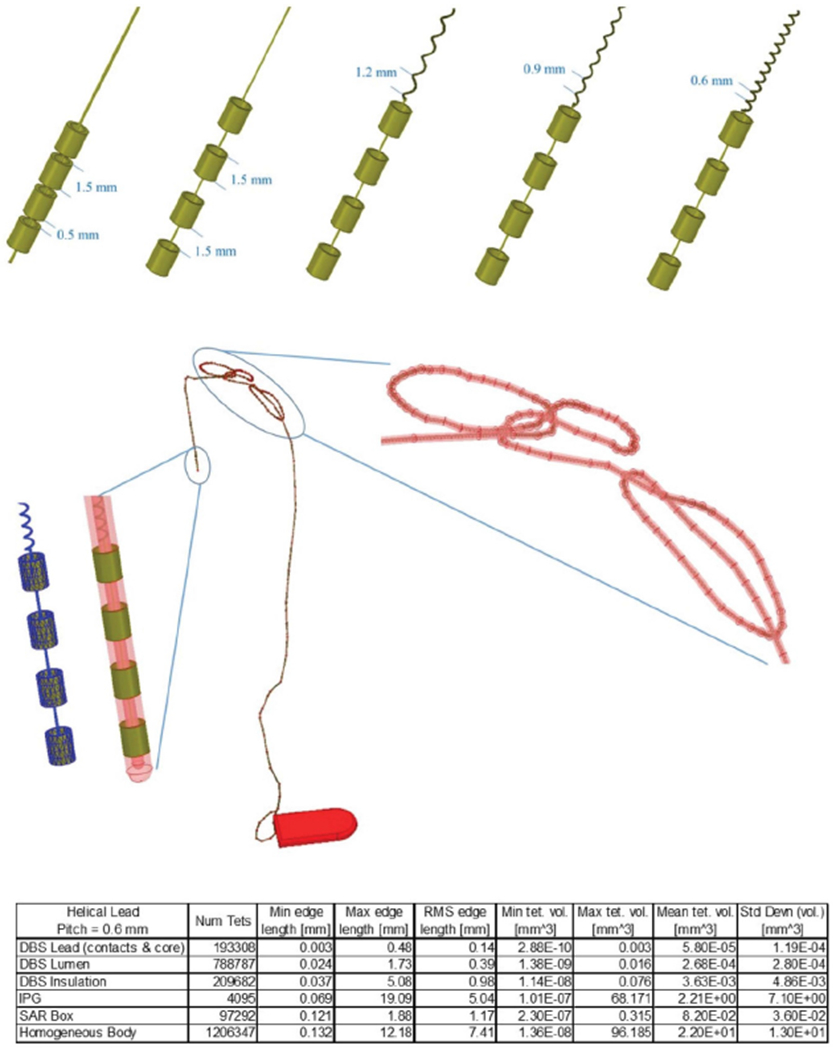
Top row: DBS leads with different internal geometries. Middle row: snapshot of DBS lead trajectory with helical core (0.6 mm pitch) inside a hollow insulation connected to extension lead and an IPG. The snapshot shows the helical lead was successfully created along the looped segments and the mesh was carefully inspected to ensure no short-circuit was created between tightly wound loops. Bottom row: details of mesh statistics for the above simulation.

2.6. Numerical convergence

ANSYS HFSS uses an adaptive mesh refinement method, which solves the fields based on an initial mesh (which can be controlled by the user), and then re-meshes based on where the fields have a high concentration and/or gradient. Each re-meshing step is called an ‘adaptive pass’. Importantly, at each adaptive pass, scattering parameters (S-parameters) are evaluated at each port, and compared to the previous pass. The change in magnitude of the S-parameters between two consecutive passes is called ‘delta S’. The maximum delta S is defined as $Ma{x}_{ij}\left|S_{ij}^N-S_{ij}^{N-1}\right|$, where i and j cover all ports and N represents the number of iterative pass. Simulations were considered to be converged when the maximum delta S fell below a set threshold of 0.02. All simulations converged after less than 3 iterative passes. Details of mesh statistics after convergence for an example simulation are included in figure 4.

3. Results

3.1. Sensitivity of SAR to dielectric properties of body model

Figure 5 shows the variation of MaxSAR1g in a 2 cm × 2 cm × 2 cm cubic area around the tip of the DBS leads during MRI at 64 MHz and 127 MHz in the heterogeneous body model when the conductivities of different tissues were varied by 40% around their nominal values. All results were normalized such that both 1.5T and 3T coils produced a head SAR of 3.2 W kg⁻¹. At 1.5T, the variation in conductivity of the grey matter generated the largest variation in SAR amounting to 7%, followed by CSF (3.9%), white matter (3.7%), fat (1.2%), and muscle (0.8%). At 3T, SAR at DBS tip was most sensitive to variation in conductivity of white matter (10.6%) and grey matter (9.4%), followed by substantially smaller sensitivity to variation in conductivity of CSF (2.6%), fat (0.5%) and muscle (0.2%).

Figure 5.

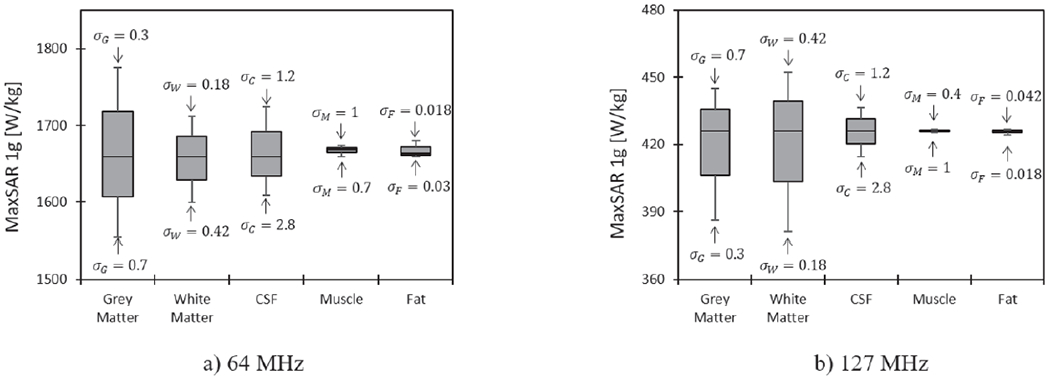
MaxSAR1g around DBS electrodes in the heterogeneous body model during RF exposure at 64 MHz and 127 MHz when conductivities of grey matter, white matter, CSF, muscle and fat was varied by ± 40% around their nominal values. For each simulation, the input power of the coil was adjusted to generate the global head SAR of 3.2 W kg⁻¹.

3.2. Homogeneous vs heterogeneous body models

Figure 6 compares the influence of the conductivity variation in homogeneous body model versus those variations in heterogeneous model on prediction of MaxSAR1g during RF exposure at 64 MHz and 127 MHz. Figure 7 shows predicted values of MaxSAR1g when the conductivity of homogeneous body model was varied from 0.01 s m⁻¹ to 1 s m⁻¹. MaxSAR1g in the heterogeneous body model with nominal values of tissue conductivities is also given as a reference. As it can be observed, the homogeneous body model with conductivities varied in a range of low to high values for tissue (0.01 S m⁻¹ → 1 S m⁻¹) could cover the full range of SAR values predicted by the heterogeneous body model. Simulation times and memory requirement for simulations with heterogeneous and homogeneous bodies were 10 h 35 min and 438 GB, and 5 h 50 min and 367 GB, respectively.

Figure 6.

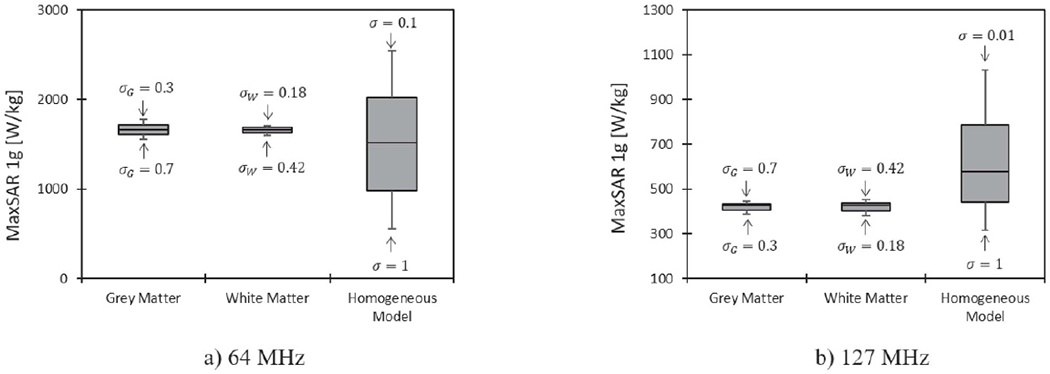
MaxSAR1g around DBS electrodes in the homogeneous body model during RF exposure at 64 MHz and 127 MHz, when the conductivity of the tissue was changed from 0.01 s m⁻¹ to 1 s m⁻¹. The variation of MaxSAR1g due to changes in grey matter and white matter conductivities in the heterogeneous body model are also given for comparison. For each simulation, the input power of the coil was adjusted to generate the global head SAR of 3.2 W kg⁻¹.

Figure 7.

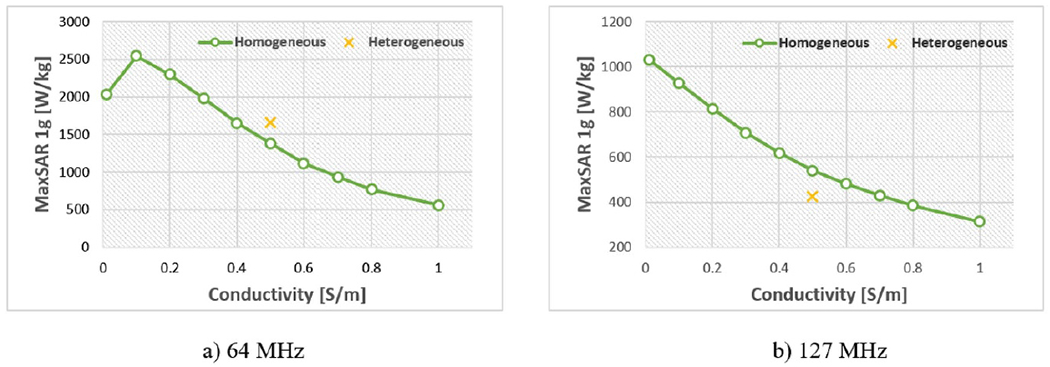
Conductivity response of MaxSAR1g for homogeneous body model at 64 MHz and 127 MHz.

Table 3 shows the changes of predicted MaxSAR1g when the homogeneous body/implant model was truncated right below the IPG and below the neck. Truncating the homogeneous model below the IPG changed the SAR by 16% at 64 MHz, and by 32% at 127 MHz, while saving 250% in simulation time (1 h 40 min) and 148% in memory allocation (148 GB). On the other hand, truncating below the neck changed the SAR drastically by 66% at 64 MHz, and by 63% at 127 MHz, while saving 465% in simulation time (1 h 2 min) and 225% in memory allocation (113 GB). These results indicate that truncating the body models can be considered to save computational time and resources as long as the full length of implanted device remains intact.

Table 3.

Truncation effects on MaxSAR1g.

	MaxSAR1g W kg−1
Body truncation	at 64 MHz	at 127 MHz
Full model	1367	548
Truncated below IPG	1138	368
Truncated below neck	463	205

3.3. The effect of implant geometry

Despite allocating high computational resources to simulations (1.5 TB RAM, 64 processors), realistic features of implant geometry such as coiled interconnections could not be incorporated in simulations with heterogeneous body model. Incorporating these features in the homogeneous model by replacing the straight core wire with helical interconnecting wires of different pitch (1.2 mm, 0.9 mm and 0.6 mm) led to a significant change in SAR, amounting to 51% at 64 MHz and 67% at 127 MHz (table 4). Interestingly, increasing the number of loops (i.e, decreasing the pitch of helix) did not always reduce the SAR. At 3T for example, the lead with the helical core with 1.2 mm pitch generated 62% higher SAR compared to the lead with the straight core.

Table 4.

Effects of internal geometry of the leads on MaxSAR1g.

		MaxSAR1g (W kg−1)
Contact separation (mm)	Helix pitch (mm)	at 64 MHz	at 127 MHz
0.5	Straight	1367	548
1.5	Straight	1100	289
1.5	1.2	664	469
1.5	0.9	625	456
1.5	0.6	544	94

Varying the spacing between electrode contacts (0.5 mm to 1.5 mm) changed the SAR by 20% at 64 MHz and by 47% at 127 MHz. These results indicate that comparing to other model simplification strategies, the errors associated to simplification in lead geometry are not negligible. This suggests that in safety applications where determination of worst-case heating scenarios is the goal, modeling the realistic implant structure, should not be simply dismissed at the expense of using more realistic body models.

4. Discussion and conclusion

There is a steady growth in the use of implantable electronic devices for therapeutic applications in the US and globally. In the field of neuromodulation, the market for DBS devices Is expected to grow at an annual rate of 18% to reach $3.2 billion by 2023 (Global Market Insights 2020). Similarly for cardiac disease, permanent pacemakers, implantable cardioverter-defibrillators and cardiac resynchronization therapy devices are implanted more frequently. Today, there are more than 3 million patients with cardiovascular implantable electronic devices (CIEDs) in the US (Greenspon et al 2012) with the number growing by 80,000 annually (Sommer et al 2006). The trend is likely to continue with new indications for use and technological advancements in device manufacturing (Roguin 2009, Higgins et al 2014).

Because of its excellent soft tissue contrast and non-invasive nature, MRI is considered the modality of choice for a majority of neurologic, cardiac and musculoskeletal disorders. It is estimated that 50–75% of patients with electronic implants will need to undergo MRI over their lifetime (Kalin and Stanton 2005), with many patients requiring repeated examinations (Naehle et al 2009). Until very recently, MRI was contraindicated in these patients due to concerns for hazardous interactions between MRI fields and the implanted device. The major restriction was, and still is, due to the interaction of MRI RF fields and implanted leads. The coupling of MRI transmitters’ electric field with long conductive leads induces electric currents on lead wires, which once injected into the low-conductivity tissue surrounding the lead, can cause excessive heating and potential tissue damage (Rezai et al 2004, Rezai et al 2005). Serious injuries have underscored these safety concerns, especially in cases where leads were implanted in sensitive organs such as the brain. As a result, the conditions under which patients with implants are indicated for MRI are restrictive. In the case of DBS patients for example, only MRI at field strength of 1.5T is allowed and only pulse sequences with a whole-head SAR of 0.1 W kg⁻¹ (~ 30 fold below the FDA-approved clinical level) or $B_1^{+}<2\mu T$ are recommended. However, it is noted that although total B field and total E field are correlated under electromagnetic mechanism, $B_1^{+}$ as only component of B field that is responsible for the excitation of the protons, is not correlated to the E field that directly affects the SAR distribution. There are technical difficulties due to these restrictions. First, following the low SAR recommendation in a clinical setting is problematic as MRI protocols that optimally image leads and their target structures tend to have much higher SARs than current recommendations allow (Larson et al 2008). Second, there is an inherent degradation of the signal-to-noise ratio (SNR) of MR images at low field intensities which tends to limit the image resolution. In the near future, MRI of these patients will become more problematic as high-field clinical scanners proliferate (Ibrahim et al 2007) and parallel transmit technology spreads (Dormont et al 2010).

Significant effort has been dedicated to mitigating the problem of RF heating of implants during MRI. These include, for example, modification of MRI hardware (Golestanirad et al 2016, McElcheran et al 2016, Golestanirad et al 2017b, Golestanirad et al 2017c, McElcheran et al 2017a, McElcheran et al 2017b, McElcheran et al 2017c, Wei et al 2018, Golestanirad et al 2019b, McElcheran et al 2019, Kazemivalipour et al 2019) or the implant’s trajectory (Golestanirad et al 2017a, Golestanirad et al 2017d, Golestanirad et al 2019c) to reduce the coupling of electric fields and implanted leads, modification of lead’s geometry and/or material to reduce induced RF currents (Bottomley et al 2010, Serano et al 2015, McCabe and Scott 2017, Golestanirad et al 2019a), and protocol optimization (Golestanirad et al 2016, Golestanirad et al 2019d). These and many other MRI safety studies rely on use of numerical simulations to predict the interaction of MRI electric and magnetic fields with human body and the implant (Neufeld et al 2011, Golestanirad et al 2012, Wolf et al 2013, Li et al 2015, Alon et al 2016, Navarro de Lara et al 2018, Liu et al 2018, Liu et al 2019, Golestanirad etal 2020, Navarro de Lara et al 2020). Another possible approach makes use of thermal modeling and MR thermometry together that may help determine the heating and improve patient safety online (Shrivastava et al 2012).

High resolution body models originally developed to evaluate MRI fields in the human body at ultra-high fields are now suggested to assess RF heating of implants, but this has only been possible with the tradeoff of simplifying implant geometry. An important question in the context of numerical simulations for the assessment of MRI RF heating in the presence of conductive implants is the sensitivity of the results to the complexity of the human body and/or implant model. As the available amount of computational resources are limited in terms of memory and time, as well as reconstructing the details of body/implant model is often difficult and time consuming, it is crucial to determine which model parameters have the highest impact on the end point results and devise a defeaturing strategy accordingly.

To date, the majority of studies that aimed to assess RF heating of implants in MRI environment and have opted to use anatomically realistic body models have done so at the expense of simplifying the implant’s geometry. In this study, the influence of simplifications in the human body and implant geometry on the accuracy of SAR calculation was investigated in a patient with a DBS implant undergoing MRI at 64 MHz and 127 MHz. In simulations with a heterogeneous body model consisting of 30 tissue classes, we found that SAR amplification at the tip of DBS lead was most sensitive to changes in conductivities of the tissue directly surrounding the implant, such as brain white matter and grey matter. A total of 22 simulations were performed by changing the conductivity of white matter, grey matter, CSF, muscle and fat tissue separately at each step while keeping other tissue properties the same. The total simulation time was ~ 240 h. At 1.5T, SAR was also sensitive to changes in conductivity of CSF, varying by 3.9% when we changed conductivity of CSF by 40% around its nominal value. At 3T however, SAR sensitivity dropped for tissues that were further away from the exposed tip of the lead. It should be noted however, that our approach was limited as it did not explore the full space of all possible combinations of tissue conductivities. Such exhaustive search with 486 simulations (5 tissues, 3 variations each) would have amounted to ~ 5280 h of continuous simulation (~ 220 days) on a server with 1.5 TB RAM and 64 processors.

We assessed whether a homogeneous body model could predict the worst-case SAR scenario predicted by the heterogeneous body model. SAR calculations with a homogeneous body model with a range of low to high conductivities (0.01 S m⁻¹ → 1 S m⁻¹) covered a range of SAR values 43% and 128% wider than what were predicted by the heterogeneous model at 64 MHz and 127 MHz, respectively. The computational time for each simulation was reduced to 5 h 50 min. When the body model was truncated below the IPG, predicted SAR changed by 16% at 1.5T and by 32% at 3T, and simulation time was further reduced to 1 h 40 min. Thus, a total of 20 simulations with a truncated homogeneous body model could allow us to predict the worst-case SAR scenario in 33 h compared to 240 h simulations with heterogeneous model. It is important to note, however, that although here we used an example of a heterogeneous body model which is assumed to be a better representative of an in vivo scenario, such models have not been validated to predict induced electromagnetic fields, and thus SAR, in human body during MRI. Moreover, in majority of simulations, electrical properties assigned to different body tissues are driven from a single series of ex vivo experiments ran in 1996 (Gabriel et al 1996a, Gabriel et al 1996b, Gabriel et al 1996c) which may not be representative of variations in the population.

The important role of the implant’s internal geometry, especially multi-electrode configuration and coiled internal wires, has been recently emphasized in the context of MRI RF heating (Kozlov and Kainz 2020, Nguyen et al 2020a, Nguyen et al 2020b). This is important, because in contrast to simulations that represent implanted leads with straight wires, commercial leads have interleaved helical core wires. The advantage of such geometry is two-folded: helical core will add to mechanical flexibility of the lead, allowing it to be bent and looped easier during the implantation. A coiled core could also help reduce MRI RF heating by increasing the overall inductance of the lead which in turn reduces included currents (Bottomley et al 2010, Olsen et al 2010, Atalar et al 2011). Theoretically, however, a lead with helical wires could generate substantially different RF heating compared to a lead with straight wires when routed along different trajectories. We observed that the error arising from simplification of lead geometry well surpasses the error associated with inaccuracies in body model anatomy. This indicates that a simplified approach to MRI safety, where body models with a large number of tissue classes are used along with dramatically simplified implant structures could give a false sense of accuracy, and that an accurate modeling of the implant’s geometry is of paramount importance to provide confidence in numerical predictions of RF heating.