Abstract
We provide a protocol for measuring the absolute concentration of the oxidized and reduced state of cytochrome c oxidase (CCO) in the cerebral cortex of mice, using broadband continuous-wave NIRS. The algorithm (NIR-AQUA) allows for absolute quantification of CCO and deoxyhemoglobin. Combined with an anoxia pulse, this also allows for quantification of total hemoglobin, and tissue oxygen saturation. CCO in the cortex was 4.9 ± 0.1 μM (mean ± SD, n=6). In normoxia, 84% of CCO was oxidized. We include hypoxia and cyanide validation studies to show CCO can be quantified independently to hemoglobin. This can be applied to study oxidative metabolism in the many rodent models of neurological disease.
1. Introduction
Near-infrared spectroscopy (NIRS) has an optical window that allows one to measure absorption of oxyhemoglobin (HbO), deoxyhemoglobin (dHb) and cytochrome C oxidase (CCO). NIRS has been widely used to study cerebral physiology, with the focus mainly on the strong absorption feature of hemoglobin (Hb) [1–3]. Hb data can provide indirect information about hemodynamics, oxygen delivery, and oxygen saturation in the tissue (StO2). CCO plays an essential role in oxidative energy metabolism as it is the terminal electron acceptor of the electron transport chain [4]. By measuring CCO with NIRS one can assess the redox state of the CuA center located in the enzyme [5].
Here we present a novel NIRS approach that allows for the simultaneous quantification of the absolute redox state of CCO, the total amount of the enzyme (totCCO), the total hemoglobin (tHb) concentration and StO2. As rodent models are foundational in our studies of neurological processes, we focused in developing this method for use in rats and mice.
Several clinical and pre-clinical studies have confirmed the importance of CCO as an intracellular biomarker of O2 metabolism and energy state of the brain [6]. These include studies investigating brain injury in adults [7] and neonates [8], and functional activation in adults and infants [9,10]. It has been argued that CCO redox data are a more sensitive indicator of brain O2 deficiency and energy failure than the change of O2 saturation in blood [11–13].
Quantifying CCO in the presence of strong hemoglobin absorption is challenging, mainly because its concentration is about one order of magnitude lower than Hb, and the absorption peak of the CuA centre is very broad [6]. The current state of quantification is done by measuring the spectral change in the difference between the oxidized and the reduced forms of the enzyme known as the “difference spectra of CCO” or ΔoxCCO. This allows one to report relative changes over time in the oxidation state of CCO in arbitrary units (AU) or ΔμM [6,8,9,14–16].
NIRS methods used to resolve ΔoxCCO are based on multi-wavelength data acquisition and fitting. Many algorithms, based either on the modified Beer-Lambert law (MBLL) [8,17] or on an analytical solution to the diffusion approximation (DA) [18,19], have been developed to analyse NIRS data and report ΔoxCCO. NIRS methods, along with the combination of appropriate algorithms for data analysis, such as the UCLn algorithm, have been shown to be capable to accurately separate ΔoxCCO signals from those of Hb [8,15,16]. Advances in optical instrumentations have increased the reliability of monitoring ΔoxCCO with NIRS [6,20]. Although studies have shown that it is possible to reduce the number of wavelengths required to extract ΔoxCCO data, to 16 or less, the data are still analysed as relative changes [21,22]. As NIRS technology has evolved, so have other combinations been developed. It has been shown that hybrid NIRS systems which combine a broadband spectrometer with a frequency-domain spectrometer can be successful at resolving ΔoxCCO [23,24]. Time-Resolved (TR) NIRS has also been used [22]. A Diffuse Optical spectroscopy (DOS) study, which combined frequency-domain and broadband NIRS, studied the impact of cyanide toxicity and treatment on oxidized and reduced CCO in the thigh muscles of a rabbit model [24]. However, all these studies have reported relative changes over time.
Since the total concentration of CCO should not change over short-time periods, using the difference spectra of CCO to report changes in the redox state of the enzyme would be sufficient to indicate a change in the cellular oxidative metabolism. However, knowing the absolute redox state of the enzyme or the concentration of the oxidized form relative to the reduced form would allow better comparison between subjects and provide novel information. For instance, the concentration of CCO is likely to change with maturity and energy metabolism of the brain tissue [25]. A change in the concentration of CCO would indicate a change in the mitochondria density or a change in the number of respiratory complexes per mitochondrion.
In this study, we introduce a new absolute quantification algorithm, titled “NIR-AQUA”, to quantify absolute concentrations of oxidized CCO (oxCCO), reduced CCO (reCCO) and totCCO, in addition to dHb from broadband NIR data. Combining this approach with a brief anoxia pulse, allows the quantification of tHb, and therefore HbO and StO2. As we are focusing on using rodents, the anoxia pulse is acceptable.
One issue, when trying to resolve data from multi-wavelength absorption spectra, is that spectra of one absorber can impact those of another (crosstalk). In early animal studies, CCO NIRS signals were investigated using blood-free or perfluorocarbon-exchange animal models where hemoglobin was completely removed from the animal, to facilitate CCO detection [26]. Other studies investigated crosstalk between Hb and CCO NIRS signals, by changing one absorber independently from another. At low doses, cyanide (CN) inhibits the electron flow through CCO without compromising cerebral oxygenation. Therefore, CN was used to change CCO conditions of differing oxygenation [14,27].
To validate the ability of NIR-AQUA to independently quantify these absorbers in vivo, two studies were conducted with a custom-built broadband CW-NIRS system. In the first study, spectral data were non-invasively collected from the cerebral cortex of anesthetized and spontaneously ventilated mice, under different fractions of inspired oxygen (FiO2), to change hemoglobin saturation and CCO. In the second study, CN was administered to uncouple Hb and CCO, to help confirming the assumption that we are measuring real changes in CCO redox state and not crosstalk caused by the changes in dHb and HbO concentrations.
2. Methods
2.1. Instrumentation
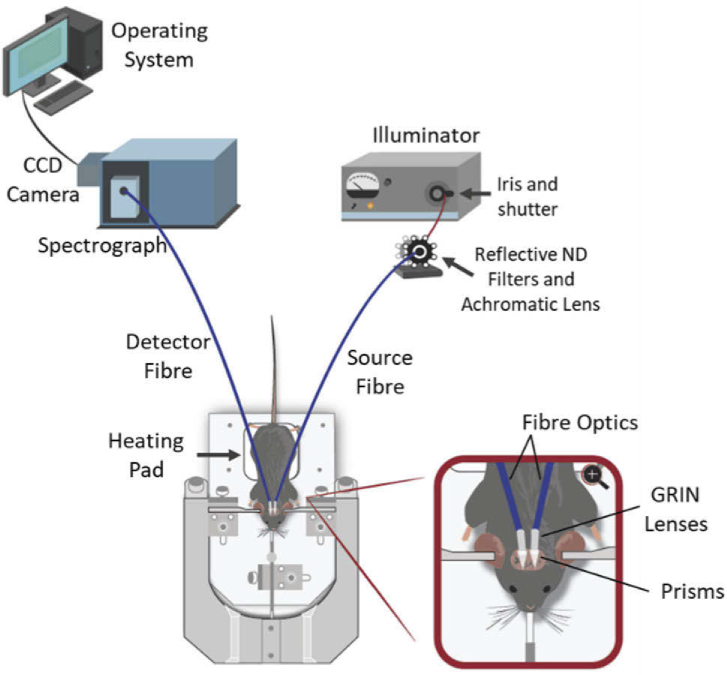
A custom-built continuous wavelength (CW) NIRS system, with a broadband white light source, a spectrograph, and a charge-coupled device (CCD) were employed to collect in vivo data from the cerebral cortex of mouse models. A schematic of the experimental setup is shown in Fig. 1. The system was briefly described in previous studies [28,29]: A Hard-Clad Silica Core Multimode optical fibre with a 1000 μm core diameter and 0.39 NA (FT1000EMT, Thorlabs Inc, USA) was used to deliver the broadband NIR light provided by the fiber optic illuminator (model 77501, Oriel Instruments Inc., USA) to the mouse head. The illuminator features a 100-Watt broadband quartz tungsten-halogen light bulb and emits light in the VIS-NIR range. A focal lens (AC127-019-B-ML, Thorlabs Inc, USA) was used to focus the output light onto the fibre optic. In addition, an iris and a shutter were used to moderate the light entering the fibre. A GRIN lens with a 1.80 mm diameter and 0.55 NA (#64-525, Edmund Optics, USA) and a 90°prism with a leg length of 2 mm (#45-524, TECHSPEC N-SF11, Edmund Optics, USA) were glued with a cyanoacrylate containing adhesive (Krazy Glue, Elmer’s Products, Inc, USA) to the end of the fiber to collimate the light and direct it into the tissue. A thin layer of dental cement was applied to strengthen the connection between the end of the fibre, the lens, and the prism.
Fig. 1.
Schematic design of the custom-built CW NIRS system used to non-invasively collect broadband NIR data from the mouse cortex. Inset shows a closeup view of the optic fibres positioned on the shaved scalp of the mouse.
A similar fibre-GRIN lens-prism assembly was used to transport the NIR light collected from the mouse head to the spectrograph (Shamrock 303i, Andor Technology Inc, Northern Ireland). The spectrograph has a f/4 aperture and a 303 mm focal length with a mechanical scan range of 0-1450 nm, a motorized input slit and a motorized triple grating turret (68 mm × 68 mm). The light collected by the receiver fibre, was delivered into the input slit of the spectrograph which was set to 350 μm. The spectrograph spread the input NIR light along wavelengths, using the diffraction grating with a density of 300 lines/mm blazed at 500 nm providing a wavelength resolution of 3.7 nm, 281 nm bandwidth, and an effective quantum efficiency (QE) range of 250-1150 nm with a peak efficiency of 80%. Complete absorption spectra were collected over the range 700.23-967.82 nm. The diffracted light was then projected onto a back-illuminated CCD camera (DU420-BR-DD, Andor Technology Inc, Northern Ireland), which has a two-dimension array of 1024 × 256 pixels with 26μm × 26 µm pixel size. The QE of the detector is ≥ 90% in the 700-900 nm range, with a peak QE of 94% at 800 nm, and ≤ 70% above 960 nm. The CCD camera was cooled to -40℃ to significantly reduce the dark noise contribution.
Collected data were transmitted to a computer via an internally installed controller card (Andor Technology). In-house software developed with Matlab (The MathWorks, Inc. USA) was used to communicate with the spectrograph and the CCD camera.
2.2. In vivo experiments
Animals.
Male C57BL/6J mice were purchased from Charles River, Québec, Canada, housed and maintained in the University of Calgary Animal Care facility with a 12 h light and dark cycle with access to water and food pellets ad libitum. Animal protocols were approved by the Animal Care Committee of the University of Calgary and conformed to the guidelines established by the Canadian Council of Animal Care (CCAC).
In-vivo Setup.
The mice were anesthetized with 5% isoflurane added to a gas mixture of 70% N2 and 30% O2. Anesthesia was reduced, after induction, to 2% (balance N2), and further reduced during the studies if needed to maintain breathing. The mice were fixed in a stereotactic, laid on a heating pad and stabilized with two ear bars and a nose cone (Fig. 1). Hair from the mice head were removed using depilatory cream (Nair; Church & Dwight Co. Inc., USA) to reduce the scattering effect and improve the coupling between the optic fibers and the head. To enhance the light transmission through the skin, the prisms on the optic fibres were covered by a thin layer of Glycerol. The fibers were secured on top of the animal head, near bregma, by covering the area with masking tape connected to the outside ear bars, to keep them pressed down on the head of the mouse. Fibers were spaced with a black rubber separator to keep the optimal distance constant between the source and detector fibers (4 mm width) and to help reduce direct light transmission between the source and detector. Breathing rate was monitored to ensure a stable physiology. Two sets of experiments were conducted to validate the use of our custom-built system and the proposed algorithm in vivo, and are detailed below:
Varying FiO2 Study.
6 mice (14-15 weeks old), weighing 38.5 ± 1.2 g (mean ± SEM) were used in this study. Breathing rates and NIRS absorption spectra were stable prior to data acquisition. NIR spectra were collected over a time course of 30-35 minutes, under 4 different levels of inhaled O2 (100%, 30%, 10%, and 0%). The experiments started with a baseline measurement where the animals were supplied by a 70% N2, 30% O2 mixture for 5 minutes. The FiO2 level was then changed to 100%, 30%, and 10% respectively, each for 5 minutes. This was to induce a wide range of oxygenation from hyperoxia to hypoxia. A short anoxia pulse (45 seconds) was given to the animals, where the air mixture ratio was altered to 100% N2 / 0% O2. After the anoxia pulse, the O2 level was restored to 30% for recovery.
The collected spectra were converted into absolute chromophores concentrations using NIR-AQUA. To obtain a mean concentration of the chromophores at each FiO2 level, the concentrations were averaged from when a steady state was achieved, to the end of that block of FiO2. Statistical significance was determined using a one-way ANOVA test with repeated measures and a Bonferroni post-hoc analysis, to compare between chromophores values at different FiO2 level. All data were expressed as mean ± SD, and p ≤ 0.05 was considered statistically significant. All statistical analyses were performed in IBM SPSS Statistics v24.
NaCN Study.
Prior to NIR data acquisition, the mice were anesthetized with 2% isoflurane, and a catheter was placed in the lateral tail vein to administer continuous intravenous NaCN. The catheter (Intramedic PE10 tubing) was drawn down to a fine diameter with a 45° bevel on the end and primed with saline containing 10 IU/ml heparin. 10 mice (8-9 weeks old), weighing 25.7 ± 0.6 g (mean ± SEM) were used to test a range of NaCN doses (10-35 mg/kg) in order to determine the dose that would cause an uncoupling between Hb and CCO without affecting the cardiac system. The study dose was a solution of 0.4 mg NaCN in 124 µl saline infused at 2 µl/min, to deliver appropriate final dose of 15 mg NaCN/kg animal weight, through the tail vein catheter. During NIR data acquisition, the mice were maintained on 2% isoflurane and core temperature was 36.6 ± 0.5 °C. Heart rate, breathing rate and arterial oxygen saturation were monitored by the MouseOx MRI-compatible pulse oximeter (Starr Life Sciences, USA) placed on the shaved right thigh of the animal.
NIRS data were collected before NaCN infusion at 30% (10 min), 0% (45 sec) and 100% FiO2 (10 min) with balanced levels of N2. Afterwards, NaCN was delivered over 55 minutes at 100% FiO2 and 1.5% isoflurane. Data collection was continued after the completion of NaCN infusion, for 10 min at 100% FiO2, and an additional 10 min at 30% FiO2. A short anoxia pulse (45 seconds) was given to the animal at the end, where the air mixture ratio was altered to 100% N2 and 0% O2. The whole experiment lasted for 3 hours per mouse, including surgery time. Mice were sacrificed directly after the experiment by intravenous injection of sodium pentobarbital. The spectra collected pre-, during and post- NaCN, were converted into absolute chromophores concentrations using NIR-AQUA.
2.3. Acquisition protocol
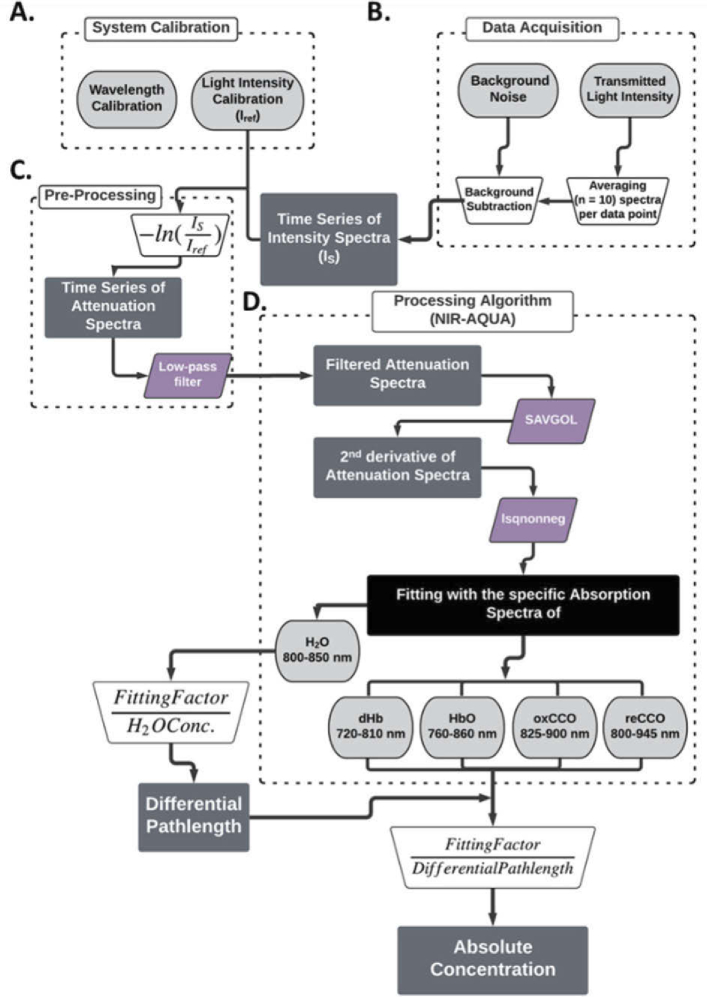
The in-house Matlab software controlling the NIRS system incorporated 3 steps: system calibration, signals acquisition, and signals pre-processing (Fig. 2(A-C)).
Fig. 2.
Flow diagram of the acquisition protocol and the proposed algorithm (NIR-AQUA). The acquisition protocol includes System Calibration (A), Data Acquisition (B), and Pre-Processing (C) steps. Attenuation spectra are transferred to the Processing Algorithm (NIR-AQUA) (D) which estimates the differential pathlength and derives the absolute concentration of the chromophores.
System Calibration.
The calibration process included a wavelength-calibration, and light intensity calibration. During the wavelength calibration, the detector fiber was pointed to the neon lamp located on the front panel of the illuminator, and the spectrum was collected. This lamp has a known standard spectrum, which was provided by Newport Corporation (California, USA). The measured spectrum was compared to the standard spectrum, and a linear best fit between the two spectra was found. The calibration coefficients were derived and used to match pixel number on the CCD camera with spectrum wavelength. The wavelength resolution after calibration is approximately 0.33 nm. Next, the light intensity calibration was performed to determine the spectra of the reference light (Iref) penetrating the investigated tissue [30]. For this, the source and detector fibres were lined one against the other, so the light coming out from the source entered directly to the detector. First, background measurements were collected, with no light coming in. And then the same measurements were repeated when the light source was turned on, so the detector fibre directly collected the broadband light coming out of the illuminator. The background measurements were subtracted from the high-intensity measurements to eliminate any background signals, and to form the spectrum of the reference light (Iref). After being fully calibrated, the system was ready to acquire signals from the desired subject.
Signal Acquisition.
During the signal acquisition, a background reading (illuminator off) was taken from the mouse head and repeated 100 times. The average background signal was calculated over 1024 pixels which were translated to wavelengths using the wavelength calibration step. Next, the illuminator was turned on and the spectra from the mouse cortex were collected continuously at a sampling rate of 6 Hz. In order to increase the signal-to-noise ratio (SNR), every 10 spectral acquisitions were averaged to give a temporal resolution of 1.7s.
Signal Pre-Processing.
The average background reading was subtracted from the collected raw spectra, and the resulted spectra were converted into light attenuation by applying the natural logarithm to the ratio of the incident light intensity (Iref) determined in the calibration step, and the light intensity (IS) transmitted through the sample, which is the mouse head in this case [31]:
| (1) |
To overcome the sensitivity of the second derivative analysis to noise in the data, a Parks-McClellan filter was applied on the calculated attenuation, with passband ripple of 0.1 dB at 0.3π, and stopband attenuation of 80 dB at 0.4π [30]. The filtered time-series attenuation was then transferred to the processing algorithm (NIR-AQUA) for further processing and calculation of absolute concentrations of the chromophores.
2.4. Algorithm (NIR-AQUA)
NIR-AQUA is the new processing algorithm suggested, to quantify the absolute concentrations of oxCCO, reCCO, HbO, dHb, in addition to tHb and StO2, from broadband data acquired from the mouse cortex, using broadband CW-NIRS equipment and a brief anoxia pulse.
2.4.1. Principles and assumptions
NIR-AQUA uses the modified Beer-Lambert law [32] to relate the wavelength-dependent light attenuation to chromophores concentration:
| (2) |
A denotes the attenuation of light at a given wavelength λ. d·DPF denotes the total path length of photons travelling through the tissue to the detector. Ci is the absolute concentration of the chromophore of interest, i. G(λ) represents photon losses owing to scattering.
The main assumption underlying this algorithm is that tissue scattering, and water content remain constant throughout the measurement period. Therefore, NIR-AQUA is based on the second derivative approach, commonly applied in broadband NIRS methods [3,33], to remove the scattering effect. It also uses the water absorption features and its known concentration in the brain tissue to estimate the mean optical pathlength that the photons travel. The algorithm applies multi-linear regression to fit the second differential spectra of the attenuation with the known second differential spectra of the pure chromophores over a specific range of wavelengths, for each chromophore. The absolute concentration of the chromophores is obtained by dividing the fitted curve of each chromophore by the estimated pathlength. A flow diagram summarizing the processing steps is shown in Fig. 2(D). The main factors affecting the reliability and adequacy of the algorithm are described below:
2.4.2. Scattering effect
Due to its wavelength linear dependence, the scattering coefficient G(λ) can be eliminated from the modified Beer-Lambert law (Eq. (2)), by applying the second differential method [34], so that . The relationship between the derivative and the concentration is conserved:
| (3) |
The Savitsky-Golay (SAVGOL) smoothing algorithm [35] was employed to obtain the second derivative of the spectra. This step is used for computing derivatives of spectra and eliminating high-frequency noises and baseline shifts. The algorithm calculates the derivative value for each point of the spectra based on the moving average (MA) principle [35]. To apply the SAVGOL algorithm on the measured spectra, the number of smoothing points, the polynomial order, and the derivative order should be considered. In our case, a quartic polynomial and a 45-points smooth span were found to remove high frequency noise without sacrificing the spectral features [36].
2.4.3. Pure chromophores spectra
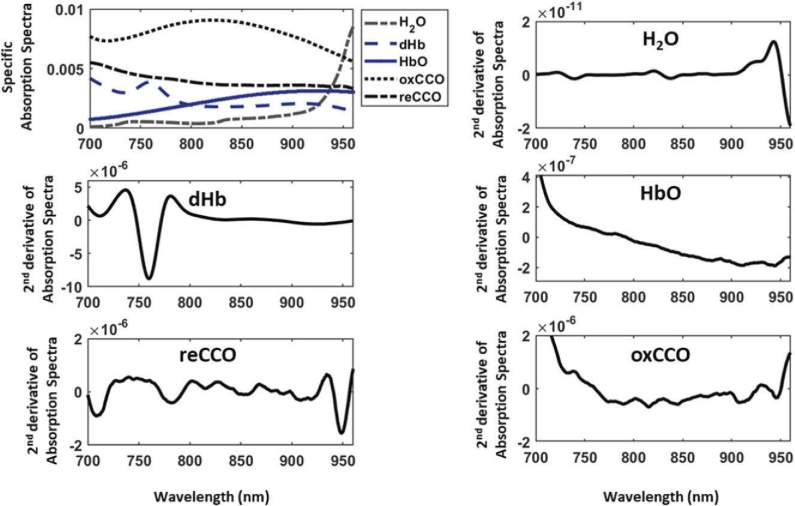
The specific absorption spectra of Hb and CCO have been previously identified and characterized in vitro and in vivo [3,26,33]. In order to determine the concentration of these chromophores in the tissue, the algorithm fit the in vivo collected spectra with the reference spectra of the pure chromophores. For this purpose, the matlab function “lsqnonneg” was used to solve a non-negative least square problem and find the best-fitting. For consistency purposes, SAVGOL with the same smoothing and fitting parameters, was applied on both the in vivo measured spectra and the pure chromophores spectra before performing multilinear regression fitting. The data sets for the specific absorption spectra of the pure chromophores were downloaded from the medical physics UCL website [37] and reproduced in Fig. 3. In these experiments, the dHb and HbO data were obtained by measuring known concentrations of lysed blood samples using a commercial scanning spectrometer [33]. The specific extinction spectra of oxCCO and reCCO were obtained from bovine heart, measured by Dr. John Moody at the University of Plymouth.
Fig. 3.
Specific absorption spectra and second differential spectra of the five chromophores in living tissues: dHb, HbO, oxCCO, reCCO, and H2O. The data are downloaded from the medical physics UCL website; dHb and HbO data were obtained by measuring known concentrations of lysed blood samples using a commercial scanning spectrometer. oxCCO and reCCO were measured from bovine heart.
2.4.4. Mean optical pathlength
Since water concentration usually stays within a narrow range, it is often used as a reference chromophore to assess the optical pathlength of photons in the area of interest [26]. Water has three well-defined features in the NIR region, around 740 nm, 840 nm, and 960 nm. To determine the amplitude of the water features, NIR-AQUA applied the “lsqnonneg” function to perform a non-negative least-squares fit of the second differential of the in vivo measured attenuation spectra, with the second differential of pure water spectrum taken from University College of London medical physics website [37]. The algorithm based the pathlength estimation on the second spectral feature of water (840 nm) and performed the non-negative least squares fitting (lsqnonneg) over the wavelength range of 800-850 nm. This fitting resulted in a scale factor which was divided by the assumed concentration of water in the cerebral cortex of the rodent and provided the mean pathlength of light. Our algorithm is mostly used to estimate the concentration of the chromophores in the cerebral cortex of mice, therefore, the cerebral water content was assumed to be 80% [38] which is equivalent to 44.4 M.
2.4.5. Wavelength range
The broadband NIRS system used here offers a range of measurement wavelengths (705–960 nm), spanning the spectral range of dHb, HbO, oxCCO and reCCO. Since the absorption features of these chromophores partially overlap in this wavelength range, a separate wavelength window was carefully allocated for each chromophore. Theoretically, the optimal wavelength window that allows a reliable fitting for each chromophore would be located around its maximum absorption feature and should be wide enough to allow accurate fitting. To identify these optimal wavelengths windows, modeling of artificial datasets was employed. The purpose of the analytical modeling is to fine-tune the upper and lower bounds of the wavelength range for each chromophore (see details in next section). The model was also used to test the NIR-AQUA on an artificial dataset and assess its accuracy in quantifying each chromophore, in the absence of interfering features of other chromophores, before applying it on the animal model.
Analytical modeling for wavelength allocation
An analytical model was written with Matlab to generate attenuation spectra of artificial datasets replicating physiological parameters in the cortex of a living mouse model. The artificial datasets were generated using an analytical diffusion theory through an infinite-slab geometry. The diffusion theory expresses the relation between light attenuation, absorption, and scattering coefficients. It has been shown that this model accurately describes the light transport in tissue, and it has been used previously to validate similar NIRS algorithms [3]:
| (4) |
is the apart distance between the source-detector optode pair; ; is the wavelength-dependent tissue total absorption coefficient, is the concentration and is the specific absorption coefficient of the chromophore i at NIR wavelengths range; is the tissue reduced-scattering coefficient, given at wavelength λ, by the following formula: [39].
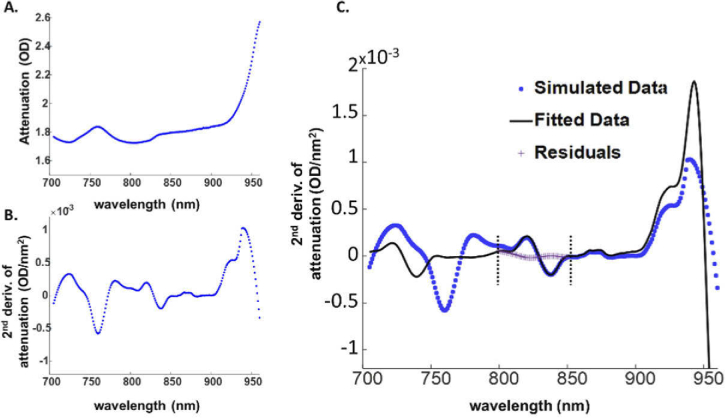
The current model considered the five main chromophores in biological tissues: H2O, dHb, HbO, oxCCO, and reCCO. Each chromophore concentration was set to be independent and varying within its physiological range. The concentration of water was fixed at 80%, which is equivalent to 44.4 M in mice brains [38]. The nominal concentration of dHb and HbO varied between 10 µM and 60 µM, while oxCCO and reCCO concentrations varied between 1.5 µM and 6 µM. The absorption coefficient µa of each chromophore is the product of its standard absorption spectra (Fig. 3) and its nominal concentration. The overall absorption coefficient of the tissue is the linear combination of the absorption coefficients of the five chromophores together. The separation distance of the source-detector pair ρ was 4 mm to mimic the case of mouse models, and the wavelength (λ) range was set from 705 nm to 960 nm. Equation (4) was used to convert the overall µa, together with all the parameters mentioned above to several attenuation spectra (A) with different concentrations of chromophores. NIR-AQUA was applied on these artificial datasets to derive the concentrations of the chromophores. The first step of the processing algorithm was to get the second derivative of the attenuation spectra by applying the SAVGOL function. The attenuation of one of the artificial spectra and its corresponding second differential spectrum are shown in Fig. 4(A-B). Figure 4(C) shows the non-negative least-squares model fit of this second differential spectrum with the second derivative of the specific absorption spectrum of water around its second spectral feature (800-850 nm). The wavelength-independent residuals distributed around zero show the accuracy of the fitting model over this wavelengths range.
Fig. 4.
(A) The attenuation spectra of one of the artificial datasets generated by the simulation, where [H2O] = 44.4 M, [dHb] = 20 μM, [HbO] = 40 μM, [oxCCO] = 3.5 μM, [reCCO] = 2 μM. (B). The second differential of the generated spectra in (A). (C). The second-differential spectrum in (B) (blue dots) and the non-negative least-squares model fit of this spectrum with the second derivative of the specific absorption spectrum of H2O (black line). The fitted data show the absorption features of H2O around 740 nm, 840 nm, and 960 nm. Fitting H2O was performed around the second spectral feature (800-850 nm). Residuals (purple plus signs) show the accuracy of the fitting model over this wavelengths range. Dashed vertical lines indicate the wavelength range chosen for the fitting.
As the test attenuation spectra had nominal concentrations of the chromophores, they can be used to optimize the fitting process and find the optimal wavelength range for each chromophore. The main criteria guiding the selection of these wavelength ranges were: 1) inclusion of the main absorption feature of the chromophore of interest, 2) having a wide fitting range, as a higher number of wavelengths allows more accurate fitting, and 3) having minimal overlap with other chromophores features to avoid distortions caused by these chromophores. An iterative approach was taken to optimize the wavelength windows for each chromophore. In each iteration, the chromophore concentration was calculated using NIR-AQUA. The derived concentrations were compared to the nominal ones and the percentage error was calculated. The wavelength range yielding minimum percentage error was defined as the optimal wavelength range to be used in the NIR-AQUA when applied to in vivo data:
dHb and HbO.
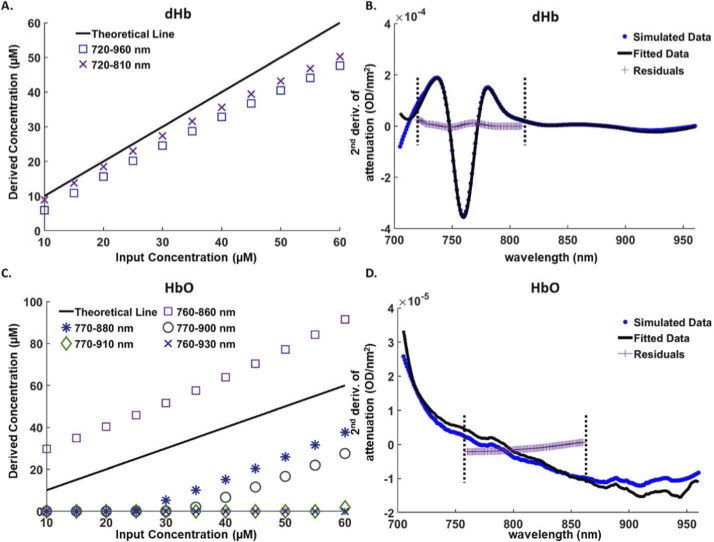
dHb has a well-defined absorption peak at 760 nm, therefore by using the model, we tried to find the optimal wavelength range that includes 760 nm, and fulfills the criteria mentioned above. Figure 5(A) shows the concentrations of dHb derived by NIR-AQUA versus the nominal concentrations set in the artificial datasets. These datasets consist of 10-60 µM dHb, 60-10 µM HbO and 44.4 M H2O. An example of two different wavelength windows used to extract the concentration of dHb from the spectra of these datasets are shown. The optimal wavelength window for dHb fitting was found to be 720-810 nm. The mean absolute percentage error (MAPE) over this wavelength window is 5.6%. Figure 5(B) shows the fitting of the second differential of one simulated dataset (20μM dHb) over the range of 720-810 nm. The wavelength-independent residuals indicate a good fit over this range.
Fig. 5.
The absolute concentration of dHb (μM) (A) and HbO (μM) (C) derived by NIR-AQUA, versus the input concentration of simulated datasets. Different wavelength windows were applied in the fitting process, to find the most accurate wavelength range. The theoretical concentration line (black) where derived = input concentration is shown for comparison. (B) A Second-differential spectrum of a simulated dataset (blue dots) consisting of 20 μM dHb and (D) 40 μM HbO, and their non-negative least-squares model fit with the second derivative of the specific absorption spectra (black line). The fitted data show the strong absorption feature of dHb around 760 nm (B) and the weak features of HbO (D) between 760 nm and 860 nm. Fitting dHb and HbO was found to be optimal over the wavelength range 720 - 810 nm and 760 - 860 nm, respectively. Residuals (purple plus signs) show the accuracy of the fitting model over these wavelength ranges. Dashed vertical lines indicate the wavelength range chosen for the fitting.
Despite the flat absorption spectra of HbO, a very broad feature can be seen in its specific absorbance spectra around 770–925 nm (Fig. 3). Therefore, wide ranges of wavelengths were tested in the fitting process, as it would be more accurate to fit over a high number of wavelengths. Figure 5(C) shows an example of some of the tested wavelength ranges used to fit artificial spectra consisting of 10-60 µM dHb, 60-10 µM HbO and 44.4 M H2O. The wavelength range that provided the most accurate concentration of HbO, with an error ranging from 1.5% to 30%, was 760-860 nm. Figure 5(D) shows the results of the fitting process of the second differential of one simulated dataset consisting of 40μM HbO over the wavelength range of 760-860 nm. Reasonable estimates of HbO were obtained with this wavelength range (Fig. 5(D)), indicating that such quantification is possible. Even though the algorithm could calculate HbO values from fitting, for this study, HbO values in vivo will be back calculated by using an anoxia pulse and setting tHb = dHb at the peak of the pulse. This anoxia pulse method has been previously validated and is more commonly used [11,28,29]. A 45-50 sec period of 0% O2 inhalation was proved to be sufficient to reach steady state of dHb with no significant effect on other physiological parameters [11,28].
oxCCO and reCCO.
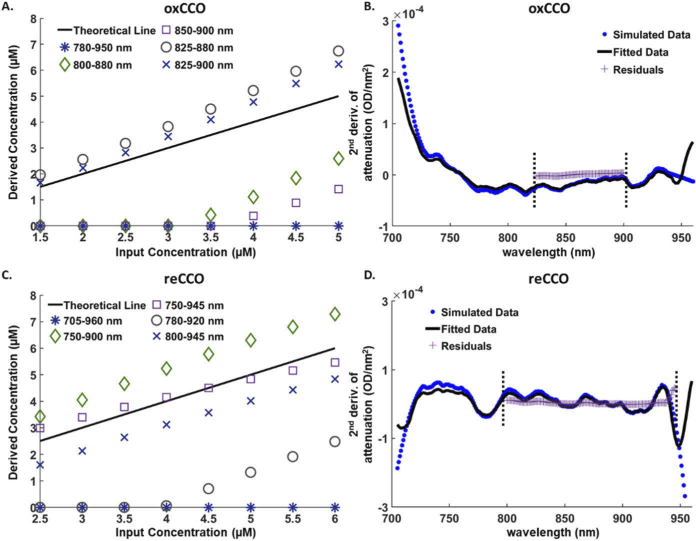
CCO has a broad dominant absorption feature in its oxidised form (oxCCO) around 830 nm, while its reduced form (reCCO) has relatively featureless spectra (Fig. 3). To report absolute values of oxCCO and reCCO, the current algorithm fit the measured attenuation to the specific absorption spectra of oxCCO and reCCO independently, rather than to the difference absorption spectra (oxidized-reduced CCO). To determine the optimal wavelength range reflecting, as accurate as possible, the concentration of each of the CCO forms, several wavelength sets were examined. To our knowledge, we are the first to look at the pure spectra of oxCCO and reCCO separately and at distinct wavelength windows. Figure 6(A) and Fig. 6(C) show examples of the concentration of oxCCO and reCCO respectively, derived by NIR-AQUA versus the nominal concentration set in the artificial datasets which consist of 1.5-5 µM oxCCO, 2.5-6 µM reCCO and 44.4 M H2O. Examples of different sets of wavelength windows that were used in the fitting process are shown. For oxCCO, the optimal wavelength set was found to be 825–900 nm with a MAPE of 16%. This wavelength range includes the dominant feature around 830 nm and has the highest number of wavelengths with minimum overlap with the dominant features of H2O (960 nm) and dHb (760 nm).
Fig. 6.
The absolute concentration of oxCCO (μM) (A) and reCCO (μM) (C) derived by NIR-AQUA, versus the input concentration of simulated datasets. Different wavelength windows were applied in the fitting process, to find the most accurate wavelength range. The theoretical concentration line (black) where derived = input concentration is shown for comparison. (B) A Second-differential spectrum of a simulated dataset (blue dots) consisting of 3 μM oxCCO and (D) 5μM reCCO, and their non-negative least-squares model fit with the second derivative of the specific absorption spectra (black line). Fitting oxCCO and reCCO was found to be optimal over the wavelength range 825 - 900 nm and 800 - 945 nm, respectively. Residuals (purple plus signs) show the accuracy of the fitting model over these wavelength ranges. Dashed vertical lines indicate the wavelength range chosen for the fitting.
Although reCCO has flat spectra relative to oxCCO, its second derivative still shows weak features around 780 and 850 nm (Fig. 6(D)). Fitting over a wider range such as 750-945 shows smaller percentage error, however it would overlap with the dominant features of dHb and H2O. Therefore, the optimal fitting range was found to be 800-945. Although this range overlaps with the oxCCO features, wider fitting range was prioritized in this case. The MAPE for this wavelength window is 23%. Examples of the fitting of the second differential of a simulated dataset consisting of 3μM oxCCO and 5μM reCCO with their specific absorption spectra over the optimal wavelength windows are shown together with the wavelength-independent residuals in Fig. 6(B) and Fig. 6(D), respectively.
2.5. Comparison between NIR-AQUA and the published algorithm (UCLn)
To provide supporting evidence for the absolute measurements of the chromophores by NIR-AQUA, data from the “Varying FiO2 study” were analyzed using the modified Beer-Lambert law (MBLL) as applied with the UCLn algorithm. This algorithm was originally described by Matcher et al. [17] and applied in previous studies [8,16,21,22]. This is a least-squares fitting procedure based on multiple regression analysis, used to calculate the change in concentrations (ΔdHb, ΔHbO, ΔoxCCO), formulated as:
| (5) |
where ΔA is the attenuation change measured over n number of wavelengths, λ. ΔA(λn) is defined as: , with being the average signal recorded during the first 3-5 mins of the experiment at 30% FiO2, and being the recorded signal at time t. , , are the specific extinction coefficient provided in [9]. The log10 is applied here to calculate the attenuation, and the specific extinction coefficients are used to resolve the change in concentrations of the chromophores. Also, is used to resolve the change in the redox state of CCO, which is denoted here as . The wavelength range used for the calculation is 770 to 900 nm. Since this is the first time, to our knowledge, that NIRS data from the mouse cortex is analysed, there is no published pathlength that we could use here. Therefore, we used the mean optical pathlength calculated with NIR-AQUA, which is similar to the method described in Matcher et al. [33]. In order to examine the effect of the wavelength-dependency of the pathlength, the same wavelength-dependence used in [8] was applied. Although there was no significant difference in concentrations when compared to calculations using mean optical pathlength only, we still included this, to be consistent with previous studies that used UCLn.
To facilitate the comparison between the two algorithms, absolute concentrations quantified with NIR-AQUA were converted into relative changes. The change in the redox state of CCO was calculated as the difference between the absolute concentration of oxCCO and reCCO.
3. Results
3.1. Validation under varying levels of FiO2
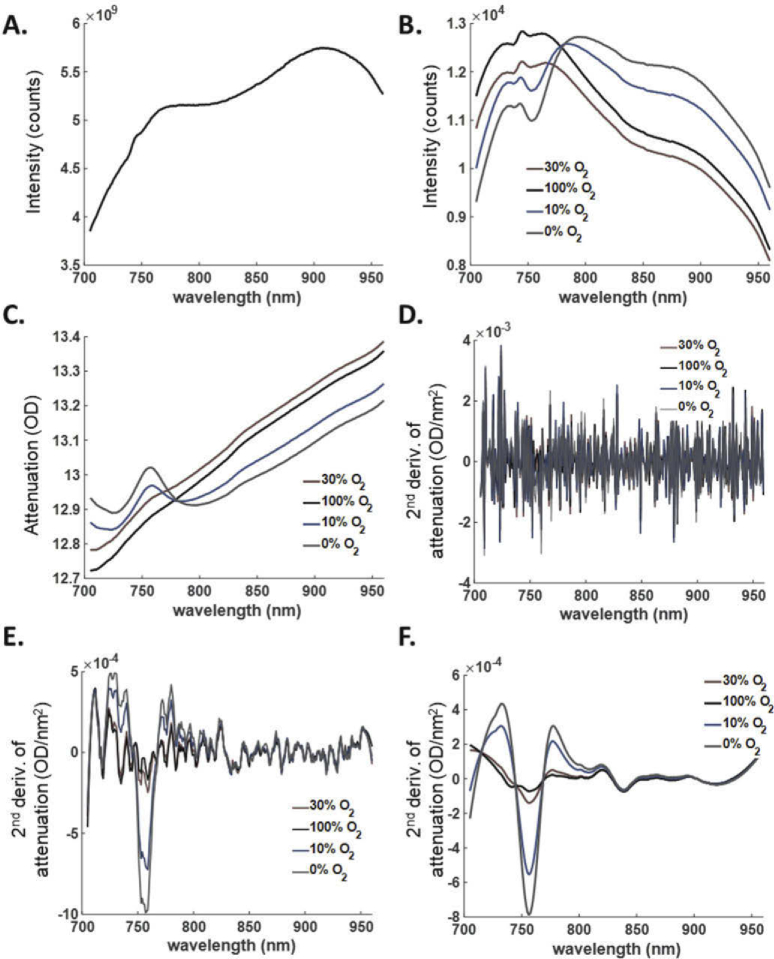
In order to validate the algorithm, we first assessed the impact of varying levels of inhaled oxygen on the absolute values of dHb, HbO, oxCCO, reCCO, tHb and StO2. A time-series of NIRS signals were recorded in 6 mice over a time course of 30-35 minutes for each mouse, under 4 different levels of inhaled O2 (100%, 30%, 10%, and 0%). Figure 7 shows an example of the intensity of the light source spectra (Iref) after calibration (Fig. 7(A)), and the light intensity (Is) recorded from the cortex of a representative mouse during the 4 different levels of FiO2 (Fig. 7(B)). For clarity, each spectrum displayed here is the average of all the continuously collected spectra over the period of the corresponding FiO2 which is 3-5 minutes for 10%, 30% and 100% FiO2 and 45s for the anoxia pulse. The change in the shape of these spectra reflects the change in the concentration of the chromophores due to varying O2 conditions. Figure 7(C) shows the attenuation of these spectra calculated with Eq. (1). The second derivative of the attenuation spectra shown in Fig. 7(D) eliminates baseline shifts, however high-frequency noises are dominating. Figure 7(E) and 7(F) show the effect of the SAVGOL algorithm on eliminating these noises with two different numbers of smoothing points. The parameters used in our algorithm are: Polynomial order = 4, Number of smoothing points = 45, and the derivative order = 2 (Fig. 7(F)). These data clearly showed the distinct absorption peaks of dHb at 760 nm and H2O at 840 nm, whereas the absorption features of oxCCO and reCCO were less recognizable. H2O peak was constant, while the features of dHb and CCO varied with the level of FiO2. The same smoothing is applied to the specific absorption spectra of the chromophores. Higher number of smoothing points (not shown here) causes over-smoothing which may lead to sacrificing small features of chromophores and therefore to calculation errors.
Fig. 7.
Representative NIR spectra collected from the cortex of one mouse. A. Spectra of the light source after calibration (Iref). B. Light intensity (IS) recorded from the cortex of the mouse during different FiO2 levels. Each line represents the average of all the spectra collected during the period of the corresponding O2 challenge. C. Attenuation spectra of the mouse cortex calculated with . D. Second derivative of the attenuation spectra in (C). E. Second derivative of the attenuation spectra in (C) using the smoothing algorithm SAVGOL with the number of smoothing points = 15. F. Second derivative of the attenuation spectra in (C) using the smoothing algorithm SAVGOL with the number of smoothing points = 45.
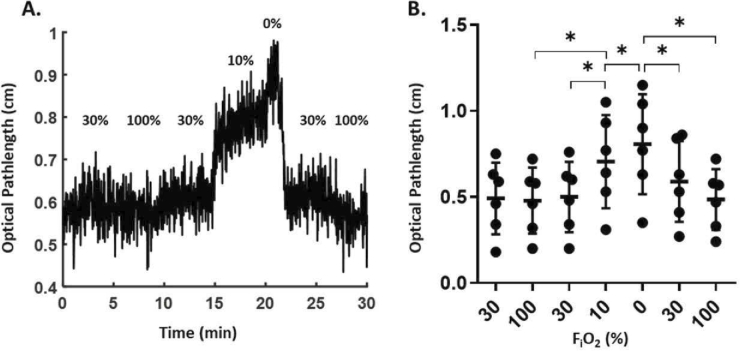
The mean optical pathlength in the mouse cortex was estimated using the second absorption peak (800-850 nm) of H2O and its assumed concentration in the brain tissue (80%). Fitting the second differential of the attenuation collected from the mouse cortex to the second differential of H2O over the wavelength range 800-850 nm, yields a scaling factor which is the apparent mean optical pathlength through the cortex. Figure 8(A) shows the mean optical pathlength from a representative mouse calculated from the recorded spectra over a time course of 30 minutes. Figure 8(B) shows this measurement from 6 mice. The average pathlength did not change significantly between 30% FiO2 (0.50 ± 0.20 cm) and 100% FiO2 (0.48 ± 0.19 cm). At 10% FiO2, the average pathlength was significantly higher (0.70 ± 0.22 cm, p ≤ 0.05) than its value at 30% and 100%. During the anoxia pulse, the average pathlength was significantly higher than its value at the three other FiO2 levels (0.81 ± 0.29 cm, p ≤ 0.05).
Fig. 8.
A. The mean optical pathlength from a representative mouse calculated by fitting the recorded spectra with H2O absorption spectra over the range 800-850 nm under 4 different FiO2 (100%, 30%, 10%, 0%). B. Measurement of mean optical pathlength under varying FiO2 levels in a group of control mice. Each black dot represents the average value at the corresponding FiO2 level for each mouse (mean ± SD, n = 6). Statistical analysis was performed to compare these values under the different FiO2 using one-way ANOVA with repeated measures and a Bonferroni post-hoc test (*- p ≤ 0.05). Significance between repeated FiO2 levels is not shown for clarity.
Figure 9(A) shows the absolute concentrations of the 4 chromophores (dHb, HbO, reCCO, oxCCO) extracted by NIR-AQUA, from the raw NIRS spectra, under the different levels of FiO2. As expected, dHb and reCCO concentrations increased in low levels of O2, while HbO and oxCCO concentrations decreased. tHb concentration is equal to the concentration of dHb at the peak of the anoxia pulse. dHb, and tHb concentrations were used to determine HbO and the oxygen saturation in tissue (StO2) with the following equation:
| (6) |
Fig. 9.
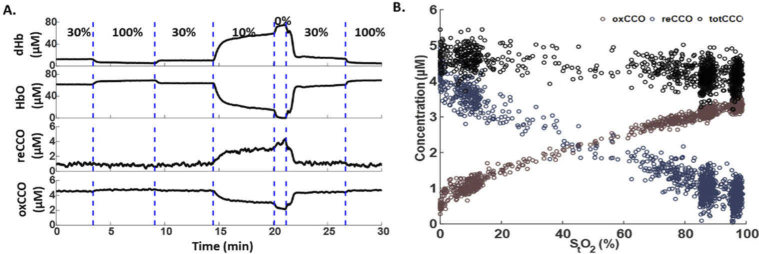
A. The absolute concentration (µM) of cortical dHb, HbO, reCCO, and oxCCO, under varying FiO2 levels, quantified from the raw spectra of a representative mouse, using NIR-AQUA. Dashed lines indicate the initiation of a different level of inhaled O2. B. The correlation between the concentration of oxCCO (red circles), reCCO (blue circles), totCCO (black circles) and StO2 levels. oxCCO has a positive linear correlation, reCCO has a negative linear correlation and totCCO remains constant with StO2.
The correlation between the concentration of oxCCO, reCCO, totCCO and the calculated levels of StO2 in a representative mouse is shown in Fig. 9(B). oxCCO shows a positive linear correlation with StO2, while reCCO shows a negative linear correlation, and the total concentration of the enzyme (totCCO) remains constant with the different levels of StO2.
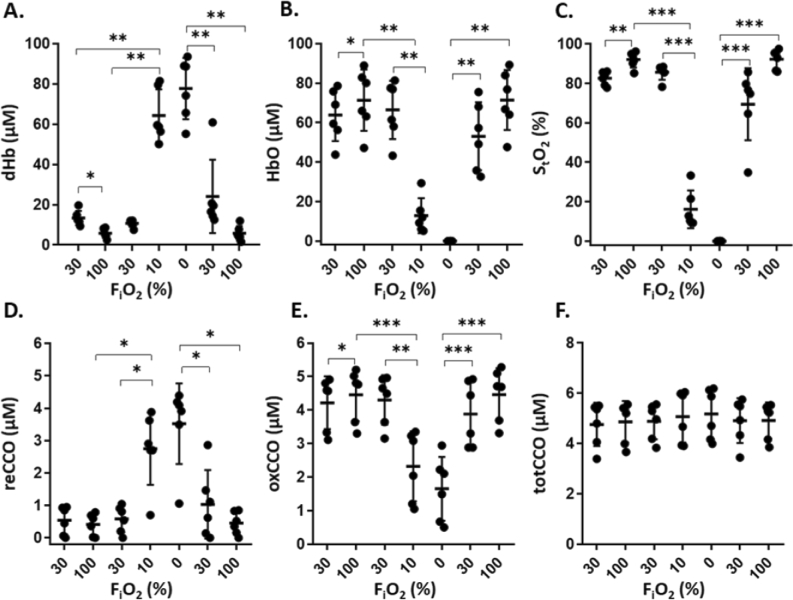
Figure 10 summarizes all the parameters quantified with NIR-AQUA in 6 mice, under varying levels of FiO2. For each mouse, the value of each correlate at a particular FiO2 level is obtained by averaging the concentrations extracted from all the spectra collected at the same FiO2 level. The average concentration of dHb and HbO ranged from 5.8 ± 2.3 μM to 77.7 ± 15.2 μM (16.1 ± 7.8 μM at normoxia), and 0.02 ± 0.04 μM to 71.4 ± 15.2 μM (61.1 ± 15.4 μM at normoxia) respectively. StO2 values were 0.03 ± 0.07% at 0% FiO2, 79.2 ± 12.6% at 30% FiO2, and 92.3 ± 4.9% at 100% FiO2. oxCCO and reCCO concentration ranged from 1.6 ± 0.9 μM to 4.5 ± 0.8 μM (4.0 ± 0.8 μM at normoxia), and 0.4 ± 0.3 μM to 3.5 ± 1.2 μM (0.9 ± 0.6 μM at normoxia), respectively. totCCO concentration was constant over the different O2 levels (4.9 ± 0.1 μM). For all the parameters shown in Fig. 10 (except of totCCO), there was a significant difference between their values at the different FiO2 levels, however, between 0% and 10% FiO2 there was no significant difference.
Fig. 10.
In vivo measurement of cortical dHb, HbO, StO2, oxCCO, reCCO and totCCO under varying FiO2 levels in a group of control mice. Absolute concentrations are extracted from the raw attenuation spectra using NIR-AQUA. Each black dot represents the average value extracted from all the spectra collected at the corresponding FiO2 level in each mouse (mean ± SD, n = 6). Statistical analysis was performed to compare these values under the different FiO2 using one-way ANOVA with repeated measures and a Bonferroni post-hoc test (* - p ≤ 0.05, ** - p ≤ 0.01, *** - p ≤ 0.001). Significance between repeated FiO2 levels is not shown for clarity.
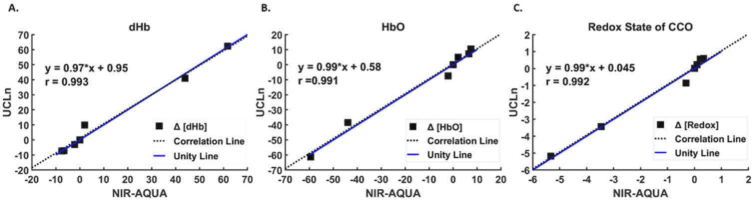
To verify the changes of the chromophores concentrations under varying FiO2, changes in dHb, HbO and the redox state of CCO were calculated using the conventional UCLn algorithm described in the Methods section. Absolute values quantified with NIR-AQUA were converted into relative changes and compared to the relative changes quantified with UCLn. Figure 11 shows the comparison between the relative changes obtained from one mouse using the two algorithms. A strong correlation (r = 0.99) was found between the two methods, with a slope that is very close to the unity line.
Fig. 11.
Broadband NIR data from a representative mouse were analyzed with UCLn and NIR-AQUA. A strong correlation (r = 0.99) was found between the two methods, with a slope that is not significantly different from the unity line.
3.2. Validation in the presence of cyanide
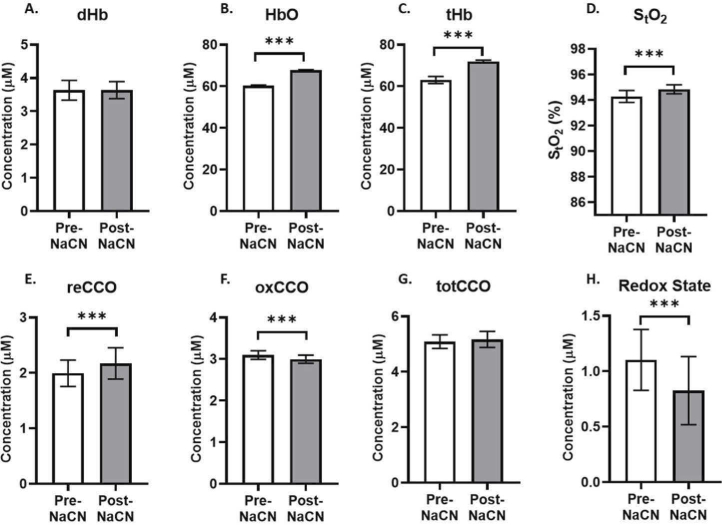
In this study, NaCN was employed as a mitochondrial inhibitor, to demonstrate that the NIR-AQUA can quantify the absolute concentrations of oxCCO and reCCO, independently of changes in dHb and HbO. A range of NaCN doses (10-35 mg/kg) was tested to determine the dose that would cause an uncoupling between Hb and CCO without affecting the heart rate, under spontaneous ventilation. The data presented here are from 2 mice that were infused with 15 mg/kg NaCN. Baseline measurements were recorded pre-NaCN infusion at 100% FiO2. After 55 minutes of NaCN infusion, collecting data continued for additional 10 minutes to investigate the effect of NaCN on the different chromophores. A brief anoxia pulse was given pre and post NaCN to quantify tHb under both conditions. Figure 12 shows a comparison between Hb and CCO correlates pre and post NaCN infusion. All the data collected over 10 minutes at each condition were averaged for each mouse. While dHb concentration did not change, a significant increase in HbO (+7.5 µM, - p ≤ 0.0001), tHb (+8.9 µM, - p ≤ 0.0001), and StO2 (+0.6%, - p ≤ 0.0001) was observed. In terms of CCO, there was a significant increase in reCCO (+0.2 µM, - p ≤ 0.001), decrease in oxCCO (-0.1 µM, - p ≤ 0.001) and the redox state which is equal to the difference between the concentrations of oxCCO and reCCO (-0.3 µM, - p ≤ 0.001). The total concentration of CCO (totCCO) did not change.
Fig. 12.
In vivo measurement of Hb and CCO pre, and post NaCN infusion. NIR spectra were collected from 2 mice pre and post NaCN (15 mg/kg) infusion at 100% FiO2. Spectral data were collected over 10 minutes under each condition and used to quantify the chromophores from the 2 mice (mean ± SD). t-test was used to compare values pre and post NaCN infusion (*** - p ≤ 0.0001).
Over the time course of NaCN infusion, dHb concentrations showed a decrease while reCCO showed an increase (data not shown here). dHb was restored after the termination of the cyanide challenge, while a part of CCO was locked in its reduced state. This shows that CCO quantification does not mirror the change in dHb.
4. Discussion
4.1. Algorithm
The overall goal of this study was to show that NIRS quantification of chromophores is possible in a mouse brain and to further advance the quantification from broadband NIR spectroscopy. To this end, the algorithm NIR-AQUA, which is based on the modified Beer-Lambert law, was proposed. It is an evolution of previous algorithms, such as [8,15–19,40]. NIR-AQUA differs in that the output is an absolute quantification of concentrations. The main assumptions underlying this algorithm are that tissue scattering and water content remain constant throughout the in vivo measurement period. Spectral features ascribed to tissue scattering, along with baseline shifts and linear trends were eliminated from the attenuation spectra by applying the second derivative. This approach increases the sensitivity and selectivity of the features in the original spectra and allows easier distinguishing of little changes in the position, intensity, and shape of the different chromophores features [1,34].
Mean Optical Pathlength.
Converting in vivo attenuation data into absolute concentrations of chromophores requires a real-time estimation of the optical pathlength. The wavelength-dependent pathlength has been suggested as a solution for distinguishing between chromophores and reducing crosstalk issues [41]. However, CW-NIRS cannot measure the wavelength-dependent pathlength [42]. In such cases, researchers have used tabular values or a constant differential pathlength factor that was experimentally determined with time or frequency resolved NIRS in prior studies [32,43].
In the current study we estimated the mean optical pathlength by fitting the second differential of the recorded spectra to the second differential of H2O absorption spectra over the wavelength range 800-850 nm. This approach has been demonstrated to provide an accurate assessment for the mean optical pathlength in the tissue [33]. Previous fitting algorithms based their calculation on either one or two of the three water absorption features (740, 840, and 960 nm) [3,17,33]. Since the 840 nm feature is located within the range of wavelengths usually used to extract chromophores concentrations (700-960 nm), it contains more accurate wavelength-dependent information and thus is a better pathlength estimator. Moreover, it has been demonstrated that fitting against the 840 nm water feature yields pathlength estimates which are consistent with those measured with time-resolved systems, without the need for correction factors or prior knowledge regarding the absorption and scattering coefficients in the tissue [33]. Therefore, in this study, we did not correct for the wavelength-dependency of the mean optical pathlength. Additionally, such experiments have not been done in mouse brain before, therefore using tabular values extracted from other animal models or neonates would not be accurate, as optical properties and hence pathlength vary with species, tissue layers, age, and individuals [44].
Wavelength Range.
An additional important factor affecting the accuracy of calculating concentrations from attenuation spectra, is the selection of wavelengths corresponding to each chromophore. The optimal wavelength window for chromophores, especially those which lack dominant and well-defined features, would be the result of a good compromise between the number of wavelengths used in the fitting process, and their location relative to other chromophore absorption peaks [17,21]. Since CCO has a broad absorption feature, partially overlapping with the absorption feature of the dominant dHb, NIR-AQUA uses the higher number possible of wavelengths and excludes shorter wavelengths to reduce the contribution from dHb which has a sharp, well-defined peak at 760 nm. The wavelength ranges selected for the fitting of dHb (720-810 nm) and oxCCO (825-900 nm) do not overlap. reCCO has weaker absorption features, therefore the wavelength range selected was wider (800-945). Although the analytical model showed that a higher number of wavelengths provided a slightly better fit, the selected range for reCCO was a good compromise between accuracy and minimizing contamination from the well-defined features of dHb and H2O. The range of wavelengths were selected iteratively. The ranges that gave the smallest %error in concentration, when inputting known concentrations, were selected (Fig. 5,6).
Validity of the algorithm.
The first step in validating the algorithm was to apply it to artificial spectra of known chromophore concentrations. The comparison between nominal and derived concentrations (Fig. 5,6) showed that the algorithm underestimated dHb and reCCO by a mean absolute percentage error (MAPE) of 5.6% and 23% respectively. It overestimated oxCCO by a MAPE of 16%. These percentage errors between nominal and derived concentrations are expected in such algorithms mainly because the second differential approach cannot completely remove the scattering effects. The scattering effect induced in these artificial data, and in vivo scattering effects as well, may still have residuals contaminating the signals of the chromophores of interest. In addition, the consideration of water, dHb, HbO,oxCCO and reCCO as the only main chromophores contributing to the absorption in the tissue may also result in errors. Another source of error may be due to the fact that the wavelength-dependency of the pathlength was not considered.
Such an algorithm can be adopted as a simple and inexpensive NIRS method for the quantification of Hb and CCO in vivo. Although there are errors, they are in a predictable direction and so, to some extent, can be accounted for in the interpretation.
4.2. In vivo validation
While the previous section assessed the errors using model spectra, the current section adds to the validation of the algorithm by quantifying in vivo data under conditions aimed at causing differential changes in the chromophores, such as changing inspired oxygen and inhibiting CCO with cyanide. Broadband NIR data were collected non-invasively from the cortex of a mouse model and analysed with NIR-AQUA.
4.2.1. Impact of oxygenation on pathlength
Estimating the mean optical pathlength in each mouse was critical to obtain reliable quantification of chromophores. An inter-subject variation in the pathlength was observed, justifying the need to estimate this parameter in each subject independently. Similar variations were observed in neonates with CW, time- and phase-resolved spectroscopy [1,44–46] showing that intrinsic anatomical variations affect the optical properties in the tissue and hence the measured pathlength. Such variations are likely due to the inhomogeneous nature of the brain, the thickness of the layers that may vary between subjects [43,45] and the variability in scattering [46].
The pathlength was significantly affected by severe hypoxia (10% FiO2) and anoxia (0% FiO2), however, it didn’t change when the chromophore concentrations changed between 100% and 30% FiO2. The optical pathlength in this model is determined by scattering. Therefore, an increase in the pathlength under hypoxia and anoxia indicates an increase in scattering. Cellular nuclei and mitochondria are the main components causing light scattering [47]. It has been shown that anoxia causes shrinkage in the matrix of mitochondria and therefore a reversible increase in light scattering [48,49]. These optical changes are not due to the change in the density or total mitochondrial volume [48,49]. A change in light scattering was also observed in studies where brain oxygen saturation was decreased by lowering FiO2 below 10% [50,51]. These changes show the importance of concurrent estimation of the pathlength for accurate quantification of chromophores under varying oxygen conditions.
4.2.2. Impact of oxygenation on chromophores
This study showed how the chromophore concentrations derived by NIR-AQUA reflect physiological alterations due to changes in cerebral oxygenation. An increase in oxCCO and a decrease in reCCO was observed when high levels of O2 were inhaled (Fig. 9, 10). Since O2 is the final electron acceptor in the electron transport chain, lack or reduced levels of O2 causes to an accumulation of electrons leading to the reduction of CCO. Consistent with this, there was an increase in reCCO and a decrease in oxCCO levels during hypoxia. In normoxic conditions (30% FiO2), 84% of the enzyme was in its oxidized form while 16% was in its reduced state.
This is consistent with the observation that, in an in vitro mixture of CCO and Cytochrome C under normal physiological conditions, 15% of the CuA site of CCO was available for reduction by the electron donor, Cytochrome C [52]. Moreover, in a previous NIRS study, the fraction of oxidized CuA in the adult rat brain was calculated to be 82.0 ± 16.6% [11]. In hyperoxia (100% FiO2) the percentage of the oxidized form was higher (91%) because of the higher availability of O2, but the enzyme was not fully oxidized due to the presence of the electron donor, Cytochrome C which constantly re-reduces the CuA site. During the anoxia pulse where FiO2 was switched to 0% for a period of 45 s, only 75% of the enzyme was in its reduced state. This indicates that such short durations of 0% O2 do not result in total reduction of CCO.
The total concentration of CCO, which was calculated as the sum of oxCCO and reCCO, remained constant and was not affected by the oxygenation level. This is consistent with the fact that the content of the enzyme should not change over such short periods of time [6]. The quantification of the absolute concentration of the enzyme (totCCO) makes it possible to study regulation of CCO content. totCCO would be a marker for mitochondrial damage in some diseases that are expressed for instance, by an abnormal number of mitochondria and/or abnormal number of respiratory complexes per mitochondrion. Knowing the absolute concentration of CCO in addition to its absolute redox state allows us to compare between subjects, without any prior baseline measurements and without any external interventions such as applying O2 challenges.
There is no gold standard for the measurement of absolute levels of CCO in vivo. To our knowledge, this is the first time the absolute concentration of CCO has been non-invasively measured in the brain of living mice. A previous study used visible spectral changes in a homogenized suspension of extracted rat brains and reported an absolute concentration of CCO ranging from 1.2 μM at birth and 5.5 μM in adult rats [53]. The concentration of CCO reported here is 4.9 ± 0.1 μM (mean ± SD, n=6), which falls in the range reported in the in vitro study.
In addition to CCO quantification, dHb and HbO, were also quantified and changed with FiO2. The concentration of tHb (77.7 ± 15.2 μM, Fig. 10) falls within previously measured values in rats [3,11]. StO2 of 79.2 ± 12.6% (Fig. 10) was also similar to that observed in an isoflurane anesthetized mouse and rat models while breathing 30% O2 [29,40].
A brief anoxia pulse [11,28,54] was needed in order to measure tHb (and therefore HbO and StO2). Applying such manipulation may be a drawback of the 2nd derivative approach, as it is unable to report HbO concentrations through direct quantification from NIR spectra. As we are focusing on using rodents, the anoxia pulse is acceptable. This method has been previously validated and proved to allow a steady state of dHb with no significant effect on other physiological parameters [11,28,29]. However, this approach is not applicable in humans. An alternative approach, using “Graded Hypoxia”, has been shown previously by us and others to report similar results to those reported by the anoxia pulse method [28,55–57]. Therefore, the graded hypoxia method could be applied alternatively, to facilitate the quantification of tHb in humans.
Decreases in cerebral StO2 have been shown to correlate with decreases in the mean arterial blood pressure, which could cause reduced cerebral blood flow and oxygen delivery [58]. As we did not maintain blood pressure or heart rate during hypoxia, there is a possibility that the reduction in Hb saturation and CCO redox is larger than if we had maintained cardiovascular function. In addition, it has been shown that severe hypoxic-ischemic injury disrupts the metabolic response to anoxia, leading to a difference in the response of CCO [59]. However, the data presented here do represent the whole-body physiological changes that occur in a mouse under isoflurane anesthesia at these levels of inspired oxygen.
The absolute concentration changes calculated with NIR-AQUA were found consistent with the relative changes calculated with the UCLn algorithm, a conventional NIRS algorithm based on the MBLL [8,9,16,17,21,22]. This supports the conclusion that NIR-AQUA is reliable for quantifying the absolute values of dHb, HbO, oxCCO and reCCO.
4.2.3. Impact of cyanide on chromophores
The purpose of this study was to demonstrate that the values of CCO quantified with NIR-AQUA are independent of Hb concentration. This validation is important as crosstalk between Hb and CCO quantification is a major issue that NIRS algorithms try to overcome [11,27]. We used cyanide which is known to target the active sites of CCO and inhibit the reduction of oxygen, leading to the uncoupling of CCO and Hb saturation.
In this study, a reduction in the redox state of CCO occurred during the infusion of mild doses of NaCN (15 mg/kg) under spontaneous ventilation. The concentration of reCCO increased by 9%, while the concentration of oxCCO decreased by 3% in average. The redox state of CCO decreased by 25% in average at the end of the NaCN infusion. Such reduction in ΔoxCCO have been reported previously in ΔμM [27,60] and arbitrary units (AU) [14]. The changes in the concentration of oxCCO and reCCO detected in the current study may be relatively smaller, compared to other published data [24,27,60]. This may be due to the different animal models and setups that have been used previously in order to induce full reduction of CCO. In addition, high levels of inhaled oxygen led to increased oxidation level of CCO which could decrease the rate of NaCN binding to CCO [61,62]. It is important to note that the change in the concentration of oxCCO and reCCO was not equal. It has been proved that although cyanide binds with both the reduced and the oxidized forms of the enzyme [62,63], the interaction rate with reCCO is two order of magnitudes faster than its reaction with the oxidized form [63]. This may contribute to the difference in the change observed between oxCCO and reCCO and explain why the change is observed more in reCCO than in oxCCO.
The transient inhibition of CCO during NaCN infusion caused a decrease in cerebral oxygen consumption, and thus a lower oxygen extraction. This led to an increase in StO2 (0.6%) and HbO (12%). tHb increased (14%) significantly as well, indicating that the blood volume increased due to CN poisoning. This is consistent with the increase of relative blood volume reported in literature [27,61]. It has been shown that in such cases, where sublethal doses of CN were used, the relative blood volume increased but the mean arterial pressure didn’t drop below the autoregulatory threshold [27,61], therefore oxygen delivery was not compromised.
The reduction in the redox state of CCO, along with a higher tissue oxygenation are both evidence that the mild NaCN dose impacted mitochondria and that inhibiting CCO impacted the relationship between tissue oxygenation and redox. The ability to quantify the opposite change in redox state of CCO and tissue oxygenation support the conclusion that NIR-AQUA is able to differentiate CCO from Hb.
The mild CN doses applied here did not appear to critically impair the cardiovascular system. The mice remained alive after the infusion, and dHb returned to pre-CN levels after CN infusion ended, while reCCO did not fully recover. Additional evidence for this being an acceptably mild dose of CN was that CCO was not fully inhibited and did not become locked in a reduced state. If CCO were fully inhibited by CN, reducing FiO2 would lead to a drop in HbO and an increase in dHb without additional reduction of CCO. This was not the case here since the response of CCO to the different FiO2 challenges, was similar pre- and post- CN infusion.
4.3. Summary of validation
Previous measures of CCO with NIRS use algorithms that measure relative change. When comparing between animals, or over time, in metabolic disease models, it would be useful to have a more quantitative metric. The following summarizes the validations we noted above.
The total CCO concentrations quantified with our algorithm were within the range of reported values [53,54]. In addition, when animals were measured repeatedly over days, similar values were obtained. For instance, we measured totCCO in 6 mice and found the baseline to be 4.9 ± 0.1 μM with a coefficient of variation of 2%. This is an excellent coefficient of variation (CV<15%) for between animal studies. We also showed that repeated measures of CCO in the varying levels of FiO2 experiment, had large shifts in oxCCO and reCCO while totCCO didn’t change. These had an average within animal repeated measures CV of 6.9% between the 7 measures of totCCO in each animal (Fig. 10(F)).
We suggest that the comparison with UCLn based algorithms is helpful. This algorithm has been used multiple times to quantify changes in the oxidation state of CCO. We compared the relative changes quantified with the UCLn algorithm with those obtained with NIR-AQUA, where we quantified the absolute value at each FiO2, but then converted the values to relative changes. These compare very well with the UCLn data (Fig. 11).
Finally, we note that many factors could impact the absolute values such as adding additional chromophores (fat, other cytochromes), correcting for the spectral responsivity of the camera, improving the fit with additional modeling, changing the water concentration etc. As a result, we acknowledge that the absolute values have error. However, the variation between measurements is relatively low, and the values are in an expected range, making this method useful for looking at metabolic changes between strains and over time.
5. Conclusions
We present a new NIRS analysis (NIR-AQUA), that enables continuous monitoring and quantification of absolute values of oxCCO, reCCO and totCCO in the cerebral cortex of living mice, in addition to tHb and tissue oxygenation, which were quantified using a brief anoxia pulse. An analytical modeling was used to identify wavelength ranges suitable for each chromophore and optimize the fitting process. In vivo experiments were used to validate the suggested approach; Changes in CCO redox state were measured under different levels of FiO2, showing capability of the suggested algorithm to identify cerebral metabolic perturbations. The NIR-AQUA algorithm was able to detect changes in the concentration of oxCCO and reCCO, caused by the mitochondrial inhibitor CN, independently of cerebral oxygenation, and in the presence of hemoglobin. This provides the first absolute quantitative assessment of oxCCO, reCCO and totCCO, simultaneously with dHb, HbO, tHb and StO2, in a mouse model.
The novel approach presented here will prove useful in expanding our understanding of how hemodynamics, redox state and concentration of CCO, and cerebral oxygen saturation respond to many physiological perturbations. It also lays the groundwork for future research into neurological diseases where alterations in oxygen metabolism and mitochondrial damage are known to be involved.
Acknowledgments
We would like to thank David Rushforth, the technical operations manager of the Experimental Imaging Centre, Department of Radiology, University of Calgary, for performing the animals surgery in the cyanide experiment, and the graphic designer Rindala Hachem for illustrating the schematic design of the NIRS system in Fig. 1.
Funding
National Institutes of Health10.13039/100000002 (R21 EB021397); Canada Foundation for Innovation10.13039/501100000196 (Project 4933); Natural Sciences and Engineering Research Council of Canada10.13039/501100000038 (RGPIN-2015-06517); Eyes High International Doctoral Scholarship; Alberta Graduate Excellence Scholarship (AGES).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Cooper C. E., Elwell C. E., Meek J. H., Matcher S. J., Wyatt J. S., Cope M., Delpy D. T., “The noninvasive measurement of absolute cerebral deoxyhemoglobin concentration and mean optical path length in the neonatal brain by second derivative near infrared spectroscopy,” Pediatr Res 39(1), 32–38 (1996). 10.1203/00006450-199601000-00005 [DOI] [PubMed] [Google Scholar]
- 2.Delpy D., Cope M., “Quantification in tissue near–infrared spectroscopy,” Phil. Trans. R. Soc. Lond. B 352(1354), 649–659 (1997). 10.1098/rstb.1997.0046 [DOI] [Google Scholar]
- 3.Matcher S. J., Cooper C. E., “Absolute quantification of deoxyhaemoglobin concentration in tissue near infrared spectroscopy,” Phys. Med. Biol. 39(8), 1295–1312 (1994). 10.1088/0031-9155/39/8/008 [DOI] [PubMed] [Google Scholar]
- 4.Fontanesi F., Soto I. C., Barrientos A., “Cytochrome c oxidase biogenesis: new levels of regulation,” IUBMB Life 60(9), 557–568 (2008). 10.1002/iub.86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jobsis F. F., “Noninvasive, infrared monitoring of cerebral and myocardial oxygen sufficiency and circulatory parameters,” Science 198(4323), 1264–1267 (1977). 10.1126/science.929199 [DOI] [PubMed] [Google Scholar]
- 6.Bale G., Elwell C. E., Tachtsidis I., “From Jobsis to the present day: a review of clinical near-infrared spectroscopy measurements of cerebral cytochrome-c-oxidase,” J. Biomed. Opt 21(9), 091307 (2016). 10.1117/1.JBO.21.9.091307 [DOI] [PubMed] [Google Scholar]
- 7.Tisdall M. M., Tachtsidis I., Leung T. S., Elwell C. E., Smith M., “Increase in cerebral aerobic metabolism by normobaric hyperoxia after traumatic brain injury,” JNS 109(3), 424–432 (2008). 10.3171/JNS/2008/109/9/0424 [DOI] [PubMed] [Google Scholar]
- 8.Bale G., Mitra S., Meek J., Robertson N., Tachtsidis I., “A new broadband near-infrared spectroscopy system for in-vivo measurements of cerebral cytochrome-c-oxidase changes in neonatal brain injury,” Biomed. Opt. Express 5(10), 3450–3466 (2014). 10.1364/BOE.5.003450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kolyva C., Tachtsidis I., Ghosh A., Moroz T., Cooper C. E., Smith M., Elwell C. E., “Systematic investigation of changes in oxidized cerebral cytochrome c oxidase concentration during frontal lobe activation in healthy adults,” Biomed. Opt. Express 3(10), 2550–2566 (2012). 10.1364/BOE.3.002550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Siddiqui M. F., Lloyd-Fox S., Kaynezhad P., Tachtsidis I., Johnson M. H., Elwell C. E., “Non-invasive measurement of a metabolic marker of infant brain function,” Sci Rep 7(1), 1330 (2017). 10.1038/s41598-017-01394-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cooper C. E., Delpy D. T., Nemoto E. M., “The relationship of oxygen delivery to absolute haemoglobin oxygenation and mitochondrial cytochrome oxidase redox state in the adult brain: a near-infrared spectroscopy study,” Biochem J. 332(3), 627–632 (1998). 10.1042/bj3320627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bainbridge A., Tachtsidis I., Faulkner S. D., Price D., Zhu T., Baer E., Broad K. D., Thomas D. L., Cady E. B., Robertson N. J., Golay X., “Brain mitochondrial oxidative metabolism during and after cerebral hypoxia-ischemia studied by simultaneous phosphorus magnetic-resonance and broadband near-infrared spectroscopy,” NeuroImage 102(1), 173–183 (2014). 10.1016/j.neuroimage.2013.08.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tsuji M., Naruse H., Volpe J., Holtzman D., “Reduction of cytochrome aa3 measured by near-infrared spectroscopy predicts cerebral energy loss in hypoxic piglets,” Pediatr. Res. 37(3), 253–259 (1995). 10.1203/00006450-199503000-00001 [DOI] [PubMed] [Google Scholar]
- 14.Thiele R. H., Ikeda K., Osuru H. P., Zuo Z., “Comparison of broadband and discrete wavelength near-infrared spectroscopy algorithms for the detection of cytochrome aa3 reduction,” Anesthesia & Analgesia 129(5), 1273–1280 (2019). 10.1213/ANE.0000000000003572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tisdall M. M., Tachtsidis I., Leung T. S., Elwell C. E., Smith M., “Near-infrared spectroscopic quantification of changes in the concentration of oxidized cytochrome c oxidase in the healthy human brain during hypoxemia,” J. Biomed. Opt. 12(2), 024002 (2007). 10.1117/1.2718541 [DOI] [PubMed] [Google Scholar]
- 16.Kolyva C., Ghosh A., Tachtsidis I., Highton D., Cooper C. E., Smith M., Elwell C. E., “Cytochrome c oxidase response to changes in cerebral oxygen delivery in the adult brain shows higher brain-specificity than haemoglobin,” NeuroImage 85, 234–244 (2014). 10.1016/j.neuroimage.2013.05.070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Matcher S. J., Elwell C. E., Cooper C. E., Cope M., Delpy D. T., “Performance comparison of several published tissue near-infrared spectroscopy algorithms,” Analytical Biochemistry 227(1), 54–68 (1995). 10.1006/abio.1995.1252 [DOI] [PubMed] [Google Scholar]
- 18.Nosrati R., Lin S., Ramadeen A., Monjazebi D., Dorian P., Toronov V., “Cerebral hemodynamics and metabolism during cardiac arrest and cardiopulmonary resuscitation using hyperspectral near infrared spectroscopy,” Circ J 81(16), 1225 (2017). 10.1253/circj.CJ-16-1225 [DOI] [PubMed] [Google Scholar]
- 19.Yeganeh H. Z., Toronov V., Elliott J. T., Diop M., Lee T. Y., St Lawrence K., “Broadband continuous-wave technique to measure baseline values and changes in the tissue chromophore concentrations,” Biomed. Opt. Express 3(11), 2761–2770 (2012). 10.1364/BOE.3.002761 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Scholkmann F., Kleiser S., Metz A. J., Zimmermann R., Mata Pavia J., Wolf U., Wolf M., “A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology,” NeuroImage 85(1), 6–27 (2014). 10.1016/j.neuroimage.2013.05.004 [DOI] [PubMed] [Google Scholar]
- 21.Arifler D., Zhu T., Madaan S., Tachtsidis I., “Optimal wavelength combinations for near-infrared spectroscopic monitoring of changes in brain tissue hemoglobin and cytochrome c oxidase concentrations,” Biomed. Opt. Express 6(3), 933–947 (2015). 10.1364/BOE.6.000933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lange F., Dunne L., Hale L., Tachtsidis I., “MAESTROS: a multiwavelength time-domain NIRS system to monitor changes in oxygenation and oxidation state of cytochrome-c-oxidase,” IEEE J. Select. Topics Quantum Electron. 25(1), 1–12 (2019). 10.1109/JSTQE.2018.2833205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ghosh A., Tachtsidis I., Kolyva C., Highton D., Elwell C., Smith M., “Normobaric hyperoxia does not change optical scattering or pathlength but does increase oxidised cytochrome C oxidase concentration in patients with brain injury,” in Oxygen Transport to Tissue XXXIV (Springer, 2013), pp. 67-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee J., Armstrong J., Kreuter K., Tromberg B. J., Brenner M., “Non-invasive in vivo diffuse optical spectroscopy monitoring of cyanide poisoning in a rabbit model,” Physiol. Meas 28(9), 1057–1066 (2007). 10.1088/0967-3334/28/9/007 [DOI] [PubMed] [Google Scholar]
- 25.Blomgren K., Hagberg H., “Free radicals, mitochondria, and hypoxia-ischemia in the developing brain,” Free Radical Biology and Medicine 40(3), 388–397 (2006). 10.1016/j.freeradbiomed.2005.08.040 [DOI] [PubMed] [Google Scholar]
- 26.Wray S., Cope M., Delpy D. T., Wyatt J. S., Reynolds E. O., “Characterization of the near infrared absorption spectra of cytochrome aa3 and haemoglobin for the non-invasive monitoring of cerebral oxygenation,” Biochim. Biophys. Acta 933(1), 184–192 (1988). 10.1016/0005-2728(88)90069-2 [DOI] [PubMed] [Google Scholar]
- 27.Cooper C. E., Cope M., Springett R., Amess P. N., Penrice J., Tyszczuk L., Punwani S., Ordidge R., Wyatt J., Delpy D. T., “Use of mitochondrial inhibitors to demonstrate that cytochrome oxidase near-infrared spectroscopy can measure mitochondrial dysfunction noninvasively in the brain,” J. Cereb. Blood Flow Metab. 19(1), 27–38 (1999). 10.1097/00004647-199901000-00003 [DOI] [PubMed] [Google Scholar]
- 28.Zhang Q., Srinivasan S., Wu Y., Natah S., Dunn J. F., “A near-infrared calibration method suitable for quantification of broadband data in humans,” Journal of Neuroscience Methods 188(2), 181–186 (2010). 10.1016/j.jneumeth.2010.01.037 [DOI] [PubMed] [Google Scholar]
- 29.Hashem M., Zhang Q., Wu Y., Johnson T. W., Dunn J. F., “Using a multimodal near-infrared spectroscopy and MRI to quantify gray matter metabolic rate for oxygen: a hypothermia validation study,” NeuroImage 206, 116315 (2020). 10.1016/j.neuroimage.2019.116315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhang Q., “Development and application of a broadband near-infrared system using the second differential spectrum method,” (University of Calgary, 2008). [Google Scholar]
- 31.Wahr J. A., Tremper K. K., Samra S., Delpy D. T., “Near-infrared spectroscopy: theory and applications,” Journal of Cardiothoracic and Vascular Anesthesia 10(3), 406–418 (1996). 10.1016/S1053-0770(96)80107-8 [DOI] [PubMed] [Google Scholar]
- 32.Delpy D. T., Cope M., van der Zee P., Arridge S., Wray S., Wyatt J., “Estimation of optical pathlength through tissue from direct time of flight measurement,” Physics in medicine and biology 33(12), 1433–1442 (1988). 10.1088/0031-9155/33/12/008 [DOI] [PubMed] [Google Scholar]
- 33.Matcher S. J., Cope M., Delpy D. T., “Use of the water absorption spectrum to quantify tissue chromophore concentration changes in near-infrared spectroscopy,” Phys. Med. Biol. 39(1), 177–196 (1994). 10.1088/0031-9155/39/1/011 [DOI] [PubMed] [Google Scholar]
- 34.Dehghani H., Leblond F., Pogue B. W., Chauchard F., “Application of spectral derivative data in visible and near-infrared spectroscopy,” Phys. Med. Biol. 55(12), 3381–3399 (2010). 10.1088/0031-9155/55/12/008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Savitzky A., Golay M. J., “Smoothing and differentiation of data by simplified least squares procedures,” Anal. Chem. 36(8), 1627–1639 (1964). 10.1021/ac60214a047 [DOI] [Google Scholar]
- 36.Chen H., Song Q., Tang G., Feng Q., Lin L., “The combined optimization of Savitzky-Golay smoothing and multiplicative scatter correction for FT-NIR PLS models,” ISRN Spectroscopy 2013(2), 642190 (2013). 10.1155/2013/642190 [DOI] [Google Scholar]
- 37.Biomedical Optics Research Laboratory UCL , “Tissue Spectra,” (2005), retrieved April 20 2020, https://web.archive.org/web/20170716153131/http://www.ucl.ac.uk/medphys/research/borl/resources/intro-spectra.
- 38.Reinoso R. F., Telfer B. A., Rowland M., “Tissue water content in rats measured by desiccation,” Journal of Pharmacological and Toxicological Methods 38(2), 87–92 (1997). 10.1016/S1056-8719(97)00053-1 [DOI] [PubMed] [Google Scholar]
- 39.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 40.Sakata Y., Abajian M., Ripple M. O., Springett R., “Measurement of the oxidation state of mitochondrial cytochrome c from the neocortex of the mammalian brain,” Biomed. Opt. Express 3(8), 1933–1946 (2012). 10.1364/BOE.3.001933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Skov L., Greisen G., “Apparent cerebral cytochrome aa3 reduction during cardiopulmonary bypass in hypoxaemic children with congenital heart disease. A critical analysis of in vivo near-infrared spectrophotometric data,” Physiol. Meas. 15(4), 447–457 (1994). 10.1088/0967-3334/15/4/006 [DOI] [PubMed] [Google Scholar]
- 42.Talukdar T., Moore J. H., Diamond S. G., “Continuous correction of differential path length factor in near-infrared spectroscopy,” J. Biomed. Opt 18(5), 056001 (2013). 10.1117/1.JBO.18.5.056001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Scholkmann F., Wolf M., “General equation for the differential pathlength factor of the frontal human head depending on wavelength and age,” J. Biomed. Opt 18(10), 105004 (2013). 10.1117/1.JBO.18.10.105004 [DOI] [PubMed] [Google Scholar]
- 44.Zhao H., Tanikawa Y., Gao F., Onodera Y., Sassaroli A., Tanaka K., Yamada Y., “Maps of optical differential pathlength factor of human adult forehead, somatosensory motor and occipital regions at multi-wavelengths in NIR,” Phys. Med. Biol. 47(12), 2075–2093 (2002). 10.1088/0031-9155/47/12/306 [DOI] [PubMed] [Google Scholar]
- 45.Ferrari M., Wei Q., De Blasi R. A., Quaresima V., Zaccanti G., “Variability of human brain and muscle optical pathlength in different experimental conditions,” in Photon Migration and Imaging in Random Media and Tissues (International Society for Optics and Photonics, 1993), 466-472. [Google Scholar]
- 46.Lange F., Dunne L., Tachtsidis I., “Evaluation of haemoglobin and cytochrome responses during forearm ischaemia using multi-wavelength time domain NIRS,” in Oxygen Transport to Tissue XXXIX (Springer, 2017), pp. 67-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang L. V., Wu H.-I., Biomedical Optics: Principles and Imaging (John Wiley & Sons, 2012). [Google Scholar]
- 48.Fujii F., Nodasaka Y., Nishimura G., Tamura M., “Anoxia induces matrix shrinkage accompanied by an increase in light scattering in isolated brain mitochondria,” Brain Research 999(1), 29–39 (2004). 10.1016/j.brainres.2003.11.017 [DOI] [PubMed] [Google Scholar]
- 49.Mane M., Muller M., “Temporo-spectral imaging of intrinsic optical signals during hypoxia-induced spreading depression-like depolarization,” PLoS One 7, e43981 (2012). 10.1371/journal.pone.0043981 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yoshida K., Nishidate I., Ishizuka T., Kawauchi S., Sato S., Sato M., “Multispectral imaging of absorption and scattering properties of in vivo exposed rat brain using a digital red-green-blue camera,” J. Biomed. Opt. 20(5), 051026 (2015). 10.1117/1.JBO.20.5.051026 [DOI] [PubMed] [Google Scholar]
- 51.Mustari A., Kanie T., Kawauchi S., Sato S., Sato M., Kokubo Y., Nishidate I., “In vivo evaluation of cerebral hemodynamics and tissue morphology in rats during changing fraction of inspired oxygen based on spectrocolorimetric imaging technique,” IJMS 19(2), 491 (2018). 10.3390/ijms19020491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vilhjalmsdottir J., Gennis R. B., Brzezinski P., “The electron distribution in the “activated” state of cytochrome c oxidase,” Sci Rep 8(1), 7502 (2018). 10.1038/s41598-018-25779-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Brown G. C., Crompton M., Wray S., “Cytochrome oxidase content of rat brain during development,” Biochim. Biophys. Acta 1057, 273–275 (1991). 10.1016/s0005-2728(05)80109-4 [DOI] [PubMed] [Google Scholar]
- 54.Springett R., Newman J., Cope M., Delpy D. T., “Oxygen dependency and precision of cytochrome oxidase signal from full spectral NIRS of the piglet brain,” American Journal of Physiology-Heart and Circulatory 279(5), H2202–2209 (2000). 10.1152/ajpheart.2000.279.5.H2202 [DOI] [PubMed] [Google Scholar]
- 55.Wyatt J. S., Cope M., Delpy D. T., Richardson C. E., Edwards A. D., Wray S., Reynolds E. O., “Quantitation of cerebral blood volume in human infants by near-infrared spectroscopy,” Journal of Applied Physiology 68(3), 1086–1091 (1990). 10.1152/jappl.1990.68.3.1086 [DOI] [PubMed] [Google Scholar]
- 56.Elwell C. E., Cope M., Edwards A. D., Wyatt J. S., Delpy D. T., Reynolds E. O., “Quantification of adult cerebral hemodynamics by near-infrared spectroscopy,” Journal of Applied Physiology 77(6), 2753–2760 (1994). 10.1152/jappl.1994.77.6.2753 [DOI] [PubMed] [Google Scholar]
- 57.Hashem M., Dunn J. F., “Brain oximetry and the quest for quantified metabolic rate: applications using MRI and near-infrared spectroscopy,” Appl. Magn. Reson. 52, 1–35 (2021). 10.1007/S00723-021-01345-Y [DOI] [Google Scholar]
- 58.Tsuji M., duPlessis A., Taylor G., Crocker R., Volpe J. J., “Near infrared spectroscopy detects cerebral ischemia during hypotension in piglets,” Pediatr Res 44(4), 591–595 (1998). 10.1203/00006450-199810000-00020 [DOI] [PubMed] [Google Scholar]
- 59.Bale G., Rajaram A., Kewin M., Morrison L., Bainbridge A., Diop M., St Lawrence K., Tachtsidis I., “Broadband NIRS cerebral cytochrome-C-oxidase response to anoxia before and after hypoxic-ischaemic injury in piglets,” in Oxygen Transport to Tissue XL (Springer, 2018), pp. 151-156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lee J., Keuter K. A., Kim J., Tran A., Uppal A., Mukai D., Mahon S. B., Cancio L. C., Batchinsky A., Tromberg B. J., “Noninvasive in vivo monitoring of cyanide toxicity and treatment using diffuse optical spectroscopy in a rabbit model,” Military medicine 174(6), 615–621 (2009). 10.7205/MILMED-D-02-7408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Piantadosi C. A., Sylvia A. L., Jobsis F. F., “Cyanide-induced cytochrome a,a3 oxidation-reduction responses in rat brain in vivo,” J. Clin. Invest. 72(4), 1224–1233 (1983). 10.1172/JCI111078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Nicholls P., van Buuren K. J., van Gelder B. F., “Biochemical and biophysical studies on cytochrome aa 3 . 8. Effect of cyanide on the catalytic activity,” Biochim. Biophys. Acta 275(3), 279–287 (1972). 10.1016/0005-2728(72)90208-3 [DOI] [PubMed] [Google Scholar]
- 63.Yonetani T., Ray G. S., “Studies on cytochrome oxidase. VI. kinetics of the aerobic oxidation of ferrocytochrome c by cytochrome oxidase,” Journal of Biological Chemistry 240(8), 3392–3398 (1965). 10.1016/S0021-9258(18)97230-3 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.