Bacteriophage self-counting in the presence of viral replication

Significance

Viral dormancy, in which the infected cell is not killed but rather becomes the long-term residence of the parasite, is a hallmark of viruses across kingdoms from bacteriophages to HIV. When and how viruses decide to opt for this lifestyle remains mysterious. Phage lambda, which serves as a paradigm for viral dormancy, is reported to count the number of coinfecting viruses and then uses this value to assess the abundance of potential hosts and decide whether to become dormant. Here, we use a single-cell measurement of viruses and messenger RNA together with mathematical modeling to illuminate how lambda performs this task.

Abstract

When host cells are in low abundance, temperate bacteriophages opt for dormant (lysogenic) infection. Phage lambda implements this strategy by increasing the frequency of lysogeny at higher multiplicity of infection (MOI). However, it remains unclear how the phage reliably counts infecting viral genomes even as their intracellular number increases because of replication. By combining theoretical modeling with single-cell measurements of viral copy number and gene expression, we find that instead of hindering lambda’s decision, replication facilitates it. In a nonreplicating mutant, viral gene expression simply scales with MOI rather than diverging into lytic (virulent) and lysogenic trajectories. A similar pattern is followed during early infection by wild-type phage. However, later in the infection, the modulation of viral replication by the decision genes amplifies the initially modest gene expression differences into divergent trajectories. Replication thus ensures the optimal decision—lysis upon single-phage infection and lysogeny at higher MOI.

Following genome entry into the host cell, temperate bacteriophages must choose between two developmental pathways (1). In the default lytic pathway, rapid viral replication typically culminates in the death of the host cell (lysis) and release of viral progeny. By contrast, in the lysogenic pathway, phages suppress their virulent functions and enter a dormant prophage state (1). To decide on the infected cell’s fate, temperate phages assess the environmental abundance of potential hosts (1, 2). If susceptible host cells are scarce, then producing hundreds of new phages via the lytic pathway would be futile, and, instead, lysogeny should be chosen. To evaluate the relative abundance of viruses and cells, phages use diverse methods. Some achieve this by measuring the number of simultaneously coinfecting phages (multiplicity of infection, MOI) and increasing the frequency of lysogeny at higher MOI (3, 4). Other bacteriophages harness cell–cell communication to assess the frequency of virus–host encounters in their vicinity (5, 6). Notwithstanding the mechanism by which the measurement is performed, a regulatory circuit encoded by the virus must interpret a biological signal reflecting the relative abundance of viruses and host cells and use it to bias a decision between the two possible outcomes of infection.

Phage lambda, a temperate bacteriophage that infects Escherichia coli, has long served as the paradigm for viral self-counting (7–10). Direct measurements both in bulk (10, 11) and in single cells (12) demonstrated that a higher number of coinfecting phages increases the probability of lysogeny. Decades of experimental interrogation have resulted in a comprehensive genetic understanding of the virus and the identification of key players involved in the lambda postinfection decision (13–15). However, despite this detailed molecular knowledge of the underlying circuitry, our system-level understanding of how MOI drives the infection outcome is far from complete (12, 16, 17). In contrast to the two-gene “switch” governing lysogenic maintenance (18), the network driving the lysis/lysogeny decision comprises multiple genes, regulating each other through diverse molecular interactions (13). The common theoretical view of the decision is that this genetic network is biased by MOI toward either of two attractors, one corresponding to lytic onset, another to lysogeny (7, 9, 16, 17, 19–22). However, the way this takes place varies between models. Further challenging our ability to decipher the circuit’s function is the fact that, while the eventual gene expression patterns in lysis and lysogeny clearly differ, the initial gene expression cascade following infection appears indistinguishable for both pathways (23).

Complicating phages’ task of measuring MOI—and our attempts to decipher how they do it—is the fact that the viral copy number is rapidly increasing inside the infected cell (Fig. 1). Phage replication begins within minutes of genome entry (22) and coincides with the expression of early genes in the decision circuit (23) (Fig. 2). In other words, the initial MOI, which the viral circuitry presumably attempts to measure (24, 25), is soon obfuscated by the presence of additional phage genomes in the cell. Elucidating how lambda succeeds in distinguishing the initial genome number from the instantaneous number present in the cell has remained a challenge partly because of experimental limitations. Within a population, single-cell MOI is broadly distributed (10, 12) (SI Appendix, Fig. S1), necessitating measurements at the level of the individually infected cell. However, simultaneous measurement of the viral copy number and the expression of phage genes has previously not been possible at single-cell resolution.

Fig. 1.

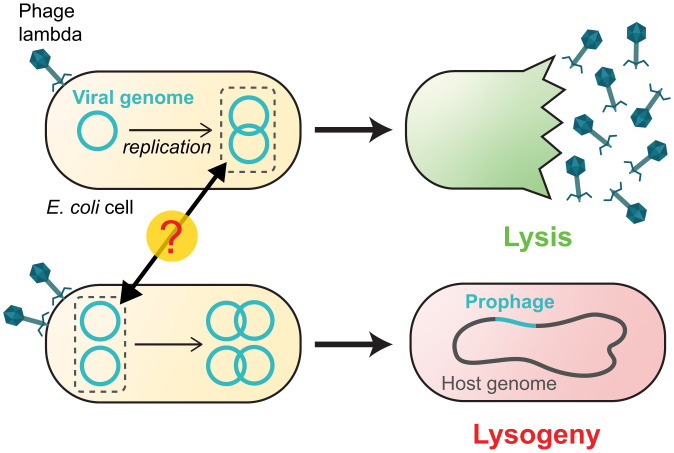
The lambda decision circuit measures the MOI even as the viral copy number is changing. A higher MOI increases the propensity to lysogenize. Here, infection by a single lambda phage (Top) results in lysis, whereas coinfection by two phages (Bottom) leads to lysogeny. In choosing cell fate, the infecting phage must respond to the initial number of viral genomes in the cell but ignore the subsequent increase in number because of viral replication.

Fig. 2.

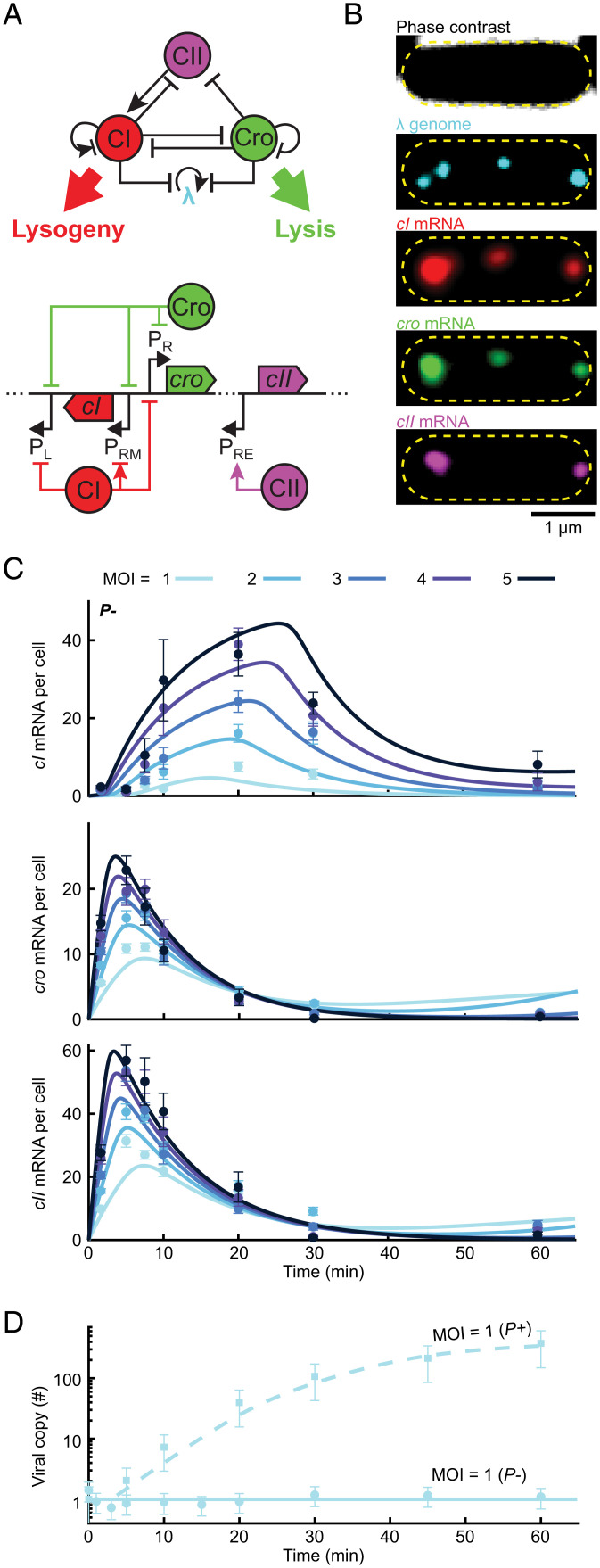
A simplified model of the decision network captures the kinetics of mRNA and viral copy number following infection. (A, Top) The three-gene circuit at the heart of the lysis/lysogeny decision. (Bottom) The corresponding segment of the lambda genome. Upon viral entry, P_R expresses both cro and (following a leaky terminator) cII. CII then activates cI expression from P_RE. CI and Cro repress P_R and P_L as well as phage replication. In a lysogen, CI regulates its own expression from P_RM. (B) Images of a single E. coli cell at 10 min following infection by λ cI857 Pam80 P1parS. Phage genomes are labeled using ParB-parS and the mRNA for cI, cro, and cII using single-molecule fluorescence in situ hybridization. The yellow dashed line indicates the cell boundary. (C) The numbers of cI, cro, and cII mRNA per cell at different times following infection by P− phage (λ cI857 Pam80 P1parS) at MOI = 1 to 5. Markers and error bars indicate experimental mean ± SEM per sample (refer to SI Appendix, Table S6 for detailed sample sizes). Solid lines indicate model fit. (D) Viral copy number measured using qPCR following infection at MOI = 1 by P+ and P− phages. Markers and error bars indicate experimental mean ± SD because of qPCR calibration uncertainty. Lines indicate model fits. Refer to SI Appendix for detailed information.

Here, we combine single-molecule detection of messenger RNA (mRNA) and phage genomes during infection with mathematical modeling of network dynamics to identify how lambda measures the number of coinfecting phages. To circumvent the complication of a time-varying genome number, we first examined infection by a replication-deficient lambda strain. At various times after infection, we measured, in individual cells, the viral copy number (which, in this case, equals the MOI) and mRNA levels of key lambda genes—cI, cro, and cII. To our surprise, we found no divergence of the mRNA trajectories between low and high MOI, indicative of a transition between the lytic and lysogenic attractors. Instead, gene expression simply scaled with viral dosage. This led us to hypothesize that viral replication is required for obtaining an MOI-dependent lysis/lysogeny decision. To test this hypothesis, we constructed a data-calibrated model for the decision network that included the coupling of phage replication to gene expression. Our model revealed that, indeed, viral replication is inextricably coupled to the lysogeny decision. Early in infection, during a time window set by the dynamics of CII, a short-lived activator, expression of the lysogenic repressor CI scales with MOI, similarly to what we observed in the absence of replication. However, subsequent replication—and its modulation by the decision genes—drive a sharp divergence of cell fates as a function of MOI. Specifically, the initial accumulation of CI at MOI > 1 leads to repression of both cro expression and viral replication, enabling the lysogenic choice. In contrast, at MOI = 1, accumulated CI is insufficient to repress cro expression and replication. Consequently, Cro production from a rapidly increasing number of cro gene copies activates the lytic pathway. We thus find that, rather than hindering lambda’s decision by obscuring the initial MOI, viral replication ensures the appropriate choice of lysis upon infection by a single phage and lysogeny upon coinfection.

Results

In the Absence of Viral Replication, Gene Expression Does Not Diverge into Lytic and Lysogenic Trajectories.

To characterize the behavior of the lambda decision circuit, we sought to measure gene expression kinetics during infection across a range of single-cell MOI values. To decouple the gene-regulatory aspects from the effects of time-varying dosage, we first followed the approach of Kourilsky (10) and Arkin et al. (7) and examined infection by a replication-deficient mutant (Pam80, henceforth denoted P−) (10). We focused on the expression of three lambda genes at the heart of the decision circuit—cI, cro, and cII (9, 19, 22) (Fig. 2A). Cro, transcribed from P_R, is a repressor that inhibits transcription of multiple lambda genes (including itself) from the two early promoters P_R and P_L (14). Cro is required for successful lysis to prevent the accumulation of CI and the overproduction of lambda proteins deleterious to later development (14). Transcription of cro can also be used as a proxy for the presence of Q, a critical lytic gene produced from the same polycistronic transcript (23). CI too inhibits transcription from P_R and P_L in addition to regulating its own expression from P_RM and is required for establishing and maintaining lysogeny (23). CII is a short-lived protein that activates early transcription of cI from P_RE, a critical event for the establishment of lysogeny (14). Both CI and Cro also suppress viral replication by inhibiting expression of the lambda replication proteins O and P (23) and by repressing transcription from P_R, required for early replication (13).

To measure the MOI dependence of expression dynamics in this three-gene subnetwork, we combined single-molecule quantification of mRNA and phage genomes in individual cells (26) (Fig. 2B). Following infection by a replication-deficient phage (cI857 Pam80 P1parS; refer to SI Appendix, Experimental Methods and Tables S1–S6 for strain construction and experimental protocols), samples were taken at different time points and chemically fixed. The lambda genomes present in each cell were detected and counted using the ParB-parS system (27, 28) (SI Appendix, Experimental Methods and Fig. S2). In the same cells, mRNA copy numbers for cI, cro, and cII were measured using single-molecule fluorescence in situ hybridization (26, 29). The cells were then grouped based on the measured single-cell MOI, and the averaged mRNA level for each gene, time, and MOI was calculated (Fig. 2C).

All three genes exhibited a transient pulse of expression, with mRNA numbers first rising and then decaying (Fig. 2C). The main difference between genes was in the timing of the expression peak, with cro and cII reaching their highest level ∼10 min after the entry of viral genomes and cI peaking later at about ∼20 min. Biological replicates yielded consistent results (SI Appendix, Fig. S3). The observed dynamics were consistent with our current understanding of the gene expression cascade following infection (Fig. 2A): upon viral entry, cro and cII are transcribed from P_R (SI Appendix, Figs. S4 and S5), and this promoter is later repressed by Cro (23). cI transcription requires activation of the P_RE promoter and is hence delayed until enough CII protein, driving this activation, has accumulated (23).

Multiple theoretical models previously developed for the lysis/lysogeny decision have predicted distinct gene expression trajectories at low and high MOI, whereby in the former case, the lytic proteins accumulate while lysogenic ones remain low, and in the latter case, the reverse takes place (9, 16, 19–21). In light of this prevailing picture, we were surprised to observe no clear divergence of mRNA trajectories between low and high MOI, reflecting a transition from lysis to lysogeny. Instead, we found that for each of the genes, a simple scaling by a factor MOI^ε [suggested previously by Joh and Weitz (16)], with ε ≈ 1 for cI and ε ≈ 0.5 for cro and cII, yielded a near collapse of the different MOI-gated trajectories to a single curve (SI Appendix, Fig. S6). Thus, gene expression kinetics following P− infection did not reveal a clear signature of a transition from lysis to lysogeny as MOI increases.

Modeling Network Dynamics Reveals that a Lytic Decision Cannot Be Reached in the Absence of Viral Replication.

The absence of clear MOI-driven changes in gene expression profiles following infection by a nonreplicating phage may indicate that divergence only takes place at the protein level, even if absent from the short-lived mRNA species. Alternatively, this absence may reflect a more fundamental point; namely, that viral replication is required for a lysis-to-lysogeny transition. To explore these possibilities, we constructed a deterministic mathematical model that describes the regulatory interactions between cI, cro, and cII as well as the coupling between gene expression and viral replication (Fig. 2A and SI Appendix, Theoretical Methods). Building on previous theoretical efforts (9, 19, 22), our model captures, phenomenologically, both direct interactions between the three genes (e.g., the activation of cI transcription from P_RE by CII and the repression of cro transcription from P_R by CI) and indirect ones mediated by players that are not modeled explicitly [e.g., CIII-mediated suppression of CII degradation (30)]. As its output, the model produces the population-averaged temporal dynamics of the viral copy number and mRNA and protein concentrations for a given initial MOI. To estimate the parameters governing gene regulation in the network, we fitted the model to the experimental mRNA kinetics during P− infection by minimizing an objective function measuring the agreement between the two using particle swarm optimization (PSO) (31) (SI Appendix, Theoretical Methods). This procedure yielded a good agreement between the model and experiments (Fig. 2C and SI Appendix, Fig. S7) and allowed us to predict cellular variables that are not directly measurable in the experiments, such as protein concentrations and the activity of individual phage promoters.

To relate the gene expression dynamics computed by our model with the infection outcome, we assumed that cell fate is determined by whether Cro or CI concentration in the cell reaches a threshold value (16). The Cro threshold captures its multiple putative roles in establishing lysis: repressing cI transcription from P_RM and (indirectly, by repressing cII transcription from P_R) from P_RE and the requirement that Q (encoded by the same transcript as Cro) reaches sufficient level to enable readthrough of the late lytic genes transcribed from P_R’ (17). As will be seen, our model suggests that it is the latter feature that sets the required Cro threshold. The lysogenic threshold, on the other hand, corresponds to CI levels sufficient to turn off the P_L and P_R promoters, thereby repressing the expression of lytic genes and phage replication (23).

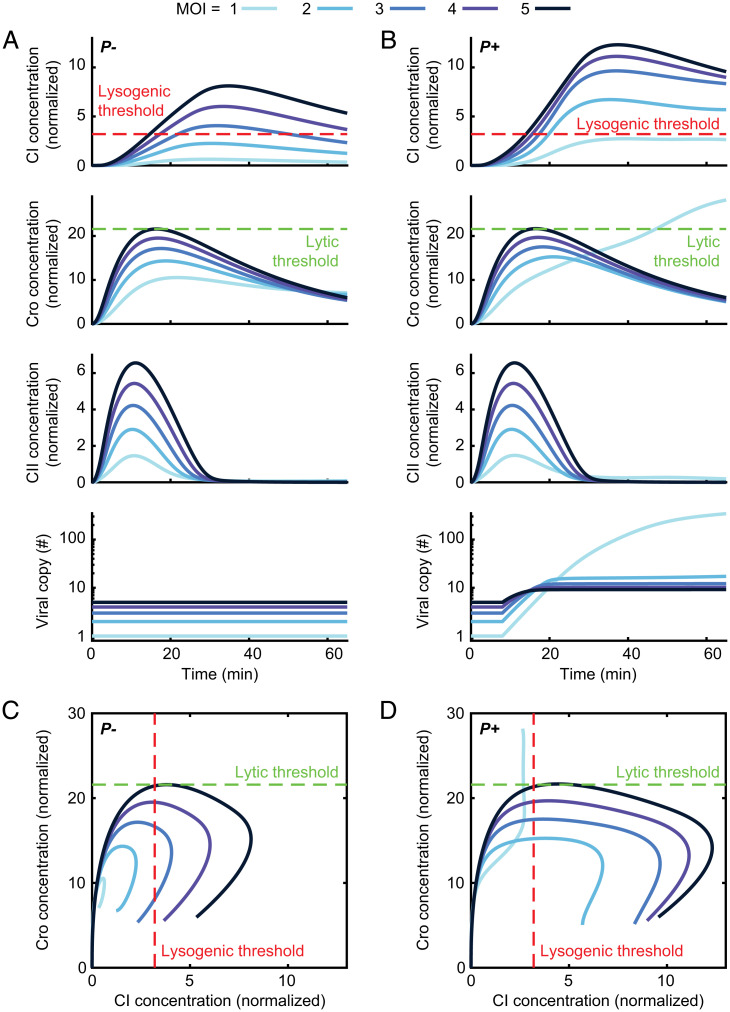
Using our model to infer protein concentration dynamics following P− infection, we found that, consistent with what we inferred from the mRNA data above, there is no obvious divergence in the trajectories. Cro, CI, and CII concentrations first rise and then decrease, with the maximal value reached by each protein increasing with MOI (Fig. 3A). As was the case with mRNA, this value is approximately linear for CI and sublinear (partially dose compensated) for Cro (SI Appendix, Fig. S8). Crucially, these dynamics are inconsistent with the requirement that cells reach a lytic decision threshold in Cro at low MOI but fail to reach it at higher MOI. In other words, no Cro threshold can be defined, which results in a lytic decision only below a critical MOI (SI Appendix, Theoretical Methods). In contrast, a range of CI thresholds that ensure lysogeny above some critical MOI can be defined (demonstrated by the dashed red line in Fig. 3A). Therefore, the inferred protein dynamics suggest that the lytic threshold is never reached during P− infection and that, at low MOI, neither lysis nor lysogeny is selected (Fig. 3C). This interpretation is consistent with the known absence of lysis following infection by P− phages (22, 32) but suggests that this failure reflects the state of the decision circuit rather than merely a failure to execute the chosen lytic pathway, which was the implicit assumption in previous works (7, 16, 21).

Fig. 3.

Phage replication is required for an MOI-driven lysis-to-lysogeny transition. (A) Model-predicted CI concentrations (normalized by threshold for CI repression of cro transcription), Cro concentrations (normalized by threshold for Cro repression of P_RM), CII concentrations (normalized by threshold for CII activation of P_RE), and viral copy number during the first 65 min following infection by P− (nonreplicating) phage at varying MOI. (B) Same as A during P+ infection. (C) Trajectories in the CI–Cro phase plane for the scenarios in A. (D) Same as C during P+ infection. Refer to SI Appendix for detailed information.

To test the robustness of our prediction that infection at low MOI by a nonreplicating phage results in a failure to reach a decision, we employed an ensemble modeling approach (33–35). To this end, we supplemented the best-fit model used in Fig. 3 with an ensemble of models with distinct parameter values, obtained by repeating the PSO procedure (>100 times) using random starting seeds and selecting an ensemble of 44 parameter sets that produce objective functions within 4% of the best fit (SI Appendix, Fig. S7 and Theoretical Methods). As expected, some model parameters were well constrained, whereas others varied several folds between the different models within the ensemble (SI Appendix, Table S7). However, despite this variation, 100% of the models were consistent with the prediction by the best-fit model that, in the absence of viral replication, the maximal Cro concentration increases with MOI, and therefore, a low MOI lytic decision is not possible (SI Appendix, Table S8).

Viral Replication Modifies Protein Dynamics and Enables an MOI-Dependent Lysis–Lysogeny Decision.

We next sought to evaluate what effect viral replication would have on the system’s behavior. To calibrate the model parameters pertaining to lambda replication and its regulation, we used qPCR measurements of genome number kinetics from low MOI infection by a replicating (P+) phage (Fig. 2D) as well as published data for cI and cII expression following infection with P+ phages, cI−, cro−, and cro−P− mutants (22) (SI Appendix, Figs. S9 and S10). The resulting model allowed us to predict the kinetics of CI and Cro concentrations trajectories following infection by replicating phages at various MOIs (Fig. 3B).

Comparing these dynamics (Fig. 3B) to what we found for a nonreplicating phage (Fig. 3A), we find the CI’s behavior is qualitatively similar, with a transient peak whose magnitude is again nearly linear with MOI (SI Appendix, Fig. S8), albeit higher in the presence of viral replication. Cro dynamics, in contrast, now exhibit a clear divergence between low and higher MOI, very unlike what was seen in the nonreplicating phage. Specifically, for MOI > 1, Cro levels in P+ phage are hardly affected by replication and remain very similar to P−. However, for MOI = 1, Cro continuously increases during the time simulated (65 min), eventually exceeding the maximal level reached at higher MOIs. The divergence between low and high MOI is also observed in the dynamics of viral copy number (Fig. 3B): replication is suppressed at early ∼20 min postinfection for MOI > 1 but continues throughout the simulation for MOI = 1.

The qualitative differences in behavior between P− and P+ phages are further illustrated by examining the trajectories in the plane of Cro and CI concentrations (Fig. 3 C and D). For nonreplicating phages, the trajectories for different MOIs are similar in shape and simply scale with MOI (Fig. 3C and SI Appendix, Fig. S8). For replicating phage, in contrast, trajectories clearly diverge between MOI = 1 and higher MOIs and, in particular, support a transition from lysis (Cro threshold crossing) to lysogeny (CI threshold crossing) with increasing MOI (Fig. 3D). Moreover, a single choice of thresholds is simultaneously consistent with the experimental phenotypes of both P− and P+ phages in terms of the MOI value at which the transition to lysogeny occurs (∼3 to 4 and 2 for P− and P+ respectively; SI Appendix, Theoretical Methods and see Fig. 6D) (10). Notably, these predictions are robustly observed for the whole ensemble of fitted models. For replicating phage, all models show 1) a divergence of trajectories between MOI = 1 and higher MOI and 2) a lower minimal MOI required for crossing the lysogeny thresholds as compared to nonreplicating phages (SI Appendix, Table S8).

Fig. 6.

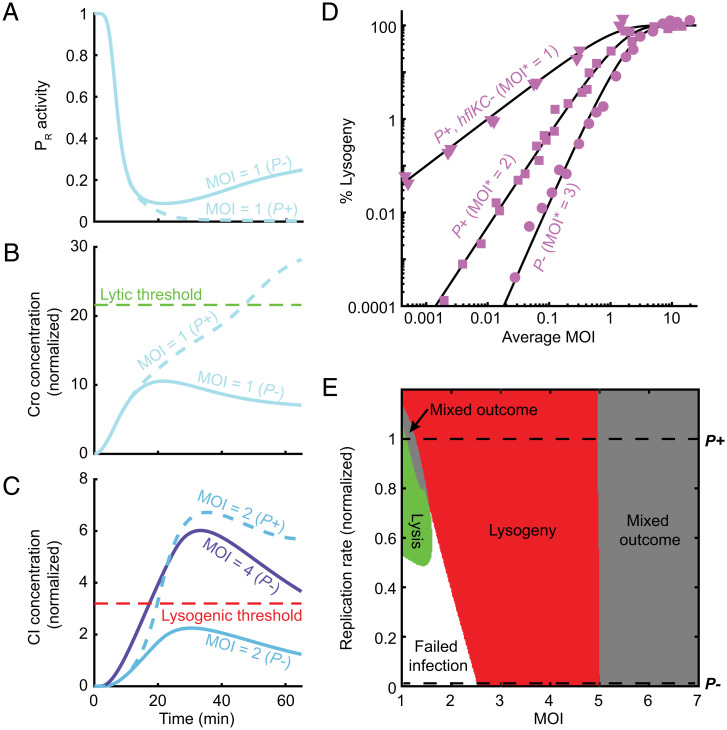
Replication is required for the lytic outcome and lowers the MOI required for lysogeny. (A) Model-predicted P_R activity per phage during P− (solid blue line) and P+ (dashed blue line) infection at MOI = 1. (B) Cellular Cro concentration (normalized as in Fig. 3) for the cases modeled in A. (C) Cellular CI concentration (normalized as in Fig. 3) during P− infection at MOI = 2 and 4 (solid light and dark blue lines, respectively) and during P+ infection at MOI = 2 (dashed line). (D) The fraction of cells undergoing lysogeny as a function of average MOI during bulk infection with P− (circles), P+ (squares), and phages with prolonged CII lifetime (P+ phages infecting hflKC− hosts; triangles). The experimental data were normalized and fitted to a model (black lines) in which virus–cell encounters follow Poisson statistics, and infection at MOI ≥ MOI* results in lysogeny (10) as described in SI Appendix. The hflKC− strains are either ΔhflK or ΔhflC (SI Appendix, Table S1). (E) Predicted infection outcome as a function of MOI and viral replication rate (normalized by the fitted replication rate of P+ phage). Refer to SI Appendix for detailed information.

CII Activation of P_RE Defines a Time Window for the Network’s Response to MOI.

Having successfully recapitulated the decision phenotype, we next sought to understand how lambda reliably responds to the initial MOI even in the presence of viral replication. Since establishing lysogeny requires reaching a critical CI concentration, we focused on the response of cI expression to MOI. Two lambda promoters drive cI transcription, P_RE (activated by CII) and P_RM (autoregulated by CI) (23). P_RM is solely responsible for CI production in a lysogen (23), but whether it plays a role during the initial decision has remained unresolved (36). Our model indicates that the MOI-driven increase in CI is caused by transcription from P_RE, and removing cI autoregulation does not eliminate that response (SI Appendix, Fig. S11). Analyzing the whole ensemble of fitted models, we confirmed that the MOI-dependent transition to lysogeny requires cI transcription from P_RE but not P_RM (SI Appendix, Table S8). This finding is consistent with reports that a wide range of mutations in P_RM permit the establishment of lysogeny (37, 38), whereas mutating P_RE or CII prevents it (23). The lower translation rate of CI from P_RM versus P_RE transcripts (a feature not modeled here) is expected to further diminish P_RM’s role. Thus, to elucidate CI’s response to MOI, we focused on characterizing the CII-activated expression of cI during infection.

Our model indicates that CII-activated P_RE expression occurs in a single pulse, taking place within the first ∼30 min of infection (Fig. 4A). The amplitude (per phage) and duration of this P_RE activation pulse depend only weakly on MOI (Fig. 4A and SI Appendix, Fig. S12), reflecting the fact that CII reaches its P_RE activation threshold at all MOIs (Fig. 3 A and B). These predictions contrast with previous suggestions of an ultrasensitive increase in cI transcription with MOI (17, 20) but are robustly observed in our ensemble of fitted models (SI Appendix, Table S8). Notably, these model predictions are supported by direct measurements of nascent cI mRNA level at individual phage genomes (SI Appendix, Fig. S13) and are also consistent with our findings that, in nonreplicating phages, cellular cII numbers are dosage compensated, whereas cI level scales linearly with MOI (SI Appendix, Fig. S6). The MOI independence of cI expression from individual viral copies during P_RE activation explains the approximately linear scaling of cellular CI concentration with increasing MOI (Fig. 3B and SI Appendix, Fig. S8). This scaling nevertheless satisfies a necessary condition for the lysogeny decision by allowing the maximal CI concentration at MOI ≥ 2 to reach the critical level sufficient to repress both cro expression (Fig. 4B) and viral replication (Fig. 4C). This repression is established during the P_RE activation window and persists throughout infection leading to lysogeny.

Fig. 4.

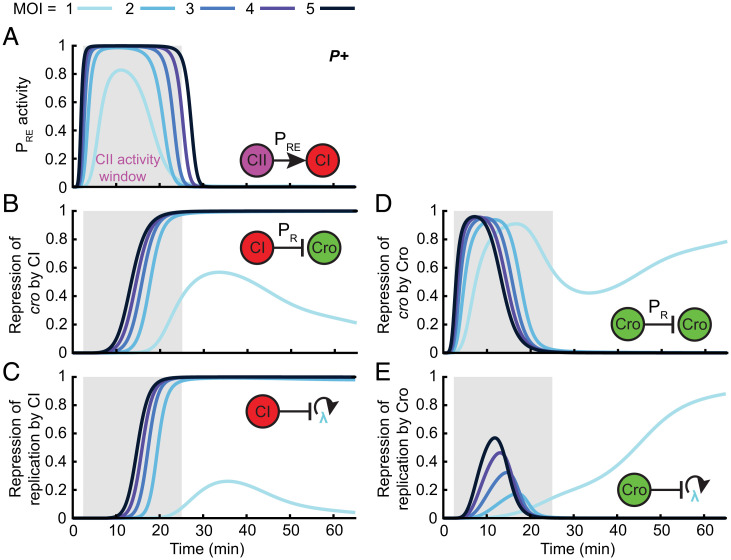
CII activation of P_RE defines a time window for the network’s response to MOI. (A) Model-predicted P_RE promoter activity (per phage) following infection by P+ phage at MOI = 1 to 5. Gray shading indicates the MOI-averaged CII activity window defined as the period during which P_RE activity is greater than 10% of its maximum. (B) The strength of cro repression by CI calculated as the magnitude of the CI repression term in the P_R transcription rate following infection by P+ phage at MOI = 1 to 5. (C) The strength of repression of replication by CI calculated as the magnitude of the CI repression term in the viral replication rate following infection by P+ phage at MOI = 1 to 5. (D) The strength of cro repression by Cro calculated analogously to the term in B. (E) The strength of repression of replication by Cro calculated analogously to the term in D. Refer to SI Appendix for detailed information.

As for Cro, the divergence of its dynamics between low and high MOI manifests itself in qualitative changes in its ability to repress P_R and viral replication (Fig. 4 D and E). Cro’s role in regulating viral replication during the decision appears minor relative to CI (Fig. 4C), becoming dominant only at later stages of lytic development at MOI = 1 (Fig. 4E). However, early in the P_RE expression window, Cro does play an important role in repressing P_R, and thereby CII, at all MOIs, to ensure the closing of the CII activity window. Notably, for MOI = 1, Cro continues to play a role in repressing P_R transcription at later times, as CI levels are insufficient to keep it fully repressed (Fig. 4 B and D).

The results above pinpoint key features of the decision network that must be in place to enable an MOI-dependent choice—activation of P_RE by CII, repression of P_R by Cro, and repression of replication and cro expression by CI. Perturbations to our ensemble of models, which eliminate these interactions, destroy the lysis-to-lysogeny transition (SI Appendix, Table S9). In addition, ensemble perturbations predict two other features that are necessary for the existence of the MOI-insensitive time window: high cooperativity of CII activation of P_RE and rapid CII degradation (SI Appendix, Table S9). In contrast, repression of viral replication of Cro plays a major role in only some of the parameter sets within the ensemble (SI Appendix, Table S9) and may therefore be a redundant mechanism, increasing the robustness of the decision (39).

Finally, examination of the system’s dynamics during the CII activity window provides a mechanistic insight for defining the lytic Cro threshold: this threshold is unlikely to reflect the repression of P_RM (which is unnecessary for the decision, SI Appendix, Fig. S11) or of P_R (which takes place for all MOIs, Fig. 4D). Accordingly, in our ensemble, the regulatory thresholds for these processes lie considerably below the lytic decision threshold (SI Appendix, Table S10). While the Cro threshold for repressing viral replication is of the same order as the lytic threshold, this repression is not needed in the majority of ensemble models (SI Appendix, Table S9). These observations suggest that the lytic threshold serves as a proxy for the accumulation of sufficient Q protein to enable readthrough of the late lytic genes transcribed from P_R’ (17).

Changes in Viral Copy Number Outside the CII Activity Window Do Not Alter the Decision.

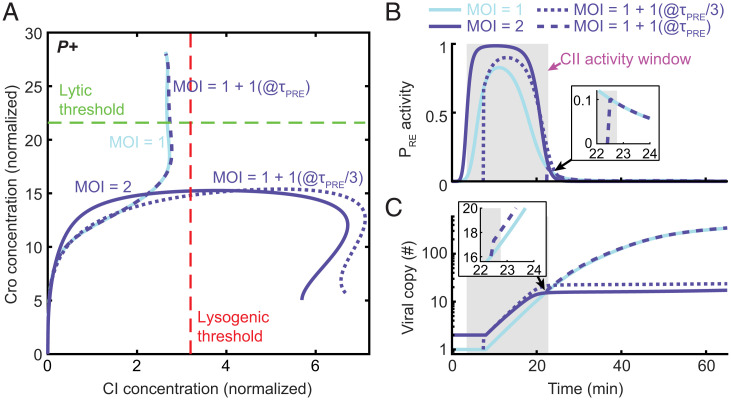
The findings in the preceding section reveal how CI levels—and the propensity to lysogenize—increase with MOI. However, a reliable MOI-based decision also requires that viral replication inside the cell will not obfuscate the initial response to MOI. We reasoned that, for this to hold, the system should become insensitive to changes in viral dosage once the window for CII activation of P_RE is closed. To test this hypothesis, we followed the approach of Cortes et al. (20) and used the model to examine what happens in the case of delayed infection. Specifically, we modeled an infection by a single phage followed by a second single-phage infection at time τ_d later (Fig. 5). We found that, indeed, if the second infection takes place after the end of the CII activity window τ_PRE, the outcome is lysis, and the CI and Cro trajectories are indistinguishable from those at MOI = 1 (Fig. 5A). If, in contrast, the delayed infection occurs early enough within the CII activity window, and the infection results in lysogeny, with CI and Cro trajectories similar to those for a synchronized infection at MOI = 2 (Fig. 5A). Infecting with higher numbers of late-arriving viruses prolongs the time window in which the late phages can affect the decision but not beyond τ_PRE (SI Appendix, Fig. S14). Thus, the infection outcome is insensitive to changes in viral copy number that take place outside the time window determined by CII activity. This prediction robustly holds across all models of the ensemble (SI Appendix, Table S8).

Fig. 5.

Changes in viral copy number outside the CII activity window do not alter the decision. (A) Model-predicted system trajectories in the plane of Cro and CI concentrations (normalized as in Fig. 3) during the first 65 min following infection by P+ phages at four different scenarios: infection by a single phage (solid line, light blue), infection by a single phage followed by a second phage at time τ_PRE/3 (with τ_PRE the end of the CII activity window at MOI = 1; dotted line, dark blue) and τ_PRE (dashed line, dark blue), and simultaneous infection by two phages (solid line, dark blue). (B) P_RE activity from the second arriving phages for the cases modeled in A. The shaded gray region indicates the CII activity window at MOI = 1. (Inset) Infection by a second phage at time τ_PRE. (C) Viral copy number over time for the cases modeled in A. (Inset) Infection by a second phage at time τ_PRE. Refer to SI Appendix for detailed information.

Why does delayed infection result in a diminished response? Our model indicates reduced P_RE expression from the second virus since that virus is not present for the entire duration of the CII activity pulse (Fig. 5B). This results in lower cellular accumulation of CI during that time window as compared to simultaneous coinfection (Fig. 5A). Furthermore, the delay impacts not only the late-infecting virus itself but also all viruses produced subsequently through viral replication (Fig. 5C). We note that, through the combination of Cro repression of P_R and active CII degradation (23), the decision network constrains CII activity to a single time window. Subsequent changes in viral copy number after the initial infection cannot overcome this constraint. These features of the system’s response to delayed infection can also explain why rampant viral replication during infection at MOI = 1 does not cause a switch to lysogeny: While replication generates >100 additional genome copies (Fig. 2D), viruses produced outside the CII activity window are unable to express cI from P_RE (SI Appendix, Fig. S15). The opportunity to “flip” the decision switch has already been lost.

Phage Replication Enables the Lytic Choice and Lowers the MOI Required for Lysogeny.

We have thus seen how phage replication is tolerated, that is, how a reliable response to the initial MOI is achieved despite the subsequent change in viral copy number. Recall, however, that comparing CI–Cro trajectories in replicating (Fig. 3D) and nonreplicating (Fig. 3C) phages indicated that viral replication is not only tolerated but, in fact, required for the existence of an MOI-dependent lysis-to-lysogeny transition. To understand why that is the case, we first addressed the absence of a lytic choice following P− infection at MOI = 1. Our model indicates that, in both P+ and P−, cro transcription from P_R (per phage) is repressed greater than twofold within ∼10 min of infection (Fig. 6A and SI Appendix, Fig. S16 depicts the corresponding experimental data). However, the presence of additional gene copies in the P+ case results in higher Cro concentration later in the infection, sufficient to cross the lytic threshold (Fig. 6B). Viral replication thus serves to boost total Cro expression despite repression of its transcription at the individual phage level.

As for the effect of replication on the lysogenic choice, we find that cI transcription from P_RE during P− infection follows a similar pattern to P+, namely, a single pulse whose duration and amplitude per phage depend only weakly on MOI (SI Appendix, Fig. S17; compare to Fig. 4A and SI Appendix, Fig. S12). However, as in the case of Cro, the presence of added gene copies during P+ infection leads to considerably higher CI accumulation than for P− (Fig. 6C). Consequently, while replicating phages reach the lysogenic CI threshold at MOI = 2, nonreplicating ones require a higher MOI to reach that threshold and establish lysogeny. The theoretical prediction that P− phage lysogenizes at higher MOI than P+ is consistently observed across the ensemble of fitted models (SI Appendix, Table S8) and is borne out in experiments (10) (Fig. 6D).

To generalize the effect of viral replication on the lysis/lysogeny decision, we simulated infections at MOI in the range 1 to 7 while varying the phage replication rate from zero to 1.5× that of P+ phage. Determining the infection outcome at each MOI and replication rate yielded the two-dimensional “fate diagram” shown in Fig. 6E. Consistent with the preceding discussion, we find that both the existence of a lytic outcome and the minimal MOI at which the transition to lysogeny occurs depend on the viral replication rate. The ability to replicate is not by itself sufficient to enable the lytic pathway. Rather, there is a minimum required replication rate below which MOI = 1 infections fail to achieve either outcome. As for lysogeny, the MOI at which this fate is chosen decreases with the viral replication rate (Fig. 6E). When replication is sufficiently rapid, the model predicts a lysogenic outcome even at MOI = 1 (Fig. 6E and SI Appendix, Table S9). While we are unaware of an experimental test for this prediction, we note that the model predicts a similar behavior when the CII activity window is extended by inhibition of CII degradation (SI Appendix, Fig. S18 and Table S9), a result validated by experiments (30) (Fig. 6D).

Interestingly, there are two regions where the system’s trajectories cross both the lytic and lysogenic thresholds in the course of infection (Fig. 6E). The first of those occurs at high replication rates in the MOI range between lysis and lysogeny. We are uncertain how to interpret this feature, but it is intriguing to note that, at the single-cell level, it may correspond to the range of infection parameters in which stochastic effects become important, and consequently, individual cells exhibit different fates as reported experimentally (11, 12, 40). The analysis of cellular heterogeneity is outside the premise of our current model, which captures the population-averaged behavior only. A second region where mixed outcomes are predicted is found for MOI ≳ 5 and may correspond to a scenario in which the overexpression of viral proteins results in the halting of cell growth rather than a lytic or lysogenic outcome, consistent with experimental data (12).

Discussion

The combination of single-molecule genome and mRNA measurement in individual cells with theoretical modeling provided us with insights into the way lambda counts coinfecting phages to bias the lysis–lysogeny decision. Early theoretical studies of the postinfection decision sought insight to the phage’s binary choice in the toggle switch comprised of the mutually antagonistic CI and Cro, which governs lysogenic maintenance and lytic induction (9, 19, 41, 42). This famous “genetic switch” exhibits bistability (43) with well-defined states characterized by high CI (lysogeny) and high Cro (lytic onset), respectively. These features, and the tremendous body of experimental and theoretical knowledge that has accrued about the pairwise CI/Cro interactions (14, 18), explain the focus on this element as the key to the decision. Moreover, theoretical work has shown that MOI could indeed drive a bifurcation of the CI/Cro switch’s steady state, consistent with a transition from lysis to lysogeny (9, 19). Our analysis, however, suggests that this is not how the lambda decision unfolds. Instead, each phage initially attempts to execute a preset pattern of gene expression independent of the MOI. In this cascade of events, cI transcription takes place predominantly through the transient activation of P_RE by CII, while cI autoregulatory expression from P_RM is unnecessary. The resulting cellular CI expression is approximately linear in MOI, indicating the absence of an ultrasensitive response to CII as previously suggested (17, 20, 44). This linearity holds despite the high Hill coefficient of P_RE activation because even a single phage produces enough CII to activate P_RE. Given the fixed gene expression cascade at the individual phage level, it is the introduction of time-varying gene dosage due to viral replication—rather than the standalone topology of the viral circuit—that enables the subsequent divergence of gene expression trajectories and cell-fate choices at low and high MOI.

The time-varying viral copy number is found to be critical for both possible outcomes of infection. The choice of lysogeny depends on the number of lambda copies present during the early decision window, set by CII activation of P_RE (Fig. 4A). The finite response window immunizes the lambda decision to changes in viral copy number that take place outside it, thus allowing reliable detection of the initial MOI. However, the role of viral copy number does not end then and is, in fact, crucial for reaching the protein threshold required for establishing either fate: Cro for lysis or CI for lysogeny. Cro (and by proxy, the lytic activator Q) continues to accumulate through late infection, reaching the lytic decision threshold ∼50 min postinfection (Fig. 6B). Cro’s continued accumulation is driven by late viral replication, despite the repression of P_R at the single-phage level (Fig. 6A). As for lysogeny, while this fate is achievable in the absence of viral replication, it is replication that ensures that coinfection by more than one phage is sufficient to drive lysogeny; in the absence of replication, CI accumulates insufficiently, and higher MOI is required to reach the lysogenic threshold (Fig. 6C).

Our ensemble modeling approach enables us to pinpoint the critical regulatory interactions and their parametric regimes, which underlie the formation of the MOI response window and subsequent cell-fate decision (SI Appendix, Table S9 and Figs. S19 and S20). Fast initial accumulation of CII past its P_RE activation threshold makes CI concentration linearly scale with the viral dosage, whereas Cro autorepression makes its concentration partially dosage compensated. Repression of P_R by Cro, fast degradation of CII, and cooperativity of P_RE activation together lead to the closing of the time window at all MOIs. If enough CI to keep P_R and viral replication repressed has accumulated during that time, cells follow the lysogenic pathway. Otherwise, continued viral replication overrides the per-copy repression of cro and leads to sufficient Cro (and Q) accumulation to trigger lysis.

The ensemble modeling also leads to several robust predictions (SI Appendix, Table S8). Some of those provide interpretations for previous observations. For example, the failure to lyse following infection by P− phage at low MOI (22, 32) is explained by the inability of Cro (as a proxy for Q) to reach the lytic threshold. And the increase in minimal MOI required for lysogeny in P− versus P+ phages (Fig. 6D) (10, 22) is found to reflect faster accumulation of CI due to replication-driven increase in gene dosage. Other predictions will await future experimental validation. For instance, the existence of a finite (∼20 to 30 min) window during which an increase in viral gene dosage via reinfection or replication can affect cell-fate decisions, or the strong effect that perturbing viral replication rate is predicted to have on the lysis/lysogeny decision.

The relation between gene dosage and the output of genetic networks has been explored in diverse biological contexts, both natural (45–47) and synthetic (48–51). In some instances, changes in gene copy number were found to have a significant effect on phenotype (52–54), whereas in other cases, mechanisms of dosage compensation buffer the network output from such changes (51, 55–58). The lambda decision exhibits a richness of dosage response beyond what was previously documented, with the transcriptional output either linear in dosage or partially compensating it, for different genes in the network at different times during the infection. Consequently, viral replication is found to facilitate rather than hinder the implementation of a reliable decision. Since cellular decisions frequently take place even as gene copy number is changing (59–61), this inextricable coupling of gene dosage and network output cannot be ignored if one aims for a predictive description of cellular decision making.

Materials and Methods

All bacterial and phage strains, experimental procedures, microscopy, data analysis, and theoretical modeling used in this study are described in SI Appendix.

Data Availability

Bacterial and phage strains are available upon request. All simulation codes can be found in Zenodo: https://doi.org/10.5281/zenodo.5639007. Previously published data were used for this work (22).