Ensemble learning to predict opioid-related overdose using statewide prescription drug monitoring program and hospital discharge data in the state of Tennessee

Abstract

Objective

To develop and validate algorithms for predicting 30-day fatal and nonfatal opioid-related overdose using statewide data sources including prescription drug monitoring program data, Hospital Discharge Data System data, and Tennessee (TN) vital records. Current overdose prevention efforts in TN rely on descriptive and retrospective analyses without prognostication.

Materials and Methods

Study data included 3 041 668 TN patients with 71 479 191 controlled substance prescriptions from 2012 to 2017. Statewide data and socioeconomic indicators were used to train, ensemble, and calibrate 10 nonparametric “weak learner” models. Validation was performed using area under the receiver operating curve (AUROC), area under the precision recall curve, risk concentration, and Spiegelhalter z-test statistic.

Results

Within 30 days, 2574 fatal overdoses occurred after 4912 prescriptions (0.0069%) and 8455 nonfatal overdoses occurred after 19 460 prescriptions (0.027%). Discrimination and calibration improved after ensembling (AUROC: 0.79–0.83; Spiegelhalter P value: 0–.12). Risk concentration captured 47–52% of cases in the top quantiles of predicted probabilities.

Discussion

Partitioning and ensembling enabled all study data to be used given computational limits and helped mediate case imbalance. Predicting risk at the prescription level can aggregate risk to the patient, provider, pharmacy, county, and regional levels. Implementing these models into Tennessee Department of Health systems might enable more granular risk quantification. Prospective validation with more recent data is needed.

Conclusion

Predicting opioid-related overdose risk at statewide scales remains difficult and models like these, which required a partnership between an academic institution and state health agency to develop, may complement traditional epidemiological methods of risk identification and inform public health decisions.

INTRODUCTION

We sought to develop and validate implementable predictive models for the state of Tennessee (TN) to predict (1) fatal and (2) nonfatal opioid-related overdose risk by leveraging statewide data sources provided by the Tennessee Department of Health (TDH). Through our academic-state partnership, we applied ensemble learning to fatal and nonfatal overdose prediction using statewide controlled substance prescription data, hospital discharge diagnoses, and causes of death from vital records.¹

BACKGROUND AND SIGNIFICANCE

The link between the current opioid epidemic in the United States and the over-prescribing of opioid pain relievers (OPRs) has been well established. Over-prescribing and OPR-related harms were first observed in the 1990s and some states including TN have experienced higher rates of prescribing and the subsequent harms.^2,3 Near the opioid prescribing peak in 2010, TN providers wrote more OPR prescriptions than there were residents in the state.⁴ Between 2014 and 2018, OPR-related deaths rose 49% to an annual cost of 1307 lives.^5,6 The United States meanwhile has seen a near-universal adoption of prescription drug monitoring programs (PDMPs) with intentions to combat the opioid epidemic by monitoring prescribing histories, informing providers, and identifying concerns with varying success.^7–10 Although PDMPs have seldomly been used to predict imminent risk at the patient level, prevention at the practice, county, or regional levels might be possible if accurate algorithms are developed, validated, and implemented.^11–14 Severely affected by the opioid crisis, TN has already linked its controlled substance PDMP (II–V scheduled and gabapentin) to statewide mortality data and hospital discharge data.^15,16 In this study, researchers at TDH and Vanderbilt University Medical Center (VUMC) partnered to develop and validate the first scalable predictive models from statewide datasets in TN for the related but disparate outcomes: (1) fatal and (2) nonfatal opioid overdose.^17,18

The application of machine learning to predict individual risk is not new in the biomedical literature nor in OPR overdose prevention. Prior studies have predicted overdose risk using Medicare claims, self-reported substance use patterns, and demographics.^13,19–21 Many studies have also utilized electronic health records with or without vital records including at Mt. Sinai, in the state of Colorado, and at the Veteran’s Health Administration (VHA).^22–25 Few US states, however, have specifically used PDMP data to predict overdose—namely Maine, Oregon, and Maryland.^11,26,27 In Maryland, hospital discharge, healthcare utilization, and criminal justice data have been linked to predict future OPR overdose risk for individuals.^12,14,28 Our study likewise combines predictive modeling with comprehensive statewide data. No previous studies to our knowledge have assembled these kinds of data for a large, southern US state like TN where the rates of OPR prescribing are much higher than the national average.

In 2019, a federal investigation led by the Department of Justice (DOJ) uncovered fraud and inappropriate opioid prescribing in TN and resulted in the arrests of multiple physicians, pharmacists, and other health professionals.²⁹ Such measures relied upon descriptive analytics for harms that had already occurred years prior. While monitoring and descriptive analytics may provide a lens into the current state of the opioid epidemic, they cannot identify the next patient, practice, or community at risk. The goal of this work was to supplement these traditional epidemiological methods of identifying and characterizing risk with precise and automated predictive models. Part of our efforts was to leverage known sociodemographic and economic factors relating to mental and physical health. Community characteristics have been known to be predictive of OPR overdose risk.³⁰

Seeking to predict future risk by combining linked PDMP and overdose data, TDH partnered with VUMC to help the state understand the opioid epidemic statewide, target interventions, and allocate scarce resources accordingly. Adhering to the architectural and implementation requirements of TDH, the VUMC team derived a data management strategy, sourced a wide array of social determinant variables to help quantify risk, and evaluated our approach. Once implemented in TDH systems, such models might allow TN to further support the greatest at-risk communities and identify intervention touch points within the community health system.

MATERIALS AND METHODS

This study was approved by the VUMC Institutional Review Board (#171323).

Data sources

Controlled Substance Monitoring Database (CSMD, TN’s PDMP) data, Hospital Discharge Data System (HDDS) data, and TN death certificates were combined to produce a 6-year observational cohort that spanned from the beginning of 2012 through the end of 2017. Publicly available socioeconomic indicators relating to health, healthcare utilization, and treatment access were compiled and mapped to either ZIP codes or counties.

The following were mapped to residential ZIP codes: Area Deprivation Index (ADI); statistics on employment from the U.S. Census Bureau; and Medication-Assisted Treatment (MAT) locations including buprenorphine providers, methadone clinics, and Opioid Treatment Programs (OTPs) from data aggregated by TDH.^31,32 TN age-adjusted morbidity rates from TDH; the Tennessee Vulnerability Index (TVI) from TDH; statistics on income, poverty, college education, crowding, and private insurance from the American Community Survey (ACS); Rural–Urban Continuity Codes (RUCC) from the U.S. Department of Agriculture; the Social Vulnerability Index (SVI) from the Centers for Disease Control and Prevention (CDC); and Anti-Drug Abuse Coalition services from TDH were mapped to individual counties.^33–36 A full list of sourced data is available within the Supplementary Material.

Outcome ascertainment

The outcomes of interest in this study were fatal and nonfatal opioid-related overdose events that occurred within 30 days of a controlled substance prescription fill. The 30-day time window was chosen after plotting the accumulation of overdoses over time after a prescription fill (Supplementary Material). Fatal and nonfatal overdoses were identified consistent with methods used by TDH in their annual Prescription Drug Overdose Reports.³⁷ Fatal overdoses were identified from TN death certificates using International Classification of Disease, revision 10 (ICD-10) codes.³⁸ Nonfatal overdoses were identified in the HDDS with specified opioid-related diagnostic codes (Supplementary Material).

Predictive modeling details

Our modeling choices were as follows: (1) establish a vector of socioeconomic indicators based on a patient’s last reported location from the PDMP (from the time of the previous prescription); (2) count the cumulative number of prior medications, diagnostic codes, and hospital visits by type a patient has accumulated thus far; and (3) add age, sex, and derived variables that represent a patient’s prescription history for controlled substances.¹⁵ Variables chosen included the sums of distinct practitioners, distinct pharmacies, distinct hospital identifiers, total prescriptions, total morphine milligram equivalents, short/long-acting OPR prescriptions, overlapping OPR and benzodiazepine prescriptions, prior medications for opioid use disorder, and opioid-naïve prescriptions as defined as not having an OPR prescription within the last 45 days (Supplementary Material). Race and ethnicity were not explicitly represented in our models. Modeling at the prescription level was done to create time-dependent and granular risk predictions which could then be aggregated to practice, pharmacy, local, county, and regional levels. This approach intended to potentially guide planning and response activities at varying levels of detail.

Data preprocessing

Patient linkage across our datasets relied on TDH-determined master patient indexing.³⁹ Only records with valid person identifiers were retained, and records determined to be related to a nonhuman patient (ie, veterinary prescription records) were removed. Hospital records from the HDDS were limited to verified inpatient encounters.

Precise ADI and RUCC features were developed from the minimum, maximum, and mean values of each ZIP code. Other ZIP code features were developed from county data using the TN county that contained the majority area of each ZIP code. OTP and methadone clinic availability were modeled using a 60-mile radius, representing a practical range for driving a normal distance in TN (90–120 minutes driving time).

To reduce the dimensionality of PDMP and HDDS features, prior medications and diagnoses were grouped to higher-order categories using the National Drug File-Reference Terminology (NDF-FT), Pharmacologic Classes and Clinical Classification Software (CCS), Level 2 groupings from National Drug Codes (NDCs) and International Classification of Disease, revision 10, Clinical Modification (ICD-10-CM) codes.^40–42 In total, 342 features were used for model training after this dimensionality reduction and only entries in patient records prior to prediction dates were used.

Sampling strategy and model training

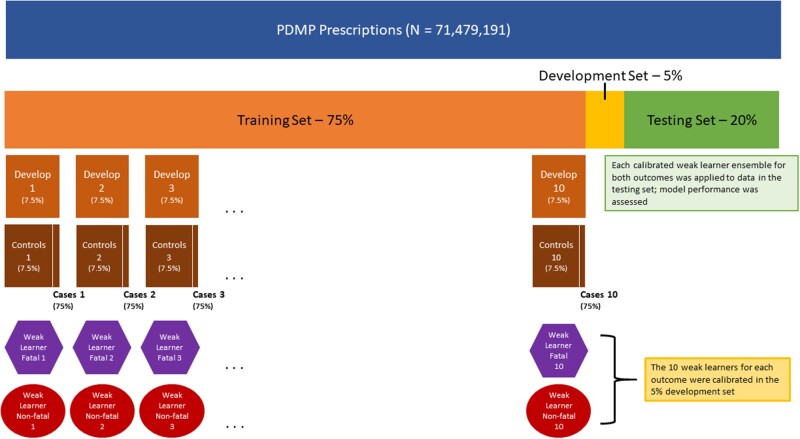
We separated the data into 75% training, 5% development, and 20% testing partitions to ultimately derive one model for fatal overdose and one model for nonfatal. All prescriptions in the data that were associated with an individual were added together to only one set to prevent leak between training and testing within individuals. Models were trained in the training set and then calibrated, ensembled, and evaluated in the development set.

The training set was equally divided into 10 smaller training partitions or subsets due to computational limits. To help combat case imbalance, all cases and their associated records were added to each training set, but only 10% of all the controls from the entire training set were included in an individual training set (ie, only one training set contained any one control). Ten random regression forest “weak learners” were then developed from the training subsets using the ranger R package with an estimated response variance splitting criteria.⁴³ To help limit memory consolidation, 200 trees were used for each random forest. In total, 20 random forests were developed from the 20 training subsets—10 for each of the 2 outcomes.

During training, each training subset itself was split into a 90% training set and a 10% testing set to allow predictions to be made for each case. Each case was placed in the testing set of each subset exactly one time which guarantied all case data were used in training and at least one prediction for each associated record was generated. After the weak learners were ensembled and calibrated in the development set, the resulting ensembled models were validated in a final held-out testing set. A conceptual diagram of this training scheme is shown (Figure 1).

Figure 1.

Conceptual diagram of training data splits, weak learners, the ensembling/calibration development step, and the testing step.

Calibration

A development set consisting of 5% of the data was reserved to correct the miscalibrations from the under-sampled controls in the training subsets. We compared 7 methods of ensembling and calibration. Either the minimum, maximum, mean, or median prediction was taken from the 10 weak learner predictions and passed through logistic calibration, or the 10 weak learner predictions were used as inputs for ridge regression, random forest, or penalized regression (LASSO).^43–46

Logistic calibration, when applied, was defined by training a univariate logistic regression in the calibration set where the sole predictor was the aggregate in question (eg, max) and the outcome was either fatal or nonfatal overdose. The resulting generalized linear models along with the aggregation methods were then considered as ensemblers. The more complex ensembling methods trained multivariate models using the 10 weak learners as predictors. Random forest was used for comparison for 2 types of penalized logistic regression: L1-regularized (LASSO) and L2-regularized (RIDGE) regression. All resulting models were expected to be calibrated as they were either trained on the calibration set or calibrated via logistic calibration.

Final ensembled and calibrated algorithms were then tested on the test set. Weak learners were tested on the calibration set. We note that no additional calibration was performed on the test set, making it a pure test of calibration as well as discrimination.

Performance assessment methods

Discrimination performance metrics included area under the receiver operating curve (AUROC), area under the precision recall curve (AUPRC), and risk concentration. Risk concentration was performed by dividing the predictions from the test set into 10 quantiles and calculating the proportion of all the cases those quantiles held.

Calibration was assessed using Spiegelhalter z-test. The ridge regression ensembles were further assessed for performance differences by subgroups consisting of race, ethnicity, and gender as determined by hospital records as well as age and RUCC codes from residential ZIP codes for urbanicity/rurality. To test how performance varied when the number of partitions in the training set was changed, additional models were trained using N = 5 or N = 15 and compared using AUPRC. For both fatal and nonfatal overdose, we ranked each feature by taking the mean of the important values from the 10 weak learners—determined by the variance of responses from each random forest.⁴³ A full list is available within the Supplementary Material.

RESULTS

Study data

Study data included 71 479 191 controlled substance prescriptions across 3 041 668 TN patients. As sourced from hospital records, when available: 1 409 556 (46.3%) patients were Female; 958 440 (31.5%) patients were Male; and 673 672 (22.1%) patients were Unknown. Patients by coded race showed 7104 (0.23%) patients were Asian-American; 360 314 (11.8%) patients were Black; 704 (0.023%) patients were Native American; 20 147 (0.66%) patients were Other; 1 851 324 (61.0%) patients were White; and 802 075 (26.4%) patients were Unknown. Patients by coded ethnicity also showed 16 061 (0.53%) patients were Hispanic; 2 064 654 (67.8%) patients were non-Hispanic; and 960 953 (32.0%) patients were Unknown. Within 30 days, 2574 fatal overdoses occurred after 4912 (0.0069%) prescriptions and 8455 nonfatal overdoses occurred after 19 460 (0.027%) prescriptions. Nearly 60% of all fatal and nonfatal overdoses in the data occurred within 30 days of a prescription (Supplementary Material).

Weak learner and ensembling model performance

Both the fatal and nonfatal weak learner models had similar prevalence rates throughout the training set and showed consistent AUROC and AUPRC values when applied to the development set (Table 1). AUROC was useful to compare these models simply despite having known problems when assessing absolute performance with case imbalance. The total number of cases and controls in the training set were 3725 and 53 591 596 (0.0069%) for fatal and 14 695 and 53 580 626 (0.027%) for nonfatal overdose.

Table 1.

Characteristics of both the 20 weak learner models in the development set and the 14 ensemble models in the test set for fatal and nonfatal overdose

	Fatal overdose					Nonfatal overdose
Weak learner/ensemble	AUROC	AUPRC	Cases	Controls	% Outcomes	AUROC	AUPRC	Cases	Controls	% Outcomes
WL1	0.77	0.00024	224	3 566 077	0.0063	0.79	0.0018	1131	3 580 452	0.032
WL2	0.73	0.00023				0.78	0.0016
WL3	0.76	0.00023				0.79	0.0019
WL4	0.75	0.00024				0.78	0.0016
WL5	0.72	0.00026				0.79	0.0021
WL6	0.73	0.00027				0.80	0.0019
WL7	0.71	0.00023				0.79	0.0017
WL8	0.78	0.00024				0.80	0.0017
WL9	0.75	0.00025				0.79	0.0017
WL10	0.72	0.00026				0.78	0.0015
Maximum	0.83	0.00040	963	14 316 606	0.0067	0.82	0.0014	4031	14 309 753	0.028
Minimum	0.67	0.00032				0.76	0.0014
Mean	0.83	0.00042				0.83	0.0015
Median	0.80	0.00041				0.82	0.0015
LASSO	0.79	0.00038				0.82	0.0015
Ridge	0.83	0.00042				0.83	0.0016
Random forest	0.38	0.00007				0.49	0.0004

Note: Ensemble models combined and calibrated weak learner model predictions from the development set.

AUPRC: area under the precision recall curve; AUROC: area under the receiver operating curve.

Discrimination varied by ensembling method when applied to the test set for both fatal and nonfatal overdose (Table 1). Averaging or selecting the minimum or maximum predictions from the 10 weak learner models for both fatal and nonfatal produced similar results to using more complex methods of aggregation (eg, ridge, LASSO). Random forest performed worse compared to other methods of aggregation. The top 2 performing ensembles, mean and ridge regression, were further evaluated in the risk concentration and calibration analyses.

Risk concentration and calibration performance

Risk concentration showed that, in the test set, the mean and ridge regression ensembling methods concentrated 47–52% of the overdose outcomes within the top quantiles of predicted probabilities (Table 2). Both top quantiles contained 10% of the test set predictions. Overlapping quantiles where the predictions had the same values were combined as seen by the number of prescriptions in the first quantile of the fatal mean ensembling method.

Table 2.

Risk concentration of the ensembled fatal and nonfatal prediction models which were validated in the test set

Fatal/Nonfatal	Ensembling method	Quantile	Prescriptions	Cases	Proportion of cases	Inclusive lower bound	Exclusive upper bound
Fatal	Mean	1	4 106 507	32	0.033	0.00E+00	1.65E−08
		2	210 474	4	0.004	1.65E−08	6.28E−08
		3	1 412 596	14	0.015	6.28E−08	3.33E−05
		4	1 429 211	33	0.034	3.33E−05	3.53E−04
		5	1 431 757	40	0.042	3.53E−04	7.07E−04
		6	1 432 104	66	0.069	7.07E−04	1.46E−03
		7	1 434 688	100	0.104	1.46E−03	2.92E−03
		8	1 428 476	171	0.178	2.92E−03	6.80E−03
		9	1 431 756	503	0.522	6.80E−03	3.34E−01
	Ridge regression	1	1 431 758	81	0.084	3.85E−05	5.47E−05
		2	4 776 940	43	0.045	5.47E−05	5.48E−05
		3	950 091	4	0.004	5.48E−05	5.48E−05
		4	1 443 236	55	0.057	5.48E−05	5.54E−05
		5	1 420 274	60	0.062	5.54E−05	5.66E−05
		6	1 431 800	103	0.107	5.66E−05	6.00E−05
		7	1 431 716	159	0.165	6.00E−05	6.73E−05
		8	1 431 754	458	0.476	6.73E−05	3.19E−01
Nonfatal	Mean	1	1 929 336	43	0.011	0.00E+00	1.93E−08
		2	933 421	25	0.006	1.93E−08	8.68E−06
		3	1 437 802	67	0.017	8.68E−06	2.50E−04
		4	1 425 055	81	0.020	2.50E−04	6.91E−04
		5	1 432 474	123	0.031	6.91E−04	1.41E−03
		6	1 430 183	143	0.035	1.41E−03	2.55E−03
		7	1 431 883	290	0.072	2.55E−03	4.50E−03
		8	1 431 048	415	0.103	4.50E−03	8.04E−03
		9	1 431 205	835	0.207	8.04E−03	1.59E−02
		10	1 431 377	2009	0.498	1.59E−02	2.86E−01
	Ridge regression	1	1 431 493	106	0.026	1.33E−04	2.11E−04
		2	2 073 804	45	0.011	2.11E−04	2.11E−04
		3	788 932	19	0.005	2.11E−04	2.11E−04
		4	1 431 285	96	0.024	2.11E−04	2.14E−04
		5	1 432 043	143	0.035	2.14E−04	2.21E−04
		6	1 430 714	172	0.042	2.21E−04	2.31E−04
		7	1 431 378	239	0.059	2.31E−04	2.49E−04
		8	1 431 379	478	0.119	2.49E−04	2.85E−04
		9	1 431 378	807	0.200	2.85E−04	3.85E−04
		10	1 431 378	1926	0.478	3.85E−04	9.97E−01

Calibration measured the degree to which the predictions reflected the true outcome prevalences. The ensembled models predicting fatal overdose showed nonsignificant calibration from mean ensembling and significant calibration from ridge regression as indicated by the nonsignificant Spiegelhalter z-test. The ensembled models for nonfatal overdose showed better calibration for ridge regression than for mean ensembling although both were nonsignificantly calibrated (Table 3). The ridge regression ensembling method was subsequently used to analyze performance variations by subgroups.

Table 3.

Calibration statistics for the mean and ridge regression ensembling methods for the fatal and nonfatal overdose models after application in the test set

Ensembled model	Brier score	Intercept	Slope	Sz	Sp
Fatal mean	0.0001305	−5.5329	0.6205	−191.59	0.00
Fatal ridge regression	0.0000673	−0.3313	0.9599	1.55	0.120
Nonfatal mean	0.0004239	−4.0305	0.7625	−272.14	0.00
Nonfatal ridge regression	0.0002923	−1.7524	0.7942	−9.34	0.00

Subgroup performance differences and partition variation

Both the fatal and nonfatal ridge regression ensembles were tested on subgroups in the test set. AUROC and AUPRC values varied by subgroup in age, sex, race, ethnicity, and RUCC values of residential ZIP codes (Table 4). Case and control percentages among the subgroups also varied.

Table 4.

AUROC and AUPRC for various subgroups in the test set for the fatal and nonfatal ridge regression ensembled models

Characteristic	Subgroup	Fatal				Nonfatal
		AUROC	AUPRC	Cases (%)	Controls (%)	AUROC	AUPRC	Cases (%)	Controls (%)
Age	20–29	0.83	0.00030	16 (1.74)	393 406 (3.22)	0.75	0.0014	141 (3.50)	381 438 (3.12)
	30–39	0.79	0.00036	126 (13.74)	1 417 833 (11.60)	0.75	0.0011	502 (12.48)	1 421 592 (11.63)
	40–49	0.79	0.00054	233 (25.41)	1 934 651 (15.83)	0.80	0.0013	590 (14.66)	1 945 431 (15.91)
	50–59	0.80	0.00062	351 (38.28)	2 583 639 (21.14)	0.82	0.0021	966 (24.01)	2 606 848 (21.32)
	60–69	0.84	0.00045	172 (18.76)	2 695 746 (22.06)	0.82	0.0019	1036 (25.75)	2 704 083 (22.12)
	70–79	0.91	0.00022	14 (1.53)	1 876 554 (15.36)	0.83	0.0015	546 (13.57)	1 856 381 (15.18)
	80–89	0.95	0.00020	5 (0.55)	948 381 (7.76)	0.78	0.0013	217 (5.39)	945 839 (7.74)
Sex	F	0.84	0.00048	470 (48.81)	7 633 488 (53.42)	0.81	0.0016	2439 (60.61)	7 657 711 (53.61)
	M	0.81	0.00044	447 (46.42)	4 556 799 (31.89)	0.80	0.0015	1570 (39.02)	4 542 227 (31.80)
	U	0.74	0.00006	46 (4.78)	2 100 560 (14.70)	0.99	0.0009	15 (0.37)	2 084 944 (14.60)
Race	Asian-American	N/A	N/A	0 (0.00)	12 253 (0.090)	N/A	N/A	0 (0.00)	11 428 (0.080)
	Black	0.86	0.00023	35 (3.63)	1 101 369 (7.71)	0.79	0.0010	198 (4.92)	1 105 227 (7.74)
	Native American	N/A	N/A	0 (0.00)	1 888 (0.010)	N/A	N/A	0 (0.00)	1947 (0.010)
	Other	0.78	0.00021	2 (0.21)	32 659 (0.23)	0.88	0.0006	4 (0.10)	32 400 (0.23)
	Unknown	0.79	0.00041	105 (10.90)	2 794 866 (19.56)	0.92	0.0031	413 (10.26)	2 763 247 (19.34)
	White	0.83	0.00045	821 (85.25)	10 347 812 (72.41)	0.80	0.0015	3409 (84.72)	10 370 633 (72.60)
Ethnicity	Hispanic	0.83	0.00034	2 (0.21)	25 870 (0.18)	0.81	0.0009	5 (0.12)	25 665 (0.18)
	Non-Hispanic	0.81	0.00035	709 (73.62)	10 404 402 (72.80)	0.80	0.0014	3080 (76.54)	10 448 420 (73.14)
	Unknown	0.86	0.00066	252 (26.17)	3 860 575 (27.01)	0.89	0.0021	939 (23.33)	3 810 797 (26.68)
RUCC	1, metro, >1 000 000	0.86	0.00064	357 (37.07)	4 856 038 (33.98)	0.84	0.0021	1593 (39.59)	4 898 834 (34.29)
	2, metro, 250 000–1 000 000	0.83	0.00042	301 (31.26)	3 852 307 (26.96)	0.83	0.0015	1006 (25.00)	3 829 032 (26.8)
	3, metro, <250 000	0.78	0.00021	76 (7.89)	1 491 989 (10.44)	0.83	0.0010	325 (8.08)	1 491 254 (10.44)
	4, urban, >20 000+ metro adjacent	0.80	0.00046	67 (6.96)	1 346 081 (9.42)	0.81	0.0016	398 (9.89)	1 330 476 (9.31)
	5, urban, >20 000+	N/A	N/A	0 (0.00)	94 940 (0.66)	0.88	0.0007	13 (0.32)	101 859 (0.71)
	6, urban, 2500–19 999 metro adjacent	0.82	0.00030	101 (10.49)	1 714 426 (12.00)	0.80	0.0013	459 (11.41)	1 709 034 (11.96)
	7, urban, 2500–19 999	0.71	0.00014	26 (2.70)	453 522 (3.17)	0.82	0.0016	108 (2.68)	442 912 (3.10)
	8, rural, <2500, metro adjacent	0.68	0.00020	21 (2.18)	320 187 (2.24)	0.82	0.0011	86 (2.14)	312 688 (2.19)
	9, rural, <2500	0.80	0.00510	14 (1.45)	161 357 (1.13)	0.82	0.0011	36 (0.89)	168 793 (1.18)

AUPRC: area under the precision recall curve; AUROC: area under the receiver operating curve; RUCC: Rural–Urban Continuity Codes.

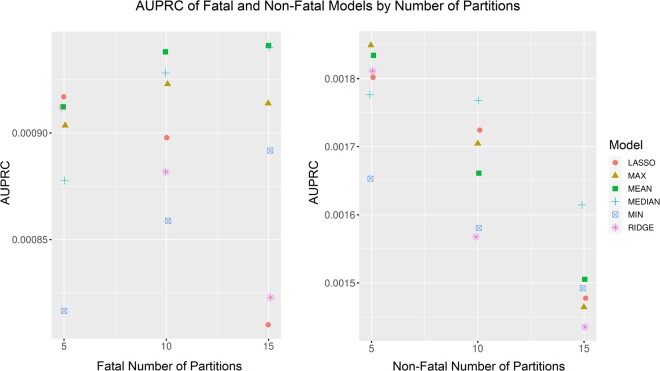
Repeating the modeling experiments for N = 5 and N = 15 showed no differences in AUPRC values when the number of partitions was changed (Figure 2). Absolute change by partition choice was minimal as evidenced by the small absolute differences in y-axes shown (eg, <0.0001 change in AUPRC by number of folds for the fatal model).

Figure 2.

AUPRC of the LASSO, max, mean, median, min, and ridge regression ensembling methods for fatal and nonfatal overdose models when the number of partitions was changed. Note: compressed y-axes used to visualize minimal differences in models by number of partitions. AUPRC: area under the precision recall curve.

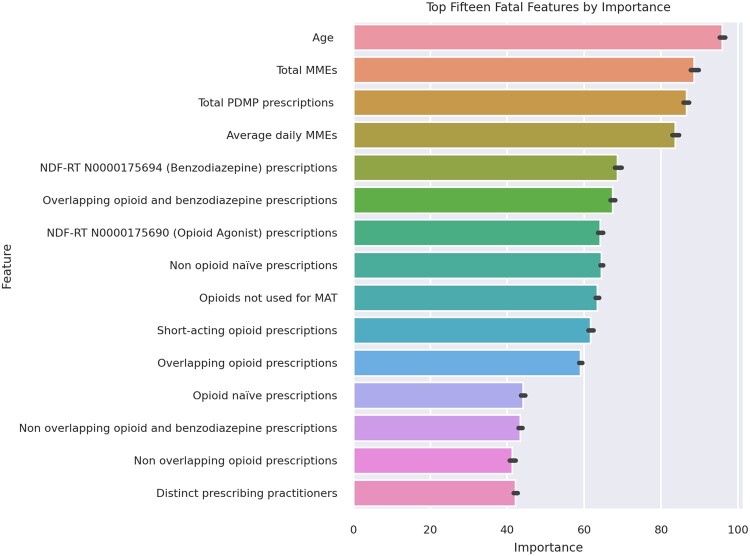
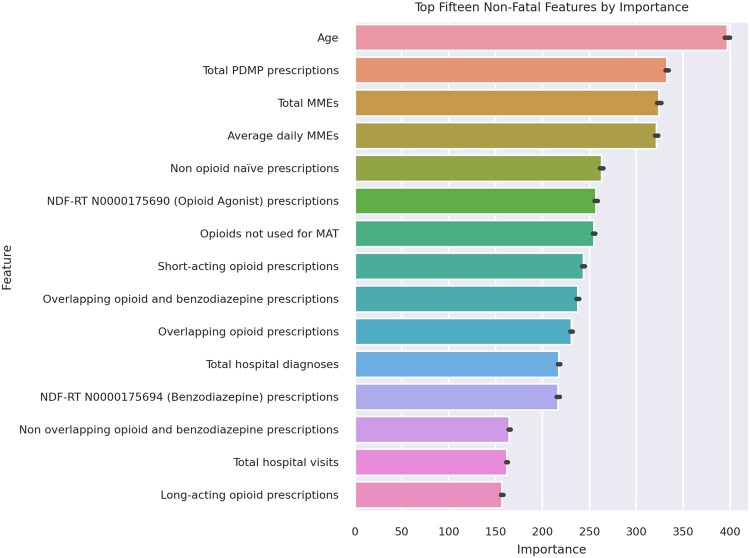
Weak learner feature importances

The top 15 model features from the 10 weak learner models for fatal and nonfatal overdose were determined by ranking their mean response variances (Figures 3 and 4). Twelve features were within the top 15 of both the fatal and nonfatal overdose models.

Figure 3.

Top 15 predictive features by mean rank of importance for the fatal opioid overdose model.

Figure 4.

Top 15 predictive features by mean rank of importance for the nonfatal opioid overdose model.

DISCUSSION

This study supports the validity of combining statewide PDMP data with clinical discharge and socioeconomic data to predict fatal and nonfatal opioid overdose within 30 days of a controlled substance prescription fill. Partitioning and ensembling the data allowed us to use all study data despite computational limits. We modeled risk at the prescription level, making these models applicable to any individual prescription with historical data. Aggregating these predictions enables risk to be calculated at varying levels of detail for better informed public health decision-making.

AUROCs and AUPRCs of the fatal and nonfatal models in the development set improved in the test set after ensembling (Table 1). Risk concentration analyses consistently captured half the outcomes of interest in the top quantiles of risk (Table 2). Given the presence of case imbalance, the highest risk quantiles may enable TN to focus prevention efforts more efficiently. Both ensembles were miscalibrated when predicting nonfatal overdose, but the ridge regression ensemble was calibrated when predicting fatal overdose (Table 3). Future recalibration efforts should reduce these gaps. Predicting fatal overdose in the future may enable better prevention. Prospective evaluation with more recent data is needed.

The subgroup performance analysis showed that the ridge regression models resulted in disparate performance in terms of AUPRC and AUROC for race and age despite small absolute AUPRC differences (Table 4). Case imbalance may be driving these differences. Correcting performance differences is necessary for accurately assessing risk in the state. When the number of training partitions was varied, AUPRCs varied minimally if at all (Figure 2).

In the fatal overdose model, the top predictors were face valid as known risk factors for opioid-related overdose (Figure 3). The total quantity of controlled substances prescribed was close to the top of the list. Notably, overlapping benzodiazepine prescriptions were more important in the prediction of fatal opioid-related overdose than nonfatal. Multidrug combinations have been known to play a large role in the fatality potential of opioid-related overdoses and benzodiazepines have a synergistic respiratory depressant effect when taken with opioids.⁴⁷

Informatics implications of this study include the importance of partitioning and sampling to lessen overfitting in settings with high stake, but rare (at state scale), outcomes. Efforts to predict risk at an actionable timepoint, for example, a prescription fill event, do not obviate aggregating risk analyses to levels relevant for public health intervention such as the community and regional levels. US states have long implemented PDMPs, but most have not disseminated predictive modeling approaches at this scale and none of the nearby states in the southern United States have done so. Characterizing OPR risk in our state might inform better prevention both in TN and in neighbor states, as the overdose crisis varies considerably near and across state lines.

Several attributes of this overdose modeling problem increased its complexity. First, extreme case imbalance resulted from the rarity of fatal and nonfatal overdoses at statewide scale—prevalence less than a fraction of 1%. Second, person disambiguation in data that were manually entered by pharmacists into the CSMD resulted in reliance on constructed, probabilistic patient mapping indices. Ongoing work within TDH continues to refine and improve this disambiguation. Third, CSMD data in TN contain human and nonhuman controlled substance prescription data. Removing those prescriptions known to be nonhuman was straightforward but ensuring nonhuman data are not miskeyed as human was not.

Neither the fatal nor nonfatal models are suitable for direct clinical application. Given the resulting model AUPRCs, high false-positive rates are expected at virtually every cutoff. While it is possible that clinically actionable subgroups may exist within the high-risk tiers, given the size of this study, most localized clinical interventions would likely see highly variable calculated individual risk and unacceptably high false positives. Current actionability of these models rests upon their ability to ascribe relative risk geographically within TN. Studies of their ability to predict counties and regions at highest risk in need of public health resource allocation are underway. Overdose prevention is currently directed after harm has already occurred—for example, basing “high impact area” designations on deaths that have already occurred, not those we seek to prevent.

Strengths

The training-development-test framework in this study enriched case data in the presence of case imbalance without discarding valuable noncase comparator data. Our weak learner approach overcame computational constraints which may apply to other groups attempting similarly scaled experiments. Our academic-public partnership catalyzed and made possible a modeling study at this scale coupled with design choices to enable implementation at TDH.

This study included the use of comprehensive real-world data derived from statewide operational datasets. Vital records, validated by medical examiners, and certified hospital discharge records were used in the context of our partnership with stakeholders at TDH to ensure modeling decisions reflected the implementation environment and were responsive to public health informatics requirements for overdose prevention. We leveraged the broad expertise among our TDH and VUMC multidisciplinary partnership, working in close communication throughout.

Limitations

Statewide data used in this study were limited to a 6-year time period ending in 2017. Given the changing face of the opioid epidemic, validation with more recent data is needed. Carceral, other criminal justice data, and ambulatory clinical data were not available here, but have been previously used to predict opioid overdose risk.¹⁴ Our decision to predict overdose within 30 days, supported by measuring outcomes over time was chosen empirically and in discussion with TDH (Supplementary Material). Tools to identify patients at longer-term risk may be important for future prevention efforts.

While our models did not explicitly use race as a predictor, other variables were still likely proxies for race and health inequalities in our predictions. Our subgroup analysis showed that race and age vary in both AUROC and AUPRC (Table 4). Understanding the cause and impact of inaccurately calculating risk for different subgroups may have critical policy implications. Sampling may improve this disparity. More data are needed and a dedicated investigation in collaboration with experts in health inequalities is indicated. A large percentage of prescriptions had unknown race and gender given a lack of hospital discharge data for those individuals.

In addition, our outcome ascertainment strategy did not seek to determine if the patient’s last prescription was the actual cause of the overdose outcome nor was it used in those risk calculations. Historical clinical and demographic information were also added to these models from batched HDDS data. Calculating risk in real-time remains challenging given the additional steps necessary to incorporate data entered close to the time of prediction.

Future work

Implementation of these models into internal state systems is currently being reviewed. The choice to do so may provide a platform for prospective validation opportunities and public health perspectives unprecedented in TN. While a small number of proprietary risk scores exist in this domain, none are being used at the state level in TN. Implementing these models would complement traditional epidemiologic methods that identify risk and guide planning for prevention. Future work includes a need to study the interpretability of these models and the need to assess for drift and apply recalibration prospectively. Outcome rates and prescription rates have changed since 2017. More advanced feature engineering and additional external data sources might improve these models further.

CONCLUSION

Historical statewide PDMP data, hospital discharge data, and death certificates from vital records were linked to socioeconomic indicators to produce ensembled opioid-related overdose risk models for TN. Through an academic-state partnership, our models we able to granularly predict fatal and nonfatal overdose risk within 30 days of receiving a controlled substance prescription. These predictions when aggregated may lead to more informed prevention efforts at the local, county, and regional levels.

FUNDING

This work was supported by the Harold Rogers Prescription Drug Monitoring Program Grant No. 2016-PM-BX-K002 and Comprehensive Opioid Abuse Site-based Program Grant No. 2018-PM-BX-0007 awarded by the Bureau of Justice Assistance. The Bureau of Justice Assistance is a component of the Department of Justice’s Office of Justice Programs, which also includes the Bureau of Justice Statistics, the National Institute of Justice, the Office of Juvenile Justice and Delinquency Prevention, the Office for Victims of Crime, and the SMART Office. Points of view or opinions in this document are those of the author and do not necessarily represent the official position or policies of the U.S. Department of Justice.

The above funders had no role in any of the following: design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication (authors BT, AR, CC, and SL).

RFS #34301-29519—Predicting opioid overdose in TN using controlled substance monitoring data and vital statistics (authors CGW, MR, DW, KR, QC, and CEF).

Funding for the Research Derivative and BioVU Synthetic Derivative is through UL1 RR024975/RR/NCRR, PI: Gordon Bernard.

AUTHOR CONTRIBUTIONS

MLM, BT, and CGW outlined the study. QC investigated study validity. KR coordinated the work as performed. SCL, CEF, and AR compiled and analyzed prior research. MR, SCL, DW, and ML processed all reference data. DW delineated study outcomes. MR transformed study data, trained the weak learners, and performed the subgroup analysis. CGW performed the weak learner ensembling. DW analyzed the modeling results and repeated the analysis with varying partitions. MR, DW, and CEF produced figures. All authors contributed to writing and revisions. MR and CGW take responsibility for the integrity and accuracy of the study.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.