A predictive model for next cycle start date that accounts for adherence in menstrual self-tracking

Abstract

Objective

The study sought to build predictive models of next menstrual cycle start date based on mobile health self-tracked cycle data. Because app users may skip tracking, disentangling physiological patterns of menstruation from tracking behaviors is necessary for the development of predictive models.

Materials and Methods

We use data from a popular menstrual tracker (186 000 menstruators with over 2 million tracked cycles) to learn a predictive model, which (1) accounts explicitly for self-tracking adherence; (2) updates predictions as a given cycle evolves, allowing for interpretable insight into how these predictions change over time; and (3) enables modeling of an individual's cycle length history while incorporating population-level information.

Results

Compared with 5 baselines (mean, median, convolutional neural network, recurrent neural network, and long short-term memory network), the model yields better predictions and consistently outperforms them as the cycle evolves. The model also provides predictions of skipped tracking probabilities.

Discussion

Mobile health apps such as menstrual trackers provide a rich source of self-tracked observations, but these data have questionable reliability, as they hinge on user adherence to the app. By taking a machine learning approach to modeling self-tracked cycle lengths, we can separate true cycle behavior from user adherence, allowing for more informed predictions and insights into the underlying observed data structure.

Conclusions

Disentangling physiological patterns of menstruation from adherence allows for accurate and informative predictions of menstrual cycle start date and is necessary for mobile tracking apps. The proposed predictive model can support app users in being more aware of their self-tracking behavior and in better understanding their cycle dynamics.

INTRODUCTION

Background and significance

Mobile health (mHealth) tracking apps enable users to self-manage their personal health by tracking information anytime, anywhere.^1,2 In particular, self-tracking apps allow users to flexibly and easily track conditions and behaviors ranging from endometriosis³ and fertility care⁴ to compliance and chronic diseases,^5,6 resulting in increased awareness of and autonomy over individual health.

While such apps offer the opportunity for users to better understand their behaviors, they present the issue of adherence, namely how consistently a user engages with the app to track their health. Studies have shown that such adherence can vary widely among users, impacted by factors like the app’s user interface and notification system, as well as device fatigue.^7–9 Well-designed apps are crucial to user engagement.^10,11 For apps that provide predictions and analytics to the user, insights can only be derived from what is actually tracked by the user, raising the question of how to distinguish true health phenomena from tracking behavior to provide the most accurate picture of an individual’s health.

To explore this question, we ground our work in the context of menstrual trackers, a category of mobile tracking apps that has risen in popularity—they are the second most popular app for adolescent girls and the fourth most popular for adult women.^12,13 Users of these apps are interested in knowing when their next period will occur and what symptoms to expect. Responding to this need, various apps provide prediction and insight into menstrual behavior, fertility, and more, allowing users to gain a deeper understanding of their menstrual experience,¹⁴ but may fall short in providing accurate predictions.¹⁵ With access to large-scale, longitudinal menstrual datasets from these trackers, there has been a surge in research on how to best characterize menstruation,^16–19 including efforts to describe menstrual cycles and symptoms,^18–20 as well as related physiological events like ovulation,^17,21 quantitatively. Nonetheless, menstrual trackers are subject to adherence artifacts that may obscure health-related conclusions: if a user forgets to track their period, their cycle length computations are inflated.

Owing to the inherent variability of the menstrual experience, it can be difficult to predict the time to each user’s next cycle start. Prior studies based on survey results have shown that menstrual experiences vary both within and between individuals, encompassing not only period and cycle length (the number of days between subsequent periods),²² but also qualitative symptoms like period flow, physical pain, and quality-of-life characteristics.^22–32 Combined with the aforementioned possibility of inconsistent adherence (eg, some users may track their information consistently, while others may skip tracking, whether intentionally or by accident), the difficulty of modeling menstruation holds especially true for such self-tracking data, as researchers must take into account multiple sources of uncertainty. As such, there exists a need for accurate predictive models that can address the specific nature of data from mobile apps.

Objective

Our goal is to provide users with more accurate predictions of next cycle start date (ie, next period date) by characterizing the underlying mechanisms (both physiological and behavioral) implicit in menstrual data as collected via self-tracking apps. Specifically, we aim at disentangling true cycle lengths from self-tracking artifacts that result from inconsistent adherence, allowing for better understanding of collected mHealth data and greater predictive power. We also aim to provide predictions that evolve over time. To that end, we take a probabilistic machine learning approach.

We aim at a model with 3 key features. First, it shall account explicitly for the possibility that users may adhere differently to the app by factoring in the possibility that the observed cycle lengths are not the true, experienced cycle lengths. Second, it should dynamically update predictions each day as the cycle proceeds, providing insights into how predictions evolve over time. Third, it must prioritize each individual’s unique menstrual experience by modeling user-specific cycle length history and providing individual user predictions, while also harnessing the power of population-wide knowledge.

MATERIALS AND METHODS

This study leverages de-identified data. The research was approved as exempt by the Columbia University Institutional Review Board.

Self-tracked menstruator data

We leverage a de-identified self-tracked dataset from Clue by BioWink,³³ comprising 117 014 597 self-tracking events over 378 694 users. A “self-tracking event” refers to an instance when a user logs a symptom in their menstrual tracking app (eg, “heavy flow” or “headache”). For this full dataset, users have a median age of 25 years, a median of 11 cycles tracked, and a median cycle length of 29 days. Clue app users input personal information at sign-up, such as age and hormonal birth control type; information on race or ethnicity is not collected. The dataset contains information from 2015 to 2018 for users worldwide, covering countries within North and South America, Europe, Asia, and Africa.

Users can self-track symptoms over time—for this work, we focus on period self-tracking events, ie, the users' self-reports on which days they have period flow, which we use to compute cycle lengths. A period consists of sequential days of bleeding (greater than spotting and within 10 days after the first greater than spotting bleeding event) unbroken by no more than 1 day on which only spotting or no bleeding occurred. We consider a menses duration longer than 10 days as an outlier, as it would exceed mean period length plus 3 standard deviations for any studied population.²² In addition, a user has the opportunity to specify whether a cycle should be excluded from their Clue history—eg, if the user feels that the cycle is not representative of their typical menstrual behavior due to a medical procedure, changes in birth control, or other relevant events like pregnancy or miscarriage, they may elect to exclude it. To focus the scope and consistency of our dataset, we exclude these cycles from our analysis.

Our cohort consists of users 21 to 33 years of age (because cycles are more likely to be ovulatory and less variable in their lengths during this age interval)^{22,24,25,34,35} with natural menstrual cycles (ie, no hormonal birth control or intrauterine device). To rule out cases that indicate insufficient engagement with the app or instances where a user may not be menstruating (for instance, due to pregnancy), we remove users who have only tracked 2 cycles and cycles for which the user has not provided period data within 90 days. We use the first 11 cycles for all 186 106 menstruators with more than 11 cycles tracked (because 11 is the median number of cycles tracked in the full Clue dataset).

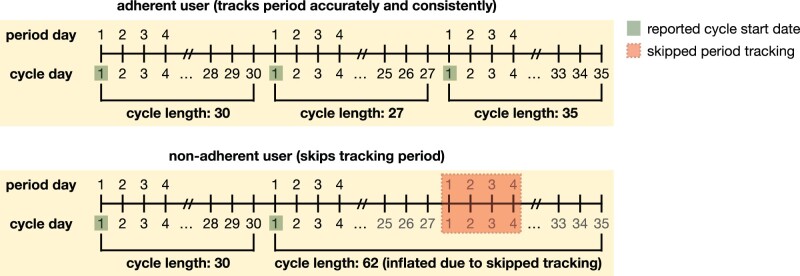
We only use cycle lengths as input to our proposed model, in which we define a menstrual cycle as the span of days from the first day of a period through to and including the day before the first day of the next period.²² Because the tracking of period exactly determines cycle length, if a period is not tracked by the user, their observed cycle length may not accurately reflect their true experience. A “self-tracking (or adherence) artifact” refers to a mismatch between true, experienced physiological phenomena and the self-tracked event: eg, a user had their period on a given day, but they did not log such an event in the app. In the context of this article, we focus on how such self-tracking artifacts impact cycle length computation and result in instances where a cycle appears to be skipped because a user did not track accurately; see Figure 1 for an illustrative example.

Figure 1.

Example cycle tracking history for the same user, demonstrating 2 scenarios: in which they track all of their periods (top) and in which they skip tracking of 1 of their periods (bottom). Cycle start dates are highlighted in green and the skipped period tracking is highlighted in red. The bottom panel showcases how skipping tracking of 1 period can result in inflated observed cycle lengths—instead of 2 subsequent cycles of lengths 27 and 35, respectively, because the user skips tracking of a period, it appears that they have 1 cycle of length 62. This is because cycle length is determined by the number of days between tracked periods. This phenomenon holds analogously if a user skipped more than 1 period (in which case 3 subsequent cycle lengths would appear as if it were a single, inflated cycle length).

Proposed model

We propose a probabilistic machine learning model that accounts explicitly for self-tracking artifacts, utilizes population-wide information and individual-level tracking histories, and updates predictions over days of the next cycle.

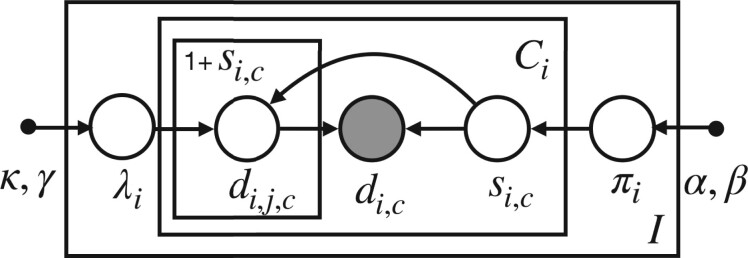
Our model is generative, meaning that we propose the distributions from which each of these quantities (variables) are drawn and hypothesize how the observed variables are related to one another.³⁶ We showcase all the relevant variables in our generative model as a probabilistic graphical model³⁷ in Figure 2. A generative process is a candidate probabilistic model for generating the observed data. A graphical model is a visual representation for explaining and reasoning about such a probabilistic model. In this representation, shaded circles represent observed data, open circles represent latent (unobserved) variables, and dots represent hyperparameters. Latent variables are quantities we wish to infer from the data. Lines in a graphical model represent conditional dependencies between variables. “Plates” (the rectangular boxes) represent groups of variables that share the same repeated conditional dependence relations; for example, a plate could represent many users or many instances of time for representing a temporal process.

Figure 2.

Hierarchical graphical model for the proposed generative process. In our graphical model, variables within the outer plate are replicated for users $i=1,\dots ,I$, variables within the inner plate are replicated for each per-user cycle $c=1,\dots ,C_i$, and variables within the innermost plate are replicated for each skipped cycle $j=0,\dots ,s_{i,c}$. Individual-level parameters ${\mathrm{\lambda }}_i$ (average cycle length without skipping) and ${\mathrm{\pi }}_i$ (probability of skipping a cycle) are drawn from population-level distributions characterized by hyperparameters $u=\left[\mathrm{\kappa },\mathrm{\gamma },\mathrm{\alpha },\mathrm{\beta }\right].\mathrm{ }{s}_{i,c}$ represents number of skipped cycles for user $i$ and cycle number $c$; $d_{i,c}$ represents observed cycle length. We model observed data (cycle lengths $d_{i,c}$) as the sum of true (unobserved) cycle lengths $d_{i,j,c}$ skipped $s_{i,c}$ times (so that an observed cycle length $d_{i,c}$ contains $1+s_{i,c}$ unobserved cycle lengths $d_{i,j,c}$).

Our model posits that each user can be characterized by 2 latent quantities that govern the observed data: their typical cycle length ${\lambda }_i$ (ie, their expected cycle length patterns) and their likelihood to skip tracking ${\mathrm{\pi }}_i\mathrm{ }$(ie, their typical adherence behavior). We model observed data (cycle lengths $d_{i,c}$ for user $i$ and cycle $c$) as the sum of latent, true (unobserved) cycle lengths $d_{i,j,c}$ skipped $s_{i,c}$ times ($j\mathrm{ }$indexes these skipped cycles).

By proposing separate probability distributions from which each of these per-user variables are drawn, we can disentangle true, per-user cycle behavior from self-tracking adherence. Consequently, in addition to predicting cycle length, we can also gain interpretable insight into cycle skipping behavior on a per-individual basis. To that end, we must learn the per-user parameters of interest on the basis of observed self-tracked cycle lengths, accommodating the latent (unobserved) variables via marginalization of their uncertainties (see the Supplementary Appendix for details on inference).

The generative nature of our model enables us to update predictions each day for the next cycle, which we refer to as “current day.” In addition, it allows us to provide predictions for how likely a user is to have skipped tracking of their period on each day of the cycle. Finally, it offers 2 possibilities for computing predictions—one in which we assume that the next reported cycle will be truth and one in which we assume that the next reported cycle may not be truth. $s$ represents the number of possible skipped cycles in the observed cycle length: $s=0$ indicates that we assume the next observed cycle length to be the true cycle length (ie, that the next observed cycle will not be skipped), while $s\ge 0$ indicates that there may be a nonzero number of skipped cycles in the next observed cycle length (ie, accounting for the user possibly skipping their next cycle tracking). When we assume that the next reported cycle may not be truth (ie, $s\ge 0$), we can account for as many skipped cycles as is desired. This allows us to assess how valuable accounting for self-tracking artifacts is for predictive performance. See the Supplementary Appendix for details on how we compute predictions.

An ideal model for menstrual cycle start date is able to borrow information between users (ie, take advantage of population-wide knowledge), while also maintaining the integrity of each individual’s unique experience. In order to achieve this, we utilize a hierarchical model, which means we incorporate different levels of information into our model: the aforementioned individual-level variables for typical cycle patterns and self-tracking adherence, as well as a broader level of information that represents population-wide characteristics (ie, common patterns that exist across the studied population). Population-wide information is learned as hyperparameters that influence the distributions from which the individual-level quantities are drawn. That is, if on a population scale the most likely cycle length is around 30 days, the population-wide distribution will represent this. Individual-level typical cycle length drawn from population-wide distribution will then be influenced by each person’s own cycle tracking history.

Model training and prediction task

We train our model (see the Supplementary Appendix for details on inference) on the full dataset of 186 106 users described in Table 1. We train on the first 10 cycle lengths and predict each user’s next cycle start and likelihood to have skipped tracking on each day of the user’s 11th cycle (see Figure 1 for definition of cycle length and cycle start). For instance, a user could have 10 cycle lengths of $d=\left[\mathrm{30,40,32,35,34,33,50,48,32,31}\right]$; the 11th cycle is used for testing. On each day of the 11th cycle, we predict each user’s next cycle start and likelihood to have skipped tracking.

Table 1.

Summary statistics for selected self-tracked menstruator dataset

Summary statistic	Selected cohort	Selected cohort (first 11 cycles only)
Total number of users	186 106	186 106
Total number of cycles	3 857 535	2 047 166
Number of cycles	20.73 ± 8.35, 18.00	11.00 ± 0.00, 11.00
Cycle length, days	30.45 ± 7.73, 29.00	30.71 ± 7.90, 29.00
Period length, days	4.07 ± 1.76, 4.00	4.13 ± 1.80, 4.00
Age, years	26.07 ± 3.56, 26.00	25.59 ± 3.61, 25.00

Values are n or mean ± standard deviation, median.

Evaluation metrics

We use root mean square error (RMSE) to evaluate the average prediction accuracy of our model across all users. For a given model and $N$ users, an RMSE is computed at each current day of the next cycle, where each of the $N$ users has their own prediction. RMSE of true cycle lengths $d_i$ and predicted cycle lengths $\widehat{d_i}\mathrm{ }$is computed as $\mathit{RMSE}\mathrm{ }=\mathrm{ }\sqrt{\frac{{\sum }_{i=1}^N{\left(d_i-\widehat{d_i}\right)}^2}{N}}$.

We use absolute error and median absolute error to evaluate prediction accuracy of our model on a per-user basis. Absolute error between an actual data point $d_i$ and prediction $\widehat{d_i}\mathrm{ }$is computed as $|d\_i\mathrm{ }-\mathrm{ }\widehat{d\_i|}.$

We use median cycle length difference (CLD) as a metric for evaluating menstrual regularity, based on previous work characterizing menstruation.¹⁹ CLDs are computed per user as the absolute differences between consecutive cycle lengths, measuring the variability from one cycle to the next—for a user whose $C$ cycles are defined as $d=\left[d_0,d_1,d_2,\dots d_C\right]$, the CLDs are computed as CLDs = $\left[\left|d_1-d_0\right|,\left|d_2-d_1\right|,\dots \left|d_C-d_{C-1}\right|\right]$. For instance, a user with cycle lengths $d=\left[\mathrm{30,40,25,30}\right]$ will have CLDs of $5,\mathrm{ }10,\mathrm{ }\mathrm{and}\mathrm{ }15$ and a median CLD of 10. Users with higher median CLD are generally more volatile in their cycle tracking histories, and vice versa.¹⁹

Alternative baselines

To evaluate the predictive performance of our proposed model, we consider summary statistic–based and neural network–based baselines:

• Mean and median baselines: the predicted next cycle for each user is the average (or median) of their previously observed cycle lengths.

• Convolutional neural network: a 1-layer convolutional neural network with a 3-dimensional kernel.

• Recurrent neural network: a 1-layer bidirectional recurrent neural network with a 3-dimensional hidden state.

• Long short-term memory network: a 1-layer long short-term memory neural network with a 3-dimensional hidden state.

We train these baselines in the same way as the proposed model, training on the first 10 cycle lengths and predicting next cycle start of the 11th cycle. Because these models are not generative, we cannot predict the likelihood of skipping or update predictions dynamically by day. Note that we also test other neural network architectures (increasing number of layers and changing kernel or hidden state dimensionality) and find no meaningful performance difference—see the Supplementary Appendix for details.

We utilize summary statistic-based baselines because of the common conception that menstrual cycles are “regular,” and that therefore the mean or median of several cycle lengths would provide a reasonable estimate for the predicted next cycle length. We choose neural network–based baselines because they have been shown to be powerful predictive models in a variety of healthcare applications. While menstrual trackers utilize their own proprietary solutions for cycle prediction (and therefore we are unable to evaluate our predictions against theirs), our baselines provide a reasonable and fair picture of alternative approaches to consider for our predictive task.

RESULTS

Self-tracked menstruator data

We show summary statistics for the selected self-tracked menstruator cohort for all cycles, as well as for the selected first 11 cycles only in Table 1. The total number of users and age are the same in both cohorts, as they represent the same set of users. We see that cycle length and period length statistics differ very minimally between cohorts, indicating that using the first 11 cycles is a reasonable representation of each user's history.

Summary of results

We demonstrate below our model's ability to successfully detect self-tracking artifacts, which can be utilized in mHealth apps to alert users of possible missed tracking. We showcase our proposed model's ability to outperform alternative baselines on predicting next cycle start on the menstruator data, especially on later days of the next cycle and in particular, as the typical cycle length has passed. This demonstrates the benefit of being able to dynamically update beliefs about both cycle length and likelihood of cycle skips and can help users better understand their cycles as they proceed. In addition, we examine the effect of individual variability on cycle length predictions and the importance of considering individual experiences.

Accounting for potential cycle skips enables detection of tracking artifacts

As noted in Figure 1, identifying when a user has skipped tracking of their period is vital to modeling self-tracked cycle lengths accurately, since a failure to do so results in mistaking observed, artificially-inflated cycle lengths for true ones.

We display our model’s ability to detect when a user has skipped period tracking by utilizing simulated data, in which we know the ground truth of when in their cycle tracking history a user has skipped. As with our real menstruator data experiments, we simulate 10 cycles per user and predict likelihood of skipping on the 11th cycle (details on simulated data in the Supplementary Appendix).

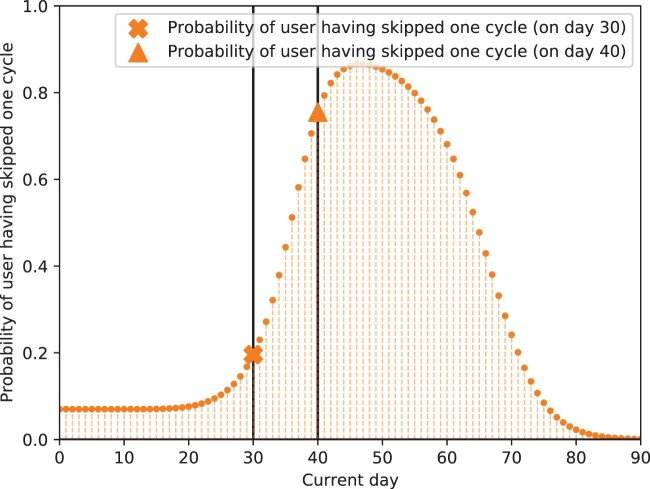
In Figure 3, we showcase that for a user who has skipped a cycle before (in their set of 10 training cycle lengths), their probability of skipping 1 cycle in the 11th (unseen) cycle is low up until around current day 30 of cycle 11, but increases substantially after this day (eg, on day 40, it is around 0.8). That is, before the average cycle length of this user (30 days) has passed, the likelihood that the user has skipped tracking their period is low; however, when the cycle proceeds past this typical cycle length, this probability spikes. This demonstrates that our model can accurately detect when a user is likely to have skipped an upcoming cycle based on their individual cycle length histories and update these beliefs over time.

Figure 3.

Predicted probability of skipping 1 cycle over time for a simulated user. Orange curve represents probability of user having skipped 1 cycle; markers indicate probability of having skipped 1 cycle on day 30 or 40 of the upcoming cycle. We see that the probability of having skipped 1 cycle in the upcoming cycle is low until day 30. However, past day 30, we see that this probability increases; on day 40, it is around 0.8 (vs 0.2 on day 30). Thus, the model detects that the user is likely to have skipped a cycle on day 40, when their typical cycle length has been passed. Because data in this experiment are simulated, we know that this user has skipped a cycle before in their history and does actually skip the next cycle. Our inferred probabilities recover this, showing that our model can accurately detect when a user is likely to have skipped an upcoming cycle based on their individual cycle length histories and update these beliefs over time.

Note that we can compute probabilities of skipping a specific number of cycles, not just whether a cycle was skipped or not—for instance, we can model the likelihood that a user has skipped 0 cycles, 1 cycle, 2 cycles, and so on in the upcoming reported cycle. See the Supplementary Appendix for a deeper illustration of our ability to detect cycle skips.

Proposed model outperforms baselines in cycle length prediction, particularly as the cycle proceeds

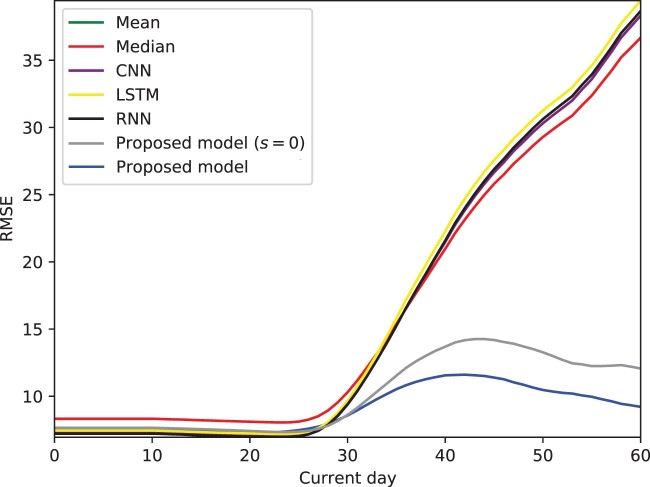
Our model outperforms the studied baselines in prediction accuracy, particularly as the cycle proceeds—it updates predictions on each day of the next cycle, which we refer to as current day in Figure 4.

Figure 4.

Prediction root mean square error (RMSE) for proposed model and baselines over current day of the next cycle on the menstruator data, averaged over all users. Our models' superior performance is magnified past around day 30 of the next cycle; they are able to update predictions dynamically, as compared with static baselines. In particular, accounting for skipped cycles (full version of our proposed model, blue line) proves especially beneficial to prediction accuracy vs assuming the next reported cycle is truth (alternative version of our proposed model, gray line)—by anticipating the possible presence of skipped cycles, we are able to make more accurate predictions and avoid the bump in RMSE seen in the gray line. CNN: convolutional neural network; LSTM: long short-term memory; RNN: recurrent neural network.

On the first day of the next cycle (day 0), our model outperforms all alternative baselines, as seen in Table 2. As seen in Figure 4, this superior performance is especially apparent as the cycle evolves past day 29—our models (gray line, $s=0$ and blue line, $s\ge 0$) display much lower RMSE than baselines. In particular, accounting for potential skipped cycles (blue line) proves more advantageous as the cycle proceeds, in comparison to assuming the next observed cycle contains no self-tracking artifacts (gray line).

Table 2.

Prediction RMSE for proposed model and baselines on different days of the next cycle for the full menstruator dataset (averaged over 186 106 users)

Model	Day 0	Day 14	Day 21	Day 28	Day 30	Day 40
Mean	7.50	7.43	7.29	7.81	8.99	21.92
Median	7.49	7.43	7.32	7.99	9.35	23.39
CNN	8.03	7.97	7.85	8.23	9.55	24.51
LSTM	7.40	7.34	7.20a	7.72a	8.98	22.68
RNN	7.76	7.70	7.56	7.92	9.07	22.95
Proposed model (predict with s = 0)	7.56	7.51	7.36	7.80	8.59	14.78
Proposed model	7.38a	7.32a	7.22	7.93	8.58a	11.77a

Our model typically outperforms summary statistic-based and neural network–based baselines when we account for skipped cycles.

CNN: convolutional neural network; LSTM: long short-term memory; RMSE: root mean squared error; RNN: recurrent neural network.

^aBest-performing model on each day.

We showcase specific RMSE values on different days of the next cycle in Table 2 and further illustrate that after the typical cycle length of around 29 days has passed, our model’s ability to account for skipped cycles becomes especially important for accurate predictions. This is because the possibility of a cycle skip becomes more likely, a scenario that our model is able to incorporate into its predictions, whereas baselines cannot—regardless of the model, the likelihood of a cycle skip becomes more likely as time progresses, but not all models can account for this fact in predicting next cycle length. Our model's ability to outperform baselines as the cycle proceeds demonstrates the value of being able to dynamically update predictions, a benefit offered by our proposed generative model.

We have evaluated the robustness of our training and predictive performance with respect to different modeling choices, namely dataset size and ordering of cycle lengths. We find that our model is generally stable across different training set sizes. To account for possible time dependencies across tracked cycles, we experimented with shuffling the order of each user's cycles and found no significant difference in results. See the Supplementary Appendix for details.

Variability in cycle tracking history impacts prediction accuracy

The menstrual experience is unique, differing within and between individuals, and it is imperative for models relating to menstruation to maintain the integrity of this inherent variability. In addition to averaging results over the whole population, we also consider results on an individual level and examine the role that menstrual variability may play in producing accurate predictions. The ability to learn population-wide information while also making individualized predictions is a direct benefit of our hierarchical modeling approach.

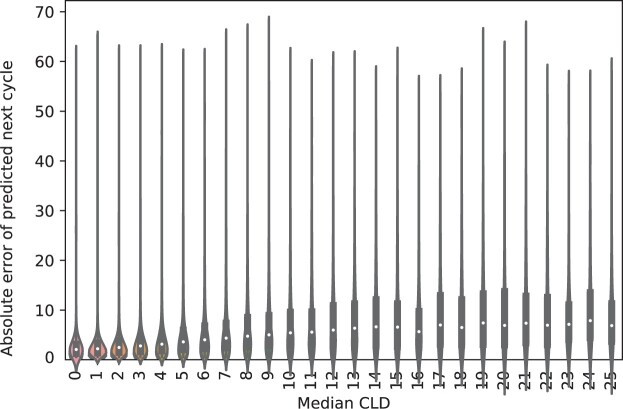
To assess how predictive accuracy depends on cycle length variability, we showcase a violin plot of per-user median CLD vs absolute error in predicted cycle length in Figure 5—the middle white point represents the median absolute error for each group (as defined by the median CLD value on the x-axis), and the thick gray bar represents the interquartile range. We see that variability impacts prediction accuracy, with more variable users being generally more difficult to predict. This underscores the importance of considering each individual's experience.

Figure 5.

Violin plot of per-user absolute error of predicted next cycle length, stratified by user median cycle length difference (CLD) on the menstruator data. We see from the increasing trend in absolute error with median CLD that more variable users are typically more difficult to predict, showcasing that consideration of per-individual behavior is vital to the integrity of our model.

We also note the presence of outliers within a user's cycle length history, eg, instances in which users may have never skipped in their history, but skip the last cycle. These represent a small proportion of the user base, but skew RMSE computations; for instance, for users with very consistent cycle lengths (ie, a median CLD of 0), the median absolute error is as low as 1.5 days, despite the RMSE for this group being 6.15.

DISCUSSION

Our proposed model offers opportunities to characterize the underlying mechanisms of the varied experience of menstruation as collected via mobile tracking apps, a step to a deeper understanding of menstruation as a whole. One particular advancement of our model is the ability to flexibly account for adherence artifacts. While heuristics have been proposed for identifying such self-tracking artifacts, such as locating cycle lengths that are anomalous on a per-user basis,¹⁹ such definitions can be limiting. Because our method explicitly considers the possibility that users track their information inconsistently and separates this cycle-skipping behavior from typical cycle length patterns, we can examine the likelihood of skipped cycles specifically and in a probabilistic manner. This enables us to distinguish true cycle lengths from self-tracking adherence, which not only allows us to gain insight into both menstrual and tracking behavior, but also has practical implications for mHealth users and designers.

In particular, our dual predictions (ie, predictions of both cycle length and possible cycle skips) allow us to provide users with more accurate predictions, even when they are not necessarily consistent in their tracking, and can allow apps to alert users when they may have skipped tracking. Rather than providing an option for users to exclude self-identified faulty cycles after the fact, apps can proactively alert users when their probability of skipping tracking is high, helping users to better self-manage their menstruation. For instance, users could be alerted when their cycle skipping probability is near a peak, as in Figure 3. Because cycle variability is common, longer cycle lengths can also be the result of physiological phenomena and not just skipped tracking—this context, captured by our proposed model, can be provided to users in such alerts. This type of informed alerting helps avoid user notification fatigue (ie, targeted alerts instead of everyday alerts to ensure that they are tracking) and increases efficacy and accuracy of self-reporting, which is crucial to creating more reliable datasets for the future. This demonstrates the importance of considering the specific nature of mHealth data that not only enables researchers and users alike to better understand menstruation and the underlying reason behind the observed cycle lengths, but also provides insight for mHealth app developers into how to alert users about possible inconsistent adherence in a nuanced way. As self-tracking apps continue to grow in popularity and serve as an increasingly important source of information for healthcare interventions, these insights can aid researchers in improving the quality of mHealth data and ensuring it is being treated responsibly.

Other efforts to model menstrual cycle lengths using user-reported data focus on issues like how to represent between-women and within-women variability. Researchers have represented this variability utilizing hierarchical models³⁸; linear random effects models,³⁹ accounting for the fact that menstrual cycle behavior evolves with age⁴⁰; and mixture models of standard cycles (cycles 43 days and shorter) and nonstandard cycles (cycles longer than 43 days).⁴¹ While these studies capture many important aspects of menstruation (like consideration of each woman's individual cycle behavior) and include exclusion criteria for women who may not have reported their cycles accurately, they do not explicitly address the user adherence issues encountered when using self-reported mHealth data. Without this consideration, it may be difficult to determine whether nonstandard cycles are the result of skipped tracking. In addition, the definition of a standard or nonstandard cycle may be limiting in itself, and these studies may also be limited in the size or scope of the dataset used. For instance, one advantage of our analysis is that we are able to utilize a large dataset of natural menstrual cycles only.

Furthermore, because sparsity is a prevalent issue with self-tracked data, it is beneficial to have a performant model with the minimal type of information needed. In this case, that is cycle length information (which is also the information most commonly tracked by users who use menstrual tracking apps). By using observed cycle lengths as our only data source, we are able to achieve comparable error to prior studies. In previous work⁴² for instance, an RMSE of 1.6 is achieved; however, this RMSE is based on standard cycles only and uses self-tracking data from a mHealth app designed for female athletes, a specific subset of individuals that does not necessarily represent the diversity of women. In our study, when we consider nonvariable cycles only (based on the definition of menstrual regularity as represented in Figure 5) our model is able to achieve a similar median absolute error of 1.5 days, but the presence of outliers in more broadly used apps like Clue (due to unexpected cycle skips) increases the RMSE. Beyond predictive accuracy, model calibration is also useful to provide less uncertain cycle length predictions.⁴³

We acknowledge that there are limitations to this study. A limitation inherent to our work is the lack of access to ground truth (ie, knowledge of what the actual experienced cycle lengths are); however, this limitation holds for all studies utilizing self-tracking data. Relatedly, we do not have explicit user information about events that may disrupt menstruation, such as pregnancy or miscarriage; we account for this by conservatively removing cycles that are identified by the user as anomalous and removing cycles longer than 90 days. Another limitation of our work is that we do not currently leverage any menstrual symptom information from Clue. However, symptom observations offer great potential to extend our model. In our previous work,¹⁹ we found that there is a relationship between cycle timing and symptom experiences; other studies have also included symptom covariates, like cramps and period flow, to examine how these impact reported menstrual cycle length.⁴² Including information beyond cycle lengths is crucial to understanding cycle variability more holistically⁴⁴ and may have significant impact on cycle prediction accuracy.

CONCLUSION

Our work on predicting menstrual patterns showcases the potential that self-tracking data holds to further understanding of previously enigmatic physiological processes. We have demonstrated our proposed model's ability to successfully detect self-tracking artifacts and outperform alternative baselines on predicting next cycle start on real-world menstruator data. By utilizing a generative model, we have gained insight into the mechanisms of self-tracking behavior, and in particular, users' propensity to skip tracking.

FUNDING

KL is supported by the National Science Foundation's Graduate Research Fellowship Program Award #1644869. IU and NE are supported by National Library of Medicine award R01 LM013043.

AUTHOR CONTRIBUTIONS

KL, IU, CHW, and NE conceived the proposed research and designed the experiments. KL and IU processed the dataset and conducted the experiments. KL wrote the first draft of the manuscript. IU, CHW, AD, AS, VJV, and NE reviewed and edited the first draft. All authors read and approved the manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.