Strategies for building robust prediction models using data unavailable at prediction time

Abstract

Objective

Hospital-acquired infections (HAIs) are associated with significant morbidity, mortality, and prolonged hospital length of stay. Risk prediction models based on pre- and intraoperative data have been proposed to assess the risk of HAIs at the end of the surgery, but the performance of these models lag behind HAI detection models based on postoperative data. Postoperative data are more predictive than pre- or interoperative data since it is closer to the outcomes in time, but it is unavailable when the risk models are applied (end of surgery). The objective is to study whether such data, which is temporally unavailable at prediction time (TUP) (and thus cannot directly enter the model), can be used to improve the performance of the risk model.

Materials and Methods

An extensive array of 12 methods based on logistic/linear regression and deep learning were used to incorporate the TUP data using a variety of intermediate representations of the data. Due to the hierarchical structure of different HAI outcomes, a comparison of single and multi-task learning frameworks is also presented.

Results and Discussion

The use of TUP data was always advantageous as baseline methods, which cannot utilize TUP data, never achieved the top performance. The relative performances of the different models vary across the different outcomes. Regarding the intermediate representation, we found that its complexity was key and that incorporating label information was helpful.

Conclusions

Using TUP data significantly helped predictive performance irrespective of the model complexity.

INTRODUCTION

Clinical decision support models based on artificial intelligence and machine learning are enjoying rapid adoption in clinical practice.^1–4 One such area is risk modeling,^3,5 where the risk of a future outcome is assessed at a particular point in time to inform the patient’s care decisions. For example, risk models can be used to assess the 30-day risk of hospital-acquired postoperative complications at the end of the surgery. Pre-existing longitudinal electronic health records (EHRs) are often utilized for training such models. In a typical analysis, a cross-section of the patients at an index date (at the end of surgery in this example) is taken, their state of health is summarized into “predictors” using information before the index date (from the “past”) and their “future” 30-day outcomes are extracted from the existing data. Besides the “future” outcomes, EHR data also contains “future” data about patients’ state of health at and around the time of the outcome. When the model is applied in practice, the “past” data (predictors) are available, but “future” outcomes and “future” data are not yet generated. Therefore, we categorize data in the EHR as available at prediction time (APT) or temporally unavailable at prediction time (TUP) depending on whether they precede or follow the index date. TUP data cannot be directly used as predictors in a prediction model and are thus overwhelmingly ignored. In this article, we proposed methods to utilize TUP data and improve the resulting risk model’s predictive performance.

We hypothesize that TUP data, which is in the “future” relative to the index date, is between the “future” outcomes and the APT data (retrospective or “past” predictors). TUP data can thus be used to partition the potentially complex relationship between the APT data and the outcome into a set of simpler relationships between the APT data and the TUP data and another set of even simpler relationships between the TUP data and the outcomes. Such partitioning is most useful if data availability is limited, outcome labels are scarce, or positive outcomes are rare.

In this study, we build models using perioperative data as predictors for 8 related 30-day postoperative complication outcomes: pneumonia (PNA), urinary tract infection (UTI), sepsis, with and without shock, superficial, total, and organ-space surgical site infection (SSI). At our institution, EHR data exists in very large quantities, covering over 100 000 surgeries for this study. Unfortunately, the number of reliable outcomes is limited. While diagnosis codes for these outcomes exist, their definition involves clinical judgment, and thus the EHR system does not capture them with high fidelity.^6–8 EHR diagnosis codes have more mistakes compared to vetted National Surgical Quality Improvement Program (NSQIP) outcomes, partly due to diagnostic challenges^6,7 or non-medical reasons, such as patient relocation. To obtain reliable outcomes, manual adjudication by trained professionals in a labor-intensive process is needed. This high cost limits the availability of adjudicated outcomes; at our institution, they exist only for 9785 out of 116 067 surgeries and among these 9785 surgeries, positive outcomes (presence of complications) are very rare, less than 1% for some outcomes. Given the scarcity of adjudicated outcomes, particularly positive outcomes, being able to use TUP data is very promising.

The typical solution to the scarcity of outcome labels is semi-supervised learning,^9,10 where unsupervised knowledge about the data (eg, cluster structure) is used to complement the small number of existing labels. Our application can be viewed as a special case of semi-supervised learning, where the TUP data are used to provide information about the missing adjudicated outcomes. Compared with the semi-supervised learning approach, which only uses the APT data, our approach can provide extra knowledge using the TUP data. For example, the computable phenotypes identified by the TUP data will be more informative and accurate than those identified using the APT data. Another related area is transfer learning,^11–13 where a model is trained on a large external data set, and the trained model is adjusted to the small local data set. Our problem is different because the features in the external data (TUP data) are semantically different from the features in the risk model. A third general solution is knowledge distillation (KD).^14–17 In KD, a detailed teacher model is constructed on the external data, and this teacher model helps a student model fit to the local data.¹⁸ KD differs from our setup because it assumes that the outcome labels are available equally for the local and external data.

OBJECTIVE

In this article, we present a comprehensive comparison of 12 methods to incorporate the TUP data in the model training process. Four of these methods are commonly used and we developed the remaining 8. We look at these methods from 3 perspectives. First, since the APT data and the TUP data have features with different semantics, a common representation is necessary to be able to transfer information from the TUP data. We look at 4 different approaches to construct this intermediate representation. Second, the adjudicated outcome labels are scarce, leading to a sample-size perspective. We compare low-complexity models (logistic/linear regression) and models of varying complexity (deep learning). Third, we also consider single versus multi-task learning, where the intermediate representation can (or cannot) share information among the 8 related outcomes.

MATERIALS AND METHODS

Cohort description

For this retrospective cohort study, data are collected between 2011 and 2019 from M Health Fairview (FV), a health system comprised of a flagship academic hospital, the University of Minnesota Medical Center (UMMC), and 11 community hospitals located in Minnesota. The study population consists of 116 067 adult surgical cases from 62 787 patients with 22 194 patients having multiple surgeries. We divide our population into 2 cohorts: the NSQIP cohort consists of 9785 patients with adjudicated outcomes and the non-NSQIP cohort of 106 282 patients with the outcomes missing.

Outcomes and variables

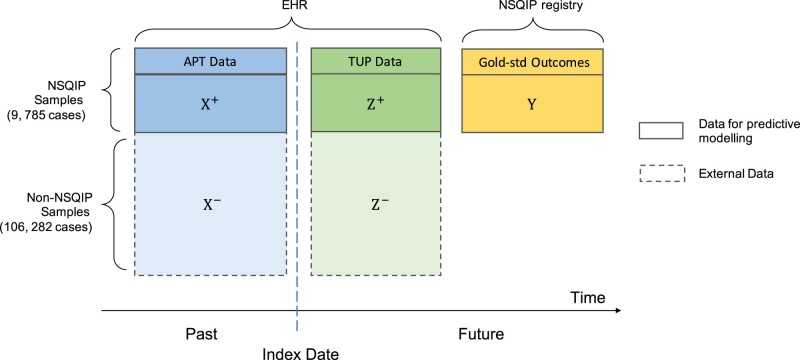
Figure 1 provides an overview of the data types and sources. The outcomes are PNA, UTI, 3 kinds of SSI: superficial, organ-space, and total; and 3 sepsis-related outcomes: sepsis (non-severe without shock), septic shock, and any sepsis (sepsis or septic shock, SESS). We use the NSQIP definition of these outcomes, and the outcome data were obtained from the NSQIP registry. The positive rates for the outcomes vary from 0.7% to 5.3%.

Figure 1.

Overview of data type and source in the predictive models. The data temporally unavailable at prediction time (TUP data) are available for training the predictive models but are not available at the time the model is applied (index date). The data available at prediction time (APT data) are depicted in blue and the TUP data in green. Adjudicated outcomes are obtained from the NSQIP registry and are available only for 9785 out of 106 282 surgeries. They are depicted in yellow. We aim to make predictions for all cases.

Predictor variables, perioperative (APT) and postoperative (TUP), are derived from the structured EHR data collected from the Clinical Data Repository (CDR) of the University of Minnesota. Perioperative data consists of (1) preoperative variables, including medical history, laboratory results, and vital signs up to 30 days prior to surgery; and (2) intraoperative variables including orders, medications, and high-resolution laboratory results and vital signs during the surgery. Continuous variables with repeated measurements are aggregated to mean values as described in Zhu et al.¹⁹ Postoperative data consists of diagnosis codes, orders, procedures, microbiology, and lab test results and vital measurements, which occur during the time window from days 3 to 30 after surgery. In order to account for the recovery period, during which abnormal measurements are common, the first 2 postoperative days were excluded.

Table  1 summarizes the 2 study cohorts, including demographic information, outcomes, the most important variables in the APT data (X), and the TUP data (Z). For binary variables, we show the number (and percent) of positive cases and for continuous features, we show the mean (and interquartile range).

Table 1.

Cohort description

	NSQIP	Non-NSQIP
Total surgical cases	9785	106 282
	Demographics
Age	54 (41, 65)	56 (44, 66)
Gender (male)	4180 (42.7%)	50 649 (47.7%)
	Outcomes
SESSa	219 (2.2%)
PNAa	214 (2.2%)
UTIa	230 (2.4%)
Superficial SSIa	218 (2.2%)
Organ-Space SSIa	219 (2.2%)
Total SSIa	515 (5.3%)
Sepsis	156 (1.6%)
Septic shock	64 (0.7%)
	APT datab ($\mathrm{X}$)
sch_mnts (scheduled surgery length in minute)	180 (120, 275)	90 (60, 180)
rgn_abdomen_pelvis (abdomen, pelvic region)	6961 (71.1%)	39 146 (36.8%)
dx_htn (history of hypertension)	1823 (18.6%)	28 527 (26.8%)
dz_pna (history of PNA)	128 (1.3%)	3926 (3.7%)
dz_uti (history of UTI)	197 (2.0%)	2744 (2.6%)
med_dm_insulin_1y (insulin during prior 1 year)	1413 (14.4%)	24 158 (22.7%)
med_abx_30d (antibiotics during prior 30 days)	4042 (41.3%)	50 057 (47.1%)
med_steroid_in (intraop steroid)	2955 (30.2%)	23 838 (22.4%)
ph_art_in_mean (intraop arterial pH)	7.39 (7.35, 7.43)	7.38 (7.34, 7.42)
rdw_in_mean (intraop red cell distribution width)	14.3 (13.4, 15.6)	14.4 (13.4, 16.0)
	TUP datab ($\mathrm{Z}$)
ICD_SE (sepsis-related diagnosis codes recorded)	248 (2.5%)	3662 (3.5%)
ICD_PNA (PNA-related diagnosis codes recorded)	485 (5.0%)	7272 (6.8%)
ICD_UTI (UTI-related diagnosis codes recorded)	419 (4.3%)	4071 (3.8%)
ICD_SSI (SSI-related diagnosis codes recorded)	659 (6.7%)	4396 (4.1%)
IMAGING_SE_TREAT (sepsis-related imaging treatment ordered)	290 (3.0%)	3081 (2.9%)
Abscess (abscess culture ordered)	135 (1.4%)	761 (0.7%)
Wound (wound culture ordered)	227 (2.3%)	2032 (1.9%)
Microbiology test positive (Enterococcus)	315 (3.2%)	3744 (3.5%)
Microbiology test positive (Escherichia coli)	248 (2.5%)	2122 (2.0%)
Microbiology test positive (Gram-positive)	353 (3.6%)	3488 (3.3%)
PNA_MED (Pneumonia antibiotics ordered)	2767 (28.3%)	35 075 (33.0%)
Respiratory rate (maximum)	20 (18, 21)	20 (18, 24)
Blood (blood culture ordered)	989 (10.1%)	13 253 (12.5%)
Temperature (maximum)	98.9 (98.3, 99.8)	98.8 (98.2, 99.7)
Calcium (minimum)	8.2 (7.8, 8.7)	8.3 (7.8, 8.8)

Note: For the binary variables, the label shows the count and the percentage of the positive samples in both the NSQIP and non-NSQIP groups. For the continuous variables, the label shows the mean value and the interquartile range in both the NSQIP and non-NSQIP groups. The non-NSQIP group does not have labels, so the outcome column remains empty.

^aPNA: pneumonia; SESS: sepsis or septic shock; UTI: urinary tract infection; SSI: surgical site infection.

^bAPT data: data available at prediction time; TUP data: data temporally unavailable at prediction time.

Model description

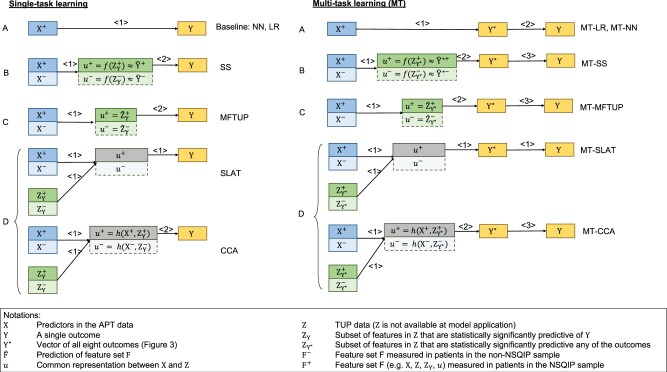
Figure  2 provides an overview of the 12 methods considered. We describe these methods from 3 perspectives: (1) the approach they used for constructing a common representation for the external and internal data, (2) the complexity of the models, and (3) single versus multi-task learning.

Figure 2.

Overview of proposed models. X represents features (predictors) in the APT data, Z in the TUP data, and Y represents a single outcome, while Y* represents the vector of all 8 outcomes. Arrows signal predictive relationships and the numbers above the arrows denote the order in which the predictions are made. When multiple numbers coincide (eg, SLAT), the corresponding predictions are made at the same time. Modeling approaches can be classified into 4 categories, denoted by the different capital letters, according to the intermediate features they build. Approach A does not construct any intermediate features. Instead, it models Y directly without Z (these are the baseline models). Approach B uses the estimates of (the probability of) Y as intermediate features. Approach C uses Z or a subset of Z as the intermediate feature to model Y. Finally, Approach D constructs a shared hidden layer from X and Z as the intermediate feature. The colors correspond to Figure  1, and gray represents the intermediate features. Saturated colors denote the NSQIP sample (samples with the adjudicated outcome labels), and the less saturated colors denote the non-NSQIP sample (with missing outcome labels). Positive superscripts denote the NSQIP sample, negative superscripts denote the non-NSQIP samples (missing labels), and the absence of a superscript denotes the entire dataset. APT: available at prediction time; SLAT: Shared LATent layer; TUP: temporally unavailable at prediction time.

Approaches

Since the APT data X and the TUP data Z contain different features, a common representation u is necessary to transform information from Z to X. Four approaches are presented to construct this intermediate representation u.

Approach A represents the baseline models where Y is directly modeled from X without Z. This approach yields 2 baseline methods: logistic regression (LR) and neural network (NN) with bottleneck. With no Y labels for the non-NSQIP patients, LR and NN can only use the NSQIP samples. Details of the model construction are described later in the Experimental Setting section.

Approach B constructs a single intermediate feature, which is the estimated probability of Y: $u=\widehat{\mathrm{Y}}=\mathrm{ }f\left({\mathrm{Z}}_{\mathrm{Y}}\right)$. The Silver-Standard model (SS)¹⁹ uses this approach and is trained in 2 steps. First, a detection model $\mathrm{Y}\sim \mathrm{Z}$ is constructed using only NSQIP patients. This model then provides risk estimates ${\widehat{\mathrm{Y}}}^{-}$ for the non-NSQIP samples (the negative superscript denotes the lack of NSQIP labels). In the second step, a LR model is constructed to predict $\widehat{\mathrm{Y}}$ based on X. Details of the model construction procedure are provided in ref.19 When the models are applied to previously unseen samples, only the model from the second step is used.

Approach C methods model a subset ${\mathrm{Z}}_{\mathrm{Y}}\mathrm{ }$of Z, which is predictive of Y, using X, and then model Y based on the predicted ${\mathrm{Z}}_{\mathrm{Y}}$. The intermediate features in this approach are the estimates of ${\mathrm{Z}}_{\mathrm{Y}}$, that is, $u={\widehat{\mathrm{Z}}}_{\mathrm{Y}}=\mathrm{ }f\left(\mathrm{X}\right)$. This approach yields one method, Modeling Features Temporally Unavailable at Prediction time (MFTUP). It first builds multiple regression models ${\mathrm{Z}}_{\mathrm{Y}}\sim \mathrm{X}$, one for each significant TUP feature in ${\mathrm{Z}}_{\mathrm{Y}}$ in the combined NSQIP and non-NISQP samples. Then, it models the outcome using the predicted TUP features, that is, $\mathrm{Y}\sim {\widehat{\mathrm{Z}}}_{\mathrm{Y}}$. At the time of prediction, first estimates for ${\widehat{\mathrm{Z}}}_{\mathrm{Y}}$ are obtained from X, and then the outcome is estimated based on ${\widehat{\mathrm{Z}}}_{\mathrm{Y}}$.

Approach D creates a shared representation of X and Z, which is then used to model Y. Two methods use this approach, and they differ in the way they construct this shared representation. The first is Canonical Correlation Analysis (CCA),²⁰ which computes a transformation of both X and ${\mathrm{Z}}_{\mathrm{Y}}$ that maximizes the correlation between the transformed X and ${\mathrm{Z}}_{\mathrm{Y}}$. The intermediate representation is the transformed X, which is then used to model Y. The second method is NN with Shared LATent layer (SLAT). It builds a NN with a shared latent layer to decode $\mathrm{Y}$ and ${\mathrm{Z}}_{\mathrm{Y}}$ simultaneously. The idea is similar to the supervised autoencoder.²¹ The main modification is that SLAT tries to decode TUP features ${\mathrm{Z}}_{\mathrm{Y}}$ instead of recovering input X from the shared latent layer. In the implementation, the dimension of the shared latent layer is set to a value smaller than other hidden layers, which makes it become a bottleneck,^22–24 as shown in Figure  4 (b). There are 2 losses in SLAT, the reconstruction loss of Z and the classification loss of Y. In the experiment, we update the reconstruction loss on both the NSQIP and the non-NSQIP datasets while we update the classification loss only on the NSQIP dataset. These 2 losses are weighed equally. When we make predictions on previously unseen data X, we only use the left path of the model in Figure  4(b), namely the X-Bottleneck-Y path.

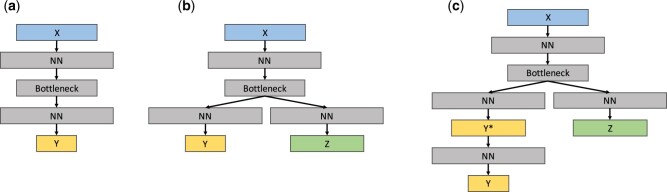
Figure 4.

The structure of 3 deep learning models: (A), (B), and (C) are the structures of NN Baseline, SLAT, and MT-SLAT, respectively. Color coding is consistent with Figure  1. NN block denotes the neural network structure with multiple layers. Bottleneck block denotes a one-layer neural network whose dimension is smaller than other NN blocks. The setting for each block is provided in the Experimental Setting section. NN: neural network; SLAT: Shared LATent layer;

Multi-task learning-based methods

The second perspective from which we describe the algorithms is single versus multi-task learning. The 8 outcomes in this study form a hierarchy as shown in Figure  3. While the single-task learning method builds models for each outcome independently, the multi-task learning method builds them simultaneously, allowing information to be shared among the models. In general, multi-task and single-task learning methods use the same approaches, but multi-task methods learn all related outcomes Y* simultaneously, and then create a mapping from all outcomes Y* to the outcome $\mathrm{Y}$ of interest. The names of multi-task learning methods have an “MT” prefix in Figure  2.

Figure 3.

Levels of outcomes for multi-task learning approaches.

Model complexity

Finally, the third perspective is model complexity. Given the scarcity of outcome labels, when applicable, we construct both linear regression models (of low complexity) and deep learning methods (of varying complexity). When the modeling step involves scarce outcome labels, a low complexity model is preferable; when the modeling task does not involve outcome labels (eg, construction of the intermediate representation), a deeper, more complex model is preferred. Figure  4 shows the architectures of the deep learning models used in this study.

Experimental setting

Data analysis

Missing values in the analytical matrix were imputed using median imputation. Due to the high dimensionality of the feature space, feature selection was performed using causal variable screening through the PC-Simple algorithm^25,26 followed by backward elimination. Specifically, given an outcome Y, we use the univariate correlation to select the retrospective features $\mathrm{X}$, and we use the PC-Simple algorithm with a maximum condition set size of 2 followed by backward elimination to select the significant TUP features ${\mathrm{Z}}_{\mathrm{Y}}$. Lasso-penalized LR was used to build the detection models (Y/Y* ∼g(Z)) in SS and MFTUP. For all other modeling steps except for CCA, and NN-based models, LR models were used to model binary outcomes, and multiple linear regression models were used to model continuous outcomes. In SS, MFTUP, and CCA, there are additional feature selection steps (PC-Simple algorithm with a maximum condition set size of 2) before all LR models.

Performance evaluation

Bootstrap estimation²⁷ with 20 replications was used. NSQIP and non-NSQIP samples were sampled separately. In the non-NSQIP samples, where the same patient can have multiple records, the sampling unit was a patient. In the NSQIP data, each patient only has one record. On each replica dataset, all models were constructed and evaluated on the out-of-bag NSQIP samples, yielding 20 performance estimates. With no adjudicated outcomes, the non-NSQIP samples could not be used for evaluation. The confidence interval was computed using the normal approximation of the 20 performance estimates, and a paired t-test with Bonferroni correction was used to compare the methods. Three main performance metrics: the area under the receiver operating characteristic curve (AUC) (also known as C-statistic), the mean, and the empirical 95% confidence interval were reported. We do not report biases because the last step of the modeling is a calibration step (to account for differences between the NSQIP and non-NSQIP samples); hence bias is removed.

Hyperparameters for NN-based models

The performance of the NN depends on hyperparameters like the number of hidden layers, learning rate, etc. We tune these hyperparameters on a 20% leave-out portion of the training set separately for all the 20 bootstrap replications. The choices for the number of nodes in the hidden layer are 32, 64, 128, 256, 512, and 1024; for the bottleneck, they are 8, 16, 32, 64, 128, and 256; and for the number of hidden layers, the choices are 4 or 8; and the learning rate is set to 1e-4. An early stopping strategy is adopted on the validation set to avoid overfitting to the training set.

RESULTS

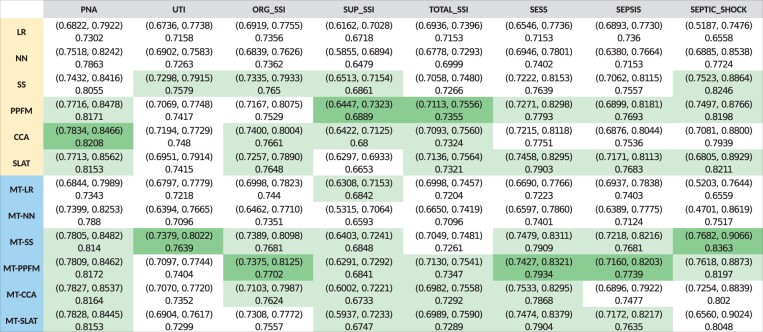
Figure 5 shows the performance of each model across the 8 outcomes. Columns of Figure 5 correspond to methods. The column header is color-coded: yellow indicates single-task learning models, and blue indicates multi-task learning models. Rows correspond to the 8 outcomes. Each cell contains the mean AUC across the 20 bootstrap replications and its 95% confidence interval in parenthesis.

Figure 5.

Performance of each model across 8 outcomes. Rows correspond to methods. Yellow row header indicates single-task learning models, while blue headers indicate multi-task learning models. Columns correspond to the 8 outcomes. In each column, one cell is colored, dark green, which identifies the model with the highest performance for the specific outcome. Light green cells in each column identify models with AUC not significantly different from the best performance.

For each outcome (in each row), the cell corresponding to the method that achieved the highest mean AUC (“top performance”) is colored dark green, and cells corresponding to methods that achieved statistically equivalent performance (P-value > 0.1 in the 2-sided t-test), “top-equivalent performance,” are colored light green. All the models corresponding to green cells (both dark and light green) have equivalent performance and represent the best choice for the corresponding outcome.

All methods managed to achieve reasonable predictive performance for all outcomes. Superficial SSI, with the least objective clinical definition, observed the lowest performance (AUC of ∼.68) followed by total SSI (superficial SSI is a component of total SSI). The performance on other outcomes was high, with AUC in the range of .7 to .8.

The use of TUP data was always advantageous. Baseline (Approach A) methods never achieved the top performance, and MT-LR achieved top-equivalent performance for only one outcome (superficial SSI).

Multi-task learning achieved slightly higher performance. There are 19 single-task and 25 multi-task outcome-method combinations with top-equivalent performance. For 3 of the 8 outcomes, the top performance was achieved by a single-task learning method, and for 5 outcomes, by a multi-task learning method.

Among the 4 approaches, Approach C (MFTUP and MT-MFTUP) achieved top performance for 5 of the 8 outcomes and top-equivalent performance for all outcomes except UTI. Approach B (SS and MT-SS) achieved top performance for 2 of the 8 outcomes and top-equivalent performance for all outcomes except total SSI. Although Approach D methods did not achieve top performance for any outcome, their performance was similar, achieving top-equivalent performance for all outcomes except UTI.

Lower complexity models, those using linear regression instead of deep learning, achieved high performance: MFTUP or MT-MFTUP achieved top performance on 5 of the 8 outcomes, MT-SS on 2, and CCA on the remaining outcome. The more complex models, SLAT and MT-SLAT, achieved top-equivalent performance on all outcomes except UTI.

DISCUSSION

Summary

In this study, we tested and compared 12 different machine learning methods to predict the risk of 8 related hospital-acquired infections (HAIs) by leveraging TUP data and unlabeled instances. We examined these methods from 3 perspectives: (1) the approach they use to construct an intermediate representation to bridge the different feature sets in the TUP data (postoperative) and APT data (perioperative), (2) the complexity of the models, and (3) whether sharing information about the related outcomes helps the methods.

Discussion of the results

TUP data always improved performance

The baseline methods (Approach A) achieved substantially lower performance than methods that utilized TUP data. With a scarcity of labels, the complex relationship between the APT data X and the outcome Y could not be modeled correctly. To avoid overfitting, NN-based methods became just too simple. MT-LR does not utilize TUP data, yet it managed to achieve top-equivalent performance on superficial SSI mostly because this outcome is the least objective and is hence noisier than others. Multi-task learning helped because it managed to relate superficial SSI to more reliable SSI outcomes: “If it is (total) SSI and not organ-space SSI, it is more likely superficial SSI.”

Multi-task learning helped low-complexity models more than varying-complexity models

All methods, except those based on NNs, benefited from multi-task learning. SS experienced the largest improvement. Multi-task learning increased the size of its internal representation from 1 variable to 10, resulting in a better fit. Similarly, MFTUP experienced improvement with its internal representation growing from (an average of) 3 variables to 38. For NN-based models (NN and SLAT), the size of the internal representation did not change, resulting in a representation that is less specific to each outcome, yielding a worse fit. We tried more and less complex network architectures, too, but the performance did not improve.

Complexity of the intermediate representation is key

Among the approaches, Approach C (MFTUP, MT-MFTUP) achieved the highest performance. (Single-task) MFTUP had an intermediate representation of 3 variables on average and MT-MFTUP had 38. MFTUP and MT- MFTUP had equivalent performance for all outcomes except organ-space SSI, which favored the more complex MT-MFTUP. SS, a model that can utilize external data but has lower complexity (a single intermediate variable), underfits. On the other extreme, MT-SLAT, with substantially more complexity (on average 87 variables), overfits. We believe that SS underfits because MT-SS achieved higher performance and MT-SLAT overfits because (single-task) SLAT achieved higher performance. If we had more labels, we could have constructed a more a complex Y∼u model, which would have favored SLAT. Conversely, if we had fewer (or noisier) labels, it would have favored the less complex SS.

Incorporating label information into the intermediate representation is helpful

In single-task learning, there is a significant difference between the 2 Approach D methods: SLAT outperforms CCA. There are 2 possible reasons for this: CCA is linear while SLAT is more flexible, and SLAT uses the outcome label for constructing intermediate representation, while CCA does not.

TUP data helps because it partitions complexity

The TUP data Z is closer to the outcome than the APT data X. The relationship between X and outcome Y is complex, and the number of instances with outcome labels does not support modeling this complexity. Conversely, the relationship between Z and Y is simpler; thus the lower number of outcome labels suffices to build a good model. The relationship between X and Z can be arbitrarily complex since modeling Z based on X is not constrained by the availability of outcome labels. Successful methods managed to create an intermediate representation u, such that the relationship between u and Y is simple, and most complexity is pushed into modeling u based on X and Z.

Generalizability and limitations

Due to data availability, we evaluated our methods on the HAI-prediction application. This application does not have any special properties that would limit the generalizability of our findings. The use of TUP data is impacted by the scarcity of the outcome labels, the availability of the unlabeled data, and the complexity of the TUP data–outcome relationship. If the TUP data–outcome relationship is too complex (relative to the available sample size), even the proposed methods may fail to build a model. Conversely, if the complexity of the relationship between the APT data and the outcome is sufficiently supported by the available outcome labels, the proposed method is unnecessary. Otherwise, our findings would generalize, and the use of the proposed methods would be advantageous. One possible limitation of the use of NNs can be poor calibration. Therefore, we assessed the calibration of methods. The results show that all methods achieved similar calibration. LR, SS, CCA, and MFTUP are well-calibrated since their last step utilizes LR models, while SLAT and NN show slightly worse calibration, probably due to the use of NNs.²⁸ We report the Model calibration results in the Supplementary Material.

Relationship to knowledge distillation and transfer learning

There is a connection between our SS model and KD framework.^14,29,30 The vanilla KD builds a complex teacher model to guide a simpler student model. The transferred knowledge is the logits (the output value before binarization) of the teacher, which is also known as “soft-label” (after applying the softmax function to the logits). The student learns from the teacher by approximating the “soft-label,” as well as from the ground truth, which is the “hard-label.” In the second step of our SS model, we predict the “soft-label” for both the NSQIP and the non-NSQIP samples, and we use the “soft-label” to build the model $\widehat{\mathrm{Y}}$ ∼ X. This step can be seen as a special case of KD in the semi-supervised learning scenario. MFTUP can be seen as a special case of transfer learning because in MFTUP, we build 2 model ${\mathrm{Z}}_{\mathrm{Y}}\sim \mathrm{X}$, $\mathrm{Y}\sim {\widehat{\mathrm{Z}}}_{\mathrm{Y}}$, which follows the structure of transfer learning.

CONCLUSION

We found that using TUP data significantly helped predictive performance irrespective of the model complexity and single versus multi-task learning. Among the methods for constructing intermediate features, we found MFTUP to have the best performance for single- and multi-task learning, with SLAT offering similar performance for single-task learning and SS for multi-task learning. Multi-task learning helped SS the most and failed to improve the NN-based methods.

FUNDING

This work was supported in part by NIGMS award R01 GM120079, AHRQ award R01 HS024532, and the NCATS University of Minnesota CTSA UL1 TR002494. The views expressed in this manuscript are those of the authors and do not necessarily reflect the views of the funding agencies.

AUTHOR CONTRIBUTIONS

GS, RT, YZ, and HY conceived and planned the experiments. HY and YZ carried out the experiment. GBM, GS, RT, and YZ contributed to data acquisition. HY and GS drafted the manuscript. All authors provided critical feedback and helped shape the manuscript. GS, MS, and VK supervised the project.

SUPPLEMENTARY MATERIAL

Supplementary materials are available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST STATEMENT

None declared.

DATA AVAILABILITY

The data that support the findings of this study are not publicly available since they contain patient health information. Authorization to access patient data can be requested from University of Minnesota Institutional Review Board.