Divergence-Free Constrained Phase Unwrapping and Denoising for 4D Flow MRI Using Weighted Least-Squares

Abstract

A novel divergence-free constrained phase unwrapping method was proposed and evaluated for 4D flow MRI. The unwrapped phase field was obtained by integrating the phase variations estimated from the wrapped phase data using weighted least-squares. The divergence-free constraint for incompressible blood flow was incorporated to regulate and denoise the resulting phase field. The proposed method was tested on synthetic phase data of left ventricular flow and in vitro 4D flow measurement of Poiseuille flow. The method was additionally applied to in vivo 4D flow measurements in the thoracic aorta from 30 human subjects. The performance of the proposed method was compared to the state-of-the-art 4D single-step Laplacian algorithm. The synthetic phase data were completely unwrapped by the proposed method for all the cases with velocity encoding (venc) as low as 20% of the maximum velocity and signal-to-noise ratio as low as 5. The in vitro Poiseuille flow data were completely unwrapped with a 60% increase in the velocity-to-noise ratio. For the in-vivo aortic datasets with venc ratio less than 0.4, the proposed method significantly improved the success rate by as much as 40% and reduced the velocity error levels by a factor of 10 compared to the state-of-the-art method. The divergence-free constrained method exhibits reliability and robustness on phase unwrapping and shows improved accuracy of velocity and hemodynamic quantities by unwrapping the low-venc 4D flow MRI data.

I. Introduction

4D flow magnetic resonance imaging (MRI) allows for in vivo acquisition of time-resolved three-dimensional (3D) blood flow, thus enabling quantitative analysis of volumetric, time varying hemodynamic quantities such as flow rates, wall shear stress (WSS), pressure difference, etc [1], [2], [11], [3]–[10]. 4D flow MRI has demonstrated its potential to improve the diagnostics of cardiovascular and cerebrovascular diseases [3], [5]–[7], [12]–[15]. 4D flow MRI is based on the phase contrast (PC) technique which encodes the blood velocity along all dimensions into the MRI signal phase data. A predefined velocity encoding sensitivity parameter (venc) determines the maximum and minimum velocity that can be recorded in the phase data as π and −π, respectively. Therefore, the velocity field can be obtained by multiplying the phase with venc/π. Whenever a velocity component is greater than venc or lower than -venc, the acquired phase is wrapped and leads to velocity aliasing. To avoid aliasing, the venc is suggested to be set approximately 10% higher than the maximum expected velocity [12], [15]. However, high venc leads to high noise level since the velocity-to-noise ratio (VNR) is inversely proportional to venc [16].

One strategy to capture the wide dynamic range associated with physiologic blood flow while maintaining the low noise level associated with low venc data is to perform acquisitions with a set of two or more vencs [14], [16]–[21]. The acquired high-venc data can then be employed for unwrapping the low-venc data. However, despite the efforts to accelerate the multi-venc acquisition [14], the total scan time with a 4-point low venc encoding is still unavoidably longer than a single scan, which is the major limitation of the approach. Using undersampled parallel encoding methods and Bayesian processing of phase data can further accelerate the 4D flow acquisition and enable flexible choice of velocity encoding ranges [22]–[24]. Another strategy is algorithmically unwrapping the wrapped phase data. Several algorithms have been proposed for 4D flow MRI [25]–[29]. However, these algorithms are either untested or unreliable for low-venc acquisitions with large aliased areas or repeatedly wrapped regions. Phase noise also dramatically affects the performances of the unwrapping algorithms.

The purpose of this study was to introduce and evaluate a robust and reliable phase unwrapping method for 4D flow MRI. The proposed method, divergence-free constrained weighted least-squares (CWLS), incorporates the divergence-free constraint of incompressible flow with the estimated phase variations to formulate an optimization problem. The divergence-free constraint has been used in previous studies to reconstruct the velocity field from 3D phase contrast MRI and 4D flow MRI [30]–[32]. The unwrapped phase is obtained using WLS with weights generated based on the phase variation uncertainty. CWLS also utilizes the temporal phase information to enhance the robustness by unwrapping from timepoints least-likely to be wrapped towards those likely to be wrapped. The CWLS method was tested using synthetic phase data of left ventricular (LV) flow and in vitro Poiseuille flow measured using 4D flow MRI. The method is then applied to in vivo aortic 4D flow MRI data from 30 subjects.

II. THeory

Phase wrapping in 4D flow MRI can be presented as:

$$\psi =\mathcal{W}(\varphi )=\varphi +2n\pi withn=-round\left(\frac{\varphi }{2\pi }\right)\in Z,$$ (1)

where ψ is the wrapped phase, ϕ is the unwrapped phase, $\mathcal{W}()$ represents the wrapping operation which adds a multiple of 2π to ϕ such that ψ is within the range (−π, π), round() means rounding to the nearest integer, and Z is the set of integers. ϕ is related with the underlying velocity component v as $\varphi =\frac{\pi }{venc}v$. If v is out of the dynamic range (−venc, venc), phase wrapping occurs as ψ differs from ϕ by a multiple of 2π. The objective of phase unwrapping is to find ϕ based on the acquired ψ so that the underlying velocity can be properly determined.

To unwrap the phase field, one common approach is to integrate the phase variation estimated as:

$$\widehat{\mathrm{\Delta }\varphi }=\mathcal{W}(\mathrm{\Delta }\psi ),$$ (2)

where Δψ is the spatial or temporal variation of the acquired (wrapped) phase, $\widehat{\mathrm{\Delta }\varphi }$ is the estimated variation for the unwrapped phase by wrapping Δψ as in (1). Equation (2) assumes that the phase variation between neighboring voxels is within the range of (−π, π), which is generally valid since the blood velocity varies continuously across the field. The phase variation integration can be treated as an optimization process and solved in a least-squares sense [33]–[35]. This approach has been tested with 2D synthetic phase images, and the robustness can be improved by assigning proper weights to the objective function [33]. The weighted least-squares (WLS) method has been demonstrated to improve the pressure integration with the weights generated based on the accuracy of pressure variation [11]. A similar WLS approach can be developed and applied to the phase unwrapping of 4D flow MRI. Moreover, the divergence-free constraint can be incorporated into the WLS minimization to further improve the accuracy of the unwrapping and denoise the phase field.

III. Methodology

A. Phase Unwrapping With CWLS

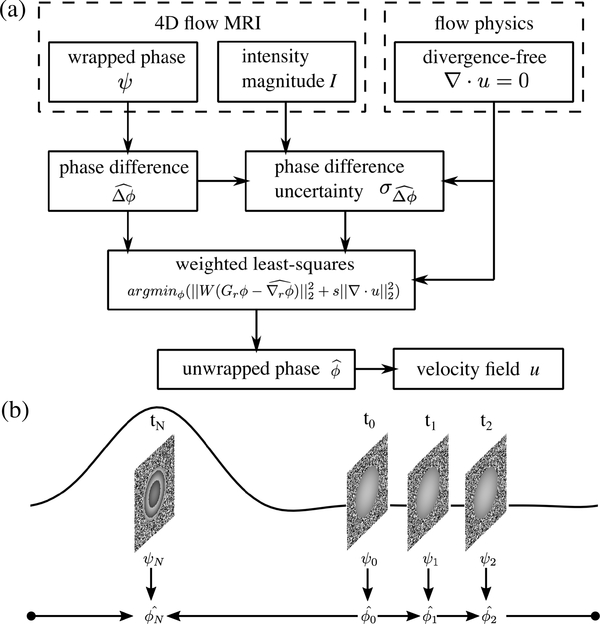
The procedure of phase unwrapping with CWLS is presented in Fig. 1(a). First, the phase variation Δψ was calculated from the wrapped phase field ψ. Specifically, the spatial phase variation was the difference between neighboring voxels, and the temporal phase variation was the difference between consecutive cardiac frames. Then $\widehat{\mathrm{\Delta }\varphi }$ was estimated using (1). The phase gradient was calculated as the phase variation divided by the corresponding spatial or temporal resolution, e.g.,

$$\widehat{{\nabla }_{\text{r}}\varphi }=\widehat{{\mathrm{\Delta }}_{\text{r}}\varphi }/\mathrm{\Delta }r,$$ (3)

where $\widehat{{\nabla }_{\text{r}}\varphi }$ is the spatial phase gradient, $\widehat{{\Delta }_{\text{r}}\varphi }$ is the spatial phase variation, and Δr is the voxel size. The subscript r represents the spatial dimension. The unwrapped phase $\widehat{\varphi }$ is spatially related to the phase gradient $\widehat{{\nabla }_r\varphi }$ as:

$$D_r\widehat{\varphi }=\widehat{{\nabla }_r\varphi },$$ (4)

where D_r is the discrete spatial gradient operator consisting of D_x, D_y, and D_z. In addition, the divergence-free constraint reveals the following relationship between the phases of u, v, and w velocity components (denoted as ϕ_u, ϕ_v, and ϕ_w) as:

$$\begin{array}{l}\nabla \cdot \stackrel{\rightharpoonup }{u}\equiv D_{x}u+D_{y}v+D_{z}w=\frac{ven{c}_u}{\pi }{D}_x{\varphi }_u\\ +\frac{ven{c}_v}{\pi }{D}_y{\varphi }_v+\frac{ven{c}_w}{\pi }\\ D_z{\varphi }_w=0,\end{array}$$ (5)

where ∇· represents the discrete divergence operator, $\stackrel{\rightharpoonup }{u}$ is the velocity vector containing three components as $\stackrel{\rightharpoonup }{u}={[u,v,w]}^T$, venc_u, venc_v, and venc_w are the vencs used for measuring the three velocity components u, v, and w, D_x, D_y, and D_z are the discrete gradient operators constructed as matrices, and ϕ_u, ϕ_v, and ϕ_w are the vectors of phases for the three velocity components. Equations (4) and (5) formulate a minimization problem which can be solved using weighted least-squares as:

$$\begin{array}{l}\widehat{\varphi }=argmi{n}_{\varphi }({\Vert W\left(D_r\varphi -\widehat{{\nabla }_r\varphi }\right)\Vert }_2^2+s\Vert \frac{ven{c}_u}{\pi }{D}_x{\varphi }_u\\ +\frac{ven{c}_v}{\pi }{D}_y{\varphi }_v+\frac{ven{c}_w}{\pi }{D}_z{\varphi }_w{\Vert }_2^2),\end{array}$$ (6)

with

$$W=diag\left(\frac{1}{{\sigma }_{\widehat{{\nabla }_r\varphi }}^2}\right),$$ (7)

where ‖ ‖₂ represents the L2 norm, D_r is the combined discrete gradient operator constructed by vertically stacking D_x, D_y, and D_z, ϕ is the vector consisting of ϕ_u, ϕ_v, and ϕ_w, $\widehat{{\nabla }_r\varphi }$ is the vector of the spatial phase gradients determined using (3), W is the weight matrix generated based on the uncertainty of the phase gradient ${\sigma }_{\widehat{{\nabla }_r\varphi }}$, diag() generates the diagonal matrix with the given diagonal elements, and s is the constant controlling the level of regularization by the divergence-free constraint. The term ${\Vert W\left(D_r\varphi -\widehat{{\nabla }_r\varphi }\right)\Vert }_2$ is the weighted residual of phase variations, and the term ${\Vert \frac{ven{c}_u}{\pi }{D}_x{\varphi }_u+\frac{ven{c}_v}{\pi }{D}_y{\varphi }_v+\frac{ven{c}_w}{\pi }{D}_z{\varphi }_w\Vert }_2$ is the velocity divergence. The divergence-free constraint is considered to be more reliable than the phase gradients since the divergence-free constraint is based on the flow-physics while the phase gradients were estimated from the measurement containing noise and errors. In order to minimize the velocity divergence, s was assigned to be significantly larger than the mean of the phase gradient weights $(\overline{W})$. The residual divergence in the resulting velocity fields can be completely eliminated by using an s value greater than ${10}^4\overline{W}$, thus s was set to ${10}^4\overline{W}$ unless specified otherwise in this work. LSQR, an iterative algorithm for sparse least-squares problems [36], [37], was employed to obtain the solution from (6). The discrete gradient and divergence operators were constructed using the second order central (SOC) difference scheme.

Fig. 1.

(a) Procedure of phase unwrapping with CWLS. (b) The sequence of temporal phase unwrapping start form the time point with lowest average velocity at t₀ to the time point with highest average velocity at t_N along the forward and backward directions in a cyclic manner. The waveform demonstrates the flow rate in one cardiac cycle.

B. Field of View (FOV) Division

To properly apply the divergence-free constraint, the FOV was divided into three regions denoted as the region of blood flow $\left({\mathcal{D}}_{ROI}\right)$, the reference points $\left({\mathcal{D}}_{ref}\right)$, and the rest of the FOV. The divergence minimization in Equation 6 was only applied to the voxels within ${\mathcal{D}}_{ROI}$ since the divergence-free constraint might be invalid outside the flow. The D_ref is defined as a layer of voxels surrounding the ${\mathcal{D}}_{ROI}$, and was obtained by performing one iteration of morphological dilation of ${\mathcal{D}}_{ROI}$ then subtracting ${\mathcal{D}}_{ROI}$ from the dilated region. ${\mathcal{D}}_{ref}$ located in the tissue adjacent to the blood flow, which can be dynamic or static depending on the imaging location. The phase values in ${\mathcal{D}}_{ref}$ were set to zeros prior to the unwrapping for noise elimination, and used as the boundary condition for the CWLS phase unwrapping via gradient integration. The term ${\Vert W\left(D_r\varphi -\widehat{{\nabla }_r\varphi }\right)\Vert }_2$ in (6) was minimized in the combined region ${\mathcal{D}}_{ROI}\cap {\mathcal{D}}_{ref}$. The phase unwrapping via gradient integration was first performed with an arbitrary point set to zero. Then the median of $\widehat{\varphi }$ in D_ref was evaluated and subtracted from the $\widehat{\varphi }$ in the whole field in order to enforce a zero median of $\widehat{\varphi }$ in ${\mathcal{D}}_{ref}$ in order to be consistent with the boundary condition and ensure the robustness since the median is not affected by the extreme values obtained in ${\mathcal{D}}_{ref}$ due to noise. The rest of the FOV was excluded from the CWLS unwrapping to save computational effort.

C. Uncertainty Estimation of Phase Variation

The uncertainty ${\sigma }_{\widehat{{\nabla }_r\varphi }}$ of each $\widehat{{\nabla }_r\varphi }$ value needed for generating the weight matrix W in (7). ${\sigma }_{\widehat{{\nabla }_r\varphi }}$ was estimated as the standard deviation of the distribution of the phase variation error ${ϵ}_{\widehat{{\nabla }_r\varphi }}\equiv \widehat{{\nabla }_r\varphi }-{\nabla }_r\varphi$, where ∇_rϕ is the true phase gradient. ${ϵ}_{\widehat{{\nabla }_r\varphi }}$ can be decomposed into two components:

$${ϵ}_{\widehat{{\nabla }_r\varphi }}={ϵ}_{\widehat{{\nabla }_r\varphi }}^N+{ϵ}_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}},$$ (8)

where ${ϵ}_{\widehat{{\nabla }_r\varphi }}^N$ is the error component due to the measurement noise in ψ, and ${ϵ}_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}}\equiv {ϵ}_{\widehat{{\mathrm{\Delta }}_r\varphi }}^{\mathcal{W}}/\mathrm{\Delta }r$ is caused by the incorrect phase variation estimation by (2). Since the two error components in (8) are uncorrelated, the uncertainty ${\sigma }_{\widehat{{\nabla }_r\varphi }}$ can be determined as

$${\sigma }_{\widehat{{\nabla }_r\varphi }}=\sqrt{{\left({\sigma }_{\widehat{{\nabla }_r\varphi }}^N\right)}^2+{\left({\sigma }_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}}\right)}^2},$$ (9)

where ${\sigma }_{\widehat{{\nabla }_r\varphi }}^N$ and ${\sigma }_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}}$ are the uncertainties of ${ϵ}_{\widehat{{\nabla }_r\varphi }}^N$ and ${ϵ}_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}}$,respectively.

The magnitude of ${ϵ}_{\widehat{{\mathrm{\Delta }}_r\varphi }}^{\mathcal{W}}$ can be inferred from the integration of $\widehat{{\nabla }_r\varphi }$ along closed loops in space [38]. The smallest possible loops are 2 × 2 voxel rectangular loops denoted as loop elements. The integration $(\oint \widehat{{\nabla }_r\varphi })$ of each loop element equals the sum of the four ${ϵ}_{\widehat{{\mathrm{\Delta }}_r\varphi }}^{\mathcal{W}}$ values on the loop element. Since each $\widehat{{\mathrm{\Delta }}_r\varphi }$ value can be on multiple loop elements, the phase variation uncertainty ${\sigma }_{\widehat{{\mathrm{\Delta }}_r\varphi }}^{\mathcal{W}}$ was approximated as the sum of $\frac{1}{4}|\oint \widehat{{\nabla }_r\varphi }|$ from all the loop elements. The $\oint \widehat{{\nabla }_r\varphi }$ was calculated for all possible 2×2 voxel loop elements in the 3D field, and the value of ${\sigma }_{\widehat{{\mathrm{\Delta }}_r\varphi }}^{\mathcal{W}}$ was additively updated. The phase gradient uncertainty ${\sigma }_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}}$ was then determined as ${\sigma }_{\widehat{{\mathrm{\Delta }}_r\varphi }}^{\mathcal{W}}/\mathrm{\Delta }r$.

The uncertainty ${\sigma }_{\widehat{{\nabla }_r\varphi }}^N$ for the noise component was estimated based on the spurious divergence of the velocity field as well as the intensity magnitude field I. First, the velocity-divergence field ∇·u was calculated from $\widehat{{\nabla }_r\varphi }$ using (5). According to the divergence-free constraint, ∇ · u is related to the phase noise ${ϵ}_{\widehat{\varphi }}^N$ as:

$$\frac{ven{c}_u}{\pi }{D}_x{ϵ}_{\widehat{{\varphi }_u}}^N+\frac{ven{c}_v}{\pi }{D}_y{ϵ}_{\widehat{{\varphi }_v}}^N+\frac{ven{c}_w}{\pi }{D}_z{ϵ}_{\widehat{{\varphi }_w}}^N=\nabla \cdot \stackrel{\rightharpoonup }{u}.$$ (10)

Similar to the velocity error estimation from velocity divergence [11], ${ϵ}_{\widehat{\varphi }}^N$ was obtained by solving (10) in a least-squares sense. The ${ϵ}_{\widehat{\varphi }}^N$ was convolved with a 3D Gaussian kernel with a width of 2Δr corresponding to the three-point stencil-size of the SOC scheme to obtain the phase uncertainty field ${\sigma }_{\widehat{\varphi }}^{N,G}$. In addition, the root-mean-square (RMS) of ${ϵ}_{\widehat{\varphi }}^N$ in ${\mathcal{D}}_{\text{ROI}}$ was calculated to represent the global phase noise level as ${\overline{\sigma }}_{\widehat{\varphi }}^N$. Since the noise in the phase is inversely proportional to the intensity magnitude [16], [39], the ratio between the local and global phase noise uncertainty equals the reciprocal of the ratio between the local and global intensity. Thus, the phase noise uncertainty can be estimated based on the intensity field and the global phase noise uncertainty ${\overline{\sigma }}_{\widehat{\varphi }}^N$ as:

$${\sigma }_{\widehat{\varphi }}^{N,I}={\overline{\sigma }}_{\widehat{\varphi }}^N\overline{I}/I,$$ (11)

where $\overline{I}$ is the average of the intensity magnitudes in ${\mathcal{D}}_{\text{ROI}}$. The quadratic mean of the two estimations of phase noise uncertainty was calculated as:

$${\sigma }_{\widehat{\varphi }}^N=\sqrt{\frac{1}{2}\left[{\left({\sigma }_{\widehat{\varphi }}^{N,G}\right)}^2+{\left({\sigma }_{\widehat{\varphi }}^{N,I}\right)}^2\right]},$$ (12)

which was then propagated through the calculations of phase variation and phase gradient to acquire the phase gradient uncertainty ${\sigma }_{\widehat{{\nabla }_r\varphi }}^N$.

D. Sequential Frame Unwrapping

Based on the temporal continuity of the velocity field, an unwrapped frame can be used to infer the temporally neighboring frames [25] as:

$${\widehat{\varphi }}_{i\pm 1}^t={\widehat{\varphi }}_i+\mathcal{W}\left({\mathrm{\Delta }}_t\psi \right),\text{with}{\mathrm{\Delta }}_t\psi ={\psi }_{i\pm 1}-{\psi }_i,$$ (13)

where ${\widehat{\varphi }}_i$ is the unwrapped phase at i^th cardiac frame, Δ_tψ is the temporal phase variation, and ${\widehat{\varphi }}_{i\pm 1}^t$ is the temporally unwrapped phase at the neighboring frames i ± 1. The temporally unwrapped phase ${\widehat{\varphi }}^t$ was utilized in the CWLS unwrapping. First, the spatial variation of ${\widehat{\varphi }}^t$ was combined with the estimation from (2) to obtain the spatial phase variation as:

$$\widehat{{\Delta }_r\varphi }=\frac{1}{2}\left({\mathrm{\Delta }}_r{\widehat{\varphi }}^t+\mathcal{W}\left({\mathrm{\Delta }}_r\psi \right)\right),$$ (14)

which was employed in the phase variation integration by (6). Second, the deviation between ${\mathrm{\Delta }}_r{\widehat{\varphi }}^t$ and $\mathcal{W}\left({\mathrm{\Delta }}_r\psi \right)$ was used to update the phase gradient uncertainty as:

$${\sigma }_{\widehat{{\nabla }_r\varphi }}=\sqrt{{\left({\sigma }_{\widehat{{\nabla }_r\varphi }}^N\right)}^2+{\left({\sigma }_{\widehat{{\nabla }_r\varphi }}^{\mathcal{W}}\right)}^2+{\left(\frac{{\mathrm{\Delta }}_r{\widehat{\varphi }}^t-\mathcal{W}\left({\mathrm{\Delta }}_r\psi \right)}{\mathrm{\Delta }r}\right)}^2},$$ (15)

which was employed to generate the weight matrix W in (7). In addition, ${\widehat{\varphi }}^t$ was used as the initial field for solving (6) with the iterative LSQR algorithm.

Since the reliability of ${\widehat{\varphi }}_{i\pm 1}^t$ depends on the accuracy of ${\widehat{\varphi }}_i$, it is preferable to perform the temporal phase unwrapping from a less-wrapped frame towards a more-wrapped one. We adopted the frame sequences to start from the frame with lowest average velocity magnitude towards the frame with highest average velocity magnitude along both the forward and backward temporal directions as demonstrated in Fig. 1(b). The frame with highest flow rate was unwrapped twice with the two temporal sequences as both neighboring timeframes had lower flow rates. Each of the two unwrapping operations on the frame with highest flow rate was performed independently and initialized with one of the neighboring frames, yielding two unwrapping results which were similar in general. The average of the two unwrapped fields were taken as the final result since taking the average can reduce the uncertainty compared to a single sample. The proposed temporal sequences can prevent the propagation of unwrapping errors from severely wrapped frames to the less-wrapped ones. The starting and the ending timepoints can be approximated as the peak diastole or peak systole depending on the locations in the cardiovascular system.

E. Synthetic Phase Data Generation

To evaluate the performance of the CWLS method, synthetic phase data was generated from computational fluid dynamics (CFD) simulated left ventricular (LV) flow velocity fields [40]. The CFD results were obtained on unstructured computational mesh with 180,000 tetrahedral cells and linearly interpolated to a fine Cartesian grid with spatial resolution of 0.2 mm. Complex-valued signal was generated at each grid node based on each velocity component as:

$$M_{fine}=Iexp\left(\frac{i\pi u}{venc}\right),$$ (16)

where M_fine denotes the complex signal at the fine grid node, I is the signal magnitude, and u is the velocity component at grid node. Another Cartesian grid with a resolution of 2.5 mm was employed as the MRI grid (G_MRI ) with each grid point corresponding to a voxel-center, in order to be consistent with the typical resolutions of heart scans [15]. The complex-valued signal at each voxel-center of the synthetic 4D flow MRI data was generated by convolving the signal on the fine Cartesian grid with a sinc-function kernel (K) as:

$$K(x,y,z)=sinc\left(\frac{x}{\mathrm{\Delta }x}\right)\times sinc\left(\frac{y}{\mathrm{\Delta }y}\right)\times sinc\left(\frac{z}{\mathrm{\Delta }z}\right),$$ (17)

with $sinc(x)=\frac{sin(\pi x)}{\pi x}$, where Δx, Δy, and Δz represent the spatial resolution of the MRI grid. Previous studies have shown that the spatial blurring of Cartesian 4D flow MRI measurement due to limited coverage of the k-space equals to the convolution with the sinc-function kernel [41], and convolving with the sinc-function kernel has been used to simulate 4D flow MRI acquisitions [42]–[44]. One reference (M₀) and 3 flow-sensitive datasets (M_u, M_v, and M_w) were simulated following a four-point reference method. Each flow-sensitive dataset was created based on the field of a velocity component, and the reference dataset was generated from a zero phase field such that the phase difference between the flow-sensitive and the reference datasets was consistent with the velocity field as in real applications. The signal noise ϵ in each component of the complex-valued data was assumed to be normally distributed with a standard deviation of ${\sigma }_I=\overline{I}/SN{R}_I$, where SNR_I is the intensity magnitude based SNR [45]. The wrapped phase data ψ for each velocity component was generated from the complex-valued data, e.g.:

$${\psi }_u=angle\left(M_u\ast M_0^{*}\right),$$ (18)

where ψ_u is the phase for u velocity component, $M_0^{*}$ is the complex conjugate of M₀, and angle( ) means calculating the angle from a complex signal as:

$$angle(a+bi)=\arctan \left(\frac{b}{a}\right).$$ (19)

Since the reference dataset was shared among the three flow-sensitive datasets, the phase noise of different velocity components were correlated in a similar way as the real phase data [46].

The intensity magnitude field I was allowed to vary spatially as commonly seen from the FOV of 4D flow MRI. The spatial distribution of I was defined as:

$$I=1.0-0.5\left(\frac{x}{L_{domain}}\right),$$ (20)

where L_domain is the total length of the FOV along the x direction. The I outside D_ROI was multiplied with 0.2 to mimic the low intensity outside the lumen. In addition to the predefined bulk variation, I would also vary locally due to the noise and the intravoxel dephasing effect caused by the spatiotemporal variation of velocity.

Since the SNR of MRI acquisitions can be greater than 100 for in vitro measurements and less than 10 for in vivo measurements [14], [17], [18], [47], [48], we employed the following 6 values to represent a wide range of SNRI as: 100, 50, 20, 10, 5, and 2. A wide range of vencs was also employed to test CWLS on different levels of phase wrapping. The venc ratio (VR) defined as the ratio between the venc and the maximum flow velocity was varied from 0.1 to 0.9 in increments of 0.1. In total, 54 test cases were created with different combinations of SNRI and VR.

To determine the effect of spatial resolution on CWLS unwrapping, several additional datasets were created using the same approach with MRI grid resolution varying from 2 to 6 mm in increments of 1 mm. For each spatial resolution, 10 datasets were created with an SNR of 10 and VR from 0.1 to 1.0 in increments of 0.1.

The mask of ${\mathcal{D}}_{ROI}$ was generated for each dataset and each time frame based on the geometry available from the CFD simulation. A voxel was considered to be in the blood flow domain if the voxel-center was within the geometry at the time instant.

F. In Vitro 4D Poiseuille Flow Measurement

Steady, laminar Poiseuille flow in a circular pipe was measured using 4D flow MRI with different vencs. The working fluid was a blood mimicking water-glycerol (60:40 by volume) solution with a density of 1110 kg/m³ and viscosity of 0.00372 Pa·s. A small amount (0.66 mg/mL) of Gadolinium contrast was added to enhance the SNR of the scan without altering the rheology of the fluid. A computer-controlled gear pump was used to drive the working fluid at a steady flow rate of 7.6 mL/s. The diameter of the pipe was 12.7 mm, and the length was sufficiently long prior to entering the FOV such that the velocity profile was fully developed. Three dual-venc (DV) acquisitions [14] (denoted as A, B, and C) were performed on a Siemens 3T PRISMA scanner with a spatial resolution of 0.85 × 0.85 × 0.8mm³. The dual-venc acquisitions were split up, and the low and high venc acquisitions were analyzed separately, thus yielding 6 datasets with vencs ranging from 4 to 16 cm/s as presented in Table I. The expected maximum velocity in the field was 12 cm/s. Each dataset contained 12 time frames with a temporal resolution of 120.4 ms. The echo time (TE) and repetition time (TR) are presented in Table I. The bandwidth was 455 kHz and flip angle was 15°. The mask of ${\mathcal{D}}_{ROI}$ was generated based on the position and radius of the pipe. A voxel was considered to be within the flow if the distance from its center to the centerline of the pipe was less than the pipe radius. The SNR_I values were calculated for each acquisition as $SN{R}_I=\overline{I}/{\sigma }_I$, where σ_I is the standard deviation of I across the 12 frames, and $\overline{I}$ is the average of I within ${\mathcal{D}}_{ROI}$. The SNR_I values are given in Table I.

TABLE I.

The Venc, Intensity Based Signal-to-Noise Ratio (SNR_I), Number of Wrapped Voxels (N_W), Velocity-to-Noise Ratio (VNR), Mean WSS Magnitude, and Relative WSS Magnitude Error (ϵ_WSS) for the Each in vitro Poiseuille Flow Dataset With CWLS and 4D Lap Unwrapping

DV acquisitions		A	B	C	A	B	C
venc (cm/s)		4	6	8	8	12	16
TE (ms)		7.47	6.47	5.87	7.47	6.47	5.87
TR (ms)		10.2	9.2	8.6	10.2	9.2	8.6
SNRI		60.9	54.1	47.9	60.9	54.1	47.9
Nw		41919	32819	24128	23434	3925	1
Nw	CWLS	1	0	0	0	0	0
	4D Lap	104	2	20	38	4	10
VNR	CWLS	33.2	38.4	28.1	16.0	18.5	14.4
	4D Lap	23.7	26.4	17.5	10.7	13.3	9.4
VNR improve (%)		40	46	61	50	39	53
mean WSS (Pa)	CWLS	0.17	0.16	0.17	0.20	0.18	0.20
	4D Lap	0.20	0.17	0.19	0.23	0.20	0.22
relative ϵWSS	CWLS	0.45	0.37	0.42	0.68	0.51	0.65
	4D Lap	0.70	0.56	0.78	1.38	1.02	1.50
ϵWSS reduction (%)		56	53	85	105	102	130

G. In Vivo Aortic 4D Flow MRI Measurement

In vivo aortic 4D flow MRI data was used to evaluate the performance of CWLS. Aortic flow was measured from 12 patients with bicuspid aortic valve (BAV), 12 patients with tricuspid aortic valve and aortic aneurysm (TAV-AA), and 6 healthy control subjects with tricuspid aortic valve. The scans were performed in a sagittal oblique volume on a 1.5 T scanner (MAGNETOM Avanto, Aera, Siemens, Erlangen, Germany) with prospective ECG gating and during free-breathing. All patients (BAV and TAV-AA) except the control subjects were imaged with gadolinium-based contrast (Magnevist, Ablavar, or Gadavist). The voxel sizes were 2–2.5 mm isotropic in-plane with a slice thickness of 2.4–3.2 mm. The temporal resolution was 37.6–39.2 ms with 10–25 cardiac time frames. TE/TR were 2.184–2.463 ms/4.6–4.9 ms, flip angle was 7° in controls and 15° in patients, and the bandwidth was 446–460 kHz. A single venc was used for each scan. The venc was 150–350 cm/s for BAV patients, 150–200 cm/s for TAV-AA patients, and 150 cm/s for control subjects. All patient data for this HIPPA compliant and IRB approved study were retrospectively included with waiver of consent. The mask of ${\mathcal{D}}_{ROI}$ for each dataset was approximated by thresholding the time-averaged product of the intensity and the magnitude of the phase components $\left(I\cdot \sqrt{{\psi }_u^2+{\psi }_v^2+{\psi }_w^2}\right)$ [49] and manually corrected by an expert observer using Mimics (Materialise NV, Belgium).

In vivo datasets were assessed for aliasing, with four TAV-AA and four BAV datasets containing velocity aliasing, while no velocity aliasing was observed in the remaining 22 datasets. Phase unwrapping was applied to the datasets with velocity aliasing, and the resulting velocity fields were analyzed to assess the performance. For datasets without aliasing, the phase data were artificially wrapped based on virtual vencs that were lower than the vencs from original scans as $\mathcal{W}\left(\frac{\pi V}{venc}\right)$, where V is the original velocity data and venc is the virtual venc. This wrapping operation maintains the mathematical relationship between wrapped and unwrapped phase data without bringing additional noise or error to the phase field. Five VRs ranging from 0.1 to 0.5 were employed to set the virtual vencs based on the maximum velocity value within the blood flow. Outliers were excluded from the maximum velocity calculation using universal outlier detection (UOD) [50] followed by median filtering on the unaliased velocity data. The originally unaliased datasets were used as the benchmark to assess unwrapping performance. Since the measurement noise in the benchmark datasets could affect the error analysis on the unwrapped phase fields, UOD was applied to the benchmark phase field to remove outliers.

H. Performance Evaluation

The performance of CWLS on phase unwrapping and denoising was assessed by analyzing the unwrapped phase field as well as the resulting velocity field obtained by multiplying the unwrapped phase by venc/π. The current state-of-the-art 4D single-step Laplacian algorithm [29] (4D Lap) was also employed in this study and compare to CWLS. 4D Lap unwraps time-resolved phase data along temporal dimension and all three spatial dimensions by evaluating the phase Laplacian with Fourier transform. All of the preprocessing was kept constant between CWLS and 4D Lap such that the input phase data were same between the unwrapping techniques.

To assess the overall performance on each test case for the synthetic phase data of LV flow, the unwrapped phase $\widehat{\varphi }$ was compared to the true phase ϕ generated from CFD results voxel by voxel at each cardiac frame. A voxel was considered as wrapped if the deviation $|\widehat{\varphi }-\varphi |$ was greater than π. The success rate (SR) of phase unwrapping was calculated as:

$$SR=1-\frac{N_{\mathcal{W},\widehat{\varphi }}}{N_{\mathcal{W},\psi }},$$ (21)

where $N_{\mathcal{W},\widehat{\varphi }}$ is the total number of wrapped voxels in the unwrapped data, and $N_{\mathcal{W},\psi }$ is the total number of wrapped voxels in the synthetic data. $N_{\mathcal{W},\widehat{\varphi }}$ and $N_{\mathcal{W},\psi }$ were counted within D_ROI for each of the 3 velocity components at each frame, which were then summed together as $N_{\mathcal{W},\widehat{\varphi }}=\sum _{i=1}^N(N_{\mathcal{W},{\widehat{\varphi }}_u}^i+N_{\text{W},{\widehat{\varphi }}_v}^i+N_{\mathcal{W},{\widehat{\varphi }}_w}^i)$, where the superscript i indicates the i^th cardiac frame. SR=1 means that all voxels were correctly unwrapped. The SR can be less than 0 if the unwrapping created more wrapped voxels than the original data. The error in the resulting velocity (ϵ_V) was calculated as the deviation from the CFD results. To evaluate the accuracy of the resulting velocity fields, the velocity error level (V_error) was calculated as:

$$V_{error}=\frac{RMS\left({ϵ}_V\right)}{\left|\overline{V}\right|}\times 100\%,$$ (22)

where $\left|\overline{V}\right|$ is the average velocity magnitude in D_ROI, and RMS (ϵ_V) represents the RMS velocity error in D_ROI.

For the in vitro 4D Poiseuille flow, the unwrapped phase $\widehat{\varphi }$ data was compared with the true phase ϕ generated from the analytical velocity fields described by:

$$u_r=0,u_{\theta }=0,u_z(r)=\frac{2Q}{\pi R^4}\left(R^2-r^2\right),$$ (23)

where u_r is the radial velocity component, u_θ is the circumferential velocity component, u_z is the axial (along z-axis) velocity component (m/s), r is the radial distance from the pipe centerline (m), R is the pipe radius (m), and Q is the volumetric flow rate (m³/s). The number of wrapped voxels N_W,Ψ and $N_{W,\widehat{\varphi }}$ were calculated from the acquired phase fields and the unwrapped phase fields, respectively. To quantify the noise level, the VNRs were determined from the resulting velocity fields as:

$$VNR=\frac{\overline{\left|V\right|}}{RMS\left({\sigma }_V\right)},$$ (24)

where σ_V is the velocity standard deviation across 12 frames, and RMS (σ_V ) is the RMS of all the σ_V within D_ROI. The wrapped voxels were excluded from the VNR calculation such that the VNR only represented the noise level. From the unwrapped velocity fields using CWLS and 4D Lap, the WSS was calculated from the velocity gradients determined using thin-plate spline radial basis function interpolation [10], [51] with the non-slip (zero velocity) boundary condition applied on the wall. The WSS error (ϵ_WSS) was determined by comparing the magnitude of the WSS vector to the analytical value determined as:

$$\left|WSS\right|=\frac{4\mu Q}{\pi R^3},$$ (25)

where μ is the dynamic viscosity of the fluid (Pa·s). For each dataset, the relative ϵ_WSS was calculated as the RMS of ϵ_WSS in D_ROI normalized by the analytical WSS magnitude.

To evaluate the performance with the in vivo aortic 4D flow data, the SRs defined by (21) on the artificially wrapped datasets were determined by comparing the unwrapped phase to the benchmark (the originally unaliased datasets). Because benchmark data is not available for the eight datasets with real aliasing, the error in the resulting velocity fields were estimated based on the velocity divergence using the least-squares algorithm [11], which was then employed to calculate the V_errors using (22). To indicate the level of wrapping in the original phase data, the venc ratio was estimated based on the average of the maximum velocity values from the CWLS and 4D Lap unwrapped fields.

IV. Results

A. Synthetic Phase Data of LV Flow

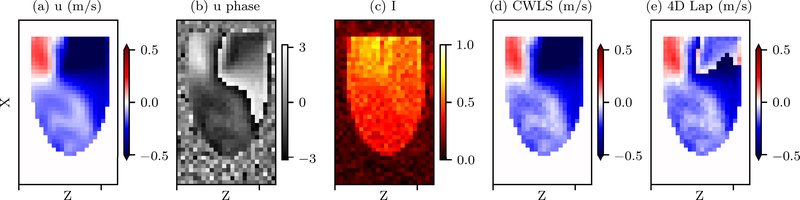
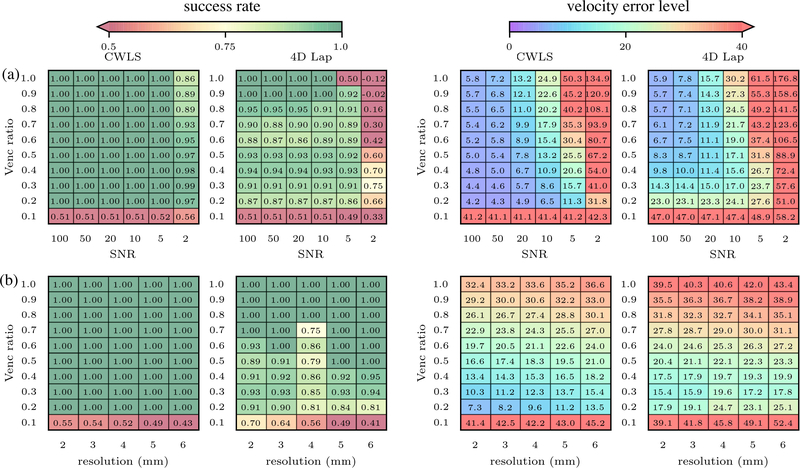
The u velocity field at peak diastole on the MRI grid is shown in Fig. 2(a). The generated phase and magnitude intensity fields for VR=0.2 and SNR_I = 10 are shown in Fig. 2(b–c). The unwrapped u-component velocity fields at peak diastole are compared in Fig. 2(d) and (e) for the case of SNR_I =10 and VR = 0.2. With 4D Lap, the large region of wrapped voxels in inflow jet remained, while all voxels were correctly unwrapped by CWLS. The SRs and V_errors of all the cases are compared in Fig. 3(a) between CWLS and 4D Lap. The CWLS completely unwrapped the phase data for most cases with VR ≥ 0.2 and SNR_I ≥ 5. Even with significant amount of noise (SNR_I = 2), the SRs were consistently greater than 0.8. Compared to 4D Lap, CWLS was more robust to noise and more reliable for low-venc acquisitions. The CWLS method effectively reduced the V_error in most cases compared to 4D Lap. The improvement was significant for the cases where 4D Lap failed to unwrap all the voxels and led to V_error reduction as much as 500%. It is also worth noting that CWLS reduced the V_errors by around 20% compared the 4D Lap results for the low-SNR_I cases where both methods completely unwrapped the phase.

Fig. 2.

(a) The u velocity field at peak diastole on the center x-z plane. (b-c) The u phase and magnitude intensity fields at peak diastole for the case with VR = 0.2 and SNR_I = 10. (c-d) The resulting u velocity fields on the center x-z plane at peak diastole unwrapped with CWLS and 4D Lap, respectively, for the same case.

Fig. 3.

(a) The unwrapping SRs and V_errors (%) by CWLS and 4D Lap for the synthetic cases with different VRs and SNRs on 2.5 mm resolution grid. (b) The SRs and V_errors (%) on the synthetic datasets of LV flow generated with a SNR of 10, grid resolution from 2 to 6 mm, and VR from 0.1 to 1.0.

The effects of spatial resolution on the performances of CWLS and 4D Lap were presented in Fig. 3(b) in terms of the SRs and V_errors from the datasets with an SNR of 10, VR from 0.1 to 1.0, and grid size from 2 to 6 mm. The SR by CWLS remained around 1.0 for all the cases with VR>0.1, whereas the SR by 4D Lap decreased with the increase of grid size for cases for VR from 0.2 to 0.4. Thus, greater improvement was achieved by CWLS compared to 4D Lap for cases with larger voxel size. The V_errors by CWLS were consistently lower than 4D Lap for all the cases with VR > 0.1. At each VR, the V_error by CWLS slightly increased with the increase of grid size due to the voxel-averaging effect.

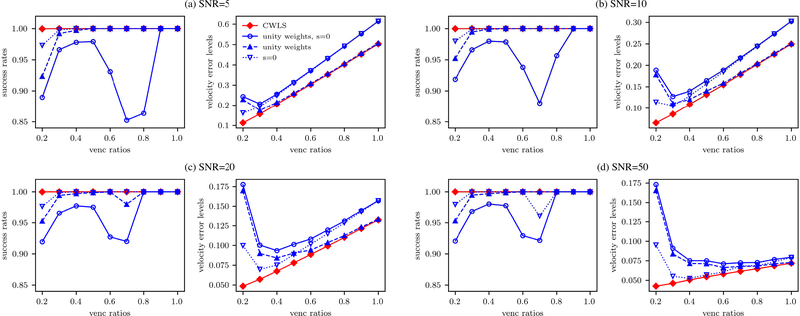
The effect of the uncertainty-based weighting and the divergence-free regularization was demonstrated by comparing CWLS with the unwrapping frameworks with unity weights or zero regularization constant s. With a SNR of 10 and VR from 0.2 to 1.0, the SRs and V_errors of the different unwrapping frameworks are presented in Fig. 4 as functions of VR. The method of “unity weights” means applying unity weights while “s = 0” means setting s to zero, and “unity weights, s = 0” employed both unity weights and zero regularization constant. As shown in Fig. 4, CWLS yielded a SR around 1.0 for all the cases. Without either the uncertainty-based weighting or the divergence-free regularization, the SRs were affected for cases with VR<0.4, indicating that both operations improved the unwrapping results at low VR. The “unity weights, s = 0” yielded the lowest SRs for all cases with VR < 0.8. For the cases with VR ≥ 0.8, the phase data were unwrapped completely by all the methods as SR = 1.0, and the V_errors of the two methods with divergence-free regularization were lower than the other two, indicating the denoising effect of the divergence-free regularization.

Fig. 4.

The SRs and Verrors (%) by the four different unwrapping methods with or without the uncertainty-based weighting and the divergence-free regularization for the synthetic cases with VRs from 0.2 to 1.0 and SNRs of 5, 10, 20, and 50.

B. In Vitro 4D Poiseuille Flow

For the Poiseuille flow, the analytical solution had a maximum axial velocity (w_max) of 12 cm/s at centerline. The VRs of the 6 acquisitions were determined accordingly and given in Table I. The intensity magnitude and phase fields from 3 datasets are presented in Fig. 5. The intensity magnitude was higher near the center of the FOV, while it was lower near the pipe wall (partial volume effect[52]) and on the edges of the FOV. The voxels along the centerline of the phase field were wrapped twice at venc = 4 cm/s and were wrapped once at venc = 8 cm/s.

Fig. 5.

The intensity magnitude fields (a) and the streamwise velocity phase fields (b) from 3 acquisitions with vencs of 4, 8, and 16 cm/s. The fields are shown on the x-z plane along the centerline of the pipe.

The unwrapped phase $\widehat{\varphi }$ data was compared with the true phase ϕ generated from the analytical velocity fields. The number of wrapped voxels $N_{\mathcal{W},\psi }$ and $N_{\mathcal{W},\widehat{\varphi }}$ are presented in Table I. As a reference, the total number of voxels within D_ROI (N_ROI) was 63720. One aliased voxel existed in the dataset with venc = 16 cm/s, which was due to measurement noise. The 4D Lap unwrapped most of the voxels and failed to unwrap 2 to 104 wrapped voxels for each dataset, while CWLS completely unwrapped 5 datasets and failed to unwrap only 1 wrapped voxel for venc = 4 cm/s. With venc = 16 cm/s, the 4D Lap created 9 more wrapped voxels compared to the unprocessed data. The VNRs of the resulting velocity fields are presented in Table I together with the percentage increase of VNR by CWLS compared to 4D Lap. Compared to 4D Lap, the CWLS VNRs were 40–61% higher, demonstrating the denoising effect by CWLS unwrapping on velocity accuracy. With CWLS, the VNR was 131% higher using a venc of 4 cm/s than the VNR at a venc of 16 cm/s.

The mean WSS and relative ϵ_WSS from the velocity fields unwrapped with CWLS and 4D Lap are presented in Table I for the six datasets, together with the error reduction achieved by CWLS compared to 4D Lap. As a reference, the analytical WSS magnitude is 0.141 Pa. The WSS accuracy was consistently higher with CWLS for all datasets, with an error reduction of as much as 130% compared to 4D Lap. The relative ϵ_WSS was lowest for the CWLS-processed velocity fields at venc of 6 cm/s. Using a venc of 4 or 6 cm/s improved the relative ϵ_WSS by 31 and 43%, respectively, compared to using a venc of 16 cm/s.

C. In Vivo Aortic 4D Flow MRI

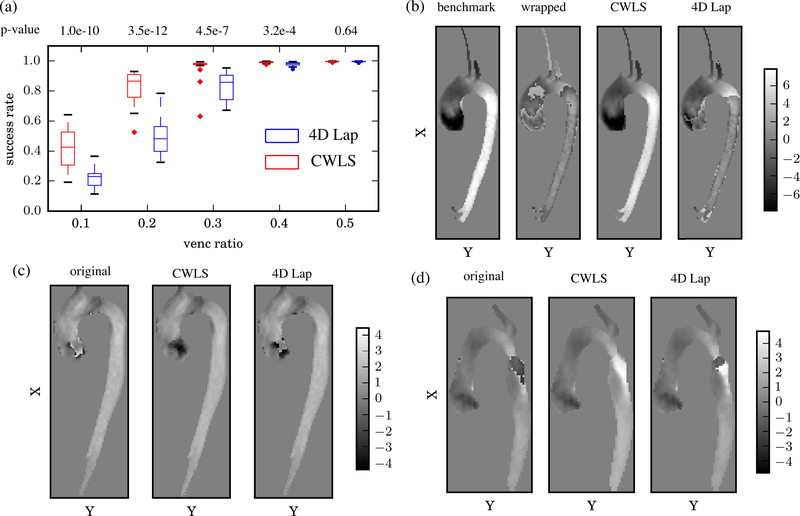
The SRs of 22 datasets for each VR are presented in Fig. 6(a) using boxplot [53]. The p-values from paired sample t-test between the SRs by CWLS and 4D Lap are also reported in Fig. 6(a), which indicated statistically significant difference (p-value < 0.05) between the performances of the two methods at VRs of 0.1 to 0.4. The median SR is given in Table II. Compared to 4D Lap, the improvement by CWLS was dramatic for VRs at 0.2 and 0.3. At a VR of 0.2, the median SR value was 81% higher by CWLS compared to 4D Lap. Examples of the unwrapped phase fields are given in Fig. 6(b) for a BAV dataset with a VR of 0.3 together with the benchmark ϕ and the wrapped phase ψ. Doubly-wrapped voxels can be observed in ψ near the aortic valve and in the descending aorta. CWLS completely unwrapped these voxels, while a large portion of wrapped voxels still remained from 4D Lap.

Fig. 6.

(a) Boxplots of the statistical distributions of SRs from the 22 artificially wrapped datasets for each VR. The centerline of each box indicates the median, while the edges are the 25^th and 75^th percentiles. (b) The u phase fields on the center x-y plane at peak systole of an artificially wrapped BAV dataset with VR = 0.3. (c-d) With real-aliasing, the u phase fields at peak systole on the center x-y plane at peak systole for one BAV dataset (c) and one TAV-AA dataset (d) where the patient additionally had a repaired coarctation causing a high speed jet in the proximal descending aorta.

TABLE II.

The Median Success Rates (SR) for Each venc Ratio (VR) of the Artificially Wrapped in vivo Aortic Datasets With CWLS and 4D Lap

VR		0.1	0.2	0.3	0.4	0.5
median of SRs	CWLS	0.43	0.87	0.98	0.99	1.0
	4D Lap	0.23	0.48	0.86	0.98	1.0

The VRs and V_errors for the in vivo datasets with real velocity aliasing are given in Table III. The V_errors of the 4D Lap processed fields were minimally 10 times higher than the V_errors of the CWLS results. The unwrapped phase fields from one BAV case and one TAV-AA case with real aliasing are presented in Fig. 6(c) and (d). With 4D Lap unwrapping, phase jumps were observed near the aortic valve for the BAV case, as well as wrapped voxels in the descending aorta for the TAV-AA case. The CWLS completely unwrapped the voxels in the displayed field. The computational costs by CWLS on the aliased in vivo datasets were quantified with respect to the number of voxels (N_voxels) within D_ROI ∪ D_ref. As N_voxels increased from 17640 to 35574, both the number of LSQR iterations and time-cost per iteration increased, resulting in a linear increase of the total time-cost per timeframe from 100 to 310 s. It should be noted that the computations were carried using a workstation with 16 cores (Intel Xeon CPU E5–2450 v2), and the time-cost may change with different computational capacity.

TABLE III.

The Venc Ratios (VR) of the Acquisitions and the Velocity Error Levels (V_ERROR) of the Resulting Velocity Fields for the 8 in vivo Aortic Datasets With Real Aliasing by CWLS and 4D Lap Unwrapping

BAV	VR		0.51	0.70	0.63	0.72
	Verror (%)	CWLS	2.9	2.6	2.3	1.9
		4D Lap	55.9	34.0	41.9	30.8
TAV-AA	VR		0.54	0.64	0.95	0.71
	Verror (%)	CWLS	1.7	2.1	1.7	2.8
		4D Lap	36.7	30.1	30.5	35.3

V. Discussion and Conclusions

The proposed CWLS method algorithmically unwraps the phase data without the need of additional high-venc acquisition. The performance of CWLS was evaluated and demonstrated with synthetic phase data, in vitro measurement of Poiseuille flow, and in vivo aortic 4D flow data. By incorporating the divergence-free constraint and using the robust WLS integration algorithm, CWLS reliably and robustly unwrapped the phase data with a venc as low as 20% of the maximum velocity and a SNR as low as 5, and also reduces the phase noise. As a consequence, CWLS improved the accuracy of the obtained velocity and hemodynamic quantities.

The CWLS method allows for the use of lower venc to obtain more accurate velocity and subsequent hemodynamic quantities in clinical applications of 4D flow MRI. Overall, a VNR increase of more than 100% can be achieved by using lower-venc acquisitions and the CWLS unwrapping according to the analysis on the in vitro Poiseuille flow. In addition, the CWLS method does not require any change in the 4D flow MRI acquisition in comparison with the multi-venc approaches which need additional high-venc acquisition with a 25–75% increase in scan time [14], [17]. In applications where two 4D flow MRI scans are typically required for measuring venous and arterial flow with different vencs such as in the liver or brain, CWLS can reduce the scan time by omitting the high-venc acquisition and unwrapping the low-venc data.

Compared to 4D Lap, CWLS is more reliable for severely wrapped data, and more robust to noise and low spatial resolution. Unlike the 4D Lap method which unwraps along 4 dimensions in a single step [29], CWLS sequentially unwraps each time frame and employs WLS for spatial unwrapping. The time sequence proposed in section III–D prevents the error propagation from more-wrapped frames to less-wrapped frames, and the WLS integration mitigates the error propagation across the field. Moreover, CWLS incorporates the divergence-free constraint to regularize and denoise the phase field. Thus, CWLS better handles phase singularity and reduces noise during unwrapping. The advantage of 4D Lap over CWLS is its ease of use and low computational cost. Neither method needs aliasing-free reference timeframes as required by other temporal unwrapping algorithms [25]. Compared to the unwrapping method which resolves phase singularity with branch cut surfaces [54], the CWLS method does not rely on the estimation of phase singularity loops, making it more scalable for large and complex datasets. The advantage of CWLS over the 4D gradient based phase unwrapping [27] is that CWLS can unwrap voxels wrapped multiple times and large wrapped regions.

There are several limitations of the CWLS method. First, the computational cost of CWLS was expensive compared to 4D Lap. Using a workstation with 16 cores (Intel Xeon CPU E5–2450 v2), the processing of each in vivo dataset took 1–2 hrs, whereas 4D Lap completed the unwrapping within seconds. Another limitation of CWLS was that the FOV needed to be segmented prior to unwrapping, which can be difficult for acquisitions with tissue movement despite the recent development on 3D segmentation algorithms [55]. The segmentation applied to the in vivo aortic data based on the time-averaged quantity did not consider the motion of aorta and might affect the CWLS unwrapping. However, the CWLS still showed superior performance compared to 4D Lap on the in vivo aortic data with this segmentation. It is also worth noting that the CWLS unwrapping depends on the phase variation estimated using (2) with the assumption that the phase variation between neighboring voxels are within (−π, π). Using an extremely low venc can violate the assumption and therefore affect the performance of CWLS as suggested by the low SRs from the cases with VR = 0.1 in Fig. 3.

Furthermore, there are a number of limitations of this study. First, the benchmark phase data for the eight real-aliasing in vivo datasets was unavailable to evaluate the SR of unwrapping. Instead, we estimated the velocity errors from the velocity divergence and compared the V_errors between results from CWLS and 4D Lap. However, it should be noted that this divergence-based error metric could underestimate the error level from CWLS which penalized the velocity divergence during phase unwrapping. In vivo dual-venc datasets can be acquired in future studies and used as benchmark to evaluate the performance of phase unwrapping on low-venc acquisitions. Moreover, further investigation on CWLS unwrapping needs to be performed for severely wrapped in vivo datasets with VRs lower than 0.5. In addition, the intra-voxel phase dispersion due to the aortic valve pathologies was not considered in the synthetic data generation or the in vitro experiment, limiting the performance evaluation of CWLS on data with this artifact.

In conclusion, this study introduces a divergence-free constrained phase unwrapping method for 4D flow MRI and evaluates its performance with synthetic phase data, in vitro measurement of Poiseuille flow, as well as in vivo aortic 4D flow data. The proposed method is reliable with severely wrapped data and robust to noise. The method also denoises the phase field and thus enhances the VNR of the resulting velocity data. The method can benefit clinical applications of 4D flow MRI as it improves the accuracy of acquired velocity and hemodynamic quantities.