Keywords: binary pursuit, cerebellum, multi-contact electrodes, spike sorter, spike sorting
Abstract
We evaluate existing spike sorters and present a new one that resolves many sorting challenges. The new sorter, called “full binary pursuit” or FBP, comprises multiple steps. First, it thresholds and clusters to identify the waveforms of all unique neurons in the recording. Second, it uses greedy binary pursuit to optimally assign all the spike events in the original voltages to separable neurons. Third, it resolves spike events that are described more accurately as the superposition of spikes from two other neurons. Fourth, it resolves situations where the recorded neurons drift in amplitude or across electrode contacts during a long recording session. Comparison with other sorters on ground-truth data sets reveals many of the failure modes of spike sorting. We examine overall spike sorter performance in ground-truth data sets and suggest postsorting analyses that can improve the veracity of neural analyses by minimizing the intrusion of failure modes into analysis and interpretation of neural data. Our analysis reveals the tradeoff between the number of channels a sorter can process, speed of sorting, and some of the failure modes of spike sorting. FBP works best on data from 32 channels or fewer. It trades speed and number of channels for avoidance of specific failure modes that would be challenges for some use cases. We conclude that all spike sorting algorithms studied have advantages and shortcomings, and the appropriate use of a spike sorter requires a detailed assessment of the data being sorted and the experimental goals for analyses.
NEW & NOTEWORTHY Electrophysiological recordings from multiple neurons across multiple channels pose great difficulty for spike sorting of single neurons. We propose methods that improve the ability to determine the number of individual neurons present in a recording and resolve near-simultaneous spike events from single neurons. We use ground-truth data sets to demonstrate the pros and cons of several current sorting algorithms and suggest strategies for determining the accuracy of spike sorting when ground-truth data are not available.
INTRODUCTION
Neuroscientists now routinely apply complex computer algorithms to identify and classify the spikes (“spike sorting”) from multiple neurons in voltage traces recorded by probes that have from one to thousands of electrically sensitive contacts. The goal of spike sorting is to identify all the spikes that come from neurons near the probe and to cluster those spikes according to the neuron they belong to (1, 2). Insofar as the sorting is done correctly, the resulting data allow deep insight into how information is encoded by populations of neurons and also into the connections among the neurons in local microcircuits. The power of successful identification of the action potentials from many individual neurons simultaneously is indisputable.
Spike sorters—the algorithms used to perform spike sorting—face many challenges, and it is difficult to compare or rank them. Different sorters exist at different locations in the space of the competing constraints of spike-sorter challenges. Furthermore, a given research goal will require that resolution of some challenges of spike sorting takes precedence, while other known failure modes are tolerable. For example, a research project that plans to draw conclusions based on spike-timing cross-correlograms (CCGs) between nearby neurons will need to use a spike sorter that resolves all situations where the waveforms produced by spikes from two neurons overlap (3). Overlaps are a general issue when multiple nearby neurons fire simultaneously either because they are responding to a discrete event, or simply by chance because the neurons have high spontaneous firing rates. Because of our interest in the brainstem and cerebellum, we needed a spike sorter that was ideal for resolving spike overlaps with high reliability for multiple neurons that have firing rates close to 100 spikes/s. We present such a sorter here, called “full binary pursuit” or “FBP.”
We designed FBP to have five characteristics that would allow us to reach our scientific goals. 1) When neurons fire at a high rate and spike overlaps occur with a high probability, the sorter should resolve the overlaps and assign the overlapping waveforms to the correct neurons. 2) The sorter should degrade gracefully as signal-to-noise ratio decays to levels too low for reliable sorting. 3) The sorter should be resilient to drift across a long recording session when spike waveforms can change in size or shape and shift gradually from one contact to another. 4) The sorter should avoid creation of false or contaminated output units that are either combinations of real neurons and noise or multiunit activity from more than one neuron. 5) Failures to deliver the spikes from single neurons should be as straightforward as possible to identify and correct during both automated and manual postprocessing steps. FBP incorporates these characteristics by borrowing pieces of existing sorters, modifying and combining them, and adding procedures to generate a spike-sorting pipeline that achieves these objectives. Our approach focuses on the overall quality of sorting output and how to evaluate it, rather than optimizing the implementation of the sorting algorithm itself. As a result, our FBP algorithm is a brute force approach that examines the principles of our methodology but sacrifices computational speed on high channel count data compared with other spike sorting algorithms.
We set out to enable our own scientific goals, but we discovered many cautions about spike sorting as we validated FBP and compared its strengths and weaknesses with those of three other spike sorters in common use: MountainSort4 (4), SpyKING-CIRCUS (5), and KiloSort2 (6). As a result, our goal here is not to demonstrate that FBP is “better” than the other sorters, but rather to develop a framework to consider the failure modes of spike sorting and strategies for avoiding them. We conclude that “caveat emptor” should be the slogan of anyone using a spike sorter. It is critical to understand the failure modes of a sorter, consider how the failures may or may not compromise the specific scientific goals of a project, and deploy postprocessing analyses and criteria that assist in identifying those failures.
MATERIALS AND METHODS
Overview
Our data comprise an nC-channels by nS-samples matrix of the continuously sampled and digitized raw recorded voltage. Our analysis has two phases that operate more or less independently. First, we perform multistep dimension reduction to create an average template that concatenates waveforms across channels to identify uniquely each neuron in the recording. The steps are as follows: 1) filter the voltages and divide a long recording into shorter segments so that the voltages are quite stable in space and time; 2) analyze each channel separately for each segment to identify clips of voltage that cross a threshold and gather the clips into clusters of like waveforms; 3) condense across channels, remove duplicates, and average across clusters of clips to define a set of template waveforms, concatenated across channels, that define all the neurons in the segment. Second, we abandon the clips and work from the concatenated-template waveforms, stepping through the voltage traces across channels to identify waveforms that statistically are assigned to the neuron represented by each concatenated template. The steps are as follows: 1) perform “binary-pursuit” template matching on the segment to identify voltages that belong with each neuron’s concatenated template; 2) disambiguate overlapping waveforms and define the spike times of each waveform; 3) stitch the data back together across all segments to define the total set of recorded neurons.
Data Preprocessing
We apply a zero-phase bandpass digital filter to each channel in the raw voltage matrix. Then, we break the voltage into segments of 5-min duration, with each segment overlapping the previous segment by 2.5 min. Breaking the data into smaller segments speeds the clustering procedure because shorter segments yield fewer clusters with fewer spike clips. The use of reasonable length segments with temporal overlap between adjacent segments also enables strategies to compensate for drift in the waveform shape or amplitude of individual spikes across time and for spatial drift across channels on a multicontact probe. The user can choose segment lengths and amount of overlap between segments based on the particular needs of their data.
Next, we find a threshold (Thc) for event detection on each channel c as follows:
| (1) |
Here, the “median absolute deviation” over time of the time-varying voltage (Vc) on channel c is divided by 0.6745 to provide an estimate of the standard deviation of the voltage that is robust to outliers. The factor α scales the number of standard deviations to use as the threshold. A good choice of α will typically avoid random noise events. Very low values of α will lead to an excessive number of clips being admitted as potential spike waveforms and needlessly slow the algorithm without improving the output. Because the spike times will be determined by binary pursuit in a second and independent run through the data, the exact value selected for α is fairly robust and we default to a value of 4. We define the signal-to-noise ratio (SNR) on a channel as the maximum minus the minimum voltage of the average waveform template on that channel divided by Thc.
We remove the correlations between channels by spatially whitening the data using a “zero-phase component analysis sphering” (ZCA) transform (7). We estimate the covariance matrix for the ZCA transform for each pair of channels by randomly sampling 106 datapoints from the “noise” by choosing voltage points that are within ±αThc on both channels. We compute the inverse correlation matrix and multiply it by the raw voltage matrix to obtain the ZCA-transformed voltage for each segment. The ZCA-transformed voltage is thus whitened and has a channel-wise covariance matrix for subthreshold datapoints that is the identity matrix. All subsequent analyses are performed on the ZCA-transformed voltage, which we will henceforth simply refer to as the voltage.
Event Detection
Our first spike-sorting step breaks the voltage into “spike-event clips” that will define the characteristic shape of the voltage deviation associated with each particular neuron’s firing event. Each clip has a specified duration encompassing a window of time centered on a spike event. The goal of an ideal clip width is to capture the full characteristic deviation of a spike event without being long enough to exceed the unit’s absolute refractory period. To define all clips, we recompute Thc for each channel from the whitened data using Eq. 1. We find all positive or negative deflections of the voltage trace that cross ±αThc, and we identify the local absolute maximum or minimum within one clip width of each threshold crossing (Fig. 1, top left). This local extremum is selected as the tentative spike event time, and we extract clips centered at this time point. We ignore any threshold crossings that follow a spike-event clip by less than a clip width, so that each spike-event clip indicates a local positive-negative (or negative-positive) excursion that is likely to correspond to a single action potential. We assemble the full set of spike-event clips by extracting snippets of the voltage traces from cwpre samples before to cwpost samples after each putative spike event time, where cwpre + cwpost + 1= cwtotal, the total number of time samples comprising each clip.
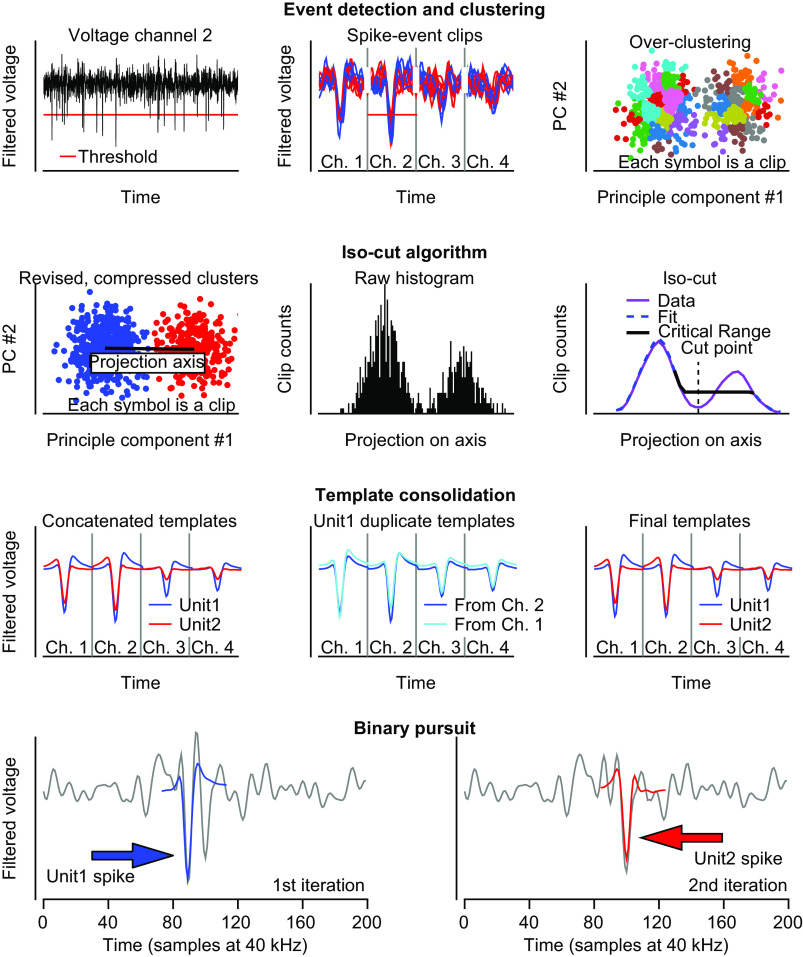
Figure 1.
Details of sorting procedure for each step of spike sorting pipeline. First row: detection of spike events, clips and clustering space. Left: filtered and zero-phase component analysis (ZCA) transformed voltage example for channel 2. Horizontal red line shows the spike event detection threshold. Middle: spike clips for threshold crossing events. Clips are taken separately for each of the 4 channels and concatenated across all channels. Only a subset of clips is shown for clarity. Right: principal component (PC) projection of all spike clips onto the first 2 PCs. The colored clips show the results of intentional overclustering. Second row: isocut algorithm. Left: clusters are compared pairwise with their nearest neighbor (final comparison shown). Data for each cluster are whitened and projected onto the line connecting their average centroids (black line). Middle: the projected PCs for the pair are converted into a one-dimensional histogram. Right: the actual data histogram is smoothed (purple) and a null distribution is formed using unimodal isotonic regression (dashed blue). The data and null distribution histogram bin counts are compared within the critical range (black) using a multinomial goodness of fit test. Third row: template consolidation across channels. Left: ground-truth templates used to create the artificial data set. Different color templates represent the average spike waveform for different units. Middle: due to noise, clips for unit 1 sometimes have maximal deviation on channel 1, and other times on channel 2, causing two different templates to be output, both of which correspond to unit 1. Right: the spike clips corresponding to unit 1 on channel 1 and channel 2 merge and so they are combined to form a single template for unit 1. Fourth row: binary pursuit template matching. Only data for channel 2 are shown for clarity. Left: first iteration of binary pursuit. Voltage trace (gray curve) showing overlapping spikes from unit 1 (blue arrow) and unit 2 (red arrow). Binary pursuit finds a maximal match for unit 1 template (blue curve) and adds a spike event to unit 1. Right: second iteration of binary pursuit. The voltage trace (gray curve) is the residual voltage trace after the template of unit 1 was subtracted during the first iteration. Red arrow indicates the remaining spike waveform of unit 2 that is identified and assigned correctly (red curve).
We refine the temporal alignment for each spike-event clip using a Mexican hat wavelet because our initial, tentative, choice of the time of a spike relies solely on local extrema, which are susceptible to outliers due to noise. Moreover, because of the choice of the absolute extreme voltage as the time of a clip, spikes that are roughly equal in positive and negative going magnitude will be aligned arbitrarily on their peak or trough in different instances due to random fluctuations. To correct this, we compute the cross-correlation between the clips and Mexican hat wavelets of a series of frequencies and find the frequency that gives the maximal absolute (positive or negative) cross-correlation for a given clip. We then adjust the spike-event time for the clip so that it is aligned optimally with the wavelet and resample the spike event clips to be centered on the newly adjusted spike-event times. The cross-correlation gives a better measure of spike timing that takes all datapoints in the voltage clip into account, rather than only the local extrema. Extra care in choice of spike-event time is critical for accurate principal components analysis and clustering in subsequent steps.
Once the clips are optimally aligned on the channel we are sorting, we collect the simultaneous voltage clips from across all nearby channels in the current channel’s neighborhood. The neighborhood is a user-specified set of nearby channels whose data will be used during the clustering procedure to identify single units. The neighborhood must be chosen in a manner that is specific to the brain region of recording and the electrode configuration of the recording probe. We concatenate the clips from all individual neighborhood channels to form a single multichannel clip for each spike event (Fig. 1, top middle). We then remove all clips that have their absolute maximum value on a different channel than the one we currently are sorting. We do so on the assumption that they belong to a different set of neurons and will be sorted when their respective channel is being considered. Later, we address the exception to this assumption, where an individual neuron has a variable spike amplitude that causes it to appear with a maximum that varies across neighboring channels in different clips.
Clustering
We identify the neurons present in a recording and their individual waveform shapes through a multistep procedure. We initially cluster the clips defined only on the channel we are currently sorting. At the end of clustering, we use the concatenated multichannel clips to take advantage of any additional information afforded by the spike waveform shapes across all channels in the neighborhood. To specify the space to be used for clustering, we use principal component analysis (PCA). We select principal components (PCs) based on their reconstruction accuracy, where the goal is to identify the minimal number of PCs that maximizes the average clip reconstruction (8). Briefly, we compute the PCs across our matrix of spike-event clips, X. For each of the identified PCs, we compute the mean squared error between the clips and the linear reconstruction using solely the current PC. The reconstructed spike-event matrix, M, is computed as a linear model of X and the matrix of principle component vectors, Q, as:
| (2) |
where M[n] is the reconstruction derived from the nth PC and qn is the nth PC column vector of Q. The reconstruction error for the nth PC, REn, is computed as the mean sum of squared error between the original spike-event clips and their PC reconstruction:
| (3) |
where nClips is the total number of spike-event clips (rows in X) and nSamples is the total number of samples in each clip (columns of X). We then reorder the PCs from smallest to greatest reconstruction error. Note that this method deviates from the standard method of ordering PCs by the eigenvalue “variance accounted for” (VAF). Ordering the PCs on eigenvalue-based VAF serves to maximize the variance accounted for across clips rather than the variance within clips. In instances where there is substantial noise across clips, eigenvalue-based VAF ordering of the PCs may result in a choice of PCs that overfits the noise. In contrast, ordering the PCs by reconstruction accuracy more strongly weights the within clip variance, which generally corresponds to the waveform characteristics of individual neurons’ spikes.
After ordering the PCs, we determine the optimal number of PCs that should be used to subsequently cluster the spike waveforms. We iteratively add the reordered PCs one at a time to the linear reconstruction model and compute the residual error at each step.
| (4) |
| (5) |
Here M[N] is the reconstruction derived from the first N PCs, and Q[N] represents the first N columns of the matrix Q. This yields the corresponding residual error REN, which is the residual of the reconstruction based on the first N PCs. From REN we define a function quantifying the change in the mean residual error after the addition of each PC, computed from the ratio of the residual error between steps as follows:
| (6) |
ΔRE(N) quantifies the relative improvement in the residual error of the reconstruction by the addition of the Nth PC to the model. We define RE0 by computing the residual error with respect to the mean value over all Xij in X. Local maxima of ΔRE indicate points where addition of a PC to the reconstruction provides no improvement. We choose the basis of our clustering space to be the first k PCs, where ΔRE(k) is the first local maximum of ΔRE.
Next, we project all spike-event clips from the channel being sorted onto the k PCs chosen as the clustering space and begin a clustering procedure similar to that proposed by Chung et al. (4). We begin by over-clustering the data (Fig. 1, top right). We start with the full set of clips in PC space and follow an iterative strategy to select a point as a new cluster center, and then reassign all spike-event clips to their nearest cluster centroid. Our strategy uses the k-means++ algorithm, which randomly selects a point in the data with a probability that is proportional to the distance of each point to its current centroid (9). We complement this approach with a deterministic cluster seeding that always chooses the datapoint at the 95th percentile of distances from its cluster center. We continue the over-clustering process until the median cluster size is the smaller of 100 or the number of clips divided by 1,000. At this point, we have many more clusters than unique waveforms in the original recording.
The next step is to determine how the clusters should be separated and combined on each individual channel (we combine across channels later). We mimic the central concepts of the iso-cut algorithm (4) but with key differences in smoothing and statistical tests. The main idea is to assess the degree of similarity and difference pairwise by considering each pair of clusters that are mutually closest to one another, measured as centroid to centroid distance, and asking whether the two clusters should be merged or split. We first whiten the pair and project their points onto the axis that connects the two centroids to obtain a decorrelated, one-dimensional (1-D) representation of the clusters that allows us to capitalize on low-dimensional statistical analyses (Fig. 1, second row). Given the 1-D distribution of datapoints for each pair of nearest neighboring clusters, we ask whether the distribution is consistent with our null hypothesis of a unimodal distribution, or whether it is multimodal and should be split into separate clusters. We smooth the distribution using a nonparametric kernel density estimator that is robust to multimodal distributions (10) and therefore substantially improve the ensuing fits and statistical tests. We treat the smoothed distribution as our “observed” data (Fig. 1, second row, right, violet curve) and derive all subsequent analyses from it.
To decide whether to separate or combine two distributions, we obtain a null hypothesis for their combined distribution by fitting the observed data with an optimal unimodal distribution via isotonic regression (Fig. 1, second row, right, dashed blue curve). We choose a critical region of comparison between the unimodal and observed distributions as a subset of the two distributions such that 1) the difference between the null and observed distributions is maximized and 2) the first and last points are identical for both distributions, or lie at the peak of the unimodal distribution (Fig. 1, second row, right, black). Intuitively, this means finding a window that lies to the left or right of the unimodal peak where the observed data dips below the unimodal fit maximally for consecutive observations. Such regions are easily discovered, if they exist, due to the monotonicity of the isotonic fit.
We use a multinomial goodness-of-fit test to compare the null and observed distribution bin counts within the critical range, instead of the score suggested by Chung et al. (4), because we found it to be adequately but not overly sensitive. The multinomial goodness-of-fit test can be computed exactly for relatively small sample sizes. For larger samples, we performed a permutation test version. If the statistical test yields a P value greater than a user-defined threshold (e.g., P = 0.05), then we accept the null hypothesis and combine the two clusters. If the P value is less than the criterion, then we separate the two clusters at the maximum difference between the isotonic regression fit and the observed distribution within the critical range (Fig. 1, second row, right, vertical dashed line). Data from the two clusters are reassigned on each side of the cut point and thrown back into the clustering algorithm. We repeat the entire pairwise comparison of mutually closest cluster pairs until no additional merges occur. The remaining clusters form a first hypothesis for the set of individual neurons on the sorted channel.
Next, we refine our clusters further. We compute a template, defined as the average clip waveform for each cluster, align each individual clip in the cluster on the average template by centering the index of their maximal cross-correlation, and recompute all clips by shifting their time to be aligned on their newly aligned event times. Within each cluster, we perform “branch-PCA” (4) by repeating the clustering procedure described earlier. Because the PCs are now calculated within each cluster instead of across all clips, we obtain a different PCA space that may be more sensitive to differences between clips within each cluster: this step can only increase the number of clusters. Finally, we perform the branch-PCA procedure on the multichannel clips created by concatenating the voltage clips across all channels in the current channel’s neighborhood. Differences in waveform voltage traces across channels further separate out individual neurons, resulting in our final set of neurons on the current channel.
Extracting and Consolidating Templates
Next, we consolidate the clusters, which were independently sorted one channel at a time, into a refined set of putative neurons across all channels, still working one 5-min segment of data at a time. Consolidation involves two considerations.
The first consideration is whether a cluster may represent spikes from two separate units that overlap with each other reliably enough to form their own cluster. Assume that clusters A and B each have characteristic waveform shapes, and a third cluster C has a waveform that is a sum of the waveforms A and B. To assess this possibility, we iteratively assign each cluster in the channel to be “C” and compute a “template” defined as the average clip for C across all channels in the recording, regardless of the input neighborhood. We then shift and add combinations of any two other templates, A and B, to find the pair and shift that creates a vector most similar to template C. We then take advantage of our analysis of the noise-induced variance of the likelihood functions to ask the probability that the binary pursuit algorithm will confuse template C with template A + B at an acceptable level (see Noise variance and threshold). If the probability of confusion is too high, template C is removed. We no longer consider cluster C to be a candidate to be a separate neuron because it is either 1) a combination of A and B or 2) so similar to a combination of A and B that our algorithm will not reliably discriminate it. We therefore remove cluster C and associated data from any further consideration. To eliminate C as a separate neuron, we additionally require that:
1) nA > 4 × nC and nB > 4 × nC
2)A ‡ B ‡ C
3)−cwpre ≤ Δt ≤ cwpost,
where nX indicates the number of clips in cluster X, and Δt is the shift between A and B for their sum to be compared with C (derived from the clip width). Note that removing cluster C does not eliminate its clips from consideration as spikes from neurons. They may be assigned to neurons in the later, template matching stage of sorting.
The second consideration is whether a single neuron has given rise to clusters on more than one channel. Due to noise, spike variance, amplitude drift, and other intangible factors, the spikes from a single neuron could sometimes be maximal on channel N, and other times on channel M. Because we sorted N and M independently, we could have two copies of the neuron, one on each channel (Fig. 1, third row). Working with templates that are concatenated across all channels in the recording, we search iteratively through the average templates pairwise for all pairs of clusters from individual channels. For each pair, we find an optimal time-shift (Δt) based on the cross-correlation in the concatenated templates and compute the Euclidean distance, d, between average templates (Ti) at that time shift:
| (7) |
Templates with similar overall shape will have small values of d and suggests that the template pair may have originated from the same neuron’s spikes. Optimal Δt > 0.5 × cwtotal are ignored. For the pair with the smallest d, we then create a more meaningful set of channels to consider based on the signal-to-noise ratio (SNR) in the templates (Tc) for each individual channel. We define SNR for each channel as:
| (8) |
| (9) |
where σc is the estimated standard deviation of the noise and Thc and α are from Eq. 1. We use the optimally aligned clips to create a new set of concatenated clips only for channels where SNRc is greater than 0.5 for at least one of the units. We now have two new clusters, and we test whether the two clusters merge using the clustering algorithm described in the earlier section. Here, we use a two-dimensional space by projecting all clips onto the average templates for the two clusters being compared rather than a PC-based space. If the clusters merge across channels, they are considered to come from the same neuron and their spike-event clusters are combined. If they do not merge, the clusters are considered to be distinct and are not checked further against any other clusters. We repeat the merging procedure iteratively until none of the remaining clusters merge with their nearest template pair. This leaves us with spike-event clips corresponding to single putative units from a set of unique neurons across channels.
Assigning Spike Times and Unit Labels: Modified Binary Pursuit
At this point, clustering has identified a set of clips corresponding to each putative neuron in the recording. To identify the spike event times for each neuron, we compute the average template concatenated across all channels for each neuron and use template matching to assign all spikes in the voltage trace to the appropriate unit. In effect, we now discard all previously found spike event times and clips and start over, but with rich knowledge about the voltage signature across channels of the different neurons in the recording.
We adapted the binary pursuit algorithm of Pillow et al. (3) to perform template matching (Fig. 1, bottom row). Briefly, their procedure models the recorded voltage traces as a linear combination of the spike waveform templates and noise. They use Bayesian inference to compute the posterior likelihood of the distribution of spikes across space and time, given the recorded voltage and a prior estimate of the probability of detecting a spike from a given neuron (i.e., the firing rate of each identified unit). After some derivation, this means maximizing the change in the log-likelihood objective function across all channels in the recording, L(t, T):
| (10) |
| (11) |
Here V(s)2 is the squared deviation of the recorded voltage at time s, t is time with respect to the start of the segment being sorted, and s spans the clip width centered on t. The template, Tc(s) is the template of a given neuron on channel c, and p(T) is the Bernoulli probability of observing a spike from the neuron with template T at a given time point. Intuitively, the first term of the equation indicates the current sum of squares residual voltage in the window centered at time t, and the second term indicates what the sum of squares residual voltage would become if we were to subtract the template from the voltage. Thus, values of L(t, T) > 0 imply that the residual sum of squares will be decreased (the likelihood is increased) via subtraction of template T at time t.
We do not have an accurate estimate of the prior probability of observing a spike. We therefore chose to drop the prior probability term and instead adopt a threshold for each template (N(T)) that is proportional to the variance of each template’s objective function due to noise (explained in further detail in Noise variance and threshold). This yields our objective function
| (12) |
Expanding the (Vc(s)–Tc(s))2 term and simplifying yields
| (13) |
And finally summing across all channels
| (14) |
We optimize this function in three iterative steps using the greedy binary-pursuit algorithm (3) as follows:
Compute L(t, T) for all t in V and all templates/neurons T.
If all values L(t, T) ≤ N(T), then the algorithm has converged, all spikes are assigned to neurons, and we are done.
-
For the values of t and T that maximize L(t, T), if L(t, T) > N(T):
Add a spike event at time t to the neuron with template T.
Subtract template T from V in the window centered on t.
Repeat starting from step 1 with the new residual voltage, V.
In words, the binary-pursuit algorithm adds a spike at the time point t for the neuron with template T that maximally increases the posterior likelihood over all t and T. In our formulation of binary-pursuit without a prior probability but with a noise threshold, this strategy optimally reduces the residual voltage by subtraction of templates, given that the change in posterior likelihood due to the subtraction of T exceeds a statistical noise threshold N(T).
Noise variance and threshold.
In its raw form, the binary pursuit equations require only that the voltage at any given time is sufficiently similar to a unit template that subtracting it reduces the residual voltage, i.e., L(t, T) in Eq. 14 is greater than 0. Due to random noise fluctuations in the voltage, L(t, T) is a random variable. The variance of L(t, T) is determined by the covariance of the noise within the time window of a clip width. In this section, we provide equations for the noise estimates using templates and voltage on a single channel to simplify the equations. All of the equations generalize linearly to any number of channels. We estimated the noise of the likelihood function separately for each template vector T by computing the covariance of the nclips × cwpre + cwpost + 1 matrix of spike clips. The covariance of this matrix over columns (time points) yields Ncov, the covariance matrix of the noise over the time duration of a clip width. This covariance matrix represents the uncertainty in L(t, T) due to noise fluctuations in the voltage. With this covariance matrix it can be shown that:
| (15) |
We can take advantage of the variance of the likelihood functions to ask how discriminable each template is from noise. The expected value of our zero-centered voltage trace is 0 given that no signal is present. Therefore, the expected value of the first term in Eq. 13, VT, given no signal, is also 0. Substituting this into Eq. 13 we have:
| (16) |
Assuming normally distributed noise, our objective function L(t, T) is normally distributed with mean E[(L(t, T|VT = 0)] (Eq. 16) and variance Var(L(t, T)) (Eq. 15) when the underlying voltage V(s) (Eq. 13) is only noise.
We minimize false positives during binary pursuit by defining a statistical threshold based on the distribution of L(t, T) given that V(s) is noise. We call this the noise threshold, N(T), for each template chosen according to
| (17) |
| (18) |
Here σbpn is a user-defined threshold scaling parameter (default 2.326) indicating the number of standard deviations above E[(L(t, T|VT = 0)] to set the threshold. The value of N(T) is therefore directly related to the probability of observing a value L(t, T) >= N(T) given that there is no signal present, i.e., the probability of assigning a false positive spike due to random noise fluctuations. We require that L(t, T) > N(T) in order for a spike to be added, and impose the optimization requirement that the threshold be nonnegative (Eq. 18) so that each spike added decreases the residual sum of squares of the voltage trace.
We can take further advantage of knowing the variance of the likelihood functions to ask how discriminable each template is from noise. To do so, we estimate the distribution of L(t, T) given that a true spike is present, i.e., that the true underlying voltage is the waveform given by T. Assuming that V = T, from Eq. 13 we see that:
| (19) |
A template whose E[(L(t, T|V = T)] is sufficiently close to the decision boundary, N(T), indicates that true positive spikes will likely be missed due to noise fluctuations. We flag such templates as candidates for deletion if:
| (20) |
We do not delete all templates that lie near the decision boundary because many times the presence of these templates improves the sorting of other well isolated units. Binary pursuit only has the option to assign voltage deflections to the templates that are input. In particular, removing a noisy unit’s template can result in their waveforms (or other noise induced “spikes”) being erroneously added to well-isolated units. However, we can again use our variance estimates of L(t, T) and our binary pursuit noise induced error tolerance to determine whether removal of a given noisy template is likely to affect the sorting of other units. Suppose we have two templates, TN and T, where TN is near the decision boundary. We can analyze the distribution of L(t, T) given that an event from TN is present by plugging these values into Eq. 13.
| (21) |
This yields a normal distribution with mean E[L(t, T|V = TN)] and variance Var(L(t, T)). The probability of misclassifying a spike from unit TN to unit T when only the template T is available (i.e., if we were to remove TN) is therefore given by:
| (22) |
where Pmis(TN to T) is the probability of assigning a true spike from TN to unit T and CDF(x, µ, Var) is the normal cumulative distribution function evaluated at x for a normal distribution with mean and variance µ and Var. We derive our acceptable approximate error tolerance as:
| (23) |
We can now see that if
| (24) |
holds, keeping the unit with template TN might improve the sorting of unit T, and we therefore choose to keep template TN. If Eq. 24 does not hold for any of the templates T that were not flagged as noisy, then we can safely remove TN from further consideration without degrading the sorting accuracy of other units. Removing templates near the decision boundary not only reduces the number of poor units output from the sorting algorithm but also substantially speeds computation time by preventing overfitting of noisy templates to the voltage trace and reducing the number of templates tested.
Finally, we can leverage our knowledge of the delta likelihood function distributions for each template to estimate the probability of pairwise misclassification errors during binary pursuit. We note that the exact classification errors of the algorithm are more complicated because binary pursuit compares all templates simultaneously, not just pairwise comparisons. However, pairwise comparisons are much more analytically tractable and provide a useful estimate of the discriminability between templates given their shape and the noise characteristics. Suppose that we have two templates TA and TB. Binary pursuit will exhibit a misclassification error by assigning an event V = TB to the unit with template TA if:
| (25) |
| (26) |
where:
| (27) |
| (28) |
Because both likelihood functions are normally distributed, their difference is also a normal distribution with mean and variance:
| (29) |
| (30) |
The probability of observing a misclassification is therefore the probability of observing a value from this distribution that is less than 0:
| (31) |
where P(TB to TA) is the probability of assigning a true voltage of TB to the unit with template TA; CDF(0, µ, Var) is evaluated at x = 0 for the distribution with mean and variance given by Eqs. 29 and 30.
We use Eqs. 25–31 to determine whether a given template, TC might be the result of a sum of two templates TA and TB by substituting template TC and template TA + B. We remove template TC because it is not discriminable from a sum of templates A and B if:
| (32) |
That is, if the probability of misclassification between TC and TA + B exceeds the acceptable error rate indicated by the tolerance derived from σbpn, we remove TC because binary pursuit cannot reliably discriminate spike matches to TC versus TA + B.
Overlap detection and correction.
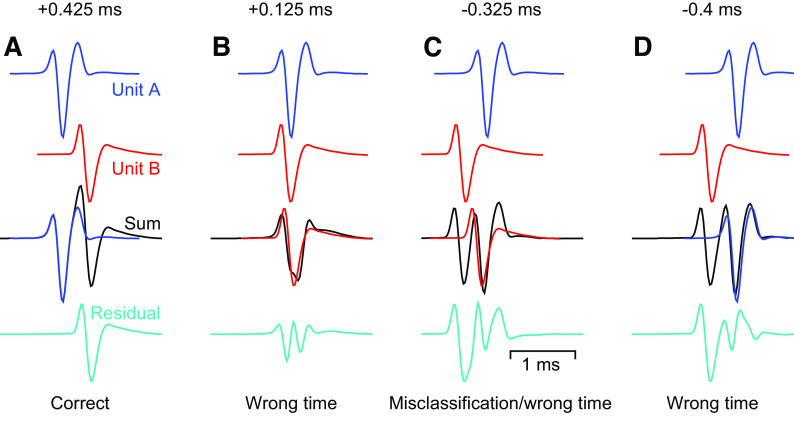
Optimization algorithms for template fitting, such as binary pursuit, tend to be greedy (3). Greed can guarantee algorithm convergence, but in the presence of spike overlaps it can lead to deterministic failures. These failures are generally the result of the algorithm’s attempt to reduce the residual voltage trace as much as possible using only a single spike template when the actual voltage deflection was caused by more than one spike. To demonstrate, we created two single channel voltage templates without any noise (Fig. 2). We added the unit A template (blue) and the unit B template (red) at different time shifts relative to unit A to obtain a pseudo spike voltage trace containing overlapping spikes (black).
Figure 2.
Greedy template matching systematically fails at certain temporal offsets when spikes from two neurons overlap. Top two rows: average spike waveform templates for two units, unit A (blue) and unit B (red) at slightly different time lags. Third row: a noiseless pseudo voltage trace (black) created by adding the two templates at the temporal offset shown. The binary pursuit algorithm chooses to assign a spike according to the overlaid template. Bottom row: the residual voltage after subtraction of the selected template from the original pseudo-voltage. This is the voltage available to the subsequent iteration of binary pursuit. A–D: examples for 4 separate time lags of a spike from unit B relative to a spike from unit A.
When the two spikes are sufficiently separated in time, binary pursuit is able to accurately identify the two spikes (Fig. 2A). The first iteration of binary pursuit correctly identifies the unit A spike at exactly the correct time (third row) and subtraction of the template from the net voltage yields a residual voltage trace that looks almost exactly like the unit B template (Fig. 2A, bottom row, cyan). The subsequent iteration of binary pursuit easily identifies a unit B spike event, resulting in a perfect sort.
When the unit B spike follows unit A by only 0.125 ms (Fig. 2B), the summed voltage contains a single, extra wide waveform (third row, black). The first iteration of binary pursuit now assigns unit B at a time point that is incorrect by only two samples (red trace overlaying black trace) because subtracting the unit B waveform at that time maximizes the decrease in the residual deviation of the voltage trace (it is greedy). The residual voltage (Fig. 2B, bottom) does not resemble a spike from either unit and does not attract the addition of a spike event during the next iteration of binary pursuit. The unit B spike is detected at a time that was off by two samples, but the unit A spike is missed.
When unit B precedes unit A by 0.325 ms (Fig. 2C), the algorithm assigns unit B at nearly the unit A spike time. The end result is a misclassified spike assignment that is not at the correct spike time for either unit. The residual voltage trace is a mess, and binary pursuit assigns the unit A template at the unit B spike time.
A larger negative deviation where unit B spikes 0.4 ms before unit A (Fig. 2D) pushes the unit A optimal template match away from the true unit A spike time. The resulting residual voltage, although inaccurate, still allows the second iteration of binary pursuit to correctly identify the unit B spike in the noiseless example of Fig. 2. However, the waveforms clipped out of the voltage at the times assigned to each unit will be poor representations of the true spikes and a realistic level of noise in the recording will increase the risk of total failure.
We amended the binary pursuit algorithm of Pillow et al. (3) to search specifically for spike waveform overlaps and accommodate these shortcomings of binary pursuit. Our strategy asks whether each spike found in binary pursuit belonging to template T might have a combination of T and another template A, such that:
| (33) |
over a range of values of ΔtT and ΔtA; the maximum shift width is limited to +/− one clip-width minus 1. If Eq. 33 is satisfied, then we remove the spike that had been created at time t, add the previously deleted template back to the residual voltage, and create a new spike event according to:
If L(t + ΔtT, T) >= L(t + ΔtA, A), then create a spike for template T at t + ΔtT.
If L(t + ΔtA, A) > L(t + ΔtT, T), then create a spike for template A at t + ΔtA.
Subtraction of the best matching template of the pair from the residual voltage then leaves binary pursuit to find the second spike in the overlap pair during a subsequent iteration.
The benefit of considering whether each spike event is more likely to have arisen from a sum of two overlapping spikes is a guarantee to resolve detected spike events arising from up to two overlapping spikes, provided SNR is sufficient and templates are accurate. Our approach can still considerably enhance spike detection in instances of three or more overlapping spikes, but performance may still suffer from the types of deterministic errors shown in Fig. 2.
Stitching Segments
The final step in our algorithm is a postsorting processing procedure to clean up the sort for each segment and then stitch together the neurons across segments to obtain a final output that represents each neuron’s spikes for the duration of the recording session. This step takes advantage of the overlap between adjacent segments, where we sorted identical voltages in each channel.
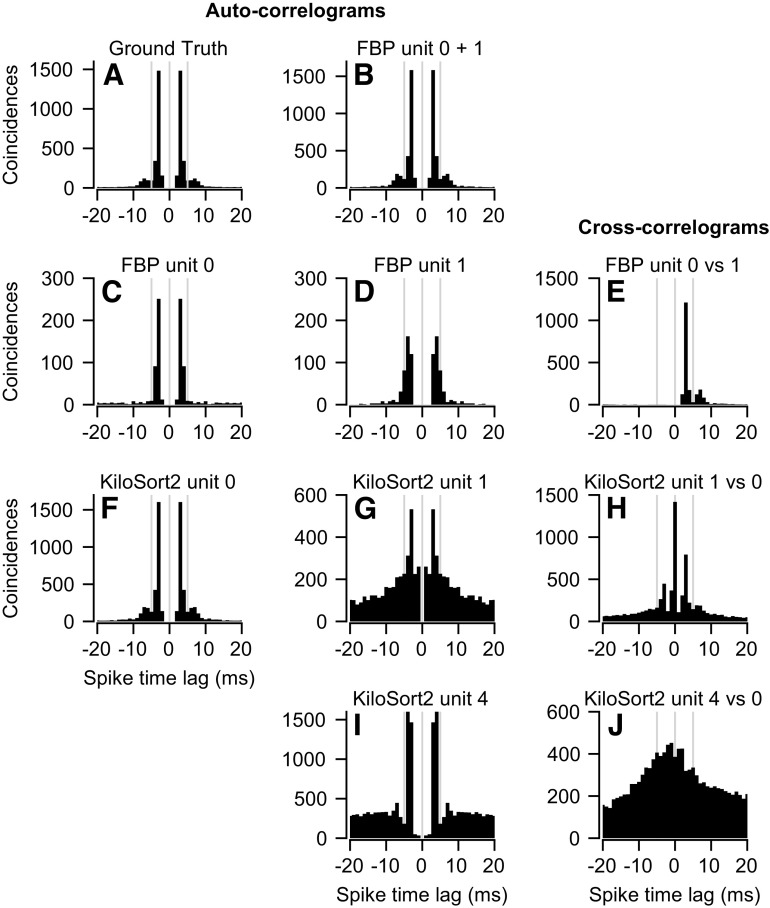
We begin by creating new templates in each segment based on the spike event times assigned by binary-pursuit to the different neurons. We then take three very conservative steps to remove units that are unlikely to represent well-isolated neurons. First, we delete any units whose templates have a SNR less than 1.5. Second, we delete any units with a high degree of multiunit activity, as ascertained by analyzing their interspike interval (ISI) distributions to assess the number of violations of a specified absolute refractory period. We create a histogram of all ISIs less than 500 ms for each unit and compute a “multiunit activity ratio” as the ratio between the number of ISI counts within the absolute refractory period and the maximum ISI count across all bins. Units are deleted if their multiunit activity ratio exceeds 0.2. Third, we remove units that appear redundant with other units based on CCGs computed in 1 ms bins for all pairs of units in the sort for the given segment. Iteratively, we find the pair with the greatest number of identical spike event times (bin count at t = 0 in the CCG) and ask whether there is sufficient evidence of redundancy that one of them should be deleted. If the jump in the spike count between neighboring bins at t = 0 is twice as big as the jump between any other two neighboring bins, then we conclude that the CCG is physiologically implausible and the two units are redundant. We preferentially keep the unit that has the lower multiunit activity ratio and the template with the larger SNR. If neither unit satisfies both criteria, then we delete them both.
Working with the cleaned-up data, we assign each neuron within a segment to a specific channel, chosen as the channel where that neuron’s template has the highest SNR. Using a concatenated-template based on only the channels within the user-defined neighborhood of the assigned channel, we attempt to match each neuron to itself from segment to segment. We do so in two steps.
First, we test and attempt to take advantage of the assumption that each unit is likely to be stationary on its assigned channel across segments, S. We take our complete set of neurons to be the set of neurons present in the first segment. Starting with S = 1, we proceed in temporal order of the segments, from first to last, considering one channel at a time as follows:
- Compare all templates in segment S pairwise with those for the same set of neighboring channels in segment S + 1. Using cross-correlation between the templates, find the optimal shift that minimizes the vector distance between the pair:
Here TSi indicates template i in segment S and T(S + 1)j indicates template j in segment S + 1.(34) For the pair of templates with the smallest distance between them, align the spike clips assigned to those neurons according to the optimal shift, truncating as needed.
Compute the principal components of the two concatenated-templates (not their clips) and choose the best components defined by the reconstruction error approach of Eqs. 3–6.
Project the spike clips from both neurons into this principal component space and define the two neurons as two separate clusters, skipping the initial over-clustering procedure.
Test whether the two clusters merge, using the fitting and statistical approach described earlier.If the two clusters merge statistically, then both are assigned to the neuron in segment S and the template in segment S + 1 is removed from any further comparisons.If the two clusters do not merge, then the template in segment S + 1 is different from the most similar template in segment S. It is assigned tentatively as a novel neuron and added to our full set of neurons; the templates from segments S and S + 1 are removed from any further comparisons.
Return to step 1 and iterate until no more merges occur between any templates in the two segments under consideration.
Any further templates in segment S + 1 that did not find a match from segment S are assigned as novel neurons and added to the full set of neurons.
Increment the segments under consideration and repeat the entire procedure starting from step 1.
Second, we consider whether a unit may have drifted spatially across segments to a new, presumably neighboring, set of channels. We again implement a nearest pair iterative procedure that advances segment by segment as follows:
From the results of the channel stitching aforementioned, we define “orphan” neurons as all neurons in segment S that did not find a match in segment S + 1 plus all neurons in segment S + 1 that did not find a match in segment S. The orphan neurons might have drifted across channels on the recording probe between segment S and S + 1.
Compute the proportion of spike coincidences, within 1 clip width, between each orphan neuron in one segment and all other neurons in the adjacent segment during the segment overlap time period, when the sorting is based on identical voltages placed in different segments.
Find the pair with the maximal proportion of spike coincidences. If this proportion exceeds 75%, then combine the neurons and remove both from further consideration.
Repeat steps 2 and 3 until no pairs remain with proportion of coincidences above 75%.
Proceed to the next adjacent segments and repeat.
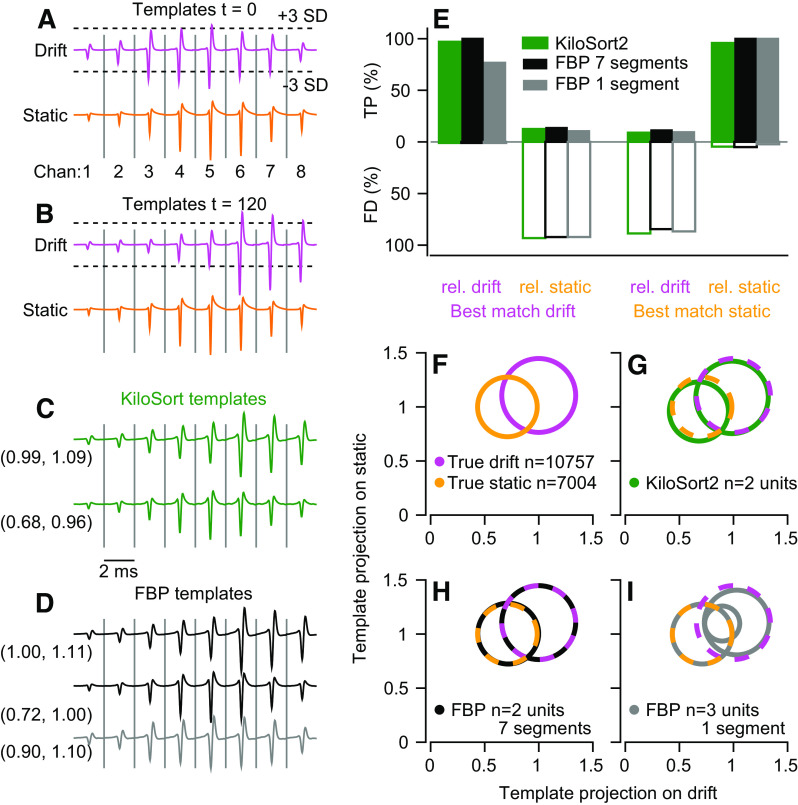
Our drift correction procedure is deliberately strict in that it requires spikes from the same unit to appear across segments and to be detected separately during sorting of the overlapping window in each adjacent segment. It is designed to allow compensation for drift that is relatively slow and purposefully will tend to reject stitching together units that may have abruptly shifted. If an observed unit disappears from any or all channels, and another reappears on some other channel(s), it is difficult to know for sure the circumstances under which we can be certain that it is in fact the same unit. Such a decision is further likely to depend on the exact geometry of the recording array and brain region under investigation. We therefore make no attempt to automatically correct for such abrupt shifts and chose a drift correction procedure that deliberately avoids making such decisions, leaving them instead to the user.
As a final step, we remove the duplicate spikes that necessarily are present due to the overlap time between segments. We do so by removing any spikes within a spike width of each other, preferentially retaining the spike that best matches the template. The spike width is computed as twice the interval between the maximum and minimum values of the neuron’s template. We chose this interval to define overlaps to be small enough so that autocorrelograms remain valid and can be used to identify interspike intervals that violate the neuron’s absolute refractory period, but large enough to account for the fact that waveform shapes and alignments might not be constant across segments and channels.
Data sets
Synthetic data sets.
To create synthetic data, we first generated voltage traces of bandlimited noise from 300 to 8,000 Hz. Noise was Gaussian white noise with random phase and scaled to a standard deviation of 0.33, such that 3 standard deviations of the noise was roughly equal to 1 voltage unit. Noise on each channel (Vc) was 30% correlated by creating a shared voltage across channels and adding it to independent noise on each channel separately:
| (35) |
where ηs represents the shared noise across all channels and ηc the independent noise for channel c. Simulated spiking events were created by adding templates to the noisy voltage traces. The spike templates were taken from actual recordings, and their waveform shape was identical but multiplicatively scaled separately for each channel as shown in the figures. The timing location of the spike events was determined by a random Poisson process with a refractory period of 1.5 ms or by the spike times output by the leaky integrate-and-fire neural network simulation.
Neural network simulation.
Our simulated feedforward leaky integrate-and-fire network was created using the freely available Brian2 software package (11). Our feedforward network consists of two units, where the inhibitory unit provides direct inhibition to the second unit, its target unit. The input drive I, to each unit was a 5 Hz square wave modulation from 60 to 80 mV that provided constant excitation that kept both units firing at high rates. The voltages of the inhibitory unit Vi and its target neuron VT were defined by
| (36) |
| (37) |
| (38) |
Here, e is the equilibrium potential of each unit (ei = −80 mV, eT = −60 mV), τ is the membrane time constant (τi = 7 ms, τT = 8 ms), and η represents Gaussian independent noise added to each unit with standard deviations of 30 mV. The inhibitory current onto the target neuron is defined by gi. The inhibitory postsynaptic potential was set at −10 mV and driven by spikes in the inhibitory unit through their modeled connectivity with a time constant of τgi = 4 ms. Both units fired spikes at a threshold of −30 mV and had refractory periods of 1.5 and 2 ms for the inhibitory and target units, respectively.
Ground-truth data sets.
The ground-truth data sets were taken from the SpikeForest2 (12) website from the Kampff ground-truth data set (13, 14). The sorting results for MountainSort4, SpyKING-CIRCUS, and KiloSort2 were also downloaded and taken as given from the SpikeForest2 website.
Spike Sorter Parameters
The spike sorters evaluated in this paper have many parameters. To simply for our analysis, we used the default parameters of each sorter with the exception of clip width. Clip width is a critical parameter that is highly dependent on the data. KiloSort2 uses a clip width of 2 ms and does not include clip width as a user-modifiable parameter. For MountainSort4 and SpyKING-CIRCUS, we used a clip width of 2 ms for our synthetic and cerebellum data. For the same data sets, we used our default FBP parameters (Table 1), as these are generally tuned to the smaller spike waveform widths we observe in our own cerebellar data and used in our simulated data sets. For the ground-truth SpikeForest2 Kampff data sets, the default settings for KiloSort2, MountainSort4, and SpyKING-CIRCUS were used as reported by SpikeForest2. We found that the ground-truth data sets contained units with much wider spike widths than observed in our cerebellum data and so increased the FBP clip width to [1.0, 2.5] ms for these recordings, but continued to use the remaining default inputs shown in Table 1.
Table 1.
Default parameters of FBP sorter
| Input Variable | Default Value |
|---|---|
| Threshold (α) | 4 |
| Sigma binary pursuit noise | 2.326 |
| Clip width | [0.8, 0.8] ms |
| Filter band | 300–6,000 Hz |
| Check components | 20 |
| Max components | 5 |
| Min firing rate | 0.1 Hz |
| P value cut | 0.01 |
| Segment duration | 300 s |
| Segment overlap | 150 s |
| Overlap spike % | 75% |
| Clip width (Kampff) ground truth | [1.0, 2.5] ms |
FBP, full binary pursuit.
Algorithm Implementation
Two key features of our algorithm implementation involve parallelization and could be expanded upon in the future. The clustering procedure runs in parallel processes using the Python Multiprocessing module. Clustering is performed by initiating multiple “work items,” each of which sorts a single channel’s data for a single segment. The binary pursuit algorithm runs in massively parallelized fashion on a GPU. Each GPU worker computes the objective function L(t, T) within a time window equal to 3 clip widths and stores the results for all windows in GPU memory. In effect, the entire voltage data are chopped up and analyzed in pieces the size of the clip width. Then, a second wave of workers adds a spike in window W if max(L(t, T)) in W is larger than max(L(t, T)) in both adjacent windows W – 1 and W + 1 and L(t, T) ≤ 0 in the next earlier window, W − 2. The logic for this set of requirements is that subtracting the voltage associated with a spike from the residual voltage in W cannot affect any time points beyond its neighboring windows, but the voltage residual in the neighboring window W – 1 is technically not resolved until its neighbor W – 2 is resolved. Thus, we enforce the policy that addition of spikes defers to windows to the left. For the ensuing iteration of binary pursuit, we need to update L(t, T) only in windows where a spike was added and their neighbors. We then recheck whether or not L(t, T) > 0 in windows where L(t, T) either was updated or was greater than zero on the previous iteration. Our strategy tremendously speeds up the binary pursuit algorithm as it reaches convergence, but still is practical only using the massive parallelization afforded by GPU processing. We refer the reader to the source code for any further implementation details.
Hardware
We used a desktop computer running Windows 10 Enterprise N, 64-bit, with two Intel(R) Xeon(R) Gold 5122 processors (3.60 GHz) with 8 cores each and 384 GB RAM. The graphics card used for GPU processing was an NVIDIA GeForce GTX 1660 Ti with 6 GB dedicated memory.
Software
The software was written and distributed in Python code using Python 3 and additional packages from the standard Anaconda distribution 4.8.3. Software is publicly available at https://github.com/njh27/spikesorting_fullpursuit.git. Parallelization was implemented with the Python Multiprocessing module. The GPU code was written with OpenCL and implemented via the PyOpenCL Python wrapper version 2019.1.2. Several algorithms were further optimized with Cython v. 0.29.12.
RESULTS
We start with a broad overview of the sorting algorithm, leaving a detailed treatment to the materials and methods. We then assess the performance of FPB by comparison to three other popular sorters: SpyKING-CIRCUS, MountainSort4, and KiloSort2. Our goal is not to demonstrate that FBP is better than these other sorters (although it is for our needs). Indeed, different sorters make different kinds of tradeoffs and errors. Instead, our goal is to highlight the issues faced when using spike sorters and the possible contaminants those issues can introduce into analyses. We consider the challenges of overlaps between the spikes of different neurons, performance under different conditions of signal-to-noise ratio (SNR) in the recordings, drift in space and time, and the identification of contaminated units. Finally, we examine various combinations of pitfalls revealed by comparing the performance of all four spike sorters on “ground-truth” data, including the difficulty faced when assessing performance itself.
Algorithm Overview
The FBP sorter has two distinct steps. A “clustering” step thresholds the raw data and goes through a series of computations designed to discover templates across recording channels for each of the neurons in the recording. Then, we discard the thresholded clips used to make the templates and start over with a “template matching” step that uses the templates to find the individual spike event times that correspond to each of the neurons discovered by the clustering algorithm. Spikes are assigned to neurons entirely on the basis of the probabilistic agreement of a snip of the recorded voltages and one of the templates. The overall pipeline is outlined schematically in Fig. 3.
Figure 3.
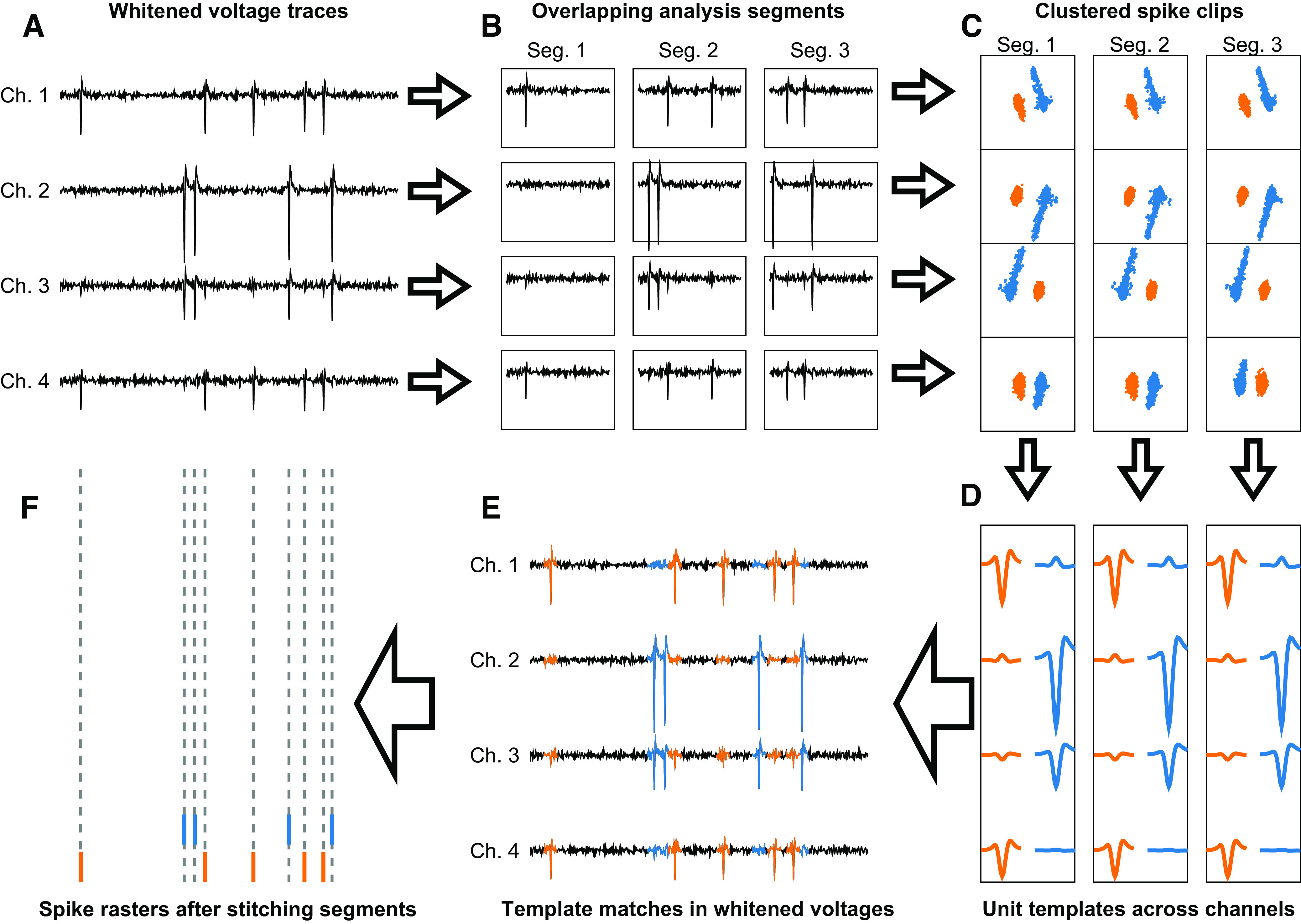
Schematic pipeline of spike sorting procedure. A: synthetic voltage trace for a 4-channel data set with spike signatures from 2 separate units. B: the voltage is broken into 3 serial time segments for each channel, which are thresholded independently to find the spike clips (not shown). C: spike clips projected into principal component analysis (PCA) space for each channel and segment. The projected data are clustered to identify putative single units. D: average spike clip templates from each cluster are concatenated across channels to create a single set of templates representing the voltage waveform of all putative units found in each time segment. E: binary pursuit template matching uses the template set from D to identify the spike events for each unit in each time segment. F: the spike times discovered by binary pursuit are stitched together across segments, yielding a single train of spike event times for each unit output by the sorter. In C–F, different colors show data for different neurons.
Clustering.
Our sorting pipeline begins by whitening the noise across channels via zero-phase component analysis [ZCA; for a review, see Kessy et al. (7)]. This transformation decorrelates any features across channels that are due to noise, making the features due to spiking activity from neurons easier to detect. This yields the transformed voltage trace on which sorting will be performed (Fig. 3A). To avoid the problems of drift across space and time, we next divide the voltage into shorter time segments, and initially analyze each channel and time segment independently (Fig. 3B). We threshold the whitened voltage traces to obtain brief spike event clips that form the basis for clustering. We perform principal component analysis (PCA) on the spike clips for each channel and time segment and use an automated reconstruction accuracy-based procedure (8) to select the optimal principal component features. We cluster these spike clips in PCA space, again separately for each time segment and each channel (Fig. 3C). Clustering is performed following a modified version of the MountainSort “iso-cut” algorithm (4). Briefly, we massively over-cluster the data and compare each cluster with its mutually nearest neighbor, making a binary statistical decision whether or not to merge the two clusters into a single cluster, or optimally split them into two distinct clusters. This iterative process results in a set of clusters, each corresponding to a set of spike events produced from a putative single neuron during a given time segment on a particular channel.
Next, we combine clusters across channels to obtain a single set of neuron waveform templates for each time segment (Fig. 3D). We compute the average across the spike clips for each cluster along with the averages across all other channels for the times of the spike clips. Then, we concatenate the averages across channels to represent each cluster as a single template over all channels. Because we discovered the clusters, and thus the templates, independently on each channel, a single neuron might be represented by more than one cluster. We therefore condense the templates by finding the pairs of templates that are most similar to one another and using the same merge test as in the clustering algorithm to ask whether these two clusters should be combined. We repeat the process pairwise until no clusters combine, leaving templates that correspond to the waveforms across channels of a unique set of neurons irrespective of the channel they were detected on.
Template matching.
The goal of our template-matching algorithm is to find the individual spike event times that correspond to each of the neurons discovered by the clustering algorithm (Fig. 3E). We discard the individual clips used during the clustering step and use the unique templates from the clustering algorithm to perform a slightly modified version of binary pursuit template matching (3). Thus, the spike times output by FBP are determined fully by binary pursuit and not by threshold crossings.
Binary pursuit is a greedy, iterative approach to template matching. Each iteration detects the optimal fit of a template to a site in the voltage, labels that time as a spike, and subtracts the template from the voltage trace to create a residual voltage trace. Template matching has three major benefits over thresholding and clustering. 1) Binary pursuit considers information in the recorded voltage across multiple channels and multiple time points to determine the time of a spike and the identity of the neuron that produced it. 2) Multiple spikes overlapping in time can be assigned to multiple neurons, improving detection of overlapping spike events. 3) We include a noise term that equips the algorithm to reject voltage deviations that are more likely to have been generated by noise or artifacts. FBP also includes an explicit procedure to identify and resolve voltage deflections that result from the temporal overlap of spikes from two neurons. For each spike event detected by binary pursuit, we ask whether the spike event is better explained as a sum of two templates than as a waveform from the originally assigned template alone.
Last, we stitch the sorted neurons back together across the individual time segments on which the data were sorted to yield the spike trains for each putative neuron (Fig. 3F). We again use the merge test from our clustering algorithm in pairwise fashion, taking advantage of abundant overlap between adjacent time segments. We also assess the possibility that what appear to be two neurons are actually a single neuron whose recording has drifted across contacts on a multicontact probe or has changed amplitude across the duration of the recording. Postsort processing removes any units with excessive refractory period violations in their autocorrelograms, assesses combined autocorrelograms of pairs of units to identify single neurons that have been sorted into two units, and asks whether a set of spikes might have been assigned to two neurons by analyzing cross-correlograms (CCGs) between pairs of units. If a pair of units exhibits an excessive peak at time zero in their CCG, the unit with lower quality is removed. This renders a final output that minimizes the number of “neurons” that are actually multiunit activity or mixtures of well-isolated units.
The key parameters in our algorithm are user assignable. We recognize that different recording sites and use cases will be served best by optimizing the sorter through experiments with, and strategic choices about, the exact values of the key parameters. Indeed, our philosophy is that spike sorting should not be strictly automatic. User input and assessment are essential to guarantee the desired confidence about the assignment of spikes to neurons. Maximizing the quality of spike sorting requires that users make choices based on an understanding of their use case and their data.
Resolution of Overlapping Spikes
Overlapping spikes result from the voltage deviation of two distinct neurons, within roughly a spike width of each other and roughly in the same spatial location across electrodes. They present a problem that has a potential impact on neural data quality and interpretation, especially when spike rates are high. Overlaps can cause spikes to be missed, reduce the recorded firing rate, alter measured responses to a given stimulus, and contaminate neural cross-correlograms. Even for experiments that simply investigate stimulus response properties, nearby neurons frequently share tuning properties and will thus disproportionately tend to fire spikes at the same time. Without resolution of overlaps, spike detection during sorting will be worst during the epoch of greatest experimental interest.
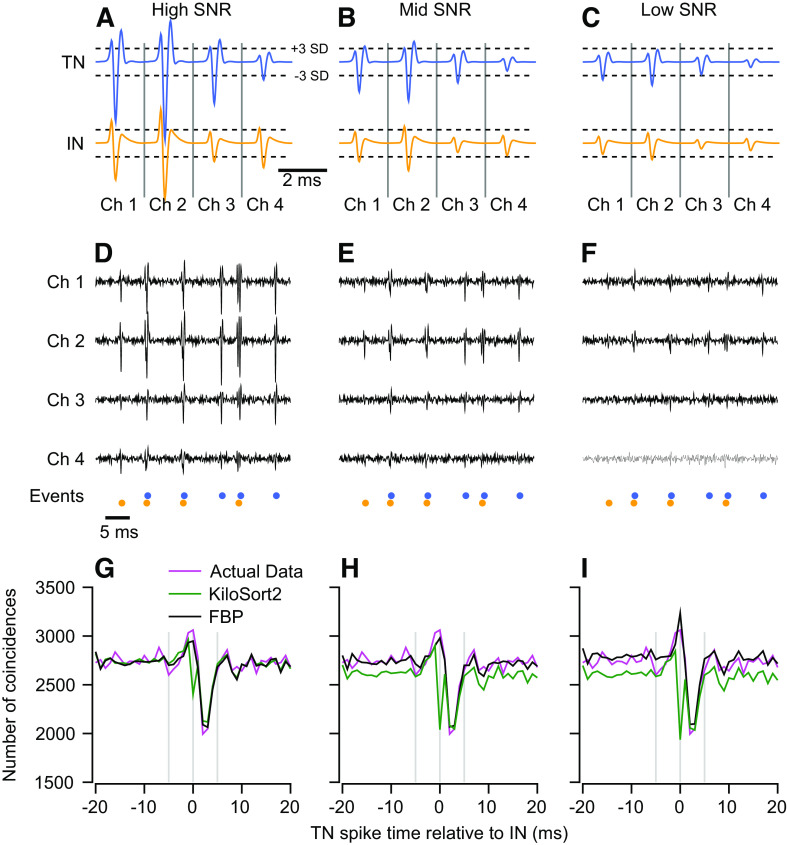
Random overlaps.
We first consider a simulation with two model neurons that fire independently at rates that roughly mimic our own use case in the cerebellum: one at 60 Hz and the other at 90 Hz. We ran the simulation for 200 s, generating 12,095 and 18,055 spikes, respectively (Fig. 4A). Both units have Poisson random firing rates with a 1.5-ms refractory period. The data were generated using two templates with largely nonoverlapping spatial distributions and very high SNR (10.5 and 6.1; Fig. 4C). The two spikes could be sorted perfectly by choosing a threshold beyond the noise envelope and assigning any threshold crossings on channel 1 to unit 2, and any threshold crossings on channel 2 to unit 1 (Fig. 4B).
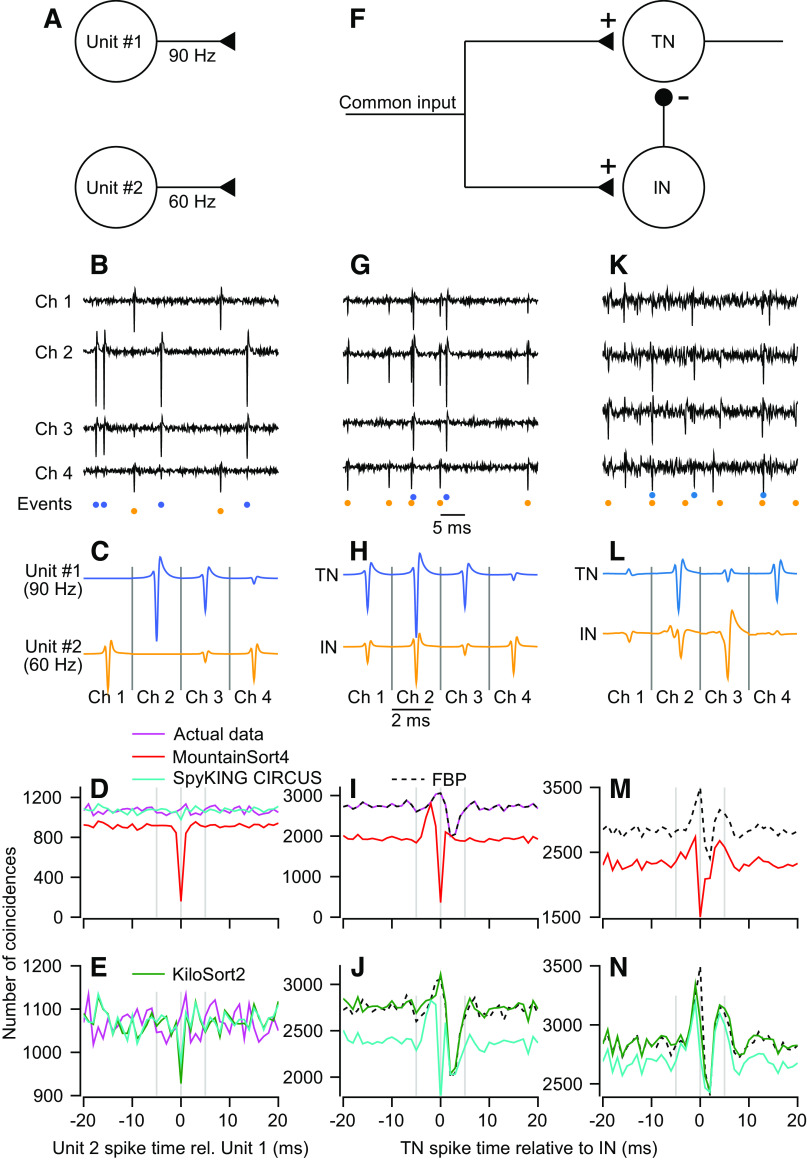
Figure 4.
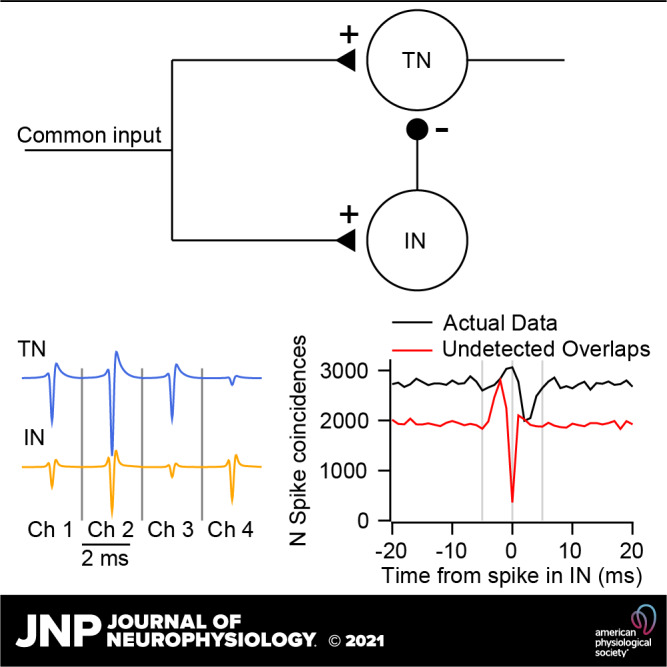
Sorting accuracy for overlapping spikes in synthetic and real data. A: simulated network of two independent units with Poisson firing rates. B: sample voltage trace from synthetic data set generated from the templates in C. Colored symbols below the traces indicate time points where templates in C were added to noise that was partially correlated across channels. D and E: magenta trace shows the cross-correlogram (CCG) for the synthetic data. Other traces show CCGs between the top 2 units for each sorter. Full binary pursuit (FBP) output was identical to the actual data and is not shown for clarity. F: simulated feedforward inhibition circuit. The inhibitory neuron (IN) inhibits the target neuron (TN). G–J: same as B–E with spike times taken from the feedforward inhibition circuit. K: sample voltage traces from four channels of data from the cerebellar cortex. Colored symbols below the traces show the event times discovered by FBP. L: average templates of two units discovered by FBP. M and N: dashed black trace shows the CCG between the two FBP output units. Other traces show the CCG for the two closest matching units from the other sorters.
FBP detected all spikes correctly and produced a CCG that matched the actual dataset exactly (not shown). In contrast, the other three spike sorters missed overlapping spikes to some degree (Fig. 4, D and E). The actual dataset (magenta trace) contained 1,085 overlapping spikes at t = 0, ∼9% and 6% of the spikes of units 1 and 2, respectively. MountainSort4 has a powerful clustering algorithm but does not implement a templated matching procedure and produced a CCG with a dip at time zero (Fig. 4D, red curve), indicating that it had missed or misclassified most overlaps. Both SpyKING-CIRCUS and KiloSort2 take a very similar approach as FBP by performing clustering followed by template matching, and both performed reasonably well. Both detected the majority of overlapping spikes in the simulated dataset (Fig. 4D, cyan curve; Fig. 4E, green curve). However, a higher gain on the y-axis of the CCG (Fig. 4E) reveals that each of these sorters missed in excess of 100 overlapping spikes, nearly 10% of the total overlaps in the dataset (CCGs for the two sorters overlap almost perfectly). These failures did not impact the overall firing rates greatly but could have altered the shape and size of small responses and correlations.
Performance on a modeled feedforward inhibition motif.
We next simulated a feedforward inhibition neural circuit as a common scenario in physiological recordings. Here, the spike times are no longer independent and the neurons’ templates have considerable spatial overlap across channels. The circuit consists of two leaky integrate-and-fire neurons (see materials and methods) that receive a powerful shared input of constant excitation with a square wave modulation (Fig. 4F). The target neuron (TN) is inhibited directly by the inhibitory neuron (IN). We added our selected neuron templates (Fig. 4H) to noise at spike times determined by the model to create the synthetic test dataset (Fig. 4G). We again used high SNR (TN, 10.5 and IN, 6.1) and very high firing rates (TN, 21,622 spikes, ∼108 Hz; IN, 25,155 spikes, ∼128 Hz) to remove signal detection confounds and emulate the firing rates of cerebellar neurons or neurons under stimulus drive.
FBP missed a single spike in this simulated dataset. It revealed a CCG (Fig. 4I, black dashed trace) that matched the actual data (magenta trace) nearly perfectly. The CCG exhibits the hallmark features of feedforward inhibition with an increase in spike synchrony for several ms before the IN fires followed by inhibition of the TN. By contrast, because MountainSort4 does not consider overlapping spikes, its CCG is severely distorted and the effect of inhibition on the TN is not evident (Fig. 4I, red trace). SpyKING-CIRCUS detects many more of the overlapping spikes, yet it produces a CCG that distorts the overall feedforward inhibition motif (Fig. 4J, cyan trace). The CCG suggests a much larger proportion of TN spikes preceding an IN spike and a much lower level of inhibition than exists in the actual data. Finally, KiloSort2 misses some overlapping spikes but largely reproduces the correct CCG (Fig. 4J, green trace). We note that KiloSort2 and FBP use different computational strategies to detect overlaps, so their performance may diverge on more challenging data sets.
Performance on cerebellum recording.
We next compared the four spike sorters on 10 min of actual data recorded from the primate cerebellum using low-density 32 contact linear array electrodes (Fig. 4K). The templates from FBP reveal two units with a moderate degree of spatial overlap and sufficient SNR for an accurate sort (Fig. 4L). The putative TN had a firing rate of 48 Hz and a SNR of 3.5; the putative IN had a firing rate of 94 Hz and a SNR of 4.3. Based on the sort delivered by FBP, the CCGs of these two units exhibit the signature increase, then decrease, of feedforward inhibition circuitry (Fig. 4M, dashed black trace). As before, MountainSort4 largely misses overlapping spikes and has a CCG with a dip at t = 0 (Fig. 4M, red trace). KiloSort2 and SpyKING-CIRCUS (Fig. 1N, green and cyan traces) both provide a CCG that is consistent with the CCG from FBP, but with a lower estimate of the number of overlapping spikes. We do not know ground-truth in the cerebellum dataset, but the consensus among FBP, SpyKING CIRCUS, and KiloSort2 is that the recording contains two units whose firing rates are correlated at fine timescales.
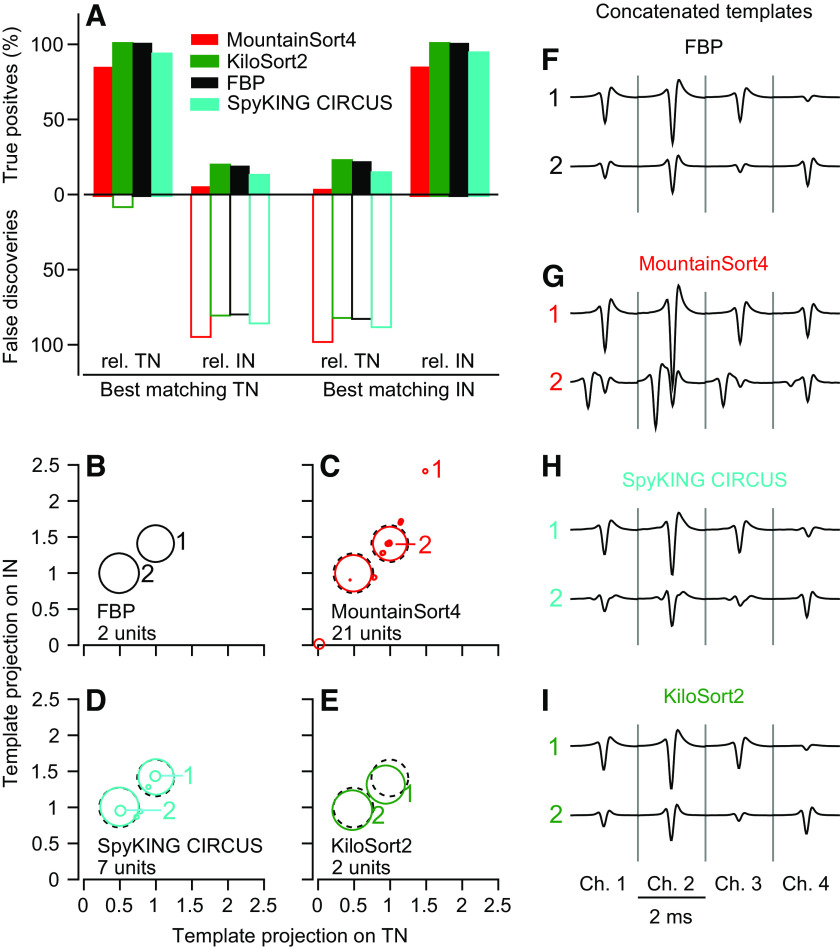
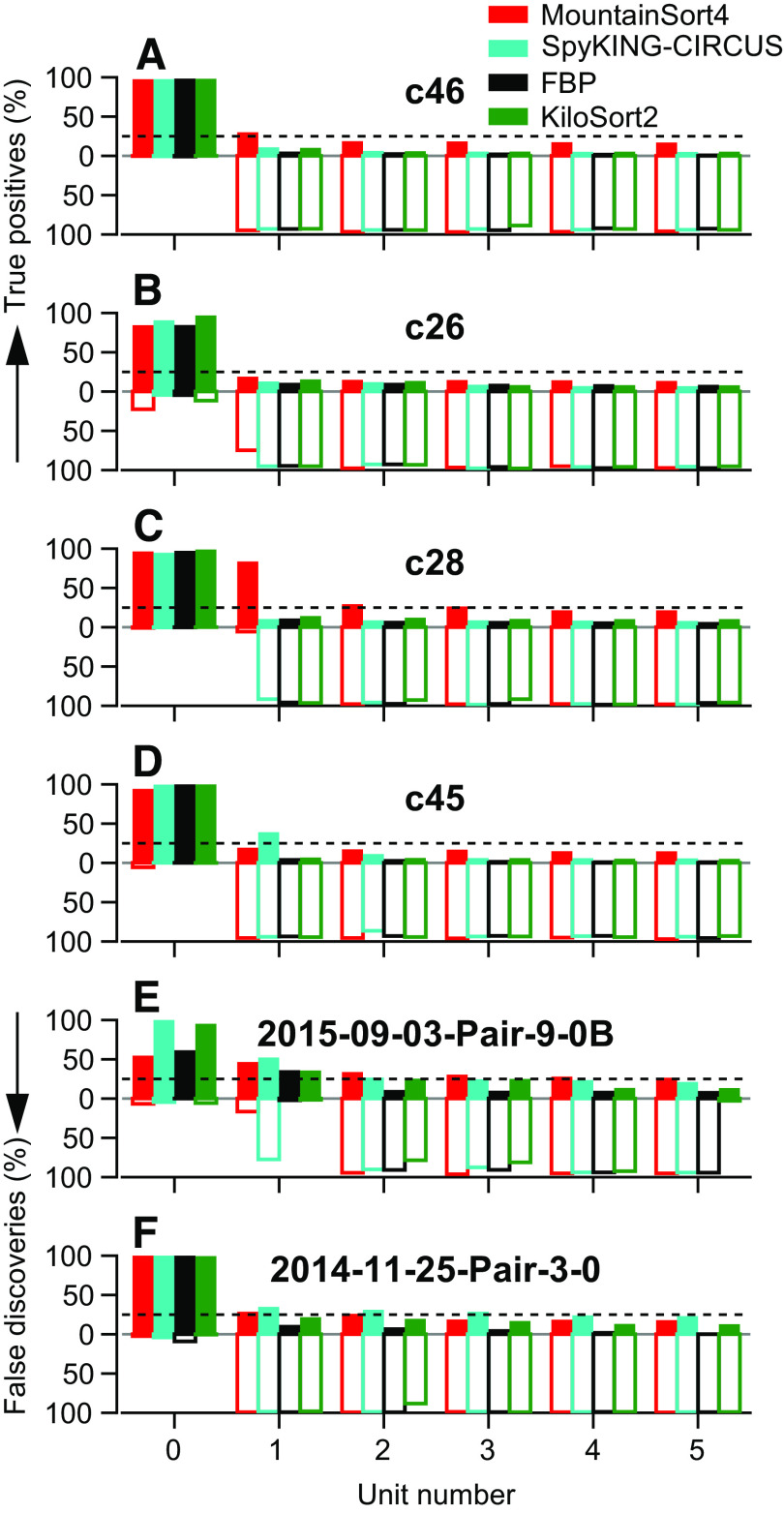
True positives and false discoveries.
We can learn more about the strengths and weaknesses of a spike sorter by assessing performance in synthetic data sets where spike timing and neuron identity are known. For the model TN and IN used in Fig. 4, F–J, we computed true positive (TP) rate for each sorted unit relative to each ground-truth neuron as:
where a sorted unit was credited with a “true detection” if it contained at least one spike event time within ±1 ms of a ground-truth spike time. By this definition, a unit’s TP rate cannot exceed 100%. For example, a unit containing a spike 0.5 ms before and after every ground-truth spike would contain twice the number of ground-truth spikes, but still have a TP rate = 100%. This definition of TP also implies that nonzero TP rates for nonground-truth neurons are not necessarily errors. Accurately sorted spikes from the nonground-truth neuron can occur within ±1 ms of a ground-truth spike and be credited as “true detections.” On the other hand, a TP rate below 100% indicates that ground-truth spikes went undetected. Throughout the paper, we match the sorted unit with the highest TP rate to the ground-truth neuron when assessing sorter accuracy.
We complement the TP rate with the false discovery (FD) rate for each sorted unit. We define the FD rate as:
Intuitively, FD rate indicates the percentage of the spikes assigned to a neuron that are not ground-truth spikes: it is the percentage of a unit’s spikes discovered by the sorter that do not lie within +/−1 ms of a ground-truth spike. The FD rate is necessary because our formula for TPs does not penalize a spike sorter for being overly permissive. In our simplistic example mentioned earlier, the unit containing two spikes for every ground-truth spike will have a FD rate = 50%, in contrast to its TP rate of 100%. Taken together, an ideal sorter would deliver TP = 100% and FD = 0% for its best matching ground-truth unit, and low rates of TPs accompanied by high FD rates for the other units. Again, FD rates under 100% are acceptable because of the way “true detections” are attributed to each unit.
We analyzed the TP and FD rates of the sorters relative to both the IN and TN units that comprise the synthetic feedforward data set of Fig. 4, F–J. We define the best matches as the sorted units with the largest TP rates and we call them the “best matching IN unit” and the “best matching TN unit.” The performance of FBP on this dataset was perfect and can be taken as the ground-truth sorting result (Fig. 5A, black bars). KiloSort2 (Fig. 5A, green bars) has a TP rate of nearly 100% for both its best matching TN and IN units. The TP rates were ∼10%–15% for both FPB and KiloSort2 for the best matching IN unit relative to the true TN and the best matching TN unit relative to the true IN, as expected given the actual number of overlapping spikes. MountainSort4 (Fig. 5A, red bars) and SpyKING CIRCUS (cyan bars) both had TP rates below 100% for the best matching TN unit and the best matching IN unit, confirming their poorer detection of overlapping spikes indicated by the CCG analysis.
Figure 5.
Quantitative analysis of sorting accuracy. A: histograms showing true positive (TP) and false discovery (FD) rates for all 4 sorters for synthetic feedforward-inhibition data set from Fig. 4. Different colors indicate results for different sorters. The left two groups of bars vs. the right two groups of bars show results for the sorted unit best matching the true target neuron (TN) and the true inhibitory neuron (IN), respectively. Within each group, TP and FD rates are computed against the real TN spike times (“rel TN”) and the real IN spike times (“rel IN”). B–E: scatterplots showing the projection of each unit’s template against the true TN and true IN templates for each sorter. The area within each symbol is linearly related to the number of spikes discovered in each unit. Dashed circles indicate the projections of the true TN and IN templates, which overlapped perfectly with the projections for full binary pursuit (FBP) and therefore do not appear in B. F–I: templates for 2 example units discovered by each sorter as labeled with “1” and “2” in B–E.
FD rate is also critical to understanding sorter performance. Only KiloSort2 has a nonzero FD rate (7.3%) for the best matching TN (Fig. 5A, open green bar). Because KiloSort2 had 99.9% TPs for both the TN unit and the IN unit, nearly all ground-truth spikes are accounted for. The presence of FDs therefore indicates an excess of spikes added to the best matching TN unit. For the other sorters, the TN and IN units were generally free of FDs (leftmost and rightmost sets of open bars). Finally, as expected, all sorters have high FD rates for the best matching IN unit relative to the true TN and vice versa.
Sorted templates versus ground truth.
We further quantified how well the sorters classified ground-truth spikes by comparing the average template for each unit identified by each sorter with the ground-truth templates. This step is necessary because the TP rates alone for a sorted unit do not reveal the extent to which TP detections are due to a spike sorter correctly detecting a ground-truth spike as opposed to some other event in close temporal proximity. We reasoned that if a sorted unit’s spike events are the direct result of the detection of ground-truth spikes, then voltage clips centered on each spike time should be consistently aligned with ground-truth spikes. Thus, the average voltage trace centered on each spike time (i.e., the template) should look like the ground-truth template to the extent that a unit’s TP detections directly resulted from ground-truth spikes.
The four scatterplots in Fig. 5, B–E provide a succinct visual summary of how well the templates found by the four spike sorters matched the ground-truth templates. We quantified the similarity between each unit’s template and the ground truth using the scalar projection between templates. The scalar projection was taken as the peak value of the cross-correlation function between the templates to allow for small alignment differences between sorters. The scalar projections were normalized by the magnitude of the ground-truth template so that the true TN and IN templates lie at (1, y) and (x, 1). Each point in the scatterplots shows the template projection onto the TN and IN templates for one unit. The area of each circle is linearly related to the number of spikes placed in each unit. FBP (Fig. 5B), MountainSort4 (Fig. 5C), and SpyKING-CIRCUS (Fig. 5D) all found two units that overlay the ground-truth template projections (black dashed circles) almost perfectly, indicating that these units represent correct classification of ground-truth spikes. The template for the best matching TN unit for KiloSort2 is shifted from the ground-truth TN (Fig. 5E), in a direction that suggests it looks more similar to the IN than expected.
Direct inspection of the templates suggests the types of errors made by the sorters (Fig. 5, F–I). The templates for KiloSort2 (Fig. 5I) are similar to the ground-truth templates (Fig. 5F) except that the TN unit template has a slightly diminished amplitude. Together with the high FD rate for the TN, the shifts in template amplitude and location suggest that KiloSort2 double counted some of the IN spikes and classified them as TN spikes. Both MountainSort4 and SpyKING-CIRCUS output more than two units (21 and 7, respectively), largely because they mishandled overlapping spikes and placed them into separate clusters. For MountainSort4 (Fig. 5G), example template 1 results from nearly direct overlapping of TN and IN spikes whereas example template 2 shows overlapping spikes at a longer time lag. For SpyKING-CIRCUS (Fig. 5H), the two templates shown are close to the correct location in the scatterplot. However, there are extra units with a small number of spikes whose templates lack the smoothness expected from the ground-truth template, probably because of poor spike timing alignments caused by overlapping spike events.
Sorting under Reduced SNR
All spike sorters will eventually fail as SNR decreases toward zero. One goal of FBP is to remain roughly as likely to miss nonoverlapping and overlapping spikes across a range of SNR. Here, we evaluate the performance of FBP and KiloSort2 on three synthetic data sets that vary in SNR but otherwise contain the same spike times from the TN and IN neurons from our feedforward inhibition model. We chose templates that are more difficult to distinguish from one another (Fig. 6, A–C) and varied the SNR of the templates across three levels (SNR = 8.7, 4.4, 2.6 for the TN and 6.6, 3.3, 2.0 for the IN). SNR is taken from the channel with maximal SNR according to Eq. 8. We omit the performance of the other two sorters in this more difficult dataset for clarity, because their performance already was degraded at higher SNR (Fig. 4).
Figure 6.
Sorter performance as signal-to-noise (SNR) ratio degrades. A–C: templates used to generate the synthetic spike trains. Dashed horizontal lines indicate 3 standard deviations of the noise used to create the synthetic data. D–F: example synthetic voltage traces for each value of SNR. Spike event times are the same in each panel and were taken from the synthetic feedforward inhibition data set of Fig. 4, F–J. G–I: magenta, green, and black traces show cross-correlograms (CCGs) constructed by plotting the distribution of the spike times for the best matching target neuron (TN) unit relative to the time of the best matching inhibitory neuron (IN) spike for the synthetic data, KiloSort2, and full binary pursuit (FBP). Values of true positive (TP) and false discovery (FD) in each graph are for the TN and IN, in that order.
FBP performs extremely well under conditions of high SNR (Fig. 6, left column). It detects 100% of IN spikes and 99.3% of TN spikes without any FDs for either unit. The sorted units reproduce the ground-truth CCG well (Fig. 6G, black vs. magenta traces), including the peak at time 0. KiloSort2 misses ∼4% of IN spikes (TP = 96.2%) and detects 99.5% of TN spikes with 17.4% FDs. The CCG shows a large dip at time 0 (Fig. 6G, green curve) suggesting that overlapping spike events are more likely to be missed.
Performance is similar for the middle SNR (Fig. 6, middle column): FBP misses a small percentage of spikes (TP = 99.3 and 99.9% for the TN and IN), has nearly zero FDs, and reproduces the ground-truth CCG fairly accurately (Fig. 6H, black vs. magenta curves). KiloSort2’s TP rates (98.6% and 96.5% for the TN and IN) are very similar to those for the high SNR condition and, interestingly, it no longer has a large number of FDs. KiloSort2’s bias toward missing overlapping spikes has increased further, causing a larger dip in the CCG at time 0 (Fig. 6H, green curve).
The performance of both sorters degrades for low SNR (Fig. 6, right column). TP rates fall and FD rates increase, though the CCGs (Fig. 6I) indicate that FBP’s detection of overlapping spikes is not degraded selectively as there is not a large dip in the CCG at time 0. In contrast, KiloSort2 has become further biased and its dip at time 0 has increased in magnitude. Overall, the performance of FBP in detecting overlapping spikes is comparable with its detection of nonoverlapping spikes as overall accuracy drops. For the low SNR data, FPB had TP rates of 98.8% and 99.2% and FD rates of 1.79% and 1.83% for the TN and IN. Kilosort2 did somewhat worse and had TP rates of 98.0% and 95.1% and FD rates of 1.2% and 0.9% for the TN and IN.
Sorting a Single Channel
FBP was designed to sort accurately based on data from a single channel, whether from a conventional microelectrode or from the individual contacts that are part of an array but are too far apart to allow neurons to register on more than one contact. We tested sorting on a single channel using the synthetic data from channel 2 of Fig. 6 for three different SNRs. FBP performed well on the high SNR and mid SNR data, with true positive rates greater than 98.7% for both the TN and the IN, and false discover rates lower than 1.88%. For the low SNR data, true positive rates fell to 95%–96% and false discoveries were in excess of 10%. Thus, FBP remains accurate on single-channel data when sufficient information is present, but performs better when multiple informative channels are available.
Compensation for Drift in Space and Time
In actual neural recordings, the waveforms of individual neurons may drift in amplitude and/or move to different channels across time. FBP compensates for drift by explicitly dividing the recording into short adjacent segments that overlap in time. Sorted units in one segment are joined with units in an adjacent segment if their spike clips merge together via our clustering algorithm or their spike times are largely identical within the interval of overlap. We chose to perform drift compensation by working in time because it is a directly measured variable during neural recordings and the investigator has a good intuition for adjusting the length of segments and their degree of overlap for their specific experimental setup. For our recordings, we typically choose 5-min segments and an overlap of half the segment duration, 2.5 min. This requires that all data be sorted twice (except the first and last 2.5 min) and is a conservative way to ensure drift is captured at the selected timescale. Our procedure is deliberately conservative in that it will only detect continuous drifts. Any sudden changes in a neuron’s shape or spatial profile are left to the user’s discretion, as there is no way of knowing whether abrupt shifts represent the same or different neurons. Here, we benchmark our drift correction procedure against that of KiloSort2, which is the only other sorter we tested with an explicit drift correction procedure. Unlike FBP’s time-based correction, KiloSort2 conducts drift correction in PCA space.
To evaluate compensation for spatial and temporal drift, we generated a synthetic dataset with two ground-truth units defined on eight voltage channels. A “static” neuron fired spikes at 60 Hz and did not drift (Fig. 7, A and B, orange templates) and a “drift” neuron fired spikes at 90 Hz and had a template whose amplitude across channels drifted rapidly over time (Fig. 7, A and B, magenta templates); the speed and magnitude of the drift exaggerate what happens in real life, but simplify our analysis and allow us to work with only 120 s of data. Both units had independent Poisson random spike times with a 1.5 ms refractory period. The drift neuron’s template started as shown in Fig. 7A at time t = 0, with a peak amplitude on channel 5 and ended at time t = 120 s with a peak amplitude on channel 6.
Figure 7.
Drift correction for a synthetic data set. A: unit templates used to add spikes at the beginning (time = 0 s) of the synthetic data set for the drifting unit and static unit. B: unit templates used to add spikes at the end of the data set (time = 120 s). The drift template moved across channels exponentially throughout the data set whereas the static template remained stable. C and D: templates of the units found by KiloSort2 using PC-based drift correction (green traces) and by full binary pursuit (FBP) using time-based drift correction. For FBP, the 2 black traces show the templates discovered by dividing the data into 7 overlapping segments while the gray trace shows the template found for an extra unit without drift correction. Coordinates to the left of each template indicate their location in scatterplots in F–I. E: true positive (TP) and false discovery (FD) rates for each sorter’s best matching drift and static units. Conventions are the same as Fig. 5A. Black bars show FBP results using 7 time segments for drift correction and gray bars show FBP results for 1 time segment, without drift correction. F–I: scatterplots of the projection of each unit’s template against the true static and drift templates for each sorter. The area within each symbol is linearly related to the number of spikes in its corresponding unit. Dashed circles in G–I indicate the projections of the true static and drift templates for reference.
KiloSort2 performs well even under rapid drift rates and with interference from the static unit (Fig. 7E, green bars; drift unit: 96.0% TP, 0.0% FD; static unit: 94.8% TP, 3.6% FD). FBP performs slightly better with a segment duration of 30 s to account for the rapid time scale of the drift and 15 s overlap between segments (Fig. 7E, black bars). By contrast, FBP performs poorly when sorting the drifting dataset with a single time segment, disabling explicit compensation for drift (Fig. 7E, gray bars).
Analysis of the templates produced by averaging the spikes detected by each sorter tells a similar story (Fig. 7, C and D). The best-matching static and drift templates for both KiloSort2 and FBP are qualitatively very similar to the true templates. The quantitative template projections show that the KiloSort2 drift template is a near perfect match for the ground-truth drift template (Fig. 7G), with some small errors for the static template. The templates for FBP project nearly perfectly onto the ground-truth templates with drift compensation enabled (Fig. 7H) but poorly when data were sorted in a single segment (Fig. 7I). Without drift compensation, FBP splits the drifting and static neurons into multiple units with smaller numbers of spikes in each unit (Fig. 7I, gray circles). Thus, both sorters perform well in the face of severe spatial-temporal drift. Our approach of working in the time domain compares well with KiloSort2’s approach in PC space, with the benefit of being explicit but the cost of being more computationally expensive.
Parsing True versus False Units in Real Neural Recordings with Ground Truth
Typical neural recordings from multicontact electrode arrays yield complex data sets that pose substantial challenges to spike sorting algorithms and the assessment of sorting quality. In real neural recordings, many neurons are present across multiple contacts, and their isolation quality, SNR, and similarity to nearby neurons spans a spectrum of possibilities. Spike sorter confusion between individual neurons and noise is inevitable, leading all sorters (including FBP) to the discovery of “false units,” units output by a sorter that do not accurately represent any neurons actually present in the data. We developed FBP with a bias to output units that are well separated from each other and make fewer errors of confusion, at the expense of being more likely to split true neurons, miss spikes, or delete units. Our assumption was that we could not exclude false units entirely, so we targeted a strategy that would allow us to most easily identify false units due to multiunit activity or contamination by noise in automated and manual postprocessing steps.
Recordings with ground truth provide an objective assessment of spike-sorter performance. The challenge is that the recordings include spikes from the ground-truth neuron plus many other neurons, and the sorters find many units. Even if sorting accuracy is excellent for the ground-truth neuron, there is no way to assess sorting accuracy for the other units found by the sorters. Focusing solely on the accuracy for the ground-truth unit risks severely overestimating overall sorting quality.
We explore the identification of false units created by the four spike sorters on the “ground-truth” “PAIRED_KAMPFF” dataset contributed to SpikeForest2 (12) by the Adam Kampff laboratory (13, 14). This dataset consists of patch clamp recordings from one neuron aligned with simultaneous extracellular recordings using a dense Neuropixels microelectrode array. The extracellular data comprised 32 channels surrounding the channel with the best extracellular isolation of the intracellularly recorded ground-truth unit. This dataset poses both an opportunity and a challenge. The opportunity is to determine how well each sorter can identify the ground-truth neurons and to understand their failings.
We take a more holistic approach and attempt to gain insight into the separation between the ground-truth unit and other sorted units by evaluating sorting accuracy across all units discovered by a sorter. Our evaluation begins by considering six ground-truth data sets and identifying the top six units discovered by the sorters in decreasing order of TP detections of the ground-truth spikes (Fig. 8). If we consider only the unit with the highest TP rate (unit 0), then the output units for all sorters on most of the data sets look good to excellent, with TP rates near 100% and FD rates near 0%. However, inspection of the TP rates across the next five units reveals that in many cases, nonground-truth units have fairly high TP rates. An ideal spike sorter will yield a binary result: output units are either the ground-truth neuron or not. The best matching unit (unit 0) should have 100% TPs and 0% FDs and the remaining units should have low TPs and high FDs. Even in a perfect sort, nonground-truth units will exhibit nonzero TPs due to temporal coincidence of their spikes within +/− 1 ms of ground-truth spikes. However, coincident spikes near a rate of 25% seem physiologically implausible: it implies an extraordinary level of neuron-neuron spike correlation with a very high level of temporal precision. High TP rates and/or low FD rates in units beyond the ground-truth unit 0 suggest the presence of false units.
Figure 8.
Quantitative assessment of spike sorter accuracy for 6 files of the SpikeForest Kampff data set. Each graph presents data for a different recording and plots the true positive (TP) and false discovery (FD) rates for the 6 units with the highest TP detections of the ground-truth unit ordered by TP rate. Bars above the abscissa (filled) show TP rates, those below the abscissa (unfilled) show FD rates. Data are shown for each of the 4 sorters tested. Full binary pursuit (FBP), black; SpyKING-CIRCUS, cyan; MountainSort4, red; KiloSort2, green. Horizontal dashed line indicates 25% true positives as an arbitrary reference point. The signal-to-noise ratio (SNR) and maximum SNR channel (see materials and methods) for each recording are: file c46, 5.25 on channel 17 (A); c26, 3.67 on channel 16 (B); c28, 6.70 on channel 16 (C); c45, 5.65 on channel 16 (D); 2015-09-03-Pair-9-0B, 12.50 on channel 9 (E); 2014-11-25-Pair-3-0, 10.50 on channel 3 (F).
Consider, for example, the performance of MountainSort4 for file c28 (Fig. 8C). Unit 0 is an excellent representation of the ground-truth neuron. But the high TP and low FD rates of unit 1 indicate it is a redundant copy of the ground-truth neuron. Units 2–5 have TP rates larger than those of the units discovered by every other sorter coupled with high FD rates. This pattern suggests that many units discovered by MountainSort4 have an excess of spikes that overlap the ground-truth spikes, suggesting that these units are either MUA and/or other units contaminated by noise spikes that fell within 1 ms of ground-truth spikes. For the data set 2014-11-25-Pair-3-0 (Fig. 8F), SpyKING-CIRCUS has a near perfect sort of the ground-truth neuron but shows a similar pattern of high TPs and FDs for units 1–5. In the same dataset, KiloSort2 unit 2 has over 19% TPs and only 88% FD, suggesting a unit that either is very strongly correlated with the ground-truth unit or is a mixture of ground-truth spikes with other events. FBP, on the other hand, shows little evidence of false units for this dataset but has a greater FD rate for unit 0 than any of the other sorters at ∼9%. Finally, all sorters performed poorly on file 2015-09-03-Pair-9-0B (Fig. 8E). To varying degrees, they appear to have split the ground-truth spikes across at least units 0 and 1, with high TP rates for units 2–5. We consider a similar spike-sorting failure in detail for another ground-truth dataset in Fig. 9.
Figure 9.
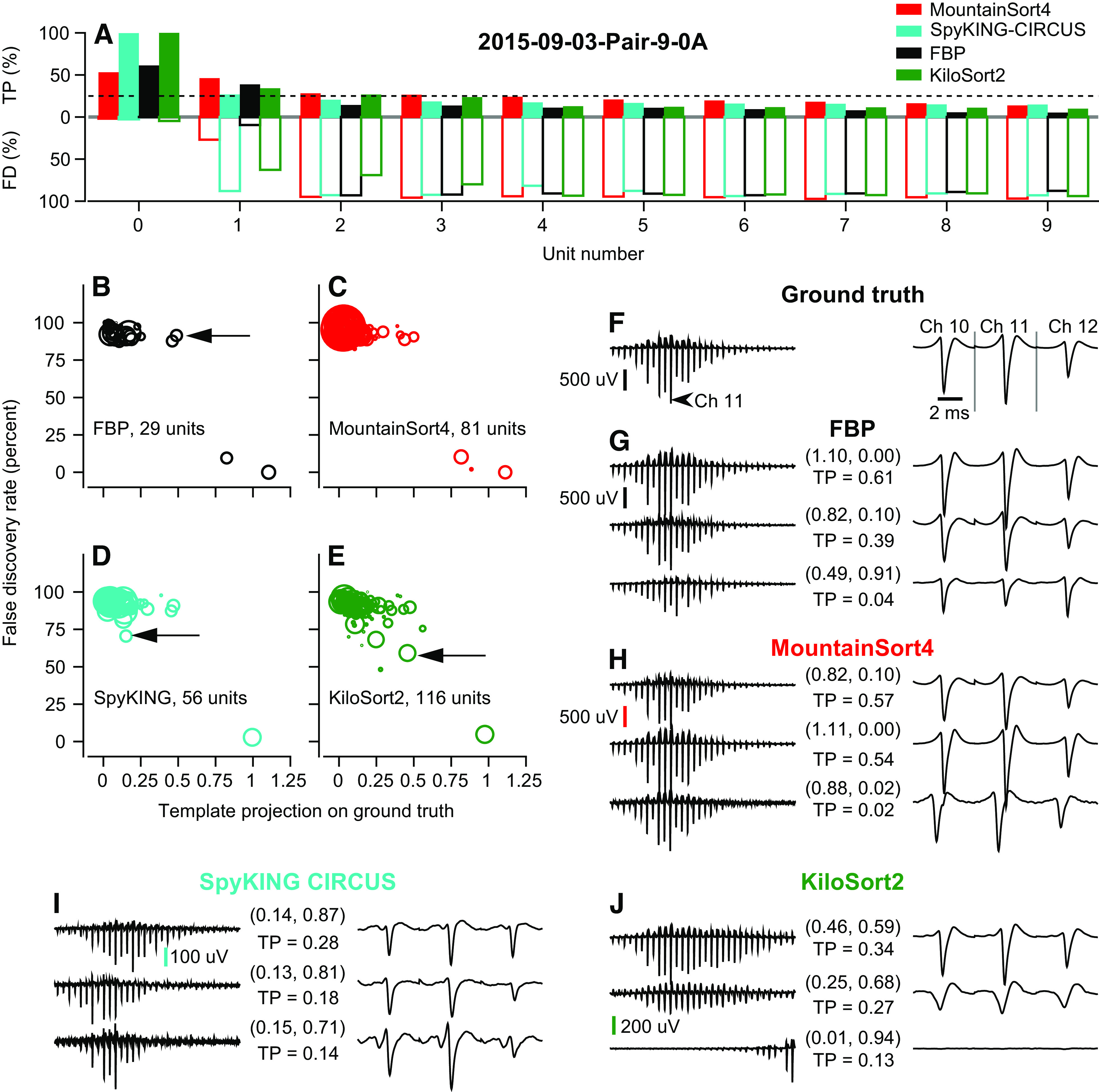
Detailed assessment of spike sorter performance on ground-truth data from the SpikeForest Kampff 2015-09-03-Pair-9-0A data set. A: the true positive (TP) and false discovery (FD) rates for the 4 spike sorters. Conventions are the same as Fig. 8. B–E: scatterplots of FD rate vs. normalized template projection on the ground-truth template for all units found by each sorter. The actual ground-truth unit would plot at (1, 0). Arrows point to symbols for the units that show evidence of greatest spike sorter error. The area within each symbol is linearly related to the number of spikes discovered for its corresponding unit. F–J: three example templates from each sorter. The best matching templates for both SpyKING CIRCUS and KiloSort2 plot at the points (1.0, 0.03) and (0.97, 0.05), respectively. Both templates are nearly identical to the ground-truth template and are not shown for clarity. In the left column, the templates include all 32 channels in the data set. In the right column, the templates show the same data for 3 channels centered on the channel with greatest signal-to-noise ratio (SNR) for the ground-truth unit. In G–J, each pair of traces has numbers in parenthesis above the traces that give that unit’s coordinates in scatterplots in B–E and numbers below the traces that give the TP rate. The ground-truth SNR is 10.00 on channel 11. FBP, full binary pursuit.
The preponderance of high values of TP rate for units 1–5 across the data sets in Fig. 8 suggests the presence of false units for many of the sorters. FBP has the lowest TP rates among the sorters for units 1–5 almost uniformly. We suggest that the lack of TPs in the sorts from FBP reflects fewer false units and good separation between the ground-truth unit and other neurons in the recording, possibly combined with a conservatism that caused FBP to miss a few spikes. It is unlikely to be the result of poor detection of coincident spikes because FBP outperforms the other sorters in resolving overlapping spikes (Fig. 4).
We dig deeper into the issue of false units using another dataset that gave all four sorters difficulty, file 2015-09-03-Pair-9-0A from the Kampff dataset (Fig. 9). FBP appears to sort the ground-truth unit poorly (Fig. 9A, black). Unit 0 has a TP rate of 61% and a FD rate of 0%: it is missing a large number of ground-truth spikes but is not contaminated with other events. Unit 1 has a TP rate of 39% and 9% FDs: 91% of its spikes correspond to the ground-truth neuron but a large number of spikes are missing and other events have been incorrectly added. The remaining FBP units, units 2–9 show much lower TP rates, indeed the lowest of all four sorters and very high FD rates. Together, the TP and FD rates suggest that FBP split the ground-truth unit nearly in half into units 0 and 1, but otherwise isolated the ground-truth unit.
Performance for the other three sorters is varied. For the most part, the TP rates of units 1–3 are higher than we would expect from random overlap with the ground-truth spikes (Fig. 9A). MountainSort4 (red bars) appears to split the ground-truth neuron in a manner similar to FBP. However, its unit 1 has a high 27% FD rate suggesting that the unit is contaminated by nonground-truth spikes. Units 2 and 3 have TP rates in excess of 25% (dashed horizontal line) and very high FD rates, suggesting that they represent activity from a large number of ground-truth spikes plus many other events. SpyKING-CIRCUS’s (Fig. 9A, cyan bars) unit 0 is a near perfect representation of the ground-truth neuron with nearly 100% TPs and 0% FDs. However, units 1 and 2 contain 27% and 21% ground-truth spikes and have high FD rates implying that these two units are likely to be false units. KiloSort2’s (Fig. 9A, green bars) unit 0 is also a near perfect representation of the ground-truth neuron. However, units 1–3 have TP rates of 34%, 27%, and 24% and relatively low FD rates, implying that the ground-truth spikes comprise an unexpectedly large proportion of their spike events.
To understand the situation better, we again computed the ground-truth neuron’s template (Fig. 9F) and the average concatenated templates for all sorted units. We projected the template for each sorted unit onto the template of the ground-truth neuron and made scatterplots that are slightly different from the ones we used in Figs. 5 and 7 (Fig. 9, B–E). Here, we plotted the FD rate versus the template projection on ground truth. In these scatterplots, an ideal sorter would deliver one unit with a FD rate of 0% and a template projection of 1, corresponding exactly with the ground-truth unit and plotting at the point (1, 0). All remaining units would plot along a horizontal line near a FD rate of 100%. They would vary along the vertical axis according to legitimate spike overlaps within 1 ms of spikes in the ground-truth neuron and along the horizontal axis only insofar as their average templates happen to have a shape similar to the ground-truth waveform.
Units near the center of the scatterplots in Fig. 9, B–E indicate spike sorter confusion. A relatively lower FD rate means that a unit has a high proportion of its spike events in close temporal proximity to ground-truth spike events. Relatively higher template projections on the ground-truth template indicate units whose average spike waveform is similar to the ground truth. Although we do not know the ground truth for other neurons in the recording, these two pieces of evidence imply that the sorted unit includes a high proportion of spike events that are consistently temporally aligned with ground-truth spikes: i.e., events that are the direct result of detecting and misclassifying ground-truth spikes. Units near the center of these scatterplots are thus likely to be false units.
Analysis of the templates for the units discovered by FBP supports the impression that it split the ground-truth neuron. The two best matching units have low FD rates and high ground-truth template projections (Fig. 9B, bottom right). The templates for these two units bear a strong resemblance to the ground truth (Fig. 9G, top 2 examples). The middle template has a distinctly smaller amplitude and reduced hyperpolarization phase compared with the top template, causing FBP to split them into two separate units. Of the 22 units discovered by FBP, the worst is indicated by the arrow in Fig. 9B. About 10% of this unit’s spikes corresponded to ground-truth spikes. This unit’s template (Fig. 9G, bottom example) also bears some resemblance to the ground-truth template with a much smaller amplitude: it is possible this unit represents a false unit or unit contaminated with ground-truth spikes.
MountainSort4 appears to split the ground-truth neuron into two units with a relatively large number of spikes and a third unit with a small number of spikes: all three units plot in the lower right of the scatterplot (Fig. 9C). Their templates (Fig. 9H) all resemble the ground-truth template and the bottom one indicates that the unit with a low spike count arose from alignment errors.
SpyKING-CIRCUS (Fig. 9D) does an excellent job of sorting the ground-truth neuron, but finds other units that are contaminated with ground-truth spikes or may include noise. Unit 0 plots in the bottom right corner of the graph at (1.0, 0.03). Its template is a near-perfect match to the ground-truth template and is not shown in Fig. 9I because this information is redundant with the template shown in Fig. 9F. One other unit lies toward the center of the scatterplot (Fig. 9D, arrow) and has a template that bears some resemblance to the ground-truth template (Fig. 9I, top example). However, its template has a rather small amplitude (note the scale bar change in Fig. 9, I and J), suggesting that the unit may be a mixture of noise with occasional ground-truth spikes.
KiloSort2 (Fig. 9E) does an excellent job of sorting the ground-truth neuron but finds several units that appear to be contaminated with ground-truth spikes. Unit 0 plots in the bottom right corner of the graph at (0.97, 0.05). It’s template is a near-perfect match to the ground-truth template and again is not shown in Fig. 9J. Several other units plot near the center of the scatterplot, including one (Fig. 9E, arrow) with nearly the same number of spikes as the ground-truth unit, ∼60% FDs, and a projection that is about a 46% match for the ground-truth template. The other two example templates (Fig. 9J, bottom examples) suggest similar errors, but with much smaller overall amplitudes.
Finally, we note differences in the number of units found by the different sorters: FBP, 29 units; MountainSort4, 81 units; SpyKING-CIRCUS, 56 units; KiloSort2, 116 units. The small number of units found by FBP reflects an intentional philosophy. FBP is conservative about identifying units, avoids placing spikes that actually are noise into units, and has an automated procedure to delete likely false units. The other sorters identify many units; most plot in the top left corner of the scatterplots in Fig. 9, C–E, but a few plot in the middle indicating undesirable overlap with the ground-truth neuron. Many have an extremely large number of spikes (large circles) suggesting that they represent large mixtures of multiunit activity and/or noise. The output of all sorters on this dataset would require further postprocessing to correctly identify well-isolated single neurons and to eliminate units that probably are not single-unit recordings.
Identifying Sorter Errors in Postprocessing
Strategy.
In the absence of ground-truth data, can we assess the quality of a sort, decide whether a neuron was split into pieces, and identify putative units that actually are contaminated by noise or multiunit activity? Attempts to manually repair and improve the individual units output from a spike sorter for multichannel data sets with multiple neurons are futile. The sorting algorithms work in a higher dimensional space and objectively consider far more information for every spike detection and assignment than could any human. Instead, we advocate simple decision-making rules for postprocessing.
After sorting, we eliminate units with 1) values of SNR that are low, 2) too many interspike intervals (ISI) less than an absolute refractory period, or 3) too low a number of spikes. Then, we compare the templates, autocorrelograms (ACGs), and CCGs of all remaining units pairwise with one another and make a simple decision. Either 1) the two units should be combined because they show evidence of being the same unit, 2) one of the two units should be deleted because it shows evidence of being a mixture of spikes from the other unit, or 3) the two units should be tentatively accepted because they are legitimate and different. We show an example of how this could work for the ground-truth recording analyzed above (Fig. 9).
Kampff 2015-09-03-Pair-90A.
The ACGs of FBP units 0 and 1 (Fig. 10, C and D) have zero refractory period violations (empty bins at t = +/− 1 ms) indicating that both are well isolated (Figs. 9 and 10). Combining units 0 and 1 yields an ACG without refractory period violations (Fig. 10B) as would be expected from two pieces of the same neuron. The CCG between units 0 and 1 (Fig. 10E) shows that unit 0 has a large number of spikes at short ISIs of ∼3–4 ms after spikes of unit 1, consistent with unit 0 corresponding largely to the second spike of bursts in the ground-truth neuron. The same CCG does not show a feature we would expect if these were different neurons, namely overlapping spikes in time bins from −2 to 2 ms. It also does not show the sharp peak we would expect at zero if the two units contained identical spikes. Returning to the templates for units 0 and 1 in Fig. 9G shows that they differ subtly, as might be expected of the first and subsequent spikes in a burst. Even if we had not had ground-truth data, consideration of the templates, the individual ACGs, the combined ACGs, and the CCGs for each of the 29 × 28 pairs of units would lead to the conclusion that one of the neurons in the recording was split between units 0 and 1. We would therefore choose to combine units 0 and 1 into a single unit. Comparison of the combined ACG of units 0 and 1 (Fig. 10B) to the ground-truth ACG (Fig. 10B) confirms that this would have been a good decision.
Figure 10.
Postprocessing analysis of the units discovered by full binary pursuit (FBP) and KiloSort2 in the SpikeForest Kampff 2015-09-03-Pair-9-0A data set. Autocorrelograms (ACGs) and cross-correlograms (CCGs) are derived from the sorts included in Fig. 9. A: ACG of the ground-truth spike times. B: ACG of a unit made by combining the spike times of FBP units 0 and 1. C and D: ACGs of FBP units 0 and 1. E: CCG of the spike times of FBP unit 0 with respect to the spikes on unit 1. Note the change in scale of the y-axis. F–H: same as C–E but for KiloSort2 units 0 and 1. I and J: ACG of KiloSort2 unit 4 and its CCG with unit 0. All unit numbers correspond to the units from Fig. 9A.
The same postprocessing strategy for KiloSort2’s units 0 and 1 suggests a different, but equally good decision. The ACG for unit 0 (Fig. 10F) is clean. The ACG for unit 1 (Fig. 10G) shows evidence of refractory period violations, with many ISIs shorter than 1.5 ms (bins at t = −1 and t = 1). The CCG between unit 1 and unit 0 (Fig. 10H) indicates that one of the two units is likely a mixture of the other because there are a large number of spikes with identical event times. Without ground-truth data, we would conclude that unit 1 contains unit 0 spikes that are contaminated with multiunit activity and/or noise. We would choose to delete unit 1 and keep unit 0. Comparison of the ACG for unit 0 (Fig. 10F) with the ground-truth ACG (Fig. 10A) confirms that this would be a good decision. Even in the absence of ground-truth data, our postprocessing strategy would have allowed FBP and KiloSort2 to find different paths to the same correct conclusion.
Postprocessing also reveals that KiloSort2 unit 4 is well separated from the ground-truth neuron. We previously posited that additional units with very high levels of true positives indicated mixtures of the ground-truth neuron (e.g., KiloSort2 units 1–3, Fig. 9A). This is confirmed for unit 1 by the CCG analysis in Fig. 10H. By contrast, KiloSort2 unit 4 has fewer than 13% true positives. It has an ACG that is largely free of ISI violations (Fig. 10I). The CCG of KiloSort2 unit 4 with unit 0 does show a high level of temporally coordinated spike events (Fig. 10J). However, here the coincident spike events are not nearly as temporally specific as would be expected from contamination (Fig. 10H). The large smooth hump in the CCG instead suggests units whose firing properties are plausibly correlated with one another. Indeed, the CCG suggests that the ∼13% true positives in unit 4 may result from legitimate spikes that are temporally coordinated with ground-truth spikes. In this instance, we would conclude that unit 4 is well isolated from unit 0 and choose to keep both units in the sorted output.
Limitations of the FBP Algorithm
The FBP algorithm provides a proof-of-concept framework as a baseline for future developments. But it also has limitations. These include relatively slow runtimes and poor scaling to large channel numbers (>32 contacts). These limitations tradeoff favorably against the virtue of better sorts that allow us to resolve overlaps so that we can measure small changes in firing rate accurately, properly assess trial-by-trial variation in neural firing, and obtain accurate measures of noise correlations and spike-timing cross-correlograms. Thus, our primary focus is to ask how well approaches to sorting can isolate individual neurons and what types of analyses are required to understand the limitations of the sorted data.
In developing our algorithm, we emphasized the larger principles of sorting strategy and accuracy assessment rather than the details of software and hardware optimizations. We therefore opted for a direct, brute force approach to template matching, overlap detection, and drift correction to keep our assessment more tractable. As a result, the sorter is slow by comparison with other sorters. It is difficult to quantify FBP runtime because it depends not only on the number of data channels and recording duration, but also on the number of units detected, the number of spikes they fire, and the number of overlapping spikes. These factors interact in complex ways because every additional spike detected requires recursion of the binary pursuit algorithm within a window near the spike event (see Algorithm Implementation in materials and methods). Furthermore, our drift correction procedure requires sorting almost all of the data twice. As a rough point of reference, our typical cerebellum data sets use 32-channel linear probes for a duration of 70 min to record tens to hundreds of thousands of spikes from each of 3–10 different neurons. Sorting takes from 2 to 4 h up to about a day for more complex data sets, orders of magnitude longer than other sorting algorithms such as KiloSort2 and SpyKING CIRCUS.
The challenge of scaling to recordings from electrodes with hundreds of contacts is a limitation of FBP. Other sorters were optimized to work with recordings using much larger numbers of contacts and they implement advanced methods of template matching pursuit and drift correction to achieve rapid performance. However, they fail to varying degrees on exactly the kind of data that was important to us. As a result of the optimization to work with large channel numbers, they can stumble on data sets with fewer channels. FBP works best on recordings with a modest number of channels, but also can sort the data from recordings with a single microelectrode. Of course, additional information and better sorting can be derived from recordings using multiple contacts with sufficiently dense spacing that neurons are detected on multiple channels. More contacts improve the discrimination of spike events but increase the computational complexity of the spike sorting problem. Finally, FBP could sort recordings from a NeuroPixel probe with 384 contacts by breaking the contacts into smaller neighborhoods. Perhaps the optimal solution would be to sort the full NeuroPixel recording quickly with KiloSort2, identify the neighborhoods that have the key neurons needed for the scientific question at hand, and sort those neighborhoods with FBP.
Ultimately, the runtime for any sorting algorithm is limited by hardware. The clustering aspect of our algorithm is implemented in parallel with each channel initially clustered independently. Thus, this step will be limited by the number of available CPUs and their available memory storage. An ideal use of the binary pursuit template matching algorithm requires full knowledge of the voltage and templates across all channels in a dataset. Although there is no theoretical limit to the number of channels that can be sorted using binary pursuit, in practice it is limited by time and hardware. Our six GB GPU hardware could store sufficient data to perform binary pursuit on 64 channels for 5-min segments. Sorting of larger data sets would require more powerful hardware and/or breaking the data into groups of channels and recombining the resulting sort.
DISCUSSION
Caveat emptor should be the motto of anyone who embarks on spike sorting. We analyzed the sorting quality of four different algorithms on contrived synthetic data sets and actual neural recordings from multicontact arrays with ground truth. We conclude that no current spike sorter is definitively the best in all situations. All sorters exhibit failure modes and each has its own strengths and weaknesses. Because of the tendency of sorters to discover false units that are either multiunit activity or a combination of a single neuron and noise, the output of each sorter tested requires automated and/or manual curation if the research goal is to have well isolated single neurons. Our new sorting algorithm, FBP, was designed to avoid specific failure modes that are critical to our scientific objectives, and to enable a rational and feasible postprocessing strategy.
The broad rule for choosing a spike sorter should be its performance on a particular application. We require resolution of overlapping spikes from single units to resolve small changes in firing rate and perform CCG analyses on data collected from low-density 16- to 32-contact recording probes with nearby neurons firing spikes at rates as high as 100 spikes/s in baseline conditions. For these purposes FBP is the best choice. It resolves pairs of spike overlaps optimally and is conservative enough to minimize false units arising from multiunit activity or contamination of a single unit with noise. FBP’s conservatism discovers a small enough number of units to enable manual curation using ACGs and CCGs. Other spike sorter use cases may vary in tolerance for recordings of multiunit activity versus isolation of single neurons, resolution of overlapping spikes, contamination by noise, and other factors.
We learned that FBP was ideal for our use case through 1) careful design and a full understanding of the sorting algorithm and 2) tests using synthetic data that mimicked our use case. The other three sorters we tested have been similarly demonstrated to perform well in their designed use conditions where FBP might show weaknesses. The spike sorting challenge is that the number of variables present in real neural recordings creates an infinite set of possible test cases and failures dependent on a specific experiment, e.g., the number of channels, their proximity to one another, the density of neurons, neuron firing rates, temporal/spatial overlap of neighboring neurons, and similarity between neurons’ templates, to name a few common characteristics to consider. Thus, we advocate that the best sorter be chosen by testing on realistic use cases with synthetic or ground-truth data.
The known advantages for the sorters we tested appear to be features specifically designed into them. Some are designed to sort quickly and produce a large number of units, whereas FBP was designed to be conservative and deal with overlapping spikes and drift in space and time. We created FBP to generalize consistently across single-electrode recordings, tetrodes, as well as low-density and high-density arrays. We demanded that given sufficient SNR, and two discriminable neurons, FBP could sort the units perfectly in synthetic data. We included a noise criterion to reduce the number of false units. The penalties for these decisions are slowness of sorting and a high threshold for spike detection. Both KiloSort2 and SpyKING-CIRCUS are aimed at sorting numerous channels from high-density arrays. They are capable of sorting these types of data sets much faster than FBP but are less strict in their output units. KiloSort2 was designed to sort data from NeuroPixels and, not surprisingly has occasional problems sorting lower channel count, low density data sets (e.g., Fig. 6G).
Finally, we have shown that a rigorous postprocessing step is necessary if the goal is to obtain single-unit recordings. Refractory period violations in ACGs reveal whether a unit includes multiunit activity or contamination by noise. A high probability of coincident spikes in CCGs reveals units that share spikes, implying that they should be combined or one should be deleted. Combined ACGs between pairs of units provides evidence about whether they should or should not be combined into one unit. Postprocessing is not fool-proof, but we have provided some examples where it can lead to a good decision in the absence of ground-truth data. We designed FBP with these postprocessing steps in mind because postprocessing scales poorly with increases in the number of units discovered by a sorter. With 20 units, postprocessing could involve as many as 400 CCGs. With 100 units, inspection of 10,000 CCGs is implausible. To us, though, the effort to perform rigorous postprocessing seems valuable to ensure the validity of neuroscience data derived after spike sorting.
GRANTS
The study was supported by the U.S. Department of Health and Human Services (HHS) National Institutes of Health (NIH) National Institute of Neurological Disorders and Stroke (NINDS) under Grant No. R01 NS092623 (to S.G.L.).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
N.J.H., D.J.H., and S.G.L. conceived and designed research; N.J.H. performed experiments; N.J.H. and D.J.H. analyzed data; N.J.H., D.J.H., and S.G.L. interpreted results of experiments; N.J.H. and S.G.L. prepared figures; N.J.H. drafted manuscript; N.J.H., D.J.H., and S.G.L. edited and revised manuscript; N.J.H., D.J.H., and S.G.L. approved final version of manuscript.
REFERENCES
- 1.Rey HG, Pedreira C, Quian Quiroga R. Past, present and future of spike sorting techniques. Brain Res Bull 119: 106–117, 2015. doi: 10.1016/j.brainresbull.2015.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Carlson D, Carin L. Continuing progress of spike sorting in the era of big data. Curr Opin Neurobiol 55: 90–96, 2019. doi: 10.1016/j.conb.2019.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pillow JW, Shlens J, Chichilnisky EJ, Simoncelli EP. A model-based spike sorting algorithm for removing correlation artifacts in multi-neuron recordings. PLoS One 8: e62123, 2013. doi: 10.1371/journal.pone.0062123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chung JE, Magland JF, Barnett AH, Tolosa VM, Tooker AC, Lee KY, Shah KG, Felix SH, Frank LM, Greengard LF. A fully automated approach to spike sorting. Neuron 95: 1381–1394.e6, 2017. doi: 10.1016/j.neuron.2017.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yger P, Spampinato GLB, Esposito E, Lefebvre B, Deny S, Gardella C, Stimberg M, Jetter F, Zeck G, Picaud S, Duebel J, Marre O. A spike sorting toolbox for up to thousands of electrodes validated with ground truth recordings in vitro and in vivo. eLife 7: e34518, 2018. doi: 10.7554/eLife.34518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pachitariu M, Steinmetz N, Kadir S, Carandini M, Kenneth DH. Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels (Preprint). bioRxiv 061481, 2016. doi: 10.1101/061481. [DOI]
- 7.Kessy A, Lewin A, Strimmer K. Optimal whitening and decorrelation. Am Stat 72: 309–314, 2018. doi: 10.1080/00031305.2016.1277159. [DOI] [Google Scholar]
- 8.Abdi H, Williams LJ. Principal component analysis. WIREs Comput Stat 2: 433–459, 2010. doi: 10.1002/wics.101. [DOI] [Google Scholar]
- 9.Arthur D, Vassilvitskii S. k-means++: the advantages of careful seeding. In: SODA '07: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2007, p. 1027–1035. [Google Scholar]
- 10.Botev ZI, Grotowski JF, Kroese DP. Kernel density estimation via diffusion. Ann Stat 38: 2916–2957, 2010. doi: 10.1214/10-AOS799. [DOI] [Google Scholar]
- 11.Stimberg M, Brette R, Goodman DFM. Brian 2, an intuitive and efficient neural simulator. eLife 8: e47314, 2019. doi: 10.7554/eLife.47314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Magland J, Jun JJ, Lovero E, Morley AJ, Hurwitz CL, Buccino AP, Garcia S, Barnett AH. SpikeForest, reproducible web-facing ground-truth validation of automated neural spike sorters. eLife 9: e55167, 2020. doi: 10.7554/eLife.55167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marques-Smith A, Neto JP, Lopes G, Nogueira J, Calcaterra L, Frazão J, Kim D, Phillips MG, Dimitriadis G, Kampff AR. Recording from the same neuron with high-density CMOS probes and patch-clamp: a ground-truth dataset and an experiment in collaboration (Preprint). bioRxiv 370080, 2018. doi: 10.1101/370080. [DOI]
- 14.Neto JP, Lopes G, Frazão J, Nogueira J, Lacerda P, Baião P, Aarts A, Andrei A, Musa S, Fortunato E, Barquinha P, Kampff AR. Validating silicon polytrodes with paired juxtacellular recordings: method and dataset. J Neurophysiol 116: 892–903, 2016. doi: 10.1152/jn.00103.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]