Modeling the native ensemble of PhuS using enhanced sampling MD and HDX-ensemble reweighting

Abstract

The cytoplasmic heme binding protein from Pseudomonas aeruginosa, PhuS, plays two essential roles in regulating heme uptake and iron homeostasis. First, PhuS shuttles exogenous heme to heme oxygenase (HemO) for degradation and iron release. Second, PhuS binds DNA and modulates the transcription of the prrF/H small RNAs (sRNAs) involved in the iron-sparing response. Heme binding to PhuS regulates this dual function, as the unliganded form binds DNA, whereas the heme-bound form binds HemO. Crystallographic studies revealed nearly identical structures for apo- and holo-PhuS, and yet numerous solution-based measurements indicate that heme binding is accompanied by large conformational rearrangements. In particular, hydrogen-deuterium exchange mass spectrometry (HDX-MS) of apo- versus holo-PhuS revealed large differences in deuterium uptake, notably in α-helices 6, 7, and 8 (α6,7,8), which contribute to the heme binding pocket. These helices were mostly labile in apo-PhuS but largely protected in holo-PhuS. In contrast, in silico-predicted deuterium uptake levels of α6,7,8 from molecular dynamics (MD) simulations of the apo- and holo-PhuS structures are highly similar, consistent only with the holo-PhuS HDX-MS data. To rationalize this discrepancy between crystal structures, simulations, and observed HDX-MS, we exploit a recently developed computational approach (HDXer) that fits the relative weights of conformational populations within an ensemble of structures to conform to a target set of HDX-MS data. Here, a combination of enhanced sampling MD, HDXer, and dimensionality reduction analysis reveals an apo-PhuS conformational landscape in which α6, 7, and 8 are significantly rearranged compared to the crystal structure, including a loss of secondary structure in α6 and the displacement of α7 toward the HemO binding interface. Circular dichroism analysis confirms the loss of secondary structure, and the extracted ensembles of apo-PhuS and of heme-transfer-impaired H212R mutant, are consistent with known heme binding and transfer properties. The proposed conformational landscape provides structural insights into the modulation by heme of the dual function of PhuS.

Significance

The cytoplasmic heme binding protein from Pseudomonas aeruginosa, PhuS, is essential for heme uptake and iron homeostasis and thus for infection and virulence. However, in vitro biophysical studies have suggested significant local discrepancies with crystal structures and ensuing molecular dynamics (MD) simulations, pointing to a more heterogeneous conformational landscape in solution. We have employed a strategy combining enhanced sampling MD together with a hydrogen-deuterium exchange mass spectrometry (HDX-MS)-based ensemble reweighting to model the local conformational landscape of apo-PhuS. Demonstrating the utility of HDX-MS-based ensemble refinement approaches to model native structural ensemble, we reveal large conformational rearrangements consistent with in vitro biophysical and functional data, yielding new, to our knowledge, mechanistic insights and potentially revealing cryptic drug binding sites.

Introduction

Iron, because of its redox properties, is an essential element found in cellular processes ranging from oxygen transport and energy transduction to nitrogen fixation (1). Iron is an essential micronutrient in bacterial metabolism, and, in bacterial pathogens, it has been shown to be critical for survival and virulence (2, 3, 4). As such, competition for iron resources within the host is a major determinant of infection and virulence. The hosts of these pathogens have developed strategies to limit the availability of free iron as a defense mechanism to combat bacterial pathogens (5). In return, many pathogens have evolved multiple iron acquisition strategies to overcome the limited amount of free iron available. Pseudomonas aeruginosa is one such pathogen that can adapt its iron uptake strategies in response to different physiological environments (6,7). P. aeruginosa is a Gram-negative opportunistic pathogen that infects individuals with compromised immune systems. Notably, in cystic fibrosis patients, chronic P. aeruginosa infection leads to increased morbidity and mortality as a result of chronic airway inflammation and decreased lung function (8).

P. aeruginosa can acquire host iron through one of three strategies: 1) the secretion of siderophores such as pyochelin, which scavenges host ferric iron (9); 2) the uptake of ferrous iron through the Feo uptake system (10); and 3) the acquisition and degradation of host heme through heme acquisition and uptake pathways (11). Genetic (12), proteomic (13), and metabolic studies have suggested that in longitudinal studies of chronically infected cystic fibrosis lungs, P. aeruginosa adapts to rely largely on heme uptake as a preferential iron acquisition strategy. Heme acquisition and uptake by P. aeruginosa is achieved through two nonredundant systems: the heme assimilation system (has) and the Pseudomonas heme utilization system (phu) (14). Both systems encode for an outer membrane heme receptor protein (HasR and PhuR, respectively) that binds either free heme or hemophore HasA-bound heme. The extracellular heme is then transported to the periplasmic space, where it is bound by the periplasmic heme binding protein, PhuT, and then translocated into the cytoplasm through the inner-membrane ATP-binding cassette transporter, PhuUV. There, the cytoplasmic heme binding protein, PhuS, sequesters heme and delivers it to the iron-regulated heme oxygenase (HemO) for degradation and release of iron along with CO and biliverdin IXβ and IXδ (15). PhuS has been shown to be a titratable regulator of heme flux into the cell, as the deletion of PhuS results in inefficient heme utilization, causing a disruption in iron homeostasis (16). Consequently, deletion results in a slow-growth phenotype and potentially reduced virulence (17). Recently, a combination of DNA binding studies and quantitative polymerase chain reaction (qPCR) have also revealed a previously uncharacterized heme-dependent regulatory role of PhuS in the transcription of iron and heme-regulated small RNAs (sRNAs) PrrF and PrrH, respectively (18), which in turn are involved in the post-transcriptional regulation of genes regulating virulence and iron homeostasis (19). In vivo, the deletion of PhuS was shown to affect transcriptional levels of PrrF and PrrH (18). In parallel, in vitro DNA binding studies have shown that in its apo form, PhuS binds DNA sequences in the promoter region of the PrrF/H gene, overlapping the iron-regulated Fur box (18). In addition, DNA binding is inhibited in heme-bound holo-PhuS, providing a potential molecular mechanism for the integration of its metabolic heme flux role with its role in the regulation of gene expression involved in heme or iron homeostasis and virulence. However, critical questions remain regarding the structural understanding of how PhuS binds heme and subsequently transfers it to HemO or how heme and DNA binding are mutually exclusive.

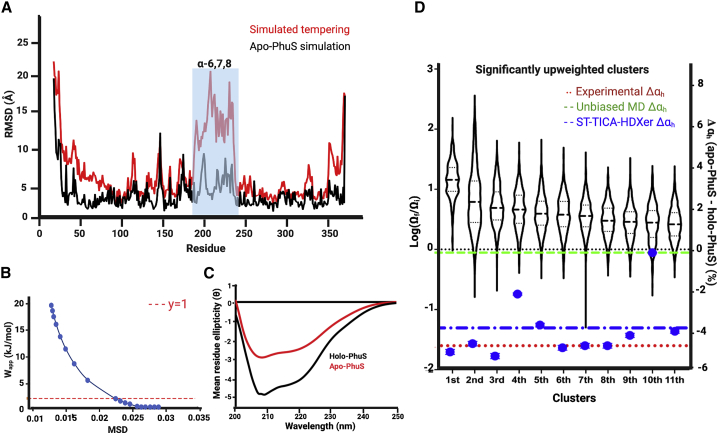
High-resolution crystal structures of both the unliganded PhuS (20) (apo-PhuS, 4IMH) and the heme-bound PhuS (21) (holo-PhuS, 4MF9) reveal a high degree of structural similarity with a backbone root mean-square deviation (RMSD) of 0.3 Å. With a molecular mass of 39 kDa, PhuS is composed of a core of two curved β-sheets stacked together, each containing nine anti-parallel β-strands. Each β-sheet is structurally flanked on both ends by α-helices to form two structurally identical units connected by a long loop from Arg168 to Val189 (20). The heme binding site is located in the unit closer to the C-terminal end. α-helices α6, 7, and 8 (α6,7,8) form an α-loop-α-loop-α motif that precedes the β-sheet in the C-terminal unit. This motif contributes to the heme binding pocket, with conserved residue His209, at the N-terminal end of helix α7, serving as the proximal ligand to the heme in the holo-PhuS structure (Fig. 1 A). Unique among homologous heme trafficking proteins, PhuS has three additional histidine residues within α7: His210, His212, and His218. Highlighting a dynamic heme binding pocket, crystallographic (20), spectroscopic, and mutagenesis (5) studies have shown that His212 can serve as an alternate ligand and is critical for heme transfer to HemO. Moreover, in contrast to the high degree of similarity between the apo- and holo-PhuS crystal structures, biophysical evidence suggests significant differences in the conformational landscapes of apo- and holo-PhuS in solution and points toward a more dynamic heme binding pocket in apo-PhuS. In the first of such studies, analytical ultracentrifugation, limited trypsin digests, and PhuS-HemO binding studies suggested that heme binding induces large conformational changes in PhuS that drive the interaction of PhuS with HemO (23). Subsequently, hydrogen-deuterium exchange mass spectrometry (HDX-MS) studies (22) provided corroborating evidence for a conformational change upon heme binding, as large decreases in deuterium uptake were observed in various localized regions in holo-PhuS when compared with apo-PhuS (Fig. 1, B, C, and D). In particular, the C-terminal α6,7,8 segment (red in Fig. 1 A) displayed the most intense decrease in deuterium uptake (Fig. 1 B), with the largest decrease observed in segments of the motif that do not form direct contacts with the heme, such as α6, located more than 8 Å away (Fig. 1 C). In apo-PhuS, the deuterium uptake behavior of peptides spanning α6,7,8 (Fig. 1 D) rapidly reached saturation levels of 100% exchange. Such rapid exchange is more consistent with a largely unstructured and labile motif rather than the ordered secondary and tertiary structure observed in the apo-PhuS crystal structure (Protein Data Bank (PDB): PDB: 4IMH (20)). Although conventional molecular dynamics (MD) simulations of apo-PhuS and holo-PhuS have suggested some differences in the dynamics of the heme binding pocket, loss of secondary and tertiary structure was not observed during 500 ns simulations (22). Hydrogen-deuterium exchange rate predictions from the resulting in silico ensembles suggested that the minor conformational differences between apo and holo simulations could not account for the large difference in HDX-MS observed experimentally ((22); Fig. 1 D). Rather, the calculated deuterium uptake in α6,7,8 for both apo- and holo-PhuS simulations was consistent with the experimental HDX-MS data for holo-PhuS in solution (Fig. 1 D). These observations suggest that the structural protection afforded by direct heme contacts alone cannot explain the large difference in experimental deuterium uptake in α6,7,8. More importantly, these results suggest that the crystal structure of apo-PhuS likely adopts a holo-like conformation and that conventional MD simulations initiated from that structure are unable to sufficiently explore the conformational landscape of α6,7,8 or sample alternative states during typical simulation timescales.

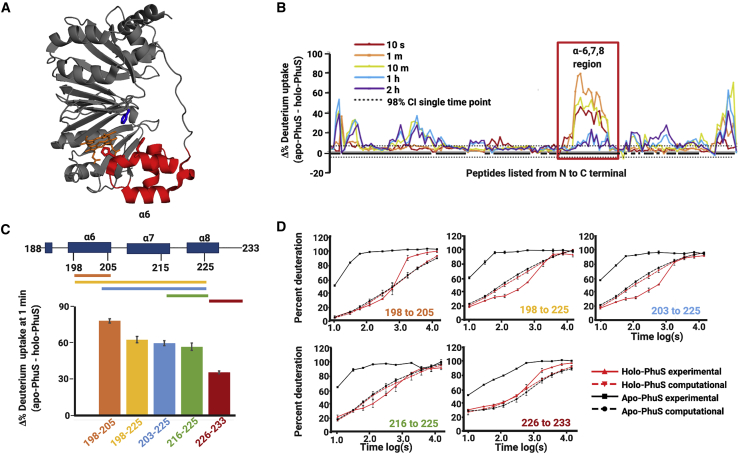
Figure 1.

HDX-MS and MD simulations point to conformational rearrangements in proximal α6,7,8. (A) Crystal structure of holo-PhuS (PDB: 4MF9) with the α6,7,8 region colored in red with the heme-coordinating H209 and H212 displayed as red stick representations, F114 as a blue stick representation, and heme shown as orange sticks. (B) HDX-MS percent difference plot highlighting the change in deuterium uptake (apo-PhuS − holo-PhuS) at each individual peptide listed on the x axis from N- to C-terminus and monitored for five deuterium exposure times (colored lines) (22). Peptides with percent deuterium difference values greater than the 98% confidence interval (gray dotted lines) are considered significantly different. The α6,7,8 region of PhuS is highlighted in a red box and shows the largest magnitude in difference. (C) Schematic of representative peptides encompassing the α6,7,8 region (top) coupled with a bar graph of the difference (apo-PhuS − holo-PhuS) in percent deuterium uptake of the same peptides after 1 min of deuterium exchange reaction, error bars represent the propagated standard error for triplicate apo-PhuS and holo-PhuS HDX-MS data. (bottom). (D) Kinetic uptake plots of the same representative peptides in the α6,7,8 region with the experimentally determined uptake of apo-PhuS (black solid line) and holo-PhuS (red solid line) compared with the calculated deuterium uptake from apo-PhuS MD simulations (black dashed line) and holo-PhuS MD simulations (red dashed line), error bars respresent the standard error for the HDX-MS experiments and MD simulations done in triplicate.

A more thorough structural characterization of apo-PhuS is therefore necessary to facilitate the mechanistic interpretation of experimental data investigating heme binding and transfer to HemO and of the newly revealed DNA binding properties of PhuS. In addition, structure-based drug design efforts targeting apo-PhuS require a detailed and accurate understanding of the structural dynamics of the apo state. In this work, therefore, we have expanded the conformational exploration of apo-PhuS with a particular emphasis on the conformational dynamics of α6,7,8. To that end, we have implemented and applied a workflow combining enhanced sampling MD simulations, which widen the conformational space and overcome the sampling limitations of unbiased MD simulations, with hydrogen-deuterium exchange ensemble reweighting (HDXer), a maximal entropy reweighting approach that optimally fits a candidate ensemble of structures to a target set of HDX-MS data, taking into account all forms of uncertainty in the modeling process (24,25).

In the first stage of our workflow, enhanced sampling MD was performed using simulated tempering (ST). ST broadens the conformational landscape explored by employing a Metropolis algorithm to periodically change the simulation temperature, providing a boost in temperature as a means to overcome conformational energy barriers (26, 27, 28). Next, the candidate ensemble of apo-PhuS structures generated by our simulations is subjected to ensemble reweighting using HDXer. HDXer first predicts peptide-level deuterated fractions by estimating the protection factors of each exchangeable amide hydrogen. Protection factors are quantitative estimates of the structural determinants that result in the reduction of hydrogen-deuterium exchange at a given amide hydrogen when compared to an unstructured conformation. Here, they are calculated using the phenomenological equation introduced by Best and Vendruscolo (29), which correlates the local structural protection from exchange to the hydrogen bonds and heavy atom contacts involving each individual amide hydrogen, averaged across an ensemble of structures. Next, the relative populations of frames in the candidate structural ensemble are minimally biased such that the predicted hydrogen-deuterium exchange data of the final reweighted ensemble conform to the experimental data, within a chosen level of uncertainty. Finally, the reweighted ensemble is structurally analyzed to identify conformations that are statistically upweighted relative to the other frames and that therefore, on average, most accurately reflect conformational states present in the experimental data. The interpretation of the reweighted ensemble from HDXer is aided by a dimensionality reduction approach, time-lagged independent correlation analysis (TICA), to determine and rank the populations of structural clusters from the ST simulations. The structural observations from the application of this computational and HDX-MS workflow to apo-PhuS were then further corroborated by circular dichroism (CD) and mutagenesis studies. Using this workflow, we have therefore extracted ensembles that we propose to be representative of the conformation of apo-PhuS in solution.

Materials and methods

Protein expression and purification

All bacterial strains and plasmids used in these studies were previously reported (5,15). Site-directed mutagenesis to create the PhuS H212R variant was performed as previously described (18,22). Expression and purification of the wild-type (WT) PhuS and H212R proteins were carried out as previously described (15,18,22,23) with slight modifications. Briefly, the PhuS or PhuS H212R mutant lysate was applied to a Sepharose-G column (Cytiva, Marlborough, MA) equilibrated in 20 mM Tris-HCl (pH 8.0) and washed with 5 column volumes of the same buffer. The column was further washed with 10 column volumes of 20 mM Tris (pH 8.0) containing 20 mM NaCl and the PhuS protein eluted in the same buffer with a linear gradient of 50–500 mM NaCl. Eluted fractions were analyzed by sodium dodecyl sulphate–polyacrylamide gel electrophoresis (SDS-PAGE), and the peak fractions were pooled and dialyzed against 4 L of 20 mM Tris (pH 8.0) containing 100 mM NaCl. The protein was concentrated in a Pierce Protein Concentrator (30 K) (Thermo Fisher Scientific, Waltham, MA) and purified to homogeneity on an AKTA FPLC system fitted with a 26/60 Superdex 200 pg size exclusion column (Cytiva) equilibrated with 20 mM Tris (pH 8.0) containing 100 mM NaCl. Peak fractions as judged by the A₂₈₀ were subjected to SDS-PAGE and the homogenous fractions pooled, concentrated (10 mg/mL), and stored at −80°C until further use.

Locally unfolded model generation

Chain A from the crystal structure of apo-PhuS (4IMH) was used for all computational work. N-terminal residues 1–7, for which no electron density was observed, were modeled using Modloop (30,31). Modloop was further used for the generation of models with different degrees of local unfolding in the α6,7,8 motif. Specific residue ranges used for that modeling were selected so that the models would reflect a progressive unfolding of all three helices in the α6,7,8 motif. A schematic of the residue ranges used in each locally unfolded model is shown in Fig. S1.

MD simulations

MD simulations of each of the five locally unfolded models, as well as the apo-PhuS crystal structure and an in silico mutant H212R apo-PhuS, were performed using OpenMM v7.5 (32) as follows. Inputs for the MD simulations were generated using the CHARMM graphical user interface (CHARMM-GUI) Input Generator web application (33). Simulations were carried out using OpenMM with the CHARMM36m additive force (34) field and the TIP3P water model (35). The system was solvated in a periodic water box containing 0.15 M KCl, with box boundaries no closer than 1 nm to any solute atom. For the Lennard-Jones interaction calculations, a force switching function was applied over the range from 1.0 to 1.2 nm. The particle mesh Ewald approach, with an Ewald error tolerance of 0.0005, was used for the calculation of long-range electrostatic interactions. A 2 fs time step was used for integration with temperature and pressure held constant at 298.15 K and 1 atm, respectively. Temperature was maintained at 298.15 K using a Langevin thermostat with a friction coefficient of 1 ps⁻¹. Pressure was isotropically held constant at 1 bar using an MC (Monte Carlo) barostat with a pressure coupling frequency of 2 ps. Before the production run, the system energy was minimized using the L-BGFS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm) method, in which 5000 steps of minimization were performed and a convergence tolerance of 100 kJ/mol was utilized. The system was then equilibrated for 125 ps in the NVT ensemble using a 1 fs timestep. During both minimization and equilibration, positional restraints were applied to the protein’s backbone and side chain atoms with a force constant of 400 and 40 kJ/mol/A², respectively. For production runs, each model and the crystallographic form were simulated for 50 ns, with structural coordinates written to the trajectory every picosecond of simulated time, resulting in 50,000 frames total. To sample a longer timescale, the simulations initiated from the crystallographic apo-PhuS conformation and the modeled H212R mutant apo-PhuS were both repeated, resulting in 5-μs-long trajectories each.

Enhanced sampling MD simulations

The enhanced sampling method ST was performed on the apo-PhuS crystal structure conformation (4IMH, chain A) with N-terminal missing residues built in as described above. Input generation, energy minimization, and equilibration steps were performed as described above. The resulting system was then used as the starting structure for the ST, which was carried out using OpenMM (32), the CHARMM36m force field, and the TIP3P water model (35). A 2 fs time step was used for integration, with pressure held constant at 1 atm and a minimal temperature of 300 K.

To identify the optimal parameters for the ST runs of PhuS, preliminary calculations were carried out with maximal temperature values between 420 and 520 K in increments of 20 K, the number of temperature levels (between which transitions were attempted) set to between 75 and 150, and the number of time steps between 2.5 × 10⁷ and 5.0 × 10⁸. The temperature steps are equally spaced, and each is assigned a weight to promote equal temperature sampling throughout the course of the simulation. ST was performed with temperature transitions attempted every 25 ps. Optimal parameters were identified by the extent of conformational excursion away from the crystallographic conformation based on the trajectory-averaged C_α RMSD of both individual residues (local) and whole protein (average) with respect to the initial input structure. After the optimization, 5.0 × 10⁷-step-long ST runs were performed in six repeats for WT and H212R apo-PhuS respectively, with the following conditions: 100 temperature steps and maximal temperature of 520 K for WT and 440 K (three runs) or 420 K (three runs) for H212R. Structural coordinates were reported every 1000 steps per trajectory, resulting in 50,000 frames in total. C_α RMSD calculations were used to assess whether significant local and global deviations from the crystallographic conformation had occurred (Fig. S2). The trajectories of the six repeats were then combined for ensemble reweighting purposes.

Hydrogen-deuterium exchange calculations and maximal entropy reweighting

The calculation of percent deuterium uptake from computational ensembles and the subsequent maximal entropy reweighting were performed using the HDXer approach described in Bradshaw et al. (24) and subsequent work (25). To calculate deuterium uptake, the following phenomenological equation (29), Eq. 1, was used to compute protection factors at individual backbone amide hydrogens through the course of a given simulation.

$$\ln \left(P_i\right)={\beta }_C{N}_{C,i}+{\beta }_H{N}_{H,i}$$ (1)

The protection factor (P_i) at residue i is the ensemble average of the sum of the number of nonhydrogen atoms within 6.5 Å of the backbone nitrogen atom of the residue (N_{C, i}) multiplied by a scaling factor (β_C) and the number of hydrogen bonds formed by the backbone amide hydrogen of the residues (N_{H, i}) multiplied by a second scaling factor (β_H). In the calculation of (N_{C, i}), the atoms of the neighboring two residues on each side of the residue were omitted. In this study, scaling factors of 0.35 and 2.0 are used for β_C and β_H, respectively (29).

Protection factors were then used to calculate peptide-level deuterium fractional uptake $\left(D_{j,t}^{sim}\right)$ as a function of time (t) of exchange as in Eq. 2:

$$D_{j,t}^{sim}=\frac{{\sum }_{i=m_j+1}^{i=n_j}1-\text{exp}(-\frac{k_i^{int}}{P_i}t)}{n_j-m_j},$$ (2)

where m_j and n_j are the starting and ending residue numbers of the i^th peptide and were chosen to match the experimental peptide segments observed in HDX-MS. Prolines, which do not have a backbone amide hydrogen, and the first residue of each segment were omitted from the calculations. The empirically determined intrinsic rate of exchange, k_int, was obtained from Bai et al. and subsequent updates (36,37). As discussed previously (22,24,38), these calculations are only applicable to the EX2 kinetic exchange regime of hydrogen-deuterium exchange. Therefore, for the purposes of ensemble reweighting, any peptides or deuterium incubation time points displaying EX1 characteristic bimodal behavior were excluded. For PhuS, EX1 kinetics was observed and reported in various regions of the protein in both apo- and holo-PhuS (22). However, the first instance of detectable bimodal behavior was observed after 5 min of deuterium incubation. Thus, the peptide centroid data before 5 min deuterium incubation were assumed to reflect structural fluctuations of the EX2 kinetic regime, and all deuterium incubation time points collected after 5 min were discarded from the data set before reweighting.

After the calculation of peptide segment deuteration fractions, maximal entropy reweighting was implemented to fit the relative populations (“weights”) of the structures in the combined simulation ensembles to a target experimental data set. Reweighting was performed using HDXer as previously established (24,25), and a detailed description of the methodology is outlined in Bradshaw et al. (24) and in the Supplemental methods of the Supporting materials. Before reweighting, the initial weight Ω_i for each structure in the ensemble is equal to $\left(1/n\right)$ (where n is the total number of structures in the ensemble). After reweighting, an optimized weight (Ω_f) for each frame is obtained such that frames that more closely represent the data are given Ω_f > Ω_i, whereas frames that do not represent the data well are given values of Ω_f < Ω_i.

To prevent overfitting of the final optimized weights, the tightness of fit between the simulated and the experimental data can be controlled by a parameter (γ). The choice of γ affects both the final mean-square deviation (MSD) of the fitted data to the experimental data and the apparent work (W_app, in kJ/mol) applied to the initial ensemble to adjust the conformational populations. The relationship between these variables was inspected by way of a “decision plot” of W_app vs. MSD, in which a point of inflection denotes the onset of overfitting, characterized as a rapid increase in W_app for very little reduction in MSD. To fairly compare the final reweighted ensembles resulting from different initial ensembles or fitted to different HDX-MS data sets, we always selected a γ-value that resulted in a constant work (∼2 kJ/mol) applied to the initial ensemble.

Dimensionality reduction by TICA

A dimensionality reduction strategy was used to extract structural clusters from ensembles and assess the distribution of reassigned HDXer weights across clusters. Trajectories were clustered by applying TICA (39). TICA was implemented using the PyEMMA software (40), and backbone dihedral angles were used as the input structural parameter. The resulting TICA plots were visualized, and the number of clusters and cluster boundaries were determined using the PyEMMA software. The reassigned weights from HDXer for each frame were mapped to the TICA-delineated clusters. For complex ensembles resulting from the combination of six ST trajectories, TICA clustering was performed iteratively by isolating individual clusters and subjecting each to further TICA-based clustering. Endpoints of the iterative clustering were set when a cluster either 1) displayed a pairwise C_α RMSD < 3 Å for all pairwise comparisons within the cluster or 2) contained fewer than 1000 frames (Fig. S3). Once the endpoints have been met for all clusters, the average weight reassignment for a given cluster was calculated as the mean of the log fold change in weight, log(Ω_f/Ω_i), of each frame in the cluster. The clusters with a mean log(Ω_f/Ω_i) > 0 are upweighted clusters. The distribution of log(Ω_f/Ω_i) assigned to the frames was plotted as a histogram to check for normalcy, and the standard deviations of each cluster were plotted (Figs. 5 and 6; Fig. S4). For the upweighted clusters, a z score was calculated to determine the statistical significance of the change in weights of individual clusters as in Eq. 3,

$$z=\frac{(x-\mu )}{s},$$ (3)

where x is the average log(Ω_f/Ω_i) of a given cluster, μ is the average log(Ω_f/Ω_i) over all clusters, and s is the standard deviation in average log(Ω_f/Ω_i) values of all clusters. z scores were then converted to percentiles using a z score to percentile table (a z score >1.7 has a significance ≥95%), from which p-values were derived. p-values below 0.05 were selected as significantly upweighted clusters. The significantly upweighted clusters were ranked based on their average log(Ω_f/Ω_i) value.

Figure 5.

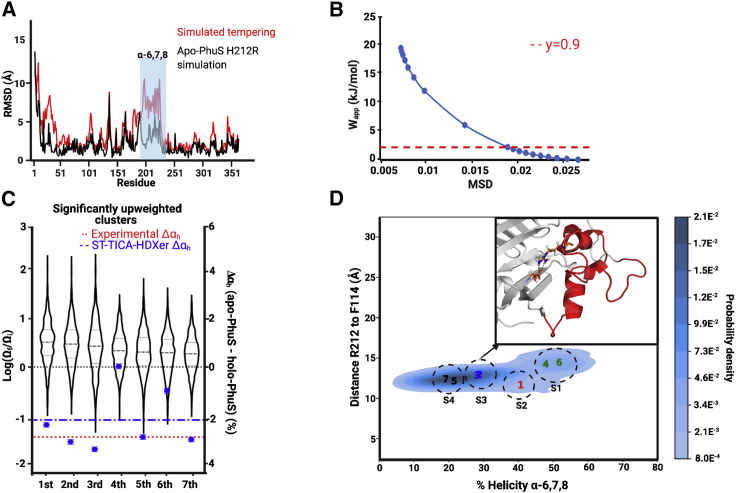
Ensemble refinement of H212R apo-PhuS by ST, HDXer, and CD. (A) Plot of the average RMSD (Å) of the C_α at each residue for a 5-μs-long conventional MD simulation of H212R apo-PhuS simulation (black) and the six combined ST simulations of H212R apo-PhuS (red). (B) Decision plot resulting from the reweighting of the combined H212R apo-PhuS ST runs to the target H212R apo-PhuS HDX-MS data. The apparent work obtained using selected γ of 0.9 is indicated with a red dashed line. (C) Violin plots of the seven significantly upweighted clusters ranked in order of average change in weight (log(Ω_f/Ω_i)). The tails represent the minimal and maximal weight in the cluster, the thick dashed lines indicate the mean change in weight, and the thin dashed lines bracket 50% of the population. The change in percent α-helicity (Δα_h) observed between each cluster and the holo-PhuS computational simulations (blue dots) is shown alongside a weighted average for all clusters (blue dot-dashed line). The red dotted line indicates the experimental Δα_h. (D) The KDE plot generated from the seven significantly upweighted clusters using the distance between the C_α of Arg212 and Phe114 (Å) and the percent α-helicity in the α6,7,8 region. Each number represents the average coordinate of one of the seven significantly upweighted clusters, numbered according to its corresponding average upweighting rank (most upweighted to least upweighted). The scale bar represents the probability desnsity at each point. The inset shows the Arg212 residue is within 2.2 Å of Glu318 (sticks), an interaction observed in all but clusters 4 and 6.

Figure 6.

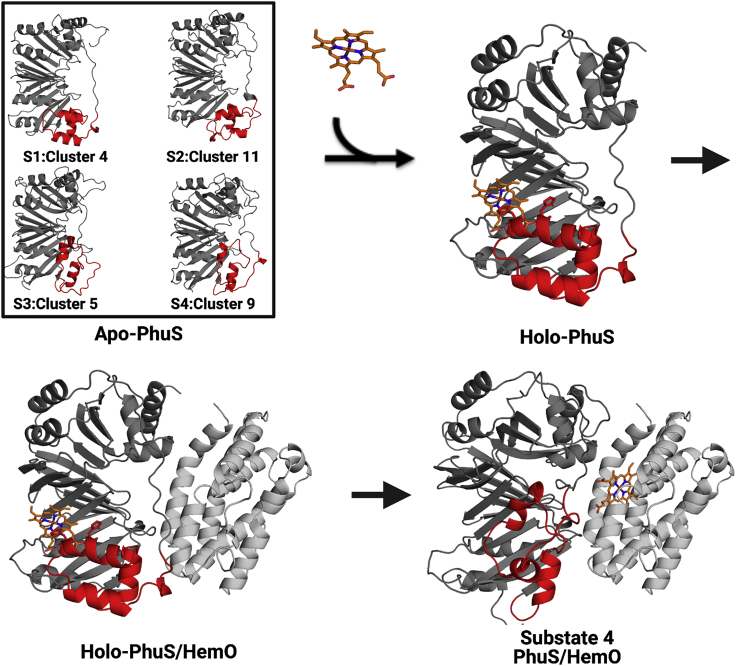
The proposed mechanism of heme binding to PhuS and subsequent transfer to HemO. Apo-PhuS exists in multiple conformational substates, represented here by the four major substrates (top left) extracted by ST and HDXer. Heme binding is accompanied by a conformational rearrangement to coordinate the heme on the proximal side as in the crystallographic form (top right). Heme binding drives the formation of the holo-PhuS/HemO complex, modeled by cross-linking and mass spectrometry and docking studies (22) (bottom left). Transfer of heme to HemO may occur through a conformation in which the α6,7,8 helices reorient toward HemO; this putative conformation might consist of one similar to the representative structure from substate 4, shown aligned with PhuS within the context of the PhuS-HemO complex (bottom right). The α6,7,8 helices are colored red.

Circular dichroism

Experimental CD spectra of the apo-PhuS and holo-PhuS for WT and H212R mutants were obtained on a JASCO J-810 spectropolarimeter (Oklahoma City, OK). All samples were recorded in 10 mM potassium phosphate (pH 7.4) at 25°C from 190 to 260 nm, with 0.2 mm resolution and a 1.0 cm⁻¹ bandwidth. The mean residue ellipticity (deg ⋅ cm² ⋅ dmol⁻¹) was calculated using CDPRO software as recommended by JASCO. Theoretical CD spectra were modeled from computational ensembles using chosen trajectories as inputs to DISICL (Dihedral-based segment identification and classification) (41). The resulting predicted and experimental spectra were then deconvoluted using the BeStSel webtool (42,43) to estimate percent secondary structure content to calculate differences in percent helicity.

Distance and local percent helicity calculations

To characterize the conformational landscape of the heme binding pocket, kernel density estimation plots (KDE plots) were generated as a function of percent helicity of α6,7,8 and the distance between residue 212 (His or Arg) and Phe114 across the heme binding pocket. For each frame of the upweighted clusters, as well as the unbiased apo- and the unbiased holo-PhuS simulations, the distance between the α-carbons of Phe114 and His212 (or Arg212 for mutant) was measured using mdtraj (44), and percent helicity of the α6,7,8 region (residues 188 to 233) was calculated using the “dssp” function of mdtraj (44).

Solvent-accessible surface area calculations

Distal and backside contact residues to the heme in holo-PhuS (PDB: 4IMH) were identified using the Ligand Contact Tool from the Firesuite Home (http://firedb.bioinfo.cnio.es/). Residues within 0.5 Å, plus van der Waals radii, of the ligand were considered to contact the heme. Residues present in the α6,7,8 helices were not considered. Solvent-accessible surface area (SASA) was calculated for the apo- and holo-PhuS MD simulations and for the significantly upweighted clusters of the WT and H212R ST simulations in Visual Molecular Dynamics using a 1.4 Å probe radius.

Results

Locally unfolded models of α6,7,8

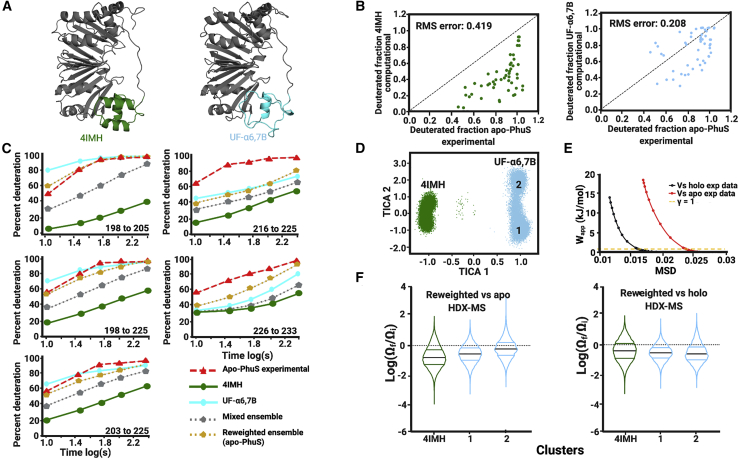
As an initial attempt to probe the conformational landscape of C-terminal helices α6,7,8 in silico, models were generated with various degrees of unfolding of α6,7,8 qualitatively guided by experimental HDX-MS observations (Fig. 1). A schematic of the secondary structure elements replaced by unstructured loops in the locally unfolded models is shown in Fig. S1. The models consist of 1) UF-α6, in which α6 (residues 195–207) is unfolded; 2) UF-α6,7A, in which α6 and the N-terminal half of α7 (residues 195–215) are unfolded; 3) UF-α6,7B, in which both α6 and α7 (residues 195–220) are unfolded; 4) UF-α7, in which α7 (residues 207–220) is unfolded; and 5) UF-α6,7,8 (residues 188–233), in which all three helices are unfolded. Model UF-α6,7B and the apo-PhuS crystal structures are shown in Fig. 2 A. Using these models, as well as the apo-PhuS crystal structure (4IMH, chain A), short (50 ns) unbiased MD simulations were performed. As expected, the trajectory-averaged C_α RMSD of individual residues with respect to the starting crystal structure showed that the remodeling of loops in α6,7,8 resulted in greater local structural deviations and dynamic behavior (Fig. S7). From these resulting ensembles, the predicted HDX-MS deuterated fractions were then calculated for peptide segments corresponding to the experimental data and as a function of the experimental deuterium exposure times. The calculated deuterated fractions were plotted versus the corresponding experimental apo-PhuS HDX-MS data, taking into account either all peptide segments (Fig. S8 B) or just the peptides covering the C-terminal α6,7,8 motifs (Fig. 2 B; Fig. S8 A). The root mean-square (RMS) error to the line of identity (y = x) provides a simple assessment of the accuracy of the structures sampled in each ensemble. The RMS error for each of the unfolded model simulations showed an improved accuracy over all peptide segments covering the entire protein, but particularly so for α6,7,8 (Table S1). In the α6,7,8 region, therefore, the ensembles generated from all five locally unfolded models are more consistent with the experimental apo-PhuS HDX-MS than the ensemble resulting from the apo-PhuS crystal structure, at least for the peptides in that region. Interestingly, the greatest improvement in RMS error was observed for ensembles generated from models in which α6 was unfolded (UF-α6, UF-α6,7A, UF-α6,7B, and UF-α6,7,8). Moreover, model UF-α6,7B, in which both α6 and α7 are unfolded, resulted in the lowest RMS error (Fig. 2 B) of 0.208 for peptides in the α6,7,8 region. In contrast, the ensemble generated from the apo crystal structure shows an RMS error value of 0.419.

Figure 2.

Modeled local unfolding of α6 and α7 improves correlation to apo-PhuS HDX-MS data. (A) The crystal structure of apo-PhuS (PDB: 4IMH) and the best fitting model UF-α6,7B, with the α6,7,8 region highlighted (green and cyan, respectively). (B) Plots of the calculated deuterium uptake versus experimentally measured apo-PhuS deuterium uptake for all peptides spanning the α6,7,8 motif and deuterium exchange reaction time points up to 5 min. The calculated deuterium uptake was obtained from MD simulations of the apo-PhuS structure 4IMH (left) or of the UF-α6,7B locally unfolded model (right); the RMS error to the line of identity is also shown. (C) Kinetic deuterium uptake plots of representative peptides in the α6,7,8 region including the traces for the apo-PhuS experimental data (red dashed line), the 4IMH MD simulations (green solid line), the UF-α6,7B MD simulations (cyan solid line), the mixed ensemble (silver dotted line), and the HDXer reweighted ensemble (gold dotted line). (D) TICA separation of the mixed ensemble. Frames are mapped based on simulation of origin (4IMH, green and UF-α6,7B, cyan). (E) The work versus MSD plots or decision plot obtained for the reweighting the mixed ensemble to the experimental apo-PhuS target data (red) and to the experimental holo-PhuS target data (black) with the chosen γ-value of 1 displayed as the dashed yellow line. (F) Violin plots of the log(Ω_f/Ω_i) of individual frames mapped to the clusters generated by TICA and colored accordingly. Within the violins, black lines indicate the average log(Ω_f/Ω_i) and the color lines bracket 50% of the population.

The above data reflect analysis over all the peptides covering α6,7,8. However, the same data can be visualized for individual peptide segments using kinetic deuterium uptake curves. Fig. 2 C shows the experimental and calculated kinetic deuterium uptake traces for five peptides covering the entire α6,7,8 motif. For peptide 198–205, which spans α6, the experimental curve rapidly reaches saturation and reflects a mostly unprotected region (red dashed line). For the same peptide, the calculated fractional deuterium uptake for the ensemble generated from the UF-α6,7B model (cyan solid line) is more consistent with the experimental data than the ensemble generated from the apo crystal structure (green solid line). This preliminary approach based on targeted local unfolding therefore confirms that in solution, the structure of apo-PhuS is more consistent with a significantly less structured conformational landscape of α6,7,8, and in particular of α6.

TICA and maximal entropy reweighting

Using the trajectories generated from the targeted UF models, we then validated the use of TICA together with HDXer, particularly in the context of large and uneven conformational landscapes. First, we tested TICA’s ability to discriminate frames with significant deviations in secondary structure using the MD simulations generated from the locally unfolded models. To that end, the ensemble from model UF-α6,7B was combined with the ensemble from the apo-PhuS crystal structure to generate a mixed ensemble, which was then subjected to TICA. TICA consistently separated the frames based on the simulation of origin (Fig. 2 D) in the first dimension of separation (TICA1). The separation is also seen after randomization of the frames in the mixed ensemble. It is worth noting that in the second TICA dimension (TICA2), distinct secondary clustering was observed for the frames originating from the UF model simulation (Fig. 2 D), possibly reflecting the more dynamic behavior of the UF-α6,7B.

Separately, HDXer was applied to the mixed ensemble using experimental HDX-MS data either from apo- or holo-PhuS as the target data. A suitable γ-value at which to analyze the reweighed ensemble was first selected from a range (0.1–9) by means of a decision plot, apparent work W_app vs. MSD. To restrict our analysis to a regime in which reweighting did not result in overfitting, a γ-value corresponding to a W_app of ∼2 kJ/mol was selected, well below the point of inflection on the decision plot (Fig. 2 E), and the final weights (Ω_f) of each frame were obtained for this value. It is worth noting that at the same W_app, reweighting the mixed ensemble to the holo-PhuS HDX-MS data achieved greater agreement than when reweighting to the apo-PhuS HDX-MS data (at W_app of 2 kJ/mol, MSD versus apo is 0.025 and MSD versus holo is 0.016). To determine the extent to which the weights were redistributed within and between each cluster, the fold change in weight (log(Ω_f/Ω_i)) of each individual frame of the mixed ensemble was mapped onto their respective TICA clusters (Fig. 2 F). When reweighting was performed against the apo-PhuS HDX-MS target data, the average log(Ω_f/Ω_i) of the cluster originating from the apo crystal structure was downweighted (Fig. 2 F, left). On the other hand, clusters originating from the UF models displayed mixed behavior. One subcluster was seen to be downweighted, whereas the other displayed the highest average log(Ω_f/Ω_i) (Fig. 2 F, left).

To further illustrate the improvement resulting from reweighting of the mixed ensemble, the fractional deuterium uptake curve at the individual peptide level was calculated from the mixed ensemble before and after reweighting by HDXer. The mixed ensemble (gray) displayed a calculated deuterium uptake behavior intermediate between that of UF-α6,7B (cyan) and the 4IMH ensemble (green) (Fig. 2 C), as expected. However, reweighting of the mixed ensemble to the apo-PhuS data resulted in greater agreement between the calculated (gold) and the experimental (red) deuterium uptake behavior. Finally, when reweighting was performed against holo-PhuS HDX-MS target data and the corresponding change in weights were mapped onto the TICA clusters (Fig. 2 F, right), the cluster containing frames generated from the apo crystal structure simulations displayed the greatest average log(Ω_f/Ω_i), consistent with the suggestion that the apo crystal structure better reflects the holo ensemble in solution than the apo conformation in solution.

Our validation so far focused on the mixture of conformations derived from the locally unfolded model UF-α6,7B. This validation process was repeated using all locally unfolded models, and the results are described in detail in the Supplemental results of the Supporting materials and in Fig. S9. Overall, probing the α6,7,8 motif by applying TICA and HDXer using locally unfolded models confirms that in solution, α6 and α7 are significantly less structured than is implied by the crystallographic form and that the apo crystal structure locally adopts a holo-like conformation. Importantly, it also demonstrates that a workflow that combines HDX-MS-based maximal entropy reweighting with dimensionality reduction by TICA can discriminate distinct structural clusters with differential distribution of reassigned weight.

ST, TICA, and HDXer

Although modeling of the α6,7,8 helices as disordered regions resulted in improved agreement of predicted HDX-MS data with experiment, the manual selection of the regions to model can be biased by the inaccuracies in the structural interpretations of the HDX-MS data. Hence, a more rigorous and objective approach to explore the conformational landscape of apo-PhuS is desirable. To this end, we used ST to achieve enhanced conformational sampling of apo-PhuS.

In ST, the temperature of the simulation is periodically increased with the idea of boosting the system up out of energy wells, allowing for a more thorough exploration of the conformational landscape. We identified a suitable protocol for ST simulations of apo-PhuS across a range of different maximal temperatures, temperature steps, and simulation length by monitoring the extent of sampling away from the crystallographic conformation and structural integrity of the protein using both local and protein-averaged C_α RMSD. At the highest tested maximal temperature of 520 K, ST runs resulted in an average C_α RMSD of 4.8 Å, indicating that such conditions allow a more expansive sampling of conformational space than conventional MD simulations yet do not lead to global unfolding (Fig. S2). For comparison, the average C_α RMSD of a 5-μs-long conventional MD simulation was 2.4 Å. Similarly, the average C_α RMSD of our previously published 500-ns-long apo-PhuS simulation was 2.3 Å (22). Under the chosen conditions of maximal temperature, six repeats of apo-PhuS ST simulations were performed and combined to make up an enhanced conformational ensemble of 300,000 frames. C_α RMSD analysis of the combined ensemble revealed an average C_α RMSD of 4.7 Å and that local C_α RMSD values do not exceed 22 Å (Fig. 3 A). This strategy was preferred over the acquisition of fewer yet longer ST runs for two reasons. First, ST runs with increased number of steps resulted in significant protein unfolding. Second, multiplying repeats of shorter ST runs may allow more efficient sampling of conformation space by multiplying the paths of conformational sampling explored (45).

Figure 3.

Ensemble refinement of WT apo-PhuS by ST, HDXer, and CD. (A) Plot of the trajectory-averaged RMSD (Å) of the C_α at each residue for the 5 μs conventional MD simulations of WT apo-PhuS (PDB: 4IMH) (black) and the combined six ST simulations of WT apo-PhuS (red). (B) The decision plot resulting from the reweighting of the combined ST ensemble to the target WT apo-PhuS HDX-MS data. The selected γ of 1 is displayed as a red dashed line. (C) Experimental CD spectra for apo-PhuS (red) and holo-PhuS (black). (D) Violin plots of the 11 significantly upweighted clusters ranked in order of average change in weight (log(Ω_f/Ω_i)). The tails represent the minimal and maximal weight in the cluster, the thick dashed lines are the mean weight, and the thin dashed lines bracket 50% of the population. The green dashed line represents the percent change in overall α-helicity (Δα_h) observed between apo- and holo-PhuS unbiased MD simulations. The blue dots represent the Δα_h between each of the 11 clusters and the holo-PhuS unbiased MD simulations, with the blue dashed-dot line representing the weighted average of the 11 blue dots. The red dotted line is the experimental Δα_h measured by CD.

A structural examination of the combined enhanced ensemble of apo-PhuS revealed that the greatest structural deviations were observed in unstructured loops, in particular the N- and C-termini and the loop connecting the N- and C-terminal domains (Fig. 3 A). However, whereas most secondary structural elements were largely stable, the motif composed of α6, α7, and α8 displayed substantial deviations (Fig. 3 A). In agreement with experimental HDX-MS and calculations with locally unfolded models, enhanced sampling by ST indicated that this structural motif was either unstructured, highly dynamic, or most prone to large conformational rearrangements. Upon visualization of the trajectories, α6 was consistently observed to be the first to lose secondary structure. Interestingly, α1 and α2 at the N-terminal end of the PhuS also displayed large fluctuations, occasionally unraveling. Although distant from the heme binding site, the dynamics of α1/α2 have been shown to be associated with heme binding by HDX-MS and have also been implicated in HemO binding by cross-linking studies (22).

Ensemble reweighting using HDXer was performed against apo-PhuS HDX-MS target data using the resulting 300,000-frame ST-enhanced ensemble. We again selected a suitable γ-value from a range (0.1–9) using a decision plot and a W_app criterion of ∼2 kJ/mol (Fig. 3 B). In parallel, TICA analysis was performed on the ST-enhanced ensemble to reduce the dimensionality of the data. A first round of analysis revealed five major clusters (Fig. S3), of which four of the five displayed significant conformational heterogeneity. Mapping the log(Ω_f/Ω_i) values onto the clusters, all clusters were downweighted on average. It is worth noting here that it is not unexpected that all the clusters appear downweighted, considering the clusters remain largely heterogeneous and their average reweighting is assessed as the average of the log transform of the fold change in weight. However, clusters 2 and 3 were, on average, less downweighted, whereas clusters 1, 4, and 5 were substantially downweighted. To obtain clusters of manageable size and conformational homogeneity, TICA dimension reduction was performed iteratively on subsequent clusters until the cutoff criteria described in the methods were reached for all clusters. A total of 221 clusters were obtained (Fig. S10; Table S2). The size of each cluster varied from 38 to 10,256 frames, and the average size was 1034 (Table S2). The average log(Ω_f/Ω_i) values resulting from HDXer were mapped onto each subcluster (Fig. S10). Table S2 shows all subclusters ranked by average log fold change in weights. Of these, the significantly upweighted subclusters were identified by calculating a z score and selecting those clusters whose z score correspond to a p-value of 0.05 or below. This yielded 11 significantly upweighted clusters with average log(Ω_f/Ω_i) values ranging from 0.43 to 1.16. The resulting clusters are plotted in a violin plot in Fig. 3 D. In 9 out of 11 clusters, structural examination revealed that α6 was entirely unfolded and α7 was in various states of unfolding and reorientation with respect to the apo crystal structure.

Conformational landscape of the heme binding pocket

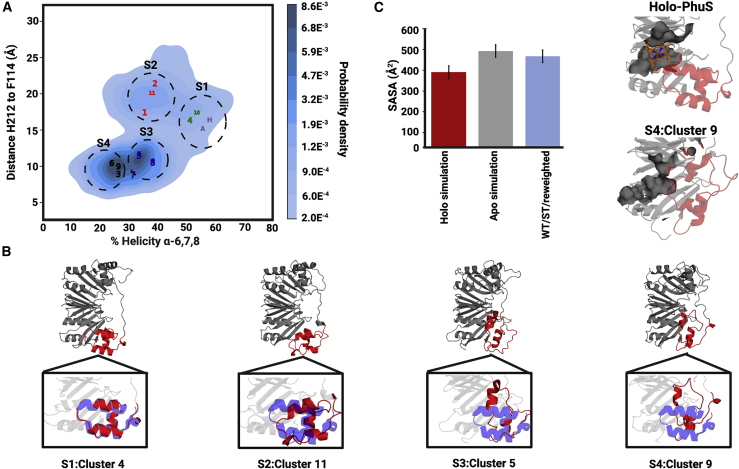
To quantitatively describe the structural dynamics of the heme binding pocket in the ensemble of the 11 upweighted clusters, the conformational landscape was mapped out using two collective variables, namely 1) the percent helicity of the α6,7,8 motif on the proximal side of the heme and 2) the distance between H212, a proximal alternate heme-coordinating residue, and Phe114, a residue on the distal side that interacts with the heme vinyl group. A KDE plot of the α6,7,8 helicity and the distance was plotted, revealing four distinct populations or substates (Fig. 4 A). To assess how individual upweighted clusters populated these substates, the average structure of each individual cluster was computed and mapped on the KDE plot and compared to the position of the apo- and holo-PhuS crystal conformation as a reference. Interestingly, two upweighted clusters (cluster 4 and 10) form a distinct substate (substate 1), which displays a crystal-structure-like conformation with α-helicity of α6,7,8 between 50 and 60% and a His212-Phe114 distance between 15 and 17 Å (Fig. 4 A). A distinct substate (substate 2) composed of three clusters (cluster 1, 2, and 11), including the top two most upweighted clusters, displays a significant decrease in α-helicity (30–40%) but a slight increase in distance across the binding pocket (∼20 Å) (Fig. 4 A). An examination of these clusters indicates that the loss of secondary structure results mostly from the unraveling of α6, and the increase in distance results from a downward tilt of α7 away from the distal side of the binding pocket (Fig. 4 B).

Figure 4.

The local conformational landscape of α6,7,8 in apo-PhuS. (A) The kernel density estimation (KDE) plot generated from the 11 significantly upweighted clusters using the distance between the C_α atoms of H212 and F114 (Å) versus the percent α-helicity of the α6,7,8 region. Numbered points indicate the average coordinate of one of the 11 significantly upweighted clusters, labeled according to its corresponding average upweighting rank (most upweighted to least upweighted). The coordinates of apo- and holo-PhuS structures are indicated as an A and an H, respectively. From the KDE plot, four substates (S1–S4) are delineated as indicated by the gray circles. The scale bar represents the probability desnsity at each point. (B) A representative structure from each of the four substates, with the close-up highlighting the α6,7,8 region (red) overlaid with that in 4IMH (purple). (C) SASA calculations of the distal and backside heme-interacting residues. Bar graphs show the SASA of the contact residues in the holo-PhuS MD simulations (red), apo-PhuS MD simulations (gray), and significantly upweighted clusters (blue) the error bars are the standared error of the SASA calculated over each frame. To the right, the corresponding residues are shown in surface rendering for a representative frame from the holo-PhuS MD simulations and from a significantly upweighted cluster in substate S4.

The remaining clusters populate two major and neighboring substates in the conformational space defined by the collective variables. The first of these, substate 3 (composed of clusters 5, 7, and 8), also displays an α-helicity of ∼30–40% largely due to the unraveling of α6. However, the His212-Phe114 distance decreases to ∼10 Å because of the translational displacement of α7 toward the distal side of the heme binding pocket (Fig. 4, A and B). Consequently, residues within helix α7, including His212, contact residues from the distal and backside β-sheet, β5, β6, β12, and β13. Finally, substate 4 (comprising clusters 3, 6, and 9) is similar to substate 3 and results from a loss in α-helical content of α7, accounting for a further ∼10% decrease in a helicity of α6,7,8 (Fig. 4, A and B). It is worth noting that substates 3 and 4 are adjacent in the collective variable space and may reflect distinct microstates within a common substate. Video S1, with substates and clusters annotated, illustrates the conformational rearrangements in α6 and α7 while the remainder of the structure remains largely intact.

Video S1. Movie of the native ensemble of apo-PhuS as refined through ST, HDXer and TICA analysis

This video shows the concatenated frames of each significantly upweighted cluster ordered by substate. This video demonstrate the heterogeneity of the apo-PhuS conformational landscape and illustrates the progressive unfolding and rearrangement of the α-678 region of apo-PhuS.

Importantly, structural alignment of these conformations with the holo-PhuS crystal structure suggests that the new contacts observed in substates 3 and 4 have minimal overlap with the heme contact surface on the distal side. To quantify the extent to which the heme-contacting residues are solvent accessible in the significantly upweighted ensemble, we computed the SASA of 10 distal and backside heme contact residues identified based on the holo-PhuS crystal structure (Leu103, Arg112, Phe114, Met257, Phe259, Lys307, Gln329, Phe331, Arg334, and Pro336) and compared it with its respective value in the apo- and holo-PhuS simulations. The SASA of these 10 residues was found to be lower in the holo-PhuS simulations by ∼80–100 Å² than in the apo-PhuS simulations or in the reweighted ensemble (Fig. 4 C, mean for holo simulation: 380.3 Å², apo simulation: 487.1 Å², ST HDXer apo-PhuS: 460.6 Å²). The similar SASA in the apo-PhuS and reweighted ensembles suggests that the heme binding site remains largely accessible to heme in the various upweighted substates (Fig. 4 C).

Overall, the conformational landscape of the heme binding pocket in the ensemble made up of all the upweighted clusters from HDXer of the ST-enhanced ensemble hints at a heterogeneous and dynamic nature of the α6,7,8 region in solution. Although this region can sample a holo-like conformation, it can also sample conformations that significantly deviate from it in terms of secondary and local tertiary structures. In particular, the analysis of the reweighted ensemble suggests that the unraveling of α6 is critical and allows the movement of α7 toward the β-sheets on the distal side of the heme binding pocket.

Circular dichroism of apo- and holo-PhuS

The experimental support for the loss in secondary structure described above comes exclusively from HDX-MS data. To provide independent verification of this observation, and in particular the loss of α-helical content, experimental CD spectra were acquired for both apo- and holo-PhuS (Fig. 3 C). The spectra were processed, and secondary structure content was deconvoluted using BeStSel. CD spectral deconvolution suggests that heme binding results in an ∼4% increase in α-helical content, an observation that is qualitatively consistent with HDX-MS data but also HDXer reweighted clusters. In parallel, theoretical CD spectra were modeled from each of the significantly upweighted clusters as well as from the apo- and holo-PhuS simulation ensembles. The resulting CD spectra were then deconvoluted into percent secondary structure using BeStSel. The difference in percent α-helical (Δα_h) content between the individual upweighted clusters and the holo-PhuS simulation was then computed along with the Δα_h between apo-PhuS and holo-PhuS simulation ensembles. These experimental and theoretical Δα_h-values were then plotted together with the violin plots displaying the log fold change in weight of each of the significantly upweighted clusters (Fig. 3 D). Whereas the Δα_h of the apo- and holo-PhuS MD simulations suggest no difference in α-helicity (−0.1%, green dashed line), 9 out of 11 clusters displayed a Δα_h of ∼−4% (blue circles), a value that is in very close agreement with the experimental Δα_h (red dotted line). The weighted average Δα_h of all 11 upweighted clusters was determined by weighting the Δα_h of each cluster with the number of frames in the cluster. The Δα_h of all 11 upweighted subclusters was calculated to be −3.7% (Fig. 3 D, blue dashed line). The greater agreement of the HDXer reweighted clusters with the experimentally derived CD data provides orthogonal corroboration that the upweighted clusters are more representative of apo-PhuS conformations in solution.

ST and HDXer of H212R

His212, located in α7, has been shown to serve as an alternate proximal coordinating residue for heme (5,23). It has also been proposed to play a role in heme transfer, in which the holo-PhuS/HemO interaction would trigger a ligand switch from His209 to His212 (23). Consistent with these proposed roles, a histidine to arginine substitution at position 212 (H212R) was seen to affect the rate of transfer of heme to HemO without inhibiting the interaction between holo-PhuS H212R and HemO (22). In addition, spectroscopic studies revealed that the apo-PhuS H212R mutant binds heme marginally faster and with slightly greater affinity (22) but binds DNA with a marginally lower binding affinity than WT apo-PhuS (18). Similarly, whereas HDX-MS of apo- and holo-PhuS H212R suggested largely similar protection upon heme binding compared with WT, subtle local differences in deuterium uptake were observed. For instance, the α6,7,8 regions of apo-PhuS H212R were observed to be slightly more protected from deuterium uptake than in WT (22). We therefore asked whether the H212R mutant exhibits a different conformational landscape for this region in silico. Initial ST runs using the optimized conditions used for WT apo-PhuS (minimal temperature of 300 K and maximal temperature of 520 K) resulted in trajectories with an average C_α RMSD of 7.0 Å, suggestive of a substantially more significant exploration of conformational space than for the WT apo-PhuS ST using the same parameters. This observation was supported by the substantially greater local C_α RMSD values (Fig. S2) and visualization of the trajectory. To reduce the conformational exploration to a level similar to that of WT PhuS, the maximal temperature was optimized over the range of 400–500 K in increments of 20 K. Trajectories with global average C_α RMSD values less than 5.0 Å and with minimal local deviations were obtained using maximal temperatures of either 420 or 440 K (Fig. S2). Subsequently, the HDXer workflow was carried out using three 5 × 10⁷ step ST simulations with a maximal temperature of 420 K and three 5 × 10⁷ step ST simulations with a maximal temperature of 440 K. The resulting six trajectories were combined, resulting in an ensemble comprising 300,000 frames and an average C_α RMSD of 3.8 Å. As observed for WT apo-PhuS, the local C_α RMSD reveals that the most significant deviations in this data set are localized to the α6,7,8 motif (Fig. 5 A).

Maximal entropy reweighting against HDX-MS data previously measured for apo-PhuS H212R (22) was performed using the resulting ST ensemble. Again, γ-values from 0.1 to 9 were explored, and an optimal γ-value of 0.9 was selected via the decision plot method (Fig. 5 B). TICA clustering, which was performed using the same endpoint criteria as for PhuS WT, yielded 183 clusters (Fig. S11; Table S3) with sizes varying from 316 to 11,674, and an average cluster size of 1578 conformers. Of those 183 clusters, seven were found to be significantly upweighted (Fig. 5 C). Like WT apo-PhuS, experimental CD (Fig. S12) and modeled CD of the significantly upweighted clusters display a good agreement (Fig. 5 C). Here again, an examination of the clusters suggested that the loss in secondary structure is characterized by a loss in α-helicity in α6 and α7. It is noteworthy that both experimental and calculated differences in percent helicity are slightly lower for H212R PhuS than for WT (experimental Δα_h H212R: −2.9, experimental Δα_h WT: −4.6, calculated Δα_h H212R: 2.2, calculated Δα_h WT: 3.7); this agrees with HDX-MS data that suggest α6,7,8 is marginally yet significantly more protected in H212R than WT (22).

Mapping the same collective variables as for WT highlights the overall similarity, but also some differences, between the conformational landscapes of the heme binding pocket extracted for WT versus H212R apo-PhuS (Fig. 5 D). Just as for WT apo-PhuS, the upweighted clusters populate four distinct substates. Substate 1 with two clusters (clusters 4 and 6) populates a crystal-like conformational substate characterized by an Arg212-Phe114 distance of ∼15 Å and α-helicity of α6,7,8 between 45 and 60%. However, unlike WT apo-PhuS, H212R apo-PhuS does not populate any substates with increased distance across the heme binding pocket. Instead, cluster 1 populates a substate (substate 2) with a decreased Arg212-Phe114 distance of ∼12 Å. Interestingly, in substate 2, α6 remains structured, as reflected by the high α-helicity (∼40%). As in WT PhuS, helix α7 undergoes a similar downward tilt and translational displacement that places its C-terminal end close to β5, β6, and β12. Finally, clusters 2 and 3 and clusters 5 and 7 populate two additional substates, substates 3 and 4, respectively. As in WT PhuS, these substates are characterized by reduced α-helicity in α6,7,8 at ∼20–30%. Again, an examination of these clusters indicates that the loss of α-helicity results from the loss of secondary structure of α6. However, the distance across the heme binding pocket remains at an average of 12–13 Å, whereas it decreased to an average of ∼10 Å in WT PhuS. Interestingly, Arg212 from α7 is seen to engage in an electrostatic interaction with Glu318 (Fig. 5 D, inset) in all substates except substate 1, the crystal-like conformation. This electrostatic interaction can potentially lock α7 and hinder a complete displacement of α7 toward the distal side, as observed in WT PhuS.

Overall, the application of our workflow incorporating ST-enhanced sampling and HDXer to the H212R mutant recapitulates most of the features of the conformational landscape described for WT PhuS, including the unraveling of α6 and the tilt and displacement of α7 toward the distal side of the heme binding pocket. However, subtle differences are nevertheless observed. Notably, H212R displays a more significant population of the conformation in which α6 maintains secondary structure (substate 2) and the displacement of α7 appears to be hindered by an electrostatic interaction between Arg212 and Glu318 that is absent in WT PhuS.

Discussion

The role of PhuS as a regulator of exogenous heme flux to HemO for degradation has been extensively investigated both in vitro and in vivo (17,22,23,46, 47, 48). Biochemical and biophysical studies have shown that apo-PhuS does not bind HemO, whereas heme binding drives the interaction of PhuS with HemO (23) (Fig. 6 A). In turn, it has been proposed that HemO binding to holo-PhuS triggers a ligand switch from His209 to His212 that then facilitates the transfer of heme from its binding site in holo-PhuS toward the HemO active site, which has been modeled to be >20 Å away by cross-linking and docking studies (22) (Fig. 6). More recently, the transcriptional regulatory role of PhuS was revealed by DNA binding studies (18). In contrast to its metabolic role, it is in the apo form that PhuS binds DNA in the sRNA PrrF/H promoter region, whereas heme binding disrupts DNA binding. This observation suggests that PhuS interactions with HemO and DNA are mutually exclusive, pointing to a heme-dependent conformational mechanism for the integration of its metabolic heme flux role and its transcriptional role. Structurally, these data suggest a complex conformational landscape of PhuS in which heme binding results in a large rearrangement that allows HemO binding but hinders DNA binding. Such a large rearrangement is supported by numerous solution-based biophysical measurements. For example, analytical ultracentrifugation (23) and CD of apo- and holo-PhuS have reported significant differences in sedimentation coefficient distributions and secondary structure, respectively. These changes have been localized, using limited trypsin digest and HDX-MS (22), to the C-terminal unit (or domain) and in particular to motif α6,7,8, for which increased trypsinization and large increases in deuterium uptake were observed in the apo form. This large rearrangement is also further corroborated by the reported slow kinetics of heme binding, measured to be on the millisecond timescale by spectroscopic studies. Stopped-flow ultraviolet-visible spectroscopy and rapid freeze quench resonance Raman spectroscopy suggested that heme binding is initially driven by noncoordinating π-stacking and hydrophobic interactions with the distal β-sheets followed by a slow (millisecond timescale) conformational rearrangement in the C-terminal domain that leads to the coordination of the heme iron (22). In contrast, the high similarity of the crystal structures of apo- and holo-PhuS does not support such large rearrangements, and MD simulations of those structures for up to 700 ns (and extended to 5 μs in this study) have not revealed conformational changes consistent with the HDX-MS data (22). However, the slow timescale of the conformational change reported by the spectroscopic studies may be prohibitively slow for MD simulations without enhanced sampling techniques.

In this study, we have implemented and applied a workflow that combines enhanced sampling MD simulations to overcome sampling limitations with HDX-MS-based maximal entropy reweighting to model the conformational landscape of α6,7,8 in apo-PhuS. The resulting ensemble depicts a complex conformational landscape populated both by crystal-like conformations and conformations with large deviations or rearrangements. These rearrangements are characterized by the unraveling of α6, and the tilt, partial unfolding, and progressive displacement of α7 toward β5-β6 of the distal side β-sheet. This ensemble is consistent with orthogonal experimental measurements performed using CD as well as with previous in-solution biophysical data. For instance, although α6 does not contact the heme in the structures, HDX-MS data have revealed that it is the site of the greatest relative decrease in deuterium uptake upon heme binding. Accordingly, it was found to be unstructured in most clusters extracted by our workflow. Furthermore, structural features of the rearrangements are consistent with the model previously proposed for heme binding (22). Indeed, the loss in secondary structure in α6 allows the tilt and displacement of α7, which can then interact with residues in β-strands and loops belonging to the distal (β5-β6 and β11-β12) and backside (β16) of the heme binding cleft. However, structural alignments of these rearranged conformers with the holo-PhuS structure indicate that these interactions do not overlap with the contact surface of the heme porphyrin ring. In fact, SASA calculations for heme contact residues across the upweighted clusters indicate that the heme binding site on the distal and backside β-sheet is similarly solvent accessible in the rearranged conformations as in the crystallographic apo-PhuS conformation. Thus, the rearrangements observed in the modeled conformational landscape would not occlude access of heme to the binding site for the initial binding step and are consistent with the model of heme binding to distal and backside β sheets initially with noncoordinating interactions, followed by conformational rearrangements of α6,7,8 to achieve the crystallographic conformation for proximal coordination of the heme.

The modeled conformational landscape of α6,7,8 also provides some structural insights into the mechanism of transfer of heme to the active site of HemO. This transfer was proposed to involve an “exit from the side” mechanism, based on the holo-PhuS/HemO complex modeled by cross-linking mass spectrometry and docking (22). In this model, the heme binding site in HemO is located >30 Å from the heme in holo-PhuS. In such a case, the heme must be translocated across a significant distance, and the structural mechanism of this translocation remained unclear. The physical transport of heme could potentially be mediated by multiple ligand-switch events with limited conformational changes. However, spectroscopic studies of heme transfer from PhuS to HemO have only reported one change in the spin state of heme, from six-coordinated low spin to six-coordinate high spin (48). Alternatively, heme translocation might involve a large conformational change with a limited number of ligand switches. A comparison of representative structures from substates 3 and 4 with the conformation of holo-PhuS in the context of the PhuS-HemO model shows that His209 and His212 are located along the path of side exit between the two heme binding sites (Fig. 6). Indeed, when comparing average structures from clusters 3, 6, and 9 from substate 4 to the holo-PhuS conformation, the α-carbons of His209 and His212 were found to be ∼9 and ∼4 Å closer, respectively, to the iron center of the heme positioned in the HemO active site. This shift is also observed in the average structures of clusters 5, 7, and 8 from substate 3, in which the α-carbon of His209 and His212 are ∼8 and ∼3.0 Å closer, respectively. Thus, the large conformational rearrangements exhibited in the reweighted α6,7,8 landscape may reflect mechanistically important motions involved in the translocation of heme to HemO. However, the path between the heme binding sites of PhuS and HemO is occluded in these conformations because of the new contacts between the displaced α7 and the distal and backside β-sheet (Fig. S13). As such, substates 3 and 4 seem unlikely to represent an intermediate or transition state. Rather, it is more likely that these conformations reflect a state of PhuS after heme transfer and dissociation from HemO: a state that would be DNA binding competent but would readily undergo conformational changes into the HemO binding competent state upon heme binding to the distal and back side β-sheets. Regardless, the complete understanding of the biophysical and mechanistic importance of these conformations will require further investigation.

The application of the workflow to the H212R mutant, which is impaired in heme transfer to HemO, provided further corroboration of the mechanism of heme binding and transfer. Solution-based studies have pointed to small but significant differences in apo-H212R, including protection from deuterium exchange in α6,7,8, when compared to WT apo-PhuS (22). In addition, spectroscopic studies have revealed that the coordination step after the initial heme binding step is also slightly faster than in WT PhuS (22). The interpretation of these findings was that the slightly more structured nature of apo-H212R α6,7,8 leads to a faster rearrangement upon binding. Finally, with a K_d of 90 nM, H212R apo-PhuS was found to bind the PrrF1 promoter sequence with slightly lower affinity than WT apo-PhuS (K_d of 64 nM) (18). Overall, the solution-based data suggested that the conformational landscape of H212R apo-PhuS largely resembles that of WT apo-PhuS but with some subtle differences characterized by a more structured nature. When compared to WT, the reweighted conformational landscape of the H212R mutant reflects this overall similarity but also the subtle yet significant differences in structure. Indeed, the unraveling of α6 and displacement of α7 is observed in H212R as it is in WT. However, a distinct population (substate 2) in which α6 is structured is upweighted in H212R but absent in WT PhuS. In addition, the displacement of α7 is less pronounced across the entire upweighted ensemble. These differences are assumed to be due to an electrostatic interaction formed during ST runs between Arg212 and Glu318, which is absent in WT (Fig. 5 D, inset). SASA calculations suggest that the distal or backside heme binding site is accessible to heme with an average increase in SASA of 128 Å compared with the holo-PhuS simulation. Structural examination also suggests that the reweighted conformational landscape is consistent with a faster coordination step, as reported by spectroscopic approaches. This is supported by a decreased displacement of His209 away from its holo crystallographic conformation in the upweighted ensembles of H212R mutant compared with that of the WT protein, as evidenced by the average C_α RMSD (H212R C_α RMSD_His209 of 3.5 Å vs. WT C_α RMSD_H209 of 4.9 Å).

The work performed in this study aimed at modeling conformational landscapes by integrating MD simulations with HDX-MS through HDXer. The HDXer approach belongs to a growing trend in computational approaches to leverage experimental methods for broader ensemble refinement purposes, including fluorescence resonance energy transfer (FRET), double electron-electron resonance (DEER), small-angle X-ray scattering (SAXS), and cross-linking mass spectrometry, among others (49, 50, 51). HDX-MS is advantageous from this perspective because it provides ensemble-averaged, time-resolved, peptide-level resolution structural observables that capture local conformational dynamics. In addition, typical HDX-MS data are information rich, with simultaneous reporting on potentially as many observables as there are amide hydrogens in a protein. As such, HDX-MS-based ensemble refinement could be well suited to modeling both global and local conformational heterogeneity of a protein’s structural ensemble in solution. Such an approach is particularly valuable if typical high-resolution structural determination approaches and subsequent conventional MD simulations are suspected of undercharacterizing the complexity of the ensemble.

In this study, the use of HDXer allowed for the modeling of a native ensemble with large conformational heterogeneity involving local changes in secondary structure, which are thought to be responsible for a significant portion of the protection from deuterium uptake. In such cases, adequate sampling of the conformational landscape is critical, and coupling HDXer with a modeling strategy or, preferably, an untargeted enhanced sampling strategy is necessary. Although the enhanced sampling method we chose for this work was ST, the same overall approach is compatible with other enhanced sampling methods. Replica exchange has long been one of the most popular unguided enhanced sampling techniques. For a system the size of PhuS in explicit solvent, the number of replicas required for efficient sampling would necessitate large computational resources, but replica exchange could successfully be used in this workflow. Accelerated MD and Gaussian accelerated MD are also potential methods that could be used. Regardless, HDXer was also able to distinguish subtle differences in conformational landscapes characterized by subtle differences in deuterium uptake arising from the H212R substitution. Therefore, this study demonstrates the applicability of HDX-MS-based maximal entropy reweighting as an ensemble refinement approach to study both large- and small-scale heterogeneity or perturbations, potentially including protein folding and unfolding, protein-protein interactions, protein-ligand interactions, or amino acid substitutions. In the case of PhuS, ongoing efforts will focus on using reweighted conformational landscapes for structure-based drug design.

Author contributions

K.C.K., R.T.B., P.L.W., L.R.F., A.W., and D.J.D. conceived the work. K.C.K. and D.J.D. designed the research and developed the methodology. K.C.K. and A.K.S. performed the calculations, K.C.K., R.T.B., and D.J.D. analyzed the calculations. T.W. and A.W. performed and analyzed the circular dichroism. K.C.K., T.W., A.K.S., R.T.B., P.L.W., L.R.F., A.W., and D.J.D. wrote and revised the manuscript.

Editor: Lucie Delemotte.