Abstract
Loop extrusion convincingly describes how certain structural maintenance of chromosome (SMC) proteins mediate the formation of large DNA loops. Yet most of the existing computational models cannot reconcile recent in vitro observations showing that condensins can traverse each other, bypass large roadblocks, and perform steps longer than their own size. To fill this gap, we propose a three-dimensional (3D) “trans-grabbing” model for loop extrusion, which not only reproduces the experimental features of loop extrusion by one SMC complex but also predicts the formation of so-called Z-loops via the interaction of two or more SMCs extruding along the same DNA substrate. By performing molecular dynamics simulations of this model, we discover that the experimentally observed asymmetry in the different types of Z-loops is a natural consequence of the DNA tethering in vitro. Intriguingly, our model predicts this bias to disappear in the absence of tethering and a third type of Z-loop, which has not yet been identified in experiments, to appear. Our model naturally explains roadblock bypassing and the appearance of steps larger than the SMC size as a consequence of non-contiguous DNA grabbing. Finally, this study is the first, to our knowledge, to address how Z-loops and bypassing might occur in a way that is broadly consistent with existing cis-only 1D loop extrusion models.
Significance
Understanding how structural maintenance of chromosome (SMC) proteins form DNA loops is an outstanding challenge. Models that assume cis-only extrusion cannot recapitulate recent in vitro observations such as Z-loops. To address this, we propose an interstrand loop extrusion model that predicts the formation of Z-loops and explains the observed asymmetry in the appearance of different Z-loops as due to tethering and tension-mediated topology. Intriguingly, it predicts a new type of Z-loop not identified in experiments and rationalizes observations of roadblock bypassing and large step sizes. Our model paves the way for a new class of 3D trans-grabbing non-topological loop extrusion models.
Introduction
Cells exert an impressive control over genome folding to confine long chromosomes inside the small space of a nucleus. Structural maintenance of chromosome (SMC) proteins are now well known to fundamentally contribute to the large-scale folding of DNA in vivo (1). Cohesin and condensin, ring-shaped SMC protein complexes, can bring together two DNA segments and form DNA loops (2, 3, 4). Current evidence shows that yeast condensin (5), human cohesin (6, 7), human condensin (8), and both cohesin and condensins in Xenopus egg extracts (9) processively extrude loops in vitro. At the same time, bacterial SMCs also appear to extrude loops in vivo (10, 11, 12). On the other hand, currently there is no direct evidence that yeast cohesin can extrude loops in vitro (13, 14, 15), although there is indirect evidence for translocation of yeast cohesin in vivo (16, 17, 18).
The formation and growth of long DNA loops is well described by the loop extrusion model (2, 19, 20, 21, 22). In this popular framework, loop extrusion factors (LEFs) such as condensin (5) or cohesin (6, 7) bind DNA and stem a short loop by grabbing two contiguous DNA segments; they then move along the DNA until they either unbind or stop (e.g., in vivo, when they encounter a zinc-finger protein CCCTC binding factor (23, 24, 25)). Evidence and models for entropic diffusion (13, 26, 27, 28), Brownian ratchet (26, 29), or bridging (30) have also been reported.
Although loop extrusion convincingly describes the principles behind the formation and growth of DNA loops, the mechanical details of how SMC protein complexes extrude loops are still debated. Proposed loop extrusion models include the pumping (31, 32), scrunching (33, 34), tethered inchworm (35), and safety belt (36) mixed with power stroke (37), all inspired by the shape and structure of the SMC complexes (32, 38, 39).
Most of the previously proposed models have a common feature: they assume the extrusion to happen in cis, i.e., by reeling in contiguous DNA contour length. An exception to these is the diffusion-capture model (41), which posits that DNA-bound SMCs can dimerize and form stable loops when they meet in trans by three-dimensional (3D) diffusion. While both classes of models compare favorably well with experiments in vivo (42, 43), they cannot explain some recent observations in vitro. For instance, cis loop extrusion with topological entrapment cannot explain the formation of so-called Z-loops (40), i.e., non-trivial positioning of SMCs yielding cross-looping topologies (Fig. 1 B), nor the bypassing of roadblocks several times the size of condensin (44), nor the fact that condensin single steps can reel in DNA longer than its own size (45). At the same time, loop-capture mechanisms (41, 43) cannot explain the observed processive extrusion of condensin on tethered DNA (5).
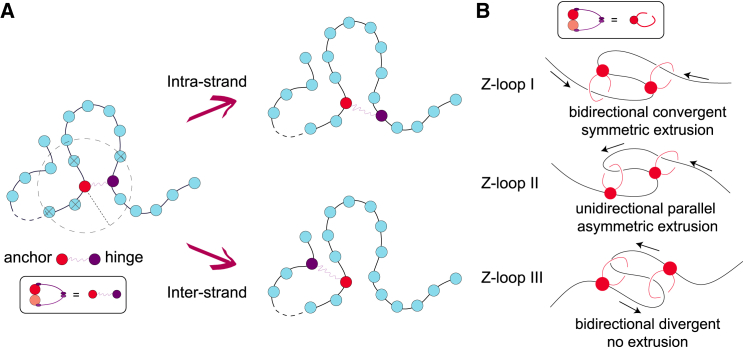
Figure 1.
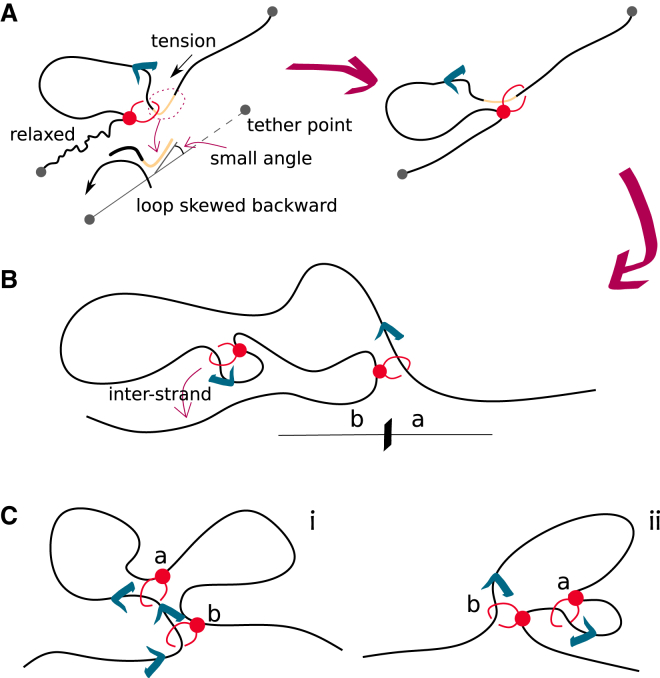
A three-dimensional (3D) or “trans-grabbing” model for loop extrusion. (A) We model LEFs as springs connecting two polymer beads; one of these beads is denoted as the “anchor” that does not move while the other is denoted as the “hinge” that can jump to 3D proximal but non-contiguous polymer segments. By updating the position of the hinge via a mix of intra- and interstrand moves, the system is driven to form Z-loops. (B) We identify three types of Z-loops: Z-loop I () has both hinges pointing outward, thus yielding symmetric extrusion; Z-loop II () has both hinges pointing in the same direction and thus yields asymmetric extrusion; finally, Z-loop III () has both hinges pointing inward and displays no net extrusion. Only and were observed in experiments (40).
To fill this gap, and motivated by the fact that cohesin's main role is to bridge sister chromatids in vivo (which cannot be achieved via a pure cis-looping mechanism) (46, 47, 48), here we propose a trans-grabbing model for loop extrusion. By performing molecular dynamics (MD) simulations, we discover that Z-loops are a natural consequence of introducing occasional interstrand capture in a standard loop extrusion model (Fig. 1). Furthermore, we find that the experimentally observed bias for Z-loop I over Z-loop II (Fig. 1 B) is a consequence of DNA tethering of the in vitro assay in (40). Finally, we find that under certain conditions, i.e., when SMCs are initiated in series and in a convergent orientation, a third type of (non-growing) Z-loop, which we dub , appears.
We note that the novelty of our model is that it is the first to explain the formation of Z-loops in a natural way that is broadly consistent with existing models of loop extrusion. Indeed, while models accounting for non-contiguous reeling of DNA (29, 34) or extending the original LEF model to allow bypassing have been proposed (10, 11), they have not extensively explored the topological issues arising from the interaction of multiple loop extruding factors on the same DNA substrate, nor have they addressed the abundance and evolution of different Z-loop topologies.
Finally, our model also naturally rationalizes recent observations of SMCs bypassing large roadblocks in vitro (44) and in vivo (11), and performing steps larger than their own size (45). Our model—in agreement with these recent findings—supports the view that SMCs may perform non-topological loop extrusion composed by discrete jumps in which SMCs grab a non-contiguous DNA segment, in turn reeling in the subtended contour.
Materials and methods
To simulate loop extrusion on DNA, we employ a well-established coarse-grained model (19, 49). We perform MD simulations of a segment of torsionally relaxed DNA modeled as bead-and-spring polymer made of beads of size basepairs. Consecutive beads are connected by finite-extension-nonlinear-elastic (FENE) bonds, i.e.,
| (1) |
where and . Beads interact with each other via pure excluded volume, via a Weeks-Chandler-Andersen (WCA) potential,
| (2) |
where r denotes the separation between the bead centers and . The stiffness of DNA is accounted for by introducing a Kratky-Porod potential acting on triplets of consecutive beads along the polymer,
| (3) |
where is the position of ith bead, and and are, respectively, the separation vector between beads i and j and its modulus. We set to achieve the known persistence length of DNA nm (50). We use the LAMMPS (51) engine to integrate the equations of motion with implicit solvent (Langevin dynamics) with friction (where the Brownian time is ) being related to the thermal noise amplitude via the fluctuation-dissipation theorem. Finally, the integration step size is .
Implementation of the 3D loop extrusion model
In this section we explain in detail our interstrand loop extrusion model. In essence, we generalize the standard cis loop extrusion model (19, 20) by introducing the possibility of trans (3D) moves in which LEFs can grab a DNA segment that is proximal in 3D.
Each SMC is modeled as a spring connecting two DNA beads (segments), and is described by the harmonic potential
| (4) |
where is the resting distance between the centers of the two beads and is the elastic constant. The rest length is chosen to be nm, comparable with the minimum size of condensin. We then fix one of the two ends of the spring (the anchor) for the duration of the simulation, whereas the other (the hinge) is periodically updated as follows.
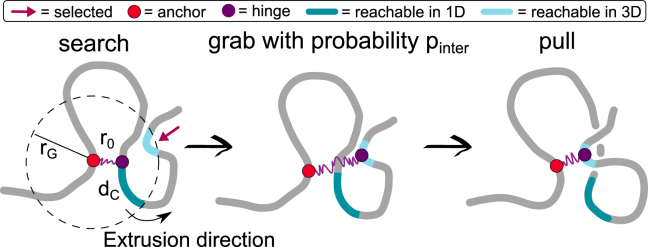
First, after a LEF is loaded with its anchor at bead l and hinge at bead m, we randomly choose an extrusion direction. Then, at each extrusion step, all the beads within a certain “grabbing” Euclidean distance nm (smaller than the size of condensin) from the anchor l are identified (Fig. 2). Out of those 3D proximal beads, we select two groups: the first contains all the “cis” beads that are within five beads from the hinge m and to its left or its right (according to the extrusion direction). The second group contains the beads farther than in one dimension (1D) from both the hinge m and the anchor l. In this way we distinguish beads that are close in 3D but far in 1D and at the same time disallow back-steps, which are only rarely seen in experiments. After the creation of these two groups, we randomly select one bead, n, from either the first (1D) group or, if not empty, from the second (3D) group, with a small probability . Finally, we update the position of the LEF by connecting l to the new selected bead n (and remove the bond between l and m). In the case that the move is in 3D, we select a new extrusion direction at random as we assume that the SMCs cannot distinguish forward/backward on a newly grabbed DNA segment. Finally, we note that setting and maps our model back to standard cis-only loop extrusion models (19).
Figure 2.
Implementation of 3D extrusion. A LEF is modeled as a spring connecting two non-contiguous beads and with rest length . Every 8000 simulations steps ( s), we attempt to move the LEF by gathering the 3D neighbors within a Euclidean distance from the anchor. Of these, the ones that fall within the nearest neighbors are classified as 1D beads. A random bead from the list of 3D “trans” neighbors is selected with probability (in supporting material we show results with a different choice of this parameter) and a random bead from the 1D list otherwise. Finally, we update the beads connected by the spring and evolve the equations of motion of the beads so that the spring relaxes to its equilibrium rest length . We note that setting and maps back to the standard cis-only loop extrusion model (19, 21).
We implement this algorithm in LAMMPS (51) by loading it as an external library within a C++ program. Every 8000 integration steps (or with s), we extract the coordinates of all the beads and loop over the positions of LEFs. The bonds are then updated using the “delete bond” and “create bond” commands to connect new pairs of beads as described above. Sample codes can be found at https://git.ecdf.ed.ac.uk/dmichiel/translefs.
Results
Calibration of the model using one LEF
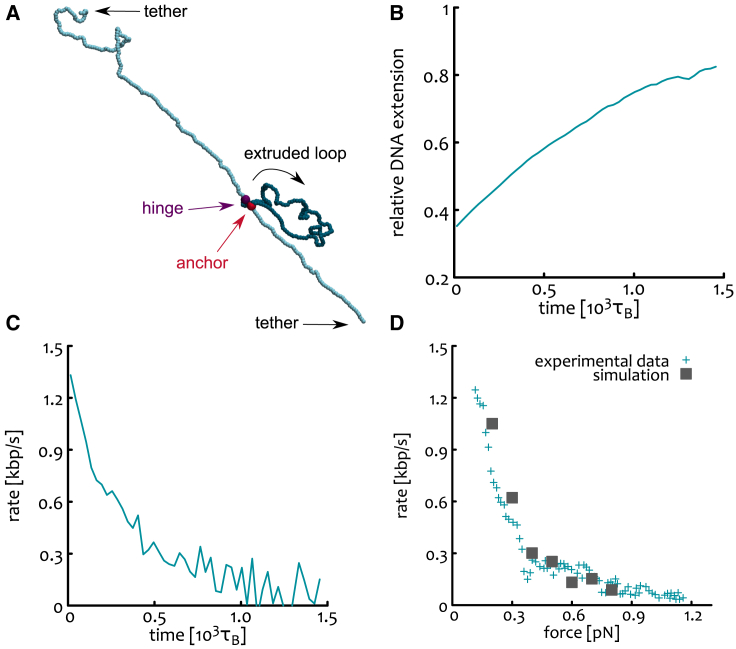
We first calibrate our model on doubly tethered DNA beads long loaded with one (asymmetric) LEF (Fig. 3 A). Each initial conformation is obtained by equilibrating for a long time () a polymer with the constraint that the Euclidean distance between its two ends is equal to one-third of its total length when pulled taut. This mimics the experimental setup in (5) and is practically implemented by applying a force to the chain ends until they reach a distance of in a presimulation step and then by equilibrating the chain with its ends fixed in space. After equilibration, an LEF is loaded either at bead and with positive extrusion direction (i.e., the moving side of the spring with progressively larger bead index) or at bead and with negative extrusion direction. In this way, we prevent the extrusion process to end because of the LEF reaching the end of the polymer.
Figure 3.
(A) MD simulations of doubly tethered DNA (cyan) loaded with one asymmetric LEF (violet and red) extruding a loop (blue). (B) Mean relative DNA extension as a function of time. The relative extension is defined as the end-to-end distance divided by the difference between the total length of the DNA and the length of the extruded loop. (C) Extrusion rate as a function of time. (D) Extrusion rate as a function of tension: comparison between our simulations (dark-gray squares) and experimental data from (5) (cyan “+”).
Importantly, in our simulations the extrusion rate is not a fixed parameter but depends on the tension experienced by the polymer during the loop extrusion as this enters in competition with the tethered ends. For instance, in Fig. 3 B, one can appreciate that the relative DNA extension, i.e., the ratio between the end-to-end distance () and the difference of DNA length (N) and extruded loop length (), or , grows in time because the difference becomes smaller and is kept constant. At large times, when the loop extrusion step is balanced by the tension on the DNA, one expects to see a plateau in the relative extension. This stalling is due to the fact that in the LEF update rule, new segments are searched within a radius from the LEF anchor point. If the LEF bond connecting anchor and hinge is (note that nm), segments outside the extruded loop do not fall within the grabbing range of the LEFs. In other words, the tension along the polymer leads to stretching of the LEF bond and then to stalling via the depletion of available cis (and trans) segments that can be grabbed.
The extrusion rate is thus computed from the simulations by taking the (discrete) time derivative of the length of the extruded loop as in experiments (Fig. 3 C), i.e., . We then plot the rate as a function of the tension by converting the extension of the polymer to force as done in (5), i.e., by using a tabulated conversion.
The free parameters of the model, i.e., LEF update time , LEF spring stiffness k, and Brownian time were progressively tuned to closely match the experimental data in (5). With this calibration we thus lock in a combination of these parameters that match experimental data on single LEF extrusion on tethered DNA and leave the trans-grabbing (or interstrand) parameter free to be explored when studying multiple LEFs, which is the main aim of this work. Fig. 3 D shows the rate-force curve we ultimately obtain by simulating 100 DNA molecules with the optimal parameters (see supporting material for other choices of our free parameters).
Modeling interactions of two LEFs
After having calibrated our model using one LEF to match the experimentally observed behavior, we now perform MD simulations of two LEFs along the same DNA substrate (Fig. 4, H and I). To align with the experimental setup in (40), we simulate doubly tethered polymers beads long and choose to load the LEFs in a nested state, as typically observed in experiments. This is done by (1) loading the first LEF immediately after equilibration in a random position and with random extrusion direction and then (2) by attempting to load a second LEF inside the loop formed by the first some time after the simulation starts. We can distinguish between two further cases: in one half of the simulations, the two LEFs are nested and extruding in the same direction (Fig. 4 F) while in the second half the LEFs have opposite extrusion direction (Fig. 4 G).
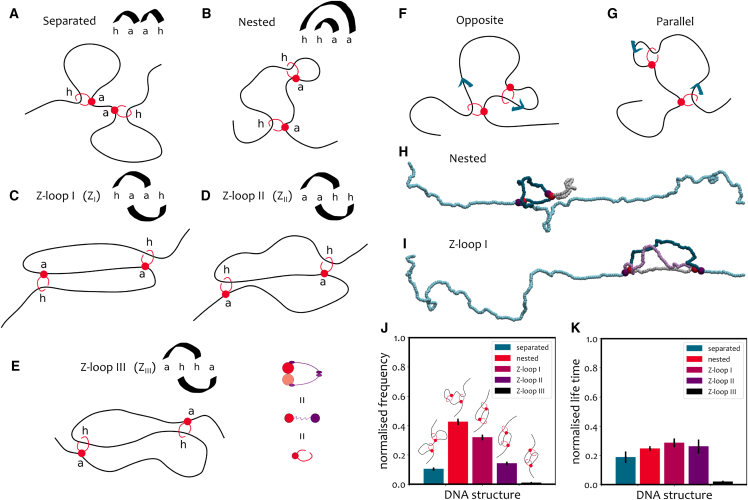
Figure 4.
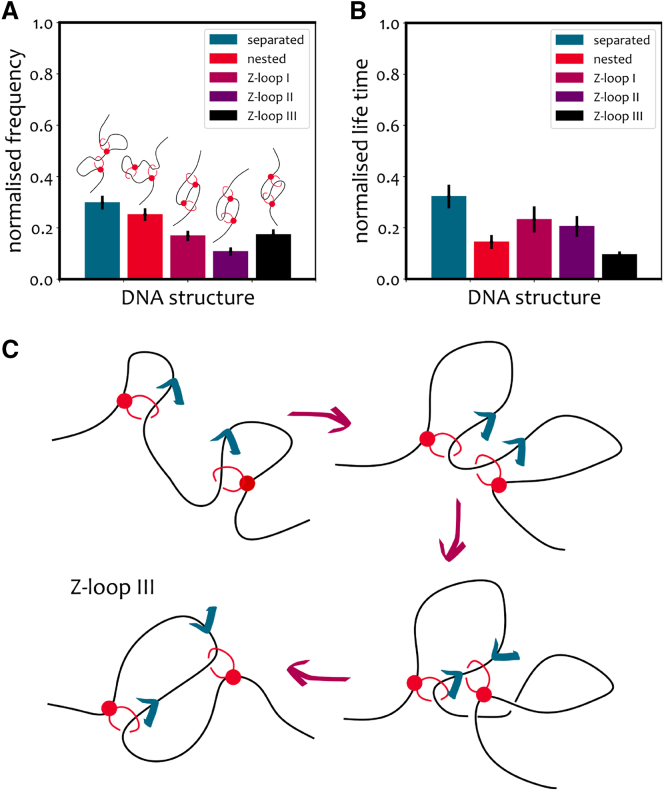
(A–E) A summary of the five Z-loop topologies observed in simulations with two LEFs (the anchored bead “a” and the moving hinge “h”): (A) separated; (B) nested; (C) Z-loop I (this structure grows as DNA is reeled in from the outward-facing hinges); (D) Z-loop II (only one of the boundaries moves with respect to the structure); (E) Z-loop III (both boundaries of the structure are fixed as the anchors are facing inward). See also Fig. S5 in the supporting material for a stepwie scheme on the formation of these loop topologies. (F and G) Schematic illustration of the initial configuration of MD simulations with two nested LEFs. When the second LEF is loaded, its extrusion direction either opposes (F) or copies (G) the extrusion direction of the first one. Blue arrows indicate in which direction DNA is reeled inside a loop. (H and I) MD simulations of doubly tethered DNA loaded with two LEFs. (H) When the LEFs are nested, one of the loops (gray) extruded by the two protein complexes is part of the other loop (gray + blue). (I) Two condensins can fold a Z-loop (type I in the figure). One of the three segments (gray) involved in a Z-loop is shared between the loops extruded by the two condensins (gray + blue and gray + lilac). (J and K) Frequency (J) and survival times (K) of topological structures in simulations of two nested LEFs on doubly tethered DNA.
To check the evolution of the polymer topology over time, we reconstruct the position of the ends of the LEFs and draw a corresponding arch diagram for each observed configuration. As shown in Fig. 4, A–E, we observe separated, nested, and three types of Z-loop topologies. It should be noted that all these structures are non-equilibrium topologies, since the LEFs are unidirectionally moving along the DNA and thus displaying an absorbing non-extruding state at large times. We take our simulations’ total runtime to be typically shorter than the time it takes for the LEFs to reach the absorbing state. Additionally, the same topology can appear more than once for each simulation: it can form, undo, and eventually form again at a later time. A stepwise scheme of loop formation and disassembly is reported in Fig. S5. We stress that it is not the loops themselves that are undone (our LEFs are never unloaded from the substrate), but the Z-loop topologies formed by the interaction of the two loops that evolve in time.
To best compare with experiments, we align to the method of (40) and record (1) the number of times we observe a given loop topology and (2) its relative survival time over a fixed total simulation runtime. Fixing a total runtime is important, as the final states are absorbing and would therefore dominate the spectrum of topologies in the very large time limit.
In Fig. 4, J and K we show the relative frequency and survival times of the five different topologies. As one can observe, while the nested state is the most likely topology, Z-loops I and II are also significant. Remarkably, we observe a spontaneous asymmetry in topologies, whereby Z-loop I () is more than twice as likely to form than Z-loop II (), i.e., . This asymmetry emerges naturally, without imposing any bias favoring the formation of a particular Z-loop type. Additionally, it is in good agreement with experiments, as they report (40). We find that this asymmetry is assay and tension dependent, and that singly tethered DNA displays a far weaker bias in the ratio of ZI/ZII (see next section).
We finally highlight that while we observe Z-loop III () in simulations (Fig. 4 E), they have not been detected in experiments (40). Accordingly, the frequency with which they appear in our simulations is tens of times smaller than in the other Z-loop topologies. Again, we predict that this result is assay dependent (see below).
Z-loop asymmetry is due to tension and assay geometry
We can think of at least two reasons that may bias the formation of over . As sketched in Fig. 5, because of the geometry of the doubly tethered assay, more frequent intergrabbing events are expected to occur on the side of the anchor of the outermost LEF (labeled b in Fig. 5, A and B). This is because the extrusion is unidirectional and the DNA, being tethered, has a preferred structural direction in the 3D space (the line passing through the two fixed ends). Each time a loop extruded by the external LEF grows, a new segment of DNA is brought inside the loop. Since the DNA is tethered, and especially when the relative DNA extension is close to 1, the angle between this newly added segment and the geometric line passing through the two ends of the DNA is small (Fig. 5 A).
Figure 5.
Asymmetry in the frequency of and on DNA with two tethered ends. (A) At each extrusion step, the segment of DNA (cream) on the intake side is likely to be pulled taut and roughly parallel to the line connecting the two ends of the tethered DNA. The anchor-side part is instead relaxed as no tension is applied. (B) This effective alignment biases the extruded loop to fold over the anchor side of the most external LEF. In turn, this favors the nested LEF to grab segments of DNA from over the anchor side (b) rather than over the hinge side (a) (see Fig. 3A). (C) (i) If the two nested LEFs are extruding in the same direction and the internal LEF, labeled a, approaches the other one (b), a is formed when a's hinge jumps other b's hinge. When the jump is attempted, however, b's hinge is running away from a's hinge. (ii) If instead the LEFs are extruding in opposite directions, a is formed when a's hinge jumps the other b's anchor, which does not move. Move (ii) (yielding ) is more likely to succeed due to the slower dynamics of the polymer near an LEF anchor.
As shown in Fig. 5 A (see also snapshots in Figs. 3 A and 4 H), as the extrusion goes on, the geometry of the extruding complexes biases the extruded DNA loop to fold over the anchor (where there is no force applied by the LEF). As a consequence, due to closer proximity, it then becomes easier for the nested LEF to grab a segment behind the anchor of the external LEF (side b), in turn forming a loop (Fig. 5 B), rather than grabbing a segment over the hinge of the other LEF (side a) to eventually form a loop.
Moreover, when two nested LEFs are both extruding in the same direction along the DNA, one of them is “running away” from the other. As shown in Fig. 5 C, this hinders the hinge of the nested LEF to jump over the other when folding a . This suggests that directionality of LEFs also plays a role in the balance of Z-loop topologies (see also supporting material).
Singly versus doubly tethered DNA
We hypothesize that the tethering of the DNA may bias the local conformation of extruded loops, especially in the limit where the relative extension is close to 1. To test this, we simulate two nested LEFs on singly tethered DNA.
While this setup was considered in experiments (40), the imaging resolution did not allow a clear interpretation of the looped topologies. On the contrary, in our simulations we can always precisely classify and distinguish different Z-loop topologies. As before, we can also distinguish between nested LEFs extruding in parallel versus opposite directions. In Fig. 6 we show that, compared with the doubly tethered case, the frequencies at which and appear are closer to each other. We argue that this should also hold for free DNA. The fraction of is now larger than before but still significantly lower than ; yet the corresponding mean (normalized) lifetime is substantially larger (Fig. 6 D), meaning that it forms relatively rarely, but when it does it is a stable topology.
Figure 6.
Results of simulations of nested LEFs on singly tethered DNA. (A, C, and E) Frequency of topologies folded by two LEFs loaded with the same (A) or opposite (C) initial directions. (B, D, and F) Mean normalized lifetime of the loop topologies.
We note that loops are clearly stable due to their topology. The anchors point outward, therefore making it a non-extruding Z-loop structure. Without polymer fluctuations, a should be an absorbing state for the system as it cannot evolve by pure 1D extrusion. Thanks to polymer fluctuations and 3D moves this topology can come undone by, e.g., bypassing a hinge over the other anchor (thus going into a nested state).
These results confirm that, as hypothesized in the previous section, tethering the ends of DNA favors the formation of . We may thus conjecture that the statistics of Z-loop formation in vivo could differ from those observed in vitro (40). To test our prediction that DNA tension and assay affect the statistics of Z-loops, more in vitro experiments with a different choice of setups are needed.
Z-loop formation depends on initial loading
Until now we have only considered situations in which the LEFs started from a nested configuration. This is frequently observed in experiments, as condensins favor binding to bent or supercoiled substrates (52, 53, 54). On the other hand, in our simulations we can also study the case in which LEFs start in a serial (separated) state rather than nested.
To this end we load two LEFs at random on an equilibrated doubly tethered polymer and impose them to have opposite extrusion directions. We simulate 50 polymers and collect the results in Fig. 7: the measured frequencies (Fig. 7 A) and mean normalized lifetimes (Fig. 7 B) differ substantially from those estimated for two initially nested LEFs. Specifically, the frequency of remains larger than that of ; however, the fraction of is much more significant, as it rivals the fraction of . This is not surprising: the formation of is expected when the hinges of two LEFs meet and one jumps over the other (Fig. 7 C).
Figure 7.
(A and B) Results of simulations of two initially separated LEFs loaded on doubly tethered DNA with opposite initial extrusion directions. Frequency (A) and mean normalized lifetime (B) of the topologies. (C) Scheme of the formation of a in simulations with two initially separated LEFs and opposite extrusion directions. is formed if one of the hinges jumps over the other.
Conclusions
Motivated by the observation that SMCs can tie Z-loops, bypass roadblocks, and take steps larger than their own size, we have proposed a generalization of the original cis-only loop extrusion picture to allow “trans” grabbing of 3D proximal DNA segments.
First, we have calibrated our model to match the experimental force-rate curve of a single condensin extruding loops on doubly tethered λ-DNA (5). Using the parameters thus determined, we then have studied the balance and stability of loop topologies that can emerge when two LEFs are extruding on the same DNA substrate.
Importantly, we have identified five different loop topologies: separated (or serial), nested (or parallel), and three types of Z-loops. These are most clearly classified in terms of their net extrusion capability: can extrude from both boundaries, can extrude from only one of the two boundaries, and (never seen in experiments so far) cannot extrude loops because the anchors of the LEFs are facing outward. We highlight that the ratio of observed in our simulations is in good agreement with the one in recent experiments (40) (). More interestingly, this asymmetry emerges spontaneously and is not introduced by hand in our simulation. We have shown that this asymmetry is assay dependent and that loop extrusion on doubly tethered DNA induces geometric conformations that favor the formation of loops (Fig. 5 B). To test this hypothesis, we studied the formation of Z-loops on singly tethered DNA and indeed observed that are in this case as likely as . The singly tethered DNA assay was also performed in (40) but, due to the limits of optical resolution, the authors could not classify the type of the Z-loops formed.
We have also discovered a new type of Z-loop () which is expected to be a rare, but very long-lived, loop topology due to the fact that the anchors point outward, thereby rendering it a non-extruding form of Z-loop. We find that it appears frequently in the case that LEFs are initially separated and extruding in opposite directions. This is a prediction of our simulations that could be tested in experiments by forcing the loading of condensins on two separated sites rather than nested.
We conclude by highlighting that the precise mechanics of DNA loop extrusion are still highly debated. Here we have not attempted to give a precise biochemical characterization of the steps involved in extrusion (for this see, e.g., (31, 55)). Instead, we have focused on relaxing the assumption of cis extrusion, which is now difficult to reconcile with recent experimental findings (such as condesin-condensin and condensin-roadblock bypassing). Additionally, Ryu et al. (45), using high-resolution magnetic tweezers, recently observed that condensin collapses DNA in discrete steps and that it can reel in more than 100 basepairs in a single step. These observations may not be compatible with cis-only loop extrusion, and it is clear that new models of loop extrusion are needed.
We argue that two types of experiments may help to disentangle this problem. First, single-molecule setups using two entangled DNA molecules in an “X” configuration as in (14) could provide clear evidence of SMCs jumping/bridging in trans while extruding. Our model would predict that the complex should try, if close enough, to grab a sister DNA strand while being anchored to the first. Second, experiments performed on bulk solutions of entangled DNA with and without SMCs may display different viscoelastic properties depending on whether SMCs can extrude only in cis (1D) or also in trans (3D). We hope to report on both these types of assays in the near future.
In conclusion, the novelty of our work is that, to the best of our knowledge, it is the first to rationalize recent observations (Z-loops, roadblock bypassing, and large condesin step sizes) in a manner that is compatible with existing successful models of loop extrusion. In fact, our model is a generalization of cis loop extrusion that allows occasional 3D grabbing events. Additionally, and perhaps most importantly, we feel that our work suggests that more comprehensive models of loop extrusion may be needed to explain the organization of DNA in vivo. Currently, many models for interphase and mitotic genome organization employ cis loop extrusion (19, 20), yet it is well known that cohesin bridges sister chromatids together and without it the mitotic structure would fall apart (46, 47, 48). We thus argue that some SMCs, and in some conditions, may be able to activate a trans-loop extrusion mechanism, or bridging mode (15), with profound consequences on the organization and dynamics of genomes in vivo.
Author contributions
D.M. and A.B. designed research. A.B. developed the code, performed the simulations, and conducted the analysis. D.M. and A.B. wrote the paper.
ACKNOWLEDGMENTS
D.M. is a Royal Society University Research Fellow. This work was supported by the ERC (TAP, 947918). The code to simulate interstrand loop extrusion was developed by A.B. and is deposited for open access at https://git.ecdf.ed.ac.uk/dmichiel/translefs.
Editor: Andrew Spakowitz.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.11.015.
Supporting material
References
- 1.Hirano M., Hirano T. Hinge-mediated dimerization of SMC protein is essential for its dynamic interaction with DNA. EMBO J. 2002;21:5733–5744. doi: 10.1093/emboj/cdf575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nasmyth K. Cohesin: a catenase with separate entry and exit gates? Nat. Cell Biol. 2011;13:1170–1177. doi: 10.1038/ncb2349. [DOI] [PubMed] [Google Scholar]
- 3.Uhlmann F. SMC complexes: from DNA to chromosomes. Nat. Rev. Mol. Cell. Biol. 2016;17:399–412. doi: 10.1038/nrm.2016.30. [DOI] [PubMed] [Google Scholar]
- 4.Hirano T. Condensin-based chromosome organization from bacteria to vertebrates. Cell. 2016;164:847–857. doi: 10.1016/j.cell.2016.01.033. [DOI] [PubMed] [Google Scholar]
- 5.Ganji M., Shaltiel I.A., et al. Dekker C. Real-time imaging of DNA loop extrusion by condensin. Science. 2018;360:102–105. doi: 10.1126/science.aar7831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Davidson I.F., Bauer B., et al. Peters J.-M. DNA loop extrusion by human cohesin. Science. 2019;366:1338–1345. doi: 10.1126/science.aaz3418. [DOI] [PubMed] [Google Scholar]
- 7.Kim Y., Shi Z., et al. Yu H. Human cohesin compacts DNA by loop extrusion. Science. 2019;366:1345–1349. doi: 10.1126/science.aaz4475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kong M., Cutts E.E., et al. Greene E.C. Human condensin I and II drive extensive ATP-dependent compaction of nucleosome-bound DNA. Mol. Cell. 2020;79:99–114.e9. doi: 10.1016/j.molcel.2020.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Golfier S., Quail T., et al. Brugués J. Cohesin and condensin extrude DNA loops in a cell cycle-dependent manner. eLife. 2020;9:1–34. doi: 10.7554/eLife.53885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brandão H.B., Paul P., et al. Mirny L.A. RNA polymerases as moving barriers to condensin loop extrusion. Proc. Natl. Acad. Sci. USA. 2019;116:20489–20499. doi: 10.1073/pnas.1907009116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brandão H.B., Ren Z., et al. Wang X. RNA polymerases as moving barriers to condensin loop extrusion. Nat. Struct. Mol. Biol. 2021;28:642–651. [Google Scholar]
- 12.Anchimiuk A., Lioy V.S., et al. Gruber S. A low Smc flux avoids collisions and facilitates chromosome organization in Bacillus subtilis. eLife. 2021;10:1–22. doi: 10.7554/eLife.65467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stigler J., Çamdere G.Ö., et al. Greene E.C. Single-molecule imaging reveals a collapsed conformational state for DNA-bound cohesin. Cell Rep. 2016;15:988–998. doi: 10.1016/j.celrep.2016.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gutierrez-Escribano P., Newton M.D., et al. Aragon L. A conserved ATP- and Scc2/4-dependent activity for cohesin in tethering DNA molecules. Sci. Adv. 2019;5:1–16. doi: 10.1126/sciadv.aay6804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ryu J.-K., Bouchoux C., et al. Dekker C. Bridging-induced phase separation induced by cohesin SMC protein complexes. Sci. Adv. 2021;7:eabe5905. doi: 10.1126/sciadv.abe5905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Glynn E.F., Megee P.C., et al. Gerton J.L. Genome-wide mapping of the cohesin complex in the yeast Saccharomyces cerevisiae. PLoS Biol. 2004;2 doi: 10.1371/journal.pbio.0020259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lengronne A., Katou Y., et al. Uhlmann F. Cohesin relocation from sites of chromosomal loading to places of convergent transcription. Nature. 2004;430:573–578. doi: 10.1038/nature02742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Paldi F., Alver B., et al. Marston A.L. Convergent genes shape budding yeast pericentromeres. Nature. 2020;582:119–123. doi: 10.1038/s41586-020-2244-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fudenberg G., Imakaev M., et al. Mirny L.A. Formation of chromosomal domains by loop extrusion. Cell Rep. 2016;15:2038–2049. doi: 10.1016/j.celrep.2016.04.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goloborodko A., Marko J.F., Mirny L.A. Chromosome compaction by active loop extrusion. Biophys. J. 2016;110:2162–2168. doi: 10.1016/j.bpj.2016.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sanborn A.L., Rao S.S.P., et al. Aiden E.L. Chromatin extrusion explains key features of loop and domain formation in wild-type and engineered genomes. Proc. Natl. Acad. Sci. USA. 2015;112:201518552. doi: 10.1073/pnas.1518552112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alipour E., Marko J.F. Self-organization of domain structures by DNA-loop-extruding enzymes. Nucleic Acids Res. 2012;40:11202–11212. doi: 10.1093/nar/gks925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Phillips J.E., Corces V.G. CTCF: master weaver of the genome. Cell. 2009;137:1194–1211. doi: 10.1016/j.cell.2009.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tang Z., Luo O.J., et al. Ruan Y. CTCF-mediated human 3D genome architecture reveals chromatin topology for transcription. Cell. 2015;163:1611–1627. doi: 10.1016/j.cell.2015.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Oti M., Falck J., et al. Zhou H. CTCF-mediated chromatin loops enclose inducible gene regulatory domains. BMC Genomics. 2016;17:252. doi: 10.1186/s12864-016-2516-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brackley C., Johnson J., et al. Marenduzzo D. Nonequilibrium chromosome looping via molecular slip links. Phys. Rev. Lett. 2017;119:138101. doi: 10.1103/PhysRevLett.119.138101. [DOI] [PubMed] [Google Scholar]
- 27.Davidson I.F., Goetz D., et al. Peters J. Rapid movement and transcriptional re-localization of human cohesin on DNA. EMBO J. 2016;35:2671–2685. doi: 10.15252/embj.201695402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yamamoto T., Schiessel H. Osmotic mechanism of the loop extrusion process. Phys. Rev. E. 2017;96:1–4. doi: 10.1103/PhysRevE.96.030402. [DOI] [PubMed] [Google Scholar]
- 29.Higashi T.L., Pobegalov G., et al. Uhlmann F. A Brownian ratchet model for DNA loop extrusion by the cohesin complex. eLife. 2021;10:1–35. doi: 10.7554/eLife.67530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ryu J.-K., Bouchoux C., et al. Dekker C. Bridging-induced phase separation induced by cohesin SMC protein complexes. Sci. Adv. 2021;7:1–10. doi: 10.1126/sciadv.abe5905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Marko J.F., De Los Rios P., et al. Gruber S. DNA-segment-capture model for loop extrusion by structural maintenance of chromosome (SMC) protein complexes. Nucleic Acids Res. 2019;47:6956–6972. doi: 10.1093/nar/gkz497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Diebold-Durand M.L., Lee H., et al. Basfeld A. Structure of full-length SMC and rearrangements required for chromosome organization. Mol. Cell. 2017;67:334–347. doi: 10.1016/j.molcel.2017.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Terakawa T., Bisht S., et al. Greene E.C. The condensin complex is a mechanochemical motor that translocates along DNA. Science. 2017;676:eaan6516. doi: 10.1126/science.aan6516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Takaki R., Dey A., et al. Thirumalai D. Theory and simulations of condensin mediated loop extrusion in DNA. Nat. Commun. 2021;12:5865. doi: 10.1038/s41467-021-26167-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nichols M.H., Corces V.G. A tethered-inchworm model of SMC DNA translocation. Nat. Struct. Mol. Biol. 2018;25:906–1001. doi: 10.1038/s41594-018-0135-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kschonsak M., Merkel F., et al. Haering C.H. Structural basis for a safety-belt mechanism that anchors condensin to Chromosomes. Cell. 2017;171:588–600.e24. doi: 10.1016/j.cell.2017.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nomidis S.K., Carlon E., F. M.J., et al. DNA tension-modulated translocation and loop extrusion by SMC complexes revealed by molecular dynamics simulations. bioRxiv. 2021 doi: 10.1093/nar/gkac268. 2021.03.15.435506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ryu J.K., Katan A.J., Dekker C., et al. AFM images of open and collapsed states of yeast condensin suggest a scrunching model for DNA loop extrusion. bioRxiv. 2019 2019.12.13.867358. [Google Scholar]
- 39.Kamada K., Suétsugu M., et al. Hirano T. Overall shapes of the SMC-ScpAB complex are determined by balance between constraint and relaxation of its structural parts. Structure. 2017;25:603–616. doi: 10.1016/j.str.2017.02.008. [DOI] [PubMed] [Google Scholar]
- 40.Kim E., Kerssemakers J., et al. Dekker C. DNA-loop extruding condensin complexes can traverse one another. Nature. 2020;579:438–442. doi: 10.1038/s41586-020-2067-5. [DOI] [PubMed] [Google Scholar]
- 41.Cheng T.M., Heeger S., et al. Uhlmann F. A simple biophysical model emulates budding yeast chromosome condensation. eLife. 2015;4:1–22. doi: 10.7554/eLife.05565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gibcus J.H., Samejima K., et al. Dekker J. A pathway for mitotic chromosome formation. Science. 2018;359:6376. doi: 10.1126/science.aao6135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gerguri T., Fu X., et al. Uhlmann F. Comparison of loop extrusion and diffusion capture as mitotic chromosome formation pathways in fission yeast. Nucleic Acids Res. 2021;49:1294–1312. doi: 10.1093/nar/gkaa1270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pradhan B., Barth R., Dekker C., et al. SMC complexes can traverse physical roadblocks bigger than their ring size. bioRxiv. 2021 doi: 10.1101/2021.07.15.452501. [DOI] [PubMed] [Google Scholar]
- 45.Ryu J.-K., Rah S.-H., Dekker C., et al. Condensin extrudes DNA loops in steps up to hundreds of base pairs that are generated by ATP binding events. bioRxiv. 2020 doi: 10.1101/2020.11.04.368506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nasmyth K., Haering C.H. Cohesin: its roles and mechanisms. Annu. Rev. Genet. 2009;43:525–558. doi: 10.1146/annurev-genet-102108-134233. [DOI] [PubMed] [Google Scholar]
- 47.Murayama Y., Samora C.P., et al. Uhlmann F. Establishment of DNA-DNA interactions by the cohesin ring. Cell. 2018;172:465–477.e15. doi: 10.1016/j.cell.2017.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Piskadlo E., Tavares A., Oliveira R.A. Metaphase chromosome structure is dynamically maintained by condensin I-directed DNA (de)catenation. eLife. 2017;6:1–22. doi: 10.7554/eLife.26120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Brackley C.A., Liebchen B., et al. Marenduzzo D. Ephemeral protein binding to DNA shapes stable nuclear bodies and chromatin domains. Biophys. J. 2017;112:1085–1093. doi: 10.1016/j.bpj.2017.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bustamante C., Marko J.F., et al. Smith S.B. Entropic elasticity of lambda-phage DNA. Science. 1994;265:5–6. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 51.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995;117:1–19. [Google Scholar]
- 52.Kimura K., Hirano T. ATP-dependent positive supercoiling of DNA by 13S condensin: a biochemical implication for chromosome condensation. Cell. 1997;90:625–634. doi: 10.1016/s0092-8674(00)80524-3. [DOI] [PubMed] [Google Scholar]
- 53.Kimura K., Rybenkov V.V., et al. Cozzarelli N.R. 13S condensin actively reconfigures DNA by introducing global positive writhe: implications for chromosome condensation. Cell. 1999;98:239–248. doi: 10.1016/s0092-8674(00)81018-1. [DOI] [PubMed] [Google Scholar]
- 54.Kim E., Gonzalez A.M., et al. Dekker C. bioRxiv. 2021 2021.05.15.444164. [Google Scholar]
- 55.Nomidis S.K., Caraglio M., et al. Carlon E. Twist-bend coupling, twist waves, and the shape of DNA loops. Phys. Rev. E. 2019:022402. doi: 10.1103/PhysRevE.100.022402. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.