Abstract
Ionizable residues can release and take up protons and this has an influence on protein structure and function. The extent of protonation is linked to the overall pH of the solution and the local environments of ionizable residues. Binding or unbinding of a single proton generates a distinct charge microstate defined by a specific pattern of charges. Accordingly, the overall partition function is a sum over all charge microstates and Boltzmann weights of all conformations associated with each of the charge microstates. This ensemble-of-ensembles description recast as a q-canonical ensemble allows us to analyze and interpret potentiometric titrations that provide information regarding net charge as a function of pH. In the q-canonical ensemble, charge microstates are grouped into mesostates where each mesostate is a collection of microstates of the same net charge. Here, we show that leveraging the structure of the q-canonical ensemble allows us to decouple contributions of net proton binding and release from proton arrangement and conformational considerations. Through application of the q-canonical formalism to analyze potentiometric measurements of net charge in proteins with repetitive patterns of Lys and Glu residues, we determine the underlying mesostate pKa values and, more importantly, we estimate relative mesostate populations as a function of pH. This is a strength of using the q-canonical approach that cannot be replicated using purely site-specific analyses. Overall, our work shows how measurements of charge equilibria, decoupled from measurements of conformational equilibria, and analyzed using the framework of the q-canonical ensemble, provide protein-specific quantitative descriptions of pH-dependent populations of mesostates. This method is of direct relevance for measuring and understanding how different charge states contribute to conformational, binding, and phase equilibria of proteins.
Significance
The net charge of a protein in solution is governed by the overall pH as well as solution conditions and conformational contexts. Measurements of net charge are accessible via techniques, such as potentiometry, that quantify the buffering capacity of a protein solution. Here, we use the formal structure of the q-canonical ensemble to identify charge states that are compatible with a measured net charge profile as a function of pH. Our approach highlights how measurements of charge, decoupled from measurements of conformation, can be used to identify the ensembles of charge states that contribute to the overall population for given solution conditions. The methods introduced will be useful for measuring charge states and interpreting these measurements in different contexts.
Introduction
Ionizable residues make key contributions to protein structure and function (1, 2, 3, 4, 5, 6). They influence protein stability, solubility, and interactions mediated by the surfaces of the folded states of proteins (7, 8, 9, 10, 11, 12, 13, 14, 15), specifically in active sites of enzymes (16, 17, 18). Ionizable residues also feature prominently in intrinsically disordered proteins (IDPs) (19,20). Several studies have documented the important contributions made by ionizable residues to conformational (21, 22, 23, 24, 25, 26), binding (27, 28, 29, 30, 31, 32, 33), and phase equilibria of IDPs (34, 35, 36, 37, 38, 39, 40, 41, 42).
The charge states of ionizable residues can be regulated or altered through a variety of mechanisms that are collectively known as charge regulation (43, 44, 45). Active processes enable charge regulation through enzyme catalyzed reactions that enable posttranslational modifications (46), such as lysine acetylation (47), arginine citrullination (48), serine/threonine/tyrosine phosphorylation (49, 50, 51), and deamidation of asparagine/glutamine (52). In addition to enzyme catalyzed charge regulation, the charge states of ionizable residues can also be altered by spontaneous processes, such as binding or release of protons (2,3,7,53, 54, 55, 56, 57, 58, 59). In addition to charge regulation, preferential accumulation or exclusion of solution ions around regions of high charge density can lead to charge renormalization (60, 61, 62, 63, 64, 65, 66, 67).
Charge regulation via proton uptake or release is influenced by a combination of sequence contexts, solution conditions, and the linked effects of conformational equilibria (68, 69, 70). Importantly, multiple charge states are accessible depending on solution conditions. As a result, each protein sequence is an ensemble of charge microstates, with each microstate being a distinct sequence defined by the charge states of ionizable residues. We recently introduced the q-canonical ensemble to describe ensembles of charge microstates and conformations associated with each of the microstates (71).
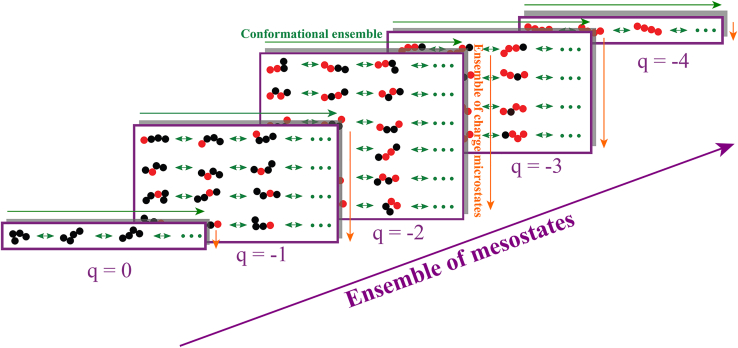
The structure of the q-canonical ensemble, see Fig. 1, is as follows: we consider a protein sequence comprising nq ionizable residues, Nfixed atoms that do not change with protonation/deprotonation, and a net charge of q when protons are bound to the protein sequence. If there are gq ways in which protons can be bound, then there are gq distinct charge microstates for a net charge of q. At temperature T, in a solution volume V, each charge microstate i with net charge q will access a canonical ensemble of conformations. For this ensemble, the partition function is written as:
| (1) |
Figure 1.
Structure of the q-canonical ensemble. The ensemble of mesostates (purple arrow) encompasses all mesostates (purple rectangles). Each mesostate encompasses an ensemble of charge microstates (orange arrows) corresponding to the different ways residue in their charged state (red circles) can be arranged with respect to those in their uncharged state (black circles). Finally, each microstate has a distinct conformational ensemble (green arrows).
Summing over the gq ways in which when protons can be bound, leads to a sum over canonical partition functions written as:
| (2) |
The partition function, written as the sum over the different numbers of protons that can be bound, becomes:
| (3) |
The states summed being over in Eq. 3 are the set of conformations accessible for each charge microstate, with the outer two summations running over all possible microstates. The partition function Ξ describes the q-canonical ensemble. Next, we rewrite Ξ to account for the chemical potential of the proton, which is defined by the pH of the solution. Accounting for pH, Ξ becomes:
| (4) |
The conformational ensemble for each charge microstate contributes to , and the sum over all microstates with a charge q, which we refer to as a charge mesostate, contributes to wq. A mesostate is made up of all charge microstates that have the same net charge, and the sum over q is a sum over all mesostates. Accordingly, we rewrite the sum over q as a sum over mesostates such that the probability that the protein of interest will have a charge q at a given pH can be written as pq(pH), and this is computed as:
| (5) |
Given this formalism, the net charge as a function of pH can be written as:
| (6) |
Note that is the probability associated with mesostate i that has charge qi. Potentiometric measurements provide a direct readout of net charge as a function of pH. Here, we present a new approach to analyze potentiometric data. The approach relies on the structure of the q-canonical ensemble, which allows for a formal decoupling of measurements of charge from measurements of structure. This is achieved by estimating the mesostate weights from potentiometric measurements using a Monte-Carlo-based fitting procedure. This information can be subsequently combined with simulations as well as measurements of conformational averages or populations, performed as a function of pH, to identify microstates that contribute most significantly to a mesostate. The key point is that subsequent computations of microstate probabilities and conformational distributions can be constrained by the values for that we obtain using potentiometric measurements.
In the following sections, we summarize the challenges posed by acid-base equilibria of proteins with multiple ionizable residues. Such systems are referred to as polyacids (54,72, 73, 74, 75). We then describe how the q-canonical formalism can be interfaced with potentiometric measurements (76, 77, 78). This is followed by a presentation of our results from application of the q-canonical formalism to analyze potentiometry data for three model systems that are repeats of Lys and Glu. We conclude with a discussion of the broader implications of our findings, the general use of our approach, and the insights that will be forthcoming through joint use of the q-canonical ensemble, conformational sampling, and separate measurements of proton binding and conformational equilibria.
Theory
Acid-base equilibria for polyacids
For a sequence with n ionizable residues, there are, in theory, 2n distinct charge microstates to consider. However, for sequences that are mixtures of acids and bases, the number of thermodynamically relevant charge microstates can be significantly reduced by eliminating forbidden states (71). Any microstate that involves the coexistence of neutral versions of acidic and basic residues can, to first approximation, be ignored as forbidden microstates. This is because the intrinsic pKa values are such that the protonation of acids and deprotonation of bases are unlikely to occur simultaneously. Classification of microstates as being forbidden and ignoring these in subsequent calculations does not materially alter the estimated partition function (71). After the pruning of forbidden microstates, the number of thermodynamically relevant charge microstates is designated as Ωmicro. Even with pruning to eliminate forbidden microstates, Ωmicro will increase exponentially with the number of ionizable residues n (Fig. S1). Comparative descriptions of acid-base equilibria for simple systems versus polyacids show how the large number of charge microstates must be accounted for when assessing pH-dependent titrations for polyacids.
For a monoacid, such as a single glutamic acid, the pKa value is defined for the reaction . Here, e and E, respectively denote the protonated and deprotonated versions of Glu, and H+ refers to the proton that is released upon deprotonation. The standard state ionization free energy is: . The picture becomes more complicated for polyacids because of the increase in the number of reactions that involve the loss of a proton (79). To illustrate this point, we consider the case of ac-(Glu)2-nme, where ac and nme, respectively, refer to N-acetyl and N'-methylamide. There are four separate reactions that involve the loss of a single proton. These are:
| (7) |
Each of the reactions shown in Eq. 7 can be assigned a pKa value. We refer to these as primary pKa values, as they involve the loss of exactly one mole of protons from a single site for each mole of advancement of the reaction. For a system with n ionizable residues, there will be a set of n2n−1 primary pKa values. These cannot be measured, although they can be approximated (80, 81, 82).
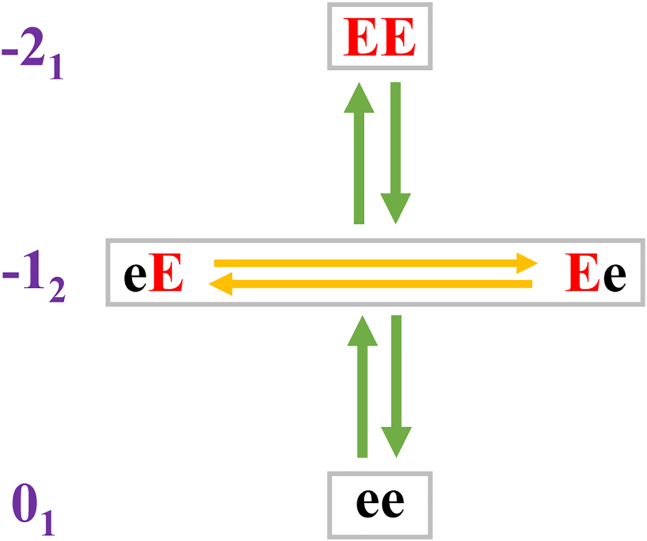
A mesostate is made up of all charge microstates that have the same net charge—see Eqs. 4 and 5. Each mesostate is assigned a label qk where q denotes the net charge associated with each microstate within the mesostate and k denotes the total number of microstates within the mesostate. For example, the designation of +13 implies that there are three microstates in the mesostate, and all these microstates have a net charge of +1. The total number of mesostates, denoted as Nmeso, scales linearly with the number of ionizable residues (Fig. S2). We can rewrite the acid-base equilibria in Eq. 7 using the notation for mesostates (Fig. 2) and rewrite the relevant reactions for the release of one mole of protons as follows:
| (8) |
Here, (01,–12) and (−12,–21) are two pairs of adjacent mesostates. Adjacency refers to mesostates whose net charge differs by ±1e. Each reaction in Equation (8) can also be assigned a pKa value. These mesostate pKa values are different from the set of primary pKa values. For Nmeso mesostates, there will be Nmeso–1 mesostate pKa values corresponding to transitions between pairs of adjacent mesostates. While the set of primary pKa values cannot be measured, the set of mesostate pKa values can be inferred from measurements of net charge as a function of pH, providing we are able to extract the pH-dependent populations of mesostates—a problem we solve here by leveraging the structure of the q-canonical ensemble.
Figure 2.
Schematic showing charge microstates and the grouping into mesostates for ac-(Glu)2-nme. Here ace and nme refer to N-acetyl and N'-methylamide, respectively. Protonated and deprotonated Glu residues are depicted as e and E, respectively. The charge microstates ee, eE, Ee, and EE can be grouped into mesostates, and the designation of mesostates, shown in qk format, is shown in purple.
For the case of the ac-(Glu)2-nme system, there are at least two distinct scenarios that could correspond to a seemingly reasonable definition of unshifted pKa values. According to one assumption, the pKa value for a transition between two mesostates would be identical to the intrinsic pKa value. This would imply that . However, this assumption ignores the number of reactions within a single mesostate, each involving a distinct microstate that can contribute to the loss of a proton. The second model for unshifted pKa values corresponds to the assumption that: . This model assumes that the primary pKa values can only be assigned to reactions involving individual microstates rather than collections of microstates. Here, the unshifted pKa values associated with transitions between mesostates can be derived through proper accounting of the diversity of charge microstates per mesostate. We illustrate these points using reactions for the ac-(Glu)2-nme system. The mesostate −12 includes the microstates Ee and eE. Therefore, the concentration of mesostate −12, denoted as [–12] is written as: [–12] = [Ee] + [eE]. Accordingly, the equilibrium constant for dissociation of a mole of protons from mesostate −12 is written as:
| (9) |
The free energy of ionization of a single mesostate, for the specific example considered here, may be written as:
| (10) |
If we assume that primary pKa values correspond to those of model compounds, we can use Eq. 10 for polyacids by accounting for the number of microstates per each mesostate. The free energy of ionization that transforms mesostate qk to (q–1)L of a polyacid, through the release of one mole of protons, may be written as:
| (11) |
Here, and refer to the number of charge microstates within mesostates qk and (q–1)L, respectively; and are the context-dependent free energies of ionization; nq-1,i and nq,j are the numbers of ionizable residues within microstates i and j that are in their basic forms. For example, nq = 1 for microstates eE, eEe, kK, KKk, etc. Likewise, nq = 2 for microstates eEE, kkK, etc. Here, k is the deprotonated version of lysine (K). For the transformation of mesostate 01 to mesostate −12, nq-1,i = 1 for each of the microstates Ee and eE, whereas nq,j = 0 for the microstate ee.
Equation 11 reduces to Eq. 10 if we set and . If all microstates within a mesostate are equiprobable, implying that the ionization free energy is independent of sequence context, then Eq. 11 reduces to:
| (12) |
Upon further rearrangement, Eq. 12 becomes:
| (13) |
Equation 13 highlights the importance of microstate entropy that features in two terms: and . These are the microstate entropies of mesostates qk and (q–1)l, respectively. The implication is that, even for the simple scenario of context-independent pKa values, the free energy difference between a pair of adjacent mesostates, which is a measure of the pKa values associated with the transition between a pair of adjacent mesostates, must account for the contributions of different microstate entropies for each mesostate. In general, the microstate weights will be nonidentical. In this scenario, the pH-independent standard state free energy change associated with transformation from mesostate qk to (q–1)l is written as:
| (14) |
Here, is the standard state free energy of microstate i. In the following sections we show how potentiometry, which measures the buffering capacity of a solute as a function of pH, can be used in conjunction with Eq. 14 to derive mesostate populations as a function of pH.
Extracting mesostate populations from potentiometry measurements
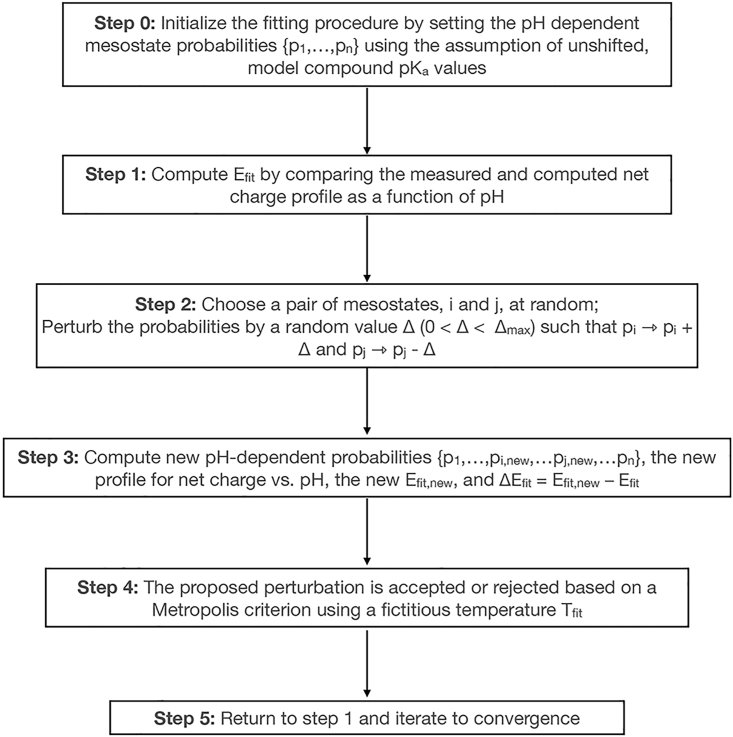
We use potentiometry to estimate the net charge of a protein as a function of pH. This is achieved by titrating the solution pH using a strong acid or a strong base. The buffering capacity of a protein solution, referenced to the buffering capacity of the protein-free solution, is used to estimate the profile of net charge versus pH. Given the ensemble-averaged net charge versus pH as an input, we can fit the measured profile to extract the pH-dependent population of mesostates. This information allows us to extract the contributions made by distinct mesostates to the pH-dependent net charge profile. The measured net charge qnet as a function of pH is given in Eq. 6, where qi is the charge associated with mesostate i and pi(pH) is the probability of populating mesostate i for a given pH. Given knowledge of qnet(pH), and the charge associated with each mesostate, we can estimate the pH-dependent mesostate probabilities by fitting the measured profiles to Eq. 6. The fitting procedure is based on a Metropolis Monte Carlo method (83) that minimizes the deviation between the measured and estimated charge profile by minimizing a cost function defined as:
| (15) |
We choose absolute values rather than signed values to keep the cost function bounded between 0 and a positive number. In Eq. 15, qest and qnet are the estimated and measured net charge values for a given pH. The fitting procedure, summarized in Fig. 3, can be seeded by assigning mesostate probabilities using intrinsic pKa values; however, as discussed in the supporting material, this is not essential. We use 10.7 and 4.34 for intrinsic pKa values of Lys and Glu, respectively (84). The parameter Δmax (see Fig. 3) is set so that the maximal change in relative free energies of states i and j that are being perturbed will be no more than 0.01 kcal/mol. The Metropolis criterion for accepting or rejecting a proposed change in mesostate probabilities is of the form: . Here, ΔEfit quantifies how the cost function Efit has changed with the newly proposed mesostate probabilities. The parameter Tfit is a scalar parameter, which is a fictitious and unitless temperature that is chosen to enable efficient convergence of the Monte-Carlo-based fitting procedure. The optimal temperature will be system-specific, and is chosen by inspecting the acceptance ratio and making sure it is not close to 1 or below a numerical tolerance. Data from potentiometry measurements (see below) converted into profiles of net charge versus pH are used to quantify how the mesostate probabilities evolve as a function of pH.
Figure 3.
Flowchart summarizing the workflow for fitting data from potentiometric titrations to Eq. 6.
Smoothing of the raw data was performed using a Savitzky-Golay algorithm (85) as implemented in the SciPy python package (https://scipy.github.io). The prescribed output resolution was set to 100 points per pH unit, with a window size of 101, and a second-order polynomial. Results of the smoothing procedure are shown in Fig. S3. To enhance sampling efficiency, especially in the first steps of the fit, we introduce a drift correction, which returns the fitting parameters to the parameters of the best fit found to that point if the current fit has a cost function of more than 125% of the best fit cost function. The best fit as a function of step number is depicted for two different priors in Video S1 (all pKa values set to 7) and Video S2 (pKa values set to their intrinsic pKa values). Each Monte Carlo fitting procedure comprises 150,000 steps. For each construct, we performed a total of 10 independent runs. The best fits obtained in each run are depicted as the blue curves of Fig. S5. These fits show clear convergence, especially for the neutral pH region.
The gray curve is the smoothed, interpolated experimental data, the orange curve is the current fit. The red dashed lines correspond to the fitted pKa values which in the q-canonical approach are defined as the pH at which two mesostates with a net charge difference of one have an equal population.
Colors are the same as in Video S1.
It is worth emphasizing that the fitting procedure generates estimates for mesostate populations as a function of pH. Further parsing of these mesostate-specific weights to unearth the contributions of mesostate-specific microstates will require additional information in the form of the full q-canonical Monte Carlo simulation that assesses the contributions of microstates and their conformations. These simulations can be constrained by the mesostate populations we derive using the procedures summarized in Fig. 3.
Materials and methods
Reagents and peptides
Potassium chloride (KCl), hydrochloric acid (HCl), potassium hydroxide (KOH), and potassium hydrogen phthalate (KHP) were purchased from Sigma (St. Louis, MO, USA). We assessed the purity of KOH using titrations of a standard with a known pKa, which confirm that contaminants, if present are miniscule and do not affect the potentiometric titrations. Peptides were purchased from GenScript (Piscataway, NJ, USA) at >95% purity as HCl salts with acetylated N-termini and amidated C-termini. Salt content was determined by mass spectrometry. The identities of the peptides were confirmed using mass spectrograms provided by the vendor. Peptides were stored in lyophilized form at −20°C in sealed containers in the presence of desiccant until they were used for experiments. We performed measurements for three peptides, excised from proteins with single α-helical domains. The amino acid sequences of the three peptides were as follows: ac-G-(E4K4)n-GW-NH2, where n = 1, 2, or 3. The peptides were capped at the N- and C-termini using N-acetyl (ace) and an amide, respectively. This avoids confounding effects from charged termini. Trp was used to enable precise measurements of concentration.
Sample preparation
A sealed flask of ultrapure water was depleted of CO2 using a custom-built Schlenk line to apply alternating cycles of nitrogen gas and vacuum. The resulting CO2-depleted water and all solutions and samples prepared from this water were kept in sealed flasks or vials and stored in a glove bag (AtmosBag, Millipore-Sigma, Burlington, MA, USA, Z530204) filled with nitrogen gas. To further decrease the concentration of dissolved CO2, solutions prepared with the CO2-purged water were allowed to equilibrate with the nitrogen-filled (CO2-depleted) atmosphere in the glove bag before sealing the flask or vial. All transfers of these liquids between flasks or vials were carried out within the nitrogen-filled glove bag or using gas-tight Hamilton syringes (Fisher Scientific, San Francisco, CA, USA) to access sealed vials without exposing the contents to air. A stock solution of background solvent was prepared by dissolving KCl in CO2-depleted ultrapure water to which HCl had been added. The final solution contained 10 mM KCl and 5 mM HCl. This solution was further depleted of CO2 using the Schlenk line, after which it was sealed and stored in a nitrogen-filled glove bag until further use.
A 50 mM KOH solution was used as the titrant for all potentiometry experiments. A 200 mM KOH stock solution was prepared in the glove bag using CO2-depleted ultrapure water. This stock was further diluted to 50 mM KOH with CO2-depleted ultrapure water and sealed in a glass vial with a Teflon-coated rubber septum while in the nitrogen-filled glove bag. Peptides were dissolved in the CO2-depleted background solution at a concentration of ∼200 μM. The final peptide concentrations used were 215 μM for (E4K4)1, 95 μM for (E4K4)2, and 180 μM for (E4K4)3. Immediately before each potentiometry experiment, the peptide concentration was measured by UV-visible spectroscopy using Trp absorbance at 280 nm and an extinction coefficient of 5500 M−1 cm−1. A KHP solution at a concentration of 1 mM was prepared by massing a quantity of KHP powder into a glass vial using a precision mass balance, transferring the vial to the nitrogen-filled glove bag, and then adding CO2-depleted ultrapure water directly to the vial to dissolve the material. The sample was stored in a sealed vial in the nitrogen-filled glove bag until further use.
Potentiometry
All measurements were carried out in a custom sample vial consisting of a glass screw-cap vial sealed with a Teflon-coated rubber septum with a 5 mm hole (created with a biopsy punch) that accommodated the pH probe while still forming a seal. Titrant was delivered to the sealed vial through the rubber septum using a precision gas-tight μL syringe fitted with a repeating dispenser (Hamilton). Potentiometric measurements were carried out on an Orion Star A215 potentiometer (Thermo Scientific, Waltham, MA, USA) using a pHT-micro combination probe with a platinum/Silamid double junction (YSI, Yellow Springs, OH, USA). A 2 mL sample was titrated with 50 mM KOH in 2 μL increments in all cases.
The concentration of the KOH solution was verified by titrating a known concentration of KHP having a well-documented pKa of 5.4, as follows: a 2 mL volume of KHP solution was titrated with ∼50 mM KOH solution in 2 μL increments, and the pH of the solution was measured after each addition. A titration of 2 mL of background solution was carried out in the same manner. The resulting potentiometry curves (KHP and background) were analyzed by Gran analysis (86,87) as well as by first- and second-derivative analyses to determine the precise KOH concentration (88,89).
For each peptide, a 2 mL volume of peptide solution was titrated with ∼50 mM KOH solution in 2 μL increments, and the pH of the solution was measured after each addition. A titration of 2 mL of background solution was carried out in the same manner. For each peptide titration, the KOH solution used as the titrant was prepared fresh and calibrated with a KHP titration as described above.
A stable pH reading is essential for accurate potentiometric measurements, and this can be difficult to achieve under conditions of low solute concentration. For example, it is extremely difficult, if not impossible, to obtain a stable pH reading in a sample of ultrapure water due to the lack of buffering capacity and the lack of salt ions in the sample. In our experiments, we found that 10 mM salt was sufficient to ensure signal stability, as demonstrated by successful measurement of stable pH in background titrations of 10 mM KCl and 5 mM HCl with no peptide (Figs. S8–S10). In peptide-containing samples, the presence of buffering moieties at millimolar concentrations (1.72 mM for E4K4, 1.52 mM for (E4K4)2, and 4.32 mM for (E4K4)3) provided further stability to pH readings. Additional measurement stability was facilitated by the use of a pH probe with a platinum wire junction, which allows optimum electrolyte flow, and by allowing the signal to plateau and stabilize for a minimum of 50 s (longer near neutral pH) for each data point.
Calculation of peptide net charge
Since KOH is a strong base, we can assume that for each mole of OH added, one mole of protons is consumed, resulting in water as the product. We use the known concentration of the KOH solution to calculate the number of moles of KOH from the volume of KOH added. The difference in KOH volume added between the titration curves for peptide and background represents a quantity that is proportional to the number of moles of protons introduced by the peptide. Since the peptide concentration is known, we can calculate the number of protons per peptide. The number of protons released over the course of the titration is equivalent to the change in net charge of the peptide. Therefore, the net charge of the peptide can be determined as a function of pH if the net charge is known at the starting point of the titration. Since the titration is started at a low pH (∼2.0), which is below the pKa values of all ionizable groups present, we assume that all ionizable groups are protonated at the low pH, and the net charge on the peptide should be equal to the number of cationic residues (Lys in the case of (E4K4)n peptides).
Following the approach of Nozaki and Tanford (90), the data were transposed to facilitate comparison of the volume of KOH added in the background titration versus the peptide titration at each pH value (2,91). A linear interpolation between each data point within a given titration curve was carried out so that the background curve could be subtracted from the peptide curve at any pH value. The resulting quantities represent the difference in KOH volume added in the background titration versus the peptide titration at a given pH value. Multiplying these values by the known concentration of KOH gives the difference in number of moles of KOH between the two curves, and this is equivalent to the number of protons introduced by the peptide. Dividing this value by the number of moles of peptide (calculated as peptide concentration multiplied by sample volume) quantifies the moles of protons per moles of peptide, which is equivalent to relative change in net charge (Figs. S11–S13).
As explained above, for (E4K4)n peptides, the number of Lys residues provides the offset value needed to shift the calculated moles of protons per peptide to the appropriate register for reporting the net charge of the peptide. In practice, there are a few sources of uncertainty that may require adjustments to both the scaling and the offset of the net charge curve. These include any uncertainties in measurements of concentration, and the presence of trace amounts of residual acid in the peptide sample. To account for these errors, we scale the protein net charge curve such that the inflection point around neutral pH has a charge of 0. This is the most parsimonious rescaling, since any other rescaling would lead to mesostates with nonzero charge being the dominant population around pH 7.0, implying that the 01 mesostate would never be dominant in the ensemble. The rescaling factors used are 0.92, 0.76, and 0.79 for (E4K4)1, (E4K4)2, and (E4K4)3, respectively.
Results
Sequences with a consensus repeat consisting of (E4X4)n or (E3X3)n, where X is either an Arg or Lys have been shown to form α-helical conformations (92, 93, 94, 95). These single α helicx forming sequences belong to larger proteins (94). Helicity is known to increase with the number of repeats (92). The single α helices are thought to be useful in force transduction in myosin (93) and have been deployed as spectroscopic rulers for Förster resonance energy transfer measurements, in vitro and in cells (96). The overall helicity has been ascribed to a network of intrahelical salt bridges between residues i and i + 4 (92,95).
Here, we ask if a single mesostate viz, 01, dominates over the entire accessible pH range, irrespective of the number of repeats. This question is motivated by observations showing a remarkable stability of the α-helical conformations across a wide range of pH values (95,97). We reasoned that it is unlikely for networks of salt bridges to be operative under conditions where Glu is protonated, or Lys is deprotonated. A definitive assessment of the curious pH insensitivity requires knowledge of how the net charge varies with pH, and we measure this directly. We can then use these data, in conjunction with the q-canonical ensemble, to infer the populations of each of the relevant mesostates as a function of pH. The measurements reveal a series of insights that are summarized next.
Fitting of potentiometric data
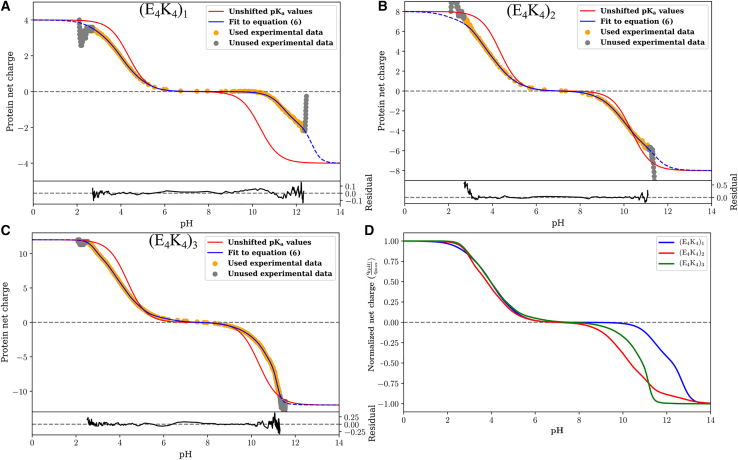
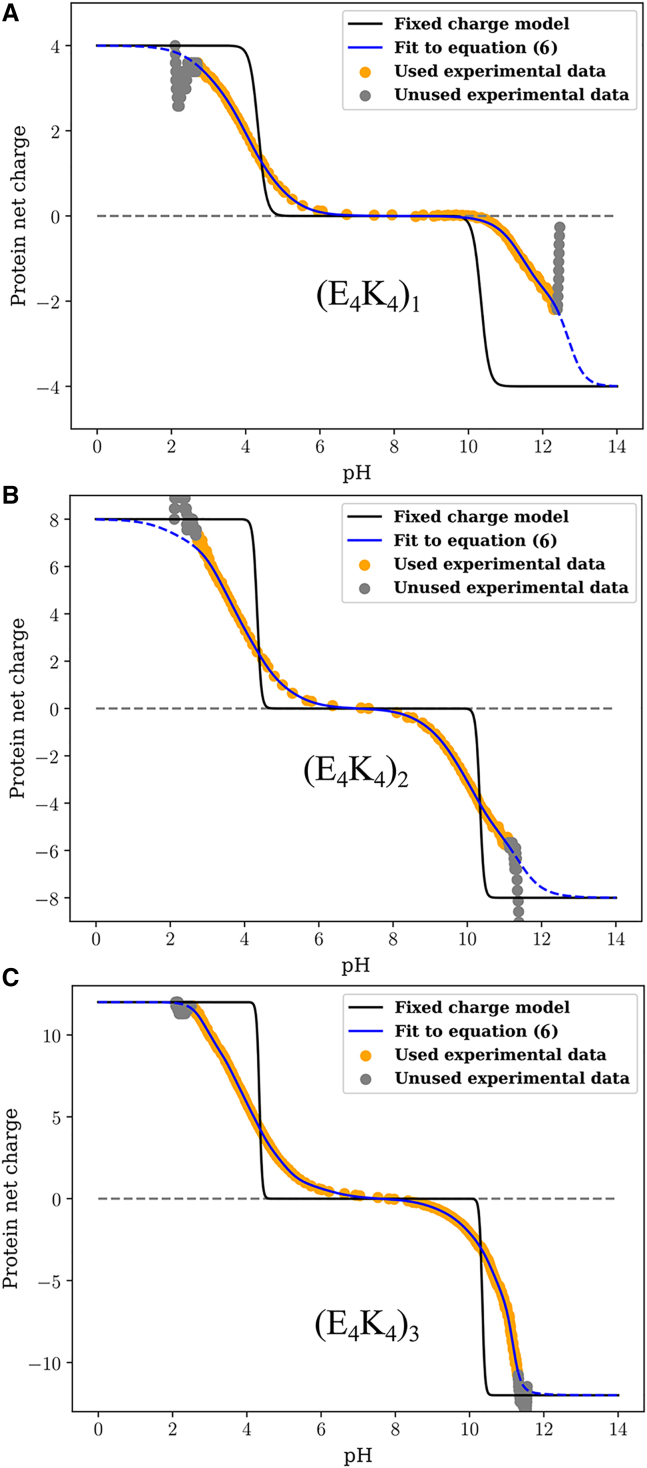
Figs. 4A–4 C show the quality of the fits obtained for each of the three peptides. Further, Video S1 provides a direct visualization of how the fitting procedure evolves. In each panel of Fig. 4, the gray circles denote the raw experimental data that are not used in the fitting procedure. The orange points are the raw data used for the fitting procedure. The fitting procedure was applied to the smoothed version of the data to have a uniform resolution across the pH range. This ensures that evaluation of the cost function is uniformly distributed. The raw data and comparisons to the smoothed data are shown in Fig. S3. Fits to the data are shown using two models, depicted using blue versus red curves. The red curves are charge profiles calculated by assuming model compound pKa values for all the ionizable residues, although the microstate entropies per mesostate are different. In this model, the only parameters that distinguish different mesostates are net charge and the microstate entropy per mesostate. These fits, which do not describe the data well, clearly indicate that there are shifted pKa values in each of the three sequences. The blue curves show the quality of fits obtained through the Monte Carlo fitting procedure that uses Eq. 6. The quality of the fits is shown in terms of residuals included at the bottom of each panel. The mesostate probabilities change with respect to the unshifted model, and these changes are reflected in the improved fits to the net charge versus pH profiles. We further assessed the quality of the fits by calculating the pH-dependent derivatives of the net charge profiles, for the experimental data and for the numerical fits. These comparisons are shown in Fig. S4. Fig. 4 D shows a comparison of the normalized net charge versus pH for the three peptides. If the unshifted model were to be valid, then the three curves should collapse on one another. Clearly, this is not the case, and it points to sequence- and context-dependent contributions and the increasing diversity of mesostates with peptide length.
Figure 4.
Raw data and results obtained from fitting the model based on unshifted pKa values versus the full model—Eq. 6—to the profile of net charge versus pH obtained from potentiometric titrations. Panel A shows results for (E4K4)1; Panel B shows results for (E4K4)2 and panel (C) shows results for (E4K4)3. (D) A comparison of the fitted profiles for the three peptides. To enable these comparisons, the ordinate is rescaled to be normalized by the magnitude of the maximal charge realizable for each system.
We also compared charge profiles calculated using a fixed charge model to the measured profiles from potentiometry. Here, we assume that Lys is always protonated below its intrinsic pKa values and Glu is always deprotonated above its intrinsic pKa values. The results are shown in the three panels of Fig. 5. Again, each panel includes the gray circles, orange points, and blue curves that are identical to those in Fig. 4. Clearly, the fixed charge model does not recapitulate how the measured charge varies with pH, at least not for the (E4K4)n series of peptides.
Figure 5.
Comparison of the raw data, fits obtained using the full model, and a model that uses fixed charges. The results are shown for each of the three peptides: (E4K4)1 (A), (E4K4)2 (B), and (E4K4)3 (C). In each panel, the black curve corresponds to the fixed charge model. This model does a poor job of recapitulating the titration curve.
Interpretations from the measured charge profiles
The profile for (E4K4) shows a plateau in the pH range between 7 and 9 (Fig. 4 A). This observation is confirmed by calculations of the derivative as a function of pH, which show that the derivative is essentially zero in the pH range between 7 and 9 (Fig. S4 A). The implication is that none of the acids or bases are titrating their charge states in this pH range. Therefore, a single mesostate dominates in the pH range between 7 and 9 for the E4K4 peptide. It is noteworthy, however, that the plateau region of the blue curve in Fig. 4 A is larger than that of the red curve. The latter corresponds to the model that uses unshifted, model compound pKa values while accounting for differences in microstate entropies of the different mesostates. Thus, the data indicate a downshift versus an upshift in the pKa values for the acids and the bases, respectively. In contrast to the (E4K4) peptide, the two longer peptides (E4K4)2 and (E4K4)3 do not have a pH range where the charge profile plateaus (Figs. 4 B and 4 C), and this is confirmed by the absence of a pH region where the derivative is zero (Figs. S4 B and S4 C). This suggests that at every pH, there is at least more than one mesostate (and hence microstate) that contributes to the measured charge profiles.
Insights from pH-dependent mesostate populations
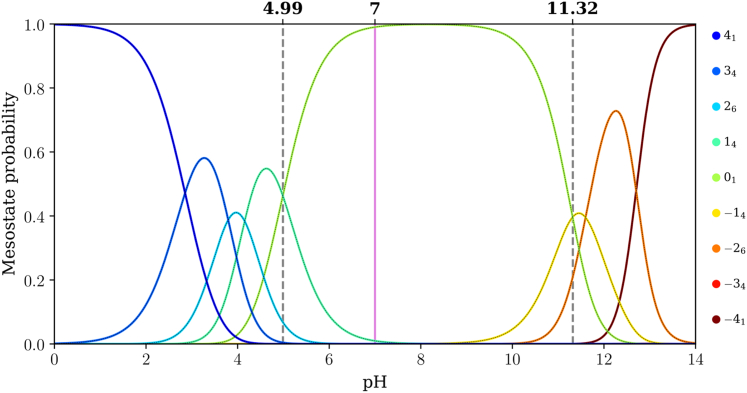
Fitting of the data for net charge versus pH using the q-canonical ensemble formalism yields the pH dependence of mesostate populations. The results are shown in Figs. 6, 7, and 8 for E4K4, (E4K4)2, and (E4K4)3, respectively. The dashed vertical lines in Fig. 6 help quantify mesostate pKa values. For E4K4, the +14 and 01 mesostates have equal likelihoods of being populated at a pH of 4.99. This implies that the pKa value associated with the transition between +14 and 01 mesostates is 4.99. Using a similar approach, we find that the pKa value associated with the transition between 01 and −18 mesostates is 11.32. Therefore, the 01 mesostate is dominant within the pH range between 4.99 and 11.32, with the gap between the two mesostate pKa values being 6.33 pH units. However, the dominance of the 01 mesostate weakens with increasing numbers of E4K4 repeats, and the prominence of the mesostates with net charges of ±1 increases as the numbers of E4K4 repeats increase.
Figure 6.
Mesostate probabilities, plotted against pH, for the E4K4 peptide. The dashed lines in each panel mark the pH values at which mesostates adjacent to the 01 mesostate have equal likelihoods of being populated. The pink line corresponds to a pH of 7.0.
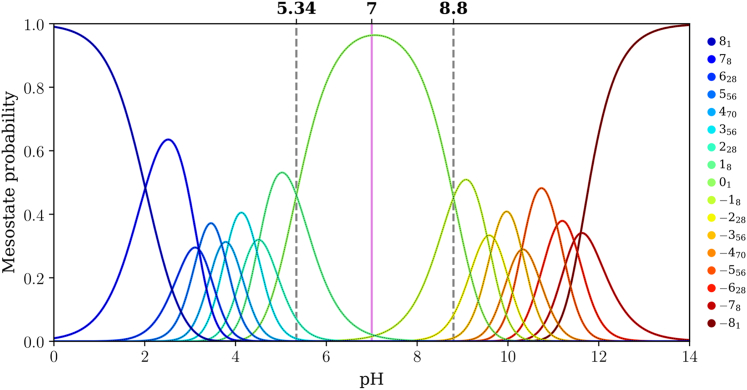
Figure 7.
Mesostate probabilities, plotted against pH, for the (E4K4)2 peptide. The dashed lines in each panel mark the pH values at which mesostates adjacent to the 01 mesostate have equal likelihoods of being populated. The pink line corresponds to a pH of 7.0.
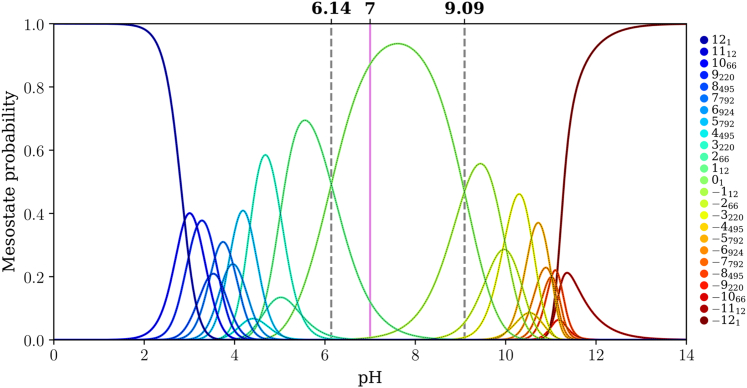
Figure 8.
Mesostate probabilities, plotted against pH, for the (E4K4)3 peptide. The dashed lines in each panel mark the pH values at which mesostates adjacent to the 01 mesostate have equal likelihoods of being populated. The pink line corresponds to a pH of 7.0.
For (E4K4)2 the pKa values for the transitions +18 ↔ 01 and 01 ↔ −18 are 5.34 and 8.80, respectively (Fig. 7), implying a gap of 3.46 pH units. This gap between the two pKa values, which corresponds to transitions between 01 and its adjacent mesostates, further narrows for (E4K4)3 (Fig. 8). Here, the pKa values for the transitions +112 ↔ 01 and 01 ↔ −112 are 6.14 and 9.01, respectively (gap of 2.87 pH units). The mesostate pKa for transitions between the mesostate with net charge +1 and the 01 mesostate shifts up with increasing numbers of repeats. In contrast, the pKa value for transitions between the mesostate with net charge −1 and 01 shows nonmonotonic variation with the number of repeats. This derives from the steeper variation of net charge with pH as the intrinsic pKa value of Lys is approached. In contrast, the mesostate with charge +1 is accessible in a pH range where the net charge shows a weaker pH dependence.
The gap between pKa values for transitions between the 01 and adjacent mesostates that have a net charge of ±1 narrows from 6.33 to 3.46 and 2.87 pH units as the number of E4K4 repeats increases from 1 to 2 to 3. It is likely that this gap further narrows as the numbers of repeats increase. One of the main takeaways is that for (E4K4)3, the mesostate +112 contributes significantly, in addition to the 01 mesostate at pH 7.0 (see pink line in Fig. 8). This contribution weakens in favor of the −112 mesostate as the pH increases above 7.4. Therefore, even at pH 7.0, there are at least 13 distinct microstates whose contributions to the conformational ensemble must be considered.
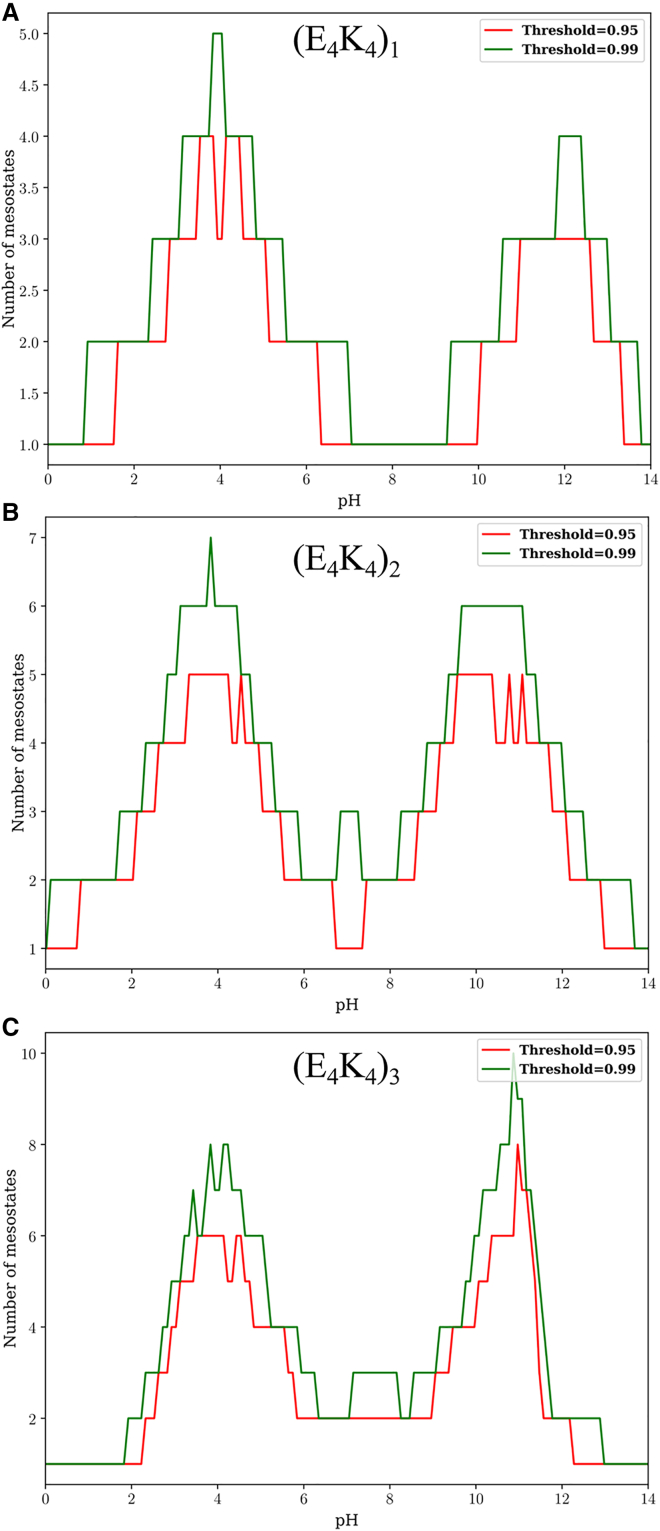
The importance of charge state heterogeneity increases as the pH increases or decreases from the value of 7.0. The pH-dependent populations of mesostates can be used to quantify the numbers of mesostates that contribute to 95 versus 99% of the overall population as a function of pH. The results are summarized in Fig. 9. Fig. 9 A shows that a single mesostate, 01, and hence a single microstate, contributes to 99% of the population for the E4K4 peptide across a wide pH range. For the (E4K4)2, two to three mesostates are required to account for 90–99% of the preferred mesostates in the pH range of 7–9 (Fig. 9 B). We obtain similar results for the (E4K4)3 system (Fig. 9 C).
Figure 9.
Minimum number of mesostates that are required to account for 95 and 99% of the population, as a function of pH, for each of the three peptides: (E4K4)1 (A), (E4K4)2 (B), and (E4K4)3 (C).
Discussion
Here, we have introduced a method for analyzing potentiometric data by leveraging the formal structure of q-canonical ensemble, which allows us to decouple the interpretation of measurements of charge from measurements of conformations. Our methods are likely to be of particular use for uncovering the dual impacts of charge state and conformational heterogeneity for IDPs, as these systems tend to be rich in ionizable residues, with a large fraction featuring more than 30% of ionizable residues (19). This number increases when we include the contributions of neutral residues that become ionizable after posttranslational modifications such as Ser/Thr phosphorylation.
The prothymosin α system that has been studied extensively by the Schuler group (27,98, 99, 100, 101, 102, 103), as well as acid-rich disordered proteins that function as transactivation domains of transcription factors (104), are examples of well-known IDPs that are among the closest mimics of homo polyacids, which are seldom fully deprotonated in solution (53,54). Indeed, single-molecule electrometry measurements performed by Ruggeri et al. (102) suggest that only 28.5 ± 1.2 out of the 46 D/E residues in prothymosin α are, on average, charged at pH 8.8. Whether this is purely due to charge regulation or if there are contributions from charge renormalization remains to be resolved. Given the growing interest in the conformational, binding (105), and phase equilibria of polyampholytic, polyzwitterionic (106,107), and polyelectrolytic IDPs (108), it will be important to measure net charge profiles and extract the contributions of charge state heterogeneity to these profiles. Here, we demonstrate the feasibility of such analyses by extracting mesostate populations using the q-canonical ensemble formalism. In follow-up work, we propose to adopt this approach for analysis of cross sections of IDPs.
The apparent insensitivity of helicity of single α helices to changes in pH (95,97) might derive from the helicity associated with microstates that have a net charge. In this scenario, it cannot solely be the network of salt bridges that contribute to stabilizing helical conformations. Instead, the interplay among differences in free energies of solvation of charged and neutral forms of Glu and Lys (109), as well as the higher intrinsic helical propensity of neutral Glu versus charged Glu (110, 111, 112, 113), are likely contributors to the intriguing robustness of measured helicities to large-scale changes in pH. Accounting for the totality of these interactions requires a combination of charge measurements, presented here, and measurements of conformational equilibria, that are jointly used in a suitable molecular simulation framework for describing the total q-canonical ensemble.
Features of the q-canonical ensemble
It is worth noting that the semigrand ensemble developed by Mugnai and Thirumalai (70) also bears resemblance to the q-canonical ensemble used here and introduced our earlier work (71). Their efforts were motivated by the molecular transfer model developed for describing pH effects on single-molecule pulling experiments of proteins (114). The structure of the q-canonical ensemble allows us to decouple measurements of charge from measurements of conformation. By leveraging this decoupling, through the mesostate description of the net charge extracted from the q-canonical ensemble, we can analyze potentiometry-based charge profiles as a function of pH to quantify the number and types of mesostates that are thermodynamically relevant for a given set of solution conditions. We find that the microstate entropy per mesostate makes significant contributions to the distribution of thermodynamically accessible mesostates. Importantly, the contributions of microstate entropy grow with the number of ionizable residues. Whether or not this heterogeneity can be overcome by dominant conformational preferences of specific microstates can only be decided by decoupling the measurements of charge from other readouts such as measurements of conformation and/or binding.
It is worth emphasizing the intrinsic differences between a site-specific representation of ionizable groups, and a description in terms of mesostates afforded by the q-canonical ensemble. If one were to measure pKa values using site-specific titrations, aided by appropriate spectroscopic approaches such as nuclear magnetic resonance (8,82,115) or infrared spectroscopy (112), the inferred variations in site-specific pKa values would be much lower than the variations that we can uncover using the mesostate representation and measurements of global charge profiles.
Potentiometry
The simplicity of potentiometric titrations is a key to its robustness (116). The buffering capacity can be measured to obtain net charge profiles as a function of pH by fixing solution conditions, such as salt concentration, salt type, and the solution temperature. Therefore, with suitable automation, potentiometry can provide direct access to charge profiles as a function of pH for a range of systems and solution conditions. These data, when analyzed using the q-canonical formalism, will be essential for understanding the extent of sequence- and composition-specific effects of charge regulation via proton binding and release.
Being one of the earliest methods to characterize acid-base equilibria in chemical species, several methods for the interpretation of potentiometric curves, especially for monoacids, have been developed (116). However, as noted by Ghasemi and Larson, the interpretation of potentiometric data has remained an unsolved problem for polyacids (54). We propose that our q-canonical ensemble-based approach provides an alternative route to obtain more complete descriptions of the measured charge profiles.
Historically, potentiometry measurements have been used to assess the presence of anomalous or shifted pKa values (2). This is typically achieved by using model compound pKa values, ignoring the microstate entropy, and querying whether the measured net charge profiles match or deviate from the calculated profiles. Qualitative assessments from analysis of potentiometry are typically used to set up detailed site-specific measurements of local pKa values using nuclear magnetic resonance spectroscopy or other types of spectroscopies that rely on isotopic labeling at specific sites.
The net charge profiles extracted using potentiometry have also been analyzed by prescribing model conformations and the calculation of conformation-specific electrostatic potentials (54). The goal in these endeavors is to assess the extent to which local sequence contexts can be implicated as modifiers of local pKa values that cause deviations of measured charge profiles from expectations based on model compounds. While these efforts highlight the importance of charge regulation, they ignore the contributions of microstate entropy. Here, we leverage the structure of the q-canonical ensemble and show how this can be deployed to extract insights regarding the pH dependence of mesostate populations.
Potentiometry versus other methods to measure charge
Methods to measure charge are of considerable interest, especially for studies of IDPs. Several methods, such as capillary electrophoresis (57,117) and single molecule electrometry (102), have been introduced and deployed for measuring the net charges of IDPs and other flexible polymers. A limitation of these methods is the reliance on measurements of molecular mobility in the presence of a potential drop or a spatially patterned electric field. Analysis of data from mobility-based measurements requires the a priori assumption of a preferred conformational state. Further complications arise because electrophoretic mobility measurements require the use of ultralow salt concentrations to avoid confounding effects that arise from the adsorption or release of solution ions. Accordingly, we propose that potentiometry, which is the most direct approach for measuring net charge, should be the preferred route for quantifying charge profiles of IDPs.
Summary and prognosis
We have developed and deployed a formalism, leveraging the recently introduced q-canonical ensemble, to analyze potentiometric titrations. We showcase the approach using measurements and analyses for three related systems. The formalism is applicable for analyzing multisite binding isotherms (118, 119, 120) for arbitrary ligands, not just protons. A large-scale deployment of potentiometry, aided by the analysis introduced in this work, will be forthcoming for a cross section of IDPs that include residues, such as Asp, Glu, Lys, Arg, His, and other more complex features. This will allow us to dissect the contributions of different compositions and sequence contexts to charge state heterogeneity.
The results presented here help highlight the importance of charge state heterogeneity and the fact that heterogeneity makes significant contributions with increasing numbers of ionizable residues. Potentiometric measurements, combined with separate measurements of the pH dependence of conformational properties, can be analyzed using the q-canonical ensemble to extract mesostate populations as well as microstate populations. The latter is being pursued for a series of systems, using sampling methods developed for the q-canonical ensemble (71). The results, which will be published elsewhere, will likely move us in the direction of quantifying the extent to which charge state and conformational heterogeneity either enhance or antagonize one another. These studies are likely to be important for understanding and modeling the conformational, binding, and phase equilibria of IDPs. Such studies take on additional significance given various observations of pH-responsive equilibria for IDPs (42), recent measurements highlighting the significant extent of charge regulation in polyelectrolytic IDPs, and the presence of compartments of highly variable pH environments within cells.
Author contributions
Conceptualization, M.J.F. and R.V.P.; development of the formal theory and analysis, M.J.F.; potentiometry setup, troubleshooting, and measurements, A.E.P.; numerical analysis of potentiometry data, M.J.F. and R.V.P.; writing of the manuscript, M.J.F. and R.V.P.; editing, M.J.F., A.E.P., and R.V.P.; funding, R.V.P.
Acknowledgments
We thank Furqan Dar, Mina Farag, Andrew Lin, Kiersten Ruff, Min Kyung Shinn, and Xiangze Zeng for careful reading of the manuscript. This work was supported by grant FA9550-20-1-0241 from the Air Force Office of Scientific Research, grants R01NS089932 and 5R01NS056114 from the US National Institutes of Health, and the St. Jude Children’s Research Collaborative on Membraneless Organelles.
Editor: Scott Showalter.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.11.2886.
Supporting material
References
- 1.Pace C.N., Grimsley G.R., Scholtz J.M. Protein ionizable groups: pK values and their contribution to protein stability and solubility. J. Biol. Chem. 2009;284:13285–13289. doi: 10.1074/jbc.R800080200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Whitten S.T., Garcia-Moreno E.B. pH dependence of stability of staphylococcal nuclease: evidence of substantial electrostatic interactions in the denatured state. Biochemistry. 2000;39:14292–14304. doi: 10.1021/bi001015c. [DOI] [PubMed] [Google Scholar]
- 3.Whitten S.T., Wooll J.O., et al. Hilser V.J. The origin of pH-dependent changes in m-values for the denaturant-induced unfolding of proteins. J. Mol. Biol. 2001;309:1165–1175. doi: 10.1006/jmbi.2001.4726. [DOI] [PubMed] [Google Scholar]
- 4.Castle P.E., Karp D.A., et al. Cone R.A. Human monoclonal antibody stability and activity at vaginal pH. J. Reprod. Immunol. 2002;56:61–76. doi: 10.1016/s0165-0378(02)00013-x. [DOI] [PubMed] [Google Scholar]
- 5.Mehler E.L., Fuxreiter M., et al. Garcia-Moreno E.B. The role of hydrophobic microenvironments in modulating pKa shifts in proteins. Proteins. 2002;48:283–292. doi: 10.1002/prot.10153. [DOI] [PubMed] [Google Scholar]
- 6.Schlessman J.L., Abe C., et al. Garcia-Moreno E.B. Crystallographic study of hydration of an internal cavity in engineered proteins with buried polar or ionizable groups. Biophys. J. 2008;94:3208–3216. doi: 10.1529/biophysj.107.122473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Whitten S.T., Garcia-Moreno E.B., Hilser V.J. Local conformational fluctuations can modulate the coupling between proton binding and global structural transitions in proteins. Proc. Natl. Acad. Sci. U S A. 2005;102:4282–4287. doi: 10.1073/pnas.0407499102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Castaneda C.A., Fitch C.A., et al. Garcia-Moreno B.E. Molecular determinants of the pKa values of Asp and Glu residues in staphylococcal nuclease. Proteins. 2009;77:570–588. doi: 10.1002/prot.22470. [DOI] [PubMed] [Google Scholar]
- 9.Harms M.J., Castaneda C.A., et al. Garcia-Moreno E.B. The pK(a) values of acidic and basic residues buried at the same internal location in a protein are governed by different factors. J. Mol. Biol. 2009;389:34–47. doi: 10.1016/j.jmb.2009.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Isom D.G., Castaneda C.A., et al. Garcia-Moreno E.B. Charges in the hydrophobic interior of proteins. Proc. Natl. Acad. Sci. U S A. 2010;107:16096–16100. doi: 10.1073/pnas.1004213107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kitahara R., Hata K., et al. Royer C.A. Structural plasticity of staphylococcal nuclease probed by perturbation with pressure and pH. Proteins. 2011;79:1293–1305. doi: 10.1002/prot.22966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Peck M.T., Ortega G., et al. Garcia-Moreno E.B. Local backbone flexibility as a determinant of the apparent pKa values of buried ionizable groups in proteins. Biochemistry. 2017;56:5338–5346. doi: 10.1021/acs.biochem.7b00678. [DOI] [PubMed] [Google Scholar]
- 13.Petrosian S.A., Makhatadze G.I. Contribution of proton linkage to the thermodynamic stability of the major cold-shock protein of Escherichia coli CspA. Protein Sci. 2000;9:387–394. doi: 10.1110/ps.9.2.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Permyakov S.E., Makhatadze G.I., et al. Berliner L.J. How to improve nature: study of the electrostatic properties of the surface of alpha-lactalbumin. Protein Eng. Des. Sel. 2005;18:425–433. doi: 10.1093/protein/gzi051. [DOI] [PubMed] [Google Scholar]
- 15.Chan C.H., Wilbanks C.C., et al. Wong K.B. Electrostatic contribution of surface charge residues to the stability of a thermophilic protein: benchmarking experimental and predicted pKa values. PLoS One. 2012;7:e30296. doi: 10.1371/journal.pone.0030296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hofer F., Kraml J., et al. Liedl K.R. Catalytic site pKa values of aspartic, cysteine, and serine proteases: constant pH MD simulations. J. Chem. Inf. Model. 2020;60:3030–3042. doi: 10.1021/acs.jcim.0c00190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bartlett G.J., Porter C.T., et al. Thornton J.M. Analysis of catalytic residues in enzyme active sites. J. Mol. Biol. 2002;324:105–121. doi: 10.1016/s0022-2836(02)01036-7. [DOI] [PubMed] [Google Scholar]
- 18.Harris T.K., Turner G.J. Structural basis of perturbed pKa values of catalytic groups in enzyme active sites. IUBMB Life. 2002;53:85–98. doi: 10.1080/15216540211468. [DOI] [PubMed] [Google Scholar]
- 19.Holehouse A.S., Das R.K., et al. Pappu R.V. CIDER: resources to analyze sequence-ensemble relationships of intrinsically disordered proteins. Biophys. J. 2017;112:16–21. doi: 10.1016/j.bpj.2016.11.3200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pujato M., Bracken C., et al. Tasayco M.L. pH dependence of amide chemical shifts in natively disordered polypeptides detects medium-range interactions with ionizable residues. Biophys. J. 2005;89:3293–3302. doi: 10.1529/biophysj.105.060384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mao A.H., Crick S.L., et al. Pappu R.V. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. U S A. 2010;107:8183–8188. doi: 10.1073/pnas.0911107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mao A.H., Lyle N., Pappu R.V. Describing sequence-ensemble relationships for intrinsically disordered proteins. Biochem. J. 2013;449:307–318. doi: 10.1042/BJ20121346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.van der Lee R., Buljan M., et al. Babu M.M. Classification of intrinsically disordered regions and proteins. Chem. Rev. 2014;114:6589–6631. doi: 10.1021/cr400525m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Marsh J.A., Dancheck B., et al. Peti W. Structural diversity in free and bound states of intrinsically disordered protein phosphatase 1 regulators. Structure. 2010;18:1094–1103. doi: 10.1016/j.str.2010.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marsh J.A., Forman-Kay J.D. Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J. 2010;98:2383–2390. doi: 10.1016/j.bpj.2010.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu B., Chia D., et al. Gradinaru C.C. The effect of intrachain electrostatic repulsion on conformational disorder and dynamics of the Sic1 protein. J. Phys. Chem. B. 2014;118:4088–4097. doi: 10.1021/jp500776v. [DOI] [PubMed] [Google Scholar]
- 27.Borgia A., Borgia M.B., et al. Schuler B. Extreme disorder in an ultrahigh-affinity protein complex. Nature. 2018;555:61–66. doi: 10.1038/nature25762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bugge K., Brakti I., et al. Kragelund B.B. Interactions by disorder—a matter of context. Front. Mol. Biosci. 2020;7:110. doi: 10.3389/fmolb.2020.00110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.O'Shea C., Staby L., et al. Skriver K. Structures and short linear motif of disordered transcription factor regions provide clues to the interactome of the cellular hub protein radical-induced cell death1. J. Biol. Chem. 2017;292:512–527. doi: 10.1074/jbc.M116.753426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sottini A., Borgia A., et al. Schuler B. Polyelectrolyte interactions enable rapid association and dissociation in high-affinity disordered protein complexes. Nat. Commun. 2020;11:5736. doi: 10.1038/s41467-020-18859-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Prestel A., Wichmann N., et al. Kragelund B.B. The PCNA interaction motifs revisited: thinking outside the PIP-box. Cell Mol. Life Sci. 2019;76:4923–4943. doi: 10.1007/s00018-019-03150-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Millard P.S., Weber K., et al. Burow M. Specificity of MYB interactions relies on motifs in ordered and disordered contexts. Nucleic Acids Res. 2019;47:9592–9608. doi: 10.1093/nar/gkz691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Borg M., Mittag T., et al. Chan H.S. Polyelectrostatic interactions of disordered ligands suggest a physical basis for ultrasensitivity. Proc. Natl. Acad. Sci. U S A. 2007;104:9650–9655. doi: 10.1073/pnas.0702580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pak C.W., Kosno M., et al. Rosen M.K. Sequence determinants of intracellular phase separation by complex coacervation of a disordered protein. Mol. Cell. 2016;63:72–85. doi: 10.1016/j.molcel.2016.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kaur T., Raju M., et al. Banerjee P.R. Sequence-encoded and composition-dependent protein-RNA interactions control multiphasic condensate morphologies. Nat. Commun. 2021;12:872. doi: 10.1038/s41467-021-21089-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Alshareedah I., Moosa M.M., et al. Banerjee P.R. Phase transition of RNA−protein complexes into ordered hollow condensates. Proc. Natl. Acad. Sci. U S A. 2020;117:15650. doi: 10.1073/pnas.1922365117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fisher R.S., Elbaum-Garfinkle S. Tunable multiphase dynamics of arginine and lysine liquid condensates. Nat. Commun. 2020;11:4628. doi: 10.1038/s41467-020-18224-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yeong V., Wang J.-w., et al. Obermeyer A.C. Intracellular phase separation of globular proteins facilitated by short cationic peptides. bioRxiv. 2021 doi: 10.1101/2021.07.08.450573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chang L.W., Lytle T.K., et al. Perry S.L. Sequence and entropy-based control of complex coacervates. Nat. Commun. 2017;8:1273. doi: 10.1038/s41467-017-01249-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Knoerdel A.R., Blocher McTigue W.C., Sing C.E. Transfer matrix model of pH effects in polymeric complex coacervation. J. Phys. Chem. B. 2021;125:8965–8980. doi: 10.1021/acs.jpcb.1c03065. [DOI] [PubMed] [Google Scholar]
- 41.Last M.G.F., Deshpande S., Dekker C. pH-controlled coacervate–membrane interactions within liposomes. ACS Nano. 2020;14:4487–4498. doi: 10.1021/acsnano.9b10167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Quiroz F.G., Fiore V.F., et al. Fuchs E. Liquid-liquid phase separation drives skin barrier formation. Science. 2020;367:eaax9554. doi: 10.1126/science.aax9554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lund M., Jönsson B. Charge regulation in biomolecular solution. Q. Rev. Biophys. 2013;46:265–281. doi: 10.1017/S003358351300005X. [DOI] [PubMed] [Google Scholar]
- 44.Avni Y., Andelman D., Podgornik R. Charge regulation with fixed and mobile charged macromolecules. Curr. Opin. Electrochem. 2019;13:70–77. [Google Scholar]
- 45.Burton R.F. The protein content of extracellular fluids and its relevance to the study of ionic regulation: net charge and colloid osmotic pressure. Comp. Biochem. Physiol. A Comp. Physiol. 1988;90:11–16. doi: 10.1016/0300-9629(88)90998-x. [DOI] [PubMed] [Google Scholar]
- 46.Bah A., Forman-Kay J.D. Modulation of intrinsically disordered protein function by post-translational modifications. J. Biol. Chem. 2016;291:6696–6705. doi: 10.1074/jbc.R115.695056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gil J., Ramírez-Torres A., Encarnación-Guevara S. Lysine acetylation and cancer: a proteomics perspective. J. Proteomics. 2017;150:297–309. doi: 10.1016/j.jprot.2016.10.003. [DOI] [PubMed] [Google Scholar]
- 48.Fuhrmann J., Thompson P.R. Protein arginine methylation and citrullination in epigenetic regulation. ACS Chem. Biol. 2016;11:654–668. doi: 10.1021/acschembio.5b00942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bah A., Vernon R.M., et al. Forman-Kay J.D. Folding of an intrinsically disordered protein by phosphorylation as a regulatory switch. Nature. 2015;519:106–109. doi: 10.1038/nature13999. [DOI] [PubMed] [Google Scholar]
- 50.Kennelly P.J. Protein Ser/Thr/Tyr phosphorylation in the Archaea. J. Biol. Chem. 2014;289:9480–9487. doi: 10.1074/jbc.R113.529412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Eymann C., Becher D., et al. Hecker M. Dynamics of protein phosphorylation on Ser/Thr/Tyr in Bacillus subtilis. Proteomics. 2007;7:3509–3526. doi: 10.1002/pmic.200700232. [DOI] [PubMed] [Google Scholar]
- 52.Bischoff R., Kolbe H.V.J. Deamidation of asparagine and glutamine residues in proteins and peptides: structural determinants and analytical methodology. J. Chromatogr. B Biomed. Appl. 1994;662:261–278. doi: 10.1016/0378-4347(94)00203-7. [DOI] [PubMed] [Google Scholar]
- 53.Salehi A., Larson R.G. A molecular thermodynamic model of complexation in mixtures of oppositely charged polyelectrolytes with explicit account of charge association/dissociation. Macromolecules. 2016;49:9706–9719. [Google Scholar]
- 54.Ghasemi M., Larson R.G. Role of electrostatic interactions in charge regulation of weakly dissociating polyacids. Prog. Polym. Sci. 2021;112:101322. [Google Scholar]
- 55.Fitch C.A., Whitten S.T., et al. Garcia-Moreno E.B. Molecular mechanisms of pH-driven conformational transitions of proteins: insights from continuum electrostatics calculations of acid unfolding. Proteins. 2006;63:113–126. doi: 10.1002/prot.20797. [DOI] [PubMed] [Google Scholar]
- 56.Hilser V.J., Garcia-Moreno E.B., et al. Whitten S.T. A statistical thermodynamic model of the protein ensemble. Chem. Rev. 2006;106:1545–1558. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- 57.Sharma U., Negin R.S., Carbeck J.D. Effects of cooperativity in proton binding on the net charge of proteins in charge ladders. J. Phys. Chem. B. 2003;107:4653–4666. [Google Scholar]
- 58.Simonson T., Carlsson J., Case D.A. Proton binding to proteins: pKa calculations with explicit and implicit solvent models. J. Am. Chem. Soc. 2004;126:4167–4180. doi: 10.1021/ja039788m. [DOI] [PubMed] [Google Scholar]
- 59.Shiao D.D.F., Sturtevant J.M. Heats of binding protons to globular proteins. Biopolymers. 1976;15:1201–1211. doi: 10.1002/bip.1976.360150613. [DOI] [PubMed] [Google Scholar]
- 60.Anderson C.F., Record M.T. Salt dependence of oligoion-polyion binding: a thermodynamic description based on preferential interaction coefficients. J. Phys. Chem. 1993;97:7116–7126. [Google Scholar]
- 61.Grosberg A.Y., Nguyen T.T., Shklovskii B.I. Colloquium: the physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002;74:329–345. [Google Scholar]
- 62.Roosen-Runge F., Heck B.S., et al. Schreiber F. Interplay of pH and binding of multivalent metal ions: charge inversion and reentrant condensation in protein solutions. J. Phys. Chem. B. 2013;117:5777–5787. doi: 10.1021/jp401874t. [DOI] [PubMed] [Google Scholar]
- 63.Zhang F., Weggler S., et al. Schreiber F. Universality of protein reentrant condensation in solution induced by multivalent metal ions. Proteins. 2010;78:3450–3457. doi: 10.1002/prot.22852. [DOI] [PubMed] [Google Scholar]
- 64.Winkler R.G., Gold M., Reineker P. Collapse of polyelectrolyte macromolecules by counterion condensation and ion pair formation: a molecular dynamics simulation study. Phys. Rev. Lett. 1998;80:3731–3734. [Google Scholar]
- 65.Butler J.C., Angelini T., et al. Wong G.C.L. Ion multivalence and like-charge polyelectrolyte attraction. Phys. Rev. Lett. 2003;91:028301. doi: 10.1103/PhysRevLett.91.028301. [DOI] [PubMed] [Google Scholar]
- 66.Angelini T.E., Liang H., et al. Wong G.C.L. Like-charge attraction between polyelectrolytes induced by counterion charge density waves. Proc. Natl. Acad. Sci. U S A. 2003;100:8634. doi: 10.1073/pnas.1533355100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Annunziata O., Paduano L., Albright J.G. Multicomponent diffusion of lysozyme in aqueous calcium chloride. The role of common-ion effects and protein−salt preferential interactions. J. Phys. Chem. B. 2007;111:10591–10598. doi: 10.1021/jp072404k. [DOI] [PubMed] [Google Scholar]
- 68.Zheng Y., Cui Q. Microscopic mechanisms that govern the titration response and pKa values of buried residues in staphylococcal nuclease mutants. Proteins. 2017;85:268–281. doi: 10.1002/prot.25213. [DOI] [PubMed] [Google Scholar]
- 69.Pahari S., Sun L., Alexov E. PKAD: a database of experimentally measured pKa values of ionizable groups in proteins. Database. 2019;2019:baz024. doi: 10.1093/database/baz024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Mugnai M.L., Thirumalai D. Molecular transfer model for pH effects on intrinsically disordered proteins: theory and applications. J. Chem. Theor. Comput. 2021;17:1944–1954. doi: 10.1021/acs.jctc.0c01316. [DOI] [PubMed] [Google Scholar]
- 71.Fossat M.J., Pappu R.V. q-Canonical Monte Carlo sampling for modeling the linkage between charge regulation and conformational equilibria of peptides. J. Phys. Chem. B. 2019;123:6952–6967. doi: 10.1021/acs.jpcb.9b05206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Mandel M., Leyte J.C. Some remarks on the titration equation of weak polyacids. J. Electroanal. Chem. Interfacial Electrochem. 1972;37:297–301. [Google Scholar]
- 73.Müller M., Wirth L., Urban B. Determination of the carboxyl dissociation degree and pKa value of mono and polyacid solutions by FTIR titration. Macromol. Chem. Phys. 2021;222:2000334. [Google Scholar]
- 74.Borukhov I., Andelman D., et al. Orland H. Polyelectrolyte titration:theory and experiment. J. Phys. Chem. B. 2000;104:11027–11034. [Google Scholar]
- 75.Woodbury C.P. The titration curve of weak polyacids. J. Phys. Chem. 1993;97:3623–3630. [Google Scholar]
- 76.Fitch C.A., Platzer G., et al. McIntosh L.P. Arginine: its pKa value revisited. Protein Sci. 2015;24:752–761. doi: 10.1002/pro.2647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Bakker E., Pretsch E. Modern potentiometry. Angew. Chem. Int. Ed. 2007;46:5660–5668. doi: 10.1002/anie.200605068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Smith L.A., Glasscott M.W., et al. Dick J.E. Enzyme kinetics via open circuit potentiometry. Anal. Chem. 2020;92:2266–2273. doi: 10.1021/acs.analchem.9b04972. [DOI] [PubMed] [Google Scholar]
- 79.Gunner M.R., Murakami T., et al. Chodera J.D. Standard state free energies, not pKas, are ideal for describing small molecule protonation and tautomeric states. J. Comput. Aided Mol. Des. 2020;34:561–573. doi: 10.1007/s10822-020-00280-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Szakács Z., Kraszni M., Noszál B. Determination of microscopic acid–base parameters from NMR–pH titrations. Anal. Bioanal. Chem. 2004;378:1428–1448. doi: 10.1007/s00216-003-2390-3. [DOI] [PubMed] [Google Scholar]
- 81.Bashford D., Karplus M. Multiple-site titration curves of proteins: an analysis of exact and approximate methods for their calculation. J. Phys. Chem. 1991;95:9556–9561. [Google Scholar]
- 82.Onufriev A., Case D.A., Ullmann G.M. A novel view of pH titration in biomolecules. Biochemistry. 2001;40:3413–3419. doi: 10.1021/bi002740q. [DOI] [PubMed] [Google Scholar]
- 83.Metropolis N., Rosenbluth A.W., et al. Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 84.Platzer G., Okon M., McIntosh L.P. pH-dependent random coil 1H, 13C, and 15N chemical shifts of the ionizable amino acids: a guide for protein pKa measurements. J. Biomol. NMR. 2014;60:109–129. doi: 10.1007/s10858-014-9862-y. [DOI] [PubMed] [Google Scholar]
- 85.Savitzky A., Golay M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964;36:1627–1639. [Google Scholar]
- 86.Gran G. Determination of the equivalence point in potentiometric titrations. Part II. Analyst. 1952;77:661–671. [Google Scholar]
- 87.Gran G., Johansson A. Automatic titration by stepwise addition of equal volumes of titrant. Part VI. Further extension of the Gran I method for calculation of the equivalence volume in acid-base titrations. Analyst. 1981;106:231–242. [Google Scholar]
- 88.Yan J.F. A method for the determination of equivalence point in potentiometric titrations using unequal volume increments. Anal. Chem. 1965;37:1588–1590. [Google Scholar]
- 89.Fortuin J.M.H. Method for determination of the equivalence point in potentiometric titrations. Anal. Chim. Acta. 1961;24:175–191. [Google Scholar]
- 90.Nozaki Y., Tanford C. Methods in Enzymology. Academic Press; 1967. Examination of titration behavior; pp. 715–734. [Google Scholar]
- 91.Huang Y., Bolen D.W. Methods in Enzymology. Academic Press; 1995. Probes of energy transduction in enzyme catalysis; pp. 19–43. [DOI] [PubMed] [Google Scholar]
- 92.Baker E.G., Bartlett G.J., et al. Woolfson D.N. Local and macroscopic electrostatic interactions in single α-helices. Nat. Chem. Biol. 2015;11:221–228. doi: 10.1038/nchembio.1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Peckham M., Knight P.J. When a predicted coiled coil is really a single α-helix, in myosins and other proteins. Soft Matter. 2009;5:2493–2503. [Google Scholar]
- 94.Süveges D., Gáspári Z., et al. Nyitray L. Charged single α-helix: a versatile protein structural motif. Proteins. 2009;74:905–916. doi: 10.1002/prot.22183. [DOI] [PubMed] [Google Scholar]
- 95.Wolny M., Batchelor M., et al. Peckham M. Characterization of long and stable de novo single alpha-helix domains provides novel insight into their stability. Sci. Rep. 2017;7:44341. doi: 10.1038/srep44341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Malik R.U., Dysthe M., et al. Sivaramakrishnan S. ER/K linked GPCR-G protein fusions systematically modulate second messenger response in cells. Sci. Rep. 2017;7:7749. doi: 10.1038/s41598-017-08029-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Wang E., Wang C.-L.A. (i,i+ 4) ion pairs stabilize helical peptides derived from smooth muscle caldesmon. Arch. Biochem. Biophys. 1996;329:156–162. doi: 10.1006/abbi.1996.0204. [DOI] [PubMed] [Google Scholar]
- 98.Mueller-Spaeth S., Soranno A., et al. Schuler B. Charge interactions can dominate the dimensions of intrinsically disordered proteins. Proc. Natl. Acad. Sci. U S A. 2010;107:14609–14614. doi: 10.1073/pnas.1001743107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Hofmann H., Soranno A., et al. Schuler B. Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. Proc. Natl. Acad. Sci. U S A. 2012;109:16155–16160. doi: 10.1073/pnas.1207719109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Brucale M., Schuler B., Samori B. Single-molecule studies of intrinsically disordered proteins. Chem. Rev. 2014;114:3281–3317. doi: 10.1021/cr400297g. [DOI] [PubMed] [Google Scholar]
- 101.Wuttke R., Hofmann H., et al. Schuler B. Temperature-dependent solvation modulates the dimensions of disordered proteins. Proc. Natl. Acad. Sci. U S A. 2014;111:5213–5218. doi: 10.1073/pnas.1313006111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Ruggeri F., Zosel F., et al. Krishnan M. Single-molecule electrometry. Nat. Nanotechnol. 2017;12:488–495. doi: 10.1038/nnano.2017.26. [DOI] [PubMed] [Google Scholar]
- 103.Holmstrom E.D., Holla A., et al. Schuler B. Accurate transfer efficiencies, distance distributions, and ensembles of unfolded and intrinsically disordered proteins from single-molecule FRET. Methods Enzymol. 2018;611:287–325. doi: 10.1016/bs.mie.2018.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Staller M.V., Holehouse A.S., et al. Cohen B.A. A high-throughput mutational scan of an intrinsically disordered acidic transcriptional activation domain. Cell Syst. 2018;6:444–455.e6. doi: 10.1016/j.cels.2018.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Dyla M., Kjaergaard M. Intrinsically disordered linkers control tethered kinases via effective concentration. Proc. Natl. Acad. Sci. U S A. 2020;117:21413. doi: 10.1073/pnas.2006382117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Sørensen C.S., Kjaergaard M. Effective concentrations enforced by intrinsically disordered linkers are governed by polymer physics. Proc. Natl. Acad. Sci. U S A. 2019;116:23124. doi: 10.1073/pnas.1904813116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Greig J.A., Nguyen T.A., et al. Jedd G. Arginine-enriched mixed-charge domains provide cohesion for nuclear speckle condensation. Mol. Cell. 2020;77:1237–1250.e4. doi: 10.1016/j.molcel.2020.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Wiggers F., Wohl S., Dubovetskyi A., Rosenblum G., Zheng W., Hofmann H. Diffusion of a disordered protein on its folded ligand. Proc. Natl. Acad. Sci. U S A. 2021;118 doi: 10.1073/pnas.2106690118. e2106690118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Fossat M.J., Zeng X., Pappu R.V. Uncovering differences in hydration free energies and structures for model compound mimics of charged side chains of amino acids. J. Phys. Chem. B. 2021;125:4148–4161. doi: 10.1021/acs.jpcb.1c01073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Nick Pace C., Martin Scholtz J. A helix propensity scale based on experimental studies of peptides and proteins. Biophys. J. 1998;75:422–427. doi: 10.1016/s0006-3495(98)77529-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Myer Y.P. The pH-induced helix-coil transition of poly-L-lysine and poly-L-glutamic acid and the 238-mμ dichroic band. Macromolecules. 1969;2:624–628. [Google Scholar]
- 112.Donten M.L., Hamm P. pH-jump induced α-helix folding of poly-l-glutamic acid. Chem. Phys. 2013;422:124–130. [Google Scholar]
- 113.Fonin A.V., Stepanenko O.V., et al. Turoverov K.К. Folding of poly-amino acids and intrinsically disordered proteins in overcrowded milieu induced by pH change. Int. J. Biol. Macromol. 2019;125:244–255. doi: 10.1016/j.ijbiomac.2018.12.038. [DOI] [PubMed] [Google Scholar]
- 114.O’Brien E.P., Brooks B.R., Thirumalai D. Effects of pH on proteins: predictions for ensemble and single-molecule pulling experiments. J. Am. Chem. Soc. 2012;134:979–987. doi: 10.1021/ja206557y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Donnini S., Ullmann R.T., et al. Grubmuller H. Charge-neutral constant pH molecular dynamics simulations using a parsimonious proton buffer. J. Chem. Theor. Comput. 2016;12:1040–1051. doi: 10.1021/acs.jctc.5b01160. [DOI] [PubMed] [Google Scholar]
- 116.Buck R.P. Ion selective electrodes, potentiometry, and potentiometric titrations. Anal. Chem. 1972;44:270–295. doi: 10.1021/ac60313a011. [DOI] [PubMed] [Google Scholar]
- 117.Plasson R., Cottet H. Determination and modeling of peptide pKa by capillary zone electrophoresis. Anal. Chem. 2006;78:5394–5402. doi: 10.1021/ac060406f. [DOI] [PubMed] [Google Scholar]
- 118.Gill S.J., Richey B., et al. Wyman J. Generalized binding phenomena in an allosteric macromolecule. Biophys. Chem. 1985;21:1–14. doi: 10.1016/0301-4622(85)85001-8. [DOI] [PubMed] [Google Scholar]
- 119.Di Cera E., Gill S.J., Wyman J. Binding capacity: cooperativity and buffering in biopolymers. Proc. Natl. Acad. Sci. U S A. 1988;85:449. doi: 10.1073/pnas.85.2.449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Gill S.J., Gaud H.T., et al. Barisas B.G. Analysis of ligand binding curves in terms of species fractions. Biophys. Chem. 1978;8:53–59. doi: 10.1016/0301-4622(78)85022-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The gray curve is the smoothed, interpolated experimental data, the orange curve is the current fit. The red dashed lines correspond to the fitted pKa values which in the q-canonical approach are defined as the pH at which two mesostates with a net charge difference of one have an equal population.
Colors are the same as in Video S1.