Abstract
We combined theory and experiments to depict physical parameters modulating the phospholipid (PL) density and tension equilibrium between a bilayer and an oil droplet in contiguity. This situation is encountered during a neutral lipid (NL) droplet formation in the endoplasmic reticulum. We set up macroscopic and microscopic models to uncover free parameters and the origin of molecular interactions controlling the PL densities of the droplet monolayer and the bilayer. The established physical laws and predictions agreed with experiments performed with droplet-embedded vesicles. We found that the droplet monolayer is always by a few percent (∼10%) less packed with PLs than the bilayer. Such a density gradient arises from PL-NL interactions on the droplet, which are lower than PL-PL trans interactions in the bilayer, i.e., interactions between PLs belonging to different leaflets of the bilayer. Finally, despite the pseudo-surface tension for the water/PL acyl chains in the bilayer being higher than the water/NL surface tension, the droplet monolayer always has a higher surface tension than the bilayer because of its lower PL density. Thus, a PL density gradient is mandatory to maintain the mechanical and thermodynamic equilibrium of the droplet-bilayer continuity. Our study sheds light on the origin of the molecular interactions responsible for the unique surface properties of lipid droplets compared with cellular bilayer membranes.
Significance
Organelles' biogenesis and function rely on membrane mechanics and phospholipid composition. Lipid droplets (LDs) are unique cell organelles because of their neutral lipid oil core shielded by a single phospholipid monolayer. LD biogenesis happens in the endoplasmic reticulum (ER) bilayer, which unzips to encapsulate the developing LD, which subsequently buds off in the cytoplasm. The ER cytoplasmic monolayer leaflet thus equilibrates with that of the forming LD. Experimental data and simulations support that this equilibration happens with different phospholipid densities and tensions between the bilayer and monolayer, but the underlying mechanisms remain unknown. A theoretical framework combined with experiments enabled us to reveal these mechanisms.
Introduction
Except for lipid droplets (LDs), most cellular organelles are bilayer bounded (1). LDs are made of neutral lipids (NLs), which are non-membrane lipids and often oily molecules. These NLs are encapsulated in the core of the LDs, covered by a single phospholipid (PL) monolayer in which proteins are embedded. LDs form in the endoplasmic reticulum (ER) bilayer following a multiple-step process (2,3). NLs are synthesized and sheltered in the ER bilayer's hydrophobic region. The NL phase separates from the ER bilayer at a critical concentration and condenses into an LD (4, 5, 6). At this stage, the LD is contiguous with the ER bilayer and can exchange proteins and lipids with its membrane (7). The nucleated LDs grow by acquiring more NLs and proteins. At maturation, LDs can be physically disconnected from the ER bilayer but may reconnect with it later to exchange content (8,9). Hence, the droplet monolayer surface is functionally connected to the ER bilayer to maintain the homeostasis of lipids and proteins of the LDs (10, 11, 12). A crucial question is how these organelles manage to share PLs and proteins while keeping their respective identities. Answering this question will help understand LD biogenesis and protein targeting principles (13, 14, 15, 16, 17). In particular, understanding how the density of PLs is set between contiguous bilayer and monolayer interfaces will allow better understanding of the mechanisms of LD assembly and protein binding (13,16, 17, 18).
Important parameters controlling LD biogenesis are the monolayer and bilayer surface tension and curvature (19, 20, 21), which depend on the PL composition of the organelles (16,22,23). The PL density regulates both the LD monolayer surface tension and its accessibility to proteins (8,16,24, 25, 26, 27, 28). First, while the ER bilayer can behave as an infinite PL reservoir to the connected LD, reconstitution approaches, cell data, and molecular dynamics simulations suggest that the droplet monolayer is less packed with PLs than the ER bilayer (25,29, 30, 31). Such a discrepancy partly explains the higher recruitment of peripheral or monotopic membrane proteins to LDs than bilayer membranes (24,25,30,32,33). Second, while the ER bilayer is of low surface tension, circa 0.01 mN/m (34), cellular LDs, made from and contiguous with the ER, have a surface tension above 1 mN/m (19,20), two orders of magnitudes higher. This tension difference is crucial for the proper emergence of LDs from the ER bilayer (16,17,19). Reasons for the discrepancies in PL densities and surface tensions between LDs and the ER bilayer are unclear as yet. Understanding the molecular basis of such differences between the two contiguous organelles will improve our knowledge of their biology.
Whether the physical properties of PL bilayers and monolayers are identical was raised several decades ago (35, 36, 37, 38) because both are self-assembled interfaces with essential functions and applications in biology and physical science. For example, early studies focused on the kinetics and mechanics of the PL monolayers of air/water or water/oil interfaces for better understanding the dynamics of lung surfactants (39) or emulsions' stability for digestion purposes (32,33,40), and so forth. In the meantime, biophysical approaches allowed studying the mechanics and dynamics of PL bilayers, an important branch of membrane biology (41, 42, 43). Altogether, these pioneer focuses on PL interfaces led to the genesis of several theoretical frameworks describing the mechanics and thermodynamics of PL-coated fluid interfaces (35,36,44). However, because LDs have gained focus relatively recently, little or no effort was devoted to studying the case of the PL monolayer interface covering an LD emerging from the ER bilayer. Mechanisms controlling the PL density and surface tension equilibrium between a droplet monolayer joined to a bilayer are currently unknown. We decided to capitalize on the established theoretical frameworks to uncover them.
This paper aims to unveil the molecular origin of mechanisms maintaining the uneven PL density between a droplet monolayer connected to a bilayer (Fig. 1 A). We customized macroscopic and microscopic frameworks of such a situation and established the relationship between the free parameters of the system.
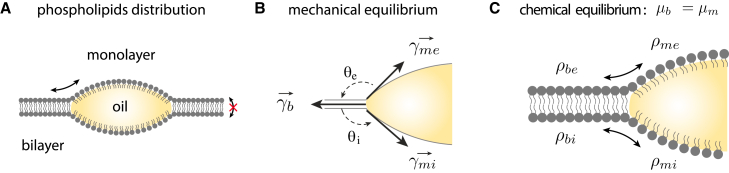
Figure 1.
Equilibrium conditions of a lipid droplet connected to a PL bilayer. (A) Schematic view of a lipid droplet embedded in a bilayer. The two PL monolayers covering the oil droplet are in continuity with the leaflets of the bilayer allowing PL exchanges. (B) The mechanical equilibrium, resulting from the balance of the surface tension forces acting on the contact line, imposes the shape of the droplet reported by the two contact angles and . The bilayer tension, the external monolayer tension, and the internal monolayer tension are respectively , , and . (C) Chemical equilibrium between PLs in the bilayer leaflet and in the monolayer. The equilibrium distribution between PLs in contiguous bilayer leaflet and LD monolayer is determined by the balance of their chemical potentials and . PLs of a given membrane leaflet are free to exchange by lateral diffusion between the contiguous LD monolayer and the bilayer leaflet but PL flip-flop is considered irrelevant. and are the PL density in the external and internal monolayer, and are the density in the external and internal leaflet of the bilayer.
Experiments validated our theoretical predictions, and this agreement allowed us to highlight molecular interactions underlying the difference in PL densities and surface tensions between the droplet monolayer and bilayer. These interactions involve (1) the adhesion between the PL monolayer leaflets forming the bilayer, which does not exist on a droplet monolayer; and (2) a pseudo-surface tension—resulting from the interaction between water molecules and PL acyl chains of the bilayer—higher than the classical water/oil surface tensions. Keeping a PL density difference is essential for the mechanical and thermodynamic equilibrium of the droplet and bilayer contiguity.
Material and methods: theory
Definition of the intensive thermodynamic quantities
The surface tension and chemical potential of a PL monolayer are defined by (supporting material, section 2),
| (1) |
where fm is the free energy per surface unit of a monolayer and the prime denotes the derivative of the function. For each monolayer, and the chemical potential of a bilayer leaflet is
| (2) |
where fb is the free energy per surface unit of a bilayer, is the density of the considered leaflet and that of the opposite leaflet, so that and . The surface tension of the bilayer is defined as
| (3) |
Materials and methods
Preparation of GUVs
All experiments were performed in the following HKM buffer (20 mM HEPES pH 7.4, 150 mM potassium acetate, 2 mM magnesium chloride): 50 mM HEPES, 120 mM K acetate, and 1 mM MgCl2 (in Milli-Q water) at pH 7.4 and 275 ± 15 mOsm.
Giant unilamellar vesicles (GUVs) were prepared by electro-formation. PLs and mixtures thereof in chloroform at 0.5 μM were dried on an indium tin oxide (ITO)-coated glass plate. The lipid film was desiccated for 1 h. The chamber was sealed with another ITO-coated glass plate. The lipids were then rehydrated with a sucrose solution (275 ± 15 mOsm). Electro-formation is performed using 100 Hz alternating current (AC) voltage at 1.0 to 1.4 Vpp and maintained for at least 1 h. This low voltage was used to avoid hydrolysis of water and dissolution of the titanium ions on the glass plate. GUVs were either stored in the chamber at 4°C overnight or directly collected with a Pasteur pipette.
GUV composition
1,2-Dioleyl-sn-3glycero-3-phosphocholine (DOPC) GUVs: 99% DOPC stained with 1% rhodamine 1,2-dioleyl-sn-glycero-3-phosphoethanolamine-N-lissamine rhodamine B sulfonyl (DOPE).
1,2-Dioleoyl-sn-glycero-3-phosphate (DOPA)-DOPC GUVs: 30% DOPA, 69% DOPC, and 1% rhodamine-DOPE.
Polyunsaturated fatty acid (PUFA)-DOPC GUVs: 30% PUFA (18:0–20:4) (1-stearoyl-2-arach- idonoyl-sn-glycero-3-phosphocholine), 69% DOPC, and 1% rhodamine-DOPE.
Preparation of DEVs (GUVs plus oil droplet)
To prepare the oil droplets, 5 μL of the oil (triolein or squalene) was added to 45 μL of HKM buffer. (20 mM HEPES pH 7.4, 150 mM potassium acetate, 2 mM magnesium chloride). The mixture was sonicated. The diameter of the resulting droplets is on the order of a few hundred nanometers. To make droplet-embedded vesicles (DEVs), GUVs were then incubated with the LDs for 5 min. The GUV-LD mixture was then placed on a glass coverslip (pretreated with 10% (w/w) BSA and washed three times with buffer).
Confocal microscope images
All micrographs of DEVs were made on a Carl ZEISS LSM 800 with ×10 air objective, and observed samples were held by glass coverslips (Menzel Glaser, 24 × 36 mm #0).
Micromanipulation and surface tension measurements by microaspiration
Micro-pipettes were made from capillaries drawn out with a Sutter Instruments pipette puller. They were used to manipulate the DEVs in order to get a side view of the system.
Additionally, surface tensions were measured and modulated using the same pipettes. As shown in (Fig. 2 B), the micromanipulation of the external LD monolayer (or the DEV's bilayer) enables the measurement of the external monolayer surface tension (or the bilayer surface tension). Using Laplace's law and the measurement of the diameter, droplet (or bilayer) diameter, and suction pressure, the surface tension of the interface can be determined:
where ΔPsuc, Rp, and Rd are the suction pressure, the pipette radius, and the droplet external radius. The suction was carried out using a syringe. The resulting pressure was measured with a pressure transducer (DP103 provided by Validyne Engineering, United States), the output voltage of which was monitored with a digital voltmeter. The pressure transducer (range 55 kPa) was calibrated prior to the experiments.
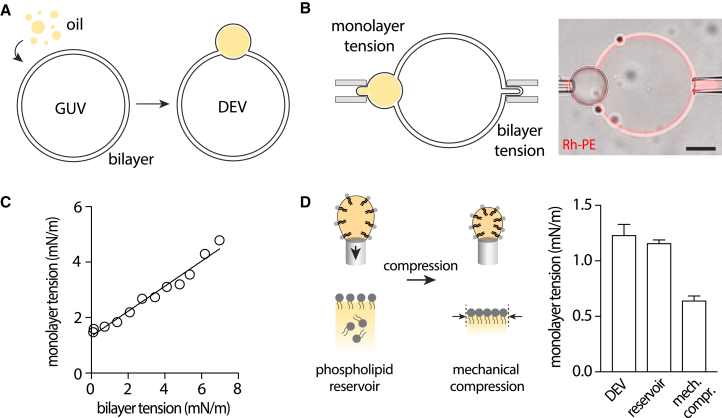
Figure 2.
Experimental determination of the interdependence between surface tensions. (A) Formation of the DEV system: GUVs are mixed with nano emulsion droplets that are incorporated into the intermonolayer space of the GUVs to form DEVs. (B, left) schematic view of micropipette measurement of the monolayer surface tension of a DEV while simultaneously measuring and increasing its bilayer surface tension with a second micropipette. (Right) Representative confocal micrograph showing a brightfield image of a triolein-DOPC DEV merged with the fluorescence image of the PLs reported by rhodamine-DOPE. Scale bar represents 10 μm. (C) Monolayer-bilayer surface tension diagram of a triolein-DOPC DEV. This DEV was selected with a droplet symmetrically positioned with respect to the bilayer; i.e., identical contact angles and . See Fig. S1A for confocal images of the experiment. See Fig. S1B and C for monolayer-bilayer tension diagram of DEVs with asymmetric droplet position and of DEVs with other phospholipidic compositions. A trend line is drawn to highlight the linear dependence of the tensions. (D) (Left) Scheme of the droplet tensiometer method: an oil-in-water droplet is generated at the tip of a tube, with PLs added in excess in the oil phase. Compression is achieved by decreasing the droplet volume through withdrawing the oil phase. (Right) Quantification of the surface tension of DOPC monolayer at triolein-buffer interface, respectively for a monolayer in continuity with a lipid bilayer with tension <0.01mN/m (DEV), a monolayer in contact with a large PL reservoir dissolved in the oil phase, and a monolayer mechanically compressed. Data are represented as mean ± SD. Related to Fig. S1D and E.
External monolayer and bilayer tension of DEVs were measured simultaneously while increasing the bilayer surface tension to obtain the monolayer tension-bilayer tension graph shown in (Fig. 2 C).
Tension measurements of triolein-buffer interface covered with PLs
A pendant droplet tensiometer designed by Teclis Instruments was used to measure the interfacial tension of oil/water interfaces. All experiments were conducted at room temperature. DOPC PLs stored in chloroform were dried under argon and mixed with triolein oil. This mix was then sonicated and store at room temperature for 2 h. To generate a PL monolayer at the oil-buffer interface, PL-in-triolein droplets (5–16.0 μL) were formed at the tip of a J-needle submerged in 5 mL of HKM buffer. The surface tension of the interface was automatically measured by the tensiometer.
Tension of an interface at equilibrium with a large reservoir of PLs dissolved in the oil phase
Triolein was supplemented with 0.5% (w/w) DOPC to get above the critical micellar concentration. This mix was used in the pendant droplet tensiometer to form a DOPC monolayer at the oil-water interface. As the PLs exceeded the critical micellar concentration, the oil phase acted as a PL reservoir in supplying PLs to the monolayer. Surface tension was measured until a plateau was reached (Fig. S1 D). This plateau of tension is the tension designated as the tension of a monolayer connected to a PLs reservoir.
The tension of a mechanically compressed PL monolayer
Triolein was supplemented with 0.05% (w/w) DOPC. This mix was used in the pendant droplet tensiometer to form a DOPC monolayer at the oil-water interface. The PLs relocated at the oil-buffer interface, resulting in a decrease of surface tension. After tension stabilization, we started to record tension while gradually sucking up the oil back into the needle. This resulted in the compression of the PL monolayer at the interface, increasing the PL density and decreasing surface tension. At some compression level, a tension plateau was reached (Fig. S1 E). This plateau of tension is the tension designated as the tension of a monolayer mechanically compressed at its maximal PL density.
PLs monolayer characterization (DOPC)
A DOPC monolayer was formed at the triolein-buffer interface using the pendant droplet tensiometer using the same condition as described in the above paragraph. After tension stabilization, the droplet area was decreased while recording surface tension (Fig. S2 A and B). This surface tension-droplet area isotherm is then fitted by Eq. 14, with given by the van der Waals equation of state and is the number of PLs on the droplet interface. It allows deducing the values of the parameters , (and ).
Determination of the contact angles between the droplet and the bilayer
DEVs were imaged at their equatorial plane (side view). Two osculating circles are adjusted to delimit the droplet and bilayer of the DEV. θe, the contact angle formed by the two tangents originating from the intersection point of the two circles (see Fig. S3 A–D), can be determined geometrically using the following equation derived from the law of cosines:
where () is the radius of the droplet auscultating circle, () is the radius of the bilayer auscultating circle, and () is the distance between the two centers of the two osculating circles.
Quantification and statistical analysis
Statistical analysis
Unless mentioned, all values shown in the text and figures are mean ± SD.
Equipment and reagents
Equipment
All micrographs were made on a Carl ZEISS LSM 800. Glass coverslips: Menzel Glaser (24 × 36 mm #0). Micro-pipettes were made from capillaries (1.0 mm outside diameter × 0.58 mm inside diameter × 150 mm length, 30-0017 GC100-15b Harvard Apparatus) with a micropipette puller (Sutter instrument model P-2000). Micromanipulation was with an Eppendorf TransferMan 4r. Pressure measurement unit (DP103) was provided by Validyne Engineering (United States). Plasma cleaner was purchased from Harrick Plasma (PDC-32G-2) (230 V) and used at 0.8 mbar of air pressure.
Chemical product list
PLs
DOPC, DOPA, PUFA (18:0–20:4) (1-stearoyl-2-arach- idonoyl-sn-glycero-3-phosphocholine), and rhodamine-DOPE were from Avanti Polar Lipids (Alabaster, AL). Triolein (glyceryl trioleate T7140), squalene (S3626), sterol ester (C9253 1G), HEPES (54457–250-F), K acetate (P1190), MgCl2 (M8266-100G), BSA 98% (A7906-100G), sucrose 99.5% (59378-500G), and mPEG5K-silane (JKA3037) were from Sigma-Aldrich.
Results
The results section is organized as follow. We first present the thermodynamic equilibrium relations, which govern the droplet morphology and the PL distribution between the droplet monolayer interfaces and the bilayer. In the second part, we analyze one important and experimentally testable consequence of the equilibrium conditions: the interdependence between the surface tensions of the droplet and the bilayer, which reflects the coupling between the monolayer and bilayer PL densities. The theoretical predictions made from this second part are successfully verified experimentally in the third part. In the fourth part, we present a microscopic theoretical description of the contiguous monolayers and bilayer, enabling us to derive the state equations of these interfaces. These equations are then used to understand the molecular origin of the density difference (part five) and surface tension difference (part six) between the monolayers and the bilayer. In the last part, a quantitative comparison between theory and experiments is made to validate the theoretical approach and its underlying hypothesis.
Thermomechanical equilibrium of a lipid droplet connected to a PL bilayer
We consider a droplet of fixed volume, above tens of nanometers in size, connected to a PL bilayer (Fig. 1 A). At this scale, the contribution of the bending elasticity and long-range interactions of the different interfaces is negligible (17,19). Hence, the PL bilayer and the droplet interfaces can be described as homogeneous fluid interfaces joining at the droplet edge (17). A line tension arises at this contact, but its contribution to the order of tens of pN is negligible with respect to surface tension forces (17) (discussion of the origin and influence of the line tension in supporting material sections 1 and 3). The free energy of the droplet embedded in a bilayer is then
| (4) |
where , , and are the area of the three interfaces (bilayer and monolayers covering the LD at the “external” and “internal” side); , are the PL surface density in each bilayer leaflet and each monolayer (Fig. 1 C); and and are the free energy per surface unit of a PL bilayer and a PL monolayer at the water/oil interface. (A more thorough discussion of the assumptions leading to Eq. 1 is provided in supporting material section 1). We consider that PLs freely diffuse and equilibrate between the droplet and the bilayer (Fig. 1 A). PL flip-flop, which takes several hours or days under passive conditions (45,46), is much slower than the lateral diffusion of PLs (∼μm2/s) (21) and is negligible at relevant time scales (Fig. 1 A). Also, experimentally, PLs are insoluble in the NL oil phase, which is why they self-assemble into droplet interface bilayers (19); therefore, PL exchange does not occur through the droplet in the relevant time scales. Under these conditions, the PL number of each leaflet is constant,
| (5) |
where and can be different.
At equilibrium, the morphology of the connected droplet and bilayer, as well as the distribution of PL between the droplet and the bilayer, minimizes the free energy (Eq. 4), under the constraints of Eq. 5 and of fixed droplet volume. This minimization yields the usual equilibrium conditions presented in the following.
The droplet and bilayer shapes obey the laws of three-fluid phase wetting systems (47). The interfaces must have a constant mean curvature (Laplace’s law). We focused on axisymmetric geometries for which the droplet interfaces are spherical caps, and the bilayer can either be flat or bear a constant curvature. The droplet morphology is fully characterized by the contact angles between the droplet interfaces and the bilayer, and (Fig. 1 B). These angles are fixed by the balance of the forces acting at the contact line (Fig. 1 B): or,
| (6) |
where , , are respectively the surface tension of the external and internal monolayers of the droplet (, ), and the bilayer (). In vitro experiments (20) confirmed the validity of Eq. 6 to describe the morphology of large membrane-embedded droplets. In the particular case where the bilayer is tensionless, , the angles are not unequivocally determined but must be such that , which implies that the droplet is spherical.
The PL partitioning between the bilayer and droplet monolayers (Fig. 1 C) is controlled by the chemical potential equilibrium,
| (7) |
where , , , respectively denote the chemical potential of the external and internal monolayers of either the droplet (, ) or the bilayer (). A monolayer and its contiguous bilayer leaflet have equal chemical potentials. Because of the rapid diffusion of PLs, the chemical potential equilibrium is quickly reached, much faster than the growth rate of a cellular LD (∼minutes) or the time scale of perturbations imposed in DEVs (16,20).
Surface tensions and chemical potentials are functions of the PL densities: , , , where , can be expressed in terms of the free energy densities and defined in Eq. (4) and their derivatives, Eq. 1, 2, and 3 (section, “materials and methods”). It follows that the relations (6) and (7) are interdependent: a variation in PL densities modulates tensions, which alter the contact angles (Eq. 6) and interface areas, as the droplet volume is fixed. Conversely, changes in morphology, and, hence, in interfacial areas, redistribute PLs because of mass conservation (Eq. 5) and, subsequently, modify chemical potentials (Eq. 7).
In conclusion, for a given oil volume, number of PLs in each membrane leaflet, and bilayer tension, the PL densities, , , , , and the contact angles, , , adjust in a coupled manner to fulfill the thermomechanical equilibrium conditions (Eq. 6 and 7).
Coupling between PL densities and between surface tensions
The above equilibrium relations impose an interdependence between the different interfaces' PL densities and, thus, the droplet and bilayer surface tensions via two distinct mechanisms.
The first coupling mechanism pertains to the chemical potential equilibriums, Eq. 7. Indeed, a slight variation in surface tension of one interface will modify the density of this interface. In response, PLs will redistribute between the adjacent interfaces to re-establish the equilibrium of the chemical potentials (Eq. 6). Such an adjustment will change the respective PL densities and, hence, the surface tensions. The link between variations of surface tension and chemical potentials of an interface, due to variation of its PL density, is expressed by the Gibbs-Duhem relations,
| (8) |
Combining these relations and the differentials of Eq. 7, , we obtain a general link between surface tension variations,
| (9) |
This first coupling due to the chemical potential equilibrium (7) is the unique coupling in two practical and biologically interesting situations: a symmetric bilayer and an infinite bilayer reservoir.
In a symmetric membrane, and , the balance of chemical potentials (Eq. 7) reads and therefore imposes an unequivocal relation between bilayer and monolayer tensions, and . Thereupon, Eq. 9 becomes,
| (10) |
This relation indicates that the droplet interfacial tension increases with the bilayer one with a slope proportional to the ratio of their PL densities.
For a droplet embedded in a large ( and possibly asymmetric membrane, the bilayer behaves as an infinite PL reservoir of fixed PL density, independent of the state of the droplet. This configuration is more relevant in cell conditions when nascent LDs form in the ER membrane. In this case, a similar relation to Eq. 10 holds,
| (11) |
and with (derivation of Eq. 11 and definition of in supporting material, section 6.3). This equation shows that the monolayer tension should also increase linearly with the bilayer ones as for a symmetric membrane, but with a numerical pre-factor depending on the membrane asymmetry; if the external leaflet is less dense than the internal one and vice versa.
A second density coupling mechanism exists for small (bilayer area comparable with droplet area) and asymmetric membranes. This coupling arises from the PL number conservation (Eq. 5) and the mechanical equilibrium (Eq. 6), together linking the PL distribution to the system's morphology. A change in surface tension affects the morphology (Eq. 6), i.e., the surface area of the interfaces, which in turn affects the densities (Eq. 5), and hence tensions. No simple mathematical relations resembling Eq. 9 expressing this coupling can be derived.
Experimental determination of the interdependence between surface tensions
We wanted to experimentally test the theoretical findings by probing the interdependence between the droplet and bilayer surface tensions. For this purpose, we used the DEV system (19,48) (Fig. 2 A), which mimics the theoretically described situation of an oil droplet in contiguity with a bilayer. DEVs were formed by inserting triolein droplets within the bilayer of GUVs made of DOPC (48).
The external droplet monolayer and the bilayer of the DEV were captured by two micro-pipettes (Fig. 2 B). We selected DEVs with a symmetrically positioned droplet, i.e., identical contact angles , which, consequently, have similar tension, (Eq. 6). These DEVs meet the symmetric condition leading to Eq. 10, which can be tested experimentally. To establish the tension dependency predicted by this equation, we imposed the DEV bilayer tension step by step, by fixing the aspiration pressure of the micropipette, and concomitantly measured the micropipette-aspiration-applied surface tension of the external monolayer of the droplet (Fig. 2 B). We found that the monolayer tension increased with the bilayer tension (Fig. 2 C), agreeing with the theoretical description: increasing the bilayer tension decreases the chemical potential in the bilayer leaflets; to keep the chemical potential equilibrium, the droplet must, therefore, supply PLs to the bilayer, resulting in its tension increase.
Interestingly, the tensions' dependency followed a linear trend line (Fig. 2 C). Based on Eq. 10, this linear dependency suggests that the ratio of the monolayer-to-bilayer PL density did not vary, independently of the bilayer tension. The slope of 0.45 ± 0.02 indicates that the bilayer PL density is slightly higher than the monolayer one, agreeing with our previous fluorescence and droplet tensiometer measurements where this value was 0.435 (30).
The PL density is maximum, i.e., close to full packing, in a tensionless bilayer. Since the droplet monolayer PL density evolves like the bilayer one, one may speculate that it also reaches near close packing when the bilayer is tensionless. Thereupon, the monolayer tension would also be close to zero. Such assumption was not valid as, when the bilayer tension fell to almost zero (<0.01 mN/m), the monolayer tension was non-negligible, around 1.5 mN/m (Fig. 2 C). We initially hypothesized that the non-zero tension of the monolayer could be due to the nature of the tensionless bilayer of the DEV, which may have been unable to supply PLs to the droplet. To test this hypothesis, we changed the system and put the droplet in contact with another type of PL reservoir.
At the tip of a tensiometer apparatus, we generated a triolein oil-in-buffer droplet, over-supplied with PLs in the oil (0.5% w/w to triolein) (Fig. 2 D, left). In this setting, the oil phase acts as a PL reservoir to the droplet interface. As soon as the droplet was formed in the buffer solution, the surface tension dropped, due to the spontaneous adsorption of PLs to the interface, to reach an equilibrium value of 1.15 mN/m (Figs. 2 D and S1 D); without PLs, the triolein/buffer tension is ∼34 mN/m. Thus, even with this reservoir, the monolayer tension was non-zero and close to the ∼1.5 mN/m obtained with DEV (Fig. 2 C). Next, starting from the equilibrium tension at 1.15 mN/m, we mechanically compressed the PL monolayer of the droplet by sucking off the droplet volume (Figs. 2 D and S1 E). Even under this action, surface tension decreased but was still not close to zero, ∼0.6 mN/m, compared with the tensionless bilayer (<0.01 mN/m). These results indicate that, unlike a bilayer, a droplet monolayer has specific features, detailed hereafter, that prevent it from reaching a high PL density and near-zero surface tension.
Altogether, the experiments with DEVs are consistent with the theoretical prediction (Eq. 10). For symmetric conditions, the monolayer tension responds linearly to an increase in bilayer tension, implying that the PL density ratio is constant between the bilayer and the monolayer. However, our results revealed two essential aspects: (1) although the bilayer and the droplet are connected, the PL density is lower for the droplet monolayer than the bilayer; and (2) the tensions of the droplet and the bilayer are largely different in general; even in contact with a bilayer of very low tension, the droplet remains at relatively high tension (above 1 mN/m). In the following sections, we delve deeper into these findings with a theoretical approach, subsequently validated by a quantitative analysis of the surface tension curves of DEVs.
Microscopic description of the contiguous droplet-bilayer system
To pinpoint the origin of the molecular interactions responsible for the discrepancy in tension and PL density between the monolayer and bilayer, we developed a microscopic description closely following the approach and assumptions of refs. (36,44). The goal is to express the equations of state relating surface tensions, chemical potentials, and densities, for a monolayer and a bilayer.
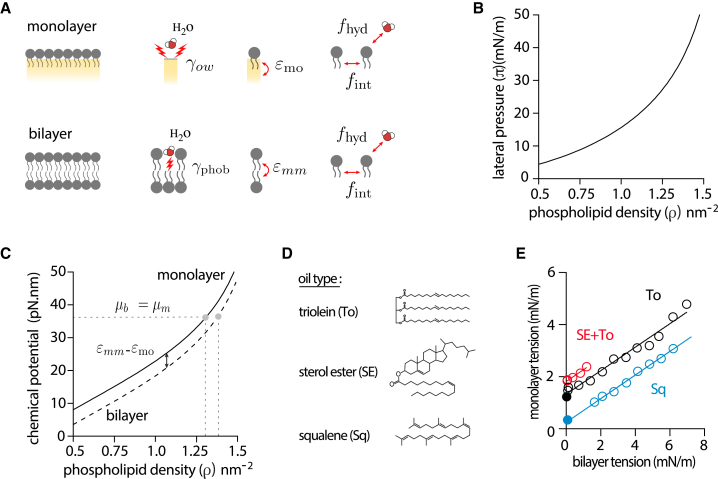
The different contributions to the free energy of a monolayer and a bilayer are depicted in Fig. 3 A. The free energy per surface unit of a monolayer at a water/oil interface function of the PL density can be written as
| (12) |
Figure 3.
Microscopic description of the contiguous droplet-bilayer system. (A) Microscopic contributions to the free energy density of a monolayer and of a bilayer. For the monolayer: the surface tension of the bare water/oil interface (), the interaction of the PL tails with the oil phase , the lateral interaction between PLs (), and the interaction of the PL headgroups with water (). For the bilayer: the unfavorable interactions of the PL tails with water (), the trans interaction between PL tails () of the apposed leaflet, the lateral interaction between PLs (), and the interaction of the PL headgroups with water (). (B) Lateral pressure as a function of PL density at the triolein-water interface deduced from a compression isotherm obtained from a pending droplet experiment (see Fig. S2A and B). (C) Chemical potential of a bilayer and a monolayer as a function of PL density. The two chemical potentials vary identically but are shifted by the amount . At equilibrium, a monolayer in contact with a bilayer has the same chemical potential () and therefore has different PL densities, whose values are directly affected by the gap. (D) Molecular structure of the different oils used to probe the effect of oil composition on monolayer-bilayer surface tension diagram. (E) Monolayer-bilayer surface tension diagram of DOPC DEVs made with different oil composition: sterol ester-triolein (1:3) (red circles), triolein (black circles), and squalene (blue circles). DEVs were selected with a droplet symmetrically positioned with respect to the bilayer. Black dot represents the average monolayer tension of osmotically deflated triolein DEVs (bilayer tension <0.03mN/m; n = 17). Blue dot represents the average monolayer tension of osmotically deflated squalene DEVs (bilayer tension <0.09mN/m; n = 9). See Fig. S2C for monolayer-bilayer tension diagram of squalene and sterol ester-triolein (1:3) DEVs with asymmetric positions of the droplet.
The four terms account respectively for the bare oil/water surface tension, lateral PL-PL interactions, hydrophilic interaction of PL head groups with water, and PL tails interaction with oil. The free energy density of the bilayer is
| (13) |
The functions and in Eq. 13, which account for the lateral interactions between PLs and from PL head -water in a bilayer leaflet, are identical to the ones in Eq. 12 for the monolayer. The term accounts for the trans interaction between the two leaflets, i.e., the interaction between the tails of PLs belonging to different leaflets. Last, accounts for the hydrophobic interaction of PL tails with water, responsible for the cohesion of bilayer in water. Following ref. (37), this contribution is supposed to be negligible for monolayer (and is thus absent in Eq. 12) and nearly constant for bilayer, with the parameter of the order 34 to 39 mN/m for DOPC. The contributions and are assumed to be linear in PL densities (37), and , i.e., the free energy per PL molecule due to PL tail interaction (with oil in a monolayer and with the tails of PL in the other leaflet in a bilayer), and are constant parameters.
The surface tension and the chemical potential of a monolayer, functions of the PL density, can be deduced from the free energy Eq. 12 and Eq. 1 (section “materials and methods”):
| (14) |
and
| (15) |
where the prime denotes the derivative of the function. The quantity , named the lateral pressure, is defined as : it arises from lateral PL-PL interactions and hydrophilic PL head interactions. This lateral pressure can be measured and well described theoretically by classical equations of state of two-dimensional fluids, such as the van der Waals equation of state (37) (see below).
The surface tension of a bilayer function and the chemical potential of one of its leaflets, functions of the leaflet densities, are deduced from Eq. 13 and Eq. 2 and 3 (section “materials and methods”), and read
| (16) |
and
| (17) |
(The chemical potential of a leaflet is independent of the density of the other leaflet under our assumptions.)
A central parameter in these state equations (14, 15, 16, and 17) is the lateral pressure . By using the pending drop experiment, described Fig. 2 C and ref. (30), we obtained for a DOPC monolayer at the water-triolein (TO) interface (Figs. 3 B and S2 A); it was well described by a van der Waals state equation, . The parameter characterizes the excluded area due to steric repulsion and the strength of the lateral interactions between PL molecules (section “materials and methods”; Fig. S2 B). The determination of enabled us to determine (up to a constant) using Eq. 15 (Fig. 3 C). Note that the exact profile of depends on the PL type, yet the global features of the curves in Fig. 3 B and C should be generic.
Combining the state equations (14, 15, 16, and 17) with the equilibrium conditions (7), we discuss in the following two sections the origin of the density difference between the connected monolayers and bilayer, and then the basis of their surface tension difference. Additionally, these equations of state allow performing a complete quantitative analysis of the surface tension curves obtained for DEVs, in particular in the case of asymmetric DEVs (last section).
Droplet-bilayer PL equilibration following the microscopic description
PL partitioning is governed by the equilibrium condition (7): the PL densities in adjacent monolayer and bilayer leaflet, and , are such that . The chemical potentials of the monolayer and bilayer leaflet, and , functions of the PL density, as given by the state Eq. (15) and (17), are shown in Fig. 3 C. The two curves have the same profiles, but are shifted by . Then, for the chemical potentials to be equal, the densities of contiguous monolayer and bilayer must be different in general, , as long as . Thereupon, the microscopic description (Eq. 17) pinpoints the parameter as the primary lever imposing the PL density difference between the monolayer and bilayer. Remember that this parameter quantifies the difference in interactions of PL tails with their underneath environments, which are the tails of PLs in the opposite leaflet for the bilayer, and the NL oil phase for the droplet monolayer (Fig. 3 A). Depending on the sign of , the monolayer lipid density is always larger or smaller than the bilayer leaflet density.
However, according to the surface tension measurements (Fig. 2 C) and Eq. 8, the PL density is expected to be lower at the droplet interface , meaning that . Consequently, trans interactions between PL tails in the bilayer are energetically more favorable than the interactions of PL tails with oil molecules in the droplet.
Assuming a slight relative difference of PL density between the droplet monolayer and bilayer leaflet, and expanding the equilibrium relation to the linear order (supporting material, section 8), one obtains
| (18) |
This equation shows that the relative density difference between the bilayer and droplet monolayer is modulated by (Fig. 3 A). A bilayer is stable only in a narrow range of PL density, near close packing, and can be stretched by only about 5% (49,50). Consequently, should be very large and, according to Eq. 18, the relative difference in density between a bilayer leaflet and its contiguous droplet monolayer should be relatively small. This interpretation agrees with the density ratio obtained from the slope of Fig. 2 C using Eq. 10 and our recent experimental finding in DEVs (30), suggesting that, for 100 PLs on a bilayer leaflet, droplet monolayer in contiguity with this leaflet has ∼90 PLs.
Surface tensions comparison following the microscopic description
Combining the previous results on the PL distribution with the state equations (14 and 16) allows understanding how the droplet tension compares with the bilayer one. In particular, we wanted to understand why the droplet remains with a non-zero tension while being in contact with a tensionless bilayer (Fig. 2 C).
According to Eq. 14, the droplet surface tension is maximal in the absence of PLs, equal to , and decreases when the PL density or the lateral pressure increases. The bilayer tension has a similar dependency on the PL density (Eq. 16), with being reminiscent of , although they have different molecular origins (Fig. 3 A). As found above, the bilayer PL density should always be slightly higher than the droplet monolayer one. Consequently, the monolayer should be of lower lateral pressure than the bilayer leaflet; i.e., .
At zero bilayer tension, the mechanical equilibrium condition (6) imposes the same tension and thus the same PL densities between the two droplet monolayers. It follows from Eq. 7 that the two bilayer leaflets also have the same density, . Under this condition, the lateral pressure in the bilayer balances exactly the hydrophobic contribution in Eq. 14, . On the droplet monolayer side, the lateral pressure is lower, i.e., < , and too small to completely cancel the tension of the droplet interface (Eq. 13), . Assuming a slight relative difference in PL density between a monolayer and a bilayer leaflet (30), the tension of a droplet embedded in a tensionless bilayer can be approximately expressed by (supporting material, section 8),
| (19) |
This equation shows that and , which controls the monolayer-bilayer density mismatch, are the two key parameters keeping the droplet monolayer tension to a non-zero value when the bilayer is tension free.
The parameters and , are functions of the oil type. Thus, changing the oil type should vary the tension of the droplet when the bilayer is tensionless (Eq. 14). To test this prediction, we established the monolayer-bilayer tension diagram of DEVs made with different oils. Namely, we used a triolein-sterol ester mixture or squalene (Fig. 3 D and E). Independently of the oil type, a linear trend was observed for symmetric DEVs, as expected from Eq. 10. The slopes were also conserved, confirming that these oils' monolayer-bilayer densities were similar (30). However, the droplet tension at zero bilayer tension was significantly different (Fig. 3 E), agreeing with our prediction from the theoretical analysis (Eq. 19). At very low bilayer tension (<0.1 mN/m), the squalene droplet had a lower tension than the triolein one (Fig. 3 E). Since was respectively 23.7 mN/m and 34 mN/m for squalene and triolein, the term I I would be lower for squalene, which, following Eq. 19, would partly explain the lower droplet monolayer tension value for squalene.
Validation of the microscopic model by the quantitative analysis of the DEV system
We wished to compare quantitatively experimental data obtained with the DEV system and theory output to go beyond the qualitative agreement between theoretical predictions and experimental observations. A quantitative agreement would eventually validate our theoretical approach and the underlying hypothesis.
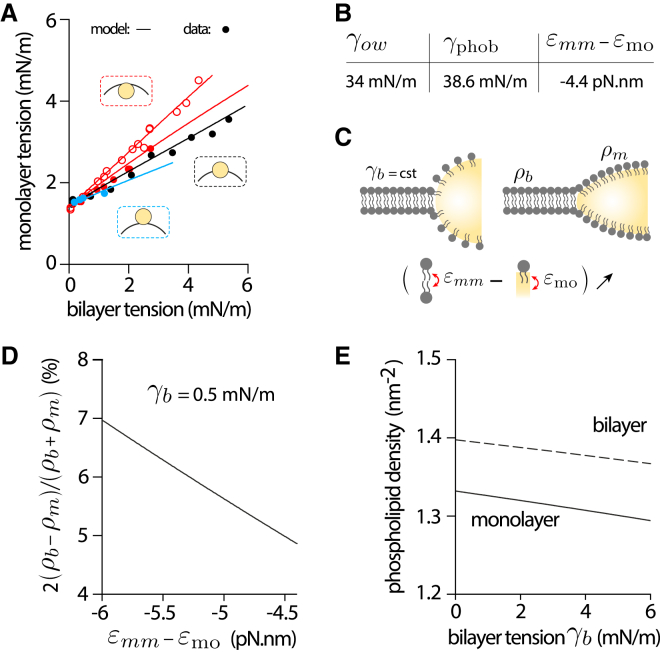
We built a complete theoretical description of the DEV system based on the thermodynamic approach developed in the preceding sections (supporting material, section 7). The model allows us to compute all the characteristics of a DEV, in particular the surface tension of the different interfaces, which are experimentally measurable and tunable observables. The parameters of the model are of two origins: geometrical and physicochemical. The geometrical parameters (oil volume, vesicle inner volume, and leaflet asymmetry in PL number) are specific to each DEV and are experimentally obtained by image analysis. The physicochemical (or microscopic) parameters are the ones in the state equations (14, 15, 16, and 17) and only depend on the PL and oil types composing the DEV. The physicochemical parameters and the lateral pressure were determined by the drop tensiometer method (Fig. S2 B). The only unknown physicochemical parameters of the model are hence and (Fig. 3 A). We adjusted these two parameters to fit the model to the surface tensions data of Fig. 2 C, obtained with a symmetric DEV. We found that mN/m, close to reported values for DOPC (36), and pN.nm (Fig. 4 B). The value of looks rather low but is sufficient to proffer a higher PL packing to the bilayer than the monolayer (Eq. 17). This means that the small differences between the PL tail-NL interactions on the droplet and the tail-tail interactions between PLs on opposite leaflets of the bilayer are sufficient to induce a PL density gradient between the bilayer and the monolayer.
Figure 4.
Validation of the microscopic model by the DEV experimental system. (A) Monolayer-bilayer surface tension diagram of a triolein-DOPC DEVs having droplets with different positions relative to the bilayer: centered droplet (, black dots), droplet budding outward of the bilayer (, blue dots), or droplet budding inward of the bilayer (, red dots). See Fig. S3A–D and section “materials and methods” for angle determination. Theoretical model was used to fit the centered experimental data (black line) and enabled to extract the microscopic parameters. Using the same parameters and only adjusting the droplet's size and position parameters, the model perfectly fit the data of the other DEVs with asymmetric droplet positions (blue and red lines). (B) Main microscopic parameters obtained by fitting the model to the centered experimental data. (C) Schematic illustration of the effect of the variation of () on PL density at the surface of a droplet in contiguity with a bilayer. If the bilayer tension is kept constant, the increase leads to a higher density of PLs on the surface of the droplet and therefore a lower surface tension of the droplets, which causes the droplet to spread. This can be achieved by increasing the affinity of the PL tails for the oil, or decreasing the strength of the trans interactions between PL tails in the bilayer. (D) Theoretical prediction of the effect of the variation of on the difference between the density of PLs in a bilayer sheet and that at the droplet surface. The bilayer surface tension () was kept at 0.5mN/m. (E) Theoretical prediction of the variation of the surface tension of the bilayer () on the PL density in the bilayer and in the monolayer of droplets. was kept constant at −4.4 pN.nm.
By definition, the above values of the different physicochemical (or microscopic) parameters should only be set by molecular interactions, exclusively depending on the PL and oil type and not on DEV geometry. Therefore, the values of these parameters should allow fitting the model for any DEV geometry. To test this prediction, we considered DEVs, made of DOPC vesicles and triolein droplets of different sizes, and different asymmetries in DOPC number between their internal and external leaflets. PL asymmetry is obvious at low bilayer tension, as the droplets are spherical (16,20) and differently positioned in the bilayer (16,20): the droplets are either centered, , or emerged outward, , or inward, (Figs. 4 A and S3 A–D). We took advantage of this variability in DEV geometry, i.e., in size and asymmetry, to test whether the microscopic parameters' values (Fig. 4 B) allow us to predict the correct DEVs tensions for all DEV geometry.
For each DEV (Fig. S3 A–D), including the one in Fig. 2 C, we measured the tension of the external droplet monolayer against the bilayer one, (Fig. 4 A, data points); we also determined by image analysis the DEV geometrical parameters (size and droplet position asymmetry). Then, using the microscopic parameters' values (Fig. 4 B), we computed as a function of for each DEV imposing specific geometrical constraints (Fig. 4 A, model, solid lines). Strikingly, the computed curves were perfectly superposed to each of the experimental data they modeled, without any adjustment of the microscopic parameters (Fig. 4 A). Given the number of experimental data points, the perfect match with the model, with the pre-adjustment of only two microscopic parameters, i.e., and , supports the validity of the theoretical approach.
Two additional features also support the validity of our model. First, at zero bilayer tension, the tensions of the droplet interfaces are the same for all the DEVs (Fig. 4 A), which had different geometries. This observation agrees with Eq. 17, which predicts in this regime that the tensions of the LD interfaces should exclusively depend on the microscopic parameters and be independent of DEV size and morphology. Second, the slope of curve depends on the droplet position at zero bilayer tension (Fig. 4 A). The more the droplet budded inward, the steeper was the slope . The exact expression of the slope at predicted by the theory is provided in supporting material, section 6.4 and, indeed, confirms that the larger at zero tension, the larger .
In conclusion, the comparison of the DEV experimental data to the theory output showed a quantitative agreement, which supports the validity of our theoretical approach and its underlying hypothesis.
Discussion
LDs have multiple biological functions that rely on the targeted proteins to their surface and their surface tension. The PL monolayer of LDs represents a barrier for proteins to access to LDs and determine their tension (13,14,18,19,51). Since LDs share a hemimembrane with the ER bilayer, at least during the steps of lipid droplet assembly (52), understanding how PLs partition between the bilayer and the droplet monolayer is crucial.
We developed macroscopic and microscopic models to establish the relationship between the system's free parameters composed of an oil droplet embedded in a PL bilayer. We subsequently set up experiments based on DEVs to test the theoretical outputs and found strong agreements. Such achievement led us to pinpoint molecular parameters or interactions responsible for the unequal PL density and surface tensions between the droplet and the bilayer.
The PL density discrepancy between the droplet monolayer and the bilayer in contiguity essentially pertains to the different environments underneath a PL layer in the bilayer and the droplet monolayer. For the bilayer, the PL tails of a leaflet interact with the PL tails of the counterpart leaflet (the interaction energy per molecule is ) while, in the monolayer, the PL tails interact with the NL oil phase beneath the monolayer (the interaction energy per molecule is ) (Fig. 3 A and C). At a constant bilayer tension, increasing , for example by increasing the affinity between oil molecules and PL acyl chains, will result in a PL flux from the bilayer to the droplet, thereby increasing the droplet PL density (Fig. 4 C, ). Such an improvement in PL cover will induce a decrease in the droplet tension and, consequently, the spreading of the droplet, according to Eq. 6. Quantitatively, a 2 pN.nm variation of , at fixed bilayer tension, will result in a variation in density of the order of a few percent (Fig. 4 D).
Should the bilayer present an asymmetry of PL composition between its two leaflets, the droplet's inner and outer PL monolayers may experience different interactions with oil molecules and therefore have different densities. Such an asymmetric monolayer PL distribution will promote the droplet emergence to the better-covered monolayer (16).
The bilayer tension also affects the PL densities (Fig. 4 E). If the bilayer tension is increased, the densities of the bilayer and monolayer will decrease simultaneously. However, the relative difference between the droplet density and the bilayer density remains almost constant.
PL packing voids occur more often when triacylglycerols are infused in a bilayer (25,27,29,32,49). Such observations already suggested, at least qualitatively, that a lipid droplet connected to a bilayer would be less packed with PLs. This is confirmed by fluorescence measurement showing that a droplet monolayer connected to a bilayer is ∼13% less packed with PLs than the bilayer. Our approach in this paper provided an alternative measurement of the relative PL densities but, most importantly, it points to the origin of such PL density gradients.
Previous experimental and theoretical studies illustrated the relevance of the surface tension difference between a lipid droplet and its host membrane (16,17,20,53). This tension gap controls, to a large extent, the morphology of droplet, its stability, and budding capacity. While the tension of organelles such as the ER is very low (34), the surface tension of LD forming in their membranes is much larger (19). This could seem surprising since the monolayers at the LD interfaces and the host membrane leaflets are connected. The present work shows how the surface tensions of the forming LD and host membrane are coupled in general and reveals the microscopic origin of the different tensions. Our results explain how a lipid droplet connected to a nearly tensionless membrane can keep a relatively high surface tension.
Finally, our theoretical approach may present two limitations. First, our model does not explicitly consider the partitioning of oil molecules from the droplet to the bilayer hydrophobic region, as seen in DEVs, which alters the membrane's biophysical properties (49). From a theoretical standpoint, it will be interesting to include the presence of these oil molecules to gain accuracy in the microscopic description. Nonetheless, the match between our theoretical predictions and experimental data, including fluorescent density measurements with DEVs (30), suggests that the oil-free description captured the dominant mechanisms controlling the PL densities, as well as the interdependence between surface tensions. Second, in the biologically relevant tensions, below 0.1 mN/m (34), the bilayer tension mostly affects the excess area stored in the thermal undulations (54,55) rather than the intermolecular distance between PLs in the bilayer. In other words, tension affects the effective density, i.e., the inverse of the projected area per molecule, rather than the real surface density. This effect of thermal undulations is not included in our theoretical description, in particular in the equation of state (16) for the bilayer tension. Our model might thus be unable to precisely reproduce curves (Fig. 4 A) for very low bilayer tension, provided such curves could be obtained experimentally in this range. However, the most important effect expected is that, in the low-tension regime, the real surface density of the bilayer is always very close to the zero-tension density and then the monolayer tension close to (Eq. 19). Then, the conclusions drawn for the zero-bilayer-tension case should hold more generally in all the low-bilayer-tension regimes.
In conclusion, our present study highlights critical parameters that may modulate the PL density at the surface of LDs connected to the ER. More generally, our approach may be upgraded to study how PL mixtures, and even protein mixtures, redistribute or partition between the bilayer and the droplet, a crucial question in lipid droplet biology.
Author contributions
A.C., L.F., and A.R.T. designed the study, performed research, analyzed data, and wrote the paper.
Acknowledgments
We are thankful to our group members for their valuable comments and critical discussions about the manuscript.
This work was supported the ANR-18-CE11-0012-01-MOBIL and ANR-21-CE11-LIPRODYN to A.R.T.
Editor: Sarah Veatch.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.11.022.
Contributor Information
Lionel Forêt, Email: lionel.foret@phys.ens.fr.
Abdou Rachid Thiam, Email: thiam@ens.fr.
Supporting material
References
- 1.Thiam A.R., Farese R.V., Jr., Walther T.C. The biophysics and cell biology of lipid droplets. Nat. Rev. Mol. Cell Biol. 2013;14:775. doi: 10.1038/nrm3699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Walther T.C., Chung J., Farese R.V., Jr. Lipid droplet biogenesis. Annu. Rev. Cell Dev. Biol. 2017;33:491–510. doi: 10.1146/annurev-cellbio-100616-060608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jackson C.L. Lipid droplet biogenesis. Curr. Opin. Cell Biol. 2019;59:88–96. doi: 10.1016/j.ceb.2019.03.018. [DOI] [PubMed] [Google Scholar]
- 4.Thiam A.R., Ikonen E. Lipid droplet nucleation. Trends Cell Biol. 2020;31:108–118. doi: 10.1016/j.tcb.2020.11.006. [DOI] [PubMed] [Google Scholar]
- 5.Khandelia H., Duelund L., Ipsen J.H. Triglyceride blisters in lipid bilayers: implications for lipid droplet biogenesis and the mobile lipid signal in cancer cell membranes. PLoS One. 2010;5:e12811. doi: 10.1371/journal.pone.0012811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Choudhary V., Ojha N., Prinz W.A. A conserved family of proteins facilitates nascent lipid droplet budding from the ER. J. Cell Biol. 2015;211:261–271. doi: 10.1083/jcb.201505067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Salo V.T., Belevich I., Jokitalo E. Seipin regulates ER–lipid droplet contacts and cargo delivery. EMBO J. 2016;35:2699–2716. doi: 10.15252/embj.201695170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thiam A.R., Antonny B., Pincet F. COPI buds 60-nm lipid droplets from reconstituted water–phospholipid–triacylglyceride interfaces, suggesting a tension clamp function. Proc. Natl. Acad. Sci. U S A. 2013;110:13244–13249. doi: 10.1073/pnas.1307685110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wilfling F., Thiam A.R., Farese R.V., Jr. Arf1/COPI machinery acts directly on lipid droplets and enables their connection to the ER for protein targeting. eLife. 2014;3:e01607. doi: 10.7554/eLife.01607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jacquier N., Choudhary V., Schneiter R. Lipid droplets are functionally connected to the endoplasmic reticulum in Saccharomyces cerevisiae. J. Cell Sci. 2011;124:2424–2437. doi: 10.1242/jcs.076836. [DOI] [PubMed] [Google Scholar]
- 11.Markgraf D.F., Klemm R.W., Rapoport T.A. An ER protein functionally couples neutral lipid metabolism on lipid droplets to membrane lipid synthesis in the ER. Cell Rep. 2014;6:44–55. doi: 10.1016/j.celrep.2013.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wilfling F., Wang H., Fröhlich F. Triacylglycerol synthesis enzymes mediate lipid droplet growth by relocalizing from the ER to lipid droplets. Dev. Cell. 2013;24:384–399. doi: 10.1016/j.devcel.2013.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dhiman R., Caesar S., Schrul B. Seminars in Cell & Developmental Biology. Elsevier; 2020. Mechanisms of protein targeting to lipid droplets: a unified cell biological and biophysical perspective. [DOI] [PubMed] [Google Scholar]
- 14.Kory N., Farese R.V., Jr., Walther T.C. Targeting fat: mechanisms of protein localization to lipid droplets. Trends Cell Biol. 2016;26:535–546. doi: 10.1016/j.tcb.2016.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thiam A.R., Forêt L. The physics of lipid droplet nucleation, growth and budding. Biochim. Biophys. Acta. 2016;1861:715–722. doi: 10.1016/j.bbalip.2016.04.018. [DOI] [PubMed] [Google Scholar]
- 16.Chorlay A., Monticelli L., Beller M. Membrane asymmetry imposes directionality on lipid droplet emergence from the ER. Dev. Cell. 2019;50:25–42. doi: 10.1016/j.devcel.2019.05.003. [DOI] [PubMed] [Google Scholar]
- 17.Deslandes F., Thiam A.R., Forêt L. Lipid droplets can spontaneously bud off from a symmetric bilayer. Biophys. J. 2017;113:15–18. doi: 10.1016/j.bpj.2017.05.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Thiam A.R., Dugail I. Lipid droplet–membrane contact sites–from protein binding to function. J. Cell Sci. 2019;132:jcs230169. doi: 10.1242/jcs.230169. [DOI] [PubMed] [Google Scholar]
- 19.Ben M’barek K., Ajjaji D., Thiam A.R. ER membrane phospholipids and surface tension control cellular lipid droplet formation. Dev. Cell. 2017;41:591–604.e7. doi: 10.1016/j.devcel.2017.05.012. [DOI] [PubMed] [Google Scholar]
- 20.Chorlay A., Thiam A.R. An asymmetry in monolayer tension regulates lipid droplet budding direction. Biophys. J. 2018;114:631–640. doi: 10.1016/j.bpj.2017.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Santinho A., Salo V.T., Thiam A.R. Membrane curvature catalyzes lipid droplet assembly. Curr. Biol. 2020;30:2481–2494.e6. doi: 10.1016/j.cub.2020.04.066. [DOI] [PubMed] [Google Scholar]
- 22.Choudhary V., Golani G., Kozlov M.M. Architecture of lipid droplets in endoplasmic reticulum is determined by phospholipid intrinsic curvature. Curr. Biol. 2018;28:915–926. doi: 10.1016/j.cub.2018.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zanghellini J., Wodlei F., Von Grünberg H.H. Phospholipid demixing and the birth of a lipid droplet. J. Theor. Biol. 2010;264:952–961. doi: 10.1016/j.jtbi.2010.02.025. [DOI] [PubMed] [Google Scholar]
- 24.Caillon L., Nieto V., Thiam A.R. Triacylglycerols sequester monotopic membrane proteins to lipid droplets. Nat. Commun. 2020;11:1–12. doi: 10.1038/s41467-020-17585-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Prévost C., Sharp M.E., Walther T.C. Mechanism and determinants of amphipathic helix-containing protein targeting to lipid droplets. Dev. Cell. 2018;44:73–86. doi: 10.1016/j.devcel.2017.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kim S., Swanson J.M. The surface and hydration properties of lipid droplets. Biophys. J. 2020;119:1958–1969. doi: 10.1016/j.bpj.2020.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kim S., Oh M.I., Swanson J.M. Stressed lipid droplets: how neutral lipids relieve surface tension and membrane expansion drives protein association. J. Phys. Chem. B. 2021;125:5572–5586. doi: 10.1021/acs.jpcb.1c01795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kumanski S., Viart B.T., Moriel-Carretero M. Lipid droplets are a physiological nucleoporin reservoir. Cells. 2021;10:472. doi: 10.3390/cells10020472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bacle A., Gautier R., Vanni S. Interdigitation between triglycerides and lipids modulates surface properties of lipid droplets. Biophys. J. 2017;112:1417–1430. doi: 10.1016/j.bpj.2017.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chorlay A., Thiam A.R. Neutral lipids regulate amphipathic helix affinity for model lipid droplets. J. Cell Biol. 2020;219:e201907099. doi: 10.1083/jcb.201907099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Čopič A., Antoine-Bally S., Jackson C.L. A giant amphipathic helix from a perilipin that is adapted for coating lipid droplets. Nat. Commun. 2018;9:1332. doi: 10.1038/s41467-018-03717-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ajjaji D., Ben M’barek K., Thiam A.R. Hepatitis C virus core protein uses triacylglycerols to fold onto the endoplasmic reticulum membrane. Traffic. 2021 doi: 10.1111/tra.12825. [DOI] [PubMed] [Google Scholar]
- 33.Ajjaji D., Ben M’barek K., Small D.M. Dual binding motifs underpin the hierarchical association of perilipins1–3 with lipid droplets. Mol. Biol. Cell. 2019;30:703–716. doi: 10.1091/mbc.E18-08-0534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Upadhyaya A., Sheetz M.P. Tension in tubulovesicular networks of Golgi and endoplasmic reticulum membranes. Biophys. J. 2004;86:2923–2928. doi: 10.1016/S0006-3495(04)74343-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Marsh D. Lateral pressure profile, spontaneous curvature frustration, and the incorporation and conformation of proteins in membranes. Biophys. J. 2007;93:3884–3899. doi: 10.1529/biophysj.107.107938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Marsh D. Lateral pressure in membranes. Biochim. Biophys. Acta. 1996;1286:183–223. doi: 10.1016/s0304-4157(96)00009-3. [DOI] [PubMed] [Google Scholar]
- 37.Nagle J.F. Theory of lipid monolayer and bilayer phase transitions: effect of headgroup interactions. J. Membr. Biol. 1976;27:233–250. doi: 10.1007/BF01869138. [DOI] [PubMed] [Google Scholar]
- 38.Hamilton J.A. Interactions of triglycerides with phospholipids: incorporation into the bilayer structure and formation of emulsions. Biochemistry. 1989;28:2514–2520. doi: 10.1021/bi00432a025. [DOI] [PubMed] [Google Scholar]
- 39.Baoukina S., Monticelli L., Tieleman D.P. The molecular mechanism of monolayer-bilayer transformations of lung surfactant from molecular dynamics simulations. Biophys. J. 2007;93:3775–3782. doi: 10.1529/biophysj.107.113399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Golding M., Wooster T.J. The influence of emulsion structure and stability on lipid digestion. Curr. Opin. Colloid Interface Sci. 2010;15:90–101. [Google Scholar]
- 41.Needham D., Nunn R.S. Elastic deformation and failure of lipid bilayer membranes containing cholesterol. Biophys. J. 1990;58:997–1009. doi: 10.1016/S0006-3495(90)82444-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cooke I.R., Deserno M. Coupling between lipid shape and membrane curvature. Biophys. J. 2006;91:487–495. doi: 10.1529/biophysj.105.078683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lipowsky R. The conformation of membranes. Nature. 1991;349:475–481. doi: 10.1038/349475a0. [DOI] [PubMed] [Google Scholar]
- 44.Marsh D. Comment on interpretation of mechanochemical properties of lipid bilayer vesicles from the equation of state or pressure- area measurement of the monolayer at the air- water or oil- water interface. Langmuir. 2006;22:2916–2919. doi: 10.1021/la051216n. [DOI] [PubMed] [Google Scholar]
- 45.Pomorski T., Menon A.K. Lipid flippases and their biological functions. Cell. Mol. Life Sci. 2006;63:2908–2921. doi: 10.1007/s00018-006-6167-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Anglin T.C., Conboy J.C. Kinetics and thermodynamics of flip-flop in binary phospholipid membranes measured by sum-frequency vibrational spectroscopy. Biochemistry. 2009;48:10220–10234. doi: 10.1021/bi901096j. [DOI] [PubMed] [Google Scholar]
- 47.De Gennes P.-G. Wetting: statics and dynamics. Rev. Mod. Phys. 1985;57:827. [Google Scholar]
- 48.Chorlay A., Santinho A., Thiam A.R. Making droplet-embedded vesicles to model cellular lipid droplets. STAR Protoc. 2020;1:100116. doi: 10.1016/j.xpro.2020.100116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Santinho A., Chorlay A., Thiam A.R. Fat inclusions strongly alter membrane mechanics. Biophys. J. 2021;120:607–617. doi: 10.1016/j.bpj.2021.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kwok R., Evans E. Thermoelasticity of large lecithin bilayer vesicles. Biophys. J. 1981;35:637–652. doi: 10.1016/S0006-3495(81)84817-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kory N., Thiam A.-R., Walther T.C. Protein crowding is a determinant of lipid droplet protein composition. Dev. Cell. 2015;34:351–363. doi: 10.1016/j.devcel.2015.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Henne W.M., Reese M.L., Goodman J.M. The assembly of lipid droplets and their roles in challenged cells. EMBO J. 2018;37:e98947. doi: 10.15252/embj.201898947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang M., Yi X. Bulging and budding of lipid droplets from symmetric and asymmetric membranes: competition between membrane elastic energy and interfacial energy. Soft Matter. 2021;17:5319–5328. doi: 10.1039/d1sm00245g. [DOI] [PubMed] [Google Scholar]
- 54.Helfrich W., Servuss R.-M. Undulations, steric interaction and cohesion of fluid membranes. Il Nuovo Cimento D. 1984;3:137–151. [Google Scholar]
- 55.Rawicz W., Olbrich K.C., Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.