Abstract
Electrically excitable cells often spontaneously and synchronously depolarize in vitro and in vivo preparations. It remains unclear how cells entrain and autorhythmically activate above the intrinsic mean activation frequency of isolated cells with or without pacemaking mechanisms. Recent studies suggest that cyclic ion accumulation and depletion in diffusion-limited extracellular volumes modulate electrophysiology by ephaptic mechanisms (nongap junction or synaptic coupling). This report explores how potassium accumulation and depletion in a restricted extracellular domain induces spontaneous action potentials in two different computational models of excitable cells without gap junctional coupling: Hodgkin-Huxley and Luo-Rudy. Importantly, neither model will spontaneously activate on its own without external stimuli. Simulations demonstrate that cells sharing a diffusion-limited extracellular compartment can become autorhythmic and entrained despite intercellular electrical heterogeneity. Autorhythmic frequency is modulated by the cleft volume and potassium fluxes through the cleft. Additionally, inexcitable cells can suppress or induce autorhythmic activity in an excitable cell via a shared cleft. Diffusion-limited shared clefts can also entrain repolarization. Critically, this model predicts a mechanism by which diffusion-limited shared clefts can initiate, entrain, and modulate multicellular automaticity in the absence of gap junctions.
Significance
A mechanism of cyclic ionic potassium accumulation and depletion in diffusion-limited paracellular compartments can initiate, support, and suppress autorhythmic activity. Additionally, automaticity can emerge from electrophysiologically heterogeneous cell pairs sharing a diffusion-limited extracellular compartment, even if the individual cells are excitable but not autorhythmic in isolation. Sustained and entrained autorhythmic activity can occur in the absence of gap junction coupling. Last, the shared diffusion-limited extracellular compartment can also reduce dispersion of repolarization.
Introduction
Cyclic behavior is frequently observed in multicellular preparations. At the cellular level, oscillations often occur secondary to linked processes with different reaction time constants, positive and negative feedback, and reagent availability. Oscillators can synchronize or continue to function independently with minimal energy or resource transfer. In the context of excitable cells such as neurons or cardiac myocytes, autorhythmic electrical activity arises from regenerative sarcolemmal ion exchange or other intracellular ionically dependent processes. For example, there are two predominant theories that describe the origin of the heartbeat in specialized cells within the sinoatrial node. It is well accepted that the “funny current,” linked to the hyperpolarization-activated, cyclic-nucleotide gated family of genes (HCN), is a steady-state pacemaking current that predominates in late diastole, permitting slow membrane depolarization that eventually triggers an action potential (1, 2, 3, 4). According to oscillatory systems theory, some type of feedback that can be positive or negative is required to reset, limit, or select for a dominant frequency. In the case of the cardiac myocyte membrane potential (Vm), this is accomplished by the voltage- and time-dependent activation, inactivation, deactivation, and conductance of a host of ion handling proteins known as channels, exchangers, and pumps. The setting of intrinsic cyclic depolarization by sarcolemmal channels is referred to as the “membrane clock” hypothesis, and the structure, function, and modulation of the HCN channels were elegantly summarized by Wilders in 2007 (5).
The “calcium clock” hypothesis, which can operate in conjunction with the membrane clock, was reviewed carefully by Lakatta et al. (6) In short, the calcium clock operates with the assumptions that calcium regulatory channel proteins called ryanodine receptors on the sarcoplasmic reticulum (SR) will spontaneously and nearly synchronously release calcium into the cytosol. Some of that calcium will leave the cell through a sodium-calcium exchanger. The exchange of one calcium for three sodium ions depolarizes the myocyte by a net inward charge transfer, providing feedback for additional calcium entry through the activation of L-type calcium channels, further raising intracellular calcium. Some of this calcium leaves the cell again, but the majority of the calcium is taken back into the SR through a pump. As the system equilibrates between action potentials, increased SR calcium increases the likelihood of spontaneous calcium release again.
Potassium handling has also been implicated as an important mechanism of electrical automaticity in cardiomyocytes. Specifically, many excitable cells have a negative resting Vm, and this is generally attributed to inwardly rectifying potassium channels that polarize the membrane closer to the equilibrium potential of potassium. The role of potassium channels and many other sarcolemmal currents that modulate automaticity was summarized by Irisawa et al. (7). In brief, enhanced conductance of the inward rectifier potassium channels are thought to inhibit automaticity, and therefore, altering potassium permeability is a second membrane clock mechanism that can modulate intrinsic cyclic behavior. In cardiac electrophysiology, this is what is thought to underlie the different and increasingly slower spontaneous action potential rates distal to the sinoatrial node, atrioventricular nodes, His bundle, Purkinje fibers, and eventually, the working myocardium. Beyond the heart, spontaneous and cyclic electrical behavior has been described in the brain (8, 9, 10), hair cells (11), skeletal myotubes (12), stomach (13), intestines (14), and uterine myometrium (15,16). In short, many excitable tissues are associated with varying degrees of spontaneous, cyclic, and coordinated action potentials.
The next requirement for pacemaking is that groups of cells are sufficiently synchronized to electrically activate adjacent excitable cells. Consider that the probability of a group of cardiac cells depolarizing sufficiently to initiate coordinated and near simultaneous depolarization is low. Some have estimated that upwards of 10,000 cardiomyocytes would need to simultaneously depolarize to produce sufficient current to excite neighboring myocardium (17). Given this statistical improbability, pacemaking was proposed to occur from “master” pacemakers (18, 19, 20) or entrainment of intrinsically active pacemaker cells (21, 22, 23, 24, 25). Importantly, the computational models of master pacemakers and entrained pacemakers require that the cells composing the autorhythmic tissue have relatively similar autorhythmic frequencies. However, only a fraction of cells isolated from autorhythmic cardiac tissues like the sinoatrial node, atrioventricular node, and His-Purkinje systems are spontaneously active in isolation (26, 27, 28). Setting aside a concern that our understanding of cellular automaticity is mainly understood from cell selection bias, it is clear that newer theories are required to understand how electrically heterogeneous cells can produce a population effect of rhythmic electrical activity. With that objective in mind, Quinn and Kohl (29) proposed that mechanosensitivity is a candidate mechanism to coordinate entrained activity throughout the spatially extensive cellular network of the sinoatrial node, and a recent experimental study by Bychkov et al. (30) demonstrated that heterogeneous subcellular and subthreshold cellular signaling can macroscopically synchronize action potentials in tissue like the sinoatrial node.
Importantly, our study does not challenge any of the aforementioned work. Rather, this report describes the logic and modification of two different mathematical action potential models—Hodgkin-Huxley (HH) (31) and Luo-Rudy (LRd) (32)—to demonstrate how a single cell with no intrinsic autorhythmic activity can gain autorhythmic activity when coupled to a neighboring cell via a shared diffusion-limited extracellular compartment. Importantly, this theory can occur in the absence of gap junctional coupling, and it overcomes the issues concerning the heterogeneous electrophysiology found in multicellular tissues.
The premise of the study is rooted in neuroscience. As early as 1956, Frankenhäuser and Hodgkin (33) noted extracellular potassium accumulation during the firing of axon impulses. It is now well established that the neural support cells called astrocytes modulate extracellular potassium, which in turn determine neuronal excitability (34, 35, 36, 37, 38, 39). Central to this hypothesis is the importance of the inward rectifier potassium current Kir4.1 (40). When Kir4.1 is genetically downregulated, extracellular potassium rises, the resting Vm of neurons rises, neuronal activity dramatically increases, and the risk of seizures is elevated. Recent corollary evidence from the cardiac field demonstrates that the inward rectifier potassium channel Kir2.1 is densely expressed in the intercalated disk of ventricular myocytes (41,42). More specifically, Kir2.1 can be found in the gap junction-adjacent perinexus (43), first identified by Rhett et al. (44) as a gap junction-adjacent nanodomain with high expression of voltage-gated sodium channels as well. Importantly, the perinexus is a candidate structural node for ephaptic propagation to occur. In brief, ephaptic coupling occurs by the alteration of electrical potentials and ionic concentrations in diffusion-limited extracellular nanodomains, on the order of 15 nm wide, that modulate the electrophysiology of adjacent cell membranes (45).
We hypothesized that potassium accumulation and depletion in these restricted extracellular nanodomains can initiate, sustain, and modulate autorhythmic activity in significantly different cell models. Importantly, this hypothesis may appear similar to action potential propagation mediated via potassium fluxes through the cleft as summarized by Sperelakis and McConnell (46), but this manuscript discusses how potassium fluxes between electrically active cells confer autorhythmicity in otherwise quiescent cells. This study also demonstrates that shared diffusion-limited extracellular volumes can entrain excitable and inexcitable cells. The simulations suggest sustained automaticity can arise from cyclic potassium ion accumulation and depletion within shared extracellular diffusion-limited nanodomain.
Materials and methods
The first significant assumption of our model is based on studies demonstrating that a subpopulation of inward rectifier potassium channels such as Kir2.1 are localized to the relatively restricted nanodomains of the ventricular myocardial intercalated disk (43), which is referred to as the “cleft” in this model. The second assumption is that extracellular potassium concentration in the cleft can vary more than, and independently of, intracellular and bulk extracellular potassium. For context, the extracellular volume in working ventricular myocardium is tens of microns wide and spatially extensive throughout tissue, intracellular dimensions of the adult human ventricular cardiomyocyte are ∼20 by 100 μm (47,48), and the perinexus is ∼20 nm wide and 100 nm long (49,50). Thus, the perinexus is several orders of magnitude smaller than cardiomyocytes and the bulk interstitial volume.
Given these assumptions, the HH model of a single cell was altered according to Fig. 1. Specifically, membrane currents were considered to consist of two components, the lateral membrane with membrane area Am and the junctional membrane, i.e., the membrane lining the cleft, with membrane area Aj. Each of the membrane currents consist of capacitive and ionic currents with sodium, potassium, and leak ionic currents for the lateral membrane and sodium and potassium ionic currents for the junctional membrane. Consequently, the total transmembrane current is
| (1) |
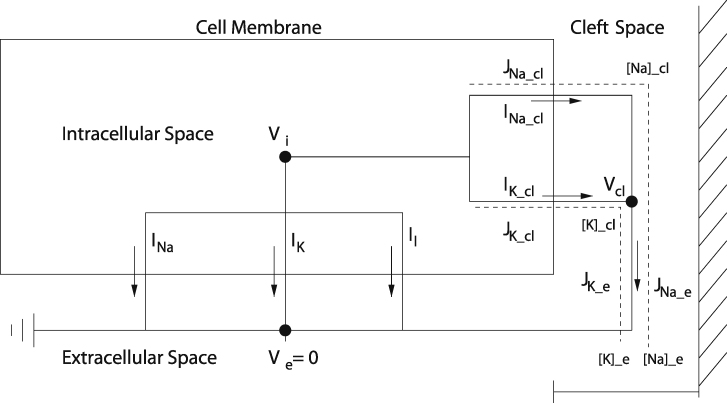
Figure 1.
Circuit diagram for a single Hodgkin-Huxley (HH) cell modified to include sodium and potassium currents into a diffusion-limited cleft region. Model includes standard HH transmembrane ionic currents for the lateral membrane and potassium and sodium transmembrane currents for the junctional membrane into the diffusion-limited cleft region. Currents out of the cleft region are governed by a Goldman-Hodgkin-Katz current relationship. The two-cell model has a single and shared cleft potassium concentration [K]cl, cleft sodium concentration [Na]cl, cleft width wf, and cleft resistance rj parameters. Cellular capacitance and fraction (FIK) of total potassium current IK,cl in the cleft can be varied independently for both cells. Supporting materials and methods single_cell_potassium_cleft.m and double_cell_potassium_cleft.m are MATLAB (The MathWorks, Natick, MA) source codes for the single and dual cell models, respectively.
The lateral membrane has transmembrane potential Vm = Vi − Ve (with Ve = 0), and the junctional membrane has transmembrane potential Vj = Vi − Vcl, where Vcl is the potential in the cleft and is not the same as Ve. The junctional membrane current must balance the cleft current Icl:
| (2) |
The lateral membrane ionic currents are gated in a voltage-dependent way by Vi, whereas the junctional membrane ionic currents are gated in a voltage-dependent way by Vj. Furthermore, the driving force (the Nernst potentials) for the lateral membrane ionic currents are fixed at standard values; however, the Nernst potentials for the junctional ionic currents fluctuate with the cleft concentrations according to
| (3) |
Because the cleft volume is so small, we track the cleft potassium and cleft sodium concentrations by
| (4) |
| (5) |
where the cleft volume is vcl = Aj w, and w is the cleft width. Ionic fluxes J and currents I are related through Faraday’s constant:
| (6) |
Finally, for the cleft currents and ion fluxes, we take the Goldman-Hodgkin-Katz fluxes with z = 1. Notice that if Vcl = 0, these reduce to Fickian diffusion, whereas with no concentration gradient, these reduce to
| (7) |
| (8) |
| (9) |
which is Ohm’s law. Thus, because there are two ions involved, we take
| (10) |
where rcl is the cleft resistance.
The model has three adjustable parameters. These are FIK, FINa, and wf. FIK and FINa, respectively, specify the fraction of potassium and sodium ion channels in the junctional membrane, and they have values between zero and one. Unless otherwise noted, FINa = 0, so that the junctional membrane has no sodium current. The cleft width factor wf appears in two places: in the cleft volume vcl = Aj wf w0, where w0 is the nominal cleft width, and in the cleft resistance . Nominal cleft resistance is based on a myoplasmic resistance ρmyo of 150 Ω⋅cm (51) and a radial resistance defined as ρext/8πw (52,53) rounded to 4000 kΩ. Nominal intermembrane cleft width wo is based on measurements of synaptic clefts (54) and the cardiomyocyte perinexus (15 nm) (49,55). The model does not incorporate gap junctional coupling. Nominal cleft volume is based on the diameter of some axons, boutons (54,56), and cardiomyocytes (15 μm) (48). Consequently, cleft permeability is . Model parameters and initial conditions are in Table 1.
Table 1.
HH model cellular parameters with adjacent cleft
| Parameter | Definition | Value |
|---|---|---|
| w0 | nominal cleft width | 1.5 × 10−6 cm |
| Am | lateral membrane surface area | 6.9 × 10−5 cm2 |
| Aj | junctional membrane surface area | 3.8 × 10−6 cm2 |
| vcl | nominal cleft volume | 5.7 × 10−12 cm3 |
| nominal cleft resistance | 4000 kΩ | |
| [Na]i | intracellular sodium concentration | 50 mM |
| [Na]e | extracellular sodium concentration | 457 mM |
| [K]i | intracellular potassium concentration | 397 mM |
| [K]e | extracellular potassium concentration | 20 mM |
| 25.8 mV |
Bifurcation analysis
Because oscillatory solutions are hysteretic with respect to changes in parameters, Figs. 2, 5, and 6 are computed using a slowly varying “double ramp,” first increasing and then decreasing the underlying parameter over the range of interest. For example, for Fig. 2, [K]e is varied from 20 to 65 mM and then back to 20 mM at a rate of 1.8 × 10−2 ms−1. Fig. 2 is then constructed by plotting Vm versus [K]e, eliminating those portions where there is overlap, thus creating a “quasisteady” bifurcation diagram for periodic solutions. The forward sweep and backward sweep each require 2500 ms. For Fig. 5, FIK is varied from 0.6 to 0.875 and then back to 0.6 at a rate of 1.1 × 10−4 ms−1. The forward and backward parameter sweeps each require 2500 ms.
Figure 2.
(A) Solution diagram for the HH model as a function of extracellular potassium concentration [K]e. Black curves represent stable steady-state solutions, and the blue curve represents stable autorhythmic solutions. (B) Spontaneous oscillatory solution manifest as autorhythmic action potentials for the HH model with [K]e = 30 mM.
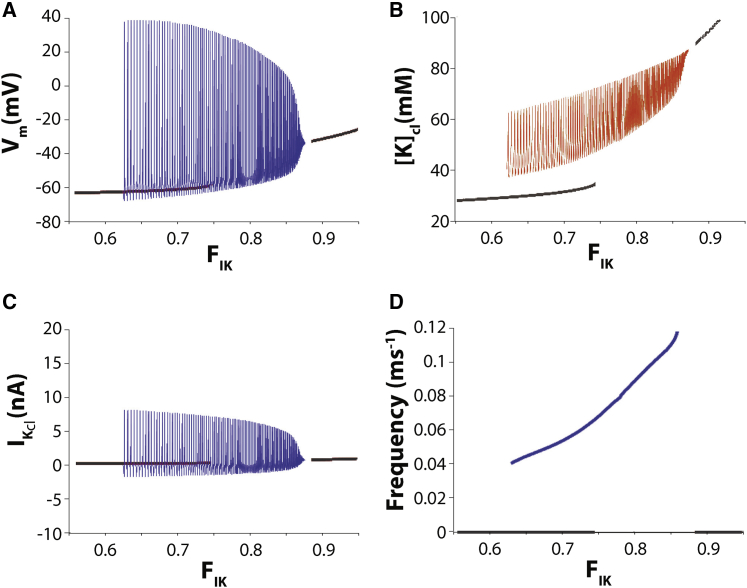
Figure 5.
Solution diagram for the modified HH cleft model as a function of fractional potassium cleft current FIK with cleft width fixed wf = 1. Black curves represent stable steady-state solutions, and blue curves represent stable autorhythmic solutions. (A) Spontaneous autorhythmic solutions exist for 0.62 < FIK < 0.87. Peak membrane potential Vm decreases and minimal membrane potential increases as FIK increases until minimal Vm inactivates sodium current and abolishes oscillations. (B) Maximal and minimal cleft potassium concentrations [K]cl increase when FIK increases. (C) Potassium currents in the cleft IK,cl decrease when FIK increases. (D) Autorhythmic frequency increases in response to increasing FIK.
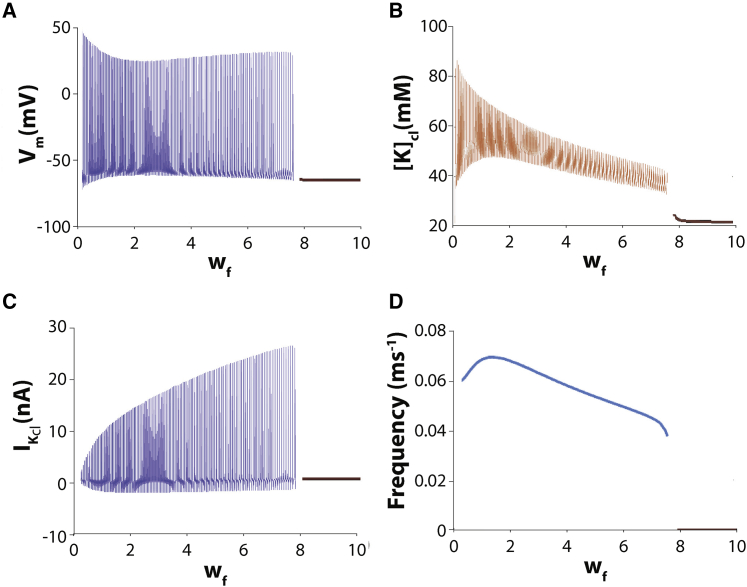
Figure 6.
Solution diagram for the modified HH cleft model as a function of cleft width wf with fixed fractional potassium cleft current FIK = 0.75. (A) Spontaneous autorhythmic solutions (blue curves) cease for wf> 7.5 (black curve), and the soloution is at a stable steady state. (B) The amplitude of cleft potassium concentration [K]cl oscillations and the average value of potassium cleft concentration is a decreasing function of wf. (C) Peak cleft potassium current IK,cl increases when wf increases. (D) The frequency response to wf is biphasic and when FIK = 0.75.
Cardiac tissue model
To investigate spontaneous activity in a tissue, we next generalize the one- and two-cell model to a “chain” of 30 cells, with each adjacent set of cells sharing a diffusion-limited cleft. Membrane currents are now represented by the dynamic LRd model, a detailed biophysical model of the guinea pig ventricular myocyte (32). As in our prior work (57, 58, 59) and the HH cleft model above, channels are nonuniformly distributed between the lateral and junctional membranes. In these simulations, we vary the fractional inward-rectifying potassium current (FIK1), whereas the fractional sodium cleft current (FINa = 0) is fixed. All other currents are assumed to be only present on the lateral membrane. Importantly, there is no gap junctional coupling between myocytes (i.e., a direct electrical connection between intracellular spaces), such that coupling only occurs through the shared clefts.
Results
Oscillatory behavior with potassium diffusion-limited clefts
The HH model is not autorhythmic with standard parameter values without the addition of a transient or persistent depolarizing current. However, it does exhibit autorhythmic behavior if [K]e is elevated. This fact is demonstrated in Fig. 2. In Fig. 2 A, the black curves represent stable steady-state solutions, and the blue curve represents stable autorhythmic solutions. Consequently, for 29 mM < [K]e < 58 mM, autorhythmic action potentials occur. An example of a stable and autorhythmic action potential train is shown in Fig. 2 B for [K]e = 30 mM. The mechanism underlying automaticity is easy to understand. Increased [K]e raises resting Vm to a value in which sodium channel kinetics are biased toward increasing activation and depolarization through positive feedback between membrane and current.
To explore whether autorhythmic activity can be initiated by [K]e control in our modified model, the total potassium current IK was distributed between channels facing an invariant potassium compartment along the lateral membrane and the cleft where potassium concentration ([K]cl) can change. Fig. 3 demonstrates that with the fraction of potassium channels facing the cleft, FIK = 0.7, there is spontaneous and stable autorhythmic behavior.
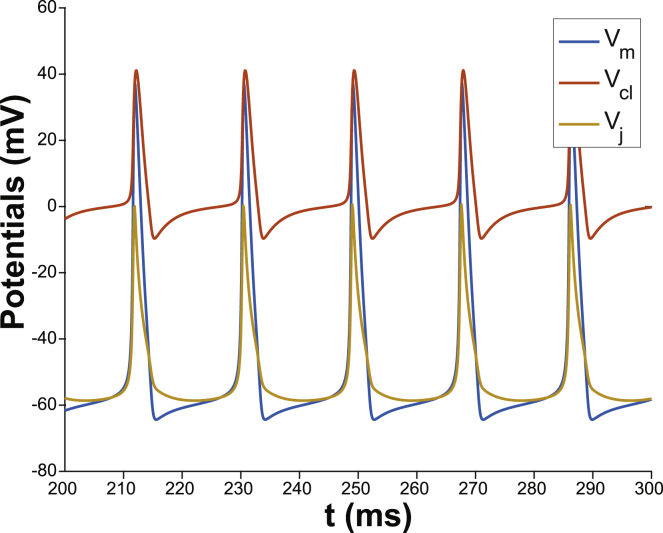
Figure 3.
Spontaneous autorhythmic behavior for the membrane potential Vm= Vi, the cleft potential Vcl, and the junctional transmembrane potential Vj = Vi− Vcl with fraction of potassium cleft current FIK = 0.7 and nominal cleft width wf = 1.
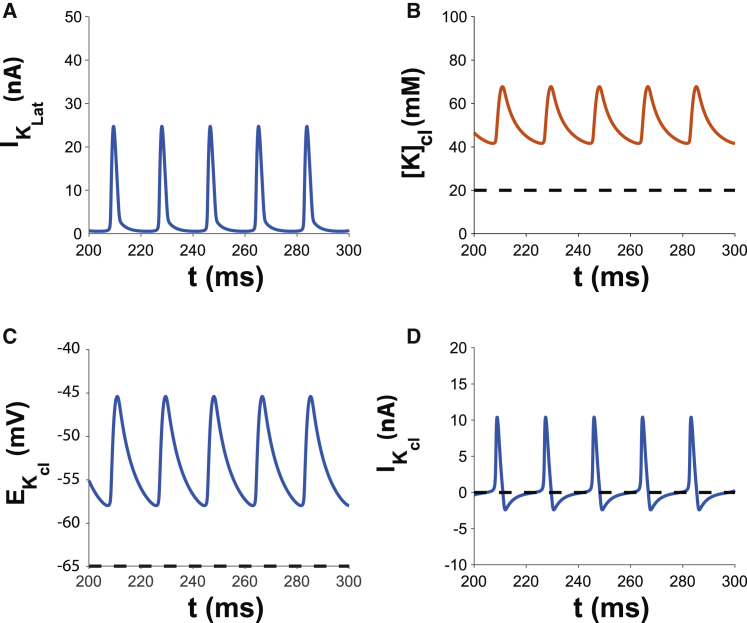
The mechanism behind the spontaneous activity is illustrated in Fig. 4. First, lateral Vm does not drop below EK, because EK = −65 mV (dashed black trace) is the most negative reversal potential for the lateral membrane. As a result, potassium current along the lateral membrane (IK,Lat) facing an unrestricted volume can only ever be outward (Fig. 4 A). Fig. 4 B demonstrates that facilitating a change in [K]cl, resulting from IK,cl, permits transient cyclic [K]cl increases. In the cleft, [K]cl does not drop below 40 mM, which is higher than the lateral and invariant [K]e of 20 mM. The consequence is that the junctional Nernst potential EK can transiently and cyclically rise above minimal Vm (Fig. 4 C). When EK,cl rises above Vm, then IK,cl reverses to become an inward current (Fig. 4 D), which relatively quickly becomes negligible. Therefore, the mechanism of spontaneous autorhythmic activity under these conditions is a result of outward IK,cl during the action potential loading [K]cl, which maintains Vj above lateral Vm, which in turn activates an inward sodium window current. In other words, the cleft creates a condition that permits endogenous accumulation of [K]cl, which is in contrast to the case in Fig. 2 requiring exogenous [K]e elevation. Therefore, given the prevalence of strongly inward-rectifying potassium channels in multiple cell types (60,61), all of which can exhibit some form of autorhythmic and organized activity, the model suggests that a relatively small, shared extracellular domain can initiate cyclic depolarizations in otherwise quiescent cells.
Figure 4.
(A) Potassium current on the lateral membrane IK,Lat is always outward and rapidly changes during an action potential because extracellular potassium [K]e and reversal potential EK,e are invariant along the membrane facing bulk unrestricted volumes. (B) Extracellular potassium in the cleft [K]cl (red curve) is elevated relative to invariant bulk extracellular potassium [K]e = 20 mM (dashed black trace) between action potentials. (C) The cleft potassium equilibrium potential EK,cl (blue curve) is elevated relative to bulk (dashed black trace). Between action potentials, EK,cl decreases early after repolarization and begins to rise as the lateral membrane begins to depolarize. (D) Cleft potassium current IK,cl (blue curve) is inward early between action potentials, becomes transiently outward as the cell begins to depolarize, becomes strongly outward during the early phase of the action potential, and becomes strongly inward for a prolonged period of time during repolarization.
Effects of varying fractional cleft potassium current
The behavior of the model as a function of the cleft potassium current fraction FIK can be seen in Fig. 5. Below the threshold of FIK = 0.62, there is no spontaneous autorhythmic activity. Below this threshold value, diastolic Vm is a gradually increasing function of FIK (Fig. 5 A, black curve), as is [K]cl (Fig. 5 B). However, once FIK exceeds 0.62, autorhythmic activity begins. The autorhythmic behavior in this parameter range is associated with the increased average [K]cl, similar to the behavior of the HH model without a cleft. The oscillation of [K]cl is a direct consequence of the oscillation of Vm, which drives an oscillatory potassium current IK,cl (Fig. 5 C). The maximal IK,cl in Fig. 5 C is inversely proportional to the maximal [K]cl in Fig. 5 B, and the minimal IK,cl is directly proportional to minimal [K]cl. Interestingly, increasing FIK in the range that supports autorhythmic activity can increase the frequency of spontaneous activity (Fig. 5 D). For this model and parameter space, the increased autorhythmic frequency may be a result of the increasing [K]cl that increases the sodium window current. However, as FIK increases beyond 0.87, the average level of [K]cl is too high to sustain oscillations.
Importantly, this model is highly dependent on the simplistic nature of IK, which does not account for the complex kinetics of the many inward rectifier potassium channel protein families, subtypes, heteromeric combinations, and accessory subunits. Nonetheless, one expects that subcellular potassium channel localization, coupled with the unique biophysical channel properties, can produce emergent stable autorhythmic behaviors even in different cell types.
Effects of increasing cleft width
Based on the results above, we further hypothesize that increasing cleft width (wf) should decrease the likelihood of spontaneous oscillations. In Fig. 6 A, we see the effect of varying wf while keeping FIK = 0.75 fixed. At small values of wf, i.e., for a narrow cleft, [K]cl accumulation is substantial and has large amplitude oscillations (Fig. 6 B). As wf increases, the amplitude of [K]cl oscillation decreases as does the average [K]cl. For sufficiently large wf, (wf > 0.75), [K]cl is too small to drive oscillations, such that autorhythmic behavior ceases, and [K]cl is not much different from [K]e.
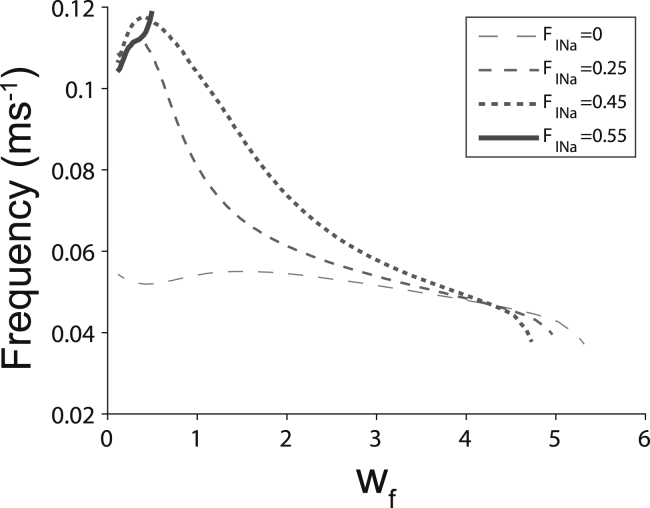
Interestingly, the amplitude of the oscillatory potassium current IK,cl is increasing as wf increases (Fig. 6 C), for the simple reason that the EK,cl is decreasing, hence increasing the amplitude of the driving force for IK,cl. Just as in Fig. 5, B and C, maximal IK,cl in Fig. 6 C is inversely proportional to the maximal [K]cl in Fig. 6 B, and the minimal IK,cl is directly proportional to minimal [K]cl. Also, similar to the findings in Fig. 5 D, autorhythmic activity in Fig. 6 D is not constant but is dependent on wf. In this case, the autorhythmic frequency can be complex and multiphasic, and appears to once again follow diastolic [K]cl values in Fig. 6 D. Additionally, increasing the fraction of sodium current (FINa) in the cleft increases autorhythmic frequencies particularly for low wf and decreases the range of wf over which automaticity is initiated (Fig. 7). As a result, significantly elevating FINa can initiate and attenuate automaticity. These data reveal that potassium regulation in diffusion-limited extracellular clefts can initiate, modulate the frequency, and repress spontaneous activity.
Figure 7.
Increasing fractional sodium current in the cleft FINa increases the maximal autorhythmic frequency at narrow cleft widths wf while decreasing the range of wf that support autorhythmic activity.
Extracellular coupled oscillator synchronization
Based on the ability of a single cell to oscillate in predictable patterns when a portion of its potassium channels face a restricted volume, it should come as no surprise that two cells sharing a restricted cleft will oscillate and entrain. Note that the autorhythmic frequency of the two cells is not an average of the two cells’ cleft-mediated autorhythmic frequencies nor is the dominant frequency governed by the “fastest” activating cell. Importantly, the frequency of two cells sharing a cleft can be higher or lower than the individual cell frequencies because both cells simultaneously modulate [K]cl.
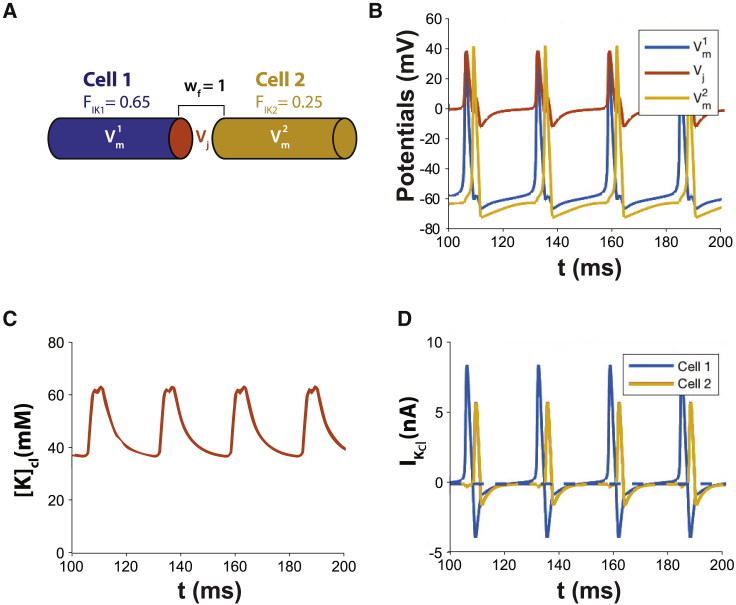
With parameter values FIK = 0.65 and wf = 1, the single cell model does not spontaneously oscillate. When FIK = 0.65 for two cells sharing a restricted volume, they entrain and simultaneously depolarize as will be discussed shortly in a different context. First, we consider the effects of introducing intercellular electrophysiologic heterogeneity between two cleft-coupled cells (Fig. 8 A). Fig. 8 B demonstrates that with FIK = 0.65 in cell 1 and FIK = 0.25 in cell 2, there is spontaneous and temporally coordinated, although not simultaneous, automaticity. Specifically, the two cells concurrently increase [K]cl in the shared cleft more rapidly than the individual cells alone (Fig. 8 C), but there is a delay between action potential activations, demonstrating the synchronization can be the result of extracellular potassium-mediated electrical propagation. Fig. 8 D reveals that IK,cl for cell 1 becomes positive after action potential initiation, and the shared [K]cl rises dramatically. The rapid rise in shared [K]cl causes IK,cl in cell 2 to transiently conduct inwardly and depolarize cell 2 by a potassium-mediated pathway. The amplitude of IK,cl of cell 2 is less than IK,cl in cell 1 because of cleft priming caused by IK,cl in cell 1 and the smaller fraction of IK,cl for cell 2. Interestingly, this inward IK,cl in cell 1 prolongs the late phase of the action potential in cell 1 (Fig. 8 A), suggesting that dispersion of repolarization between electrically active cells can be reduced by a gap junction-independent mechanism.
Figure 8.
(A) Diagram of two cells sharing a cleft. The two cells are not autorhythmic when they do not share a cleft and FIK = 0.65 in cell 1 and FIK = 0.25 in cell 2. (B) Autorhythmic activity is initiated when they share a cleft with cleft width factor wf = 1. (C) Heterogeneous FIK in cells 1 and 2 results in multiphasic potassium cycling resulting from temporally shifted [K]cl dynamics. The action potential of cell 1 increases [K]cl, and activation of cell 2 further increases [K]cl to create a second peak in [K]cl. (D) IK,cl is phase shifted, and the peak amplitudes are different for the two apposing cell ends sharing the cleft. IK,cl for both cells 1 and 2 are biphasic during the respective action potentials, but the outward amplitude is reduced in cell 2 concurrent with the inward IK,cl of cell 1.
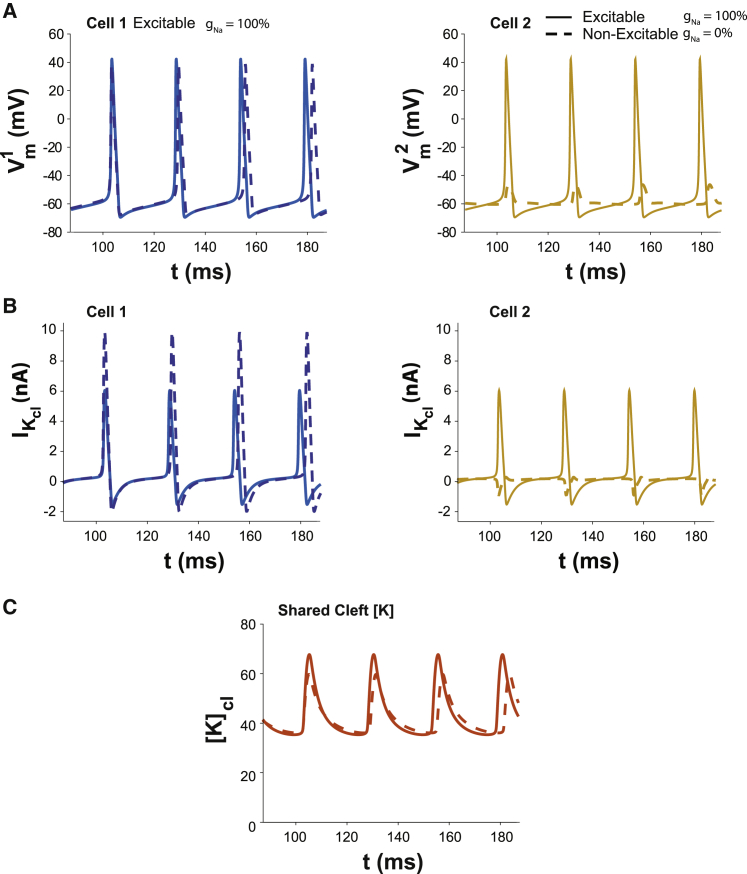
Representative action potentials in Fig. 9 A demonstrate what happens when an excitable cell (left) is coupled with an inexcitable cell (right). Specifically, cell 1 has currents of the original HH constants and kinetics. Cell 2 is either excitable with normal gNa similar to cell 1, or it is inexcitable with gNa = 0 (dashed trace). Importantly, neither cell 1 or 2 are autorhythmic in isolation or even if they each had their own nonshared cleft (nominal gNa, and FIK = 0.65). Yet, they will both synchronously oscillate when they share a restricted cleft (Fig. 9 B, solid traces). When cell 2 is rendered inexcitable by setting gNa = 0, it is noteworthy that IK,cl in cell 2 is mostly inward (Fig. 9 B, right panel, dashed trace), partially depleting [K]cl, but the amplitude of IK,cl in cell 1 is substantially enhanced compared with the situation in which the two cells are identical (Fig. 9 B, comparing dashed to solid traces). As a result, peak [K]cl in Fig. 9 C is only modestly reduced in the heterogeneous cell pair (dashed trace) relative to the homogeneous cell pair.
Figure 9.
(A) Oscillatory solutions for the dual cell model with cells coupled via a common diffusion-limited cleft domain (wf = 1), fractional potassium cleft current FIK = 0.65 for both cells, cell 2 with standard sodium channel density (solid curves), and gNa=0 (dashed curves), hence inexcitable. Neither cell 1 nor 2 are autorhythmic on their own. Excitable cell 1 gains automaticity when sharing a cleft with an inexcitable cell 2 (dashed traces). Making cell 2 excitable confers automaticity to cell 2 that is synchronized with cell 1 and increases the autorhythmic frequency of cell 1. (B) Cleft potassium currents corresponding to the Vm oscillations in (A). (C) Peak [K]cl is modestly reduced in the electrophysiologically heterogeneous cell pairs because the integral of outward IK,cl is partially balanced by the small inward current into cell 2.
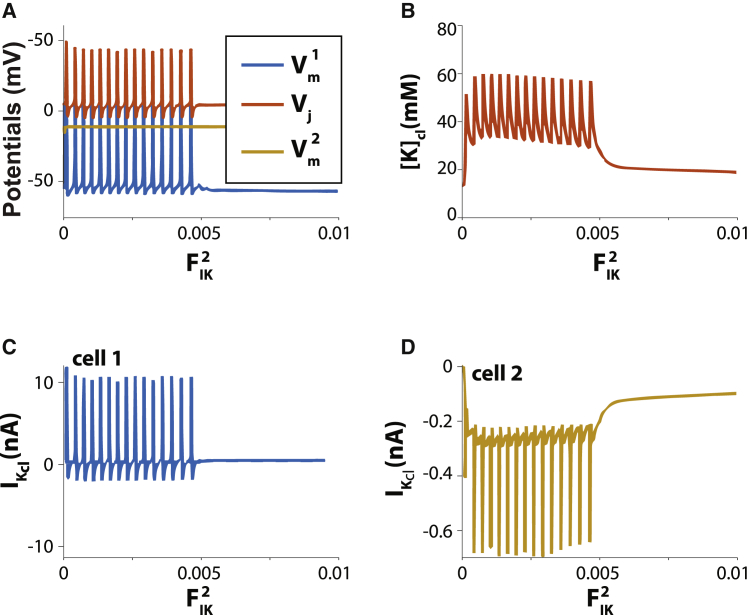
To simulate an inexcitable support cell like a fibroblast, intracellular potassium ([K]i) of the inexcitable cell 2 (gNa = 0) is reduced to 35.77 mM to establish a depolarized lateral resting Vm (62,63). In this case, excitable cell 1 is spontaneously autorhythmic (blue trace) as long as FIK of inexcitable cell 2 is below 0.0055 (Fig. 10 A, yellow trace), and this is driven by [K]cl oscillations (Fig. 10 B). With very low FIK, IK,cl in cell 1 (Fig. 10 C) is predominantly outward, and FIK is always inward in cell 2 (Fig. 10 D). As soon as FIK in cell 2 increases beyond 0.0055, the nonexcitable cell withdraws sufficient [K]cl to abolish automaticity in cell 1. Taken together with Fig. 8, this model predicts that inexcitable cells can suppress and initiate automaticity.
Figure 10.
Support cells that are depolarized can suppress automaticity in an excitable cell sharing a diffusion-limited cleft. (A) Cell 1 is excitable and shares a cleft with inexcitable cell 2 (gNa = 0). Minimal membrane potential of cell 2 (yellow trace) is depolarized relative to cell 1 (blue trace). Cells are coupled via a shared cleft domain with nominal wf = 1 and high fractional potassium cleft current = 0.8 in cell 1. in cell 2 is varied as the independent variable and ranges from 0 to 0.01. Automaticity is supported for 0 < < 0.005 in cell 2. (B) Relationship between extracellular cleft potassium [K]cl and fractional. (C) Cleft potassium current IK,cl for cell 1. (D) Cleft potassium current IK,cl for in cell 2.
Automaticity in cardiac tissue
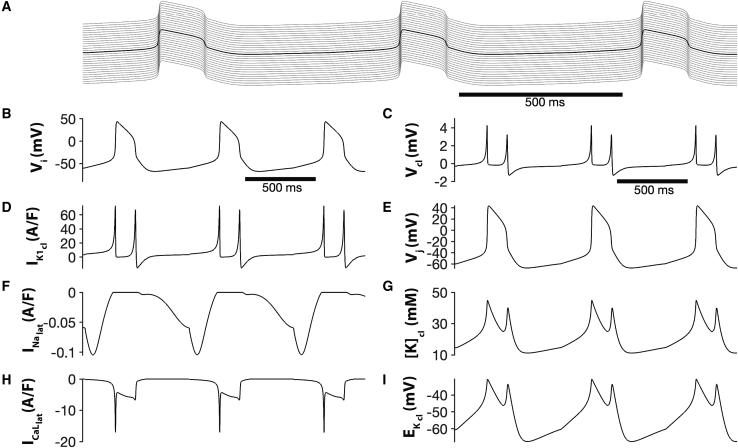
Next, we demonstrate the generality of the findings from individual and pairs of HH cells and expand the discussion to a chain of coupled cardiac myocytes with membrane currents now represented by the dynamic LRd cardiac model. Once again, all adjacent myocytes share a restricted cleft. As in the HH cleft model, high fractional inward rectifier cleft current (FIK1) drives entrained spontaneous electrical activity throughout the entire cardiac strand (Fig. 11 A). Action potentials exhibit physiological duration and periods on the order of 150 and 600 ms, respectively (Fig. 11 B). A large IK1 at the cleft is active between action potentials, which drives [K]cl accumulation and increases EK,cl (Fig. 11, D, G, and I). Additionally, we find that a small but persistent lateral membrane sodium current is active during the gradual phase-4 depolarization that occurs between action potentials, and the action potential upstroke is driven by a lateral membrane calcium window current (Fig. 11, F and H).
Figure 11.
(A) Entrained spontaneous activity in a chain of 30 cardiac myocytes, with adjacent cells coupled via a common diffusion-limited cleft domain w = 8 nm and high fractional potassium cleft current FIK1 = 0.8. (B) Intracellular potential Vi, (C) cleft potential Vcl, (D) cleft inward rectifier potassium current IK1, (E) junctional potential Vj, (F) lateral membrane sodium current I current, (G) cleft potassium concentration K, (H) lateral membrane L-type calcium current , and (I) cleft K+ reversal potential are shown as a function of time for the middle cell or cleft, respectively. Supporting materials and methods LRd_EpC_Automaticity.zip contains the MATLAB source code.
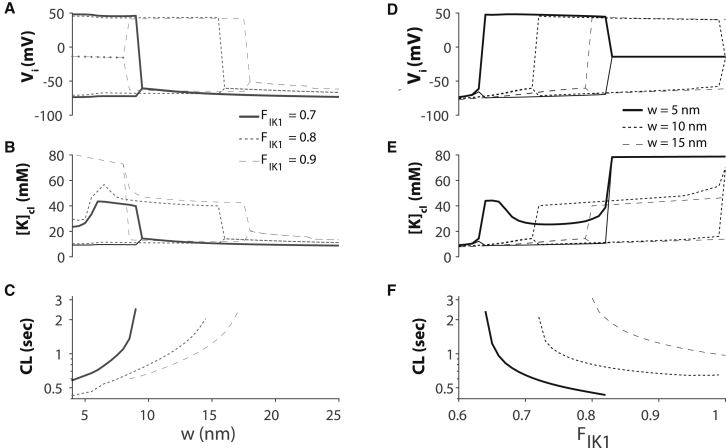
We next investigate the autorhythmic behavior in the cardiac tissue model as a function of cleft width w and FIK1. Importantly, we observe the same trends and relationships as in the HH cleft model. For large w, there are no oscillations (Fig. 12 A). As w decreases, [K]cl increases until spontaneous activity occurs in the strand (Fig. 12 B). Higher FIK1 results in automaticity for large cleft widths. Further, autorhythmic cycle length decreases as w decreases (Fig. 12 C). Similarly, for a given w, increasing FIK1 elevates [K]cl, promotes autorhythmic activity (Fig. 12, D and E), and decreases spontaneous cycle length (Fig. 12 F). For very small cleft widths and high FIK1, [K]cl is elevated to such an extent that spontaneous activity ceases.
Figure 12.
Spontaneous activity in cardiac tissue for diffusion-limited cleft widths (w) and high fractional inward rectifier cleft current FIK1. (A–C) The range of intracellular potentials Vi, cleft potassium concentrations [K]cl, and spontaneous cycle lengths (CL) are shown as a function of w for different values of fractional inward rectifier potassium current in the cleft FIK1. (D–F) The range of Vi and [K]cl values and spontaneous CL are shown as a function of FIK1 for different cleft w.
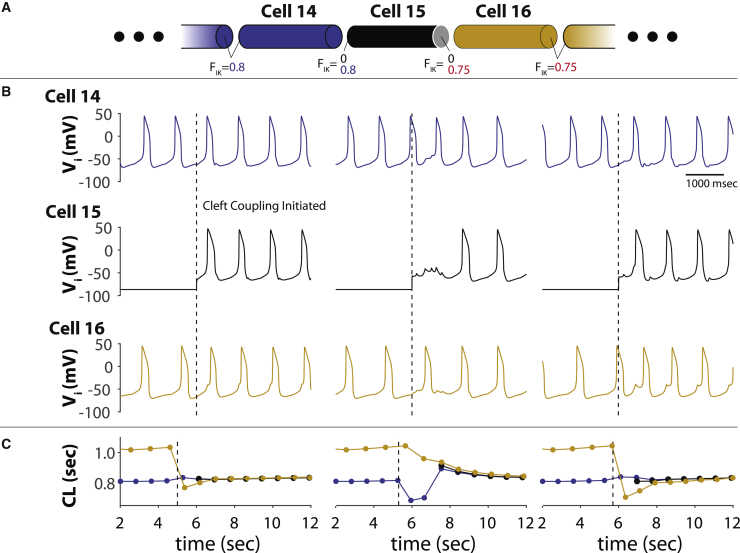
Finally, we investigate the temporal aspects of entrained automaticity for two parts of the cable spontaneously activating at different cycle lengths. Fig. 13 A contains the schematic showing cells 1–14 with FIK1 = 0.8 and cells 16–29 with FIK1 = 0.75. The w is 8 nm for all cells. FIK1 in cell 15 is initially set to 0. The first half of the traces in Fig. 13 B reveal that cells 1–14 and 16–19 are autorhythmic with different intrinsic cycle lengths plotted in Fig. 13 C. The different columns in Fig. 13, B and C show the temporal synchronization of the two halves of the strand when FIK1 on the left side of cell 15 is set to 0.8 and the right side is set to 0.75. The two halves of the strand synchronize between one and three beats depending on the time cleft coupling is initiated, and the cycle length of the entire strand follows the cells with the lower cycle length. Furthermore, much like Fig. 7 A above, the faster-firing half of the strand entrains the slower half of the strand as evidenced by the phase shift between cells 14 and 16.
Figure 13.
Temporal synchronization of an LRd strand with distinct autorhythmic cycle lengths. (A) Diagram of strand. FIK1 = 0.8 for cells 1–14, FIK1 = 0 for cell 15, and FIK1 = 0.75 for cells 16–29. Cleft width w = 8 nm for all cells. (B) Lateral transmembrane voltages Vi for cells 14, 15, and 16, demonstrating that cells 14 and 16 are autorhythmic with shared clefts at different cycle lengths. When FIK1 = 0.8 on the left side of the cell and 0.75 on the right side (dashed trace) are changed to initiate cleft coupling at the boundary of the two strands, cell 15 becomes autorhythmic. (C) The autorhythmic cycle length (CL) of cells 1–14 in blue is shorter than cells 16–29 until cleft coupling is initiated. After one to three beats, cell 15 and cells 16–28 entrain with cells 1–14 at a cycle length very close to the intrinsic cycle lengths of cells 1–14.
Discussion
Summary and conclusions
In this manuscript, we demonstrate that 1) the addition of an extracellular volume with limited potassium diffusivity can induce spontaneous autorhythmic behavior in otherwise quiescent in silico cell models, 2) multicellular entrainment can occur in the absence of gap junctional coupling, 3) induction and entrainment can occur via the same mechanism even if cells are not autorhythmic in isolation, and 4) the autorhythmic rate of multiple cells coupled by diffusion-limited spaces can be higher than the intrinsic frequency of the individual cell. The mechanism is a result of potassium channels in the cleft raising [K]cl, which increases cleft EK,cl, junctional transmembrane potential Vj, intracellular potential Vi, and ultimately lateral Vm. The result is that a low-amplitude and persistent sodium or calcium window current can ultimately trigger the all-or-none action potential that is necessary to reset [K]cl. Under or overdamping [K]cl suppresses automaticity. The data also support previous studies suggesting that shared extracellular volumes can reduce dispersion of repolarization (64).
Gap junctions and cardiac automaticity
In the cardiac field, the centrality of gap junctional electrical communication continues to dominate the theories of spatially extensive sinoatrial node automaticity, which has significant clinical implications for diseases like sick sinus syndrome. The two main hypotheses relating gap junctional coupling to sinoatrial node automaticity are that gap junctions propagate the action potential from master pacemaker cells and that gap junctions permit entrainment of spontaneously active sinoatrial node cells. These hypotheses are not mutually exclusive. There is general agreement that gap junctional coupling in sinoatrial nodal tissue is significantly lower and heterogeneously distributed relative to working atrial and ventricular myocardium, but elegant experimental studies like the “sucrose-gap” experiments established that gap junctional coupling is capable of synchronizing autorhythmic activity (21).
Much of the work suggesting that pacemaking arises from master pacemaker cells and propagates to the remainder of the sinoatrial node through gap junctions occurred throughout the 1970s and early 1980s (18, 19, 20). Later, the hypothesis that gap junctions synchronize a large number of cells over a relatively extensive volume by mutual electrical entrainment through gap junctions (21,22) was important to explain sinoatrial node phase resetting (24). Notably, the master pacemaker cell hypothesis could not explain the phenomenon by conduction alone (25). Both hypotheses are still salient to pacemaking because master pacemaker cells require some type of entrainment to overcome electrotonic load and synchronize automaticity, and the autorhythmic signal must propagate to the remainder of the specialized conduction system and cardiac myocardium.
Conversely, the experimental consensus is that gap junction modulation (65, 66, 67, 68, 69, 70, 71) with memetic peptides or derivatives (72) or genetically (73, 74, 75) is not associated with any change in heart rate. In the few studies that report modulating gap junction coupling alters heart rate, the effect is reported as modest (76,77). This study and others (78,79) support experimental findings that suggest gap junctions do not play a significant role in setting the sinus or intrinsic rhythms of cells in the heart.
Sodium channels and cardiac automaticity
The importance of sodium channels to cardiac automaticity arise from studies demonstrating that functional downregulation of voltage-gated sodium channels alters the autorhythmic frequency by slowing and even blocking conduction out of the compact sinoatrial node (80). Yet, sodium channels can also induce autorhythmic activity as demonstrated by Denis Noble nearly half a century prior (81). Specifically, he showed that a sodium window current can create autorhythmic Purkinje fiber-like action potentials (81). Unlike Noble’s model, our model demonstrates that arrhythmic activity can occur without revising sodium channel kinetics but by utilizing a diffusion-limited extracellular domain capable of cyclic potassium accumulation and depletion. Our results also demonstrate that even without gap junctional coupling, cellular models can gain autorhythmic activity and entrain by sharing extracellular nanodomains. This is distinct from the aforementioned studies demonstrating how gap junctional coupling modulates multicellular automaticity comprised from cells that are autorhythmic in isolation. Additionally, neither the HH nor LRd model in this study are autorhythmic without a cleft. Thus, the mechanism of extracellularly mediated automaticity by diffusion-limited clefts (EMA-DL) as an initiator and modulator of autorhythmic activity should be interpreted as a generalized but not cell-type specific phenomenon separate from gap junction coupling.
Repolarization
Gap junctions also modulate repolarization between cardiomyocytes (82,83) and between cardiomyocytes and support cells like fibroblasts (84). Electrotonic homogenization of repolarization via an intracellular gap junction-mediated pathway occurs over a relatively larger spatial extent of millimeters as described by a space constant. The proposed cleft mechanism can synchronize repolarization over extracellular gaps with a spatial extent on the order of nanometers. Specifically, cleft sodium regulation, as opposed to potassium in this study, can conceal or unmask whole-heart action potential duration prolongation in models with enhanced late sodium currents (57, 58, 59,85). The proposal that extracellular spaces modulate dispersion of repolarization was proposed by Hubbard and Henriquez (64), but the biophysical mechanisms in this study are different. Specifically, EMA-DL modulates dispersion of repolarization via ionic depletion and subsequent alterations to ionic reversal potentials, whereas the electric field ephaptic mechanism proposed previously occurs via electric field generation between junctional membrane. Multicellular EMA-DL synchronization occurs when individual cells are conjoined across nanometer cleft spaces, and ion channel distributions meet the requirements to entrain activation and homogenize repolarization. Undoubtedly, future studies incorporating both ionic and electric field ephaptic mechanisms with gap junction coupling will reveal that Vm changes driven by intracellular potentials (gap junctions) and extracellular potentials (ephaptic coupling) will further dynamically modulate automaticity, conduction, and repolarization.
Structural determinants
EMA-DL, in this study, was achieved with cleft volume of 5.7 × 10−12 cm3 and 60% of potassium channels (HH) or inward rectifier potassium channels IK1 (LRd) localized to the junctional membrane. Although the shapes and dimensions of cardiomyocytes are heterogeneous, the volume of the intercellular cleft was based on estimates of ventricular myocyte diameters of ∼15–20 μm (47,48). Cleft width was based on estimates of gap junction-adjacent perinexal separation (43,49,50) and other zonula occludens-1-associated intercalated disk structural junctions (86,87). The intercalated disk between cardiomyocytes is a highly complex and tortuous structure with a surface area much greater than the cross-sectional area of a myocyte, and the number and extracellular cluster volumes of Kir2.1 nanodomains are unknown. Therefore, the cleft volume utilized in this model may be consistent with realistic cleft widths, but nanodomain volumes will need to be established for detailed cellular geometry studies (88) and complex three-dimensional tissue models (89).
EMA-DL also requires dense potassium channel expression to the diffusion-limited clefts, and the LRd simulations above reveal automaticity can be achieved with assumed cleft volumes when 60% of the inward rectifier potassium current through Kir2.1 is localized to the cleft. This is consistent with recent estimates that ∼45% of total Kir2.1 can be found within the intercalated disk (43).
Based on evidence that sodium channels are localized to specific cellular membrane domains (49,53,90, 91, 92), our work has important implications for the effects of sodium channel localization on automaticity, particularly as voltage-gated sodium channels can co-localize with Kir2.1 in the intercalated disk (43,93,94). Fig. 7 demonstrates that increasing sodium channel expression in the cleft modulates the frequencies and ranges of the autorhythmic behaviors shown above. In the LRd model, calcium channel window currents are more important than sodium channels for automaticity. Our study also has implications for HCN channels that can simultaneously conduct potassium and sodium in opposite directions. It is possible that HCN channels may also simultaneously exhibit preferential ionic species conductances based on their cellular localization to membrane nanodomains that themselves maintain different Vm and extracellular ionic compositions. Future structural biology studies are needed to explore this hypothesis.
Broader implications
EMA-DL may also have implications in the heart, where fibroblasts are densely expressed in the pacemaking sinoatrial node (95,96) and where macrophages can be found in the atrioventricular node (97). As suggested previously (98), this ephaptic mechanism may further expand the understanding of the degree of gap junctional coupling needed by much smaller and inexcitable nonmyocytes to alter cardiomyocyte electrophysiology (99,100).
There are also striking similarities in the extracellular domains between cardiomyocytes and neurons. The synaptic cleft is estimated to be between 15 and 25 nm (54), the distance from astrocytes to neurons is ∼10–40 nm (101), axon diameters range from 0.1 to 10 μm (102), and Kir4.1 is densely expressed at astrocyte-neuron interfaces (40). Regardless of the cell types, future studies are needed to elucidate whether cells involved in autorhythmic activity meet the requirement for EMA-DL by estimating shared cleft volumes and the distribution of ion channels, hemichannels, pumps, aquaporins, and exchangers capable of modulating extracellular nanodomains.
Conclusions
This study demonstrates that shared extracellular nanodomains can create emergent phenomenon that cannot be solely accounted for by homogenized transmembrane and intercellular pathways. Incorporating extracellular electric fields (103) and ionic tracking into models of electrically active cells may offer new avenues to develop therapies for autorhythmic dysregulation in diverse tissues like the heart, brain, skeletal muscles, intestine, and uterine myometrium that to date have focused on gap junctional coupling as the exclusive mode of intercellular electrical communication.
Author contributions
S.P. conceptualized the original hypothesis, designed the research, and wrote the manuscript. J.P.K. designed, validated, and executed the EMA-DL-modified HH model and the bifurcation analysis and wrote the manuscript. J.P.K. identified that EMA-DL will occur in computational models that gain spontaneous automaticity when the resting membrane potential is elevated. S.H.W. designed, validated, and executed EMA-DL-modified LRd for isolated cells and a cable and wrote the manuscript. S.H.W. identified that the sodium or calcium window currents drive EMA-DL automaticity in HH and LRd, respectively.
Acknowledgments
This study was supported by funding from the National Institutes of Health, with grants R01HL141855 (S.P.), R01HL102298 (S.P. and J.P.K.), and R01HL138003 (S.P. and S.H.W.).
Editor: Brian Salzberg.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.10.034.
Supporting material
References
- 1.DiFrancesco D. Pacemaker mechanisms in cardiac tissue. Annu. Rev. Physiol. 1993;55:455–472. doi: 10.1146/annurev.ph.55.030193.002323. [DOI] [PubMed] [Google Scholar]
- 2.Pape H.C. Queer current and pacemaker: the hyperpolarization-activated cation current in neurons. Annu. Rev. Physiol. 1996;58:299–327. doi: 10.1146/annurev.ph.58.030196.001503. [DOI] [PubMed] [Google Scholar]
- 3.Mitsuiye T., Shinagawa Y., Noma A. Sustained inward current during pacemaker depolarization in mammalian sinoatrial node cells. Circ. Res. 2000;87:88–91. doi: 10.1161/01.res.87.2.88. [DOI] [PubMed] [Google Scholar]
- 4.Biel M., Schneider A., Wahl C. Cardiac HCN channels: structure, function, and modulation. Trends Cardiovasc. Med. 2002;12:206–212. doi: 10.1016/s1050-1738(02)00162-7. [DOI] [PubMed] [Google Scholar]
- 5.Wilders R. Computer modelling of the sinoatrial node. Med. Biol. Eng. Comput. 2007;45:189–207. doi: 10.1007/s11517-006-0127-0. [DOI] [PubMed] [Google Scholar]
- 6.Lakatta E.G., Maltsev V.A., Vinogradova T.M. A coupled SYSTEM of intracellular Ca2+ clocks and surface membrane voltage clocks controls the timekeeping mechanism of the heart’s pacemaker. Circ. Res. 2010;106:659–673. doi: 10.1161/CIRCRESAHA.109.206078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Irisawa H., Brown H.F., Giles W. Cardiac pacemaking in the sinoatrial node. Physiol. Rev. 1993;73:197–227. doi: 10.1152/physrev.1993.73.1.197. [DOI] [PubMed] [Google Scholar]
- 8.McCormick D.A., Bal T. Sleep and arousal: thalamocortical mechanisms. Annu. Rev. Neurosci. 1997;20:185–215. doi: 10.1146/annurev.neuro.20.1.185. [DOI] [PubMed] [Google Scholar]
- 9.Ramirez J.M., Richter D.W. The neuronal mechanisms of respiratory rhythm generation. Curr. Opin. Neurobiol. 1996;6:817–825. doi: 10.1016/s0959-4388(96)80033-x. [DOI] [PubMed] [Google Scholar]
- 10.Raman I.M., Bean B.P. Ionic currents underlying spontaneous action potentials in isolated cerebellar Purkinje neurons. J. Neurosci. 1999;19:1663–1674. doi: 10.1523/JNEUROSCI.19-05-01663.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Levic S., Lv P., Yamoah E.N. The activity of spontaneous action potentials in developing hair cells is regulated by Ca(2+)-dependence of a transient K+ current. PLoS One. 2011;6:e29005. doi: 10.1371/journal.pone.0029005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guo X., Greene K., et al. Hickman J. In vitro differentiation of functional human skeletal myotubes in a defined system. Biomater. Sci. 2014;2:131–138. doi: 10.1039/C3BM60166H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reddivari A.K.R., Mehta P. StatPearls; Treasure Island, FL: 2021. Gastroparesis. [Google Scholar]
- 14.Takaki M. Gut pacemaker cells: the interstitial cells of Cajal (ICC) J. Smooth Muscle Res. 2003;39:137–161. doi: 10.1540/jsmr.39.137. [DOI] [PubMed] [Google Scholar]
- 15.Arrowsmith S., Robinson H., et al. Wray S. What do we know about what happens to myometrial function as women age? J. Muscle Res. Cell Motil. 2012;33:209–217. doi: 10.1007/s10974-012-9300-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chow L., Lye S.J. Expression of the gap junction protein connexin-43 is increased in the human myometrium toward term and with the onset of labor. Am. J. Obstet. Gynecol. 1994;170:788–795. doi: 10.1016/s0002-9378(94)70284-5. [DOI] [PubMed] [Google Scholar]
- 17.Xie Y., Sato D., et al. Weiss J.N. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys. J. 2010;99:1408–1415. doi: 10.1016/j.bpj.2010.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bleeker W.K., Mackaay A.J., et al. Becker A.E. Functional and morphological organization of the rabbit sinus node. Circ. Res. 1980;46:11–22. doi: 10.1161/01.res.46.1.11. [DOI] [PubMed] [Google Scholar]
- 19.Pollack G.H. Cardiac pacemaking: an obligatory role of catecholamines? Science. 1977;196:731–738. doi: 10.1126/science.16342. [DOI] [PubMed] [Google Scholar]
- 20.Sano T., Sawanobori T., Adaniya H. Mechanism of rhythm determination among pacemaker cells of the mammalian sinus node. Am. J. Physiol. 1978;235:H379–H384. doi: 10.1152/ajpheart.1978.235.4.H379. [DOI] [PubMed] [Google Scholar]
- 21.Jalife J. Mutual entrainment and electrical coupling as mechanisms for synchronous firing of rabbit sino-atrial pace-maker cells. J. Physiol. 1984;356:221–243. doi: 10.1113/jphysiol.1984.sp015461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Michaels D.C., Matyas E.P., Jalife J. Dynamic interactions and mutual synchronization of sinoatrial node pacemaker cells. A mathematical model. Circ. Res. 1986;58:706–720. doi: 10.1161/01.res.58.5.706. [DOI] [PubMed] [Google Scholar]
- 23.Michaels D.C., Matyas E.P., Jalife J. Mechanisms of sinoatrial pacemaker synchronization: a new hypothesis. Circ. Res. 1987;61:704–714. doi: 10.1161/01.res.61.5.704. [DOI] [PubMed] [Google Scholar]
- 24.Guevara M.R., Shrier A., Glass L. Phase resetting of spontaneously beating embryonic ventricular heart cell aggregates. Am. J. Physiol. 1986;251:H1298–H1305. doi: 10.1152/ajpheart.1986.251.6.H1298. [DOI] [PubMed] [Google Scholar]
- 25.Anumonwo J.M., Delmar M., et al. Jalife J. Phase resetting and entrainment of pacemaker activity in single sinus nodal cells. Circ. Res. 1991;68:1138–1153. doi: 10.1161/01.res.68.4.1138. [DOI] [PubMed] [Google Scholar]
- 26.Guo J., Noma A. Existence of a low-threshold and sustained inward current in rabbit atrio-ventricular node cells. Jpn. J. Physiol. 1997;47:355–359. doi: 10.2170/jjphysiol.47.355. [DOI] [PubMed] [Google Scholar]
- 27.Shinagawa Y., Satoh H., Noma A. The sustained inward current and inward rectifier K+ current in pacemaker cells dissociated from rat sinoatrial node. J. Physiol. 2000;523:593–605. doi: 10.1111/j.1469-7793.2000.t01-2-00593.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vaidyanathan R., O’Connell R.P., et al. Anumonwo J.M. The ionic bases of the action potential in isolated mouse cardiac Purkinje cell. Heart Rhythm. 2013;10:80–87. doi: 10.1016/j.hrthm.2012.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Quinn T.A., Kohl P. Mechano-sensitivity of cardiac pacemaker function: pathophysiological relevance, experimental implications, and conceptual integration with other mechanisms of rhythmicity. Prog. Biophys. Mol. Biol. 2012;110:257–268. doi: 10.1016/j.pbiomolbio.2012.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bychkov R., Juhaszova M., et al. Lakatta E.G. Synchronized cardiac impulses emerge from heterogeneous local calcium signals within and among cells of pacemaker tissue. JACC Clin. Electrophysiol. 2020;6:907–931. doi: 10.1016/j.jacep.2020.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Livshitz L.M., Rudy Y. Regulation of Ca2+ and electrical alternans in cardiac myocytes: role of CAMKII and repolarizing currents. Am. J. Physiol. Heart Circ. Physiol. 2007;292:H2854–H2866. doi: 10.1152/ajpheart.01347.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Frankenhaeuser B., Hodgkin A.L. The after-effects of impulses in the giant nerve fibres of Loligo. J. Physiol. 1956;131:341–376. doi: 10.1113/jphysiol.1956.sp005467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Moody W.J., Futamachi K.J., Prince D.A. Extracellular potassium activity during epileptogenesis. Exp. Neurol. 1974;42:248–263. doi: 10.1016/0014-4886(74)90023-5. [DOI] [PubMed] [Google Scholar]
- 35.Lothman E., Lamanna J., et al. Somjen G. Responses of electrical potential, potassium levels, and oxidative metabolic activity of the cerebral neocortex of cats. Brain Res. 1975;88:15–36. doi: 10.1016/0006-8993(75)90943-9. [DOI] [PubMed] [Google Scholar]
- 36.Kager H., Wadman W.J., Somjen G.G. Simulated seizures and spreading depression in a neuron model incorporating interstitial space and ion concentrations. J. Neurophysiol. 2000;84:495–512. doi: 10.1152/jn.2000.84.1.495. [DOI] [PubMed] [Google Scholar]
- 37.Bolton S., Greenwood K., et al. Butt A.M. Regulation of the astrocyte resting membrane potential by cyclic AMP and protein kinase A. Glia. 2006;54:316–328. doi: 10.1002/glia.20384. [DOI] [PubMed] [Google Scholar]
- 38.Kager H., Wadman W.J., Somjen G.G. Seizure-like afterdischarges simulated in a model neuron. J. Comput. Neurosci. 2007;22:105–128. doi: 10.1007/s10827-006-0001-y. [DOI] [PubMed] [Google Scholar]
- 39.Somjen G.G., Kager H., Wadman W.J. Computer simulations of neuron-glia interactions mediated by ion flux. J. Comput. Neurosci. 2008;25:349–365. doi: 10.1007/s10827-008-0083-9. [DOI] [PubMed] [Google Scholar]
- 40.Nwaobi S.E., Cuddapah V.A., et al. Olsen M.L. The role of glial-specific Kir4.1 in normal and pathological states of the CNS. Acta Neuropathol. 2016;132:1–21. doi: 10.1007/s00401-016-1553-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Melnyk P., Zhang L., et al. Nattel S. Differential distribution of Kir2.1 and Kir2.3 subunits in canine atrium and ventricle. Am. J. Physiol. Heart Circ. Physiol. 2002;283:H1123–H1133. doi: 10.1152/ajpheart.00934.2001. [DOI] [PubMed] [Google Scholar]
- 42.Ponce-Balbuena D., Guerrero-Serna G., et al. Jalife J. Cardiac Kir2.1 and NaV1.5 channels traffic together to the sarcolemma to control excitability. Circ. Res. 2018;122:1501–1516. doi: 10.1161/CIRCRESAHA.117.311872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Veeraraghavan R., Lin J., et al. Poelzing S. Potassium channels in the Cx43 gap junction perinexus modulate ephaptic coupling: an experimental and modeling study. Pflugers Arch. 2016;468:1651–1661. doi: 10.1007/s00424-016-1861-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rhett J.M., Jourdan J., Gourdie R.G. Connexin 43 connexon to gap junction transition is regulated by zonula occludens-1. Mol. Biol. Cell. 2011;22:1516–1528. doi: 10.1091/mbc.E10-06-0548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Veeraraghavan R., Gourdie R.G., Poelzing S. Mechanisms of cardiac conduction: a history of revisions. Am. J. Physiol. Heart Circ. Physiol. 2014;306:H619–H627. doi: 10.1152/ajpheart.00760.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sperelakis N., McConnell K. Electric field interactions between closely abutting excitable cells. IEEE Eng. Med. Biol. Mag. 2002;21:77–89. doi: 10.1109/51.993199. [DOI] [PubMed] [Google Scholar]
- 47.Ashley L.M. A determination of the diameters of ventricular myocardial fibers in man and other mammals. Am. J. Anat. 1945;77:325–363. doi: 10.1002/aja.1000770303. [DOI] [PubMed] [Google Scholar]
- 48.Sorenson A.L., Tepper D., et al. Capasso J.M. Size and shape of enzymatically isolated ventricular myocytes from rats and cardiomyopathic hamsters. Cardiovasc. Res. 1985;19:793–799. doi: 10.1093/cvr/19.12.793. [DOI] [PubMed] [Google Scholar]
- 49.Veeraraghavan R., Lin J., et al. Poelzing S. Sodium channels in the Cx43 gap junction perinexus may constitute a cardiac ephapse: an experimental and modeling study. Pflugers Arch. 2015;467:2093–2105. doi: 10.1007/s00424-014-1675-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Raisch T., Khan M., Poelzing S. Quantifying intermembrane distances with serial image dilations. J. Vis. Exp. 2018:58311. doi: 10.3791/58311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shaw R.M., Rudy Y. Ionic mechanisms of propagation in cardiac tissue. Roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ. Res. 1997;81:727–741. doi: 10.1161/01.res.81.5.727. [DOI] [PubMed] [Google Scholar]
- 52.Katz B. McGraw-Hill; New York: 1966. Nerve, Muscle, and Synapse. [Google Scholar]
- 53.Kucera J.P., Rohr S., Rudy Y. Localization of sodium channels in intercalated disks modulates cardiac conduction. Circ. Res. 2002;91:1176–1182. doi: 10.1161/01.res.0000046237.54156.0a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Savtchenko L.P., Rusakov D.A. The optimal height of the synaptic cleft. Proc. Natl. Acad. Sci. USA. 2007;104:1823–1828. doi: 10.1073/pnas.0606636104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Raisch T.B., Yanoff M.S., et al. Poelzing S. Intercalated disk extracellular nanodomain expansion in patients with atrial fibrillation. Front. Physiol. 2018;9:398. doi: 10.3389/fphys.2018.00398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Innocenti G.M., Caminiti R. Axon diameter relates to synaptic bouton size: structural properties define computationally different types of cortical connections in primates. Brain Struct. Funct. 2017;222:1169–1177. doi: 10.1007/s00429-016-1266-1. [DOI] [PubMed] [Google Scholar]
- 57.Greer-Short A., George S.A., et al. Weinberg S.H. Revealing the concealed nature of long-QT type 3 syndrome. Circ. Arrhythm. Electrophysiol. 2017;10:e004400. doi: 10.1161/CIRCEP.116.004400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Nowak M.B., Greer-Short A., et al. Poelzing S. Intercellular sodium regulates repolarization in cardiac tissue with sodium channel gain of function. Biophys. J. 2020;118:2829–2843. doi: 10.1016/j.bpj.2020.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Weinberg S.H. Ephaptic coupling rescues conduction failure in weakly coupled cardiac tissue with voltage-gated gap junctions. Chaos. 2017;27:093908. doi: 10.1063/1.4999602. [DOI] [PubMed] [Google Scholar]
- 60.Ransom C.B., Sontheimer H. Biophysical and pharmacological characterization of inwardly rectifying K+ currents in rat spinal cord astrocytes. J. Neurophysiol. 1995;73:333–346. doi: 10.1152/jn.1995.73.1.333. [DOI] [PubMed] [Google Scholar]
- 61.Hibino H., Inanobe A., et al. Kurachi Y. Inwardly rectifying potassium channels: their structure, function, and physiological roles. Physiol. Rev. 2010;90:291–366. doi: 10.1152/physrev.00021.2009. [DOI] [PubMed] [Google Scholar]
- 62.Kamkin A., Kiseleva I., et al. Günther J. Mechanically induced potentials in fibroblasts from human right atrium. Exp. Physiol. 1999;84:347–356. [PubMed] [Google Scholar]
- 63.Chilton L., Ohya S., et al. Giles W.R. K+ currents regulate the resting membrane potential, proliferation, and contractile responses in ventricular fibroblasts and myofibroblasts. Am. J. Physiol. Heart Circ. Physiol. 2005;288:H2931–H2939. doi: 10.1152/ajpheart.01220.2004. [DOI] [PubMed] [Google Scholar]
- 64.Hubbard M.L., Henriquez C.S. Increased interstitial loading reduces the effect of microstructural variations in cardiac tissue. Am. J. Physiol. Heart Circ. Physiol. 2010;298:H1209–H1218. doi: 10.1152/ajpheart.00689.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kojodjojo P., Kanagaratnam P., et al. Peters N.S. The effects of carbenoxolone on human myocardial conduction: a tool to investigate the role of gap junctional uncoupling in human arrhythmogenesis. J. Am. Coll. Cardiol. 2006;48:1242–1249. doi: 10.1016/j.jacc.2006.04.093. [DOI] [PubMed] [Google Scholar]
- 66.Lan W.R., Hou C.J., et al. Yeh H.I. Effects of carbenoxolone on flow-mediated vasodilatation in healthy adults. Am. J. Physiol. Heart Circ. Physiol. 2011;301:H1166–H1172. doi: 10.1152/ajpheart.00967.2010. [DOI] [PubMed] [Google Scholar]
- 67.Papp R., Gönczi M., et al. Végh A. Gap junctional uncoupling plays a trigger role in the antiarrhythmic effect of ischaemic preconditioning. Cardiovasc. Res. 2007;74:396–405. doi: 10.1016/j.cardiores.2007.02.021. [DOI] [PubMed] [Google Scholar]
- 68.Isobe T., Honda M., et al. Tabo M. Conduction and contraction properties of human iPS cell-derived cardiomyocytes: analysis by motion field imaging compared with the Guinea-pig isolated heart model. J. Toxicol. Sci. 2018;43:493–506. doi: 10.2131/jts.43.493. [DOI] [PubMed] [Google Scholar]
- 69.Masumiya H., Oku Y., Okada Y. Inhomogeneous distribution of action potential characteristics in the rabbit sino-atrial node revealed by voltage imaging. J. Physiol. Sci. 2009;59:227–241. doi: 10.1007/s12576-009-0032-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Hennan J.K., Swillo R.E., et al. Crandall D.L. Rotigaptide (ZP123) prevents spontaneous ventricular arrhythmias and reduces infarct size during myocardial ischemia/reperfusion injury in open-chest dogs. J. Pharmacol. Exp. Ther. 2006;317:236–243. doi: 10.1124/jpet.105.096933. [DOI] [PubMed] [Google Scholar]
- 71.Miura T., Ohnuma Y., et al. Shimamoto K. Protective role of gap junctions in preconditioning against myocardial infarction. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H214–H221. doi: 10.1152/ajpheart.00441.2003. [DOI] [PubMed] [Google Scholar]
- 72.De Vriese A.S., Van de Voorde J., Lameire N.H. Effects of connexin-mimetic peptides on nitric oxide synthase- and cyclooxygenase-independent renal vasodilation. Kidney Int. 2002;61:177–185. doi: 10.1046/j.1523-1755.2002.00122.x. [DOI] [PubMed] [Google Scholar]
- 73.Thomas S.A., Schuessler R.B., et al. Saffitz J.E. Disparate effects of deficient expression of connexin43 on atrial and ventricular conduction: evidence for chamber-specific molecular determinants of conduction. Circulation. 1998;97:686–691. doi: 10.1161/01.cir.97.7.686. [DOI] [PubMed] [Google Scholar]
- 74.Danik S.B., Liu F., et al. Gutstein D.E. Modulation of cardiac gap junction expression and arrhythmic susceptibility. Circ. Res. 2004;95:1035–1041. doi: 10.1161/01.RES.0000148664.33695.2a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Stein M., van Veen T.A., et al. van Rijen H.V. Combined reduction of intercellular coupling and membrane excitability differentially affects transverse and longitudinal cardiac conduction. Cardiovasc. Res. 2009;83:52–60. doi: 10.1093/cvr/cvp124. [DOI] [PubMed] [Google Scholar]
- 76.Howarth F.C., Qureshi M.A. Effects of carbenoxolone on heart rhythm, contractility and intracellular calcium in streptozotocin-induced diabetic rat. Mol. Cell. Biochem. 2006;289:21–29. doi: 10.1007/s11010-006-9143-5. [DOI] [PubMed] [Google Scholar]
- 77.Garcia-Dorado D., Inserte J., et al. Soler-Soler J. Gap junction uncoupler heptanol prevents cell-to-cell progression of hypercontracture and limits necrosis during myocardial reperfusion. Circulation. 1997;96:3579–3586. doi: 10.1161/01.cir.96.10.3579. [DOI] [PubMed] [Google Scholar]
- 78.Kostecki G.M., Shi Y., et al. Tung L. Optogenetic current in myofibroblasts acutely alters electrophysiology and conduction of co-cultured cardiomyocytes. Sci. Rep. 2021;11:4430. doi: 10.1038/s41598-021-83398-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Yu J.K., Liang J.A., et al. Trayanova N.A. Computational modeling of aberrant electrical activity following remuscularization with intramyocardially injected pluripotent stem cell-derived cardiomyocytes. J. Mol. Cell. Cardiol. 2021;162:97–109. doi: 10.1016/j.yjmcc.2021.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Lei M., Zhang H., et al. Huang C.L. SCN5A and sinoatrial node pacemaker function. Cardiovasc. Res. 2007;74:356–365. doi: 10.1016/j.cardiores.2007.01.009. [DOI] [PubMed] [Google Scholar]
- 81.Noble D. A modification of the Hodgkin--Huxley equations applicable to Purkinje fibre action and pace-maker potentials. J. Physiol. 1962;160:317–352. doi: 10.1113/jphysiol.1962.sp006849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lesh M.D., Pring M., Spear J.F. Cellular uncoupling can unmask dispersion of action potential duration in ventricular myocardium. A computer modeling study. Circ. Res. 1989;65:1426–1440. doi: 10.1161/01.res.65.5.1426. [DOI] [PubMed] [Google Scholar]
- 83.Viswanathan P.C., Shaw R.M., Rudy Y. Effects of IKr and IKs heterogeneity on action potential duration and its rate dependence: a simulation study. Circulation. 1999;99:2466–2474. doi: 10.1161/01.cir.99.18.2466. [DOI] [PubMed] [Google Scholar]
- 84.Jacquemet V., Henriquez C.S. Loading effect of fibroblast-myocyte coupling on resting potential, impulse propagation, and repolarization: insights from a microstructure model. Am. J. Physiol. Heart Circ. Physiol. 2008;294:H2040–H2052. doi: 10.1152/ajpheart.01298.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Nowak M.B., Poelzing S., Weinberg S.H. Mechanisms underlying age-associated manifestation of cardiac sodium channel gain-of-function. J. Mol. Cell. Cardiol. 2021;153:60–71. doi: 10.1016/j.yjmcc.2020.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Hirokawa N., Heuser J.E. Quick-freeze, deep-etch visualization of the cytoskeleton beneath surface differentiations of intestinal epithelial cells. J. Cell Biol. 1981;91:399–409. doi: 10.1083/jcb.91.2.399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Miyaguchi K. Ultrastructure of the zonula adherens revealed by rapid-freeze deep-etching. J. Struct. Biol. 2000;132:169–178. doi: 10.1006/jsbi.2000.4244. [DOI] [PubMed] [Google Scholar]
- 88.Stinstra J.G., Poelzing S., et al. Henriquez C.S. A model for estimating the anisotropy of the conduction velocity in cardiac tissue based on the tissue morphology. Comput. Cardiol. 2007;34:129–132. [Google Scholar]
- 89.Henriquez C.S. A brief history of tissue models for cardiac electrophysiology. IEEE Trans. Biomed. Eng. 2014;61:1457–1465. doi: 10.1109/TBME.2014.2310515. [DOI] [PubMed] [Google Scholar]
- 90.Cohen S.A., Levitt L.K. Partial characterization of the rH1 sodium channel protein from rat heart using subtype-specific antibodies. Circ. Res. 1993;73:735–742. doi: 10.1161/01.res.73.4.735. [DOI] [PubMed] [Google Scholar]
- 91.Petitprez S., Zmoos A.F., et al. Abriel H. SAP97 and dystrophin macromolecular complexes determine two pools of cardiac sodium channels Nav1.5 in cardiomyocytes. Circ. Res. 2011;108:294–304. doi: 10.1161/CIRCRESAHA.110.228312. [DOI] [PubMed] [Google Scholar]
- 92.Rhett J.M., Ongstad E.L., et al. Gourdie R.G. Cx43 associates with Na(v)1.5 in the cardiomyocyte perinexus. J. Membr. Biol. 2012;245:411–422. doi: 10.1007/s00232-012-9465-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Gillet L., Rougier J.S., et al. Abriel H. Cardiac-specific ablation of synapse-associated protein SAP97 in mice decreases potassium currents but not sodium current. Heart Rhythm. 2015;12:181–192. doi: 10.1016/j.hrthm.2014.09.057. [DOI] [PubMed] [Google Scholar]
- 94.Milstein M.L., Musa H., et al. Jalife J. Dynamic reciprocity of sodium and potassium channel expression in a macromolecular complex controls cardiac excitability and arrhythmia. Proc. Natl. Acad. Sci. USA. 2012;109:E2134–E2143. doi: 10.1073/pnas.1109370109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.De Mazière A.M., van Ginneken A.C., et al. Bouman L.N. Spatial and functional relationship between myocytes and fibroblasts in the rabbit sinoatrial node. J. Mol. Cell. Cardiol. 1992;24:567–578. doi: 10.1016/0022-2828(92)91041-3. [DOI] [PubMed] [Google Scholar]
- 96.Kohl P., Kamkin A.G., et al. Noble D. Mechanosensitive fibroblasts in the sino-atrial node region of rat heart: interaction with cardiomyocytes and possible role. Exp. Physiol. 1994;79:943–956. doi: 10.1113/expphysiol.1994.sp003819. [DOI] [PubMed] [Google Scholar]
- 97.Hulsmans M., Clauss S., et al. Nahrendorf M. Macrophages facilitate electrical conduction in the heart. Cell. 2017;169:510–522.e20. doi: 10.1016/j.cell.2017.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Nattel S. Electrical coupling between cardiomyocytes and fibroblasts: experimental testing of a challenging and important concept. Cardiovasc. Res. 2018;114:349–352. doi: 10.1093/cvr/cvy003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Rubart M., Tao W., et al. Soonpaa M.H. Electrical coupling between ventricular myocytes and myofibroblasts in the infarcted mouse heart. Cardiovasc. Res. 2018;114:389–400. doi: 10.1093/cvr/cvx163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Quinn T.A., Camelliti P., et al. Kohl P. Electrotonic coupling of excitable and nonexcitable cells in the heart revealed by optogenetics. Proc. Natl. Acad. Sci. USA. 2016;113:14852–14857. doi: 10.1073/pnas.1611184114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Octeau J.C., Chai H., et al. Khakh B.S. An optical neuron-astrocyte proximity assay at synaptic distance scales. Neuron. 2018;98:49–66.e9. doi: 10.1016/j.neuron.2018.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Perge J.A., Niven J.E., et al. Sterling P. Why do axons differ in caliber? J. Neurosci. 2012;32:626–638. doi: 10.1523/JNEUROSCI.4254-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Roberts S.F., Stinstra J.G., Henriquez C.S. Effect of nonuniform interstitial space properties on impulse propagation: a discrete multidomain model. Biophys. J. 2008;95:3724–3737. doi: 10.1529/biophysj.108.137349. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.