Dynamics of Heterogeneous Catalytic Processes at Operando Conditions

Abstract

The rational design of high-performance catalysts is hindered by the lack of knowledge of the structures of active sites and the reaction pathways under reaction conditions, which can be ideally addressed by an in situ/operando characterization. Besides the experimental insights, a theoretical investigation that simulates reaction conditions—so-called operando modeling—is necessary for a plausible understanding of a working catalyst system at the atomic scale. However, there is still a huge gap between the current widely used computational model and the concept of operando modeling, which should be achieved through multiscale computational modeling. This Perspective describes various modeling approaches and machine learning techniques that step toward operando modeling, followed by selected experimental examples that present an operando understanding in the thermo- and electrocatalytic processes. At last, the remaining challenges in this area are outlined.

Introduction

Heterogeneous catalysis is at the heart of the chemical industry, where a high-performance catalyst with a fast conversion of the reactants and a high selectivity toward targeted products is greatly desired.¹⁻³ However, the rational design of catalysts is hindered by the lack of molecular-level knowledge about the structures of active sites and the reaction pathways under reaction conditions. It has been observed that, during the reaction, most heterogeneous catalysts undergo a structural reconstruction accompanied by a varying catalytic performance.⁴ Moreover, the concept of “dynamic fluxionality” reminds us to see the active structure as a collection of many structures that dynamically interconvert with a low energy barrier. It is therefore significant to characterize the changing surface morphology, short-lived intermediates, and stepwise reaction kinetics under the reaction conditions, which can be addressed by the fast-developing operando characterization.

In the definition, operando refers to the real-time measurement of a catalyst at its working place under real reaction conditions, with the simultaneous online analysis of catalyst performance.⁵ With the establishment of structure/composition-performance correlations, the operando characterizations provide a dynamic insight into the atomic and electronic structures of heterogeneous catalysts under working conditions, which help to deeply understand the interfacial behavior and the catalytic mechanism.⁶ As a comparison, the ex situ characterization presents the pre- and postchemical states, which may not truly reflect the dynamic nature of the heterogeneous catalysts during the reaction.⁴

For a complete understanding of a working catalyst system at an atomic scale, a theoretical investigation that can realistically simulate operando conditions is necessary. However, the operando conditions have been significantly simplified in the current widely used computational model. A typical example is the periodic slab model for a heterogeneous catalysis, which is created by cutting a crystal through a specific crystalline plane and adding a vacuum in the direction orthogonal to the surface. However, its validity can be expected only when the active structure of a catalyst system is known (or correctly guessed) and is not dramatically affected by the reaction environment.⁷ It was reported that, without an explicit consideration of the solvent effect, a density functional theory (DFT) calculation outputs a result contradictory to the experimentally observed high activity of Ni single atom over graphene.⁸

The interaction between the environment and the reaction intermediate species plays an important role in the exploration of the catalytic mechanism, which should not be ignored.¹ It gives rise to the concept of operando modeling that describes the catalyst behavior in an experimentally spatiotemporal scale under true reaction conditions.⁷ A schematic depiction of the operando modeling is illustrated in Figure 1. Compared with the simplified periodic slab model, operando modeling further considers the temperature, pressure, and/or solvent effect on the active structure of the catalyst. Beyond that, given that catalysts can undergo a constant structural change during the reaction, a long-term, large-scale simulation is expected to track this dynamic process. With numbers of intermediates and reaction pathways being visited, a large reaction network is thus possible to be established, providing a way to fully reveal the catalytic mechanism under the operando condition.

Figure 1.

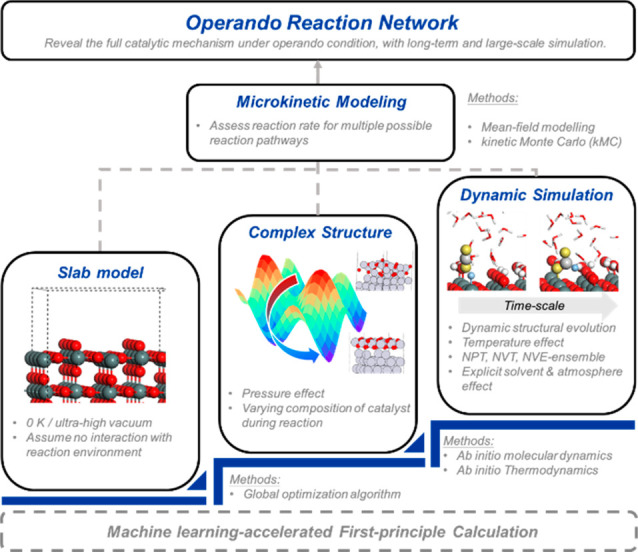
Schematic depiction of the concept of operando modeling. The ML technique significantly accelerates the first-principle calculation and makes a long-term, large-scale, and accurate simulation possible. The operando modeling is aimed to reveal the full catalytic mechanism under operando conditions, within which the catalyst behavior should be described in an experimentally spatiotemporal scale under true reaction conditions with both thermodynamic and kinetic aspects.

Because of the overwhelming complexity, a comprehensive operando modeling cannot be achieved by a single computational method (e.g., DFT calculations).^4,7Operando modeling should be achieved through a multiscale computational modeling, with multifaceted physical and chemical methodologies being involved. The most stable structure of a heterogeneous catalyst under operando conditions can be obtained by global optimization (GO) techniques, which can also help to study the dynamic fluxionality of the catalyst. Ab initio thermodynamics (AITD) can be utilized to assess the thermodynamic stabilities under the varying reaction conditions, while ab initio molecular dynamics (AIMD) can identify the dynamic interfacial structure of the heterogeneous catalyst. With the numbers of intermediates and reaction pathways being visited, kinetic modeling is required to explain the stepwise kinetics to build up the reaction network. Considering the huge computational cost of the above method, the machine learning (ML) technique can serve as a surrogate model to accelerate the time-consuming simulation by orders of magnitude.

This Perspective describes the current progress and remaining challenges in this area. Beginning with the brief introduction of the operando technique, this Perspective will illustrate how the above-mentioned computational techniques link with each other, achieve the concept of operando modeling, and help clarify the underlying mechanism in a heterogeneous catalysis. In the end, we will present how a joint effort by experimental and theoretical studies can be made toward an atomistic understanding of the thermo- and electrocatalytic processes.

Operando Characterization

The term operando was coined by Eric Gaigneaux, Gerhard Mestl, Miguel A. Bañares, and Bert M. Weckhuysena at the 220th ACS National Meeting in 2000 and first appeared in the catalytic literature in 2002 with several publications putting the idea of operando into practice.⁹⁻¹⁴ Recently, various operando techniques, including optical spectroscopies (Raman, IR, etc.), X-ray-based characterizations (X-ray diffraction (XRD), X-ray absorption near edge structure (XANES), etc.), microscopies (scanning/transmission electron microscopes (S/TEM), scanning tunneling microscopy (STM), etc.), Mössbauer spectroscopy, and other methods have been successfully implemented to track the dynamic behavior of a catalyst under reaction conditions. Table 1 briefly lists some representative operando techniques with their main function.

Table 1. Representative Operando Techniques for Atomic-Scale Studies of Surface Catalysis.

operando technique	function
infrared (IR) spectroscopy	Monitor chemisorbed species on the catalyst
Raman spectroscopy	Monitor the intermediates’ formation
X-ray diffraction (XRD)	Monitor the crystal structural change and phase transitions.
Mössbauer spectroscopy	Clarify the chemical state and spin state (for specific elements)
X-ray absorption near edge structure (XANES) spectroscopy	Monitor electronic/oxidation states of the target atoms.
extended X-ray absorption fine structure (EXAFS) spectroscopy	Provide information about the coordination environments of target atoms, including their coordination number and the bond distance.
X-ray photoelectron spectroscopy (XPS)	Provide information about elemental composition, chemical and electronic state information on the catalyst.
X-ray emission spectroscopy (XES)	Clarify the local electronic structure and bonding configuration of the absorbing atom.
nuclear magnetic resonance (NMR) spectroscopy	Observe the chemical components and their interactions with active sites.
electron paramagnetic resonance (EPR) spectroscopy	Monitor the evolution of redox reactions.
scanning/transmission electron microscopes (S/TEM)	Provide sub-Ångström spatial resolution with compositional information and electronic structure.
atomic force microscopy (AFM)	Detect evolution in surface morphology and surface potential.
scanning electrochemical microscopy (SECM)	Monitor the electrochemical activity, kinetics, and adsorbate coverages.
differential electrochemical mass spectrometry (DEMS)	Detect the reaction products and adsorbates for studying kinetics.
electrochemical quartz crystal microbalance (EQCM)	Monitor mass change on the catalyst electrode.

It is worth noting that it is difficult to achieve an in-depth and comprehensive understanding of a catalytic mechanism through only a single operando technique. When multiple operando techniques are combined, the dynamic catalytic behavior can be identified from complementary aspects.⁴ For example, Zakharov et al.¹⁶ combined the operando XANES, extended X-ray absorption fine structure (EXAFS), and S/TEM measurements to characterize all-metal species present in a silica-supported Pt catalyst (0–5 nm), while EXAFS alone cannot achieve this characterization due to a poor spatial resolution. Weckhuysen and co-workers have developed several combined operando techniques to get a full insight into the reactions. Figure 2 presented their combined operando XRD and UV–vis setup for studying the lattice expansion of zeolite catalysts caused by the formation of hydrocarbon species. The evolution of the hydrocarbon pool was measured using operando UV–vis spectroscopy, and the resulting zeolite lattice expansion was measured using operando XRD.¹⁵ More combined operando instruments developed by Weckhuysen and co-workers included luminescence thermometry/Raman spectroscopy to simultaneously obtain local thermal and chemical information, X-ray powder diffractometry (XRPD)/Raman spectroscopy that monitors the simultaneous evolution of phases and various formed species during the reaction, etc.¹⁷⁻²¹

Figure 2.

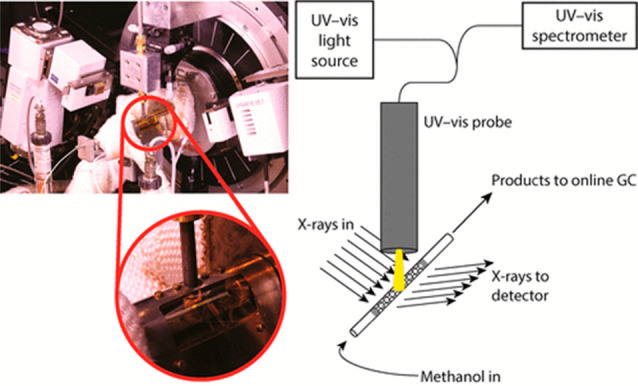
Schematic of the combined operando XRD/UV–vis setup showing the X-ray diffractometer with the mounted capillary; in the middle of the capillary, the spot of the UV–vis light source can be seen. Reprinted with permission from ref (15) . Copyright 2018 American Chemical Society.

Modeling Strategies for Realistic Simulation

Prediction of Surface Structure for Heterogeneous Catalyst under Operando Conditions

The actual surface structure of the catalyst mostly is the lowest energy-point on the potential energy surface (PES), the so-called global minimum (GM). Finding the GM of a working catalyst constitutes a GO problem. During the GO process, metastable structures of the catalyst can be obtained. Note that a recent study by Sun and Sautet shows which of some metastable structures might contribute more to the total activity than the global minimum structures.²² Because of their importance, the controllable synthesis of metastable structures has received extensive attention in the experiment.^23,24

In the past decade, there has been significant progress in developing GO algorithms and software packages for chemical structure optimization. The frequently used GO algorithms and their representative software packages are listed in Table 2.

Table 2. Frequently used GO algorithm for chemical structure optimization and their representative software package.

GO algorithm	software package
genetic algorithm	USPEX,25 XtalOpt,26 BCGA,27,28 BPGA,29 GA module of ASE,30,31 HAGA,32 GOFEE33
differential evolution	PDECO34
covariance matrix adaptation evolution strategy (CMA-ES)	Clinamen35
stochastic surface walking (SSW)	LASP36
particle swarm optimization	CALYPSO37
artificial bee colony	NWPEsSe,38 ABCluster39
basin and minima hopping	TGMin,40 Basin and Minima Hopping module of ASE31
Bayesian optimization	BOSS,41 BASC42

As this Perspective especially focuses on operando modeling that highlights the characterization of the catalyst surface, the following content is about the interface structure of the heterogeneous catalyst. Owing to the periodicity of the crystal and the presence of strong covalent bonds to the underlying support, the optimization of the surface structure is more geometrically restricted than that of free particles.⁷ For the application of GO algorithms in free particles like metal clusters and nanoalloys, we refer the reader to some recent reviews.⁴³⁻⁴⁵

The existence of a support can make the catalyst structure very different from that in the gas phase because of the strong metal–support interaction.⁴⁶ Davis et al.²⁸ performed the Birmingham parallel genetic algorithm (BPGA) to reveal that the existence of the MgO(100) support could suppress the spin of Au–Ir clusters, causing a huge difference in the gas-phase and MgO-supported structure. For the metal–organic framework (MOF)-supported systems, Vilhelmsen et al.⁴⁷ investigated MOF-supported Au, Pd, and Au–Pd clusters and concluded that Pd could bind more tightly with the MOF support than Au. Compared with the aromatic ring, the open metal site in the MOF did not provide much tighter binding sites, which provided an understanding of how the local environment effects the catalyst structure. It is worth noting that whether the support has a significant effect rests on the nature of the support and catalysts.⁴⁶ For example, Pt₁₃ catalysts in the gas phase hold a similar structure with that upon a graphene surface,⁴⁸ but the structure significantly changes when on a CeO₂ surface.⁴⁹

GO algorithms can provide insights into the defective structure, like steps, vacancies, and adgrowths,⁷ which commonly occur in realistic conditions. Some examples include the exploration of the ⟨111⟩ and ⟨001⟩ step edges of the TiO₂(110) surface⁵⁰ and the oxidized edge of graphene sheets on the Ir(111) surface.³³ Arrigoni et al.³⁵ have developed a GO software package, named Clinamen, that helps to discover the low-energy defective structure, and its capabilities have been demonstrated in an optimization of TiO₂ anatase with oxygen vacancies. Moreover, the catalyst structure can be different when deposited on the defective surfaces and the stoichiometric surface. After confirming the F_s defect could profoundly modify the absorption features,⁵¹ Fortunelli and co-workers have presented series of GO studies for Au,^52,53 Ag,^54,55 Pd–Ag⁵⁶ clusters adsorbed on the F_s-defected MgO(100) surface.

For alloy catalysts, the catalytic properties can be dramatically different with even a small change in composition. The GO algorithm plays a role generally when the number of atoms is correctly guessed. For the catalyst system in which the composition of the GM remains unclear, the GO method needs to be modified to search over composition space and to perform fixed-stoichiometry searches at many compositions.

Upon exposure to oxygen, reactant gas, and additional adsorbates, the supported catalysts can undergo a structural change. As shown in Figure 3, Sierka et al.⁵⁷ showed that the one-dimensional (1D) and two-dimensional (2D) silica structures deposited upon a Mo(112) surface are subject to the oxygen pressure and amount of deposited Si atoms.³² Later the same technique was applied in a search of the stable structure of p(1 × 2)-, p(1 × 3)-,³² and O(2 × 3)-⁵⁸ on a Mo(112) surface, with full support from experimental observations. Moreover, Liu et al.⁵⁹ applied GA to identify surface phases of Pt, Pt₃Ni, and Pt₃Au surfaces with high oxygen coverages and concluded that the existence of oxygen created oxide skins with a different morphology. The adsorbed GM is the foundation of the further analysis of catalytic behavior. For example, after obtaining the GM of the fully CO-saturated alumina-supported Pt₁₀, Yin et al.⁶⁰ found that this structure can coadsorb O₂ at the interface, which is beneficial to catalytic activity through the OOCO mechanism. In the case of the Ag/Pt catalyst, a complete CO → CO₂ reaction catalytic cycle was drawn after the GM was obtained, as the OOCO mechanism still got supported.

Figure 3.

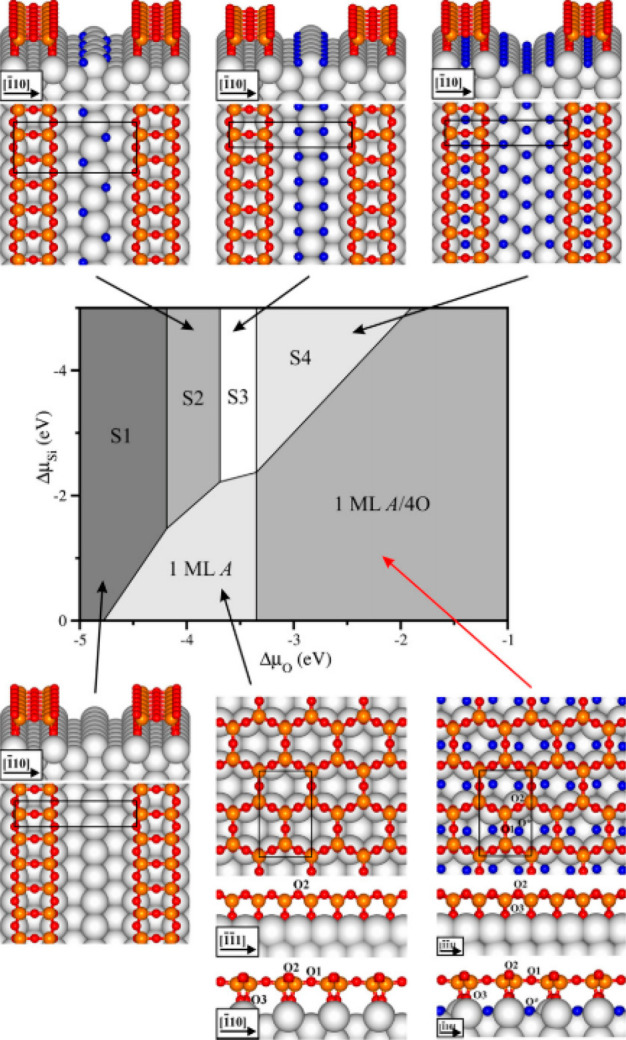
Calculated phase diagram of 1D and 2D crystalline silica over a Mo(112) substrate as a function of Δμ_O and Δμ_Si chemical potentials. Reprinted with permission from ref (73). Copyright 2010 Elsevier.

The GM obtained from the GO algorithm for catalysts with different sizes can help to understand the size-evolution trend in the catalyst growth mechanism. As shown in Figure 4a, Wang et al.⁶¹ revealed that the CeO₂(111)-supported Pd_n (n = 1–21) catalysts first grow on the base layer and then on the second layer to undermine the metal–support interactions. For the Cu_n (n = 1–10) catalysts on a ZnO(1010) surface, Cu atoms prefer an adsorption between the Zn and O or a direct adsorption to an O atom, and the interface of Cu_n (n > 5) and ZnO(1010) presents a continuum between Cu(111) and (110) structures.⁶² Moreover, the GO algorithm can optimize nanosized particle systems. Di Valentin and co-workers⁶³⁻⁶⁷ have performed GO algorithms to model nanosize TiO₂ particles with water to study their photoexcitation processes, proton transfer mechanism, etc.

Figure 4.

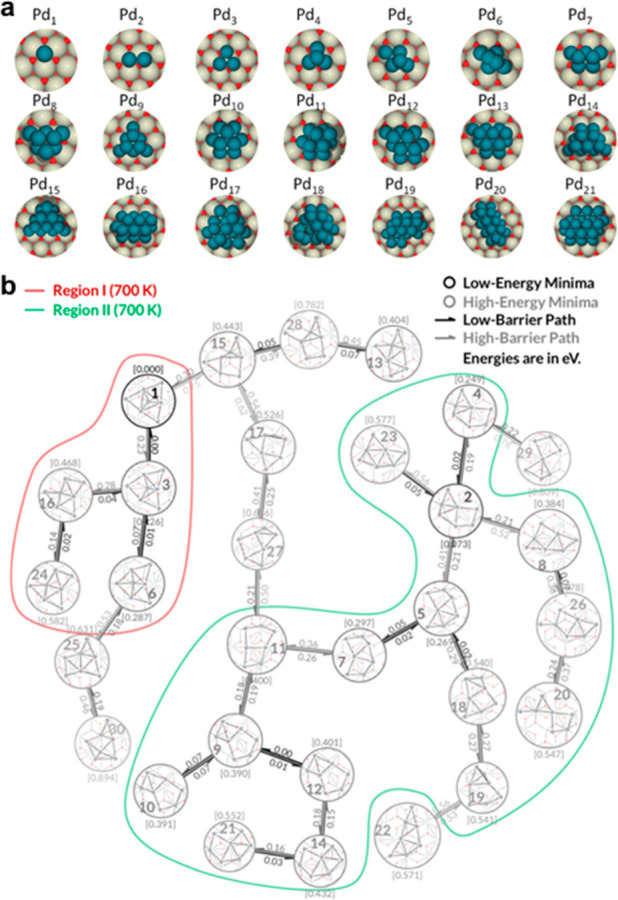
(a) GM of Pd_n catalyst (n = 1–21) over CeO₂(111). Reprinted with permission from ref (61). Copyright 2020 American Chemical Society. (b) Minimal energy paths of Pt₇ on Al₂O₃ obtained using a bipartite matching algorithm, showing the picture of the fluxional behavior of Pt₇. Reprinted with permission from ref (75). Copyright 2018 American Chemical Society.

Not only the GM but also some metastable isomers of the catalyst obtained during the GO process can play a significant role in building the reaction network. Fang et al.⁶⁸ selected some metastable isomers to build the whole reconstruction process of a Au(100) surface induced by the adsorption of CO. Earlier, Fortunelli and co-workers^69,70 have developed kinetics-driven Reactive Global Optimization (RGO) to study a reaction network for supported catalysts, in which reaction rates are calculated during the GO process and are used to guide the GO. The RGO has been successfully applied to study the propylene partial oxidation by MgO(100)-supported Ag₃ and the CO oxidation by MgO(100)-supported Ag_xAu_3–x.^71,72 However, it suffers a great cost of searching.³⁸

In some cases, metastable isomers may even lead to a higher activity. It was shown that the catalytically relevant sites of the Mo catalyst over γ-Al₂O₃ do not correspond to its GM.⁷⁴ And for Pt₁₃, the highest activity toward methane activation corresponds to its second lowest-lying isomer, rather than GM.²² Furthermore, many metastable isomers are energetically accessible, and thermodynamic equilibration between them is kinetically possible. It reminds us not to see the active structure as a single GM but as a statistical ensemble representation, a collection of many structures that dynamically interconvert with a lower energy barrier.⁴⁶ This concept is the so-called “dynamic fluxionality”, which implies that the single structure obtained from the GO algorithm represents the most abundant isomer in the ensemble of structures.⁴⁴

An experimental observation of the dynamic fluxionality under an operando condition has been reported on a silica-supported Pd for ethylene hydrogenation,⁷⁶ ceria-supported Pt for water gas shift,⁷⁷ Al₂O₃-supported Cu oxide,⁷⁸ etc. Recently, Alexandrova and co-workers have presented series of works that contribute to the deeper theoretical understanding of dynamic fluxionality. Using the GO technique, they revealed the highly fluxional behavior of Pt₇ over Al₂O₃,⁷⁵ Cu oxide at a high temperature and different O₂ pressures,⁷⁹ and hexagonal boron nitride in the oxidative dehydrogenation of propane.⁸⁰ They found that dynamic fluxionality may break the scaling relationships,⁸¹ cause non-Arrhenius behavior,⁸² or accelerate the Ostwald ripening of a supported catalyst.⁸³ Moreover, a bipartite matching algorithm was introduced to connect low-lying isomers obtained from the GO technique and to build the whole picture of the fluxional behavior,⁷⁵ as shown in Figure 4b. More discussion about dynamic fluxionality can be seen in their recently published review.^2,46,84

Dynamic Modeling of Reaction Environment

The structure of the catalyst also depends on the realistic chemical environment (solvent, electrochemical potential, and temperature). Indeed, GO has been used to identify the GM of water clusters^85,86 and microsolvated ions⁸⁷ and to reveal explicitly solvated transition state^88,89 and reaction mechanisms.⁹⁰ However, it more represents a static snapshot of what a stable structure looks like, so a GO is seldom applied to operando descriptions of surface systems with an explicit description of a chemical environment⁴⁶ when a dynamic interaction between catalyst and environment matters.

Solvents play a crucial role in electrocatalytic reactions. To mimic operando conditions and illustrate the active surface structure, an explicit consideration of the solvent is necessary. The AIMD technique can identify the dynamic interfacial structure of heterogeneous catalysts with an explicit solvent. Ren et al.⁴⁹ used the AIMD to study the CeO₂-supported Pt₁₃ catalyst in an aqueous phase, whose structure is significantly different from that in the gas phase, as shown in Figure 5a. Greeley and co-workers have presented a series of works using the AIMD to study the solvation effects on the catalytic mechanism, which revealed that an explicit solvent molecule can interact with a defect and active site, transfer the electron, alter the adsorption behavior of catalytic spices, and so on.⁹¹⁻⁹⁵ The AIMD can also help to unravel the atomistic structures of electric double layers (EDL) and to understand the dynamic behavior of catalytic species at the interface, a field in which Cheng and co-workers have presented a series of significant works recently.⁹⁶⁻¹⁰⁰ More examples include the explicit description of a mixture solvent, like supercritical CO₂/H₂O.¹⁰¹ Similarly, the transition state may suffer a strong explicit solvent effect. Herron et al.¹⁰² used AIMD to study the methanol electrooxidation on Pt(111) and reveal that a water solvation reduces the barriers for both the C–H and O–H bonds of methanol, while the effect is more pronounced for a C–H bond activation. Moreover, the dynamics of electrons can be also modeled by AIMD as shown in Figure 5b. Selcuk et al.^65,103 thus found that the behavior of excess electrons on anatase surfaces depended strongly on the nature of the exposed facet, the environment, and the character of the electron donor during the photocatalytic reaction.

Figure 5.

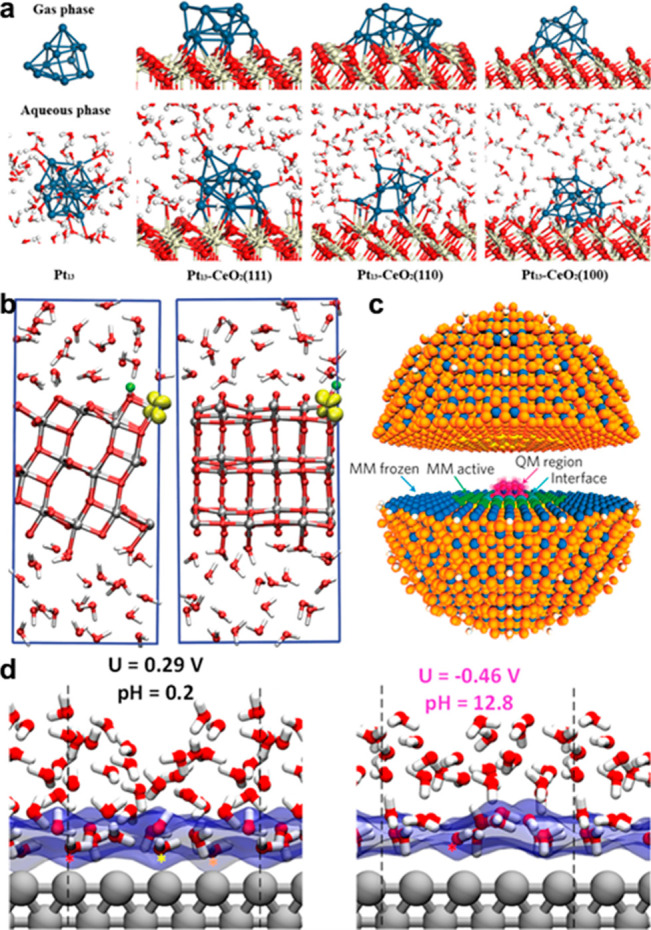
(a) Electron density difference plots for the optimized CeO₂-supported Pt₁₃ cluster in the gas and aqueous phases. Reprinted with permission from ref (49). Copyright 2018 American Chemical Society. (b) Hydroxylated anatase (101) slab immersed in water; the e_ex^– is shown as a yellow iso-surface plot. Reprinted from ref (103). Copyright 2018 Nature Portfolio. (c) Graphic of the QM/MM cluster used for rutile in the positive charge state. The cluster is divided into hemispheres to highlight the different regions in the model. Hole density iso-surfaces are shown in the QM region. Reprinted from ref (105). Copyright 2018 Nature Portfolio. (d) The snapshots with atomic details of the interfaces are shown at U = +0.29 V and at U = −0.46 V. The first layer of water is highlighted by a plot of the van der Waals surface of oxygen as transparent blue. Reprinted with permission from ref (106). Copyright 2018 American Chemical Society.

Another simulation method is the hybrid quantum mechanics/molecular mechanics (QM/MM) approach, which retains an ab initio consideration at the interface and leaves other surrounding molecules for the force field.¹⁰⁴ As shown in Figure 5c, Scanlon et al.¹⁰⁵ found the band alignment of −0.4 eV for the anatase–rutile phase junction by using QM/MM, which explains the robust separation of photoexcited charge carriers between the two phases. Moreover, to investigate the pH-dependent hydrogen oxidation reaction (HOR) and hydrogen evolution reaction (HER) performance, Cheng et al.¹⁰⁶ calculated the hydrogen binding energy (HBE) as a descriptor and simulated the full solvent water/Pt(100) interface using a QM/MD approach at an applied voltage from +0.29 to −0.46 V, which is equivalent to pH from 0.2 to 12.8 at 0.3 V applied voltage. The snapshots with atomic details of the interfaces were shown in Figure 5d. The results revealed that the pH-dependent HBE was mainly due to the distinct water adsorption under different pH values, and its changing trend was very close to the experimental observation.

In the thermo-catalytic processes, the above-mentioned methods can also be applied to observe dynamic structural changes induced by the reaction atmosphere. He et al.¹⁰⁷ used AIMD to study the structure of CeO₂-supported Au₁₉ under a CO atmosphere. Being consistent with our experimental observations, the AIMD result confirmed that Au₁₉ undergoes a layer-to-three-dimensional transition after an exposure to a CO atmosphere, caused by an extraction and motion of Au atoms in the form of gold–carbonyl species. Besides the solvent/atmosphere effect, the catalyst structure can change significantly under a high temperature/pressure. The temperature/pressure effect can also be described in an ab initio calculation. With different temperatures, the ab initio calculation revealed that the supported catalyst undergoes a different adsorption behavior,¹⁰⁸ solvent interaction,¹⁰⁹ and reactive pathway.¹¹⁰ Besides AIMD, AITD is routinely employed in this case. Originally introduced by Reuter and co-workers, AITD highlights the thermodynamic stabilities (of intermediates, active sites, etc.) under the varying reaction conditions, which are currently widely used in heterogeneous systems like reactive surfaces and nanoporous spaces.^111,112 Senftle et al.¹¹³ applied AITD to assess the stability of CeO₂-supported Pd₇O_x catalysts for a methane conversion, as a function of temperature and oxygen pressure. The stability of intermediates can also be analyzed by AITD to confirm the proposed mechanism under the operando conditions. Using the AITD analysis, Li et al.¹¹⁴ analyzed the stability of the potential molybdenum (oxy)carbide species form during the methane dehydroaromatization and finally concluded that the binuclear [Mo₂C₂]²⁺ site is a more likely candidate for the active sites. A surface Pourbaix diagram can be obtained through AITD to study the stable surface phases under different potential/pH conditions.¹¹⁵ Moreover, combining GO methods with AITD is a powerful strategy to construct structural models. After obtaining a series of GM of Cu(111)-supported Zn_yO_x catalysts through GO, Reichenbach et al.¹¹⁶ performed AITD to further assess, and ensure, the thermodynamic stabilities of these structures under different temperatures and O₂ pressures.

In the experiment, the reaction intermediates detected by operando techniques comprehensively understand the reaction mechanisms. With an explicit description of the reaction environment, the computational mechanisms obtained from an ab initio simulation can better explain the experimental observation from an atomistic view. As a representative example, Li and co-workers have presented series of works using AIMD to systemically study the dynamic catalytic behavior of a supported Au single-atom catalyst upon exposure to a reactant gas, including its formation, size effect, and reaction mechanism for CO oxidation,^{107,117−120} which provide insights into the existing experimental finding. Moreover, they have applied a similar strategy to identify intermediates and to study the catalytic mechanism of a Pt single-atom catalyst for a CO oxidation and Fe for a nonoxidative conversion of methane.^121,122

The inconsistency between the experimental result and the output of an ab initio calculation is sometimes due to the failing capture of rare events (like chemical reactions) and the limited time-scale of simulation. For a complex reaction mechanism with multiple reaction channels, an enhanced sampling technique can be applied to facilitate the crossing of energy barriers and extend the sampling time scales of ab initio calculation, like umbrella sampling, meta-dynamics, and so on.¹²³ Goddard and co-workers^124−127 have presented a series of works that combine meta-dynamics to identify the complex reaction pathway for a CO₂ reduction reaction (CRR) and CO reduction reactions (CORR) on a Cu (100) surface with an explicit solvent. The intermediates captured from a picosecond-level simulation can successfully interpret the experimental operando spectrum.⁵ For nanoporous catalysts, Speybroeck and co-workers used molecular dynamics (MD) techniques with enhanced sampling to describe their phase stability/transformation, active site, and reaction kinetics,^94,128−130 together with the diffusion behavior and nucleation process of solvent/reactant inside the nanoporous cages.^131−133

To fully reveal the reaction network, microkinetic modeling is required to assess the reaction rate for multiple possible reaction pathways and eventually explain the macroscopic kinetics under operando conditions.¹³⁴ Taking the H₂ oxidation over Ru as an example, the microkinetic modeling was successfully applied to simulate the local oscillation frequency and to support the local reaction kinetics observed from imaging microscopies.^135−138 Two widely utilized modeling methods in this field are mean-field microkinetic modeling and kinetic Monte Carlo (kMC).¹³⁹ An emerging alternative is a hybrid method called extended phenomenological kinetics (XPK), which is proposed by Xu and co-workers and is specially designed to describe complex catalytic kinetics under operando conditions.¹⁴⁰ With enhanced accuracy and efficiency, XPK has been successfully described as a complex reaction network on the surface, including syngas conversion,¹⁴¹ formic acid decomposition,¹⁴² and CO oxidation.¹⁴³ Besides, some automatic techniques has been applied to automatically generate microkinetic mechanisms for the surface catalytic process like graph theory-driven software Reaction Mechanism Generator (RMG) for an oxidative coupling over a Pt surface and the combustion of methane over a Ni surface,^144,145 CatNet for a syngas conversion over Rh(111),^146,147 stochastic surface walking (SSW) for a water gas shift reaction over Cu(111),¹⁴⁸ and the artificial force induced reaction (AFIR) method for a CO oxidation over Pt(111).¹⁴⁹

After a full reaction network is constructed, it is of greater importance to determine the optimal pathway based on the calculated kinetics. The practice developed by Xiao and co-workers is worth considering, which is to introduce an energy optimization to determine the pathway with minimal ΔG-limiting energy.¹⁵⁰ As illustrated in Figure 6, the optimal pathway of NO₂ conversion over anatase TiO₂(101) was studied in their recent work, which helped to clarify the activity and selectivity of NO₂ conversion over different active sites under photo and dark conditions.¹⁵¹

Figure 6.

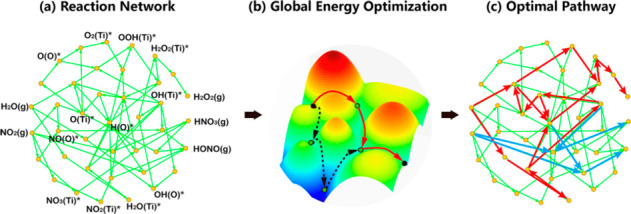
(a) The complete reaction network of NO₂ conversion with stable intermediates marked. (b) The algorithm of determining the pathways from global energy optimization. (c) The optimal reaction pathway over the perfect anatase TiO₂(101) surface (blue, NO₂ evolutional paths; red, H₂O evolutional paths). Reprinted with permission from ref (151). Copyright 2021 American Chemical Society.

Machine Learning for Accelerating Heterogeneous Catalysis Research

Recently, the data-driven ML technique emerged as a useful tool and surrogate model to accelerate the time-consuming simulation. Machine learning potentials (MLP), which directly learns the potential surface from ab initio calculations, have been developed to act as a cheap energy calculator with a high accuracy (within a few meV/atom for energies, ∼0.1 eV/Å for forces) while maintaining the large speedup (with several orders of magnitude faster). Once a successful MLP has been derived, it has the potential to be used efficiently on much larger systems than the one on which it was trained, significantly lowering the computational cost for the simulation of large-scale systems.¹⁵²

In recent years, an increasing number of MLP has been published, including a variety of neural network potentials (NNP), graph networks, Gaussian approximation potentials, and many others.¹⁵³ This Perspective especially focuses on the application of the ML technique in simulating realistic catalyst systems under operando conditions. For a comprehensive review of the technical details of ML techniques that are widely used in materials science, we refer readers to a few recent reviews.^153,154

Coupling the ML technique with the GO provides significant advantages in the acceleration of searches. Performing a search on the ML model provides a cheap energy calculator without requiring expensive DFT calculations. It is worth noting that the ML model fitted to DFT data can show better accuracy than the empirical potential for a GO search.¹⁵⁵ Liu and co-workers combined a neural network (NN) with their own developed SSW global optimization method to develop the SSW-NN method as implemented in the LASP code,^156,157 which can explore complex reactions systems unbiasedly and automatedly. A more detailed introduction and application of the LASP code on heterogeneous catalyst systems can be seen in the review.^36,158−160 ML can also be combined well with a population-based GO method like GA to formulate an active learning framework, that is, on-the-fly training.¹⁶¹ Kolsbjerg et al.¹⁶² showed that, with an active learning framework, the number of DFT calculations required to obtain the GM of MgO-support Pt₁₃ was significantly reduced from 8900 to 260. An ML model trained during the GO can be further utilized to search for the transition barrier and then to build up the complete image of a Pt₁₃ structural transformation, which is extremely time-consuming at the DFT level. Further, the Bayesian concepts can be introduced to accelerate the GO search not only by reducing the number of required DFT calculations but also by balancing “exploration” (probing uncertain regions of configuration space) and “exploitation” (exhausting the local region known to have low-energy structures).¹⁶³ Hammer and co-workers have utilized Bayesian concepts in the context of Gaussian processes to develop the open-source GA-based software package GOFEE³³ for the surface system, which outperforms by 2 orders of magnitude a DFT-based GA in reducing computational cost. Other ML methods, like cluster analysis, have also been used to increase the structural diversity by suppressing similar structures¹⁶⁴ and to bias searching toward lower energy basins after clustering and characterizing local atomic environments,¹⁶⁵ both of which accelerate the GO search for surface structure.

The ML-accelerated GO can be applied to predict phase diagrams for alloy catalysts with an unfixed composition or in the situation that the catalyst composition changes during the reaction. Hajinazar et al.¹⁵⁵ used an NN-accelerated GO to obtain the phase diagram of ternary Cu–Pd–Ag nanoalloys, which showed an encouraging agreement between the NN and the DFT methods. By utilizing the SSW-NN method, Ma et al.¹⁶⁶ established the phase diagram of a ZnCr oxide catalyst for a syngas-to-methanol conversion and then identified an active Zn₃Cr₃O₈ phase containing [ZnO₆] octahedra in bulk that is experimentally known for high activity. Moreover, for a catalyst under operando conditions, the compositions and the total number of atoms can change dynamically. The SSW-NN method was also utilized to study the operando formation of PdH_x during an acetylene semihydrogenation and identified the Pd₄H₃ phase as the most responsible for the deep hydrogenation to ethane at high H₂ pressures.¹⁶⁷ Besides, the temperature effect can be included in a predicting phase diagram by using an ML descriptor for the temperature-dependent contribution G^δ(T) to the Gibbs energy G(T).^168,169

The understanding of reaction intermediates and catalysts’ active sites has been classically studied by operando techniques, and the determination of active sites is crucial for clarifying the reaction mechanism. However, the correct modeling of these species remains a huge challenge due to the enormous number of possible adsorption configurations. Using NNP as a surrogate model, Ulissi et al.¹⁷⁰ discover an unexplored active site of Ni/Ga intermetallic catalysts with the best thermodynamics for CO reduction and step-like kinetic behavior. The number of ab initio calculations was reduced by an order of magnitude in this study. This high-throughput framework was then applied to accelerate the discovery of CO₂ electrocatalysts, resulting in the identification of Cu–Al catalysts with the highest Faradaic efficiency.¹⁷¹ Not only the thermodynamics for active sites, the evaluation of kinetic properties like reaction rate can also be accelerated by ML, even in a microstructure with a large size.¹⁷² Apart from directly modeling the structure, ML can be trained using experimental spectra like XANES or Raman spectroscopy and then directly predict the local atomic environment of reaction intermediates.^173−176

The overwhelming complexity of reaction networks limits the modeling of the experimental behavior in surface catalytic reactions at the DFT level, which can be addressed by MLP. A typical reaction network contains not only the relevant intermediates but also transition states that connect between intermediates. A nudged elastic band (NEB) calculation is the most popular method for transition-state searching, which can also be accelerated by MLP.^139,177,178 It is worth noting that, when preparing a training data set that is used to build MLP for reaction networks, the imbalance between the number of reactants and product configurations versus the number of transition state structure needs to be considered.¹⁷⁹ Ulissi et al.¹⁸⁰ performed Gaussian process models that are trained on-the-fly, to iteratively optimize reaction networks of the syngas reaction over Rh(111) under the guidance of uncertainty. Moreover, Kang et al.¹⁵⁸ used SSW-NN to study the reaction network of the water gas shift reaction over Cu(111). An optimal network was built after 375 000 minima were sampled and more than 10 000 reaction pairs were collected, which is almost impossible for a DFT calculation. The final reaction network was shown in Figure 7, revealing the lowest-energy pathway for this reaction.

Figure 7.

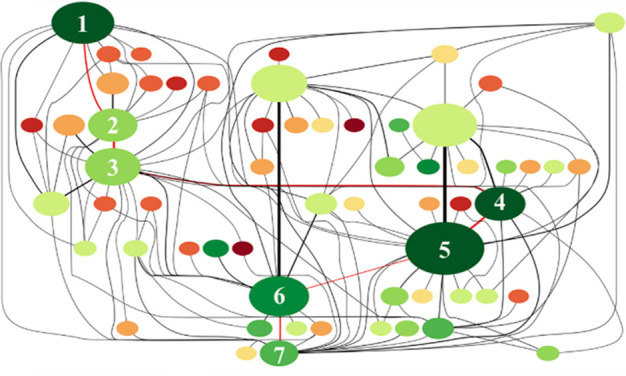
Reaction network for water gas shift reaction (WGSR) on Cu(111). The system starts from two CO and two H₂O on the Cu(111) surface. The key intermediates along the WGSR lowest-energy pathway are marked by red lines, e.g., (1) 2CO+2H₂O; (2) 2CO + H₂O + OH + H; (3) COOH + CO + H₂O + H; (4) HCOOH + CO+H₂O; (5) HCOO+CO+H₂O + H; (6) CO₂+CO+H₂O+H+H; (7) CO₂+CO+H₂O + H₂. The color of the circles from dark green to dark red indicates the energy from low to high; the area of the circle represents the frequency of the state encountered during the search; the width of the line corresponds to the occurrence number of the transformation in simulation. Reprinted with permission from ref (158). Copyright 2021 Elsevier.

Using MLP can significantly extend the spatial and time scale of atomistic simulations, providing more opportunities to simulate large-scale catalyst systems while maintaining a high accuracy.^139,183 Cheng et al.¹⁸¹ used NNP to perform molecular dynamics simulation (NN-MD) and to describe the realistic and dynamic oxide-derived copper (OD-Cu) surface models during CO₂ electro-reduction to C₂₊ products, as shown in Figure 8a,b. After scanning over 150 surface sites, three square-like sites for C₂₊ products were identified finally, providing fundamental insights into the origin of activity and selectivity over Cu-based catalysts. In this study, the error of *CO and *COCO adsorption energy between the NNP and DFT calculation is as low as 0.08 and 0.13 eV, respectively. The ML-enhanced large-scale modeling also enables simulations of complex systems such as electrolytes or solid–liquid interfaces. Natarajan et al.¹⁸⁴ investigated the behavior of interfacial water molecules at the low-index Cu(111), (100), and (110) surfaces, using a model containing 128 explicit water. Quaranta et al.¹⁸⁵ even showed that MLP can well capture the surface reactions such as proton transfer, taking the water-ZnO(1010) interface as an example. Furthermore, Artrith et al.¹⁸² used NNP with Monte Carlo (MC) simulations for bimetallic Au/Cu nanoalloys with up to 3915 atoms (∼6 nm). With the consideration of explicit solvent molecules, the different preferred structures in a vacuum and aqueous solution were further revealed. The simulation results are in agreement with an experimental EXAFS analysis. The same method was also used to model the surface structure after an interaction with solvent, as depicted in Figure 8c.

Figure 8.

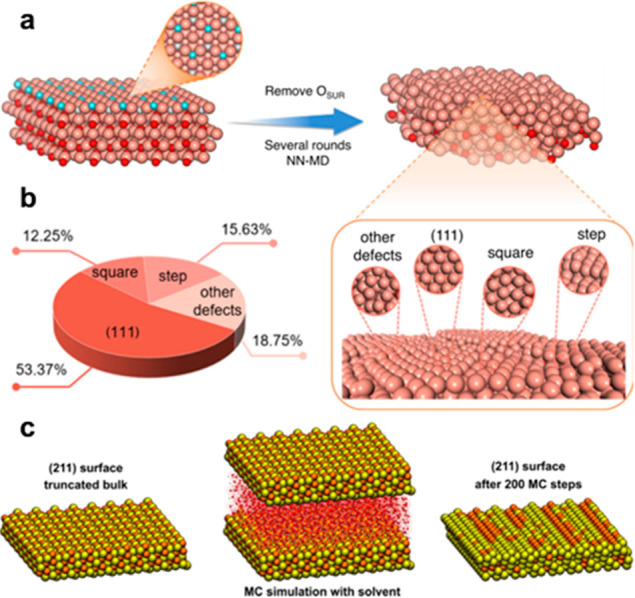
(a) Illustration of the procedure to construct an OD-Cu model with an NN-MD simulation. (b) Proportions of different surface structures of the OD-Cu model. Reprinted from ref (181) under a Creative Commons CC BY License. (c) Snapshots from the MC simulation of a large (211) surface slab model with solvent, containing in total ∼6500 atoms. (left) Initial truncated-bulk structure. (center) The same structure of water including the hydration shell of water molecules. (right) The optimized composition after 200 MC steps. Reprinted with permission from ref (182). Copyright 2014 American Chemical Society.

Besides, ML can accelerate enhanced sampling simulations to predict the long-time-scale surface reaction by using an ab initio calculation. Jiang and co-workers^186−191 have presented a series of works that fit NN to construct a high-dimensional reactive PES for AIMD simulations. A simulation lasting tens of picoseconds was achieved in their studies, which required a tremendous computational cost without ML. The gas-surface reaction dynamics (nonadiabatic effect, dissociative/adsorptive behavior, etc.) of the surface system, like CO₂ on Ni(100), H₂O on Pt(110), etc., were revealed, without losing accuracy (∼1 meV/atom root-mean-square error (RMSE) for energy and ∼10 meV/Å for atomic force).

Experimental Operando Application

Thermocatalytic Processes

A typical feature of thermocatalysis is that catalytic species are exposed to an atmosphere that contains reactants, with high reaction temperatures. The catalytic reactions are driven by heat, and the catalyst undergoes a continuous structural change during the thermocatalysis. Thus, clarifying the dynamic evolution of thermocatalyst is essential for the understanding of overall catalytic performance. According to the different driving factors of dynamic evolution, we divide the section into two parts: atmosphere and temperature.

Atmosphere-Induced Dynamic Evolution

The gas–solid interface is a focus of the thermocatalysis process. When passed through such an interface, reactants will continuously absorb and react on the surface, which will also induce the changing morphologies or composition of catalyst. The CO oxidation reaction is generally treated as a model system for studying the gas–solid interface, and Au is a typical catalyst for studying the dynamic features of a catalyst. Wang et al.¹¹⁸ investigated the formation process of a Au single-atom catalyst induced by the adsorption of CO molecules. As shown in Figure 9a, AIMD showed that the adsorption of CO enhanced the reconstruction of Au particles and generated more low-coordination sites to bind with CO. Besides, CO would diffuse on the support surface that was accompanied by one Au atom formed by the strong interaction between Au and CeO₂.

Figure 9.

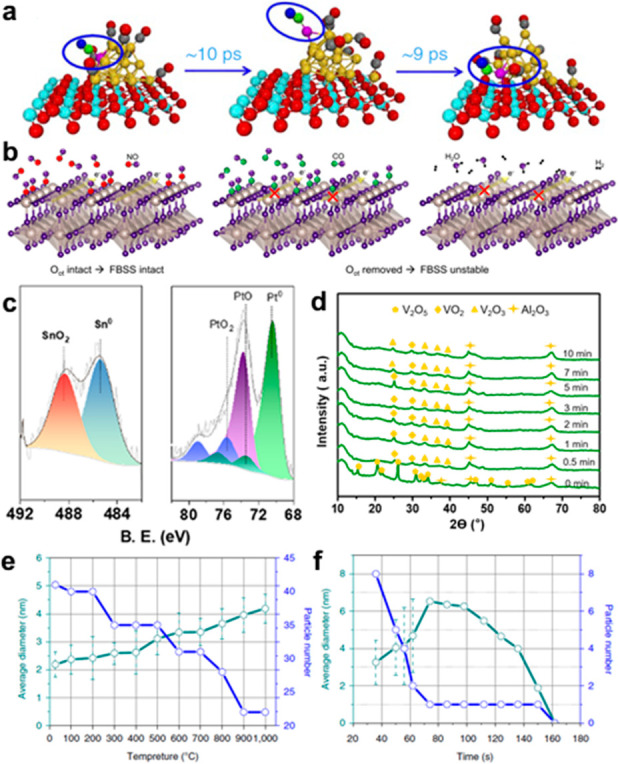
(a) Selected snapshots of the MD trajectory for Au₂₀/CeO₂ with a circled Au-CO unit to show the diffusion process. Reprinted from ref (118) under a Creative Commons CC BY License. (b) FBSS state induced by different absorbates on RuO₂. Reprinted from ref (193). Copyright 2021 American Chemical Society. (c) Quasi in situ XPS of Pt–Sn/SBA-15 reduced by H₂. Reprinted from refs (195) and (196). Copyright 2021 American Chemical Society. (d) XRD pattern of Mo-doped VO_x/Al₂O₃ at 500 °C during the dehydrogenation step for 0–10 min. Continuous phase variation from V₂O₅ to V₂O₃ via VO₂ was observed due to the induction by a lattice evolution under the propane stream. Reprinted from ref (197). Copyright 2021 American Chemical Society. (e) Average diameter and number of particles as a function of heating temperatures. (f) Average diameter and number of particles vs pyrolyzing time at 1000 °C. Reprinted from ref (198). Copyright 2018 Nature Portfolio.

For the CO oxidation that uses nanoparticles, Albinsson et al.¹⁹² pointed out the importance of bridging the gap between local and averaging characterization methods. With operando plasmonic nanoimaging, they revealed that both surface and bulk oxidation states changed by the CO oxidation of a Cu catalyst. For the larger particle, where a periodic surface calculation is appropriate, Jovic et al.¹⁹³ focused on the RuO₂ surface and its unique change of electronic structure during the CO adsorption process by operando angle-resolved photoemission spectroscopy. They pointed out the flat-band surface state (FBSS) promoted catalytic charge transfer processes and the corresponding CO oxidation reaction (Figure 9b). Nguyen et al.¹⁹⁴ further considered the function of O₂ reactant during a CO oxidation, and they found O₂ would produce a missing row reconstruction on a Rh(110) surface, while the origin Rh(110) structure was retained even under one monolayer of CO coverage.

H₂ is another typical composition of the atmosphere during the thermocatalytic process, acting as a reactant or product. The morphology of metal nanoparticles will be prominently affected by H₂, as Johnson et al.¹⁹⁹ pointed out that H₂ would lead to a phase transformation in Pd nanoparticles. According to in situ XRD patterns, the α-phase disappeared while the β-phase was generated after the catalyst was exposed to H₂, which strengthened the adsorption of hydrogen on Pd nanoparticles. But the situation on Pt nanoparticles is quite different. The existence of the H atom will lead to the sintering and growth of Pt particles rather than to the formation of another phase. Song et al.²⁰⁰ showed that Pt–H interactions could weaken the adhesion of Pt on MoS₂ and accelerate particle migration and coalescence. Introducing Au to form a Pt–Au alloy could inhibit sintering prominently by decreasing the interaction with Pt atoms. Liu et al.²⁰¹ draw a similar conclusion after studying a Pt species on MCM-22 zeolite; they showed how highly dispersed Pt was reduced and agglomerated into clusters in the reductive atmosphere, while an oxidative atmosphere had an opposite function. A Pt–Sn alloy is another important system for the dehydrogenation of propane. Combining in situ XPS, TEM, and DFT calculations, Wang et al.¹⁹⁵ revealed the phenomena of migration of Sn atoms from the inner core to the surface during a reduction induced by H₂ (Figure 9c) and the formation of the Pt–Sn alloy surface structure.

The redox reactions under a reductive/oxidative atmosphere also induce a dynamic structural change of catalyst, together with a changing valence state. Zichittella et al.¹⁹⁶ utilized operando EPR spectroscopy to quantify the oxidation state of representative CrPO₄ and EuOCl catalysts during a propane oxychlorination reaction. They found the number of redox-active centers (Cr²⁺ or Eu²⁺) can be directly correlated with the space-time yield of propylene. Chen et al.¹⁹⁷ investigated the reduction process of Mo-doped vanadia (Figure 9d) by XRD. They observed the phase transformation process from V₂O₅ to VO₂, V₂O₃ under a reductive propane atmosphere, which explained the change of propane dehydrogenation performance. Koch et al.²⁰² considered the application of perovskites in an alkane oxidation, showing that steam added to the feed could increase the selectivity of the partial oxidation product propylene. By analyzing the surface of the working catalyst, they found Mn in a low oxidation state (2⁺/3⁺), an increased concentration of hydroxyl groups, and a higher abundance of adsorbed activated oxygen species on the catalyst surface is the origin of the better performance of the two-dimensional MnO_x surface phase.

Temperature-Induced Dynamic Evolution

Temperature is another factor that induces the dynamic evolution of the catalyst. In a thermocatalytic process, the catalyst will experience a heating-up process under reaction conditions. The results from an in situ environmental TEM performed by Wei et al.¹⁹⁸ show that the particle size of Pd will increase with rising temperature under 900 °C. When the temperature rises to 1000 °C, a N dopant could help anchor the Pd atoms and form Pd single atoms, as shown in Figure 9e,f.

Adjusting the reaction temperature can alter the catalytic performance in some cases. Passos et al.²⁰³ reported how heating versus cooling cycles influence the single nanoparticle elastic energy landscape. The highly compressive and tensile strain distribution was accordingly changed with temperature and so was the CO oxidation performance. Another important application of changing the temperature is the thermal annealing process. Kozlovskiy et al.²⁰⁴ investigated the phase transformation process of FeCo-Fe₂CoO₄/Co₃O₄ nanocomposites that was induced by an annealing. Increasing the annealing temperature can help the catalyst keep a crystal structure with fewer deformations and distortions and can release its lattice oxygen more easily to act as an oxidant. The kMC model proposed by Zhou et al.²⁰⁵ can simulate the structural evolution during annealing, which may boost the further development of research in the annealing process.

(Photo) Electrochemical Catalytic Processes

It has been well-known that most catalysts would undergo a structural reconfiguration during the electrochemical reaction. Here we summarize the combination of theoretical calculations and operando characterization to track this information from three aspects, including (i) the reconstruction of the catalysts (phase, morphology, etc.) under actual operating conditions (pH values, potential, etc.), (ii) the determination of the oxidation states of the active centers, and (iii) the recording of the reaction intermediates.

Reconstruction of the Catalysts during the Reaction

Because of the unique electrochemical environment, the structural evolution of the catalysts can be affected by pH values and potential.²⁰⁶ Currently, many studies have used the DFT calculation to understand the interfacial structures at the atomic scale. Hansen et al.²⁰⁷ constructed surface Pourbaix diagrams based on the computational hydrogen electrode (CHE) approach, which described the most stable surface structures of Pt(111), Ag(111), and Ni(111) in an aqueous environment as a function of pH values and potential for an oxygen reduction reaction (ORR). As mentioned above, an explicit solvent model is also adopted. Zhao et al.⁸ included the effect of surface charge and hydrogen bonding by using AIMD with enhanced sampling and successfully clarified the experimentally observed high activity and selectivity of Ni single-atom anchored in graphene, which a previous DFT calculation without an explicit consideration cannot.

By the operando characterization, the changing catalyst surface structure under different pH values can be observed. Pi et al.²⁰⁸ showed that IrNi_x nanoparticles exhibited distinct composition-segregated features under acidic and alkaline conditions during the oxygen evolution reaction (OER). Coincidentally, by combining operando XAFS and photoelectron spectroscopic measurements, Cao et al.²⁰⁶ visualized a chameleon-like structural self-optimization of Co₉S₈ supported by a single-walled carbon nanotube under neutral/alkaline conditions during the OER. They identified that the precatalyst self-optimized into CoOOH with residual S species under alkaline conditions, while the oxygenated CoS was formed under neutral conditions. Gao et al.²⁰⁹ utilized the photothermal effect to enhance the OER activity of NiFe₂O₄ nanoparticles. Operando Raman spectroscopy revealed that the photothermal effect facilitated the surface reconstruction into high-active oxyhydroxides, and a lower kinetics barrier under applied anodic potentials was confirmed by DFT.

The operando characterization can also help to explore how the potential affects the reconstruction of the catalysts. Dionigi et al.²¹⁰ utilized operando wide-angle X-ray scattering (WAXS) to study the phase-transition process of NiFe and CoFe layered double hydroxides as OER electrocatalysts under applied anodic potentials and found that they all transformed from the as-prepared α-phase to the active γ-phase. Moreover, these measured results were in excellent agreement with the DFT calculations and AIMD simulations, indicating that the operando scattering analysis can accurately identify the catalytically active phases. Using operando XRD, Reikowski et al.²¹¹ studied the relationship between the potential-dependent structure of thin Co₃O₄(111) and CoOOH(001) films and the electrochemical current. It was found that CoOOH(001) could maintain good stability at a wide OER current densities range, while they observed the fast and fully reversible structural changes on Co₃O₄(111). Su et al.²¹² reported a NiFe Prussian blue analogue as OER electrocatalyst and revealed that Ni(OH)₂ was the active species. Through operando X-ray spectroscopy, the in situ generated Ni(OH)₂ was detected to transform into NiOOH_2–x, which contained Ni⁴⁺, under an applied potential. The amount of Ni⁴⁺ was a function of the applied potential.

Determination of the Oxidation States of the Active Sites

Identifying the oxidation states of the active site under reaction conditions plays a crucial role in the electrocatalyst design. For CRR, copper has been proved a promising electrocatalyst for converting CO₂ to C₂ products among all of the explored metals.^213,214 To improve the catalytic performance of Cu-based catalysts, the relationship between the oxidation states of Cu and catalytic properties has been extensively studied using operando characterization. Chou et al.²¹⁵ found that the CRR mechanism is related to the oxidation state distribution on a Cu surface by employing in situ surface-enhanced infrared absorption spectroscopy (SEIRAS) and in situ soft X-ray absorption spectroscopy (XAS). As shown in Figure 10a, the results showed that C₁ hydrocarbon products could be obtained on a Cu(I) dominant surface, whereas a Cu(0) dominant surface inhibits hydrocarbon formation. The selectivity of ethylene was further enhanced on the surface with the coexistence of Cu(I) and Cu(0). Likewise, by employing operando seconds-resolved XAS, Lin et al.²¹⁶ reported an oxide-derived Cu electrocatalyst with a steady chemical state of half Cu(0) and half Cu(I), which could produce C₂H₅OH with a considerably high selectivity in a wide potential range. By employing DFT calculations, it was revealed that the equal numbers of Cu and Cu(I) on the top layer of Cu₂O could facilitate the coupling of dual carbon monoxide to form the *OCCO intermediate, which improved the CRR selectivity toward C₂ products. Zhou et al.²¹⁷ correlated the oxidation state of copper with the preference for the electrosynthesis of C₂ hydrocarbon and utilized boron to tune the average copper valence state at +0.35, which was confirmed by in situ XANES, achieving a high Faradaic efficiency for C₂ hydrocarbons of ∼80%.

Figure 10.

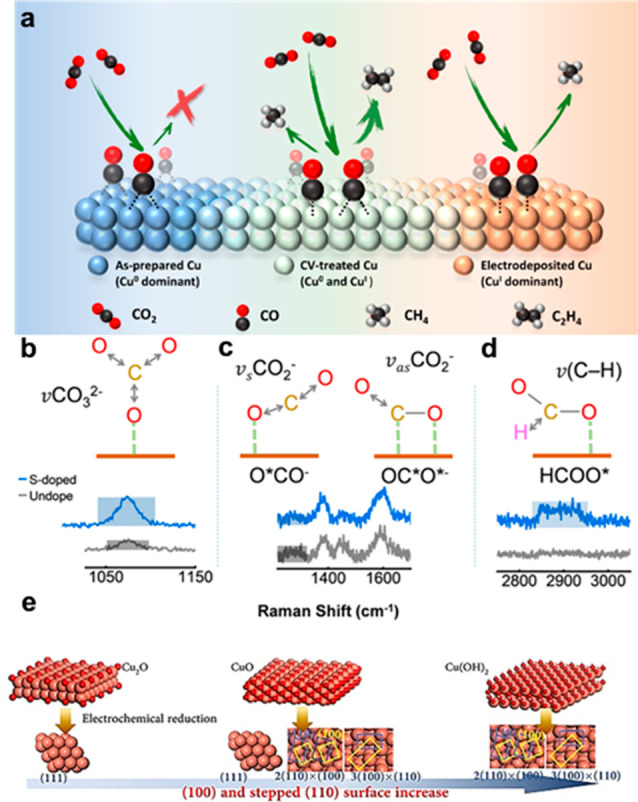
(a) Schematic illustration of the electrochemical CRR on the Cu Surface. Reprinted from ref (215). Copyright 2020 American Chemical Society. (b–d) Absorption structure of the intermediate with relative Raman spectra. Reprinted from ref (220). Copyright 2020 American Chemical Society. (e) Illustration of the preparation of Cu(OH)₂-derived/Cu foil, CuO-derived/Cu foil, and Cu₂O-derived/Cu foil. Reprinted from ref (222). Copyright 2020 Wiley.

The oxidation state of single-atom active sites is difficult to determine during an electrochemical reaction. By using operando XAFS, Cao et al.²¹⁸ revealed that the coordination-unsaturated single Co₁–N₄ site transformed into a high-oxidization HO-Co₁–N₂ moiety with a hydroxyl adsorption under an alkaline HER. A DFT calculation demonstrated that this highly oxidized Co site could enhance the HER activity. In contrast, Fang et al.²¹⁹ revealed that the single Pt atom tended to release from the nitrogen–carbon support and exhibited a close-to-zero valence state during the HER, which optimized the adsorption energies of the reactants.

Detection of the Reaction Intermediates

Using some operando characterization, such as Fourier transform infrared spectroscopy (FTIR) and Raman spectroscopy, the formation of the adsorbed species on a catalyst surface can be recorded under the actual operating conditions in aqueous media and obtain a deeper understanding of the reaction mechanism.⁴ To enhance the CO₂-to-formate selectivity in CRR, Pan et al.²²⁰ employed in situ Raman spectroscopy to monitor the vibration models of CO₂^– intermediates on Cu-based electrocatalysts. It was found that introducing the S atom can change the adsorption state from coexisting O*CO^– and OC*O*^– to the dominating OC*O*^–, resulting in a high selectivity and activity toward formate (Figure 10b–d). Furthermore, to improve the CRR selectivity toward C₂ products, Chen et al.²²¹ reported a controllable boundary-rich copper catalyst (GB-Cu) with the high C₂ selectivity of 70%. In situ attenuated total reflection surface-enhanced infrared absorption spectroscopy (ATR-SEIRAS) and DFT calculation revealed that the key intermediate *CO was binding more strongly on the Cu surface in the presence of a large number of grain boundaries, which promote the C–C coupling. In addition, Zhong et al.²²² synthesized a series of Cu catalysts with different exposed surfaces in a controlled manner by modifying the structures of precursors (Cu(OH)₂, CuO, and Cu₂O). By employing in situ ATR-SEIRAS, in situ Raman spectroscopy, and DFT calculations together, the facet effect of copper crystals toward the C₂ selectivity/activity was investigated at the atomic level (Figure 10e). The results unveiled that the stepped Cu(110) and Cu(100) are crucial, which facilitated the CO adsorption and promoted a CO dimerization. Guo et al.²²³ utilized in situ Raman spectroscopy to explore the HER mechanism during photocatalytic processes on MoS_2xSe_2(1–x) nanosheets. They demonstrated that H atoms were bonded to active S and Se atoms and a guideline to directly assess the HER performance owing to the exponential relationship between the number of reactive electrons and the Raman intensity of intermediate species.

The large noises in the spectrum make the operando FTIR and Raman spectroscopy limited in identifying the atomistic structure of the reactive intermediates.¹²⁴ A theoretical calculation is an effective tool providing an atomistic understanding, but sometimes the results do not match with the experimental observation due to an unrealistic modeling. To solve this issue, Cheng et al.¹²⁴ utilized QM/MD with an explicit solvent and applied a potential at 298 K to resemble the operando experimental condition and identified reactive intermediates in CRR. The results showed that the value of the predicted C–O stretch of *HOC–COH and the C–C stretch of *C–COD is consistent with that of the experimental peak. In addition, to explore how to improve the hydrocarbon product selectivity and reaction rates, they¹²⁶ further performed AIMD to calculate the CRR pathways and kinetics on the water/Cu(100) interface with five layers of the explicit water at pH 7. It was found that hydrocarbon products could be obtained selectively and efficiently with an applied potential greater than −0.60 V (RHE) and that accelerating the CO dimerization was an efficient way to improve the reaction rates.

Operando methods are also commonly used in photocatalysis to explore the reaction mechanism. Xu et al.²²⁴ combined operando NMR spectroscopy, DFT calculations, and AIMD simulations to understand the dynamic behaviors of the methanol–water cluster intermediates on the surfaces of rutile-TiO₂ in a photocatalytic reaction. The results demonstrated that the motions of the methanol–water clusters govern the number of methanol molecules that reach the surface of the photocatalyst per unit time and, in turn, determine the yields of methanol-reforming products.

Challenges and Opportunities

The union of operando characterization with the modeling strategies for a realistic reaction represents an exciting area for new insight into heterogeneous catalysis. Here, we discuss a few of the most recent advances, challenges, and opportunities in this area: the more accurate description of a reaction environment, the further consideration of a highly dynamic fluxionality of catalyst structure, along with the deeper incorporation of the ML technique.

Improved Operando Techniques with High Spatiotemporal Resolutions

Despite the fast-developing operando techniques, the gap between experimental and theoretical spatiotemporal windows still exists, which can result in a difference between experimental results and theoretical prediction. Currently, operando microscopy, like liquid-cell S/TEM, can achieve a nanometer and even an atomic-scale spatial resolution, while attosecond spectroscopy even enables a visualization of the electron motion in atoms, molecules, and solids.^{152 ,225 ,226} In heterogeneous catalysis, theoretical investigations generally provide an atomistic model of reaction intermediates whose lifetime is approximately a few hundred femtoseconds or even much shorter.²²⁷ However, simultaneously obtaining such high temporal and spatial resolutions remains highly challenging.⁵ It implies that current operando techniques may only capture the (quasi)stable states of reaction intermediates.²²⁸ Not to mention, heterogeneous catalysts have a completely different structure with their specificities and reaction environments that cause even more complex heterogeneities in spatiotemporal windows. In a word, to further combine the experimental and theoretical techniques, the development of novel operando techniques with high spatiotemporal resolutions is desired.

Dynamic Fluxionality of Catalyst Structure

The concept of dynamic fluxionality reminds us to see the active structure under operando conditions as an ensemble representation of many structures that dynamically interconvert with a lower energy barrier.⁴⁶

The Unclear Importance of Each Isomer

The possible number of dynamically accessible isomers is large, which even grows exponentially as the number of atoms increases.⁷⁵ Unfortunately, there is no a priori knowledge of which isomers play a more important role than others in the dynamic reaction.⁴⁶ The GM is believed to be the most abundant isomer in an ensemble of structures at low temperatures. However, some metastable structures might contribute more to the total activity than the most stable ones.²² The situation can be further complicated with varying reaction environments (temperature, adsorbates coverage, etc.).⁸⁴ Boltzmann statistics have revealed that the populations of different isomers can change with temperatures; thus, different ensemble-averaged properties are expected.²²⁹ In short, the dynamic fluxionality somehow leaves the true active structure in doubt.

The Interconversion Pattern of Possible Isomers

The ensemble representation of active structure implies that the actual reaction mechanism might be not one but many, with slightly different mechanisms and rates.² However, it is even unclear whether the catalyst undergoes an interconversion concurrently with the reaction step or sequentially with it, which should depend on the reaction energy barrier and cluster interconversion barrier.⁸⁴ Things can become extremely complicated if the reaction and interconversion happen concurrently, as the transition state of such a process is almost impossible to obtain.⁴⁶ Under operando conditions, as the catalyst undergoes continuous structural changes, the complexity to accurately describe its dynamic reaction mechanism is daunting.

In Alexandrova and co-workers’ recent review,^2,46 they proposed that a full theoretical description of a dynamic catalyst system calls for the all-around development of correlated electronic structure methods, efficient PES sampling, statistical mechanics, and accelerated dynamics. As for the experiment, it is expected for operando tools with the per-site resolution and the ability to find the minority sites that govern the catalytic activity and the combination of multiple operando techniques to build a coherent picture.^46,228

The Accurate Description of the Reaction Environment

The active structure of the catalyst highly depends on the reaction environment (solvent, electrochemical potential, and temperature). However, realistic simulations of surface catalytic reactions under operando conditions remain a grand challenge from many perspectives, and continuous efforts are required.

The Consideration of Coverage Effect

The coverage effect can be a decisive factor that causes deviations between simulations and experimental measurables, especially for the high-coverage system with a surface nonuniformity and strong self-/cross-interactions of adsorbates. As is well-known, the kMC method can be used to study how the surface coverage affects the reaction kinetics by quantitatively altering rate coefficients, whose calculated turnover frequencies (TOF) and product selectivity show good agreement with the experimental data.^230−232 However, it is noteworthy that the catalyst can undergo a different structural change with different coverage, which can be analyzed with the help of GO techniques as mentioned above. To fully illustrate the coverage effect, a combinational view of both thermodynamics and kinetics is expected.

Constant Potential in Electrocatalytic Modeling

The explicit consideration further raises problems of how to keep a constant applied potential in electrocatalytic modeling, which is significant especially for electron-transfer reactions.²³³ With an explicit solvent, the applied potential can be modulated by charges or extra hydrogen atoms. In this case, a constant potential is hard to maintain, as the work function (which needs to be fixed to keep the potential constant) is sensitive to the coordinates of an explicitly treated solvent.¹⁰⁴ A constant potential model with numerous explicit solvent molecules in a continuum dielectric may be a potential solution for this issue.²³⁴ Also, Chan and co-workers have presented series of works to extend the constant charge model to the constant potential model, using methods like charge extrapolation, effective charge, etc.^235−238 However, a generally accepted constant potential method is currently not yet available.^104,239

Take Advantage of the Machine Learning Technique

As mentioned above, the data-driven ML technique significantly accelerates the time-consuming simulation. For the further development and integration of ML technique on operando modeling, the following points are worth attention.

Lack of Benchmark for Heterogeneous Catalysis

As a data-driven technique, the most important strategy for the application of MLP in heterogeneous catalysis is the development of an open-source data set. Not only for training but a benchmark data set is also critical to establishing a consensus on testing and reporting newly developed ML models, and will ultimately improve data veracity in this field.²⁴⁰ For the prediction of molecular properties, today’s benchmark is the QM9 data set containing DFT-computed properties for ∼134 000 molecules with up to nine heavy atoms.^241,242 However, a universally recognized benchmark is still lacking in the study of heterogeneous catalysis. Moreover, another concern is that, currently, operando experiments have not been explored fully, causing a lack of refined experimental data to guide the development of ML methods.²⁴³

Lack of a Large Data Set of Heterogeneous Catalysis

The data sets for heterogeneous catalysis are relatively difficult to collect due to the structural complexity and higher computational cost, and the number remains small.²⁴⁴ The currently available data sets include the Catalysis Hub, Open Catalyst 2020 (OC20) Data set, CMR project, etc.^244−247 Except for the limited number of data sets, the data set’s chemical diversity also limits the generalizability of ML predictions.²⁴⁸ One more thing to take care of is the inconsistency of data sets, as they may obtain from different levels of theory.¹⁰⁴ A potential solution to the limited numbers of the data set is a hybrid approach based on an active learning framework with an uncertainty quantification, where training data are generated on-the-fly whenever needed.²⁴⁹

Next-Generation MLP

In Behler’s recent review, he pointed out that the next generation of MLP focus on the consideration of global charge distribution. The current construction of MLP depends on the local environments inside a cutoff sphere. However, in some cases, the atomic charge can strongly relate to structural changes very far away, of which current MLP fails to produce an accurate result.¹⁵³ Another challenging area is the interpretability of MLP. Some well-developed interpretable ML models include TinNet,²⁵⁰ SISSO,²⁵¹ and iGAM,²⁵² which have been applied to study the surface alloy and doped catalysts, like its prediction of the structural stability, to study adsorption behavior, to screen high-performance catalysts, etc.^252−256 The advantage of these methods is the physical transparency, as the obtained ML models are the explicit and analytic functions of input physical quantities, which can shine some light on the underlying structure–property relationship. Moreover, the transferability of MLP may be improved by active learning that can achieve high accuracy and data efficiency with fixed training data.²⁵⁷

Path to a Long-Term and Large-Scale Simulation

There is certainly a need for even larger and longer simulations at heterogeneous interfaces on the experimental scales, particularly with ab initio accuracy. Advances in both methods and software/hardware were pivotal to be developed successfully. For example, the MLP software DeePMD-kit was applied in the millisecond-level MD simulation of 100 million atoms water and Cu system.²⁵⁸ Moreover, the ability of a graphics processing unit (GPU)-based architecture to improve computational efficiency was demonstrated by simulating a massive 200 million atoms and was adopted in the popular MD software like GROMACS and NAMD.^152,259,260 With the help of these emerging techniques, the concept of hybrid machine learning/molecular mechanics (ML/MM) methods (proposed by Aspuru-Guzik) may be achieved before long, which can substantially accelerate the QM/MM simulations for the substantially larger systems and longer time scales, from microscopic (nm/ns) to macroscopic (μm/μs) systems.²⁴⁹ The development of a facile multiscale modeling method with the integration of ML still requires a continuous effort in the coming years.

Summary and Outlook

The fast-developing operando characterization allows the real-time detection of the dynamic structure of the catalyst, reaction intermediates, and catalytic products, which is helpful to precisely understand the catalytic mechanism and rational design of high-performance catalysts. For a complete understanding of a working catalyst system at an atomic scale, a theoretical investigation that simulates operando conditions is a must, which can be achieved through a multiscale computational modeling approach. In this Perspective, we describe various modeling approaches and machine learning techniques that step toward operando modeling. GO mostly helps in finding the most stable structure of the heterogeneous catalyst, while ab initio techniques can include the dynamic effect of the reaction environment. Microkinetic modeling can help explain the stepwise kinetics and build up the full reaction network, while the ML technique can serve as a surrogate model to accelerate the time-consuming simulation by orders of magnitude.

The real active intermediate under the interaction with the reaction environment species plays an important role in the exploration of the catalytic mechanism, which should not be ignored. We hope that this short Perspective can provide a useful guide to how to model the catalyst behavior on an experimentally spatiotemporal scale under true reaction conditions. Indeed, there are still significant challenges on the way to operando modeling: the limited spatiotemporal resolutions of operando techniques, the huge computational cost of ab initio calculation for a long-time/large-scale simulation, the unclear extremely dynamic nature of the catalyst, etc. However, considering the fast progress in recent years, especially the huge improvement of computational efficiency with the help of the ML technique, we can expect that, soon, it will become a new normal to describe the catalyst behavior in a spatiotemporal manner under true reaction conditions, with an affordable computational cost. With structure–activity relationships and reaction mechanisms being revealing, the rational design of highly efficient heterogeneous catalysts is expected to be greatly promoted.

Glossary

Abbreviations

AITD

ab initio thermodynamics

AIMD

ab initio molecular dynamics

BPGA

Birmingham parallel genetic algorithm

CRR

CO₂ reduction reaction

CORR

CO reduction reactions

EXAFS

X-ray absorption fine structure

EPR

electron paramagnetic resonance

GA

genetic algorithm

GO

global optimization

GM

global minimum

HER

hydrogen evolution reaction

IR

infrared

kMC

kinetic Monte Carlo

ML

machine learning

MLP

machine learning potentials

MOF

metal–organic framework

NNP

neural network potentials

NEB

nudged elastic band

OER

oxygen evolution reaction

PES

potential energy surface

QM/MM

quantum mechanics/molecular mechanics

RGO

reactive global optimization

RMG

reaction mechanism generator

S/TEM

scanning/transmission electron microscopes

SSW

stochastic surface walking

XRD

X-ray diffraction

XANES

X-ray absorption near edge structure

XPS

X-ray photoelectron spectroscopy

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.