Adaptation and the Mortality Effects of Temperature Across U.S. Climate Regions

Abstract

We estimate how the mortality effects of temperature vary across U.S. climate regions to assess local and national damages from projected climate change. Using 22 years of Medicare data, we find that both cold and hot days increase mortality. However, hot days are less deadly in warm places while cold days are less deadly in cool places. Incorporating this heterogeneity into end-of-century climate change assessments reverses the conventional wisdom on climate damage incidence: cold places bear more, not less, of the mortality burden. Allowing places to adapt to their future climate substantially reduces the estimated mortality effects of climate change.

1. Introduction

The prospect of rising global temperatures over the 21st century has focused attention on understanding how climate change affects human well-being and whether adaptation or mitigation strategies can offset its harmful effects (IPCC, 2014). One common approach to estimating climate change effects is to first estimate economic damages due to weather and then calculate climate damages using shifts in the future weather distribution predicted by climate models (Deschênes and Greenstone, 2011). Applications of this approach have generally assumed that the relationship between weather and mortality is uniform across regions and is constant over time. For example, Hsiang et al. (2017) estimate that excess mortality will account for about 70% of end-of-century (2080–2099) climate damages in the United States and that northern, cooler regions will generally bear lower mortality costs from climate change than warmer regions. However, both the overall magnitude and geographic distribution of climate damages could deviate substantially from these predictions if the mortality effects of weather vary geographically or if places adapt to their future climate.

In this paper, we estimate how the mortality effects of temperature vary across U.S. climate regions and use these estimates to predict local and national end-of-century climate change impacts on U.S. elderly mortality. We assess climate change impacts for three cases: assuming homogeneous effects of temperature across regions, incorporating heterogeneity in a region’s current temperature-mortality relationship, and allowing for both current heterogeneity and future adaptation. Our analysis leverages Medicare administrative data on dates of death and ZIP codes of residence for all elderly U.S. beneficiaries from 1992–2013, daily weather monitor readings, and end-of-century climate change predictions from 21 climate models and two different emissions scenarios.

Our analysis proceeds in two parts. In the first part, we conduct a nonparametric analysis aimed at establishing the extent to which mortality effects of temperature vary across climate regions. While both hot and cold days increase mortality, on average, relative to a moderate day, we find that hot days are much deadlier in cool regions than in warm ones. The reverse is true for cold days. This heterogeneity implies that, absent future adaptation, a warming climate will increase mortality more in cool places—and less in warm places—than would be implied by homogeneous temperature effects. In addition, these results suggest that attempts to account for adaptation to hot weather under a warming climate must also account for the potential for regions to simultaneously de-adapt to cold weather.

In the second part, we assess the mortality effects of projected end-of-century climate change. Informed by our heterogeneity analysis, we first estimate the mortality effects of temperature as a smooth, semi-parametric function of temperature and local (ZIP code level) climate. We then calculate climate damages for each ZIP code by combining temperature effects with projected shifts in the future weather distribution for each ZIP code. This approach allows us to model both heterogeneity in the current temperature-mortality relationship based on a region’s historical climate and the potential for the region to adapt to its future climate.

We find that accounting for heterogeneity and adaptation substantially influences the sign, magnitude, and geographic distribution of predicted climate damages relative to a conventional approach that assumes homogeneous current temperature effects and no future adaptation. Using the conventional approach, we predict an overall increase in elderly mortality of 0.76%, with warm regions bearing larger burdens and cool regions benefiting from mortality reductions, similar to conclusions by Houser et al. (2014) and Hsiang et al. (2017). However, accounting for heterogeneous current temperature effects implies a much larger aggregate mortality increase of 2.15% and reverses the distribution of predicted climate damages: cold places bear more, not less, of the mortality burden.

Further allowing places to adapt to their future climate yields mortality effects of climate change that are systematically lower than estimates that do not allow for adaptation. When we account for both current heterogeneity and future adaptation, we estimate an overall decrease in U.S. elderly mortality of approximately 0.53% by the end of the century, compared to the overall mortality increase of 2.15% for the case of heterogeneous effects with no adaptation. This finding is best interpreted as quantifying the potential scope for adaptation to future climate change using currently available technologies that regions have found worthwhile to adopt given historical costs and their current climates. Because we model neither the future cost of adaptation nor the nonmortality effects of climate change on elderly welfare, our findings do not imply that climate change will necessarily improve elderly well-being.

Our paper contributes to a growing literature that explores adaptation to climate change.¹ Methodologically, the studies most closely related to ours are Butler and Huybers (2013) and Auffhammer (2017), which use a similar approach to consider regional adaptation in maize production and in energy use, respectively. In contemporaneous work, Portnykh (2017) considers weather, adaptation, and mortality using Russian data. Our paper also contributes to studies of how the mortality effects of temperature vary across climate regions. For example, Curriero et al. (2002) and Barreca et al. (2016) find that cold days tend to have larger effects in southern climates, while hot days tend to have larger effects in northern climates. Barreca et al. (2015) more thoroughly examine how the mortality impacts of hot days vary across U.S. states according to the frequency at which they occur.

Our work expands on these studies in three primary ways. First, we use more spatially and temporally granular data spanning the United States to characterize graphically, and in a statistically precise way, how the entire temperature-mortality relationship varies with local climate. This is important because climate change can affect the likelihood of both hot and cold days, varying by region. Second, we combine climate-specific temperature effects with location-specific climate change projections to predict end-of-century climate damages both locally and in aggregate. Third, we predict the scope for adaptation to climate change using cross-sectional heterogeneity in the observed temperature-mortality relationship, simultaneously accounting for adaptation to heat and possible de-adaptation to the cold.

The remainder of this paper proceeds as follows. Section 2 describes our data. In section 3, we estimate climate-specific temperature-mortality relationships. Section 4 makes predictions of long-run climate change-induced mortality, with and without climate-based regional heterogeneity and with and without adaptation. Section 5 concludes.

2. Data

2.1. Data Description

Our analysis leverages a novel combination of three primary data sources: daily weather monitor readings from the National Oceanic and Atmospheric Administration’s (NOAA) Global Historical Climate Network (GHCN), elderly mortality and place of residence from Medicare administrative data, and climate projections from the NASA Earth Exchange Global Daily Downscaled Projections (NEX-GDDP). We briefly describe the weather and mortality data and variable construction in this section. Section 4.1 describes the climate model projections. Appendix section A.1 provides more detailed data descriptions.

The primary geographic units for our analysis are ZIP codes, as defined by the 2010 U.S. Census Bureau’s ZIP Code Tabulation Areas (ZCTAs). ZCTAs aggregate census blocks to form real representations of United States Postal Service (USPS) ZIP Code mail delivery routes. For most areas, the ZCTA code is the same as the USPS ZIP Code.

We obtain daily minimum and maximum temperatures from NOAA’s GHCN database, which provides climate summaries for weather stations across the 50 U.S. states, the District of Columbia, and Puerto Rico. For each ZIP code, we construct daily high and low temperatures as the inverse distance-weighted average of all available maximum and minimum temperatures, respectively, for monitors within 20 miles of the ZIP code centroid, following the monitor aggregation method used by Currie and Neidell (2005) and Beatty and Shimshack (2014). The daily average temperature is defined as the midpoint of the daily high and low temperatures.²

We categorize ZIP codes into climate regions based on their cooling degree days (CDD), derived from NOAA’s 1981–2010 Climate Normals for U.S. weather stations. CDD are based on daily average temperatures and are designed to reflect the energy needed to cool a building to a base temperature, typically 65°F. For example, one day with an average temperature of 75°F represents 10 CDD, while a day with temperatures below the base temperature represents 0 CDD. A weather station’s CDD Normal is a three-decade average of its annual CDD, which is the sum of daily CDD values across all days in the year. The CDD Normal for a ZIP code is the inverse distance-weighted average of CDD Normals at the nearest weather station and any other stations within a 20-mile radius of the ZIP code centroid.

Finally, we measure mortality using Medicare enrollment files from 1992–2013. These files provide demographic data on all individuals eligible for Medicare in each year, including date of birth, date of death, and ZIP code of residence. We restrict our sample to elderly beneficiaries aged 65–100, who represent over 97% of the U.S. elderly resident population (appendix figure B.1). We define daily mortality for a ZIP code as those who die within a given time period (e.g., within three days of the index date) as a fraction of all beneficiaries residing in the ZIP code who were alive and eligible for Medicare as of the index date.

2.2. Summary Statistics

The primary sample for our analysis contains 32,860 ZIP codes, yielding over 250 million ZIP-code-day observations over the sample period (1992–2013). Appendix figure B.2 shows how climate varies across the sample. The Medicare population-weighted average ZIP code CDD Normal is 1,404. The coolest third of ZIP codes have fewer than 787 CDD, with some parts of Alaska and Colorado having 0 CDD, as the average temperature never exceeds 65°F. The warmest third of ZIP codes have at least 1,442 CDD, with some very hot ZIP codes in Arizona, California, Florida, and Puerto Rico exceeding 4,500 CDD.

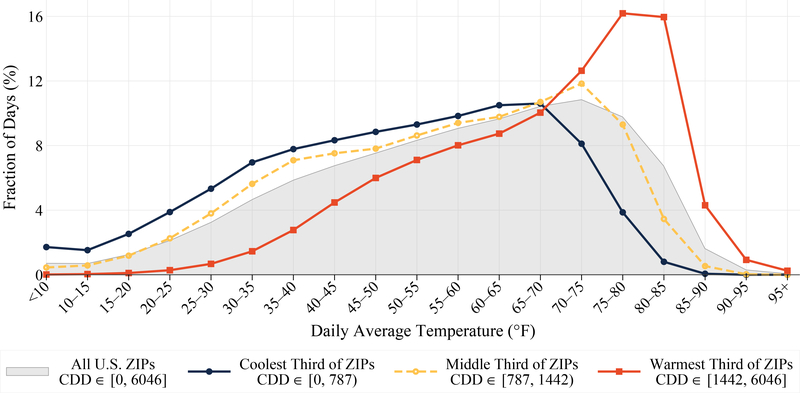
Figure 1 summarizes the distribution of realized temperature over the sample across each of 19 temperature bins ranging in 5°F increments from < 10°F to > 95°F. The gray-shaded region presents the distribution of daily average temperature for the United States as a whole, while the blue, gold (dashed), and orange curves present respective distributions for the coolest, middle, and warmest thirds of U.S. ZIP codes.

Figure 1:

U.S. Daily Average Temperature Distribution

Notes: This figure summarizes the distribution of daily average temperature in the United States from 1992–2013. Distributions are reported separately for the entire United States and for the coolest, middle, and warmest population-weighted thirds of ZIP codes based on CDD Climate Normals. Daily temperature data come from the Global Historical Climatology Network land surface station database. Appendix tables B.1a–B.1b report numerical values of the points in this figure.

Appendix tables B.1a–B.1b summarize daily mortality by temperature bin for each of the three climate terciles and for the United States as a whole, respectively. Average three-day mortality was 39.4 deaths per 100,000 beneficiaries, corresponding to an annual mortality rate of 4.8%. However, mortality was systematically lower on warmer ZIP days, with the lowest three-day mortality rate of 35 deaths per 100,000 occurring after days with average temperatures above 95°F. A naïve interpretation of this pattern is that replacing cool days with very hot days reduces mortality. Yet this conclusion could be flawed either because hot days tend to occur during the summer, confounding the temperature effect with seasonality, or because the population residing in regions where hot days occur most often differs systematically from cooler regions. The richness of our data allows us to address these potential confounders by controlling flexibly for both location and seasonality.

3. Heterogeneous Mortality Effects of Temperature

In this section, we examine the extent to which the mortality effects of temperature vary across climate regions. For this analysis, we define climate regions as the coolest, middle, and warmest population-weighted third of ZIP codes based on CDD Normals. We then nonparametrically estimate the temperature-mortality relationship for each climate tercile.

3.1. Empirical Strategy

We use year-over-year variation in daily temperature to identify the causal effect of temperature on mortality, inspired by the approach of Deschênes and Greenstone (2011). Our analysis uses daily observations of mortality and temperature at the ZIP code level. Our primary outcome of interest, mortality_zd, is the number of deaths per 100,000 beneficiaries in ZIP code z within three days after index day d.³ Our estimating equation is

$$\begin{gathered} {\mathit{mortality}}_{zd}=\sum _{{}_{b\in B\backslash \{65-70\}}}{\beta }_b^{cool}tempbi{n}_{zd}^b\times 1(ZIPzincoolestthirdofregions) \\ +\sum _{{}_{b\in B\backslash \{65-70\}}}{\beta }_b^{mid}tempbi{n}_{zd}^b\times 1(ZIPzinmiddlethirdofregions) \\ +\sum _{{}_{b\in B\backslash \{65-70\}}}{\beta }_b^{hot}tempbi{n}_{zd}^b\times 1(ZIPzinwarmestthirdofregions) \\ +ZipDa{y}_{zd}+L_{zd}+StY{r}_{zd}+{\epsilon }_{zd}. \end{gathered}$$ (1)

The primary independent variables of interest in equation 1 are temperature indicators $tempbi{n}_{zd}^b$ defined by which of the 19 temperature bins b∈B = {< 10,10−15,...,90−95,> 95} the average temperature in ZIP code z falls in on day d. The temperature bins are then interacted with indicators for the climate tercile containing the ZIP code. This specification allows for arbitrary nonlinearities in the relationship between temperature and mortality and further allows this relationship to vary arbitrarily by climate region.

Because equation 1 includes ZIP code fixed effects, the coefficients on the set of temperature indicators for each climate region are only identified up to a common constant (i.e., a vertical shift in the temperature-mortality relationship). This corresponds to arbitrarily omitting one temperature bin in the regression, which we choose to be the 65°F–70°F bin. As a result, the coefficients ${\beta }_b^c$ describe the mortality effect in climate region c of replacing a day with an average temperature in bin b with a 65°F–70°F day. Identification up to a common constant also implies that all statements we make about heterogeneous treatment effects reflect differences in the curvature of the temperature-mortality relationship, not differences in mortality levels across regions.

We identify the effects of temperature on mortality by isolating year-over-year variation in temperature and mortality, controlling for both geography and seasonality using fixed effects ZipDay_zd for each ZIP code and day of year combination. This control strategy accounts for seasonal mortality patterns that may vary by ZIP code, such as elevated winter mortality and reduced summer mortality. To account for serial correlation in daily temperature and potentially lagged mortality effects, L_zd includes three fully interacted sets of 5-degree average temperature bins for the preceding two and six days and the subsequent two days, which are further allowed to vary by climate tercile. Finally, we include state-by-year fixed effects, StYr_zd, to control for arbitrary annual shocks that may vary by state, such as changes to Medicare or Medicaid policy. All regressions are weighted by the ZIP code’s Medicare population. We two-way cluster standard errors at the county and state-date levels to allow for arbitrary correlations within groups of nearby ZIP codes over time and across all ZIP codes in the state at a particular point in time.

3.2. Results

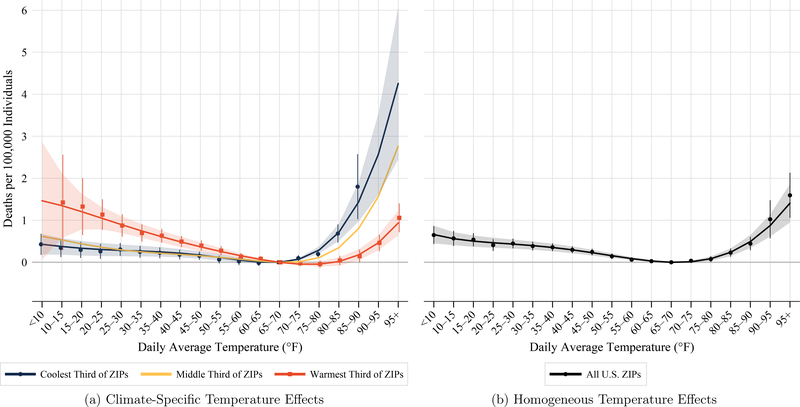
Figure 2a depicts results from estimating equation 1 with three-day mortality as the outcome. Markers with whisker lines plot the nonparametric temperature bin estimates and associated 95% confidence intervals. Nonparametric estimates are shown only for the coolest and warmest climate terciles and for binned temperatures that occur with a frequency of at least one day per decade in the climate region. Solid lines plot estimates from a semi-parametric version of equation 1, where temperature bin indicators are replaced by a 5th-degree polynomial in the temperature bin. The semi-parametric and nonparametric estimates agree closely for temperatures occurring at least one day per decade. Shaded regions, representing 95% confidence intervals on the semi-parametric estimates, are shown for the coolest and warmest terciles. For comparison, figure 2b shows the results of estimating equation 1 under the assumption of homogeneous temperature effects.⁴

Figure 2:

Morality Effects of Temparature

Notes: This figure plots estimated three-day mortality effects of temperature. In panel A, effects are allowed to differ by the coolest, middle, or warmest third of ZIP codes as defined in figure 1. In panel B, effects are restricted to be common to all U.S. ZIP codes. Effects reflect excess mortality on a day with a given average temperature relative to a day with an average temperature of 65°F–70°F. Markers with whisker lines plot nonparametric temperature bin estimates and associated 95% confidence intervals. Markers are only shown for binned temperatures that occur with a frequency of at least one day per decade in the climate region. Solid lines and shaded regions plot semi-parametric polynomial estimates and associated 95% confidence intervals. Confidence intervals are based on two-way clustered standard errors at the county and state×date levels. Numerical values for all point estimates and standard errors are reported in appendix tables B.1a–B.1b.

Figure 2a reveals substantial heterogeneity in temperature effects by climate tercile. In the warmest third of ZIP codes, depicted in orange, mortality effects are lowest on days with average temperatures of 75°F–80°F. For the coolest third of ZIP codes, depicted in blue, mortality is minimized on days with temperatures of 60°F–65°F. As temperatures increase above 75°F, the colder regions feature a stark increase in mortality, while warmer regions exhibit much more modest effects. For example, an 85°F–90°F day increases the mortality rate in the coldest decile by 1.8 deaths per 100,000 but has nearly no effect (0.15 additional deaths per 100,000) in the warmest decile. On the other hand, mortality increases 2.6–4.8 times more on days at or below freezing in the warmest region than in the coolest one.

Figure 2a suggests that regions are both relatively good at dealing with temperatures they experience frequently and are relatively bad at dealing with temperatures they experience infrequently. Comparing the temperature-mortality relationships in figure 2a with the temperature frequency plots in figure 1 reveals that for days with temperature greater than 65°F, which occur with greater frequency relative to a 65°F day in the warmest region than the coolest, mortality effects are larger in the warmest region than in the coolest. The opposite is true for days below 65°F. Although the reference category of 65°F is a choice, it is also true that the curve for the warmest tercile is flatter than the curve for the coolest tercile for days above 65°F and is steeper for days below 65°F.

Comparing the climate-specific heterogeneous effects in figure 2a with the homogeneous effects in figure 2b illustrates how properly accounting for temperature effect heterogeneity can affect the projected impact of climate change. The homogeneous effects curve lies between the curves for the warmest and coolest regions, implying that using homogeneous effects understates the mortality effects of hot days in cool regions and overstates them in warm ones. The opposite is true for cold days. So while the homogeneous effects estimates imply that replacing a cold 25°F–30°F day with a hot 85°F–90°F day has little effect on mortality in any region, this replacement actually increases mortality by 1.49 deaths per 100,000 in the coolest tercile and reduces mortality in the warmest tercile decrease by 0.75 deaths per 100,000. In addition, the homogeneous effects are not a simple average of the heterogeneous effects but instead lie closer to the cooler regions’ curve for cold temperatures and closer to the warmer regions’ curve for hot temperatures. Thus, the homogeneous effects do not reflect the national average effects of temperature.

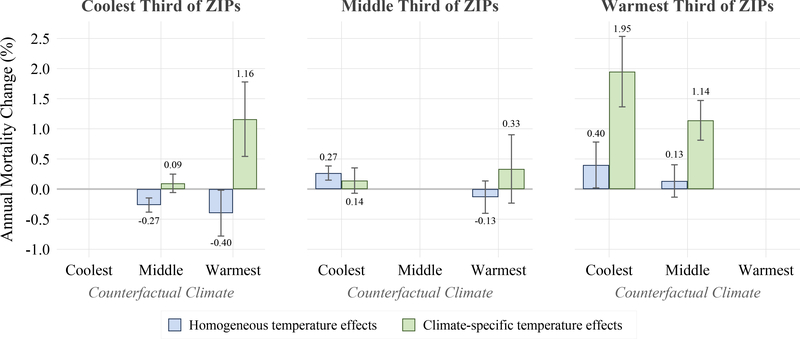
As further illustration of the importance of allowing for heterogeneous temperature effects when assessing climate change effects, figure 3 presents predicted mortality impacts of replacing the climate of each tercile by the climate of one of the other terciles. When homogeneous effects are assumed (blue bars), warming is always associated with decreased mortality. However, taking into account current climate-specific heterogeneity (green bars), a qualitatively different pattern emerges. Under heterogeneous effects, we see that warming the coolest tercile’s temperature distribution to that of either the middle or warmest tercile, or warming the middle tercile’s temperature distribution to that of the warmest tercile, increases mortality, the opposite of what occurred in the homogeneous effects case. Further, for each of the current climate terciles, a change in a region’s temperature increases mortality whether that change involves warming or cooling. Thus the heterogeneity we observe is not simply due to some regions being better at dealing with all temperatures than other regions. Rather, whatever factors determine a region’s temperature-mortality curve, they tend to perform particularly well given the region’s actual climate relative to other climates.

Figure 3:

Predicted Mortality Effects of Regional Climate Swaps

Notes: This figure summarizes mortality impacts from counterfactual scenarios in which each of these climate region’s current temperature distribution is replaced by the current distribution of one of the other two climate regions, shown in figure 1.

3.3. Regional Heterogeneity as Adaptation

Regional heterogeneity in the temperature-mortality relationship could arise due to regional adaptation, whether technological, behavioral, and/or biological in nature, or due to regional differences in characteristics that are correlated with current climate but do not result from human choices or physiology. This distinction is important for interpretation because if regional differences are caused by factors that are immutable, then even though Chicago in the future may face the climate that Dallas does now, we should not expect the Chicago of the future to be as good at dealing with heat as Dallas currently is. Thus, understanding the extent to which current heterogeneity is due to adaptation is important for understanding the extent to which future adaptation may mitigate the impact of climate change.

The nonlinear pattern of temperature effect heterogeneity that we document with respect to baseline climate is informative of the underlying mechanisms driving this heterogeneity. For example, the effects of hot days are smaller but the effects of cold days are larger in warm regions than in cooler ones. This pattern is not readily explained by factors that reduce sensitivity to both cold and hot days. In particular, the treatment effect heterogeneity we document seems unlikely to reflect regional differences in wealth or underlying health endowments since these differences plausibly reduce sensitivity to both hot and cold weather. By contrast, this nonlinear pattern is consistent with a wide variety of adaptation behaviors.

There are numerous ways in which people and communities may adapt to their climate, such as through biological acclimatization, migration to different regions based on health, infrastructure investments, or architectural design. In appendix section A.4, we provide evidence that air conditioning (AC) adoption is strongly associated with differences in heatrelated mortality across regions but not with cold-related mortality. Since AC adoption can be correlated with many other adaptive behaviors that also reduce the mortality effects of heat (e.g., designing buildings to optimize thermal performance), our estimates should not be interpreted as identifying the causal effect of AC. Nevertheless, the AC results provide additional, albeit suggestive, evidence that adaptive behaviors can explain the regional heterogeneity we document.

Our finding that places seem well-adapted to their current climate suggests it is reasonable to expect that regions could continue to find it worthwhile to adapt to a changing climate. It is important to note, however, that this statement concerns the observed degree of historical adaptation to the current range of climates given current technology. The degree to which places continue to adapt to climate change will depend on the future cost of available adaptation technologies and on the ability of currently hot places to adapt to climates much hotter than any U.S. regions currently experience.

4. Climate Change-Induced Mortality and Adaptation

In this section, we develop estimates of the end-of-century mortality impact of climate change accounting for heterogeneity and adaptation. To fix ideas, let $m_z^p(t)$ denote the mortality effect in ZIP code z and period p of a day with average temperature in bin t. We will consider both the current and future periods by p = current and p = future, respectively. Let $g_z^p(t)$ be the number of days per year in which the temperature falls in bin t in period p. Current annual mortality (CAM_z) is therefore

$$CA{M}_z=\sum _t{m}_z^{current}(t)g_z^{current}(t).$$

We are interested in the change in excess mortality due to climate change. Let $m_z^{future}(t)$ denote the future mortality effect of temperature bin t in location z. In this case, the change in excess mortality would incorporate both the change in the temperature distribution and the change in the temperature-mortality relationship:

$$FA{M}_z-CA{M}_z=\sum _t{m}_z^{future}(t)g_z^{future}(t)-\sum _t{m}_z^{current}(t)g_z^{current}(t).$$ (2)

4.1. Empirical Implementation

Computing the estimated change in excess mortality involves the four functions on the right hand side of equation 2: current and future temperature distributions and current and future temperature-mortality relationships. The current temperature distribution is that observed for the ZIP code in the sample from 1992–2013. Our predictions of future temperature distributions are based on ZIP-code-specific projected changes in the daily temperature distribution between the current period (1992–2013) and the end of the century (2080–2099).

We derive projected changes in temperature for each of the 21 climate models for which daily scenarios are produced and distributed as part of the NEX-GDDP dataset. The NEX-GDDP data include daily minimum and maximum temperature predictions on a 25km by 25km grid (0.25-degree spatial resolution). We focus on climate model projections made under the Representative Concentration Pathway (RCP) 8.5 “business as usual” scenario, where emissions continue to rise throughout the 21st century (Meinshausen et al., 2011). Finally, we aggregate the gridded model projections to the ZIP code level using inverse distance weighting of all climate model grid points within 20 miles of the ZIP code centroid.⁵

To create a consensus projection from the 21 models, we average over all of the models using the weights employed by the Fourth National Climate Assessment (Sanderson, Knutti and Caldwell, 2015; Sanderson and Wehner, 2017). These weights, shown in column 1 of appendix table B.2a, positively value model predictive skill but penalize codependency between models. We refer to the weighted average model as the meta-model and the weighted average predicted temperature distribution as the meta-distribution.

The meta-model projects that average annual temperatures in the United States will rise by 8°F by the end of the century under the RCP 8.5 emissions scenario. Appendix figure B.6 maps the projected changes in temperature and CDD. Although predicted warming tends to be higher in areas that are currently cooler, comparing appendix figures B.2 and B.6 shows that there is significant variation in predicted warming even among regions that currently have quite similar climates.⁶

With sufficient observations for each ZIP code, we could estimate the temperature-mortality relationship nonparametrically for each ZIP code using equation 1 in the same way that we estimated it nonparametrically at the climate tercile level. In practice, however, there are not enough observations for each ZIP code to estimate this relationship precisely. Instead, we estimate the daily temperature-mortality relationship as a semi-parametric, smooth function f(t,CDD) that depends on both daily average temperature and climate, as captured by the ZIP code’s CDD Normal.

The regression equation used to estimate this semi-parametric function of temperature and climate is identical to equation 1 except the temperature and climate indicators are replaced by this smooth function f(t,CDD) of temperature and climate, yielding the estimating equation:

$$mortalit{y}_{zd}=f\left(t_{zd},CD{D}_z\right)+ZipDa{y}_{zd}+L_{zd}+StY{r}_{zd}+{\epsilon }_{zd}.$$ (3)

We define f(t,CDD) to be a linear spline in temperature with knot points at 10-degree increments from 30°F to 90°F, which is then fully interacted with a spline in log CDD with knot points at the 33rd and 66th percentiles of the current distribution of ZIP-code-level CDD normals (the same cutoff points used to define the climate terciles). Specifically, if F_CDD is the cumulative distribution function of the current CDD Normal distribution, then

$$f(t,CDD)=s(t,\beta )+\sum _{p=0}^2\max \left(\log CDD-\log F_{CDD}^{-1}(0.33p),0\right)\times s\left(t,{\beta }^p\right),$$

where

$$s(t,\beta )={\beta }_{0}t+\sum _{k=3}^9{\beta }_k\max (t-10k,0).$$

Since f(t,CDD) is identified up to a constant, we always evaluate it relative to a reference temperature of 65°F. We compare the parametric estimates from equation 3 to the nonparametric temperature bin results from equation 1, and we reestimate equation 1 but with fitted, three-day mortality values $mort\widehat{a}lit{y}_{zd}=\widehat{f}(t,CDD)$ as the outcome and controlling only for temperature bin indicators. As shown in appendix figure B.7, the parametric estimates broadly align with the nonparametric estimates in each climate tercile.

Appendix figure B.8 further illustrates the parametric estimates from equation 3 by plotting the fitted temperature-mortality relationship $\widehat{f}(t,CDD)$ for two cold ZIP codes (Fargo, ND, and Minneapolis, MN), one moderate ZIP code (Chicago, IL), and two hot ZIP codes (Dallas, TX, and Miami, FL), evaluated at each ZIP code’s current CDD Normal. As with the nonparametric tercile-based regressions presented in figure 2a, cold places suffer the most from hot days, while hot places suffer the most from cold days. This figure also previews how we will model adaptation to future climate. The climate models we use project Chicago’s end-of-century CDD to be 2,327, which is very close to Dallas’s current climate with 2,668 CDD. When we consider adaptation, we will use the temperature-mortality curve for a region with 2,327 CDD—essentially that of current-Dallas—to proxy for future-Chicago, assuming the region fully adapts to its new climate.

Finally, we can relate the estimate of f(t,CDD) to the mortality effect $m_z^p(t)$ of a day with average temperature t in ZIP code z in period p, introduced in our general framework above. If $M{65}_z^p$ represents mortality on a 65°F day in ZIP code z and period p, then

$$m_z^p(t)=M{65}_z^p+f\left(t,CD{D}_z^p\right).$$

4.2. Adaptation Predictions

We estimate the change in mortality between the current period (1992–2013) and the end of the century (2080–2099) using the meta-predictions of climate change under the RCP 8.5 emissions scenario. To investigate the importance of accounting for regional heterogeneity and adaptation, we construct these estimates under three different sets of assumptions about how the mortality effects of temperature vary spatially and over time.

4.2.1. Homogeneous Current Effects with No Future Adaptation

Our first set of predictions relies on two simplifications commonly made when predicting the mortality effects of climate change. The first simplification is to use a homogeneous mortality estimate, m^period(t), rather than region-specific estimates, $m_z^{period}(t)$. The second is to estimate health damages under an assumption of no adaptation (i.e., to define $m_z^{future}(t)$ to be equal to $m_z^{current}(t)$). We implement this empirically by estimating a version of equation 3 where we drop all terms in f(t,CDD) that depend on CDD to get a single temperature-mortality relationship m(t)^current = M65 + f(t). We then use that relationship for all ZIP codes in both current and future periods. Note that while we use the same mortality function f(t) for all regions, each ZIP code’s mortality change is computed with respect to its own projected future temperature distribution. We call this the case of homogeneous current effects with no future adaptation.

4.2.2. Current Climate Heterogeneity with No Future Adaptation

Our second set of predictions allows each ZIP code to have its own temperature-mortality relationship, $m_z^{current}(t)$, by estimating equation 3 where f(t,CDD) is permitted to depend on the ZIP code’s current CDD Normal. Thus, any two ZIP codes with the same current CDD Normals will have the same estimated temperature-mortality curve. Using this mortality relationship to capture both current and future conditions, we continue to assume there is no adaptation. We call this the case of current climate heterogeneity with no future adaptation.

4.2.3. Current Climate Heterogeneity with Future Adaptation

In our third set of predictions, we account for both climate-specific heterogeneity in the temperature-mortality relationship and adaptation over time. We operationalize this by evaluating the future mortality effects of temperature, f(t,CDD), in ZIP code z under the projected future climate (CDD) in that ZIP code. Intuitively, this approach assumes that if Chicago’s climate changes so that its end-of-century CDD is equal to Dallas’s current CDD, then Chicago’s end-of-century temperature-mortality relationship will be the same as Dallas’s is today, up to a constant.

Since under our approach to adaptation, the current and future temperature-mortality relationships are allowed to differ, the constant terms in $m_z^{current}(t)$ and $m_z^{future}(t)$, which are not identified empirically, do not drop out of the calculation of climate change mortality effects (equation 2). For our computations, we assume that mortality on a 65°F day does not change over time (i.e., $M{65}_z^{current}=M{65}_z^{future}$). Our justification for this assumption is that when the average temperature is near 65°F, individuals typically do not choose to heat or cool their homes. This assumption is appropriate if regional differences in mortality on 65°F days, after adjusting for seasonal and other fixed effects, reflect baseline differences in mortality across ZIP codes that are not affected by differences in climate. We call this the current climate heterogeneity with future adaptation case.

Our approach to modeling adaptation assumes that adaptation is complete in the sense that if future-Chicago has Dallas’s current climate, future-Chicago will respond to temperature like Dallas does today. This need not be the case if the cost of adaptation changes or if some characteristics of current-Chicago are immutable. In addition, our approach assumes that a region’s past adaptation to its current climate has no long-lasting effects in the sense that if Chicago has Dallas’s climate in the future, after it adapts it will be no better at dealing with cold temperatures than Dallas is now, even though Chicago currently has a significant advantage over Dallas in this area.⁷ Finally, this approach ignores the possibility of technological progress, which may moderate the temperature-mortality relationship beyond what we capture.

4.2.4. Example: Chicago

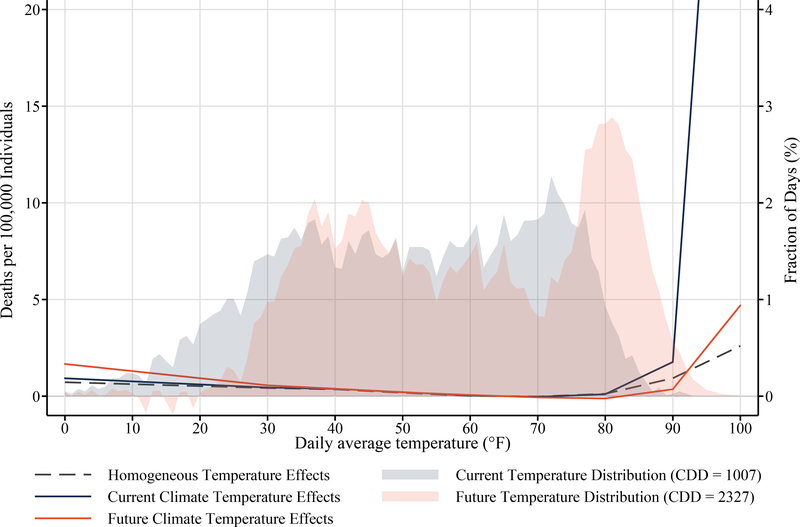
Figure 4 depicts the relevant pieces of equation 2 for computing the projected end-of-century change in mortality for Chicago. Chicago’s current and future temperature distributions are depicted by the blue and orange shaded regions, respectively. To compute the mortality effect with homogeneous effects and no adaptation, we use the dashed homogeneous temperature-mortality relationship in both the current and future periods. For the current climate heterogeneity with no future adaptation case, expected mortality is computed using Chicago’s current temperature-mortality relationship in both periods. Finally, to allow for current climate heterogeneity and future adaptation, we compute current mortality using Chicago’s current temperature-mortality curve and its current temperature distribution (both shown in blue), and we compute future mortality using Chicago’s future curve its future temperature distribution (both shown in orange).

Figure 4:

Climate Change Assessment for Chicago, IL

Notes: This figure depicts the components used by equation 2 to assess end-of-century (2080–2099) climate change impacts on mortality in Chicago, IL. The end-of-century temperature distribution is based on the meta-model projection for Chicago under the RCP 8.5 greenhouse gas emissions scenario.

4.3. End-of-Century Mortality Prediction Results

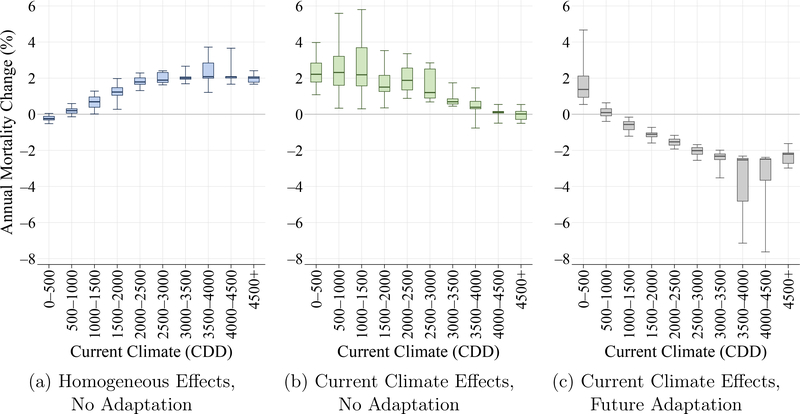
Figure 5 presents the results from assessing annual mortality effects of end-of-century climate change as predicted by the meta-model under the RCP 8.5 emissions scenario. Panel A depicts results under the conventional approach of assuming homogeneous current effects and no adaptation. Each box and whisker plot summarizes percentage changes in predicted annual mortality by the end of the century (2080–2099, vertical axis) for ZIP codes whose current climate falls in the bin depicted on the horizontal axis. Boxes stretch from the 25th percentile (lower hinge) to the 75th percentile (upper hinge) of mortality effects. The median is plotted as a line across the box, and whiskers stretch from the 5th–95th percentiles. In this case, mortality effects increase with CDD up to around 2,000 CDD, which is well into the warmest climate tercile (which begins at 1,442 CDD), and then flatten out as CDD continue to increase. These findings are further summarized by column 5 of table 1, who shows the aggregate percentage mortality change for each of the climate terciles and for the United States as a whole.⁸ The average mortality effects increase in magnitude from the coolest to the warmest third of ZIP codes, with a 0.76% increase in mortality overall. This pattern agrees with the conventional wisdom that the effects of climate change will be largest in regions that are currently hot.

Figure 5:

End-of-Century Climate Change Mortality Effects

Notes: The figure summarizes annual mortality effects of end-of-century (2080–2099) climate change as projected by the meta-model, an average of the 21 NEX-GDDP climate models, under the RCP 8.5 emissions scenario. Effects are calculated for each ZIP code based on the ZIP code’s current and future (projected) climates. Panel A reports climate effects under the assumption of homogeneous temperature effects. Panel B reports climate effects that allow for heterogeneous temperature effects based on current climate but do not allow for future adaptation. Panel C reports climate effects that incorporate both current heterogeneity and future adaptation. Box and whisker plots summarize the distribution of climate change effects across ZIP codes in each climate range. Boxes stretch from the 25th percentile (lower hinge) to the 75th percentile (upper hinge). The median is plotted as a line across the box. Whiskers stretch from the 5th percentile to the 95th percentile.

Table 1:

End-of-Century Climate Change Effects

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
					Annual Mortality Change (%)
	Avg. Temp. (°F)		Annual CDD		Homogeneous Effects	Climate Heterogeneity
	Current	Future	Current	Future	No Adaptation	No Adaptation	Future Adaptation
Coolest third of ZIPs	49.4	58.1	525	1,661	−0.03 (0.12)	2.25*** (0.50)	0.84** (0.35)
Middle third of ZIPs	55.2	63.5	1,079	2,491	0.54*** (0.16)	2.89*** (0.93)	−0.41 (0.35)
Warmest third of ZIPs	66.5	73.6	2,600	4,397	1.75*** (0.28)	1.33*** (0.31)	−1.97*** (0.67)
All U.S. ZIPs	57.1	65.1	1,413	2,864	0.76*** (0.18)	2.15*** (0.47)	−0.53* (0.32)

Notes: The table summarizes ZIP code-level climate change impacts, aggregated to climate terciles and to the United States as a whole. Columns 1–4 summarize the current climate of each region as well as the end-of-century (2080–2099) climate projected by the meta-model under the RCP 8.5 greenhouse gas emissions scenario. Columns 5–7 are based on the ZIP-code-level annual mortality effects summarized in figure 5. Column 5 reports climate effects under the assumption of homogeneous temperature effects. Column 6 reports “business as usual” climate effects that allow for heterogeneous temperature effects based on current climate but do not allow for future adaptation. Column 7 reports climate effects that incorporate both current heterogeneity and future adaptation.

The results change markedly once heterogeneity, with respect to current climate, is incorporated into the climate assessment. Panel B of figure 5 illustrates the heterogeneous current climate effects and the no-adaptation case. Here, the pattern is reversed relative to the conventional approach, with the mortality effect being flat up to 1,500 CDD (which includes the coolest and middle ZIP code terciles), and then declining as CDD continue to rise. The large average increases in mortality in cool and moderate ZIP codes result from two factors in combination: these regions are currently poorly adapted to very hot days, but climate models project increased exposure to such days in the future.⁹

Aggregate results for the case of heterogeneous effects by climate with no future adaptation are presented in column 6 of table 1. Mortality increases are larger in the coolest third of ZIP codes (2.25%) than in the warmest (1.33%). The mortality increase in the middle (2.89%) tercile is slightly larger than in the coolest, as these ZIP codes expect, on average, to experience more very hot days in the future than the coolest ones. Overall, our analysis predicts an increase in mortality across all U.S. ZIP codes of 2.15%, almost three times larger than is implied by homogeneous effects (0.76%). To put this number in perspective, this increase is roughly equivalent to the share of U.S. elderly deaths in 2013 due to chronic kidney disease (2.1%), accidents (2.4%), or influenza (2.5%) and around 10% of the share of elderly deaths due to cancer (21.4%).¹⁰

Panel C of figure 5 presents results under heterogeneous current climate effects with future adaptation. Three features emerge. First, net of adaptation, climate change is expected to be worse in the coolest regions than in the warmest ones. Second, incorporating adaptation to future climate yields mortality effects of climate change that are systematically lower than the no-adaptation estimates in panel B. Third, the predicted mortality change under adaptation is negative for regions with a current climate of 1,000 CDD (e.g., current-Chicago) and up. Column 7 of table 1 summarizes these findings at a more aggregate level. For each climate tercile and the United States overall, the mortality effect with future adaptation is smaller than without (column 6); i.e., adaptation reduces the assessed mortality effects of climate change. In each case, the magnitude of these differences is large, with the mortality effect shrinking by over 60% for the coolest third of ZIPs and actually becoming negative for the two other terciles and for the United States overall.

These findings indicate that climate change could reduce elderly mortality in the United States if places adapt to the future climates the way places are adapted to their current climates. That currently hot regions appear better adapted to heat than cooler places suggests that the benefits of adaptation exceed the cost within the domain of current climates. At the same time, there remains uncertainty about which adaptation technologies will be available in the future, how much they will cost to use, and how effective they will be at mitigating the effects of climates that are much hotter than any currently being experienced in the United States.

One aspect of adaptation where these concerns are particularly salient is migration. If the adaptation to hot temperatures we currently observe is driven by migration based on current climates, with individuals who are particularly vulnerable to heat moving to cooler climates, then their ability to continue to migrate in this way in the future depends on the continued availability of similarly desirable locations with cool climates in the future.

Even if climate change reduces mortality, it is important to note that this does not necessarily imply an improvement in elderly welfare. If adaptation to heat involves staying indoors and running the AC, then a decrease in utility from outdoor activities may offset some or all of the mortality benefit of adaptation relative to the current situation. In addition, warmer global temperatures may lead to changes in sea levels, agriculture, vector-borne disease prevalence, and other factors that may directly reduce human well-being.

4.4. Alternative Climate Projections

Our primary climate assessment results use climate change projections from the weighted meta-model under the RCP 8.5 emissions scenario. In appendix A.3, we show results for the RCP 4.5 emissions scenario, a mid-range projection under which emissions peak around 2,040 and then decline. Mortality effects under the RCP 4.5 scenario are qualitatively similar to, but more muted than, the effects under the RCP 8.5 scenario.

Appendix figures B.9b–B.9w and appendix tables B.2a–B.2d present separate prediction results for each of the 21 individual climate change models and an unweighted version of the meta-model. These results are broadly consistent with those of our main projections. Because the NEX-GDDP dataset contains a single realization of daily temperatures for each model, we are unable to consider uncertainty within a particular model that could arise due to uncertainty about appropriate choices of parameter values or realizations of stochastic quantities. However, the individual models predict end-of-century changes in average temperature ranging from about 5°F to 11.5°F. Comparing effects for the individual models provides insight into the range of possible outcomes in models that exhibit a relatively high or low degree of warming.

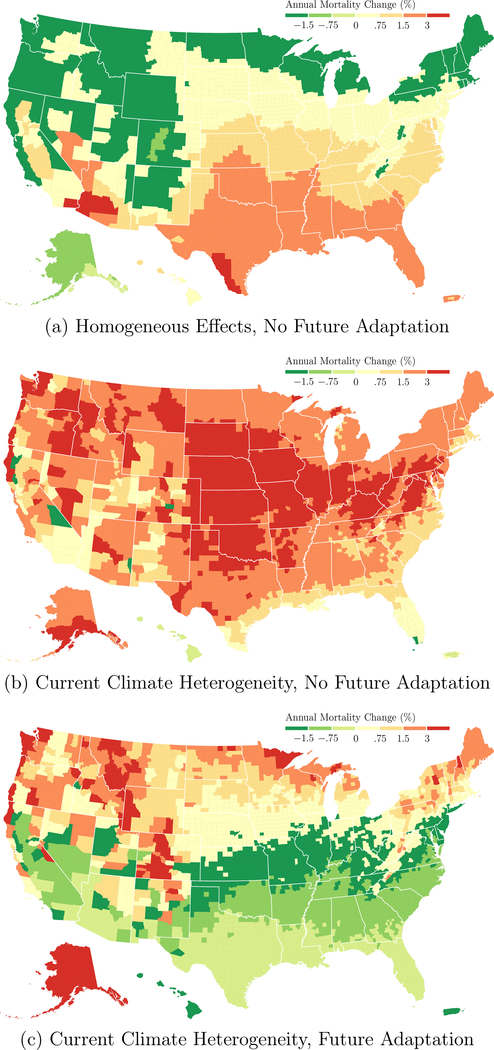
4.5. Geography of the Mortality Effects of Climate Change

Figure 6 maps the estimated mortality impact of end-of-century climate change under the three cases that we simulate, aggregated by county to facilitate comparison with prior studies. Panel A, which assumes homogeneous temperature effects, shows that the areas that are currently the hottest, the Deep South and Desert Southwest, will tend to suffer the largest mortality increases. Many of the coldest parts of the country, in the Northeast, Upper Midwest, and Northwest, are predicted to see a decrease in mortality due to the decrease in very cold days resulting from climate change. This geographic pattern mirrors the all-age mortality result of Hsiang et al. (2017) (see figure 2 of that paper), which also assumes homogeneous effects and no future adaptation.

Figure 6:

Geography of End-of-Century Climate Change Effects

Notes: The map shows county-level aggregates of the ZIP-code-level climate change impacts on annual mortality summarized in figure 5. Panel A reports climate effects under the assumption of homogeneous temperature effects. Panel B reports climate effects that allow for heterogeneous temperature effects based on current climate but do not allow for future adaptation. Panel C reports climate effects that incorporate both current heterogeneity and future adaptation.

Panel B of figure 6, which maps mortality predictions allowing for current climate heterogeneity but not future adaptation, reverses the geographic distribution of climate damages relative to assuming homogeneous temperature effects. Here, the mortality impacts are the smallest in the warmest regions of the country. The largest effects are expected to be felt in a swath across the Midwest and Central Plains, which expect a large increase in hot days and are currently poorly adapted to dealing with heat.

Panel C of figure 6 maps mortality predictions that incorporate both current heterogeneity and future adaptation to climate change. Here we see that adaptation has the potential to significantly moderate the impact of warming over much of the country, with the yellow and green areas exhibiting small positive to negative mortality effects. In isolation, these negative effects do not necessarily imply a benefit due to adaptation itself since some regions are projected to benefit from climate change even without additional adaptation in the future (panel B). However, many of the areas that are medium or dark green in panel C are also dark orange or red in panel B, indicating a large adaptation benefit. These regions would be expected to have the largest per-capita willingness to pay for adaptation to climate change.

5. Conclusion

This paper demonstrates the importance of accounting for regional heterogeneity and adaptation in predicting the impact of climate change on U.S. elderly mortality. Incorporating heterogeneous mortality effects of temperature into a climate change assessment substantially increases the estimated mortality impact of warming and changes which regions are likely to suffer the most. Allowing for adaptation yields estimated mortality impacts of climate change that are much lower than those calculated without adaptation and possibly even negative. Although we do not consider the future cost of adaptation, our results show that regions have chosen to engage in adaptation that significantly reduces elderly mortality given currently available technologies and current/historical costs, suggesting that there is significant ability to moderate the mortality impact of future warming even using technologies that are readily available today. The potential for future technological change to reduce the costs of adaptation may lower the mortality effect of climate change even further.

Our paper has focused on the mortality effects of climate change among the U.S. elderly. While the elderly are a relatively vulnerable group, the United States is a wealthy and geographically diverse country where the opportunity to adapt to climate change may be particularly high. Effects of climate change could differ for other populations, especially those in poorer or more geographically constrained countries (e.g., Bangladesh) with less opportunity to adapt to future climate change. Although we do not consider the nonelderly, other countries, or nonmortality outcomes, the methods we employ could be applied to estimating climate-change impacts in these environments as well.

Finally, it is important to recognize that our estimates of heterogeneity and adaptation are based on current experience and that our climate change assessments extrapolate from this experience to a future as simulated by climate models. However, the climate of the future may move outside of our present experience or even beyond what is projected by climate models. Because of this, there remains significant uncertainty about the future damages from climate change and the likelihood of large-scale, potentially catastrophic changes that is not fully incorporated into our model and could not be without quantifying these risks through additional assumptions. This uncertainty could easily dominate the statistical uncertainty expressed in the standard errors of our estimates. As Martin Weitzman wrote in this journal when deriving his “Dismal Theorem” and arguing in favor of a precautionary principle with respect to climate policy (Weitzman, 2009), “it is not possible to learn enough about the frequency of extreme tail events from finite samples alone to make [utility-based welfare calculations] independent of artificially imposed bounds on the extent of possibly ruinous disasters. … Climate-change economics generally—and the fatness of climate-sensitivity tails specifically—are prototype examples of this principle, because we are trying to extrapolate inductive knowledge far outside the range of limited past experience.”