Object displacement-sensitive visual neurons drive freezing in Drosophila

Summary

Visual systems are often equipped with neurons that detect small moving objects, which may represent prey, predators, or conspecifics. While the processing properties of those neurons have been studied in diverse organisms, links between the proposed algorithms and animal behaviors or circuit mechanisms remain elusive. Here, we have investigated behavioral function, computational algorithm, and neurochemical mechanisms of an object-selective neuron, LC11, in Drosophila. With genetic silencing and optogenetic activation, we show that LC11 is necessary for a visual object-induced stopping behavior in walking flies, a form of short-term freezing, and its activity can promote stopping. We propose a new quantitative model for small object selectivity based on the physiology and anatomy of LC11 and its inputs. The model accurately reproduces LC11 responses by pooling fast-adapting, tightly size-tuned inputs. Direct visualization of neurotransmitter inputs to LC11 confirmed the model conjectures about upstream processing. Our results demonstrate how adaptation can enhance selectivity for behaviorally relevant, dynamic visual features.

Graphical Abstract

eTOC Blurb

Tanaka and Clark show that Drosophila initiates brief freezing upon sighting small moving objects. This behavior depends on LC11 neurons, which show a high selectivity for translating objects that is not expected from existing models of object selective neurons. Spatial pooling of size-tuned, fast-adapting units explains the observed selectivity.

Introduction

Sighted animals rely on the ability to visually locate other animals, including prey, predators, and conspecifics, to successfully survive and reproduce. From a distance, other animals often appear as small moving objects. As a consequence, neurons that selectively respond to small objects have been found in diverse visual systems, ranging from vertebrate retinae [1–4] to insect brains [5–9], and animals exhibit diverse behavioral responses to small objects, possibly utilizing these neurons [3,5,10–13]. Detecting small moving objects is a challenging computational problem. Based on physiological recordings, different algorithmic architectures have been proposed to explain small object sensitive neurons in vertebrate retinae [1] and in insect brains [14]. However, it is not well understood how neural circuits implement such object detection algorithms or how they influence behavior. There are some object-sensitive neurons with well-established neurochemical mechanisms (e.g., glutamatergic amacrine cells in mice retina [4,15]) or with strong connections to behavioral functions (e.g., zebrafish AF7 retinal ganglion cells [3] and Drosophila LC10 cells [5]), but these neuron types lack quantitative, algorithmic descriptions of their computation. Since behavioral relevance, algorithm, and mechanisms of a neural circuit all constrain each other, it is important to address these three functional aspects together to understand the function of a circuit [16]. In this study, we aim to establish a link between behavioral function, computational algorithm, and circuit implementation of a small object sensitive neuron, using the fruit fly Drosophila as a model system, where sophisticated neurogenetic tools allow us to monitor and manipulate specific cell types [17,18].

In Drosophila’s visual system, two types of small object sensitive neurons have been studied: lobula columnar cell type 10 (LC10) [5] and cell type 11 (LC11) [9,19]. Lobula columnar (LC) cells are among approximately 40 known types of visual projection neurons (VPNs) in the Drosophila brain, which send information from the optic lobe, the center of visual computation in arthropod brains, to the central brain [19–22]. Unlike second- and third-order visual neurons that have relatively simple receptive field properties [23–25], VPNs are thought to encode more elaborate, behaviorally relevant visual features [19]. For instance, VPNs encode full-field optic flow [26,27] and looming stimuli [19,28]. However, it remains largely unknown how VPNs, especially columnar ones, achieve their feature selectivity algorithmically and mechanistically.

The neuron LC11 responds selectively to small (~10°) objects moving in any direction [9,19]. The links reported between LC11 activity and behavior are less clear than those of LC10, whose activation and silencing respectively results in robust induction and reduction of male courtship behaviors [5]. For instance, experiments that activated LC11 using optogenetic methods did not observe obvious behavioral phenotypes [19]. One study found that silencing LC11 in male flies compromised tracking of females [29], while another did not [5]. One study has also reported that silencing LC11 impairs a reduction of minute time-scale freezing in response to looming stimuli when flies are in groups [30]. Beyond connections to behavior, the algorithm and mechanism by which LC11 achieves selectivity to small moving objects remain largely unknown.

In the present study, we have investigated LC11’s role in behavior, its functional properties, and its neurochemical inputs. In particular, we wished to: (1) connect LC11 activity to behavior, (2) describe its response properties algorithmically, and (3) identify circuit and neurochemical mechanisms underlying that algorithm. First, we combine genetic silencing and activation of LC11 with single-fly psychophysics to show that LC11 is necessary for a previously-undocumented, short-timescale freezing behavior triggered by the presentation of small moving objects. Second, we show that LC11 differs critically from existing models of small object sensitive neurons because it responds selectively to translating small objects and not to localized flickers. Inspired by the observation that input neurons to LC11, T2 and T3, tile the broad dendritic arbor of LC11, we propose a computational model that features spatial pooling of fast-adapting, center-surround antagonistic units, which can qualitatively capture many features of the responses of LC11. Third, using fluorescent indicators of neurotransmitters and voltage, we test the mechanistic supposition of the model: that LC11 inherits size-tuning and flicker insensitivity from upstream neurons. Last, we test a potential extension to the model where nonlinear pooling enhances object displacements, but find that the outputs of LC11 reflect approximately linear summation of its inputs. Our results demonstrate how adaptation coupled with spatial pooling can enhance selectivity to translating small objects, which are relevant to diverse behaviors.

Results

Drosophila freezes briefly when presented with small visual objects

To identify behaviors that involve LC11, we first measured wild type flies’ walking responses to the presentation of small objects. Flies were tethered to the tips of surgical needles with UV cured epoxy, and placed on air-floated balls (Figure 1A). Translational and rotational velocities of the flies were inferred by monitoring the rotation of the balls [31,32]. Visual stimuli were presented from DLP projectors onto panoramic screens surrounding the flies [33]. For visual stimuli, we presented either 10° × 10° black squares or 10° × 106° black vertical bars against a gray background, which appeared in front of or to the sides of the flies, remained stationary for 1 second, then moved horizontally at 180°/s in either direction for 1/12 s, then remained stationary again for 1 second before disappearing (Figures 1B, S1A). We observed that when small objects were presented, average walking speed was reduced (Figures 1C, D, S1C), regardless of the position of the object. The decrease in mean walking speed was triggered by the appearance, movement, and disappearance of small objects, and its magnitude was larger than corresponding slowing caused by long, vertical bars. The recovery from the slowing caused by small objects was also slower than those caused by bars, and the decreased average walking speed lasted for more than a second after the offset of the small objects.

Figure 1. Flies initiate stopping upon detecting small objects.

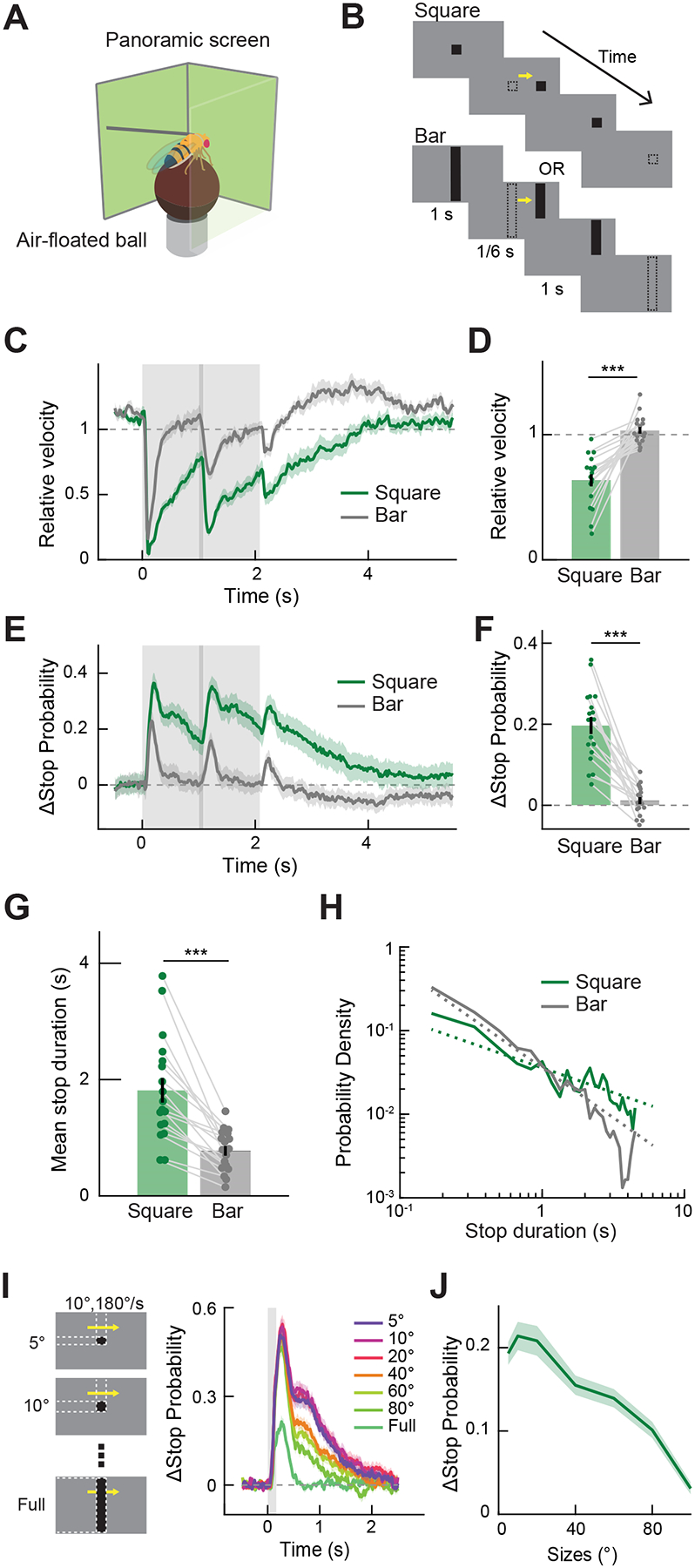
(A) Behavioral responses of flies to stimuli projected on the panoramic screen were measured by the rotation of an air-floated ball. (B) Visual stimuli, either a 10° × 10° square or a 10° × 106° bar, appeared and remained stationary for 1 s, moved at 180°/s for 1/12 s, then remained stationary for another second before disappearing. (C) Relative forward velocity (fold change) averaged across flies. The gray shaded region corresponds to the period during which stimuli were presented, and the area with a darker shade indicates when the stimuli were moving. (D) Relative forward velocity by stimulus type, averaged over 4 seconds after the stimulus onset. Data points from the same flies are connected with gray lines. (E) Change in instantaneous stop probability averaged across flies. (F) Change in instantaneous stop probability, averaged over 4 seconds after the stimulus onset. (G) Mean duration of stop triggered by the movement of the stimuli. (H) Log-log histogram of the duration of stop triggered by the movement of the stimuli. Dotted lines are the across-fly average of the linear functions fit to individual log-log histograms (See Figure S1E). (I) (left) As visual stimuli, 10° wide rectangular object with various heights were presented for 1/6 s, while moving at 180°/s. (right) Change in instantaneous stop probability triggered by moving objects with different sizes. (J) Change in instantaneous stop probability by object size, averaged over 2 seconds after the stimulus onset. Throughout the paper, time traces and bar graphs indicate averages across flies and error bars indicate one standard error of the mean (s. e. m.). (C - H) n = 18 flies. (I, J) n = 18 flies. *** p < 0.001 in Wilcoxon sign-rank test.

The average walking speed could be slower because all walking speeds have slowed, or because there is a larger fraction of flies in a stopped state [34,35]. To better understand the nature of the slowing, we plotted the probability of flies being stopped at every time point during the stimulus presentation (Figures 1E, F, S1D). The stop probability followed similar kinetics to the average walking speed, indicating that increased stop probability (or reduced frequency of walking bouts) contributed to the observed slowing. The duration of quiescence triggered by the appearance of small squares was longer compared to those triggered by bars (Figures 1G, H, S1E). We did not observe strong turning responses to either squares or bars (Figure S1B).

Next, we measured the size tuning of the observed freezing behavior by briefly presenting flies with moving objects of various sizes (Figure 1I). Brief presentations of moving objects again triggered an increase in stop probability with slow kinetics, especially when objects were small (Figure 1I, J). The time-averaged stop probability increase was largest when the object was 10° × 10°, and decreased as the size of the object increased to the full extent of the screen (Figure 1J).

LC11 is necessary for small object-induced freezing

We then asked whether LC11 is involved in the observed freezing behavior. We silenced the output of LC11 by expressing shibire^ts [36] under the control of a split-Gal4 tailored to selectively target LC11 [19]. We compared behavior of those LC11-silenced flies with genetic controls with either only UAS-shibire^ts or only split-Gal4. Silencing LC11 significantly reduced the stopping behavior, measured both in terms of average walking speed (Figures 2A, B) and stop probability (Figures 2C, D). However, LC11-silenced flies still showed residual stopping, suggesting either that silencing with shibire^ts was incomplete or that parallel, unsilenced pathways also contribute to this behavior. In addition to stimulus-triggered changes in stop probability, the baseline stop probability during the pre-stimulus period was also reduced in flies with LC11 silenced (Figure 2E). The duration of quiescence triggered by the movement of small objects was also significantly shorter in flies with LC11 silenced (Figures 2F, G, S1F). In contrast, slowing in response to bars was not reduced in LC11-silenced flies (Figures S1G, H). These results indicate that synaptic output from LC11 is necessary for flies to exhibit wild-type stopping in response to small objects.

Figure 2. LC11 is causally involved in object-induced slowing.

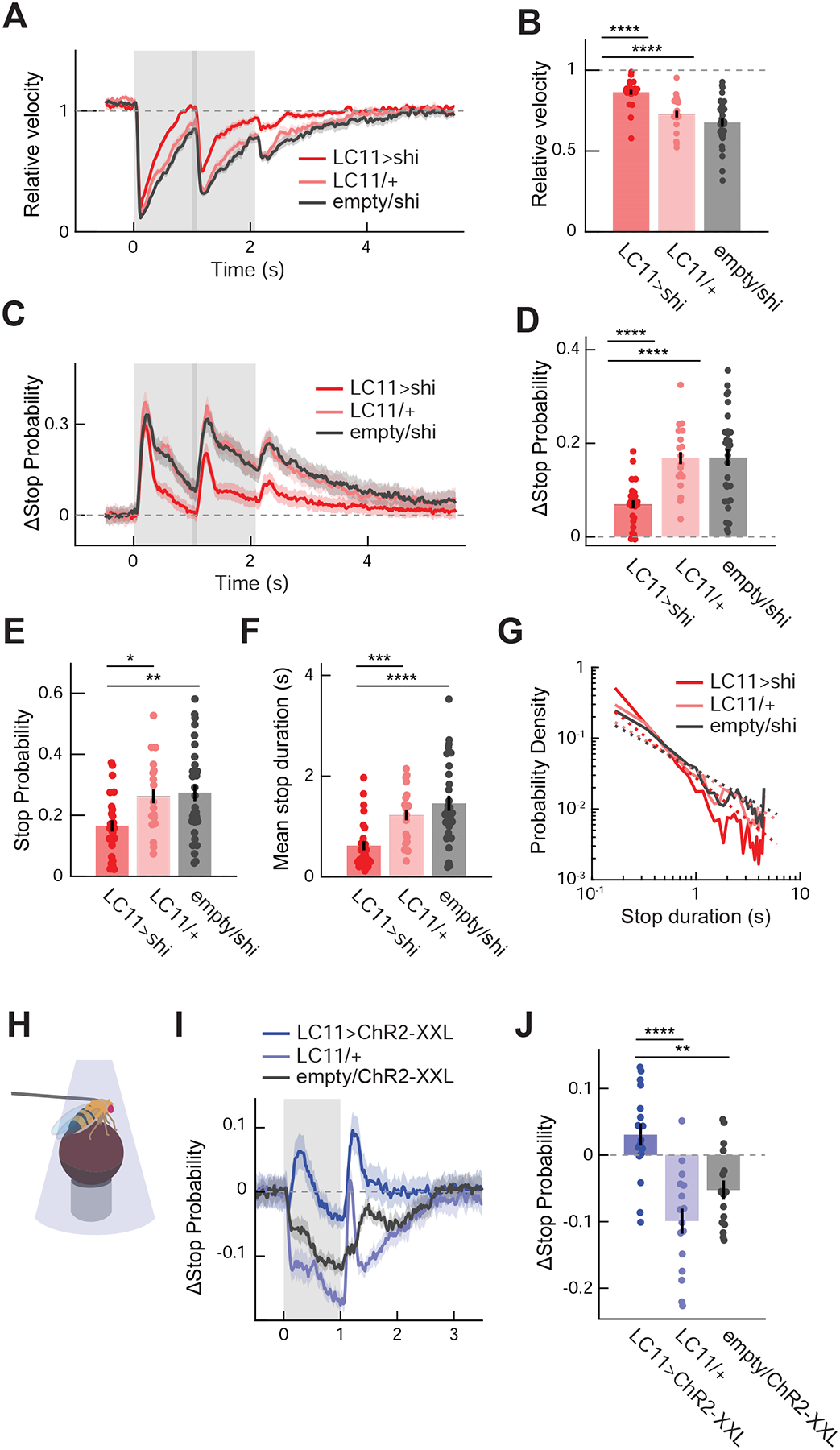
(A) Average relative walking speed of LC11-silenced flies in response to presentation of small squares, with corresponding Gal4 and UAS controls. The gray shaded region indicates the period during which stimuli were presented, and the area with a darker shade indicates when the stimuli were moving. (B) Relative walking speed of LC11-silenced and control flies, averaged over 4 seconds after the stimulus onset. (C) Change in instantaneous stop probability in LC11-silenced and control flies in response to presentation of small squares. (D) Time-averaged change in instantaneous stop probability in LC11-silenced and control flies. (E) Baseline stop probability during the pre-stimulus period by genotypes. (F) Mean duration of stop triggered by the movement of squares in LC11-silenced and control flies. (G) Log-log histogram of the duration of stop triggered by the motion of small squares by genotypes. Dotted lines are the across-fly average of the linear functions fit to individual log-log histograms (See Figure S1F). (H) A schematic of optogenetic activation experiment. (I) Average change in stop probability of flies expressing ChR2-XXL in LC11 and control flies. The gray shaded region indicates the period during which blue lights from the DLP projectors were applied to the fly. (J) Change in stop probability in response to optogenetic activation of LC11 in flies expressing ChR2-XXL and control flies, averaged over one second during the stimulation. (A – G) n = 25 flies (LC11/shi), 18 (LC11/+), 30 (empty/shi) (flies). (I, J) n = 17 flies (LC11>ChR2-XXL), 16 (LC11/+), 16 (empty/ChR2-XXL). * p<0.05; ** p<0.01; *** p < 0.001; **** p<0.0001 in Wilcoxon rank-sum test. See also Figure S2.

How specific is the mapping between LC11 and the small object-induced freezing? Conceivably, the observed decrease in stopping could simply be a manifestation of broad impairment in visual-motor capability of flies caused by the manipulation. A complementary possibility is that any deficiency in object- or motion-sensitive visual neurons can compromise the observed freezing. To test the first possibility, we compared a series of visual behaviors that involve either turning or walking speed modulation [5,10,31,37–40] between LC11-silenced flies and genetic controls. We found that none of the tested behaviors other than small object induced freezing was significantly affected by silencing LC11 (Figure S2). This shows that LC11 contributes specifically to the stopping behavior in response to small objects. Second, silencing another small object sensitive cell, LC10, along with several other visual and descending neurons, did not affect the freezing, indicating that the observed phenotype also depends on LC11 fairly specifically (Figures S3A–E). The exception was T4/T5, the first direction-selective neurons in the fly visual system (Figure S3B), which also affected walking speed modulation [31]. However, unlike LC11 (Figure S3F), the effect of T4/T5-silencing was dependent of position of the visual objects (Figure S3G), suggesting that LC11 and T4/T5 contribute to stopping through parallel pathways.

These experiments showed that LC11 is necessary for the wild-type object-induced stopping behavior (and not for other behaviors), but can the activity of LC11 cause the fly to stop? To test this, we measured flies’ translational velocity while optogenetically activating LC11. Optogenetic activation of LC11 using Chrimson [41] had previously failed to produce any observable phenotype [19], but we hypothesized that the null result could be because the inward current generated by Chrimson was insufficient to activate the LC11 neurons. We therefore optogenetically stimulated LC11 using ChR2-XXL [42], a variant of channelrhodopsin-2 that generates larger photocurrents. Blue light from a DLP projector was directly shone onto tethered flies and was flickered at 30Hz, while flies walked on the air-floated balls (Figure 2H) [33]. Applying the blue light induced a transient, significant increase in stop probability in flies whose LC11 expressed ChR2-XXL compared to corresponding genetic controls (Figures 2I, J). This indicates that activity in LC11 can promote stopping.

Last, we compared the size tuning of the freezing behavior (Figures 1I, J) with the physiological size tuning of LC11 neurons. To measure the size tuning of LC11 neurons, we presented visual stimuli on panoramic screens surrounding the fly [33] (Figure 3A), expressed the fluorescent calcium indicator GCaMP6f [43] in LC11, and imaged its neuronal activity with two-photon microscopy. LC11 has extensive dendrites in the lobula layers 2 and 3 (Lo2/3) and likely presynaptic neurites in lobula layer 5 (Lo5), and sends axon terminals to posterior ventrolateral protocerebrum (PVLP), where the terminals form an optic glomerulus [9,19,20]. We imaged the main dendritic stalks of LC11 between Lo5 and PVLP, where individual LC11 neurons are easily discernable (Figure 3B). To localize the receptive field (RF) center of the each LC11 cell, we first presented black, 10° × 10° squares translating vertically or horizontally at various azimuths or elevations, similar to previous experiments [9] (Figure 3C). Gaussian functions were fitted to the time-averaged calcium responses to identify the location and size of the RFs. The widths of the RF, measured as the full-width quarter-maximum (FWQM) of the fitted Gaussian [9], were 32.9 ± 2.0° vertically and 33.9 ± 1.2° horizontally (mean ± s.e.m.) (Figure 3D). These RF size estimates are larger than those previously reported [9], which is likely due to different imaging location (soma vs. dendritic stalks). In the following single-stalk experiments (Figures 3E–O), all visual stimuli were centered around the RF center estimated in this way. We presented a set of black moving objects with various sizes, identical to the stimuli used to measure size tuning of the stopping behavior (Figure 1I). Consistent with the stopping behavior, the response of LC11 was stronger when the object was small, peaking at about 20°, and the response decreased approximately linearly as the size of the object increased (Figure 3E, F). The size-tuning curve of LC11 neurons deviated from that of the stopping behavior at the smallest size of objects we tested.

Figure 3. Existing models of small object detection do not explain response properties of LC11.

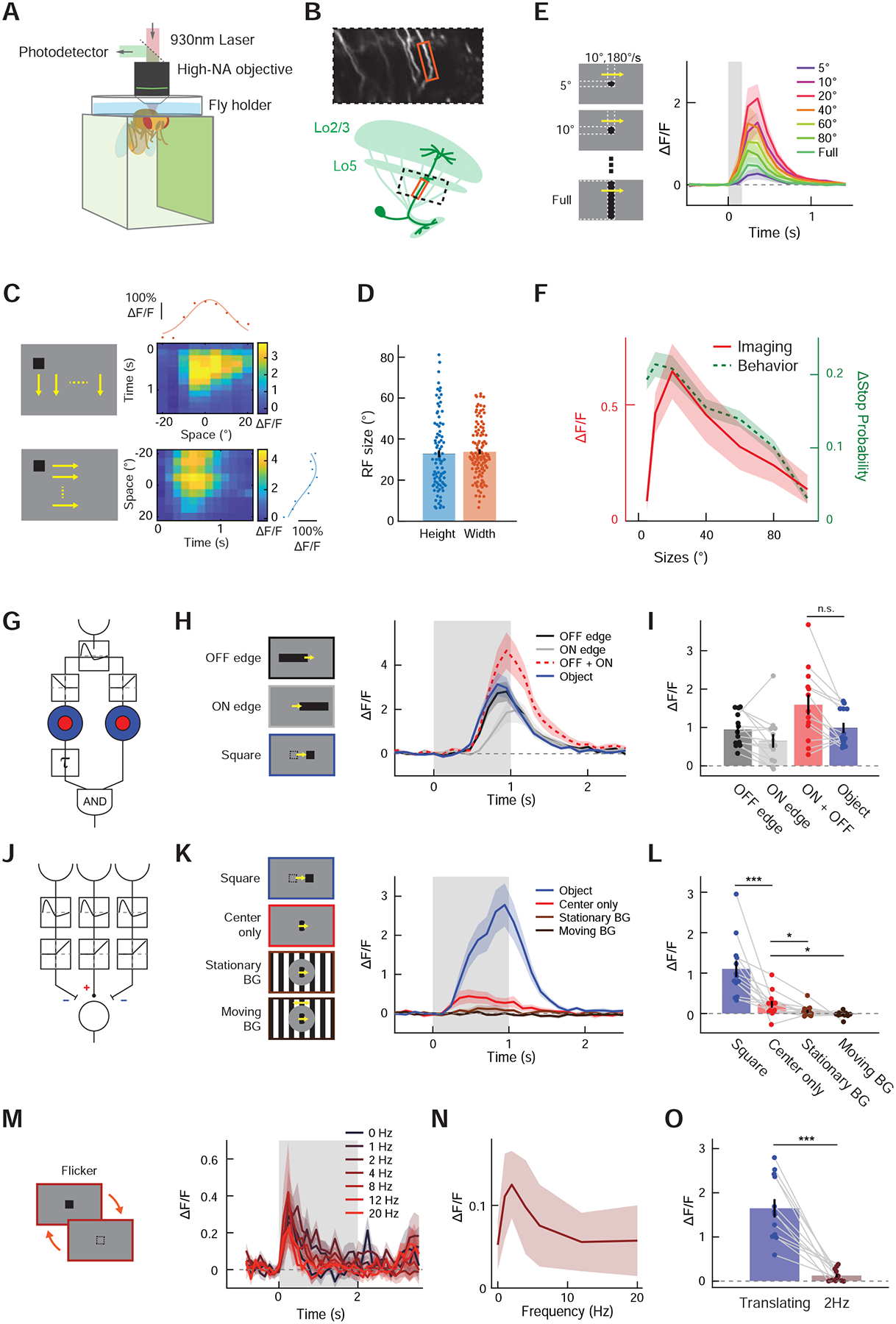
(A) Neuronal responses to visual stimuli projected on the panoramic screen were measured with two-photon microscopy. (B) (top) Frame from a typical recording during single-stalk LC11 calcium measurements. (bottom) Schematic showing the imaging region. At the region between proximal lobula and optic glomerulus, the main stalks of dendritic tree of individual LC11 cells are easily discernible. (C) (left) A single, 10° × 10° black square swept the visual field vertically (top) or horizontally (bottom) at different azimuths and elevations, with the resolution of 5°. (right) Calcium responses of a typical LC11 stalk to vertically (top) or horizontally (bottom) translating squares are shown as heatmaps. The calcium responses were averaged over time for each azimuth/elevation to generate horizontal/vertical spatial tuning curves of the stalk (red/blue dots), to which Gaussian functions were fitted (red/blue solid lines) to estimate the center and the width of each RF. (D) The size of horizontal and vertical RF, calculated as FWQM values of the Gaussian functions fitted to the spatial tuning curves. (E) (left) Stimuli used for size-tuning measurement, which were identical to those used in size-tuning measurement of stopping behavior (Figure 1I). (right) Average calcium responses of LC11 neurons to translating squares with different sizes. (F) Calcium response of LC11 to translating objects as the function of object size (red), averaged over 1 seconds after the stimulus onset. Overlaid on top is the size tuning curve of object-induced stopping behavior (green dotted, Figure 1J). (G) Schematic of STMD model [7,14]. The model detects small objects by computing coincidence between size-tuned ON signal with size-tuned and delayed OFF signal. See Figures S4A–D for expected responses of the STMD model to the stimuli used. (H) Average calcium responses of LC11 neurons to either translating decoupled edges or a black square, along with the simulated linear sum of ON- and OFF-edge responses. The STMD model predicts that the responses to an object (blue) is greater than the sum of responses to decoupled edges (red) (Figure S4B). (I) Calcium responses of LC11 to either a square or decoupled edges, averaged over 2 seconds after the stimulus onset. (J) Schematic of the OMS model [1], which features temporal high-pass filtering followed by a center-surround antagonism. See Figures S4A–D for expected responses of the OMS model to the stimuli used. (K) LC11’s calcium response to either a translating square or a localized, drifting square-wave grating, with or without stimuli in the background. The OMS model predicts that stimuli in the surround suppresses the response (red vs. light and dark brown), but does not predict the greater responses to translating objects than to localized gratings (blue vs. red) (Figure S4C). (L) Calcium responses of LC11 to translating squares and localized gratings, averaged over 2 seconds after the stimulus onset. (M) Average calcium responses of LC11 to flicker stimuli with various temporal frequencies. (N) Calcium responses of LC11 as a function of flicker frequency, averaged over 2 seconds after the stimulus onset. (O) Comparison of calcium responses of LC11 to a translating square and the same square flickering at 2 Hz. (C) n = 88, 115 cells for vertical and horizontal spatial tuning curves, respectively. (E) n = 13 cells. (H, I) n = 13 cells. (K, L) n = 13 cells. (M - O) n = 12 cells. n.s.: non-significant; * p<0.05; *** p < 0.001; **** p<0.0001 in Wilcoxon sign-rank test.

Existing models of object motion detection do not explain LC11’s displacement selectivity

Having established that LC11 is causally involved in object-induced freezing, we next sought to understand the algorithm that enables the selectivity of LC11 to small moving objects. We first asked whether existing models of non-direction selective, small object selective neurons could account for the response properties of LC11. One such model was proposed to explain small target motion detector (STMD) neurons in hoverfly and dragonfly brains [7,14].

In the STMD model (Figures 3G, S4A–D), photoreceptor inputs are first high-pass filtered over time to detect changes in luminance, creating a contrast signal. This signal is then split into two separate pathways that detect either contrast decrements (i.e., OFF contrasts) or increments (i.e., ON contrasts). Each pathway undergoes lateral inhibition to establish selectivity for small objects. Then, a downstream neuron detects coincidence between delayed OFF contrast signals and ON contrast signals. The intuition behind the delayed OFF-ON coincidence detection is as follows: When an object darker than the background traverses the RF of a neuron, the luminance within the RF first decreases and then increases. Therefore, by detecting an OFF contrast followed by an ON contrast localized to small neighborhood, a neuron could selectively respond to small moving objects. To test if LC11 employs an algorithm similar to the STMD model, we measured the response of LC11 to translating squares and to “decoupled edge” stimuli. In the decoupled edge stimuli, a 10° tall vertical edge, either gray-to-black or black-to-gray, traversed the RF of a LC11 neuron, providing isolated OFF or ON contrasts, while the squares provided OFF and ON contrasts in rapid succession (Figure 3H, left). If LC11 were detecting successive occurrences of OFF and ON contrasts, as in the STMD model, it should respond to decoupled ON or OFF edges only minimally, while responding to successive occurrences of OFF and ON edges vigorously (Figure S4B). LC11 responded positively to both decoupled edges, indicating that it is an ON-OFF cell. However, the sum of the responses to the two edges were statistically no different from its response to a translating square, arguing against the STMD model (Figures 3H, I).

Another model for small object sensitivity was proposed to explain object motion sensitive (OMS) retinal ganglion cells in vertebrate retinae [1] (Figures 3J, S4A–D). In the OMS model, photoreceptor inputs are first high-pass filtered in time to detect luminance changes, similar to the STMD model. Then, the signals are thresholded to detect only ON contrast. Lastly, a lateral inhibition step establishes selectivity for spatially localized inputs. In short, this model detects objects by responding to contrast changes at the RF center that are asynchronous from changes in the surround, or background. We tested whether the spatial antagonism hypothesized in the OMS model exists in LC11 by presenting small square stimuli as before, as well as localized square wave grating stimuli, which are commonly used in OMS retinal ganglion and amacrine cell literature [1,44] (Figure 3J). In these grating experiments, a full contrast drifting square wave grating (wavelength λ =20°, 60°/s) was presented to LC11 cells within a circular aperture with 20° diameter centered at the RF center. It was accompanied by the backgrounds of either mean gray, a full-contrast stationary square wave grating (λ =20°), or a moving square wave grating (λ =20°, 60°/s) (Figure 3K). The central aperture and background were separated by a 20°-thick annulus of mean gray to prevent background stimuli from affecting the RF center. The responses of LC11 to central gratings were significantly reduced by the presence of either stationary or moving gratings in the surround (Figures 3K, L), as predicted by the OMS model (Figure S4C). However, the response of LC11 to the square wave grating was far smaller than its response to translating squares even when there was no background, which is not expected from the OMS model (Figure S4C).

Why did LC11 strongly prefer translating squares over localized gratings? One possibility is that the size of the aperture (20° diameter) was already large enough to activate a putative inhibitory portion of the LC11 RF, whereas the 10° square was small enough to fit within the excitatory portion of the RF. To exclude this, we presented stationary black squares that flickered at various temporal frequencies, which had the identical size to the translating squares, at the RF center of LC11 neurons (Figure 3M, left). While previous studies showed that axon terminals of LC11 are insensitive to isolated changes in contrast [9,45], it is unknown how the cell responds to repetitive flicker, especially at the level of dendrites. Both STMD and OMS models should prefer such localized, repetitive flickers to translating squares, since local repetitive stimuli activate the models for longer durations (Figures S4C, D). However, similarly to the localized square wave gratings, flickering squares only weakly and transiently activated LC11 at all frequencies tested (Figures 3M, N). Time-averaged response of LC11 to flickering squares was only about one tenth of its response to translating squares with identical size, even at the peak frequency of 2 Hz (Figure 3O).

Pooling size-tuned, fast-adapting units captures response properties of LC11

To summarize the findings thus far, LC11 (1) does not enhance successive occurrences of OFF and ON contrasts, (2) is suppressed by motion and contrast in the background, (3) is only transiently and weakly responsive to local flickers, yet (4) is highly responsive to translating objects in any direction. One parsimonious model that could explain all the above observations is that LC11 pools the output of size-tuned, fast-adapting neurons over space (Figure 4A). Intuitively, such a model rejects large objects or full-field stimuli by the upstream center-surround antagonism. At the same time, local flickers are suppressed by fast presynaptic adaptation. As a result of these two properties, this model should be strongly activated only when small stimuli are sequentially presented at displaced locations within its RF, as observed experimentally. The proposal that LC11 receives size-tuned inputs is consistent with the recent finding that size-tuned columnar neurons, T2 and T3, are presynaptic to LC11 [45], which we have confirmed using independent methods (Figures S5–7). In addition, the proposed pooling motif agrees with the morphology of LC11’s primary dendrites, which span 8 ~ 15 columns (corresponding to 40 ~ 75° of visual space) [9,19]. Moreover, using a recently published connectome dataset [46], we found that T2 and T3 neurons tile the entirety of LC11 dendrites (Figures 4B, C, S7C–I), further supporting the pooling mechanism. The pooling motif could also explain the discrepancy between optimal object size (~20°) and LC11’s excitatory RF size, which extends well beyond 30° (Figures 3C, D, 6A). Henceforth, we call this model the displacement detector (DD) model.

Figure 4. Displacement detector (DD) model of small object motion detection.

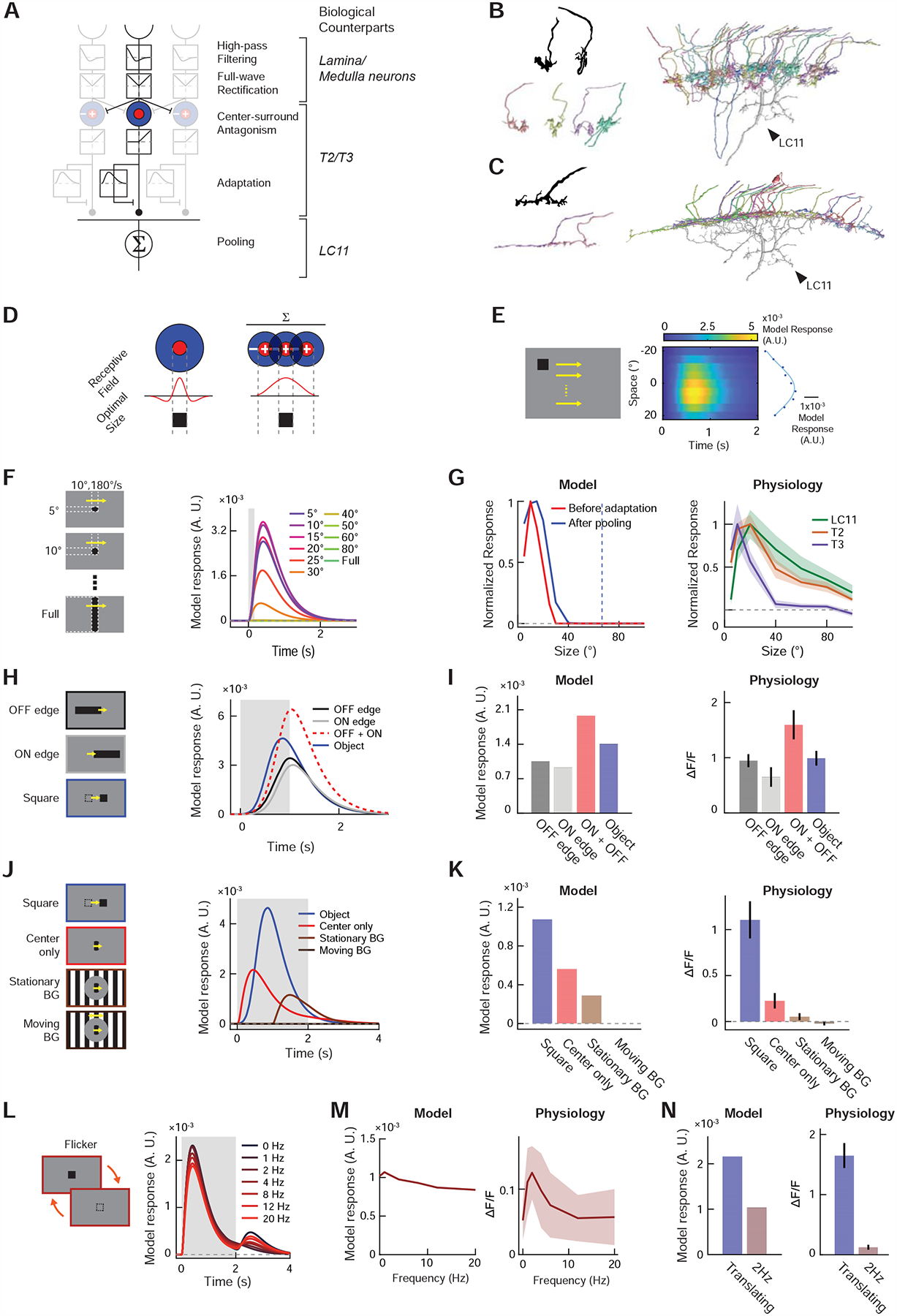
(A) The DD model consists of initial temporal high-pass filtering and full-wave rectification, center-surround antagonism, adaptation by divisive inhibition, and spatial pooling (see STAR Methods). Putative neuronal bases of each algorithmic step are indicated in italic. (B) (top left) Golgi-staining based camera lucida drawing of T3 terminals, from [22]. (bottom left) Putative T3 terminals found among presynaptic neurons of the particular LC11 neuron shown in Figure S7B. (right) The 33 putative T3 terminals we identified among the presynaptic cells of the LC11 shown in Figure S7B. See Table S1 for their unique identifiers in the hemibrain dataset. T3 appears to tile the entire dendritic arbor of LC11 in Lo2/3, supporting the proposed pooling motif in the DD model. (C) (top left) Golgi-staining based drawing of a T2 terminal, from [22]. (bottom left) Putative T2 terminals found among presynaptic neurons of the same LC11 neuron. See Table S1 for their unique identifiers in the hemibrain dataset. (right) The 23 putative T2 cells identified among presynaptic partners of the LC11 neuron. Similar to T3, T2 also appears to tile the entirety of the LC11 dendrite in Lo2/3. (D) In a neuron where center-surround antagonism establishes its size tuning, the size of excitatory receptive field and its optimal object size must be equal. Neurons that pool already size-tuned inputs can have larger receptive field sizes than the optimal object size. (E) Model responses (right) to horizontally translating squares (left) used for RF mapping in Figure 3C. Blue dots indicate time-averaged responses by each elevation, and the blue curve a Gaussian function fitted to the dots. (F) Model responses to objects with various sizes, as in Figure 3E. (G) (left) Size-tuning curves of the output unit (red) and input unit before adaptation (blue). The blue dotted line indicates the RF size, calculated as the FWQM value of the Gaussian function in (E). (right) Physiologically measured size-tuning curves of LC11 and its putative inputs, T2 and T3, replotted from Figures 3F, S6F, S5G, respectively. (H) Model responses to decoupled edge stimuli, along with simulated sum of its responses to ON and OFF edges, as in Figure 3H. (I) Time-averaged model responses to decoupled edge stimuli (left), along with corresponding physiological results (right), replotted from Figure 3I. (J) Model responses to localized gratings with or without stimuli in the background and a translating square, as in Figure 3K. (K) Time-averaged model responses to localized grating stimuli (left), along with corresponding physiological results (right), replotted from Figure 3L. (L) Model responses to stationary squares that flickered at different temporal frequencies, as in Figure 3M. (M) Temporal frequency tuning curve of the model (left) and LC11 cells (right). The latter was replotted from Figure 3N. (N) Comparison of model (left) and physiological responses (right) to either translating or flickering square at 2Hz. The latter was replotted from Figure 3O.

Figure 6. LC11 inherits size tuning and fast adaptation from upstream neurons.

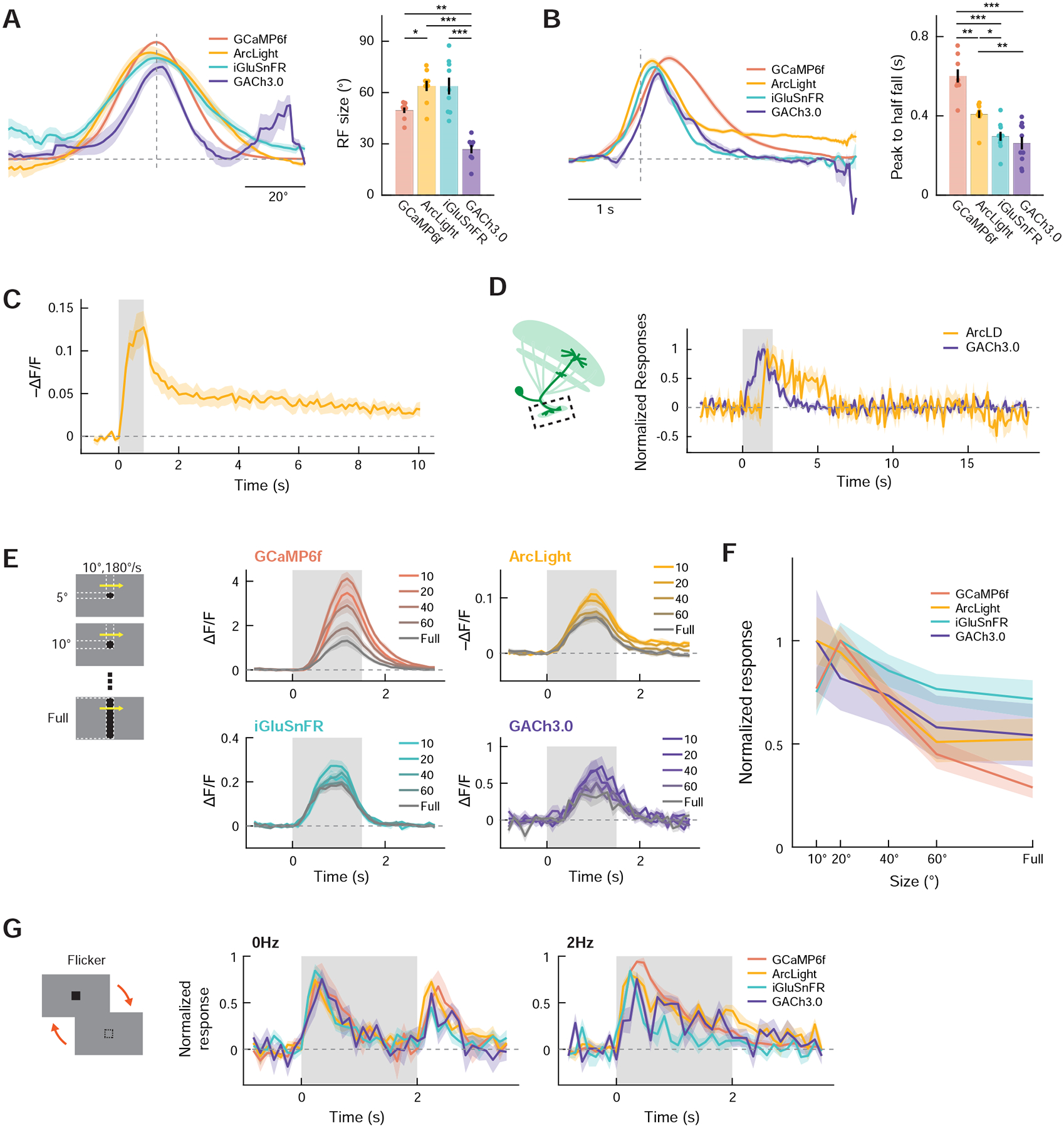
(A) Spatial receptive field of LC11 dendrites measured with either GCaMP6f (red), ArcLight (yellow), iGluSnFR (green), or GACh3.0 (violet). (left) Average normalized azimuthal spatial tuning curves by indicator type. The vertical dotted line indicates the estimated RF center and the horizontal dotted line zero response. (right) RF size by indicator type. (B) (left) Average normalized kinetics of LC11 to translating squares, measured with the four indicators. The vertical dotted line indicates the time the square hit the estimated RF center. (right) Peak-to-half-fall duration of the response kinetics, by indicator type. (C) Voltage response of LC11 distal dendrites to vertically translating squares traversing their RF center, measured with ArcLight. The sustained hyperpolarization lasts more than 10 seconds after the offset of the stimulus. (D) Normalized responses of LC11 glomerular axon terminals to translating squares, measured with either ArcLight (yellow) or GACh3.0 (violet). The axons also possess sustained dynamics of membrane voltage similar to those in dendrites, but the sustained dynamics were not reflected in neurochemical outputs. (E) Responses of LC11 dendrites to translating objects with different sizes, measured with the four indicators. Note that, since the responses of each ROI were not aligned to the timing of when the stimuli reached its RF, the average response kinetics do not represent the kinetics of each ROI. (F) Size tuning curve of LC11 dendrites by indicator type. Responses were averaged within the temporal window between 0 to 3 s after the stimulus onset. (G) Peak-normalized responses of LC11 dendrites to either a constant (left) or 2 Hz flickering (right) single black square. (A) n = 8 flies (GCaMP6f), 9 (ArcLight), 9 (iGluSnFR), 8 (GACh3.0). (B) n = 8 flies (GCaMP6f), 9 (ArcLight), 10 (iGluSnFR), 10 (GACh3.0). (C) n = 11 flies. (D) n = 10 flies (ArcLight), 10 (GACh3.0). (E, F) n = 14 (GCaMP6f), 14 (ArcLight), 13 (iGluSnFR), 10 (GACh3.0). (G) n = 8 flies (GCaMP6f), 12 (ArcLight), 11 (iGluSnFR), 10 (GACh3.0). * p < 0.05; ** p < 0.01; *** p<0.001; **** p<0.0001 in Wilcoxon rank-sum test after Bonferroni correction. Note that statistical tests were repeated for every indicator pair in (A) and (B), and non-significant pairs were not indicated for visual clarity.

We implemented a quantitative version of the DD model to test if the model reproduces the experimentally observed features: size tuning and suppression by background motion, flicker insensitivity, and decoupling of RF size from size tuning. In our model (Figures 4A, see STAR Methods), visual stimuli are first spatially down-sampled at the resolution of Drosophila ommatidia, and then temporally high-pass filtered to match typical medulla processing [23,24,47]. Next, the signals are full-wave rectified, as suggested by ON-OFF responses of LC11, and the signals are then spatially pooled with a center-surround antagonism to generate size tuning in the inputs to LC11 [45]. After another half-wave rectification, the signals undergo fast adaptation. The adaptation is modeled using a feedforward divisive inhibition motif, where input is divided by a temporally low-pass filtered version of the same input [49]. Lastly, the pooling by LC11 is modeled as low-pass spatial pooling of excitatory inputs and low-pass filtering in time (Figure S4F). With this model architecture fixed, we found that a range of parameters (size and time constants of filters and gains of divisive inhibition) could qualitatively reproduce physiological observations (Figures S4J–L).

The most characteristic response property of LC11 is that it is tuned to small objects of ~10–20°. Our model qualitatively captured the tight size tuning of LC11 in response to briefly presented moving objects with various sizes (Figures 4F, G, 3E, F, S4F). Because of the pooling motif, the optimal size of stimuli was smaller than the excitatory RF of the model (Figures 4D, E, G, S4L). Interestingly, the output of the model was tuned to larger sizes than the size-tuned input units (Figures 4G, S4J), similar to LC11 and T3. This is because an object slightly larger than the optimal size for the input units can activate more input units, albeit sub-optimally, resulting in overall larger activity after spatial pooling. Second, the DD model was not sensitive to a time-lag coincidence between contrast decrement and increment (Figures 4H, I), paralleling our physiological observation (Figures 3H, I). Third, the response of the model to localized gratings was completely abolished by moving gratings in the surround, and was also dampened by the appearance of stationary gratings in the surround (Figures 4J, K, 3K, L), which was due to strong lateral inhibition in the input units (Figure S4F). Lastly, the model response to localized stimuli, either drifting gratings or flickers, were transient and weaker than its response to translating squares (Figures 4L–N). This property is due to the fast adaptation in the model (Figure S4F). Both the relative response amplitudes and kinetics matched well with the physiological observations (Figures 3M–O). In several cases, the model responses appear less selective than corresponding calcium imaging results (e.g., Figures 4K, M, N). This could be partly due to supralinearity in the voltage-to-calcium transformation and in calcium binding of GCaMP6f [50], which we did not model explicitly. Taken together, these simulation results indicate that the proposed adaptation-and-pooling based architecture of the DD model is sufficient to explain many physiological response properties of LC11.

LC11 inherits size-tuning and fast-adaptation from upstream neurons

The DD model, based on the results of calcium imaging and the anatomy of LC11, suggests that excitatory inputs into LC11 are already size-tuned and fast-adapting. To more directly test these aspects of the model, we characterized fast neurochemical inputs to LC11 and intracellular signal transformation with LC11 using genetically-encoded fluorescent sensors of fast neurotransmitters (acetylcholine: GACh3.0 [51]; glutamate: iGluSnFR [52]; GABA: iGABASnFR [53]) and membrane voltage (ArcLight [54]). To first establish the feasibility of using these sensors in LC11, we presented flies with a battery of stimuli while imaging LC11’s distal-most dendrites at lobula layer 2/3 (Lo2/3) (Figure 5A) using the four fluorescent sensors in addition to GCaMP6f. The battery consisted of translating bars, full-field drifting gratings, and full-field flashes (Figure 5B). We observed that the acetylcholine indicator, glutamate indicator, voltage indicator, and calcium indicator all showed similar patterns of responses to the battery of stimuli. They responded most strongly to translating bars and less strongly to drifting square wave gratings, while responses to full-field flashes were non-detectable except in GABA and membrane voltage signals (Figures 5C, E–G). Interestingly, the voltage response to translating bars had a sustained component that lasted for more than a second, which was not observed in any other modalities. In contrast, the GABA indicator responded broadly to the all types of stimuli with a similar amplitude (Figure 5D). The GABA indicator responses to flashes could be reflected in the transient membrane hyperpolarization caused by flashes (Figure 5F).

Figure 5. Calcium, voltage, and neurochemical imaging in LC11 dendrites.

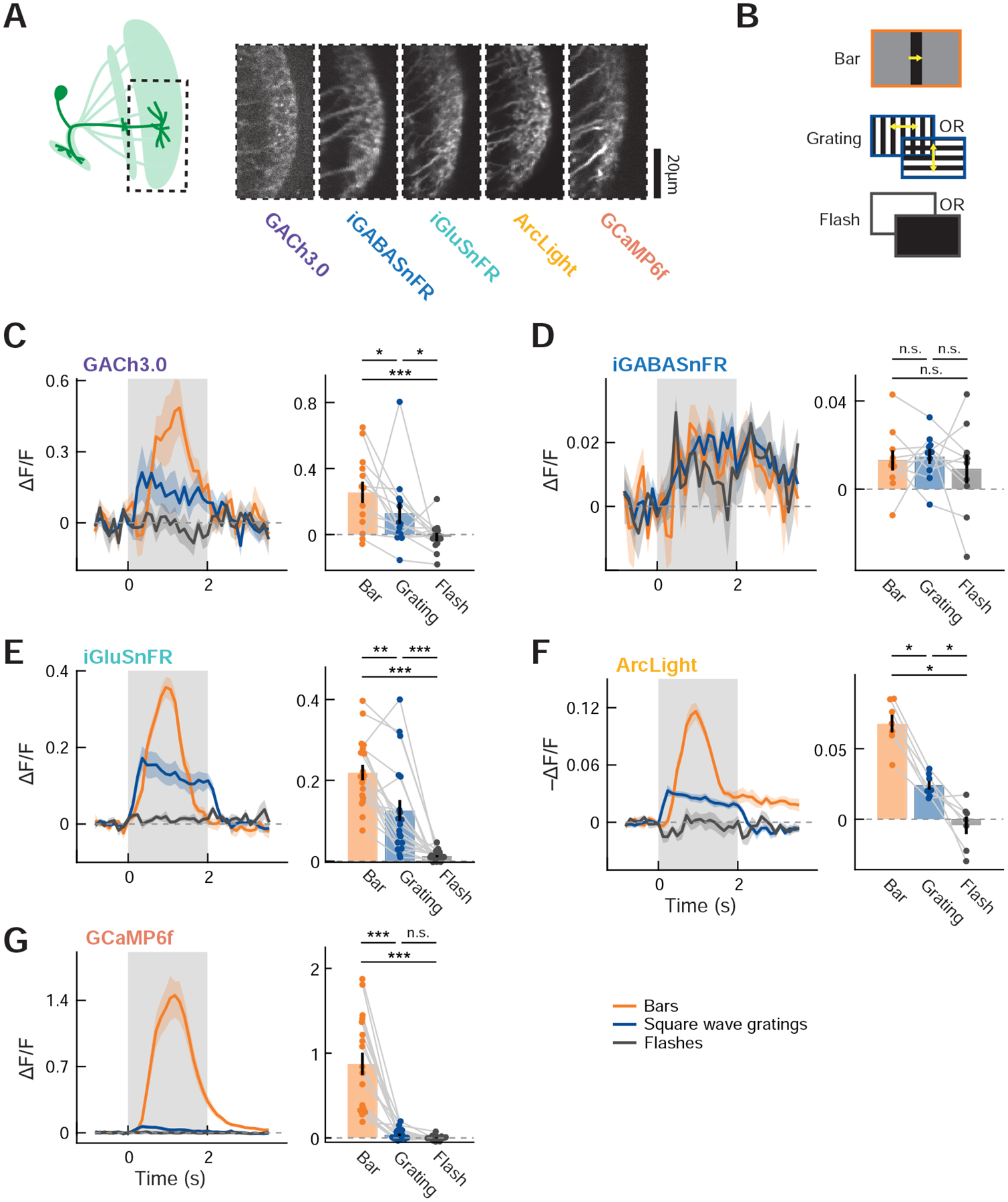
(A) (left) Distal dendrites of LC11 in Lo2/3 were imaged using the five indicators. (right) Frames from typical dendritic recordings using the five indicators. (B) Schematics of visual stimuli used. Bars moved either rightward or leftward, and the square wave grating moved in four cardinal directions. The responses to different directions of bar/grating and polarities of flash were averaged. (C – G) (left) Average responses of LC11 to the three types of stimuli, measured with (C) GACh3.0, (D) iGABASnFR, (E) iGluSnFR, (F) ArcLight, or (G) GCaMP6f. Note that since we did not align the responses according to the RF of each ROI, the kinetics of the responses to moving bars shown here are not representative of the kinetics of individual ROIs’ responses. (right) Time-averaged responses of LC11 to the three types of stimuli, measured with the five indicators. Temporal averaging windows were 0 to 1.5 s for bars, and 0 to 2 s for the rest. The data points from the same flies are connected with gray lines. (C) n = 13 flies, (D) n = 10 flies, (E) n = 19 flies, (F) n = 7 flies, and (G) n = 18 flies. n.s.: non-significant; * p<0.05; ** p < 0.01; *** p<0.001 in Wilcoxon sign-rank test.

We next characterized spatiotemporal RF structures of cholinergic and glutamatergic inputs as well as membrane voltage and calcium concentration. To this end, we presented a 10° × 10° black square translating horizontally or vertically at various elevations and azimuths. For each dendritic region-of-interest (ROI), we first obtained vertical and horizontal spatial tuning curves by time-averaging the responses to squares by elevations and azimuths, to which we fitted spatial Gaussian functions. The average sizes of RFs ranged between 30° and 60°, with cholinergic inputs being narrowest and membrane voltage and glutamatergic input being broadest (GCaMP6f: 50.0 ± 2.7°; ArcLight: 63.9 ± 3.2°; iGluSnFR 63.8 ± 5.2°; GACh3.0: 26.9 ± 2.7°) (Figure 6A). None of the four spatial tuning curves had obvious inhibitory surround that could account for LC11’s size tuning, consistent with the DD model supposition that size tuning is established in upstream neurons. Each ROI’s response to translating squares was then aligned to the time when the squares crossed its RF center, and ROIs were averaged (Figure 6B). The duration between when the response peaked and when it decayed back to the half-peak value (half-fall time) was calculated as a summary measure of response kinetics (Figure 6B). The half-fall time measured with the four indicators ranged between 300 and 600 ms, where cholinergic and glutamatergic signals were fastest and the calcium signal slowest (GCaMP6f: 530 ± 25 ms; ArcLight: 409 ± 20 ms; iGluSnFR: 297 ± 23 ms; GACh3.0: 262 ± 32 ms). These values are longer than the decay time constants of the fluorescent sensors [43,51,52,54]. We again found that membrane voltage stayed continuously depolarized at about 25% of its peak depolarization (Figure 6B). In a separate experiment, we confirmed that, surprisingly, this sustained depolarization did not decay back to the original level over 10 seconds (Figure 6C). The sustained dynamics of membrane voltage was also observed at axon terminals in the optic glomerulus, but was not reflected in synaptic output (Figure 6D).

Next, we measured the size tuning of cholinergic and glutamatergic dendritic signals, as well as membrane voltage and the calcium signals in the dendrites (Figures 6E, F). We presented flies with horizontally translating objects with various heights at different elevations. For each ROI, the vertical center of its RF was determined as the elevation at which 10° × 10° squares gave rise to maximum time-averaged responses, and its size tuning curve was calculated as the time-averaged responses to objects with different sizes that traversed the estimated vertical RF center. Responses measured with the four indicators were all size-tuned, with peak responses at 10° to 20° object height. This observation is consistent with the model’s conjecture that the size tuning of LC11 is established in circuitry upstream of LC11.

Lastly, we tested whether fast adaptation to flickering stimuli already exists in LC11’s input (Figure 6G). We presented flies with 10° × 10° black squares at various locations that were either sustained or flickered at 2 Hz. The RF center of each dendritic ROI was again estimated post hoc, and the time courses of responses to the squares presented closest to the estimated RF center was averaged across ROIs within each fly. The resulting response kinetics were strikingly similar across the indicators: the four signals all responded transiently but slowly to both the onset and the offset of the sustained square, whereas they all quickly adapted to 2 Hz flicker. This observation confirmed the model’s hypothesis that the fast adaptation to flicker happens upstream of LC11.

Synaptic output of LC11 reflects linear summation

A reasonable extension to the DD model would be that LC11 supralinearly summates successive occurrences of stimuli at neighboring points in space (Figure 7A). Such a nonlinearity on top of fast adaptation of LC11 inputs would further increase the cell’s selectivity to translating objects. This sort of nonlinear enhancement of spatially offset, successive inputs is a key computation in direction-selective motion detection and underlies popular models of motion detection [55,56]. Enhanced responses to successive stimuli have been observed in calcium signals in visual direction-selective neurons in Drosophila [32,50,57,58]. To test this possibility, we presented flies with a series of 10° × 10° squares either separately or as a spatiotemporally continuous sequence (i.e., apparent motion) (Figure 7B). If LC11 were sensitive to successive occurrence of displaced inputs, its response to the apparent motion stimulus should be greater than the linear sum of its responses to separately presented squares (Figure 7C). We first imaged LC11’s responses to the apparent motion stimuli in its distal dendrites (Lo2/3) using the four indicators (GCaMP6f, ArcLight, iGluSnFR, and GACh3.0). There, we observed apparent motion responses significantly greater than the linear expectation from component responses only in GCaMP6f, but not in other indicators, raising a possibility that nonlinear voltage-to-calcium transformation could be implementing supralinearity over space and time in LC11 (Figure 7D). This voltage-to-calcium transformation has been suggested as an origin of direction-selectivity in motion sensing neurons in Drosophila [50,59–61]. We also found that the long-lasting depolarization measured with ArcLight was only present in the apparent motion response, but not in the linear expectation from separately presented squares (Figure 7D).

Figure 7. Sensitivity of LC11 to sequential inputs over space.

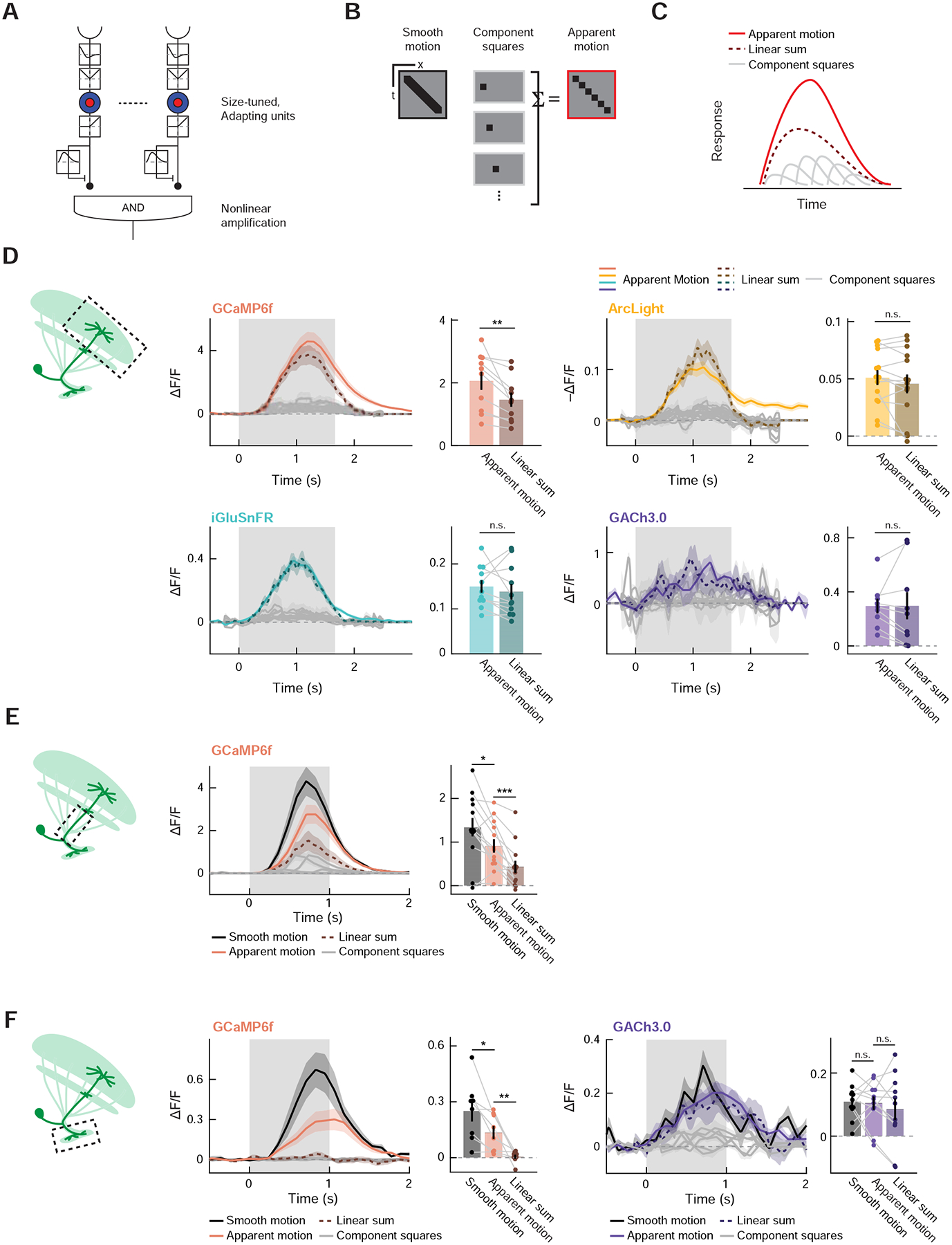
(A) An extended DD model with nonlinear amplification, instead of the linear spatial pooling proposed in Figure 4A. (B) To test whether LC11 has nonlinear sensitivity to sequential inputs spanning space and time, we presented a spatially contiguous set of squares, either separately (middle) or in a spatiotemporal sequence, namely apparent motion (right). In some experiments, we also presented a velocity-matched, smoothly translating square as a reference. (C) The extended DD model with nonlinear spatial amplification detection predicts that LC11’s response to the apparent motion (red) should be greater than the sum of its responses to the individually presented component squares (dotted dark red). (D) Responses of distal dendrites of LC11 to apparent motion stimuli measured with GCaMP6f, ArcLight, iGluSnFR, and GACh3.0, either over time (line plots) or time-averaged between 0 and 2.5 s after the stimulus onset (bar graphs). Only calcium responses showed a statistically significant difference between the time-averaged apparent motion response and the sum of component square responses. (E) Response of LC11 stalks to apparent motion stimuli, measured with GCaMP6f. The temporal averaging window was between 0 and 2 s after the stimulus onset. (F) Response of LC11 axon terminals to apparent motion stimuli, measured with either GCaMP6f or GACh3.0. The temporal averaging window was between 0 and 2 s after the stimulus onset. (D) n = 10 flies (GCaMP6f), 14 (ArcLight), 11 (iGluSnFR), 9 (GACh3.0). (E) n = 13 cells (GCaMP6f). (F) n = 8 flies (GCaMp6f), 11 (GACh3.0). n.s. non-significant (p > 0.05); * p<0.05; ** p<0.01; *** p < 0.001; **** p<0.0001 in Wilcoxon sign-rank test. See also Figures S4–S6.

We then asked whether the same response nonlinearity could be observed throughout different sub-cellular compartments of LC11. When we repeated the same apparent motion presentation while imaging the main dendritic stalks (Figure 7E) or glomerular axon terminals (Figure 7F) with GCaMP6f, we again observed significantly greater responses to apparent motion stimuli than to linear expectations. Qualitatively, it appeared that the magnitude of nonlinearity increases as the signals are transmitted from dendrites to axons, while the absolute amplitude of calcium responses was increasingly dampened (Figures 7D–F). This reduction of calcium response amplitude between dendrites and axons is similar to findings in third order neurons in the fly visual system [62].

Last, we tested if the same nonlinearity is present in the synaptic output of LC11. Since LC11 has been shown to be ChAT positive [45], we used GACh3.0 to monitor its synaptic outputs at the optic glomerulus. Surprisingly, we found no significant difference between cholinergic responses of LC11 to apparent motion stimuli and the linear expectation based on separately presented squares. This was true in part because we observe acetylcholine signals in response to component squares even when calcium responses were almost undetectable (Figure 7F). The lack of nonlinearity in the cholinergic outputs, combined with the observation that the stimuli which evoked no detectable calcium response could drive synaptic release, suggests that the apparent nonlinearity in calcium signals is likely due to nonlinearities in GCaMP6f fluorescence, rather than nonlinearities in the voltage to calcium transformation. Note that muscarinic cholinergic receptor on which GACh is based [51] has only a single acetylcholine binding site and thus is approximately linear [63], while GCaMP6f has Hill-coefficient of ~2.7 [64]. Intracellular dampening of voltage deflection [62] combined with the nonlinear activation curve of GCaMP6f [64] would also parsimoniously explain the gradual increase of the nonlinearity within LC11 from dendrites to axons. Overall, these results suggest that LC11 linearly pools successive inputs, and its strong selectivity for small, moving objects arises from surround antagonism and fast adaptation in its inputs.

Discussion

By silencing, activating, and recording from LC11, we have demonstrated that it is necessary for a newly-documented short-timescale freezing behavior in Drosophila induced by small objects, and that its activity promotes stopping (Figures 1, 2, 3A–F). The response properties of LC11 deviated critically from existing models of object-selective neurons in vertebrates and insects because LC11 distinguished translating small objects from localized flickers (Figure 3). A simple algorithmic model for the neuron was inspired by the anatomical connectivity between putative upstream neurons and LC11, as well as the discrepancy between LC11’s excitatory RF size and its preferred object size. In this displacement detection (DD) model, which captured response properties of LC11 well, outputs of size-tuned, fast-adapting neurons are pooled over space (Figure 4). We used fluorescent sensors of calcium, membrane voltage, and neurotransmitters to track signal transformations in LC11 from input to output (Figure 5), revealing that the size tuning and fast adaptation to flicker are established in circuitry upstream to LC11 (Figure 6), in agreement with the proposed model. Last, we showed integration of spatially offset inputs by LC11 appears quite linear, unlike integration in direction-selective cells (Figure 7).

Ethological relevance of object-induced freezing

What is the ethological function of the observed object-induced freezing? It is hard to infer function because freezing can be a part of diverse behavioral programs with different goals. Moreover, different ethologically relevant entities, like predators and conspecifics, can all appear as small moving objects. This makes it difficult to draw direct connections, as one might for instance between escape behaviors and looming stimuli [65,66]. Indeed, flies are known to avoid or approach small object depending on their behavioral or olfactory contexts [10,12,67]. Previous studies have revealed a variety of cases in which flies slow or freeze. For example, flies slow to stabilize their walking speed in response to translational optic flow [31], but also slow as they navigate to odor sources [68]. Flies also stop walking to avoid colliding with conspecifics [37], but also to initiate long lasting freezing in response to looming stimuli, presumably to avoid detection by predators [69]. Our results do not exclude that LC11 activity represents either predators or conspecifics. It is potentially informative that LC11’s activity is significantly suppressed by stationary contrast in the background (Figures 3K, L). This observation favors the hypothesis that LC11 is tuned to objects moving against a uniform background, such as flying predators against the sky, as seen by walking flies. From this perspective, the freezing could be interpreted as a defensive behavior to avoid detection by a non-approaching predator. Translating aerial objects trigger defensive freezing behavior in rodents, whereas looming triggers rapid escape behavior [11]. Given that flies also respond to looming stimuli with rapid escape [65], it is appealing to think that flies and rodents developed parallel flight/freeze strategies to different visual features.

Circuitry surrounding LC11

How is the activity of LC11 translated into the stopping behavior through the downstream circuitry? A large-scale characterization of descending neurons in Drosophila identified only a single type of descending neuron, DNp35, whose dendrites overlap with the optic glomerulus projections of LC11 [70]. However, we did not observe any significant reduction of the freezing by silencing DNp35 (Figure S2L). We also saw no effect of silencing DNp09, a descending neuron that is implicated in loom induced freezing [69] and forward walking [29] and that is functionally connected to LC11 [29] (Figure S2K). These results imply that, unlike some VPNs that are directly presynaptic to descending neurons (e.g., LPLC2/LC4 to the giant fiber motor neuron [71]), outputs of LC11 undergo more nuanced computation in downstream circuitry before reaching command neurons. One likely downstream pathway that mediates the observed stopping is glomerular interneurons. Dipteran optic glomeruli are connected by local interneurons [72], and indeed we found that the majority of output synapses of LC11 are onto those interneurons (Figures S7J–N), including ones that resembled previously documented small object sensitive neurons (PDL09z, Figure S7K) [48].

While silencing LC11 resulted in robust decreases in object-induced stopping, LC11-silenced flies still showed size-tuned slowing/stopping in response to objects. This observation points to the existence of parallel visual pathways contributing to the small object induced freezing. Consistent with this hypothesis, we observed that silencing T4 and T5, which are thought not to provide inputs into LC11 [45], significantly reduced freezing. The effect silencing T4 and T5 differed from silencing LC11 because the phenotype depended stimulus position (Figure S3G), further suggesting that T4 and T5 contribute to the object-induced freezing in a LC11-independent manner, probably through columnar VPNs innervating lobula plate (for instance, LPLCs, LLPCs, LPCs). Another hypothesis is that other small object-sensitive LCs that have not been studied in detail (for instance, LC26 [73]) contribute to the object-induced freezing. Since LC11 has presynaptic terminals within lobula [9,19], it is also possible that LC11 signals are transmitted to the central brain through other LC types, similar to the LPLC2-LC4 pair [71].

In addition to the short-timescale freezing we studied here, LC11 has been suggested to mediate long-term reduction of loom-induced freezing when it is among conspecifics, constituting a “safety in numbers” phenomenon [30]. The fact that LC11 can trigger superficially opposite behaviors in different time scales — freezing on the timescale of seconds, reduction of freezing on the timescale of minutes — supports the idea that the outputs of LC11 are processed by divergent downstream circuits and may be strongly context dependent. Paralleling the multiple timescales of LC11 dependent behaviors, we found the activity of LC11 itself has two timescales: immediate object responses and long-lasting subthreshold depolarization (Figures 6B–D). Previous studies found that the LC11-dependent freezing reduction depended on the total amount of object motion a fly experienced, rather than just the number of objects [30]. This observation interestingly agrees with our finding that the long-lasting depolarization requires translation of objects (Figure 7D), and supports the possibility that the two timescales in LC11 activity correspond to the two timescales in LC11-dependent behaviors.

Neurochemical basis of the LC11 receptive field

Using fluorescent sensors of neurotransmitters, we found that LC11 receives input from all three fast neurotransmitters at the same layer (Figure 5). Our model of LC11 activity only posits excitatory input into LC11, which likely corresponds to the cholinergic input. Thus, the functions of the other two inputs, GABA and glutamate, remain unclear. Previous work showed that bath application of picrotoxin, a GABA_A receptor antagonist, abolished LC11’s sensitivity to small objects and made it sensitive to large bars or full-field motion [9]. The tuning of the excitatory inputs into LC11 (Figures 6E, F) suggests that at least some of the previously observed loss of size-tuning reflected effects of picrotoxin on upstream neurons, rather than LC11 itself. This is in agreement with results showing that conditional knockout of GABA_A receptors from LC11 does not abolish its size tuning [45]. At the same time, we also identified direct GABAergic release onto LC11, which was broadly sensitive to full-field stimuli (Figure 5D). Although our DD model suppressed LC11 activity by full-field motion without invoking direct inhibition onto LC11 (Figure 4K), it seems likely that the observed GABAergic inputs function as an additional mechanism to reject full-field changes.

The most puzzling among the three neurochemical inputs we observed is the glutamatergic release onto LC11. The observed iGluSnFR signal closely paralleled both the cholinergic input and calcium signals in T2/T3 in terms of its size-tuning and adaptation dynamics (Figures 5C, E, 6E–G). One concern is the potential for crosstalk between cholinergic signaling and iGluSnFR. To our knowledge, the specificity of iGluSnFR has not been directly tested in flies in vivo, but in vitro iGluSnFR does not bind any neurotransmitter except glutamate [52]. In addition, the iGluSnFR signal differed from the cholinergic input and from T2 and T3 by its larger spatial receptive field, further suggesting iGluSnFR and GACh3.0 signals originated from different sources. A simple hypothesis to reconcile these observations is that there is a glutamatergic neuron that pools T2/T3 outputs and innervates LC11. One functional interpretation of this putative glutamatergic input is that it works as a redundant excitatory input into LC11 along with the cholinergic one. However, glutamatergic transmission in Drosophila sensory systems appears most frequently to be inhibitory [26,74–78], though visual neurons generically express both inhibitory and excitatory glutamate receptors [79]. If glutamate is indeed inhibitory to LC11, its function would be less intuitive: why would an object-sensitive cell receive object-sensitive inhibition? In this scenario, glutamate could be sharpening responses of LC11 by providing broad, slow inhibition following excitation. Alternatively, it could work as an additional mechanism to suppress LC11 activity when there are multiple objects in its RF [9].

T2 and T3 have complex spatiotemporal response properties

Using synaptic labeling, optogenetics, and connectomic analysis, we confirmed connectivity from T2/T3 to LC11 (Figures 4B, C, S5–7) [45], although silencing of T3 did not have similar effects on object-induced stopping to silencing of LC11 (Figure S3C). This could be due either to the relatively sparse expression of the T3 driver or to redundancy in excitatory LC11 inputs, likely with T2. Unlike LC11, the RF sizes of T2 and T3 matched their peak object size, implying that they employ strong center-surround antagonism to become size-tuned. The response properties of T2 and T3—including tight size tuning, ON-OFF responses, and fast-adaptation—are closer in complexity to T4 and T5 neurons than to most known medulla-intrinsic or trans-medullar neurons. It will be of interest to investigate the mechanisms underlying these complex properties of T2/T3 neurons.

One observation not predicted by the DD model is that T3 responds more vigorously to translating objects than to local flickers (Figure S5H). This property was specific to T3, and was not observed in T2 (Figure S6G). In calcium signals in LC11, LC11 responds slightly more to smoothly translating objects compared to velocity-matched, discretized apparent motion stimuli (Figures 7E, F), a property could be explained by T3’s motion sensitivity. Since the RF size of T3 was small (~10°), it seems unlikely that T3, like LC11, achieves its displacement sensitivity by spatial pooling. One hypothesis is that T3 is downstream of direction-selective motion detectors, T4 or T5, either directly via en passant synapses in medulla or Lo1, or indirectly through another neuron. This hypothesis could also explain the modest reduction of object-induced slowing in T4/T5 silenced flies (Figures S3B, G). An alternative origin for T3’s motion selectivity is that it might enhance responses to translating stimuli by a release-of-inhibition mechanism. That is, inhibition of T3 by a translating object passing through its inhibitory RF could de-inactivate cation channels, which could enhance its response when the object reaches the RF center.

Hierarchical elaboration of receptive fields by adaptation and pooling

We have proposed the displacement detector (DD) model of omnidirectional small object motion detection to explain response properties of LC11 (Figures 4, S4). The key features of the DD model are (1) spatial pooling of (2) center-surround antagonistic and (3) fast-adapting upstream units. In this architecture, full-field motion caused by self-movements or movements of large objects are rejected by the center-surround antagonism of the upstream units (Figure S4F). Localized (i.e., non-displaced) flickers are rejected by the fast adaptation (Figure S4F). By combining these two rejection mechanisms with spatiotemporal pooling, the DD model achieves high selectivity to small objects translating in any direction with a wide range of velocities (Figures S4G, H), similar to physiological observations [9,45]. This spatial pooling step on top of center-surround antagonism is the major feature that differentiates the DD model from the OMS and STMD models: these prior models only have single step of spatial interaction, namely center-surround antagonism, and thus do not distinguish translation from flicker. Note, however, that the DD model cannot differentiate a coherently traveling object from an object incoherently jumping around within the RF of the pooling unit, at least by the mean activity (Figure S4I). Interestingly, coherently moving objects can still generate higher peak responses than those jumping around (Figure S4I). This is because the synaptic weighting between the input units and the spatial pooling unit is distributed according to a Gaussian function, and thus a continuously translating objects can hit most highly connected central units in immediate succession [80]. The spatial pooling in the DD model conceptually parallels how complex cells in mammalian V1 achieve phase invariance by pooling simple cell outputs [81].

The DD model incorporates fast adaptation by feedforward inhibition as a critical component of visual feature computation. Adaption-like dynamics are widely observed in sensory neurons across different modalities, and various theoretical explanations have been proposed for their function [82]. For example, adaptation can adjust the dynamic range of neurons to maximize information content of their outputs [83], or can help encode salience of novel stimuli [84]. In these examples, broadly speaking, adaptation functions as a mechanism for neural circuits to incorporate contextual information into their encoding of stimulus. In contrast, in our model framework, adaptation works to enable selectivity for visual displacement over local stimuli. Similar properties of adaptation and pooling by non-direction selective neurons has been observed in locust medulla [85], and may be employed in diverse visual systems to enhance selectivity for object displacement.

An extension to the proposed DD model would be to include signal enhancing interactions between spatiotemporally displaced inputs (Figure 7A), which would make the model more selective to translating objects compared to flickers or other confounding stimuli. We found evidence against this type of enhancement in LC11’s glomerular synaptic output (Figure 7F), but the long-lasting depolarization we observed required sequential co-occurrence of inputs over space (Figure 7D). LC11-dependent, object-induced freezing also did not require translation of objects (Figure 1), mirroring the fact that presentation of a non-translating square could trigger glomerular synaptic output from LC11 (Figure 7F). Although the behavioral relevance of the long-lasting depolarization is unclear, it is interesting that LC11 exhibits different signals with different sensitivities and specificities to visual objects. Conceptually, the contrast between rejecting non-displacement and enhancing displacement parallels measurements of null-direction suppression and preferred-direction enhancement in direction-selective motion detection [32,50,57,86].

Implementing the DD model

Our excitatory pooling-based DD model is at odds with the suggestion that LC11 itself weights its inputs using center-surround antagonism [9,45]. The argument that LC11 is the locus of center-surround interaction is partly based on an observation that optimal size and RF size of LC11 approximately match at around 20° [9]. In our study, we found LC11 to have larger RF size (65° at distal dendrites, 35° at dendritic stalks). One likely source of this discrepancy is the imaging location: the previous study measured RF from somatic calcium responses. Somatic voltage responses may be strongly dampened relative to dendritic responses across several fly visual neuron types [62]. Such intracellular dampening, combined with a strong nonlinearity of calcium indicators at low calcium concentration range [64] could mask weak excitatory responses at the RF periphery and thus lead to underestimated RF sizes. This phenomenon would be similar to the absence of measured calcium responses in LC11 axon terminals in response to single stationary squares (Figure 7F). In addition, connectomic evidence shows that T3 and T2 tile the entirety of LC11 distal dendrites that span 40° to 75° of visual space, favoring the DD model (Figures 4B, C, S7C–I).

Can the DD model explain responses in other small-object sensitive neurons? LC10, another small object sensitive visual projection neuron in Drosophila, seems to be less selective to small sizes than LC11 and also has a RF with clear center-surround antagonistic structure, arguing against DD-type models [5]. On the other hand, some small object selective neurons found in other insects have dendritic arbors and excitatory RFs much broader than their size tuning, suggesting similar spatial pooling of size-tuned units as proposed in DD model [6,8,87–89]. Wide-field, small-object selective neurons have also been found in rodent superior colliculus [90,91]. It is plausible that these cells achieve their large RF and size selectivity by pooling signals from OMS retinal ganglion cells, just as LC11 pools signals from T3 neurons. Additionally, those OMS ganglion cells themselves receive excitatory inputs from small object selective amacrine cells [15], raising the possibility that each layer within the three-layer hierarchy of retinal amacrine cells, retinal ganglion cells, and superior colliculus pools size-tuned input signals.

In summary, the results presented here suggest that fly LC11 is necessary for a small-object induced freezing, and LC11 achieves its exquisite selectivity for small moving objects by pooling size-tuned, fast-adapting inputs. In this study, we took advantage of the neurogenetic tools available in Drosophila to establish a causal link between object selective cell activity and behavior, as well as to dissect circuit mechanisms for object selectivity. These links to both behavior and circuit mechanisms have been challenging in other organisms where object-selective computation has traditionally been studied. Our measurements and model of LC11 both further an integrated understanding of object-selective computation in a visual neural circuit, from mechanism and anatomy to circuit algorithm and behavior.

STAR Methods

RESOURCE AVAILABILITY

Lead contact

Damon Clark (damon.clark@yale.edu).

Materials availability

This study did not generate new unique reagents. Further information and requests for experimental data should be directed to and will be fulfilled by the Lead Contact.

Data and code availability

The code to perform numerical simulations of the models is available on GitHub (https://github.com/ClarkLabCode/DDModel). The datasets and code to analyze them have not been deposited in a public repository because of their size and nonstandard formats, but are available from the corresponding author on request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Fly Strains and Husbandry

All flies were grown at 50% relative humidity on a dextrose-based food, and non-virgin female flies were used for experiments, except that blind male flies were used for optogenetic activation experiment during imaging due to relative ease of obtaining blind male flies (Figure S5C). Flies for behavioral experiments were grown at 20° C in a 12-hour light/dark cycle. They were staged on CO₂ 12–24 hours after eclosion and experiments conducted at 50% humidity between 12 and 24 hours after staging, either within 3 hours after lights-on or within 3 hours prior to lights-off. Flies for behavioral experiments with optogenetics were placed in darkness on a food supplemented with 10 μM all-trans-retinal (ATR) for 2 to 3 days after being staged, before they were used in experiments [102]. Flies for functional imaging experiments were typically grown at 29°C, with a few exceptions grown at 25°C (+;UASGACh3.0;R22H02-Gal4; norpA/Y; R22H02-LexA, lexAop2-GCaMP6f/+; UAS-Chrimson.mVenus/+). Flies were collected 12–24 hours after eclosion on CO₂ or on ice. Flies staged on CO₂ were imaged at least 12 hours post-staging, and all surgeries used cold to immobilize flies before surgery. Flies were typically imaged at between 1 to 3 days after eclosion, while flies with weaker driver expression (R29D11-Gal4, R88C05-Gal4, R22H02-lexA) were aged up to 9 days. To amplify GCaMP6f expression in a line with weak driver expression (R88C05-Gal4), we used an additional UAS-LexA construct in combination with lexAop2-GCaMP6f. Flies for optogenetics experiments with imaging were dark-reared on the ATR-containing food for 3 to 4 days. Flies for anatomical imaging experiments were grown at 25°C and aged for up to two weeks.

Fly strains used for experiments were as follows:

		Genotype	Measurement	Figure
behavior	wild type	+;+;+	Quantification of freezing and other behaviors	1C–J, S1B–E
	LC11 > shits	w−/+; R22H02-AD/UAS-shits; R20G06-DBD/UAS-shits	LC11 silencing	2A–G, S1F–H, S2, S3F
	empty / shits (split)	w−/+; BPp65-AD/UAS-shits; BPZp-DBD/UAS-shits	UAS control for synaptic silencing with split Gal4 drivers	2A–G, S1F–H, S2, S3B, D, G
	LC11 / +	w−/+; R22H02-AD/+; R20G06-DBD/+	Gal4 control for LC11 silencing and activation	2A–G, S1F–H, S2, S3F
	LC11 > ChR2-XXL	w−/+; R22H02-AD/UAS-ChR2-XXL; R20G06-DBD/+	LC11 optogenetic activation	2I–J
	empty / ChR2-XXL	w−/+; BPp65-AD/UAS-ChR2-XXL; BPZp-DBD/+	UAS control for optogenetic activation	2I–J
	LC10 > shits	w−/+; +/UAS-shits; R22D06-Gal4/UAS-shits	LC10 silencing	S3A
	LC10 / +	w−/+; +; R22D06-Gal4/+	Gal4 control for LC10 silencing	S3A
	T4T5 > shits	w−/+; R59E08-AD/UAS-shits; R42F06-DBD/UAS-shits	T4T5 silencing	S3B, G
	T4T5 / +	w−/+; R59E08-AD/+; R42F06-DBD/+	Gal4 control for T4T5 silencing	S3B, G
	T3 > shi	w−/+; +/UAS-shits; R29D11-Gal4/UAS-shits	T3 silencing	S3C
	T3/+	w−/+; +; R29D11-Gal4/+	Gal4 control for T3 silencing	S3C
	DNp35 > shits	w−/+; +/UAS-shits; R91C05-Gal4/UAS-shits	DNp35 silencing	S3E
	DNp35 / +	w−/+; +; R91C05-Gal4/+	Gal4 control for DNp35 silencing	S3E
	DNp09 > shits	w−/+; VT023490.p65ADZp/UAS-shits; R38F04.ZpGAL4DBD/ UAS-shits	DNp09 silencing	S3D
	DNp09 / +	w−/+; VT023490.p65ADZp/+; R38F 04.ZpGAL4DBD/+	Gal4 control for DNp09 silencing	S3D
	empty / shits (single)	w−/+; +/UAS-shits; pBDP-Gal4/UAS-shits	UAS control for synaptic silencing with single Gal4 drivers	S3A, C, E
Functional Imaging	LC11 > GCaMP6f	w−/+; R22H02-AD/UAS-GCaMP6f; R20G06-DBD/+	LC11 calcium imaging	3B–O, 5A, G, 6A, B, E–G, 7D, E
		w−/+; UAS-GCaMP6f/+; R22H02-Gal4/+		7F
	LC11 > ArcLight	w−/+; R22H02-AD/+; R20G06-DBD/UAS-ArcLight	LC11 voltage imaging	5A, F, 6, 7D
	LC11 > iGluSnFR	w−/+; R22H02-AD/+; R20G06-DBD/UAS-iGluSnFR	LC11 glutamate imaging	5A, E, 6A, B, E–G, 7D
	LC11 > iGABASnFR	w−/+; R22H02-AD/+; R20G06-DBD/UAS-iGABASnFR.F 102G	LC11 GABA imaging	5A, D
	LC11 > GACh3.0	+; UAS-GACh3.0; R22H02-Gal4	LC11 acetylcholine imaging	5A, C, 6A, B, D–G, 7D, F
	T3 > Chrimson, LC11 > GCaMP6f	norpA/Y; R22H02-LexA, lexAop2-GCaMP6f/+; UAS-Chrimson.mVenus/+	T3 optogenetic activation and LC11 calcium imaging	S5C
	T3 > GCaMP6f	w−/+; UAS-GCaMP6f/+; R29D11-Gal4/+	T3 calcium imaging	S5D–H
	T2 > jGCaMP7b	w−/+; +; R29D11-Gal4/UAS-jGCaMP7b	T2 calcium imaging	S6C
	T2>GCaMP6f	w−/+; UAS-LexA, lexAop2-GCaMP6f/+; R88C05-Gal4/+	T2 calcium imaging	S6D–G
Anatomical Imaging	T3-LC11 tGRASP	y,w−/+; R22H02-lexA/Cy0; R29D11-Gal4/UAS-tGRASPpre,lexAop2-tGRASPpost	Examination of synaptic connectivity from T3 to LC11 using targeted GFP reconstitution across synaptic partners (t-GRASP)	S5B
		y,w−/+; R22H02-lexA/s; R29D11-Gal4/UAS-tGRASPpre,lexAop2-tGRASPpost
	T2-LC11 tGRASP	y,w−/+; R22H02-lexA/Cy0; R88C05-Gal4/ UAS-tGRASPpre,lexAop2-tGRASPpost	Examination of synaptic connectivity from T2 to LC11 using targeted GFP reconstitution across synaptic partners (t-GRASP)	S6B
		y,w−/+; R22H02-lexA/s; R88C05-Gal4/UAS-tGRASPpre,lexAop2-tGRASPpost

Parental lines used to generate these stains are listed in the Key Resource Table.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Anti-Bruchipilot antibody (nc82, monoclonal, mouse)	Developmental Stuidies Hybridoma Bank	RRID: AB_2314866
Anti-GFP antibody (monoclonal, rabbit)	Invitrogen	RRID: AB_2536526
Anti-mouse (polyclonal, donkey, Cy3 conjugated)	Jackson Immuno Research	RRID: AB_2340813
Anti-rabbit (polyclonal, donkey, Alexa 488 conjugated)	Thermo Fisher Scientific	RRID: AB_2556546
Chemicals, Peptides, and Recombinant Proteins
All-trans retinal	Sigma Aldrich	PubChem SID: 24899355
VECTASHIELD Antifade Mounting Medium	Vector Laboratories	RRID: AB_2336789
Experimental Models: Organisms/Strains
D. melanogaster: +;+;+	[92]	N/A
D. melanogaster: w−; UAS-shits; UAS-shits	[36]	N/A
D. melanogaster: w−; UAS-ChR2-XXL; +	[42]	N/A
D. melanogaster: w−; UAS-GCaMP6f; +	BDSC [43]	BDSC: #42747
D. melanogaster: w−; lexAop2-GCaMP6f; +	BDSC [43]	BDSC: #44277
D. melanogaster: w−; +; UAS-ArcLight	BDSC [54]	BDSC: #51056
D. melanogaster: w−; +; UAS-iGluSnFR	[52] (Gift from Marc Freeman)	N/A
D. melanogaster: w−; +;UAS-iGABASnFR.F102G	[53] (Gift from Vivek Jayaraman)	N/A
D. melanogaster: w−; UAS-GACh3.0; +	[51] (Gift from Yulong Li)	BDSC: #86549
D. melanogaster: w−; +; UAS-Chrimson.mVenus	BDSC [41]	BDSC: #55136
D. melanogaster: y,w−; sp/CyO; UAS-tGRASPpre,lexAop2-tGRASPpost/TM6B	BDSC [93]	BDSC: #79039
D. melanogaster: w−; +; R22H02-Gal4	BDSC [94]	BDSC: #49304
D. melanogaster: w−; R22H02-LexA; +	BDSC [94]	BDSC: #52699
D. melanogaster: w−; R22H02.p65ADZp; R20G06.ZpGAL4DBD	BDSC [19]	BDSC: #68362 JRC: OL0015B
D. melanogaster: w−; +; R29D11-Gal4	BDSC [94]	BDSC: #49484
D. melanogaster: w−; +; R88C05-Gal4	BDSC [94]	BDSC: #48394
D. melanogaster: w−; +; R22D06-Gal4	BDSC [94]	BDSC: #48036
D. melanogaster: w−; R59E08.p65ADZp; R42F06.ZpGAL4DBD	[95]	JRC: SS00324
D. melanogaster: w−; +; R91C05-Gal4	BDSC [94]	BDSC: #40578
D. melanogaster: w−; VT023490.p65ADZp; R38F04.ZpGAL4DBD	Ordered from Janelia Research Campus [96]	JRC: SS01540
D. melanogaster: w−; +; pBDPAL4Uw	BDSC [97]	BDSC: #68384
D. melanogaster: w−; pBPp65ADZpUw; pBPZpGAL4DBDUw	Ordered from Janelia Research Campus [98]	BDSC: #79603
D. melanogaster: w−; UAS-LexA; +	BDSC	BDSC: #7228
D. melanogaster: w−,norpA36; +; +	BDSC	BDSC: #9048
Software and Algorithms
MATLAB	Mathworks	https://www.mathworks.com/
Psychtoolbox 3	[99]	http://psychtoolbox.org/
ScanImage	[100]
neuPrint	[101]	https://github.com/connectome-neuprint/neuprint-python
Python3.8.1		https://www.python.org/

METHOD DETAILS

Fly-on-ball psychophysics

Measurements/Set-up

We used a fly-on-the-ball rig to measure flies’ turning and walking speed in response to visual stimulation, as described in previous studies [31,103]. Each fly was anesthetized on ice, fixed to a needle with UV-cured epoxy and placed above an air-suspended ball that rotated under it as it attempted to walk and turn. Rotation of the ball was recorded at 60 samples/sec at a resolution of ~0.5° using an optical mouse sensor. Panoramic screens surrounded the fly, covering 270° azimuth and 106° elevation. The stimuli were projected on to the screens by a Lightcrafter DLP (Texas Instruments, USA) using monochrome green light (peak 520 nm and mean intensity of ~100 cd/m²). Stimuli were projected such that the fly experienced a virtual cylinder [33]. The temperature of the arena was set to ~36° C to allow us to use thermogenetic tools and promote walking [31,36].

Visual stimuli

The visual stimuli used in the behavioral experiments are compiled in the following table. Each stimulus presentation was interleaved with between 1 and 5 seconds of mean gray.

Stimulus	Description (duration)	Figures
Briefly moving squares	A single 10°×10° black square or a pair of squares appear either right in front of (single) or on the both sides of (pair) a fly, remain stationary for 1 s, move horizontally for 1/12 s at 180°/s to the right or left (single), or progressively or regressively (pair), remain stationary for another 1 s, then disappear. The background is mean gray for the full 2 1/12 s.	1B–H, 2A–G, S1A–F, S3
Briefly moving bars	A single 10°×106° black bar or a pair of bars appear either right in front of (single) or on the both sides of (pair) a fly, remain stationary for 1 s, move horizontally for 1/12 s at 180°/s to the right or left (single), or progressively or regressively (pair), remain stationary for another 1 s, then disappear. The background is mean gray for the full 2 1/12 s.	1B–H, S1C, D, G, H
Object size sweep	A single black vertical or horizontal bar with variable sizes moving at 180°/s appears right in front of a fly for 1/6 s. The lengths of the bar were 5°, 10°, 20°, 40°, 60°, 80°, or the full extent of the screen (~106°). The width was fixed at 10°. The directions of the motion were either left, right (vertical bars), up, or down (horizontal bars). The responses were averaged over the direction of motion. The background is mean gray for the 1/6 s duration of the stimulus.	1I, J
Fly-mimic stimulus	A roughly fly-sized (3 mm-wide, 2 mm-high) black rectangular object moves in a virtual world parallel to the heading of the fly and 25 mm away from the fly to the left or right. The object appears 25 mm either to the front or back of the fly, remain stationary for 1 s, and then moves backward or forward at 25 mm/s for 2 s, respectively. The object then remain stationary for another second before disappearing. The object remains at zero elevation for the entire stimulus.	S2F, G
Fast translating squares and bars	A 5° × 5° black square or a 5° × 106° black vertical bar appears right behind a fly on the virtual cylinder and sweeps across the entire 360° circumference of the cylinder at 180°/s, either rightward or leftward (2 s).	S2D, E
Slow translating bars	A 10° × 106° black vertical bar appears right behind a fly on the virtual cylinder and sweeps across the entire 360° circumference of the cylinder at 18°/s, either rightward or leftward (20 s).	S2H
Full-field sine wave	A quarter-contrast full field rotational or translational sine wave moving either rightward or leftward, or the two halves moving progressively or regressively. The wavelength is 60° and temporal frequency is 8Hz (1/2 s).	S2A–C

Optogenetics

Optogenetic activation of LC11 neuron with ChR2-XXL was achieved using monochrome blue light (peak 453 nm) from the same Lightcrafter DLP used for visual stimulus presentation [33]. The panoramic screens were removed and the light was shone from the four directions (left, right, front, top) to flies to obtain higher light intensity. The light was flickered at 30 Hz and resulting average intensity from each direction was ~0.75 μW/mm².

Data Analysis

First, each walking speed trace was normalized by the average walking speed of the fly during the 500 ms periods immediately preceding the onset of each stimulus. After the normalization, the walking speed for each fly is in the unit of fold change relative to mean pre-stimulus period. Next, the normalized walking speed and turning time traces were averaged across every presentation of each stimulus type within each individual fly (‘individual mean response’). Walking and turning responses to mirror-symmetric pairs of stimuli were merged in additive or subtractive fashion, respectively. Additionally, the instantaneous probability of each fly being stopped (having zero or negative normalized walking speed) was calculated for each stimulus based on normalized walking speed. The change of instantaneous stop probability caused by stimulus presentation was calculated by subtracting the average stop probability during the 500 ms period preceding the stimulus onset from the instantaneous stop probability time traces (shown as ΔStop probability). Additionally, the average stop probability during the 500 ms of pre-stimulus period was averaged across different stimulus conditions within each experiment to generate the baseline stop probability. The group mean response time traces and their standard errors were then calculated from the mean responses of individual flies. To quantitatively compare the magnitude of behavioral responses across stimulus types and genotypes, individual mean responses were averaged over time within the temporal windows indicated in figure captions.

As an alternative measure to characterize the stopping behavior, we calculated the duration of stop triggered by the movement of objects in ‘Briefly moving squares/bars’ stimuli. For each presentation of stimulus, we labeled samples where normalized walking speed was below 0.05 as ‘stop samples’ and everything else as ‘walking samples’. Next, we labeled short (less than 1/6 s) chunks of walking samples flanked by stop samples as stop samples. We then counted the duration of the first contiguous chunk of stop samples initiated within 1/3 s after the onset of stimulus movement. If the fly was already stopped at the onset of the stimulus movement, the stop duration was computed as the time between the stimulus movement onset and the end of the chunk of the contiguous stop samples. When flies did not initiate any stopping within 1/3 s after the movement offset, stop duration of 0 was registered. The stop durations were then averaged within each stimulus condition and each fly (Mean stop duration) (Figure 1G, 2F). In addition, log-log histograms of stop duration were drawn for each stimulus condition and each fly, and averaged across flies within each genotype (Figure 1H, 2G). A linear function was fit to the log-log histograms of individual flies to quantify the slope of the log-log histograms (Figure S1E–F).

For the turning of flies in response to fast translating squares and bars (Figure S2D, E, H), we calculated the maximum (rather than mean) absolute angular velocity of individual mean turning time traces during the stimulus presentation as the summary measure of turning responses. This is because the sign of turning flips as the target the fly is fixating on moves across left and right visual fields, and therefore time-averaged turning does not necessarily reflect the magnitude of turning responses.

Two-photon Imaging

Measurements/Set-up

Neuronal activity was recorded with two-photon scanning fluorescence microscopy as described previously [32,103]. Flies expressing fluorescent indicators in neurons of interest were anesthetized on ice and head-fixed in a stainless-steel shim. To expose the optic lobe, a surgery was performed on the back of the flies’ head to remove the cuticle, fat, and trachea above the optic lobe. The exposed brain was submerged in oxygenated sugar-saline solution [104]. Imaging was performed with a two-photon microscope (Scientifica, UK) equipped with a 20x water immersion objective lens (XLUMPlanFL; Olympus, Japan), while the flies were presented with visual stimuli displayed using a digital light projector (DLP) on screens surrounding the fly [33]. The screens covered 270° azimuth and 69° elevation. Stimuli were projected such that the fly experienced a virtual cylinder, which was pitched forward 45° to account for the angle of the head of the fly in the shim. The output of the DLP was filtered with a 565/24 in series with a 560/25 filter (full width/half maximum) (Semrock, Rochester, NY, USA). The input to the PMT was also filtered with two 512/25 filters to block photons from visual stimulus (Semrock, Rochester, NY, USA). A precompensated femtosecond laser (Spectraphysics, Santa Clara, CA, USA) provided 930 nm light at power < 40 mW. Images were acquired at 8.46 Hz using ScanImage software [100]. The sequence of images acquired was processed off-line to compensate for motion of the brain tissue during imaging.

Stimulus presentation

The table below compiles the visual stimuli used in the imaging experiments. All visual stimuli were presented on a mean gray background unless otherwise noted. Each stimulus presentation was interleaved with presentations of mean gray, typically 2 to 3 seconds but ranging between 1 to 10 seconds. Two symmetric versions of each stimulus were presented an equal number of times (e.g., ‘horizontally moving objects’ moved rightward and leftward equal times), and results were averaged over directions of motion, as LC11 is non-direction selective [9]. All recordings were done on the right optic lobe, and when a stimulus is described in terms of azimuthal and elevational position, the central meridian and equator each corresponds to azimuthal/elevational zero, and positive degrees indicate rightward/downward. All coordinates are in the head coordinates of the fly, not of the microscope or screens. For stimuli involving translating objects in single cell experiments, the trajectories were all centered about the estimated RF center of a cell.

	Stimulus	Description (duration)	Figure
RF identification	Translating squares	A single 10° × 10° black square moving horizontally or vertically at 60°/s over 40° trajectories. Covers 40° × 40° square area centered about manually localized approximate RF center location with increments of 5°, resulting in 8 columns and 8 rows, each with two opposite directions. (2/3 s)	3C, D, 4E, S4A, L, S5E, F, S6D, E,
Single Cell experiment	Size sweep	A single black vertical or horizontal bar with variable sizes moving at 180°/s for 1/6 s. The lengths of the bar were 5°, 10°, 20°, 40°, 60°, 80°, or the full extent of the screen. The width was fixed at 10°. Horizontal bars moved vertically in both directions and vertical bars horizontally. (1/6 s)	3E, F, 4G, S5G, S6F
	Translating objects	A single 10° × 10° black square translating horizontally at 60°/s. (1 s)	3H, I, K, L, O, 4H–K, N 7E, S4B, C, F, I, S5H, S6G
	Decoupled edges	A single, 10° high black edge appears to the side of the RF center of a cell, extends across the RF center horizontally at 60°/s for 1 s, resulting in a 60° × 10° black bar (OFF edge). The bar remains stationary for 3 s, then the same edge travels back at −60°/s, shrinking and removing the bar (ON edge). (5 s)	3H, I, 4H, I, S4B, F
	Localized square wave gratings	Drifting full-contrast square wave grating with the wavelength of 20° and velocity of 60°/s, presented within a 20° diameter circular aperture at the center of RF. It is presented with or without a background of the same full-contrast square wave, which either remains stationary, moves syn-, or antidirectionally to the central grating. The 20° thick annulus around the central aperture was kept at the mean gray. (2 s)	3K, L, 4J, K, S4C, F
	Local flickers	A single 10° × 10° black square appearing right at the center of RF, either sustainedly presented (noted as 0 Hz) or flickers at various temporal frequencies (1, 2, 4, 6, 12, 20 Hz). (2 s)	3M–O, 4L–N, S4D, F, S5H, S6G,
	Six-step apparent motion	A spatially contiguous, horizontal series of six 10° × 10° black squares, centered about the RF center of a cell, appears and disappears one by one for 1/6 s each in sequence. (1 s)	7E, S4I
	Six-step apparent motion (component)	A solitary 10° × 10° black square flashes for 1/6 s at one of the six possible positions in the ‘six-step apparent motion’ stimulus described above. (1/6 s)	7E
Non-single cell experiment	Translating bar	A 10° wide vertical black bar extending the entire height of the screen travels horizontally at 60°/s within the azimuthal range of [−20°, 70°]. (1.5 s)	5B–G, S5D, S6C
	Full-field	Full-contrast square wave gratings with the wavelength of 20°,	5B–G,
	square wave gratings	drifting horizontally or vertically at 60°/s. (2 s)	S5D, S6C
	Full-field flash	Full field, full contrast ON (bright) or OFF (dark) flashes. (2 s)	5B–G, S5D, S6C
	Translating square	A single 10° × 10° black square moving at 60°/s, horizontally sweeping the azimuthal range of [−20°, 70°] at various elevations from −40° to 10° with 10° increments (1.5 s), and vertically sweeping the elevational range of [−40°, 10°] at various azimuths from −20° to 70° (5/6 s). For recordings with GACh3.0, horizontally translating squares were presented only at the elevation of −30° in order to keep experiments short.	6A, B
	Translating square (long interleave)	A single 10° × 10° black square moving at 60°/s, vertically sweeping the elevational range of [−40°, 10°] at various azimuths from −20° to 70° (5/6 s). With long interleaves of 10 s.	6C
	Size sweep	A single black rectangle with 10° height and variable width (10°, 20°, 40°, 60°, full vertical extent) moves horizontally at 60°/s, sweeping the azimuthal range of [−20°, 70°] at various elevations from −40° to 10° with 10° increments (1.5 s). For recordings with GACh3.0, only the elevation of −30° was used in order to keep experiments short.	6E, F
	Local flicker	A single black 10° × 10° square appears at one of the vertices of the 10° resolution grid covering the azimuthal range of [10°, 40°] and the elevational range of [−40°, −10°], either sustained or flickering at 2 Hz (2 s). For recordings with GACh3.0, only the elevation of −30° was used in order to keep experiments short.	6G
	Ten-step apparent motion	A spatially contiguous, horizontal series of ten 10° × 10° black squares, spanning across the azimuthal range of [−20°, 70°] at various elevations from −40° to 10° with 10° increments, appear and disappear one by one for 1/6 s each in sequence (10/6 s). For recordings with GACh3.0, only the elevation of −30° was used in order to keep experiments short.	7D
	Ten-step apparent motion (component)	A single 10° × 10° black square flashes for 1/6 s at one of the fifty possible positions in the ‘apparent motion’ stimulus described above (1/6 s). For recordings with GACh3.0, only the elevation of −30° was used in order to keep experiments short.	7D
Glomerular experiments	Six-step apparent motion	The same six-step apparent motion stimuli as used in single-cell experiment, centered about (azimuth, elevation) = (20°, −20°). (1 s)	7F
	Six-step apparent motion (component)	A single 10° × 10° black square flashes for 1/6 s at one of the six possible positions in the ‘six-step apparent motion’ stimulus described above (1/6 s).	7F
	Translating square	A Single 10° × 10° black square moving horizontally at 60°/s, sweeping the azimuthal range of [−40°, 80°] at the elevation of −20°. (2 s)	6D
Probe	Translating bar	A 10° wide vertical black bar extending the entire height of the screen travels rightward and leftward alternately at 60°/s sweeping the azimuthal range of [−20°, 70°], interleaved with 2 s of mean gray. (7 s)	5, 6A–C, E–G, 7, S5D, S6C
	Drifting square wave gratings	Three seconds of full-contrast square wave gratings with the wavelength of 20°, drifting towards right, left, down, and up at 60°/s, interleaved with 3 s of mean gray. (24 s)	5D
	Translating square	A single 10° × 10° black square moving horizontally at 60°/s, sweeping the azimuthal range of [−40°, 80°] at the elevations of −20°, −30°, and −40°.	6A, B, E–G, 7D
Model only	Size sweep (more sizes)	A single black vertical bar with variable sizes moving rightward at 180°/s for 1/6 s. The lengths of the bar were 5°, 10°, 15°, 20°, 25°, 30°, 40°, 60°, 80°, or the full extent of the screen. The width was fixed at 10°. (1/6 s)	4F, G, S4A, F, J, K
	Direction sweep	A single 10° × 10° black square translating at 60°/s in 8 different directions, at 45° angular resolution. (1 s)	S4G
	Velocity sweep	A single 10° × 10° black square translating horizontally for 60° at either 10°/s, 20°/s, 30°/s, 60°/s, 120°/s, or 240°/s. (1/4 – 6 s)	S4H
	Scrambled apparent motion	A spatially contiguous, horizontal series of six 10° × 10° black squares, centered about the RF center of a cell, appears and disappears one by one for 1/6 s each in a scrambled yet deterministic sequence of [1, 4, 2, 6, 3, 5]. (1 s)	S4I

Online RF identification

In single cell calcium imaging experiments (Figures 3, 7E, S5E–H, S6D–G), the receptive field (RF) center location of each cell was estimated in a similar fashion to previously reports [9]. First, structures that clearly belong to single cells (main dendritic stalks between lobula and PVLP in LC11 (Figure 3B), axon terminals in T2 and T3) were visually identified. Then, the approximate locations of their receptive field (RF) centers were probed using interactive presentation of a 10° × 10° black square on the mean gray background, moving at 60°/s. Next, to obtain a more accurate estimate of the RF center locations, a 10° × 10° black square horizontally or vertically translating at 60°/s was presented such that it swept a 40° × 40° area centered about the interactively identified approximate RF center with 5° increments. The neural response (in units of ΔF/F) were averaged over trials and directions (i.e., left and right, up and down), and integrated over time within a 1.5 s window from the onset of each stimulus, resulting in two spatial tuning curves corresponding to the vertical and horizontal dimensions of RF. Gaussian functions were independently fit to the two tuning curves, and the identified means of the distributions were used as the estimated RF center location in the subsequent experiments. In addition, the full-width quarter maximum (FWQM) values of the fitted Gaussian functions were reported as the measure of RF size [9] (Figure 3D, S5F, S6E). Only RF sizes of cells whose spatial tuning curve was fit well (R² > 0.8) by Gaussian functions are plotted.

Optogenetics

Optogenetic activation of T3 with Chrimson was achieved using a 690 nm diode laser (Thorlabs, HL6738MG) controlled via an Arduino (Figure S5C). The measured power of the laser at the sample was ~2 mW/mm². The stimulation was repeated 10 times for each fly. Each stimulation lasted for 1 s, separated by 20 s of interleave.

Imaging data analysis

Exclusion of frames and recordings

After aligning the acquired images to compensate the motion of the sample, frames that moved more than 4.3 microns from the target were excluded from the following analysis. An entire recording was also discarded if more than 5% of its frames were excluded due to excessive displacement.

Extraction of Regions of Interest

To extract regions of interest (ROIs), the mean image was generated for each recording by averaging all frames in a recording after motion compensation. For single cell imaging experiment with LC11, T2, and T3, or glomerular experiments in LC11, ROIs were manually drawn around the structure of interest based on the mean image (single cell LC11: main dendritic stalk, single cell T2 and T3: axon terminal, glomerular LC11: optic glomerulus). For non-single cell recordings, a watershed segmentation algorithm [105], as implemented in ‘watershed’ function in Matlab, was applied to the mean image to obtain ROIs with spatially contiguous pixels. Only ROIs found within appropriate anatomical location (i.e., Lo2/3) were retained.

Calculation of fractional change in fluorescence

For each ROI, ΔF/F was calculated as the proxy of intracellular calcium concentration (GCaMP6f), neurotransmitter concentration (iGluSnFR, iGABASnFR, GACh3.0), or membrane voltage (ArcLight). First, we averaged the intensity of pixels within each ROI. Then, to estimate the baseline fluorescence of the ROIs while accounting for the photobleaching of the sensors, a decaying exponential of the form Ae^−t/τ was fitted to the portion of the fluorescence time trace that corresponded to interleaves between stimulus presentations. More specifically, the fluorescence values during the entirety of each interleave were averaged over time and across the all ROIs, and the time points at the middle of each averaging window were assigned the averaged fluorescence value of that window. A single τ was fit to this average fluorescence trace in each movie, while A was individually fit to the mean amplitude of each ROI. This exponential served as the F₀ trace, and the original fluorescence time trace as F′, so that ΔF/F was computed as

$$\frac{\Delta F}{F}=\frac{F^{\prime }-F_0}{F_0}$$

In addition, each response time trace was subtracted with time-averaged ΔF/F values of immediately preceding 500ms of interleave period to account for apparent fluorescence fluctuations, possibly caused by Z-plane motion, which was not removed by fitting the exponential. In the following analyses, the responses were all analyzed in terms of ΔF/F. For voltage imaging using ArcLight, -ΔF/F was used instead of ΔF/F, as ArcLight fluorescence decreases as the membrane depolarizes.

Consistency-based Selection of Region of Interest

In non-single cell experiments, we selected responsive ROIs based on the consistency of their response during the probe presentation. The probe stimuli were presented three times before the experimental stimuli. For each ROI, the correlations between every pair of responses to the three probe presentations was computed. Then, ROIs that had average correlation below a threshold were discarded (0.4 for GCaMP6f, jGCaMP7b, and iGluSnFR; 0.3 for ArcLight and GACh3.0; 0.1 for iGABASnFR).

Calculation of average time traces

After selecting responsive ROIs, ΔF/F time traces were averaged within each ROI over multiple repetitions of each stimulus (‘individual mean response’). Responses to versions of the same stimulus with different motion directions were averaged at this step unless otherwise noted, as neither LC11, T2, nor T3 were found to be direction selective. In non-single cell experiments, individual mean responses were further averaged across ROIs within each fly. The group mean responses and their standard errors were then calculated (across ROIs in single cell experiments and across flies in non-single cell experiments). In addition, to quantitatively compare the magnitude of neuronal responses across stimulus types and genotypes, averages of individual mean responses over time were calculated within noted windows depending on the stimulus types.

Post-hoc RF identification

In some non-single cell experiments, RF centers of ROIs were identified post hoc as follows.

• RF characterization experiments with ‘translating square’ stimulus (Figures 6A, B)

  • (Characterization of spatial RF) First, for each ROI and for each stimulus (i.e., a square translating at particular elevation/azimuth in one direction), a random half of the 6 repetitions were labeled as an ‘alignment set’ and the rest as a ‘test set’. For each ROI and within each set, neural responses were averaged over the repetitions and directions (i.e., rightward and leftward, upward, and downward). Responses were then averaged over time within the time window of 1.5 s (horizontal sweep) or 2/3 s (vertical sweep), resulting in elevational and azimuthal spatial tuning curves, one each for the alignment and test sets.
  • Next, one-dimensional Gaussian functions were fit to the alignment tuning curves, and their means were used as the estimates of the RF center location. Additionally, full-width quarter-maximum (FWQM) of the fitted Gaussian functions were calculated for each ROI as the size of RF, and averaged within each fly.
  • The test set tuning curves were aligned to the estimated RF center location, and averaged over ROIs within each fly to generate ‘individual mean spatial tuning curves’.
  • In addition, maximum response rows/columns were identified as the peaks of the alignment set elevational/azimuthal tuning curves.
  • (Characterization of response kinetics) Next, the moment of impact—when horizontally/vertically-translating squares reached the azimuthal/elevational center of the RF—was calculated based on the estimated centers of ‘alignment set’ tuning curves. For each ROI, the ‘test set’ mean response time traces at the maximum response rows/columns were aligned to the estimated moment of impact at a resolution of 1 ms, then averaged over the 4 directions, and normalized to the response peak (‘normalized aligned response’). The half-fall time was calculated for each ROI as the duration between the peak of the normalized aligned response and the time when the normalized response came back to 0.5. The normalized aligned response was then averaged over ROIs within each fly to generate individual mean kinetics.
  • The group mean spatial tuning curves, response kinetics, and their corresponding standard errors were calculated based on the individual mean spatial tuning curves and the individual mean kinetics.
• Experiments using ‘translating squares with long interleaves’ stimulus (Figure 6C)

  • An ‘alignment set’ azimuthal tuning curve for each ROI was obtained to estimate the maximum response column, as described above. Then, test set response time traces at the maximum response column were averaged over ROIs.
• Size sweep experiment (Figures 6E, F)

  • A random half of 10° × 10° square presentations were labeled as the ‘alignment set’, and maximum response rows were computed from this set. For each ROI and each stimulus size, responses at the maximum response row were averaged over time (1.5 s) to obtain a size tuning curve. The ‘alignment set’ data were excluded from the size tuning curve calculation.
• Experiments with ‘local flicker’ stimulus (Figure 6G)

  • A random half of the 6 repetitions of each stimulus was labeled as an ‘alignment set’ and the rest as a ‘test set’. By averaging ‘alignment set’ responses over stimulus type (i.e., sustained and 2 Hz flicker), time (2 s) for each ROI and each location, we obtained a two-dimensional spatial tuning surface, and the maximum response location was identified as its peak. The ‘test set’ response at the maximum response location was averaged over ROIs.
• Apparent motion experiments (Figure 7D)

  • The ‘apparent motion’ and ‘apparent motion (components)’ stimuli (Figure 7D) were presented with horizontally translating 10° × 10° squares in a single recording session, which was used to identify maximum response rows for each ROI. Only the responses to ‘apparent motion’ and ‘apparent motion (components)’ stimuli presented at the maximum response rows were analyzed.

For the dendritic experiment with GACh3.0 using local stimuli (i.e., translating squares, size sweep, local flicker, apparent motion) (Figures 6A, B, E–G, 7D), stimuli were confined to the elevation of −30°. This was aimed to keep experiments short and prevent neurons expressing GACh3.0, which was dim, from photo-bleaching. To make sure that the stimuli were vertically centered about the RF of recorded ROIs, we presented horizontally translating squares at elevations of −20°, −30°, and −40° to LC11>GACh3.0 flies, and analyzed only ROIs whose integrated response to squares at −30° was larger than its responses to squares at −20° or −40°.

Linear expectation analysis

To test whether LC11 is detecting coincidence between OFF input and ON input (Figures 3H, I) or spatially offset OFF inputs (Figure 7), we compared neural responses to the sequential presentation of component inputs and linear sum of neural responses to isolated presentations of component inputs (‘linear expectation’). We constructed ‘linear expectation’ time traces by up-sampling neural responses to component stimulus presentation, shifting them temporally to the timing when the given component appears in the sequential presentation, and adding them together. Neural responses to the sequential presentations and linear expectation were all averaged over time within appropriate temporal windows, directions, and ROIs, followed by statistical comparisons between the two.

Immunohistochemistry

The brains were dissected out in PBS, fixed in 4% PFA for 15 minutes, washed 3 times for 20 minutes, blocked with 5% normal goat serum for another 20 minutes, and incubated with primary antibodies (mouse anti-Bruchipilot, 1:25; rabbit anti-GFP, 1:100) dissolved in PBS with 0.2% Triton-X for 24 hours. The brains were washed 3 times for 20 minutes again, and then incubated with secondary antibodies (Cy3-conjugated donkey anti-mouse, 1:250; Alexa 488-conjugated donkey anti-rabbit, 1:250). After another round of washing, the brains were mounted in Vectashield and imaged with a Zeiss LSM880 confocal microscope.

Computational modeling

Displacement detector (DD) model

To simulate the ommatidial resolution of fly eyes, the original visual stimuli used for behavioral and imaging experiments (1° resolution, 180 Hz, in units of contrast) were first down-sampled to 5° resolution with bilinear interpolation. The down-sampled stimuli, henceforth denoted as S(x,y,t), then underwent a sequence of filtering and non-linear operations described in the following: First, a temporal high-pass filter was applied, given by

$$k_{\text{pre}}(t)=\{\begin{array}{c}{a}_{\text{pre}}\frac{{\tau }_{\text{pre}}-t}{{\tau }_{\text{pre}}^2}{e}^{-\frac{t}{{\tau }_{\text{pre}}}}(t\ge 0)\\ 0(t<0)\end{array}$$

where τ_pre = 200 ms was convolved to the input. The amplitude a_pre was determined such that the kernel had a unit L2 norm. This was intended to mimic the impulse response functions of second order visual neurons in Drosophila visual system [103]. The filtered input was then full-field rectified such that

$$R_{\text{rect}}(x,y,t)={\left[\left(S*k_{\text{pre}}\right)(x,y,t)\right]}_{+}+{\left[-\left(S*k_{\text{pre}}\right)(x,y,t)\right]}_{+}$$

where [·]₊ stands for half wave rectification. Each pathway then undergoes spatial filtering by kernels defined by

$$h(x,y)=a_{\text{h}}\left(w_1{G}_1(x,y)-w_2{G}_2(x,y)\right)$$

$$G_{\text{i}}(x,y)=\frac{1}{2\pi {\sigma }_{\text{i}}^2}\text{exp}\left(-\frac{x^2+y^2}{2{\sigma }_{\text{i}}^2}\right)$$

where (w₁, w₂) = (1, 3.5), (σ₁, σ₂) = (5°, 15°). The amplitude a_h was determined such that the kernel had a unit L2 norm. After another half-wave rectification, the combined signal underwent adaptation. Adaptation was modeled as division of the input signal by the low-pass filtered version of itself [49], such that

$$R_{\text{adapt }}(x,y,t)=\frac{{\left[\left(R_{\text{rect }}*h\right)(x,y,t)\right]}_{+}}{1+\gamma \left(\left(k_{\text{adapt }}*{\left[R_{\text{rect }}*h\right]}_{+}\right)(x,y,t)\right)}$$

$$k_{\text{adapt }}(t)=\{\begin{array}{c}{a}_{\text{adapt }}\frac{t}{{\tau }_{\text{adapt }}^2}{e}^{-\frac{t}{{\tau }_{\text{adapt }}}}(t\ge 0)\\ 0(t<0)\end{array}$$

where γ = 10³, and τ_adapt = 300 ms The amplitude a_adapt was determined such that the kernel had a unit L2 norm. Finally, the adapted signal underwent spatiotemporal low-pass filters given as

$$R_{\text{out }}(x,y,t)=\left(R_{\text{adapt }}*k_{\text{out }}*G_{\text{out }}\right)(x,y,t)$$

$$k_{\text{out}}(t)=\{\begin{array}{c}{a}_{\text{out}}\frac{t}{{\tau }_{\text{out}}^2}{e}^{-\frac{t}{{\tau }_{\text{out}}}}(t\ge 0)\\ 0(t<0)\end{array}$$

$$G_{\text{out}}(x,y)=\frac{1}{2\pi {\sigma }_{\text{out}}^2}\text{exp}\left(-\frac{x^2+y^2}{2{\sigma }_{\text{out}}^2}\right)$$

to give rise to the model output, where τ_out = 300 ms, and σ_out = 10°. The amplitude a_out was determined such that the kernel had a unit L2 norm. For visualization, the time traces of R_out that correspond to the central pixel of the visual stimulus were plotted (Figure 4).

Small target motion detector (STMD) model

The response of STMD model was modeled as follows:

$$R_{\text{STMD}}(x,y,t)=\left(R_{\text{ON}}\times R_{\text{OFF}}\right)*k_{\text{out}})\left(x,y,t\right)$$

$$R_{\text{ON}}(x,y,t)={\left[\left(h^{\prime }*{\left[S*k_{\text{pre}}\right]}_{+}\right)(x,y,t)\right]}_{+}$$

$$R_{\text{OFF}}(x,y,t)={\left[\left(h^{\prime }*k_{\text{delay}}*{\left[-S*k_{\text{pre}}\right]}_{+}\right)(x,y,t)\right]}_{+}$$

where

$$h^{\prime }(x,y)=a_{\text{h}}^{\prime }\left(w_1^{\prime }{G}_1^{\prime }(x,y)-w_2^{\prime }{G}_2^{\prime }(x,y)\right)$$

$$G_{\text{i}}^{\prime }(x,y)=\frac{1}{2\pi \sigma {\prime }_{\text{i}}^2}\text{exp}\left(-\frac{x^2+y^2}{2\sigma {\prime }_{\text{i}}^2}\right)$$

$$k_{\text{delay }}(t)=\{\begin{array}{c}{a}_{\text{delay }}\frac{t}{{\tau }_{\text{delay }}^2}{e}^{-\frac{t}{{\tau }_{\text{delay }}}}(t\ge 0)\\ 0(t<0)\end{array}$$

and (w′₁, w′₂) = (1, 3.5), (σ₁, σ₂) = (7.5°, 20°), τ_delay = 250 ms. The amplitudes a′_h and a_delay were determined such that the kernels had a unit L2 norm.

Object motion sensitive (OMS) model

The response of OMS model was modeled as follows:

$$R_{\text{OMS}}(x,y,t)=\left({\left[h^{\prime }*{\left[S*k_{\text{pre}}\right]}_{+}\right]}_{+}*k_{\text{out}}\right)(x,y,t)$$

Note that parameters are chosen such that the STMD and OMS models had an approximately identical size tuning as the DD model (Figures 4G, S4A).

Connectomic Anaysis

All the connectomic analyses were performed on the electron micrograph-based, densely reconstructed ‘hemibrain:v1.0.1’ connectome dataset [46] available on the neuPrintExplorer website (https://neuprint.janelia.org/). The connectivity data were extracted using Cypher query [101] on the neuprint-python package, and neuronal morphology were visualized on neuPrintExplorer. To first examine the macroscopic connectivity pattern of LC11, the numbers of synapses of all the LC11 neurons in the dataset by brain regions were extracted with the following query:

MATCH (a:Neuron) 
WHERE a.type =~ ‘LC11’ 
RETURN DISTINCT a.bodyId AS bodyId, a.type AS type, a.pre AS pre, a.post AS post, a.roiInfo as roi 
ORDER BY a.pre + a.post 

which returned 71 labeled LC11 neurons (Figure S7A).

Identification of putative T3 and T2

Among the identified LC11 neurons, we chose one cell for its completeness (bodyId: 128091174) (Figure S7B). Note that bodyId is unique identifier assigned to traced neurons in the hemibrain dataset [46]. We then extracted all the optic lobe intrinsic (i.e., more than 99.9% of pre- and postsynaptic terminals are in the optic lobe) presynaptic neurons to the LC11 neuron as follows:

MATCH (a:Neuron)-[w:ConnectsTo]->(b:Neuron) 
WHERE b.bodyId=1280971174 AND a.status=‘Traced’ AND
apoc.convert.fromJsonMap(a.roiInfo)[“OL(R)”].pre/a.pre>0.999 AND
apoc.convert.fromJsonMap(a.roiInfo)[“OL(R)”].post/a.post>0.999 
RETURN DISTINCT a.bodyId AS bodyId, a.type AS type, a.pre AS pre, a.post AS post, w.weight AS weight, a.roiInfo as roi
ORDER BY a.pre + a.post

which returned 184 cells. We visually examined the 184 presynaptic cells and annotated ones that had similar morphology to T3 and T2 (Figures 4B, C, S7C, D). It is difficult to definitively identify T3 without innervation patterns in medulla — which is not included in the hemibrain dataset — but we found some reconstructed terminals that show strong resemblance to known morphology of T3 and T2 [22]. The list of the bodyId of annotated putative T3 and T2 are in Table S1.

Next, we extracted the presynaptic locations of the 184 presynaptic cells within lobula as follows:

MATCH (a:Neuron)-[:Contains]->(:SynapseSet)-[:Contains]->(s:Synapse) 
WHERE a.bodyId=<bodyId> AND s.’LO(R)’ AND s.type=‘pre’
RETURN s.location.x as x, s.location.y as y, s.location.z as z
ORDER BY a.pre + a.post DESC

which we looped through the 184 bodyIds. We applied principal component analysis to the identified presynaptic locations of each neuron, and calculated the standard deviation of the locations along the first and second principal components (SD₁ and SD₂) (Figure S7F).

Last, we extracted presynaptic neurons of three other instances of LC11 (bodyId: 1566528972, 1188885499, 1566519741), and searched for putative T3 and T2 cells by visually examining cells that had similar SD₁ and SD₂ profiles as ones we had already annotated (Figures S7G–I).

Analysis of LC11 output

We extracted the all postsynaptic target of the LC11 neurons as follows:

MATCH (b:Neuron)-[w:ConnectsTo]->(a:Neuron)
WHERE b.bodyId = %s AND a.status=‘Traced’
RETURN DISTINCT a.bodyId AS bodyId, a.type AS type, a.pre AS pre, a.post AS post, w.weight AS weight, a.roiInfo as roi
ORDER BY a.pre + a.post

which we looped through the bodyId of all the 71 LC11 neurons. We then sorted the results based on the cell type and the total synaptic weights from LC11, and visualized neurons that belonged to cell types that had a large number of synaptic inputs from LC11 (Figures S7J–N).

QUANTIFICATION AND STATISTICAL ANALYSIS

For behavioral experiments and non-single cell functional imaging experiments, each fly-cell type was counted as an independent measurement for statistical purposes. ROIs of a particular cell type within a fly were averaged together to produce each measurement for the fly-cell type. For single cell functional imaging experiments, each cell was counted as an independent measurement. All p-values presented are either results of a Wilcoxon sign-rank test (paired by fly/cell, across condition comparisons) or rank-sum test (within condition, across genotype comparisons). The p-values are Bonferroni corrected when we conduct all-to-all tests among indicator types (Figure 6). The numbers of samples and significance thresholds used are noted in figure captions.

Highlights.

1. Small visual objects elicit brief freezing in Drosophila, mediated by LC11 neurons

2. LC11 responses are inconsistent with existing models for small object detection

3. Pooling of size-tuned, adapting units explains selectivity for object displacement

4. Visualized neurochemical inputs to LC11 are consistent with this pooling model