Optimal machine learning methods for radiomic prediction models: Clinical application for preoperative T₂ *‐weighted images of cervical spondylotic myelopathy

Abstract

Introduction

Predicting the postoperative neurological function of cervical spondylotic myelopathy (CSM) patients is generally based on conventional magnetic resonance imaging (MRI) patterns, but this approach is not completely satisfactory. This study utilized radiomics, which produced advanced objective and quantitative indicators, and machine learning to develop, validate, test, and compare models for predicting the postoperative prognosis of CSM.

Materials and methods

In total, 151 CSM patients undergoing surgical treatment and preoperative MRI was retrospectively collected and divided into good/poor outcome groups based on postoperative modified Japanese Orthopedic Association (mJOA) scores. The datasets obtained from several scanners (an independent  scanner) for the training (testing) cohort were used for cross‐validation (CV). Radiological models based on the intramedullary hyperintensity and compression ratio were constructed with 14 binary classifiers. Radiomic models based on 237 robust radiomic features were constructed with the same 14 binary classifiers in combination with 7 feature reduction methods, resulting in 98 models. The main outcome measures were the area under the receiver operating characteristic curve (AUROC) and accuracy.

Results

Forty‐one (11) radiomic models were superior to random guessing during CV (testing), with significant increased AUROC and/or accuracy (P _AUROC < .05 and/or P _accuracy < .05). One radiological model performed better than random guessing during CV (P _accuracy < .05). In the testing cohort, the linear SVM preprocessor + SVM, the best radiomic model (AUROC: 0.74 ± 0.08, accuracy: 0.73 ± 0.07), overperformed the best radiological model (P _AUROC = .048).

Conclusion

Radiomic features can predict postoperative spinal cord function in CSM patients. The linear SVM preprocessor + SVM has great application potential in building radiomic models.

This study builds and analysis 98 radiomic machine learning models to predict postoperative spinal cord function in CSM, and finds out that the optimal radiomic model is better than the optimal radiological model.

1. INTRODUCTION

Cervical spondylotic myelopathy (CSM), an age‐related degenerative disease that is common worldwide, ¹ is mainly caused by the compression of the spinal cord and may possibly lead to disability. ² , ³ , ⁴ Surgery to reduce direct compression of the spinal cord might alleviate disease progression ¹ ; however, due to individual differences, some patients do not benefit from surgery. ⁵ Prognostic prediction is important because it affects subsequent treatment decision making. Currently, prognosis is generally based on magnetic resonance imaging (MRI) with a detailed macrostructural evaluation of the spinal cord. ⁶ Unfortunately, the use of conventional MRI indicators (eg, increased intensity signal [ISI]) to predict CSM outcomes has been controversial ⁵ , ⁷ because of their subjectivity or the insufficient information contained therein.

Radiomics, which makes full use of medical images with objective measurements, has contributed greatly to the study of predictive models. ⁸ , ⁹ Machine learning (ML) effectively utilities radiomic features and has the potential to build effective and reliable models. Recent studies revealed that radiomics and corresponding models demonstrated advantages in multiple tumor diseases, ¹⁰ , ¹¹ , ¹² however, their application in nontumor diseases are still in the initial stage. To date, radiomic studies in CSM are still lacking.

In this article, we constructed radiological and radiomic models based on classifiers with/without feature reduction methods and validated, tested, and compared these models. We aimed to utilize preoperative MRI and identify the optimal model to predictive postsurgical spinal cord function in CSM patients.

2. MATERIALS AND METHODS

2.1. Patients

The study design was approved by the appropriate ethics review board, which waived the requirement of informed consent due to the retrospective nature of the study. A total of 151 patients (99 men and 52 women) who underwent surgical treatment in our hospital from January 2017 to June 2017 were included in our study. The inclusion criteria were (a) diagnosed with CSM and operated on by a specific team which was led by one senior orthopedist; (b) available preoperative MRI results; (c) high‐quality image data with no motion artifacts; and (d) preoperative and long‐term follow‐up (≥3 years) modified Japanese Orthopedic Association (mJOA) score. The exclusion criteria were as follows: (a) prior head or neck surgery; and (b) a history of notable additional diseases (spinal cord tumor, multiple sclerosis, syringomyelia, spinal cord injury, or motor neuron disease). Clinical data collected included age, sex, symptom duration, and surgery. Neurological impairment was measured using mJOA. Participants were classified into a poor outcome group (postoperative mJOA score < 16) and a good outcome group (postoperative mJOA score ≥ 16), as patients with a postoperative mJOA score less than 16 still have severe residual deficits. ⁵ , ¹³

2.2. MRI methods

MR scans were performed with 3 T MR (GE Healthcare, Waukesha Wisconsin and Siemens Medical Solutions, Erlangen, Germany) and 1.5 T MR (GE Healthcare, Waukesha, Wisconsin) scanners with patients in the head‐first supine position. The parameters are shown in Table S1.

The dataset obtained from one scanner (n = 41) was regarded as the testing cohort, and the dataset obtained from the rest scanners (n = 110) was regarded as the training cohort.

2.3. Radiologic evaluation

ISI in T₂ ^*WI was classified into four types ¹⁴ : type 0, no ISI; type 1, ISI with a diffuse boundary (≥2/3 spinal cord); type 2: ISI with a diffuse boundary (<2/3 spinal cord); and type 3: ISI with a distinct boundary (<2/3 spinal cord). Two radiologists classified ISI on axial images independently under the supervision of a senior radiologist without knowledge of preoperative and postoperative neurological function, and disagreements were discussed until a consensus was reached. The compression ratio (CR) was computed automatically with the help of spinal cord toolbox (SCT) to describe the severity of the compression of the spinal cord, ¹⁵ , ¹⁶ , ¹⁷ defined as follows:

$$\text{Compression ratio}\left(\mathrm{CR}\right)=\frac{\text{Anterior‐posterior diameter}}{\text{Right‐to‐left diameter}}$$

The details of the automatic computation are described in the following section. The slice with the lowest CR, which indicated the most severe compression, ¹⁵ , ¹⁶ , ¹⁷ over the whole spine was chosen as the maximum compressed level (MCL).

2.4. Image preprocessing

To limit the differences among images, we applied a standardized MRI preprocessing pipeline. ¹⁸ First, resample the images to ensure the same resolution. Second, pre‐crop images around the centerline of the spinal cord were taken to ensure the same size. Third, the intensity of images was normalized to ensure that the intensity of the same tissue was consistent. Fourth, the 2D image at the MCL was selected, and the Z‐score was used to standardize the image. Steps 1 to 3 were achieved by SCT (Version 4.0.0; https://github.com/neuropoly/spinalcordtoolbox) ¹⁹ (Figure 1). Z‐score standardization was achieved by setting parameters in PyRadiomics (Version 3.0, git://github.com/Radiomics/pyradiomics) ²⁰ when extracting radiomic features.

FIGURE 1.

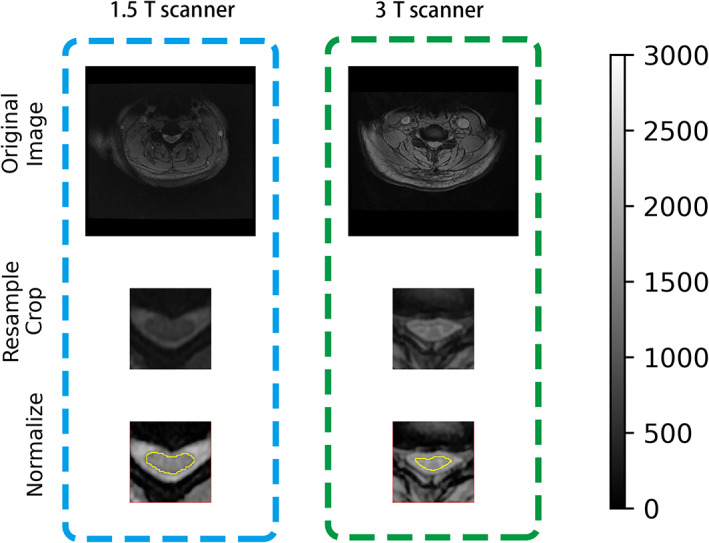
Image preprocessing pipeline. The left (right) column represents images collected from a 1.5 T scanner (3 T scanner). After resampling, cropping, and intensity normalization, images were comparable across scanners. Corresponding automatic segmentation of the spinal cord (yellow line) is shown

2.5. Radiomics: Segmentation

The spinal cord in T₂ ^*WI was segmented automatically by SCT and then manually corrected by two independent radiologists supervised by a senior radiologist. Based on two radiologists' segmentations, the dice coefficient score (DCS, a measurement of similarity) was (median [IQR, interquartile range]) 0.93 (0.90‐0.95), as were the intercorrelation coefficients (ICCs) of CR. For each patient, the slice with the minimum average CR was referred to as the MCL. Under the supervision of a senior radiologist, two independent radiologists checked the selection of MCL and finally confirmed the location of MCL.

2.6. Radiomics: Region of interest

The region of interest (ROI), whose border is widely accepted for radiomic analysis, should include sufficient pixels, refined and effective information, and repeated segmentation; this is the case for the area covered by the spinal cord at the MCL on axial T₂ ^*WI. ²¹ , ²² , ²³ Therefore, we referred to this area as the ROI. In contrast, it is difficult to find an accurate, repeatable, and widely acceptable region on sagittal images, which is why we focused our study on T₂ ^*WI.

2.7. Radiomics: Feature extraction

For the preprocessed T₂ ^*WI at the MCL, three class features (shape, first‐order statistics, and textures [e.g., gray level co‐occurrence matrix (GLCM), gray level size zone matrix (GLSZM), gray level run length matrix (GLRLM), neighboring gray‐tone difference matrix (NGTDM), and gray level dependence matrix (GLDM)]) were extracted from the ROI with/without seven built‐in suitable filters (wavelet, square, square root, logarithm, exponential, gradient, and local binary pattern) for a small ROI, resulting in 1032 features. Related details are available online (https://pyradiomics.readthedocs.io/en/latest/index.html). Excellent robust features (ICC ≥0.90 between the two radiologists' segmentations) were enrolled for subsequent analysis.

2.8. Machine learning

Machine learning (ML) is defined as programming computers to optimize a performance criterion based on previous experience or example dataset. ²⁴ ML is recommended to handle the high‐dimensional data provided by radiomics. ¹ To apply ML in radiomic studies, a general pipeline is widely accepted, including feature reduction, modeling methodology, and evaluation. ¹² Essential information is kept after feature reduction and serves as input to build a model; finally, the application value of the model is assessed. ¹² For excellent robust radiomic features, 14 widely applied built‐in binary classifiers combined with 7 compatible feature reduction methods, totaling 98 radiomic models, were constructed by auto‐sklearn (a Python package that can preprocess the input dataset, reduce the number of features, construct and validate the ML model automatically, Version 0.12.0; https://github.com/automl/autosklearn). The same classifiers were applied for the radiological features, including CR and the types of ISI, resulting in 14 radiological models. A list of the methods and their abbreviations are presented in Table 1. Five‐fold cross‐validation (CV) is a method to effectively use the small sample data. It randomizes the training set into 5‐folds and uses 4‐folds for training and the rest for validation, then repeated five times. CV was applied to train, and validate models. The testing dataset was kept unseen during the whole procedure. The pipeline of radiomic analysis is shown in Figure 2.

TABLE 1.

Abbreviations for the feature reduction methods and classifiers

Feature Preprocessor		Classifiers
Select percentile		DT	Decision tree
Select rates		RF	Random forest
Linear SVM preprocessor	Linear support vector machine preprocessor	ET	Extra trees
ET preprocessor	Extra trees preprocessor	Adaboost	Adaptive boosting
Fast ICA	Fast independent component analysis	GBDT	Gradient boosting decision trees
FA	Feature agglomeration	BNB	Bernoulli naïve Bayes
PCA	Principal component analysis	GNB	Gaussian naïve Bayes
		PA	Passive aggressive
		QDA	Quadratic discriminant analysis
		LDA	Linear discriminant analysis
		Linear SVM	Linear support vector machine
		SVM	Support vector machine
		KNN	K‐nearest neighbors
		SGD	Stochastic gradient descent

FIGURE 2.

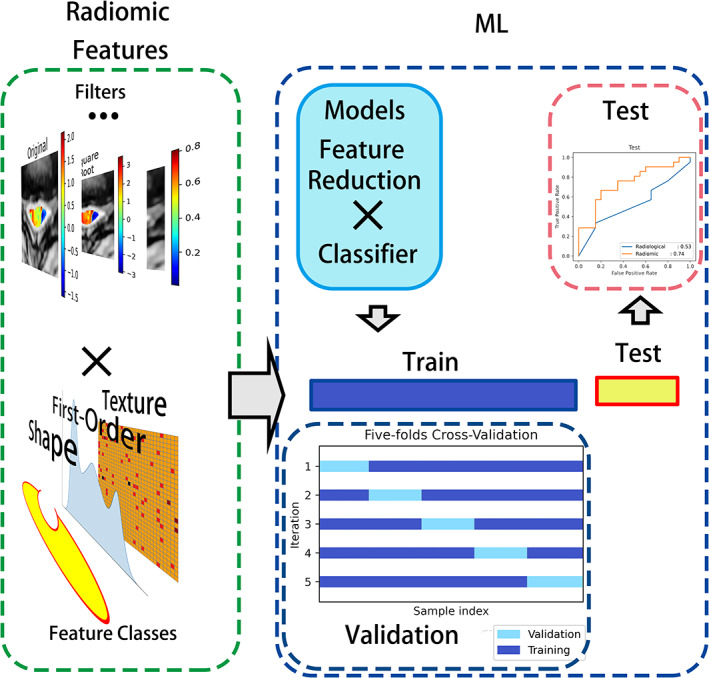
Radiomics analysis pipeline. Radiomic features were extracted from the spinal cord at the MCL of preprocessed images with or without filters. Feature reduction methods combined with binary classifiers resulted in ML models. Models were trained and cross validated on the training dataset and tested on the testing dataset. ML, machine learning; MCL, maximum compression level

2.9. Model evaluation

The area under the receiver operating characteristic (AUROC) and accuracy, widely used overall indicators in medicine and computer science, were regarded as the main evaluation index in our study. A random guessing model whose AUROC (accuracy) equals 0.5 (no information rate [NIR], denoting the best guessing given no information beyond the overall distribution of binary classes), was referred to as the baseline. We arbitrarily subdivided model performance into three groups based on their AUROC and accuracy compared with the random guessing model: (1) high potential clinical application value with significantly increased AUROC and accuracy (P _AUROC < .05, P _accuracy < .05); (2) low potential clinical application value with significantly increased AUROC or accuracy ([P _AUROC < .05, P _accuracy > .05] or [P _AUROC > .05, P _accuracy < .05]); and (3) no potential clinical application value with comparable or decreased AUROC and accuracy. If the grading of performance during CV and testing showed disagreement, the performance on the testing cohort was considered, as the performance on this cohort is more meaningful.

2.10. Model selection and comparison

For overall radiomic or radiological models, the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), a multiple criteria decision‐making method, was used by the package PyTOPS in Python (Version 0.1; http://home.iitb.ac.in/~skarmakar/index.html). This method determines the best solution from a set of alternatives with certain attributes. The best alternative is chosen based on its Euclidean distance from the ideal solution. We used PyTOPS to select the best radiomic or radiological model based on the AUROC and accuracy. The AUROC, accuracy, corresponding standard deviation (SD), and relative SD (RSD, the ratio of SD to the mean value), as well as the sensitivity, specificity, precision and F1 score, were measured and compared. The SDs were measured by a proportion test based on the binomial distribution or bootstrapping 1000 times.

2.11. Statistical analysis

2.11.1. Clinical factors and radiological evaluation

For normally (nonnormally) distributed continuous variables, we applied Student's t‐test (Mann‐Whitney U test). To compare categorical variables, we used the chi‐square test.

2.11.2. Model comparison

AUROCs (accuracy, sensitivity, specificity, precision) were compared by the DeLong test (paired or unpaired proportion test).

2.11.3. Analysis software

Overall, the above statistical analyses were performed using Python modules (SciPy, Version 1.15.0, https://www.scipy.org; Statsmodels, Version 0.13.0, https://www.statsmodels.org; Mlxtend, Version 0.18.0, https://rasbt.github.io/mlxtend/) and R language (pROC, Version 1.17.0.1, https://cran.r-project.org/web/packages/pROC/index.html; caret, Version 6.0.88, https://cran.r-project.org/web/packages/caret/vignettes/caret.html). RSD_AUROC and RSD_accuracy were compared by the Forkman J method (MedCalc, Version 0.20.3, MedCalc Software Ltd, Belgium).

3. RESULTS

3.1. Patient characteristics and conventional MRI features

Images from 80 patients with good outcomes and 71 patients with poor outcomes, comprising a total of 151 subjects, were divided into the training and testing cohorts. No significant differences in clinical factors or radiological factors were observed between the training and testing groups (P > .05) (Table 2).

TABLE 2.

Clinical and radiological factors of 151 subjects

	Train (n = 110)	Test (n = 41)	P
Clinical factors
Age (years) a	54.1 ± 10.6	56.5 ± 8.1	.194
Sex (F/M)	37/73	15/26	.883
Symptom duration (months) b	12.0 (3.3‐37.2)	12.0 (6.0‐48.0)	.359
Preoperative mJOAa	13.5 ± 2.0	13.2 ± 2.1	.435
Operation (anterior/posterior)	65/45	24/17	.901
Outcome (good/poor)	60/50	20/21	.654
Radiological factors
CRa	0.37 ± 0.08	0.38 ± 0.10	.859
ISI			.054
Type 0	23	6
Type 1	20	8
Type 2	58	17
Type 3	9	10

Abbreviations: CR, compression ratio; IQR, interquartile range; ISI, increased signal intensity; mJOA, modified Japanese Orthopedic Association score.

^a Normally distributed continuous variables (mean ± SD) were statistically analyzed by Student's t‐test.

^b Nonnormally distributed continuous variables (median [IQR]) were statistically analyzed by the Mann‐Whitney U test.

3.2. Model application value: Models vs random guessing

3.2.1. Radiological model

Radiological models yielded AUROCs and accuracy ranges of 0.51 to 0.61 and 0.51 to 0.58 (0.36‐0.53 and 0.49‐0.59) during CV (testing). The SVM revealed potential clinical application value during CV (P _AUROC = .049, P _accuracy = .255) (Figure 3 and Figure S1). However, no radiological models showed potential clinical application value in the testing cohort (Figure 4 and Figure S2).

FIGURE 3.

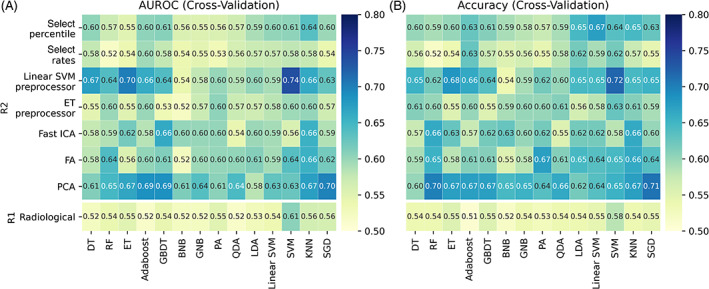
Heatmaps of AUROC and accuracy through 5‐fold CV. R1 (R2) referred radiological (radiomic) models. (A) AUROC; (B) accuracy. CV, cross‐validation; AUROC, area under the receiver operating characteristic curve

FIGURE 4.

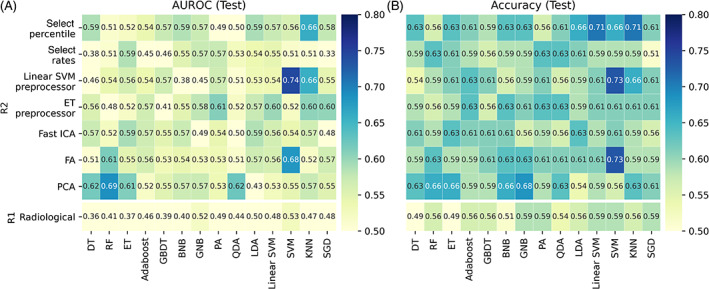
Heatmaps of AUROC and accuracy on the testing cohort. R1 (R2) referred radiological (radiomic) models. (A) ROC‐AUC; (B) accuracy. AUROC, area under the receiver operating characteristic curve

3.2.2. Radiomic model

In total, 237 excellent robust features (108 first‐order features, 9 shape features, and 120 texture features) were retained from 1032 features with ICC ≥ 0.9. During CV, 25 radiomic models demonstrated high potential clinical application value, with AUROC and accuracy ranged 0.61 to 0.74 and 0.64 to 0.72, respectively. Meanwhile, 16 radiomic models demonstrated low potential clinical application value on CV. The remaining 57 models had no potential clinical application value (Figure 3 and Figure S1). In the testing cohort, three radiomic models (linear SVM preprocessor + SVM, FA + SVM, and PCA + RF) were observed to have high potential clinical application value, with AUROCs and accuracies ranging from 0.68 to 0.74 and 0.66 to 0.73. A total of eight radiomic models had low potential clinical application value, while the remaining models had no potential clinical application value (Figure 4 and Figure S2).

3.3. Model comparison: The best radiological model vs the best radiomic model

With TOPSIS, the linear SVM preprocessor + SVM (SVM) was selected as the best radiomic (radiological) model, with an F1 score of 0.72 ± 0.08 (0.45 ± 0.11). The performance of the models is summarized in Table 3. The best radiomic model, based on 13 radiomic features ([filters] feature names), including five shape features ([no filters] pixel surface, minor axis length, maximum diameter, elongation), seven first‐order features ([wavelet‐LL, HL, and gradient] range, [wavelet‐LL] 10 percentiles, [wavelet‐HL] energy, [local binary pattern] mean, and [exponential] variance), and one texture feature ([wavelet‐LL] GLCM cluster prominence), overperformed the best radiological model, showing significantly higher AUROC, stability, and sensitivity (P _AUROC = .048, P _RSDAUROC = .008, P _RSDAccuracy = .024, P _sensitivity = .039).

TABLE 3.

Comparison between the best radiological and radiomic models in the testing cohort

	The best radiological model	The best radiomic model	P
AUROC a	0.53 ± 0.09	0.74 ± 0.08	.048
RSDAUROC b	0.17	0.11	.008
Accuracy c	0.59 ± 0.08	0.73 ± 0.07	.181
RSDAccuracy b	0.13	0.09	.024
Sensitivity c	0.33 ± 0.10	0.67 ± 0.10	.039
Specificity c	0.85 ± 0.08	0.80 ± 0.09	1.000
Precision d	0.70 ± 0.14	0.78 ± 0.10	.645

Abbreviations: AUROC, area under the receiver operating characteristic curve; RSD, relative SD.

^a AUROCs (mean ± SD) were compared by DeLong test.

^b RSDs were compared by Forkman J methods.

^c Proportion indicators (mean ± SD) were compared by paired proportion test (i.e., McNemar's test).

^d Proportion indicators (mean ± SD) were compared by nonpaired proportion test.

4. DISCUSSION

In our study, we utilized radiomics and advanced ML to predict the postoperative prognosis of patients with CSM, compared radiomic models to radiological models, reported the advantages of the radiomic models, and demonstrated the potential clinical application value of the linear SVM preprocessor + SVM, which was identified as the best algorithm for radiomic models.

The preprocessing of images and the choice of ROI are the cornerstones of this research. The repeatability of radiomics is an essential problem, as the signal intensity of MRI varies among scanners and scanning protocols. ²⁵ Normalization is a common solution to increase the reproducibility of images and has been applied in a multi‐center study in the spinal cord. ¹⁸ After normalization, some radiomic models performed well cross multi‐scanners in our study, which might due to the reduced variation of signal intensity. The choice of ROI is also crucial; it is a feasible and practical way to predict the prognosis of CSM by extracting the imaging features from the spinal cord at MCL of T₂ ^*WI rather than ISI. Although ISI is regarded as the lesion of CSM, its size is generally small. Due to the partial volume effect, the boundary is unreliable, and the radiomic features are unstable, ²⁶ indicating that ISI is not suitable for radiomic analysis. The cross‐section of the spinal cord is an alternative, as the reproducibility and repeatability of ROI and radiomic features is increased along with the increasing size of the ROI. ²⁶ , ²⁷ The information contained in the ROI includes information on not only small lesions but also the influence and changes around the ISI and over the whole spinal cord section, which are meaningful and useful. ²¹ , ²² , ²³ We have proven that the morphology, first‐order, and some texture features extracted from ROI are stable and can be used for the effective prediction of CSM.

Model selection is another important part to consider. ²⁸ Multiple algorithms are recommended and applied in spinal diseases, ²⁸ however, the best ML for radiomics in CSM remained unknown. In our study, we propose a protocol to select the best radiomic model. As the reproducibility of radiomic models determines their value for extensive application, the performance with the testing dataset is more meaningful. ²⁹ In addition, various indicators, with their specific advantages and disadvantages, can be used to measure the performance of models from different aspects, but no one alone can synthesize all metrics and comprehensively measure the performance of the models. ³⁰ , ³¹ , ³² Our study also confirmed that the changes in the AUROC and accuracy are not exactly consistent. The TOPSIS method, which has been applied in engineering, marketing management and so on, ³³ provides an alternative method to select models based on various criteria. ³⁴ In TOPSIS analysis, various dimensional criteria are converted into nondimensional criteria, the positive ideal solution with maximum benefits and minimum costs and the negative ideal solution with minimum benefits and maximum costs are formed, and an alternative is evaluated and selected based on its distance to these solutions. ³³ , ³⁵ Therefore, we applied a model selection method based on the AUROC and accuracy of the testing cohort and comprehensively evaluated the performance of the model. The selected model reported the highest AUROC and accuracy, consistent with our expectation.

Our work recommends linear SVM preprocessor + SVM as the best algorithms for radiomics in CSM. ML makes it possible to handle complex and numerous data, however, the optimal ML for radiomics is under debated ³⁶ , ³⁷ and the selection of ML depends on researchers' preference. ¹¹ , ¹² Although tree‐based models (eg, RF and Adaboost) combined with feature reduction were reported to be more preferable, ⁸ , ³⁸ the SVM combined with the linear SVM preprocessor was observed to be the best in our study. The core reason is the nonlinear nature of medical problems; along with nonlinear kernels, which could transform linear input into nonlinear input, SVM has been reported to have the ability to solve nonlinear problems, ⁸ , ³⁹ , ⁴⁰ similar to tree‐based models. As suggested by Gu et al, radiomic models based on SVM with nonlinear kernels performed better than the one with a linear kernel. ⁴¹ Additionally, SVM has special advantage for the small‐size samples. ⁴²

In conclusion, we utilized radiomics to predict CSM prognosis using numerous ML methods, validated and tested the models, and identified the optimal model, namely, the linear SVM preprocessor + SVM, which was superior to radiological models. We acknowledge that there are still some limitations to this study. Our radiomic models were trained on limited sample from a single center. Normalization and an independent testing dataset were applied to enhance models' applicability. The method can be used in future multi‐center data collection when standardization is needed. Meanwhile, we conservatively used the spinal cord on axial T₂ ^*WI but not sagittal T₂WI as the ROI in radiomic analysis. Compared with the sagittal spinal cord, the axial spinal cord at the MCL is a widely recognized ROI with better gray matter contrast, including a high intramedullary signal and the potential to provide even more information. ²¹ , ²² , ²³ Referring to it as the ROI can enhance the repeatability and reliability of radiomics. Our models based on multiple scanners suggested the credibility of this ROI and the ability of the models to be extensively used, thereby providing a foundation for further prospective multi‐center studies. Additionally, the comparisons performed in this study offer a potential reference for the development of new models that may be useful for other radiomics studies.

5. CONCLUSION

Radiomics has high potential application value for the preoperative prediction of CSM outcomes. The optimal model, the linear SVM preprocessor + SVM, provides an alternative approach for physicians to use in their clinical practice.

CONFLICT OF INTEREST

The authors declare no conflicts of interest.

Supporting information

Figure S1 Comparison of performance between constructed models and the random guessing model through 5‐fold CV. R1 (R2) referred radiological (radiomic) models. (a) P values of the difference in AUROCs between the models and the random guessing model; (b) P values of the difference in accuracy between the models and the random guessing model. CV, cross‐validation; AUROC, area under the receiver operating characteristic curve

Figure S2. Comparison of performance between constructed models and the random guessing model on the testing cohort. R1 (R2) referred radiological (radiomic) models. (a) P values of the difference in AUROCs between the models and the random guessing model; (b) P values of the difference in accuracy between the models and the random guessing model. AUROC, area under the receiver operating characteristic curve

Table S1 Parameters of the scanners

Zhang, M.‐Z. , Ou‐Yang, H.‐Q. , Jiang, L. , Wang, C.‐J. , Liu, J.‐F. , Jin, D. , Ni, M. , Liu, X.‐G. , Lang, N. , & Yuan, H.‐S. (2021). Optimal machine learning methods for radiomic prediction models: Clinical application for preoperative T₂ *‐weighted images of cervical spondylotic myelopathy. JOR Spine, 4(4), e1178. 10.1002/jsp2.1178