Density and mechanical properties of vertebral trabecular bone—A review

Abstract

Being able to predict the mechanical properties of vertebrae in patients with osteoporosis and other relevant pathologies is essential to prevent fractures and to develop the most favorable fracture treatments. Furthermore, a reliable prediction is important for developing more patient‐ and pathology‐specific biomaterials. A plethora of studies correlating bone density to mechanical properties has been reported; however, the results are variable, due to a variety of factors, including anatomical site and methodological differences. The aim of this study was to provide a comprehensive literature review on density and mechanical properties of human vertebral trabecular bone as well as relationships found between these properties. A literature search was performed to include studies, which investigated mechanical properties and bone density of trabecular bone. Only studies on vertebral trabecular bone tissue, reporting bone density or mechanical properties, were kept.

A large variation in reported vertebral trabecular bone densities, mechanical properties, and relationships between the two was found, as exemplified by values varying between 0.09 and 0.35 g/cm³ for the wet apparent density and from 0.1 to 976 MPa for the elastic modulus. The differences were found to reflect variations in experimental and analytical processes that had been used, including testing protocol and specimen geometry. The variability in the data decreased in studies where bone tissue testing occurred in a standardized manner (eg, the reported differences in average elastic modulus decreased from 400% to 10%). It is important to take this variability into account when analyzing the predictions found in the literature, for example, to calculate fracture risk, and it is recommended to use the models suggested in the present review to reduce data variability.

1. INTRODUCTION

Osteoporosis is a systemic skeletal disease that involves a reduction in the quantity and quality of bone, resulting in low mineral density and increased bone fragility. It affects more than 200 million people worldwide, ^{1 , 2 , 3} and the lifetime risk for an osteoporotic fracture, spontaneous or due to, for example, a fall, is estimated to be approximately 40%. ^{3 , 4 , 5} With the worldwide increase in the active, aging population, the number of fractures is expected to grow significantly. Women are affected by osteoporosis to a greater extent than men, and in the spine, the incidence of fractures due to osteoporosis is 1.6 to 3 times higher in women. ^{3 , 6} Although less common than osteoporosis, other diseases may also give rise to an increased fracture risk in the spine. However, the effect of other pathologies has not been widely studied except for multiple myeloma. Multiple myeloma is a chronic malignant cell disorder, which occurs in 2.5 to 7.2 people per 100 000 within Western countries. ^{7 , 8} Apart from other paraneoplastic phenomena such as anemia, renal dysfunction, or hypercalcemia, multiple myeloma is primarily associated with both widespread osteolytic bone destruction and a generalized bone loss. ^{9 , 10} The presence of lesions is related to significant disease‐related morbidity, ¹¹ and in fact, 50% to 70% of patients diagnosed with multiple myeloma will experience a spinal fracture. ¹² Metastases may also give rise to a change in vertebral morphology, with subsequent fractures and/or neurological deficit as a result. ¹³ Approximately 70% of cancer patients present metastases at the time of death, and the most common site of bone lesions is the spine. ^{13 , 14}

A disease like osteoporosis or metastatic infiltration may not become evident until fracture occurs. ^{3 , 11} Many studies have, therefore, focused on trying to estimate fracture risk, by determining bone quality through non‐invasive techniques, so that patients can be treated to possibly prevent painful fractures. Clinical fracture prediction tools are currently based on empirical models. The most common clinical method of estimating fracture risk is to measure the bone mineral density (BMD) of the patient's bone and compare it to the mean BMD of a reference group. ³ In several studies, ^{15 , 16 , 17 , 18 , 19} the BMD, together with the geometry of the vertebra, has been found to correlate with the bone strength. The areal BMD (aBMD), that is, the bone mineral content divided by the projected bone area (g/cm²), is usually determined by dual‐energy X‐ray absorptiometry (DXA), whereas the mean volumetric BMD (vBMD), that is, the bone mineral content per volume (generally as equivalent content of hydroxyapatite per volume, in gHA/cm³), can be determined using quantitative computed tomography (QCT). Areal BMD measurements are faster and give a lower dose of radiation to the patient; however, volumetric BMD measurements give 3D distribution information, which can be combined with finite element analysis (FEA) to enable 3D simulation in which element's properties are given according to respective BMD. ²⁰ FEA has also been widely used to study the mechanical behavior of human vertebral bone ^{21 , 22 , 23 , 24 , 25 , 26 , 27} based on clinical computed tomography images (CT/FEA). Studies have indicated that nonlinear CT/FEA is a better method to predict failure than lumbar spine aBMD and vBMD for vertebral fractures. ^{23 , 28 , 29} Numerical modeling could also be used to understand the biomechanics of different pathologies or to develop and improve treatments for the spine. ³⁰ Relating bone density to mechanical properties is important for the correct representation of bone tissue in computational models. ^{31 , 32 , 33} In the literature, numerous studies correlating bone density to mechanical properties can be found, with a large variation in their results, and most of them have been summarized in a comprehensive review. ³² However, the review gives no recommendation for which density‐mechanical property relationships to use. Furthermore, considering only site‐specific relationships should decrease the data scattering, since it has been found that the results are strongly anatomical site‐dependent. ^{34 , 35}

In addition, the large variation in density‐mechanical property relationships is problematic for the development of biomaterials: in vertebroplasty, for example, the development of a bone cement that matches the modulus of non‐pathological trabecular bone could be of interest, ³⁶ as the large difference in moduli between acrylic bone cement and the surrounding bone has been suggested to increase the risk of fractures in vertebrae adjacent to treated ones. ^{37 , 38} However, a target value is difficult to define due to the large variation in reported properties. One reason for this variation could be that studies have not divided vertebrae into different pathologies, which may affect the bone quality in different ways, but only related the apparent density or vBMD with, for instance, the strength. ^{19 , 39 , 40 , 41 , 42} However, different studies have confirmed that osteoporotic vertebrae or vertebrae infiltrated with lytic metastasis have notably reduced mechanical properties in terms of both local material properties, such as compressive elastic modulus and compressive yield strength of the trabecular bone ^{43 , 44} as well as structural properties such as vertebral body stiffness. ⁴⁵ On the basis of these results, the prediction of mechanical properties of pathological tissue would benefit from pathology‐specific relationships.

Reliable data of the mechanical properties of vertebral trabecular bone and how they correlate to density are, hence, required to achieve CT‐based FE methods to calculate fracture risk of vertebrae with higher precision, as well as to develop biomaterials with mechanical properties optimized for the loading scenarios in the vertebrae.

The aim of this review was to provide a comprehensive literature review on density and mechanical properties of human vertebral trabecular bone tissue as well as the relationships found between these properties with, where possible, to facilitate fracture prediction and the development of vertebral biomaterials. Furthermore, the relationships from the literature were evaluated in order to propose the use of more specific models, for use in, for example, numerical models.

2. METHODS

A literature search was carried out on the database PubMed to find relevant publications. The following keywords were used for the literature search: human AND (spine OR vertebra*) AND (trabecular OR cancellous OR spongy) AND (density OR BMD) AND (mechanical OR compress* OR tens* OR shear OR torsion* OR bending OR flex*) AND (strength OR stress OR modulus). The literature search resulted in 438 publications that were manually filtered to include only studies where a mechanical property or a density had been investigated. Furthermore, only studies on trabecular bone tissue were investigated, in total 27 publications. Therefore, studies on whole vertebrae, for example, Dall'Ara et al, ²² McBroom et al, ⁴⁶ Oravec et al, ⁴⁷ and Fields et al ⁴⁸ were excluded. All studies in this review were performed at the thoracic‐lumbar region. The reference lists of the included publications were also scanned and crosschecked to search for any other studies that encompassed the above stated criteria.

For clarity, it should be noted that all densities and mechanical properties reviewed in this study were measured on macroscopic samples, that is, local (micro‐level) trabecular properties (as evaluated through, for example, nano‐ or micro‐indentation) were not included in the scope of this study.

3. RESULTS

3.1. Bone density

Traditional density measurements (eg, weighing and/or the Archimedes method) as well as QCT measurements have been performed in order to estimate parameters such as wet, dry, and ash apparent density (ie, wet, dry, and ash weight of bone tissue per unit volume, respectively) and vBMD for vertebral trabecular bone. Table 1 summarizes the studies found for these parameters.

TABLE 1.

Density properties of vertebral trabecular bone

Parameter	Average ± SD (range)	Number of subjects, age	Further division	Reference
Volumetric density (g/cm3)
Apparent density (wet) a
Female	N/A (≈0.11‐0.15)	2F, 78 and 82y	No lesions	43
	N/A (≈0.17‐0.22)	2F, 78 and 82y	Osteoblastic lesions	43
	N/A (≈0.09‐0.13)	2F, 78 and 82y	Osteolytic lesions	43
Mixed sex	0.18 ± N/A (0.11‐0.35)	9F, 16M, 20‐90y	N/A	39
	0.17 ± 0.04 (0.11‐0.27)	6F, 5M, 32‐65y	Compression b	41
	0.19 ± 0.04 (0.11‐0.27)	6F, 5M, 32‐65y	Tension b	41
	0.18 ± 0.05 (N/A)	9F, 16M, 20‐90y	Compression b	59
	0.19 ± 0.04 (N/A)	9F, 16M, 20‐90y	Tension b	59
	0.14 ± 0.06 (0.09‐0.28)	6F, 9M, 46‐91y	N/A	58
	N/A (≈0.10‐0.35)	14, N/A	N/A	57
Apparent density (dry) c
Male	0.15 ± 0.056 (0.048‐0.297)	5M, 70‐84y	N/A	39
Mixed sex	0.22 ± 0.05 (0.15‐0.36)	10F, 12M, 47‐95y	N/A	72
Apparent density (ash) d
Male	0.091 ± 0.035 (0.028‐0.182)	5M, 70‐84y	N/A	39
	0.126 ± 0.035 (0.08‐0.217)	US, 4M, <60	Healthy inferior‐superior direction	53
	0.116 ± 0.028(0.08‐0.187)	US, 4M, <60	Healthy mediolateral direction	53
Mixed sex	0.133 ± 0.006 (0.07‐0.24)	27F, 15M, 15‐87y		55
vBMD—apparent density (CT)
Male	N/A (≈0.04‐0.2)	5M, 53‐80y	N/A	19
Mixed sex	0.124 ± 0.011 (≈0.05‐0.330)	4F, 3M, 23‐67y	N/A	42
	N/A (≈0.02‐0.21)	13F, 19M, 20‐91y	N/A	40
	N/A (≈0.1‐0.39) e	21F, 22M, 23‐93y	Healthy	44
	N/A (≈0.06‐0.19) e	21F, 22M, 23‐93y	Osteoporotic	44
	N/A (≈0.03‐0.55) e	7F, 8M, 36‐83y	Metastatic	44

^a Evaluated, after removing nonmineralized tissue in a wet state, as the wet weight divided by the apparent volume.

^b Specimens for compressive and tensile testing, respectively.

^c Evaluated, after removing nomineralized tissue and drying (ie, in furnace at 100°C for 1 h ³⁹ or room temperature 24 h ⁷² ), as the dry weight divided by the apparent volume.

^d Evaluated, after removing nomineralized tissue and ashing (ie, in furnace at 650°C for 18 h, ³⁹ 700°C for 24 h, ⁵³ or at 580°C for 24 h ⁵⁵ ), as the ash weight divided by the apparent volume.

^e Mixture of femoral and vertebral specimens.

3.2. Mechanical properties

Generally, the mechanical compressive properties are determined by cutting out trabecular bone specimens from a whole bone and loading them in a materials testing machine. In the literature, the use of different test setups can be found. ³² Most mechanical testing on vertebral trabecular bone has been performed using simple compression tests on cylindrical or cubic cores. However, a few studies have also been performed in tension, torsion, and shear. A summary of the reported mechanical properties can be found in Tables 2 and 3.

TABLE 2.

Compressive mechanical properties of vertebral trabecular bone. If not otherwise specified, the properties were measured in the inferior‐superior direction

Parameter	Average ± SD (range)	Number of subjects, age	Further division	Test geometry	Reference
Compressive strength (MPa)
Ultimate strength
Male	N/A (≈0.04‐4)	5M, 53‐80y	N/A	Cylinder	19
	N/A (≈0.05‐5)	5M, 70‐84y	N/A	Cube	39
Mixed sex	2.23 ± 0.95 (0.70‐4.33)	6F, 5M, 32‐65y	N/A	Cylinder	41, a
	0.91 ± 0.63 (0.05‐2.8)	27F, 21M, 54‐95y	N/A	Cylinder	64
	3.3 ± 2.4 (0.4‐10.6)	16F, 12M, 23‐91y	N/A	Cylinder	73
	1.3 ± 0.2 (≈0.1‐3)	4F, 3M, 23‐67y	N/A	Cube	42
	1.28 ± 1.06 (0.038‐2.92)	7, 23‐67y	N/A	Cube	54
	1.6 ± 0.9 (0.6‐3.9)	10F, 12M, 47‐95y	N/A	Cube	72
Yield strength
Male	0.86 ± 0.32 (0.4‐1.56)	4M, <60y	N/A	Cylinder	53
	0.37 ± 0.16 (0.21‐0.67)	4M, <60y	ML direction b	Cylinder	53
Mixed sex	1.92 ± 0.84 (0.56‐3.71)	6F, 5M, 32‐65y	N/A	Cylinder	41, a
	10.0 ± 2.2 (≈2‐14)	21F, 22M, 23‐93y	Healthy	Cylinder	44, c , d
	4.0 ± 2.2 (≈0.1‐7)	21F, 22M, 23‐93y	Osteoporotic	Cylinder	44, c , d
	4.0 ± 1.0 (≈0.1‐24)	7F, 8M, 36‐83y	Metastatic	Cylinder	44, c , d
	2.05 ± 0.94 (N/A)	14, N/A	Strain range 0%‐0.10%	Cylinder	57, a
	2.11 ± 0.97 (N/A)	14, N/A	Strain range 0.02%‐0.24%	Cylinder	57, a
	2.02 ± 0.92 (N/A)	9F, 16M, 20‐90y	N/A	Cylinder	59, a
	N/A (≈0.2‐5.5)	13F, 19M, 20‐91y	N/A	Cylinder	40, a
Compressive modulus (MPa)
Male	189.7 ± 67.5 (93.5‐365)	4M, <60y	IS direction b	Cylinder	53
	59.9 ± 31.7 (27.2‐143.5)	4M, <60y	ML direction b	Cylinder	53
	99.0 ± 38.5 (58‐154.2)	5M, 63‐80y	IS direction b	Cube	74
	28.1 ± 16.3 (11.9‐48.8)	5M, 63‐80y	AP direction b	Cube	74
	14.3 ± 5.1 (7.2‐19.1)	5M, 63‐80y	ML direction b	Cube	74
	N/A (20‐300)	5M, 53‐80y	N/A	Cylinder	19
	N/A (≈1‐70)	5M, 70‐84y	N/A	Cube	39
Mixed sex	319 ± 189 (≈30‐870)	13F, 19M, 20‐91y	N/A	Cylinder	40, a
	291 ± 113 (90‐536)	6F, 5M, 32‐65y	N/A	Cylinder	41, a
	356.2 ± 89.7 (≈120‐480)	21F, 22M, 23‐93y	Healthy	Cylinder	44, c
	189.9 ± 95.4 (≈20‐270)	21F, 22M, 23‐93y	Osteoporotic	Cylinder	44, c
	201.5 ± 59.7 (≈40‐640)	7F, 8M, 36‐83y	Metastatic	Cylinder	44, c
	336 ± 145 (N/A)	14, N/A	Strain range 0%‐0.10%	Cylinder	57, a
	322 ± 134 (N/A)	14, N/A	Strain range 0.02%‐0.24%	Cylinder	57, a
	165 ± 110 (32‐355)	6F, 9M, 46‐91y	Endcaps	Cylinder	58, a
	121 ± 97 (4‐261)	6F, 9M, 46‐91y	Platen	Cylinder	58
	344 ± 148 (N/A)	9F, 16M, 20‐90y	N/A	Cylinder	59, a
	75 ± 32 (10‐139)	27F, 21M, 54‐95y	N/A	Cylinder	64
	430 ± 130 (≈200‐600)	3F, 7M, 37‐84y	N/A	Cylinder	65
	317 ± 227 (51.1‐976)	16F, 12M, 23‐91y	N/A	Cylinder	73
	83 ± 16 (≈1‐200)	4F, 3M, 23‐67y	N/A Destructive testing	Cube	42
	63 ± 10 (N/A)	4F, 3M, 23‐67y	N/A	Cube	42
	29 ± 6 (N/A) 25 ± 5 (N/A)	4F, 3M, 23‐67y	AP direction b	Cube	42
	63 ± 10 (N/A)	4F, 3M, 23‐67y	ML direction b	Cube	42
	77 ± 43 (N/A) 47 ± 28 (N/A)	2F, 78 and 82y	No lesions	Cube	43
		2F, 78 and 82y	Osteolytic lesions	Cube	43
	45 ± 18 (N/A)	2F, 78 and 82y	Osteoblastic lesions	Cube	43
	58.5 ± 54 (7‐180)	7, 23‐67y	N/A	Cube	54
	32.7 ± 35 (1‐137)	7, 23‐67y	AP direction b	Cube	54
	33 ± 33 (1‐102)	7, 23‐67y	ML direction b	Cube	54
	67 ± 7 (≈9‐175) 20 ± 3 (≈5‐67)	27F, 15M, 15‐87y	N/A	Cube	55
	33 ± 33 (1‐102)	27F, 15M, 15‐87y	AP/ML direction b	Cube	55
	62.2 ± 57.8 (≈0.1‐225)	7, 23‐67y	N/A	Cube	56
	23.5 ± 22.8 (N/A)	7, 23‐67y	AP direction b	Cube	56
	22.6 ± 21.6 (N/A)	7, 23‐67y	ML direction b	Cube	56
	134 ± 81 (15‐294)	10F, 12M, 47‐95y	N/A	Cube	72
Compressive failure strain (%)
Ultimate strain	1.45 ± 0.33 (0.96‐2.30)	6F, 5M, 32‐65y	N/A	Cylinder	41, a
	2.9 ± 0.2 (N/A)	4F, 3M, 23‐67y	N/A	Cube	42
Yield strain	0.78 ± 0.06 (≈0.65‐0.87)	13F, 19M, 20‐91y	N/A	Cylinder	40, a
	0.84 ± 0.06 (0.75‐0.95)	6F, 5M, 32‐65y	N/A	Cylinder	41, a
	0.68 ± 0.11 (0.46‐0.93)	US, 4M, <60y	IS direction b	Cylinder	53
	0.88 ± 0.16 (0.65‐1.2)	US, 4M, <60y	ML direction b	Cylinder	53
	0.80 ± 0.06 (N/A)	14, N/A	Strain range 0%‐0.10%	Cylinder	57
	0.85 ± 0.06 (N/A)	14, N/A	Strain range 0.02%‐0.24%	Cylinder	57
	0.77 ± 0.06 (N/A)	9F, 16M, 20‐90y	N/A	Cylinder	59, a
	0.69 ± 0.03 (N/A)	5F, 8M, 48‐87y	On‐axis	Cylinder	60, a
	0.74 ± 0.07 (N/A)	5F, 8M, 48‐87y	45° off‐axis	Cylinder	60, a

^a Studies fulfilling the recommendations in the literature for trabecular testing (ie, endcaps with extensometer, cylindrical geometry with a diameter of at least 7.5 mm, and a height‐diameter ratio of at least 2:1).

^b Specimens tested in the IS (inferior‐superior) direction, ML (mediolateral) direction, or AP (anteroposterior) direction.

^c Mixture of femoral and vertebral specimens.

^d Average values 10 times as large were reported in the reference but due to the range found in the graphs, this was assumed to be a mistake.

TABLE 3.

Mechanical (except compressive) properties of vertebral trabecular bone. All properties were measured in the inferior‐superior (caudal‐cranial) direction

Parameter	Average ± SD (range)	Number of subjects, age	Further division	Test geometry	Reference
Tensile strength (MPa)
Ultimate strength
	2.23 ± 0.76 (1.33‐3.53)	6F, 5M, 32‐65y	N/A	Cylinder	41
Yield strength
	1.75 ± 0.65 (0.77‐2.75)	6F, 5M, 32‐65y	N/A	Cylinder	41
	1.76 ± 0.65 (N/A)	14, N/A	Strain range 0%‐0.10%	Cylinder	57
	1.82 ± 0.68 (N/A)	14, N/A	Strain range 0.02%‐0.24%	Cylinder	57
	1.72 ± 0.64 (N/A)	9F, 16M, 20‐90y		Cylinder	59
Tensile modulus (MPa)
	301 ± 100 (139‐472)	6F, 5M, 32‐65y	N/A	Cylinder	41
	338 ± 128 (N/A)	14, N/A	Strain range 0%‐0.10%	Cylinder	57
	319 ± 119 (N/A)	14, N/A	Strain range 0.02%‐0.24%	Cylinder	57
	349 ± 133 (N/A)	9F, 16M, 20‐90y	N/A	Cylinder	59
	450 ± 150 (≈190‐620)	3F, 7M, 37‐84y	N/A	Cylinder	65
Tensile strain (%)
Ultimate strain
	1.59 ± 0.33 (1.09‐2.51)	6F, 5M, 32‐65y	N/A	Cylinder	41
Yield strain
	0.78 ± 0.04 (0.71‐0.88)	6F, 5M, 32‐65y	N/A	Cylinder	41
	0.72 ± 0.05 (N/A)	14, N/A	Strain range 0%‐0.10%	Cylinder	57
	0.78 ± 0.05 (N/A)	14, N/A	Strain range 0.02%‐0.24%	Cylinder	57
	0.70 ± 0.05 (N/A)	9F, 16M, 20‐90y	N/A	Cylinder	65
Shear strength (MPa)
	3.1 ± 1.6 (1.4‐7.8)	10F, 12M, 47‐95y	N/A	Cylinder	72
	1.56 ± 0.39 (N/A)	US, 9M, 47‐98y	N/A	Cylinder disk	75
	0.68 ± 0.29 (N/A)	US, 6F, 47‐98y	N/A	Cylinder disk	75
Torsional modulus (MPa)
	88 ± 31 (≈40‐120)	3F, 7M, 37‐84y	N/A	Cylinder	65
Creep modulus (MPa)
Loading modulus
	251 ± 126	USA, 3F, 3M, 63‐85y	N/A	Cylinder	76
Unloading modulus
	274 ± 132	USA, 3F, 3M, 63‐85y	N/A	Cylinder	76

3.3. Relationship between density and mechanical properties

Several equations have been proposed to relate bone density to mechanical properties. These are summarized in Table 4. As can be seen in Table 4, in several cases, the same mechanical property was correlated with different types of density (eg, vBMD, apparent wet, dry, and ash density). To make a comparison possible among the correlations, all densities were transformed to ash density based on transformation equations from the literature, ^{49 , 50} see Table 5. However, in the case of compressive yield strength, all relationships reported were with apparent wet density, and hence, they were not transformed. For the other mechanical properties, apparent ash density was chosen to avoid more than one transformation. Keyak et al ⁴⁹ studied the relationships between apparent ash density and both apparent wet density and vBMD (using a dipotassium phosphate phantom). The relationship between apparent density and vBMD is dependent on the type of phantom used to calibrate. Schileo et al ⁵⁰ also related apparent ash density to vBMD, but used a hydroxyapatite phantom. Both types of phantoms have been used in the studies included in this review. Some authors presented both a linear and a power equation for the same analysis or reported relationships between a mechanical property and several densities; in those cases, the equation with the higher coefficient of determination (R ²) was used. It has been found, both theoretically ⁵¹ and experimentally, ⁵² that the testing direction with respect to the trabecular main direction has a significant effect on the mechanical properties of trabecular bone. Samples tested along the inferior‐superior direction have been reported to have mechanical properties more than twice those of samples tested in the mediolateral direction. ^{42 , 53 , 54} However, very few studies ^{42 , 53 , 54 , 55 , 56} investigate the mediolateral direction, and only two reported a relationship between density and mechanical properties. ^{42 , 53} Therefore, only the regressions for trabecular tissue tested along the inferior‐superior direction were included in the analysis.

TABLE 4.

Relationship between mechanical properties and density for vertebral trabecular bone

Parameter	Material model: (ρ[g/cm3])	R 2	Number of subjects, age	Further division	Test geometry	Reference
Compressive strength (MPa)
Ultimate strength
	σ u = 3.84 × 10−5 × vBMD2.12	.50	5M, 53‐80y	N/A	Cylinder	19, a , b
	σ u = −1.46 + 21.9 × ρ wet or σ u = 33.2 × ρ wet 1.53	.71 or .68	6F, 5M, 32‐65y	N/A	Cylinder	41
	σ u = −0.971 + 16.9 × ρ dry or σ u = 97.9 × ρ dry 2.3	.74 or .79	5M, 70‐84y	N/A	Cube	39
	σ u = −0.953 + 27.5 × ρ ash or σ u = 284 × ρ ash 2.27	.74 or .78	5M, 70‐84y	N/A	Cube	39
	σ u = −0.9 + 0.019 × vBMD	.91	4F, 3M, 23‐67y	N/A	Cube	42, b , c
	σ u = −1.89 + 0.021 × ρ ash or σ u = 78.2 × ρ ash 1.8	.89 or .91	27F, 15M, 15‐87y	N/A	Cube	55
Yield strength
	σ y = −0.75 + 24.9 × vBMD or σ y = 37.4 × vBMD1.39	.91 or .95	13F, 19M, 20‐91y	N/A	Cylinder	40, c
	σ y = −0.84 + 14.4 × ρ wet or σ y = 23.2 × ρ wet 1.60	.84 or .88	13F, 19M, 20‐91y	N/A	Cylinder	40
	σ y = −1.4 + 19.6 × ρ wet or σ y = 32.6 × ρ wet 1.60	.73 or .70	6F, 5M, 32‐65y	N/A	Cylinder	41
	σ y = −1.52 + 16.0 × ρ wet	.81	21F, 22M, 23‐93y	Healthy + osteoporotic	Cylinder	44, d
	σ y = −1.67 + 15.5 × ρ wet	.76	7F, 8M, 36‐83y	Metastatic	Cylinder	44, d
	σ y = 6.9 × vBMD − 0.13	.58	4M, <60y	IS direction e	Cylinder	53
	σ y = 18.81 × vBMD1.83	.70	4M, <60y	ML direction e	Cylinder	53
	σ y = 37.1 × ρ wet 1.74	.80	9F, 16M, 20‐90y	N/A	Cylinder	59
Compressive modulus (MPa)
	E = 0.00148 × vBMD2.26	.31	5M, 53‐80y	N/A	Cylinder	19, a , b
	E = 4730 × ρ wet 1.56	.73	9F, 16M, 20‐90y	N/A	Cylinder	34
	E = −34.7 + 3230 × vBMD or E = 2980 × vBMD1.05	.91 or .90	13F, 19M, 20‐91y	N/A	Cylinder	40, c
	E = −97.1 + 2130 × ρ wet or E = 2580 × ρ wet 1.34	.88 or .93	13F, 19M, 20‐91y	N/A	Cylinder	40
	E = 2100 × ρ wet or E = 2350 × ρ wet 1.20	.61 or .60	6F, 5M, 32‐65y	N/A	Cylinder	41
	E = 498 × ρ wet + 8.9	.77	21F, 22M, 23‐93y	Healthy + osteoporotic	Cylinder	44, d
	E = 433 × ρ wet + 20.8	.87	7F, 8M, 36‐83y	Metastatic	Cylinder	44, d
	E = 1493.8 × vBMD	.59	US, 4M, <60y	IS direction e	Cylinder	53
	E = 3349.1 × vBMD1.94	.79	US, 4M, <60y	ML direction e	Cylinder	53
	E = 1540 × ρ wet − 58	.64	6F, 9M, 46‐91y	Endcaps	Cylinder	58
	E = 935 × ρ wet − 15	.31	6F, 9M, 46‐91y	Platen	Cylinder	58
	E = 203 × ρ wet − 7.47 or E = 7570 × ρ dry 1.94	.54 or .70	5M, 70‐84y	N/A	Cube	39
	E = 334 × ρ wet − 7.61 or E = 1890 × ρ ash 1.92	.55 or .70	5M, 70‐84y	N/A	Cube	39
	E = −53 + 1.1 × vBMD	.82	4F, 3M, 23‐67y	Destructive testing (IS direction e )	Cube	42, c
	E = −49 + 1.0 × vBMD	.73	4F, 3M, 23‐67y	IS direction e , E measured at ε = 0.4%	Cube	42, c
	E = −21 + 0.41 × vBMD	.53	4F, 3M, 23‐67y	AP direction e , E measured at ε = 0.4%	Cube	42, c
	E = −1 + 0.23 × vBMD	.33	4F, 3M, 23‐67y	ML direction e , E measured at ε = 0.4%	Cube	42, c
Compressive failure strain (%)
Ultimate strain
	NS f vs ρ wet	N/A	6F, 5M, 32‐65y	N/A	Cylinder	41
Yield strain
	ε = 0.73 + 0.45 × vBMD	.58	13F, 19M, 20‐91y	N/A	Cylinder	40, c
	ε = 0.66 + 1.09 × ρ wet or ε = 1.24 × ρ wet 0.21	.49 or .48	6F, 5M, 32‐65y	N/A	Cylinder	41
	ε = 1.16‐2.414 × vBMD	.17	US, 4M, <60y	ML direction e	Cylinder	53
Tensile strength (MPa)
Ultimate strength
	σ u = 13.2 × ρ wet or σ u = 13.3 × ρ wet 1.07	.47 or .47	6F, 5M, 32‐65y	N/A	Cylinder	41
Yield strength
	σ y = 10.1 × ρ wet or σ y = 10 × ρ wet 1.04	.51 or .51	6F, 5M, 32‐65y	N/A	Cylinder	41
	σ y = 21.7 × ρ wet 1.52	.53	9F, 16M, 20‐90y	N/A	Cylinder	59
Tensile strain (%)
Ultimate strain
	NS f	N/A	6F, 5M, 32‐65y	N/A	Cylinder	41
Yield strain
	NS f	N/A	6F, 5M, 32‐65y	N/A	Cylinder	41
Compressive fatigue strength
	N f = 4.57 × 10−18 × (σ/E 0)−8.54 (at 1.4‐2.9 Hz)	N/A	11, 37‐101y	N/A		77
	σ = 74.3 × ρ 1.76m2.97Nf −0.069	N/A	29, 29‐86y	N/A	Cylinder	78, g

^a A dipotassium phosphate phantom was used to determine vBMD.

^b vBMD was measured in mg/cm³.

^c A hydroxyapatite phantom was used to determine vBMD.

^d Mixture of femoral and vertebral specimens. In the reference, the measured apparent density was called vBMD. However, it was defined as the product of wet tissue density times the average bone volume fraction; hence according to the present study, it is not vBMD but wet apparent density.

^e Specimens tested in the IS (inferior‐superior) direction, ML (mediolateral) direction, or AP (anteroposterior) direction.

^f NS is short for not significant.

^g ρ is the volume fraction and m = 0.00069.

TABLE 5.

Transformation equations between densities, together with coefficient of determination (R²) and when reported, SE of the estimate (SE_estimate)

Equation	R 2	SEestimate	Reference
${\rho }_{\mathrm{ash}}\left[\mathrm{g}/{\mathrm{cm}}^3\right]=0.551{\rho }_{\mathrm{wet}}-0.00478$ (1)	.992	0.00694	49, b
${\rho }_{\mathrm{ash}}\left[\mathrm{g}/{\mathrm{cm}}^3\right]=0.000953\text{vBMD}+0.0457$ a (2)	.993	0.00680	49, b
$\text{vBMD}\left[\mathrm{mg}/{\mathrm{mm}}^3\right]=1.14{\rho }_{\mathrm{ash}}-0.09$ (3)	.997	–	50, c

^a vBMD was measured in mg.

^b Equations established based on trabecular bone from proximal human tibiae.

^c Equations established based on trabecular bone from human and bovine femora.

The relationships between density and compressive ultimate strength, yield strength, and elastic modulus, respectively, are presented in Figures 1, 2, 3 (after the above described transformation). For the remaining mechanical properties (tensile strength, compressive and tensile yield strain, and ultimate strain), only one or a maximum of two relationships were reported, and they were, therefore, not reproduced graphically. All relationships were only plotted within the range of densities reported in the respective study. For the studies that included their raw data, ^{19 , 40 , 41 , 55} the raw data together with the reported relationships were also replicated in Figures 1, 2, 3. In one study, ⁴⁰ the reported relationships were found not to be the best fit for the reported raw data; in that case, both the originally reported relationship and the locally reproduced relationship based on least squares best‐fit were illustrated.

FIGURE 1.

Regressions found in the literature between compressive ultimate strength and ash apparent density for vertebral trabecular bone. Models in black represent studies following current literature recommendations for mechanical testing of bone tissue, while models in gray did not. The three calculated densities, Kopperdahl et al, ⁴¹ Lang et al, ¹⁹ and Augat et al, ⁴² were transformed from wet apparent density (Equation (1)), vBMD (Equation (2)), and vBMD (Equation (3)), respectively. To the right, the raw data for Lang et al ¹⁹ and Mosekilde et al ⁵⁵ are reproduced. The remaining studies did not include raw data, ⁴¹ or it was not possible to distinguish vertebral data from data for other anatomical locations ^{39 , 42}

FIGURE 2.

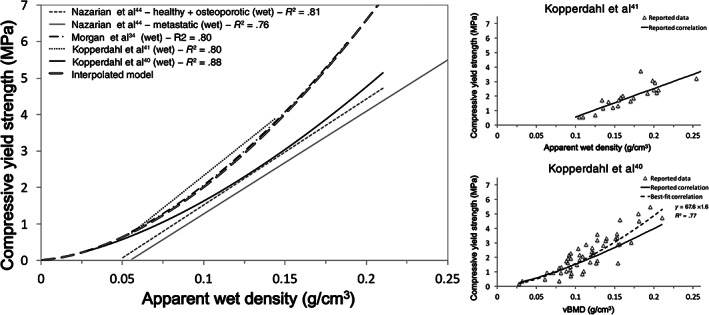
Regressions found in the literature between compressive yield strength and apparent wet density for vertebral trabecular bone, divided by pathology where reported. Models in black represent studies following current literature recommendations for mechanical testing of bone tissue, while models in gray did not. The proposed model is also included. To the right, the raw data for Kopperdahl et al ⁴¹ and Kopperdahl et al ⁴⁰ are reproduced. In the latter, the reported relationship was found not to be the best fit for the reported raw data. Both the reported relationship and the best‐fit relationship were illustrated. In the remaining studies, ^{44 , 57} it was not possible to distinguish vertebral data from data for other anatomical locations

FIGURE 3.

Regressions found in the literature between compressive elastic modulus and ash apparent density for vertebral trabecular bone, divided by pathology where reported. Models in black represent studies following current literature recommendations for mechanical testing of bone tissue, while models in gray did not. The proposed model is also included. Densities from Keaveny et al, ⁵⁸ Kopperdahl et al, ⁴¹ Kopperdahl et al, ⁴⁰ Morgan et al, ³⁴ and Nazarian et al ⁴⁴ were transformed from wet apparent density (Equation (1)), and Lang et al ¹⁹ and Augat et al ⁴² were transformed from vBMD (Equation (2) and Equation (3), respectively). To the right, the raw data for Kopperdahl et al, ⁴¹ Kopperdahl et al, ⁴⁰ and Lang et al ¹⁹ are reproduced. The remaining studies did not include raw data, ^{34 , 42 , 58} or it was not possible to distinguish vertebral data from data for other anatomical locations ^{39 , 44}

4. DISCUSSION

The aim of the present review was to collect and compare the available data in the literature on both mechanical properties and density of vertebral trabecular bone tissue, as well as to evaluate the relationships between these properties. Furthermore, the review aimed to recommend the use of more specific models for numerical modeling, to improve fracture prediction models and facilitate the development and improvement of biomaterials for the spine.

A large range of density values was found, ⁵⁸ for example, reported apparent wet density values ranged between ⁵⁷ 0.09 and 0.35 g/cm³. It has been found that the density and trabecular structure not only vary between anatomical sites, ^{34 , 35 , 59 , 60 , 61} but also between different regions in the same anatomical site. ^{62 , 63} Furthermore, underlying pathologies could have an effect on both density and bone structure. Several authors did not specify whether the vertebrae had been examined for diseases or other factors affecting the bone mineralization prior to testing. Lang et al, ¹⁹ for example, did not specify whether the vertebrae had been examined. Nevertheless, they reported that two specimens from one donor had extremely low bone mineral density. Furthermore, different protocols were used to measure the density of the bone tissue, which might have influenced the results. In the case of wet and dry density, the cleaning procedure used is of importance to obtain a correct density. ⁵⁰ Moreover, there is still a lack of a precise protocol for assessing bone density using CT; factors, such as geometrical calibration, range of density of the calibration phantom used, resolution, scanning parameters, beam hardening correction, position of the vertebra with respect to the scanner, and so forth, all influence the obtained density.

The reported mechanical properties also showed a large range of values, for example, reported average compressive elastic modulus values varied between 75 ± 32 MPa ⁶⁴ and 430 ± 130 MPa ⁶⁵ in healthy bone tested in the superior‐inferior direction. Furthermore, comparing the reported regression equations between density and mechanical properties, a large discrepancy was found in all cases (ie, for compressive elastic modulus, compressive yield and ultimate strength). For instance, for the linear relations (y = A × x + B) for elastic modulus, only including relationships with apparent wet density, a variation in A between 203 and 2100 and of B between7 and 58 was reported. This gives rise to a difference in elastic modulus of an order of magnitude, which would have a large impact on, for example, numerical modeling or development of patient‐specific biomaterials.

The differences in elastic modulus could be, partially, explained by the different testing techniques used in the included studies, that is, platen, ^{19 , 39 , 42 , 43} endcaps with an extensometer, ^{34 , 40 , 41 , 57 , 58 , 59 , 65} and step‐wise loading. ⁴⁴ It has been demonstrated that not measuring strain directly on the tissue and using the platen technique causes a systematic underestimation in elastic modulus in trabecular bone. ⁵⁸ In fact, all studies using the platen techniques ^{19 , 39 , 42} showed a lower elastic modulus (see Figure 3). Another factor that influences the mechanical properties is the cross‐sectional area of the studied trabecular bone. Since trabecular bone has a heterogeneous microstructure, a certain area is needed in order to assume it to be a continuum. Linde et al ⁶⁶ reported that the elastic modulus is directly proportional to specimen cross section (up to a diameter of 7.5 mm or a side length of 6.5 mm) and aspect ratio. The studies with a smaller diameter (4 mm ¹⁹ and 5.4 mm ⁴⁴ ) had, in fact, lower elastic moduli than the studies with larger specimen sizes (>8 mm ^{34 , 40 , 41 , 57 , 58 , 59 , 60} ). Bevill et al ³⁵ found that correction for side‐effects (ie, interruption of the trabecular network along the sides of the machined specimen) improved the prediction of mechanical properties. However, none of the other studies corrected for side effects.

Furthermore, bone tissue is a viscoelastic material and is slightly dependent on strain rate, if the strain rate is increased by an order of magnitude, the measured bone strength will increase by approximately 15%. ⁶⁷ Many of the tests were performed at the same strain rate, that is, 0.005 second⁻¹. ^{34 , 40 , 41 , 42 , 57 , 58 , 59 , 64 , 65} However, some studies used a higher ^{32 , 43} or lower ¹⁹ strain rate, which might have influenced the measured mechanical properties. Strain rates in vivo range between 0.002 second⁻¹ (walking) and 1 second⁻¹ (impact). ⁶⁷ Drying is one of the factors that affect the mechanical properties of bone tissue. It causes an increase in elastic modulus and strength and a decrease in toughness. ^{68 , 69} However, many of the studies did not specify to which degree the bone tissue was humid at the time of mechanical testing, and it is, hence, difficult to draw any conclusions whether this caused a variability in the data. Furthermore, different pre‐conditioning was applied (ranging from no pre‐conditioning to 10 cycles between 0% and 0.8% strain). It is not clear to what extent pre‐conditioning affects the mechanical properties; however, it is possible that it had an effect on the collected data.

A previous review ³² summarized most of the elasticity‐density relationships found in the literature for human bone tissue, that is, not for vertebral bone specifically. Although the studies were normalized by strain rate and type of density and further split by the main factors influencing the mechanical properties (ie, testing technique, specimen geometry, and anatomical site), variation between studies was still found. However, the studies were split by one factor at the time and not by all three of them, due to the limited number of studies. An attempt was made to group the relationships in the present review by the three remaining parameters (testing technique, specimen geometry, and strain rate). However, it was only possible for two properties, that is, compressive elastic modulus and yield strength. If including only the elasticity‐density and compressive yield strength‐density relationships fulfilling the recommendations in the literature for trabecular testing (ie, endcaps with extensometer, ⁵⁸ cylindrical geometry with a diameter of at least 7.5 mm ⁶⁶ and a height‐diameter ratio of at least 2:1 ⁷⁰ ), the variation decreased considerably (see Figures 1, 2, 3). All of those relationships were based on tests performed at the same strain rate, so in this case, there was no need to normalize by this parameter. In the case of compressive elastic modulus, it was possible to see that the range of average modulus decreased drastically, from 83‐319 MPa ^{40 , 42} to 291‐319 MPa ^{40 , 41} (the study of Nazarian et al ⁴⁴ was excluded, since it included a mixture of femoral and spinal specimens). At higher densities, the differences are however still large (eg, in Figure 3, elastic modulus was found to vary between 300 MPa ⁵⁸ and 450 MPa ³⁴ at 0.12 g/cm³), a 50% variation. For yield strength, only three studies ^{40 , 41 , 57} were performed according to the recommendations, and an average value of 1.92‐2.11 MPa was reported ^{41 , 57} (as above Nazarian et al ⁴⁴ was excluded); hence, no comparison was possible in this case. However, it should be noted that all equations, in both cases, have been subjected to a density transformation. Even though the correlations equations used (Equations (1)‐(3)) were reported to have high coefficients of determination (R ² > .99 for all three) and when reported, the SE of the estimate was low (SE_estimate < 0.007 g/cm³), and it might still have influenced the outcome, since the transformation equations were determined based on human tibial trabecular bone ⁴⁹ and femoral trabecular bone (human and bovine). ⁵⁰ It should be confirmed that the equations are valid also for human vertebral trabecular bone.

Although there is still some data scattering, the use of relationships only from studies that have tested vertebral trabecular bone specimens in a standardized way ^{34 , 40 , 41 , 58 , 59} should improve the precision. Therefore, the raw data (when available) and data points based on the reported equations, density range, and sample size were interpolated to achieve new average relationships between apparent wet density and both compressive yield strength and elastic modulus (for compressive ultimate strength only one study ⁴¹ fulfilled the criteria). Apparent wet density was chosen as the density to correlate the mechanical properties with, since most included studies had reported these relationships, Kopperdahl et al ⁴⁰ being the only exception where the raw data included was vBMD. vBMD was transformed to apparent wet density using Equations (2) and (3). In the cases were raw data were not available and both power and linear relationships, the relationship with the higher R² was chosen. The new models are the best‐fit power regression to the data points from the included studies (raw data or based on reported relationships) and can be found in Table 6. The SE of the estimates was also calculated and was found to be in the range of 0.06‐0.61 and 74‐127 MPa, for compressive yield strength and compressive modulus, respectively. It was noted that in general, the error increased with increasing density. The anisotropy and inhomogeneity of the trabecular tissue also influence the mechanical properties ⁷¹ and need to be included for improved predictions. However, the diagnostic tools of today (ie, CT) only provide density and, hence, limit the use of more complex patient‐specific models. Further studies should investigate whether the use of these new relationships improves, for example, the accuracy of numerical models of vertebral biomechanics.

TABLE 6.

Proposed relationships between mechanical properties and apparent wet density for vertebral trabecular bone and calculated SE of the estimate (SE_estimate) of the proposed model against the reported raw data or model from the literature

Parameter	Input data	N° data points	Ref.	Proposed model	SEestimate
Compressive strength (MPa)
Yield strength
	Raw data	21	41	σ y = 38.0 × ρ wet 1.77	0.57
	σ y = 37.1 × ρ wet 1.74	8 a	34		0.06
	Raw data b	52	40		0.61
Compressive modulus (MPa)
	E = 4730 × ρ wet 1.56	8 a	34	E = 3180 × ρ wet 1.38	127
	E = 1540 × ρ wet − 58	9 c	58		88
	Raw data b	73	40		96
	Raw data	22	41		74

^a 22 out 30 samples came from Kopperdahl et al; ⁴¹ therefore, eight data points were evenly distributed over the reported density range (0.11‐0.35 g/cm³), and the reported model was used to calculate the corresponding yield stress and compressive modulus.

^b vBMD was transformed to apparent wet density using Equations (2) and (3).

^c Nine samples had been used to determine the reported model; hence, nine data points were evenly distributed over the reported density range (0.09‐0.28 g/cm³), and the reported model was used to calculate the corresponding compressive modulus.

One limitation to the proposed models is that the studies they are based on all come from the same group of authors. The testing methods and sample geometries used as inclusion criteria are, however, well established and are being more and more implemented. Nevertheless, the validity of the included studies should be verified by other authors.

It was also of interest to look into differences between healthy bone and pathological bone, that is, osteoporotic and metastatic bone. However, only two of the studies included in the present review investigated pathological (osteoporotic or metastatic) trabecular bone tissue from the spine. ^{43 , 44} The results of Hipp et al ⁴³ indicated that the models based on bone density for healthy bone can also be used to estimate Young's modulus and compressive strength of bone tissue with lytic changes, but that tissue with blastic changes, associated with osseous metastases, would need the use of adjusted models. Nazarian et al ⁴⁴ found that the transaxial subregion with the minimum bone volume fraction (BV/TVmin) could estimate variations in both compressive strength and Young's modulus for trabecular bone specimens independently of skeletal site (ie, femur or vertebra) or bone pathology (ie, osteoporosis or metastatic cancer). However, no differentiation was made between lytic and blastic bone in the study of Nazarian et al ⁴⁴ Furthermore, none of the pathology‐specific studies ^{43 , 44} fulfilled the current literature recommendation of local deformation measurements (platen displacement was used in the former and a step‐wise deformation measurement in the latter). Further studies are needed to determine whether or not specific material models are needed for pathological tissue, especially for metastatic bone tissue.

5. CONCLUSIONS

New CT‐based FE methods to calculate fracture risk of vertebrae are of high importance, as well as developing biomaterials for the spine with optimal mechanical properties. Both of these need reliable data of the mechanical properties of vertebral trabecular bone and how they correlate with density. This review serves as a guide to the best relationships to implement for those purposes. A number of studies on the vertebral trabecular bone tissue were analyzed. A non‐negligible variation (more than 4‐fold) was found in the reported densities and mechanical properties, as well as the given relationships between apparent density and mechanical properties. Nevertheless, if considering only the studies meeting the inclusion criteria for trabecular bone testing (ie, using the endcap/extensometer technique and sufficiently large cross sections), the variability decreased significantly (difference in elastic modulus of approximately 10%). It is important to understand the effect of the material model when choosing the appropriate one during development of, for example, numerical models or more patient‐specific biomaterials. The authors provide evidence for the use of more specific material models, which would improve the model fidelity and proposes two interpolated models. This was based on the data found in the literature on vertebral trabecular bone meeting the discussed criteria in sample dimensions (a diameter of at least 7.5 mm and a height‐diameter ratio of at least 2:1) and the use of endcaps with extensometer. The correlations between density and elastic modulus and compressive yield strength were given, respectively:

1. E = 3180 × ρ _wet ^1.38.

2. σ _y = 38.0 × ρ_wet ^1.77.

However, further studies are needed to confirm the validity of these models.

For future studies on trabecular bone properties, the authors believe that it would be beneficial if researchers would at least:

1. Specify patient pathology, sex, and age as a minimum.

2. Follow current literature recommendations regarding the mechanical testing, that is, use endcaps, local deformation measurements (through, for example, extensometers or imaging), and adequate sample dimensions (diameter of ≥7.5 mm, height to diameter ratio of 2:1).

3. Use and report on a strain rate representative for the envisaged real situation.

CONFLICT OF INTEREST

The authors have no conflicts of interest to declare that are relevant to the content of this article.

AUTHOR CONTRIBUTIONS

The study conception and design was proposed by Cecilia Persson. The literature search and data analysis were performed by Caroline Öhman Mägi, Ondrej Holub, Dan Wu, Richard M. Hall, and Cecilia Persson. The first draft of the manuscript was written by Caroline Öhman Mägi, and all authors commented on previous versions of the manuscript.

Öhman‐Mägi, C. , Holub, O. , Wu, D. , Hall, R. M. , & Persson, C. (2021). Density and mechanical properties of vertebral trabecular bone—A review. JOR Spine, 4(4), e1176. 10.1002/jsp2.1176