Technical note: A methodology for improved accuracy in stopping power estimation using MRI and CT

Abstract

Purpose:

Proton therapy is becoming an increasingly popular cancer treatment modality due to the proton’s physical advantage in that it deposits the majority of its energy at the distal end of its track where the tumor is located. The proton range in a material is determined from the stopping power ratio (SPR) of the material. However, SPR is typically estimated based on a CT scan which can lead to range estimation errors due to the difference in x-ray and proton interactions in matter, which can preclude the ability to utilize protons to their full potential. Applications of MRI in radiotherapy have increased over the past decade and using MRI to calculate SPR directly could provide numerous advantages. The purpose of this study was to develop a practical implementation of a novel multimodal imaging method for estimating SPR and compare the results of this method to physical measurements in which values were computed directly using tissue substitute materials fabricated to mimic skin, muscle, adipose, and spongiosa bone.

Methods:

For both the multimodal imaging method and physical measurements, SPR was calculated using the Bethe Bloch equation from values of relative electron density and mean ionization potential determined for each tissue. Parameters used to estimate SPR using the multimodal imaging method were extracted from Dixon water-only and (¹H) proton density-weighted zero echo time MRI sequences and CT, with both kVCT and MVCT used separately to evaluate the performance of each. For comparison, SPR was also computed from kVCT using the stoichiometric method, the current clinical standard.

Results:

Results showed that our multimodal imaging approach using MRI with either kVCT or MVCT was in close agreement to SPR calculated from physical measurements for the four tissue substitutes evaluated. Using MRI and MVCT, SPR values estimated using our method were within 1% of physical measurements and were more accurate than the stoichiometric method for the tissue types studied.

Conclusions:

We have demonstrated the methodology for improved estimation of SPR using the proposed multimodal imaging framework.

1. Introduction

Proton therapy is becoming an increasingly popular cancer treatment modality with the number of centers in operation steadily increasing¹. Compared to more traditional photon-based radiotherapy, protons provide the distinct advantage of depositing the majority of dose immediately before stopping at the distal end, as described by the characteristic Bragg Peak². With appropriate choice of beam angles, target coverage can be achieved while imparting negligible dose to healthy tissue beyond where the beam stops. The calculation of the location of the Bragg Peak relies on a patient-specific map of the stopping power ratio (SPR) relative to water of the material being traversed. A current limitation in utilizing protons to their full potential is the proton beam range uncertainty which stems from relying on kV computed tomography (kVCT) to estimate the map of the SPR. Unlike with photons, in which there is a smaller dosimetric impact from uncertainties in relative electron density and where there is a more direct correlation between CT number and the photon attenuation for specific energies, there is a higher dosimetric impact of uncertainties in proton SPR and no one-to-one relationship between photon attenuation and proton SPR. In practice, the most common approach of estimating the SPR map from kVCT is the stoichiometric method³ which establishes a parametric fit to provide a calibration curve relating CT number and SPRs. However, the unavoidable degeneracy between proton stopping power and kVCT number results in uncertainties on the order of a couple percent.^4,5 In delving into the exact sources of these uncertainties by Paganetti⁶, he found that I_m was the largest single source of range uncertainty in the calculation of SPR by CT imaging, accounting for 1.5% out of a total 2.4% to 2.7%, with and without Monte Carlo calculation, respectively. In practice, these uncertainties are typically accounted for by adding an additional margin (typically 2.5-3.5%) to each beam’s range, which results in increased dose to healthy tissues.^6,7 There are many ongoing efforts aiming to resolve the issue of proton beam range uncertainty, including proton CT and dual-energy CT, both of which have advantages and disadvantages. Proton CT would allow for a direct relationship between CT number and SPR,^8,9 however a primary limitation of its clinical utility is the prohibitively high proton energy required to image a patient.¹⁰ Dual-energy CT (DECT), on the other hand, can be implemented currently on most CT scanners and aims to reconcile the degeneracy using two kV energies. Recent studies^11,12 have shown that DECT has the potential to significantly reduce range uncertainty, with even sub-1% uncertainty in tissues being theoretically possible. While this strategy has shown promise, practically achievable DECT accuracy has been limited by issues related to DECT derived SPR’s increased sensitivity to imaging noise^12,13 and beam hardening effects¹⁴ with the end result being more modest improvements in clinical margins used for proton therapy applications.

There has been increasing interest in using magnetic resonance imaging (MRI) in radiotherapy due to its superior soft tissue contrast compared to CT, and could potentially offer distinct advantages for proton dose calculation if able to directly provide SPR. A theoretical framework, named the Unified Compositions (UC) model, for achieving this was described by Sudhyadhom¹⁵ in which a parametrized model was introduced to estimate the mean ionization potential (I_m) in human biological tissue. Using this framework, a tissue is categorized into three components, namely water, organic tissue, and mineralized bone with their relative percentages determined predominantly through MRI. SPR can be subsequently estimated at the voxel level from I_m and the relative electron density, with the density estimated from CT.

The goal of this work was to outline and implement our multimodal imaging framework for the calculation of SPR through the estimation of relative electron density and mean ionization potential. We evaluated the accuracy of our methodology in phantom tissues for which the elemental composition was established. Our methodology was compared to the clinical standard stoichiometric method and the established physical measurements for the phantom materials. Assuming perfect image registration, we demonstrated the ability to achieve sub-1% accuracy in calculating SPR at the voxel level and attained comparable or superior accuracy to the stoichiometric method for the four phantom tissue types studied.

2. Materials and Methods

2.A. Method Overview

The location of the Bragg Peak can be determined using the SPR of the medium traversed by the proton relative to water, which can be approximated by the Bethe-Bloch equation:

$$\text{SPR}={\rho }_{\text{e},\text{water}}\frac{\text{ln}[2{\text{m}}_{\text{e}}{\text{c}}^2{\beta }^2/{\text{I}}_{\text{m}}\left(1-{\beta }^2\right)]-{\beta }^2}{\text{ln}[2{\text{m}}_{\text{e}}{\text{c}}^2{\beta }^2/{\text{I}}_{\text{water}}\left(1-{\beta }^2\right)]-{\beta }^2}$$ (1)

where ρ_e,water is the electron density of the medium relative to water, m_e is the electron mass, c is the speed of light, β is the proton velocity relative to c, I_m is the mean ionization potential of the medium, and I_water is the mean ionization potential of water. Assuming a proton energy of 115MeV, all variables in Equation 1 are constants except for ρ_e,water and I_m which must be computed for the tissue/medium of interest.

The mean ionization potential of a material can be calculated using the Bragg Additivity Rule (BAR) of elemental composition:

$$\text{ln}{\text{I}}_{\text{m}}=\left({\sum }_{\text{i}}\frac{{\text{w}}_{\text{i}}{\text{Z}}_{\text{i}}}{{\text{A}}_{\text{i}}}{\text{ln I}}_{\text{i}}\right)/\left({\sum }_{\text{i}}\frac{{\text{w}}_{\text{i}}{\text{Z}}_{\text{i}}}{{\text{A}}_{\text{i}}}\right)$$ (2)

where for each element i composing material m, w_i is the fraction by weight, Z_i is the atomic number, A_i is the atomic mass, and I_i is the mean ionization potential.

In this study, I_m was calculated using the UC method, derived from the BAR as described below, and ρ_e,water was determined from CT imaging.

2.B. Unified Compositions Model

The UC Model for computing mean ionization potential is described in detail by Sudhyadhom¹⁵. In this model, human biological tissue is modeled using three general components: water, organic, and mineralized tissues. Under this assumption, the BAR of the mean ionization potential can be computed on a per-voxel basis for the total material composing each voxel by translating Equation 2 to:

$$\text{ln}\left({\text{I}}_{\text{voxel}}\right)=\frac{\left(\frac{{\text{w}}_{{\text{H}}_2\text{O}}{\text{Z}}_{{\text{H}}_2\text{O}}}{{\text{A}}_{{\text{H}}_2\text{O}}}\text{ln}\left({\text{I}}_{{\text{H}}_2\text{O}}\right)\right)+\left({\sum }_{\text{org}}\frac{{\text{w}}_{\text{org}}{\text{Z}}_{\text{org}}}{{\text{A}}_{\text{org}}}\text{ln}\left({\text{I}}_{\text{org}}\right)\right)+\left(\frac{{\text{w}}_{\text{HA}}{\text{Z}}_{\text{HA}}}{{\text{A}}_{\text{HA}}}\text{ln}\left({\text{I}}_{\text{HA}}\right)\right)}{{\sum }_{\text{total}}\frac{{\text{w}}_{\text{total}}{\text{Z}}_{\text{total}}}{{\text{A}}_{\text{total}}}}$$ (3)

where w, Z, A, and I are the parameters listed above for water (H₂O), organic (org), and mineralized (hydroxyapatite (HA)) tissues.

In the original UC Model work, Equation 3 was simplified by assuming Z/A is identical for all biological molecules in the body, at the expense of a slight loss of accuracy, particularly in situations involving mixtures of water (Z_H2O/A_H2O=0.56) with bony tissue (Z_HA/A_HA=0.50). In this work, we were able to retain this accuracy by computing Z/A separately for the three constituents of biological tissue such that Z_H2O/A_H2O and Z_HA/A_HA are constants defined above while Z_org/A_org and Z_total/A_total were determined through a linear fit to their corresponding proton (hydrogen) densities. Using tabulated values of Z/A and the organic constituent hydrogen density by mass (h_org) for organic materials composing human biological tissues^16,17, Z_org/A_org was expressed as a function of h_org which can be determined through imaging as described below. Similarly, values of Z_total/A_total for all molecules considered in human biological tissue was expressed as a function of total hydrogen density by mass (h_total), which can also be determined through imaging. Expressions for Z_total/A_total and Z_org/A_org as functions of h_total and h_org, respectively, are shown in Equation 4:

$$\frac{Z_{tot}}{A_{tot}}=0.502h_{tot}+0.499;\frac{Z_{org}}{A_{org}}=0.490h_{org}+0.500$$ (4)

Mean ionization potential values for the three constituents of biological tissue were found using the same methodology as in the original work. I_H2O and I_HA are constants (75.3eV and 156.2eV, respectively¹⁷) while I_org was given through an exponential relationship between I_org and organic molecule hydrogen density by mass:

$${\text{I}}_{\text{org}}=\text{ A}·\exp \left({\text{Bh}}_{\text{org}}\right)$$ (5)

The constants A and B are 93.23 and −3.47, respectively, while h_org is determined through imaging as described below. Under these conditions, and assuming ∑_iw_i = 1, the mean ionization potential per voxel is reduced to the following expression:

$$\text{ln}\left({\text{I}}_{\text{voxel}}\right)=\frac{\left({\text{w}}_{{\text{H}}_2\text{O}}\frac{{\text{Z}}_{{\text{H}}_2\text{O}}}{{\text{A}}_{{\text{H}}_2\text{O}}}\text{ln}\left({\text{I}}_{{\text{H}}_2\text{O}}\right)\right)+\left(1-\left({\text{w}}_{{\text{H}}_2\text{O}}+{\text{w}}_{\text{HA}}\right)\right)\left(\text{ln}\left(\text{A}\right)-\text{B}·{\text{h}}_{\text{org}}\right)\left(\frac{{\text{Z}}_{\text{org}}}{{\text{A}}_{\text{org}}}\right)+\left({\text{w}}_{\text{HA}}\frac{{\text{Z}}_{\text{HA}}}{{\text{A}}_{\text{HA}}}\text{ln}({\text{I}}_{\text{HA}})\right)}{\frac{{\text{Z}}_{\text{total}}}{{\text{A}}_{\text{total}}}}$$ (6)

All variables in Equation 6 for computing I_m per voxel can be determined a priori except for w_H2O, w_HA, h_org (used to compute Z_org/A_org) and h_total (used to compute Z_total/A_total), which can all be calculated using the proposed multimodal imaging framework.

2.C. Multimodal imaging framework

Percent water w_H2O

The Dixon technique used is a simple gradient echo MRI sequence that has been well described for separating water and fat ¹H (proton) signals¹⁸ by exploiting the chemical shift between resonant frequencies of fat and water in a magnetic field, using in-phase and out-of-phase signals to produce water-only and fat-only images. In theory, voxels in water-only images containing higher water content will produce higher signal. In this study, percent water was determined by taking the ratio of a voxel intensity value to the voxel of highest global intensity value.

Physical density ρ and relative electron density ρ_e,water

In the proposed framework, physical density is only used to determine percent hydroxyapatite (which is then used to calculate I_m) and relative electron density is only used to calculate SPR. A calibration curve was created relating Hounsfield Unit (HU) values to physical density (ρ) and relative electron density (ρ_e,water) using a tissue surrogate phantom (Model 062; CIRS, Norfolk, VA) with known density values. Although measurements of ρ_e,water are typically derived from kVCT for treatment planning purposes, MVCT may be superior to kVCT for determination of electron density because MCVT HU values are largely independent of atomic number due to Compton scattering being the predominant mode of photon interaction. For this study, both kVCT and MVCT were used to assess and compare the accuracy of each. Physical and relative electron density calibration curves derived for both kVCT and megavoltage MVCT are shown in Figure 1.

Figure 1:

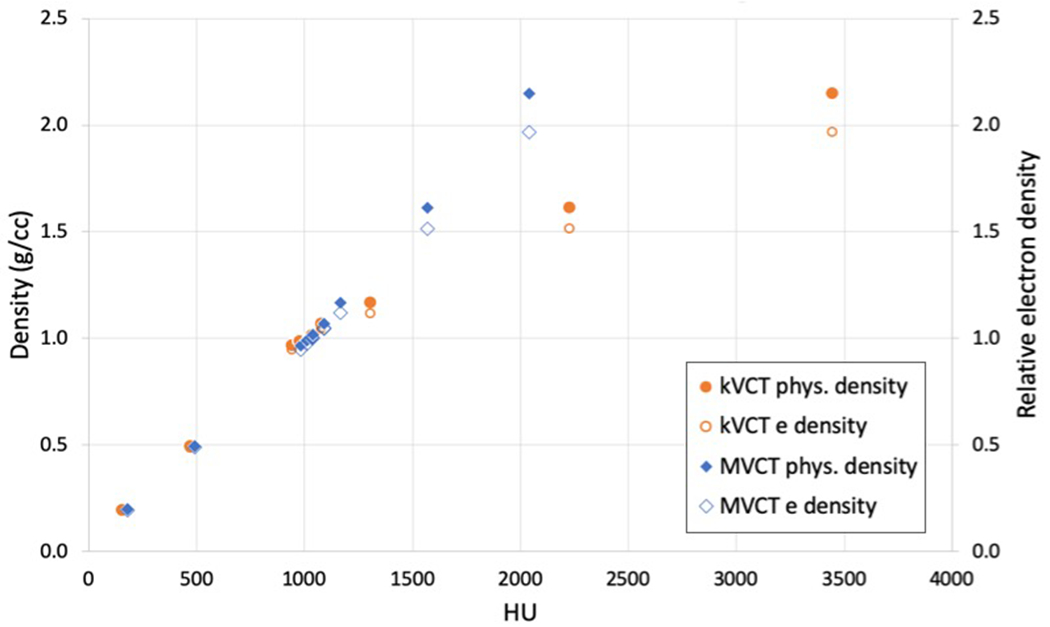
Points which make up calibration curves of HU (kVCT and MVCT) versus physical density and relative electron density determined from scans of a tissue substitute phantom. Interpolations to these points were used to determine density values of tissue substitute phantoms from kVCT and MVCT images. The kVCT distribution forms the typical bilinear calibration curve while the MVCT distribution remains linear through the range of CT numbers due to the negligible effects of the photoelectric effect at MV energies.

Percent hydroxyapatite w_HA

In this study, CT imaging was used to determine w_HA using an assumed relationship between physical density and calcium content derived from bone composition models as outlined by Zhou et al.¹⁹. Percent HA was determined using the fixed ratio of calcium mass to hydroxyapatite mass (39.9%). Percent calcium was determined empirically from physical density estimated from CT determined by a previous group, as shown in Equation 7¹⁹.

$$Ca\%=-4.796{\rho }^3+7.761{\rho }^2+32.051\rho -33.934$$ (7)

Proton (hydrogen) density h_org and h_total

A zero echo time (ZTE) gradient-echo MRI sequence²⁰ with TE<<T₂, small flip angle, and short repetition time (TR) is (¹H) proton density weighted and can provide a reasonable approximation of the voxel total hydrogen content, with higher image intensity values corresponding to higher total hydrogen content. Values of h_total were determined by dividing the total hydrogen content per voxel (in units of volume) derived from ZTE MRI by the physical density derived from CT, converting h_total to per unit mass. Materials of known hydrogen density including water, acetone, 92% (by volume) isopropyl alcohol, and propargyl alcohol, were used to create a calibration curve relating image intensity to voxel total (¹H) proton content as shown in Figure 2¹⁵. These materials were selected because they have a known (¹H) proton density (ranging from 0.07 to 0.11) and span the hydrogen density range of tissue-mimicking materials evaluated in this study (ranging from 0.09 to 0.11). Of note, this calibration curve is scanner and sequence parameter dependent (including resolution) and should be performed separately for all scanners.

Figure 2:

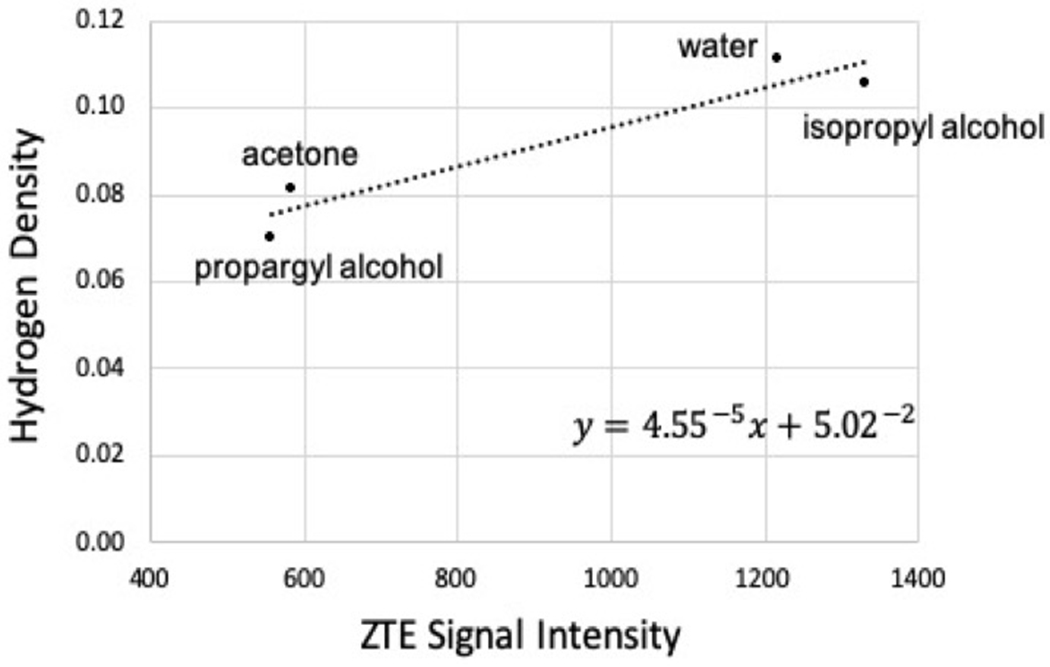
Calibration curve relating ZTE image signal intensity and hydrogen density.

The organic molecule hydrogen density (h_org) was determined by subtracting the hydrogen content contributions from water (h_H2O) and mineral (h_HA), as shown in Equation 8.

$$h_{org}=\frac{h_{tot}-(h_{\text{HA}}·w_{HA}+h_{H_{2}O}·w_{H_{2}O})}{1-(w_{H_{2}O}+w_{HA})}$$ (8)

Multimodal Imaging Pipeline

The full multimodal imaging pipeline for determining SPR is depicted in Figure 3. Both MRI datasets were acquired on a 3 Tesla scanner (MR750; GE Healthcare, Milwaukee, WI) using 3D acquisition and 2mm slice thickness, with all images acquired using a transmit/receive quadrature birdcage-type head coil. This type of head coil allowed for a highly homogenous signal acquisition²¹ not requiring specific compensation for B₁ inhomogeneities. The Dixon water-only image was acquired using flip angle of 1°, TR of 3.77ms, and TE of 2.32ms and 1.12ms for the in-phase and out-of-phase images, respectively. The ZTE scan was acquired using flip angle of 0.6°, TR of 1.34ms, and TE of 0.016ms. kVCT images were acquired on a Siemens scanner (SOMATOM Sensation; Siemens, Erlangen, Germany) using 120kVp energy and 1mm slice thickness. MVCT images were acquired on a TomoTherapy system (TomoHD; Accuray, Sunnyvale, CA) using the 3.5MV energy MVCT beam with fine pitch and 1mm slice thickness reconstruction.

Figure 3:

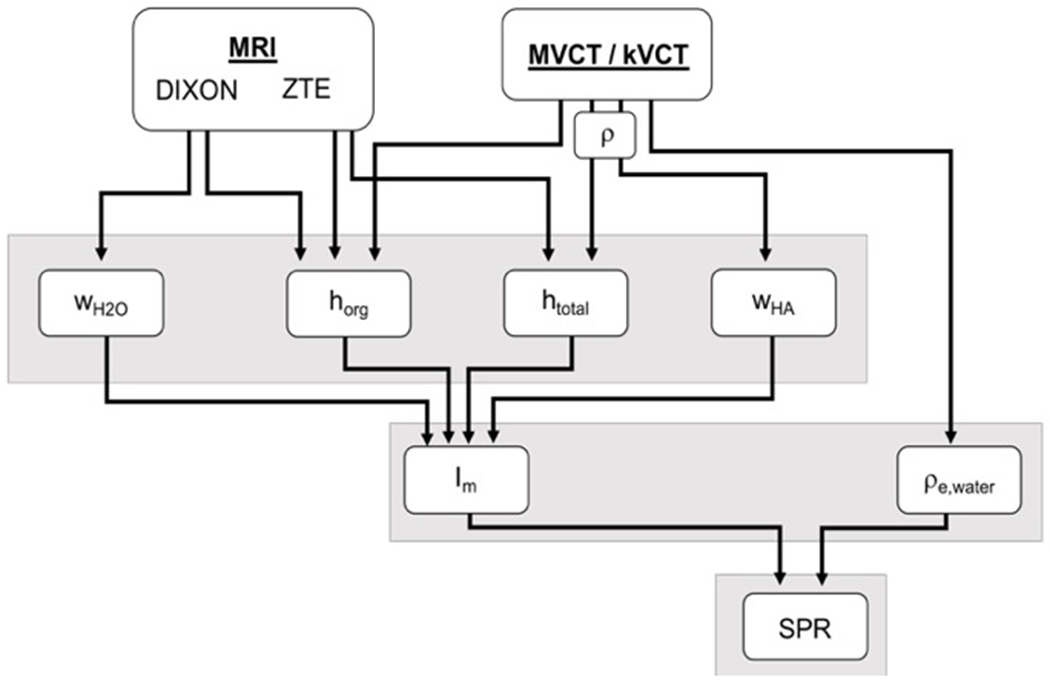
Schematic illustrating the multimodal imaging pipeline used for determination of SPR using the UC method.

2.D. Tissue Substitute Phantoms

Tissue substitute phantoms were created to mimic skin, muscle, adipose, and spongiosa based on each tissue’s molecular composition provided in ICRU Report 44²² and ICRP Report 23²³ by creating homogeneous mixtures of deionized water with appropriate ratios of gelatin (to mimic protein), coconut oil (to mimic fat), and/or pure hydroxyapatite (to mimic bone) as shown in Table 1. Constituents of each mixture were carefully weighed using a high-precision scale (Practum313-1S, Sartorius Biotech, Germany). Skin phantoms were created by mixing fixed (by mass) amounts of gelatin with hot water until dissolved and allowing for solidification. Muscle and adipose phantoms were created similarly but including coconut oil (adipose solutions were created separately for each container to prevent congealing of the predominately oil mixture). Spongiosa phantoms were created similarly to skin phantoms but including hydroxyapatite powder. Phantoms containing coconut oil included a small amount of detergent/surfactant (SDS) to encourage mixing of oil with water which improved overall homogeneity. Measurements of physical density for each phantom were calculated from volume and mass determined using volumetric pipettes and the high-precision scale. As gelatin and coconut oil are not pure molecular compounds (but rather a mixture of multiple molecules), chemical composition of these substances was determined by at a specialized microanalytical facility via combustion analysis.

Table 1.

Tabulated compositions for tissue substitute phantoms created by measurements (by mass) of appropriate ratios of water, gelatin, coconut oil, and/or pure hydroxyapatite.

	Water	Protein	Fat	Hydroxyapatite	SDS
Skin	75.00	25.00	0	0	0
Muscle	74.78	19.97	5.0	0	0.25
Adipose	46.80	2.50	49.2	0	1.50
Spongiosa	26.61	11.83	47.43	12.81	1.32

In addition to matching the molecular composition of real tissues, tissue substitutes were considered mimicking of real tissues if they demonstrated reasonable equivalence with nominal physical parameters relevant to the modalities of interest for this study. For example, tissue substitutes were considered reasonably equivalent to real biological tissues if their physical/compositional characteristics of interest for the respective modality were similar to each other including mass attenuation coefficients (for CT), water content (for the Dixon MRI), (¹H) proton density (for the ZTE MRI), and mass stopping power ratio (for proton therapy). To illustrate this, mass attenuation coefficients were computed for each phantom material from the atomic composition of each tissue substitute and elemental x-ray mass attenuation coefficients provided by NIST²⁴ assuming a single mono-energetic nominal mean energy of 80 keV for kVCT and 800 keV for MVCT. Proton mass stopping power ratios were computed for each phantom material from the atomic composition of each tissue substitute assuming a proton energy of 115MeV. Literature values for tissue mass attenuation coefficients and mass stopping power ratios were derived from tissue compositions provided in ICRU 44²². These parameters are shown for phantom and literature tissues in Table 2. Additional metrics were assessed to demonstrate reasonable tissue substitute equivalence with biological tissue composition provided in the literature^16,22,23 including affective atomic number (Z_eff), physical density, and relative electron density which are shown in Table 3. Physical measurement (PM) values for each parameter used to compute SPR were calculated directly using percentage (by mass) and elemental composition of each constituent. Uncertainties in PM values were determined from the errors in mass measurements of the phantom components and propagated through each value used to compute SPR.

Table 2.

Tabulated physical parameters for mass attenuation coefficients at mean energies of kVCT (80 keV) and MVCT (800 keV), water content, hydrogen density, and proton mass stopping power ratios derived from tissue substitute phantom elemental composition versus real tissue composition from ICRU Report 44²² and ICRP Report 23²³.

	μ/ρ (80 keV) × 10−1		μ/ρ (800 keV) × 10−2		Water content		Hydrogen density		SPR/ρ (115 MeV)
	Phantom	Literature	Phantom	Literature	Phantom	Literature	Phantom	Literature	Phantom	Literature
Skin	1.81	1.81	7.78	7.80	0.75	0.59-0.72	0.100	0.100-0.101	0.99	0.99-1.00
Muscle	1.81	1.82	7.80	7.79	0.75	0.70-0.79	0.102	0.101-0.102	0.99	0.99-1.00
Adipose	1.82	1.80	7.88	7.87	0.47	0.11-0.31	0.115	0.112-0.116	1.00	1.00-1.03
Spongiosa	1.90	1.95	7.75	7.67	0.27	0.23	0.096	0.085	0.98	0.98

Table 3.

Tabulated physical parameters for effective atomic number, physical density, and relative electron density derived from tissue substitute phantom elemental composition versus real tissue composition from ICRU Report 44²² and ICRP Report 23²³.

	Zeff		Physical density (g/cc)		Relative electron density
	Phantom	Literature	Phantom	Literature	Phantom	Literature
Skin	7.46	7.51	1.06	1.09	1.05	1.07
Muscle	7.45	7.70	1.05	1.05	1.04	1.04
Adipose	7.03	6.56	0.95	0.95	0.96	0.95
Spongiosa	9.20	10.05	1.06	1.14	1.04	1.12

The final phantom was created from nine identical containers of each tissue substitute along with calibration materials used for the MRI (¹H) proton density calibration curve. Identical containers of each tissue type and calibration material were placed in various locations at each level (top, middle, and bottom) of the phantom, resulting in a phantom consisting of 57 total containers. An axial slice of the middle of the phantom is shown in Figure 4.

Figure 4:

Axial representation of a) example phantom configuration and corresponding images of b) ZTE (¹H) proton density-weighted MRI, c) Dixon water-only MRI, d) kVCT, and e) MVCT. Each image depicts a single slice at the same level.

Image average intensity values were extracted using MIM Software (MIM Software Inc, v 6.8.3 Cleveland, OH) using regions of interest (ROIs) large enough to encapsulate all material within each container while minimizing volume averaging of the container itself.

2.E. SPR Determination Sensitivity Analysis

The sensitivity of our SPR determination methodology was evaluated by calculating changes in I_m and SPR due to variations in parameters measured using each imaging technique, specifically, HU (from CT) and water fraction and hydrogen density (from MRI). Variations in physical density and relative electron density were also separately used to assess the sensitivity of I_m and SPR on material density.

CT number variations of ± 5 HU were used for the model sensitivity analysis, which is the recommended tolerance value for CT number accuracy of water and field uniformity provided by AAPM Task Group Report 66 for simulator and treatment planning applications in radiotherapy²⁵. Although HU tolerances typically vary with imaging energy and material, ± 5 HU was considered reasonable for the purposes of assessing model sensitivity for tissue substitutes used in this study.

Quantitative MRI is a developing field that has primarily focused on methods for more specific tumor delineation, radiotherapy dose painting, interpretation of treatment response, and identification of normal tissue toxicity^26,27. Unlike in CT, MR image intensity values do not correspond to physical or electron density, i.e. a pixel value in MRI is relative to other pixel values and depends on several factors related to material composition and scan parameters. A comprehensive investigation of quantitative MRI is beyond the scope of this study; however, our model sensitivity was evaluated based on perturbations of ±10% hydrogen density and water content derived from ZTE and DIXON scans, respectively. This accuracy range is consistent with results seen in this and prior work¹⁵, and considered reasonable for the purposes of assessing model stability.

2.F. Stoichiometric Calibration

For comparison to current clinical standard, a stoichiometric calibration curve relating SECT HU and SPR was performed for the kVCT scanner used in this study. The CIRS phantom containing 10 tissue substitute plugs was scanned at 120kVp and 1mm slice thickness. Elemental composition for each plug provided by the vendor was used with corresponding atomic numbers, weights, and mean ionization potential²⁸ to determine ${\tilde{Z}}_i$ and ${\widehat{Z}}_i$ for element i, as described by Schneider et al³. A linear regression fit was used to compute scanner-specific coefficients K^ph, K^coh, and K^KN which characterize the photoelectric effect, coherent scattering, and incoherent scattering cross-sections, respectively. From these coefficients, HU values were calculated for 64 human tissues provided in the literature^23,29 and used to create a plot of tissue HU versus SPR as shown in figure 5. Each reference tissue was classified as organ-like (shown in red), fat-like (shown in green), and bone-like (shown in blue), with a separate plot generated for each of the three tissue types. The final stoichiometric curve was pieced together extending over a range of typical HU values for biological tissue from the separate fits with nodes at HU values of −200, −120, −20, +35, +100, and +140 as previously described³⁰. All calculations in the stoichiometric calibration were performed using a proton energy of 115MeV.

Figure 5:

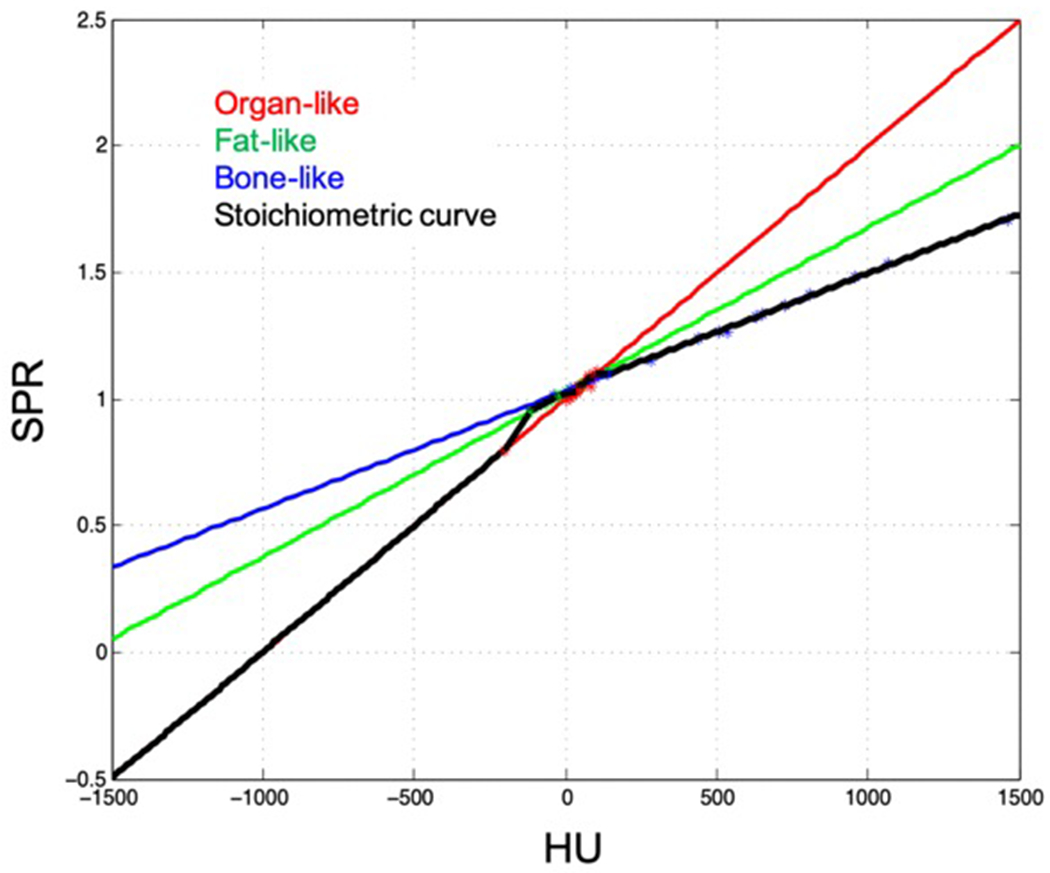
A stoichiometric calibration curve (black line) which provides SPR from HU value was created for the kVCT scanner used in this study using the CIRS tissue surrogate phantom and parametric fits to literature values of organ-like (red line), fat-like (green line), and bone-like (blue line) human tissues.

3. Results

Table 4 summarizes the results of each parameter used to calculate I_m using the multimodal imaging framework for the four tissue substitutes evaluated. W_H2O estimated from the water-only Dixon MRI deviated from PM values by approximately 8.5%, 9.1%, 9.1%, and 16.5% for adipose, muscle, spongiosa, and skin, respectively. W_HA was calculated from physical density determined from CT, therefore all tissues evaluated using the multimodal imaging method showed some amount of hydroxyapatite due to non-zero physical density. The average W_HA values estimated from kVCT differed from PM values by 0.5%, 3.0%, 4.8%, and 6.5% for adipose, spongiosa, muscle, and skin, respectively while MVCT differed from PM values by 1.5%, 4.9%, 7.6%, and 11.4% for adipose, spongiosa, muscle, and skin, respectively. kVCT was more accurate than MVCT in determining w_HA for skin, muscle, and adipose due to the higher accuracy in calculating physical density values (used as a surrogate for determining calcium content) from kVCT versus MVCT in these tissues. The average physical density estimated from kVCT was within 2% of PM values for all tissues except spongiosa, which differed by 9.8%. The average physical density estimated from MVCT was within 1.5% for muscle and spongiosa, but differed by 3.3% and 4.5% for adipose and skin, respectively. The average total hydrogen content (h_tot) estimated from ZTE MRI was within 1.5% using physical density derived from both kVCT and MVCT. The average organic hydrogen content (h_org) was within 2% of PM values derived from both kVCT and MVCT, with the exception of muscle, which deviated from PM values by approximately 20% for kVCT and 10% for MVCT. The high deviation in h_org values estimated for muscle are due to a single outlier phantom which had a higher average w_H2O value derived from the Dixon water image versus the other eight containers containing muscle. Despite this outlier, results of I_m and SPR estimated for muscle (shown below) retain accuracy due to the robustness of the multimodal imaging method, as demonstrated in the sensitivity analysis of I_m and SPR described below.

Table 4.

Tabulated values of parameters required for I_m calculation estimated from multimodal imaging (MRI, UC-kVCT and UC-MVCT) versus physical measurements (PM).

	wH2O (%)	wHA (%)	htot (%)	horg (%)	ρ (g/cc)
Skin	91.5 (MRI) 75.0 ± 0.15 (PM)	6.5 (UC – kV)	10.9 (UC – kV)	5.9 (UC – kV)	1.05 (UC – kV)
		11.4 (UC – MV)	10.3 (UC – MV)	5.4 (UC – MV)	1.11 (UC – MV)
		0 ± 0.0 (PM)	9.4 ± 0.02 (PM)	4.0 ± 0.01 (PM)	1.06 ± 0.002 (PM)
Muscle	83.9 (MRI) 74.8 ± 0.15 (PM)	4.8 (UC – kV)	11.1 (UC – kV)	24.7 (UC – kV)	1.03 (UC – kV)
		7.6 (UC – MV)	10.7 (UC – MV)	15.2 (UC – MV)	1.06 (UC – MV)
		0 ± 0.0 (PM)	9.8 ± 0.02 (PM)	5.7 ± 0.01 (PM)	1.04 ± 0.002 (PM)
Adipose	38.3 (MRI) 46.8 ± 0.09 (PM)	0.5 (UC – kV)	11.9 (UC – kV)	12.3 (UC – kV)	0.97 (UC – kV)
		1.5 (UC – MV)	11.7 (UC – MV)	12.3 (UC – MV)	0.98 (UC – MV)
		0 ± 0.0 (PM)	12.0 ± 0.02 (PM)	12.8 ± 0.03 (PM)	0.95 ± 0.02 (PM)
Spongiosa	17.5 (MRI) 26.6 ± 0.05 (PM)	15.8 (UC – kV)	9.6 (UC – kV)	11.4 (UC – kV)	1.16 (UC – kV)
		7.9 (UC – MV)	10.5 (UC – MV)	11.4 (UC – MV)	1.06 (UC – MV)
		12.8 ± 0.03 (PM)	9.0 ± 0.02 (PM)	10.0 ± 0.02 (PM)	1.06 ± 0.002 (PM)

Results of relative electron density, mean ionization potential, and relative stopping power ratio computed separately for both kVCT and MVCT, along with SPR determined from the stoichiometric method for comparison, are shown in Figure 6. Points falling on the diagonal line indicate a match to physical measurements. As expected, MVCT outperformed kVCT in determining relative electron density for all four tissues studied (Figure 6a,b), with average values within physical measurements by 2.6% for kVCT versus 0.9% for MVCT. Average ρ_e,water values differed from physical measurements by an average of 2.1%, 2.6%, 0.9%, and 2.2% for kVCT and an average of 0.3%, 0.2%, 0.9%, and 0.2% for MVCT in skin, muscle, adipose, and spongiosa, respectively. kVCT outperformed MVCT in determining mean ionization potential (Figure 6c,d), with average values differing from PM calculations for kVCT by 2.9%, 0.4%, 3.4%, and 0.8% versus MVCT by 7.6%, 3.3%, 2.5%, and 7.2% for skin, muscle, adipose, and spongiosa, respectively. Deviations in I_m values computed from MVCT are predominantly due to errors in computing physical density as described above. Our multimodal imaging approach using both kVCT and MVCT was in close agreement to physical measurement SPR values for all tissue substitutes evaluated (Figure 6e,f) and provided higher accuracy than the stoichiometric method (Figure 6g) in the cases of adipose and spongiosa bone. Because SPR varies linearly with relative electron density and logarithmically with mean ionization potential, MVCT provided higher accuracy SPR values than kVCT due to the higher accuracy of MVCT for computing relative electron density. In skin, average SPR values were within 2.0% from kVCT, 0.5% from MVCT, and 0.8% from the stoichiometric method. In muscle, average SPR values were within 2.6% from kVCT, 0.3% from MVCT, and 0.3% from the stoichiometric method. In adipose, average SPR values were within 1.0% from kVCT, 0.8% from MVCT, and 3.6% from the stoichiometric method. In spongiosa bone, average SPR values were within 2.2% from kVCT, 0.4% from MVCT, and 5.1% from the stoichiometric method.

Figure 6:

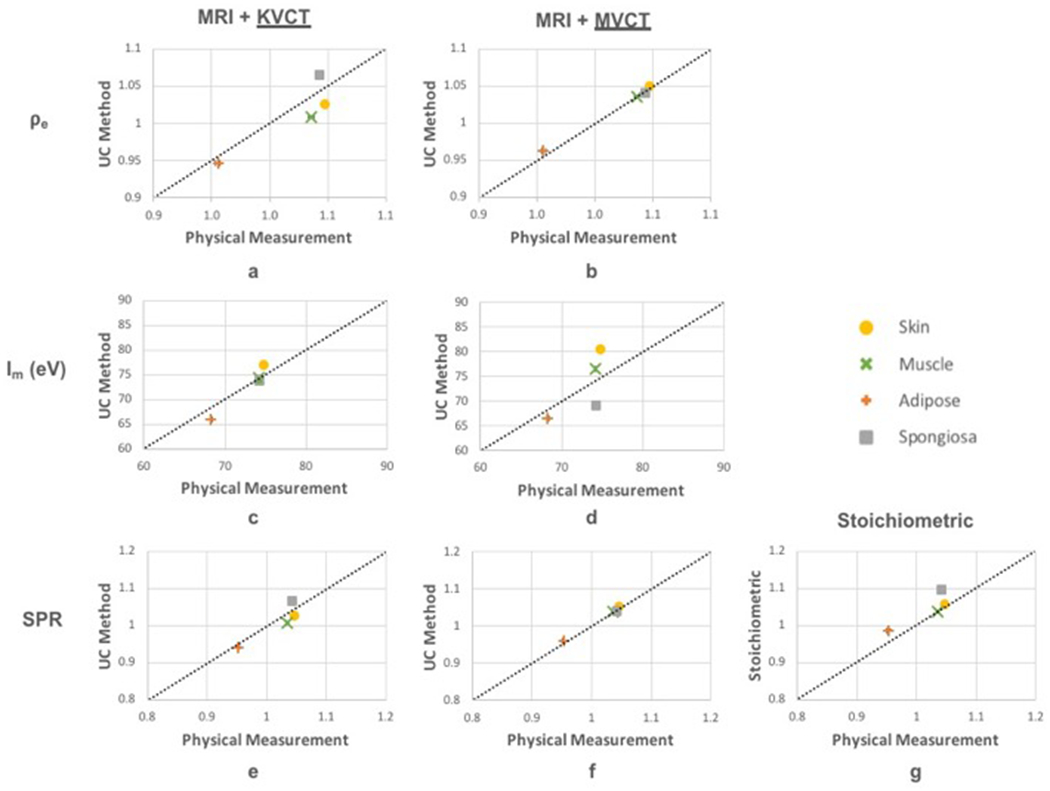
Results of relative electron density, mean ionization potential, and stopping power ratios computed using kVCT (left) and MVCT (middle) compared to physical measurements. SPR from stoichiometric method is shown for comparison (panel g).

Results of the model sensitivity analysis demonstrating changes in mean ionization potential and stopping power ratios with variations in parameters estimated from CT HU, water fraction, and hydrogen density are shown in Table 5. Variations in CT number of ±5 HU resulted in changes to I_m of up to 1.2% and SPR of up to 0.5%, with similar overall trends between kVCT and MVCT HU and subtle differences stemming from differences in their respective calibration curves. Variations in water content of ±10% led to changes in I_m of approximately ±1.8% and SPR of approximately ±0.05%. With regards to parameters extracted from MRI, our model was more sensitive to variations in hydrogen density than water content, with variations in hydrogen density of ±10% leading to changes in I_m of approximately ±3.8% and SPR of approximately ±0.1%. However, we found that the ZTE sequence used in this study for determining hydrogen density was quite accurate, with hydrogen density values well within 10% of physical measurements, as shown in the third column of table 4.

Table 5.

Tabulated values for the percentage change to I_m and SPR from errors in kVCT and MVCT of magnitude (±5 HU) and water content and hydrogen density of magnitude (±10%).

			kVCT (± 5 HU)		MVCT(± 5 HU)		wH2O (±10%)		htot (±10%)
	Im	SPR	%Im	%SPR	%Im	%SPR	%Im	%SPR	%Im	%SPR
Skin	77.8	1.05	−0.20, 0.20	−0.49, 0.49	−0.35, 1.18	−0.47, 0.46	−1.76, 1.77	−0.05, 0.05	3.65, −3.80	0.01, −0.11
Muscle	76.5	1.04	−0.20, 0.20	−0.50, 0.50	−0.18, 0.18	−0.45, 0.45	−1.77, 1.79	−0.05, 0.05	3.70, −3.82	0.01, −0.11
Adipose	67.7	0.95	−0.18, −0.63	−0.52, 0.36	−0.20, 0.20	−0.52, 0.52	−1.75, 1.78	−0.05, 0.05	3.77, −3.68	0.01, −0.11
Spongiosa	72.4	1.04	−0.42, 0.42	−0.16, 0.16	−0.18, 0.18	−0.44, 0.44	−1.78, 1.81	−0.05, 0.05	3.81, −3.69	0.01, −0.11

Results of the model sensitivity with physical density and relative electron density are shown in Table 6. In our SPR determination methodology (as in Figure 3), mean ionization potential is sensitive to physical density uncertainties because physical density is used to calculate both mineral content (through calcium content, as shown in equation 7) and hydrogen density, which are parameters used to compute I_m. Variations in physical density led to changes in SPR only through changes in I_m, as physical density is not a parameter used directly to calculate SPR. Relative electron density, on the other hand, is not used in determining I_m, therefore had no impact on this parameter. However, because SPR scales linearly with relative electron density (as shown in equation 1), variations of ±10% in relative electron density correlated with ±10% variations in SPR. As HU values were independently fit to physical and, separately, electron density, errors/uncertainties in the fitting of HU to either of these densities would manifest in SPR calculation very differently than errors/uncertainties in the HU value itself (which would affect both mass and electron density) as in Table 5.

Table 6.

Tabulated values for the percentage change to I_m and SPR from errors in physical density and relative electron density.

			ρ (± 10%)		ρe (± 10%)
	Im	SPR	%Im	%SPR	%Im	%SPR
Skin	77.8	1.05	−3.73, 3.43	−0.11, 0.09	0.0, 0.0	−9.54, 9.54
Muscle	76.5	1.04	−3.66, 3.34	−0.10, 0.09	0.0, 0.0	−9.65, 9.65
Adipose	67.7	0.95	−3.76, 2.69	−0.11, 0.07	0.0, 0.0	−10.47, 10.47
Spongiosa	72.4	1.04	−3.66, 3.54	−0.10, 0.10	0.0, 0.0	−9.58, 9.58

4. Discussion

The proposed multimodal imaging framework provides improved accuracy in estimating stopping power ratio. In the proposed methodology, MRI is used to estimate the water content using a Dixon water-fat separation technique and hydrogen density using a ZTE technique. Either kVCT or MVCT can be used to estimate physical density, hydroxyapatite content, and relative electron density, with both modalities demonstrating accurate results of SPR.

Larger discrepancies in physical density values for spongiosa were seen for kVCT versus MVCT. Differences in the spongiosa bone are more prominent than for the other tissue substitute materials because the physical density of “standard” tissues are encoded into the calibration curves and, for our phantom, the density of the spongiosa phantom differed from typical human spongiosa bone. In practice, impacts of these differences may be seen in mineralized tissues which have a physical density different than standard values for bone, for example, in cases of lower bone mineral density such as osteoporosis. Notably, while this may be problematic if using kVCT, MVCT retains accuracy of electron density even in cases of non-standard density tissues. Of note, the proposed technique using a combination of MRI and MVCT provided results closer to physical measurements than the stoichiometric method, which has been demonstrated to provide high accuracy in SPR for soft tissues with composition close to water but reported to give errors in adipose of up to 3%³¹ and bone of greater than 3.5%³². With regards to hydroxyapatite composition, a potential solution to improve accuracy in deriving w_HA from physical density could include a segmentation which differentiates soft tissue from bone and setting non-bone w_HA values to zero. While more accurate methods of determining composition are under investigation, an important advantage of the UC Method for determining mean ionization potential is that the technique is robust to deviations in content of water, organic tissue, and hydroxyapatite¹⁵ as indicated by the accuracy in estimations of SPR using either kV or MVCT. Intuitively, the robustness of the proposed technique appears to stem from the fact that data is being characterized by its individual components of water, organic material, or hydroxyapatite, which are extracted from the appropriate choice of imaging technique. For example, a water-specific MR scan (as in this proposed work) provided the data for water composition, limiting the error for this component to a relatively smaller set of possibilities relative to elemental/molecular composition and thus I_m. The robustness of the SPR determination methodology was demonstrated in the sensitivity analysis, with variations in CT number of ±5 HU and variations in water content and hydrogen density of ±10% leading to changes of I_m within a couple percent and SPR within one percent. In contrast to the findings by Paganetti⁶ for a kVCT-based stoichiometric calibration and SPR determination, our methodology limits the error due to I_m to a sub-1% level with electron density errors now dominating SPR determination.

Despite demonstrating improved accuracy in computing SPR with the proposed framework, future investigations would provide further validation on the method’s accuracy. In particular, a final validation of proton range accuracy of our methodology would necessitate proton irradiation of actual tissues as imaging studies alone can provide significant though limited amounts of information. Additionally, improvements to the imaging protocols utilized may provide increase accuracy. For example, imaging pure water for quantitative analysis can cause errors in MRI. As shown in Figure 4c, the water container (center of phantom) does not produce the highest signal, likely due to the ultra-long T₁ value of pure distilled water that would not be found biologically. In this study, tissue percent water was calculated by taking the ratio of intensity values to the highest image signal intensity, which was typically skin. Other methods that may result in more accurate water-fat separation (e.g. multi-peak models) may be useful to investigate.^33–35 In general, the proposed methodology can be applied to human biological tissues that exhibit similar physical characteristics to those provided in Tables 5 and 6, though not all materials fall within these criteria. For example, the hydrogen density of very dense bone is approximately 3-7%²², falling outside the hydrogen density range of calibration materials used in this study (7-11%). To account for this, the calibration curve shown in Figure 2 would require additional calibration materials which span the full range of hydrogen density of materials being evaluated. Furthermore, materials with both extremely short T2* values and high hydrogen content (for example, plastic) may produce erroneous results in the ZTE MRI scan as the short T2* value may result in very little signal intensity despite having high hydrogen content. Metal implants commonly produce streaking artifacts and/or signal voids in both CT and MRI, posing challenges in accurate characterization of quantitative parameters. An additional MRI source of uncertainty for clinical implementation of this technique is signal uniformity and inhomogeneity. In this study, scans were acquired using a quadrature birdcage type head coil known for its high signal homogeneity, yet current MRI technology has developed away from these types of coils due to their lower signal-to-noise ratio compared with multi-channel receive-only phased array coils. While there exist numerous techniques (including the commonly used N4 technique³⁶) to compensate for this B₁ inhomogeneity, image-based corrections operate under a set of assumptions (specifically that inhomogeneities are of low spatial frequency) with errors and biases occurring in situations outside of those. While this study serves as a proof of concept in four tissue substitute materials, a comprehensive investigation of the proposed methodology in non-biological and additional biological materials is required prior to clinical implementation.

A current limitation in the proposed framework stems from errors related to acquiring images using multiple modalities, for example, MR-to-CT image registration errors and differences in anatomical positioning of the patient between image acquisition. With perfect registration, we can expect to achieve high accuracy SPR estimation. In non-ideal cases (particularly for sites outside of the head/brain), we may expect that image registration errors between MR and CT are larger than those seen in this work. Active areas of research are being pursued to provide a framework for MRI-only dose calculation which would reduce the dependence/need for high-accuracy image registration. For SPR dose calculation in particular, an MRI-only framework may be achievable if MRI could be used to accurately quantify physical and electron density. Highly accurate MRI-only SPR calculation is challenging for a number of reasons with there being specific challenges due to ultrashort transverse relaxation time T₂/T₂* in bone. Techniques such as ultrashort time to echo (UTE) and ZTE have been developed to image materials with very short T₂/T₂*,^37,38 however, studies have indicated that while these sequences have improved contrast in bone versus air, there are still instances of mislabeling³⁹ which would be unacceptable if used in radiotherapy dose calculation. Using calcium or phosphorus MRI can, in theory, be used as a surrogate for HA content in mineralized tissues knowing the chemical form of HA is Ca₅(PO₄)₃(OH). However, the abundant isotope of calcium, ⁴⁰Ca, has no magnetic moment and is therefore not conducive to producing an MRI signal. Imaging the abundant isotope of phosphorus, ³¹P, is currently an active area of research^40–43 but has not been well established on clinical systems and has limited spatial resolution. These methods, and others, are under investigation and could potentially allow for the implementation of an MRI-only framework.

The proposed imaging methodology using MRI and MVCT has provided a proof-of-concept for achieving sub-percent accuracy in the calculation of SPR for the four types of tissue substitutes evaluated while assuming perfect image registration. While there are several potential sources of error leading to the phenomenon of proton range uncertainty, the primary sources are those resulting from the conversion of CT number to stopping power ratio, contributing about 2.5%^6,7. Reducing the beam range uncertainty caused by this conversion from 2.5% to 1% would translate to a decrease in additional margin of several millimeters for a treatment beam of moderate energy. Along with decreased dose to healthy tissues, a practical application to this improvement would be in the selection of beam angles, which are often chosen such that the distal range is not directed at a nearby critical structure because the additional margins added to account for range uncertainty result in prohibitively high dose to these structures. Reducing margins by several millimeters would potentially allow for more optimal beam arrangements and a reduction in dose to nearby healthy critical structures.

5. Conclusions

We have demonstrated the methodology for improved SPR computation at the voxel level using the proposed multimodal imaging framework. We were able synthesize several tissue substitutes and compare results from our multimodal imaging framework to values computed directly from physical measurements. Using MRI and MVCT, SPR values derived using our method were within 1% of physical measurements and were more accurate than the stoichiometric method, which is currently the clinical standard for SPR estimation.