Abstract
With the development of high-throughput biological techniques, high-dimensional omics data have emerged. These molecular data provide a solid foundation for precision medicine and prognostic prediction of cancer. Bayesian methods contribute to constructing prognostic models with complex relationships in omics and improving performance by introducing different prior distribution, which is suitable for modelling the high-dimensional data involved. Using different omics, several Bayesian hierarchical approaches have been proposed for variable selection and model construction. In particular, the Bayesian methods of multi-omics integration have also been consistently proposed in recent years. Compared with single-omics, multi-omics integration modelling will contribute to improving predictive performance, gaining insights into the underlying mechanisms of tumour occurrence and development, and the discovery of more reliable biomarkers. In this work, we present a review of current proposed Bayesian approaches in prognostic prediction modelling in cancer.
Keywords: Bayesian, cancer, prognosis, survival, single-omics, multi-omics, integrative, review
There were more than nine million deaths caused by cancer in 2018, which made it the second leading cause of death worldwide (1). Besides traditional radiotherapy, surgery and chemotherapy, targeted therapy and immunotherapy have also been developed recently, such as targeted epidermal growth factor receptor therapies, targeted vascular endothelial growth factor therapies, inhibitor of programmed cell death protein-1 and its ligand, and cytotoxic T-lymphocyte-associated protein 4 inhibitor (2). However, since cancer is a highly heterogeneous disease, these emerging therapies might not be sufficiently effective in all patients. Therefore, it is still necessary to further investigate the biological mechanism of cancer development and explore possible potential biomarkers related to tumour prognosis, diagnosis, etc.
With the development of high-throughput sequencing technology, high-dimensional data based on different omics data is constantly being generated, which provided researchers with data at the molecular level to reveal relevant biomarkers of cancer development or prognosis. At present, there are already some public cancer databases based on molecular data, such as The Cancer Genome Atlas (TCGA), Gene Expression Omnibus, International Cancer Genome Consortium, and the Catalogue of Somatic Mutations in Cancer. Among them, TCGA, known as a comprehensive database, has collected multiple omics data, including those regarding the transcriptome, methylome, somatic mutation and copy number variation, and it is the most common database used by researchers for data mining (http://cancergenome.nih.gov) (3). Different omics data can be utilized as potential biomarkers to predict the prognosis of different cancer types (4-7).
Furthermore, compared to the actual sample size (i.e., hundreds of samples), the scale of omics data is relatively large, which means that it needs to be processed (i.e., dimensionality reduction) rather than used to fit the predictive model directly. In addition, there are considerable challenges to performing better dimensionality reduction and variable selection for identification or prediction in terms of these high-dimensional omics data. Traditional frequentist approaches (i.e., regarding unknown parameters as deterministic values, which means that they can be estimated by the sample data) for coping with these challenges include ridge (8), the least absolute shrinkage and selection operator (lasso) method and its variants (9-12), and elastic net (13), amongst others. The comparison of different methods has been studied in the case of high-dimensional data (14). Benefiting from the improvement of computing capacity on computers, Bayesian methods have been developed in recent years which have better flexibility in dealing with the problem of high-dimensionality (p>>n) compared to traditional approaches. In fact, Bayesian approaches have become popular tools for medical researchers involved in clinical experimental design and drug development (15). Although some Bayesian methods have been proposed in terms of prognostic prediction, there is still a lack of relevant reviews for a comprehensive discussion.
In the present work, we review these Bayesian methods involving high-dimensional omics data proposed or applied for prognostic prediction in cancer. The primary outcome in this review focuses on relevant survival endpoints, such as overall survival, progression-free survival and relapse-free survival. We mainly explain Bayesian survival modelling from two aspects of single omics and multi-omics integration and emphasize the superiority of multi-omics integration. This survey mainly searched PubMed and Web of Science databases for articles based on key words “cancer” or “tumour”, “Bayesian”, “survival”, “omics”, “gene”, “prediction”, and “integrative”. After removing 25 reviews or meta-analyses, we found a total of 313 articles based on the above key words. Through reading the titles and abstracts, we initially excluded those involving experiments or clinical trials, which left 38 articles that involved Bayesian prognosis prediction and high-dimensional omics. After reading the full articles, we finally included 32 in this review.
Basic Bayesian Methodology
In this section, we briefly review relevant content about Bayesian inference to help readers understand the basic ideas of the Bayesian theorem. In survival analysis, semi-parametric Cox proportional hazards regression is the most common modelling tool for clinical prediction due to there being no restriction on the particular survival distribution. Another alternative is the parametric accelerated failure time (AFT) model that assumes a direct relationship between covariates and outcome (generally, the logarithm of survival time), which is able to acquire more interpretable results. Parameter estimation for both approaches is based on maximum likelihood (strictly, partial likelihood for Cox regression), which infers the most possible values of unknown parameters based on existing sample data. Differently from the view of frequentists, Bayesian theory also focuses on “experience” knowledge rather than sample data alone. Instead of considering the unknown parameter as a fixed value, Bayesian theory regards it as a random variable that follows a specific distribution. Before combining the sample data, an empirical distribution is given, regarded as a kind of pre-judgement for the unknown parameter, which is also known as the prior distribution.
Let θ and y represent the unknown parameter of interest and sample data, respectively. Then the Bayesian formula can be expressed in the following form:
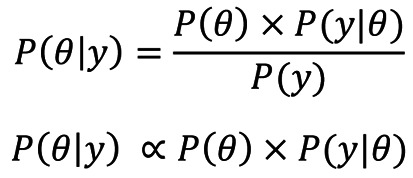
Where P(θ) represents the prior distribution of unknown parameter θ; P(y|θ) can be regarded as the likelihood function from sample data. P(y) is the so-called marginal probability and can be extended as ∫ P(θ)P(y|θ)dθ, which is irrelevant to the parameter θ to be estimated. Therefore, the formula can be re-expressed as a kernel form. P(θ|y) represents the posterior probability, which is the main aim of our inference. It can be regarded as an update of the prior information P(θ) which was utilized for Bayesian inference.
Different priors play an essential impact in the calculation and inference of the posterior distribution. Especially under a high dimension, variable selection is a necessary process and can be achieved by setting suitable priors. Reviews of these variable selection methods have been published (16-20). In particular, conjugate priors can simplify the complexity of the calculation of the posterior distribution, such as Gamma-Poisson prior, inverse-Gamma-normal prior, Beta-binomial prior, Wishart-normal prior and so on (21). However, this situation is not common in all Bayesian analyses. In addition, the integral process becomes more arduous as the parameters estimated are multi-dimensional (θ=∑θi). Therefore, approximation techniques would be an alternative choice, including Laplace approximation (22), variational inference (23) and sampling-based Markov chain Monte Carlo (MCMC). Among them, MCMC algorithms are applied widely in survival analysis. By constructing a Markov chain with a stationary distribution for simulating the sample of the posterior distribution, the posterior expectation [E(θ|D)] and variance of the corresponding parameters can be obtained. However, the original MCMC algorithm sets a relatively lower transfer acceptance ratio based on the stable property of the Markov chain, which meand it takes a long time to reach the convergence situation, especially with high-dimension data. In order to obtain a faster convergence speed, several improved algorithms have been proposed, such as Metropolis–Hastings (24), Gibbs (25), Hamiltonian Monte Carlo (26), Expectation-Maximization (EM) cyclical coordinate descent (27).
Bayesian Applications in Cancer for Prediction of Prognosis
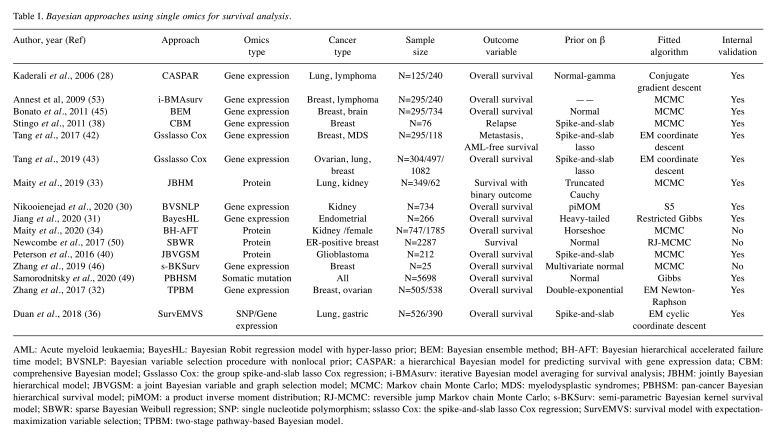
Single omics analysis. In this section, single omics analysis refers to the inclusion of single omics platform data in the study, combined with or without clinical factors for prognostic modelling. Through literature collection, we found that most of the studies were based on expression profiles, followed by proteomics and genomics. The relevant characteristics of the various studies have been summarised in Table I. Bayesian methods in these studies played a significant role in dimensionality reduction/variable selection and modelling.
Table I. Bayesian approaches using single omics for survival analysis.
AML: Acute myeloid leukaemia; BayesHL: Bayesian Robit regression model with hyper-lasso prior; BEM: Bayesian ensemble method; BH-AFT: Bayesian hierarchical accelerated failure time model; BVSNLP: Bayesian variable selection procedure with nonlocal prior; CASPAR: a hierarchical Bayesian model for predicting survival with gene expression data; CBM: comprehensive Bayesian model; Gsslasso Cox: the group spike-and-slab lasso Cox regression; i-BMAsurv: iterative Bayesian model averaging for survival analysis; JBHM: jointly Bayesian hierarchical model; JBVGSM: a joint Bayesian variable and graph selection model; MCMC: Markov chain Monte Carlo; MDS: myelodysplastic syndromes; PBHSM: pan-cancer Bayesian hierarchical survival model; piMOM: a product inverse moment distribution; RJ-MCMC: reversible jump Markov chain Monte Carlo; s-BKSurv: semi-parametric Bayesian kernel survival model; SBWR: sparse Bayesian Weibull regression; SNP: single nucleotide polymorphism; sslasso Cox: the spike-and-slab lasso Cox regression; SurvEMVS: survival model with expectation-maximization variable selection; TPBM: two-stage pathway-based Bayesian model.
Variable selection based on priors. Here, the variable selection procedure is performed by a kind of priors with the specific function of variable selection. The current main priors include shrinkage priors and spike-and-slab priors. Shrinkage priors constrain corresponding coefficients towards zero by imposing a continuous prior distribution. For instance, Kaderali et al. introduced a hierarchical Bayesian approach to predict individual survival times based on expression profiles, which imposed the normal-Gamma prior on regression parameters. It combined dimension reduction and regression in one single step to select the most discriminatory genes under study (28). This method has been proven to have better prediction performance in neuroblastoma (29). Nikooienejad et al. introduced a procedure for Bayesian variable selection that used a mixture prior comprised of a point mass at zero and an inverse moment prior, which led to lower false-positive rates in the variable selection process. Due to the Cauchy-like tail, this prior introduced comparatively small shrinkage of large coefficients (30). Considering potential pathway/structure among genes, Jiang et al. proposed a Bayesian Robit regression model with hyper-lasso priors for survival-related feature selection. It took possible group structures into account automatically without considering a pre-specific grouping structure (31). Zhang et al. proposed a two-stage pathway-based Bayesian modelling strategy for survival modelling, which imposed double-exponential prior (or Laplace/Bayesian lasso) on the coefficients (32). In short, those genes mapped into different pathways were fitted into a Bayesian hierarchical Cox model, and then the prognostic scores for each pathway, which were calculated by leave-one-out cross-validation, were regarded as new predictors to build an integrated prognostic model. Based on proteomics, Maity et al. developed a jointly Bayesian hierarchical model to model both the survival time and binary outcome, and applied a shrinkage prior (i.e., a truncated Cauchy distribution) to identify common significant proteins that affected survival and stage (33). Furthermore, the authors also presented a pan-cancer Bayesian hierarchical AFT model for survival (34). It adopted the sparse horseshoe prior for identifying the major proteomic drivers and was allowed to borrow strength across multiple cancer types by setting a correlation structure among prior distributions.
Another main prior is the spike-and-slab prior (as a kind of mixture prior), which includes a point mass at 0 (the spike) and a continuous distribution (the slab) (35). It can assign different distributions (the slab or spike) to model different effect sizes. For example, Duan et al. proposed Bayesian survival regression with the spike-and-slab prior applied on coefficients for variable selection (36). It extended EM variable selection (37) to a parametric survival model with Weibull distribution and utilized an EM algorithm to quickly obtain the posterior modes of unknown parameters. Similarly, considering the underlying structure, Stingo et al. proposed a comprehensive Bayesian model that achieved two-level selections on the pathway and genes involved. Except for the prior on coefficients, the Markov random field prior was applied for obtaining a better separation between relevant and nonrelevant pathways and fewer false-positive rates in a model with fairly small coefficients (38). The efficacy of the above Bayesian approach was further validated in lung adenocarcinoma for prognostic analysis (39). Peterson et al. proposed a joint Bayesian modelling strategy for learning relevant networks and selecting network-structure variables simultaneously. It applied a mixture prior with a normal density and a Dirac function for variable selection, which was also known as the spike-and-slab. The authors also constructed the network through a Gaussian graphical model to provide a sparse and interpretable representation of the dependency relationship from the data (40).
The above Bayesian approaches mainly imposed either a shrinkage prior or the spike-and-slab prior for regression coefficients. Recently, a kind of hybrid approach (i.e., the spike-and-slab lasso) has been proposed, which combines the advantages of shrinkage and spike-and-slab priors (41). Tang et al. presented Bayesian generalized linear models based on the spike-and-slab lasso (27) and extended the spike-and-slab framework to a Cox model for prognostic model (sslasso Cox) (42). It proposed a new EM coordinate descent algorithm to achieve faster converge speed compared to the MCMC algorithm. Compared to traditional lasso, the approach is able to estimate the effect of predictors more accurately. Later, considering possible group structures among genes, the above survival model was further extended into the sslasso Cox group, incorporating potential pathway structure information (43).
Variable selection based on non-priors. Except for above mentioned Bayesian variable selection approaches based on priors, variable selection procedures can be carried out in other ways, generally speaking, i.e., model-based selection. In this approach, the priors given to predictors (i.e., to the coefficients) tend to be assigned as flat priors (e.g., general normal distribution). Bonato et al. proposed a non-parametric Bayesian ensemble method that extended Bayesian additive regression trees to three survival models (Cox, AFT, and Weibull) using a Bayesian hierarchical framework which incorporated additive and interaction effects between genes. It achieved variable selection by Bayesian false discovery rate through the Bayesian model averaging (BMA) approach (45). Zhang et al. proposed a kind of semi-parametric Bayesian kernel survival model (46), which considered gene pathway effects related to survival outcome via a kernel function in a Gaussian process (47). It adjusted the traditional Bayes factor (48) to adapt multiple-comparison for performing robust statistical inference. It allowed taking into account the possibility of nonlinear single-gene effects and a complicated structure of interactions among genes within the same pathway. Samorodnitsky et al. proposed a novel pan-cancer Bayesian hierarchical survival model based on the somatic mutation profile. They evaluated the optimal model of fitted data and predictive importance of genes by calculating the log out-of-sample posterior predictive likelihood and mean log-posterior likelihood (i.e. model selection and forward selection) (49). Newcombe et al. considered the Weibull regression model embedded in a Bayesian framework based on Reversible Jump MCMC algorithm, which was called sparse Bayesian Weibull regression. It applied a beta-binomial prior for indicator variable γ to construct the model selection framework (if γ=1, the covariate was included in the model) (50).
Another type of approach, known as BMA, focused on coping with the model uncertainty problem (i.e. there might simultaneously exist multiple fitted-well models for the same data) (51). To accommodate high-dimensional data, iterative BMA was proposed later (52). Furthermore, Annest et al. extended iterative BMA to survival analysis through several modifications to the iterative BMA algorithm, including using Cox proportional hazards model for ranking individual genes instead of the between-group to within-group sum of squares technique, applying a user-specified number of top-rank genes for BMA algorithm iterating, and re-considering these discarded models based on an adaptive threshold after iterations (53). The risk scores of individuals were calculated by the weighted average of the risk scores calculated for each model in the set of final models. Kaplan–Meier analysis in breast cancer and diffuse large B-cell lymphoma showed a significant difference between high-risk and low-risk groups based on gene sets selected by this iterative-BMA approach (53). Similarly, the same approach was further applied in early-stage lung adenocarcinoma (54), mantle-cell lymphoma (55) and breast cancer (56).
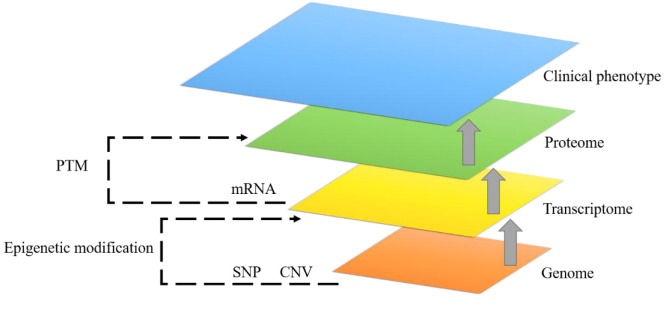
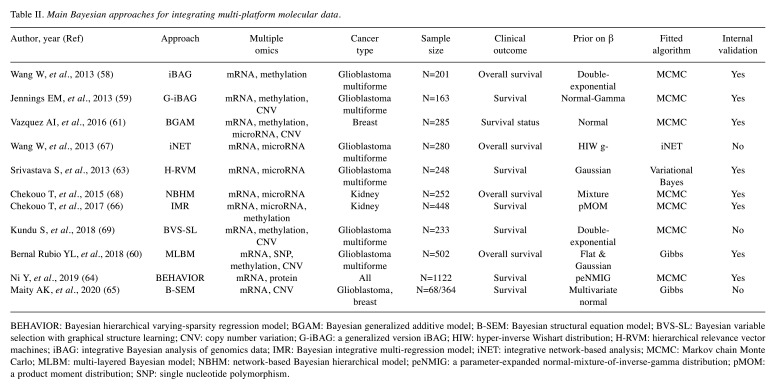
Multi-omics analysis. Considering that cancer is a highly heterogeneous disease, single omics information can only explain part of the potential mechanisms involved in the development of tumours, which means the above prognostic models based on single omics data might not be accurate enough. Therefore, in recent years, multi-omics integrated modelling analysis has provided the potential direction for us to comprehensively understand the mechanisms and find more convincing biomarkers. Moreover, except for potential structures within omics, there are often complex biological relationships between different omics platforms (Figure 1), which brings larger challenges to omics fusion modelling. Currently, the idea of integration can be divided into two categories, namely multi-stage analysis and meta-dimensional analysis (57). The former focuses on the association between omics and splits into multiple steps for analysis, while the latter considers that all data are combined simultaneously to identify complex multi-variable models (e.g., concatenation-based integration, transformation-based integration, model-based integration). However, due to distinct modelling perspectives, the Bayesian approaches discussed below might not be classified into the above types accurately. In order to describe these more logically, we briefly categorize the following literature into three types based on their approach characteristics. A brief summary of these Bayesian integrative approaches has been listed in Table II.
Figure 1. Biological relationships among different omics data and association with clinical phenotype. For example, single nucleotide polymorphism (SNP) and copy number variation (CNV) at the genome level; gene expression (mRNA) at the transcriptome level; proteins at the proteome level. Gene expression is affected by epigenetic modification, such as DNA methylation, microRNA, and long non-coding RNA. At the same time, posttranslational modification (PTM) also influences the activity of different proteins.
Table II. Main Bayesian approaches for integrating multi-platform molecular data.
BEHAVIOR: Bayesian hierarchical varying-sparsity regression model; BGAM: Bayesian generalized additive model; B-SEM: Bayesian structural equation model; BVS-SL: Bayesian variable selection with graphical structure learning; CNV: copy number variation; G-iBAG: a generalized version iBAG; HIW: hyper-inverse Wishart distribution; H-RVM: hierarchical relevance vector machines; iBAG: integrative Bayesian analysis of genomics data; IMR: Bayesian integrative multi-regression model; iNET: integrative network-based analysis; MCMC: Markov chain Monte Carlo; MLBM: multi-layered Bayesian model; NBHM: network-based Bayesian hierarchical model; peNMIG: a parameter-expanded normal-mixture-of-inverse-gamma distribution; pMOM: a product moment distribution; SNP: single nucleotide polymorphism.
Integration based on a multi-stage approach. In this approach, the idea of the integration model tended to be divided into multiple steps. For instance, Wang et al proposed the integrative Bayesian analysis of genomics data (iBAG), which modelled biological relationships among different omics by focusing on the “gene-centric” level. It was composed of two modelling stages, including a mechanistic model and a clinical model. The former was used to infer the direct effects of different features (e.g., methylation) on gene expression and the latter was used to construct a final prognostic model based on the result of the previous step (58). Jennings et al. extended the iBAG to a generalized version and focused on genes from several key cancer signalling pathways. Similar to iBAG, in the first stage, a mechanistic model was constructed by partitioning the expression of each gene into the factors explained by methylation, copy number and other features using a principal component regression model. In the second stage, the above factors were treated as predictors and established the clinical model. This study set a normal-Gamma prior on regression coefficients, which provided the sparsity (i.e. only a few genes will significantly affect the outcome while others have no or weak influence) (59). Bernal Rubio et al. developed a multi-layered Bayesian model for integrating clinical information and multi-omics. It assessed the inter-individual variation that could be explained by molecular predictors related to survival. The research process was divided into multi-stages: First, a baseline Cox regression model was used to analyse the association between clinical/demographic covariates and survival. After considering the association between omics and clinical/demographic covariates using principal components analysis, the baseline model was extended by adding omics profiles in a linear model with the logarithm of survival time as the dependent variable (60).
Integration based on the extension of existing methods. Bayesian modelling methods in this part largely focused on dealing with several specific challenges or problems in the multi-omics integration process. Vazquez et al. proposed the Bayesian generalized additive model for integrating high-dimensional multi-layer omics data (61), which was based on the generalized additive model framework (62). This modelling framework allowed the integration of high-dimension inputs from multiple omics layers, interactions between omics and different effect architectures across layers. Srivastava et al. presented the hierarchical relevance vector machines approach for addressing nonlinear patterns in the complex interactions within and between different platforms (gene expression and microRNA). Based on kernel functions, the nonlinear effects of possible interactions were considered, and it was possible to evaluate the respective contributions of different omics simultaneously (63). Ni et al. proposed a Bayesian hierarchical varying-sparsity regression model to integrate the genomic, proteomic and clinical information based on the AFT model, which contributed to identifying patient-specific prognostic biomarkers (64). Following the concept of varying coefficients, this study introduced sparsity into the model, which allowed for flexible interactions and the sparsity of the protein–outcome relationship to vary simultaneously with gene expression. Moreover, it thoroughly considered potential nonlinear relationships between the proteins and genes by spline-based semi-parametric forms. Maity et al. proposed a Bayesian structural equation model for integrating two platforms (namely copy number variation and mRNA) data (65). Considering the potential direction among different platforms (biological relationships), a latent variable in the structural equation was introduced to overcome the challenge that a specific omics component may or may not necessarily affect other specific omics components. Furthermore, a basic problem might exist in the integration analysis, that is, an insufficient valid sample size (omics data may not be available for all patients). Fortunately, Chekouo et al. proposed a novel Bayesian integrative multi-regression model for dealing with this problem. In their study, multiple regression models were constructed to make full use of the sample data of each omics rather than just the complete data across all platforms (66). The key point was to apply the Markov Random Fried prior for borrowing strength across groups, which means that it encouraged selecting the same predictors across multiple models.
Integration based on network/graph structure. Here, the integrative relationship of multiple omics was portrayed by a network/graph structure to establish prognostic models for screening key cancer biomarkers. Wang et al. developed an integrative network-based Bayesian analysis approach for analyzing multi-platform high-dimensional genomic data. It assumed one triplet as the combination of the expression level for one gene, one microRNA and the associated clinical outcome for modelling the underlying biological relationship, and considered eight possible triplet structures (models). Based on Gaussian graphical models, this study utilized Bayes factors with hyper-inverse Wishart g-prior to perform the model selection procedure (67). Chekouo et al. proposed a network-based Bayesian hierarchical model to identify microRNAs and target genes associated with survival. The microRNA regulatory network was modelled as a Bayesian network and a specific prior was constructed to link the two omics, which gave a higher probability of survival related to those highly connected biomarkers in the regulatory network (68). Kundu et al. proposed a novel multi-scale Bayesian approach that distinguished essential genomic drivers of cancer progression from integrative graphical structure learning. The process of their study was divided into two parts. Firstly, the dependence relationship within and between platform-specific features was assessed. Then identification of important prognosis-related molecular markers was performed by the above dependence relationship. Structured variable selection was implemented by identifying important cliques (i.e., the overlapping functional subgroups within/across platforms that influenced clinical outcome together) through computing corresponding marginal inclusion probabilities and eliminating unimportant covariates in cliques identified through computing Bayesian 95% credible intervals (69).
Discussion
As a summary of existing literature, the current study contributes to developing the prognostic modelling of cancer based on high-dimensional data and expanding new ideas/strategies for researchers. After briefly introducing the basic Bayesian theorem, we mainly discussed current published Bayesian approaches based on single/multiple omics data with/without clinical characteristics. As one essential part of Bayesian inference, prior information plays a critical role in the process. Notably, although variable selection can be accomplished by model-based approaches (such as BMA), Bayesian inference depends largely on the setting of suitable priors under the assumption that only a small subset of predictors significantly influence the survival situation. The correct usage of priors will help improve the performance of the predictive model but it is also a seemingly difficult task to choose appropriate priors. A previous study explored the effects of different types of Bayesian variable selection based on simulated and actual data in a relatively low-dimensional situation (20). However, in the case of high dimensions, different prior choices still need to be fully discussed. Although we perhaps find references from previous similar literature for specific analysis goals, it might be more appropriate to be guided by available data at hand.
Bayesian prognostic modelling with singe omics, to a certain extent, might improve predictive accuracy. Nevertheless, some limitations still exist. Tumour development is frequently accompanied by hundreds of distinct molecular changes, from many kinds of genomic and epigenetic alterations to their interactions. This means that interesting clinical outcomes might be affected by the use of other platforms (for example, microRNA, methylation) when single omics is utilized for prognosis modelling and screening of potential biomarkers, which might weaken the reliability of evidence for powerful targeted markers.
In fact, multi-omics integration might be more advantageous in investigating the biological mechanism of tumour progression or prognosis modelling for finding reliable targets in the era of precision medicine. A large-scale benchmark study from TCGA discovered that methods taking into account the multi-omics structure had better predictive performance, although the utility of multi-omics data was limited (70). The current methods (mainly machine learning) in the multi-omics integration field have been reported in a previous review, although it was not specifically illustrated from the Bayesian perspective (71). In relevant Bayesian articles involving multi-omics fusion, a core issue is also how to integrate different large-scale platforms, in addition to dimension reduction/variable selection. Integration based on biological relationships has better interpretability in the final result than simple merging. Then grasping the complicated relationship between multiple omics in the integration process will improve the effectiveness of the predictive model, such as interactions within/between platforms (61,63,64), non-linear relationships (63,64). Moreover, relying on the complex network or intuitive graph model in the Bayesian framework might contribute to comprehensively describing the relationship of multiple omics for better survival modelling (68,69).
However, several deficiencies exist that need to be further discussed or explored in the above approaches. i) Model validation. Nowadays, evaluating the performance of a prognostic model is increasingly relying on effective internal or external validation. Compared with external validation, internal validation is convenient to implement, such as k-fold cross-validation and bootstrapping. Although internal validation used in most literature was able to verify the performance of the models, adopting an independent external cohort would further illustrate the reliability of the predictive model. ii) The occurrence and development of cancer is a dynamic process, which also means that the integration of different omics may also be considered a dynamic process, with complex patterns of feedback loops both within and between platforms. Dynamic modelling could be a major challenge. iii) Computational complexity or burden must also be considered, especially when integrating multiple high-dimensional omics under the Bayesian framework. iv) Practicality needs to be deliberated. Most integrative studies that were validated proposed integrative Bayesian approaches on glioblastoma. The actual effect of extending these to other tumour types is still unclear, which needs more relevant literature support in the future. In addition, model interpretability is also an issue not to be ignored, primarily when multi-omics is utilized for integration into the Bayesian modelling process. The real improvement in utility of such screened biomarkers needs further evaluation after clinical transformation.
As for prognostic modelling in the future, new biostatistical methods should overcome the above limitations. Approaches based on the Bayesian theorem might provide more flexible and accurate results regarding the prognosis of cancer. Interestingly, as well as these molecular omics data, emerging radiomics might also be considered in the modelling framework for acquiring optimal predictive accuracy (72,73). The integration of these omics will help us understand the development of tumours at multiple levels for better predicting the prognosis of patients.
Conclusion
In summary, this review systematically collated the Bayesian approaches based on high-dimensional molecular data for prognostic analysis in cancer, especially the multi-omics fusion method. These approaches have been proposed chiefly in the past 10 years. From these studies, multi-omics integration methods with different strategies for feature selection have better predictive performance and more excellent value in finding biomarkers that affect prognosis in cancer. However, multi-omics integration technology often faces a key challenge, namely how to effectively integrate the relationship between multiple platforms. At the same time, the possible intractable issue involving the estimation of the complex posterior distribution is also worthy of attention. Therefore, further research is necessary.
Conflicts of Interest
The Authors declare that they have no conflicts of interest.
Authors’ Contributions
Jiadong Chu and Na Sun: Collection and writing. Wei hu and Xuanli Chen: table and graph. Yueping Shen: Design and revision. Nengjun Yi: Revision.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (project number 81973143).
References
- 1.Bray F, Ferlay J, Soerjomataram I, Siegel RL, Torre LA, Jemal A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J Clin. 2018;68(6):394–424. doi: 10.3322/caac.21492. [DOI] [PubMed] [Google Scholar]
- 2.Seebacher NA, Stacy AE, Porter GM, Merlot AM. Clinical development of targeted and immune based anti-cancer therapies. J Exp Clin Cancer Res. 2019;38(1):156. doi: 10.1186/s13046-019-1094-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cancer Genome Atlas Research Network , Weinstein JN, Collisson EA, Mills GB, Shaw KR, Ozenberger BA, Ellrott K, Shmulevich I, Sander C, Stuart JM. The Cancer Genome Atlas Pan-Cancer analysis project. Nat Genet. 2013;45(10):1113–1120. doi: 10.1038/ng.2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang HL, Liu PF, Yue J, Jiang WH, Cui YL, Ren H, Wang H, Zhuang Y, Liu Y, Jiang D, Dong Q, Zhang H, Mi JH, Xu ZM, Tian CJ, Zhang ZZ, Wang XW, Su MN, Lu W. Somatic gene mutation signatures predict cancer type and prognosis in multiple cancers with pan-cancer 1000 gene panel. Cancer Lett. 2020;470:181–190. doi: 10.1016/j.canlet.2019.11.022. [DOI] [PubMed] [Google Scholar]
- 5.Ding W, Chen G, Shi T. Integrative analysis identifies potential DNA methylation biomarkers for pan-cancer diagnosis and prognosis. Epigenetics. 2019;14(1):67–80. doi: 10.1080/15592294.2019.1568178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wu HX, Wang ZX, Zhao Q, Chen DL, He MM, Yang LP, Wang YN, Jin Y, Ren C, Luo HY, Wang ZQ, Wang F. Tumor mutational and indel burden: a systematic pan-cancer evaluation as prognostic biomarkers. Ann Transl Med. 2019;7(22):640. doi: 10.21037/atm.2019.10.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hieronymus H, Murali R, Tin A, Yadav K, Abida W, Moller H, Berney D, Scher H, Carver B, Scardino P, Schultz N, Taylor B, Vickers A, Cuzick J, Sawyers CL. Tumor copy number alteration burden is a pan-cancer prognostic factor associated with recurrence and death. Elife. 2018;7:e37294. doi: 10.7554/eLife.37294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hoerl A, Kennard R. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics. 2016;12(1):55–67. doi: 10.1080/00401706.1970.10488634. [DOI] [Google Scholar]
- 9.Tibshirani R. The lasso method for variable selection in the Cox model. Stat Med. 1997;16(4):385–395. doi: 10.1002/(sici)1097-0258(19970228)16:4<385::aid-sim380>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 10.Zou H. The adaptive lasso and its oracle properties. Journal of the American Statistical Association. 2020;101(476):1418–1429. doi: 10.1198/016214506000000735. [DOI] [Google Scholar]
- 11.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2021;68(1):49–67. doi: 10.1111/j.1467-9868.2005.00532.x. [DOI] [Google Scholar]
- 12.Simon N, Friedman J, Hastie T, Tibshirani R. A sparse-group lasso. Journal of Computational and Graphical Statistics. 2017;22(2):231–245. doi: 10.1080/10618600.2012.681250. [DOI] [Google Scholar]
- 13.Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2021;67(2):301–320. doi: 10.1111/j.1467-9868.2005.00503.x. [DOI] [Google Scholar]
- 14.Bøvelstad HM, Nygård S, Størvold HL, Aldrin M, Borgan Ø, Frigessi A, Lingjaerde OC. Predicting survival from microarray data – a comparative study. Bioinformatics. 2007;23(16):2080–2087. doi: 10.1093/bioinformatics/btm305. [DOI] [PubMed] [Google Scholar]
- 15.Berry DA. Bayesian clinical trials. Nat Rev Drug Discov. 2006;5(1):27–36. doi: 10.1038/nrd1927. [DOI] [PubMed] [Google Scholar]
- 16.O’Hara RB, Sillanpää MJ. A review of Bayesian variable selection methods: What, how and which. Bayesian Anal. 2009;4(1):85–117. doi: 10.1214/09-ba403. [DOI] [Google Scholar]
- 17.Rockova V, Lesaffre E, Luime J, Löwenberg B. Hierarchical Bayesian formulations for selecting variables in regression models. Stat Med. 2012;31(11-12):1221–1237. doi: 10.1002/sim.4439. [DOI] [PubMed] [Google Scholar]
- 18.Forte A, Garcia-donato G, Steel M. Methods and tools for Bayesian variable selection and model averaging in normal linear regression. International Statistical Review. 2019;86(2):237–258. doi: 10.1111/insr.12249. [DOI] [Google Scholar]
- 19.Van erp S, Oberski D, Mulder J. Shrinkage priors for Bayesian penalized regression. Journal of Mathematical Psychology. 2021;89:31–50. doi: 10.1016/j.jmp.2018.12.004. [DOI] [Google Scholar]
- 20.Lu Z, Lou W. Bayesian approaches to variable selection: a comparative study from practical perspectives. Int J Biostat. 2021 doi: 10.1515/ijb-2020-0130. [DOI] [PubMed] [Google Scholar]
- 21.Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. New York, Chapman and Hall/CRC. 2013. Bayesian Data Analysis, Third Version. p. pp. 580. [Google Scholar]
- 22.Tierney L, Kass RE, Kadane JB. Fully exponential Laplace approximations to expectations and variances of nonpositive functions. J Am Stat Assoc. 1989;84(407):710–716. doi: 10.1080/01621459.1989.10478824. [DOI] [Google Scholar]
- 23.Blei DM, Kucukelbir A, McAuliffe JD. Variational inference: A review for statisticians. J Am Stat Assoc. 2017;112(518):859–877. doi: 10.1080/01621459.2017.1285773. [DOI] [Google Scholar]
- 24.Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57(1):97–109. doi: 10.2307/2334940. [DOI] [Google Scholar]
- 25.Gelfand A. Gibbs sampling. Journal of the American Statistical Association. 2020;95(452):1300–1304. doi: 10.1080/01621459.2000.10474335. [DOI] [Google Scholar]
- 26.Duane S, Kennedy A, Pendleton B, Roweth D. Hybrid Monte Carlo. Physics Letters B. 2019;195(2):216–222. doi: 10.1016/0370-2693(87)91197-X. [DOI] [Google Scholar]
- 27.Tang Z, Shen Y, Zhang X, Yi N. The spike-and-slab lasso generalized linear models for prediction and associated genes detection. Genetics. 2017;205(1):77–88. doi: 10.1534/genetics.116.192195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kaderali L, Zander T, Faigle U, Wolf J, Schultze JL, Schrader R. CASPAR: a hierarchical bayesian approach to predict survival times in cancer from gene expression data. Bioinformatics. 2006;22(12):1495–1502. doi: 10.1093/bioinformatics/btl103. [DOI] [PubMed] [Google Scholar]
- 29.Schramm A, Mierswa I, Kaderali L, Morik K, Eggert A, Schulte JH. Reanalysis of neuroblastoma expression profiling data using improved methodology and extended follow-up increases validity of outcome prediction. Cancer Lett. 2009;282(1):55–62. doi: 10.1016/j.canlet.2009.02.052. [DOI] [PubMed] [Google Scholar]
- 30.Nikooienejad A, Wang W, Johnson VE. Bayesian variable selection for survival data using inverse moment priors. Ann Appl Stat. 2020;14(2):809–828. doi: 10.1214/20-AOAS1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jiang L, Greenwood CMT, Yao W, Li L. Bayesian hyper-LASSO classification for feature selection with application to endometrial cancer RNA-seq data. Sci Rep. 2020;10(1):9747. doi: 10.1038/s41598-020-66466-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang X, Li Y, Akinyemiju T, Ojesina AI, Buckhaults P, Liu N, Xu B, Yi N. Pathway-structured predictive model for cancer survival prediction: a two-stage approach. Genetics. 2017;205(1):89–100. doi: 10.1534/genetics.116.189191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Maity AK, Carroll RJ, Mallick BK. Integration of survival and binary data for variable selection and prediction: a Bayesian approach. J R Stat Soc Ser C Appl Stat. 2019;68(5):1577–1595. doi: 10.1111/rssc.12377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Maity AK, Bhattacharya A, Mallick BK, Baladandayuthapani V. Bayesian data integration and variable selection for pan-cancer survival prediction using protein expression data. Biometrics. 2020;76(1):316–325. doi: 10.1111/biom.13132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mitchell T, Beauchamp J. Bayesian variable selection in linear regression. Journal of the American Statistical Association. 2019;83(404):1023–1032. doi: 10.1080/01621459.1988.10478694. [DOI] [Google Scholar]
- 36.Duan W, Zhang R, Zhao Y, Shen S, Wei Y, Chen F, Christiani DC. Bayesian variable selection for parametric survival model with applications to cancer omics data. Hum Genomics. 2018;12(1):49. doi: 10.1186/s40246-018-0179-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ročková V, George EI. EMVS: The EM approach to Bayesian variable selection. J Am Stat Assoc. 2014;109(506):828–846. doi: 10.1080/01621459.2013.869223. [DOI] [Google Scholar]
- 38.Stingo FC, Chen YA, Tadesse MG, Vannucci M. Incorporating biological information into linear models: A Bayesian approach to the selection of pathways and genes. Ann Appl Stat. 2011;5(3):1978–2002. doi: 10.1214/11-AOAS463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jiang Y, Huang Y, Du Y, Zhao Y, Ren J, Ma S, Wu C. Identification of prognostic genes and pathways in lung adenocarcinoma using a Bayesian approach. Cancer Inform. 2020;16:1176935116684825. doi: 10.1177/1176935116684825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Peterson CB, Stingo FC, Vannucci M. Joint Bayesian variable and graph selection for regression models with network-structured predictors. Stat Med. 2016;35(7):1017–1031. doi: 10.1002/sim.6792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ročková V, George EI. The spike-and-slab LASSO. J Am Stat Assoc. 2018;113(521):431–444. doi: 10.1080/01621459.2016.1260469. [DOI] [Google Scholar]
- 42.Tang Z, Shen Y, Zhang X, Yi N. The spike-and-slab lasso Cox model for survival prediction and associated genes detection. Bioinformatics. 2017;33(18):2799–2807. doi: 10.1093/bioinformatics/btx300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tang Z, Lei S, Zhang X, Yi Z, Guo B, Chen JY, Shen Y, Yi N. Gsslasso Cox: a Bayesian hierarchical model for predicting survival and detecting associated genes by incorporating pathway information. BMC Bioinformatics. 2019;20(1):94. doi: 10.1186/s12859-019-2656-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chipman H, George E, Mcculloch R. BART: Bayesian additive regression trees. The Annals of Applied Statistics. 2021;4(1):266–298. doi: 10.1214/09-AOAS285. [DOI] [Google Scholar]
- 45.Bonato V, Baladandayuthapani V, Broom BM, Sulman EP, Aldape KD, Do KA. Bayesian ensemble methods for survival prediction in gene expression data. Bioinformatics. 2011;27(3):359–367. doi: 10.1093/bioinformatics/btq660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhang L, Kim I. Semiparametric Bayesian kernel survival model for evaluating pathway effects. Stat Methods Med Res. 2019;28(10-11):3301–3317. doi: 10.1177/0962280218797360. [DOI] [PubMed] [Google Scholar]
- 47.Seeger M. Gaussian processes for machine learning. Int J Neural Syst. 2004;14(2):69–106. doi: 10.1142/S0129065704001899. [DOI] [PubMed] [Google Scholar]
- 48.Kass R, Raftery A. Bayes factors. Journal of the American Statistical Association. 2019;90(430):773–795. doi: 10.1080/01621459.1995.10476572. [DOI] [Google Scholar]
- 49.Samorodnitsky S, Hoadley KA, Lock EF. A pan-cancer and polygenic Bayesian hierarchical model for the effect of somatic mutations on survival. Cancer Inform. 2020;19:1176935120907399. doi: 10.1177/1176935120907399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Newcombe PJ, Raza Ali H, Blows FM, Provenzano E, Pharoah PD, Caldas C, Richardson S. Weibull regression with Bayesian variable selection to identify prognostic tumour markers of breast cancer survival. Stat Methods Med Res. 2017;26(1):414–436. doi: 10.1177/0962280214548748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hoeting JA, Madigan D, Raftery AE, Volinsky CT. Bayesian model averaging: A tutorial. Stat Sc. 1999;14(4):382–401. [Google Scholar]
- 52.Yeung KY, Bumgarner RE, Raftery AE. Bayesian model averaging: development of an improved multi-class, gene selection and classification tool for microarray data. Bioinformatics. 2005;21(10):2394–2402. doi: 10.1093/bioinformatics/bti319. [DOI] [PubMed] [Google Scholar]
- 53.Annest A, Bumgarner RE, Raftery AE, Yeung KY. Iterative Bayesian Model Averaging: a method for the application of survival analysis to high-dimensional microarray data. BMC Bioinformatics. 2009;10:72. doi: 10.1186/1471-2105-10-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wu C, Zhang D. Identification of early-stage lung adenocarcinoma prognostic signatures based on statistical modeling. Cancer Biomark. 2017;18(2):117–123. doi: 10.3233/CBM-151368. [DOI] [PubMed] [Google Scholar]
- 55.Moslemi A, Mahjub H, Saidijam M, Poorolajal J, Soltanian AR. Bayesian survival analysis of high-dimensional microarray data for mantle cell lymphoma patients. Asian Pac J Cancer Prev. 2016;17(1):95–100. doi: 10.7314/apjcp.2016.17.1.95. [DOI] [PubMed] [Google Scholar]
- 56.Biermann J, Nemes S, Parris TZ, Engqvist H, Rönnerman EW, Forssell-Aronsson E, Steineck G, Karlsson P, Helou K. A novel 18-marker panel predicting clinical outcome in breast cancer. Cancer Epidemiol Biomarkers Prev. 2017;26(11):1619–1628. doi: 10.1158/1055-9965.EPI-17-0606. [DOI] [PubMed] [Google Scholar]
- 57.Ritchie MD, Holzinger ER, Li R, Pendergrass SA, Kim D. Methods of integrating data to uncover genotype-phenotype interactions. Nat Rev Genet. 2015;16(2):85–97. doi: 10.1038/nrg3868. [DOI] [PubMed] [Google Scholar]
- 58.Wang W, Baladandayuthapani V, Morris JS, Broom BM, Manyam G, Do KA. iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics. 2013;29(2):149–159. doi: 10.1093/bioinformatics/bts655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jennings EM, Morris JS, Carroll RJ, Manyam GC, Baladandayuthapani V. Bayesian methods for expression-based integration of various types of genomics data. EURASIP J Bioinform Syst Biol. 2013;2013(1):13. doi: 10.1186/1687-4153-2013-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bernal Rubio YL, González-Reymúndez A, Wu KH, Griguer CE, Steibel JP, de Los Campos G, Doseff A, Gallo K, Vazquez AI. Whole-genome multi-omic study of survival in patients with glioblastoma multiforme. G3 (Bethesda) 2018;8(11):3627–3636. doi: 10.1534/g3.118.200391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Vazquez AI, Veturi Y, Behring M, Shrestha S, Kirst M, Resende MF Jr, de Los Campos G. Increased proportion of variance explained and prediction accuracy of survival of breast cancer patients with use of whole-genome multiomic profiles. Genetics. 2016;203(3):1425–1438. doi: 10.1534/genetics.115.185181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hastie T, Tibshirani R. Generalized additive models. Statistical Science. 1986;1(3):297–310. doi: 10.1214/ss/1177013604. [DOI] [PubMed] [Google Scholar]
- 63.Srivastava S, Wang W, Manyam G, Ordonez C, Baladandayuthapani V. Integrating multi-platform genomic data using hierarchical Bayesian relevance vector machines. EURASIP J Bioinform Syst Biol. 2013;2013(1):9. doi: 10.1186/1687-4153-2013-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ni Y, Stingo FC, Ha MJ, Akbani R, Baladandayuthapani V. Bayesian hierarchical varying-sparsity regression models with application to cancer proteogenomics. J Am Stat Assoc. 2019;114(525):48–60. doi: 10.1080/01621459.2018.1434529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Maity AK, Lee SC, Mallick BK, Sarkar TR. Bayesian structural equation modeling in multiple omics data with application to circadian genes. Bioinformatics. 2020;36(13):3951–3958. doi: 10.1093/bioinformatics/btaa286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Chekouo T, Stingo FC, Doecke JD, Do KA. A Bayesian integrative approach for multi-platform genomic data: A kidney cancer case study. Biometrics. 2017;73(2):615–624. doi: 10.1111/biom.12587. [DOI] [PubMed] [Google Scholar]
- 67.Wang W, Baladandayuthapani V, Holmes CC, Do KA. Integrative network-based Bayesian analysis of diverse genomics data. BMC Bioinformatics. 2013;14(Suppl 13):S8. doi: 10.1186/1471-2105-14-S13-S8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Chekouo T, Stingo FC, Doecke JD, Do KA. miRNA-target gene regulatory networks: A Bayesian integrative approach to biomarker selection with application to kidney cancer. Biometrics. 2015;71(2):428–438. doi: 10.1111/biom.12266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kundu S, Cheng Y, Shin M, Manyam G, Mallick BK, Baladandayuthapani V. Bayesian variable selection with graphical structure learning: Applications in integrative genomics. PLoS One. 2018;13(7):e0195070. doi: 10.1371/journal.pone.0195070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Herrmann M, Probst P, Hornung R, Jurinovic V, Boulesteix AL. Large-scale benchmark study of survival prediction methods using multi-omics data. Brief Bioinform. 2021;22(3):bbaa167. doi: 10.1093/bib/bbaa167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Huang S, Chaudhary K, Garmire LX. More is better: Recent progress in multi-omics data integration methods. Front Genet. 2017;8:84. doi: 10.3389/fgene.2017.00084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zanfardino M, Franzese M, Pane K, Cavaliere C, Monti S, Esposito G, Salvatore M, Aiello M. Bringing radiomics into a multi-omics framework for a comprehensive genotype-phenotype characterization of oncological diseases. J Transl Med. 2019;17(1):337. doi: 10.1186/s12967-019-2073-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhang Y, Morris JS, Aerry SN, Rao AUK, Baladandayuthapani V. Radio-iBAG: Radiomics-based integrative Bayesian analysis of multiplatform genomic data. Ann Appl Stat. 2019;13(3):1957–1988. doi: 10.1214/19-aoas1238. [DOI] [PMC free article] [PubMed] [Google Scholar]